Советы и лайфхаки

Корень в маткаде – Mathcad

2.4.4 Поиск корней уравнений в Mathcad

Mathcad 2000 представляет ряд дополнительных возможностей для поиска корней уравнений. Функция root(f(var1, var2, …),var1, [a, b]) имеет теперь два необязательных аргумента a и b, которые определяют границы интервала, на котором следует искать корень. На концах интервала [a,b] функция f должна менять знак (f(a)f(b)<0). Задавать начальное приближение для корня не нужно. В данном варианте функция root использует алгоритм Риддера и Брента. Продемонстрируем использование расширенного варианта поиска корней на примере функции

Для оценки местоположения корней построим график этой функции

Рис. 5. График функции

На интервале [1,8] функция имеет два корня. Mathcad 2000 смог найти только один из них.

Дополнительные возможности появились и для нахождения корней полиномов. Функция polyroots может использовать два различных алгоритма поиска корней – метод Лагерра и метод сопровождающей матрицы. Переключение методов осуществляется в контекстном меню, которое вызывается нажатием правой кнопки мыши, когда указатель установлен на имя функции.

      1. 2.5 Блок-схемы

Метод половинного деления

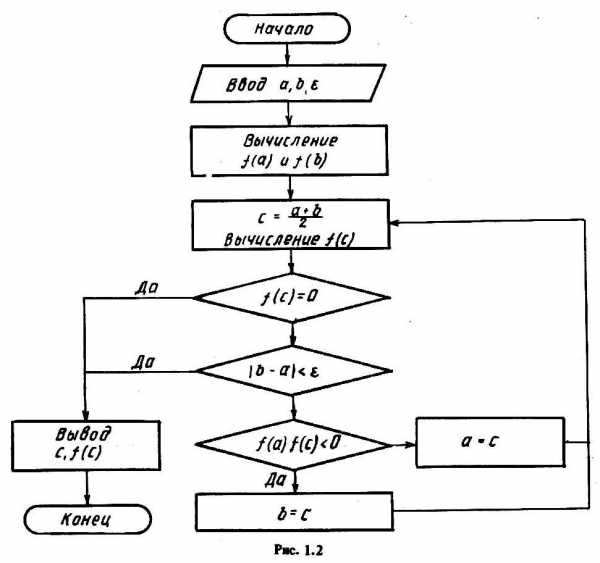
Метод простой итерации

Задание 1.

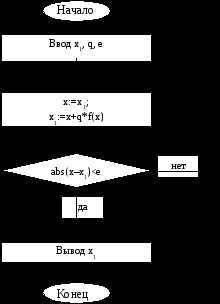
  1. Отделить минимальный по модулю корень уравнения и уточнить его методом половинного деления с точностью 0,001.

  2. Отделить минимальный по модулю корень уравнения и уточнить его методом хорд с точностью 0,001.

  3. Отделить минимальный по модулю корень уравнения и уточнить его методом Ньютона с точностью 0,001.

  4. Отделить минимальный по модулю корень уравнения и уточнить его комбинированным методом с точностью 0,001.

Образец выполнения задания

1. Уточнить с точностью до =10-2 корень х[-2;-1] уравнения х3-3х-0,4=0 методом деления отрезка пополам.

Решение. Вычисление занесем в таблицу 2.

Таблица 2

k

[ak;bk]

xk

f(xk)

Знаки функции

f(ak)

f(xk)

f(bk)

0

[-2;-1]

-1.5

0.725

—

+

+

1

[-2;-1.5]

-1.7

-0.213

—

—

+

2

[-1.7;-1.5]

-1.6

0.304

—

+

+

3

[-1.7;-1.6]

-1.65

0.058

—

+

+

4

[-1.7;-1.65]

-1.68

-0.102

—

—

+

5

[-1.68;-1.65]

-1.66

0.006

—

+

+

6

[-1.68;-1.66]

-1.67

-0.047

—

—

+

7

[-1.67;-1.66]

-1.665

-0.021

—

—

+

Получили отрезок [-1.67;-1.66], длина которого равна 0,01, и этот отрезок содержит корни уравнения. Числа -1,67 и -1,66 есть приближенные значения корня с погрешностью , не превышающей 0,01. Примем за приближенное значение корня –1,66.

Ответ: х=-1,66.

      1. 2.6 Индивидуальные задания

№1

  1. 2x +5x–3=0

  2. 3x4+4x3-12x2-5=0

  3. 0.5x +1=(x-2)2

  4. (x-3)cosx=1, -2π≤x≤2π

№2

  1. arctgx-1/3x3 =0

  2. 2x3-9x2-60x+1=0

  3. [log2(-x)]·(x+2)= -1

  4. sin(x+ π/3)-0.5x=0

№3

  1. 5x+3x=0

  2. x4-x-1=0

  3. x2-2+0.5x =0

  4. (x-1)2lg(x+11)=1

№4

  1. 2ex = 5x+2

  2. 2x4-x2-10=0

  3. x·log

    3(x+1)=1

  4. cos(x+0.5)=x3

№5

    1. 3x-1-2-x=0

    2. 3x4+8x3+6x2-10=0

    3. (x-4)2·log0.5(x-3)=-1

    4. 5sinx=x

№6

  1. 2arctgx-1/2x3=0

  2. x4-18x2+6=0

  3. x2·2x=1

  4. tgx=x+1, -π/2≤x≤ π/2

№7

  1. e-2x-2x+1=0

  2. x4+4x3-8x2-17=0

  3. 0.5x-1=(x+2)2

  4. x2cos2x=-1

№8

  1. 5x-6x-3=0

  2. x4-x3-2x2+3x-3=0

  3. 2x2-0.5x-3=0

  4. xlg(x+1)=1

№9

        1. arctg(x-1)+2x=0

        2. 3x4+4x3-12x2+1=0

        3. (x-2)22x=1

        4. x2-20sinx=0

№10

  1. 2arcсtgx-x+3=0

  2. 3x4-8x3-18x2+2=0

  3. 2sin(x+π/3)=0.5x2-1

  4. 2lgx-x/2+1=0

№11

  1. 3x+2x-2=0

  2. 2x4-8x3+8x2-1=0

  3. [(x-2)2-1]2x=1

  4. (x-2)cosx=1,-2π≤x≤2π

№12

  1. 2arctg x-3x+2=0

  2. 2x4+8x3+8x2-1=0

  3. [log2(x+2)](x-1)=1

  4. sin(x-0.5)-x+0.8=0

№13

  1. 3x+2x-5=0

  2. x4+4x3-8x2+1=0

  3. x2-3+0.5x=0

  4. (x-2)2lg(x+11)=1

№14

  1. 2ex+3x+1=0

  2. 3x4+4x3-12x-5=0

  3. xlog3(x+1)=2

  4. cos(x+0.3)=x2

№15

  1. 3x-1-4-x=0

  2. 2x3-9x2-60x+1=0

  3. (x-3)2log0.5(x-2)=-1

  4. 5sinx=x-1

№16

  1. arctgx-1/3x3=0

  2. x4-x-1=0

  3. (x-1)22x=1

  4. tg3x=x-1, -π/2≤x≤π/2

№17

  1. ex+x+1=0

  2. 2x4-x2-1+=0

  3. 0.5x-3=(x+2)2

  4. x2cos2x=-1,-2π≤x≤2π

№18

  1. 3x-2x+5=0

  2. 3x4+8x3+6x2-10=0

  3. 2x2-0.5x-2=0

  4. xlg(x+1)=1

№19

  1. arctg(x-1)+3x-2=0

  2. x4-18x2+6=0

  3. (x-2)22x=1

  4. x2-20sinx=0

№20

  1. 2arcctgx-x+3=0

  2. x4+4x3-8x2-17=0

  3. 2sin(x+ π/3)=x2-0.5

  4. 2lgx-x/2+1=0

№21

  1. 2x-3x-2=0

  2. x4-x3-2x2+3x-3=0

  3. (0.5)x+1=(x-2)2

  4. (x-3)cosx=1, -2π≤x≤2π

№22

  1. arcctgx+2x-1=0

  2. 3x4+4x3-12x+1=0

  3. (x+2)log2(x)=1

  4. sin(x+1)=0.5x

№23

  1. 3x+2x-3=0

  2. 3x4-8x3-18x2+2=0

  3. x2-4+0.5x=0

  4. (x-2)2lg(x+11)=1

№24

  1. 2ex-2x-3=0

  2. 3x4+4x3-12x2-5=0

  3. xlog3(x+1)=1

  4. cos(x+0.5)=x3

№25

  1. 3x+2+x=0

  2. 2x3-9x2-60x+1=0

  3. (x-4)2log0.5(x-3)=‑1

  4. 5sinx=x-0.5

№26

  1. arcctg(x-1)+2x-3=0

  2. x4-x-1=0

  3. (x-1)2.2x=1

  4. tg3x=x+1, -π/2≤x≤π/2

№27

  1. e -2x-2x+1=0

  2. 2x4-x2-10=0

  3. 0.5x-3=-(x+1)2

  4. x2cos2x=-1

№28

  1. 3x-2x-5=0

  2. 3x4+8x3+6x2-10=0

  3. 2x2-0.5x-3=0

  4. xlg(x+1)=1

№29

  1. arctg(x-1)+2x=0

  2. x4-18x2+6=0

  3. (x-2)22x=1

  4. x2-10sinx=0

№30

  1. 3x+5x-2=0

  2. 3x4+4x3-12x2+1=0

  3. 0.5x+1=(x-2)2

  4. (x+3)cosx=1, -2π≤x≤2π

Задание 2.

1) Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001.

2) Отделить корни уравнения аналитически и уточнить один из них методом итераций с точностью до 0,001.

Образец выполнения задания

1. Уточнить корни уравнения 3х-cosx-1=0 методом итераций с точностью до =10-5.

Решение. Отделим корни уравнения графически. Для этого запишем уравнение в виде 3х=cosx+1. Уравнение имеет единственный корень с[0,4;0,9].

Действительно, f(0,4) f(0,9)=-(0,72)1,08<0, f‘(х)=3+sin x>0 на всей числовой оси.

Запишем исходное уравнение в виде х=1/3(1+cos x) и положим:

(x)= 1/3(1+cos x).

Очевидно: 0<‘(х)<1/3. Вычисление занесем в Таблицу 3.

Таблица 3

k

xk

cos xk

xk+1

|xk+1— xk|

*

0

0.500000

0.877583

0.625861

0.125861

0.00002

1

0.625861

0.810459

0.603486

0.022375

2

0.603486

0.823362

0.607784

0.004298

3

0.607784

0.820915

0.606972

0.000812

4

0.606972

0.821378

0.607126

0.000154

5

0.607126

0.821294

0.607097

0.000029

6

0.607097

0.821307

0.607102

0.000005

Ответ: х=0,60710.

2. Найти корень уравнения с точностью до 10-2. Уравнение

f(x)  x3 – x– 1 = 0.

Решение. Уравнение имеет корень   [1; 2], так как f(1)= — 1 < 0 и f(2) = 5 > 0. Его можно записать в виде х = х3 – 1. Здесь

(х) = х3 – 1 и  (х) = 3х2;

поэтому

(х)  3 при 1  х  2

и, следовательно, условия сходимости процесса итерации не выполнены.

Если записать исходное уравнение в виде то будем иметь:

.

Отсюда при 1 х  2 и значит, процесс итерации для уравнения быстро сойдется.

Найдем корень  данного уравнения с точностью до 10-2. Вычисляем последовательные приближения хnс одним запасным знаком по формуле

Найденные значения помещены в таблицу 4:

Таблица 4

Значения последовательных приближений xi.

i

0

1

2

3

4

xi

1

1,260

1,312

1,322

1,3243

С точностью до 10-2 можно положить  = 1,324.

Ответ: х=1,324.

№1

1)

lnx+(x+1)3=0

2)

x3+2x2+2=0

№2

1)

x·2x=1

2)

x3-3x2+9=0

№3

1)

(x+1)1/2=1/x

2)

x3-2x2+2=0

№4

1)

x-cosx=0

2)

x3+3x2 -1=0

№5

1)

3x+cosx+1=0

2)

x3+x2-1=0

№6

1)

x+lnx=0.5

2)

x3+0.4x2+0.6x-1.6=0

№7

1)

2-x=lnx

2)

x3-0.2x2+0.4x-1.4=0

№8

1)

(x-1)2=1/2ex

2)

x3-0.1x2+0.4x+2=0

№9

1)

(2-x)ex=0.5

2)

x3+3x2+12x+3=0

№10

1)

2.2x-2x=0

2)

x3 -0.2x2+0.5x+-10

№11

1)

x2+4sinx=0

2)

x3-0.1x2+0.4x+1.2=0

№12

1)

2x-lgx=7

2)

x3-3x2+6x-5=0

№13

1)

5x-8lnx=8

2)

x3-0.2x2+0.5x-1.4=0

№14

1)

3x-ex=0

2)

x3+2x+4=0

№15

1)

x(x+1)2=1

2)

x3-3x2+12x-12=0

№16

1)

x=(x+1)3

2)

x3+0.2x2+0.5x+0.8=0

№17

1)

x2=sinx

2)

x3+4x-6=0

№18

1)

x3=sinx

2)

x3+0.1x2+0.4x-1.2=0

№19

1)

x=(lg(x+2))1/2

2)

x3+3x2+6x-1=0

№20

1)

x2=lg(x+1)

2)

x3-0.1x2+0.4x+-1.50

№21

1)

2x+lgx=-0.5

2)

x3-3x2+6x-2=0

№22

1)

2x+cosx=0.5

2)

x3-0.2x2+0.3x-1.2=0

№23

1)

sin0.5x+1=x2; x>0

2)

x3-3x2+12x-9=0

№24

1)

0.5x+lg(x-1)=0.5

2)

x3+0.2x2+0.5x-2=0

№25

1)

sin(0.5+x)=2x-0.5

2)

x3+3x+1=0

№26

1)

lg(2+x)+2x=3

2)

x3+0.2x2+0.5x-1.2=0

№27

1)

lg(1+2x)=2-x

2)

x3-3x2+9x+2=0

№28

1)

2sin(x-0.6)

2)

x3 -0.1x2+0.4x-1.5=0

№29

1)

x+lg(1+x)=1.5

2)

x3-3x2+6x+3=0

№30

1)

x+cosx=1

2)

x3-0.1x2+0.3x-0.=0

studfiles.net

2.4 Решение уравнений средствами MathCad

        1. 2.4.1. Функции произвольного вида

Найдем нули функции на интервале x=[–2; 7], используя Mathcad. Изобразим сначала график функции на интервале [–2; 7].

Рис. 4. График функции на интервале [–2; 7]

На заданном интервале функция три раза обращается в ноль. Определим нули функции, используя встроенную функцию root(f(x),x). Первый аргумент – функция, нуль которой необходимо найти, второй – переменная, которую необходимо варьировать. (Вообще говоря, функция f может быть функцией многих переменных и необходимо указывать, по какой именно переменной мы ищем нуль функции.) Кроме того, необходимо задать начальное приближение поиска. Точность вычислений задается встроенной переменной TOL. По умолчанию ее значение равно 0,001. Это значение можно изменить либо через меню Math/Built–In Variables или непосредственно в тексте документа:

Задаем начальное приближение:

И вычисляем корень:

Если требуется найти несколько корней, как в нашей задаче, то имеет смысл определить новую функцию:

Функция r(x) возвращает значение корня ближайшее к x1, то есть начальное приближение мы задаем через аргумент функции. Задаем вектор начальных приближений x и находим соответствующие им корни X:

Для данного примера корни легко могут быть найдены аналитически. Они равны на заданном интервале /2/2 и 2. Полученный численный результат с заданной точностью совпадает с точным решением.

Определение новой функции целесообразно и в том случае, когда мы хотим исследовать зависимость решения от параметра. Пусть функция зависит от параметра a

Первый аргумент функции z задает значение параметра, второй – начальное приближение. Найдем корни уравнения при значениях параметра 1 и 2.

Если мы хотим получить комплексный корень, то начальное приближение следует задавать комплексным:

        1. 2.4.2 Нахождение корней полиномов

Для нахождения корней полиномов имеется встроенная функция polyroots(a). Аргументом функции является вектор коэффициентов полинома , то есть для уравнения вектор а имеет вид

Если в полиноме отсутствуют некоторые степени, то на соответствующих местах следует писать 0. Пусть требуется найти корни полинома

Коэффициенты полинома могут быть и комплексными.

        1. 2.4.3 Нахождение корней уравнений путем символических преобразований

Во многих случаях, Mathcad позволяет найти аналитическое решение уравнения. Для этого необходимо воспользоваться пунктом Solve for Variable из пункта меню Symbolic. Для того чтобы найти решение уравнения необходимо записать выражение и выделить в нем переменную (поставить указатель курсора возле переменной). Это необходимо для того, чтобы показать, какая именно величина является переменной, а какая – фиксированным параметром. После этого выбираем из пункта меню Symbolic подпункт Solve for Variable

решение готово ––>

Обратите внимание! В данном случае был найден только один корень, хотя, очевидно, их бесконечно много.

В случае полинома Mathcad, а точнее – встроенный символический процессор Maple – находит все корни.

–> Для этого примера найдено 2 корня, хотя они и вырождены. Пример с комплексными корнями:––>

studfiles.net

Уравнения с одним неизвестным в Mathcad

Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение — root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.

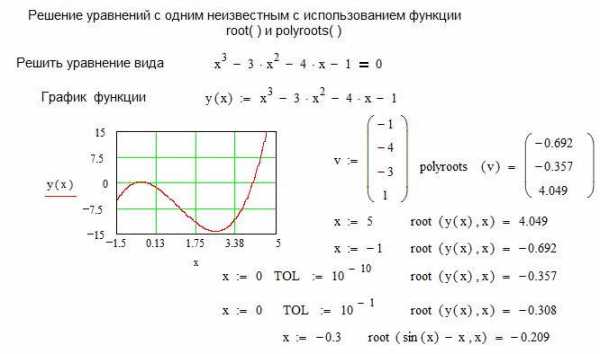
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).

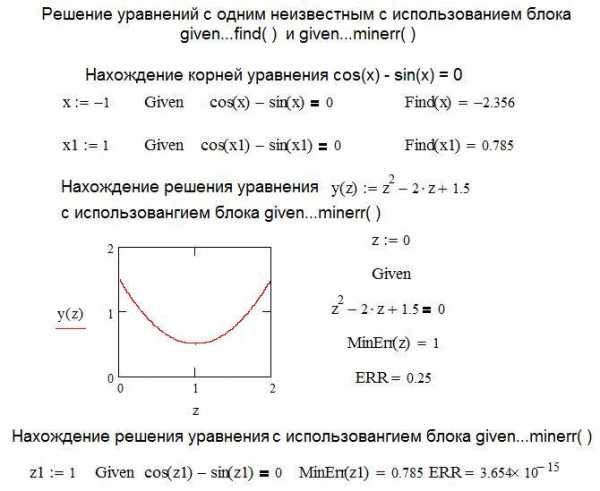
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).

Блок имеет следующую структуру:

Начальное значение искомой переменной

given

Решаемое уравнение

Выражение с использованием функции find( ) или minerr ( )

Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.

www.allmathcad.com

Как решать систему уравнений в «Маткаде»? Советы и рекомендации

Математическая программа MathCAD применяется при сложных алгебраических расчетах в то время, когда они затруднены или невозможны вручную. Данный ресурс значительно облегчает жизнь многим техническим, экономическим специальностям и студентам. Очень просто смоделировать какую-то задачу в математическом виде и получить желаемый ответ. Однако интерфейс может быть непонятен для новичков, и им тяжело адекватно воспринимать эту вычислительную среду. Одним из камней преткновения становится то, как решать систему уравнений в «Маткаде». Это очень важная функция, которую нужно изучить всем, кто желает продолжать работать в этой программе.

Как в «Маткаде» решить систему уравнений

На самом деле это не является простейшей задачей, но на рассмотренных примерах можно научиться их решать. Очень часто пользователи сталкиваются с системами уравнений и понятием «параметр». В математической рабочей среде параметр и то, как решать систему уравнений в «Маткаде», находится с помощью вспомогательной функции root. Помимо того, что нам придется привлекать эту функцию в решение, нам также понадобится значение начального приближения. Вообще, видов систем уравнений несколько, поэтому рассматривать будем конкретно на разных типах. Обсудим, с какими проблемами может столкнутся пользователь при применении функции root.

  • Уравнение в изначальном виде не имеет корней.
  • Корни уравнения находятся на достаточно далеком расстоянии от начального приближения.
  • Уравнение претерпевает разрыв между начальным приближением и корнями.
  • Уравнение имеет максимум и минимум между начальным приближением и корнями.
  • Уравнение имеет комплексный корень при условии, что начальное приближение было вещественным.

Сложная функция и ее график

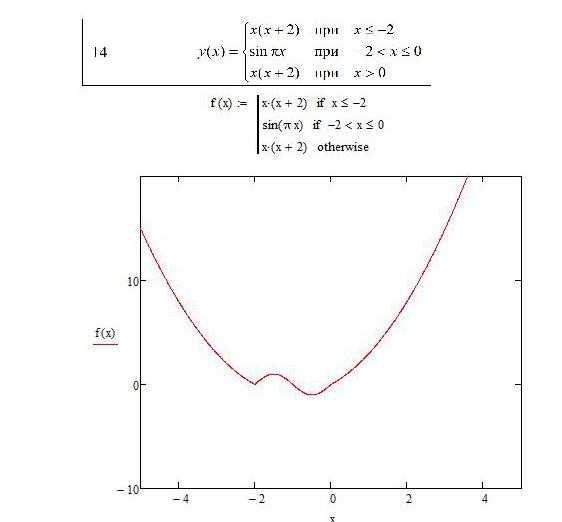
Начнем с самого простой и слегка отдаленной темы, чтобы постепенно ввести в курс дела начинающих пользователей. Это необходимо для того, чтобы символьно решить системы уравнений «Маткад», но сначала попробуем построить график для сложной функции. Пользователю нужно привести формулировку в математический вид, чтобы график функции построился корректно — так как мы имеем три участка, есть смысл воспользоваться программной конструкцией. Чтобы осуществить правильную запись уравнения, воспользуемся блоком if-otherwise.

Чтобы решить систему линейных уравнений в «Маткаде», можно использовать некоторые другие варианты. Первый способ заключается в том, что мы пишем нашу систему уравнений через оператор if. Во втором методе необходимо прибегнуть к методу логических множителей.

Строим быстрый график, нажав на сочетание клавиш Shift + 2. В появившемся окне графика вписываем функцию в средний вертикальный блок и в нижний вертикальный блок — аргумент «х».

Система нелинейных уравнений

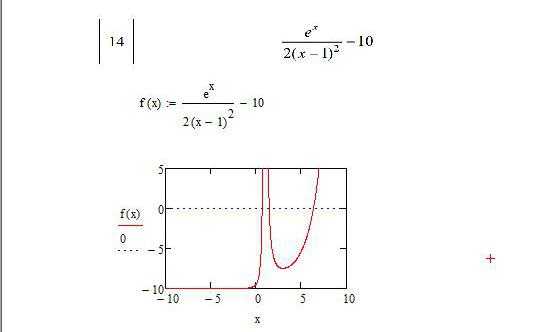
Для нелинейных уравнение порядок нахождения корней мало чем отличается от другого типа. Допустим, имеем функцию f(x) = (e^x/(2(x-1)^2)-10 в интервале от -10 до 10 включительно. Перед тем, как решить систему нелинейных уравнений в «Маткаде», нужно построить график, чтобы оценить нули и воспользоваться табуляцией.

  • Задаем данную функцию в математическом виде, который сможет обработать вычислительная среда.
  • Строим график функции клавишами Shift + 2, обозначив функцию в вертикальном среднем окошке. В горизонтальном устанавливаем границы, как и на интервале: от -10 до 10, — и вписываем аргумент «х» в среднюю ячейку.
  • Теперь нам необходимо визуально обозначить нули на графике. Сделать это можно, добавив функцию 0 (вводится в среднюю вертикальную ячейку с помощью символа «,»). Стало визуально понятнее, где находятся нули функции.
  • Время провести табуляцию на график, но при этом нужно задать диапазон значений. В рассматриваемом случае будем иметь x:=-1, 0.5 .. 7 (знак двоеточия ставится при помощи клавиши «;». Теперь отследим смену знака, оценив значения f(x).

    • Поиск корней при помощи функции root

    Перед тем, как решать систему уравнений в «Маткаде», необходимо провести операцию root. Предварительно необходимо было построить функцию и протабулировать ее. После всех операций можно приступать к поиску корней с заданным интервалом. Итак, будем на примере нелинейного уравнения отвечать на вопрос, как в «Маткаде» решать систему уравнений:

  • Необходимо отыскать первый корень функции «root». Присваиваем «х» следующую команду: x1:=root(f(x),x,-10,10). Затем выводим значение аргумента «х» и функции f(x1).
  • Отыскиваем второй корень с помощью той же функции. Единственным отличием станет то, что поиск корня будет проходить через задание начального приближения. Возьмем начальное приближение «х:=0», чтобы применить root без интервала. Задаем функцию: x2=root(f(x),x), а следом отыскиваем значение аргумента и ее функции так же, как и в предыдущем примере.

    • Поиск корней функцией find

    В отличие от предыдущей функции, здесь не используется задание интервала или начального приближения. Данная команда работает от того, что присваивается начальное условие — около корня. Разберем работу этой функции на том же примере:

  • Необходимо обозначить начальное условие: x:=7.
  • Применяем кейс Given для нашей функции и присваиваем «толстое равно» на f(x)=0.
  • Теперь используем саму функцию: x3 :=find(x).
  • Производим поиск значения аргумента и его функции.

    • Источник

    ruud.ru

    Лабораторная работа №3 Нахождение корней уравнения в MathCad

    Количество просмотров публикации Лабораторная работа №3 Нахождение корней уравнения в MathCad — 503

    Цель работы˸нахождение корней уравнения в программе MathCad с использованием встроенных функций root,polyroots, символьного решения.

    Указания к выполнению лабораторной работы˸

    IНахождение корней уравнения в программе MathCad с использованием встроенной функции root

    1. Запустить программу MathCad .

    2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.

    3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).

    4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.

    4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.

    4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.

    5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.

    6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.

    а) б)

    Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых

    ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.

    1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.

    2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.

    3. Найти корни, обратившись ко встроенной функции r˸=polyroots(v), результат будет получено относительно трансформированного вектора rT.

    4. Для интервала нахождения корня и количества элементов вектора rT создать соответствующие циклы и вычислить значение функции в точках цикла.

    5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.

    ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.

    1. Ввести левую часть уравнения.

    2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.

    3. За знаком равенства ввести правую часть уравнения.

    4. Выделить переменную, относительно которой решается уравнение.

    5. Выбрать команду Symbolіc/Varіable/Solve.

    Читайте также


  • — Функциональность доступа к MathCad

    В качестве дополнительной возможности выполнения вычислений, которые не обеспечивает непосредственно СИЛТ, в результате анализа положительных и отрицательных сторон различных коммерческих пакетов был выбран математический пакет MathCAD. Такой выбор обусловлен… [читать подробнее].


  • — Оформление текста и комментариев в Mathcad

    Текстовую область можно разместить в любом незанятом месте документа Mathcad. Чтобы до начала ввода указать программе, что требуется создать не формульный, а текстовый регион, достаточно, перед тем как ввести первый символ, нажать клавишу » (двойная кавычка). В результате на… [читать подробнее].


  • — Обращение к программе-функции Mathcad

    Для выполнения программы-функции необходимо обратиться к имени программы-функции с указанием списка фактических параметров (если в описании программы присутствует список формальных параметров), т. е. <имя — программы> (список фактических параметров) Фактические… [читать подробнее].


  • — Использование Mathcad в качестве калькулятора.

    Для набора выражения используются клавиатура и панели инструментов, которые доступны с помощью меню Просмотр\Панели. Например, для расчёта выражения необходимо набрать 1/, затем найти знак корня в панели «Калькулятор». В знаменателе выражения появится шаблон который… [читать подробнее].


  • — Язык программирования Mathcad

    Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику (например, возвращение различных значений в зависимости от условий), в одну строку не удается. Назначение… [читать подробнее].


  • — ПрограмМНЫЙ комплекс MathCad

    Для проведения измерений осциллограф нужно настроить, для чего следует задать: • расположение осей, по которым откладывается сигнал; • нужный масштаб развертки по осям; • смещение начала координат по осям, • режим работы по входу: закрытый или открытый; • режим… [читать подробнее].


  • — ПрограмМИРОВАНИЕ в MathCad

    Для написания программ в среде MathCad [4,6] существует специальная панель Programmіng (Программирование) (рис.16, а), она относится к панели Math (Математические) (рис.16, б). Язык программирования MathCad имеет предельно малое количество операторов (рис. 16, а). Чтобы написать программу,… [читать подробнее].


  • — Применение MathCad для решения прикладной задачи

    Применим возможности системы MathCad для расчета переходных процессов звеньев второго порядка. Передаточная функция W(s) звена приведена на рисунке 4.2. Обратное преобразование Лапласа, осуществляемое символьным оператором над изображением W(s)/s , позволяет получить… [читать подробнее].


  • — Оформление расчетных задач в системе MathCAD

    Пример1. Предположим, вы нашли в учебнике формулу, например, мощности некоего модуля: Nм= . Она состоит из двух частей. В первой — поясняется, из какой формулы она получена, а во второй – приведено то, что осталось после раскрытия переменных и сокращения первой части. Конечно,… [читать подробнее].


  • — Определение переменных в Mathcad

    Чтобы определить переменную, достаточно ввести ее имя и присвоить ей некоторое значение, для чего служит оператор присваивания. 1. Введите в желаемом месте документа имя переменной. 2. Введите оператор присваивания с помощью клавиши <;> или нажатием соответствующей… [читать подробнее].


    • referatwork.ru

    Основы работы в MathCAD — Стр 3

    Задача 1. Пусть надо решить систему

    3x+8y-9z=125x-9y+2z=348x-6y+5z=98.

    Для этого необходимо совершить следующие действия:

    1)Набрать начальные приближения – произвольные числа х:=1 y:=1 z:=1

    2)Набрать с клавиатуры директиву given (дано)

    3)Набрать систему уравнений, обязательно записывая знак умножения, причем знак = нужно набирать не на арифметической панели , а на панели логики ,

    которая выводится на экран кнопкой

    математической панели.

    4)Набрать выражение otvet:= find(x,y,z)

    5)Набрать otvet =

    После этого будет получен ответ в виде вектора – столбца.

    Вместо слова otvet можно использовать любой набор букв и цифр, начинающийся с буквы. Этот набор обозначает имя, которое Вы присваиваете вектору ответов. На рис.1 показано решение этой системы

    Рис.1. Решение системы линейных уравнений в решающем блоке.

    Задача 1. Решите приведенную выше систему.

    Задача 2. Решите самостоятельно приведенные ниже системы линейных алгебраических уравнений.

    А)

    5x+6y-9z+2v-7w=90

     

    3x-4y+5z-3v+4w=12

     

    9x+y +3z-2v+9w=51

     

    7x+2y-8z+v+10w=32

     

    6x+5y-4z+3v-2w=87

    Б)

    4.5x+7.9y-2.1v+6.75w+7.9u=43

     

    5.6x+7.2y+9.8z+3.9v+3.4w+8.3u=12.54

     

    5.6x+98.5y+43.7z+67.85v+4.9w+21.5u = 54.98

     

    65.75x+54.32y-78.32z-565.9v+32w+78.54u= 55.5

     

    54.2x+76.45y+32.23z+ 45.71v+43.43w+ u = 65.21

     

    8.9x+9.8y-5.6z+6.5v-4.5w+2.1u= 0

    Подобным образом можно решать и нелинейные уравнения. Однако они имеют несколько корней. Задавшись начальными приближениями, мы найдем в лучшем случае один корень, ближайший к начальному приближению. Таким способом имеет смысл искать корни трансцендентных уравнений, имеющие, как известно, бесконечное количество корней.

    Задача 3. Найти корень трансцендентного уравнения. X sin(x)+ cos(x) =25,

    ближайший x=1.

    Набираем задачу описанным выше способом и находим значение х. Однако получить решение при начальном приближении 10 нам не удастся.

    Маткад позволяет решать системы линейных алгебраических уравнений в матричной форме. Решение можно получить двумя способами.

    1 способ.

    Как известно, система линейных алгебраических уравнений в матричной форме имеет вид:

    AX=B где

    А – квадратная матрица коэффициентов, X – вектор – столбец неизвестных,

    В – вектор – столбец свободных членов системы. Решение системы в матричной форме: X= A-1B.Решим в матричной форме систему

    Для этого (см. рисунок 2):

    1)Наберем ORIGIN:=1. Как говорилось выше, это означает, что счет элементов будет производиться не от нуля, а с единицы.

    2)Введем матрицу А.

    3)Введем вектор – столбец В.

    4)Набор выражения для Х желательно выполнять, используя соответствующую кнопку матричной панели. После этого наберем X= и сразу получим вектор ответа.

    Рис.2.Решение системы линейных уравнений в матричной форме.

    2 способ

    Возможно получения решения матричного уравнения с помощью специальной функции lsolve, как показано на рис. 3.

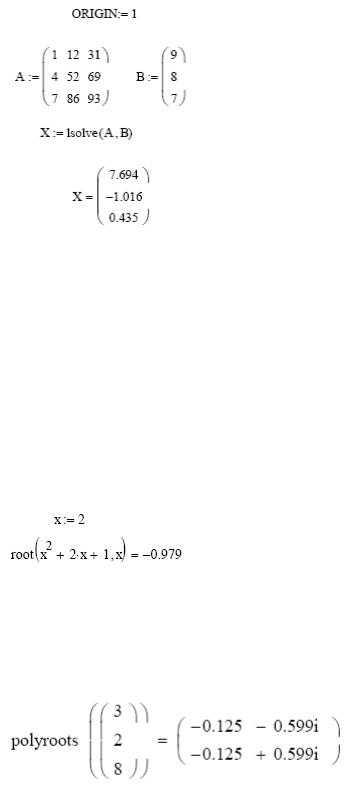
    Рис.3.Решение системы линейных алгебраических уравнений с использованием встроенной функции lsolve

    Задача 4. Решить варианты А, Б задачи 2 в матричной форме самостоятельно.

    Численное решение нелинейных алгебраических уравнений.

    В Маткад корни алгебраических уравнений и систем определяются с помощью следующих встроенных функций:

    1) Функция root (expr, var) вычисляет действительное значение переменной var, при котором выражение expr равно нулю, т.е. она вычисляет один действительный корень уравнения. При этом необходимо задать его начальное приближение. Ниже приведен пример использования этой функции для нахождения действительного корня уравнения x2 +2x+1 = 0.

    Само уравнение не набирается!

    Рис.4. Нахождение одного корня полинома.

    2) Функция polyroots (v) позволяет вычислять все корни полинома. Например, для решения уравнения 8х2 +2х +3 =0 набираем или считываем из таблицы функций (кнопка f(x)) функцию polyroots и в скобках заполняем вектор, вставляя коэффициенты уравнения. Нажимаем клавишу = и получаем ответ:

    Рис.5. Вычисление корней с помощью функции Polyroots.

    Следует обратить внимание, на то, что первый элемент вектора соответствует коэффициенту уравнения при свободном члене.

    Задача 5. Вычислить в Маткад корни приведенного выше уравнения.

    Задача 6.Вычислить все корни многочленов А) 5×5+6×3+8×2+2x=0

    Б)

    5×4+8×3+3×2+9x+8=0

    В)

    4×4+8x-3=0

    Решение алгебраических уравнений в аналитической (символьной) форме.

    Маткад предоставляет возможность решения алгебраических уравнений в символьной (аналитической) форме. Преимуществом символьного решения является возможность решения уравнений с буквенными значениями коэффициентов. Правда, более или менее сложные уравнения символьно в Маткад не решаются, поэтому приходится обращаться к численным методам.

    Решение систем линейных уравнений

    Символьное решение линейных систем алгебраических уравнений производится с помощью двух операций: Solve (Решить) иlsolve.Ниже, на рис.рис.6-10показано решение систем линейных уравнений различными методами.

    Задача 7. Система линейных алгебраических уравнений задана матрицей М коэффициентов и вектором v правых частей. Найти аналитическое решение.

    Сначала вводим матрицу и вектор.

    А) Решение с использованием встроенной функции lsolve. Функция набирается с клавиатуры или из окна встроенных функций. Стрелка набирается с панели символьных решений.

    Рис.6. Символьное решение системы линейных уравнений с использованием встроенной функции lsolve.

    Б) Решение с использованием оператора solve

    Рис.7. Символьное решение системы линейных уравнений с заданной точностью.

    Здесь помимо оператора lsolve использован операторfloat (плавающая точка) и задана точность решения – 4 знака.

    Операторы solve и float набираются последовательно.

    В) Решение в скалярной форме

    Рис.8. Символьное решение системы линейных уравнений в скалярной форме.

    Г) Решение с созданием решающего блока и директивы given. Директиваgiven и операторFind набираются с клавиатуры

    Рис.9. Символьное решение системы линейных уравнений с использованием директивы given

    Д) Решение системы с буквенными коэффициентами

    Рис.10. Символьное решение системы линейных уравнений, заданных в буквенной форме.

    Задача 8. Решить приведенную выше систему всеми рассмотренными способами.

    Задача 9.Решить самостоятельно приведенную ниже систему

    Символьное решение нелинейных алгебраических уравнений Задача 10. Решить приведенные ниже уравнения

    1Решение уравнения четвертой степени с численными коэффициентами с использованием оператора solve

    2Решение квадратного уравнения с буквенными коэффициентами

    3 Решение квадратного уравнения с буквенными коэффициентами с формированием решающего блока

    Но уже кубическое уравнение с буквенными коэффициентами не решается!

    Задача 11. Решить приведенные ниже уравнения самостоятельно

    studfiles.net

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *