Золотое сечение в фотографии примеры: Как с помощью золотого сечения сделать свой дизайн идеальным

Как с помощью золотого сечения сделать свой дизайн идеальным

Правило Золотого сечения – это необъяснимая математическая функция, которой можно описать все созданное в этой Вселенной. Золотое сечение – это соотношение сторон прямоугольника a/b=a+b/a=1,618033987, где a больше, чем b. В графическом выражении это правило выглядит вот так:

Мы согласны, с тем, что выглядит это немного страшно, и непонятно как применить на практике. При этом его используют практически везде.

Как использовать это правило в создании логотипов?

Сперва мы предлагаем взглянуть на некоторые всемирно известные логотипы. Мы не утверждаем, что все лого мира создавались именно так. Согласитесь, чем больше соблюдается это правило, тем визуально красивее выглядит логотип бренда?

У Toyоta прямоугольники со сторонами a и b формируют сетку, где расположены три овала. Также стоит отметить, что на пересечении линий прямоугольников расположено и пересечение этих овалов. Эти пересечения формируют зрительные центры, то есть, куда человек в первую очередь будет смотреть.

В логотипе Apple использовали скорей всего круги Фибоначчи, заливая черной краской или наоборот убирая цвет в определенных частях кругов. Что же, они таким образом получили один из самых идеальных логотипов.

Для лого Pepsi также использовали круги Фибоначчи.

Чтобы начать пользоваться этим правилом достаточно нарисовать рамку Золотого сечения, как показано на примере на первом рисунке статьи. После этого сформируйте сетку, которая поможет вам правильно располагать основные элементы логотипа. Если логотип округлый (например как твиттер), то стоит пользоваться круговой версией Фибоначчи.

Как применять в тексте?

Применение золотого сечения в разметке текста проще простого. Само правило звучит так: последующий большой или меньший шрифт должен быть кратным чилсу Фи. Например, если основной шрифт вы использовали размера 12, то чтобы получить размер шрифта подзаголовка, вы должны это число умножить на 1,6 (12*1,6=19) размер подзаголовка получается 19.

По тому же правилу получаем размер заголовка – 30.

Нужно взять число сетки пикселей и использовать его для построения золотого прямоугольника. И постепенно вы разбиваете сетку своего сайта на такие прямоугольники и вписываете туда основные элементы.

Начинать нужно так:

А так выглядит сетка сайта:

Казалось-бы все просто? А вот как ее строили:

Если вы не верите в это правило, то вот пример твиттера:

Превью: Depositphotos

Читайте также:

Личный опыт: как разработать современный европейский сайт. Часть 1

Личный опыт: как разработать современный европейский сайт. Часть 2

10 полезных выступлений TED о дизайне

 

Правило золотого сечения в живописи

Вероятно, вы часто встречали упоминание о «правиле золотого сечения» и его важности для художника. Что же это за правило и как его применять, расскажет этот материал.

ЧТО ТАКОЕ ЗОЛОТОЕ СЕЧЕНИЕ

Золотое сечение — это пропорциональное соотношение двух величин.

В численном выражении это бесконечное число, которое округляют до 1,618 и обозначают число золотого сечения греческой буквой Ф (фи). 

Если взять отрезок АВ и поделить его точкой С, то золотым сечением будет, когда меньший отрезок относится к большему так, как больший отрезок относится к целому.

Т.е. это пропорция, продолжающая саму себя.

Если вы посмотрите на изображение ракушки, то увидите наглядный пример этого правила — каждое последующее деление меньше предыдущего в соотношении золотой пропорции:

Мы можем найти подобные примеры во многих формах жизни: моллюски и земноводные, семечки у подсолнуха или шишки,  паутина, а также строение частей тела человека). 

Именно поэтому пропорция получила название «создающая жизнь».

Также золотое сечение называют пропорцией божественной гармонии. Это и понятно — природа столетиями оттачивала свои формы для того, чтобы получить жизнеспособные организмы в итоге пришла к этой пропорции с выражением 1,618.  

Вот еще несколько примеров правила золотого сечения:

• направление ветра в урагане
• распределение веток и листьев на деревьях
• пропорции туловища ящериц
• строение морских раковин
• основы иконографии
• строение молекулы ДНК
• конфигурация уха
• объем вдыхаемого и выдыхаемого воздуха в процессе дыхания
• соотношение длины фаланг пальцев и кисти руки в целом

ИСПОЛЬЗОВАНИЕ ПРАВИЛА ЗОЛОТОГО СЕЧЕНИЯ

Человек в своей деятельности и искусстве многое берет от природы. Зачем изобретать велосипед, когда природа уже создала гармоничный и жизнеспособный аналог?

Золотое сечение в искусстве встречается во многих произведениях мировой архитектуры, дизайна и живописи.

Египетские пирамиды, собор Парижской Богоматери, Парфенон — все это образцы использования пропорции Золотого сечения в архитектуре.

ПрОПОРЦИЯ золотого сечения в живописи

Как же использовать эту гармоничную пропорцию в живописи и графике, в изображение на плоском листе?

Правило золотого сечения в картине проявляется делением ее на части четырьмя линиями — две из них горизонтальные,  и две вертикальные. Расположены они согласно пропорции 1,618.

ЧЕМ ВАЖНО ПРАВИЛО ЗОЛОТОГО СЕЧЕНИЯ?

То, что находится на этих линиях, наиболее важно для нашего глаза. 

Картину, построенную с использование золотого сечения мы воспринимаем как правильную и красивую.

Найдя эти линии у себя в картине, мы можем расположить значимые элементы так, чтобы работа в целом производила гармоничное впечатление.

Кроме того, на пересечении линий золотого сечения находятся особые зрительные центры. Они  расположены на расстоянии примерно 3/8 и 5/8 от краев изображения. Подмечено, что человек всегда концентрирует на них свое внимание.

Если вы посмотрите на картину И.Левитана, то очень четко видно, что в ней использовано правило золотого сечения.

Луна и ее отражение стоят на линии золотого сечения. Полоса леса в центре также помещается в пропорции золотого сечения.

Еще один пример. В картине Н.Ге «Александр Сергеевич Пушкин в селе Михайловском»  фигура главного героя также расположена на одной из линий золотого сечения.

Таким образом математические закономерности помогают выстраивать картину так, чтобы она выглядела гармонично и красиво, а зритель сразу обращал внимание на главное.

Выбрав формат листа или холста, расчертите его в пропорции золотого сечения. Используйте эти линии, чтобы разместить на них значимые элементы композиции. Это придаст вашей картине гармоничную структуру и упорядоченность.

ПрИНЦИП золотого сечения:
как построить линии в картине

1) Математический вариант

Для такого просчета удобно использовать онлайн калькуляторы.

Достаточно задать один из параметров, нажать кнопку «рассчитать», и система предоставит результат.

Вот пример удобного сервиса:

— https://planetcalc.ru/1061/

Берем размер ширины или высоты картины, вводим в калькулятор и получаем размер, на каком расстоянии от края будут проходить линии золотого сечения.

Очень просто!

2) Геометрический вариант

Точки зрительных центров здесь находятся путем геометрических построений.

Посмотрите фрагмент ВИДЕО из встречи в Перископе, где я наглядно показываю, как это делать:

3) Использование шаблона

Если вы делаете много небольших эскизов, то оптимальным для построения линий золотого сечения будет использование специальной линейки.

Если взять за основу 100, то линии золотого сечения будут проходить на отметках 38 и 62. Изготовьте такую линейку самостоятельно, отметив также делениями 10, 14, 24. Эти размеры составляют продолжение золотой пропорции, их можно использовать для размеров объектов или расстояний между ними, чтобы продолжить принцип гармоничных соотношений. 

А как правильно пользоваться линейкой, посмотрите в этом фрагменте из видео:

Выбирайте любой удобный способ и обязательно опробуйте его в создании собственных композиций.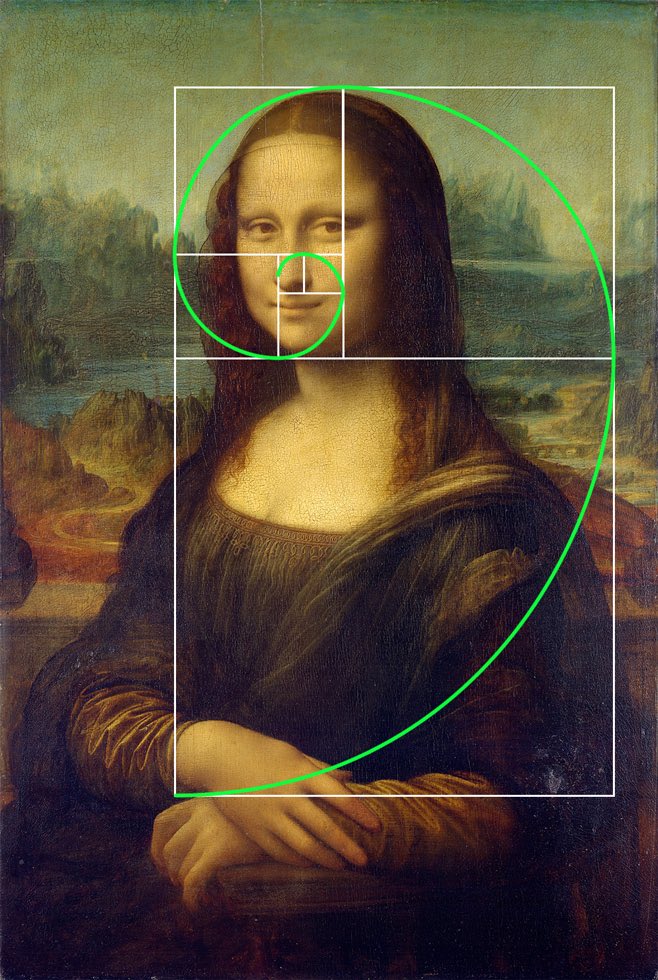

А еще рекомендую рассмотреть работы разных художников и проанализировать, как они используют линии золотого сечения. Полагаю, вы найдете массу достойных примеров.

Если вам интересна эта тема, и вы хотите узнать больше о правиле золотого сечения и его практическом применении, то обратите внимание на книгу

Ф.В. Ковалева «Золотое сечение в живописи»

Это очень полезное издание по композиции!

Если статья была вам полезна, нажмите на кнопочку и поделитесь ей в соцсетях. Спасибо!

Открыт набор на новый курс «Тайны композиции. Ритм» — будем искать и вживлять в себя код гармонии ритма в картине.

Жду первопроходцев. Стартуем 20 сентября!

Больше полезных статей:

Золотое сечение — Википедия

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

---

Первая тысяча знаков значения Φ^[1].

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия^[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число

Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}

Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }

[2],

φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}

Отсюда следует, что

φ=Φ−1{\displaystyle \varphi =\Phi -1}.

Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.

Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.

Иллюстрация к определению

Число Φ{\displaystyle \Phi } называется также золотым числом.

Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства^[3][4][5].

История

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа^[6].

Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке^[7]

или относят появление этого термина к XVI веку^[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»^[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам^[10][11], хотя некоторые авторы утверждают обратное^[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги^[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.^[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года. {2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

• Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:

  Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}

• Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби

  Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

• Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

Золотое сечение в пятиконечной звезде

• В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

Построение золотого сечения

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

• Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). {2}}{18}}}^{[источник не указан 1010 дней]}

  Золотое сечение в науке

  Общее сопротивление этой бесконечной цепи равно Фr.

  Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.

  Отношение амплитуд колебаний и частот ~ Ф.

  Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

  Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»^[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

  Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию^[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.7⁰ , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н⁺(Н₂0)₂₁, который представляет из себя ион Н₃0⁺, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра^[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра^[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды^[23].

  Золотое сечение и гармония в искусстве

  Золотое сечение и зрительные центры

  Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

  • Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
  • Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»^{[источник не указан 3378 дней]}.
  • Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.

  Примеры сознательного использования

  Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах^[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)^{[источник не указан 603 дня]}.

  Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.

  Золотое сечение в биологии и медицине

  Золотое сечение в природе

  Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов^{[25][неавторитетный источник?]} и др.

  См. также

  Примечания

  1. ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
  2. ↑ ^{1 2} Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
  3. ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
  4. ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
  5. ↑ Devlin’s Angle, The Myth That Will Not Go Away
  6. ↑ В. Лаврус, Золотое сечение
  7. ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
  8. ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
  9. ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
  10. ↑ Herz-Fischler, 2013, p. 168.
  11. ↑ Livio, 2008, p. 6-7.
  12. ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
  13. ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
  14. ↑ Herz-Fischler, 2013, p. 169.
  15. ↑ Livio, 2008, p. 7.
  16. ↑ Herz-Fischler, 2013, p. 169-170.
  17. ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know.  — Phantom Press. — 209 с. — ISBN 9785864716700.
  18. ↑ Системы счисления.
  19. ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
  20. ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
  21. ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
  22. ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
  23. ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
  24. ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
  25. ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.

  Литература

  • Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
  • Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
  • Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
  • Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
  • Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
  • Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
  • Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
  • Шмигевский Н. В. Формула совершенства // Страна знаний.  — 2010. — № 4. — С.2-7.
  • Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в

  Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.

  Ссылки

  Как использовать золотое сечение для улучшения вашей фотографии

  Узнайте, что такое золотое сечение в фотографии , как оно соотносится с правилом третей и как использовать его для композиции фотографии.

  Золотое сечение веками использовалось как мощный инструмент композиции. Это принцип конструкции, основанный на соотношении 1: 1,618. Золотое сечение, называемое «идеальным числом», может помочь в создании изображений с сильной композицией, которые привлекут внимание зрителей к вашей фотографии.

  Статья: © 2014 Сара Верко. Все права защищены. Композиция Фи — Большой Призматический источник в Йеллоустонском национальном парке Canon 7D, 24 — 70 мм, объектив серии 2. 8 L, 24 мм, ISO 100, f / 8, 1/80 сек.

  Причина этого проста: золотое сечение позволяет создать композицию, которая идеально сбалансирована с точки зрения зрителя, создавая фотографию, наиболее приятную для человеческого глаза. Мы, естественно, предпочитаем смотреть на изображение, которое сбалансировано и гармонично, и золотое сечение обеспечивает это.

  Известные произведения искусства, такие как Мона Лиза, Тайная вечеря и Рождение Венеры, среди прочего, по слухам, были созданы на основе золотого сечения. Фактически, золотое сечение также называют «числом природы», потому что, как говорят, оно встречается повсюду в природе, от раковины наутилуса до подсолнечника.

  Использование золотого сечения в фотографии в качестве элемента дизайна — отличный способ добиться сильной композиции органичным способом. Это привлечет внимание зрителей к вашей фотографии и с самого начала вызовет у них интерес.Золотое сечение также позволит вашему зрителю ориентироваться вокруг вашей фотографии.

  Это то, к чему мы, фотографы, должны стремиться. Ваши зрители не хотят работать, чтобы увидеть красивую фотографию, они просто хотят ее увидеть.

  Фотография — это создание чего-то визуально привлекательного, и использование золотого сечения в качестве принципа дизайна — лишь один из способов добиться этого.

  Золотое сечение в фотографии и спираль Фибоначчи
  

  Есть много интерпретаций того, как мы можем использовать золотое сечение в фотографии.Двумя наиболее распространенными композициями при ее применении в фотографии являются Сетка Фи и Спираль Фибоначчи.

  Говорят, что где-то в 12 веке нашей эры математик по имени Леонардо Фибоначчи разработал серию чисел, которые позволят получить эстетически приятную композицию. Эта композиция известна как спираль Фибоначчи.

  Спираль Фибоначчи была создана из серии квадратов с использованием чисел Фибоначчи, причем длина каждого квадрата является числом Фибоначчи.

  Затем набор диагональных точек на каждом квадрате создаст путь, по которому спираль может проходить через рамку. Использование спирали в качестве инструмента для компоновки фотографии позволит зрителю перемещаться по изображению в естественном потоке.

  Спиральное наложение — Художественная галерея Ванкувера и Fairmont, Ванкувер, Канада Canon 5D Mark II, 24–70 мм, объектив серии 2.8 L, 24 мм, ISO 200, f / 16, 1/60 сек.

  Сетка Фи очень похожа на принцип правила третей, но имеет одно очень важное отличие.Вместо деления кадра на равные трети 1: 1: 1 применяется золотое сечение для разделения кадра на части, в результате чего получается сетка 1: 0,618: 1.

  В результате получается набор пересекающихся линий, которые находятся намного ближе к середине кадра.

  Не существует правильных или неправильных версий Золотого сечения как принципа дизайна при создании фотографии, каждая из них уникальна и может применяться как таковая. Каждая версия может дополнять разные сцены и может помочь улучшить ваше общее изображение.

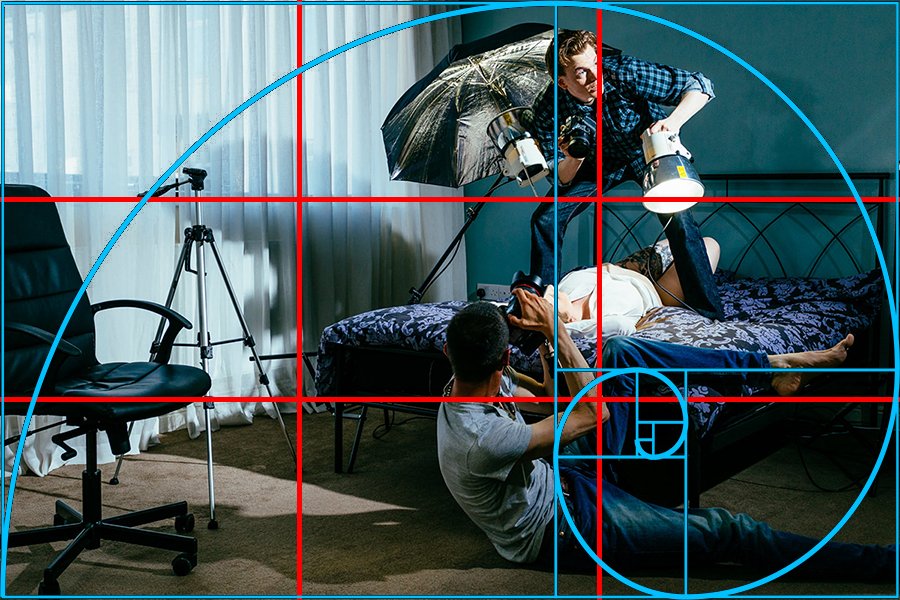
  В то время как спираль Фибоначчи может хорошо работать, например, при составлении портрета, Фи-сетка может хорошо работать для пейзажа. Прелесть в том, что эти руководства по созданию изображения гибкие и не ограничиваются какой-либо одной сценой.

  Как и во всем в фотографии, эксперименты и творчество являются ключевыми факторами. Никогда не позволяйте принципам дизайна диктовать, как вы фотографируете сцену. Просто используйте его как инструмент, который поможет вам достичь сильной композиции, способ дополнить ваше собственное творчество.

  Почему бы просто не использовать правило третей?

  Считается, что наиболее распространенный принцип дизайна, применяемый в фотографии, правило третей, является проявлением золотого сечения в фотографии. По сути, сказано, что Правило третей было разработано как простой способ для фотографов найти золотую середину золотого сечения, точку, в которую впервые обращается человеческий глаз.

  Независимо от того, появилось ли Правило третей так или нет, простая сетка из девяти частей позволяет фотографу составлять изображение на основе легко определяемых фокусных точек, в которых могут быть размещены интересные аспекты сцены.

  Хотя правило третей хорошо работает во многих ситуациях в фотографии, золотое сечение часто может быть более подходящей концепцией дизайна. Это в первую очередь потому, что это соотношение позволяет получить более сбалансированное изображение.

  Часто правило третей, особенно в пейзажной фотографии, может оставлять определенные элементы сцены, такие как линия горизонта, в неудобном положении. Простое разделение кадра на три части означает, что размещение линии горизонта может выглядеть слишком очевидным.Однако при использовании золотого сечения баланс часто может казаться более естественным и менее жестким.

  В качестве примера возьмем следующие два изображения озера Джексон в национальном парке Гранд-Тетон. Использование сетки Фи в качестве ориентира для того, где разместить линию горизонта, сместило баланс сцены, позволяя переднему плану иметь большее влияние на фотографии.

  Линия горизонта также сливается с изображением, вместо того чтобы отвлекаться. Передний план и линия горизонта, на мой взгляд, в данном случае слишком разделены по правилу третей.

  hi Композиция Пример линии горизонта — озеро Джексон, национальный парк Гранд-Тетон Canon 7D, 24–70 мм, объектив серии 2.8 L, 24 мм, ISO 100, f / 11, 1/30 сек. Manfrotto 190xprob штатив и спуск затвора

  P

  
  Пример линии горизонта композиции по правилу третей

  Композиция по золотому сечению

  Хотя сама математика может показаться довольно сложной, применение ее к фотографии — нет.

  Самый простой способ скомпоновать изображение для применения спирали Фибоначчи — это визуализировать небольшой прямоугольник из одного угла кадра, а затем разделить его пополам от угла к углу, чтобы воображаемая линия пересекала весь кадр по диагонали.

  Линия пересечет несколько фокусных точек, связанных со спиралью Фибоначчи внутри прямоугольника. Отсюда вы можете представить себе спираль, выходящую из вашего главного фокуса в широкую дугу, выходящую за пределы кадра.

  Пример состава

  Пример композиции со спиралью Фибоначчи

  При создании этого изображения пути вдоль Морской стены в Ванкувере, Канада, я использовал спираль Фибоначчи в качестве ориентира для компоновки фотографии.

  Спиральная композиция — туман на морской стене, Ванкувер, Канада Canon 5D Mark II, 24–70 мм, объектив серии 2.8 L, 32 мм, ISO 100, f / 11, 1/30 сек. Manfrotto 190xprob штатив и спуск затвора

  Был туманный поздний осенний день, и я хотел запечатлеть цвета заката, которые просачиваются сквозь туман, а также красивый малиновый цвет осенней листвы.

  Я стремился включить одного человека, который выделялся идущим по тропинке, осеннюю листву на переднем плане и линию деревьев в качестве центральной точки в моем кадре.

  Для этого я расположил эти аспекты в центре воображаемого прямоугольника, зная, что он содержит несколько ключевых точек фокусировки, связанных с соотношением, и включил туман в сцену по широкой дуге спирали.

  
  Спиральная накладка

  При компоновке для сетки Фи представьте, что кадр разделен на девять, как если бы вы делали это с Правилом третей, только вместо того, чтобы составлять равные веса для сетки, вы составите сетку, которая имеет вес 1 :.68: 1, поэтому четырем угловым прямоугольникам придается больший вес.

  В результате ваши пересекающиеся линии опускаются немного ближе к середине кадра.

  Phi Overlay — Lighthouse Park West Vancouver, Ванкувер, Канада Canon 5D Mark II, 24 — 70 мм объектив серии 2.8 L при 24 мм, ISO 100, f / 11, 1/60 сек. Штатив Manfrotto 190xprob и спуск затвора

  Как и все в фотографии, композиция для золотого сечения требует практики, точно так же, как когда-то создавалось по правилу третей. Как только вы познакомитесь с общим расположением важных фокусных точек в Золотом пайке, видеть их в видоискателе станет вашей второй натурой.

  Совершенствование композиции

  Я использую Adobe Lightroom, чтобы улучшить композицию золотого сечения во время постобработки. Программное обеспечение для редактирования фотографий имеет ряд доступных наложений кадрирования, включая наложение под названием Золотая спираль, основанное на спирали Фибоначчи.

  При использовании инструмента кадрирования перемещайтесь между различными типами наложений кадрирования с помощью сочетания клавиш [o] и [shft] + [o] для переключения между различными углами и вариантами наложения, которые доступны.
  Золотое сечение в работе

  Вот несколько изображений, которые применяют обе композиции золотого сечения, которые я обсуждал. Вы видите, как золотое сечение с его спиральной композицией было применено к композиции каждой фотографии?

  Восход солнца в лагуне Мури, Раротонга, Острова Кука Canon 7D, 24 — 70 мм объектив серии 2. 8 L, ISO 100, f / 22 HDR слияние трех изображений с различной выдержкой 1/4, 1/10, 0,6 сек. Штатив Manfrotto 190xprob и дерево спуска затвора в Стэнли-парке, Ванкувер, Канада Canon 5D Mark II, 24 — 70 мм 2.Объектив серии 8 L, 32 мм, ISO 400, f / 8, 1/40 сек. Мост, Великая океанская дорога, Виктория, Австралия Canon 7D, 24-70 мм Объектив серии 2.8 L, 24 мм, ISO 100, f / 22, 1 / 13 сек. Штатив Manfrotto 190xprob и спуск затвора Восход солнца в Кайлуа-Бич, Оаху, Гавайи Canon 7D, 24-70 мм, объектив серии 2.8 L, 24 мм, ISO 100, f / 22, 1/2 сек. Штатив Manfrotto 190xprob и спуск затвора

  Использование золотого сечения в качестве способа позиционирования точек интереса при компоновке изображения может помочь создать впечатление в сцене в целом.Это поможет провести зрителей по сцене, чтобы исследовать любые интересные места, которые вы решите включить в свою фотографию. Это также обеспечит естественный баланс сцены, который мы привыкли видеть в природе.

  Статья: © 2014 Сара Верко. Все права защищены.

  Использование золотого сечения в фотографии для улучшения композиции

  Фотография начинается с композиции. То, как вы кадрируете сцену, является основным строительным блоком для получения хорошего снимка, и один композиционный прием, который всегда был решающим, — это золотое сечение.

  Вот что это означает и как вы можете использовать это для немедленного улучшения ваших фотографий.

  Что такое золотое сечение?

  Допустим, у вас есть линия. Существует математическое правило, согласно которому любую линию можно разделить таким образом, чтобы более длинный сегмент, разделенный на более короткий сегмент, имел такое же соотношение, как и отношение полной линии к более длинному сегменту.

  Чтобы выразиться визуально:

  Длина линии равна x + y, первый сегмент — x, второй сегмент — y. Итак, уравнение: x / y = (x + y) / x = 1,6180339887498948420

  Это магическое соотношение равно 1.618 и известен как «золотое сечение» или «божественная пропорция». В математических кругах это особое число известно как Фи. Но при чем тут фотография?

  Что касается композиции изображения, вы можете использовать это соотношение, чтобы решить, как разделить кадр. Не помещайте объект прямо посередине; вместо этого используйте горизонт в качестве ориентира и поместите объект в точку 1,618. Поначалу это немного сложно понять, но мы собираемся изучить это более подробно, поэтому не отчаивайтесь, если вы чувствуете себя потерянным прямо сейчас.

  Примечание. Вы можете просто кадрировать фотографию позже, чтобы добиться аналогичного эффекта, но знайте, что хорошая исходная композиция всегда будет важнее кадрирования, не говоря уже о том, что она научит ваш глаз лучше кадрировать фотографии.

  Что такое сетка Фи?

  Некоторые фотографы предпочитают использовать сетку на основе Фи при компоновке своих снимков.Естественно, этот метод называется Phi Grid . Это вариация Правила третей, одного из основных принципов фотографии.

  Правило третей делит фрейм на три строки и три столбца равного размера, в результате чего получается 1: 1: 1 по вертикали и 1: 1: 1 по горизонтали.Сетка Фи делит рамку аналогичным образом, но делает средний ряд и средний столбец меньше в соответствии с золотым сечением, в результате чего получается 1: 1,618: 1 по вертикали и 1: 1,618: 1 по горизонтали.

  Вот быстрое сравнение:

  Пересечение линий сетки — это место, куда естественно притягивается взгляд, поэтому используйте их для выравнивания изображения.Школа цифровой фотографии предлагает пример использования Phi Grid в подробной статье, которую стоит прочитать полностью:

  Я выровнял горизонт по верхней линии сетки Фи.На мой взгляд, когда вы выравниваете горизонт с помощью сетки по правилу третей, разделение становится слишком… очевидным. Я думаю, что это оставило бы слишком много того, что не является предметом изображения. На этой фотографии небо и облака являются прекрасным дополнением к тому, что я пытаюсь передать на фотографии: церковь внизу справа и знаменитая улица Дюваля слева. Но если на фотографии больше неба, чем уже представлено на фотографии, зритель может подумать, что небо на самом деле является объектом.

  Спираль Фибоначчи

  В геометрии золотое сечение также может быть выражено в виде определенного типа прямоугольника.Предположим, вы берете линию x + y выше и превращаете ее в прямоугольник, ширина которого равна x, а длина — x + y.

  Если разделить площадь этого прямоугольника на серию квадратов, получится спираль последовательности Фибоначчи, как демонстрирует LiveScience:

  Если вы читали Код да Винчи , вы знаете последовательность Фибоначчи: вы начинаете с числа 1, складываете предыдущее целое число и составляете бесконечную серию чисел с этим шаблоном.Итак, сериал выглядит так:

  1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

  Фибоначчи обнаружил, что эта «золотая спираль» появляется в нескольких местах в природе, от молекул ДНК до лепестков цветов, от ураганов до Млечного Пути.Что еще более важно, спираль Фибоначчи приятна для человеческого глаза.

  Адриан Бежан, профессор машиностроения в инженерной школе Duke’s Pratt School of Engineering, говорит, что золотое сечение эстетично из-за эволюции человеческого зрения.

  Короче говоря, наш мозг должен обрабатывать все, что видят наши глаза.Чем быстрее он что-то обработает, тем приятнее. Любое изображение с золотым сечением быстрее обрабатывается мозгом, поэтому он посылает сигнал, что такое изображение эстетично.

  Как использовать спираль Фибоначчи

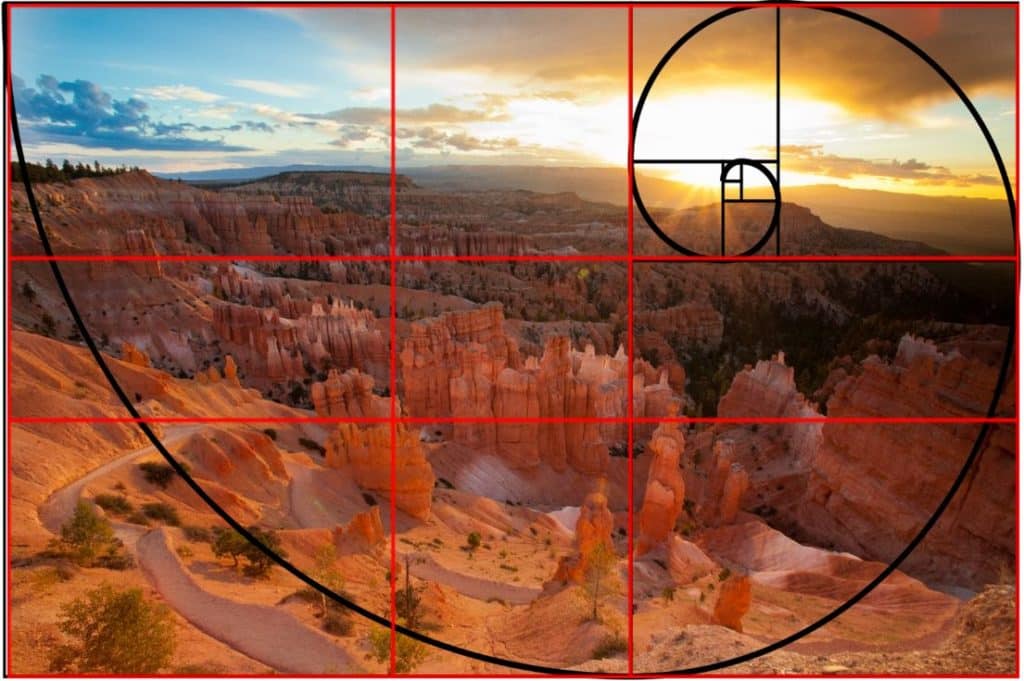
  Что касается реальной фотографии, вам не нужно беспокоиться о технических объяснениях.Спирали Фибоначчи полезны практически для любого вида фотографии, но особенно хороши для пейзажей и широких снимков.

  В Apogee Photo есть отличный пример того, как его использовать:

  Был туманный поздний осенний день, и я хотел запечатлеть цвета заката, которые просачивались сквозь туман, а также красивый малиновый цвет осенней листвы.Я стремился включить одного человека, который выделялся идущим по тропинке, осеннюю листву на переднем плане и линию деревьев в качестве центральной точки в моем кадре. Для этого я расположил эти аспекты в центре воображаемого прямоугольника, зная, что он содержит несколько ключевых точек фокусировки, связанных с соотношением, и добавил туман в сцену по широкой дуге спирали.

  Как видите, спираль в основном естественным образом направляет ваш взгляд от фокальной точки наружу.Вы можете увидеть еще несколько примеров спирали Фибоначчи, подписавшись на этих замечательных фотографов природы в Instagram.

  Лучшие приложения для золотого сечения

  Правильное приложение камеры может сделать вас лучшим фотографом, но не все приложения камеры поддерживают сетку Фи или спираль Фибоначчи.

  Если у вас телефон Android, то получите Camera Zoom FX (3 доллара).Это одно из 10 приложений, которые каждый должен сначала установить на Android, и не зря. Он поддерживает как сетку Фи, так и спираль Фибоначчи в качестве наложений. Просто выберите нужную сетку, скомпонуйте изображение и снимайте.

  Если вы используете iPhone, то в Camera Awesome [больше не доступен] есть спираль Фибоначчи, чтобы делать еще больше потрясающих фотографий.Чтобы использовать Phi Grid, вам понадобится платное приложение, такое как Phi Camera [Больше не доступно].

  Золотое сечение vs.Правило третей

  В Интернете много споров о том, что лучше: золотое сечение или правило третей.Видео выше дает некоторое представление об этих двух стилях, но мы хотим услышать от вас: какая техника композиции лучше и почему?

  Изображение предоставлено: LiveScience, Школа цифровой фотографии, Apogee Photo

  Как создать QR-код с помощью быстрого QR-кода

  Создание QR-кодов не так сложно, как вы думаете.Быстрый QR-код упрощает процесс.

  Об авторе Михир Паткар (Опубликовано 1253 статей)

  Михир Паткар уже более 14 лет пишет о технологиях и продуктивности в ведущих мировых изданиях.Он имеет академическое образование в области журналистики.

  Больше От Михира Паткара

  Подпишитесь на нашу рассылку новостей

  Подпишитесь на нашу рассылку, чтобы получать технические советы, обзоры, бесплатные электронные книги и эксклюзивные предложения!

  Еще один шаг…!

  Подтвердите свой адрес электронной почты в только что отправленном вам электронном письме.

  Золотое сечение в фотографии

  Некоторые утверждают, что правило третей является чрезмерным упрощением более сложного математического уравнения, известного как золотое сечение (также известное как золотая середина). Золотое сечение — это соотношение, которое веками удивляло художников, ученых, музыкантов и математиков. Причина в том, что золотое сечение, кажется, появляется повсюду.Мало того, что золотое сечение появляется повсюду, также кажется, что человеческий глаз очень привлекает результаты этого соотношения.

  Например, на лицах моделей есть размеры, которые удивительно близки к золотому сечению. В природе мы видим золотое сечение в растениях и ветвлениях деревьев, спирали раковин, кривые волн, в нашей ДНК и в Солнечной системе. Он также использовался в архитектуре, искусстве и музыке. Золотое сечение, кажется, есть везде.

  Он использовался в архитектурных шедеврах, таких как греческий Парфенон, пирамиды, а позже в таких великих произведениях искусства, как Нотр-Дам. Есть также основания полагать, что его использовали великие художники Микеланджело и Леонардо Де Винчи.

  Спорный вопрос о том, была ли Мона Лиза намеренно создана с использованием пропорций золотого сечения. См. Ниже

  Золотой прямоугольник — это прямоугольник, длина сторон которого находится в золотом сечении.

  Проще говоря, золотое сечение — это отношение примерно 1.618 к 1. Эта пропорция создает ощущение гармонии и баланса.

  Хотя это соотношение было вновь в течение времени, один бесспорный вехой в его истории была серия чисел Фибоначчи. В XII веке Фибоначчи произвел ряд чисел, сложив пары чисел.

  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,

  (0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8)

  Соотношение между каждой последовательной парой становится все ближе и ближе к Фи по мере прохождения серии.

  Как только вы начнете разбивать золотой прямоугольник по соотношению, вы можете продолжать делить его на части бесконечно. Спираль, которую это производит, точно соответствует росту раковины наутилуса в природе. Да, сейчас все становится немного странно.

  Скажем так, это математическое уравнение эстетически приятной композиции.

  Ниже показано, как Картье-Брессон использовал пропорции золотого прямоугольника для создания своей композиции.

  Примечательно, что этот образец также встречается в природе:

  Вот видео о золотом сечении:

  Как получить золотое сечение в Adobe Lightroom:

  Знаете ли вы, что в Adobe Lightroom можно даже включить наложение золотого сечения при кадрировании?

  Это выглядит так:
  

  Просто нажмите клавишу O при кадрировании изображения.Нажимайте клавишу O, пока не увидите свое золотое сечение. О как буква, а не цифра. Насколько это удобно ?!

  Также продолжайте нажимать кнопку O, и он будет циклически перемещаться по различным направляющим кадрирования. Еще один совет — нажмите Shift-O, и ваше руководство по обрезке золотого сечения изменит местоположение. Просто продолжайте нажимать Shift-O, и Adobe Lightroom перебирает все ваши варианты.

  Наконец, мне пришлось поместить это сюда, потому что я думаю, что это весело:

  Другие интересные страницы фотографий:
  Правило третей
  Фотография в высоком и низком ключе
  Как использовать негативное пространство в фотографии
  Ритм и узор в фотографии

  Школа фотографии Icon
  Школа фотографии Icon — это онлайн-школа фотографии.Вы можете правильно научиться фотографии в Интернете. Начни изучать фотографию сегодня!

  Что такое золотое сечение? Как применить его к своим проектам

  Хотите привлечь клиентов красивой графикой? Читайте дальше, чтобы узнать о золотом сечении и о том, как оно может повысить ставки на ваши изображения. Затем перейдите в редактор Shutterstock и используйте инструменты сетки и кадрирования для создания великолепных дизайнов, соответствующих этому мощному принципу дизайна.

  Слово «золотой» означает ценность, совершенство и успех.Мы видели, как это применимо ко всему: от редкого и драгоценного яйца до эпохи культового кино и до выигрышного лотерейного билета. Однако для маркетологов есть одна важная ссылка …

  Золотое сечение.

  Концепции золотого сечения тысячи лет. Он составляет основу многих классических произведений искусства и архитектуры, от Великой пирамиды в Гизе в Египте до «Парада цирка » художника Жоржа Сёра , и вы часто найдете его в энциклопедиях и научных статьях.Однако его историческое значение не означает, что он устарел; на самом деле золотое сечение может быть невероятно ценным для бизнеса. Использование этого при разработке маркетинговых материалов, логотипов и веб-сайта может привести к созданию более привлекательных визуальных ресурсов для вашего бренда.

  Вам просто нужно знать, как им пользоваться.

  Определение золотого сечения

  Чтобы понять золотое сечение, вы должны знать, как и где оно началось. Этот поиск ведет нас в Древнюю Грецию. Золотое сечение, также называемое греческой буквой фи , относится к числу 1.61803398875.

  С математической точки зрения это число известно как иррациональное, то есть оно состоит из бесконечного ряда цифр, которые не повторяются и не могут быть выражены в виде простой дроби (во многом как знаменитый pi ). Согласно Британской энциклопедии, математическая концепция золотого сечения возникла около 500 г. до н. Э. Некоторые считают, что греческие ученые Евклид и Пифагор отточили его.

  Однако, чтобы по-настоящему понять концепцию, вы должны посмотреть на золотое сечение так:

  (А + В) / А = А / В.

  Разделите строку на две части. Более длинная часть (A), разделенная на более короткую (B), равна всей длине линии, разделенной на более длинную часть. Чтобы создать золотое сечение, деления исходной линии должны равняться 1,618.

  Мы знаем — это сложно описать словами, поэтому вот удобная визуализация, которая поможет вам.

  Когда впервые появилась идея золотого сечения, греки поняли, что с его помощью можно создать очень визуально привлекательный прямоугольник, который мы теперь называем Золотым прямоугольником.Они стали рассматривать эту форму и ее пропорции в контексте дизайна. Оказывается, когда вы применяете соотношение от 1 к 1,61 к изображению, макету или композиции, оно будет выглядеть естественно и сбалансировано.

  Неудивительно, что с тех пор люди используют золотое сечение. Это основа многих древних построек и картин, которые мы считаем красивыми. Некоторые говорят, что золотое сечение представлено в произведениях художника Сальвадора Дали «Таинство Тайной вечери» , Микеланджело «Сотворение Адама» и даже в Стоунхендже.Сегодня вы найдете его на веб-страницах, на фотографиях и в логотипах некоторых из самых популярных мировых брендов.

  Золотое сечение в природе

  Как это актуально для вас и вашего бизнеса? Чтобы ответить на этот вопрос, мы должны исследовать золотое сечение в другой форме.

  Золотая спираль тесно связана с золотым сечением. Он создается путем рисования непрерывной дуги, которая проходит через каждую часть золотого прямоугольника, создавая плавную спираль. Возможно, греки придумали математическое объяснение того, почему существует Золотая спираль, но она появилась задолго до них.Вы найдете доказательства этого повсюду в природе в форме ракушек, цветочных лепестков, сосновых шишек, семенных головок и спиральных галактик. Это также видно на телах некоторых животных, включая дельфинов, морских звезд и пчел.

  Золотая спираль также связана с последовательностью Фибоначчи, которая станет отличным знаком для поклонников книги Дэна Брауна «Код да Винчи ». Согласно этой математической концепции, каждое число в последовательности создается путем сложения двух предыдущих чисел вместе (например, 1, 1, 2, 3, 5, 8).

  Кстати, теория итальянского математика Фибоначчи также появляется в природе. Когда вы превращаете эту последовательность в узор, вы получаете изгибающуюся спираль. Подсчитайте эти спирали, и вы обычно получите число Фибоначчи. Как поясняет Live Science, «Спираль Фибоначчи — это серия соединенных четвертьугольников, нарисованных внутри массива квадратов с числами Фибоначчи для измерений. Квадраты идеально подходят друг к другу из-за характера последовательности, где следующее число равно сумме двух перед ним.”

  Изображение предоставлено space_heater

  Что возвращает нас к Золотой спирали. Live Science продолжает: «Любые два следующих друг за другом числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1,618034. Чем больше пара чисел Фибоначчи, тем точнее приближение ». Больше не нужно задаваться вопросом, что такого особенного в объекте или форме, что делает их такими поразительными. Скорее всего, ему есть чему поблагодарить математику за его непреходящую красоту.

  Изображение Victority

  Где встречаются математика и красота

  Учитывая связь между математикой и природой, неудивительно, что человеческое тело также имеет доказательства золотого сечения.От пропорций вашей руки (длина пальца относительно предплечья и плеча) до формы лица Моны Лизы — все они соответствуют тому, что Лука Пачоли назвал Божественной пропорцией в 1509 году, и тем, что называл Леонардо да Винчи. как Золотое сечение. Да Винчи использовал золотое сечение в своем Витрувианском человеке. Его использовали и такие художники, как Рембрандт.

  Многие ученые и статистики приложили немало усилий, чтобы определить, в какой степени золотое сечение отвечает за то, как мы воспринимаем красоту лица.Согласно этим теориям, если вы вычислите ширину и длину человеческого лица и разделите длину на ширину, и вы получите число, близкое к золотому сечению, то это лицо будет красивым. Расположение глаз, носа и рта, а также расстояние между ними также влияют на наше влечение.

  Когда вы можете представить себе, как все эти формулы объединяются для создания различных форм и узоров, становится намного легче увидеть их ценность в повседневной жизни.Подобно тому, как золотое сечение можно использовать для создания привлекательных произведений архитектуры и искусства, оно жизненно важно для современного дизайна.

  Золотое сечение в дизайне

  веб-страниц, рекламных объявлений, обложек журналов и иллюстраций выигрывают от макета, основанного на этом древнем математическом принципе. Золотое сечение можно использовать для управления размещением объектов, формой логотипа и т. Д.

  Макет и контент в Интернете и за его пределами

  Давайте начнем с рассмотрения роли, которую он играет в макете и содержании.В веб-дизайне золотое сечение может применяться к тому, где и как размещаются столбцы текста. Например, страница с широким блоком содержания слева и более узким столбцом справа привлекает внимание зрителя и выделяет самое важное. Если на вашем сайте ширина 960 пикселей, ширина левого столбца должна быть 593 пикселя, а ширина правого столбца — 367 пикселей. Вместе они создают желаемую пропорцию.

  В зависимости от вашего макета, размер ваших столбцов может складываться не так, как вам хотелось бы (хотя использование калькулятора золотого сечения может помочь).Это нормально. Ваша конечная цель — максимально приблизиться к соотношению 1: 1,61, при котором основной блок контента в 1,6 раза больше, чем боковая панель.

  У этой стратегии пользовательского интерфейса (UI) есть дополнительное преимущество: она помогает читателю ориентироваться в видео, фотографиях и текстовом контенте. Вы найдете примеры такого типа макета во всем Интернете по той простой причине, что он эффективен. Взгляните на домашнюю страницу такого сайта, как Fast Company или BuzzFeed, и вы заметите характерный двухколоночный макет.

  То же самое можно сказать и о Salon.com. Помещая привлекательные фотографии и популярные видео в двух столбцах, составляющих золотое сечение, Salon обеспечивает визуальный баланс, который перенаправляет посетителя сайта от одного текущего контента к другому. Макет одновременно эстетически приятный и функциональный, помогая посетителю определить, как лучше всего перемещаться по странице, а также продвигая наиболее интересный контент Салона.

  Скриншот из Salon

  Как золотое сечение — и его круги — влияют на расстояние и форму

  Золотое сечение также может помочь вам принять решение о расстоянии: где разместить элемент дизайна по отношению к другому, оптимальное количество белого пространства и т. Д.

  Вернитесь к этому золотому прямоугольнику и подумайте, как он может помочь вам решить, где разместить меньший, менее важный блок контента на странице вашего сайта или даже как включить отрицательное пространство в ваш новый логотип. Скорее всего, вы обнаружите, что это позволяет сосредоточить вашу работу и сокращает время, необходимое для создания образа, который понравится и вам, и вашим клиентам.

  Если, однако, вы все еще не можете понять, как математика может улучшить ваши брендированные визуальные ресурсы, возможно, будет полезно принять несколько иную точку зрения.Возьмите этот золотой прямоугольник и нарисуйте идеальный круг внутри каждой его части. С точки зрения размера и пропорции эти формы, называемые золотыми кругами, соответствуют золотому сечению, и теперь их можно перемещать по своему усмотрению.

  Независимо от того, пересекаются ли они или накладываются друг на друга, золотые круги можно применять к любому дизайну, будь то полировка существующего логотипа или создание с нуля. Их наложение на текущую работу позволяет вам вносить коррективы, которые гарантируют, что ваш конечный результат будет соответствовать желанному золотому сечению.

  Если слухи верны, Золотое сечение и связанные с ним Золотые круги были задействованы в дизайне логотипа Twitter. Когда вы видите эти круги, нанесенные на культовую синюю птицу, это имеет смысл. Кажется, что логотип очень точно соответствует формуле золотого сечения, что может объяснить, почему результат так запоминается.

  Птица Twitter — далеко не единственный логотип, в котором используются Золотые круги. Говорят, что логотип Pepsi, как и логотип Google, также придерживается золотого сечения.Графические дизайнеры нередко используют эту технику для создания идеально пропорциональных форм и узоров, которые кажутся зрителю четкими и чистыми.

  Иногда простой акт перестановки ваших золотых кругов до тех пор, пока они не станут напоминать более знакомый объект, может вдохновить вас на следующий дизайн логотипа. Как и во всем, практика ведет к совершенству, и экспериментирование с тем, что могут сделать Golden Circles, является ключом к созданию жизнеспособного дизайна.

  Изображение предоставлено SAAC

  Помня об этом, в прошлом году творческий профессионал Кази Мохаммед Эрфан поставил перед собой задачу создать 25 логотипов, которые соответствуют золотому сечению.Преобразуя каждую часть формулы в коллекцию золотых кругов и используя эти формы в качестве ориентира, он смог разработать динамическую группу логотипов, которые охватывают негативное пространство, демонстрируют баланс и, что наиболее важно, воплощают суть бизнеса, который они представляют. .

  Изображение предоставлено Кази Мохаммедом Эрфаном

  Золотое сечение в фотографии

  Помимо дизайна веб-сайтов и логотипов, золотое сечение также имеет место в фотографии. Когда вам нужно создать или выбрать интересное изображение, пропорции и масштаб невероятно важны и входят в число основных строительных блоков сильной фотографической композиции.Расположение объекта таким образом, чтобы он соответствовал компоновке золотой спирали — с фокусом изображения внутри кривой спирали — может помочь вам создать более привлекательную композицию, соответствующую принципам золотого сечения.

  Чтобы упростить этот процесс, многие фотографы используют «сетку phi ». Разделив золотой прямоугольник и перекрывающую его золотую спираль на девять частей, вы получите сетку, которая поможет вам с композицией. Посмотрите, где пересекаются линии сетки.Это те области, которые естественным образом привлекают человеческий глаз, поэтому вам следует расположить различные элементы вашей фотографии, чтобы достичь визуальной гармонии.

  Сетевые войны: оценка альтернативного правила третей

  Но есть и другой подход к фотографической композиции, и это Правило третей. Этот принцип также включает сетку из девяти частей. Однако по правилу третей все фигуры на сетке имеют одинаковый размер.

  Здесь также рекомендуется размещать интересующие вас объекты на пересечении линий или вдоль самих линий.Результат предназначен для получения сбалансированной фотографии. Представьте, что вы кладете лист миллиметровой бумаги на видоискатель. Как объекты в поле вашего зрения совпадают с прямоугольниками квадратов на странице? Эти пересечения служат ориентиром для того, где вы должны разместить на фотографии основные и второстепенные достопримечательности.

  Многие цифровые фотоаппараты предлагают возможность наложить на экран сетку по правилу третей специально, чтобы пользователям было легче составлять отличную фотографию, но со временем создание изображения таким образом становится второй натурой.Однако имейте в виду, что из этого правила есть некоторые исключения. При прямом хедшоте часто лучше забыть об этих линиях сетки и центрировать лицо на экране.

  Изображение Софии Журавец

  Можно подумать, что две подобные практики — золотое сечение и правило третей — будут работать вместе в гармонии. Однако когда дело доходит до компоновки изображений, есть некоторая неуверенность в том, какая стратегия лучше. Оба служат в качестве полезных чертежей, которые могут улучшить вашу способность создавать привлекательные фотографии или дизайн.Но они не созданы равными.

  Как отмечает DNews Discovery Communications, сетка phi особенно эффективна при съемке пейзажей, поскольку она «дает более сбалансированное изображение» и «делает фотографии более естественными и менее жесткими». С Правилом третей у вас может получиться фотография, которая выглядит на слишком скомпонованной на , и это может показаться вынужденным.

  В следующий раз, когда вы будете просматривать пейзажные фотографии в поисках идеального изображения для своей кампании по электронной почте, почтовой рассылки или публикации в социальных сетях, помните о золотом сечении.Представьте себе сетку фи, наложенную на каждое изображение, и подумайте, как и куда попадают фокусные точки фотографии. Как только вы поймете, что искать, вы повсюду увидите золотое сечение и получите ценное представление о том, почему фотография может поразить вас и ваших клиентов именно так.

  Изображение Танмой Мишра

  Начало работы с золотым сечением

  Если у вас уже есть изображения, которые вы надеетесь использовать в маркетинговых и рекламных целях, но которые не соответствуют золотому сечению или Правилу третей, мужайтесь.Просто редактируя изображения, вы можете сместить фокус зрителя и воспользоваться преимуществами более мастерской композиции.

  Более плотное кадрирование может выделить самую важную часть фотографии. В редакторе Shutterstock вы можете быстро обрезать фотографию до любого размера или выбрать один из предустановленных размеров в социальных сетях для удобного обмена по каналам. Используйте инструмент сетки, чтобы нанести на карту направляющие линии золотого сечения и посмотреть, как ваше изображение работает в нем.

  На первый взгляд, Золотой прямоугольник, Золотая спираль, последовательность Фибоначчи, сетка фи и все, что с ними связано, могут показаться сложными.Идея о том, что ряд чисел может создать что-то естественное и красивое, не совсем интуитивна.

  Но, судя по тому, как его используют дизайнеры, художники-графики и фотографы, золотое сечение превратилось из малоизвестной математической теории в надежную технику, которая занимает почетное место в современном мире. Это мощное правило, которое нужно держать в заднем кармане и применять к курированию изображений, веб-дизайну и даже макетам блогов. Обладая фундаментальным пониманием, вы лучше подготовитесь к выбору изображений и разработке дизайна, которые привлекают клиентов, что повысит вовлеченность и визуальный авторитет вашего бренда.

  Откройте для себя Shutterstock Editor — простой способ персонализировать свой дизайн.

  Откройте для себя редактор

  Золотое сечение

  Подкаст Skeptoid # 325
  28 августа 2012 г.
  Расшифровка подкаста | Подписывайся
  Также доступно на русском языке | Арабский

  Спирали Фибоначчи в семенах подсолнечника Фото: Wikimedia

  Вы, наверное, слышали, что на протяжении тысяч лет человечество очаровывалось золотым сечением, которое является ценностью от 1 до φ (фи, произносится как «гонорар» в США и их родном греческом языке, и «фай» во многих других странах).φ составляет около 1,618. Это иррациональное число, которое продолжается вечно и определяется как

  .

  Золотой прямоугольник, стороны которого пропорциональны золотому сечению, чуть более приземистый, чем экран вашего телевизора высокой четкости. Этот прямоугольник считается наиболее эстетичным и, более того, встречается в природе, определяя пропорции всех видов живых существ, включая идеальное человеческое лицо. Говорят, что великие композиторы, художники и архитекторы основывали свои работы на этом соотношении.Игроки финансовых рынков создают формулы, которые полагаются на него. Повсюду в вашем доме вы найдете множество предметов, соблазнительно напоминающих золотой прямоугольник: книги, приборы, крышки электрических розеток, игральные карты, картины, окна. Люди нашли его в структуре ДНК и расположении молекул в кристаллах. Самый известный из них — греческий Парфенон, выдающийся образ архитектуры, который, как говорят некоторые, почти полностью основан на золотом сечении. Многие считают, что это соотношение настолько распространено как в природе, так и в дизайне, что его также называют божественной пропорцией.

  φ и золотое сечение известны своими уникальными математическими и геометрическими свойствами. Если вы возьмете прямоугольник, стороны которого пропорциональны золотому сечению, вы можете отрезать квадрат с одного его конца, и полученный маленький прямоугольник, который останется, будет иметь те же пропорции, что и оригинал. Вы можете вырезать из него квадрат, и вы получите прямоугольник золотого сечения еще меньшего размера, и вы можете сделать это до бесконечности. Это его основное геометрическое свойство.

  Существенным математическим свойством φ является то, что это отношение последовательных чисел в ряду Фибоначчи.Ряд Фибоначчи состоит из значений, равных сумме двух предыдущих значений: 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. 5 + 8 = 13, 8 + 13 = 21, 13 + 21 = 34 и так далее. Поскольку этот ряд продолжается бесконечно, отношение каждого числа к предыдущему становится все ближе и ближе к φ; но поскольку серия бесконечна, она никогда не достигает цели. Итак, φ — предел отношения этой последовательности. По 40-му значению в ряду Фибоначчи, которое составляет 102 334 155, φ имеет точность до 15 знаков после запятой.

  Вот, пожалуй, самое интересное проявление фи в природе.Это связано с эффективной упаковкой. Когда вы смотрите прямо на дерево сверху, дерево будет наиболее эффективным, если видно как можно больше листьев и не затенено другими листьями. По мере роста стебля необходимо знать, как часто следует производить лист и под каким углом от предыдущего листа, согласно генетической формуле. Если бы он производил каждый лист с интервалом, например, 1/4 оборота, каждый лист в конечном итоге был бы затенен четвертым листом над ним. Фактически, какую бы целую часть полного оборота мы ни использовали, в конечном итоге мы повторяем узор и закрашиваем листья.Таким образом, эволюция в конечном итоге привела к более эффективной генетической инструкции: φ. Производите φ листьев за оборот — чуть более 137,5 ° между последовательными листьями — и никакие два листа никогда не затенят друг друга. Этот угол называется золотым углом.

  Мы видим очень конкретный и очевидный пример этого рисунка в семенах в центре подсолнечника. Соцветия, которые созревают и превращаются в семена, растут из центра подсолнечника, и каждое новое выталкивает существующие семена наружу. Результатом каждого нового семени, растущего под золотым углом от своего предшественника, является подсолнечник с семенами, упакованными как можно эффективнее в круглую головку цветка, независимо от того, насколько большим становится цветок.Этот тип упаковки создает видимые спиральные узоры, пересекающиеся в обоих направлениях вокруг головы. Не случайно, что для цветка любого размера количество спиральных рукавов по часовой стрелке и спиральных рукавов против часовой стрелки всегда является двумя последовательными числами Фибоначчи. Семена в сосновой шишке и другие подобные структуры из растительного мира следуют той же схеме.

  Эта тенденция для соотношений, основанных на φ, для устранения повторения имеет инженерное применение. Один из самых известных — дизайн звуковых комнат для прослушивания музыки или просмотра фильмов, комнат, в которых мы хотим подавить стоячие звуковые волны и резонансы.Аудиоинженеры ссылаются на золотое соотношение комнаты, которое устанавливает основные идеальные размеры звуковой комнаты 10 × 16 × 26. Высота комнаты 10 × φ ≈ 16, что дает длину комнаты, и 16 × φ ≈ 26, что дает ширину комнаты. Любой диагональный прямолинейный путь, пройденный внутри золотого прямоугольника, будет отражаться бесконечно, никогда не повторяя своего курса, поэтому звуковые волны внутри комнаты таких размеров всегда рассеиваются с максимально возможной эффективностью.

  Несмотря на то, что многие книги и статьи утверждают иное, точная история понимания человеком золотого сечения неизвестна.Около 500 г. до н. Э. Греческий математик Пифагор основал пифагорейскую школу мысли, символом которой была пентаграмма. Когда вы вписываете звезду в пятиугольник, соотношение всех отрезков линии является золотым сечением; поэтому, хотя кажется, что он, должно быть, знал об этом соотношении, сам Пифагор не оставил никаких работ, которые бы рассказывали нам наверняка. Более конкретное раннее определение исходит от Евклида, который установил золотое сечение в своей книге Elements около 300 г. до н.э., назвав его крайним и средним соотношением.Кажется почти наверняка, что они должны были знать о рядах Фибоначчи; однако только примерно в 1200 году Леонардо Фибоначчи описал знаменитую последовательность, которая теперь носит его имя, но ни одно из работ Фибоначчи не показывает, что он когда-либо связывал ее с φ или золотым сечением. Сегодня концепции и отношения хорошо изучены, и теперь они являются обычными математическими приемами.

  Появление золотого сечения в мире природы почти неизбежно привело к его принятию и кооптированию многими альтернативными исследователями практически во всех дисциплинах.Возможно, самое известное псевдонаучное утверждение о золотом сечении состоит в том, что греческий Парфенон, знаменитый храм с колоннами на вершине Акрополя в Афинах, построен вокруг этого соотношения. Многие любители накладывают золотые прямоугольники на все изображения Парфенона, утверждая, что нашли совпадение. Но если вы когда-либо изучали такие изображения, вы видели, что они никогда не подходят полностью, по крайней мере, не лучше, чем любой другой прямоугольник, который вы можете попробовать. Это потому, что нет достоверных исторических или документальных свидетельств того, что дизайнеры Парфенона, которые работали более века до того, как родился Евклид, когда-либо использовали золотое сечение каким-либо образом или даже знали о его существовании.

  Еще одно псевдонаучное утверждение состоит в том, что золотое сечение присутствует во всем человеческом теле. Было написано множество чепухи, утверждающей, что всевозможные произвольные измерения тела выдают золотое сечение. Ширина плеч по сравнению с высотой головы; высота пупка относительно высоты всего тела; длина предплечья по сравнению с расстоянием от головы до кончиков пальцев; и так далее, и так далее, и так далее. Очевидно, что эти измерения у всех разные; вероятно, нет ни одного живого человека, для которого эти многочисленные утверждения верны.Более того, это совершенно произвольно. Дайте мне любое число, любое соотношение или любую форму, и я с таким же легкостью смогу составить столь же длинный список черт тела, который одинаково точен.

  Еще один хороший пример — книга. Высота и ширина обычной книги определяется удобством; мы хотим, чтобы он имел удобные пропорции в закрытом (не слишком высоком) и открытом (не слишком широком) положении. Некоторые называют 1: φ идеальной формой книги, но это неверно. Размер книги такой, чтобы ее пропорции были одинаковыми независимо от того, открыта она или закрыта — 1: √2, а не 1: φ.φ значительно больше √2. В бумажной промышленности соотношение 1: √2 называется отношением Лихтенберга.

  Простой факт заключается в том, что прямоугольники, которые не являются ни слишком квадратными, ни слишком узкими, являются наиболее привлекательными и часто наиболее удобными в дизайне. Золотое сечение попадает в диапазон обычно приятных прямоугольников, но также и √2, √3 и многие другие числа. Нет необходимости утверждать, что существует одно идеальное соотношение, которое лучше всего подходит для всех приложений.

  Хороший способ отличить реальные проявления золотого сечения от выдуманных или предполагаемых — служит ли оно цели, которой не может служить подобное число.Подсолнухи используют золотой угол для очень конкретной цели, и для этого абсолютно необходимо число φ. Примером ошибочного проявления является утверждение, что каждый сустав вашего пальца длиннее другого по золотому сечению. Это не только измеримо неверно, но и не принесет особой пользы в этом случае, и, следовательно, ничего подобного не произошло. Преимущество повышения точности при все более малых масштабах манипуляции означает, что полезно иметь постепенно уменьшающиеся сегменты пальцев, так что это то, что у нас есть.Но нет необходимости в том, чтобы это было золотое сечение или даже все в точности одинаковыми, так что это не так.

  Еще один псевдонаучный пример из природы — спиралевидная морская ракушка. Золотая спираль — это спираль, которая становится в φ раз шире с каждой четвертью оборота, и часто говорят, что раковина наутилуса следует за ней. Не правда. Золотая спираль — это только одна из бесконечного числа возможных логарифмических спиралей. Для наутилуса полезно иметь возможность сохранять ту же форму во время роста, и этой цели служит любая приблизительно логарифмическая спираль.Если коэффициент роста спирали будет основан на φ, это не принесет дополнительных преимуществ.

  φ, золотое сечение и ряд Фибоначчи математически интересны и имеют естественные проявления. Это не значит, что все или даже что-либо еще основано на них. Популярность и «громкое имя» «божественной пропорции» были реальной движущей силой ее псевдонаучного назначения практически всему и всему. Те, у кого программное обеспечение сопоставления с образцом в мозгу перегружено, вероятно, слышали о золотом сечении, и поэтому они думают о нем всякий раз, когда видят прямоугольник или великое произведение искусства (например, Мона Лизу, которая не основана на золотое сечение), или модели на фондовом рынке (которые вообще не существуют, не говоря уже о золотом сечении), или в нумерологии Библии (если любое другое число не может считаться столь же значимым).Не все утверждения о золотом сечении являются результатом гиперактивного сопоставления с образцом, но большинство таковых. Как минимум, такое заявление — всегда хороший сигнал, к которому вы должны относиться скептически.

  
  Брайан Даннинг
  Follow @BrianDunning

  Цитируйте эту статью:
  Даннинг, Б. «Золотое сечение». Подкаст Skeptoid. Skeptoid Media, 28 августа 2012 г. Интернет. 13 января 2021 г.

  Золотое сечение и правило третей

  Золотое сечение и Правило третей , возможно, самые сильные и важные правила композиции.Они, как правило, обеспечивают общую основу изображения, создавая «баланс» и позволяя другим композиционным элементам работать с вашей фотографией. По крайней мере, они являются хорошей отправной точкой при создании кадра.

  Золотое сечение или соотношение
  Когда две вещи пропорциональны друг другу в соотношении 1: 1,618, они находятся в Золотом сечении.

  Линия, разделенная на это соотношение, будет выглядеть так:

  Прямоугольник с пропорциями золотого сечения.

  Так что же такого захватывающего в этом соотношении? В природе золотая середина встречается повсюду … от классического примера оболочки Наутилуса до образования галактик, от относительного размера и расположения костей в ваших руках и руках до роста и формы деревьев и лесов, она также используется в сложные экономические уравнения, и утверждается, что это даже можно найти в самой структуре вашей ДНК.
  По какой бы то ни было причине, по которой это происходит в природе, наш разум кажется запрограммированным на распознавание этого паттерна, даже если даже подсознательно, и в результате изображения, соответствующие этому паттерну, воспринимаются как приятные для глаза.

  Итак, как это применить? В изобразительном искусстве это применяется путем разделения изображения по этому соотношению. Полученное изображение может выглядеть так.

  Обратите внимание, что даже без объекта изображение четко фокусирует взгляд на правую нижнюю часть изображения, создавая интересную точку.В этом случае вы бы разместили важную тему вокруг этой области.

  Баланс здесь тоже играет важную роль. Большее количество меньших прямоугольников справа уравновешивает общую большую, но пустую левую часть изображения. Составьте композицию вокруг этих линий, чтобы придать изображению лучший баланс.

  Хотя это отлично подходит для рисования или рисования, это довольно сложно и трудно представить в видоискателе вашей камеры, пока вы пытаетесь скомпоновать свой снимок и справиться с любыми другими отвлекающими факторами, с которыми вы можете столкнуться в поле …

  Вот где приходит на помощь правило третей.

  Правило третей — это, по сути, упрощение Золотого правила. Хотя его соотношение не соответствует соотношению 1: 1,618, его правильная реализация в композиции даст вам примерно такой же желаемый эффект, но его очень легко представить и реализовать по сравнению с золотым соотношением.

  Вот как это работает:

  1. Разделите изображение на 9 равных частей, три по вертикали и три по горизонтали (по сути, доска X и O).

  2.Используя эти линии в качестве направляющих, размещайте интересующие вас объекты на пересечениях линий, так чтобы взгляд оставался в пределах изображения. Обратите внимание, как эти местоположения более или менее совпадают с интересными точками в примере с золотым сечением.
  (Примечание. Обычно вы не можете физически переупорядочить элементы фотографии, если только вы не делаете студийную фотосъемку или фотосъемку натюрморта, поэтому под «размещением элементов» подразумевается изменение положения камеры, чтобы расположить элементы внутри рама)
  3.Вы часто слышите, как фотографы говорят о весе или балансе изображения.
  Это намного легче увидеть, если вставить эти линии. Если вы разместите элементы фотографии на две трети вправо или влево, она снова станет более приятной для глаз. Если вы снимаете вертикально, попробуйте расположить горизонт на две трети вверх или вниз.

  Правило третей очень простое, но может оказаться довольно сложным при его реализации… Не задумывайтесь. Элементы на вашей фотографии часто конфликтуют.Помещая одну вещь на две трети влево, я заставляю другой элемент находиться в месте, которое не соответствует правилу третей … так оно и есть, обычно вы сможете найти хороший баланс между конфликтующими элементами или просто нужно решить, какой из них самый сильный и самый важный, и сделать на нем акцент.

  Вы редко будете центрировать объекты или линии горизонта на изображении, но бывают случаи, когда вы можете захотеть передать сильную симметрию или, возможно, портрет или снимок головы.Помните, что эти правила должны быть гибкими и никоим образом не будут применяться всегда. На любой фотографии всегда будут элементы, которые будут противоречить самим себе или другим правилам композиции, просто нужно найти правильную комбинацию и баланс этих элементов, которые лучше всего подходят для каждой фотографии.

  Заключительные советы:

  — Попробуйте обрезать изображения в программе для редактирования фотографий, чтобы увидеть разные результаты для одного и того же изображения.

  — Разделите экран телевизора или компьютера на три части и смотрите что угодно.Рекомендую хорошие документальные фильмы или анимацию. Вы сразу увидите, как фотографы расставляют элементы в своих кадрах в соответствии с правилом третей.
  Немного ленты и веревки сделают свое дело … Раньше это было очень просто на старых телевизорах, которые собирали пыль на экране, вы могли просто нарисовать доску X и O в пыли, и это работало отлично … не так много с плоским экраном экраны, так как они не так много пыли)

  — В течение дня оглядывайтесь вокруг и пытайтесь составлять кадры на основе того, что вы видите.Представьте себе границы фотографии и подумайте, как вы разместите линии и объекты внутри этой рамки. По прошествии некоторого времени вы можете со временем обнаружить, что делаете это автоматически.

  — Многие камеры теперь накладывают график третей на свои видоискатели. Это отличный инструмент для изучения этой концепции. Постарайтесь не становиться слишком зависимым от него, поскольку это может привести к слишком жесткой интерпретации правила третей.

  Расположение элементов в этом кадре четко демонстрирует правило третей.Дерево на переднем плане выровнено по левой трети фотографии, а сарай — по правым и верхним двум третям.

  На всю фотографию нанесены трети. Чайка и столбы расположены в нижней правой трети фото. Горизонт находится примерно на верхней трети, а парусная лодка на заднем плане на фоне корабля находится примерно на пересечении линий двух третей.

  Этот снимок Ванкувера показывает, как применяется правило третей. Горизонт, разделяющий линию горизонта и квартиру на переднем плане, находится примерно на верхней трети фотографии.