Перевод чисел в различные системы счисления с решением | Онлайн калькулятор
Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую. Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку «Получить запись».
Исходное число записано в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.
Хочу получить запись числа в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.
Получить запись
=
Выполнено переводов:
Также может быть интересно:
- Калькулятор таблицы истинности.

- Калькулятор комплексных чисел
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 = 5·103+9·102+2·101+1·100. Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Число 1234.567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·103+2·102+3·101+4·100+5·10-1+6·10-2+7·10-3.
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2.
1. Перевести число 1001101.11012 в десятичную систему счисления.
Решение: 1001101.11012 = 1·26+0·25+0·24+1·23+1·22+0·21+1·20+1·2-1+1·2-2+0·2-3+1·2-4 = 64+8++4+1+0.5+0.25+0.0625 = 77.812510
Ответ: 1001101.11012 = 77.812510
2. Перевести число E8F.2D16 в десятичную систему счисления.
Решение: E8F.2D16 = 14·162+8·161+15·160+2·16-1+13·16-2 = 3584+128+15+0.125+0.05078125 = 3727.1757812510
Ответ: E8F.2D16 = 3727. 1757812510
1757812510
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
3. Перевести число 27310 в восьмиричную систему счисления.
Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421
Проверка: 4·82+2·81+1·80 = 256+16+1 = 273, результат совпал. Значит перевод выполнен правильно.
Значит перевод выполнен правильно.
Ответ: 27310 = 4218
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
4. Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 — целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 — вторая цифра результата), 0. (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён). 5·2 = 1.0
5·2 = 1.0
Ответ: 0.12510 = 0.0012
Запись числа в десятичной системе счисления Лекция 2
Запись числа в десятичной системе счисления Лекция 2
Система счисления – язык для наименования и записи чисел и выполенения действий над ними
• Непозиционные системы счисления характеризуются тем, что каждый знак всегда обозначает одно и тоже число. • Например, в римской системе счисления: • I – один • III – один да один, да один равно три • IV, VIII, IX, XII, CXXI, MMXI
• В России до XVII в. Использовалась славянская непозиционная нумерация. • Числа в такой нумерации обозначались буквами славянского алфавита, над которыми ставили особый знак – титло.
В России славянская нумерация сохранилась до конца XVII в. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранялась только в богослужебных книгах.
При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранялась только в богослужебных книгах.
• В позиционных системах один и тот же знак может обозначать различные числа а зависимости от места(позиции) • Например: 1111, 343434, 2342342
Запись чисел в десятичной системе счисления десятичная система счисления класс миллиардов класс миллионов класс единиц класс тысяч разря д сотен разря д едини ц разря д тысяч разря д сотен разря д едини ц разр яд тыс яч разр яд соте н разря д един иц 1 0 0 1 3 5 2 0 4 8 4 7
Правила нумерации • Правило прочтения чисел: • 1. Раздели число на классы справа на- лево. Каждый класс должен содержать три разряда. Только старший класс может быть неполным. • 2. Сначала называем разряды старшего класса и название класса. Затем называем разряды следующего класса и т. д.
Правило записи числа • 1. Записываем цифры старшего класса. • 2. Затем, цифры младших классов, помня о том, каждый следующий класс должен быть полным.
• 2. Затем, цифры младших классов, помня о том, каждый следующий класс должен быть полным.
• Например: • Три миллиона двести сорок пять тысяч шестнадцать. 3 _ _ _ 3 245 016
• Основа записи чисел в десятичной системе
Определение. • Десятичной записью натурального числа х называется представление в виде: где коэффициенты аi принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и аn ≠ 0
Теорема 1 • Любое натуральное число х можно представить в виде суммы разрядных слагаемых.
Доказательство существования записи числа. • Пусть тогда Разделим число x : Имеем где
• Продолжим деление. где В результате имеем Процесс деления конечен, так как Последний неравный нулю остаток обозначим a 0. ч. т. д.
Доказательство единственности. • Старшая степень числа x определяется однозначно. • Деление с остатком также однозначно. • Следовательно, представление числа в виде суммы разрядных слагаемых также однозначно.
Сравнение натуральных чисел • Теорема 2: Пусть x и y – натуральные числа, запись которых дана в десятичной системе счисления:
• Тогда число x меньше числа у (x
• Например: • 1. 34
Доказательство • 1) Если ; то Следовательно x
• 2) Если n=m, но то тогда Значит, Следовательно x
Например: • 1) x=54267; y=5426 x= 345; y= 2314 2) a=6789; b=5789 a=1245; b=3245 3) m=3456; n=3421 m=1454; n=1458
Алгоритм сложения • • • x=345; y=598. Найдем сумму чисел х+y: 345+ 598= (300+40+5)+(500+90+8)= (300+500)+(40+90)+(5+8)= 800+13= 800+(100+30)+(10+3)= (800+100)+(30+10)+3 =900+40+3=943
В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты: 1. Способ записи чисел в десятичной системе счисления; 2. Коммутативный и ассоциативный законы сложения натуральных чисел; 3. Дистрибутивный закон умножения относительно сложения; 4. Таблица сложения однозначных чисел.
Таблица сложения однозначных чисел.
Рассмотрим алгоритм сложения многозначных чисел в общем виде (для чисел x и y) • Пусть числа x и y в общем виде:
• Сумму чисел x и y можно представить:
• Но
• Применив дистрибутивный закон, имеем: Применив дистрибутивный закон для 1 и 2 , а так же для 3 и 4 слагаемых, имеем:
• Так как и то Тем самым получена десятичная запись числа
Алгоритм сложения натуральных чисел, записанных в десятичной системе счисления 1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом. 2. Складывают единицы первого разряда. Если сумма меньше 10, записывают ее в разряде единиц ответа и переходят к следующему разряду (десятков)
3. Если сумма единиц больше или равна 10, то представляют ее в виде где однозначное число
4. Повторяют те же действия с десятками, потом с сотнями и т. д. Процесс этот конечен.
д. Процесс этот конечен.
Схема алгоритма сложения x+y да нет ответ переход Сумма ст. разрядов конец -ответ 10 переносим в старший разряд
Спасибо за внимание!
Запись числа в десятичной системе счисления презентация, доклад
Запись числа в десятичной системе счисления
Лекция 2
Система счисления – язык для наименования и записи чисел и выполнения действий над ними.
Непозиционные системы счисления характеризуются тем, что каждый знак всегда обозначает одно и тоже число.
Например, в римской системе счисления:
I – один
III – один да один, да один равно три
IV, VIII, IX, XII, CXXI, MMXI
В России до XVII в. Использовалась славянская непозиционная нумерация.
Использовалась славянская непозиционная нумерация.
Числа в такой нумерации обозначались буквами славянского алфавита, над которыми ставили особый знак – титло.
В России славянская нумерация сохранилась до конца XVII в. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранялась только в богослужебных книгах.
В позиционных системах один и тот же знак может обозначать различные числа в зависимости от места(позиции)
Например: 1111, 343434, 2342342
Запись чисел в десятичной системе счисления
Правила нумерации
Правило прочтения чисел:
1. Раздели число на классы справа на- лево. Каждый класс должен содержать три разряда. Только старший класс может быть неполным.
2. Сначала называем разряды старшего класса и название класса. Затем называем разряды и название следующего класса и т. д.
Правило записи числа
1. Записываем цифры старшего класса.
2. Затем, цифры младших классов, помня о том, что каждый следующий класс должен быть полным.
Например:
Три миллиона двести сорок пять тысяч шестнадцать.
3 _ _ _ _ _ _
3 245 016
Основа записи чисел в десятичной системе
Определение.
Десятичной записью натурального числа х называется представление в виде:
где коэффициенты аi принимают значения 0,1,2,3,4,5,6,7,8,9 и аn ≠0
Теорема 1
Любое натуральное число х можно представить в виде суммы разрядных слагаемых.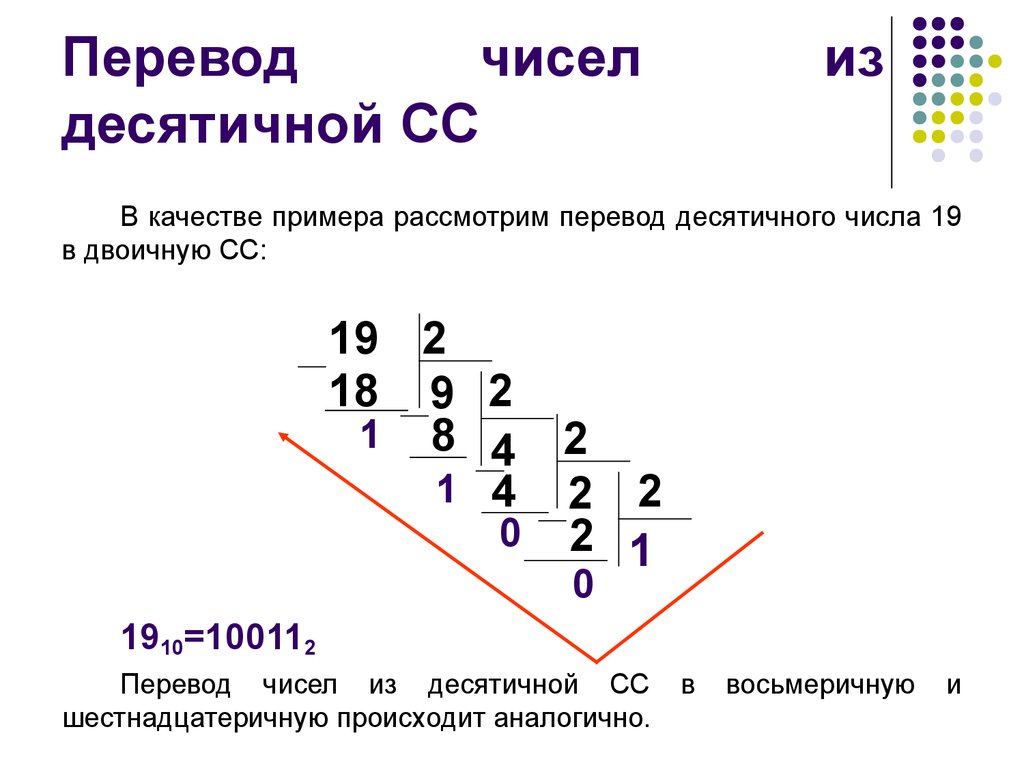
Доказательство существования записи числа.
Пусть
тогда
Разделим число x :
Имеем
где
Продолжим деление.
где
В результате имеем
Процесс деления конечен, так как
Последний неравный нулю остаток обозначим a0. ч.т.д.
Доказательство единственности.
Старшая степень числа x определяется однозначно.
Деление с остатком также однозначно.
Следовательно, представление числа в виде суммы разрядных слагаемых также однозначно.
Сравнение натуральных чисел
Теорема2: Пусть x и y – натуральные числа, запись которых дана в десятичной системе счисления:
1.
2.
3.
Например:
1. 34
2. 628
3.65734
Доказательство
1) Если
Следовательно x
;то
2) Если n=m, но
тогда
Следовательно x
то
Значит,
Например:
1) x=54267; y=5426
x= 345; y= 2314
2) a=6789; b=5789
a=1245; b=3245
3) m=3456; n=3421
m=1454; n=1458
Алгоритм сложения
x=345; y=598. Найдем сумму чисел х+y:
345+ 598= (300+40+5)+(500+90+8)=
(300+500)+(40+90)+(5+8)=
800+130+13=
800+(100+30)+(10+3)=
(800+100)+(30+10)+3 =900+40+3=943
В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты:
Способ записи чисел в десятичной системе счисления;
Коммутативный и ассоциативный законы сложения натуральных чисел;
Дистрибутивный закон умножения относительно сложения;
Таблица сложения однозначных чисел.
Рассмотрим алгоритм сложения многозначных чисел в общем виде (для чисел x и y)
Пусть числа x и y в общем виде:
Сумму чисел x и y можно представить:
Но
Применив дистрибутивный закон, имеем:
Применив дистрибутивный закон для 1 и 2 , а так же для 3 и 4 слагаемых, имеем:
Так как
и
то
Тем самым получена десятичная запись числа
Алгоритм сложения натуральных чисел, записанных в десятичной системе счисления
Записывают второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом.
Складывают единицы первого разряда. Если сумма меньше 10, записывают ее в разряде единиц ответа и переходят к следующему разряду (десятков)
Если сумма меньше 10, записывают ее в разряде единиц ответа и переходят к следующему разряду (десятков)
Если сумма единиц больше или равна 10, то представляют ее в виде
где
однозначное число
Повторяют те же действия с десятками, потом с сотнями и т.д.
Процесс этот конечен.
Схема алгоритма сложения
ответ
переход
конец
x+y
да
нет
-ответ
10 переносим в старший разряд
Сумма ст. разрядов
Спасибо за внимание!
Скачать презентацию
Запись числа в десятичной системе счисления
Похожие презентации:
Натуральные числа. Десятичная система счисления
Десятичная система счисления. Римские цифры
Римские цифры
Позиционные системы счисления, отличные от десятичной
Десятичная запись, значащие цифры, число верных знаков. Лекция 2
Системы счисления. Математические основы информатики
Числа. Натуральные числа. Действия над натуральными числами
Десятичная система счисления
Математические модели числа
Системы счисления. (Тема 2)
Позиционные системы счисления отличные от десятичной
Запись числа в десятичной
системе счисления
Лекция 2
Система счисления – язык для
наименования и записи чисел и
выполнения действий над ними.
• Непозиционные системы счисления
характеризуются тем, что каждый знак
всегда обозначает одно и тоже число.
• Например, в римской системе
счисления:
• I – один
• III – один да один, да один равно три
• IV, VIII, IX, XII, CXXI, MMXI
• В России до XVII в. Использовалась
славянская непозиционная нумерация.
• Числа в такой нумерации обозначались
буквами славянского алфавита, над
которыми ставили особый знак – титло.
В России славянская нумерация сохранилась до конца XVII в. При
Петре I возобладала так называемая арабская нумерация, которой
мы пользуемся и сейчас. Славянская нумерация сохранялась
только в богослужебных книгах.
• В позиционных системах один и тот же
знак может обозначать различные
числа в зависимости от места(позиции)
• Например: 1111,
343434,
2342342
Запись чисел в десятичной
системе счисления
Десятичная система счисления
класс миллиардов
разряд
сотен
разряд
десятко
в
разряд
единиц
класс миллионов
разряд
сотен
разряд
десятко
в
разряд
единиц
класс тысяч
разря
д
сотен
разря
д
десятк
ов
разряд
единиц
класс единиц
разря
д
сотен
разря
д
десят
ков
разряд
единиц
1
1
3
5
2
0
4
1
0
1
0
0
8
4
7
Правила нумерации
• Правило прочтения чисел:
• 1. Раздели число на классы справа налево. Каждый класс должен содержать
Раздели число на классы справа налево. Каждый класс должен содержать
три разряда. Только старший класс
может быть неполным.
• 2. Сначала называем разряды старшего
класса и название класса. Затем
называем разряды и название
следующего класса и т. д.
Правило записи числа
• 1. Записываем цифры старшего класса.
• 2. Затем, цифры младших классов,
помня о том, что каждый следующий
класс должен быть полным.
• Например:
• Три миллиона двести сорок пять тысяч
шестнадцать.
3___ ___
3 245
016
• Основа записи чисел в десятичной
системе
1 1 10
0
10 1 10
1
100 1 10
2
10
…
0 1 10
n
n
Определение.
• Десятичной записью натурального
числа х называется представление в
виде:
n
n
1
x
a
10
a
10
…
a
10
a
n
n
1
1
0
где коэффициенты аi принимают значения
0,1,2,3,4,5,6,7,8,9 и аn ≠0
Теорема 1
• Любое натуральное число х можно
представить в виде суммы разрядных
слагаемых.
n
1
x
a
10
a
10
…
a
10
a
n
n
1
1
0
n
Доказательство существования записи
числа.
• Пусть
n
n
1
x
a
10
a
10
…
a
10
a
n
n
1
1
0
n
n 1
10
x 10
тогда
Разделим число x : 10 n
Имеем
где
n
x 10
a
x
n
1
n
1
n
10
x1 10
• Продолжим деление.
где
n
1
x
10
a
x
1
n
1
2
n
2
n
1
10
x
10
2
В результате имеем
n
n
1
x
10
a
10
a
x
n
n
1
2
Процесс деления конечен, так как x x
…
1 x
2
Последний неравный нулю остаток
обозначим a0.
ч.т.д.
Доказательство единственности.
• Старшая степень числа x определяется
однозначно.
• Деление с остатком также однозначно.
• Следовательно, представление числа в
виде суммы разрядных слагаемых
также однозначно.
Сравнение натуральных
чисел
• Теорема2: Пусть x и y – натуральные
числа, запись которых дана в
десятичной системе счисления:
n
n
1
n
2
x
a
10
a
10
a
10
…
a
10
a
n
n
1
n
2
1
0
m
m
1
b
2
y
b
10
b
10
b
10
…
b
10
b
m
m
1
m
2
1
0
1.
n m
2.
n m
,an bn
3.
n
m
,a
b
…
a
b
n
n
k
k
• Например:
• 1. 34 < 341
• 2. 628 < 828
• 3.65734 < 65794
Доказательство
n
1
• 1) Если n
m
,
10
10
n
1
m
x
10
10
y
Следовательно x<y
m;то
• 2) Если n=m,
тогда
Значит,
но
a n bn
то
an 1 bn
n
n
a
10
1
b
10
n
n
n
n
x
a
1
10
b
10
y
n
n
Следовательно x<y
Например:
• 1) x=54267; y=5426
x= 345; y= 2314
2) a=6789;
a=1245;
b=5789
b=3245
3) m=3456; n=3421
m=1454; n=1458
Алгоритм сложения
x=345; y=598. Найдем сумму чисел х+y:
Найдем сумму чисел х+y:
345+ 598= (300+40+5)+(500+90+8)=
(300+500)+(40+90)+(5+8)=
800+130+13=
800+(100+30)+(10+3)=
(800+100)+(30+10)+3 =900+40+3=943
В основе алгоритма сложения многозначных
чисел лежат следующие теоретические
факты:
1. Способ записи чисел в десятичной
системе счисления;
2. Коммутативный и ассоциативный
законы сложения натуральных чисел;
3. Дистрибутивный закон умножения
относительно сложения;
4. Таблица сложения однозначных чисел.
Рассмотрим алгоритм сложения многозначных
чисел в общем виде (для чисел x и y)
• Пусть числа x и y в общем виде:
x
a
10
a
10
a
2
1
0
2
y
b
10
b
10
b
2
1
0
2
• Сумму чисел x и y можно представить:
x
y
(
a
b
)
10
(
a
b
)
10
(
a
b
)
2
2
1
1
0
0
2
• Но a
b
10
;
a
b
10
1
1
0
0
a
b
10c
1
1
1
a
b
10
c
0
0
0
2
x
y
(
a
b
)
10
(
10
c
)
10
(
10
c
)
22
1
0
• Применив дистрибутивный закон, имеем:
2 2
x
y
(
a
b
)
10
10
c
10
10
c
22
1
0
Применив дистрибутивный закон для 1 и 2 , а так же
для 3 и 4 слагаемых, имеем:
2
x
y
(
a
b
1
)
10
(
c
1
)
10
c
2 2
1
0
• Так как
и
то
a
b
1 10
1
1
c1 1 10
2 /
x
y
с
10
c
10
c
1
2
0
Тем самым получена десятичная
запись числа
Алгоритм сложения натуральных чисел, записанных в
десятичной системе счисления
1. Записывают второе слагаемое под
Записывают второе слагаемое под
первым так, чтобы соответствующие
разряды находились друг под другом.
2. Складывают единицы первого
разряда. Если сумма меньше 10,
записывают ее в разряде единиц
ответа и переходят к следующему
разряду (десятков)
1. Если сумма единиц больше или равна
10, то представляют ее в виде
a
b
1
10
c
0
0
0
где c 0
однозначное число
1. Повторяют те же действия с
десятками, потом с сотнями и т.д.
Процесс этот конечен.
Схема алгоритма сложения
x+y
да
ai bi 10
10 ci
ответ
переход
Сумма ст.
разрядов
конец
нет
ci
-ответ
10 переносим в
старший разряд
Спасибо за внимание!
English Русский Правила
Образовательный портал Лицей №14
- Кодирование информации, системы счисления
Основные определения
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
Любое целое число A, записанное в системе счисления с основанием p, можно представить в расширенной форме:
Правила перевода чисел из одной системы счисления в другую.
Перевод целых чисел в десятичную систему счисления из других систем счисления.
Для перевода целого числа, записанного в системе счисления с основанием p, в десятичную, нужно пронумеровать цифры его целой части справа налево, начиная с 0, затем найти произведение каждой цифры числа на степень основания, где показателем степени является номер цифры, и сложить полученные значения (то есть, нужно представить число в расширенной форме и вычислить).
Перевод целых десятичных чисел в другие системы счисления.
Для перевода целого десятичного числа в систему счисления с основанием p, нужно последовательно делить число и получающиеся частные на p, запоминая остатки, до тех пор, пока последнее частное не будет равно 0. После этого выписать полученные остатки в обратном порядке.
Также, для перевода целого десятичного числа в систему счисления с основанием p можно разложить это число на слагаемые, содержащие максимальную степень числа p и выписать коэффициенты (множители) при этих степенях.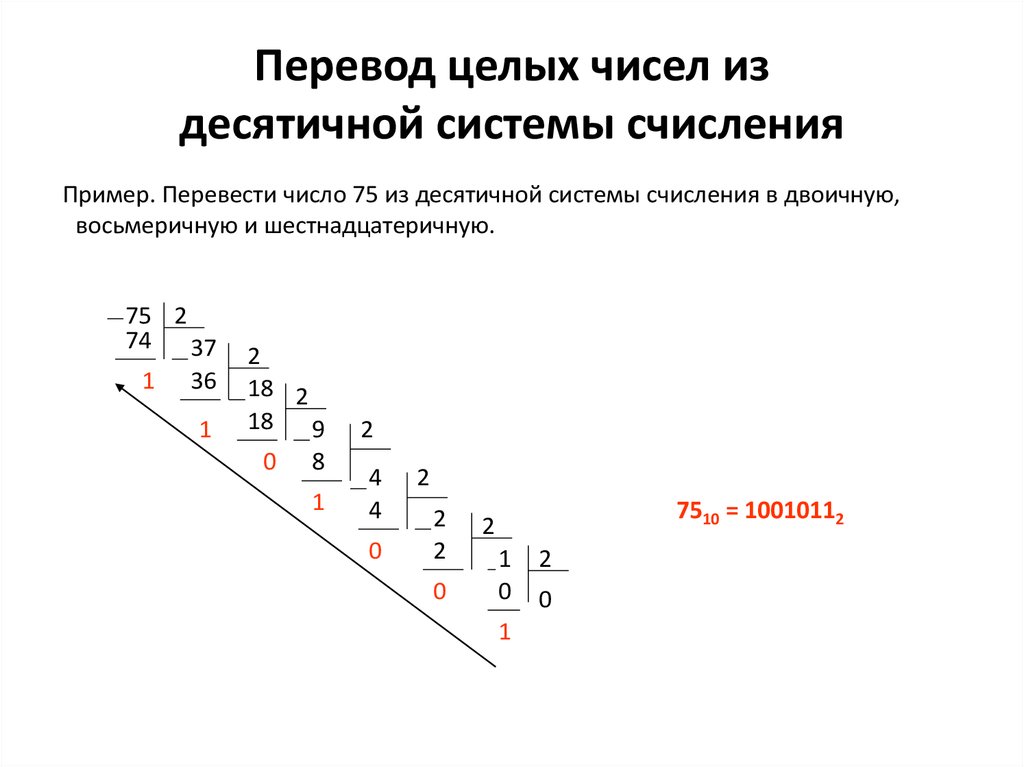 Вместо отсутствующей степени нужно записать 0.
Вместо отсутствующей степени нужно записать 0.
Легко заметить, что множители при степенях p не что иное, как остатки от последовательного деления десятичного числа на p.
Кратные системы счисления
Для перевода восьмеричного числа в двоичную систему счисления достаточно заменить каждую цифру восьмеричного числа соответствующим трехразрядным двоичным числом.
Для перевода двоичного числа в восьмеричную систему счисления нужно разбить число на триады, начиная справа. Каждую триаду записать в виде одной восьмеричной цифры.
| 0 | 0 | 000 |
| 1 | 1 | 001 |
| 2 | 2 | 010 |
| 3 | 3 | 011 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
Перевод числа из шестнадцатеричной системы счисления в двоичную выполняется аналогично. Только в этом случае каждая цифра шестнадцатеричного числа заменяется соответствующим четырехразрядным двоичным числом.
Только в этом случае каждая цифра шестнадцатеричного числа заменяется соответствующим четырехразрядным двоичным числом.
Для перевода двоичного числа в шестнадцатеричную систему счисления нужно разбить число на тетрады, начиная справа. Каждую тетраду записать в виде одной шестнадцатеричной цифры.
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
Некоторые полезные формулы
- Число в системе счисления с основанием p записывается как одна единица и N нулей:
Например, , в десятичной системе счисления.
- Число в системе счисления с основанием p записывается как N старших цифр данной системы счисления.
Например, в десятичной системе счисления. - Число в системе счисления с основанием p записывается как
N – M старших цифр данной системы счисления и M нулей.
Например, в десятичной системе счисления.
Задачи
- Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201. [Материалы ЕГЭ №16 К.Ю. Полякова, №38]
Решение:
144x + 24x = 201x, где х – искомое основание.
Запишем все числа в расширенной форме:
1∙x2 + 4∙x + 4 + 2∙x + 4= 2∙x2 + 1
x2 — 6∙x — 7= 0
x1= -1, посторонний корень, так как x>0.
x2= 7
Ответ: 7.
- Решите уравнение 1007 + x = 2305 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
[Материалы ЕГЭ №16 К.Ю. Полякова, №68]
Решение:
1007 + x = 2305 x = 2305 — 1007
1007 = 1∙72 = 49
2305 = 2∙52 + 3∙51 = 50 + 15 = 65
x = 65 – 49 = 16
16 = 2 ∙ 61 + 4 ∙ 60 = 246
Ответ: 24 - Решите уравнение 222x+ 4 = 11005. Ответ запишите в троичной системе счисления. [Материалы ЕГЭ №16 К.Ю. Полякова, №102]
Решение:
222x + 4 = 11005 , где х – искомое основание.
Запишем все числа в расширенной форме:
2∙x2 + 2 ∙x1 + 2 ∙x0 + 4 = 1 ∙53 +1 ∙52
2∙x2 + 2 ∙x – 144 = 0
x2 + x – 72 = 0
x1= -9, посторонний корень, так как x>0.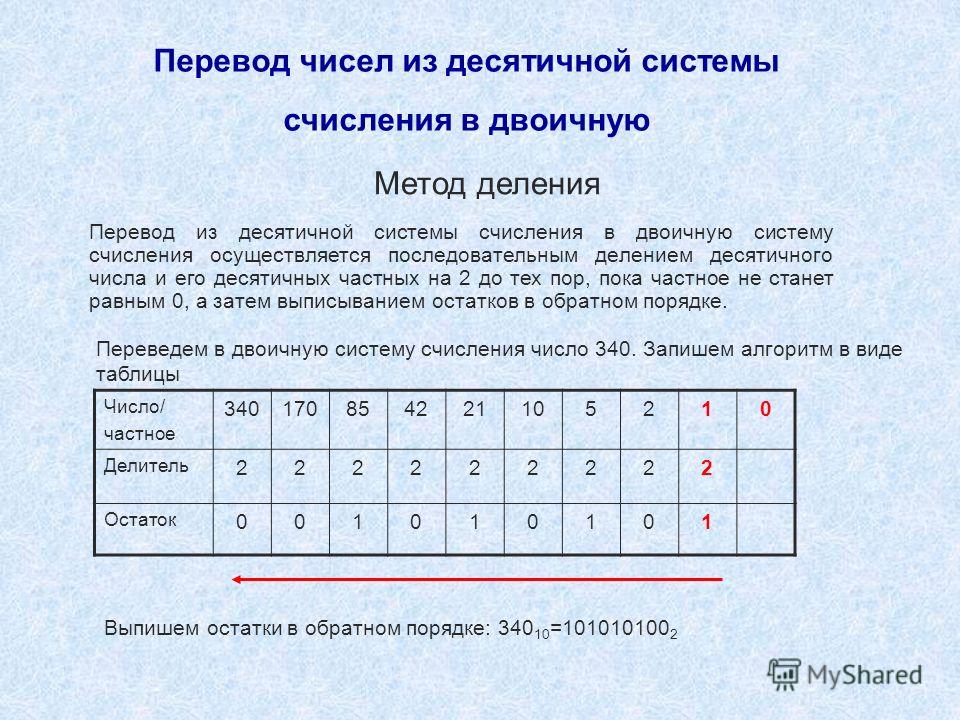
x2= 8
8 = 2∙31 + 2∙30 =223
Ответ: 22 - В системе счисления с некоторым основанием десятичное число 83 записывается в виде 123. Укажите это основание. [Материалы ЕГЭ №16 К.Ю. Полякова, №27]
Решение:
83 = 1∙x2 + 2∙x1 + 3∙x0 , где х – искомое основание.
x2 + 2∙x — 80 = 0
x1= -10, посторонний корень, так как x>0.
x2= 8
Ответ: 8 - Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 35 оканчивается на 8. [Материалы ЕГЭ №16 К.Ю. Полякова, №29]
Решение:
35 = N∙p +8, p>5 и N целое число.
N∙p = 27, тогда 27 p = {9, 27}
Ответ: 9, 27 - Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 84 оканчивается на 14.
 [Материалы ЕГЭ №16 К.Ю. Полякова, №43]
[Материалы ЕГЭ №16 К.Ю. Полякова, №43]
Решение:
Так как, известны две последние цифры записи числа 84 в системе счисления с основанием p, то
84 = N∙p2+ 1∙p1 +4∙p0, p>4
N∙p2 + p = 80
(N∙p + 1)∙p = 80
Следовательно, 80
p = {5, 8, 10, 16, 20, 40, 80}, при этом
Выполнив проверку получаем, что p={5, 80}
Ответ: 5, 80 - Запись числа 180 в системе счисления с основанием p содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления. [Материалы ЕГЭ №16 К.Ю. Полякова, №60]
Решение:
180 = a2∙p2 + a1∙p1 + 0∙p0 , где p искомое основание.
180 = a2∙p2 + a1∙p
180 = p∙( a2∙p + a1 )
Следовательно, 180 p и p2 ≤ 180 ≤ p3
p = {6, 9, 10, 12}
Ответ: 6, 9, 10, 12 - Сколько единиц в двоичной записи числа 8415 – 4162 + 2543 – 25?
[Материалы ЕГЭ №16 К. Ю. Полякова, №108]
Ю. Полякова, №108]
Решение:
8415 – 4162 + 2543 – 25 = 21245 – 2324 + 2543 – 25 = 21245 + (2543 – 2325 ) + (2324 -32) +7 = Количество единиц = 1 + 218 + 319 + 3 = 541
Ответ: 541 - Сколько значащих нулей в двоичной записи числа 4230 + 8120 – 2150 – 100? [Материалы ЕГЭ №16 К.Ю. Полякова, №115]
Решение:
Количество нулей = Количество разрядов – Количество единиц
4230 + 8120 – 2150 – 100 = 2460 + 2360 – 2151 + 2150 – 27 + 28 =
= 2460 + (2360 – 2151 )+ (2150 – 27) + 111002
461 – (1 + 209 + 143 + 3) = 461 – 356 = 105
Ответ: 105 - Значение выражения 497 + 720 – 28 записали в системе счисления с основанием 7.
 Сколько цифр «6» содержится в этой записи? [Я.Н.Зайдельман , ЕГЭ 2020. Информатика и ИКТ. Подготовка к ЕГЭ в 2020 году. Диагностические работы. ФГОС. — М.: МЦНМО, 2019., стр 64, №16]
Сколько цифр «6» содержится в этой записи? [Я.Н.Зайдельман , ЕГЭ 2020. Информатика и ИКТ. Подготовка к ЕГЭ в 2020 году. Диагностические работы. ФГОС. — М.: МЦНМО, 2019., стр 64, №16]
Решение:
497 + 720 – 28 = 714 + 720 – 49 + 21 = 720 + 714 – 72 + 3∙7 =
= 100…007 + () + 307, первое и третье слагаемые не влияют на количество цифр «6» в записи числа.
Ответ: 12
Информационные источники
- «ФИПИ. Открытый банк тестовых заданий», http://os.fipi.ru/tasks/5/a
- Материалы для подготовки к ЕГЭ по информатике К.Ю. Полякова, http://kpolyakov.spb.ru/school/ege.htm
- Образовательный портал «Решу ЕГЭ», https://ege.sdamgia.ru/
- Я.Н.Зайдельман , ЕГЭ 2020. Информатика и ИКТ. Подготовка к ЕГЭ в 2020 году. Диагностические работы. ФГОС. — М.: МЦНМО, 2019.

- Я. Н. Зайдельман, М. А. Ройтберг, Информатика и ИКТ. Подготовка к ЕГЭ в 2019 году. Диагностические работы. ФГОС.— М.: МЦНМО, 2019.
- Е.Л. Теплоухова, Как решать задачи на системы счисления? ЕГЭ. Информатика. Задание №16. — «ЛитРес: Самиздат»2019
- Ушаков Д.М. ЕГЭ-2020. Информатика. 20 тренировочных вариантов экзаменационных работ для подготовки к ЕГЭ. — М.: АСТ, 2019.
§ 1.1. Системы счисления
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- система счисления
- цифра
- алфавит
- позиционная система счисления
- основание
- развёрнутая форма записи числа
- свёрнутая форма записи числа
- двоичная система счисления
- восьмеричная система счисления
- шестнадцатеричная система счисления
1.1.1. Общие сведения о системах счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.
Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:
- 1) унарная система;
- 2) непозиционные системы;
- 3) позиционные системы.
Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:
Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Десятичная система
Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Это отчётливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».
Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
Запись числа по формуле (1) называется развёрнутой формой записиСвёрнутной формой записи числа называется его представление в виде1 ± an-1an-2…a1a0,a-1…a-m. 1 Далее будут рассматриваться только положительные целые числа.
1 Далее будут рассматриваться только положительные целые числа.
Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
- 1 • 104 + 4 • 103 + 3 • 102 + 5 • 101 + 1 • 100 + 1 • 10-1.
1.1.2. Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
На основании формулы (1) для целых двоичных чисел можно записать:
- аn-1аn-2…а1а0 = an-1 • 2n-1 + аn-2 • 2n-2 +…+ а0 • 20.
 (1′)
(1′)
Например:
- 100112 = 1 • 24 + 0 • 23 + 0 • 22 + 1 • 21 + 1 • 20 = 24 + 21 + 20 = 1910.
Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1′).
Разделим аn-1 • 2n-1 + аn-2 • 2n-2 + … + а0 • 20 на 2. Частное будет равно аn-1 • 2n-2 + … + а1, а остаток будет равен а0.
Полученное частное опять разделим на 2, остаток от деления будет равен а1.
Если продолжить этот процесс деления, то на n-м шаге получим набор цифр:
- а0, а1, а2, … аn-1,.

которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.
Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Выписывая остатки от деления в направлении, указанном стрелкой, получим: 1110 = 10112.
Пример 5. Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
- 36310 = 1011010112
1.
 1.3. Восьмеричная система счисления
1.3. Восьмеричная система счисленияВосьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1,2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
- аn-1аn-2…а1а0 = аn-1 • 8n-1 + аn-2 • 8n-2 + … + а0 • 80. (1″)
Например: 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
10310 = 1478
1.1.4. Шестнадцатеричная система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…, 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
- 3AF16 = 3 • 162 + 10 • 161 + 15 • 160 = 768 + 160 + 15 = 94310.
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
15410 = 9А16
1.
 1.5. Правило перевода целых десятичных чисел в систему счисления с основанием q
1.5. Правило перевода целых десятичных чисел в систему счисления с основанием qДля перевода целого десятичного числа в систему счисления с основанием q следует:
- 1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
- 2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
- 3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
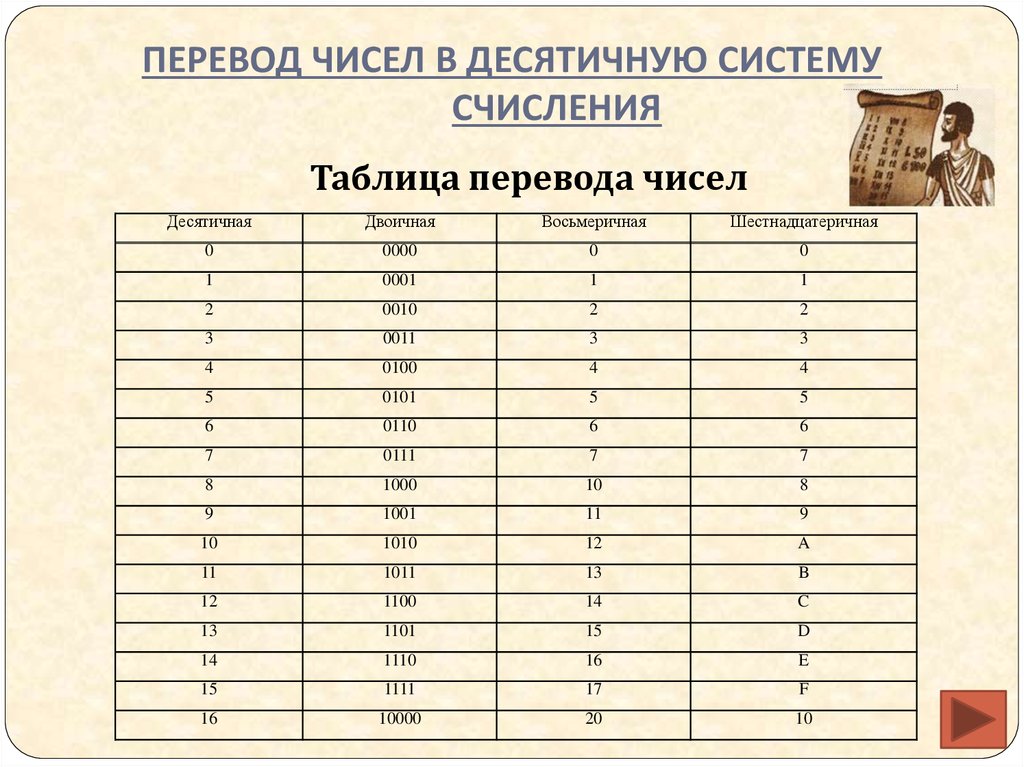
Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 2010.
В Единой коллекции цифровых образовательных ресурсов (http://sc.edu.ru/) размещена интерактивная анимация «Преобразование десятичного числа в другую систему счисления» (135050). С её помощью можно понаблюдать за переводом произвольного целого числа от 0 до 512 в позиционную систему счисления, основание которой не превышает 16.
В размещённой там же виртуальной лаборатории «Цифровые весы» (135009) вы сможете освоить ещё один способ перевода целых десятичных чисел в другие системы счисления — метод разностей.
1.1.6. Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
Пример 8. Таблица двоичного сложения предельно проста. Так как 1 + 1 = 10, то 0 остаётся в младшем разряде, а 1 переносится в старший разряд.
Пример 9. Операция умножения двоичных чисел выполняется по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Таким образом, в двоичной системе счисления умножение сводится к сдвигам множимого и сложениям.
1.1.7. «Компьютерные» системы счисления
В компьютерной технике используется двоичная система счисления, обеспечивающая ряд преимуществ по сравнению с другими системами счисления:
- двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями;
- представление информации посредством только двух состояний надёжно и помехоустойчиво;
- двоичная арифметика наиболее проста;
- существует математический аппарат, обеспечивающий логические преобразования двоичных данных.

Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
С помощью ресурса «Интерактивный задачник, раздел “Системы счисления»» (128659), размещённого в Единой коллекции цифровых образовательных ресурсов, можно проверить, насколько прочно вы усвоили изученный в этом параграфе материал.
Самое главное о системе счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
3. Цифры каких систем счисления приведены на рис. 1.1?
4. Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.
5. Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
6. Запишите в развёрнутой форме числа
7. Вычислите десятичные эквиваленты следующих чисел 172? 2EA??
8. Укажите какое из чисел 1100112, 1114, 358 и 1В16 является
9. Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
10. Верны ли следующие равенства? а) 334 = 217;
б) 338 = 214.
11. Найдите основание х системы счисления, если: а) 14х = 910;
б) 2002х = 13010.
12. Переведите целые числа из десятичной системы счисления в двоичную: а) 89; б) 600; в) 2010
13. Переведите целые числа из десятичной системы счисления в восьмеричную: а) 513; б) 600; в) 2010.
14. Переведите целые числа из десятичной системы счисления в шестнадцатеричную: а) 513; б) 600; в) 2010.
15. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
16. Выполните операцию сложения над двоичными числами: а) 101010 + 1101; б) 1010 + 1010; в) 10101 + 111.
17. Выполните операцию умножения над двоичными числами: а) 1010 · 11; б) 111 · 101; в) 1010 · 111.
18. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе: а) 1100 ? 11 ? 100 = 100000; б) 1100 ? 10 ? 10 = 100; в) 1100 ? 11 ? 100 = 0.
19. Вычислите выражения: а) (11111012 + AF16) : 368; б) 1258 + 1012 ? 2A16 ? 1418. Ответ дайте в десятичной системе счисления.
Ответ дайте в десятичной системе счисления.
20. Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?
21. Разработайте таблицы сложения и умножения для восьмеричной системы счисления.
22. Постройте граф, отражающий разновидности систем счисления.
23. Подготовьте небольшое сообщение об одной из систем счисления (когда и где применялась, какие символы использовались и т. д.).
Оглавление
§ 1.1. Системы счисления
§ 1.2. Представление чисел в компьютере
Десятичная система счисления — определение, научная система счисления и десятичная система счисления, примеры
Десятичная система счисления — это представление дроби с использованием основания 10 и десятичной точки. Другими словами, число представляется с десятичной точкой в соответствии со значением десятичного разряда. Десятичное число — это число, состоящее из двух частей, то есть целого числа и дробной части, которая записывается с помощью разделителей, таких как точка (.), которая называется десятичной точкой. Давайте узнаем больше десятичных обозначений, определений и решим несколько примеров, чтобы лучше понять концепцию.
Десятичное число — это число, состоящее из двух частей, то есть целого числа и дробной части, которая записывается с помощью разделителей, таких как точка (.), которая называется десятичной точкой. Давайте узнаем больше десятичных обозначений, определений и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Определение десятичной системы счисления |
| 2. | Научное обозначение и десятичное представление |
| 3. | Часто задаваемые вопросы о десятичной системе счисления |
Определение десятичной системы счисления
Представление числа в виде дроби с основанием 10 и десятичной точкой называется десятичной записью. Эти цифры от 0 до 9состоит из двух частей: целого числа и дробной части, разделенных точкой, называемой десятичной запятой. Поскольку в десятичных дробях используется основание равное 10, система разряда также записывается в соответствии с ней. На приведенном ниже изображении разрядное значение до десятичной точки записывается единицами, за которыми следуют десятки, сотни и т. д., а после десятичной точки записываются десятые доли, за которыми следуют сотые, затем тысячные и т. д. Значение разряда после запятой представляет собой дробную часть числа. Например, число 0,48 состоит из 4 десятых и 8 сотых. Это также можно записать как 0,48 = 0,4 + 0,08. Другими словами, это означает, что 0,48 = 4/10 + 8/100. Преобразование дробей в десятичные и наоборот может быть выполнено в любое время, поскольку они означают одно и то же, но пишутся по-разному.
На приведенном ниже изображении разрядное значение до десятичной точки записывается единицами, за которыми следуют десятки, сотни и т. д., а после десятичной точки записываются десятые доли, за которыми следуют сотые, затем тысячные и т. д. Значение разряда после запятой представляет собой дробную часть числа. Например, число 0,48 состоит из 4 десятых и 8 сотых. Это также можно записать как 0,48 = 0,4 + 0,08. Другими словами, это означает, что 0,48 = 4/10 + 8/100. Преобразование дробей в десятичные и наоборот может быть выполнено в любое время, поскольку они означают одно и то же, но пишутся по-разному.
Цифры слева от десятичной точки, т. е. целое число, могут быть выражены как кратные положительной степени десяти, а цифры справа выражены как кратные отрицательной степени десяти, поскольку десятичные дроби используют основание как 10. Например, дробь 13,24 записывается как 1324/100, а с основанием 10 записывается как 1 × 10 1 + 3 × 10 0 + 2 × 10 -1 + 4 × 10 -2 .
Научное обозначение и десятичное представление
Научное представление похоже на десятичное представление, в котором числа записываются с учетом основания 10. По определению, когда число записывается в виде произведения двух чисел, где первое число больше или равно единице, но меньше чем 10, а второе число — это степень 10, записанная в экспоненциальной форме, это называется научной записью. Эта форма используется учеными и инженерами, когда они имеют дело с большими или очень маленькими числами. Положительные показатели демонстрируют большие числа, в то время как отрицательные показатели демонстрируют маленькие числа от 1 до 10. Десятичная точка в экспоненциальном представлении перемещается в соответствии со степенью влево или вправо в зависимости от того, является ли число положительным или отрицательным. Когда число равно 10 или больше, десятичная точка должна двигаться влево, а степень числа 10 положительна. Когда число меньше 1, десятичная точка должна двигаться вправо, поэтому степень числа 10 отрицательна. Например, 0,0076 записывается как 7,6 × 0,001 = 7,6 × 10 -3 . Другими словами, научное представление записывается в виде a × 10 b , где a — десятичное число или число, которое больше 1 и меньше 10, а b — степень числа 10.
Например, 0,0076 записывается как 7,6 × 0,001 = 7,6 × 10 -3 . Другими словами, научное представление записывается в виде a × 10 b , где a — десятичное число или число, которое больше 1 и меньше 10, а b — степень числа 10.
Преобразование десятичного числа в экспоненциальное представление
Шаги для преобразования десятичной записи в экспоненциальную запись:
- Переместите десятичную точку так, чтобы первое число было больше или равно 1, но меньше 10.
- Подсчитайте количество перемещенных десятичных знаков (n).
- Запишите число в виде произведения степени 10. Если число больше 1, степень 10 будет равна 10 n , а если оно находится между 0 и 1, степень 10 будет равна 10 -n .
- Перепроверьте окончательный результат.
Давайте рассмотрим пример. Запишите 0,0025 в экспоненциальном представлении.
Шаг 1: Переместите десятичную точку, чтобы число было больше 1. Переместите десятичную точку вправо.
Переместите десятичную точку вправо.
0,0025 = 2,5
Шаг 2: Подсчитайте количество мест, на которые он был перемещен.
n = 3.
Шаг 3: Запишите произведение в степени 10. Поскольку десятичная запятая сместилась вправо, после запятой она будет отрицательной.
2,5 × 10 -3
Шаг 4: Поперечная проверка
2,5 × 10 -3 = 2,5 × 1/10 3 = 2,5 × 1/1000 = 2,5 × 0,001 = 0,0035.
Преобразование научного представления в десятичное
Шаги для преобразования научной записи в десятичную:
- Найдите показатель степени (n) в степени 10.
- Переместите десятичные точки на n позиций, если число положительное, сдвиньте вправо, если показатель степени отрицательный, сдвиньте влево. При необходимости добавьте нули.
- Перепроверьте окончательный результат.
Давайте рассмотрим пример. Преобразуйте 4,8 × 10 -2 в десятичную форму.
Шаг 1: Найдите значение показателя степени (n)
n = -2
Шаг 2: Переместите десятичную точку на 2 разряда влево, так как она имеет отрицательное значение.
4,8 = 0,048
Шаг 3: Поперечная проверка
4,8 × 10 -2 = 4,8 × 1/10 2 = 4,8 × 1/100 = 4,8 × 0,01 = 0,048
.
Ниже перечислены некоторые темы, связанные с десятичной записью.
- Десятичные числа и дроби
- Экспоненты
- Калькулятор десятичной системы счисления
- Стандартное обозначение
Часто задаваемые вопросы о десятичной системе счисления
Что означает десятичная запись?
Десятичная система счисления представляет собой форму выражения десятичных чисел в виде дроби вместе с выражением числа с основанием 10. Числа выражаются в соответствии с их порядковым значением, поэтому записывается показатель степени с основанием 10.
Что такое десятичная запись 1?
Десятичная запись 1 равна 1. Поскольку десятичная точка стоит после 1 и записывается как 1,0. В этом случае нулем можно пренебречь. Но в случае 0,1 1 ставится после запятой, и в соответствии со значением десятичного разряда 1 записывается как одна десятая.
Что такое десятичная запись 79%?
79% в виде дроби равно 79/100. В десятичной системе счисления это выражается как 79/100 = 0,79.
Может ли десятичная запись быть целым числом?
Нет, десятичная запись не может быть целым числом, поскольку все, что находится справа от запятой, меньше 1. Однако десятичное число состоит из двух частей: целой части и дробной части. Дробная часть – это десятичная запись десятичного числа.
Как записывать числа в десятичной системе счисления?
Когда десятичное число выражается с основанием 10 вместе со степенью кратных, мы можем записать десятичную запись в соответствии с экспоненциальным числом. Показатель степени также определяет, в каком направлении должно двигаться десятичное число. Если показатель степени положительный, десятичная точка перемещается вправо. Если показатель степени отрицательный, десятичная точка перемещается влево. Например, 9,31 × 10 5 = 931000,
Если показатель степени положительный, десятичная точка перемещается вправо. Если показатель степени отрицательный, десятичная точка перемещается влево. Например, 9,31 × 10 5 = 931000,
Преобразование научной системы счисления в десятичную систему счисления
Результаты обучения
- Определение десятичной и научной системы счисления
- Преобразование экспоненциального представления в десятичное представление
- Преобразование десятичной записи в экспоненциальную
Определение научного представления
Помните работу с разрядным значением для целых чисел и десятичных дробей? Наша система счисления основана на степенях [латекс]10[/латекс]. Мы используем десятки, сотни, тысячи и так далее. Наши десятичные числа также основаны на степенях десятков — десятых, сотых, тысячных и так далее.
Рассмотрим числа [латекс]4000[/латекс] и [латекс]0,004[/латекс]. Мы знаем, что [латекс]4000[/латекс] означает [латекс]4\умножить на 1000[/латекс], а [латекс]0,004[/латекс] означает [латекс]4\умножить на {\Large\frac{1}{1000} }[/латекс]. {-3}\hfill \end{array}[/latex]
{-3}\hfill \end{array}[/latex]
Когда число записывается как произведение двух чисел, где первый множитель представляет собой число больше или равное единице, но меньше [латекс]10[/латекс], а второй множитель представляет собой степень [латекс] 10[/latex], записанный в экспоненциальной форме, говорят, что он имеет научный формат .
Прежде чем мы сможем преобразовать экспоненциальную и десятичную систему счисления, нам нужно знать разницу между ними. S научная запись используется учеными, математиками и инженерами при работе с очень большими или очень маленькими числами. Используя экспоненциальную запись, большие и маленькие числа можно записать так, чтобы их было легче читать.
Когда число записывается в экспоненциальном представлении, показатель степени говорит вам, является ли член большим или маленьким числом. Положительная экспонента указывает на большое число, а отрицательная экспонента указывает на малое число, которое находится между [латекс]0[/латекс] и [латекс]1[/латекс]. Трудно понять, насколько велики миллиард или триллион. Вот способ, который поможет вам подумать об этом.
Трудно понять, насколько велики миллиард или триллион. Вот способ, который поможет вам подумать об этом.
| Ворд | Сколько тысяч | Номер | 9{n}[/latex], где коэффициент a равен [latex]1\leq{a}<10[/latex], а n – целое число.
| Номер | Научное обозначение? | 9{3}[/латекс] | нет | 10 не < 10 |
Преобразование из десятичной записи в экспоненциальную
Теперь давайте сравним некоторые числа, выраженные как в экспоненциальной записи, так и в стандартной десятичной системе счисления, чтобы понять, как преобразовать из одной формы в другую. Взгляните на таблицы ниже. Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.
Взгляните на таблицы ниже. Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.
Если мы посмотрим, что происходит с десятичной точкой, мы увидим метод простого преобразования десятичной записи в экспоненциальную.
В обоих случаях десятичная дробь была перемещена [latex]3[/latex] разряда, чтобы получить первый множитель, [latex]4[/latex], сам по себе.
Чтобы записать большое число в экспоненциальном представлении, переместите десятичную точку влево, чтобы получить число между [латекс]1[/латекс] и [латекс]10[/латекс]. Поскольку перемещение десятичной точки изменяет значение, вам нужно умножить десятичную дробь на степень [latex]10[/latex], чтобы выражение имело то же значение. 9{5}\end{array}[/latex]
Обратите внимание, что десятичная точка была перемещена на [latex]5[/latex] позиций влево, а показатель степени равен [latex]5[/latex].
В примерах, показанных ниже, мы будем следовать этой общей стратегии преобразования десятичных чисел в экспоненциальное представление:
Преобразование десятичного представления в экспоненциальное представление
- Переместите десятичную точку так, чтобы первый множитель был больше или равен [латекс]1[/латекс], но меньше [латекс]10[/латекс]. 9{-n}[/латекс].
- Чек.
В приведенных ниже примерах мы преобразовываем большие десятичные значения в экспоненциальное представление.
пример
Напишите [латекс]37,000[/латекс] в экспоненциальном представлении.
Решение
| Шаг 1 : Переместите десятичную точку так, чтобы первый множитель был больше или равен [латекс]1[/латекс], но меньше [латекс]10[/латекс]. | |
| 9{4}[/латекс] |
Пример
Запишите следующие числа в экспоненциальном представлении.
- [латекс]920 000 000[/латекс]
- [латекс]10 200 000[/латекс]
- [латекс]100 000 000 000[/латекс]
Показать решение
попробуйте
Теперь давайте рассмотрим преобразование очень маленького десятичного числа в экспоненциальное представление. Чтобы записать небольшое число (от [latex]0[/latex] до [latex]1[/latex]) в экспоненциальном представлении, вы перемещаете десятичную дробь до 9.{-5}\end{array}[/latex]
Вы можете заметить, что десятичная точка была перемещена на пять знаков вправо , пока вы не дошли до числа 4, которое находится между [latex]1[/latex] и [латекс]10 [/латекс]. Показатель степени равен [латекс]−5[/латекс].
пример
Запишите в экспоненциальном представлении: [латекс]0,0052[/латекс]
Показать решение
Пример
Запишите следующие числа в экспоненциальном представлении.
- [латекс]0,0000000000035[/латекс]
- [латекс]0.
 0000000102[/латекс]
0000000102[/латекс] - [латекс]0.00000000000000793[/латекс]
Показать решение
попробуй
В следующем видео представлены примеры преобразования больших и малых чисел из десятичной записи в экспоненциальную.
Преобразование из экспоненциального представления в десятичное
Как мы можем преобразовать экспоненциальное представление в десятичное представление? Давайте посмотрим на два числа, записанные в экспоненциальном представлении, и посмотрим. 9{-4}\hfill \\ 9,12\times 10,000\hfill & & & 9,12\times 0,0001\hfill \\ 91,200\hfill & & & 0,000912\hfill \end{array}[/latex]
Если мы посмотрим на расположение десятичной точки, мы можем увидеть простой способ преобразования числа из экспоненциального представления в десятичную форму.
В обоих случаях десятичная точка переместилась на 4 разряда. Когда показатель степени был положительным, десятичная дробь сдвигалась вправо. Когда показатель степени был отрицательным, десятичная точка перемещалась влево. 9{-8}=\underset{\longleftarrow}{0.00000005.}=0.00000005\end{массив}[/latex]
Для каждой степени f[latex]10[/latex] вы перемещаете десятичную точку на одно место. Будьте осторожны и не увлекайтесь нулями — количество нулей после запятой всегда будет [latex]1[/latex] меньше , чем показатель степени, потому что он занимает одну степень [latex]10[ /latex], чтобы сдвинуть первое число слева от десятичной дроби.
Практикуя преобразование экспоненциальной системы счисления в десятичную форму, мы будем выполнять следующие шаги:
Преобразовать экспоненциальное представление в десятичную форму
- Определить показатель степени [латекс]n[/латекс] для множителя [латекс]10[/латекс].
- Переместите десятичные [латекс]n[/латекс] разрядов, при необходимости добавив нули.

- Если показатель степени положительный, переместите десятичную точку [latex]n[/latex] знаков вправо.
- Если показатель степени отрицательный, переместите десятичную точку [латекс]|n|[/латекс] разрядов влево.
- Чек.
Начнем с преобразования большого числа в экспоненциальном представлении в десятичную форму. 9{6}[/латекс]
Показать решение
Подумай об этом
Чтобы лучше понять взаимосвязь между знаком экспоненты и относительным размером числа, записанного в экспоненциальном представлении, ответьте на следующие вопросы. Вы можете использовать текстовое поле, чтобы написать свои идеи, прежде чем раскрыть решение.
1. Вы пишете число, которое больше, чем [latex]1[/latex] в экспоненциальном представлении. Будет ли ваш показатель положительным или отрицательным?
2. Вы пишете число между [латекс]0[/латекс] и [латекс]1[/латекс] в экспоненциальном представлении. Будет ли ваш показатель положительным или отрицательным?
Будет ли ваш показатель положительным или отрицательным?
3. Какую мощность нужно приложить к [латексу]10[/латексу], чтобы получить результат [латекс]1[/латекс]?
Показать решение
В следующем видео вы увидите, как преобразовать число, записанное в экспоненциальном представлении, в десятичное представление.
Сводка
Большие и маленькие числа можно записывать в экспоненциальном представлении, чтобы их было легче понять. В следующем разделе вы увидите, что выполнение математических операций, таких как умножение и деление больших и малых чисел, упрощается с помощью экспоненциального представления и правил возведения в степень.
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Десятичная запись
Назад на страницу с десятичными дробями Назад к математике 187A страница Назад к математике Страница отдела электронная почта Вопросы и предложения |
Понимание десятичной системы счисления – Математика для торговли: Том 1
Десятичные числа
Мы начали с целых чисел, затем перешли к дробям, а теперь рассмотрим десятичные дроби.
Начнем эту историю с Чада. Теперь Чад не ученик, как люди в первых двух историях, а скорее человек, который несколько лет назад получил свой электронный талон с красной печатью. Затем он основал собственную электротехническую компанию, которой руководит до сих пор.
После нескольких лет владения собственным бизнесом Чад осознал тот факт, что ученики, проходящие через систему, могут воспользоваться некоторыми советами по созданию и управлению компанией, особенно когда речь идет о деньгах. Поскольку у Чада есть некоторый опыт в этом, он решил начать курс для учеников, желающих начать свой собственный бизнес.
Поскольку у Чада есть некоторый опыт в этом, он решил начать курс для учеников, желающих начать свой собственный бизнес.
Имея дело с числами, мы не всегда можем позволить себе роскошь работать только с целыми числами. Если бы мы вернулись к предыдущей главе и рассмотрели дроби, то увидели бы, что дробь представляет собой часть целого числа. Десятичные числа одинаковы в том, что они представляют собой часть целого числа. Разница в том, что десятичные дроби записываются иначе, чем дроби. Десятичная система счисления позволяет нам визуально определить, с какой частью целого числа мы имеем дело.
На первом занятии Чад начинает с разговора о ценах на инструменты и материалы. Он начинает с молотка по цене 12,47 доллара. Обратите внимание, что стоимость молотка составляет не ровно 12 долларов, а чуть больше 12 долларов. Здесь в игру вступают десятичные дроби. Числа после точки (.), также известные как десятичная точка, называются десятичными.
Каждый доллар содержит 100 центов. На самом деле слово «цент» означает 100. Подумайте о веке: в нем 100 лет. Все десятичные дроби основаны на числе 10 и могут называться основанием 10. Эти числа включают 10, 100, 1000, 10000 и так далее. Если бы мы относили это к дробям, то имели бы дело с дробями, знаменатель которых равен 10, 100, 1000, 10000 и так далее.
На самом деле слово «цент» означает 100. Подумайте о веке: в нем 100 лет. Все десятичные дроби основаны на числе 10 и могут называться основанием 10. Эти числа включают 10, 100, 1000, 10000 и так далее. Если бы мы относили это к дробям, то имели бы дело с дробями, знаменатель которых равен 10, 100, 1000, 10000 и так далее.
Несмотря на то, что у нас есть только два десятичных знака, о которых нужно беспокоиться, когда мы имеем дело с деньгами, мы можем продолжать десятичную дробь столько, сколько захотим. Например, число пи (3,14 или π) на самом деле продолжается вечно и не имеет конца. Проверьте это:
Это просто показывает число пи с точностью до первых нескольких десятков знаков после запятой, но есть и другие числа.
Что нам нужно сделать, так это получить представление о десятичной системе и о том, как она работает. Взгляните на следующий номер.
Еще в главе 1 мы имели дело с разрядной системой целых чисел (см. «Система разрядных значений»). Десятичные числа следуют аналогичному шаблону, который начинается с первого числа справа от десятичной дроби. В нашем примере 5,9, шаблон будет начинаться с 9.
В нашем примере 5,9, шаблон будет начинаться с 9.
Назад в Чад. В лекции Чад подчеркивает важность подробного учета при ведении собственного бизнеса. Теперь мы все знаем, что в одном долларе 100 центов, и важно убедиться, что вы правильно используете центы при учете. Округление в большую или меньшую сторону до ближайшего доллара и «достаточно близкое значение» не помогут. Точные суммы в долларах и центах важны, поэтому Чад имеет дело с числами, которые идут до второго десятичного знака. Взгляните на число ниже (которое, как мы могли бы предположить, представляет собой доллары и центы), чтобы увидеть, в каких местах стоят цифры до и после десятичного знака. Давайте возьмем пример с молотком в размере 12,47 доллара.
Думайте о 0,47, как о деньгах. Это будет представлять 47 центов из возможных 100 центов. Что представляет собой 4 сама по себе? Что ж, в пересчете на доллар это 40 центов, или 40 из 100. Все это хорошо, за исключением того факта, что 4 на самом деле находится на так называемом десятом месте. Число указывает на то, что у нас есть 4 из 10 возможных частей. Десятое место можно рассматривать как разделенное на 10 частей, и у нас есть 4 полных части.
Число указывает на то, что у нас есть 4 из 10 возможных частей. Десятое место можно рассматривать как разделенное на 10 частей, и у нас есть 4 полных части.
Следующий шаг — визуализировать, что такое 7. 7 стоит на сотом месте, значит, у нас 7 из 100 возможных.
Идея состоит в том, чтобы взять каждую коробку и разбить ее на еще более мелкие части. Первые четыре коробки уже окрашены в серый цвет, потому что они представляют собой 4 полных коробки или 40 центов. Далее мы берем пятую коробку и разбиваем ее на 10 частей.
Вопрос : Если бы мы разбили все 10 ящиков на 10 маленьких частей, сколько бы у нас было?
[латекс]\БОЛЬШОЙ10\times10=100[/латекс]
В итоге у нас будет 100 деталей, или мы можем рассматривать это как 100 центов. Теперь выньте пятую коробку, разделите ее на 10 частей и заполните 7 из них.
Представьте, что каждый из исходных 10 ящиков разделен на 10 четных частей. Что еще более безумно, так это то, что мы могли бы затем взять каждую из этих 100 коробок и разделить их еще на 10 частей каждую. Это оставит нас с числом, которое приведет нас к тысячным разрядам, потому что мы разделим все на 1000 частей. Что мы действительно делаем с десятичными дробями, так это берем целое число и разбиваем его на части, как дроби. На самом деле, если бы мы смотрели на десятичные дроби как на дроби, мы бы думали об этом так:
Это оставит нас с числом, которое приведет нас к тысячным разрядам, потому что мы разделим все на 1000 частей. Что мы действительно делаем с десятичными дробями, так это берем целое число и разбиваем его на части, как дроби. На самом деле, если бы мы смотрели на десятичные дроби как на дроби, мы бы думали об этом так:
[латекс]\БОЛЬШОЙ\dfrac{1}{10}=0,1[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{1}{100}=0,01[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{1}{1000}=0,001[/латекс]
Теперь, когда у нас есть первые три цифры после запятой, давайте продвинемся дальше. Взгляните на число ниже. Слева от запятой стоит целое число, а справа — десятичная дробь или часть целого числа.
[латекс]\БОЛЬШОЙ123.456789[/латекс]
Примечание: 1, 2 и 3 являются частью целого числа, а 4, 5, 6, 7, 8 и 9все являются частью десятичной дроби. Используя позиционную систему как для целых чисел, так и для десятичных, мы получим следующее:
- 1 = разряд сотен
- 2 = разряд десятков
- 3 = разряд единиц
- (.
 ) = десятичное число
) = десятичное число - 4 = десятое место
- 5 = сотые доли
- 6 = разряд тысячных
- 7 = разряд десятитысячных
- 8 = разряд сотен тысячных
- 9 = разряд миллионных
Давайте рассмотрим пару быстрых примеров, просто чтобы убедиться, что мы все на одной странице.
В приведенном ниже числе укажите, какая цифра стоит в тысячном разряде.
[latex]\LARGE57.29652[/latex]
Проще всего это сделать, выписав число, а затем, начиная слева, указать разрядное значение каждой из цифр.
- 5 = разряд десятков
- 7 = разряд единиц
- 2 = десятое место
- 9 = сотые доли
- 6 = разряд тысячных
- 5 = разряд десятитысячных
- 2 = разряд сотен тысячных
6 стоит на тысячном разряде.
Попробуйте другой пример.
В приведенном ниже числе укажите, какая цифра стоит в стотысячном разряде.
[латекс]\LARGE369.246813[/латекс]
Еще раз, чтобы найти ответ, запишите число, а затем укажите разрядное значение каждой из цифр.
- 3 = разряд сотен
- 6 = разряд десятков
- 9 = разряд единиц
- 2 = десятое место
- 4 = сотые доли
- 6 = разряд тысячных
- 8 = разряд десятитысячных
- 1 = разряд сотен тысячных
- 3 = разряд миллионных
1 стоит на стотысячном разряде.
Преобразователь научной записи
Базовый калькулятор
Конвертер научных обозначений
введите число или экспоненциальное представление
Операнд 1
Ответ:
= 3,456 × 10 11
экспоненциальное обозначение
= 3,456e11
научная запись
= 345,6 × 10 9
инженерная запись
миллиардов; Префикс Giga- (g)
= 3,456 × 10 11
Стандартная форма
11
Порядок величины
для научных и стандартных форм
= 345600000000
(реальное число)
= Три Сто на 55600000000. сто миллионов
сто миллионов
словоформа
Чем может быть лучше этот калькулятор?
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Использование калькулятора
Преобразование числа в экспоненциальную запись, электронную запись, инженерную запись, стандартную форму и действительные числа и обратно. Введите число или десятичное число или экспоненциальное представление, и калькулятор преобразует его в экспоненциальное представление, электронное обозначение, инженерное обозначение, стандартную форму и формат словесной формы. 9б где a — число или десятичное число, такое что абсолютное значение a больше или равно единице и меньше десяти или 1 ≤ | и | < 10. b – степень числа 10, необходимая для того, чтобы научная запись была математически эквивалентна исходному числу.
b – степень числа 10, необходимая для того, чтобы научная запись была математически эквивалентна исходному числу.
- Перемещайте десятичную точку в вашем номере, пока не останется только одна ненулевая цифра слева от десятичной точки. Полученное десятичное число равно и .
- Подсчитайте, на сколько знаков вы передвинули десятичную точку. Этот номер b .
- Если вы переместите десятичную запятую влево b будет положительным.
Если вы переместите десятичную запятую вправо b будет отрицательным.
Если не нужно было перемещать десятичную дробь b = 0 . - Напишите свой номер научной записи как 9b и читать как « a умножить на 10 в степени b «.
- Удалять конечные 0, только если они изначально были слева от десятичной точки.

Пример: преобразование 357 096 в экспоненциальное представление
- Переместите десятичную дробь на 5 знаков влево, чтобы получить 3,57096
- а = 3,57096
- Мы переместили десятичную дробь влево, чтобы b было положительным 9-4 = 3,456 x 0,0001 = 0,0003456
- часть числа , называемая «с» (число больше или равно 1, но меньше 10)
- число с основанием 10, возведенным в целую степень .
- Если число находится в диапазоне от 0 до 1, то показатель степени по основанию 10 отрицательный.
- Если число больше 1, показатель степени по основанию 10 положительный.
- Конечное положение исходной десятичной точки должно быть прямо справа от первого ненулевого числа .
- Здесь вы получите число, называемое «c». Его значение должно быть больше или равно 1, но меньше 10.
- Когда десятичная дробь смещается влево , показатель степени по основанию 10 должен быть положительным .
- Когда десятичная дробь смещается вправо , показатель степени основания 10 должен быть равен 9n}
Примеры записи десятичных чисел в экспоненциальном представлении
Пример 1 : Перепишите заданное десятичное число 5 800 в экспоненциальном представлении.
Начнем с определения исходного положения десятичной точки и ее нового положения.

Теперь мы перемещаем десятичную точку из начальной точки в конечную точку, подсчитывая количество знаков после запятой.
- Помните вышеприведенное правило, если десятичная дробь перемещается влево , показатель степени по основанию 10 равен положительному .
Получается, что наше значение «c» равно c = 5,8, а степень числа 10 равна 10 3 . Объединив их в требуемом формате, мы получим окончательный ответ:
. Всегда помните, что значение «c» всегда имеет десятичную точку сразу после первой цифры , что и имеет место здесь. Большой!
Пример 2 : Переписать данное десятичное число 1 730 000 в экспоненциальном представлении.
Начните с определения начальной десятичной точки и того, куда она идет.
Похоже, мы собираемся передвинуть десятичную дробь влево. Помните, что такой тип движения будет иметь положительный показатель степени для основания 10.

Коэффициент или значение «c» равно c = 1,73, а степень числа 10 равна 10 6 . Это должно дать нам окончательный ответ
Пример 3 : Перепишите данное десятичное число 33 335 000 000 000 в экспоненциальном представлении.
Начальная десятичная точка находится справа. Нам нужно переместить его на влево , пока мы не получим десятичное число от 1 до 10.
Перемещение десятичного числа справа налево означает, что степень 10 будет иметь положительное целое число.
Значение коэффициента равно c = 3,3335, а степень числа 10 становится равной 10 13 . Следовательно, окончательный ответ нашей научной системы обозначений равен 9.0003
Пример 4 : Перепишите данное десятичное число 0,0009 в экспоненциальном представлении.
Очевидно, что исходная десятичная точка стоит слева от отличной от нуля цифры.
 Мы переместим десятичную дробь к вправо . Вышеприведенное правило гласит, что
Мы переместим десятичную дробь к вправо . Вышеприведенное правило гласит, что- Когда десятичная дробь смещается на вправо , показатель степени основания 10 должен быть минус .
Перемещение десятичной точки вправо должно дать отрицательный показатель для основания 10 .
Значение c равно c = 9, а степень числа 10 равна 10 -4 . Наш окончательный ответ в научной записи должен быть
Пример 5 : Перепишите данное десятичное число 0,00000000086 в экспоненциальной записи.
Может быть, вы можете предсказать, что, поскольку заданное десятичное число находится между 0 и 1, у нас должна быть научная запись с отрицательной степенью. Во-первых, определите начальную десятичную точку и куда она идет.
Давайте продолжим и переместим исходную десятичную запятую вправо, пока десятичная запятая не окажется на справа от первой ненулевой цифры , которая равна 8.

Дополнительные ресурсы
См. Калькулятор научной нотации для сложения, вычитания, умножения и деления чисел в научной нотации или E-нотации.
Для округления значащих цифр используйте Калькулятор значимых цифр.
Чтобы увидеть, насколько стандартная форма похожа на научное обозначение, посетите Калькулятор стандартной формы.
Если вам нужен научный калькулятор, см. наши ресурсы на научные калькуляторы.
Подпишитесь на CalculatorSoup:
Запись чисел в экспоненциальном представлении
Поиск Научное обозначение позволяет выразить очень маленькое или очень большое число в компактной форме . Основные компоненты числа, записанного в экспоненциальном представлении, следующие:
Основные компоненты числа, записанного в экспоненциальном представлении, следующие:
Итак, в двух словах, экспоненциальное представление состоит из
, умноженное на
Ниже приведены распространенные числа, записанные в экспоненциальном представлении. Попробуйте посмотреть, сможете ли вы найти какую-то закономерность.
Краткий обзор:
Теперь давайте поговорим об общих шагах, связанных с преобразованием десятичного числа в научное представление.
ШАГ 1 : Определите начальное положение исходной десятичной точки.
ШАГ 2 : Определите конечное местоположение или «назначение» исходной десятичной точки.
ШАГ 3 : Переместите исходную десятичную точку в ее конечное положение.