Решение
Вычисление матрицы $D$ начнем с нахождения результата произведения $AB$. Матрицы $A$ и $B$ можно перемножать, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. Обозначим $F=AB$. При этом матрица $F$ будет иметь три столбца и три строки, т.е. будет квадратной (если этот вывод кажется неочевидным, посмотрите описание умножения матриц в первой части этой темы). Найдем матрицу $F$, вычислив все её элементы:
$$
F=A\cdot B=\left(\begin{array} {cccc}
1 & 0 & -1 & 2 \\
3 & -2 & 5 & 0 \\
-1 & 4 & -3 & 6
\end{array} \right)\cdot \left(\begin{array} {ccc}
-9 & 1 & 0 \\
2 & -1 & 4 \\
0 & -2 & 3 \\
1 & 5 & 0
\end{array} \right)\\
\begin{aligned}
& f_{11}=1\cdot (-9)+0\cdot 2+(-1)\cdot 0+2\cdot 1=-7; \\
& f_{12}=1\cdot 1+0\cdot (-1)+(-1)\cdot (-2)+2\cdot 5=13; \\
& f_{13}=1\cdot 0+0\cdot 4+(-1)\cdot 3+2\cdot 0=-3;\\ \\
& f_{21}=3\cdot (-9)+(-2)\cdot 2+5\cdot 0+0\cdot 1=-31;\\
& f_{22}=3\cdot 1+(-2)\cdot (-1)+5\cdot (-2)+0\cdot 5=-5;\\
& f_{23}=3\cdot 0+(-2)\cdot 4+5\cdot 3+0\cdot 0=7;\\ \\
& f_{31}=-1\cdot (-9)+4\cdot 2+(-3)\cdot 0+6\cdot 1=23; \\
& f_{32}=-1\cdot 1+4\cdot (-1)+(-3)\cdot (-2)+6\cdot 5=31;\\
& f_{33}=-1\cdot 0+4\cdot 4+(-3)\cdot 3+6\cdot 0=7.
Умножим матрицы в правой части равенства на соответствующие числа (т.е. на 2, 3 и 7):
$$ 2\cdot \left(\begin{array} {ccc} -7 & 13 & -3 \\ -31 & -5 & 7 \\ 23 & 31 & 7 \end{array} \right)-3\cdot \left(\begin{array} {ccc} -5 & 10 & 3 \\ -20 & 12 & -15 \\ 13 & 9 & 8 \end{array} \right)+7\cdot \left(\begin{array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)=\\= \left(\begin{array} {ccc} -14 & 26 & -6 \\ -62 & -10 & 14 \\ 46 & 62 & 14 \end{array} \right)-\left(\begin{array} {ccc} -15 & 30 & 9 \\ -60 & 36 & -45 \\ 39 & 27 & 24 \end{array} \right)+\left(\begin{array} {ccc} 7 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 7 \end{array} \right) $$
Выполним последние действия: вычитание и сложение:
$$
\left(\begin{array} {ccc}
-14 & 26 & -6 \\
-62 & -10 & 14 \\
46 & 62 & 14
\end{array} \right)-\left(\begin{array} {ccc}
-15 & 30 & 9 \\
-60 & 36 & -45 \\
39 & 27 & 24
\end{array} \right)+\left(\begin{array} {ccc}
7 & 0 & 0 \\
0 & 7 & 0 \\
0 & 0 & 7
\end{array} \right)=\\
=\left(\begin{array} {ccc}
-14-(-15)+7 & 26-30+0 & -6-9+0 \\
-62-(-60)+0 & -10-36+7 & 14-(-45)+0 \\
46-39+0 & 62-27+0 & 14-24+7
\end{array} \right)=
\left(\begin{array} {ccc}
8 & -4 & -15 \\
-2 & -39 & 59 \\
7 & 35 & -3
\end{array} \right).
2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right).
Ответ: $f(A)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right)$.
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
2.4. Возведение матрицы в целую положительную степень
Операция возведения квадратной матрицы в степень определяется в виде:
.
По определению полагают . Легко показать, что .
Замечание 1.3. Возведение в степень матрицы может привести к нулевой матрице.
Замечание 1.4. Операция возведения в степень определена только для квадратных матриц.
Пример выполнения задания:Найдите значение матричного многочлена
.
Решение:
Ответ: .
Для самостоятельного решения:
а) Найдите матрицу .
1. ; 2. ; 3. .
б) Найдите значение матричного многочлена .
1. ; 2. ;
3. . 4. .
2.5. Транспонирование матрицы
Транспонирование – это замена строк столбцами. Например, пусть дана матрица А размерностью :
.
Если в матрице А поменять местами строки и столбцы, то получится матрица, транспонированная к данной, обозначаемая :
.
Приведем основные свойства операции транспонирования
1. Двойное транспонирование возвращает исходную матрицу: .
2. Транспонирование суммы матриц эквивалентно сумме транспонирования слагаемых: .
3. Транспонирование
произведения двух матриц эквивалентно
произведению транспонированных матриц,
взятых в обратном порядке: .
4. Произведение матрицы на свою транспонированную или всегда имеет результатом симметричную квадратную матрицу.
5. Если матрица А – квадратная, то значение ее определителя не зависит от транспонирования: .
Примеры выполнения заданий:
Задача 1. Транспонируйте матрицу .
Решение:
Записывая первую и вторую строки матрицы А как первый и, соответственно, второй столбец матрицы , получим матрицу .
Ответ: .
Задача 2. Транспонируйте матрицу .
Решение:
Так как у матрицы А две строки и три столбца, то у матрицы будет три строки и два столбца: .
Ответ: .
Для самостоятельного решения:
а) Найдите матрицу
1. ; 2. ;
3.
; 4.
;
5. .
б) Найдите произведение матриц и .
1. ; 2. ;
3. ; 4. .
2.6. Вычисление обратной матрицы
Определение. Матрица называется обратной для квадратной матрицы А, если .
Определение. Матрица называется невырожденной, если ее определитель не равен нулю.
Квадратная матрица А, определитель которой не равен нулю, имеет единственную обратную матрицу
, где матрицы А. алгебраическое дополнение к элементу матрицы А.
Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)
1. Найти определитель
матрицы А. Если определитель отличен
от нуля, то матрица имеет обратную
матрицу.
2. Поменять местами столбцы матрицы (транспонировать матрицу) А.
3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы А его алгебраическим дополнением: , – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i-ой строки и j-го столбца.
4. Вычисляем обратную матрицу .
5. Проверить правильность вычисления обратной матрицы по формуле: .
Примеры выполнения заданий:
Задача 1. Найти матрицу, обратную к матрице А, если дана матрица .
Решение: Применим алгоритм нахождения обратной матрицы.
1. Найти определитель матрицы А. Если определитель отличен от нуля, то матрица имеет обратную матрицу.
Матрица имеет
обратную матрицу, так как .
2. Найдем матрицу , транспонированную к матрице А: .
3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы
.
4. Вычисляем обратную матрицу .
5. Проверим правильность вычисления обратной матрицы по формуле:
.
Ответ:
Задача 2. Найдите матрицу, обратную к данной матрице .
1. Найдем .
2. Найдем матрицу :___________________________.
3. Найдем алгебраические
дополнения элементов матрицы
:___________________
.
4. Вычисляем обратную матрицу :
_____________________________________________________________________________
.
5. Проверим правильность вычисления обратной матрицы по формуле:
______________________________________________________________________________.
Ответ: .
Элементарными преобразованиями строк (столбцов) матрицы называются:
а) умножение i-ой строки (столбца) матрицы на число ;
б) прибавление к i-ой строке (столбцу) j-ой строки (столбца), умноженной на ;
в) перестановка i-ой и j-ой строк (столбцов) матрицы.
Возведение матрицы в степень | Brilliant Math & Science Wiki
Возводить в степень диагональные матрицы проще всего. Все остальные матрицы могут быть факторизованы, чтобы иметь диагональный множитель, что делает это полезным.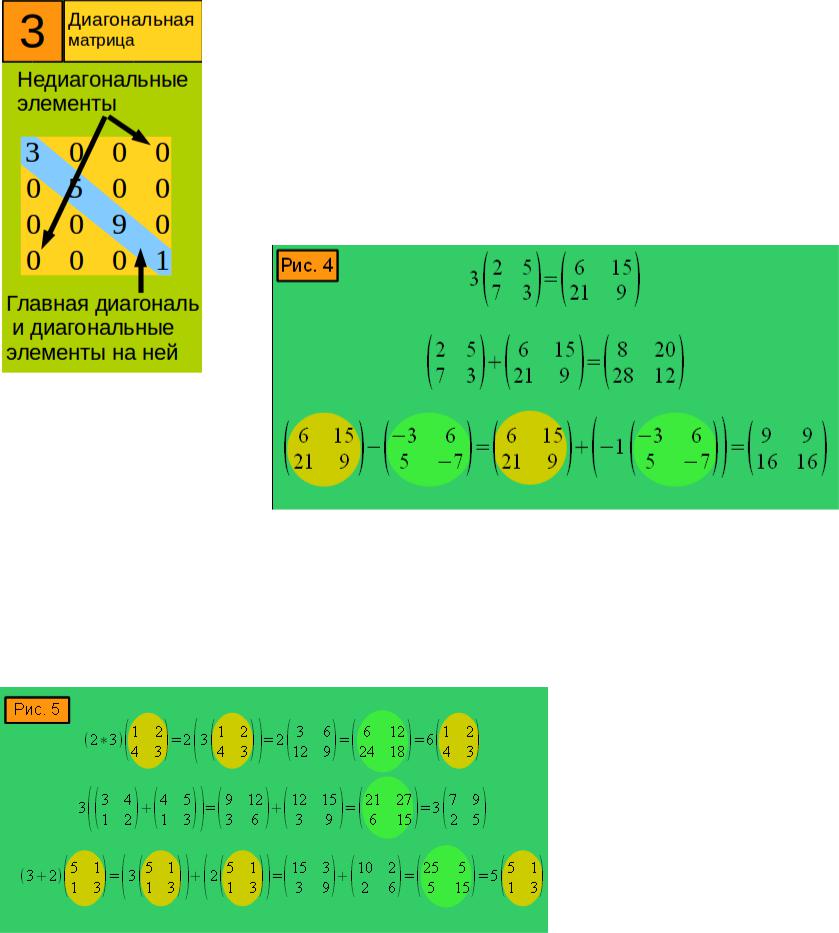
Если AAA является диагональной матрицей (т.е. все числа не на диагонали равны 0):
A=[a1,10⋯⋯00a2,2⋯⋯0⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯00⋯⋯an,n],A= \begin{bmatrix} a_{1,1}&0&\cdots&\ cdots&0\\0&a_{2,2}&\cdots&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ \cdots& \cdots&\cdots&\cdots&\cdots\\0&0&\cdots&\cdots&a_{n,n} \end{bmatrix},A=⎣⎢⎢⎢⎢⎡a1,10⋯⋯00a2,2⋯⋯0⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯00⋯⋯an,n ⎦⎥⎥⎥⎥⎤, 9{tr(A)}det(eA)=etr(A) для диагональной матрицы AAA, где tr(A)tr(A)tr(A) — след матрицы или сумма по ее диагонали.
Используйте тот факт, что определитель диагональной матрицы равен
∣a1,10⋯⋯00a2,2⋯⋯0⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯00⋯⋯an,n∣=a1,1a2,2⋯an,n. \begin{vmatrix} a_{1,1}&0&\cdots&\cdots&0\\0&a_{2,2}&\cdots&\cdots&0\\ \cdots&\cdots&\cdots&\cdots&\cdots\\ \cdots& \cdots&\cdots&\ cdots&\cdots\\0&0&\cdots&\cdots&a_{n,n}\end{vmatrix}=a_{1,1}a_{2,2}\cdots a_{n,n}.∣∣∣∣∣∣∣∣ ∣∣a1,10⋯⋯00a2,2⋯⋯0⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯00⋯⋯an,n∣∣∣∣∣∣∣∣∣∣ =a1,1a2,2⋯an,n. 92-5\лямбда+6&=0\\ \лямбда&= 2,3. \end{выровнено}det(A−λI)=∣∣∣∣1−λ2−14−λ∣∣∣∣=0⟹(1−λ)(4−λ)+2λ2−5λ+6λ =0=0=2,3.
Находим собственные векторы для обоих собственных значений:
- λ=2 ⟹ [−1−122][x1x2]=0.\lambda=2\ подразумевает \begin{bmatrix} -1&-1\\2&2\end{bmatrix}\begin{bmatrix}x_1\\x_2 \end{bmatrix}=0.λ=2⟹[−12−12][x1x2]=0. Одно решение, которое мы выберем, это [1−1]. \begin{bmatrix}1\\-1\end{bmatrix}.[1−1].
- λ=3 ⟹ [−2−121][x1x2]=0.\lambda=3\ подразумевает \begin{bmatrix} -2&-1\\2&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\ end{bmatrix}=0.λ=3⟹[−22−11][x1x2]=0. Одно решение, которое мы выберем, это [−12]\begin{bmatrix}-1\\2\end{bmatrix}[−12]. 93\конец{bматрица}, \end{aligned}eA=[1−1−12][e200e3][2111]=[1–1−12][2e2e3e2e3]=[2e2–e3 −2e2+2e3e2−e3−e2+2e3],
и это ответ. □_\квадрат□
Как было сказано во введении, матрицы действительно можно использовать для решения дифференциальных уравнений. Ниже приведены некоторые примеры:
Дана система дифференциальных уравнений
{dx1dt=x2dx2dt=x1,\begin{case} \dfrac{dx_1}{dt}=x_2\\ \dfrac{dx_2}{dt}=x_1,\end{case}⎩⎪⎨⎪⎧dtdx1 =x2dtdx2=x1,
решить для всех переменных через t.
Хитрость заключается в том, чтобы рассмотреть матрицу U=[x1x2]U=\begin{bmatrix}x_1\\x_2\end{bmatrix}U=[x1x2]. Итак,
dUdt=[x1′x2′]=[x2x1]=[0110][x1x2] ⟹ dUdt=[0110]U. \dfrac{dU}{dt}=\begin{bmatrix}x_1’\\x_2’\end{bmatrix}=\begin{bmatrix}x_2\\x_1\end{bmatrix}=\begin{bmatrix}0&1\\1&0 \end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix}\имплициты \dfrac{dU}{dt}=\begin{bmatrix}0&1\\1&0\end{bmatrix}U.dtdU=[ x1′x2′]=[x2x1]=[0110][x1x2]⟹dtdU=[0110]U. 9{-t}\end{bmatrix}U_0.\ _\squareU=21[et+e-tet-e-tet-e-tet+e-t]U0. □
t.t.Это было утомительно. В случае двух систем матрицы часто не являются оптимальным путем. Но по мере роста систем матрицы становятся лучшими решениями. В следующем примере возникает проблема с начальным значением.
Дана система дифференциальных уравнений
{dx1dt=x2dx2dt=x1,\begin{case} \dfrac{dx_1}{dt}=x_2\\ \dfrac{dx_2}{dt}=x_1,\end{case}⎩⎪⎨⎪⎧dtdx1 =x2dtdx2=x1, 9{-t}\end{bmatrix}, \end{aligned}U=21[et+e-tet-e-tet-e-tet+e-t][10]=21[et+e-tet-e-t ],
, и это действительно удовлетворяет уравнениям и граничным условиям.
□_\квадрат□Matrix Exponentiation · USACO Guide
| Resources | ||||
|---|---|---|---|---|
| CP2 | 5.9 — Powers of a Square Matrix | |||
| CPH | 23 — Matrices | |||
| CF | Errichto — Matrix Exponentiation | video + problemset | ||
| CF | Cool tricks using Matrix Exponential | interesting applications of mat exp | ||
| Mostafa | Matrix Power Applications | powerpoint возведения матрицы в степень | ||
