Внутреннее сопряжение дуг двух окружностей: 3.5. Сопряжение двух окружностей

Построение сопряжений. — Студопедия

Поделись  

Сопряжением называется плавный переход от одной линии к другой. Плавный переход может быть выполнен как с помощью циркульных линий
(дуг окружностей), так и с помощью лекальных кривых (дуг эллипса, параболы или гиперболы). Мы будем рассматривать только случаи сопряжений с помощью дуг окружностей. Из всего многообразия сопряжений различных линий можно выделить такие основные виды сопряжений: сопряжение двух различно расположенных прямых линий с помощью дуги окружности, сопряжение прямой линии с дугой окружности, построение общей касательной к двум окружностям, сопряжение двух окружностей третьей. Любой вид сопряжений следует выполнять в такой последовательности:

– находят центр дуги сопряжения,

– находят точки сопряжения,

– заданным радиусом проводят дугу сопряжения.

 

Различные виды сопряжений приведены в таблице 2:

Таблица 2

 

Графическое построение сопряжений	Краткое объяснение к построению
Сопряжение пересекающихся прямых дугой заданного радиуса
	Провести прямые, параллельные сторонам угла на расстоянии R. Из точки О, взаимного пересечения этих прямых, опустив перпендикуляры на стороны угла, получим точки сопряжения 1 и 2. Радиусом R провести дугу сопряжения между точками 1 и 2.
Сопряжение окружности и прямой с помощью дуги заданного радиуса
	На расстоянии R провести прямую, параллельную заданной прямой, а из центра О1 радиусом R+R1 – дугу окружности. Точка О – центр дуги сопряжения. Точку 2 получим на перпендикуляре, опущенном из точки О на заданную прямую, а точку 1- на пересечении прямой ОО1 и окружности радиуса R.

 

Продолжение таблицы 2

 

Сопряжение дуг двух окружностей прямой линией
	Из точки О провести вспомогательную окружность радиусом R-R1. Отрезок ОО1 разделить пополам и из точки О2 провести окружность радиусом 0,5 ОО1.Эта окружность пересекает вспомогательную в точке К0.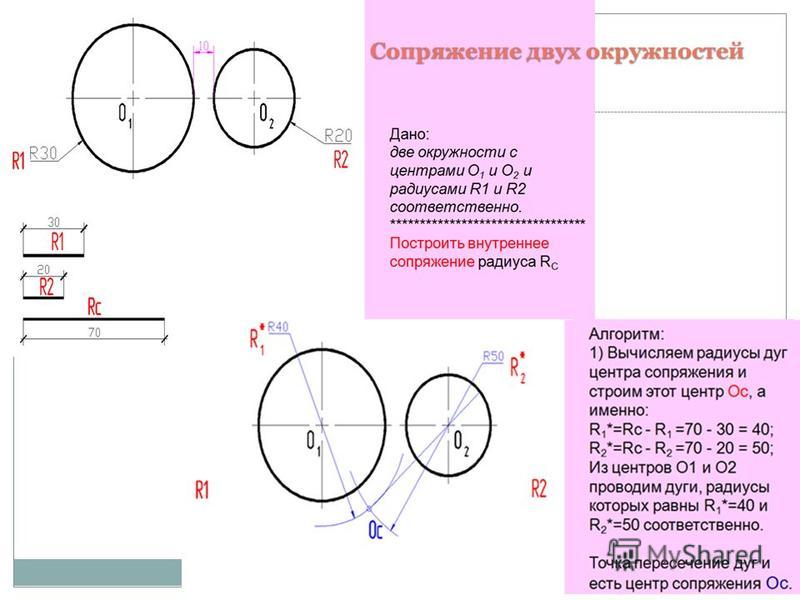 Соединив точку К0 с точкой О1 получим направление общей касательной. Точки касания К и К1 находим на пересечении перпендикуляров из точек О и О1 с заданными окружностями.
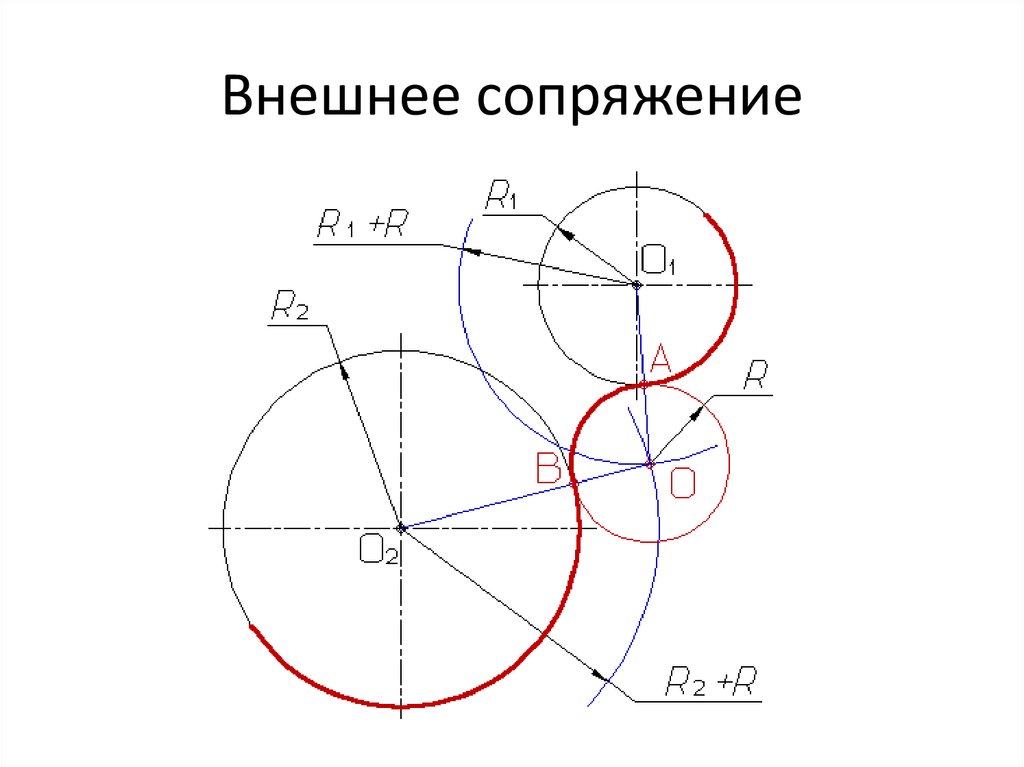
Сопряжение дуг двух окружностей дугой заданного радиуса (внешнее сопряжение)
	Из центров О1 и О2 провести дуги радиусов R+R1 и R+R2. При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединить точки О1 и О2 с точкой О. Точки К и К1 являются точками сопряжения. Между точками К и К1 провести дугу сопряжения радиусом R.

 

Продолжение таблицы 2

 

 

Сопряжение дуг двух окружностей дугой заданного радиуса (внутреннее сопряжение)
	Из центров О1 и О2 провести дуги радиусов R-R1 и R-R2.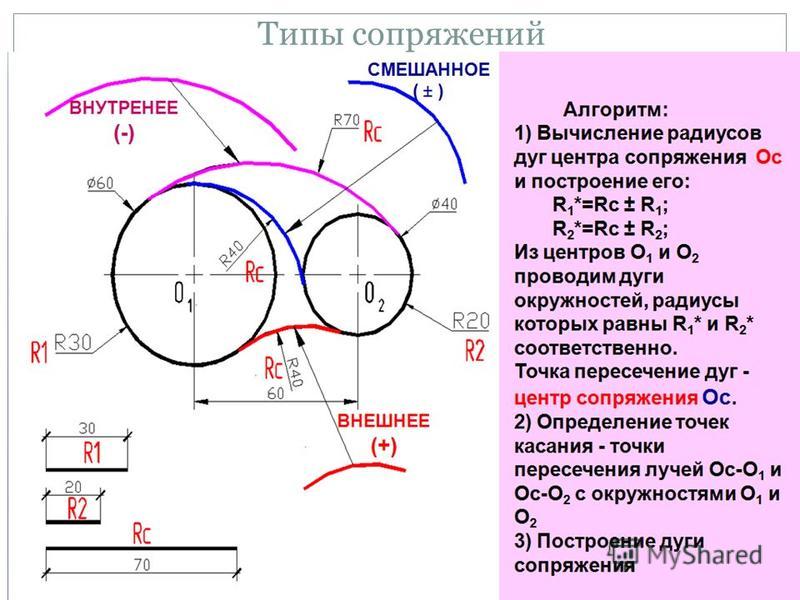 При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединить точки О1 и О2 с точкой О до пересечения с заданными окружностями. Точки К и К1 – точки сопряжения. Между точками К и К1 радиусом R проводим дугу сопряжения.
Сопряжение дуг двух окружностей дугой заданного радиуса (смешанное сопряжение)
	Из центров О1 и О2 провести дуги радиусов R-R1 и R+R2 . При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединяем точки О1 и О2 с точкой О до пересечения с заданными окружностями. Точки 1 и 2 – точки сопряжения. Между точками 1 и 2 радиусом R проводим дугу сопряжения.

 

 

 



Сопряжение линий с примерами и образцами выполнения (Инженерная графика

Содержание:

1. Сопряжение двух сторон угла дугой окружности и заданного радиуса
2. Сопряжение прямой с дугой окружности
3. Сопряжение дуги с дугой
4. Построение внешнего сопряжения
5. Построение смешанного сопряжения

Рис.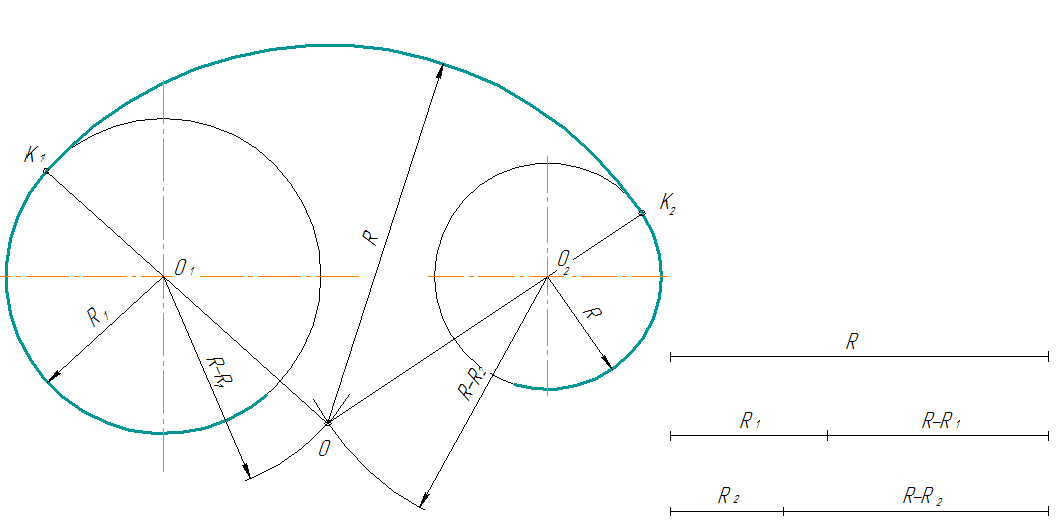 60

При вычерчивании деталей, контуры очертаний которых состоят из прямых линий и дуг окруж­ностей с плавными переходами от одной линии в другую, часто выполняют сопряжения. Сопряже­нием называется плавный переход одной линии в другую. На рис. 60 показаны примеры примене­ния сопряжений.

Контур рычага (рис. 60, а) состоит из отдель­ных линий, плавно переходящих одна в другую, например, в точках А, виден плавный переход от дуги окружности к прямой линии, а в точках В, В₁ — от дуги одной окружности к дуге другой окружности (рис. 60, б). На рис. 60, в изображен двурогий крюк. На чертеже контура крюка (рис. 60, г) в точке А виден плавный переход от дуги окружности (200) к прямой линии, а в точке В — от дуги окружности (R 460) к дуге окружности (R260).

Для точного и правильного выполнения черте­жей необходимо уметь выполнять построения сопряжений, которые основаны на двух поло­жениях.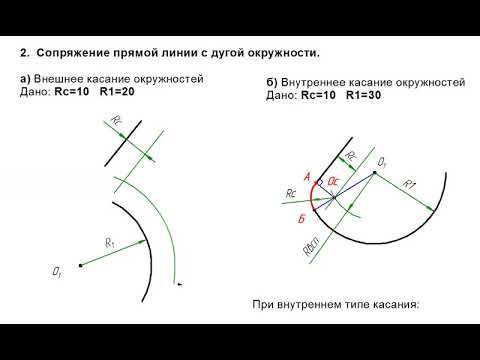

1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к пря­мой, восставленном из точки сопряжения (рис. 62,

а).

2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку со­пряжения (рис. 61, б).

Рис. 61

Сопряжение двух сторон угла дугой окружности и заданного радиуса

При выполнении чертежей деталей, показан­ных на рис. 62, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 62, а выполнено по­строение сопряжения сторон острого угла дугой, на рис. 62, в — тупого угла, на рис. 62, д — пря­мого.

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса Rвыполняют следующим образом (рис. 62, а и в).

Параллельно сторонам угла на расстоянии, равном радиусу дуги R,проводят две вспомога­тельные прямые линии.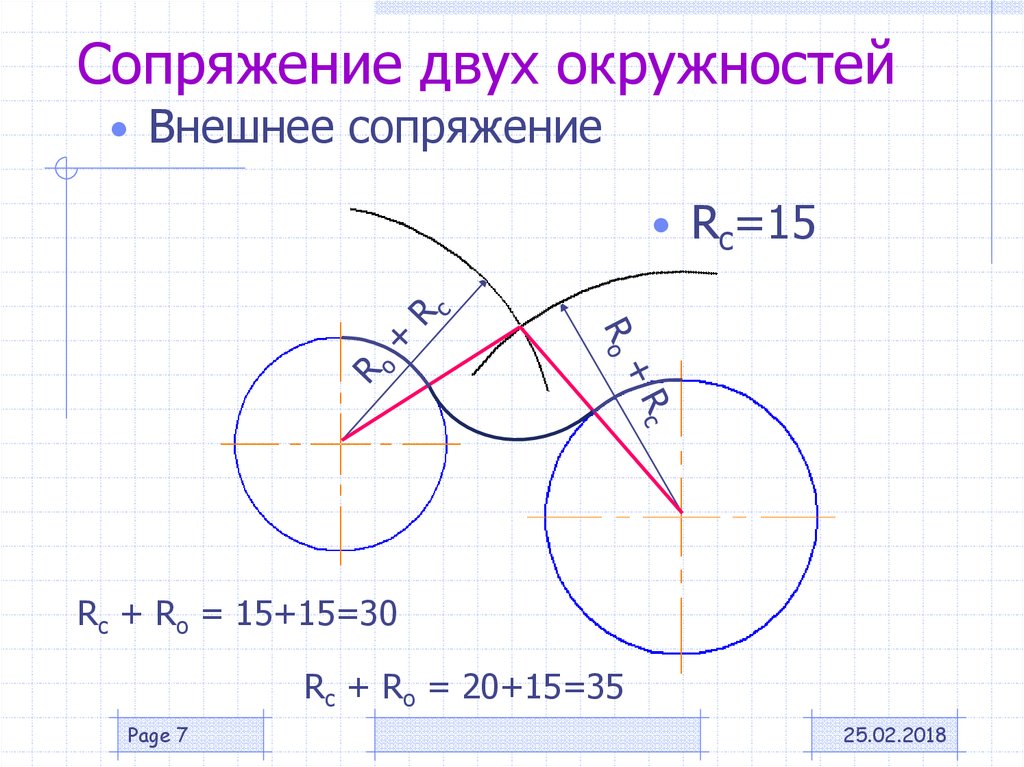 Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла. Дугу заканчивают в точках сопряжения п и п₁ которые являются основаниями перпендику­ляров, опущенных из центра О на стороны утла.

При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рис. 62, д). Из вершины угла А проводят дугу радиусом R,равным радиусу сопряжения. На сторонах утла получают точки сопряжения п и п₁. Из этих точек, как из цен­тров, проводят дуги радиусом Rдо взаимного пересечения в точке О, являющейся центром со­пряжения. Из центра О описывают дугу сопряже­ния.

Рис. 62

Сопряжение прямой с дугой окружности

Сопряжение прямой с дугой окружности может быть выполнено с помощью дуги с внутренним касанием (рис.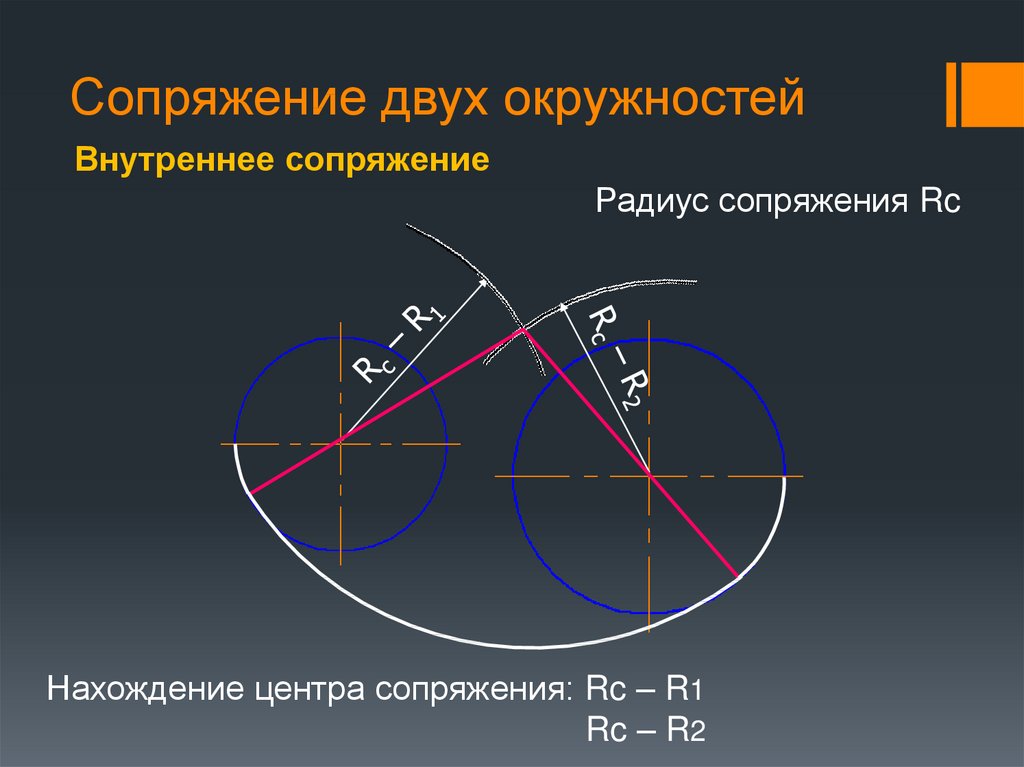 63, в) и дуги с внешним касанием (рис. 63, а).

На рис. 63, а показано сопряжение дуги окруж­ности радиусом Rи прямой АВ дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую AB. Параллельно заданной прямой на расстоянии, равном радиусу r (радиус сопрягаю­щей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сум­ме радиусов R и г, до пересечения ее с прямой ab в точке O₁. Точка О₁ является центром дуги со­пряжения.

Точку сопряжения с находят на пересечении прямой ОO₁ с дугой окружности радиуса R. Точка сопряжения c₁ является основанием перпендику­ляра, опущенного из центра O₁ на данную пря­мую АB. С помощью аналогичных построений могут быть найдены точки О₂c₂c₃

На рис.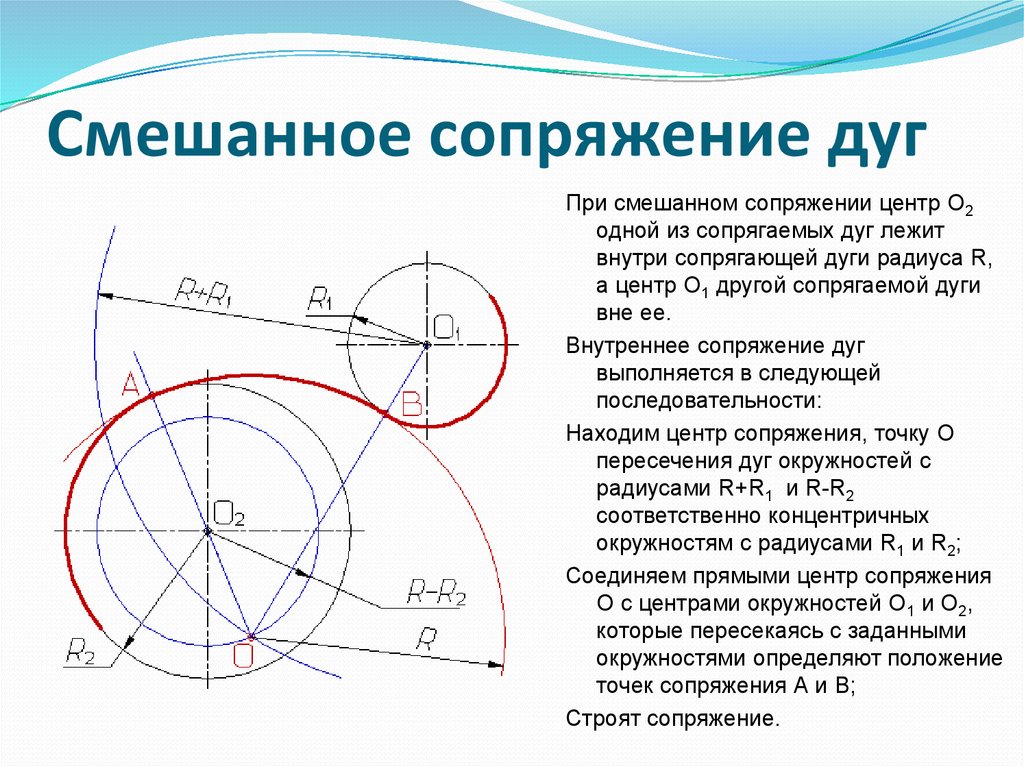 63, б показан кронштейн. При вы­полнении изображения контура этой детали необходимо выполнить построения, описанные выше.

На рис. 63, в выполнено сопряжение дуги ради­уса Rc прямой AВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О₁ находится на пересечении вспомогательной прямой, прове­денной параллельно данной прямой на расстоянии г, с дугой вспомогательной окружности, описан­ной из центра О радиусом, равным разности R—r. Точка сопряжения является основанием перпенди­куляра, опущенного из точки О₁ на данную пря­мую. Точку сопряжения с находят на пересечении прямей ОО₁ с сопрягаемой дугой. Такое сопряже­ние выполняют, например, при вычерчивании контура маховика, показанного на рис. 63, г.

Рис. 63

Сопряжение дуги с дугой

Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.

При внутреннем сопряжении центры О и О₁ сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рис.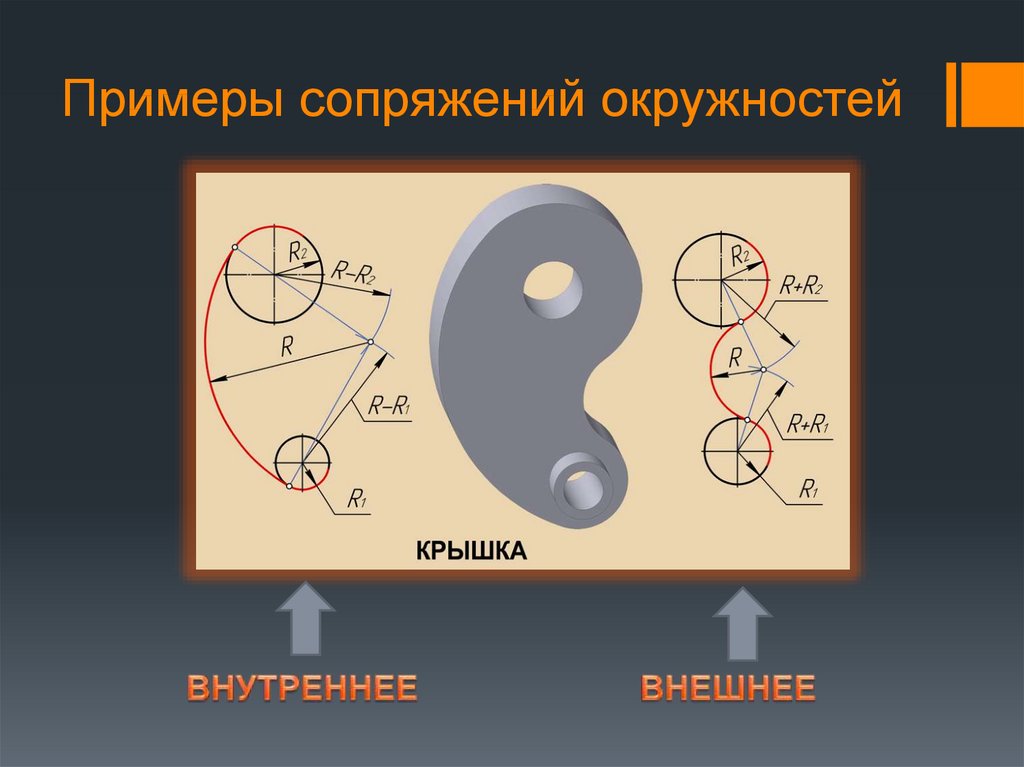 64, б).

При внешнем сопряжении центры О И О₁ сопрягаемых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рис. 64. в).

При смешанном сопряжении центр О₁ одной из сопрягаемых дут лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги вне ее (рис. 65. а).

На рис. 64, а показана деталь (серьга), при вычерчивании которой необходимо по­строение внутреннего и внешнего сопряжения (рис. 64, б—г).

Построение внутреннего сопряжения.

Задано:

а) радиусы сопрягаемых окружностей R₁ и R₂;

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

г) определить положение центра О₂ сопрягаю­щей дуги;

д) найти точки сопряжения s и s₁;

е) провести дугу сопряжения.

Построение сопряжения показано на рис. 64, б. По заданным расстояниям между центрами l₁ и l_{2на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О1 проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R2, а из цен­тра О — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R1. Вспомога­тельные дуги пересекутся в точке О2, которая и будет искомым центром сопрягающей дуги.}

Для нахождения точек сопряжения точку О₂ соединяют с точками О и О₁ прямыми линиями. Точки пересечения продолжения прямых О₂О и О₂О_{1с сопрягаемыми дугами являются искомыми точками сопряжения (точки s и s1).}

Радиусом R из центра О₂ проводят сопрягаю­щую дугу между точками сопряжения s и s_1.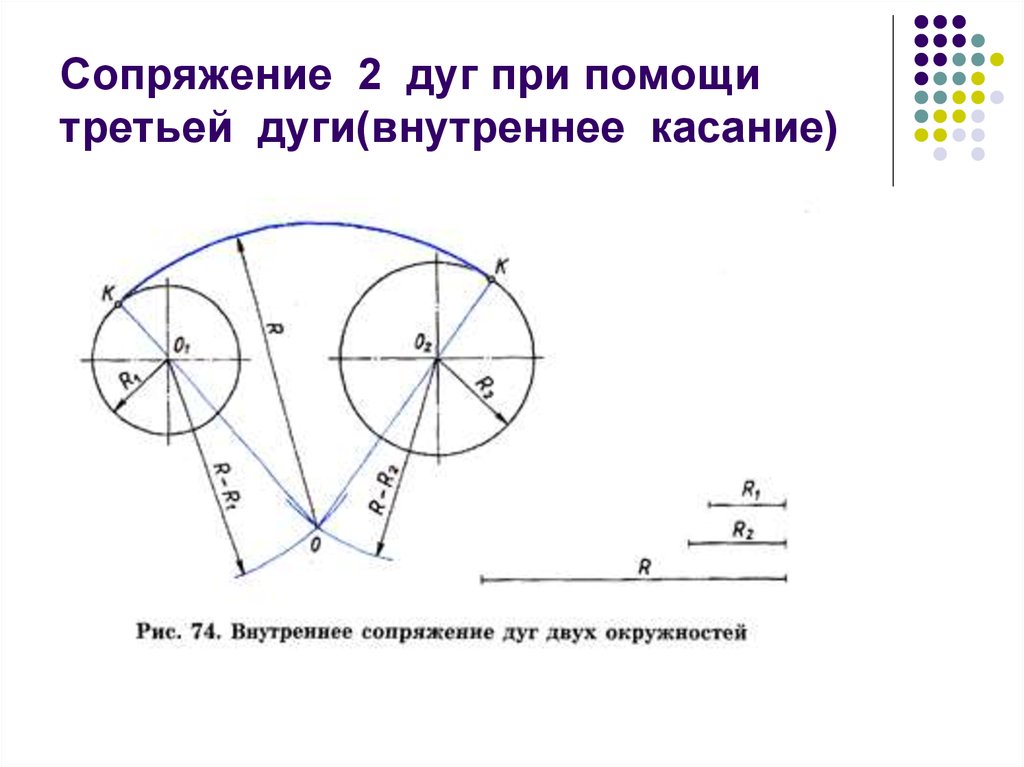

Построение внешнего сопряжения

Задано:

а) радиусы R_{1и R2сопрягаемых дуг окружнос­тей;}

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягаю­щей дуги;

б) найти точки сопряжения s и s₁;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рис. 64, в. По заданным расстояниям между цен­трами l₁ и l₂ на чертеже находят точки О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиу­сов сопрягаемой дуге R₁и сопрягающей R, а из центра О₁ — радиусом, равным сумме радиусов сопрягаемой дуги R₂ и сопрягающей R.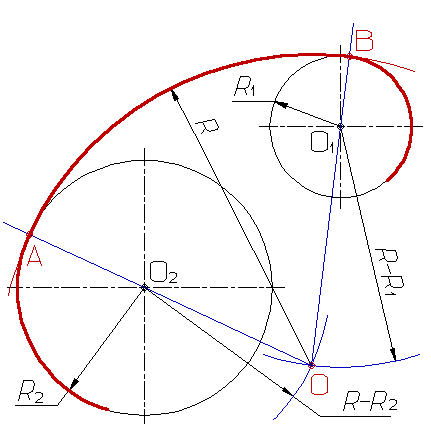 Вспомога­тельные дуги пересекутся в точке О₂, которая будет искомым центром сопрягающей дуга.

Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО₂ и О₁О₂. Эти две прямые пересекают сопрягаемые дуга в точ­ках сопряжения s и s₁.

Из центра О₂ радиусом R проводят сопрягаю­щую дугу, ограничивая ее точками сопряжения s и s_1.

Рис. 64

Построение смешанного сопряжения

Пример смешанного сопряжения приведен на рис. 65, а—в.

Задано:

а) радиусы R₁ и R₂ сопрягаемых дут окружнос­тей;

б) расстояния и l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягаю­щей дуги;

б) найти точки сопряжения s и s₁;

в) провести дугу сопряжения.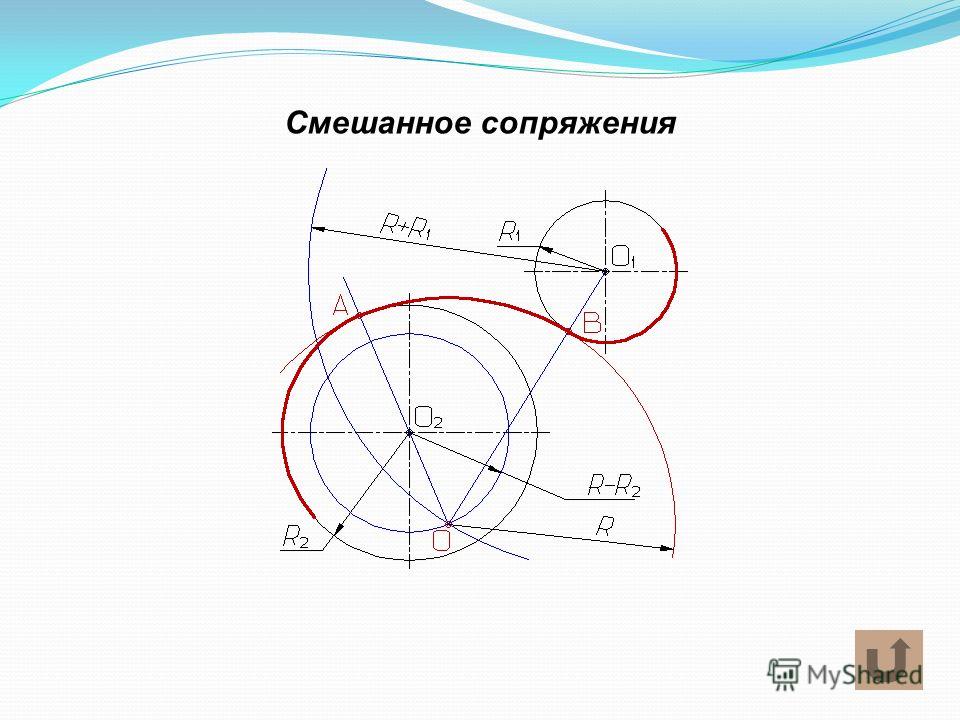

По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из ко­торых описывают сопрягаемые дуги радиусов R

1 и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиу­сов сопрягаемой дуги R₁ и сопрягающей R, а из центра О₁ — радиусом, равным разности радиусов R и R₂. Вспомогательные дуги пересекутся в точ­ке О₂, которая будет искомым центром сопрягаю­щей дуги.

Соединив точки О и О₂ прямой, получают точ­ку сопряжения s₁, соединив точки О₁ и О₂ нахо­дят точку сопряжения s. Из центра О₂ проводят дугу сопряжения от s до s₁.

При вычерчивании контуров сложных деталей важно уметь распознавать в плавных переходах те или иные виды сопряжений и уметь их вычерчи­вать.

Для приобретения навыков в построении сопря­жений выполняют упражнения по вычерчиванию контуров сложных деталей. Для этого необходимо определить порядок построения сопряжений и только после этого приступать к их выполнению.

На рис. 66 изображена деталь (кронштейн) и последовательность выполнения контурного очер­тания этой детали с построением различных видов сопряжений.

Рис. 65

Рис. 66

Примеры и образцы решения задач:

• Решение задач по инженерной графике
• Решение задач по начертательной геометрии

Услуги по выполнению чертежей:

1. Заказать чертежи
2. Помощь с чертежами
3. Заказать чертеж в компасе
4. Заказать чертеж в автокаде
5. Заказать чертежи по инженерной графике
6. Заказать чертежи по начертательной геометрии
7. Заказать черчение

Учебные лекции:

1. Инженерная графика
2. Начертательная геометрия
3. Оформление чертежей
4. Чертеж общего вида и сборочный чертеж
5. Техническое рисование
6. Машиностроительные чертежи
7. Геометрические построения
8. Деление окружности на равные части
9. Коробовые кривые линии
10. Построение уклона и конусности
11. Лекальные кривые
12. Параллельность и перпендикулярность
13. Методы преобразования ортогональных проекций
14. Поверхности
15. Способы проецирования
16. Метрические задачи
17. Способы преобразования чертежа
18. Кривые линии
19. Кривые поверхности
20. Трёхгранник Френе
21. Проецирование многогранников
22. Проецирование тел вращения
23. Развёртывание поверхностей
24. Проекционное черчение
25. Проецирование
26. Проецирование точки
27. Проецирование отрезка прямой линии
28. Проецирование плоских фигур
29. Способы преобразования проекций
30. Аксонометрическое проецирование
31. Проекции геометрических тел
32. Сечение геометрических тел плоскостями и развертки их поверхностей
33. Взаимное пересечение поверхностей тел
34. Сечение полых моделей
35. Разрезы
36. Требования к чертежам деталей
37. Допуски и посадки
38. Шероховатость поверхностей и обозначение покрытий
39. Разъемные и неразъемные соединения деталей
40. Передачи и их элементы

Объяснение урока: Углы пересекающихся прямых в окружности

В этом объяснении мы научимся находить величины углов, возникающих в результате пересечения двух хорд, двух секущих, двух касательных или касательных и секущих в окружности.

Начнем с повторения определений различных типов линий, которые встречаются или пересекаются по окружности.

• Хорда окружности — это отрезок, оба конца которого лежат на окружности окружности.
• Секущей называется прямая, пересекающая окружность ровно в двух точках. Секанту можно представить как хорду, бесконечно протянувшуюся в обоих направлениях.
• Касательная — это линия, которая касается окружности только в одной точке.

Эти три типа линий показаны на рисунке ниже.

Основное внимание в этом объяснении уделяется определению мер углов, образованных при пересечении двух таких линий внутри или вне круга. Меры этих углов связаны с мерами дуг, пересекаемых линиями, образующими их стороны. Мы должны помнить, что мера дуги определяется как мера ее центрального угла, как показано на рисунке ниже.

Сначала рассмотрим пересечения внутри круга. Наше первое определение касается мер углов, образованных пересекающимися хордами.

Теорема: углы между пересекающимися хордами

Мера угла, образованного двумя хордами, пересекающимися внутри окружности, равна половине суммы мер дуг, пересекаемых углом, и его вертикального угла.

Рассмотрим углы, образованные пересечением хорд 𝐴𝐵 и 𝐶𝐷 на рисунке ниже.

Дуга, пересекаемая углом 𝑥, равна 𝐴𝐶. Дуга, пересекаемая ее вертикально противоположным углом, равна 𝐵𝐷. Отсюда по теореме об углах между пересекающимися хордами 𝑥=12𝑚𝐴𝐶+𝑚𝐵𝐷.

Для угла 𝑦 дуги, пересекаемые этим углом и его вертикальным углом, равны 𝐵𝐶 и 𝐴𝐷. Следовательно, 𝑦=12𝑚𝐵𝐶+𝑚𝐴𝐷.

Тот же результат можно применить, чтобы найти меру угла, образованного при пересечении двух секущих внутри окружности или секущей и хорды. Это возможно, потому что секущая является продолжением хорды на неопределенный срок в обоих направлениях.

В нашем первом примере мы продемонстрируем, как применить этот результат, чтобы найти меру угла между двумя пересекающимися хордами, зная меры двух пересекаемых дуг.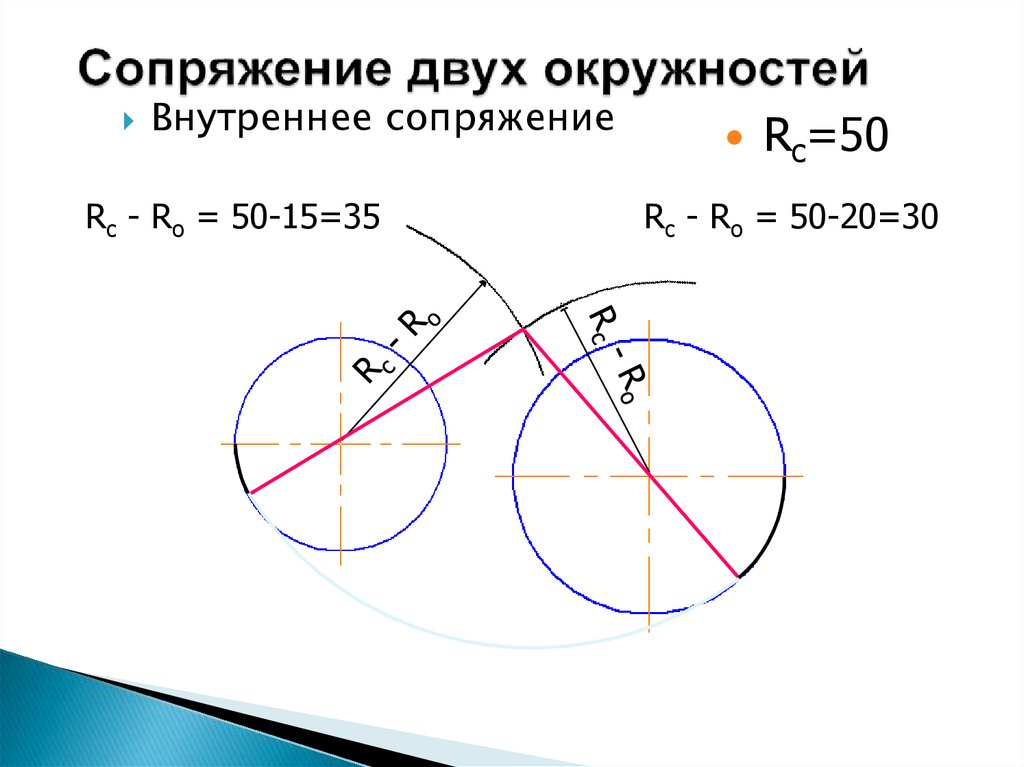

Пример 1. Нахождение меры вписанного угла между двумя пересекающимися хордами по вписанным дугам

Найти 𝑥.

Ответ

Из рисунка видно, что отрезки 𝐴𝐵 и 𝐶𝐷 являются хордами окружности, так как обе конечные точки каждого отрезка лежат на окружности окружности. Значение, которое нас просят вычислить, 𝑥, является мерой одного из углов, образованных в точке пересечения этих двух хорд. Напомним поэтому теорему об углах между пересекающимися хордами: «Мера угла, образованного двумя хордами, пересекающимися внутри окружности, равна половине суммы мер дуг, охватываемых углом, и его вертикального угла. ”

Дуги, пересекаемые для угла 𝑥 и его вертикального угла, равны 𝐴𝐶 и 𝐵𝐷. Следовательно, 𝑥=12𝑚𝐴𝐶+𝑚𝐵𝐷.

Замена 𝑚𝐴𝐶=73∘ и 𝑚𝐵𝐷=133∘ и упрощение дает 𝑥=12(73+133)=12×206=103.∘∘∘∘

Теперь рассмотрим углы, образованные пересечениями вне круга. В этом случае две пересекающиеся линии могут быть касательными или секущими, или одной из них.

Теорема: углы между пересекающимися секущими и касательными

Мера угла, образованного двумя секущими, двумя касательными или касательной и касательной, которые пересекаются в точке вне круга, равна половине положительной разности меры пересекаемых дуг.

На рисунке ниже мы иллюстрируем этот результат для угла, образованного пересечением двух секущих, ⃖⃗𝐴𝐶 и ⃖⃗𝐴𝐸.

Малая дуга, пересекаемая двумя секущими, равна 𝐵𝐷, а большая дуга равна 𝐶𝐸. Отсюда по теореме об углах между пересекающимися секущими 𝑥=12𝑚𝐶𝐸−𝑚𝐵𝐷.

Таким же образом проиллюстрируем результат для пересечения двух касательных, ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶: 𝑥=12𝑚𝐵𝐷𝐶−𝑚𝐵𝐶.

Обратите внимание, что когда две касательные пересекаются в точке вне круга, большая и малая дуги пересечения вместе образуют всю окружность. Следовательно, сумма мер двух пересекаемых дуг равна 360∘. Это важно помнить, поскольку нам может быть задана мера только одной из перехваченных дуг, и ожидается, что мы вычислим другую, применяя это знание.

Теперь рассмотрим пример, в котором мы найдем меру угла между двумя секущими, которые пересекаются вне круга, зная меры двух пересекаемых дуг.

Пример 2. Нахождение меры вписанного угла между двумя секущими по величине двух пересекаемых дуг

Найдите значение 𝑥.

Ответ

Отрезки 𝐴𝐸 и 𝐶𝐸 являются отрезками секущих окружности, поскольку каждый из них пересекает окружность ровно в двух точках. Два секущих отрезка пересекаются в точке за пределами круга, и значение, которое нам нужно вычислить, является мерой образовавшегося угла. Отсюда вспоминаем теорему об углах между пересекающимися секущими: «Мера угла, образованного двумя секущими, пересекающимися в точке вне круга, равна половине положительной разности мер пересекаемых дуг».

Две перехваченные дуги — это 𝐴𝐶 и 𝐵𝐷. Поскольку 𝐴𝐶 имеет большую меру, положительная разница находится путем вычитания меры 𝐵𝐷 из меры 𝐴𝐶. Следовательно, 𝑥=12𝑚𝐴𝐶−𝑚𝐵𝐷.∘

Подстановка размеров двух дуг, как показано на рисунке, и упрощение дает 𝑥=12(144−71)=12×73=36,5. ∘∘∘∘∘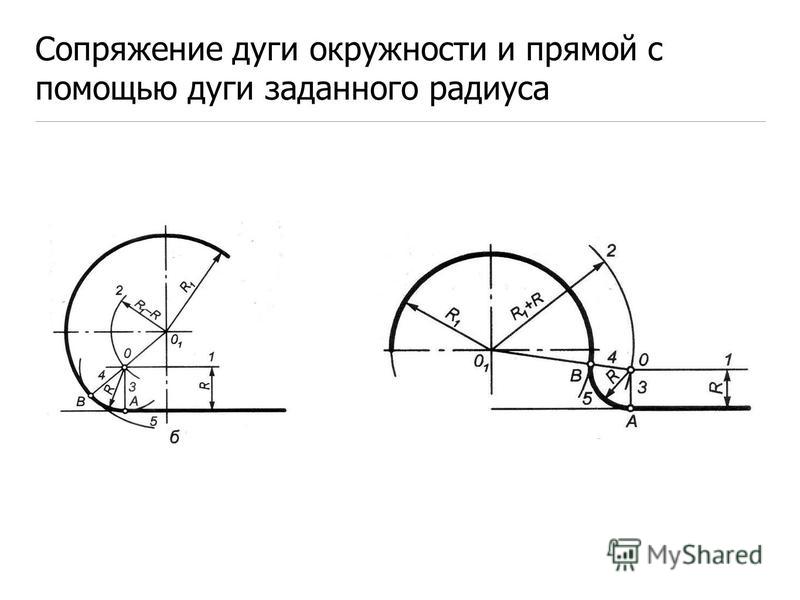

Значение 𝑥 равно 36,5.

Обратите внимание, что в предыдущей задаче значение 𝑥 было чисто числовым: наш ответ был 36,5, а не 36,5∘. Сравним это с примером 1, в котором наше решение было 𝑥=103∘. Это связано с разницей в том, была ли единица измерения (градусы) включена при обозначении угла: в примере 1 угол был обозначен просто как 𝑥, тогда как в нашем втором примере угол был помечен как 𝑥∘.

Теперь мы рассмотрели примеры того, как вычислить меру угла между двумя хордами и меру угла между двумя секущими, зная меры двух пересекаемых дуг. Также возможно работать в обратном направлении, зная меру угла между двумя хордами, секущими или касательными, чтобы определить меру одной или обеих пересекаемых дуг, при условии, что нам предоставлено достаточно другой информации. В более сложных задачах это также может потребовать от нас составить и решить алгебраическое уравнение, как мы увидим в нашем следующем примере.

Пример 3. Нахождение меры большой дуги по размерам малой дуги и вписанному углу между двумя касательными к этим дугам

Учитывая, что 𝑥∘ является мерой большой дуги 𝐵𝐶, найдите значение 𝑥.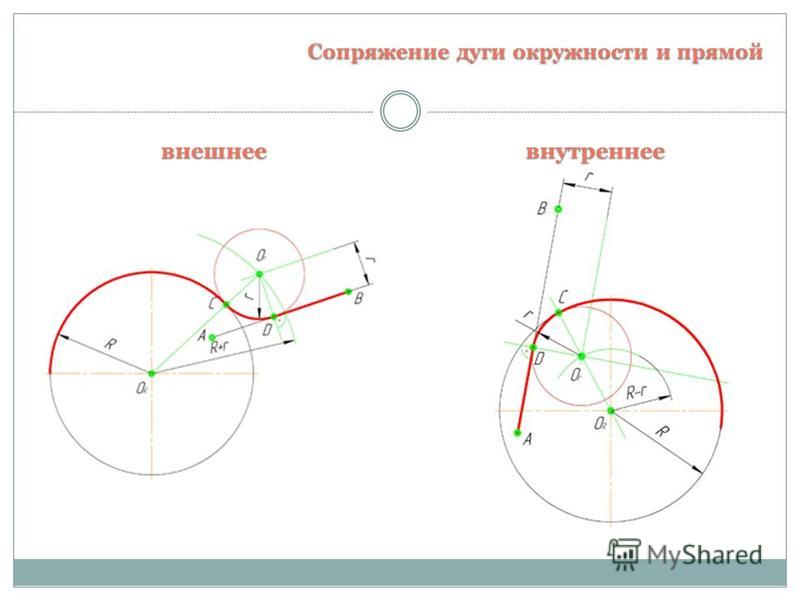

Ответ

При рассмотрении рисунка мы видим, что есть две касательные, ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶, проведенные из одной и той же внешней точки к окружности. Нас просят вычислить меру большой дуги, пересекаемой этими двумя касательными. Напомним теорему об углах между пересекающимися касательными: «Мера угла, образованного двумя касательными, пересекающимися в точке вне окружности, равна половине положительной разности мер пересекаемых дуг».

Если мы представим точку 𝐷 на окружности в любом месте на большой дуге, соединяющей 𝐵 и 𝐶, мы можем выразить этот результат для этой задачи как 𝑚∠(𝐶𝐴𝐵)=12𝑚𝐵𝐷𝐶−𝑚𝐵𝐶.

На рисунке дана мера угла между двумя касательными и алгебраическое выражение для меры большой дуги, которую мы теперь называем 𝐵𝐷𝐶. Чтобы найти выражение для меры малой дуги, вспомним, что мера полной длины окружности равна 360∘. Следовательно, мера малой дуги 𝐵𝐶 равна (360−𝑥)∘.

Теперь мы можем составить уравнение относительно 𝑥, подставив эти значения и выражения в приведенную выше формулу.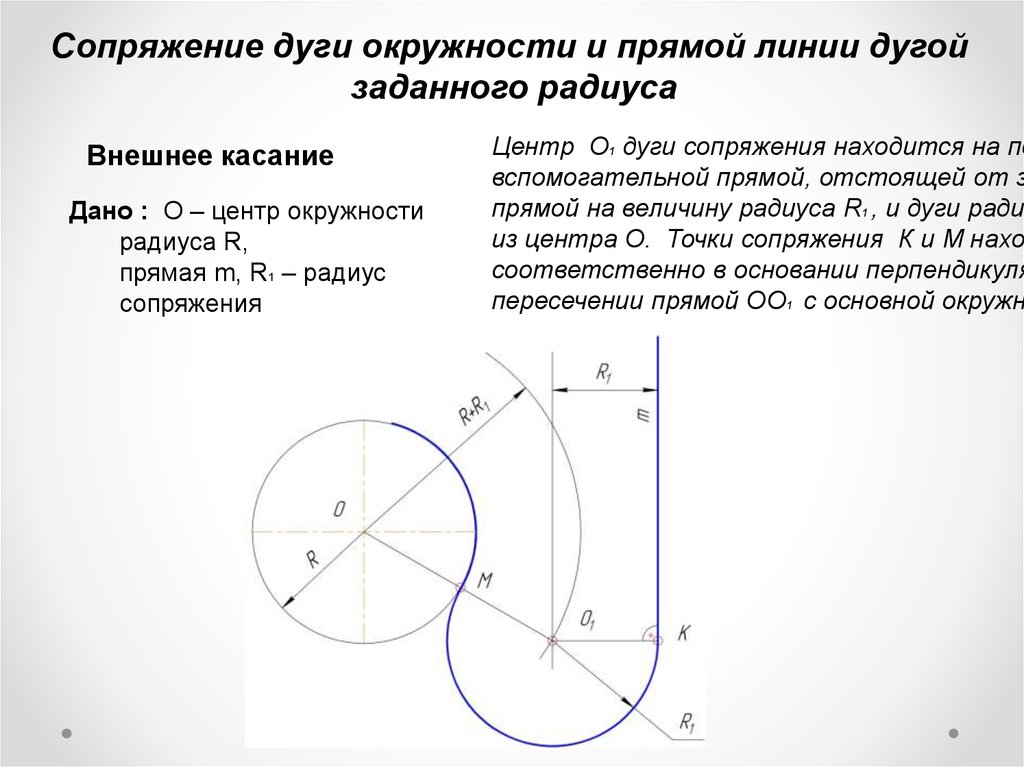 Единица измерения одинакова для всех выражений и поэтому может быть опущена. Замена 𝑥 на меру большой дуги, (360−𝑥) на меру малой дуги и 64 на меру угла между двумя касательными дает 12(𝑥−(360−𝑥))=64.

Чтобы найти 𝑥, мы сначала умножаем обе части уравнения на 2, а затем распределяем скобки: (𝑥−(360−𝑥))=1282𝑥−360=128.

Наконец, мы добавляем 360 к каждой части уравнения, а затем делим обе части на 2: 2𝑥=488𝑥=244.

Теперь рассмотрим другой пример, в котором требуется составить и решить алгебраическое уравнение, связав меру угла между секущей и касательной с мерами двух пересекаемых дуг. Обе эти меры дуги будут заданы как линейные выражения неизвестного, которое нам необходимо определить.

Пример 4. Нахождение меры двух дуг, вписанных между секущими, при заданном вписанном угле

Учитывая, что на показанном рисунке 𝑦=(𝑥−2) и 𝑧=(2𝑥+2), определите значение 𝑥.

Ответ

Из рисунка видно, что отрезок 𝐴𝐵 является касательной к окружности, поскольку пересекает окружность только в одной точке. Отрезок 𝐴𝐷 является секущим отрезком, поскольку он пересекает окружность ровно в двух точках, а его конечная точка находится на окружности окружности. Эти два отрезка пересекаются в точке вне круга, и нам дана мера угла, образованного их пересечением. Напомним теорему об углах между пересекающимися секущими и касательными: «Мера угла, образованного секущей и касательной, пересекающимися в точке вне круга, равна половине положительной разности мер пересекаемых дуг. ”

Из рисунка видно, что большая пересекаемая дуга — это 𝐵𝐷, а меньшая — 𝐵𝐶. Следовательно, мы можем составить уравнение, используя меры этих двух дуг и меру угла пересечения секущей и касательной: 50=12(𝑧−𝑦).

Нам даны выражения для 𝑦 и 𝑧 через третью переменную, 𝑥, значение которой нам нужно вычислить. Подстановка 𝑧=2𝑥+2 и 𝑦=𝑥−2 в приведенное выше уравнение дает уравнение только в 𝑥: 50=12((2𝑥+2)−(𝑥−2)).

Теперь решим это уравнение, чтобы найти 𝑥. Хотя это и не обязательно, мы начнем с того, что поменяем местами две стороны, чтобы неизвестное оказалось слева.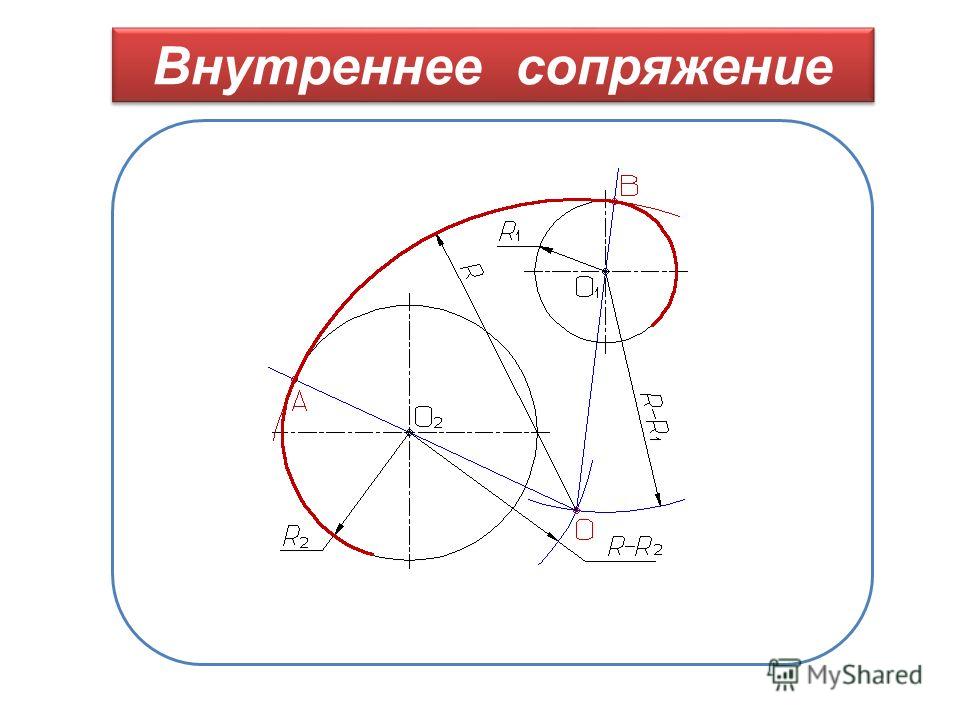 Затем мы упрощаем в скобках, чтобы дать следующее: 12(2𝑥+2−𝑥+2)=5012(𝑥+4)=50.

Умножение обеих частей уравнения на 2 дает 𝑥+4=100.

Наконец, вычитание 4 из каждой части уравнения дает 𝑥=96.

Итак, мы рассмотрели четыре примера, в которых продемонстрировано применение двух ключевых теорем как к числовым, так и к алгебраическим задачам. Результаты, которые мы представили в этом объяснении, также могут быть применены к более сложным задачам, связанным с другими геометрическими фигурами, вписанными в окружности. Теперь рассмотрим пример, в котором правильный пятиугольник вписан в окружность и требуется найти меру угла между двумя касательными к окружности.

Пример 5. Нахождение угла между двумя касательными с помощью свойств касательных к окружности и правильных многоугольников

𝐴, а ⃖⃗𝐸𝑋 является касательной к окружности в точке 𝐸. Найдите 𝑚∠𝐴𝑋𝐸.

Ответ

Изучив схему, мы видим, что угол 𝐴𝑋𝐸 — это угол, образованный пересечением двух касательных ⃖⃗𝐴𝑋 и ⃖⃗𝑋𝐸. Напомним поэтому теорему об углах между пересекающимися касательными: «Мера угла, образованного двумя касательными, пересекающимися в точке вне круга, равна половине положительной разности мер соединяемых дуг».

Мы можем счесть полезным добавить цвет к диаграмме, чтобы помочь идентифицировать перехваченные дуги, как показано ниже.

Мы будем называть большую дугу, показанную розовым, как 𝐴𝐵𝐸, а малую дугу, показанную оранжевым, как 𝐴𝐸. Следовательно, мера угла 𝐴𝑋𝐸 определяется выражением 𝑚∠𝐴𝑋𝐸=12𝑚𝐴𝐵𝐸−𝑚𝐴𝐸.

Нам не известны меры ни углов, ни дуг на рисунке. Вместо этого напомним, что пятиугольник 𝐴𝐵𝐶𝐷𝐸 правильный. Следовательно, его можно разделить на пять конгруэнтных треугольников, проведя радиусы от каждой вершины пятиугольника до центра круга. Мы проиллюстрируем один такой треугольник, нарисовав радиусы 𝐴𝑀 и 𝐸𝑀 на рисунке ниже.

Размер большой дуги 𝐴𝐵𝐸 равен углу отражения в центре окружности. Мера малой дуги 𝐴𝐸 равна острому углу в той же точке. Напомним, что сумма углов вокруг точки равна 360∘. Поскольку пятиугольник правильный, а пять треугольников конгруэнтны, острого угла 𝐸𝑀𝐴 можно найти, разделив 360∘ на 5: 𝑚∠𝐸𝑀𝐴=3605=72.∘∘

Следовательно, мера малой дуги 𝐴𝐸 равна 72∘. Размер большой дуги можно найти, вычитая это значение из 360∘, чтобы получить 288∘.

Подставив размеры двух дуг в приведенную выше формулу, мы получим 𝑚∠𝐴𝑋𝐸=12(288−72)=12×216=108.∘∘∘∘

В более сложных задачах с несколькими пересекающимися отрезками нам может понадобиться применить несколько теорем, представленных в этом объяснении. Нам также может понадобиться использовать результаты, относящиеся к другим типам углов в окружностях. Вписанный угол имеет вершину на окружности и стороны, содержащие хорды окружности. Ниже мы определим связь между мерой вписанного угла и его дугой.

Определение: мера вписанного угла

Мера угла, вписанного в окружность, равна половине длины дуги, на которую он опирается.

Для рисунка ниже этот результат может быть выражен как 𝑚∠𝐴𝐶𝐵=12𝑚𝐴𝐵.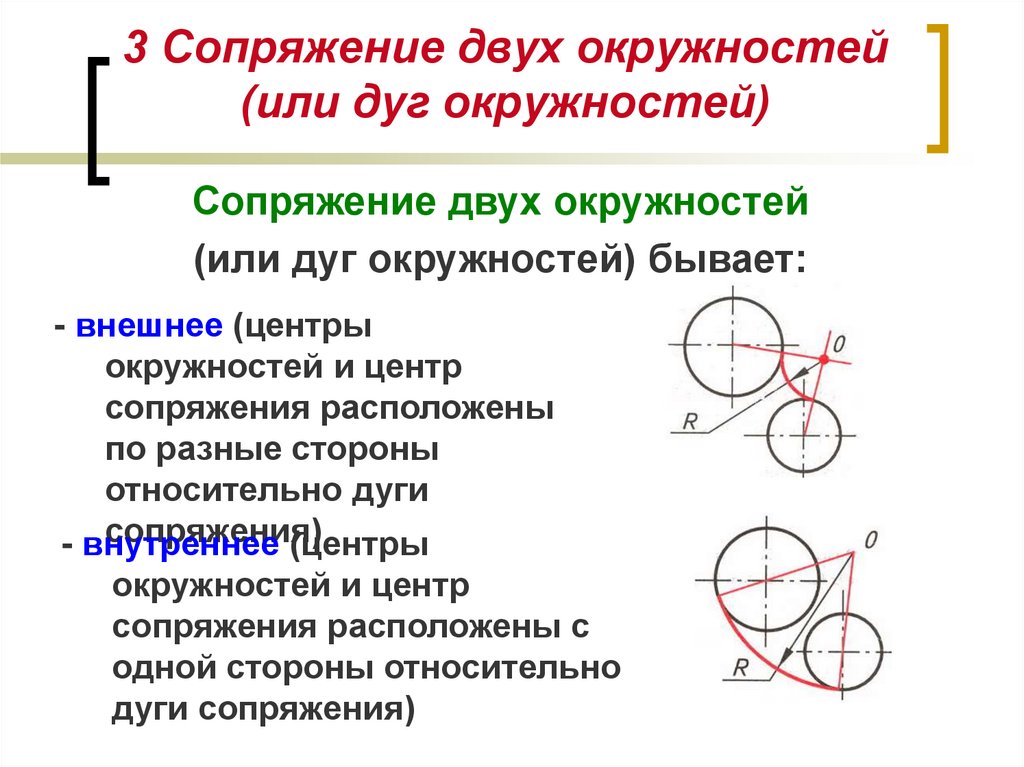

Теперь рассмотрим последний пример: многошаговую задачу, в которой мы применяем как теорему об углах между пересекающимися хордами, так и теорему об углах между пересекающимися секущими, в дополнение к нашим знаниям о вписанных углах.

Пример 6. Нахождение меры угла по мерам его большой и малой дуг

Найти 𝑥.

Ответ

Изучив рисунок, мы видим, что 𝑥∘ является мерой угла, образованного пересечением двух хорд 𝐵𝐸 и 𝐶𝐷 внутри круга. Значит, по теореме об углах между пересекающимися хордами мера этого угла равна половине суммы охватываемых дуг: 𝑥=12𝑚𝐶𝐸+𝑚𝐵𝐷.∘

Далее заметим, что один из углов, меры которых нам даны, угол 𝐵𝐴𝐷, представляет собой угол, образованный пересечением секущих отрезков 𝐴𝐶 и 𝐸𝐶 и 𝐸𝐶 вне круга. Отсюда, учитывая, что мера такого угла равна половине положительной разности охватываемых дуг, имеем 40=12𝑚𝐶𝐸−𝑚𝐵𝐷.∘

Теперь у нас есть два линейных одновременных уравнения, включающих меры 𝐶𝐸 и 𝐵𝐷, но у нас недостаточно информации для их решения. Другая информация, указанная на диаграмме, является мерой вписанного угла 𝐵𝐸𝐷. Вспоминая, что мера вписанного угла равна половине меры дуги, на которую он опирается, мы можем вычислить меру 𝐵𝐷: 12𝑚𝐵𝐷=30𝑚𝐵𝐷=2×30=60.∘∘∘

Теперь мы можем подставить это значение во второе уравнение, которое позволит нам найти меру 𝐶𝐸. Затем мы сможем подставить меры обеих дуг в наше первое уравнение, чтобы определить 𝑥.

Подстановка 𝑚𝐵𝐷=60∘ во второе уравнение дает 12𝑚𝐶𝐸−60=40.∘∘

Мы решаем определить 𝑚𝐶𝐸, сначала умножая каждую часть уравнения на 2, а затем добавляя 60∘ к каждой стороне: 𝑚𝐶𝐸−60=80𝑚𝐶𝐸=140.∘∘∘

Наконец, находим 𝑥, вычислив половину суммы мер 𝐶𝐸 и 𝐵𝐷: 𝑥=12𝑚𝐶𝐸+𝑚𝐵𝐷=12(140+60)=12×200=100.∘∘∘∘∘

Следовательно, 𝑥=100.

Давайте закончим повторением некоторых ключевых моментов этого объяснения.

Ключевые моменты

• Мера угла, образованного двумя хордами, пересекающимися внутри окружности, равна половине суммы мер дуг, пересекаемых углом, и его вертикального угла.
• Мера угла, образованного двумя секущими, двумя касательными или секущей и касательной, которые пересекаются в точке вне круга, равна половине положительной разности мер пересекаемых дуг.
• Мера угла, вписанного в окружность, равна половине дуги, на которую опирается окружность.
• Эти результаты могут быть применены как к числовым, так и к алгебраическим задачам для вычисления мер углов, возникающих в результате пересечения двух хорд, двух секущих, двух касательных или касательной и секущей в окружности.

Объяснение урока: Центральные углы и дуги

В этом объяснении мы научимся определять центральные углы, использовать их меры, чтобы найти меры дуг, идентифицировать соседние дуги, найти длины дуг и определить конгруэнтные дуги в конгруэнтных окружностях.

Начнем с точного определения того, что понимается под дугой окружности.

Определение: Дуга окружности

Дуга окружности представляет собой часть окружности окружности между двумя радиусы.

Примеры дуг окружностей можно увидеть на следующих диаграммах.

Чтобы помочь нам различать разные дуги, мы вводим понятие центральный угол.

Определение: центральный угол

Центральный угол окружности – это угол между двумя радиусами с вершиной в центр. На следующей диаграмме ∠𝐴𝐵𝐶 представляет собой Пример центрального угла.

Мы можем расширить эту идею, сказав, что центральный угол дуги является центральным угол, опирающийся на дугу.

Например, центральные углы двух заданных дуг показаны на следующем рисунке. диаграммы.

Мы видим, что чем больше центральный угол, тем больше дуга. Следовательно, это было бы полезно поговорить о мере центрального угла дуги с по поводу длины дуги. Мы делаем это, вводя следующие определение.

Определение: мера дуги

Мерой дуги является мера ее центрального угла.

Например, на диаграмме ниже мера дуги, выделенная красным цветом, равна 26∘.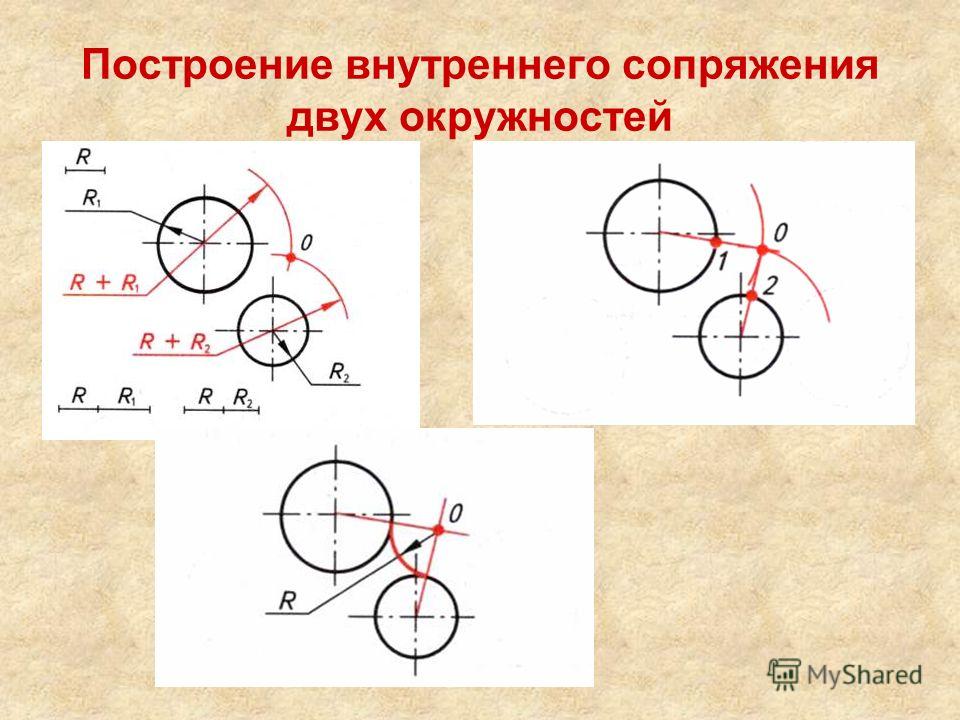

На этой диаграмме мы можем заметить кое-что интересное: есть две возможные дуги от 𝐴 до 𝐵, более короткая красная, а более длинный в зеленом цвете. Чтобы помочь нам различать эти два случая, мы называем более длинная дуга — большая дуга, а более короткая дуга — малая дуга.

Определение: большая и малая дуги окружности

Для заданных двух радиусов мы обозначаем более длинную из двух дуг между радиусами как большая дуга и более короткая дуга как малая дуга . Эквивалентно дуге с меньший центральный угол является малой дугой, а дуга с большим центральным угол — большая дуга.

Чтобы различать большую и малую дуги, мы обозначаем малую дугу как 𝐴𝐵 и обозначьте большую дугу, используя дополнительную точку (например, 𝐴𝐶𝐵).

Мы также можем использовать обозначение 𝑚𝐴𝐵 для меры малой дуги от 𝐴 до 𝐵. В этом случае мы можем использовать 𝑚𝐴𝐶𝐵 для меры большая дуга от 𝐴 до 𝐵.

Если две дуги имеют одинаковую длину, то мы называем эти полукруглых дуг .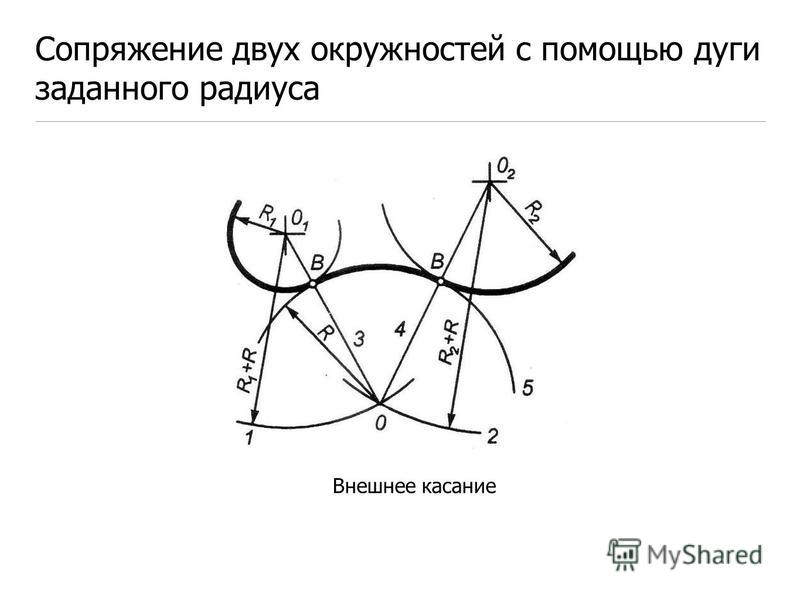 Эти возникают, когда радиусы образуют диаметр или когда их центральные углы равны меры.

Поскольку размер центрального угла дуги определяет ее размер, мы определяем главный и малые дуги с точки зрения их центральных углов. Если центральный угол больше чем 180∘, то дуга главный. Если центральный угол меньше 180∘, то дуга малая. Если центральный угол равен 180∘, то дуга полукруглый.

В нашем первом примере мы определим меру дуги по ее центральной угол.

Пример 1. Нахождение меры дуги по ее центральному углу

Найдите 𝑚𝐴𝐷.

Ответ

Напомним, что обозначение 𝑚𝐴𝐷 означает мера малой дуги между 𝐴 и 𝐷 и что мера дуги определяется как ее центральная угол. Мы выделяем эту дугу на следующей диаграмме.

Центральный угол дуги — это угол в центре окружности между два радиуса, опирающиеся на дугу. Для малой дуги 𝐴𝐷, это 33∘.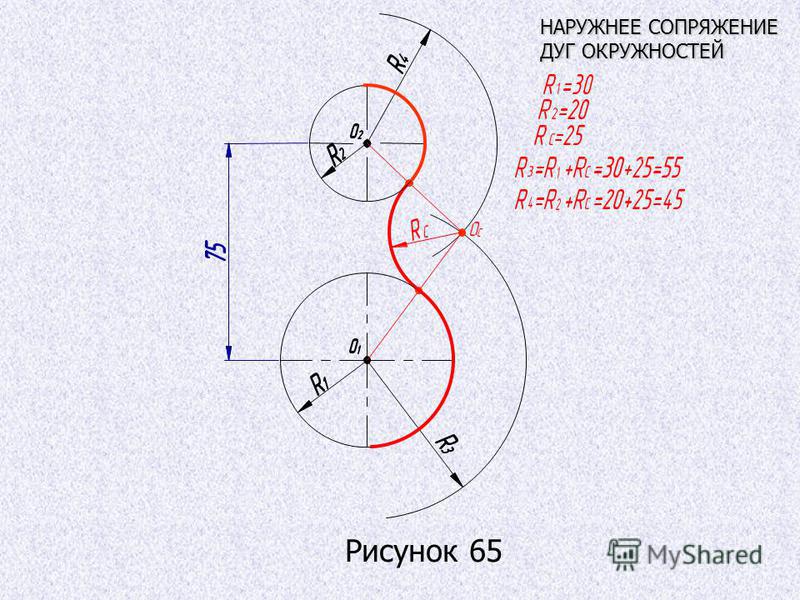 Мера дуги определяется как равная этому значению. Следовательно, 𝑚𝐴𝐷=33.∘

Перед тем, как мы перейдем к другим примерам, нам нужно определить еще одно определение. обсудить, то есть смежных дуг.

Определение: Смежные дуги

Две дуги называются смежными, если они имеют одну общую точку или если они имеют только общие конечные точки.

В круге выше 𝐴𝐵 и 𝐵𝐶 являются смежными, так как они имеют одну общую точку в общий. Точно так же 𝐴𝐶 и 𝐴𝐷𝐶 являются смежными, поскольку они разделяют только оба конечные точки общие.

Фактически, большая и малая дуги окружности между двумя точками всегда будут соседний.

Поскольку мерой дуги является мера ее центрального угла и смежных дуг будут иметь смежные центральные углы, мы можем найти меру смежных дуг по формуле добавляя свои меры. Например, в приведенном выше круге имеем 𝑚𝐴𝐶=𝑚𝐴𝐵+𝑚𝐵𝐶.

Рассмотрим пример определения смежных дуг в окружности.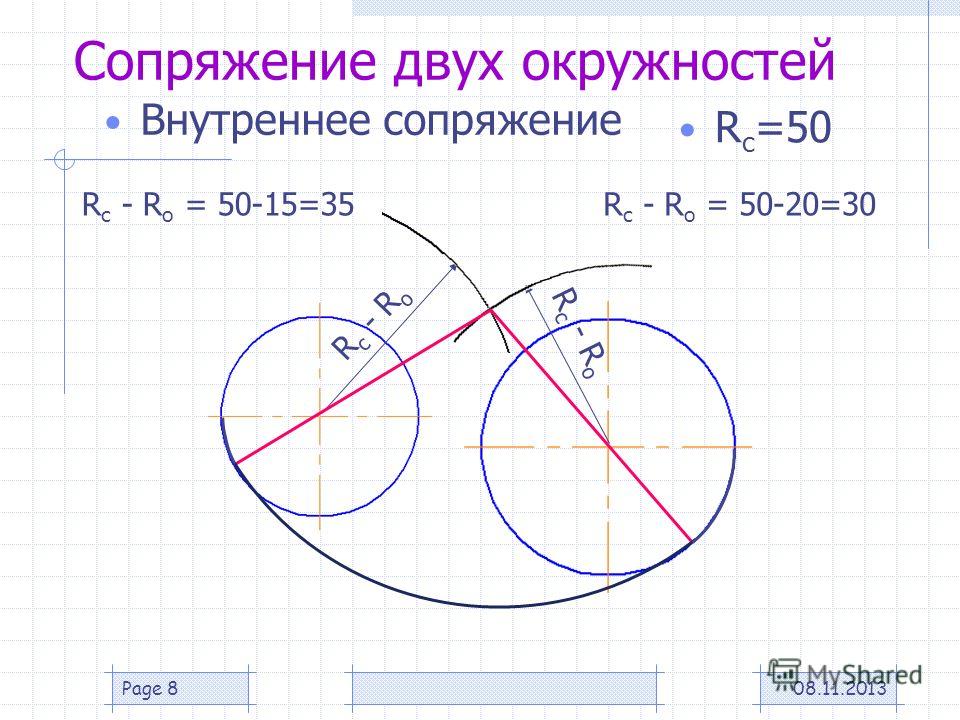

Пример 2. Определение смежных дуг в окружности

Какие из следующих дуг являются смежными в данной окружности?

1. 𝐴𝐵 и 𝐶𝐷
2. 𝐴𝐵 и 𝐵𝐶
3. 𝐴𝐷 и 𝐵𝐶
4. 𝐴𝐶 и 𝐷𝐵

Ответ

Мы помним, что две дуги находятся рядом, если они разделяют единую точку. и что обозначение 𝐴𝐵 означает минор (или меньшая) дуга от 𝐴 до 𝐵. Следовательно, мы можем ответить на этот вопрос, выделив каждую пару дуг. Начнем с 𝐴𝐵 и 𝐶𝐷.

Мы видим, что дуги не имеют общих точек, поэтому они не могут быть смежными. Затем мы выделяем 𝐴𝐵 и 𝐵𝐶.

Мы видим, что 𝐴𝐵 и 𝐵𝐶 делят только точку 𝐵 общее; это конечная точка обеих дуг, поэтому эти дуги являются соседними. Для должной осмотрительности мы также проверим другие варианты.

У нас есть 𝐴𝐷 и 𝐵𝐶.

Мы видим, что эти дуги не имеют общих точек, поэтому они не соседний.

Наконец, мы проверяем 𝐴𝐶 и 𝐷𝐵.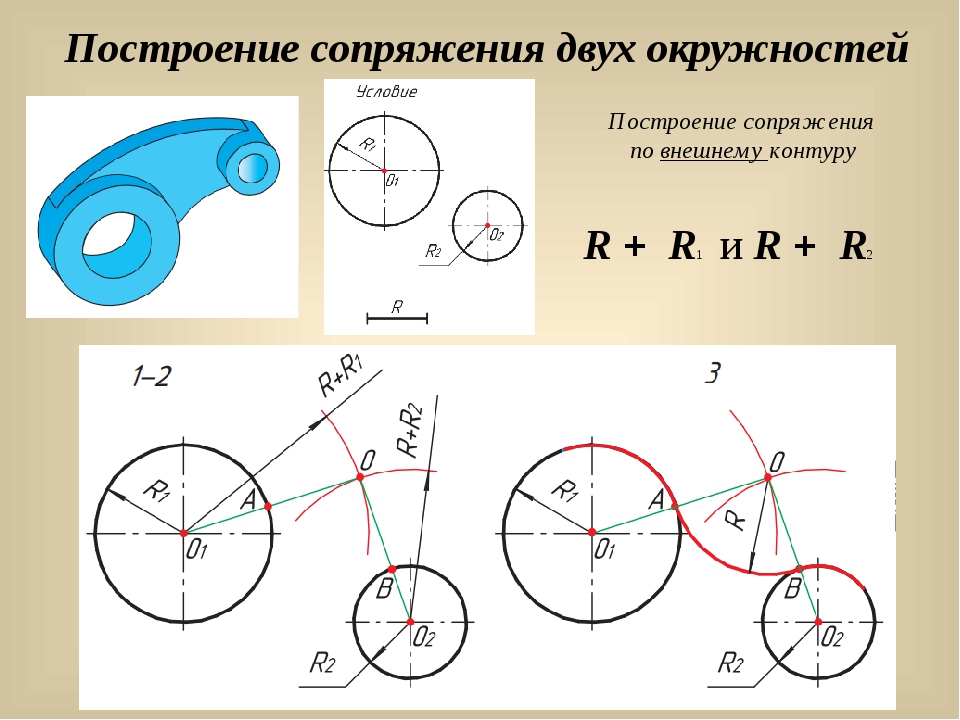

Мы видим, что каждая точка на дуге 𝐵𝐶 лежит на обеих дугах, поэтому эта пара дуг имеет более одной общей точки. Следовательно, они не являются соседними.

Единственная пара дуг, имеющих одну общую точку, это пара дуг 𝐴𝐵 и 𝐵𝐶, что является вариантом B.

В нашем следующем примере мы определим меру дуги, используя диаграмму и знание отношения двух других дуговых мер.

Пример 3. Нахождение меры дуги в окружности по данным других дуг Меры путем решения линейных уравнений

Учитывая, что 𝐴𝐵 — это диаметр в круг центра 𝑀 и 𝑚𝐴𝐶∶𝑚𝐷𝐵=85∶67, определить 𝑚𝐴𝐶𝐷.

Ответ

Мы хотим определить значение 𝑚𝐴𝐶𝐷. Напомним, что это мера дуги из 𝐴 к 𝐶 к 𝐷, как показано на следующей диаграмме.

Мы видим, что эта дуга состоит из двух смежных дуг: 𝐴𝐶 и 𝐶𝐷. Таким образом, мы можем найти меру 𝐴𝐶𝐷, найдя сумму мер 𝐴𝐶 и 𝐶𝐷.

Поскольку мера дуги равна ее центральному углу, 𝑚𝐶𝐷=𝑚∠𝐶𝑀𝐷. Нам дано 𝑚∠𝐶𝑀𝐷=28∘, поэтому мы имеем 𝑚𝐶𝐷=28.∘

Мы знаем, что сумма мер всех дуг, составляющих окружность будет 360∘. В частности, сумма мер дуг, составляющих 𝐴𝐵 будет 180∘ с 𝐴𝐵 — это диаметр. Это означает

𝑚𝐴𝐶+𝑚𝐶𝐷+𝑚𝐵𝐷 = 180𝑚𝐴𝐶+28+𝑚𝐵𝐷 = 180𝑚𝐴𝐶+𝑚𝐵𝐷 = 152.∘∘∘∘

(1)

Нам сказали, что 𝑚𝐴𝐶∶𝑚𝐷𝐵=85∶67.

Следовательно, частные каждой части отношения должны быть равны: 𝑚𝐴𝐶𝑚𝐷𝐵=8567.

Мы можем изменить это уравнение, чтобы получить 𝑚𝐷𝐵=67𝑚𝐴𝐶85.

Мы можем заменить наше выражение на 𝑚𝐷𝐵 в уравнение (1) и упростить, чтобы получить ∘∘∘∘

Наконец, 𝑚𝐴𝐶𝐷=𝑚𝐴𝐶+𝑚𝐶𝐷=85+28=113.∘∘∘

Так как дуга окружности является частью ее окружности, мы можем использовать длину окружности, чтобы определить длину дуги.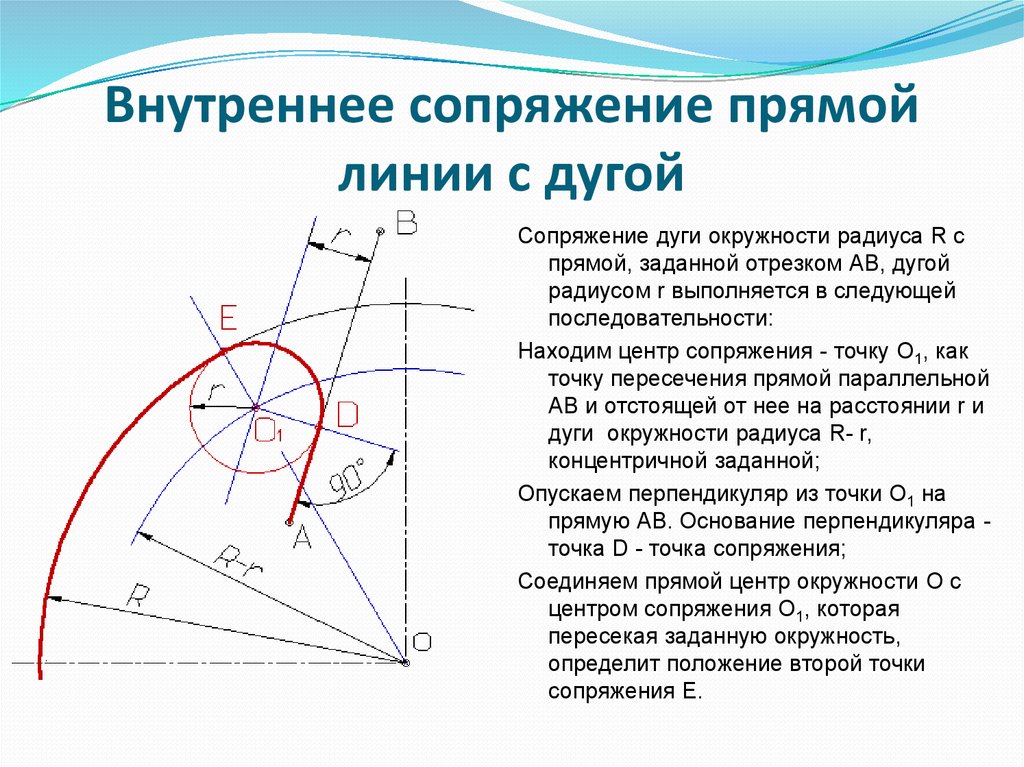 Мы можем сделать это, используя меру дуги или, что то же самое, ее центральную часть. угол.

Чтобы помочь нам определить длину дуги, начнем с пример. Мы хотим определить длину малой дуги в следующем диаграмма.

Во-первых, вспомним, что круг радиуса 𝑟 имеет длину окружности 2𝜋𝑟. Это означает, что длина окружности этого круга 2𝜋𝑟.

Мы видим, что эта дуга представляет собой четверть окружности, но это хорошо потренируйтесь, чтобы понять, почему это так. Полный оборот – это угол 360∘, так что угол 90∘

=14 круг.

Отсюда длина дуги составляет четверть окружности: длина дуги=14(2𝜋𝑟)=𝜋𝑟2.

Как правило, если центральный угол (или мера дуги) 𝜃∘, тогда длина дуги равна 𝜃360(2𝜋𝑟)∘∘. Формально мы можем сформулировать это следующим образом.

Определение: длина дуги

Если центральный угол (или мера) дуги в окружности радиуса 𝑟 это 𝜃∘, тогда длина дуги 𝑙 определяется выражением 𝑙=𝜃360(2𝜋𝑟). ∘∘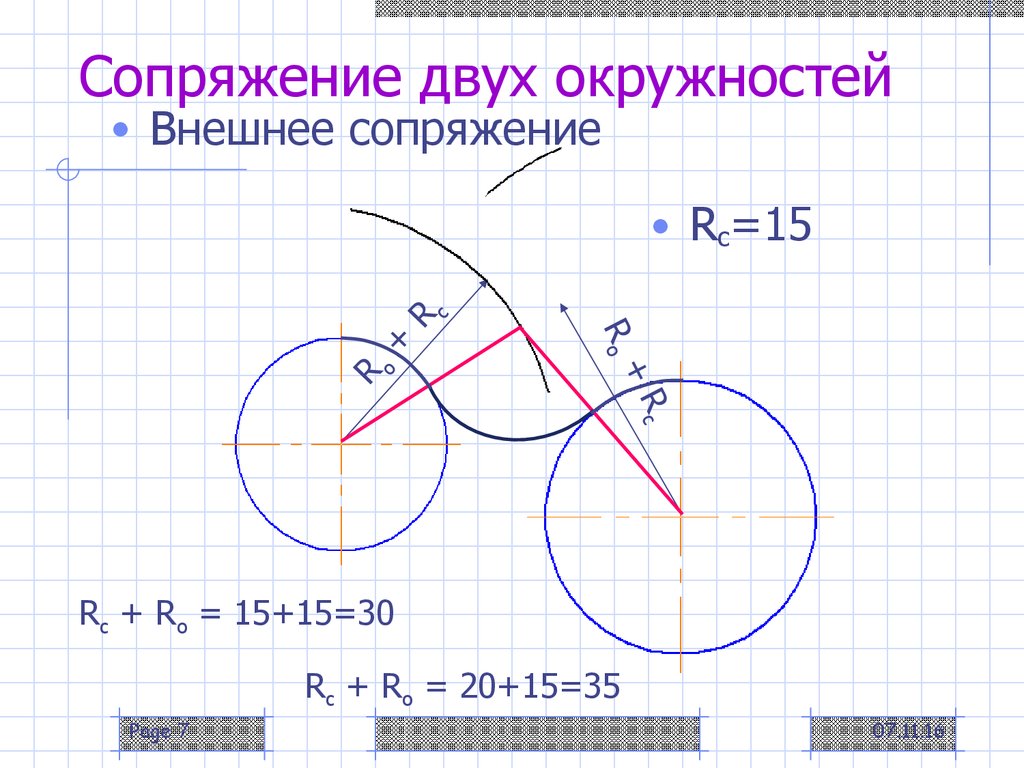

В нашем следующем примере мы будем использовать формулу длины дуги для определения мера дуги, которая дает определенную пропорцию окружности круг.

Пример 4. Нахождение меры дуги, представляющей известную часть Окружность круга

Найдите меру дуги, которая представляет 16 окружности круга.

Ответ

Чтобы ответить на этот вопрос, сначала вспомним, что длина, 𝑙, дуги измерения 𝑥∘ в окружности радиуса 𝑟 определяется выражением 𝑙=𝑥360(2𝜋𝑟).∘∘

Мы хотим, чтобы это значение было равно 16 длина окружности, и мы знаем окружность радиуса 𝑟 имеет окружность 2𝜋𝑟. Итак, мы хотим 𝑙=16(2𝜋𝑟)=13(𝜋𝑟).

Уравнивание этих двух выражений для 𝑙 дает нам 𝑥360(2𝜋𝑟)=13(𝜋𝑟).∘∘

Затем мы можем найти 𝑥∘. Делим на 𝜋𝑟, чтобы получить 𝑥360(2)=13.∘∘

Наконец, мы умножаем на 180∘ и упростить: 𝑥=13(180)=60. ∘∘∘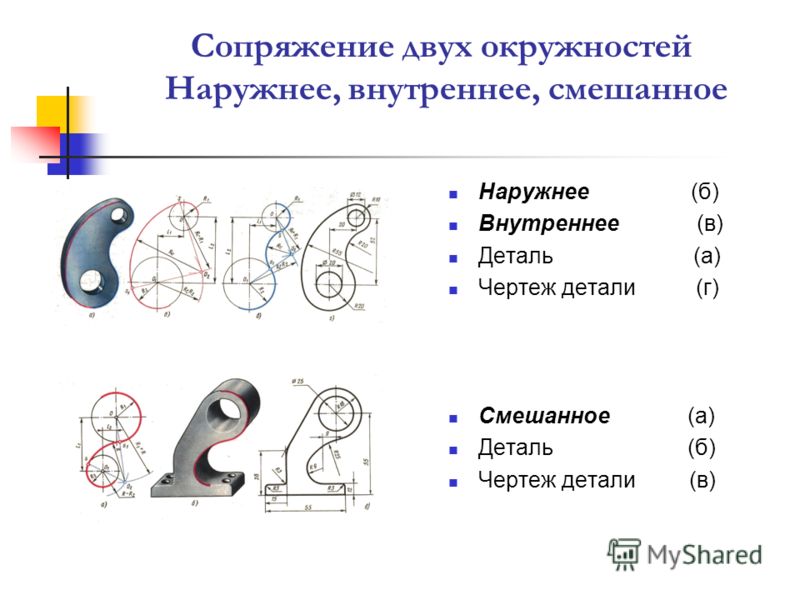

Стоит отметить, что есть и другой способ ответа на этот вопрос. Мы можем заметить, что отношение меры дуги к 360∘ точно такое же, как отношение длины дуги к длина окружности. Другими словами, 𝑥360=.∘∘длина дугиокружность

Нам сказали длина дугиокружность=16, так что у нас есть 𝑥360=16,∘∘ которое решаем и получаем 𝑥=60∘∘.

Существует важное следствие формулы длины дуги, включающее конгруэнтные дуги по кругу, о которых мы сейчас и поговорим.

Свойство: конгруэнтные дуги

Поскольку длина дуги определяется ее центральным углом (или мерой) и радиус окружности, мы можем сделать вывод, что если две дуги в окружностях с равные радиусы имеют одинаковую длину, то их центральные углы (и меры) будут равный. Другими словами, две дуги конгруэнтны тогда и только тогда, когда их центральные углы (или меры) равны.

Например, мы можем использовать эту формулу для определения длины дуги в следующую схему.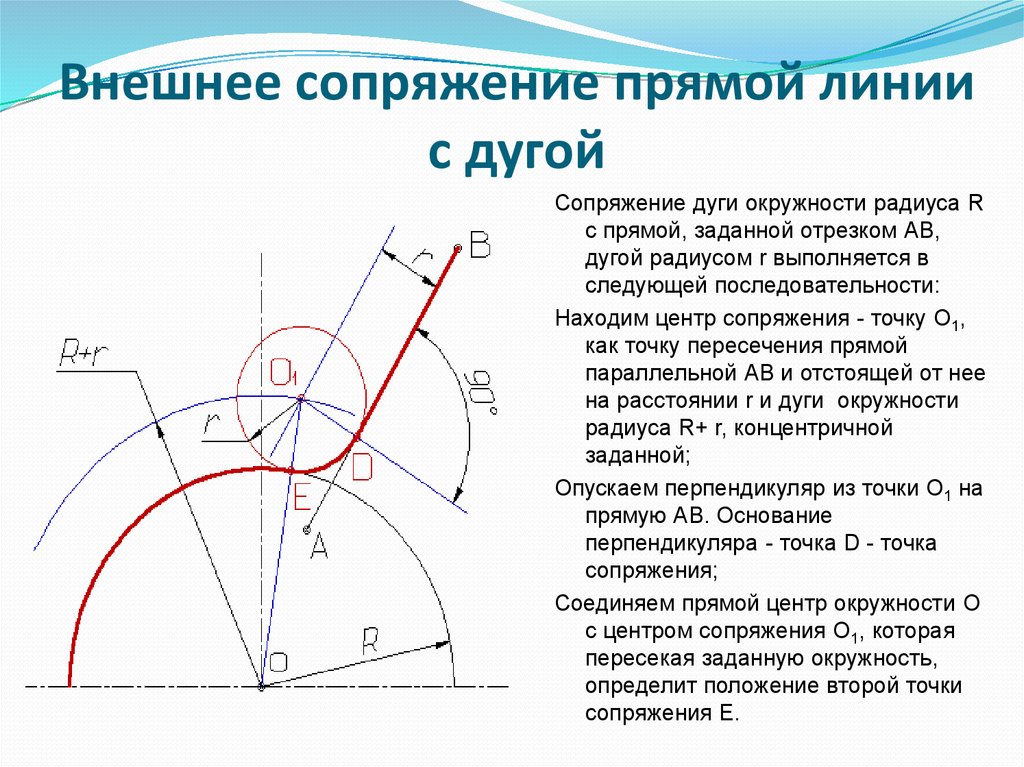

Радиус этой окружности равен 2, а центральный угол равен 30∘, поэтому имеем 𝑙=30360(2𝜋(2))=𝜋3.∘∘lengthunits

Это также говорит нам, что любая дуга длины 𝜋3 в этом круге или в любом круге радиусом 2 единицы длины будет иметь мера 30∘.

Давайте теперь посмотрим на пример того, как мы можем применить это свойство конгруэнтности дуги, чтобы определить длину дуги в окружности.

Пример 5: взаимосвязь между дугами одинаковой длины

Рассмотрим окружность 𝑀 с двумя дугами, 𝐴𝐵 и 𝐶𝐷, которые имеют равные меры. 𝐴𝐵 имеет длину 5 см. Какова длина 𝐶𝐷?

Ответить

Нам сказали, что 𝐴𝐵 и 𝐶𝐷 имеют одинаковую меру, и мы можем вспомнить что если две дуги имеют одинаковую меру, то они конгруэнтны. Так, их длины равны. Следовательно, 𝐶𝐷 имеет длину 5 см.

Хотя это и не обязательно при ответе на этот вопрос, его стоит посмотреть почему этот результат верен из формулы длины дуги.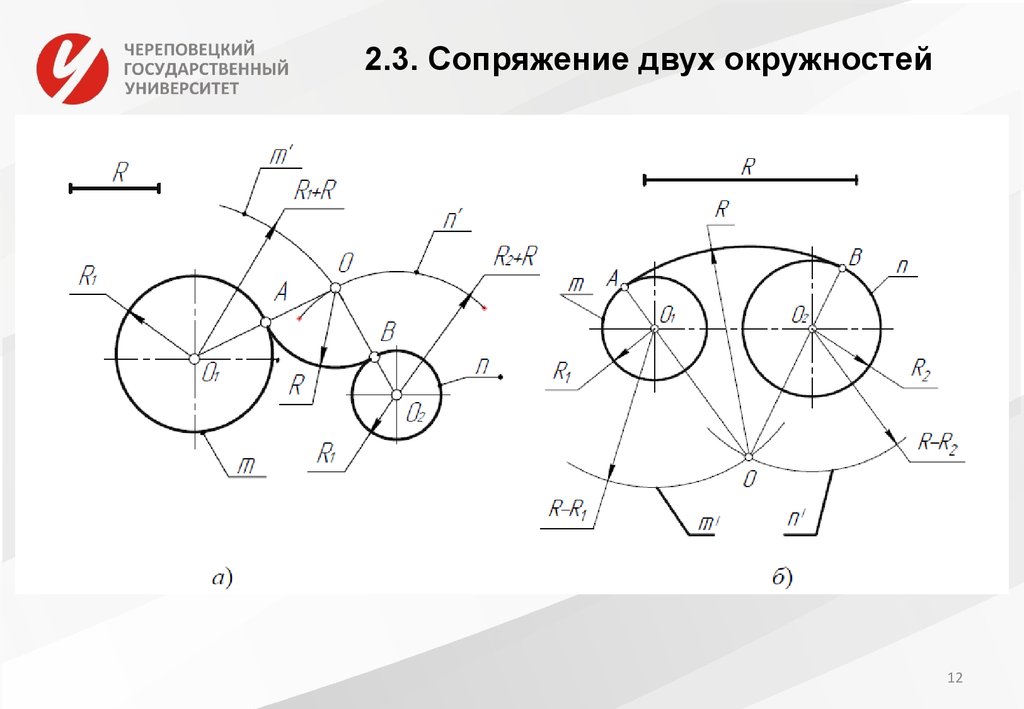 Мы напомним, что длина 𝑙 дуги между 𝑃 и 𝑄 по кругу радиуса 𝑟 находится по формуле 𝑙=𝑚𝑃𝑄360(2𝜋𝑟).

Итак, длина 𝐴𝐵 определяется выражением 𝑙=𝑚𝐴𝐵360(2𝜋𝑟).

Поскольку 𝑚𝐴𝐵=𝑚𝐶𝐷, имеем 𝑙=𝑚𝐴𝐵360(2𝜋𝑟)=𝑚𝐶𝐷360(2𝜋𝑟).

Однако это выражение равно длине 𝐶𝐷, поэтому их длины равны.

Следовательно, 𝐶𝐷 имеет длину 5 см.

Другим свойством, аналогичным свойству в приведенном выше примере, является то, что если длины хорды между концами двух дуг окружности равны, то дуги имеют равные меры. На самом деле то же самое верно и в обратном порядке; если дуги одинаковы мера, то хорды между их соответствующими конечными точками будут иметь равные длины.

Чтобы понять, почему это так, рассмотрите следующий круг.

Предположим, что 𝐴𝐵 и 𝐶𝐷 имеют равные меры. Затем меры по центральные углы равны: 𝑚∠𝐷𝑀𝐶=𝑚∠𝐴𝑀𝐵.

Мы также знаем, что 𝐴𝑀, 𝐵𝑀, 𝐶𝑀, и 𝐷𝑀 — радиусы, поэтому они имеют одинаковые длина.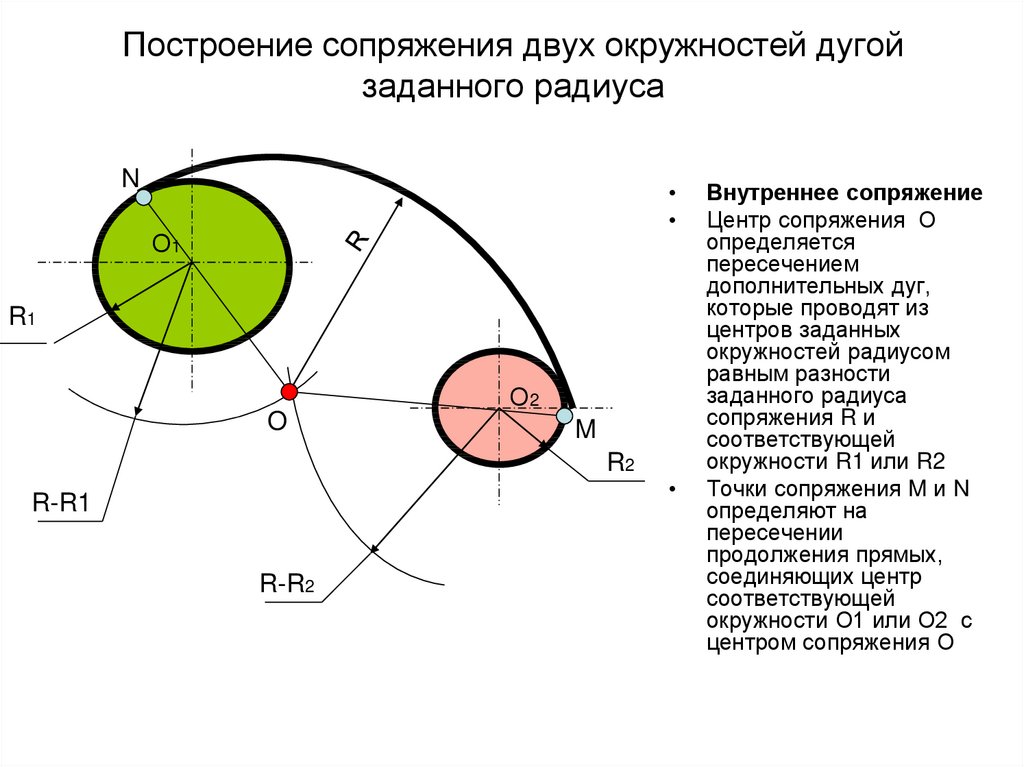 Следовательно, треугольники 𝐴𝑀𝐵 и 𝐷𝑀𝐶 конгруэнтны по правилу SAS, поэтому 𝐴𝐵 и 𝐷𝐶 должны иметь одинаковую длину.

Аналогично, если 𝐴𝐵 и 𝐶𝐷 имеют одинаковую длину, то с помощью радиусов окружности, у нас есть треугольники 𝐴𝑀𝐵 и 𝐷𝑀𝐶 конгруэнтны по правилу SSS. Так, меры внутренние углы равны. Особенно, 𝑚∠𝐷𝑀𝐶=𝑚∠𝐴𝑀𝐵.

Тогда, поскольку меры центральных углов равны, мы знаем, что их меры (и длины дуг) равны.

Свойство: конгруэнтные хорды конгруэнтных дуг

В одном и том же круге или в конгруэнтных кругах, если две дуги имеют одинаковую меру, тогда хорды между их соответствующими конечными точками будут иметь одинаковую длину. На самом деле то же самое верно и в обратном порядке; в том же круге или в конгруэнтных кругах, если две хорды между концами двух дуг конгруэнтны, то две дуги имеют одинаковую меру. Мы можем видеть это на следующей диаграмме.

1. Если 𝑚𝐴𝐵=𝑚𝐷𝐶, тогда 𝐴𝐵=𝐷𝐶.
2. Если 𝐴𝐵=𝐷𝐶, то 𝑚𝐴𝐵=𝑚𝐷𝐶.

Давайте посмотрим на пример того, как мы можем применить это свойство.

Пример 6: понимание связи между дугами и хордами

Рассмотрим круг 𝑀 с двумя хордами одинаковой длины, 𝐴𝐷 и 𝐵𝐶. Если 𝐴𝐷 имеет длину 5 см, какова длина 𝐵𝐶?

Ответ

Мы видим, что 𝐴𝐷 и 𝐵𝐶 — хорды между конечными точками дуг 𝐴𝐷 и 𝐵𝐶 как показано.

Вспомним, что если длины хорд между концами две дуги окружности равны, то дуги имеют одинаковую длину и меры. Следовательно, поскольку 𝐴𝐷 и 𝐵𝐶 имеют одинаковую длину, 𝐴𝐷 и 𝐵𝐶 также будет иметь одинаковую длину.

Следовательно, поскольку 𝐴𝐷 имеет длину 5 см, 𝐵𝐶 также имеет длину 5 см.

В нашем следующем примере мы будем использовать диаграмму и свойства центральных углов для определить меру данной дуги.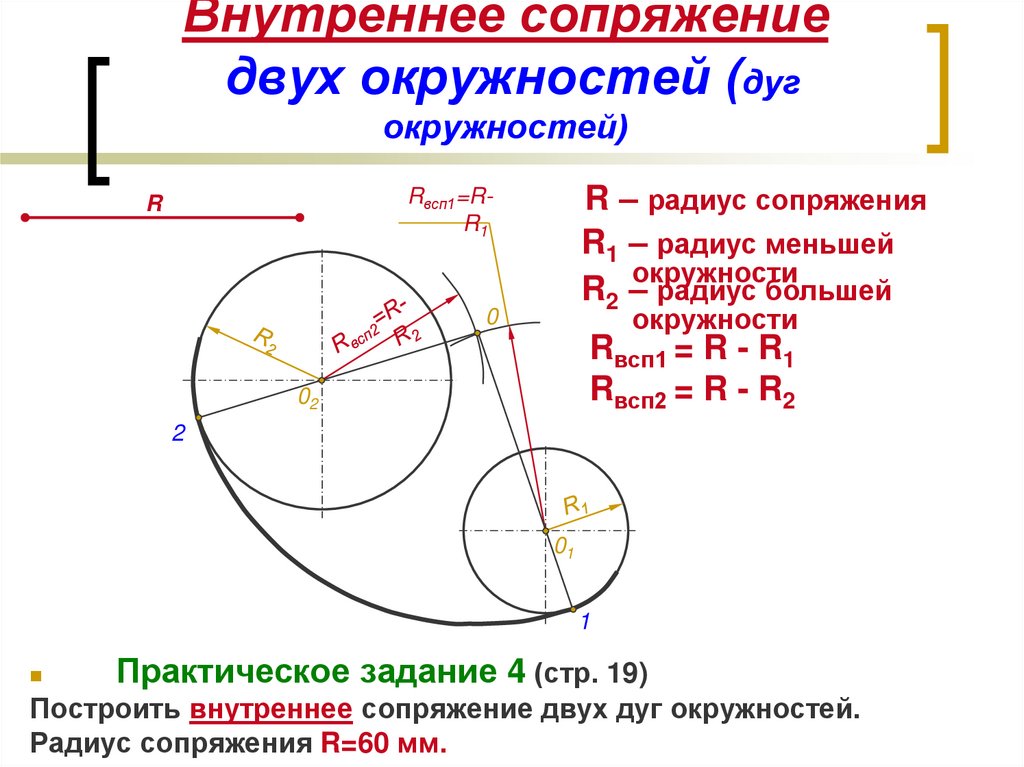

Пример 7. Нахождение меры дуги окружности по заданному диаметру и Меры двух центральных углов в виде алгебраических выражений

Учитывая, что 𝐴𝐵 — диаметр в окружности 𝑀 и 𝑚∠𝐷𝑀𝐵=(5𝑥+12)∘, определить 𝑚𝐴𝐶.

Ответ

Нас просят найти 𝑚𝐴𝐶, меру малой дуги от 𝐴 до 𝐶, показанная дуга на следующей диаграмме.

Вспомним, что мера дуги равна ее центральному углу, и мы На схеме видно, что центральный угол этой дуги равен 4𝑥∘. Итак, 𝑚𝐴𝐶=4𝑥∘. Следовательно, нам нужно определить значение 𝑥. Чтобы найти значение 𝑥, мы начнем с добавления угла, который нам дан в вопросе к схеме.

Затем заметим, что 𝐴𝐵 — это диаметр круг, что означает, что это прямая линия. Итак, мы должны иметь 𝑚 Хорошо+𝑚 Хорошо = 180 (5𝑥+12)+2𝑥 = 180.∘∘∘∘

Мы можем затем решить это для 𝑥7𝑥+12 = 1807𝑥 = 168𝑥 = 24.∘∘∘∘∘∘∘

Наконец, мы знаем, что 𝑚𝐴𝐶=4𝑥. ∘

Подставляя значение 𝑥, получаем, что 𝑚𝐴𝐶=4(24)=96.∘∘

Давайте закончим повторением некоторых важных моментов этого объяснитель.

Ключевые моменты

• Дуга окружности – это часть окружности окружности между двумя радиусы.
• Центральный угол окружности – это угол между двумя радиусами с вершиной в центр.
• Центральный угол дуги — это центральный угол, образуемый дугой.
• Мерой дуги является мера ее центрального угла.
• Для двух радиусов мы обозначаем более длинную из двух дуг между радиусами как большая дуга , и более короткая из дуг как меньшая дуга . Дуги равной длины называются дугами полуокружности; это происходит, когда радиусы образуют диаметр.
• Дуга является большой, если ее мера (или мера ее центрального угла) больше 180∘, дуга минор, если его мера (или мера его центрального угла) меньше 180∘, а дуга полукруглым, если его мера (или мера его центрального угла) равна 180∘.