В шестнадцатеричной системе счисления используются символы: Система счисления

Система счисления

Система счисления

                                                 Система счисления

Система счисления — это способ записи чисел с помощью заданного набора специальных символов.

Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес цифры (то есть тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Например, в числе 357,6  первый символ  3 означает 3 сотни; второй символ 5 означает 5 десятков, третий символ  7 означает 7 единиц, а четвертый символ  6 означает 6 десятых долей единицы.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных символов, используемых для изображения чисел в данной системе счисления.

В настоящее время, кроме хорошо известной нам десятичной системы счисления в вычислительной технике используются  двоичная, восьмеричная, и шестнадцатеричная системы счисления. Все применяемые в настоящее время системы счисления позиционные.

В десятичной системе счисления для изображения чисел используются 10 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Поэтому основанием десятичной системы счисления является число 10.

В двоичной системе счисления для изображения чисел используется 2 символа: 0,  1. Поэтому основанием двоичной системы счисления является число 2.

В восьмеричной системе счисления для изображения чисел используются 8 символов: 0, 1, 2, 3, 4, 5, 6, 7. Поэтому основанием восьмеричной системы счисления является число 8.

В шестнадцатеричной системе счисления для изображения чисел используются 16 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F, где:

А = 10;   B = 11;  C = 12;  D = 13;  E = 14;  F = 15.

Поэтому основанием шестнадцатеричной системы счисления является число 16.

 

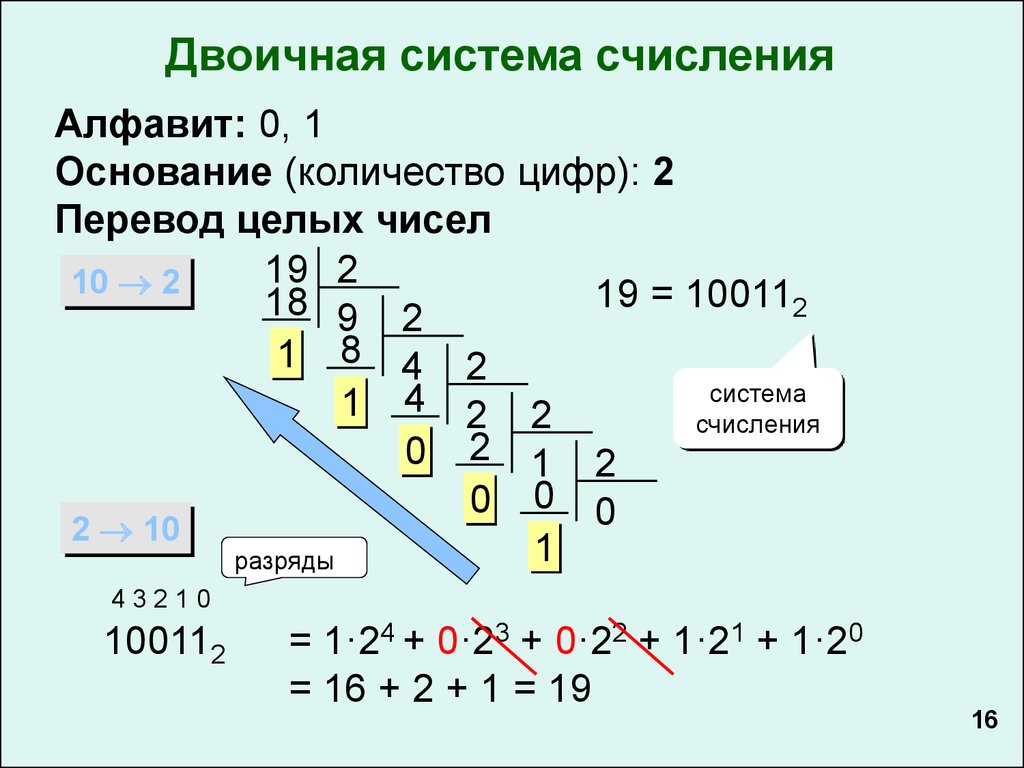
Перевод целого числа из десятичной системы счисления в любую другую систему счисления.

При переводе целого числа из десятичной системы счисления в любую другую систему счисления, нужно это число последовательно делить на основание новой системы счисления так, чтобы в остатках от деления были только символы новой системы счисления. Число в новой системе счисления записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Например,  переведём число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную системы счисления:

                                       

 

Таким образом, число 75₁₀ = 1001011₂ = 113₈ = 4В₁₆

 

Перевод дробной части числа из десятичной системы счисления в любую другую систему счисления.

При переводе дробной части числа из десятичной системы счисления в любую другую систему счисления, нужно дробную часть числа последовательно умножать на основание новой системы счисления. Дробная часть числа в новой системе счисления записывается как последовательность целых частей от умножения, записанных в прямом порядке, начиная с первого.

Например,  переведём дробное число 0, 96 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную системы счисления:

                              

 

Таким образом, число 0,96₁₀ = 0,111101₂ = 0,75341₈ = 0.F5C28F₁₆                                         

  

 Перевод чисел из любой системы счисления в десятичную систему счисления.

При переводе числа из любой системы счисления в десятичную систему счисления нужно каждый символ этого числа умножить на основание системы счисления, в которой записано это число, в степени соответствующей положению символа в записи числа и все произведения сложить.

 

Например:

1) переведём число 101100, 1011₂  из двоичной системы счисления в десятичную систему счисления:

101100, 101₂ = 1*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 0*2⁰  + 1*2^-1 + 0*2^-2 + 1*2^-3  =
 = 32 + 0 + 8 + 4 + 0 + 0 + 0,5 + 0 + 0,125 = 44, 625₁₀

 

2) переведём число 375, 624

₈  из восьмеричной системы счисления в десятичную систему счисления:

375, 624

₈  = 3*8² + 7*8¹ + 5*8⁰ + 6*8^-1 + 2*8^-2 + 4*8^-3 =

= 192 + 56 + 5 + 0,75 + 0,03125 + 0,00781835938 = 253, 78906835938

₁₀

 

3) переведём число ACF, 5D

₁₆  из шестнадцатеричной системы счисления в десятичную систему счисления:

ACF, 5D

₁₆  = 10*16² + 12*16¹ + 15*16⁰ + 5*16^-1 + 13*16^-2 =
= 256 + 192 + 15 + 0,3125 + 0,050775 = 463, 363275₁₀

 

    Перевод чисел из двоичной системы счисления в восьмеричную систему счисления.

При переводе числа из двоичной системы счисления в восьмеричную систему счисления, нужно это число влево и вправо от запятой разбить на триады символов (группы по три символа) и каждую триаду записать в виде символа восьмеричной системы счисления. В том случае, если крайняя левая или правая триады получаются неполными, нужно в этих триадах слева добавить недостающее количество до полной триады нулей.

Например, переведём число 1101111100, 11100111

₂ в восьмеричную систему счисления.

                                            

                 

 

    Перевод чисел из восьмеричной системы счисления в двоичную систему счисления.

При переводе числа из восьмеричной системы счисления в двоичную систему счисления, нужно каждый символ этого числа записать в виде триады символов двоичной системы счисления. В том случае, если при записи очередного символа триадой, триада получается неполной, нужно в этой триаде слева добавить недостающее количество до полной триады нулей.

Например, переведём число 6374, 25

₈  в двоичную систему счисления.

                                             

                                            

    Перевод чисел из двоичной системы счисления в шестнадцатеричную систему счисления.

При переводе числа из двоичной системы счисления в шестнадцатеричную систему счисления, нужно это число влево и вправо от запятой разбить на тетрады символов (группы по три четыре) и каждую тетраду записать в виде символа шестнадцатеричной системы счисления. В том случае, если крайняя левая или правая тетрада получаются неполными, нужно в этих тетрадах слева добавить недостающее количество до полной тетрады нулей.

Например, переведём число 1101111100, 11100111

₂ в шестнадцатеричную систему счисления.

                                  

                      

 

    Перевод чисел из шестнадцатеричной системы счисления в двоичную систему счисления.

При переводе числа из шестнадцатеричной системы счисления в двоичную систему счисления, нужно каждый символ этого числа записать в виде тетрады символов двоичной системы счисления. В том случае, если при записи очередного символа тетрадой, тетрада получается неполной, нужно в этой тетраде слева добавить недостающее количество до полной тетрады нулей.

Например, переведём число АЕС2, 3В

₁₆  в двоичную систему счисления.

                            

                              

                                                      

     

                                               Двоичная арифметика.

 

Сложение чисел в двоичной системе счисления.

При сложении чисел в двоичной системе счисления, нужно использовать следующую таблицу сложения:

                                                    1 + 0 = 1

                                                    0 + 1 = 1

                                                    0 + 0 = 0

                                                    1 + 1 = 10

                                            

Например, сложим числа 1101111₂    и    1011101₂                                             

                                            

 

Умножение чисел в двоичной системе счисления.

При умножении чисел в двоичной системе счисления, нужно использовать следующую таблицу умножения:

                                                    1 * 0 = 0

                                                    0 * 1 = 0

                                                    0 * 0 = 0

                                                    1 * 1 = 1

 

Например, перемножим числа 11111₂    и    101₂

                                             

 

 Вычитание чисел в двоичной системе счисления.

Вычитание чисел в двоичной системе счисления заменяется сложением уменьшаемого и  вычитаемого. Вычитаемое при этом записывается в обратном коде.

Обратный код получается из прямого кода путём замены всех нулей на 1, а всех единиц на 0.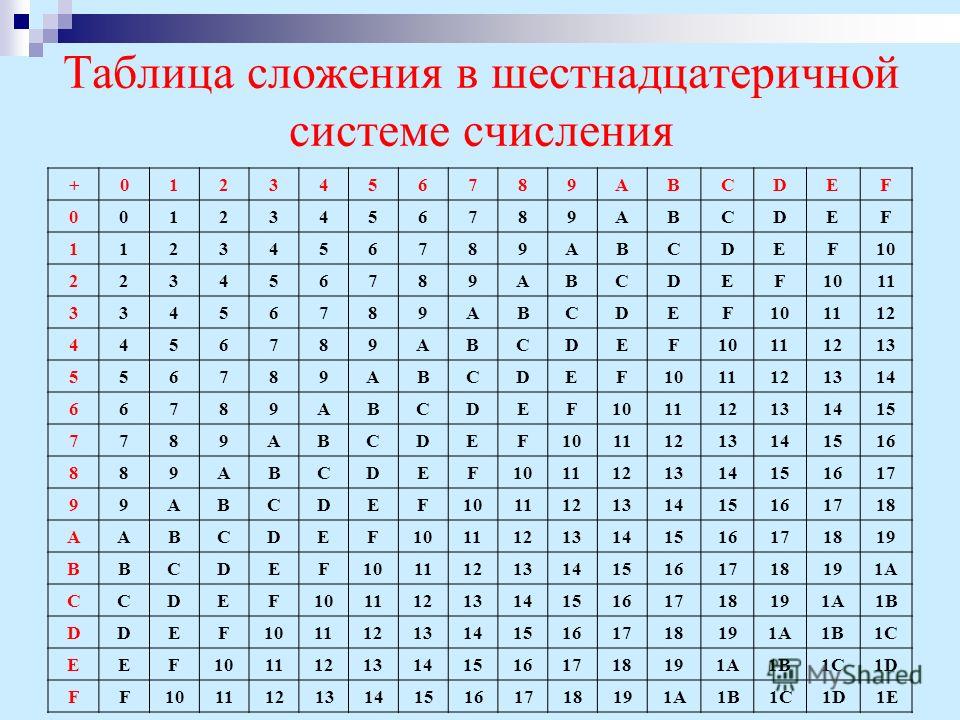

Процесс вычитания чисел в двоичной системе счисления происходит в два этапа.

На первом этапе выравнивается количество разрядов у уменьшаемого и вычитаемого и добавляются знаковые разряды. В знаковом разряде у положительного числа записывается 1, а в знаковом разряде у отрицательного числа записывается 0.

На втором этапе вычитаемое записывается в обратном коде. Для этого все нули у вычитаемого заменяются на 1 а все единицы у вычитаемого заменяются на 0.

Затем происходит сложение уменьшаемого, записанного в прямом коде с вычитаемым, записанным в обратном коде.

На этом же этапе происходит анализ полученного ответа.

 

Вычтем из большего числа меньшее число:    110111101 – 1011011₂

                         

 

Анализ ответа говорит о том, что ответ положителен (так как в знаковом разряде стоит 0), и поэтому он записан в прямом коде.

Таким образом, ответ:  101100010₂                             

 

Вычтем из меньшего числа большее число:      110111 – 11101101

 

                                                    

 

Анализ ответа говорит о том, что ответ отрицателен (так как в знаковом разряде стоит 1), и поэтому он записан пока что в обратном коде. Для получения окончательного ответа нужно преобразовать его в прямой код, то есть заменить все нули на 1 а все единицы на 0.

Таким образом, окончательный ответ:  — 10110110₂                             

 

                                                                                           В начало страницы 

 

 

 

 

 

 

Шестнадцатеричная система счисления | это.

.. Что такое Шестнадцатеричная система счисления?

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.

Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10₁₀ до 15₁₀, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

Содержание 1 Применение 2 Способы записи 2.1 В математике 2.2 В языках программирования 2.3 В электронных калькуляторах 3 Перевод чисел из одной системы счисления в другую 3.1 Перевод чисел из шестнадцатеричной системы в десятичную 3.2 Перевод чисел из двоичной системы в шестнадцатеричную и наоборот 3.3 Таблица перевода чисел 4 См. также 5 Ссылки

Применение

Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).

Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.

Способы записи

В математике

В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 1443₁₀ или как 5A3₁₆.

В языках программирования

В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:

• В Ада и VHDL такие числа указывают так: «16#5A3#».
• В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
• В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (255₁₀)
• Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
• Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
• Другие версии Бейсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
• В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.

В электронных калькуляторах

Б3-34 и ему подобные используют «-», «L», «C», «Г», «E» « » (space) на их экране.

Перевод чисел из одной системы счисления в другую

Перевод чисел из шестнадцатеричной системы в десятичную

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

5A3₁₆ = 3·16⁰+10·16¹+5·16²
= 3·1+10·16+5·256 = 3+160+1280 = 1443₁₀

Перевод чисел из двоичной системы в шестнадцатеричную и наоборот

Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведенной таблицы перевода.

Например:

010110100011₂ = 0101 1010 0011 = 5A3₁₆

Таблица перевода чисел

	0hex	=	0dec	=	0oct		0	0	0	0
	1hex	=	1dec	=	1oct		0	0	0	1
	2hex	=	2dec	=	2oct		0	0	1	0
	3hex	=	3dec	=	3oct		0	0	1	1
	4hex	=	4dec	=	4oct		0	1	0	0
	5hex	=	5dec	=	5oct		0	1	0	1
	6hex	=	6dec	=	6oct		0	1	1	0
	7hex	=	7dec	=	7oct		0	1	1	1
	8hex	=	8dec	=	10oct		1	0	0	0
	9hex	=	9dec	=	11oct		1	0	0	1
	Ahex	=	10dec	=	12oct		1	0	1	0
	Bhex	=	11dec	=	13oct		1	0	1	1
	Chex	=	12dec	=	14oct		1	1	0	0
	Dhex	=	13dec	=	15oct		1	1	0	1
	Ehex	=	14dec	=	16oct		1	1	1	0
	Fhex	=	15dec	=	17oct		1	1	1	1

См.

также

• Двоичные приставки
• Шестнадцатеричный редактор

Ссылки

• Шестнадцатеричные числа и операции с ними
• Таблица порядков двоичных, шестнадцатеричных и десятичных чисел

Простая английская Википедия, бесплатная энциклопедия. Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. Шестнадцатеричный использует десятичные числа и шесть дополнительных символов. Числовые символы, обозначающие значения больше девяти, отсутствуют, поэтому используются буквы английского алфавита, в частности A, B, C, D, E и F. Шестнадцатеричный A = десятичный 10, а шестнадцатеричный F = десятичный 15.

Люди в основном используют десятичную систему (с основанием 10), где каждая цифра может иметь одно из десяти значений от нуля до десяти. Вероятно, это потому, что у людей десять пальцев на руках. Компьютеры обычно представляют числа в двоичном формате (с основанием 2). В двоичном формате каждая «двоичная цифра» называется битом и может иметь только одно из двух значений: единицу или ноль. Поскольку два возможных значения одного бита представляют одну пятую часть информации, потенциально передаваемой десятью возможными значениями десятичной цифры, для двоичных представлений целых значений может потребоваться гораздо больше (двоичных) битов, чем десятичных цифр.

Например, трехзначное десятичное значение 219 требует, чтобы восемь битов были представлены в двоичном виде (11011011). Людям неудобно читать, запоминать и печатать длинные цепочки битов. Шестнадцатеричный формат позволяет более удобно представлять группы из четырех битов одной «шестнадцатеричной» цифрой, поэтому восьмибитное двоичное значение 11011011 требует только двух шестнадцатеричных цифр «DB».

Память компьютера организована в виде массива строк битов, называемых байтами. На современных компьютерах каждый байт обычно содержит восемь битов, которые удобно представить в виде двух шестнадцатеричных цифр. Инженеры и компьютерщики часто называют каждое из этих четырехбитных значений полубайтом (иногда пишется как nybble, см. компьютерный жаргон).

Во избежание путаницы с десятичной, восьмеричной или другими системами счисления шестнадцатеричные числа иногда пишутся с «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 в шестнадцатеричном формате.

В отличие от современных компьютеров, многие ранние компьютеры имели шестибитные байты. Программисты этих систем обычно использовали альтернативную схему группировки битов, называемую восьмеричной. Каждая восьмеричная цифра эффективно представляет три бита, а шестибитный байт может быть представлен двумя восьмеричными цифрами. Три бита, каждый из которых может быть включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7.

Шестнадцатеричная система счисления аналогична восьмеричной системе счисления (основание 8), поскольку каждую из них можно легко сравнить с двоичной системой счисления. Шестнадцатеричный использует четырехбитное двоичное кодирование.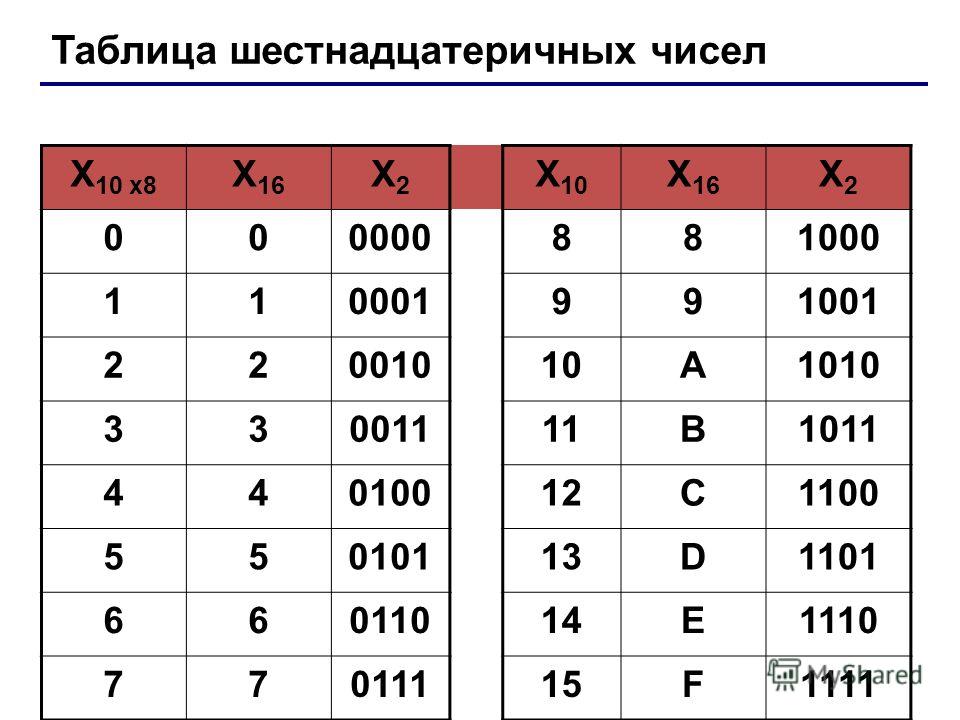 Это означает, что каждая цифра в шестнадцатеричном формате равна четырем цифрам в двоичном формате. Octal использует трехбитную двоичную систему.

В десятичной системе первая цифра — это разряда единицы, следующая слева цифра — это разряда десятков, следующая — разряда сотен и т. д. В шестнадцатеричной системе каждая цифра может иметь 16 значений , а не 10. Это означает, что цифры имеют занимает место, шестнадцать занимает место, а следующий 256 занимает место. Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 десятичный.

Пример значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.

Шестигранник Двоичный Восьмеричный Десятичный 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 А 1010 12 10 Б 1011 13 11 С 1100 14 12 Д 1101 15 13 Е 1110 16 14 Ф 1111 17 15 10 1 0000 20 16 11 1 0001 21 17 24 10 0100 44 36 5Е 101 1110 136 94 100 1 0000 0000 400 256 3E8 11 1110 1000 1750 1000 1000 1 0000 0000 0000 10000 4096 ЛИЦО 1111 1010 1100 1110 175316 64206

Двоичный в шестнадцатеричный[изменить | изменить источник]

При изменении числа с двоичного на шестнадцатеричное используется метод группировки.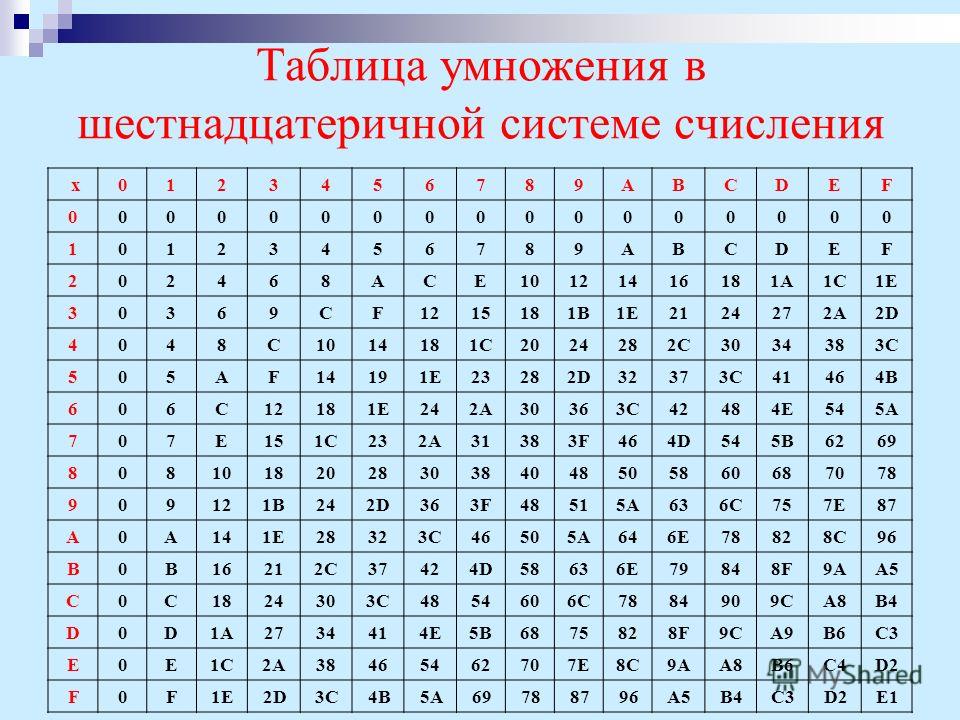 Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано в таблице выше для шестнадцатеричных чисел от 0 до F. Чтобы перейти от шестнадцатеричного, выполняется обратное. Каждая шестнадцатеричная цифра заменяется на двоичную, а группировка обычно удаляется.

Двоичный	Группировки				Шестнадцатеричный
01100101			0110	0101	65
010010110110		0100	1011	0110	4Б6
1101011101011010	1101	0111	0101	1010	Д75А

Когда количество битов в двоичном числе не кратно 4, оно дополняется нулями, чтобы это было так. Примеры:

• двоичное число 110 = 0110, то есть 6 шестнадцатеричных чисел.
• двоичный 010010 = 00010010, что составляет 12 шестнадцатеричных.

Шестнадцатеричное в десятичное[изменить | изменить источник]

Чтобы преобразовать число из шестнадцатеричного в десятичное, есть два распространенных способа.

Первый метод чаще используется при конвертации вручную:

1. Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15,
2. Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
3. Начните с младшей значащей шестнадцатеричной цифры. Это цифра справа. Это будет первый пункт в сумме.
4. Возьмите вторую наименее значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
5. Сделайте то же самое для третьей наименее значащей цифры, но умножьте ее на 16 ² (то есть 16 в квадрате или 256). Добавьте его к сумме.
6. Продолжайте для каждой цифры, умножая каждый разряд на другую степень 16. 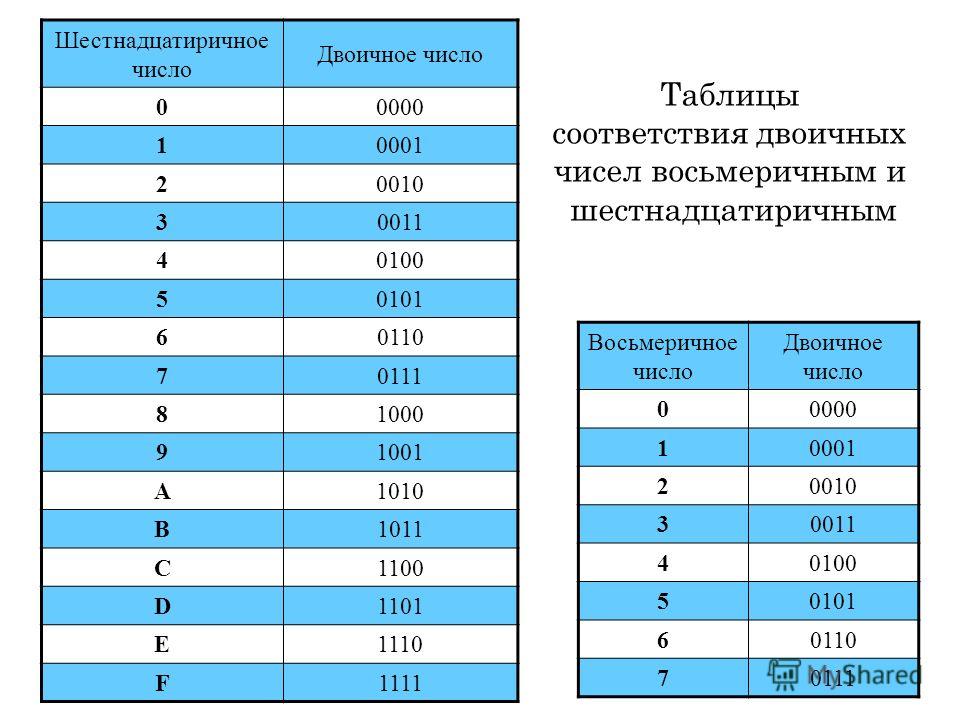(4096, 65536 и т. д.)

	Местоположение
	6	5	4	3	2	1
Значение	1048576 (16 5 )	65536 (16 4 )	4096 (16 3 )	256 (16 2 )	16(16 1 )	1 (16 0 )

Следующий метод чаще используется при преобразовании числа в программном обеспечении. Ему не нужно знать, сколько цифр в числе, прежде чем оно начнется, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.

1. Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
2. Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
3. Начните со старшей цифры (цифра крайняя слева). Это первый пункт в сумме.
4. Если существует другая цифра, умножьте сумму на 16 и добавьте десятичное значение следующей цифры.
5. Повторяйте вышеуказанный шаг, пока не закончатся цифры.

Пример: 5Fh и 3425h в десятичном виде, метод 1

5Fh до десятичного числа Шестигранник Десятичный 5фх = ( 5 х 16 ) + ( 15 х 1 ) = 80 + 15 5фх = 95

3425h в десятичной системе Шестигранник Десятичный 3425ч = (3 х 4096) + (4 х 256) + (2 х 16) + ( 5 х 1 ) = 12288 + 1024 + 32 + 5 3425ч = 13349

Пример: 5Fh и 3425h в десятичном виде, метод 2

5Fh до десятичного числа Шестигранник Десятичный сумма = 5 = (5 х 16) + 15 сумма = 80 + 15 (без цифр) 5фх = 95

3425h в десятичной системе Шестигранник Десятичный сумма = 3 = (3 х 16) + 4 = 52 сумма = (52 х 16) + 2 = 834 сумма = (834 х 16) + 5 = 13349 3425ч = 13349

• Двоичная система счисления
• Восьмеричная система счисления
• Десятичная система счисления

Система счисления

Система счисления представляет собой набор дискретных символов чисел, используемых для представления количества любых элементов. Например, система счисления, которой мы следуем в реальном мире, — это десятичная система счисления, также известная как система счисления с основанием 10. Это означает, что для представления количества используются 10 различных дискретных символов. Эти 10 дискретных символов равны 0,1,2,3,4,5,6,7,8,9.. Эта система счисления также известна как Десятичная система счисления . Какое бы число мы ни рассматривали, оно состоит только из этих 10 символов. Существуют и другие типы систем счисления. Например, Base2, Base8 и Base16. Это 4 типа систем счисления, которым мы обычно следуем. В системе счисления Base2 у нас есть только два уникальных символа: 0 и 1. Эта система счисления также известна как Двоичная система счисления . В системе счисления Base8 у нас есть только 8 уникальных символов: 0,1,2,3,4,5,6 и 7. Эта система счисления также известна как 9.0696 Восьмеричная система счисления . В системе счисления Base16 у нас есть только 16 уникальных символов: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E и F. Эта система счисления также известна как Шестнадцатеричная система счисления.

Несмотря на то, что у нас есть множество систем счисления, все они используются для представления уникальной величины. Давайте посмотрим на их эквивалентное представление для разных чисел.

Несмотря на то, что 1100 означает одну тысячу сто в десятичной системе, в двоичной системе это всего двенадцать. Из этих 4 систем счисления мы обычно используем десятичную систему счисления в реальном мире. Почему? Потому что нам рассказывали об этой системе счисления только с детства. Так что все привыкли. Это единственные системы счисления, которые у нас есть? Нет. Мы можем сформировать свои собственные системы счисления, изменив базовое значение. Мы можем сформировать систему счисления Base5, составив базу 5 только с 5 уникальными символами. В каждой системе счисления счет увеличивается за счет переноса на конце символа и размещения следующего старшего символа слева.

Почему из всех этих систем счисления для цифровых вычислений используется двоичная система счисления? Потому что у него есть только два уникальных символа для представления любого числа.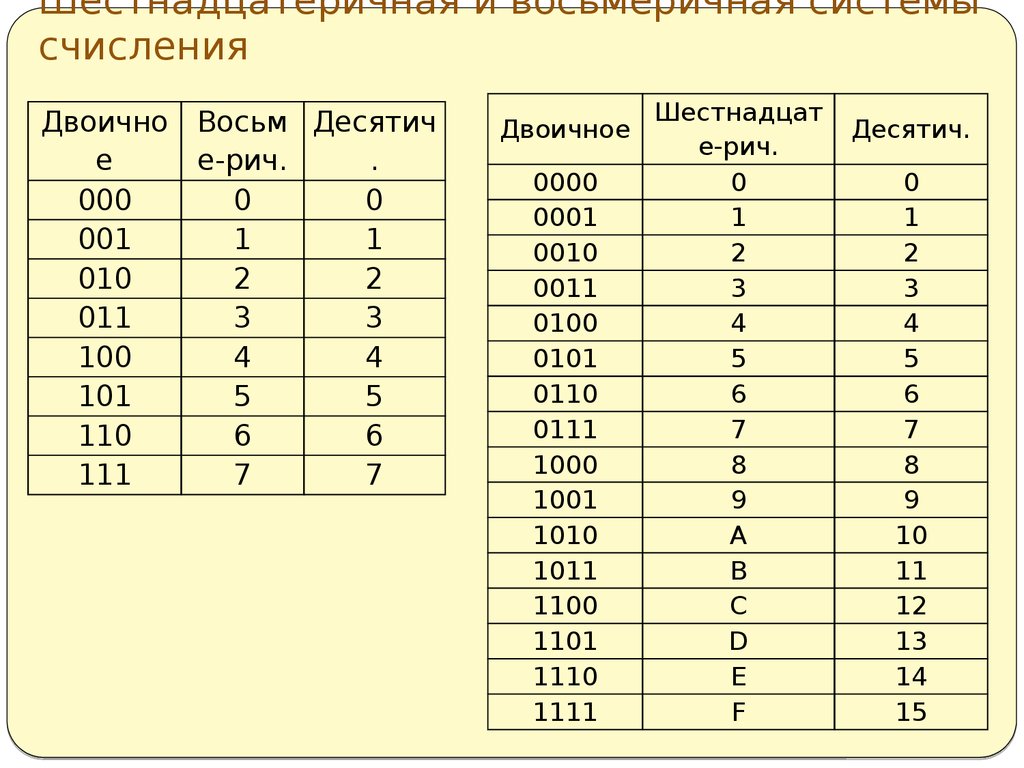 Эти два символа могут быть практически реализованы как ON, OFF переключателя. Как правило, 0 означает ВЫКЛ, а 1 — ВКЛ. Таким образом, любое число из любой системы счисления должно быть преобразовано в двоичную систему счисления, чтобы использовать его в цифровых вычислениях. Самый правый бит называется наименее значащим битом (LSB), а самый левый бит известен как старший значащий бит (MSB). Давайте посмотрим на преобразования чисел между этими основными 4-мя системами счисления.

Преобразование десятичных чисел в другие

• Преобразование десятичных чисел в двоичные:

Преобразование десятичного числа в двоичное может быть выполнено путем последовательного взятия остатков от деления десятичного числа на 2 снизу вверх до тех пор, пока частное не станет равным 0. верхний, двоичный 111000 представляет 56 .

Десятичный 29:

Взяв остатки снизу вверх, двоичное число 11101 представляет собой 29 .

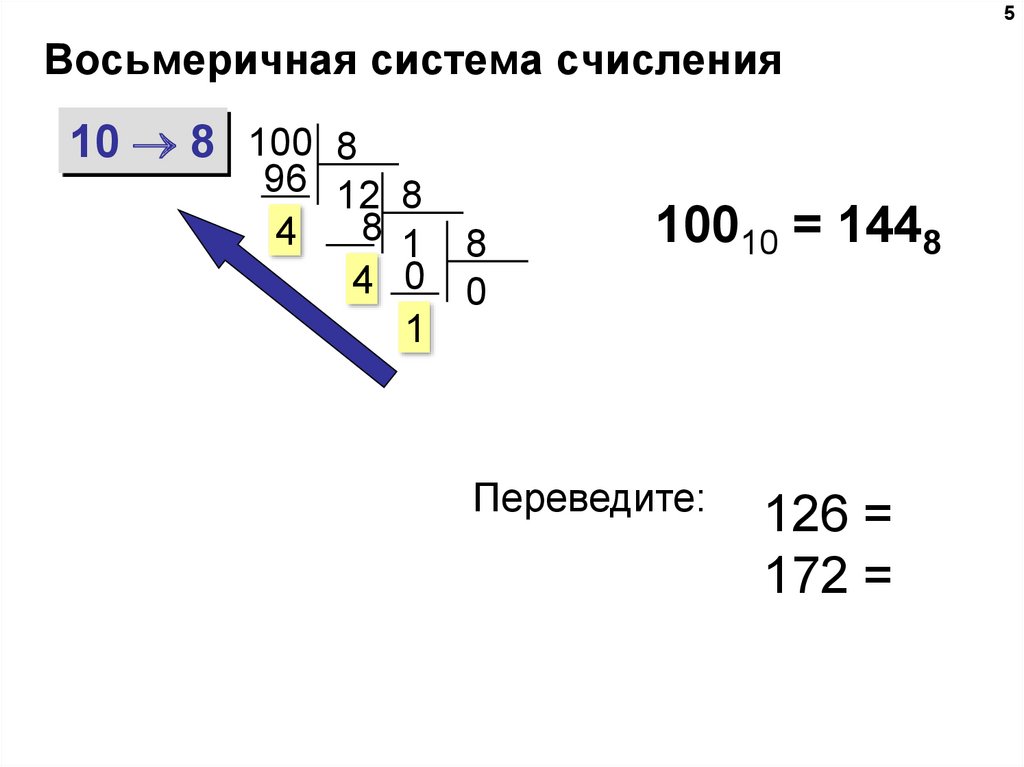
• Десятичный в восьмеричный:

Десятичное преобразование в восьмеричное может быть выполнено путем последовательного взятия остатков от деления десятичного числа на 8 снизу вверх до тех пор, пока частное не станет равным 0. вверху, восьмеричное 70 представляет 56 .

Десятичное число 29:

Взяв остатки снизу вверх, восьмеричное число 35 представляет собой 29 .

• Десятичный в шестнадцатеричный:

Преобразование десятичного числа в шестнадцатеричное может быть выполнено путем непрерывного вычисления остатков от деления десятичного числа на 16 снизу вверх до тех пор, пока частное не станет равным 0. вверху, шестнадцатеричное число 38  представляет собой 56 .

Десятичный 29:

Взяв остатки снизу вверх, шестнадцатеричный 1D  представляет 29 .

Шестнадцатеричный код в другие

• Шестнадцатеричный код в двоичный:

Преобразование шестнадцатеричных чисел в двоичные можно выполнить путем прямой записи эквивалентного двоичного представления каждого шестнадцатеричного символа и их объединения.

Шестнадцатеричный D5:

Двоичное представление D5 : 11010101 .

Шестнадцатеричный 83A:

Двоичное представление 83A : 100000111010 .

• Шестнадцатеричное число в восьмеричное:

Преобразование шестнадцатеричных чисел в восьмеричные можно выполнить в три этапа: 1) Сначала преобразовать шестнадцатеричные числа в двоичные. 2) Преобразовать двоичный файл в восьмеричный. Чтобы преобразовать двоичный файл в восьмеричный, разделите двоичный файл на группы по 3 бита с правой стороны.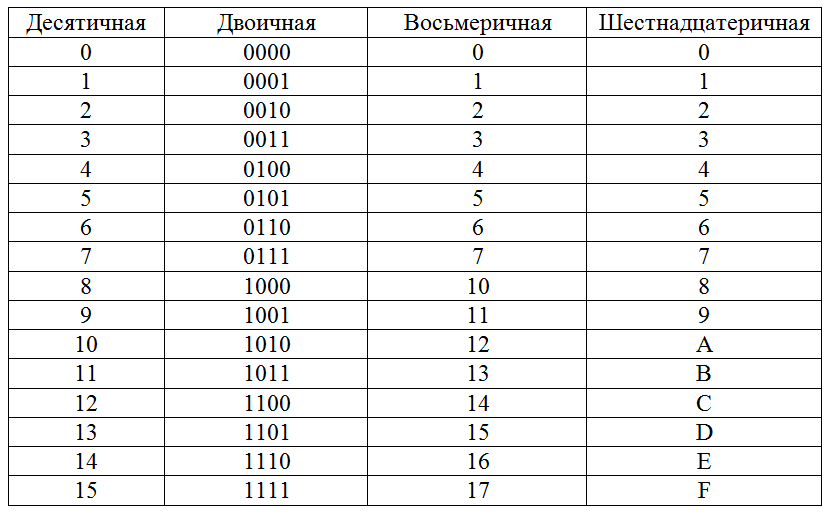 Если 3 бита недоступны для самой левой группы, добавьте 0. 3) Напишите восьмеричный эквивалент для каждой группы двоичных чисел.

Шестнадцатеричный D5:

Двоичное представление D5 : 11010101 .

Восьмеричное представление D5 равно 325 .

Шестнадцатеричный 83A:

Двоичное представление 83A : 100000111010 .

Восьмеричное представление 83A равно 4072 .

• Шестнадцатеричный код в десятичный:

Преобразование шестнадцатеричной системы в десятичную может быть выполнено путем суммирования умножения каждой цифры на 16-значный весовой коэффициент. Вес самой правой цифры равен 0.

Шестнадцатеричный D5:

Десятичное представление D5 : 213 .

Шестнадцатеричный 83A:

Десятичное представление 83A равно 2106 .

Восьмеричный в другие

• Восьмеричный в шестнадцатеричный

Восьмеричное преобразование в шестнадцатеричное можно выполнить, сначала преобразовав восьмеричное число в двоичное, а затем сгруппировав двоичное число по 4 бита справа. Заполните 0 для самой правой группы, если 4 бита недоступны. И напишите шестнадцатеричный эквивалент для каждой группы.

Восьмеричный 65:

Шестнадцатеричное представление 65 равно 35 .

Восьмеричное число 346:

Шестнадцатеричное представление 346 : E6 .

• Восьмеричный в десятичный

Восьмеричное преобразование в десятичное можно выполнить путем суммирования умножения каждой цифры на 8-значный вес.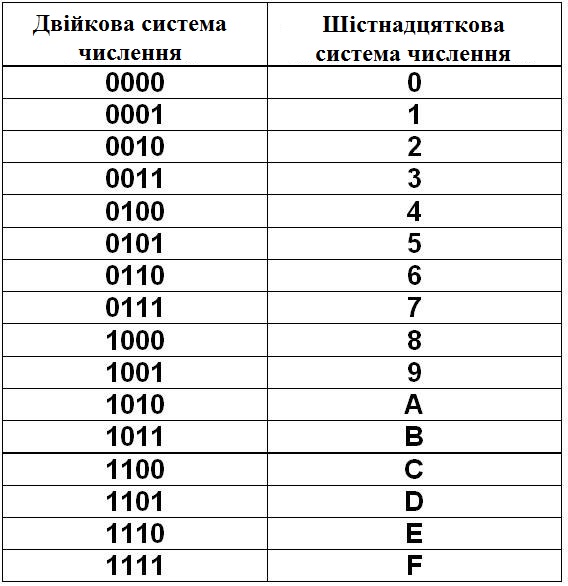 Вес самой правой цифры равен 0.

Восьмеричный 65:

Шестнадцатеричное представление 65 это 53 .

Восьмеричное число 346:

Шестнадцатеричное представление 346 : 230 .

• Восьмеричное в двоичное

Восьмеричное преобразование в двоичное может быть выполнено путем записи двоичного эквивалента для каждой восьмеричной цифры.

Восьмеричный 65:

Шестнадцатеричное представление 65 : 110101 .

Восьмеричный 346:

Шестнадцатеричное представление 346 : 011100110 .

Двоичное преобразование в другие

• Двоичное преобразование в шестнадцатеричное

Преобразование двоичного кода в шестнадцатеричный можно выполнить, записав двоичные цифры в группы по 4 бита и записав эквивалентное шестнадцатеричное значение для каждой группы.