В шестнадцатеричной системе счисления используют 16 цифр: Шестнадцатеричная система счисления | Информатика

16 в шестнадцатеричной системе. Системы счисления. Позиционная система счисления шестнадцатеричная

Шестнадцатеричная запись («Hex») — удобный способ представления двоичных значений. Так же, как десятичная система счисления имеет основание десять, а двоичная — два, шестнадцатеричная система имеет основание шестнадцать.

Система счисления с основанием 16 использует числа от 0 до 9 и буквы от A до F. Рисунок показывает эквивалентные десятичные, двоичные и шестнадцатеричные значения для двоичных чисел от 0000 до 1111. Для нас легче выражать значение в виде одной шестнадцатеричной цифры, чем в виде четырех битов.

Понимание Байтов

Учитывая, что 8 битов (байт) являются стандартной двоичной группировкой, двоичные числа от 00000000 до 11111111 могут быть представлены в шестнадцатеричной записи как числа от 00 до FF. Начальные нули всегда отображаются, чтобы завершить 8-разрядное представление. Например, двоичное значение 0000 1010 в шестнадцатеричном виде будет 0A.

Представление Шестнадцатеричных Значений

Отметьте: Важно отличать шестнадцатеричные значения от десятичных значений для символов от 0 до 9, как показано на рисунке.

Шестнадцатеричные значения обычно представляются в тексте значением, которому предшествует 0x (например 0x73), или с помощью нижнего индекса 16. Реже, они могут сопровождаться буквой H, например 73H. Однако, поскольку текст нижнего индекса не распознается ни в командной строке, ни в средах программирования, в техническом представлении шестнадцатеричных чисел им предшествует «0x» (нуль X). Поэтому, примеры выше были бы показаны в виде 0x0A и 0x73 соответственно.

Шестнадцатеричная запись используется, чтобы представлять MAC-адреса Ethernet и адреса IP Версии 6.

Шестнадцатеричные Преобразования

Преобразования чисел между десятичными и шестнадцатеричными значениями являются простыми, но быстрое деление или умножение на 16 не всегда удобно. Если такие преобразования необходимы, обычно легче преобразовать десятичное или шестнадцатеричное значение в двоичное, а затем преобразовать двоичное значение в десятичное или шестнадцатеричное, в зависимости от того, что требуется получить.

С практикой возможно распознать двоичные шаблоны битов, которые соответствуют десятичным и шестнадцатеричным значениям. Рисунок показывает эти шаблоны для некоторых 8-разрядных значений.

Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная

Системы счисления

Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще).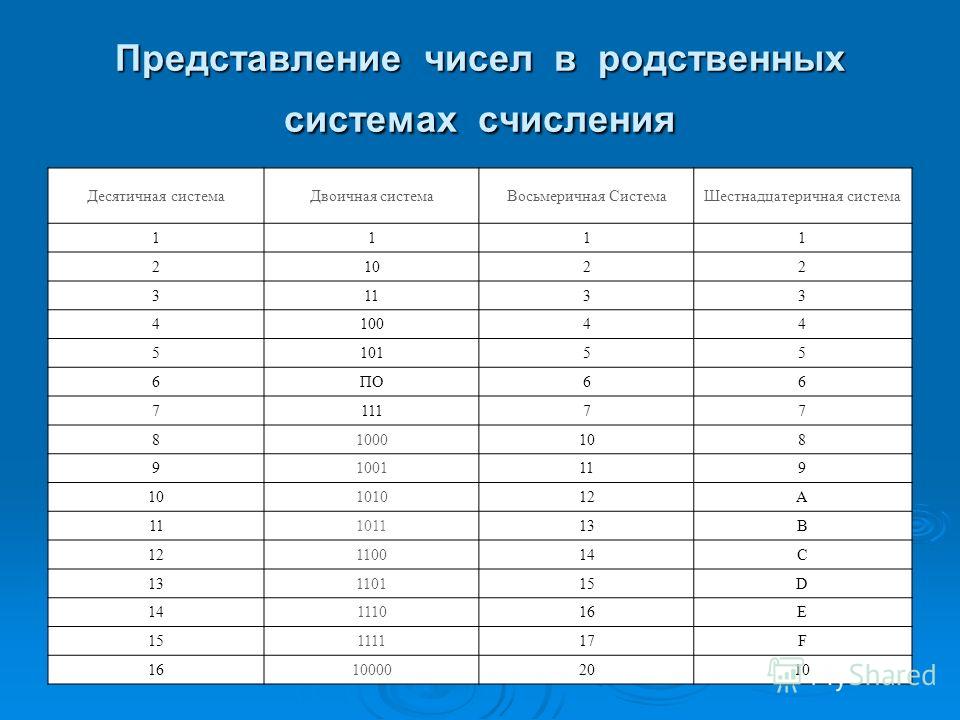 Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.

Понятие шестнадцатеричной системы

Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных — машинное слово — включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление.

Результатом также будет шестнадцатеричное число.

Где применяется

Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.

Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.

0123456789ABCDEF. Приняв за основание число 16, получаем шестнадцатеричную систему счисления. Здесь мы можем воспользоваться 10 знаками десятичной системы, добавив еще 6 знаков – буквы латинского алфавита (A, B, C, D, E, F): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 10 11 12 13 14 15 Всего 16 разных знаков составляют алфавит шестнадцатеричной системы счисления. Можно записать любое число включая все эти знаки: А37, 1В45, F302, 1A3C5… — обратите внимание: используем знаки от 0 до F. Для шестнадцатеричной системы счисления q=16. Содержание.

Слайд 32 из презентации «История счёта и систем счисления» . Размер архива с презентацией 2292 КБ.

Информатика 9 класс

краткое содержание других презентаций

««Моделирование» 9 класс» — Моделирование как метод познания. Файловая система ПК. Тест завершён. Птолемей построил модель мира. Модель человека в виде детской куклы. Удобнее всего при описании траектории движения объекта использовать информационную модель. Существующие признаки объекта. Описание дерева. Удобнее всего использовать информационную модель. Список депутатов государственной Думы. Список учащихся школы; план классных комнат.

«История счёта и систем счисления» — Основание системы счисления. Десятки. Десятичное число. Славянская кириллическая нумерация. Нумерация. Цветок лотоса. Позиция цифры в числе называется разрядом. Положение цифры. В древние времена люди ходили босиком. Позиционная система счисления характеризуется своим основанием. Деление на основание. Запись чисел нового типа. Умножение двоичных чисел. Перевод десятичного числа. Арифметические действия.

«Сортировка в электронных таблицах» — Сортировка и поиск данных в электронных таблицах. Поиск данных в ЭТ. Порядок проведения вложенной сортировки. Отдел. Условия поиска записей. Запишите фамилии. Практическая работа. Сортировка по возрастанию. Порядок следования строк. Сортировка и поиск данных. Оклад и возраст. Рефлексивный экран. Сортировка данных. Выберите примеры баз данных. Сортировка записей. Разница между записью и полем. Порядок использования автофильтра.

«Циклические программы» — Составить программу. Найти сумму. Введите целое число. Найти количество трехзначных натуральных чисел. Найти сумму натуральных чисел. Вычислить. Цикл с постусловием. Напечатать на экране таблицу. Первоначальный взнос. Цикл с предусловием. Делители. Циклические программы. Информатика. Табулирование функции. Понятие цикла. Цикл с параметром. Ввод исходных данных. Таблица перевода долларов. Найти количество чисел.

«Моделирование как метод научного познания» — Таблица типа «объекты-объекты-один». Описания объекта. Метод познания окружающего мира. Решение задач. Образовательные ресурсы. Пятеро ребят. Формализация. Этапы моделирования. Мальчик. Иерархическая модель. Описание объекта моделирования. Юра. Сирень. Обозначения серверов. Технические модели. Ярусные диаграммы. Диаграмма. Тип. Моделирование как метод познания. Модели на графах. Задачи, решаемые с помощью графов.

«Что такое электронная почта» — Адрес электронной почты. Маршутизация почты. Письмо. Как работает электронная почта. X-mailer. Вопрос появления электронной почты. Дата. Копия. Электронное письмо. Структура письма. История электронной почты. Отправитель. Электронная почта.

Привычная для человека система счисления – десятичная. В ее основу входят десять цифр от 0 до 9. Шестнадцатеричную систему отличает наличие в ней первых шести букв латинского алфавита для записи чисел помимо основных цифр. То есть после цифры 9 следует символ «A», который соответствует числу 10 для десятичной системы. Соответственно, F в шестнадцатеричной системе – это 16 в десятичной. Использование шестнадцати символов в системе – неслучайный выбор.

Единица информации – бит. Восемь бит образуют байт. Существует понятие, как машинное слово – это единица данных, представляющая собой два , то есть шестнадцать бит.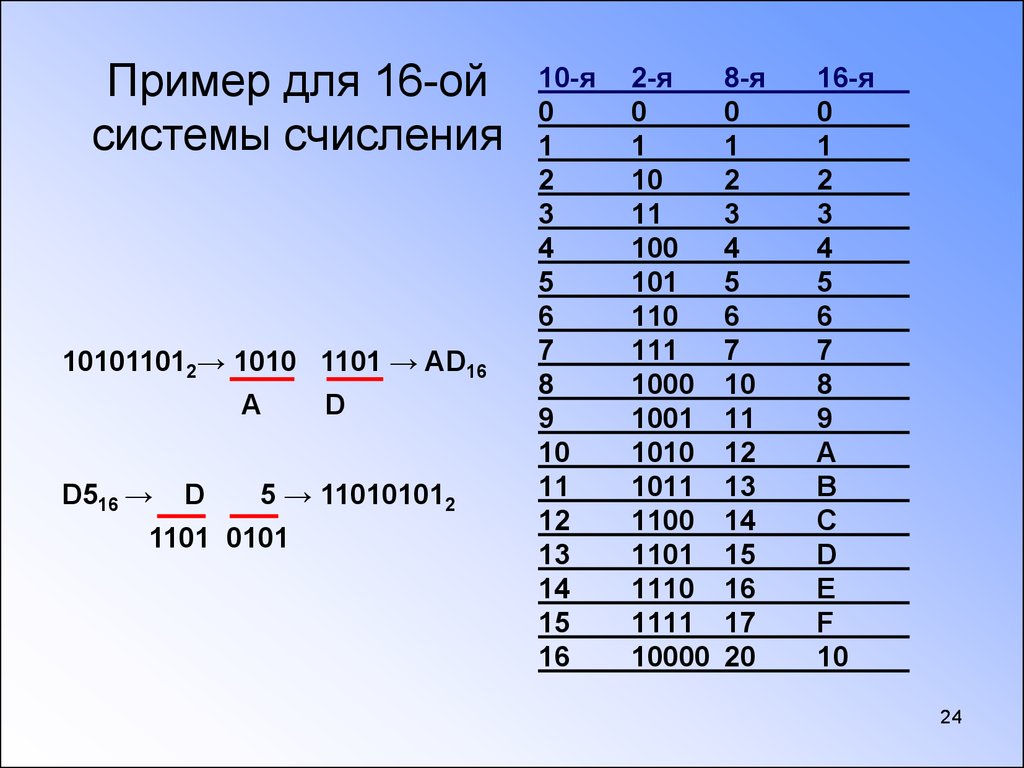 Таким образом, используя шестнадцать различных символов, можно описывать любую информацию, которая при обмене данных будет наименьшей частицей. С ними можно производить любые арифметические действия, результат, соответственно, получится тоже в шестнадцатеричной системе.

Для того чтобы отличать, что число записано в шестнадцатеричной системе, после него записывают букву «h» или нижний индекс «16».

Применение

Наиболее широкое применение шестнадцатеричной системы счисления – это коды ошибок программных продуктов, например, операционной системы. Числа, заложенные в этих кодах, стандартизированы. Имея специальную таблицу, всегда можно определить, что именно означает та или иная ошибка.

В языках низкого уровня, максимально приближенным к машинным кодам шестнадцатеричная система применяется для написания программ. Многие программисты используют ее и при работе с языками высокого уровня, потому что числа в этой системе при помощи специальной таблицы соответствия легко переводятся в двоичную систему, на которой основана работа всей цифровой техники.

Любая информация в компьютере, будь то музыкальный файл или текстовый документ, после трансляции представлена последовательностью исходного двоичного кода, а его удобнее просматривать представленным символами шестнадцатеричной системы.

Также одно из применений шестнадцатеричных символов – описание цветовых схем, то есть три компонента R, G, B описываются соответствующим данной системе способом. Данный подход к записи получил название шестнадцатеричный цвет

Возможность просмотреть программу в шестнадцатеричном коде позволяет отладить ее, внести изменения, а злоумышленниками данный подход используется для взлома программ.

Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:

• * A —10;
• * B —11;
• * C —12;
• * D —13;
• * E — 14;
• * F — 15.

Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.

Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .

Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.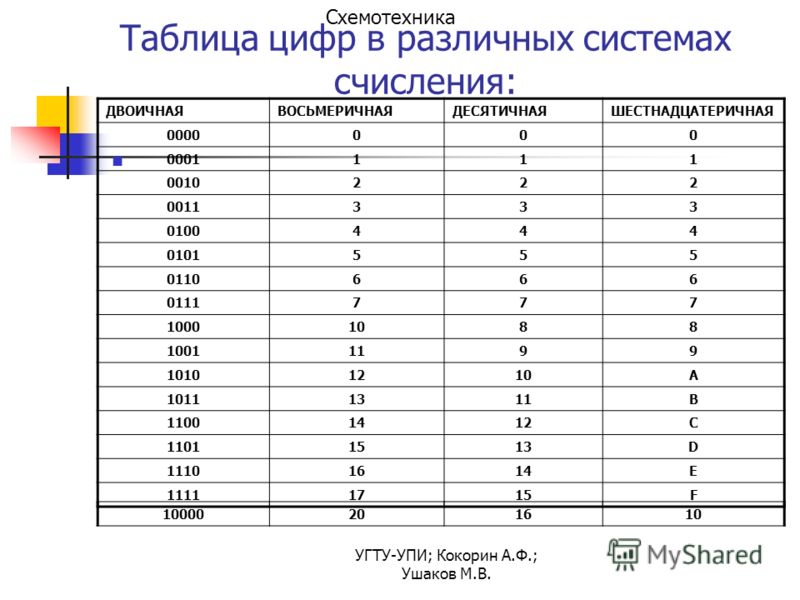

В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).

Способ записи шестнадцатеричного кода.

Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .

В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :

* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;

* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;

* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.

Как перевести шестнадцатеричный код в другую систему?

Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.

Двоичная СС	шестнадцатеричная СС

Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:

A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10

Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.

Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.

Таблица тетрад для перевода.

Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.

Двоичная СС	Восьмеричная СС

Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2

Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16

В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.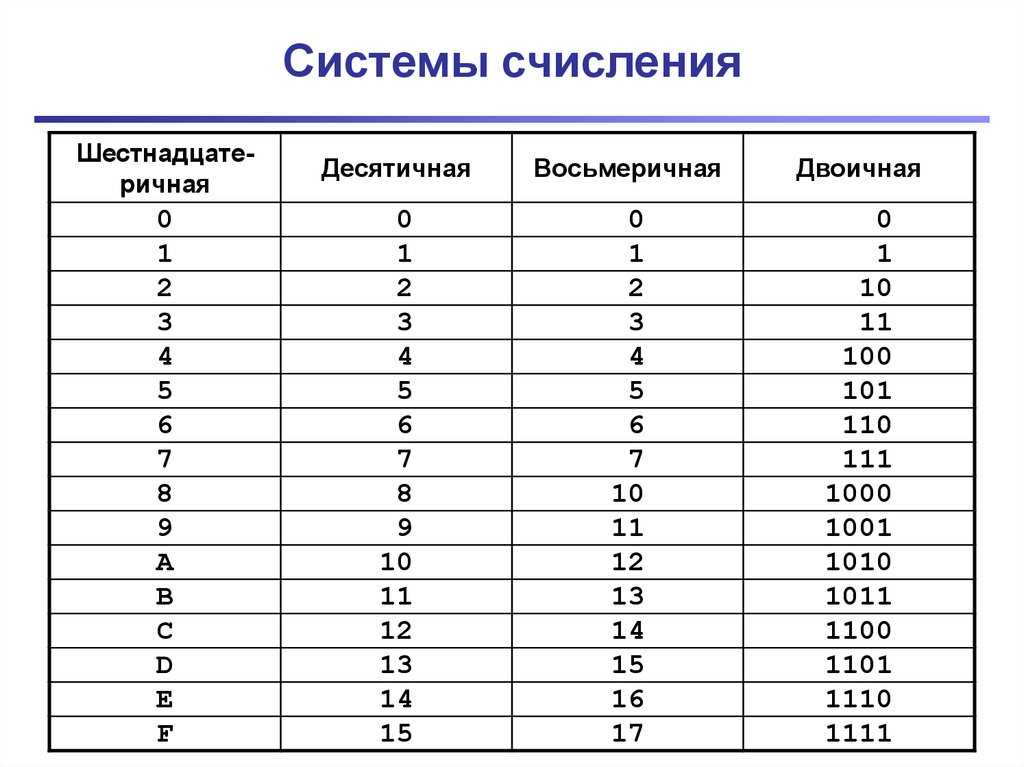

Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.

Шестнадцатеричная система счисления

Основание этой системы счисления p равно шестнадцати. Эту систему счисления можно считать ещё одним вариантом записи двоичного числа. В этой системе счисления используется шестнадцать цифр. Здесь уже не хватает десяти цифр, поэтому приходится придумать недостающие шесть цифр.

Для обозначения этих цифр можно воспользоваться первыми буквами латинского алфавита. При записи шестнадцатеричного числа неважно буквы верхнего или нижнего регистра будут использоваться в качестве цифр. В качестве цифр в шестнадцатеричной системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Так как здесь появляются новые цифры, то приведём таблицу соответствия этих цифр десятичным значениям.

Таблица 6. Таблица соответствия шестнадцатеричных цифр десятичным значениям

Шестнадцатеричная цифра	Десятичный эквивалент	Шестнадцатеричная цифра	Десятичный эквивалент
0	0	8	8
1	1	9	9
2	2	A	10
3	3	B	11
4	4	C	12
5	5	D	13
6	6	E	14
7	7	F	15

Число в этой системе счисления записывается как сумма единиц, чисел шестнадцать, двести пятьдесят шесть и так далее.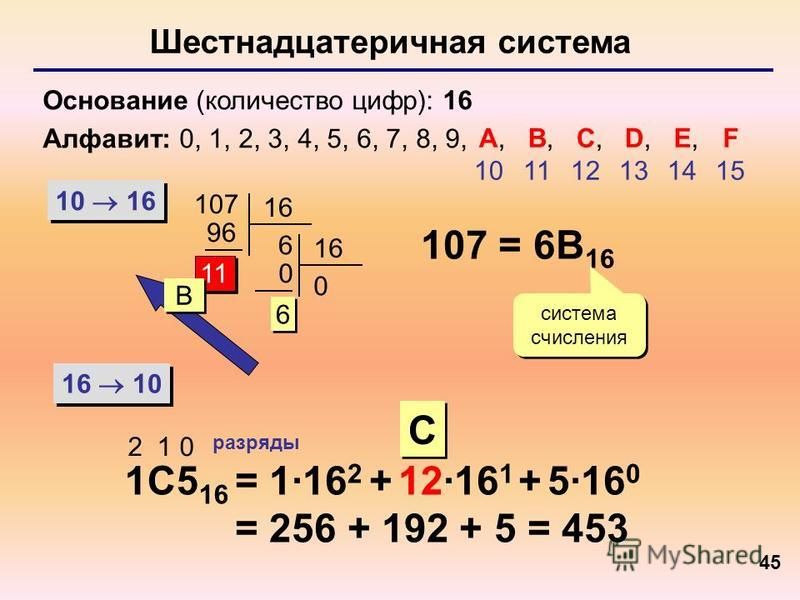 То есть веса соседних разрядов различаются в шестнадцать раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как шестнадцатые, двести пятьдесят шестые и так далее доли единицы.

Рассмотрим пример записи шестнадцатеричного числа:

A₁₆=2AF,C4₁₆=2*16²+10*16¹+15*16⁰+12*16^-1+4*16 ^-2= =512₁₀+160₁₀+15₁₀+12₁₀/16₁₀+4₁₀/254₁₀= 687,765625₁₀

Из приведённых примеров записи чисел в различных системах счисления вполне очевидно, что для записи одного и того же числа с одинаковой точностью в разных системах счисления требуется различное количество разрядов. Чем больше основание системы счисления, тем меньшее количество разрядов требуется для записи одного и того же числа.

Достаточно часто требуется уметь переводить число из одной системы счисления в другую. Давайте научимся выполнять такое действие. Преобразование целых чисел и правильных дробей выполняется по разным правилам. В действительном числе преобразование целой и дробной части производят по отдельности.

Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.

Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную систему счисления.

Возьмём десятичное число А₁₀ = 124 и поделим его на основание двоичной системы, то есть число 2.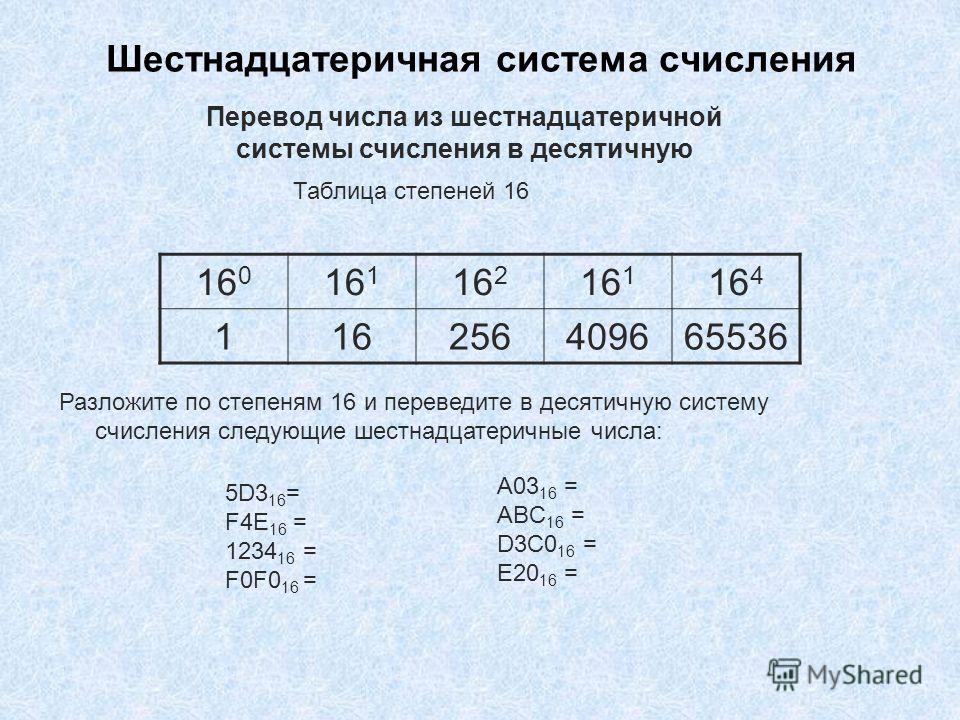 Деление будем производить уголком:

В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования мы получили двоичное число 1111100₂.

Теперь то же самое число переведём в восьмеричную систему счисления. Для этого число 124₁₀ разделим на число 8:

Как мы видим, остаток от первого деления равен 4. То есть младший разряд восьмеричного числа содержит цифру 4. Остаток от второго деления равен 7. то есть второй разряд восьмеричного числа – это цифра 7. Старший разряд получился равным 1. То есть в результате многократного деления мы получили восьмеричное число 174₈.

Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:

1×8²+7×8¹+4×8⁰=64₁₀+56₁₀+4₁₀=124

;А можно ли осуществить перевод из восьмеричной системы счисления в двоичную делением? Можно! Но деление нужно произвести по правилам восьмеричной арифметики. Правила работы в восьмеричной системе счисления мы рассмотрим в следующей главе. Тем не менее, для полноты материала, рассмотрим пример перевода в двоичную форму полученного ранее восьмеричного числа 174₈. Разделим его на основание новой системы счисления 2.

Как мы убедились выполнять деление в восьмеричной системе очень неудобно, ведь подсознательно мы делим в десятичной системе счисления. Давайте обратим внимание на то, что число 8 является степенью числа 2. То есть можно считать восьмеричную систему счисления просто более короткой записью двоичного числа. Это означает, что для представления восьмеричной цифры можно использовать три двоичных бита (8=2³). Давайте составим таблицу соответствия. Она приведена в таблице 1.

Таблица 1. Таблица соответствия восьмеричных цифр и двоичного кода

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
000	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7

Используя эту таблицу можно просто заменить каждую восьмеричную цифру тремя двоичными битами. Три двоичных бита обычно называют триадой или трибитом. Теперь давайте переведём восьмеричное число 1748 в двоичную форму при помощи таблицы 7:

Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу 7, каждой триаде ставят в соответствие восьмеричную цифру.

Аналогичным образом можно выполнить перевод числа из шестнадцатеричной формы в двоичную и обратно. В этом случае для представления шестнадцатеричной цифры потребуется четыре двоичных разряда. Четыре двоичных разряда обычно называют тетрадой. Иногда при переводе иностранных книг используется термин нибл.

Давайте составим таблицу соответствия двоичных тетрад и шестнадцатеричных цифр. Для этого мы будем просто прибавлять единицу к значению предыдущей строки в каждом столбце таблицы, в соответствии с используемой в этом столбце системой счисления. Результат приведён в таблице 2.

В качестве примера использования таблицы 2 переведем шестнадцатеричное число 7С₁₆ в двоичную форму представления:

Таблица 2. Таблица соответствия шестнадцатеричных цифр и двоичного кода

Двоичный код	Восьмеричная цифра	Десятичный эквивалент
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	a	a
1011	b	b
1100	c	c
1101	d	d
1110	e	e
1111	f	f

Пример преобразования двоичного числа в восьмеричную и шестнадцатеричную форму приведён на рисунке 1.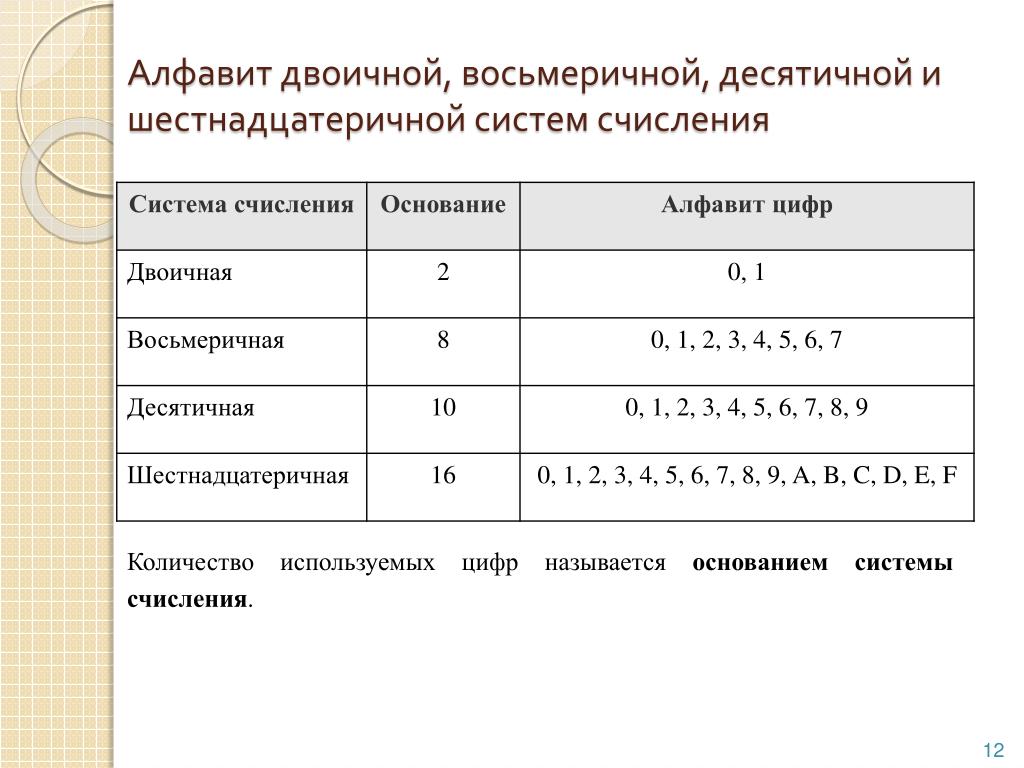

Рисунок 1. Пример преобразования двоичного числа в 8-ричную и 16-ричную форму.

На этом рисунке внизу выделены двоичные тетрады и соответствующие им шестнадцатеричные цифры. Их соответствие можно проверить при помощи таблицы 2. Сверху выделены триады и соответствующие им восьмеричные цифры. Старшая триада получилась неполной. Её нужно дополнить старшими незначащими нулями для того, чтобы можно было бы воспользоваться таблицей 1.

Шестнадцатеричные числа

Шестнадцатеричные числа

Шестнадцатеричная система счисления

Шестнадцатеричная (с основанием 16) система счисления работает так же, как и десятичная. (основание 10) система счисления, за исключением того, что она основана на шестнадцати вместо десяти. работа с десятичной системой знакома.

Ниже представлено 4-значное число с основанием 10 5826, указывающее, как значение числа получается из значений его 4 цифр.

Всем известно, что число 5826 означает пять тысяч восемьсот двадцать шесть. Но только потому, что их учили, что 1, 10, 100 и 1000 являются частью вычисление , хотя они никогда не пишутся как . Все, что есть на самом деле всего написано двадцать один (5 и 8 и 2 и 6). Только интерпретация что люди поставляют, что является чисто умственным и неписаным, информирует о том, что написано с предполагаемым значением.

Шестнадцатеричное число работает таким же образом. Каждая цифра «взвешивается» «множитель» со всеми результатами, сложенными вместе. Множители в обе системы являются степенями системной базы (10 или 16). Полномочия числа 10 1, 10, 100, 1000 и т. д., а числа 16 — 1, 16, 256, 409.6 и т.д. Так же цифры «5826», используемые в базе 16, представляют собой значение, рассчитанное следующим образом:

Хотя цифры одинаковые (5826), значения получаются совершенно разными, потому что база и ее «значения множителя» различны.

Вы увидите шестнадцатеричные числа, некоторые из цифр которых являются буквами вместо числа. Это потому, что количество цифр, необходимых для любой системы счисления, база номера. Таким образом, для основания 2 требуется 2 цифры, для основания 10 требуется 10, а для основания 16 нужно 16. База 2 имеет 0 и 1. База 10 имеет от 0 до 9. База 16 заимствует 0 хотя 9, но нужно еще 6. Для них мы могли бы придумать некоторые символы. Однако, для удобства мы используем первые 6 букв алфавита (от A до F) вместо. Когда у нас заканчиваются цифры на 9, мы используем А в качестве следующей цифры. Итак, А представляет значение 10. B следует за ним и представляет 11. Шестнадцатеричные цифры и значение, которое они обозначают:

Шестнадцатеричная цифра	Значение
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
А	10
Б	11
С	12
Д	13
Е	14
Ф	15

 

Вот вывод значения другого 4-значного шестнадцатеричного числа, но этот использует некоторые из старших цифр AF:

Максимальное число, которое вы можете сосчитать с заданным количеством цифр (в любом числе системы) — это число, в котором каждая цифра содержит максимальное значение в система счисления (1 по основанию 2, или 9 по основанию 10, или F по основанию 16). Итак, самый большой число, которое вы можете представить с помощью 4 цифр в базе 16:

Чтобы считать больше, вам потребуется использовать больше цифр. следующее число — 10000 в шестнадцатеричном формате или 65536 в десятичном. Это известное значение в информатике и называется «64К».

 

 

вариантов использования шестнадцатеричной системы счисления | Шестнадцатеричная система счисления и наборы символов

Шестнадцатеричная система KS3 (14–16 лет)

• Редактируемая презентация урока в PowerPoint
• Редактируемые раздаточные материалы
• Глоссарий, охватывающий ключевые термины модуля
• Тематические карты памяти для визуализации ключевых понятий
• Карточки для распечатки, помогающие учащимся активно вспоминать и уверенно повторять модуль

Просмотр шестнадцатеричных системных ресурсов KS3

Шестнадцатеричные ресурсы A-Level (16-18 лет)

• Редактируемая презентация урока PowerPoint
• Редактируемые раздаточные материалы для повторения
• Глоссарий, охватывающий ключевые термины модуля
• Тематические карты памяти для визуализации ключевых понятий проверить знание и понимание модуля

Просмотр шестнадцатеричных ресурсов для уровня A

1 Шестнадцатеричная система KS3 (14–16 лет)

2 Шестнадцатеричные ресурсы для уровня A (16–18 лет)

3 Система шестнадцатеричной нумерации

4 Значение места

5 Использование шестнадцатеричной

6 Преимущества шестнадцатеричной системы

6. 1 Дальнейшие показания:

Система Hexadecimal System

HexAdeCimal IS A -A -abymaling Immomering Of -Umemoring Of -Amplocmal Tummaling Tummaling — это то, что являясь в обмене. 16 цифр: от 0 до 9 и еще шесть, то есть от A до F.
В таблице ниже показано, как работает шестнадцатеричная система, и ее эквивалент десятичного числа:

Шестнадцатеричный	Decimal		Hexadecimal	Decimal
0	0		11 = (1 x 16) + 1	17
1	1		12 = ( 1 x 16) + 2	18
2	2		13 = (1 x 16) + 3	19
3	3		14 = (1 x 16) + 4	20
4	4		15 = (1 x 16) + 5	21
5	5		16 = (1 x 16. 1927			16 = (1 x 16.1927			16. (1 x 16.1927			.
6	6		17 = (1 x 16) + 7	23
7	7		18 = (1 x 16) + 8	24
8	8		19 = (1 x 16) + 9	. 27
B	11		1C = (1 x 16) + 12	28
C	12		1D = (1 x 16) + 13	29
Д	13		1E = (1 x 16) + 14	30
E	14		1F = (1 x 16) + 15	31
F	15		20 = (2 x 16) + 0	32
10 = (1 x 16) + 0	16

Значение места

IF У десятичных значений. , сотни, тысячи и т. д., шестнадцатеричные числа также имеют разрядные значения. Десятичные числа имеют степень 10, а шестнадцатеричные числа имеют степень 16.
The table below shows how the place value works for the hexadecimal numbering system:

Exponent	16 3	16 2	16 1	16 0
Value	4,096	256	16	1

Hexadecimal	Decimal
10	16
100	256
1000	4,096

Uses of Hexadecimal

The hexadecimal numbering system is often used by programmers to simplify the binary numbering system. Поскольку 16 эквивалентно 24, между числами 2 и 16 существует линейная зависимость.
Это означает, что одна шестнадцатеричная цифра эквивалентна четырем двоичным цифрам. Компьютеры используют двоичные системы счисления, в то время как люди используют шестнадцатеричные системы счисления, чтобы сократить двоичные числа и упростить их понимание.
Шестнадцатеричные числа используются в следующих случаях:

• Для определения ячеек памяти . Шестнадцатеричные числа могут характеризовать каждый байт как две шестнадцатеричные цифры только по сравнению с восемью цифрами при использовании двоичного кода.
• Для определения цветов на веб-страницах . Каждый основной цвет — красный, зеленый и синий — характеризуется двумя шестнадцатеричными цифрами. Используется формат #RRGGBB. RR означает красный, GG — зеленый, а BB — синий.
• Для представления адресов управления доступом к среде (MAC). MAC-адреса состоят из 12-значных шестнадцатеричных чисел. Используется формат ММ:ММ:ММ:СС:СС:СС или ММММ-ММСС-СССС. Первые 6 цифр MAC-адреса представляют собой идентификатор производителя адаптера, а последние 6 цифр представляют собой серийный номер адаптера.
• Для отображения сообщений об ошибках. Шестнадцатеричные числа используются для определения местоположения ошибки в памяти. Это полезно для программистов при поиске и исправлении ошибок.

Преимущества шестнадцатеричной системы счисления

Вот некоторые преимущества использования шестнадцатеричной системы счисления:

• Она очень краткая, и использование базы 16 означает, что количество цифр, используемых для обозначения данного числа, обычно меньше, чем в двоичной или десятичной системе. Это позволяет хранить больше информации, используя меньше места.
• Можно быстро и просто преобразовать шестнадцатеричные числа в двоичные. Шестнадцатеричный формат можно использовать для записи больших двоичных чисел всего несколькими цифрами.
• Это упрощает жизнь, поскольку позволяет группировать двоичные числа, что облегчает чтение, запись и понимание.