Н. И. Лобачевского Графики функций Учебно-методическое пособие
Н. И. Лобачевского Графики функций Учебно-методическое пособие
1 2 3 4 5 6 7
1 2 3 4 5 6 7 ©emirsaba.org 2023 | Басты бет Lessons Curriculum vitae Documents | ||||||||||||||||||||||||||||||||||||||||||||||||||
03.02 «Прикладная математика и информатика,
т.н., доцент В.М. Сморкалова
2.
.
Лепестковая диаграмма в Excel в полярной системе координат
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.
п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
Как построить лепестковую диаграмму в Excel
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме.
Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной». - После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.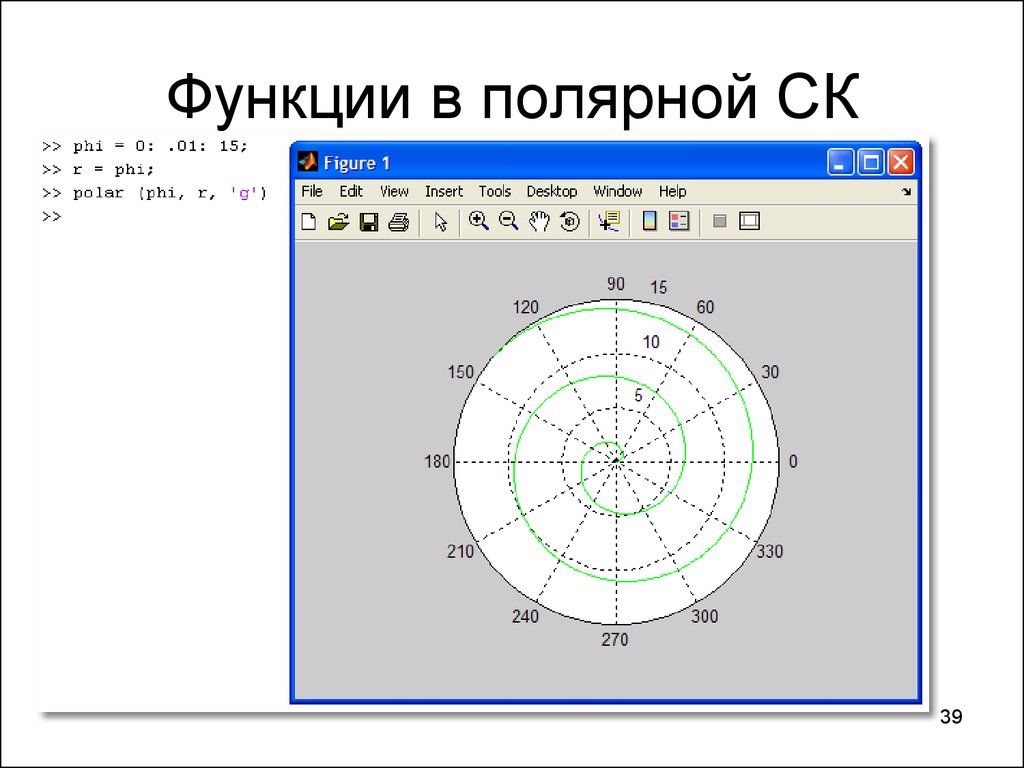
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel.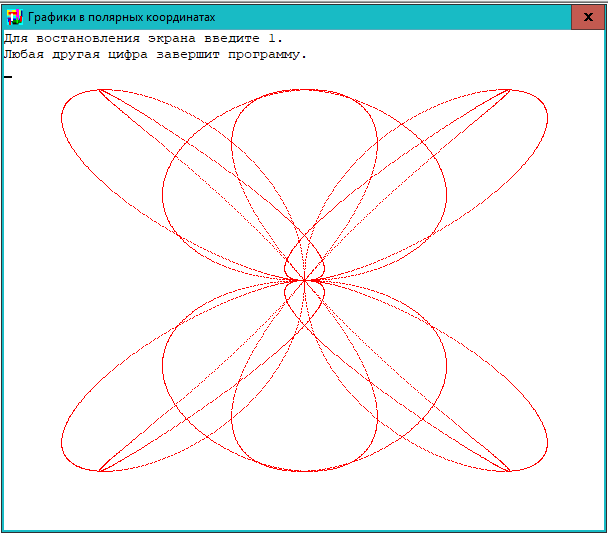
Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Интерактивировать: Полярные координаты
Наставник: Вы, вероятно, знакомы с декартовой системой координат, которая позволяет вам строить графики. точки и функции на координатной плоскости. Если вам дан набор точек в виде (x, y), вы сможете отобразить их на осях x и y графика.
Студент: Да. Если бы мне дали точку (2,3), я бы начал с начала координат и прошел две единицы до
прямо по оси x, а затем переместитесь вверх на 3 единицы в направлении y.
Наставник: Это верно. И если бы вам дали функцию, скажем, y=2x+3, вы, вероятно, могли бы построить ее график. слишком.
Ученик: Конечно, я бы выбрал значения x, которые я бы ввел в функцию, чтобы получить значения у для этой функции. Затем я нарисовал точки на графике.
Наставник: Да! Знаете ли вы, что вы также можете наносить точки на график другого типа на основе полярной диаграммы? Система координат.
Ученик: Что такое полярная система координат?
Наставник: Полярная система координат — это круговая, а не прямоугольная система координат. Ты точки графика, заданные значением r, которое представляет собой расстояние от центра; и угол мера, которая дается в градусах или, чаще, в радианах. Вы помните, что такое радианы?
Ученик: Конечно, это еще одна единица измерения углов. Круг содержит 360 градусов что совпадает с 2π радиан. Но для чего бы вы использовали эту систему?
Ментор: Ну, иногда правильнее описать локацию круговым движением.
Ученик: Как бы вы нанесли точки на полярный график?
Наставник: Полярная система координат имеет оси, подобные декартовой системе, и точку, подобную происхождения, за исключением того, что он называется столб. Он также имеет луч, который проходит горизонтально через полюс, называемый полярная ось. Вместо квадратной сетки есть концентрические круги с центром на полюсе, которые получают равномерно больше и расходятся от полюса. Полярная координатная плоскость выглядит так:
Наставник: Как и прямоугольные координаты, полярные координаты также называются упорядоченной парой, но
значение каждого из чисел разное.
Первое число в паре координат, r,
представляет собой расстояние от полюса и походит на измерение радиуса круга. Второй
номер пары, θ, представляет угол, измеренный от горизонтальной оси.
Полярная ось представляет угловую меру 0 радиан или 0 градусов. Движение против часовой стрелки
от этой оси представляет собой положительную меру угла, а по часовой стрелке — отрицательную.
Ученик: Думаю, я понял. Углы определяются в полярной системе координат так, как они единичный круг, обычно в радианах. Итак, если вам дана полярная координата (3, π/4), точка находится в трех единицах от центра под углом π/4 радиан, измеренным против часовой стрелки от полярной оси:
Ученик: Получается, что заданные координаты тоже могут быть отрицательными?
Ментор: Это отличный вопрос, и ответ положительный. Как и на единичном круге, отрицательное углы идут по часовой стрелке от полярной оси. Вы помните -3π/4 это то же самое как 5π/4?
Ученик: Да, а -4π/3 — это то же самое, что 2π/3?
Наставник: Это верно.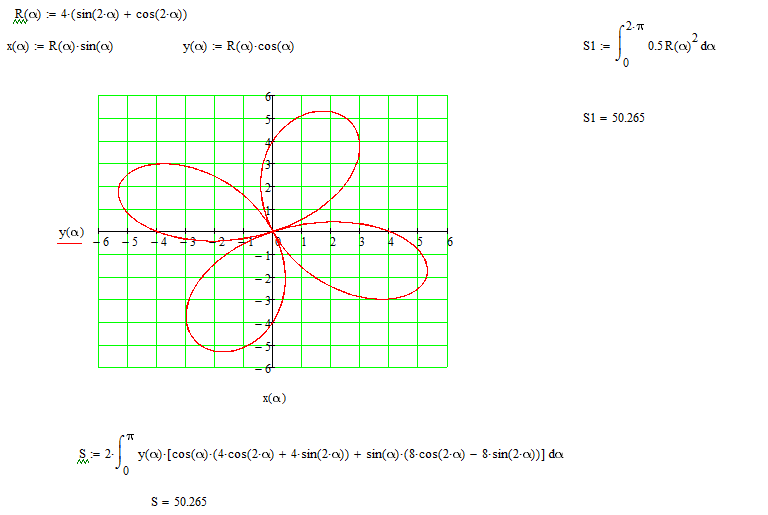
И, поскольку вы можете добавить столько вращений в виде кратных 2Ï, сколько вам нужно
хотите, любой угол может иметь бесконечное количество отрицательных и положительных значений. Кроме того, р
может быть отрицательным. Отрицательный r указывает, что точка находится в противоположном
квадрант от угла, заданного в паре координат. Например, π/4 находится в 1-м
квадрант, поэтому положительные значения r нанесены на r единиц от полюса в 1-м квадранте и
отрицательные значения нанесены в противоположном квадранте, 3-м квадранте, на угол
идентифицируется как 5π/4. Как вы думаете, где находится точка (-2, π/3)?
Ученик: Ну, так как (2, π/4) было измерено на 2 единицы вправо вдоль полярной оси, то -2 будет
указывают, что точка измеряется на 2 единицы левее вдоль полярной оси, а затем на π/4
градусов против часовой стрелки. Поскольку угол π/3 лежит в первой четверти,
затем, чтобы нанести точку (-2, π/3), вы должны нанести точку в двух единицах от полюса вдоль
угол 4π/3.
Верно?
Наставник: Это верно. Это будет выглядеть так:
Ученик: Значит, одна точка может иметь много разных значений?
Наставник: Правильно! Значения для r могут быть заданы как положительные и отрицательные значения, а θ может быть не только в положительных и отрицательных значениях, но и в виде любого значения θ + любого кратного из 2π. Таким образом, в отличие от декартовой системы, где каждая точка имеет уникальный набор координат, в В полярной системе любая точка может иметь бесконечное количество координат!
Ученик: Это означает, что точка, заданная как (2,π/4), также может быть задана как (2,-7π/4) или (2, 9π/4) или (-2,5π/4)!
Ментор: Точно. Попробуйте нанести эти точки на график с помощью действия «Полярные координаты» и убедитесь, что они тот самый момент!
Как рисовать полярные кривые — Криста Кинг Математика
Идентификация различных форм полярных кривых
Мы нарисуем полярные кривые, нанеся значения для ???r??? при известных значениях ???\theta???.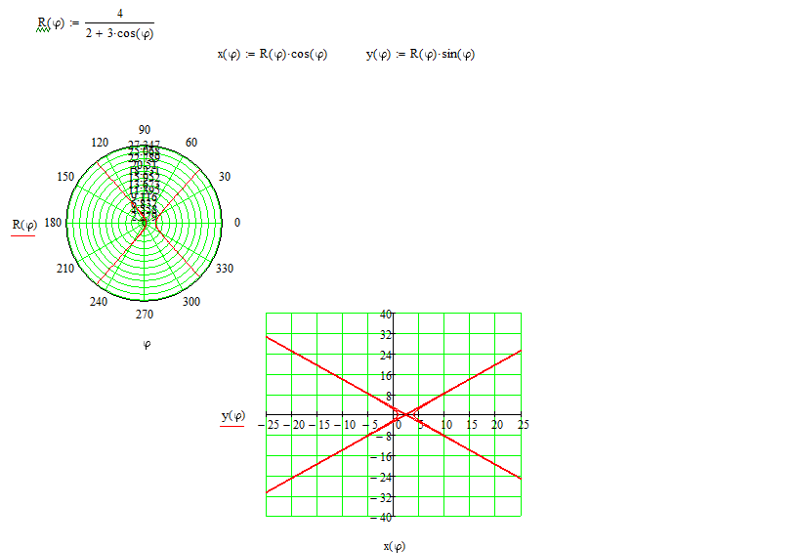
Мы также можем использовать приведенную ниже таблицу для быстрого построения полярных кривых, представленных в этих стандартных формах.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать больше.
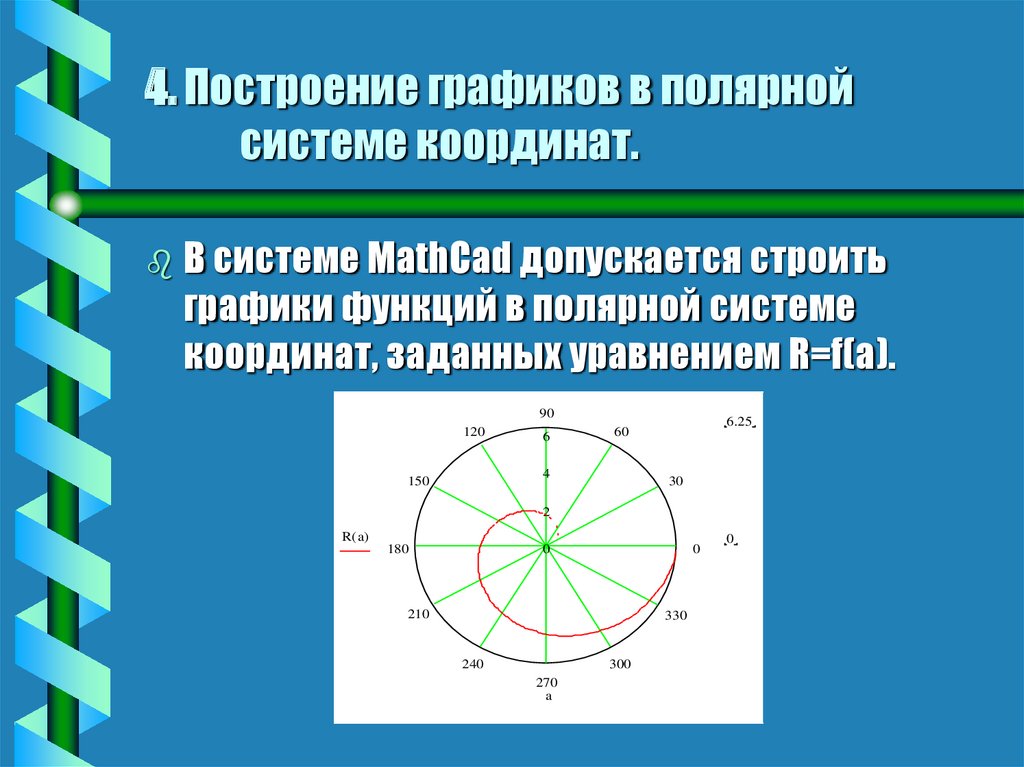
Если мы не можем использовать приведенную выше таблицу, чтобы найти стандартную форму для заданной нами полярной кривой, то мы всегда можем создать таблицу координат точек ???(r,\theta)???. Для этого мы возьмем значение внутри тригонометрической функции, включающее ???\тета???, установим его равным ???\пи/2???, а затем найдем ???\тета ???. Например, учитывая полярную кривую ???r=6\sin{3\theta}???,
???3\theta=\frac{\pi}{2}???
???\theta=\frac{\pi}{6}???
Тогда мы найдем ???r??? для приращений ???\pi/6??? на интервале ???0\leq\theta\leq 2\pi???.
Отложив эти точки на полярных осях, получим
Пошаговый пример построения полярной кривой
Пройти курс
Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого.
🙂Учить больше
График линий в полярных координатах
Пример
График полярных кривых на тех же осях.
???\theta=\frac{\pi}{3}???
???r\cos{\theta}=3???
???r\sin{\theta}=-2???
Используя таблицу стандартных кривых, мы можем построить их все на одних и тех же осях.
???\тета=\пи/3??? похоже на ???\theta=\beta???, так что это прямая линия, проходящая через начало координат под углом ???\pi/3???.
???r\cos{\theta}=3??? похож на ???r\cos{\theta}=a???, так что это вертикальная линия, проходящая через ???x=3???.
???r\sin{\theta}=-2??? похож на ???r\sin{\theta}=b???, так что это горизонтальная линия, проходящая через ???y=-2???.
Давайте попробуем несколько примеров с окружностями, заданными в полярных координатах.
Чтобы построить полярную кривую, найдите точки с шагом тета, а затем нанесите их на полярные оси.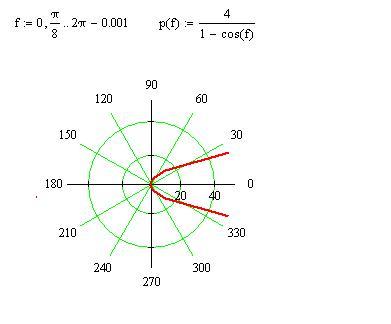
2}=\sqrt{10}???.
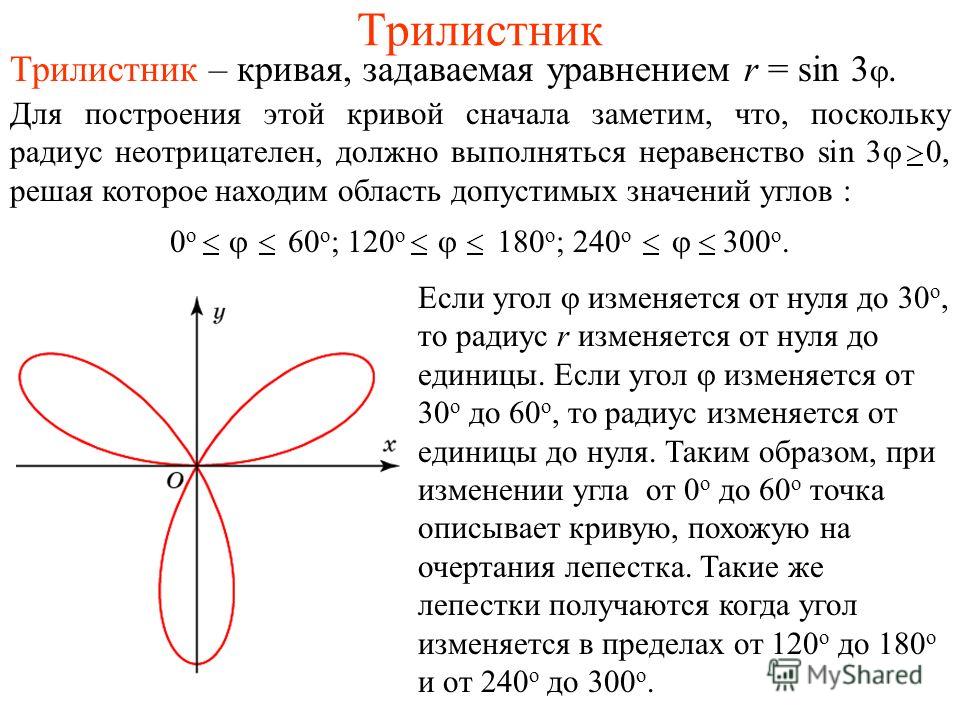
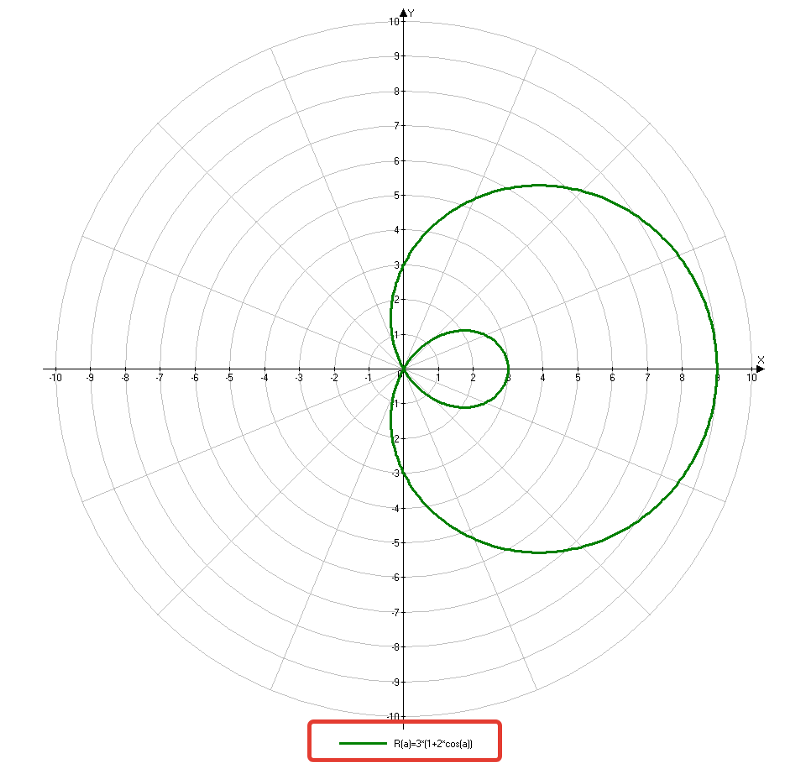
График кардиоид, лимаконов и роз
Пример
График полярных кривых.
???r=3+3\sin{\theta}???
???r=2+4\cos{\theta}???
???r=7+6\cos{\theta}???
???r=6\sin{2\theta}???
Для ???r=3+3\sin{\theta}???:
???r=3+3\sin{\theta}??? похоже на ???r=a\pm{a}\sin{\theta}???, так что это кардиоида в начале координат. Мы создадим таблицу значений на интервале ???0\le\theta\le2\pi???.
Имея эти точки и зная форму нашей полярной кривой, мы можем нарисовать график.
Для ???r=2+4\cos{\theta}???:
???r=2+4\cos{\theta}??? похоже на ???r=a\pm{b}\cos{\theta}??? с ???a Имея эти точки и зная форму нашей полярной кривой, мы можем нарисовать график. Для ???r=7+6\cos{\theta}???: ???r=7+6\cos{\theta}??? похоже на ???r=a\pm{b}\cos{\theta}??? с ???a>b???, так что это лимасон без внутренней петли. Мы создадим таблицу значений на интервале ???0\le\theta\le2\pi???. Имея эти точки и зная форму нашей полярной кривой, мы можем нарисовать график. Для ???r=6\sin{2\theta}???: ???r=6\sin{2\theta}??? не соответствует ни одной из стандартных форм в нашей таблице. В этом случае мы установим значение внутри нашей тригонометрической функции равным ???\pi/2??? а затем найти ???\тета???. ???2\theta=\frac{\pi}{2}??? ???\theta=\frac{\pi}{4}??? Тогда мы найдем ???r??? для приращений ???\pi/4??? на интервале ???0\leq\theta\leq 2\pi???. Отложив эти точки на полярных осях, получим
Получить доступ к полному курсу Calculus 2
Начать
Изучение математикиКриста Кинг