5. Графики в полярных координатах
5.1. Полярные координаты
Положение точки в полярных координатах на плоскости (см. рис. 28) определяется:
1) ее расстоянием от некоторой данной точки , называемой полюсом;
2) углом , который образует отрезок с заданным направлением прямой , которая называется полярной осью).
Рис. 28. Точка в полярных координатах.
При этом называют радиусом-вектором и — полярным углом. Если принять полярную ось за , а полюс — за начало координат, то имеем, очевидно (см. рис. 29):
Рис. 29. Точка в полярных координатах.
Данному
положению точки
соответствует одно определенное
положительное значение
и бесчисленное множество значений
,
которые отличаются слагаемым, кратным
.
Если
совпадает с
,
то и
— неопределенно.
Всякая функциональная зависимость вида (явная) или (неявная) имеет в полярной системе координат свой график.
В дальнейшем мы будем рассматривать не только положительные, но и отрицательные значения , причем если некоторому значению соответствует отрицательное значение , то условимся откладывать это значение в направлении, прямо противоположном тому направлению, которое определяется значением .
5.2. Графики кривых в полярных координатах
Для того, чтобы построить график в полярных координатах по точкам нужно заполнить таблицу, в первой строке которой записать значения угла из интересующего промежутка, а во второй — соответствующие значения функции . Затем, отметить и соединить эти точки плавной линией.
Построим графики функций, которые часто бывают заданы в полярных координатах.
Спирали. Пусть , . Рассмотрим три вида спиралей:
• спираль Архимеда: ,
• гиперболическая спираль:
• логарифмическая спираль: .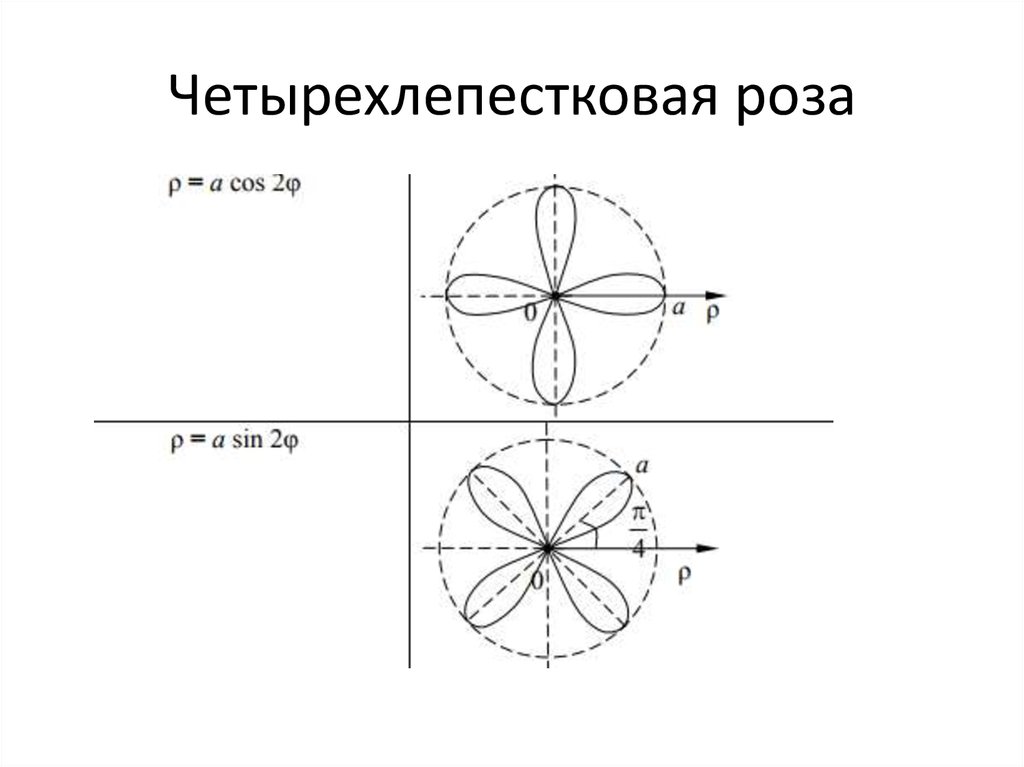
Спираль Архимеда . График функции имеет вид, изображенный на рис. 30 а), причем пунктир соответствует части кривой при . Отрицательным значениям соответствуют и отрицательные значения , и их надо откладывать в направлении, противоположном тому направлению, которое определяется значением . При этом заполнять таблицу значений и нет необходимости в силу простой функциональной завиимости между и .
Рис. 30. Графики функций , и .
Гиперболическая спираль . Особенностью этого графика (см. рис. 30 б) является то, что расстояние между любой точкой этой кривой и полярной осью не превосходит (т.е. кривая имеет асимптоту, параллельную полярной оси и проведенную на расстоянии от нее).
Предполагая и заполним таблицу для и .
Таблица 4.
Замечаем,
что
будет увеличиваться при уменьшении
.
При этом, график
не имеет общих точек с прямой, параллельной
полярной оси и проходящей на расстоянии
от неё.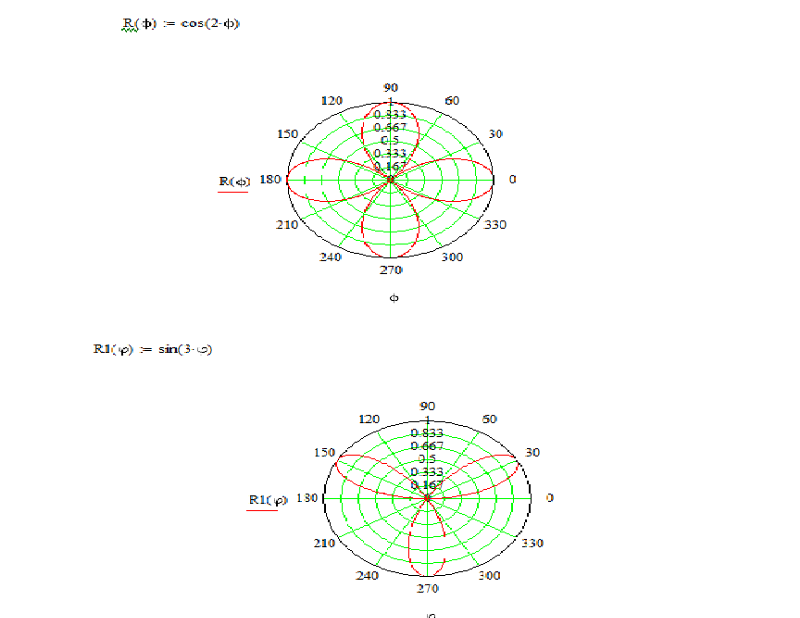
Далее, видим, что
не обращается в нуль ни при каких конечных
значениях
,
а только будет уменьшаться с увеличением
.
Кривая будет поэтому беспредельно
приближаться к полюсу
,
закручиваясь около него, но никогда не
пройдет через
в противоположность спирали Архимеда.
Отметив и соединив плавной линией точки таблицы 2, а также учитывая поведение функции при увеличении и уменьшении угла получим график функции (см. рис. 30 б).
Логарифмическая спираль . При имеем . Если , то при увеличении увеличивается и . Если , то при уменьшении радиус-вектор приближается к нулю.
Логарифмическая спираль изображена на рис. 30 в.
Розы. Розами, или кривыми Гвидо Гранди, называютя кривые, полярное уравнение которых имеет вид или . Будем рассматривать случай, когда , — целое положительное число.
Заметим,
что поскольку правая часть уравнения
розы не может превышать
,
то вся кривая находится внутри круга
радиуса
.
Так как и являются переодическими функциями, то
роза состоит из лепетков, симметричных
относительно наибольших радиусов,
каждый из которых равен
.
При этом если
нечетное число, то число лепестков равно
,
а если
— чётное, то роза имеет лепестков.
Графики функций , , и изображены на рис. 31.
Рис. 31. Графики функций , , и .
Улитка Паскаля и кардиоида. Полярное уравнение улитки имеет вид . Если , то это уравнение дает только положительные значения (см. рис. 32 a)). Если , то будет принимать и отрицательные значения (см. рис. 32 б)). Наконец, при уравнение улитки будет и в этом случае улитка представляет собою кардиоиду (см. рис. 32 в)).
В качестве примера приведем графики функций , и на рис. 32.
Рис. 32. Графики функций , и .
ПОСТРОЕНИЕ НЕКОТОРЫХ КРИВЫХ ВТОРОГО ПОРЯДКА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ, ЗАВИСИМОСТЬ КРИВЫХ ОТ КОЭФФИЦИЕНТОВ
ПОСТРОЕНИЕ НЕКОТОРЫХ КРИВЫХ ВТОРОГО ПОРЯДКА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ, ЗАВИСИМОСТЬ КРИВЫХ ОТ КОЭФФИЦИЕНТОВ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Сучков Р.
В. 1
1
Веретенникова А.Л. 1
1
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Конечно же, каждый из нас слышал о таких понятиях как график функции, система координат, гипербола и т.п. Всё это является составляющими темы «Функции», с которой знакомимся мы в школе ещё в среднем звене.
Функция — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества. Этот закон определяется уравнением , и на основе него строится график в плоской системе координат, задаваемой двумя осями X и Y. Двигаясь от 6 до 10 класса, мы усложняли уравнения и графики, вводили новые понятия, но никогда не выходили за рамки основного определения функции и принципа построения графиков.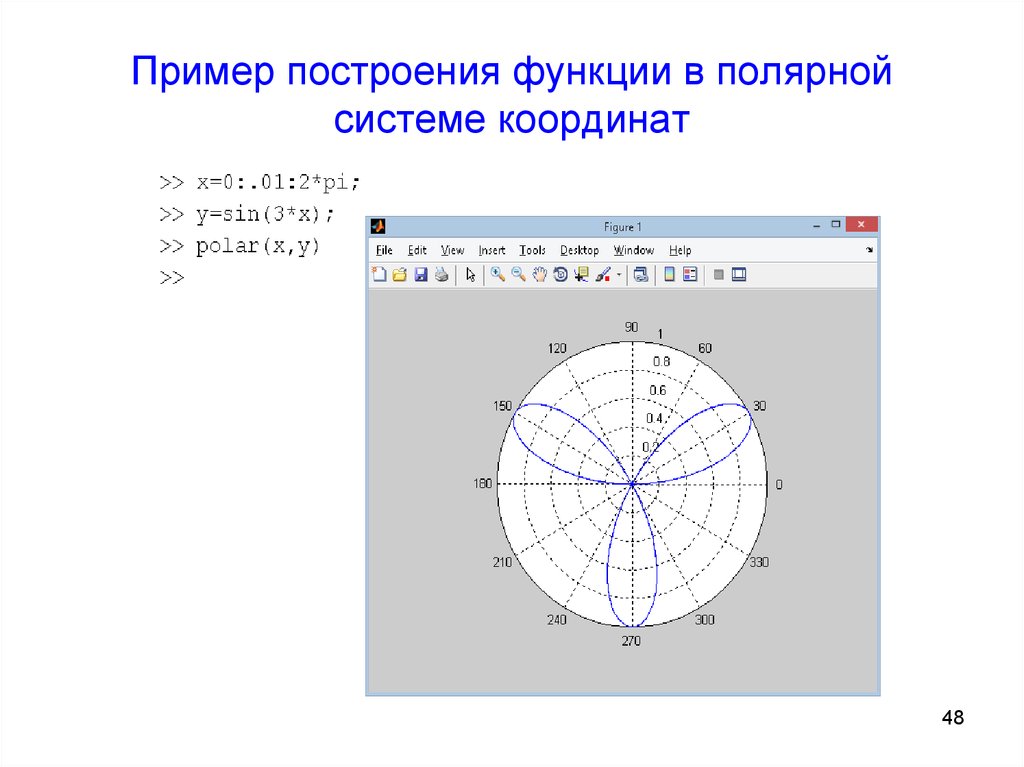
Вот главная цель работы: построить графики кривых II порядка в полярной системе координат, а также выяснить, как различаются их графики в зависимости от варьирования коэффициентов и параметров функций.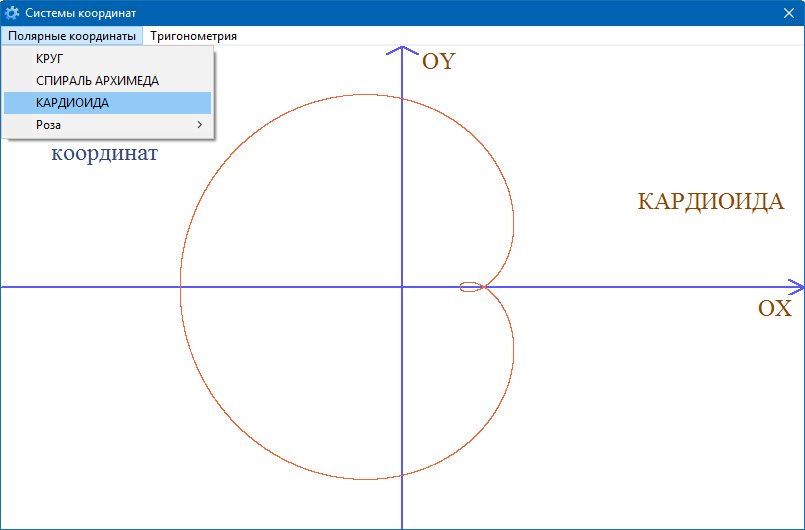
Для достижения целей работы было поставлено несколько задач:
-
пополнить знания о стандартных (невырожденных) кривых II порядка: эллипс, параболу, гиперболу;
-
рассмотреть нестандартные кривые II порядка;
-
познакомиться с полярной системой координат и сопоставить с декартовой, уже изучавшейся в школе.
Процесс решения каждой из задач был разбит на 2 этапа:
-
изучение и разбор теоретического материала, знакомство с новыми понятиями;
-
применение полученных знаний на практике, построение графиков.
Историческая справка: впервые кривые второго порядка изучались одним из учеников Платона.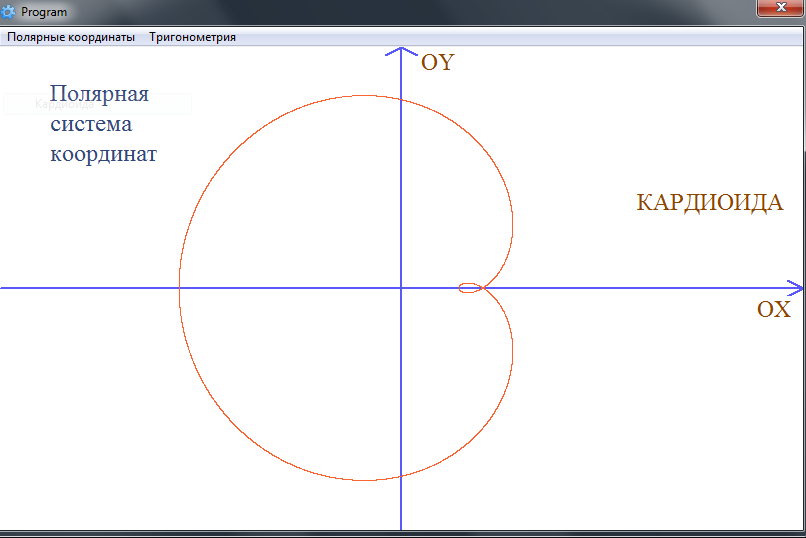
Алгебраической кривой второго порядка называется кривая , уравнение которой в декартовой системе координат имеет вид , где не все коэффициенты А, В и С равны одновременно нулю (иначе — прямая, т.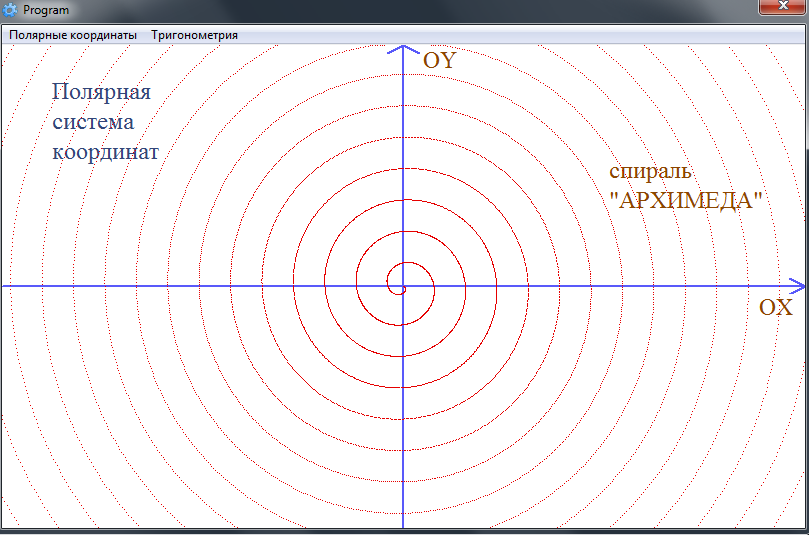
Эллипс, гипербола, парабола
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через . Фокусы эллипса обозначают буквами и , расстояние между ними — через .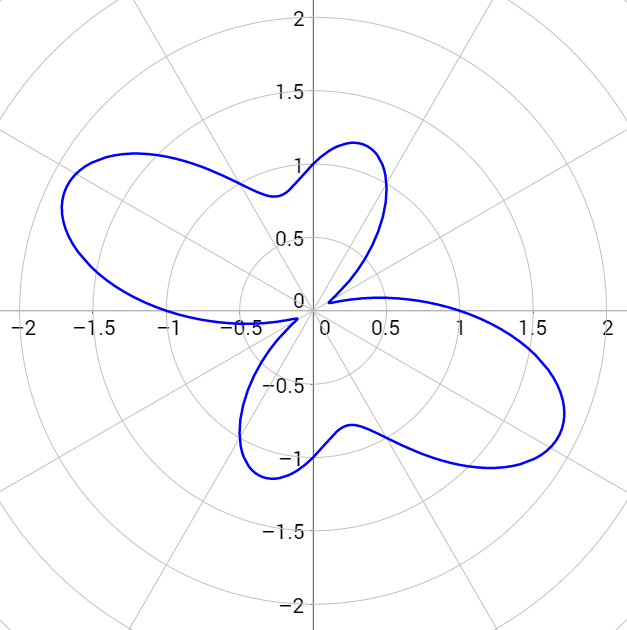
По определению эллипса .
Гиперболой называется геометрическое место точек на плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек, называемых фокусам, одинаково и равно
Параболой называется множество точек на плоскости, расстояния от которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны. С гиперболой мы часто сталкиваемся в повседневной жизни. По параболистической траектории летит брошенный вверх камень, отскакивает мяч от пола, движутся планеты вокруг Солнца.
1.2. Системы координат
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Знания обычного человека в большинстве случаев ограничиваются одной-двумя системами координат.
На самом же деле их существует великое множество: прямоугольная, полярная, аффинная, сферическая, цилиндрическая и т.д. На одном из уроков алгебры мы затрагивали кое-какие из них, а в этом исследовании я решил сопоставить две: прямоугольную (ёще называющуюся декартовой) и полярную (как хорошо знакомую и в корне отличающуюся).
Прямоугольная, или Декартова, система координат — прямолинейная система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям. Названа по имени Р Декарта. Это наиболее простая и поэтому часто используемая система координат как на плоскости, так и в пространстве.
Историческая справка: Декарт впервые ввел координатную систему в своей работе «Рассуждение о методе» в 1637 году. Она существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета.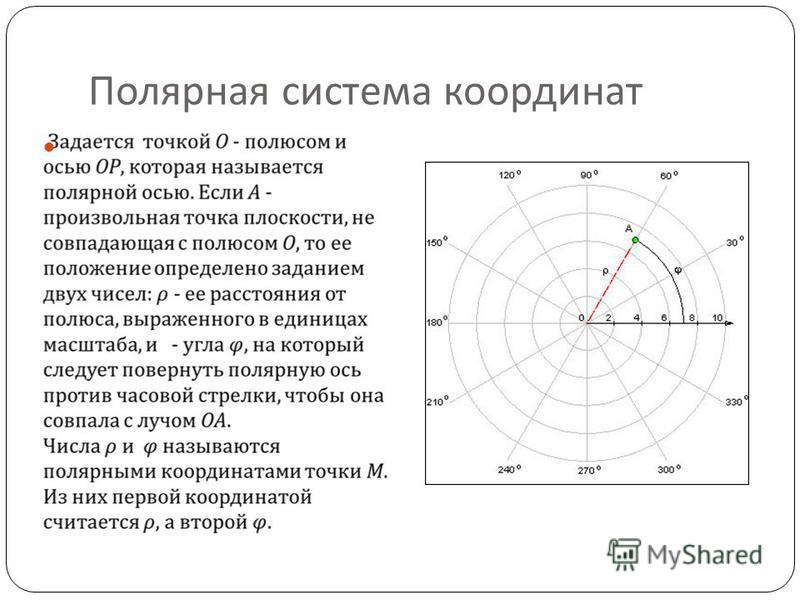
Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта.
Данная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Эти оси пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей. Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY. Четыре угла — четверти (I, II, III, IV) — образованные осями координат OX и OY, называются координатными углами.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
1.2.3. Связь между декартовыми и полярными координатамиПару полярных координат и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:
в то время как две декартовы координаты x и y могут быть переведены в полярную координату :
(по теореме Пифагора).
1.3. Нестандартные кривые второго порядка
Просмотрев этот раздел, неосведомлённый человек может подумать, что часть нестандартных кривых второго порядка можно спокойно отнести к стандартным, другая же часть не имеет с ними ничего общего.
Некоторые из них действительно представляют собой красивые витиеватые узоры, но некоторые выглядят как-то слишком просто, без изысков. Конечно, такое мнение имеет место существовать. Но ведь дело в степени и области применения кривых: одни встречаются постоянно, другие — только в узких специализированных целях — и в сложности уравнения. Хотелось бы в этом разделе рассмотреть наиболее интересные кривые: спираль Архимеда, улитка Паскаля, Розы Гранди. В разделе «Кривые II порядка в полярной системе координат» я перевел графики в другую полярную систему координат и построил их с помощью табличного процессора.
Кривые второго порядка в полярной системе координат
Эта часть является самой главной в моей работе, так как в ней описывается построение графиков в полярной системе координат в табличном процессоре MSExcel 2007. Выполняя построения мы старались акцентировать внимание на красоте математики, на том насколько все гениальное просто, ведь математика это предметная область, в которой все для жизни.
Полярная роза (Розы Гранди)
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах: ,
для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных, либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.
Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь — лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
|
— трехлепестковая роза |
— клевер |
|
|
— космея |
Два графика в одной системе |
|
Улитка Паскаля
Улитка Паскаля ― плоская алгебраическая кривая 4-го порядка. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.
Уравнение в полярных координатах:
Здесь — диаметр исходной окружности, а — расстояние, на которое смещается точка вдоль радиус-вектора.
|
В зависимости от диапазона получаются следующие графики |
||
Спираль Архимеда
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для >0, а другую для
Просмотров работы: 671
8.1: Полярные координаты и полярные графики
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14545
- Кен Каттлер
- Университет Бригама Янга via Lyryx
Результаты
- Понимание полярных координат.
- Преобразование точек между декартовыми и полярными координатами.
Вероятно, вы сталкивались с декартовой системой координат во многих аспектах математики. Существует альтернативный способ представления точек в пространстве, называемый полярными координатами . Идея подсказана на следующей картинке.
Рисунок \(\PageIndex{1}\)Рассмотрим точку выше, которая будет указана как \((x,y)\) в декартовых координатах. Мы также можем указать эту точку, используя полярные координаты, которые мы пишем как \(\left( r, \theta \right)\). Число \(r\) – это расстояние от начала координат\(\left(0,0\right)\) до точки, а \(\theta\) – это угол, показанный между положительной осью \(x\) и линия от начала до точки. Таким образом, точка может быть указана в полярных координатах как \(\left(r, \theta \right)\).
Теперь предположим, что нам дана упорядоченная пара \(\left( r,\theta \right)\), где \(r\) и \(\theta\) — действительные числа. Мы хотим определить точку, заданную этой упорядоченной парой.
Мы можем использовать \(\theta\) для идентификации луча из начала координат следующим образом. Пусть луч проходит из \(\left( 0,0\right)\) через точку \(\left( \cos \theta ,\sin \theta \right)\), как показано.
Луч идентифицируется на графике как прямая из начала координат, проходящая через точку \((\mbox{cos}(\theta),\mbox{sin}(\theta) )\). Теперь, если \(r>0,\), пройдите расстояние, равное \(r\), в направлении отображаемой стрелки, начиная с \((0,0)\). Если \(r<0,\) двигаться в противоположном направлении на расстояние \(\left\vert r\right\vert\). Это точка, определяемая \(\left( r,\theta \right)\).
Обычно предполагается, что \(\theta\) находится в интервале \([0,2\pi )\) и \(r>0.\). В этом случае существует очень простое соотношение между декартовым и полярные координаты, заданные как \[x=r\cos \left(\theta\right) ,\ \ y=r\sin \left(\theta \right) \label{cartpolcoord}\]
Эти уравнения демонстрируют, как найти декартовы координаты, когда нам даны полярные координаты точки. 2} \\ \\ \mbox{tan} \left(\theta\right ) = \frac{y}{x} \end{массив} \label{polcartcoord}\]
В следующем примере мы рассмотрим, как найти декартовы координаты точки, заданной полярными координатами.
Пример \(\PageIndex{1}\): нахождение декартовых координат
Полярные координаты точки на плоскости: \(\left( 5,\pi /6\right)\). Найдите декартовы координаты этой точки.
Решение
Точка задается полярными координатами \(\left( 5,\pi /6\right)\). Поэтому \(r=5\) и \(\theta = \pi/6\). Из \(\eqref{cartpolcoord}\) \[x= r \cos\left(\theta\right)= 5\cos\left(\frac{\pi}{6}\right) = \frac{5} {2}\sqrt{3}\nonumber \] \[y= r \sin\left(\theta\right) = 5\sin\left(\frac{\pi}{6}\right) = \frac{ 5}{2}\nonumber \] Таким образом, декартовы координаты равны \(\left( \frac{5}{2}\sqrt{3}, \frac{5}{2}\right)\). Точка показана на графике ниже.
Рисунок \(\PageIndex{3}\)Рассмотрим следующий пример случая, когда \(r < 0\).
Пример \(\PageIndex{2}\): нахождение декартовых координат
Полярные координаты точки на плоскости: \(\left(-5,\pi /6\right) . \) Найти декартовы координаты.
Решение
Для точки, заданной полярными координатами \(\left(-5, \pi /6 \right)\), \(r=-5\) и \(x\theta = \pi / 6\). Из \(\eqref{cartpolcoord}\) \[x= r \cos\left(\theta\right)= -5\cos\left(\frac{\pi}{6}\right) = -\frac{ 5}{2}\sqrt{3}\nonumber \] \[y= r \sin\left(\theta\right) = -5\sin\left(\frac{\pi}{6}\right) = -\frac{5}{2}\nonumber \] Таким образом, декартовы координаты равны \(\left( -\frac{5}{2}\sqrt{3}, -\frac{5}{2}\right) \). Точка показана на следующем графике.
Рисунок \(\PageIndex{4}\)Вспомним из предыдущего примера, что для точки, заданной \(\left( 5, \pi /6 \right)\), декартовы координаты равны \(\left( \ frac{5}{2}\sqrt{3}, \frac{5}{2}\right)\). Обратите внимание, что в этом примере при умножении \(r\) на \(-1\) результирующие декартовы координаты также умножаются на \(-1\).
На следующем рисунке показаны обе точки в двух приведенных выше примерах, чтобы подчеркнуть, что они находятся на противоположных сторонах \(\left( 0,0\right)\), но на одинаковом расстоянии от \(\left( 0,0 \правильно)\). 9{2}}=5\). Остается определить угол \(\theta\) между положительной осью \(x\) и линией от начала координат до точки. Поскольку оба значения \(x\) и \(y\) положительны, точка находится в первом квадранте. Следовательно, \(\theta\) находится между \(0\) и \(\pi /2\ \). Используя это и \(\eqref{polcartcoord}\), мы должны решить: \[\mbox{tan}\left(\theta \right)=\frac{4}{3}\nonumber \] И наоборот, мы можем используйте уравнение \(\eqref{cartpolcoord}\) следующим образом: \[3=5\cos \left( \theta \right)\nonumber \] \[4 = 5\sin \left( \theta \right)\nonumber \] Решая эти уравнения, находим, что приблизительно \(\theta =0.\, 92}\\ &= \sqrt{1 + 3}\\ &=2\end{aligned}\] В этом случае точка находится во втором квадранте, поскольку значение \(x\) отрицательно, а \( у\) значение положительное. Следовательно, \(\theta\) будет между \(\pi/2\) и \(\pi\). Решая уравнения \[-\sqrt{3}= 2 \cos \left(\theta\right)\nonumber \] \[1 = 2 \sin \left( \theta\right)\nonumber \], находим, что \ (\theta = 5\pi /6.\) Следовательно, полярные координаты этой точки равны \(\left(2, 5\pi /6 \right)\).
Рассмотрим этот пример. Предположим, мы использовали \(r=-2\) и \(\theta =2\pi -\left(\pi/6\right) = 11\pi/6\). Эти координаты указывают ту же точку, что и выше. Заметьте, что существует бесконечно много способов отождествить эту конкретную точку с полярными координатами. На самом деле каждую точку можно представить в полярных координатах бесконечным числом способов. Из-за этого обычно бывает, что \(\theta\) ограничено некоторым интервалом длины \(2\pi\) и \(r>0\), для действительных чисел \(r\) и \(\тета\).
Как и в случае с декартовыми координатами, можно использовать отношения между полярными координатами для указания точек на плоскости. Процесс рисования графиков этих отношений очень похож на тот, который используется для рисования графиков функций в декартовых координатах. Рассмотрим соотношение между полярными координатами вида \(r=f\left(\theta\right)\). Чтобы построить такое отношение, сначала составьте таблицу вида
.| \(\тета\) | \(р\) |
|---|---|
| \(\тета_1\) | \(ф(\тета_1)\) |
| \(\тета_2\) | \(е(\тета_2)\) |
| \(\вдоц\) | \(\вдоц\) |
Нанесите полученные точки на график и соедините их кривой. На следующем рисунке показано, как начать этот процесс.
Чтобы найти точку на плоскости, соответствующую упорядоченной паре \(\left( f\left( \theta \right) ,\theta \right)\), мы следуем тому же процесс, как при нахождении точки, соответствующей \(\left( r, \theta \right)\).
Рассмотрим следующий пример этой процедуры, включающей компьютерное программное обеспечение.
Пример \(\PageIndex{5}\)
График полярного уравнения Нарисуйте график полярного уравнения \(r=1+\cos \theta\).
Раствор
Для завершения этого примера мы будем использовать компьютерную программу Maple . Команда, которая создает полярный график приведенного выше уравнения: \(>\) plot(1+cos(t),t= 0..2*Pi,coords=polar). Здесь мы используем \(t\) для представления переменной \(\theta\) для удобства. Команда сообщает Maple, что \(r\) задается как \(1+\cos \left( t\right)\) и что \(t\in \left[ 0,2\pi \right]\).
Рисунок \(\PageIndex{7}\) Приведенный выше график имеет смысл, если рассматривать его с точки зрения тригонометрических функций. Предположим, \(\theta =0,r=2\) и пусть \(\theta\) увеличивается до \(\pi /2\). По мере увеличения \(\theta\) \(\cos \theta\) уменьшается до 0. Таким образом, линия от начала координат до точки на кривой должна становиться короче по мере того, как \(\theta\) идет от \(0\) в \(\пи/2\). По мере того, как \(\theta\) переходит от \(\pi /2\) к \(\pi\), \(\cos \theta\) уменьшается, в конечном итоге равняясь \(-1\) при \(\theta =\ число Пи\). Таким образом, \(r=0\) в этой точке. Этот сценарий изображен на приведенном выше графике, на котором показана функция, называемая 9.0040 кардиоида .
На следующем рисунке показана описанная выше процедура получения полярного графика \(r=1+cos(\theta)\). На этом рисунке концентрические окружности соответствуют значениям \(r\), а лучи от начала координат соответствуют углам, которые показаны на рисунке. Точка на луче, соответствующем углу \(\pi/6\), находится на расстоянии \(r = 1+cos(\pi/6)\) от начала координат. Точка на луче, соответствующем углу \(\pi/3\), находится на расстоянии \(r = 1+cos(\pi/3)\) от начала координат и так далее. Полярный график получается путем соединения таких точек плавной кривой, в результате чего получается фигура, показанная выше.
Рассмотрим еще один пример построения полярного графа.
Пример \(\PageIndex{6}\): полярный график
График \(r=1+2\cos \theta\) для \(\theta \in \left[ 0,2\pi \right]\ ).
Решение
График полярного уравнения \(r=1+2\cos \theta\) для \(\theta \in \left[ 0,2\pi \right]\) выглядит следующим образом.
Рисунок \(\PageIndex{9}\)Чтобы увидеть, как это показано на графике, рассмотрите следующий рисунок. Сначала были нанесены на график указанные точки, а затем была нарисована кривая, соединяющая точки. Когда это делается компьютером, используется гораздо больше точек для создания более точной картины.
Рассмотрим сначала следующую таблицу очков.
| \(\тета\) | \(\пи /6\) | \(\пи /3\) | \(\пи /2\) | \(5\пи /6\) | \(\пи\) | \(4\пи /3\) | \(7\пи /6\) | \(5\пи /3\) |
|---|---|---|---|---|---|---|---|---|
| \(р\) | \(\sqrt{3}+1\) | \(2\) | \(1\) | \(1-\sqrt{3}\) | \(-1\) | \(0\) | \(1-\sqrt{3}\) | \(2\) |
Обратите внимание, что некоторые записи в таблице имеют \(r<0. \) Чтобы отобразить эти точки, просто двигайтесь в противоположном направлении. Эти типы точек отвечают за маленькую петлю внутри большой петли на графике.
Процесс построения этих графиков может быть значительно облегчен с помощью компьютерного программного обеспечения. Однако использование такого программного обеспечения не должно заменять понимание необходимых шагов.
В следующем примере показан график для уравнения \(r=3+\sin \left( \displaystyle \frac{7\theta }{6}\right)\). Для сложных полярных графиков для облегчения процесса используется компьютерное программное обеспечение.
Пример \(\PageIndex{7}\): полярная диаграмма
График \(r=3+\sin \left( \displaystyle \frac{7\theta }{6} \right)\) для \(\theta \in \left[ 0,14\pi \right]\) .
Решение
Рисунок \(\PageIndex{11}\) В следующем примере показана другая ситуация, в которой \(r\) может быть отрицательным.
Пример \(\PageIndex{8}\): полярный график: отрицательный \(r\)
График \(r=3sin(4\theta)\) для \(\theta \in \left[ 0,2 \пи \справа]\).
Решение
Рисунок \(\PageIndex{12}\)Мы завершаем этот раздел интересным графиком простого полярного уравнения.
Пример \(\PageIndex{9}\): График спирали
График \(r=\theta\) для \(\theta \in [0,2\pi]\).
Решение
График этого полярного уравнения представляет собой спираль. Это так, потому что по мере увеличения \(\theta\) увеличивается и \(r\).
Рисунок \(\PageIndex{13}\)В следующем разделе мы рассмотрим два способа обобщения полярных координат на три измерения.
Эта страница под названием 8.1: Полярные координаты и полярные графики распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- кардиоидная
- полярные координаты
- Полярные графики
- источник@https://lyryx. com/first-course-linear-алгебра
- спираль
Полярные координаты
Многие системы и стили измерения широко используются сегодня. При построении графиков на плоской поверхности прямоугольная система координат и полярная система координат являются двумя наиболее популярными методами построения графиков отношений. Полярные координаты лучше всего использовать при рассмотрении периодических функций. Хотя обычно можно использовать любую систему, полярные координаты особенно полезны при определенных условиях.
Прямоугольная система координат является наиболее широко используемой системой координат. Второй по важности является полярная система координат . Он состоит из фиксированной точки 0 , называемой полюсом или исходной точкой . Из этой точки выходит луч, называемый полярной осью . Этот луч обычно располагается горизонтально и правее полюса. Любую точку P на плоскости можно определить, указав угол и расстояние. Угол θ измеряется от полярной оси до линии, проходящей через точку и полюс. Если угол измеряется против часовой стрелки, угол положительный. Если угол измеряется по часовой стрелке, угол отрицательный. Направленное расстояние, r , измеряется от полюса до точки P . Если точка P находится на конечной стороне угла θ, то значение r положительно. Если точка P находится на противоположной стороне полюса, то значение r отрицательно. полярных координат точки можно записать в виде упорядоченной пары ( r , θ). Местоположение точки можно назвать, используя множество различных пар полярных координат. На рисунке 1 показаны три разных набора полярных координат для точки 9.0150 Р (4,50°).
Рисунок 1
Полярные формы котерминальных углов.