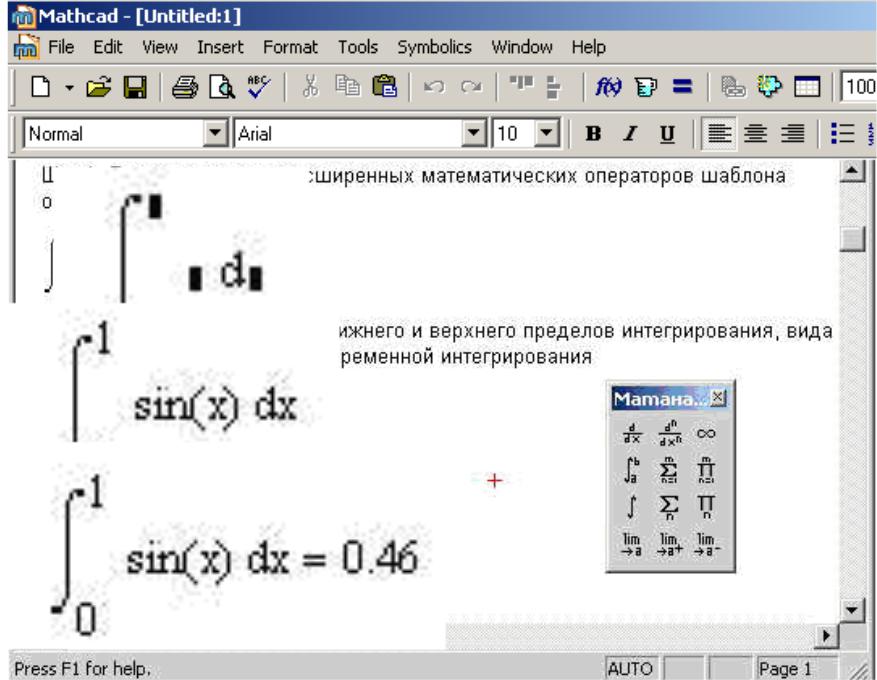
16. Тема 4. Создание программных фрагментов в MathCad. Краткие теоретические сведения
Система MathCad позволяет создавать программные фрагменты для вычисления алгоритмов, которые нельзя реализовать базовым набором средств и методов Mathcad.
Программный фрагмент можно использовать в операторе «=» или в правой части оператора «:=». Слева в операторе «:=» может находиться либо переменная, либо пользовательская функция.
Программный фрагмент состоит из строк программы, каждая из которых может содержать операторы программы.
Для создания программного фрагмента используется панель программирования, Кнопки которой имеют следующее назначение:
Add Line — Создание и расширение программного фрагмента; — Оператор внутреннего локального присваивания. IF — Оператор условия. FOr — Оператор цикла с заданным числом повторений. WHile – оператор цикла с предусловием. Оtherwise — Оператор «иначе», обычно используется совместно с If для выполнения действий в случаи невыполнения условия. Break — Оператор прерывания работы программного фрагмента. Сontinue — Оператор продолжения работы цикла после прерывания. |
Ниже приведен общий вид операторов программного фрагмента, рассмотрены правила их выполнения.
Общий вид оператора If:
Выражение if условие
Порядок выполнения: если логическое выражение, стоящее в Условии, истинно, то вычисляется Выражение, стоящее слева от оператора if.
Общий вид For :
For Var Î Nmin . . Nmax.
. Nmax.
Nmin.. Nmax – Диапазон изменения переменной цикла, организуется по правилам формирования дискретных переменных.
Порядок выполнения: переменную цикла Var изменяет свое значение в пределах от Nmin До Nmax с шагом 1 или -1, при каждом новом значении переменной цикла выполняется рабочая часть цикла.
Общий вид WHile:
While условие
Рабочая часть цикла записывается на месте шаблона
Порядок выполнения: рабочая часть цикла выполняется до тех пор, пока логическое выражение, стоящее в условии, истинно.
Результаты работы программного фрагмента передаются следующим образом: во внешнюю вычислительную область из программного фрагмента передается значение последнего выражения, вычисленного в программном фрагменте или значение переменной, имя которой записано в последней строке программы.
На рисунке 2.4.1 приведены примеры программных фрагментов. Из примера 1 видно, что программный фрагмент, реализующий линейный алгоритм, может заканчиваться оператором «=», а может быть присвоен переменной, например, k. Программный фрагмент может участвовать при создании пользовательской функции, например, y(x), которая затем вычисляется при конкретном значении ее аргумента, например, 3. Внутренние переменные программного фрагмента являются неопределенными вне его, например, переменная z, которая использовалась в программном фрагменте, не имеет конкретного числового значения вне его.
Из примера 1 видно, что программный фрагмент, реализующий линейный алгоритм, может заканчиваться оператором «=», а может быть присвоен переменной, например, k. Программный фрагмент может участвовать при создании пользовательской функции, например, y(x), которая затем вычисляется при конкретном значении ее аргумента, например, 3. Внутренние переменные программного фрагмента являются неопределенными вне его, например, переменная z, которая использовалась в программном фрагменте, не имеет конкретного числового значения вне его.
Пример1 | Пример2 |
Рисунок 2.4.1 – Примеры программных фрагментов |
Пример 2 демонстрирует программирование разветвляющихся и циклических алгоритмов. Для реализации разветвляющихся алгоритмов формируется пользовательская функция a(b), которая вычисляется по разным аналитическим зависимостям при различных значениях аргумента. Показана возможность вычисления этой функции в разных точках: при b равном -4, 9 и 15. Программирование циклических алгоритмов продемонстрировано на двух задачах. При решении задачи поиска суммы целых чисел от 1 до 5 применяется программный фрагмент с циклом for, результат получается с помощью оператора «=». Во второй части примера решается задача поиска суммы целых четных чисел от 0 до 10 с помощью оператора цикла while. Результат вычисления присваивается переменной h, хотя внутри цикла для накопления суммы используется переменная s.
Показана возможность вычисления этой функции в разных точках: при b равном -4, 9 и 15. Программирование циклических алгоритмов продемонстрировано на двух задачах. При решении задачи поиска суммы целых чисел от 1 до 5 применяется программный фрагмент с циклом for, результат получается с помощью оператора «=». Во второй части примера решается задача поиска суммы целых четных чисел от 0 до 10 с помощью оператора цикла while. Результат вычисления присваивается переменной h, хотя внутри цикла для накопления суммы используется переменная s.
| < Предыдущая | Следующая > |
|---|
7. Программирование в Mathcad
Впакете Mathcad существует богатый набор средств для решения различных математических задач, встроено огромное количество функций из различных разделов математики. Однако написать функции для всех практических задач, которые могут стоять перед пользователями пакета, невозможно. Для расширения возможностей разработчики пакета встроили достаточно простой и оригинальный язык программирования. В любом месте документа Mathcad можно вставить код программы на встроенном языке программирования. Это можно сделать при помощи «горячих клавиш» или команд из панели инструментов Programming (Программирование).
Однако написать функции для всех практических задач, которые могут стоять перед пользователями пакета, невозможно. Для расширения возможностей разработчики пакета встроили достаточно простой и оригинальный язык программирования. В любом месте документа Mathcad можно вставить код программы на встроенном языке программирования. Это можно сделать при помощи «горячих клавиш» или команд из панели инструментов Programming (Программирование).
Для визуализации панели програм-
мирования необходимо нажать на кнопку из панели математических инструментов или по-
дать команду View \Toolbars \Programming. На данной панели имеется десять команд. Щелчок по одной из этих команд создает в текущей
позиции заготовку для соответствующей программной конструкции. При частом использовании команд программирования удобнее запомнить комбинации «горячих клавиш» и команды генерировать при помощи клавиатуры.
Примечание. При составлении программ ключевые слова команд вручную писать нельзя. Заготовку команды можно получить только при помощи щелчка мыши по соответствующей кнопке или при помощи комбинаций клавиш.
Заготовку команды можно получить только при помощи щелчка мыши по соответствующей кнопке или при помощи комбинаций клавиш.
Приведем значение «горячих клавиш», использующих при программировании на Mathcadе.
Команда | Горячая клавиша | Команда | Горячая клавиша |
Add Line | ] | ← | { |
if | } | otherwise | CTR+Shift+] |
for | Ctrl+Shift+’ | while | Ctrl+] |
break | Ctrl+Shift+[ | continue | Ctrl+[ |
return | Ctrl+Shift+\ | On error | Ctrl+’ |
Предполагается, что читатель уже знаком с основными идеями программирования, изучив один из стандартных языков про-
118
граммирования: QBasic, Visual Basic, Fortran, Pascal, C++, Java, Ruby или любой другой язык программирования. Данный практикум адресован пользователям, решающим инженерные и научные задачи, для которых программирование не является основным видом деятельности. Для таких пользователей языки программирования C++ и Java противопоказаны, так как ориентированы на профессиональных специалистов. Инженерам, использующим программирование не ежедневно, для решения большинства задач достаточно и одиннадцати команд из панели программирования Mathcad.
Данный практикум адресован пользователям, решающим инженерные и научные задачи, для которых программирование не является основным видом деятельности. Для таких пользователей языки программирования C++ и Java противопоказаны, так как ориентированы на профессиональных специалистов. Инженерам, использующим программирование не ежедневно, для решения большинства задач достаточно и одиннадцати команд из панели программирования Mathcad.
Сразу же отметим недостатки программирования в среде Mathcad. Одним из главных недостатков является неразвитость отладчика программ. Ошибки, возникающие при выполнении программ, отображаются, но подробной информации о типе ошибки, значении локальных и глобальных переменных в момент останова программы оперативно получить нельзя. Отлаживать программы уже средней сложности в Mathcad не доставляет особой радости. Поэтому сложные инженерные, научные и экономические задачи удобнее и быстрее, с точки зрения автора, выполнять в рамках визуального алгоритмического языка Visual Basic [3] или последних версий языка Fortran.
Рассмотрим все команды из панели программирования Math-
cad.
1. Add Line – добавить строку в текущую позицию программы. При вводе данной команды появляется или расширяется на одну строку вертикальная линия, объединяющая отдельные операторы в блок с одним входом и одним выходом, который выполняется как один оператор.
Позиция, куда вставится строка, определяется положением курсора. Чтоб вставить новую строку в середину программы, нужно выделить (пробелами) строку перед позицией, куда будет вставлена пустая строка. Удалить лишнюю строку можно с помощью кнопки backspace на клавиатуре.
Для того чтобы начать ввод подпрограммы, необходимо набрать имя программы и в скобках через запятую перечислить формальные параметры подпрограммы, ввести нужное количество раз команду Add Line. Программа выводит последнюю переменную, обрабатываемую программой перед выходом. Вместо
119
имени подпрограммы можно указать имя переменной, куда необходимо вывести результат работы подпрограммы.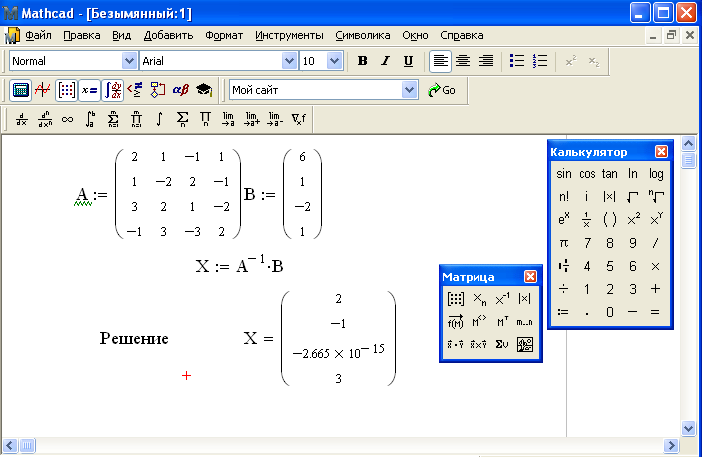
2. ← – оператор присваивания значения локальной переменной. При выходе из блока программы значения локальных переменных оказываются недоступны для других участков Mathcad файла.
В Mathcad имеются два оператора присваивания: для глобальных переменных (обозначается двумя символами «:=») и для локальных переменных «←». Глобальные переменные доступны в любом месте программы после объявления данной переменной, а локальные – только в текущем блоке.
Для пояснения действия локального и глобального оператора присваивания рассмотрим пример простейшей программы на
Mathcad.
Напишем программу для решения квадратного уравнения ax2+bx+c=0. В программе при помощи операторов глобального присваивания задаются значения глобальных переменных a, b и c. Для сравнения введем еще локальную переменную k и присвоим ей значение 4. Далее вычисляем значение корней квадратного уравнения при помощи программы, состоящей из одного блока операторов. В программе применяются три оператора локального присваивания и возвращается значения вектора x, состоящего из двух чисел.
Начало программы.
a :=1 b := −4 c := 3 k ← 4 ORIGIN :=1
x1 |
| = | D | ←b2 −4 a c | |||||
|
|
|
|
|
|
|
|
| |
x2 |
|
| x | ← | −b − | D | |||
|
|
|
|
|
|
|
| ||
|
|
| 1 |
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| x | ← | −b + | D | |||
|
|
|
|
|
|
| |||
|
|
| 2 |
|
| 2 a |
|
|
|
|
|
| x |
|
|
|
|
| |
D := | x := | k := |
|
|
| ||||
|
|
|
| ||||||
x1 =1 x2 = 3 a =1 b = −4 c = 3.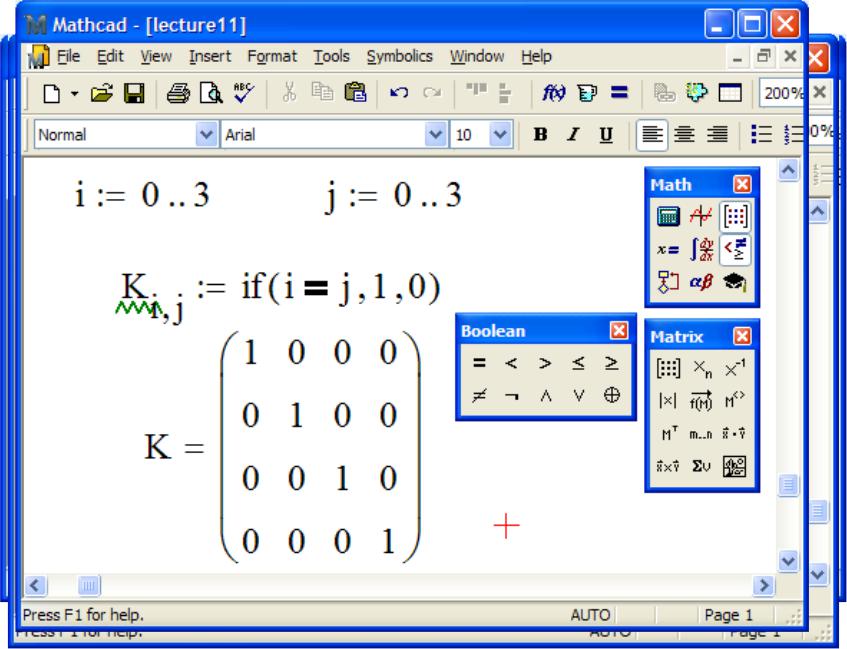
Конец программы.
3. Оператор if предназначен для организации разветвляющихся вычислительных процессов. Чтобы ввести оператор if в программу, необходимо мышкой щелкнуть по кнопке if из панели программирования или использовать горячую клавишу – }.
При этом в программу вставляется заготовка для оператора if: if .
Общий вид простого оператора if: D if L, L – логическое выражение;
D – оператор, выполняемый в случае, если условие L принимает значение «истина».
Оператор работает следующим образом:
•вычисляется логическое условие L;
•если L – истина, то выполняется оператор D, в ином случае он не выполняется;
•выполнение программы продолжается со следующего,
после if, оператора.
Как мы видим, данный оператор if идентичен аналогичному оператору из других высокоуровневых языков программирования. Единственное отличие заключаются в синтаксисе.
Для формирования сложных условий можно использовать панель инструментов Boolean, содержатся знаки логического равенства, неравенства и логических операций. В частности, «V» означает логическое «или», а «Λ» — логическое «и».
В частности, «V» означает логическое «или», а «Λ» — логическое «и».
121
Таким образом, чтобы сформулировать условие, что переменная х находится в диапазоне (–3;4), необходимо написать: x > –3 Λ x < 4.
При формулировании сложных логических условий для расстановки приоритетов можно использовать скобки.
Пример. Построить график следующей функции:
28 −6x, | x (−∞;3) | |
| +1, | x [3;−1] . |
f (x) = x2 | ||
|
| x (1,∞) |
2, |
| |
Решение.
f (x) := 28 −6 x if x > 3
x2 +1 if x ≤ 3 x ≥ −1
2if x < −1
Всложных подпрограммах
часто используется блочный оператор if: if L
D1
Dn
Где D1, …, Dn – действия, выполняемые в случае, если логическое условие L истинно.
Для того чтобы вставить подобную конструкцию, нам необходимо, на панели инструментов Programming, выбрать if , затем установить курсор на место ввода слева от оператора if и n раз нажать на Add Line.
Приведем пример программы с подобным оператором. Усовершенствуем программу для решения квадратного уравнения ax2+bx+c=0.
Начало программы.
x1 |
| = | ORIGIN :=1 a :=1 b := −1 c := 4 | |||
|
| D ←b | 2 | −4 | a c | |
x2 |
|
|
| |||
|
|
| if D ≥ 0 |
| ||
x1 ← −b2− a D x2 ← −b2+ a D
if D < 0
x1 ←»действительных корней нет» x2 ←»действительных корней нет»
x
x1 =»действительных корней нет» x2 =»действительных корней нет»
Конец программы.
В данном случае при дискриминанте меньше 0 программа выдает сообщение «действительных корней нет!».
Кроме оператора if, программа Mathcad может содержать и оператор otherwise.
4. Оператор otherwise применяется в случае, когда используется условие с двумя вариантами действия, то есть, если условие истинно, нужно выполнить одно действие (или действия), а если ложно, то другое.
Общий вид такого оператора следующий:
D1 if L
D2 otherwise
В случае если условие L истинно, выполняются действия D1, иначе выполняются действия D2. То есть otherwise аналогичен оператору else в Бейсике, Фортране и других высокоуровневых языках.
Рассмотрим пример программы, использующей операторы if и otherwise. В данном случае проверяются условия, при которых логарифм не существует (x<0 или y<0 или y=1). Если они выпол-
123
нены, выдается сообщение «error», в противном случае вычисля-
ется logyx. |
|
|
|
f _ log(x, y) := |
| «error» | if x ≤ 0 y ≤ 0 y =1 |
| |||
|
| log(x, y) | otherwise |
f _ log(−4,5) =»error» |
| ||
f _ log(8,2) = 3 |
|
|
|
Когда в блоке otherwise несколько строк, нужно установить курсор в место ввода слева от оператора otherwise и нажать Add Line необходимое количество раз.
Вернемся к программе, вычисляющей корни уравнения ax2+bx+c=0, и запишем ее с помощью операторов if и otherwise. Начало программы.
ORIGIN :=1 a :=1 b := 2 c := 2
x1 | = |
| D ←b | 2 | −4 a c |
|
|
| |||
|
|
|
| ||||||||
|
|
|
|
| |||||||
x2 |
|
| if D ≥ 0 |
|
|
| |||||
|
|
|
| x | ← |
| −b − | D | |||
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||
|
|
|
| 1 |
|
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| x | ← | −b + | D | ||||
|
|
|
|
|
| ||||||
|
|
|
| 2 |
|
|
| 2 a |
|
|
|
|
|
| otherwise |
|
|
| |||||
|
|
|
| x1 ←»действительных корней нет» | |||||||
|
|
|
| ||||||||
|
|
|
| x2 ←»действительных корней нет» | |||||||
|
|
| x |
|
|
|
|
|
|
| |
x1 = −2 |
| x2 = −1 |
|
|
| ||||||
Конец программы.
5. Оператор for используется для создания циклических вычислительных процессов. В документе Mathcad простейшие циклы могут быть заменены ранжированными векторами. Для более сложных циклов необходимо составлять программу.
Чтобы вставить оператор for в программу, необходимо мышкой щелкнуть по кнопке for из панели программирования или использовать «горячую» клавишу «Ctrl+Shift+’». При этом в программу вставляется заготовка для оператора for:
for
Общий вид оператора выбора for: for i k1..kn
D
Или
for i (k1 k2 k3 … kn)
D
Где i – счетчик цикла. Переменная, которая меняется в диапазоне от k1 до kn. Диапазон изменения счетчика цикла вводится с помощью ранжированной переменной или с помощью вектора.
D –действия, которые выполняются в цикле (тело цикла). Ниже приведен пример, в котором диапазон изменения счетчика цикла n задан с помощью вектора. Вектор вставляется с по-
мощью панели инструментов Matrix.
sum := s ← 0
for n (1 2 5 7 10 11 13 16 17 19)
s ← s + 1n
sum = 2. 285.
285.
Данная программа вычисляет сумму
Sum=1+1/2+1/5+1/7+1/10+1/11+1/13+1/16+1/17+1/19.
Если тело цикла оператора for состоит из нескольких строк, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Как и в обычных программах, циклы и условные операторы могут быть вложенными. Mathcad, впрочем, сам следит за вложенностью циклов и сделать ошибку во вложенности просто не позволит.
Пример. Написать функцию FA, создающую матрицу A, состоящую из M строк и N столбцов следующего вида:
125
1 | 2 | 4 | 8 | 16 |
| |
| 0 | 1 | 2 | 4 | 8 |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем подпрограмму, выводящую эту матрицу с помощью двух вложенных циклов:
FA(M , N ) := |
| for | i 0. |
| ||||
|
| |||||||
|
|
|
| for | j 0..N −1 |
| ||
|
|
|
|
| Ai , j | ← 1 | if | i = j |
|
|
|
|
| ||||
|
|
|
|
| Ai , j | ← 0 | if | i > j |
|
|
|
|
| Ai , j ← 2 Ai, j−1 | if i < j | ||
|
|
| A |
|
|
|
|
|
1 | 2 | 4 | 8 | 16 |
|
| ||
| 0 | 1 | 2 | 4 | 8 |
|
|
|
FA(4,5) = |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
|
|
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
Обозначим i – | строку матрицы, j – столбец матрицы. | |||||||
Тогда главная диагональ задается уравнением «i=j», элементы матрицы, расположенные выше главной диагонали, уравнением «i<j», а элементы матрицы, расположенные ниже главной диагонали, – усравнением «i<j».
Каждый элемент, расположенный выше главной диагонали, вычисляется как удвоенное произведение элемента, стоящего в этой же строке в предыдущем столбце: Ai j=2* Ai j–1.
Для проверки работы функции подали команду: FA(4,5)=. 6. Оператор цикла while используется тогда, когда цикл дол-
жен выполняться не заданное количество раз, а до тех пор, пока не будет выполнено определенное в цикле условие.
Чтобы вставить оператор while в программу, необходимо мышкой щелкнуть по кнопке while из панели программирования или использовать горячую клавишу – «Ctrl+]». При этом в программу вставляется заготовка для оператора while:
while
Общий вид оператора While: while L
D,
где L – условие, при выполнении которого выполняется цикл (условие цикла).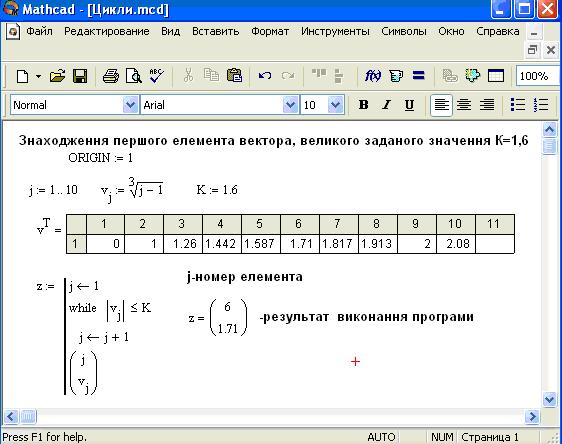 В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.
В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.
Если в теле цикла выполняемых действий должно быть несколько, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Следует заметить, что если условие L истинно всегда, то программа будет работать бесконечно (зациклится). Именно поэтому с циклом while необходимо быть очень осторожным и тщательно проверять условие выхода из цикла, прежде чем выполнять программу.
Если программа все-таки повисла, то чтобы прервать ее выполнение, необходимо нажать клавишу «Esc» и в появившемся окне нажать на кнопку OK.
Приведем пример программы, использующей цикл while.
s ← 0 |
|
|
| ||
n ←1 |
|
|
| ||
| 1 |
|
| ||
while |
|
| > tol | ||
n | |||||
|
|
|
| ||
s ← s + 1n n ← n +1
s
= 2.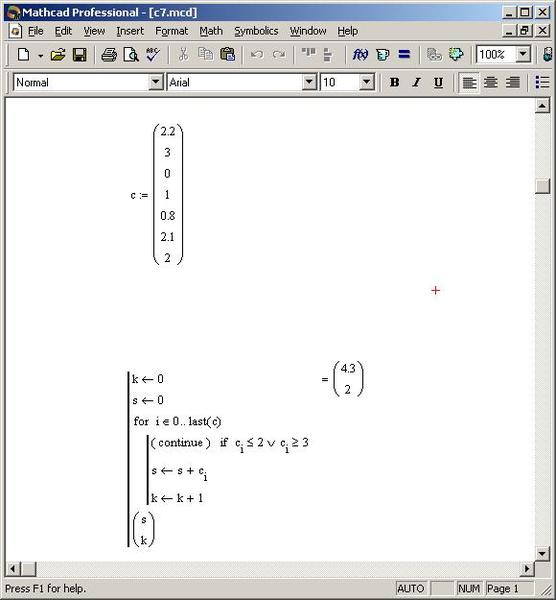 829.
829.
Вданной программе с указанной точностью (tol) вычисляется сумма s=1+1/2+1/3+1/4+1/5+1/6+1/7…
7. Оператор break обеспечивает экстренный выход из цикла. Программа при этом продолжает выполнять следующую после цикла строку. Данный оператор часто применяется, чтобы избежать «зацикливания» программы.
Вкачестве примера применения оператора break рассмотрим
∞ |
| 12n −1 |
|
|
|
задачу вычисления суммы числового ряда S = ∑ |
|
| . | В | |
n | 3 | ||||
n=1 | + 2n +1 |
|
| ||
приведенной ниже программе, суммирование членов ряда прекращается, когда достигается точность, указанная параметром tol или если число итераций цикла превышает 10000.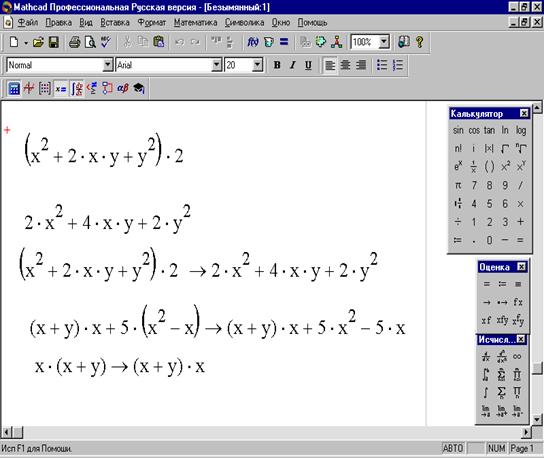
f (n) := | 12 n −1 |
| |
n3 + 2 n +1 | |||
| |||
sum(tol) := s ← 0 n ←1
while f (n) > tol s ← s + f (n)
break if n >10000 n ← n +1
s sum(0.000011) =8.726 .
В данном случае оператор break исключается возможность зацикливания программы для расходящегося ряда.
8. Оператор continue возвращает управление в первую строку цикла. Как только этот оператор встречается в программе, выполнение текущей итерации прерывается и выполняется переход на следующую итерацию цикла. Выход из цикла не производится.
Данный оператор, как и оператор break, не содержит параметров.
Пример: Найти сумму N первых членов ряда:
N |
| 1 |
|
S = ∑ |
| . | |
2n | 3 | ||
n=1 | −16 |
|
В программе, при помощи оператора continue, происходит обход слагаемого в котором знаменатель дроби равен нулю.
sum(N ) := |
| s ← 0 | |
| |||
|
| for n 1..N | |
|
|
| a ← 2 n3 −16 |
|
|
| |
|
|
| continue if a = 0 |
|
|
| s ← s + 1 |
|
|
| a |
|
| s | |
sum(100) = −0. 024.
9. Оператор return прерывает выполнение программы. В качестве результата работы программы возвращается значение, указанное в позиции для ввода, после оператора return.
При выборе на панели инструментов пункта return вставляется строка.
Пример. Подсчитать с указанной точностью tol сумму ряда:
∞ |
|
| 12n |
|
S = ∑ |
|
| . | |
n | 2 | + 2n +16 | ||
n=1 |
|
|
Если ряд получается расходящийся, программа выдаст сообщение «расходится». Ряд будет считаться расходящимся, если число итераций цикла превысило 1000000 раз.
f 1(n) := | 12n | |||||||
n2 + 2n +16 |
|
|
|
|
| |||
sum1(N ) := |
| s ← 0 | ||||||
| ||||||||
|
| n ←1 | ||||||
|
| while |
| f 1(n) |
| > tol | ||
|
|
|
| |||||
|
|
| s ← s + f 1(n) | |||||
|
|
| ||||||
|
|
| return » ряд расходится» if n >100000 | |||||
|
|
| n ← n +1 | |||||
|
| s | ||||||
129
sum1(0. 01) =» ряд расходится».
01) =» ряд расходится».
10. Оператор on error отвечает за обработку ошибок. При выборе данного оператора в программу вставляется заготовка следующего вида:
Общий вид оператора on error: D1 on error D2 .
Если при вычислении выражения D1 произошла ошибка, будет вычислено значение D2.
Данный оператор имеет смысл использовать, если при выполнении программы возможна ошибка в каком-то определенном месте, например деление на ноль.
Приведем пример программы, вычисляющей десятичный логарифм числа xy.
Если логарифм не существует, выдается сообщение об ошибке: «аргумент логарифма <0».
|
|
|
f (x, y) := |
| z ← x y |
| ||
|
| «аргумент логарифма < 0» on error log(z) |
f (0,5) =»аргумент логарифма < 0″; | ||
f (10,1) =1. | ||
Оператор on error можно применять в комплексе встроенной функцией error().
f (x, y) := z ← x y
error(«аргумент логарифма < 0») on error log(z)
В данном случае сообщение об ошибке будет показываться в стандартном для Mathcad виде. При ошибке текст вызова функции выделяется красным цветом, а при подведении мыши к этому вызову внизу отображается запрограммированный в функции error текст.
1.3.5. Программирование MathCAD 12 руководство
Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику (например, возвращение различных значений в зависимости от условий), в одну строку не удается. Назначение программных модулей как раз и заключается в определении выражений, переменных и функций в несколько строк, часто с применением специфических программных операторов.
Принцип программирования в Mathcad
При помощи элементов программирования можно определять переменные и функции (как показано в листинге 1. 19).
19).
Листинг 1.19. Функция условия, определенная с помощью программы
Традиционное программирование, упрощенный вариант которого применен в Mathcad и осуществляется при помощи панели инструментов
Programming (Программирование), имеет ряд существенных преимуществ, которые в ряде случаев делают документ более простым и читаемым:
- возможность применения циклов и условных операторов;
- простота создания функций и переменных, требующих нескольких простых шагов;
- возможность создания функций, содержащих закрытый для остального документа код, включая преимущества использования локальных переменных и обработку исключительных ситуаций.
Как видно из листинга 1.19, программный модуль обозначается в Mathcad вертикальной чертой, справа от которой последовательно записываются операторы языка программирования. Чтобы начать создание программного модуля, следует (в случае листинга 1.19 после символа присваивания) нажать на панели
Programming (Программирование) кнопку Add One (Добавить линию). Затем, если приблизительно известно, сколько строк кода будет содержать программа, можно создать нужное количество линий повторными нажатиями кнопки
Add Line (Добавить линию) (рис. 1.18).
Затем, если приблизительно известно, сколько строк кода будет содержать программа, можно создать нужное количество линий повторными нажатиями кнопки
Add Line (Добавить линию) (рис. 1.18).
Рис. 1.18. Начало создания программного модуля
В появившиеся местозаполнители введите желаемый программный код, используя программные операторы. В рассматриваемом примере в каждый местозаполнитель вводится строка, например, в средний — «positive» (рис. 1.19). Затем нажимается кнопка
If (Если) на панели Programming (Программирование) и в возникший местозаполнитель вводится выражение
х>0. После того как программный модуль полностью определен, и ни один местозаполнитель не остался пустым, функция может использоваться обычным образом, как в численных, так и в символьных расчетах.
ВНИМАНИЕ!
Не вводите с клавиатуры имена программных операторов. Для их вставки можно применять лишь сочетания клавиш, которые приведены в тексте всплывающей подсказки (рис. 1.18 и 1. 19).
19).
Рис. 1.19. Вставка программного оператора
Добавление строк программного кода
Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки Add Line (Добавить линию). Для этого следует предварительно поместить на нужное место внутри программного модуля линии ввода. Например, расположение линии ввода на строке, показанной на рис. 1.18, приведет к появлению новой линии с местозаполнителем перед этой строкой. Если передвинуть вертикальную линию ввода из начала строки (как это показано на рис. 1.20) в ее конец, то новая линия появится после строки. Если выделить строку не целиком, а лишь некоторую ее часть (рис. 1.20), то это повлияет на положение в программе новой строки кода (результат нажатия кнопки Add Line показан на рис. 1.21).
СОВЕТ
Не забывайте, что для желаемого размещения линий ввода внутри формулы можно использовать не только мышь и клавиши со стрелками, но и пробел. С помощью последовательных нажатий пробела линии ввода «захватывают» разные части формулы.
Рис. 1.20. Положение линий ввода влияет на положение создаваемой строки программы
Зачем может потребоваться вставка новой линии в положение, показанное на рис. 1.21? Новая вертикальная черта с двумя линиями выделяет фрагмент программы, который относится к условию х>0, находящемуся в его заголовке. Пример возможного дальнейшего программирования показан в листинге 1.20.
Рис. 1.21. Результат вставки новой линии в программу (из положения рис. 1.20)
Листинг 1.20. Пример усовершенствования программы
В режиме выполнения программы, а это происходит при любой попытке вычислить f (х), выполняется последовательно каждая строка кода. Например, в предпоследней строке листинга 1.20 вычисляется f (1). Рассмотрим работу каждой строки кода этого листинга.
1. Поскольку х=1, то условие х<0 не выполнено, и в первой строке ничего не происходит.
2. Условие второй строки х>о выполнено, поэтому выполняются обе следующие строки, объединенные короткой вертикальной чертой в общий фрагмент.
3. Функции f(x) присваивается значение f (x)=»positive».
4. Условие х>1000 не выполнено, поэтому значение «big positive» не присваивается f (х), она так и остается равной строке «positive».
5. Последняя строка не выполняется, т. к. одно из условий (х>0) оказалось истинным, и оператор otherwise (т. е., «иначе») не понадобился.
Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т. к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.
Локальное присваивание (<—)
Язык программирования Mathcad не был бы эффективным, если бы не позволял создавать внутри программных модулей локальные переменные, которые «не видны» извне, из других частей документа. Присваивание в пределах программ, в отличие от документов Mathcad, производится с помощью оператора Local Definition (Локальное присваивание), который вставляется нажатием кнопки с изображением стрелки (<-) на панели
Programming (Программирование).
ВНИМАНИЕ!
Ни оператор присваивания :=, ни оператор вывода = в пределах программ применять не разрешается.
В Mathcad 12 переменным, которые впервые появляются в программных модулях, по умолчанию присваивается значение 0. В прежних версиях программы использование переменных в программах без предварительного присваивания им значений приводило к генерации ошибки (как в расчетах на рабочей области документов Mathcad).
Локальное присваивание иллюстрируется листингом 1.21. Переменная z существует только внутри программы, выделенной вертикальной чертой. Из других мест документа получить ее значение невозможно. На этом же листинге вы видите пример применения оператора цикла for.
Листинг 1.21. Локальное присваивание в программе
Лекция№10 — Программирование в системе MathCAD
Функции являются важнейшим инструментом математики.
В разделе 1.9 технология работы с пользовательскими функциями, которые можно описать с помощью одного выражения. Если описания функции нельзя уместить в одно выражение, то без элементов программирования обойтись сложно.
Если описания функции нельзя уместить в одно выражение, то без элементов программирования обойтись сложно.
Язык программирования MathCAD содержит все элементы языка высокого уровня, необходимые для математических расчетов. Будучи дополненным сотнями встроенных функций и операторов системы, возможностями численного и символьного расчета различных величин, он по эффективности не уступает профессиональным системам программирования. Кроме того, у него есть одно очень крупное преимущество: язык программирования MathCAD предельно прост (а по изящности и наглядности в оформлении алгоритмов вообще не имеет аналогов).
Как правило, при использовании функций, встроенных в систему MathCAD, пользователи не задумываются о том, на основании каких методов и решений достигается цель, поставленная перед функцией. Такая встроенная функция используется по типу «черного ящика» – пользователь познакомился с ее описанием/спецификацией, вызвал для решения, получил ответ.
При программировании пользовательских функций будем придерживаться «созвучного» порядка, т.е. идти от спецификации к программированию.
4.1. Спецификации функций
Спецификация функции состоит из ее заголовка и описания назначения – выходного значения или результата работы функции. Для примера можно обратиться к мастеру функций и более внимательно посмотреть на предоставляемые им для его функций описания. На рис. 4.1 открыта страница со спецификацией функции rnorm.
Рис. 4.1. Спецификация функции, предоставляемая мастером функций
Заголовок содержит имя функции (rnorm) и список формальных параметров (m, mu, sigma). Каждая пользовательская программа-функция MathCAD должна иметь оригинальное имя, используя которое будет осуществляться обращение к этой программе-функции. Через это же имя (и только через это имя ) «возвращается» в рабочий документ результат выполнения программы-функции.
Через это же имя (и только через это имя ) «возвращается» в рабочий документ результат выполнения программы-функции.
Через формальные параметры «внутрь» программы-функции «передаются» данные, необходимые для выполнения вычислений внутри программы. В качестве формальных параметров могут использоваться имена простых переменных, массивов и функций. Формальные параметры отделяются друг от друга запятой.
При описании назначения функции необходимо сказать, что возвращает функция в качестве своего результата (в описываемой функции rnorm возвращает вектор нормально распределенных случайных значений). При этомобязательно нужно пояснить роль каждого из формальных параметров, перечисленных в заголовке (m – количество значений, mu – среднее значение, sigma – стандартное отклонение). Желательно сказать об ограничениях, т.е. невозможность расчета при … каких-либо условиях.
Для написания программ-функций в системе MathCAD предусмотрена специальная панель программироваия –Programming (Программирование), содержащая все операторы и элементы языка. Общий вид панели Programmingпредставлен на рис. 4.2. Операторы в программу вставляются только с помощью кнопок этой панели.
Общий вид панели Programmingпредставлен на рис. 4.2. Операторы в программу вставляются только с помощью кнопок этой панели.
Назначение основных команд, представленных на панели:
Add Line – добавление новой строки в программу или создание заготовки программы из двух строк, если программы еще не существует; ← – присвоение значения локальной переменной; if – условный оператор. Позволяет в зависимости от условия выполнять или не выполнять те или иные действия; otherwise – используется сразу после оператора if и позволяет выполнить определенные действия при невыполнении условия в операторе if ; for – оператор создания цикла со счетчиком; while – оператор создания цикла, выполнение которого продолжается до тех пор, пока выполняется указанное условие. continue – продолжить вычисления в цикле; break – прервать вычисления в цикле; return – оператор возврата; on error – оператор перехода при возникновении ошибки.
|
Рис.4.2. Вид панели инструментов Programming (Программирование)
Чтобы написать программу, прежде всего для нее должен быть создан специальный, обособленный от остального документа, программный блок-тело функции. Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения и операторы алгоритма. Чтобы построить единичный элемент программного блока, нажмите кнопку команды Add Line (Добавить линию) панели Programming (Программирование).
Присваивание значений в программах имеет ряд особенностей. Важнейшим из них является то, что присвоение величин используемым алгоритмом функциям и переменным может быть произведено как в самой программе, так и выше нее. Данные два подхода весьма существенно разнятся:
Если значение переменной или функции присваивается в программе посредством оператора «←» , то такая переменная или функция будет являться локальной. То есть она будет видимой только в рамках программы. Как-то повлиять на объекты вне программы она не сможет (равно, как извне к ней нельзя будет получить доступ).
Если переменная или функция задается выше программы с помощью оператора «:=», то она в программе будет обладать глобальной видимостью. То есть такая переменная или функция будет доступна любому нижележащему объекту, в том числе и коду программ.
 Однако программа может только прочитать значение глобальной переменной или вызвать глобальную функцию. Изменить каким-либо образом значение глобальной переменной или функции программа не может. Это очень важно учитывать при написании алгоритмов.
Однако программа может только прочитать значение глобальной переменной или вызвать глобальную функцию. Изменить каким-либо образом значение глобальной переменной или функции программа не может. Это очень важно учитывать при написании алгоритмов.Если программа должна осуществлять какую-то модификацию объекта, то результат своей работы она должнавозвращать.
Все программы составляемые в пакете MathCAD с точки зрения любого языуа программирования (например, Turbo Pascal) представляют собой подпрограммы – функции, которые могут возвращать в качестве результата число, вектор или матрицу.
Перед тем как использовать программу-функцию нужно ее описать. Описание программы-функции размещается в рабочем документе перед вызовом программы-функции и включает в себя заголовок функции и тело функции, соединенные в единое целое с помощью операции присваивания («:=»).
Заметим, что если программа используется для вычисления одного значения, то в своем заголовке она не содержит списка формальных параметров и называется программой-скаляром.
Программа-функция может не иметь формальных параметров и тогда, когда данные передаются через имена переменных, определенных выше описания программы-функции. Эти переменные будут являться глобальными для данной функции.
Технология создания программы-функции в рабочем документе MathCAD состоит из следующих шагов:
Ввести заголовок функции.
Ввести знак присваивания «:=».
Выполнить команду Add line, расположенную на панели Programming (Программирование). Появившейся на экране шаблон с вертикальной чертой и полями для ввода операторов будут составлять заготовку для тела программы-функции.
Вписать операторы в шаблон-заготовку. Тело программы-функции может включать любое число операторов: локальных операторов присваивания, условных операторов и операторов цикла, а также вызов других программ-функций.
Самое нижнее поле всегда предназначено для определения возвращаемого программой значения.
Пример 1. Требуется подготовить описание функции и вычислить значения этой функции приx = 4.15 и g = 1.854.
Решение. Заметим, что при вычислении y можно обойтись без описания и использования пользовательской функции и тем более без программирования, как это показано на рис. 8.4, a. Использование функции следует из требования к задаче для простоты изложения. Для нахождения значения функции «внутрь» программы-функции следует передать значения x и g, необходимые для выполнения вычислений внутри программы. Поэтому переменные x и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – y. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 8.3.
Поэтому переменные x и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – y. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 8.3.
(1-2) |
(3) | (4-5)
|
(6) |
Рис.4.3. Пошаговое создание и выполнение программы-функции
В данном примере введена вспомогательная локальная переменная t для вычисления значения функции. И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 4.4, b, c приведены другие варианты решения поставленной задачи.
И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 4.4, b, c приведены другие варианты решения поставленной задачи.
Рис. 4.4. Демонстрация элементов программирования простых выражений
В примере, представленном на рис. 4.4, в первой колонке a для вычисления значения используется базовый набор средств без элементов программирования. Во второйb и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и c) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (bи c) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.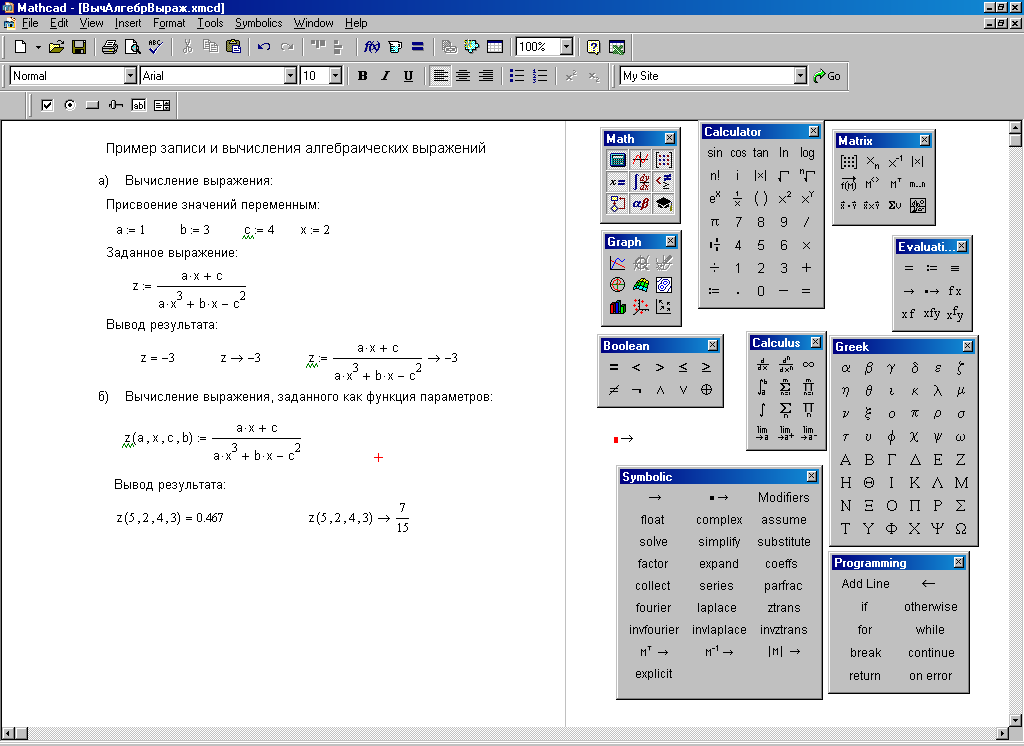
Внутри программ (b и c) используются глобальные переменные g и x из документа. Значения этих переменных определены заранее. Обе программы из примера, представленного на рис. 4.4, в своей программируемой части содержат операторы присваивания с использованием локальных переменных. Переменные, созданные внутри программы с таким видом присваивания, являются внутренними, и доступ к ним может осуществляться только в самой программе.
Впрограммной части используются глобальные переменные обычнотолько как операнды в выражениях.
Присвоить глобальным переменным значения внутри программы можно только локальным образом. После выхода из программы эти переменные сохраняют свои «глобальные» значения.
Использование «обычного» оператора присваивания «:=» в теле программы-функции приводит к синтаксической ошибке.

Последняя строка программы не должна содержать управляющих операторов. Эта строка задает значение, возвращаемое программой, т.е. получает результат вычислений и может содержать имя локальной переменной результата (рис. 4.4, c) или выражение, вычисляющее результат (рис. 4.4, b).
Обычно программа содержит больше чем две строки, поэтому рекомендуется сразу задавать блок из 5-6 маркеров.
Добавление недостающих полей для ввода дополнительных операторов производится с помощью кнопки Add lineпанели программирования. При этом поле ввода добавляется внизу выделенного к этому моменту оператора.
Для удаления того или иного оператора или поля ввода из тела программы-функции, нужно заключить его выделить и нажать клавишу <Delete> .
Программный блок можно создать и внутри уже заданного блока (вложенный блок).
 Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.
Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.Иногда при написании программы бывает нужным добавить строку к уже созданному блоку. Чтобы это сделать, поставьте курсор в ту строку блока, выше или ниже которой должна быть введена строка, и нажмите клавишу <Пробел>. При этом строка будет выделена и можно будет произвести добавление одним из стандартных способов.
Положение вставляемого маркера определяется положением вертикальной черты курсора. Если она находится слева от выделенного выражения, то маркер будет добавлен выше выделенной строки, если справа – то ниже.
Чтобы развернуть курсор в нужную сторону, нажмите клавишу <Insert>.
Чтобы добавить строку к целому блоку, его следует выделить, дважды нажав клавишу <Пробел>.

В том случае, если программа содержит блоки различных уровней, то для добавления строки, например, к первому блоку, нажмите клавишу <Пробел> несколько раз: при каждом нажатии будут выделяться блоки более низкого уровня.
Пример 2. Требуется найти действительные корни квадратного уравнения , гдеa, b, c – любые действительные числа и . Известно, что в зависимости от знака дискриминантадействительные корни уравнения могут быть получены по формуле:
Решение. Опишем вычисление корней в виде программы-функции.
Спецификацию для этой функции можно записать следующим образом. Функция R(a,b,с) возвращает значения действительных корней квадратного уравнения или сообщает о том, что уравнение не имеет корней.
Здесьa, b, с – коэффициенты уравнения.
Очевидно, что в данном случае мы имеем дело с ветвящимся процессом.
Программирование ветвящихся процессов требует проверки некоторых условий, в зависимости от которых выбирается вычислительная формула. Для реализации таких вычислений на панели программирования предусмотрен оператор if (если).
При включении оператора if в блок программирования появляется шаблон с двумя полями ввода – справа и слева от оператора:
if .
В поле ввода справа от оператора записывается условие. Для ввода условий следует использовать панельBoolean (Логические), где есть кнопки для проверки условий ( = > < ≥ ≤ ≠ ).

В поле ввода слева нужно ввести строку программы (или несколько строк), которая будет выполняться, если введенное условие истинно.
Если невыполнение условия должно привести к выполнению какой-либо другой строки (или нескольких строк), то можно в строке, следующей за оператором if , вставить оператор otherwise (иначе). В поле ввода слева от этого оператора надо ввести строку, которая будет выполняться только в том случае, если условие ложно.
Чаще всего оператор if используется для задания разрывных или кусочно-непрерывных функций.
Описание функции и примеры ее вызова представлены на рис. 4.5.
Рис. 4.5. Описание функции R(a,b,x), предназначенной для вычисления корней квадратного уравнения
Пример 3.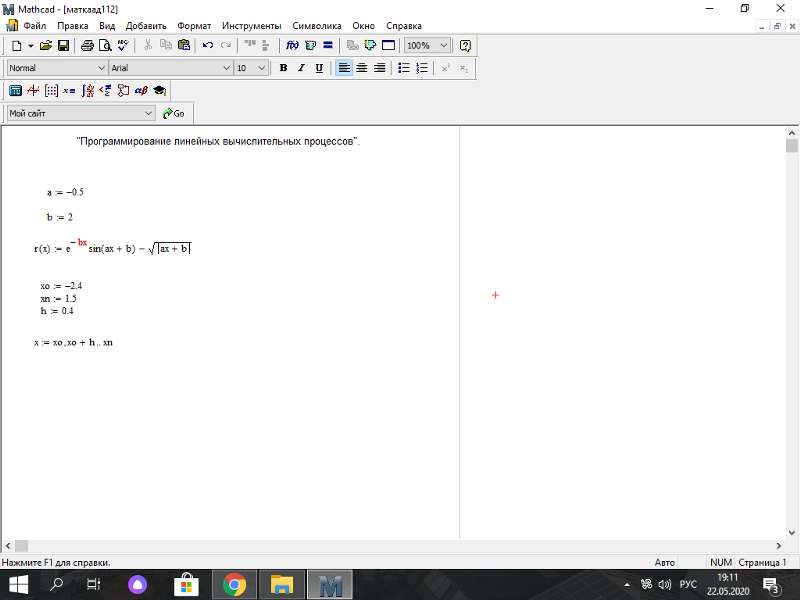 Требуется подготовить описание программы-функции и построить ее график на интервале [–2, 4] .
Требуется подготовить описание программы-функции и построить ее график на интервале [–2, 4] .
Решение. Из анализа аналитического выражения функции y видно, что функция является кусочно-непрерывной на числовой оси и алгоритм вычислений содержит три ветви. Вычисление значения y зависит от местоположения переменной x на числовой оси.
Для нахождения значения функции целесообразно ввести один формальный параметр, соответствующий переменной x.Спецификацию для этой функции можно записать следующим образом:
Функция f(x) возвращает значение функции, определенной в соответствии с условием примера 3. Здесь х – аргумент для вычисления.
В описании функции требуется проверить три условия. В зависимости от результатов проверки этих условий применяется соответствующая условию вычислительная формула.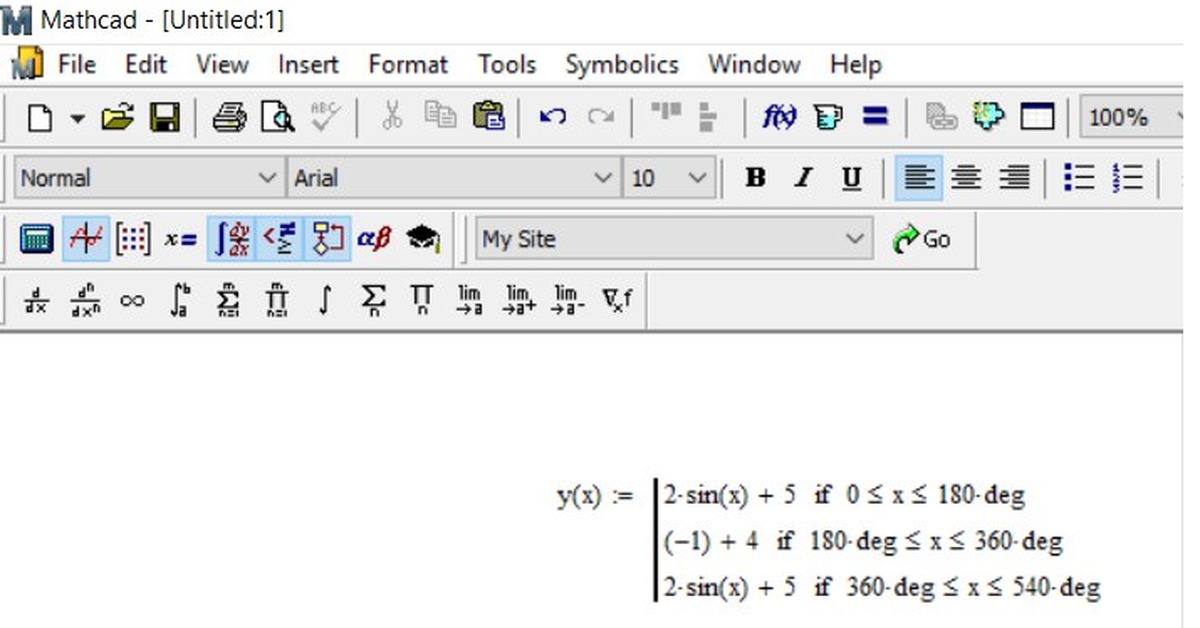 Поэтому при программировании можно с проверкой каждого из условий связать условный оператор if, как это показано на рис. 8.6. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8.7 представлен второй вариант функции-программы.
Поэтому при программировании можно с проверкой каждого из условий связать условный оператор if, как это показано на рис. 8.6. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8.7 представлен второй вариант функции-программы.
Рис. 4.6. Демонстрация элементов программирования ветвящихся процессов
Рис. 4.7. Демонстрация элементов программирования ветвящихся процессов
На рис. 4.8 представлены примеры программ-функций, реализующих вычисления, содержащие ветвящиеся процессы.
Рис. 4.8. Примеры программирования функций с проверкой условий. Здесь x – глобальная переменная
Пример 4. Требуется найти максимальный и минимальный элементы в заданном массиве.
Решение. Задача поиска наибольшего/наименьшего значений в заданном массиве относится к типовым циклическим алгоритмам .
Спецификацию для этой функции можно записать следующим образом:
Функция Fun(P) возвращает наибольшее и наименьшее значение в массиве Р.
Для создания циклов в MathCAD предусмотрено два оператора: for и while. Поскольку количество повторений цикла заранее известно и связано с числом элементов заданного массива, в данном решении целесообразно использовать оператор for.
После вставки оператораfor в строку программы его сопровождают три поля ввода, как это показано на рис. 4.9.
Рис. 4.9. Шаблон оператора цикла for
В поле ввода после слова for следует указать имя переменной-счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения.
В поле ввода после знака € следует указать диапазон значений, которые будет принимать переменная-счетчик. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В таком случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Количество повторов цикла будет равно количеству элементов массива.
В поле ввода под словом for следует ввести тело цикла
Обозначим имя переменной-счетчика, которая используется в операторе for – буквой t. Для описания алгоритма воспользуемся тем, что в операторе цикла для переменной-счетчика можно указать в качестве диапазона имя массива. Как сказано выше, в таком случае переменная t будет последовательно принимать значения всех элементов указанного вfor массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 4.10.
Отметим, что в данном случае в качестве результата работы функции нужно вернуть два значения, а специфика функции в MathCAD такова, что она позволяет вернуть только одно значение, но при этом сказано, что функция в качестве результата может вернуть, в том числе, вектор и матрицу. Поэтому при формировании результата мы определим его как вектор из двух значений.
Справа от программы-функции, представленной на рис. 4.10, написаны операторы, предназначенные для создания вектора с именем U из шести элементов. Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений.
На рис. 4.11, a представлен второй вариант программы-функции, в котором в качестве диапазона значений для переменной-счетчика цикла for берется диапазон изменения индекса массива. Поэтому в список формальных параметров в заголовок функции вносится еще один параметр n, который указывает верхнюю границу изменения индекса.
Рис. 4.10. Описание и использование функции Fun(P)
а) |
b) |
Рис. 4.11. Описание и использование функции Fun(P)
Пример 5. Требуется определить функцию, предназначенную для вычисления приближенного значения квадратного корня из числа N по формуле Ньютона:
,
где — заданное начальное приближение корня.
Решение.
Спецификацию для этой функции можно записать следующим образом:
Функция Fun(N,,x0) возвращает значение квадратного корня из числа N с заданной точностью вычислением – и заданным начальным приближением корня – x0.
Анализ блок-схемы показывает, что в представленном циклическом процессе количество повторений цикла заранее неизвестно и напрямую зависит от точности вычислений. Поэтому пользоваться оператором for не является целесообразным. Для таких циклических процессов предусмотрен оператор цикла while.
После вставки этого оператора в строку программы его сопровождают два поля ввода, как это показано на рис. 4.12.
Рис. 4.12. Шаблон оператора цикла while
В поле ввода ниже слова while следует ввести тело цикла – одна или несколько строк программы, выполнение которых нужно повторить несколько раз.
В поле ввода справа от слова while следует ввести условие. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится.
Из описания оператора цикла следует, что условие повторения цикла записывается cправа от слова while, а повторяемая часть цикла должна располагаться ниже конструкции while, а в описанной блок-схеме один из повторяемых операторов, а именно оператор, в котором вычисляется значение х, располагается до блока с условием повторения. Чтобы согласовать действия в блок-схеме с действиями оператора, сделаем перестановку — поставим определение переменной х после блока-условия. А для проверки условия введем вспомогательную переменную R, и для того, чтобы на начальном этапе пройти внутрь цикла для вычислений, определим начальное значение этой переменной значением, большим, чем указанная точность, например, значением, равным 1. И тогда функция может быть представлена в виде, как это показано на рис. 8.13.
Рис. 4.13. Описание и использование функции, предназначенной для извлечения квадратного корня
Пример 6. Требуется определить функцию, которая будет изменять значения элементов матрицы, имеющейnстрок и m столбцов следующим образом: заменить все неотрицательные элементы нулем, а отрицательные – единицей.
Решение. Алгоритм решения задача подробно рассмотрен в главе 1, блок-схема алгоритма представлена на рис. 1.11. Поэтому остановимся только на спецификации программы-функции, и ее описании. Спецификацию для этой функцииможно записать следующим образом:
Функция Fun(а,n,m) возвращает преобразованную матрицу а(nxm) по правилу: все неотрицательные элементы заменяются нулем, а отрицательные – единицей.
Анализ алгоритма показывает, что в данном случае мы имеем дело с двумя вложенными циклами, в которых переменныеi и j могут играть роль переменных-счетчиков операторов цикла типа for. Очевидно, что в качестве диапазона значений для этих переменных берется диапазон изменения индекса массива. На рис. 4.14 приведено определение функции. Описанная функция вызывается для изменения матрицы D, причем, измененная матрица заносится в матрицу T.
Рис. 4.14. Описание и использование функции, предназначенной для преобразования матрицы
Подготовить спецификацию функции.
Разработать алгоритм решения.
Установить, какие переменные помимо формальных параметров (локальные, глобальные переменные) понадобятся для реализации алгоритма.
Описать алгоритм словами или в виде блок-схемы.
Описать алгоритм в виде программы-функции на языке MathCAD.
Программирование в среде MathCAD — Docsity
ПРОГРАММИРОВАНИЕ В MATHCAD 4-курс ФМО-И-15-16 Узакбаева Үмүт В пакете MathCad могут быть реализованы два способа программирования: • безмодульное программирование – программирование без использования программных модулей; • модульное программирование – программирование с использованием программных модулей. Безмодульное программирование реализуется записью соответствующих конструкций непосредственно в математических областях документа MathCAD, и он приемлем для сравнительно простых алгоритмов. Модульное программирование предполагает разработку отдельных независимых алгоритмов в виде программных модулей, которые реализуются в виде подпрограмм-функций (сокращенно П-Ф). Программирование в пакете MATHCAD Программирование разветвляющихся алгоритмов Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких ветвей вычислений. Выбор конкретной ветви зависит от выполнения заданного условия. Условие реализуется с помощью логического выражения. Логическое выражение может включать в себя отношения, логические константы и переменные, логические функции, логические операции и круглые скобки. Для ввода знаков операций отношений и логических операций используется Панель логики. Результатом вычисления логического выражения является либо 1 (ИСТИНА), либо 0 (ЛОЖЬ). Отношения Отношение – это простейшее логическое выражение. Операции отношений: > | | < | | = | Необходимо помнить! Операции отношений имеют самый низкий приоритет, поэтому в сложных логических выражениях отношение всегда заключается в круглые скобки. Замечание. Знак сравнения (=) нельзя путать со знаком численного вывода (=). Знак сравнения имеет более жирное начертание и вводится с логической панели инструментов. Примеры вычисления отношений x 3 y 2 z 6 x y 1 x 3 z 1 0 x 5 1 x 2 y 3 z 0 Сложные логические выражения Логические операции : (NOT )| (AND ) | (OR )| (XOR ) Примеры логических выражений Пример 1. Указать порядок действий при вычислении логического выражения: (i 1) a (b (j > k)) Пример 2. Записать логическое выражение, принимающее значение 1 для точек, принадлежащих заштрихованной области. 12 3456 1 –1 0.5 x –0.5 1 y (–0.5 x 0.5) (– 1 y 1) Примеры программирования разветвляющихся алгоритмов Пример 2. Вычислить значение z по одной из трех ветвей. Решение При решении используется вложенная конструкция. x 3 z if x 1 30 if x 1 x x2 30 z 30 x 0.5 z if x 1 30 if x 1 x x2 30 z 0.5 x 3 z if x 1 30 if x 1 x x2 30 z 21 Примеры программирования разветвляющихся алгоритмов Пример 3. Вычислить значение y = max(a, b, c). Решение Рассмотрим использование условной функции для реализации структуры «ЕСЛИ-ТО». a 2 b 34 c 7 y a y if b y b y( ) y if c y c y( ) y 34 Использование функций Встроенные функции В Mathcad имеется большой набор встроенных функций, которые можно использовать при программировании, например: trunc(x) – выделение целой части числа; round(x) – округление вещественного числа х с точностью до n знаков после запятой; Ф(х) – функция Хэвисайда, значение которой равно 1 при x<0 и 0 в противном случае. Функция пользователя Функция пользователя имеет следующее описание : <Имя_функции> (<Список_формальных_аргументов>) := <Выражение> Обращение к функции имеет следующий вид: <Имя_функции> (<Список_фактических_аргументов>) Примеры программирования циклических алгоритмов Пример 1. Сформировать вектор z из n элементов, определяемых по правилу: Решение ORIGIN 1 n 5 i 1 n zi 1 i 4 z T 0.2 0.167 0.143 0.125 0.111( ) Примеры программирования циклических алгоритмов Пример 2. Вычислить значение функции: для всех значений x, изменяющихся от 0.5 до 2.5 с шагом 0.2; переменные a, b – заданные вещественные числа. Решение a 2.1 b 4.56 x 0.5 0.7 2.5 y x( ) ln x a 2 b 2 y x( ) -0.028 -0.014 -3-4.18·10 -33.782·10 0.01 0.016 0.021 0.025 0.029 0.033 0.036 Примеры программирования циклических алгоритмов Пример 3. Для переменной x, изменяющейся от 1 до 2 с шагом 0.2, сформировать вектор q, состоящий из соответствующих значений функции: Решение ORIGIN 1 n trunc 2 1 0.2 1 6 j 1 n xj 1 j 1( ) 0.2 qj xj 2 1 q T 2 2.44 2.96 3.56 4.24 5( ) Программирование итерационного цикла Решение a 9 x0 a 10 6 i 0 10 xi 1 until xi 2 a xi a xi 2 x T 9 5 3.4 3.024 3 3( ) Литература 1) http://www.mathcad.com 2) Ю.Е. Воскобойников, А.Ф. Задорожный, Л.А. Литвинов, Ю.Г. Черный «Основы вычислений и программирования в пакете MATHCAD», Новосибирск 2012», Новосибирск 2012
Программирование в MathCAD — Студопедия
В очень ранних версиях MathCAD встроенного языка программирования не было. Чтобы применять привычные операции проверки условий и организовывать циклы, приходилось изобретать причудливую смесь из встроенных функций if и until, а также комбинаций ранжированных переменных. Но надо отметить, что использование ранжированных переменных – мощный аппарат MathCAD, похожий на применение циклов в программировании. В подавляющем большинстве случаев намного удобнее организовать циклы с помощью ранжированных, чем заниматься для этого программированием.
И, тем не менее, встроенный язык программирования MathCADпозволяет решать самые различные, в том числе и довольно сложные, задачи и является серьезным подспорьем для расчетов. Поэтому последние версии MathCAD имеют не очень мощный, но весьма удобный собственный язык программирования.
Для вставки программного кода в документы MathCAD имеется специальная панель инструментов
Большинство кнопок этой панели выполнено в виде текстового представления операторов программирования, поэтому их смысл легко понятен. Операторы программирования могут быть введены только с этой панели, но никак не с клавиатуры (можно еще их вводить с помощью сочетаний клавиш, которые приведены в тексте всплывающей подсказки).
Создание программного блока начинается с команды . Нажатие этой клавиши приведет к тому, что в рабочей области документа появится вертикальная черта, а справа от нее – два пустые поля ввода.
Вертикальная черта означает, что строки, находящиеся справа от нее, образуют линейную программную последовательность операций. Эта черта является особенностью программ MathCAD. В полях ввода можно ввести две первые строки программы, а если требуется большее число строк, то необходимо нажимать клавишу столько раз, сколько необходимо строк. Не стоит забывать, что программа является полноценным выражением MathCAD. Это выражение может быть использовано для присвоения значения скалярной или векторной переменной или определения функции, или даже в составе другого выражения, в том числе и другой программы.
Внутри программы можно использовать глобальные переменные документа, но изменить их значение внутри программы никак нельзя. Можно создать в программе другие переменные, доступ к которым может осуществляться только из самой программы. Эти переменные называются локальными переменными. Локальные переменные «не видны» извне. Локальная переменная создается с помощью знака локального присвоения с панели Programming. Для оператора локального присваивания, так же как и для операторов обычного и глобального присваивания, можно изменить внешний вид так, чтобы он выглядел как обычный знак равенства. Для этого достаточно вызвать контекстное меню этого оператора и в нем выбрать команду ViewDefinitionAs/Equal.
Последняя строка любой программы не должна содержать никаких управляющих операторов. Эта строка задает значение, возвращаемое программой. В качестве этого значения может быть скаляр (число или переменная), вектор или матрица. Таким образом, последняя строка программы может содержать имя локальной переменной либо некоторое математическое выражение, куда входят как локальные, так и глобальные переменные, либо вектор или матрицу.
Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки AddLine. Для этого следует поместить на нужное место внутри программы линии ввода.
Если вертикальная линия ввода находится в начале текущей строки, то нажатие кнопки приведет к появлению новой строки перед текущей строкой, если вертикальная линия ввода находится в конце строки, то нажатие кнопки приведет к появлению новой строки после текущей. Можно выделить только часть текущей строки, что повлияет на положение новой строки в программе (например, если необходимо для некоторого условия выполнить не одно действие, а несколько). Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т.к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.
Проверка условий в программах.
Программы в MathCAD могут быть не только линейными, но и разветвленными. Одним из вариантов ветвления в программах является проверка условия. Условия могут проверять значения как локальных, так и глобальных переменных, а также выражений, содержащих эти переменные.
Для проверки условий в программах MathCAD служит оператор if . В поле ввода справа нужно ввести условие. Для ввода условий служит панель Boolean. На этой панели есть кнопки, предназначенные для проверки условий , а также кнопки, предназначенные для вставки логических операций (логическое отрицание, операция «и», операция «или», операция «исключающее или»). Вторые позволяют создавать сложные условия. В поле ввода слева нужно ввести строку программы, которая должна выполняться, если введенное условие истинно.
Если для условия «истинно» необходимо выполнение нескольких строк программы, надо воспользоваться кнопкой
.
Если невыполнение условия должно привести к выполнению какого-либо иного программного кода, можно в строке, следующей за оператором if, вставить оператор . В поле ввода слева от этого оператора необходимо ввести строку программы, которая будет выполняться только в том случае, если не выполнилось условие, заданное в операторе if.
Следует помнить, что если в программе введено подряд несколько строк с оператором if
, то выражение слева от оператора otherwise будет выполнено только в том случае, если не выполняются условия, заданные во всех операторах if.
Примеры:
Создание циклов.
Другим очень важным элементом при создании нелинейных программ являются циклы. Циклы позволяют повторять несколько раз выполнение одного и того же программного блока. Для создания циклов в MathCAD предусмотрено два оператора for и while.
Цикл for – цикл со счетчиком.
В таких циклах создается некоторая переменная-счетчик, значение которой изменяется после каждого выполнения тела цикла. Выход из цикла происходит при достижении этой переменной заданного значения. Этот оператор вводится с панели Programming клавишей for . В поле ввода после слова for следует указать имя переменной – счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения. В поле ввода после знака следует указать диапазон значений переменной-счетчика. Вводить диапазон в данном случае следует так же, как и при создании ранжированной переменной. Вместо диапазона в данном поле ввода можно указатьимя некоторого массива (вектора или матрицы). В этом случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Возможность перебора элементов массива не может быть реализована с помощью цикла while, поэтому именно в таких случаях цикл for и является незаменимым. В поле ввода под словом for следует ввести тело цикла.
Пример: Заполнить вектор числами от xнач до xкон с шагом h. Затем определить сумму элементов этого вектора и найти их среднее арифметическое значение.
Цикл while – цикл, который выполняется до тех пор, пока выполняется определенное условие.
В поле ввода справа от слова while следует ввести условие. Это условие строится по тем же правилам, что и в операторе if. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится. В поле ввода ниже слова while следует ввести тело цикла (для ввода нескольких строк в теле цикла надо воспользоваться кнопкой AddLine).
Пример1: Вычислить сумму с точностью е.
Пример2: Найти первый элемент, превышающий определенный порог.
Использование операторов break и continue.
Иногда возникает необходимость повлиять на выполнение цикла некоторым образом, например, прервать его выполнение по какому-либо условию или выполнять некоторые итерации не так, как другие. Для этого и служат операторы break и continue.
Оператор break, если он расположен внутри цикла, означает немедленное прекращение выполнения текущей итерации и выход из цикла. Если есть необходимость прекратить выполнение цикла по какому-либо условию, то следует использовать конструкцию следующего вида breakif (условие).
Пример: Выделить из массива все элементы от начала и до первого вхождения в него заданного числа.
Оператор continue используется для того, чтобы немедленно перейти в начало цикла и начать следующую итерацию. Этот оператор также обычно используется в составе конструкции вида continueif (условие). Оператор continue используется в случаях, когда необходимо чтобы некоторые вычисления производились для одних итераций и не производились для других.
Пример: Требуется заполнить элементы квадратной матрицы в шахматном порядке.
Оператор return (возврат значения).
Как было сказано ранее, результат выполнения программного модуля помещается, как правило, в последней его строке. Но можно прервать выполнение программы в любой ее точке (например, с помощью условного оператора) и выдать некоторое значение, применив оператор return. В этом случае при выполнении указанного условия значение, введенное в поле ввода после return, возвращается в качестве результата, и никакой другой код больше не выполняется. Вставляется в программу оператор return с помощью одноименной кнопки панели Programming . Пример:
Обработка ошибок.
Система MathCAD предоставляет пользователю некоторый контроль над ошибками, которые могут возникнуть при вычислении выражений или при выполнении программ. Для этой цели служит оператор onerror, который можно вставить с помощью одноименной кнопки панели Programming . В поле ввода справа следует ввести выражение или программу, которые необходимо вычислить (известно, что это выражение может содержать ошибку при определенных значениях входных параметров). В поле ввода слева следует ввести выражение, которое будет выполнено вместо правого выражения, если при выполнении последнего возникнет ошибка. Пример: Если аргументу функции присвоено нулевое значение, то в программе возникает ошибка – деление на нуль. Но за счет оператора onerror сообщение не выводится, а функции в этой точке присваивается значение, указанное слева от оператора onerror – значение машинной бесконечности.
В поле ввода слева может быть введено текстовое выражение, сообщающее об ошибке
Конечно, если программа содержит только простейшие математические операции, то никаких ошибок, кроме деления на нуль или превышения наибольшего допустимого числа в ней возникнуть не может. В таких программах оператор onerror используется редко. Но для более сложных программ, которые содержат функции решения дифференциальных уравнений, аппроксимации или другие сложные функции MathCAD, использование onerror может избавить от многих трудностей.
Иногда может возникнуть ситуация обратная той, которая была описана выше, т.е. необходимо, чтобы при определенных условиях результатом выражения было сообщение об ошибке, хотя в действительности при этом не возникает ни одной стандартной ошибки MathCAD. Для таких случаев в MathCAD предусмотрена встроенная функция error. В качестве аргумента этой функции нужно в кавычках указать текст сообщения об ошибке, который должен быть выведен. Таким образом, если необходимо, чтобы программа возвращала ошибку при определенном условии, то следует использовать конструкцию вида: error («текст ошибки») if (условие).
Пример:
Для того, чтобы иметь возможность нормально вводить текст на русском языке в аргумент функции error (а также во все другие функции со строками), следует изменить шрифт, который используется во встроенном стиле Constant. Для того чтобы этот стиль правильно отображал русские буквы, установите курсор на любом числе или строковом выражении в формульном блоке. При этом в поле на панели инструментов Formatting, отображающем текущий стиль, должно быть написано – Constant. Теперь выберите из раскрывающегося списка шрифтов шрифт, поддерживающий кириллицу.
Примеры программирования.
1. Вычислить функцию sin(x) с точностью е.
2. Даны массивы А(5) и В(5). Получить массив С, в который записаны сначала элементы массива А в порядке возрастания, а затем элементы массива В порядке убывания.
4. Дан массив натуральных чисел В(10). Определить, есть ли в нем 4 последовательных числа (например, 1, 2, 3, 4, и т.п.). Напечатать такие группы чисел.
Вопросы
1. Какая панель служит для вставки программного кода в документ MathCAD? Можно ли операторы программирования набрать с клавиатуры?
2. С какой команды начинается создание программного блока? Как с ее помощью можно создавать разветвленный программный блок?
3. Что такое определение программного блока? Обращение к программному блоку?
4. Что такое глобальные и локальные переменные для программного блока? Что может содержать последняя строка программного блока?
5. Как работает оператор if в программном блоке? Приведите пример.
6. Создание цикла с параметром в программном блоке. Приведите пример.
7. Создание цикла while в программном блоке. Приведите пример.
8. Для чего служат операторы break, continue в программном блоке? Приведите примеры.
9. Как работает оператор return в программном блоке? Приведите пример.
10. Как осуществляется обработка ошибок в программном блоке? Приведите пример.
Лекция №3
Численные методы решения задач.
Обработка экспериментальных данных средствами MathCAD
Развитие электронной вычислительной техники, создание алгоритмических языков программирования и обширного математического обеспечения ЭВМ позволяет широко использовать численные методы вычислительной математики при решении различного рода прикладных задач в науке, технике, производстве.
Численные методы – это методы решения задач через последовательность элементарных операций, которые многократно повторяются до тех пор, пока не будет получен конечный результат с наперед заданной точностью.
Численными методами часто приходится решать следующие математические задачи:
1. решение нелинейных (алгебраических и трансцендентных) уравнений;
2. вычисление определенных интегралов;
3. решение обыкновенных дифференциальных уравнений;
4. решение дифференциальных уравнений в частных производных;
5. решение задач оптимизации;
6. обработка массивов числовых данных.
Каждая из этих задач может представлять собой самостоятельную прикладную задачу или являться составной частью более сложных прикладных задач.
Решение нелинейных уравнений
Обычно нелинейные уравнения делят на трансцендентные и алгебраические. Нелинейные уравнения, содержащие тригонометрические функции или другие специальные функции, например, lg(x) или ex, называются трансцендентными. Методы решения нелинейных уравнений такого типа делятся на аналитические и численные.
Первые позволяют найти решение непосредственно с помощью формул и всегда обеспечивают получение точного решения. Известным примером такого рода является формула корней квадратного уравнения. В численных методах задается процедура решения в виде многократного применения некоторого алгоритма. Задача отыскания корней нелинейного уравнения f(x) = 0 считается решенной, если мы сумеем определить корни с нужной степенью точности.
Для решения нелинейных уравнений известны следующие численные методы: метод половинного деления (метод дихотомии), метод хорд, метод касательных (Ньютона), метод секущих, метод простой итерации. Рассмотрим метод половинного деления.
Графическая интерпретация метода показана на рис.1.
Рис.1 Графическая интерпретация метода половинного деления
В этом методе отыскание корня уравнения f(x) = 0 проходит в два этапа. На первом этапе необходимо отделить корень, т.е.выделить интервал на оси абсцисс, на котором функция f(x) меняет свой знак. Для отделения корня следует провести вычисление функции f(x) в точках, расположенных через равные интервалы по оси x, до тех пор, пока не будут найдены два последовательных значения функции f(xn) и f(xn+1), имеющие противоположные знаки.
На втором этапе производится уточнение корня. Найденный интервал [xn, xn+1], содержащий корень, делится пополам
Затем по разности знаков функции на концах интервала определяем, на каком из полученных двух интервалов находится корень уравнения. Найденный интервал снова делится пополам и т.д. В результате, интервал, на котором находится корень, сужается. Процесс повторяется до тех пор, пока f(xср) не станет достаточно близким к нулю. Блок-схема алгоритма метода показана на рис.2.
Рис.2 Блок-схема алгоритма метода половинного деления
Численное интегрирование
К численному интегрированию обращаются, когда нельзя через элементарные функции аналитически записать первообразную интеграла
или когда подобная запись имеет сложный вид.
Сущность большинства численных методов вычисления определенных интегралов состоит в замене подынтегральной функции f(x) аппроксимирующей функцией j(x), для которой можно легко записать первообразную в элементарных функциях, т.е.
Используемые на практике методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции. Дадим краткую характеристику групп наиболее распространенных методов
1. Методы Ньютона — Котеса. Эти методы требуют, чтобы значения x были заданы с постоянным шагом. Они основаны на полиномиальной аппроксимации подынтегральной функции. Алгоритмы методов просты и легко поддаются программной реализации.
2. Методы Гаусса – Кристоффеля – методы наивысшей алгебраической точности. Эти методы используют неравно отстоящие узлы, расположенные по алгоритму, обеспечивающему минимальную погрешность интегрирования. Требуют большего объема памяти, чем методы первой группы.
3. Методы Монте-Карло. В этих методах узлы выбираются с помощью датчика случайных чисел. Ответ носит вероятностный характер. Методы эффективны при вычислении большой кратности.
Рассмотрим методы первой группы. По этому методу интервал разбивается на n равных отрезков, длина каждого из которых . Для вычисления каждой элементарной площади подынтегральную функцию на данном отрезке заменяют с некоторой степенью точности более простой функцией, интеграл от которой можно вычислить, используя только ординаты на концах отрезка. Метод Ньютона -Котеса дает три формулы для приближенного вычисления определенного интеграла1. При замене f(x) на каждом отрезке прямой, параллельной оси x (рис.3,а), получим формулу прямоугольников
2. При замене f(x) на каждом отрезке прямой, соединяющей ординаты концов отрезка (рис.3,б), получим формулу трапеций
3. При замене f(x) дугой параболы, проведенной через концы трех ординат (рис.3,в), получим формулу Симпсона. При этом число отрезков должно быть четным
Точность вычисления интеграла тем выше, чем больше n и меньше h, и в пределе при n ®¥ h ® 0 указанные формулы дадут точную величину определенного интеграла.
Рис.3 Численное определение интеграла
Блок схема алгоритма численного определения интеграла с заданной степенью точности представлена на рис. 4. На блок-схеме a,b,e,n – исходные данные, е – заданная точность, n – число разбиений, i1 – начальное значение интеграла, его можно задать равным нулю, i- вычисленное значение интеграла.
Для достижения заданной точности число разбиений удваивают до тех пор, пока будет удовлетворено условие |i – i1|<e.< p=»»></e.<>
Рис.4 Блок схема алгоритма численного определения интеграла с заданной степенью точности по формуле прямоугольников
Обработка экспериментальных данных средствами MathCAD.
Инженеру на практике часто приходится сталкиваться с необходимостью определения функции, которая задана таблично. Т.е. известны экспериментально снятые аргумент и функция в узловых точках, а в промежутках эта функция неизвестна и ее надо найти.
Для анализа экспериментальных зависимостей и приведения их к наглядному виду часто используются такие средства, как интерполяция, сглаживание и аппроксимация. В некоторых задачах для анализа зависимости бывает необходимо найти ее Фурье-компоненту. Все перечисленные средства анализа можно реализовать средствами MathCad.
Интерполяция.
Интерполяцией называют заполнение отрезками кривых промежутков между заданными точками по тому или иному закону. Для проведения интерполяции в первую очередь должна быть задана экспериментальная зависимость в виде набора точек на плоскости. Для этого должны быть заданы два одномерных массива (вектора) – vx и vy, содержащие соответственно значения координат x и y каждой точки. При этом важно, чтобы значения в векторе vx были заданы в порядке возрастания.
Система MathCad позволяет проводить линейную интерполяцию и сплайн-интерполяцию наборов экспериментальных точек.
Простейшим вариантом интерполяции является линейная интерполяция. Она заключается в простом соединении точек между собой отрезками прямых. Для реализации такой интерполяции в MathCad существует встроенная функция linterp(vx,vy,x) , где vxvy – уже известные векторы, содержащие координаты последовательности точек, x – координата точки, в которой нужно вычислить значение интерполирующей функции. Пример построения линейной интерполяции приведен на рис.5
Рис.5 Линейная интерполяция
На практике линейная интерполяция применяется редко.
Из всех видов интерполяции наиболее часто используется интерполяция, где экспериментальные точки попарно соединяются отрезками полиномов. Чаще всего для этого выбирают полиномы третьей степени(поэтому такая кривая и называется кубическим сплайном). Для того чтобы найти коэффициенты этих полиномов, очевидно, недостаточно того условия, что кривая должна проходить через экспериментальные точки. Поэтому на сплайн накладываются дополнительные условия сшивки – первая и вторая производные слева и справа от каждой экспериментальной точки должны быть равны между собой. Но и после этого количество условий остается на два меньше, чем количество неизвестных коэффициентов. Дополнительные два условия должны быть наложены в начальной и конечной экспериментальных точках, поскольку в них нет условий сшивки. Эти условия можно выбрать по-разному. В MaqthCad существуют три различных функции для построения кубических сплайнов с различными дополнительными условиями.
· lspline(vx,vy) – в начальной и конечной точках накладывается условие линейности, т.е. вторая производная от функции равна нулю. Первая буква в названии функции – l , означает linear (линейный).
· pspline(vx,vy) – на первом и последнем интервале кривая является параболой, т.е. полиномиальный коэффициент при x3 равен нулю. Буква p означает parabolic (параболический).
· cspline(vx,vy) – полиномиальные коэффициенты при x3 на первых двух интервалах равны между собой точно так же, как на последних двух интервалах. Буква c означает cubic (кубический).
Результатом каждой из перечисленных функций является вектор, содержащий значения вторых производных от интерполяционной кривой во всех точках, заданных в массиве vx. Для того чтобы исходя из этого вектора построить кривую, нужно воспользоваться встроенной функцией interp(v,vx,vy,x), где vx и vy – массивы экспериментальных точек, v – массив, полученный как результат одной из трех функций, перечисленных выше, x- координата, в которой нужно вычислить значение интерполяционной кривой. Пример интерполяции кубическим сплайном приведен на рис.6.
Рис.6 Интерполяция кубическим сплайном
В приведенном примере использована функция pspline. В большинстве случаев от того, какую функцию вы используете, слабо зависит поведение кривой внутри интервала экспериментальных значений. Заметное отличие появляется лишь за границами этого интервала.
Кубический сплайн является эффективным средством построения интерполяционной кривой в подавляющем большинстве случаев. Но иногда использование кубического сплайна может привести к нежелательным результатам. Чаще всего это происходит в тех случаях, когда данные очень неравномерно распределены вдоль оси x. В таких случаях на кривой кубического сплайна могут появляться острые экстремумы в промежутках между экспериментальными точками. В некоторых подобных случаях получить лучщую интерполяционную кривую помогает использование другого вида интерполяции – В-сплайна. Основное отличие В-сплайна от всех описанных выше методов – сшивка отрезков кривых происходит не в экспериментальных точках, а между ними, в специально заданных точках. В MathCad для реализации интерполяции В-сплайном служит функция bspline(vx.vy,u,n), где vx,vy – векторы, содержащие координаты экспериментальных точек, u – вектор, содержащий координаты точек сшивки, n – порядок полинома. Результатом функции bspline является вектор, который далее следует использовать как аргумент функции interp. В-сплайн в MathCad можно построить из отрезков прямых, парабол или кубических парабол, т.е. допустимые значения параметра n – 1,2 или 3. Количество точек сшивки не является произвольной величиной и должно быть всегда на n-1 меньше, чем количество экспериментальных точек. Также на координаты точек сшивки накладываются следующее условие: первая точка сшивки должна быть не правее первой экспериментальной точки, а последняя не левее последней экспериментальной точки. Остальные точки сшивки могут произвольным образом располагаться внутри отрезка. Пример использования В-сплайна приведен на рис.7.
Экстраполяция.
Интерполяция дает возможность вычислять значения неизвестной функции в промежутках между экспериментальными точками, но иногда возникает необходимость вычислять значения функции вне области, ограниченной этими точками. Для этого используют так называемые методы экстраполяции.
При построении кубического сплайна, значение интерполяционной кривой может быть вычислено также и в любой точке за пределами «пограничной» области. Конечно, данный способ экстраполяции можно использовать только на очень небольшом расстоянии от «пограничных» точек, поскольку кривая является кубической параболой и быстро уходит в область очень больших значений, не имеющих ничего общего с реальной зависимостью.
Рис.7 Сравнение эффективности кубического сплайна и В-сплайна
Также в MathCad есть одна встроенная функция для проведения экстраполяции – predict(v,m,n), где v – вектор значений функции на том отрезке, где она известна (значения аргумента в данной функции не задаются, и считается, что точки распределены равномерно), m – количество элементов вектора v, на основании которых проводится экстраполяция ( естественно, выбираются точки, ближайшие к правой границе), n – количество точек в рассчитываемом векторе. Пример экстраполяции от осциллирующей функции приведен на рис.8
k,101+i
Рис.8 Экстраполяция с помощью функции predict
Результатом функции predict является вектор, состоящий из n элементов и задающий значения функции справа от границы выборки, т.е. в области, где она была не известна. Алгоритм, используемый в функции predict, наилучшим образом подходит для экстраполяции различного рода осциллирующих зависимостей. В некоторых случаях можно получить удовлетворительный результат экстраполяции даже для негладких зависимостей, таких как пилообразный или прямоугольный сигнал. Зато для непериодических зависимостей приемлемый результат можно получить очень редко и только на очень небольшом расстоянии.
Регрессия
Результаты экспериментов всегда содержат некоторую случайную погрешность. Причем часто погрешность оказывается величиной одного порядка с измеряемой величиной. В таких случаях интерполяционная кривая будет весьма далека от истинной зависимости. Поскольку подобные ситуации возникают довольно часто, то интерполяция редко используется при анализе результатов экспериментов. Гораздо шире здесь применяется регрессионный анализ. Регрессией называется подгон параметров той или иной простой функции для наилучшей аппроксимации экспериментальных данных (от латинскогоapproximo – приближаюсь). Если аппроксимирующая функция выбрана удачно, то значения ее параметров могут быть источником разнообразной информации об измеряемой величине.
Система MathCad содержит большое количество встроенных функций для проведения регрессионного анализа с использованием любых аппроксимирующих функций и их комбинаций. Все функции MathCad для поиска оптимальных значений параметров функций используют метод наименьших квадратов, можно еще применить метод медиан.
Линейная регрессия
Линейная регрессия является наиболее простой, но, тем не менее, используется чаще любого другого вида регрессии. Она заключается в нахождении таких значений параметров a и b, чтобы прямая y = a+bx наилучшим образом аппроксимировала заданной набор точек. Для проведения линейной регрессии по методу наименьших квадратов в MathCad существует функция line(vx,vy). Результатом функции line будет вектор, содержащий значения параметров a и b для построения регрессионной прямой. Пример линейной регрессии представлен на рис.9
Рис.9 Линейная регрессия с помощью функции line
На рис.9 для анализа эффективности линейной регрессии построена псевдоэкспериментальная последовательность точек. Для этого к точным значениям линейной функции прибавлены случайные числа, сгенерированные с помощью функции rnorm.Затем проведена линейная регрессия полученного набора точек. Ее результат можно сравнить с исходной прямой. Как видно из рис., параметры регрессионной прямой заметно отличаются от исходных, но на графике обе прямые проходят достаточно близко.
Для линейной регрессии в MathCad реализован также метод медиан с помощью функции medfit(vx,vy). Результатом этой функции является вектор, аналогичный результату line. Нельзя утверждать, что один из двух методов регрессии более точен. Метод наименьших квадратов является наиболее универсальным, поэтому функция line считается в MathCad основной функцией для проведения линейной регрессии.
Полиномиальная регрессия.
Кроме аппроксимации неизвестной функции с помощью прямой, широкое применение находит и аппроксимация с помощью полиномов различной степени. Для этой цели в MathCad существует функция regress(vx,vy,n). Последний аргумент данной функции задает степень полинома. Можно использовать полином любой степени, но не большей, чем число точек в выборке минус один. При n = 1 получится линейная регрессия. На практике наибольшее применение находит полиномиальная регрессия от второй до пятой степени.
Результатом функции regress является вектор, содержащий коэффициенты аппроксимирующего полинома. Эти коэффициенты располагаются в векторе, начиная с четвертого элемента в порядке возрастания степеней. Первые три элемента данного вектора являются служебными и используются для того, чтобы результат функции regress можно было использовать как первый аргумент функции interp по аналогии со сплайн-интерполяцией. Пример полиномиальной регрессии представлен на рис.10.
Рис.10 Полиномиальная регрессия
На рис.10 для иллюстрации полиномиальной регрессии построена псевдоэкспериментальная последовательность точек. В качестве теоретической функции был использован полином третьей степени с коэффициентами 0,1,-2,1. Как видно из примера, коэффициенты, рассчитанные функцией regress, значительно отличаются от коэффициентов исходного полинома. Тем не менее в области экспериментальных точек обе кривые достаточно близки, но за пределами этой области резко расходятся.
Аппроксимация набора точек различными элементарными функциями
Физические величины зачастую подчиняются зависимостям отличным от линейных или полиномиальных. Поэтому в MathCad существует несколько функций, позволяющих выполнить регрессию с использованием зависимостей, наиболее часто встречающихся на практике. Таких функций в MathCad всего шесть. Вот некоторые из них:
· expfit(vx,vy,vg) – регрессия экспоненциальной функцией y = a*eb*x+c.
· sinfit(vx,vy,vg) – регрессия синусоидальной функцией y = a*sin(x+b)+c.
· pwrfit(vx,vy,vg) — регрессия степенной функцией e = a*xb +c.
Перечисленные функции используют трехпараметрическую аппроксимирующую функцию, нелинейную по параметрам. При вычислении оптимальных значений трех параметров регрессионной функции по методу наименьших квадратов возникает необходимость в решении сложной системы из трех нелинейных уравнений. Такая система часто может иметь несколько решений. Поэтому в функциях MathCad, которые проводят регрессию трехпараметрическими зависимостями, введен дополнительный аргумент vg. Данный аргумент – это трехкомпонентный вектор, содержащий приблизительные значения параметров a,b и c, входящих в аппроксимирующую функцию. Неправильный выбор элементов вектора vg может привести к неудовлетворительному результату регрессии. На рис.11 приведен пример проведения экспоненциальной регрессии с помощью функции expfit, регрессия проведена для двух различных значений вектора vg.
Рис.11 Экспоненциальная регрессия
Аппроксимация набора точек функциями, заданными пользователем.
В MathCad существуют средства для проведения регрессии самого общего вида. Это означает, что можно использовать любые функции в качестве аппроксимирующих и находить оптимальные значения любых их параметров, как линейных, так и нелинейных. В том случае, если регрессионная функция является линейной по всем параметрам, т.е. представляет линейную комбинацию жестко заданных функций, провести регрессию можно с помощью встроенной функции linfit(vx,vy,F). Аргумент F – это векторная функция, из элементов которой должна быть построена линейная комбинация, наилучшим образом аппроксимирующая заданную последовательность точек. Результатом работы функции linfit является вектор линейных коэффициентов. Каждый элемент этого вектора – коэффициент при функции, стоящей на соответствующем месте в векторе F. Таким образом, для того чтобы получить регрессионную функцию, достаточно скалярно перемножить эти два вектора. Пример такой аппроксимации представлен на рис.12.
Рис.12 Использование функции linfit
Сглаживание
Система MathCad применяется для обработки различного рода сигналов. При этом очень важной процедурой является очистка сигнала от шумов. Один из вариантов решения данной задачи – это использование алгоритмов сглаживания (smoothig). Существует множество алгоритмов сглаживания данных, причем не всегда можно заранее сказать, какой из них будет наиболее эффективен для той или иной задачи. В MathCad реализовано три алгоритма сглаживания и соответственно существует три функции для их выполнения.
· medsmooth(vy,n) – реализует алгоритм «бегущих» медиан. Параметр n определяет ширину «окна» сглаживания, т.е. количество точек, которые используются при вычислении сглаженного значения в каждой точке. Параметр n должен быть целым нечетным числом. Данный алгоритм лучше всего подходит для сглаживания наборов точек, в которых лишь некоторые точки резко выбиваются из общей гладкой последовательности (см.рис.13).
· ksmooth(vx,vy,b) – алгоритм Гауссового ядра. В данном алгоритме сглаженное значение в каждой точке вычисляется как весовое среднее от всего набора данных с ядром в виде функции Гаусса. Параметр b — это параметр ширины функции ядра. Данный метод наилучшим образом подходит для фильтрации зашумленного сигнала (см.рис.14).
· supsmooth(vx,vy) – в данном алгоритме значение в каждой точке заменятся на значение регрессионной прямой, построенной с использованием некоторого количества близлежащих точек, причем данное количество выбирается по-разному для каждой точки с помощью адаптивного алгоритма.
Рис.13 Сглаживание сигнала с узкими нерегулярностями
Рис.14 Сглаживание зашумленного сигнала
Дискретное преобразование Фурье
Еще одна операция, широко применяемая при обработке сигналов , — вычисление Фурье-спектра. Для проведения данной операции с сигналами, заданными в виде массивов данных, система MathCad содержит численный алгоритм, называемый быстрым преобразованием Фурье (FastFourierTransform FFT). Для реализации данного алгоритма в MathCad существует несколько различных функций.
· В том случае, если набор данных v состоит из 2m элементов, а также все числа в наборе данных действительны, то для проведения Фурье-преобразования следует пользоваться функциями fft(v) или FFT(v). Обе эти функции выполняют Фурье-преобразование, а различие между ними заключается лишь в нормировке результата. Результатом функций fft и FFT будет массив из 2m -1+1 комплексных чисел.
· Если какое-либо из условий, перечисленных выше, не выполняется, т.е. массив содержит комплексные числа или не может быть расширен до размерности 2m, то следует пользоваться функциями cfft(v) и CFFT(v). Результатом функций cfft и CFFT будет массив комплексных чисел той же размерности, что и исходный.
Результатом каждой из перечисленных функций будет массив комплексных чисел. Исходя из этого массива, можно построить амплитудно-частотную (АЧХ) или фазово-частотную (ФЧХ) характеристику сигнала. Для построения АЧХ следует вычислить абсолютное значение каждого элемента в массиве. Пример такого построения приведен на рис.15.
Рис.15 Использование функции fft для построения АЧХ — сигнала
На рис 16 проведена фильтрация сигнала, построенного на рис.15. Конечно, такой метод фильтрации можно использовать, только если уровень шума ощутимо ниже уровня сигнала.
Рис.16 Амплитудная фильтрация сигнала
Поздравление ректора Ю.Л. Сколубовича с Днем России Уважаемые преподаватели, сотрудники, студенты, выпускники! Примите самые искренние поздравления с государственным праздником – Днем России! 12 июня 1990 года была принята «Декларация о государственном суверенитете России». Это знаменательный день для всех, кто является настоящим гражданином и патриотом Российской Федерации – великой страны с богатейшей историей и традициями, славными ратными и трудовыми подвигами. Сегодня наше государство решает сложные, стратегически важные задачи, которые определены Президентом В.В. Путиным в национальных проектах. И от поддержки, инициативы и результатов труда каждого из нас зависит, как будет развиваться Россия, и какое будущее ждет наших потомков. |
Творческие коллективы и студенческие объединения поздравляют с Днем России! Творческие коллективы и студенческие объединения Центра по внеучебной и воспитательной работе НГАСУ (Сибстрин) поздравляют сотрудников и студентов университета с Днем России! Сегодня праздник всей страны – День нашей Родины – России! Желаем в мире жить, не знать войны, чтобы всегда в любви, в достатке жили! Гордимся мы большой страной своей, Она для нас огромным домом стала, И в этот праздник мы желаем ей, Чтоб развивалась, крепла, процветала! |
Студенты института строительства приглашены на работу в известные компании «Хуавей» и «Эннова» 4 июня 2021 года состоялась встреча студентов и магистрантов института строительства НГАСУ (Сибстрин) с представителями ООО «Техкомпания Хуавэй», которая является российским подразделением компании «Huawei» – мирового лидера в области информационно-коммуникационных технологий. На встрече присутствовали операционный менеджер Андрей Александров, руководитель отдела по проектированию Рано Мирзакулова и куратор по трудоустройству выпускников Евгения Золотухина. В своем выступлении сотрудники российского подразделения «Huawei» представили основные направления деятельности компании, поделились планами на будущее и информацией о текущей потребности в кадрах. Было отмечено, что одной из задач компании является привлечение молодых специалистов для развития … |
IF (функция IF) — служба поддержки Office
Функция ЕСЛИ — одна из самых популярных функций в Excel, она позволяет проводить логические сравнения между значением и ожидаемым значением.
Таким образом, оператор IF может иметь два результата. Первый результат — если ваше сравнение — Истина, второй — если ваше сравнение — Ложь.
Например, = ЕСЛИ (C2 = «Да», 1,2) говорит ЕСЛИ (C2 = Да, тогда вернуть 1, иначе вернуть 2).
Используйте функцию ЕСЛИ, одну из логических функций, чтобы вернуть одно значение, если условие истинно, и другое значение, если оно ложно.
IF (логический_тест, значение_если_ истинно, [значение_если_ ложь])
Например:
Имя аргумента | Описание |
|---|---|
логический_тест (обязательный) | Состояние, которое вы хотите проверить. |
value_if_true (обязательно) | Значение, которое вы хотите вернуть, если результатом logic_test является ИСТИНА. |
value_if_false (необязательно) | Значение, которое вы хотите вернуть, если результатом logic_test является ЛОЖЬ. |
Простые примеры IF
В приведенном выше примере в ячейке D2 написано: IF (C2 = Да, затем вернуть 1, в противном случае вернуть 2)
В этом примере формула в ячейке D2 говорит: ЕСЛИ (C2 = 1, затем вернуть Да, в противном случае вернуть Нет) Как видите, функцию ЕСЛИ можно использовать для оценки как текста, так и значений. Его также можно использовать для оценки ошибок. Вы не ограничены только проверкой того, совпадает ли одно с другим и возвращением единственного результата, вы также можете использовать математические операторы и выполнять дополнительные вычисления в зависимости от ваших критериев.Вы также можете вложить несколько функций ЕСЛИ вместе, чтобы выполнить несколько сравнений.
В приведенном выше примере функция ЕСЛИ в D2 говорит ЕСЛИ (C2 больше B2, затем возвращается «Превышение бюджета», в противном случае возвращается «В пределах бюджета»)
На приведенной выше иллюстрации, вместо того, чтобы возвращать текстовый результат, мы собираемся вернуть математическое вычисление. Таким образом, формула в E2 говорит IF (Фактическое значение больше, чем заложенное в бюджете, затем вычтите запланированную сумму из фактической суммы, в противном случае ничего не верните).
В этом примере формула в F7 говорит IF (E7 = «Да», затем рассчитайте общую сумму в F5 * 8,25%, в противном случае налог с продаж не взимается, поэтому возвращайте 0)
Примечание: Если вы собираетесь использовать текст в формулах, вам необходимо заключить текст в кавычки (например, «Текст»). Единственное исключение из этого правила — ИСТИНА или ЛОЖЬ, которые Excel распознает автоматически.
Общие проблемы
Проблема | Что пошло не так |
|---|---|
0 (ноль) в ячейке | Не было аргументов ни для значение_если_ истинно , ни для аргументов значение_если_False .Чтобы увидеть верное возвращаемое значение, добавьте текст аргумента к двум аргументам или добавьте к аргументу ИСТИНА или ЛОЖЬ. |
# ИМЯ? в ячейке | Обычно это означает, что формула написана неправильно. |
Нужна дополнительная помощь?
Вы всегда можете спросить эксперта в техническом сообществе Excel, получить поддержку в сообществе Answers или предложить новую функцию или улучшение в Excel User Voice.
См. Также
Операторы вычисления и приоритет в Excel
Используйте вложенные функции в формуле
Использование IF, чтобы проверить, пуста ли ячейка
Видео: Расширенные функции ЕСЛИ
Функция IFS (Microsoft 365, Excel 2016 и более поздние версии)
Расширенные функции ЕСЛИ — работа с вложенными формулами и предотвращение ошибок
Обучающие видеоролики: Расширенные функции ЕСЛИ
Функция СЧЁТЕСЛИ будет подсчитывать значения на основе одного критерия.
Функция СЧЁТЕСЛИМН будет подсчитывать значения на основе нескольких критериев.
Функция СУММЕСЛИ суммирует значения на основе одного критерия.
Функция СУММЕСЛИМН суммирует значения на основе нескольких критериев.
И функция
Функция ИЛИ
Функция ВПР
Обзор формул в Excel
Как избежать неправильных формул
Обнаруживать ошибки в формулах
Логические функции
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Как использовать функцию ЕСЛИ в Excel
Функция ЕСЛИ используется для запуска логической проверки и по-разному реагирует в зависимости от того, является ли результат ИСТИНА или ЛОЖЬ.Первый аргумент, логический_тест , является выражением, которое возвращает ИСТИНА или ЛОЖЬ. И value_if_true , и value_if_false являются необязательными, но должен быть указан хотя бы один из них. Результатом IF может быть значение, ссылка на ячейку или даже другая формула.
В примере, показанном выше, мы хотим назначить либо «Пройдено», либо «Не сдано» в зависимости от результата теста. Проходной балл 70 или выше. Скопированная формула в D6:
.= ЕСЛИ (C6> = 70, «прошел», «не прошел»)
Перевод: Если значение в C6 больше или равно 70, вернуть «Пройдено».В противном случае верните «Fail».
Логическая последовательность этой формулы может быть обратной. Приведенная ниже формула возвращает тот же результат:
Перевод: Если значение в C6 меньше 70, вернуть «Fail». В противном случае верните «Пропуск».
Обе приведенные выше формулы при копировании вернут правильные результаты.
Примечание. Если вы плохо знакомы с идеей критериев формулы, в этой статье приводится множество примеров.
Другая формула
В результате функция ЕСЛИ может возвращать другую формулу.Например, приведенная ниже формула вернет A1 * 5%, если A1 меньше 100, и A1 * 7%, если A1 больше или равно 100:
Вложенные операторы IF
Функция ЕСЛИ может быть «вложенной». «Вложенный ЕСЛИ» относится к формуле, в которой по крайней мере одна функция ЕСЛИ вложена в другую, чтобы проверить наличие большего количества условий и вернуть больше возможных результатов. Каждый оператор IF должен быть тщательно «вложен» в другой, чтобы логика была правильной.
Например, следующая формула может использоваться для присвоения оценки, а не результата «прошел / не прошел»:
= ЕСЛИ (C6 <70, «F», ЕСЛИ (C6 <75, «D», ЕСЛИ (C6 <85, «C», ЕСЛИ (C6 <95, «B», «A»))))
Можно вложить до 64 функций IF.Однако в целом вам следует рассмотреть другие функции, такие как VLOOKUP или HLOOKUP, для более сложных сценариев, потому что они могут обрабатывать больше условий гораздо более оптимизированным образом.
Логические операторы
При построении теста с IF вы можете использовать любой из следующих логических операторов:
| Оператор сравнения | Значение | Пример |
| = | равно | A1 = D1 |
| > | больше | A1> D1 |
| > = | больше или равно | A1> = D1 |
| менее | A1 | |
| меньше или равно | A1 | |
| не равно | A1D1 |
Функция ЕСЛИ не поддерживает подстановочные знаки, но вы можете комбинировать ЕСЛИ с СЧЁТЕСЛИ, чтобы получить базовую функциональность подстановочных знаков.
ЕСЛИ с И, ИЛИ, НЕ
Функцию ЕСЛИ можно комбинировать с функцией И и функцией ИЛИ. Например, чтобы вернуть «ОК», когда A1 находится между 7 и 10, вы можете использовать следующую формулу:
= ЕСЛИ (И (A1> 7, A1 <10), «ОК», «»)
Перевод: если A1 больше 7 и меньше 10, вернуть «ОК». В противном случае ничего не вернуть ("").
Чтобы вернуть B1 + 10, когда A1 "красный" или "синий", вы можете использовать функцию ИЛИ следующим образом:
= ЕСЛИ (ИЛИ (A1 = «красный», A1 = «синий»), B1 + 10, B1)
Перевод: если A1 красный или синий, вернуть B1 + 10, иначе вернуть B1.
= ЕСЛИ (НЕ (A1 = "красный"), B1 + 10, B1)
Перевод: если A1 НЕ красный, вернуть B1 + 10, иначе вернуть B1.
Дополнительная информация
Дополнительные примеры функций IF см. Ниже.
Банкноты
- Для условного подсчета используйте функции СЧЁТЕСЛИ или СЧЁТЕСЛИ.
- Для условного суммирования используйте функции СУММЕСЛИ или СУММЕСЛИМН.
- Если какой-либо из аргументов IF предоставляется в виде массивов, функция IF будет оценивать каждый элемент массива.
Определение If по Merriam-Webster
\ если , əf \1а : в случае, если
б : позволяя
c : при условии, что
d : при условии, что
2 : ли спросил, пришло ли письмо, я сомневаюсь, что пройду курс3 - используется как функциональное слово, чтобы ввести восклицательный знак, выражающий желание, если будет только дождь.
4 : хотя : хотя возможно интересный, но несостоятельный аргумент
5 : и, возможно, даже не мало, если ожидаются какие-либо изменения - часто используется с , а не с сложно, если не невозможно
если что-нибудь: наоборот даже : возможно даже во всяком случае , вы должны извиниться
\ если \ 1 : состояние, условие вопрос… зависит от слишком многих «если», чтобы дать ответ - Encounterпримеров для текста, чисел, дат, пустых ячеек
IF - одна из самых популярных и полезных функций в Excel.Вы используете оператор IF для проверки условия и возврата одного значения, если условие выполняется, и другого значения, если условие не выполняется.
В этом руководстве мы изучим синтаксис и распространенное использование функции ЕСЛИ в Excel, а затем более подробно рассмотрим примеры формул, которые, надеюсь, окажутся полезными как для новичков, так и для опытных пользователей.
- Функция ЕСЛИ в Excel - синтаксис и использование
- Использование функции ЕСЛИ в Excel - примеры формул
Функция ЕСЛИ в Excel - синтаксис и использование
Функция ЕСЛИ - это одна из логических функций, которая оценивает определенное условие и возвращает указанное вами значение, если условие истинно, и другое значение, если условие - ЛОЖЬ.
Синтаксис IF следующий:
ЕСЛИ (логический_тест, [значение_если_ истинно], [значение_если_ ложь])
Как видите, функция ЕСЛИ имеет 3 аргумента, но только первый является обязательным, а два других - необязательными.
- логический_тест (обязательный) - значение или логическое выражение, которое может иметь значение ИСТИНА или ЛОЖЬ. В этом аргументе вы можете указать текстовое значение, дату, число или любой оператор сравнения.
Например, ваш логический тест может быть выражен как или B1 = "продано", B1 <12.01.2014, B1 = 10 или B1> 10.
- value_if_true (необязательно) - значение, возвращаемое, когда логический тест оценивается как ИСТИНА, т.е. если условие выполнено.
Например, следующая формула вернет текст «Хорошо», если значение в ячейке B1 больше 10:
= ЕСЛИ (B1> 10, «Хорошо») - value_if_false (необязательно) - значение, которое должно быть возвращено, если логический тест оценивается как FALSE, т.е. если условие не выполняется.
Например, если вы добавите «Плохо» в качестве третьего параметра к приведенной выше формуле, он вернет текст « Хорошо », если значение в ячейке B1 больше 10, в противном случае он вернет « Плохо ». :
= ЕСЛИ (B1> 10, «Хорошо», «Плохо»)
ЕСЛИ - что нужно помнить!
Хотя последние два параметра функции ЕСЛИ являются необязательными, ваша формула может дать неожиданные результаты, если вы не знаете скрытой логики.
- Если value_if_true опущено
Если аргумент value_if_true опущен (т.е. после логического_теста стоит только запятая), функция ЕСЛИ возвращает ноль (0), когда условие выполнено. Вот пример такой формулы:
= ЕСЛИ (B1> 10 ,, "Плохо")Если вы не хотите, чтобы в инструкции Excel IF отображалось какое-либо значение при выполнении условия, введите двойные кавычки ("") во втором параметре, например:
= IF (B1> 10, "", "Плохо ").Технически в этом случае формула возвращает пустую строку, невидимую для пользователя, но воспринимаемую другими функциями.Следующий снимок экрана демонстрирует вышеуказанные подходы в действии, и второй кажется более разумным:
- Если value_if_false опущено
Если вам все равно, что происходит, когда указанное условие не выполняется, вы можете опустить третий параметр в формулах, что приведет к следующему.
Если логический тест дает результат ЛОЖЬ, а параметр
значение_если_фальшивыйопущен (после аргументазначение_если_ истинное значениестоит только закрывающая скобка), функция ЕСЛИ возвращает логическое значение ЛОЖЬ.Это немного неожиданно, не правда ли? Вот пример такой формулы:= ЕСЛИ (B1> 10, "хорошо")Установка запятой после аргумента value_if_true заставляет ваш оператор IF возвращать 0, что тоже не имеет особого смысла:
= ЕСЛИ (B1> 10, «хорошо»)И снова самый разумный подход - поставить "" в третьем аргументе, в этом случае у вас будут пустые ячейки, когда условие не выполняется:
= ЕСЛИ (B1> 10, "хорошо", "") - Получить функцию ЕСЛИ для отображения логических значений ИСТИНА или ЛОЖЬ
Чтобы формула Excel IF отображала логические значения ИСТИНА и ЛОЖЬ, когда указанное условие выполняется и не выполняется, соответственно, введите ИСТИНА в аргументе
значение_если_ истинное значение.Параметрvalue_if_falseможет иметь значение FALSE или опускаться. Вот пример формулы:
Примечание. Чтобы ваш оператор IF возвращал TRUE и FALSE в качестве логических значений (логические значения), которые могут распознаваться другими формулами, убедитесь, что вы не заключили их в двойные кавычки. Визуальным признаком логического значения является выравнивание по центру ячейки, как вы видите на скриншоте выше.= ЕСЛИ (B1> 10, ИСТИНА, ЛОЖЬ)
или
= ЕСЛИ (B1> 10, ИСТИНА)Если вы хотите, чтобы «ИСТИНА» и «ЛОЖЬ» были обычными текстовыми значениями, заключите их в «двойные кавычки». В этом случае возвращаемые значения будут выровнены по левому краю и отформатированы как General. Никакая формула Excel не распознает такие тексты «ИСТИНА» и «ЛОЖЬ» как логические значения.
- Оператор IF для выполнения математической операции и возврата результата
Вместо того, чтобы возвращать определенные значения, вы можете получить формулу ЕСЛИ для проверки указанного условия, выполнения соответствующей математической операции и возврата значения на основе результата.Это можно сделать с помощью арифметических операторов или других функций в аргументах
value_if_trueи / илиvalue_if_false. Вот лишь пара примеров формул:Пример 1:
= ЕСЛИ (A1> B1, C3 * 10, C3 * 5)Формула сравнивает значения в ячейках A1 и B1, и если A1 больше B1, она умножает значение в ячейке C3 на 10, в противном случае на 5.
Пример 2:
= ЕСЛИ (A1 <> B1, СУММ (A1: D1), "")Формула сравнивает значения в ячейках A1 и B1, и если A1 не равно B1, формула возвращает сумму значений в ячейках A1: D1, в противном случае - пустую строку.
Использование функции ЕСЛИ в Excel - примеры формул
Теперь, когда вы знакомы с синтаксисом функции ЕСЛИ, давайте рассмотрим несколько примеров формул и узнаем, как использовать их в реальных сценариях.
Оператор Excel IF для чисел: больше, меньше, равно
Использование функции ЕСЛИ с числовыми значениями основано на использовании различных операторов сравнения для выражения ваших условий. Вы найдете полный список логических операторов, проиллюстрированный примерами формул, в таблице ниже.
| Состояние | Оператор | Пример формулы | Описание |
| Больше | > | = ЕСЛИ (A2> 5, «ОК»,) | Если число в ячейке A2 больше 5, формула возвращает «ОК»; в противном случае возвращается 0. |
| Менее | < | = ЕСЛИ (A2 <5, «ОК», «») | Если число в ячейке A2 меньше 5, формула возвращает «ОК»; в противном случае - пустая строка. |
| Равно | = | = ЕСЛИ (A2 = 5, «ОК», «Неверный номер») | Если число в ячейке A2 равно 5, формула возвращает «ОК»; в противном случае функция отображает «Неверный номер». |
| Не равно | <> | = ЕСЛИ (A2 <> 5, «Неверный номер», «ОК») | Если число в ячейке A2 не равно 5, формула возвращает «Неверное число»; в противном случае - «ОК». |
| Больше или равно | > = | = ЕСЛИ (A2> = 5, «ОК», «Плохо») | Если число в ячейке A2 больше или равно 5, формула возвращает «ОК»; иначе - «Плохо». |
| Меньше или равно | <= | = ЕСЛИ (A2 <= 5, «ОК», «») | Если число в ячейке A2 меньше или равно 5, формула возвращает «ОК»; в противном случае - пустая строка. |
На снимке экрана ниже показана формула ЕСЛИ с логическим оператором «Больше или равно» в действии:
Примеры ЕСЛИ для текстовых значений
Обычно вы пишете оператор IF с текстом, используя оператор «равно» или «не равно», как показано в паре следующих ниже примеров IF.
Пример 1. Формула ЕСЛИ без учета регистра для текстовых значений
Как и подавляющее большинство функций, IF по умолчанию нечувствительна к регистру. Для вас это означает, что логические тесты для текстовых значений не распознают регистр в обычных формулах IF.
Например, следующая формула ЕСЛИ возвращает либо «Да», либо «Нет» в зависимости от «Статус доставки» (столбец C):
= ЕСЛИ (C2 = «доставлен», «Нет», «Да»)
В переводе на простой английский формула сообщает Excel, что нужно вернуть «Нет», если ячейка в столбце C содержит слово «Доставлено», в противном случае вернуть «Да».При этом не имеет особого значения, как вы набираете слово «Доставлено» в аргументе логический_тест - «Доставлено», «Доставлено» или «Доставлено». Также не имеет значения, находится ли слово «Доставлено» в нижнем или верхнем регистре в исходной таблице, как показано на снимке экрана ниже.
Другой способ получить точно такой же результат - использовать оператор «не равно» и поменять местами аргументы value_if_true и value_if_false:
= ЕСЛИ (C2 <> «доставлен», «Да», «Нет»)
Пример 2.Формула ЕСЛИ с учетом регистра для текстовых значений
Если вам нужен логический тест с учетом регистра, используйте функцию IF в сочетании с EXACT, которая сравнивает две текстовые строки и возвращает TRUE, если строки точно совпадают с , в противном случае она возвращает FALSE. Функции EXACT чувствительны к регистру, но игнорируют различия в форматировании.
Вы используете IF с EXACT таким образом:
= ЕСЛИ (ТОЧНО (C2, «ДОСТАВЛЕНО»), «Нет», «Да»)
Где C - это столбец, к которому применяется ваш логический тест, а "DELIVERED" - текстовое значение с учетом регистра, которое необходимо точно сопоставить.
Естественно, вы также можете использовать ссылку на ячейку вместо текстового значения в аргументе 2 nd функции EXACT, если хотите.
Примечание. При использовании текстовых значений в качестве параметров для формул ЕСЛИ не забывайте всегда заключать их в «двойные кавычки».
Пример 3. Оператор Excel IF с подстановочным знаком (частичное совпадение)
Если вы хотите основывать свое условие на частичном совпадении, а не на точном совпадении, немедленное решение, которое приходит на ум, заключается в использовании подстановочных знаков (* или?) В аргументе logical_test.Однако этот простой и очевидный подход не сработает. Многие функции принимают подстановочные знаки, но, к сожалению, IF не входит в их число.
Решением является использование IF в сочетании с функциями ISNUMBER и SEARCH (без учета регистра) или FIND (с учетом регистра).
Например, если не требуется никаких действий для позиций "Доставлено" и "Отправлено для доставки", следующая формула будет работать лучше:
= ЕСЛИ (ЕЧИСЛО (ПОИСК («доставка», C2)), «Нет», «Да»)
Мы использовали функцию ПОИСК в приведенной выше формуле, так как соответствие без учета регистра лучше подходит для наших данных.Если вам нужно совпадение с учетом регистра, просто замените SEARCH на FIND следующим образом:
= ЕСЛИ (ЕЧИСЛО (НАЙТИ (" текст ", , где искать )), значение_если_ истинно, значение_если_ ложь)
Примеры формул ЕСЛИ в Excel для дат
На первый взгляд может показаться, что формулы IF для дат идентичны операторам IF для числовых и текстовых значений, которые мы только что обсудили. К сожалению, это не так.
В отличие от многих других функций Excel, IF не может распознавать даты и интерпретирует их как простые текстовые строки, поэтому вы не можете выразить свой логический тест просто как> «19.11.2014» или>> 19.11.2014.Увы, ни один из приведенных выше аргументов неверен.
Пример 1. Формулы ЕСЛИ для дат с функцией ДАТАЗНАЧ
Чтобы функция ЕСЛИ распознала дату в логическом тесте как дату, вы должны заключить ее в функцию ЗНАЧЕНИЕ ДАТЫ , как это ЗНАЧЕНИЕ ДАТЫ ("19.11.2014"). Полная формула IF может иметь следующий вид:
= ЕСЛИ (C2
Как показано на снимке экрана ниже, эта формула ЕСЛИ оценивает даты в столбце C и возвращает «Завершено», если игра была сыграна до 11 ноября.В противном случае формула возвращает «Скоро в продаже».
Пример 2. Формулы ЕСЛИ с функцией СЕГОДНЯ ()
Если вы основываете свое условие на текущей дате, вы можете использовать функцию СЕГОДНЯ () в аргументе логический_тест формулы ЕСЛИ. Например:
= ЕСЛИ (C2
Естественно, функция ЕСЛИ Excel может понимать более сложные логические тесты, как показано в следующем примере.
Пример 3. Расширенные формулы IF для будущих и прошедших дат
Предположим, вы хотите отметить только даты, которые наступят более чем через 30 дней. В этом случае вы можете выразить аргумент логический_тест как A2-TODAY ()> 30. Полная формула IF может иметь следующий вид:
= ЕСЛИ (A2-СЕГОДНЯ ()> 30, «Дата в будущем», «»)
Чтобы указать прошлые даты, которые произошли более 30 дней назад, вы можете использовать следующую формулу ЕСЛИ:
= ЕСЛИ (СЕГОДНЯ () - A2> 30, «Прошлая дата», «»)
Если вы хотите, чтобы оба показателя были в одном столбце, вам нужно будет использовать вложенную функцию ЕСЛИ, например:
= ЕСЛИ (A2-СЕГОДНЯ ()> 30, «Дата в будущем», IF (СЕГОДНЯ () - A2> 30, «Прошлая дата», «»))
Примеры IF Excel для пустых, непустых ячеек
Если вы хотите каким-то образом пометить свои данные на основе того, что определенная ячейка (я) пуста или не пуста, вы можете:
- Используйте функцию ЕСЛИ Excel вместе с ISBLANK или
- Используйте логические выражения = "" (равно пустому) или <> "" (не равно пустому).
В таблице ниже объясняется разница между этими двумя подходами и приводится пример формулы.
| Логический тест | Описание | Пример формулы | |
| Пустые ячейки | = "" | Возвращает значение ИСТИНА, если указанная ячейка визуально пуста, включая ячейки с строками нулевой длины . В противном случае оценивается как ЛОЖЬ. | = ЕСЛИ (A1 = "", 0, 1) Возвращает 0, если A1 визуально пуст.В противном случае возвращает 1. .Если A1 содержит пустую строку, формула возвращает 0. |
| ISBLANK () | принимает значение ИСТИНА, если указанная ячейка не содержит абсолютно ничего - ни формулы, ни пустой строки, возвращаемой какой-либо другой формулой. В противном случае оценивается как ЛОЖЬ. | = ЕСЛИ (ISBLANK (A1), 0, 1) Возвращает результаты, идентичные приведенной выше формуле, но обрабатывает ячейки со строками нулевой длины как непустые ячейки. То есть, если A1 содержит пустую строку, формула возвращает 1. | |
| Непустые ячейки | <> "" | Возвращает значение ИСТИНА, если указанная ячейка содержит некоторые данные. В противном случае оценивается как ЛОЖЬ. Ячейки с строками нулевой длины считаются пустыми . | = ЕСЛИ (A1 <> "", 1, 0) Возвращает 1, если A1 не пусто; в противном случае возвращает 0. Если A1 содержит пустую строку, формула возвращает 0. |
| ISBLANK () = ЛОЖЬ | Возвращает значение ИСТИНА, если указанная ячейка не пуста. В противном случае оценивается как ЛОЖЬ. Ячейки с строками нулевой длины считаются непустыми . | = ЕСЛИ (ISBLANK (A1) = FALSE, 0, 1) Работает так же, как приведенная выше формула, но возвращает 1, если A1 содержит пустую строку. |
В следующем примере демонстрируется действие логического теста «пустой / непустой».
Предположим, у вас есть дата в столбце C, только если была сыграна соответствующая игра (столбец B). Затем вы можете использовать любую из следующих формул ЕСЛИ для отметки завершенных игр:
= ЕСЛИ ($ C2 <> "", "Завершено", "")
= ЕСЛИ (ISBLANK ($ C2) = FALSE, "Completed", "")
Поскольку в нашей таблице нет строк нулевой длины, обе формулы возвращают одинаковые результаты:
Надеюсь, приведенные выше примеры помогли вам понять общую логику функции ЕСЛИ.Однако на практике вам часто может понадобиться одна формула ЕСЛИ для проверки нескольких условий, и наша следующая статья покажет вам, как решить эту задачу. Кроме того, мы также рассмотрим вложенные функции ЕСЛИ, формулы ЕСЛИ массивов, функции IFEFFOR и IFNA и многое другое. Следите за обновлениями и благодарим за чтение!
Вас также может заинтересовать:
Как использовать функцию ЕСЛИ
Простые примеры if | И / или критерии | Вложенный If | Подробнее о If
Функция ЕСЛИ - одна из наиболее часто используемых функций в Excel .Эта страница содержит множество простых примеров IF.
Простые примеры if
Функция ЕСЛИ проверяет, выполняется ли условие, и возвращает одно значение, если оно истинно, и другое значение, если ложно.
1а. Например, взгляните на функцию ЕСЛИ в ячейке B2 ниже.
Объяснение: если цена больше 500, функция ЕСЛИ возвращает High, иначе возвращает Low.
1б.Следующая функция ЕСЛИ дает точно такой же результат.
Примечание. Вы можете использовать следующие операторы сравнения: = (равно),> (больше), = (больше или равно), (не равно).
2. Всегда заключайте текст в двойные кавычки.
3а. Приведенная ниже формула вычисляет прогресс между двумя точками времени.
3б.Вы можете использовать функцию ЕСЛИ для отображения пустой строки, если конечное значение еще не было введено (см. Строку 5).
Объяснение: если конечное значение не пустое (означает, что не равно), функция ЕСЛИ вычисляет прогресс между начальным и конечным значением, в противном случае она отображает пустую строку (две двойные кавычки, между которыми ничего нет).
И / или Критерии
Используйте функцию ЕСЛИ в сочетании с функциями И и ИЛИ и станьте экспертом по Excel.
1. Например, посмотрите на функцию ЕСЛИ в ячейке D2 ниже.
Объяснение: функция И возвращает ИСТИНА, если первая оценка больше или равна 60, а вторая оценка больше или равна 90, иначе она возвращает ЛОЖЬ. Если TRUE, функция IF возвращает Pass, если FALSE, функция IF возвращает Fail.
2. Например, посмотрите на функцию ЕСЛИ в ячейке D2 ниже.
Объяснение: функция ИЛИ возвращает ИСТИНА, если хотя бы одна оценка больше или равна 60, иначе она возвращает ЛОЖЬ.Если TRUE, функция IF возвращает Pass, если FALSE, функция IF возвращает Fail.
3. Например, посмотрите на функцию ЕСЛИ в ячейке D2 ниже.
Объяснение: указанная выше функция AND имеет два аргумента, разделенных запятой (таблица, зеленый или синий). Функция И возвращает ИСТИНА, если Продукт равен «Таблица», а Цвет равен «Зеленому» или «Синему». Если ИСТИНА, функция ЕСЛИ снижает цену на 50%, если ЛОЖЬ, функция ЕСЛИ снижает цену на 10%.
Вложенный, если
Функция ЕСЛИ в Excel может быть вложенной, если необходимо выполнить несколько условий. Значение FALSE заменяется другой функцией IF, чтобы провести дальнейшую проверку.
1. Например, взгляните на вложенную формулу ЕСЛИ в ячейке C2 ниже.
Объяснение: если оценка равна 1, вложенная формула IF возвращает Bad, если оценка равна 2, вложенная формула IF возвращает Good, если оценка равна 3, вложенная формула IF возвращает отлично, в противном случае возвращает Not Valid.Если у вас Excel 2016 или новее, просто используйте функцию IFS.
2. Например, взгляните на вложенную формулу ЕСЛИ в ячейке C2 ниже.
Объяснение: если оценка меньше 60, вложенная формула IF возвращает F, если оценка больше или равна 60 и меньше 70, формула возвращает D, если оценка больше или равна 70 и меньше чем 80, формула возвращает C, если оценка больше или равна 80 и меньше 90, формула возвращает B, иначе она возвращает A.
Подробнее об If
Функция ЕСЛИ - отличная функция. Давайте взглянем на еще несколько интересных примеров.
1. Например, используйте ЕСЛИ и И, чтобы проверить, находится ли значение между двумя числами.
Объяснение: функция И возвращает ИСТИНА, если человек старше 12 и моложе 20 лет, иначе она возвращает ЛОЖЬ. Если ИСТИНА, функция ЕСЛИ возвращает Да, если ЛОЖЬ, функция ЕСЛИ возвращает Нет.
2. Вы можете комбинировать ЕСЛИ со СРЕДНИМ, СУММ и другими функциями Excel. Небо это предел!
Объяснение: функция И возвращает ИСТИНА, если входное значение больше 100, а среднее значение в именованном диапазоне Data1 больше 100, иначе возвращается ЛОЖЬ. Если ИСТИНА, функция ЕСЛИ возвращает сумму Данных2, если ЛОЖЬ, функция ЕСЛИ возвращает 0.
Запутались? Вы всегда можете использовать инструмент «Вычислить формулу» для пошагового выполнения формулы ЕСЛИ.Этот инструмент Excel поможет вам понять формулу.
3. Например, выберите ячейку G3 выше.
4. На вкладке Формулы в группе Аудит формул щелкните Вычислить формулу.
5. Нажмите кнопку «Оценить» несколько раз.
Примечание: попробуйте сами. Загрузите файл Excel и выберите одну из формул ЕСЛИ, описанных на этой странице. Вы можете использовать этот инструмент для пошагового выполнения всех видов формул.
Как составить оператор ЕСЛИ в Excel
Что такое оператор ЕСЛИ в Excel?
Оператор Excel IF проверяет заданное условие и возвращает одно значение для ИСТИННОГО результата и другое значение для ЛОЖНОГО результата. Например, если общая сумма продаж превышает 5000 долларов, то для бонуса вы должны вернуть «Да» - в противном случае - «Нет» для бонуса. Мы также можем использовать функцию ЕСЛИ для оценки одной функции или включить несколько функций ЕСЛИ в одну формулу. Несколько операторов ЕСЛИ в Excel известны как вложенные операторы ЕСЛИ.
Как финансовый аналитик Описание работы финансового аналитика В описании должности финансового аналитика ниже приводится типичный пример всех навыков, образования и опыта, необходимых для работы аналитиком в банке, учреждении или корпорации. Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, функция IF часто используется для оценки и анализа данных путем оценки конкретных условий.
Функцию можно использовать для оценки текста, значений и даже ошибок.Он не ограничивается только проверкой того, совпадает ли одно с другим, и возвратом единственного результата. Мы также можем использовать математические операторы и выполнять дополнительные вычисления в зависимости от наших критериев. Мы также можем вложить несколько функций IF вместе для выполнения множественных сравнений.
IF Formula
= IF (logic_test, value_if_true, value_if_false)
Функция использует следующие аргументы:
- Logical _ test (обязательный аргумент для - быть протестированным и оцененным как ИСТИНА или ЛОЖЬ.
- Значение _ if_true (необязательный аргумент) - значение, которое будет возвращено, если логический_тест оценивается как ИСТИНА.
- Value_if_false (необязательный аргумент) - значение, которое будет возвращено, если логический_test оценивается как FALSE.
При использовании функции ЕСЛИ для построения теста мы можем использовать следующие логические операторы:
- = (равно)
- > (больше)
- > = (больше или равно)
- < (меньше)
- <= (меньше или равно)
- <> (не равно)
Как использовать функцию ЕСЛИ в Excel
Чтобы понять использование функции оператора ЕСЛИ в Excel, давайте рассмотрим несколько примеров:
Пример 1. Простой оператор IF Excel
Предположим, мы хотим провести очень простой тест.Мы хотим проверить, действительно ли значение в ячейке C2 больше или равно значению в ячейке D2. Если аргумент верен, мы хотим вернуть текст, в котором говорится «Да, это так», а если это не так, мы хотим отобразить «Нет, это не так».
Вы можете точно увидеть, как работает оператор IF Excel в приведенном ниже простом примере.
Результат, когда истина:
Результат, когда ложь:
Загрузите простой шаблон XLS.
Пример 2 - Заявление Excel IF
Предположим, мы хотим протестировать ячейку и убедиться, что действие выполняется, если ячейка не пуста. Ниже приведены данные:
В таблице выше мы перечислили задачи, связанные с AGM, в столбце A. Примечания содержат дату завершения. В столбце B мы будем использовать формулу, чтобы проверить, пусты ли ячейки в столбце C. Если ячейка пуста, формуле будет присвоен статус «открыта».Однако, если ячейка содержит дату, формуле будет присвоен статус «закрыто». Используемая формула:
Мы получаем следующие результаты:
Пример 3 - Excel IF Statement
Продавцы часто предоставляют скидку в зависимости от приобретенного количества. Предположим, нам даны следующие данные:
Используя несколько функций ЕСЛИ, мы можем создать формулу для проверки нескольких условий и выполнения различных вычислений в зависимости от того, в какой диапазон сумм попадает указанное количество.Чтобы рассчитать общую цену для 100 наименований, формула будет такой:
Получим результат ниже:
Что следует помнить о функции ЕСЛИ
- Функция ЕСЛИ в Excel будет работать, если логический_тест возвращает числовое значение. В таком случае любое ненулевое значение трактуется как ИСТИНА, а ноль - как ЛОЖЬ.
- #VALUE! error - Происходит, когда данный аргумент logic_test не может быть оценен как ИСТИНА или ЛОЖЬ.
- Когда любой из аргументов предоставляется функции в виде массивов, функция ЕСЛИ оценивает каждый элемент массива.
- Если мы хотим подсчитать условия, мы должны использовать функции СЧЁТЕСЛИ и СЧЁТЕСЛИ.
- Если мы хотим сложить условия, мы должны использовать функции СУММЕСЛИ и СУММЕСЛИМН.
Причины использования заявления ЕСЛИ в Excel
Существует множество причин, по которым аналитик или любой, кто использует Excel, может захотеть построить формулы ЕСЛИ.
Общие примеры включают:
- Чтобы проверить, является ли аргумент истинным или ложным
- Для вывода ЧИСЛА
- Для вывода некоторого ТЕКСТА
- Для создания условной формулы (например, результат C3 + B4, если истина и N9 -E5, если ложно)
- Создание сценариев Анализ сценария Анализ сценария - это процесс изучения и оценки возможных событий или сценариев, которые могут произойти в будущем, и прогнозирования, которые будут использоваться в финансовом моделировании. Что такое Финансовое моделирование. Финансовое моделирование выполняется в Excel для прогнозирования финансовые показатели компании.Обзор того, что такое финансовое моделирование, как и зачем его создавать.
- Для расчета графика долга График долга График долга включает в себя весь долг, имеющийся у предприятия, в зависимости от срока его погашения и процентной ставки. В финансовом моделировании потоки процентных расходов или график амортизации основных средств График амортизации График амортизации требуется в финансовом моделировании для связи трех финансовых отчетов (доход, баланс, движение денежных средств) в Excel. в бухгалтерском учете
Щелкните здесь, чтобы загрузить образец файла Excel
Дополнительные ресурсы
Спасибо за то, что прочитали руководство CFI по использованию отчета IF Excel.Потратив время на изучение и освоение этих функций, вы значительно ускорите свой финансовый анализ. Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
- Расширенный курс Excel
- Расширенное руководство по формулам Excel Расширенные формулы Excel, которые необходимо знать Эти расширенные формулы Excel очень важно знать и выведут ваши навыки финансового анализа на новый уровень. Загрузите нашу бесплатную электронную книгу Excel!
- Список ярлыков Excel Ярлыки Excel для ПК Ярлыки MacExcel - список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета.Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения
- Программа финансового моделирования Станьте сертифицированным аналитиком финансового моделирования и оценки (FMVA) ®
Заявление IF - Обзор, синтаксис и Как это работает
Что такое заявление ЕСЛИ в Excel?
IF Statement - одна из популярных инструкций Excel, которую можно использовать в качестве инструкции для принятия решений.Это одна из основополагающих концепций в программировании, которая придает программе необходимый интеллект, так что программа реализует решения на основе критериев, установленных пользователем.
В Excel оператор IF используется для оценки логического или математического выражения и получения желаемого результата на основе заданных критериев. Оператор IF работает, проверяя выражение, чтобы увидеть, выполняется ли условие, и возвращает значение на основе полученных выходных данных.
Например, на основе критериев он возвращает одно предопределенное значение, если условие оказывается истинным, и другое предопределенное значение, если утверждение оказывается ложным. Оператор IF иногда называют оператором IF THEN ELSE.
Сводка- Оператор IF - это оператор принятия решений, который помогает программе принимать решения на основе заданных критериев.
- Оператор IF выполняет один набор кода, если заданное условие выполнено (ИСТИНА) или другой набор кода оценивается как ЛОЖЬ.
- Это встроенная функция в Excel, и ее можно использовать как функцию VBA в Excel.
Функция IF в Excel по сравнению с оператором IF в VBA
Операторы IF предназначены для выполнения одних и тех же функций, но они различаются по принципу работы. Оператор Excel IF работает, проверяя, выполняется ли условие, и возвращает значение (TRUE). В противном случае возвращается значение FALSE.
В отличие от оператора IF в Excel, оператор IF VBA Если Else Построение оператора VBA If Else очень похоже на построение вложенной формулы if внутри Excel.Преимущество использования VBA вместо этого заключается в том, что за ним гораздо легче следить, поскольку вложенные IF обычно осложняются заключением в несколько круглых скобок. В операторе if в VBA каждое предложение IF отделено от другого и вместо этого расположено в порядке приоритета и не возвращает никакого значения при оценке условия. Если условие оценивается как ИСТИНА, программа выполняет инструкции внутри блока IF. Однако, если условие оценивается как FALE, программа переходит к следующему блоку после блоков IF и оценивает их последовательно, пока условие не оценивается как TRUE.
Синтаксис
Ниже приведен пример синтаксиса для оператора If-Then-Else:
If condition_1 Then
statement_1
ElseIf condition_2 then statement_2
ElseIf condition_n Then
statement_n
Else
Statement_else
65в указанном порядке.Условия оцениваются как логическое значение, которое должно быть ИСТИНА или ЛОЖЬ. Если условие окажется ИСТИННЫМ, будет выполнен соответствующий код, и не будет других условий для оценки.
Ключевое слово «Then» - это директива, которая показывает, что программа управляет инструкциями, которые следуют сразу после оператора IF.
Как только программа оценивает условие как ИСТИНА, оператор, то есть оператор_1, оператор_2… .. оператор_n, представляет собой коды, которые должны быть выполнены.Заявление__else - это код, который будет выполняться, если условие_1, условие_2,… условие_n оценено как ложное.
Последняя строка синтаксиса заканчивается кодом «End If». Код сообщает программе, что это последняя строка функции ЕСЛИ и что дальнейших условий для оценки нет.
Как работает оператор IF
Все указанные условия вместе с их операторами IF оцениваются последовательно, что означает, что программа оценивает условия, начиная с Condition_1.Если программа оценивает первое условие как ИСТИНА, то все остальные условия в последовательности будут пропущены.
Однако, если условие_1 оценивается как ложное, программа перейдет к оценке второго условия в последовательности, которым является условие_2. Если условие_2 оценивается как ИСТИНА, программа выполнит все инструкции, содержащиеся в блоке ELSEIF. Все остальные условия, следующие за условием_2 в последовательности, будут пропущены. Если условие_2 оценивается как ЛОЖЬ, программа переходит к оценке condition_n.
Если condition_n оценивается как TRUE, программа выполнит инструкции в блоке ELSEIF и пропустит блок ELSE. Однако, если condition_n оценивается как FALSE, тогда программа перейдет к выполнению блока ELSE.
При последовательной оценке условий одновременно может выполняться только один блок кода. Оператор End If уведомляет программу о том, что условные операторы достигли конца.
Как написать оператор IF в VBA (пример)
Одно из приложений оператора IF - это проверка того, является ли число положительным или отрицательным.Этого можно достичь, написав программу, которая проверяет, является ли число меньше или больше 0, чтобы определить, является ли оно положительным или отрицательным.
Код VBA должен быть записан следующим образом:
Если число <0 То
MsgBox «Значение отрицательное!»
Else
MsgBox «Значение положительное!»
End If
Приведенный выше код VBA позволяет пользователям вводить случайные числа, а затем программа проверяет, больше ли введенное значение нуля или меньше нуля.Если пользователь вводит значение меньше нуля, программа отобразит результат «Значение отрицательное». Значение больше нуля отобразит результат «Значение положительное».
Использование операторов AND и OR в операторе IF
При наличии нескольких зависимых условий пользователи могут использовать логические операторы, такие как AND и OR, внутри одного оператора IF.
Синтаксис использования условий AND / OR с оператором IF следующий:
If condition_1and condition_2 Then
True_code
Else
Конец IF
В приведенной выше системе true_code выполняется, когда выполняются условие_1 И условие_2.Если условие_1 или условие_2 ложно, программа выполнит false_code. Это означает, что логический оператор «И» возвращает истинное значение только тогда, когда выполняются оба условия / Истина.
С оператором «ИЛИ», если выполняется одно из условий / True, программа выполнит true_code. Если оба условия ложны, программа выполнит false_code. Это означает, что OR возвращает TRUE, только если выполняется хотя бы одно из условий.
Ссылки по теме
CFI предлагает программу сертификации аналитика финансового моделирования и оценки (FMVA) ® Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® для тех, кто хочет вывести свою карьеру на новый уровень.Чтобы продолжить изучение и развитие своей базы знаний, ознакомьтесь с дополнительными соответствующими ресурсами ниже:
- Excel VBAExcel VBAVBA означает Visual Basic для приложений. Excel VBA - это язык программирования Microsoft для Excel и всех других программ Microsoft Office, таких как Word и PowerPoint.
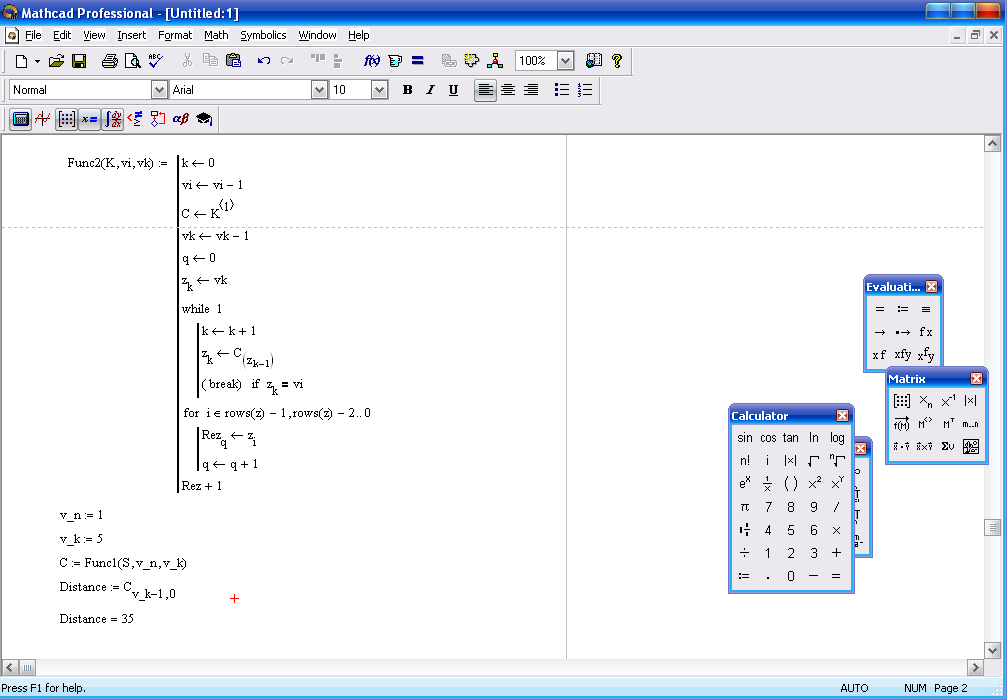
 .M −1
.M −1