Какой цифры нет в двоичной системе?
Прочее › Код › Что такое двоичный код?
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1. Примером может служить число 101.
- Какое число не может быть в двоичной системе счисления?
- Какие цифры могут быть в двоичной системе?
- Чему равен 0 в двоичной системе?
- Сколько цифр может быть в двоичной системе?
- Как будет 13 в двоичной системе счисления?
- Сколько будет 15 в двоичной системе счисления?
- Как будет 4 в двоичной системе?
- Сколько будет 5 в двоичной системе?
- Сколько будет 0 0 в информатике?
- Как будет 1 в двоичной системе?
- Почему именно 0 и 1?
- Сколько будет 3 в двоичной системе?
- Сколько будет 12 в двоичной системе?
- Как будет 8 в двоичной системе?
- Какое максимальное число можно записать в двоичной системе?
- Какие числа не могут быть в восьмеричной системе?
- Какого числа не бывает восьмеричной системы счисления?
- Какое число не может существовать в восьмеричной системе?
- Как будет 10 в двоичной системе?
- Сколько будет 45 в двоичной системе?
- Что такое 0 и 1 в двоичной системе?
- Сколько 0 в двоичной системе 16?
- Как называется 0?
- Почему 1 1 равно 10?
- Сколько будет 21 в двоичной системе?
- Какое максимальное число можно записать в двоичной системе счисления?
- Какое число не может быть записано в восьмеричной системе счисления?
- Сколько единиц содержится в двоичной записи числа?
Какое число не может быть в двоичной системе счисления?
1.
Число 1002 не может быть записано двоичной системе счисления, поскольку двоичная система предполагает использование двух знаков: 1 и 0.
Какие цифры могут быть в двоичной системе?
Двоичная запись чисел
В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу.
Чему равен 0 в двоичной системе?
Числовые системы
Десятичное число (положительное) | Двоичное число |
|---|---|
0 | 0 |
1 | 1 |
2 | 10 |
3 | 11 |
Сколько цифр может быть в двоичной системе?
Двоичная система счисления — это такое представление чисел, в котором вместо цифр 0, 1, 2, 3 и так далее до 9, которыми мы обычно пользуемся в десятичной системе счисления, используются только цифры 0 и 1.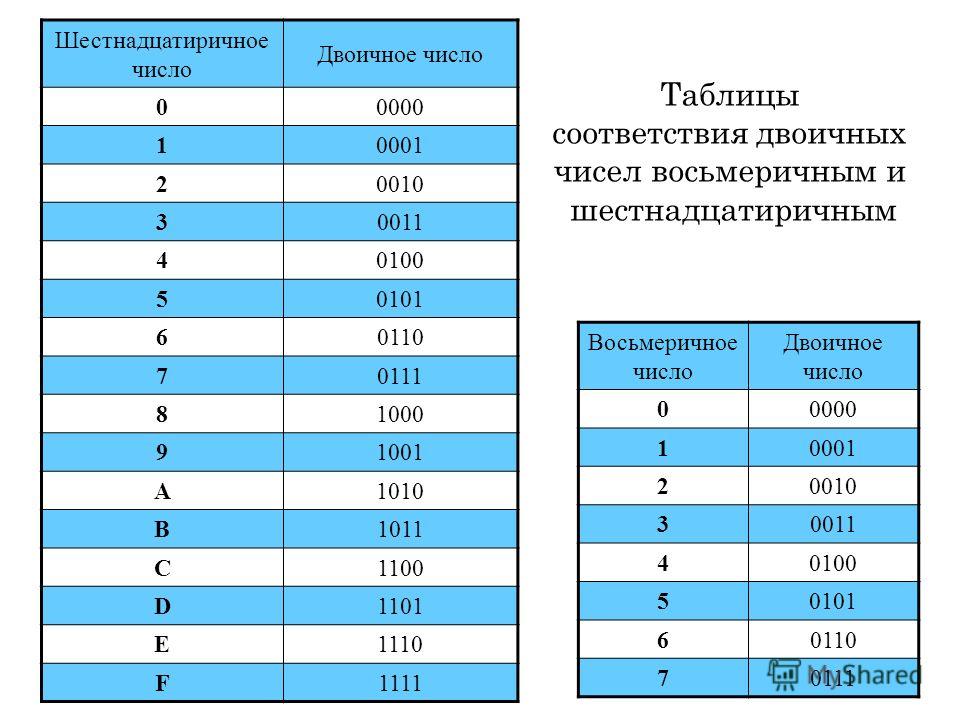
Удивительно, сколько информации можно хранить с помощью всего лишь двух цифр, 0 и 1.
Как будет 13 в двоичной системе счисления?
Перевести число 13 из десятичной системы счисления в двоичную систему: 13(10) => 1101(2).
Сколько будет 15 в двоичной системе счисления?
Шестнадцатеричная система — f. Двоичная система — 1111.
Как будет 4 в двоичной системе?
Шестнадцатеричная система — 4. Двоичная система — 100.
Сколько будет 5 в двоичной системе?
Шестнадцатеричная система — 5. Двоичная система — 101.
Выполнение таких действий как: умножение любых чисел на «0» и деление «0» на любое число (на «0» делить нельзя), всегда в ответе даст «0», то есть 1 * 0 = 0; 0 / 5 = 0; 0 * 6 = 0; 0 / 12 = 0 и тд. Отсюда следует, что пример: 0 * 0 = 0. Ответ: 0.
Как будет 1 в двоичной системе?
Примеры двоичных чисел
Десятичное число | Шестнадцатеричное число | Двоичное число |
|---|---|---|
1 | 1 | 0001 |
2 | 2 | 0010 |
3 | 3 | 0011 |
4 | 4 | 0100 |
Почему именно 0 и 1?
Почему именно \(0\) и \(1\)? Потому что в технике проще всего реализовать такие наборы цифр: если есть сигнал, то это \(1\), если нет — это \(0\).
Двоичная система кодирования появилась не с созданием компьютера, ещё задолго до этого математик Г.
Сколько будет 3 в двоичной системе?
Шестнадцатеричная система — 3. Двоичная система — 11.
Сколько будет 12 в двоичной системе?
Двоичная система — 1100.
Как будет 8 в двоичной системе?
Шестнадцатеричная система — 8. Двоичная система — 1000.
Какое максимальное число можно записать в двоичной системе?
Ответ: Максимальное число из пяти цифр в двоичной системе соответствует числу 31 в десятичной системе счисления.
Какие числа не могут быть в восьмеричной системе?
8 система счисления — система, которая содержит восемь цифр. Это 0, 1, 2, 3, 4, 5, 6, 7. Следовательно, если в числе содержаться цифры, превышающие цифру 7, то это число не может быть числом 8 системы счисления.
Какого числа не бывает восьмеричной системы счисления?
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8.
Для представления чисел в ней используются цифры от 0 до 7.
Какое число не может существовать в восьмеричной системе?
Цифр 0, 1, 2, 3, 4, 5, 6, 7. Таким образом, ответ на вопрос — г), так как в этом числе использована цифра 8, чего в восьмеричной системе счисления быть не может.
Как будет 10 в двоичной системе?
Шестнадцатеричная система — a. Двоичная система — 1010.
Сколько будет 45 в двоичной системе?
Записываем число в двоичной системе кодирования информации снизу вверх, начиная при этом с целочисленного частного. Таким образом, 45₁₀ = 101101₂.
Что такое 0 и 1 в двоичной системе?
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом.
Сколько 0 в двоичной системе 16?
В некоторых случаях двоичное представление числа 16 может быть записано следующим образом: 100002 или 0b10000 или &10000.
Cколько значащих нулей в двоичной записи числа 16? Число 16 Число 16 в шестнадцатеричной. Число 16 в восьмеричной системе.
Как называется 0?
Если запись числа совпадает с цифрой 0, то его называют «ноль».
Почему 1 1 равно 10?
Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Основание этой системы счисления равно восьми. Чтобы не выдумывать новых символов для обозначения цифр, в восьмеричной системе счисления были использованы символы десятичных цифр 0, 1, 2, 3, 4, 5, 6 и 7.
Сколько будет 21 в двоичной системе?
Шестнадцатеричная система — 15. Двоичная система — 10101.
Какое максимальное число можно записать в двоичной системе счисления?
Какое наибольшее десятичное число можно записать двумя цифрами в двоичной системе? Наибольшее двузначное число в любой системе счисления — это две самые большие цифры в этой системе счисления. В десятичной это 99, в восьмеричной — 77, в двоичной — 11.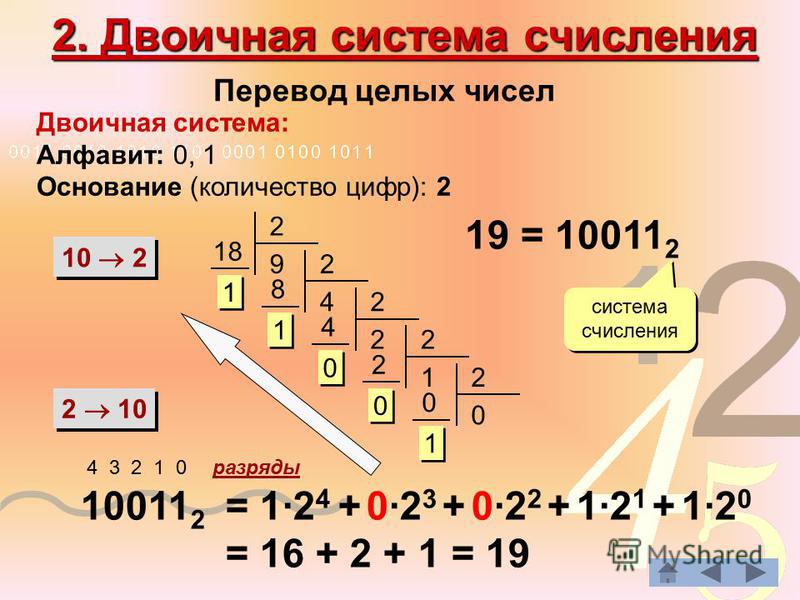
Какое число не может быть записано в восьмеричной системе счисления?
8 система счисления — система, которая содержит восемь цифр. Это 0, 1, 2, 3, 4, 5, 6, 7. Следовательно, если в числе содержаться цифры, превышающие цифру 7, то это число не может быть числом 8 системы счисления. Только число 824 под буквой D не удовлетворяет условию системы счисления.
Сколько единиц содержится в двоичной записи числа?
Запись числа в двоичной системе состоит из шести единиц. Прибавление добавляет спереди одну единицу и группу нулей.
Двоичная система счисления | Digital Music Academy
Если в десятичной системе счисления числа записываются с помощью десяти различных символов (от 0 до 9), то в двоичной системе — с помощью всего двух символов: 0 и 1. Такая система необходима для всех устройств, в которых информация представлена в виде последовательностей двух возможных состояний носителя, а это практически вся современная вычислительная техника.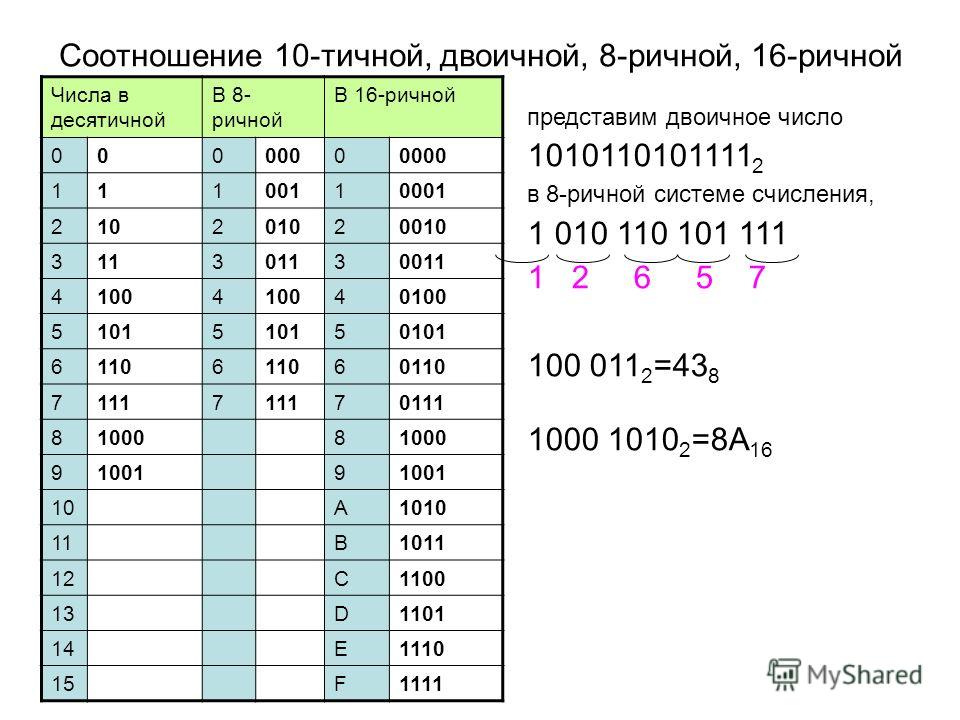
Так же, как в десятичной системе разряды являются степенями основания 10, в двоичной системе разряды являются степенями основания 2:
| 10 000 000 000 | 1 000 000 000 | 100 000 000 | 10 000 000 | 1 000 000 | 100 000 | 10 000 | 1000 | 100 | 10 | 1 |
| 1010 | 109 | 108 | 107 | 106 | 105 | 104 | 103 | 102 | 101 | 100 |
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
При этом значением числа будет сумма значений всех разрядов.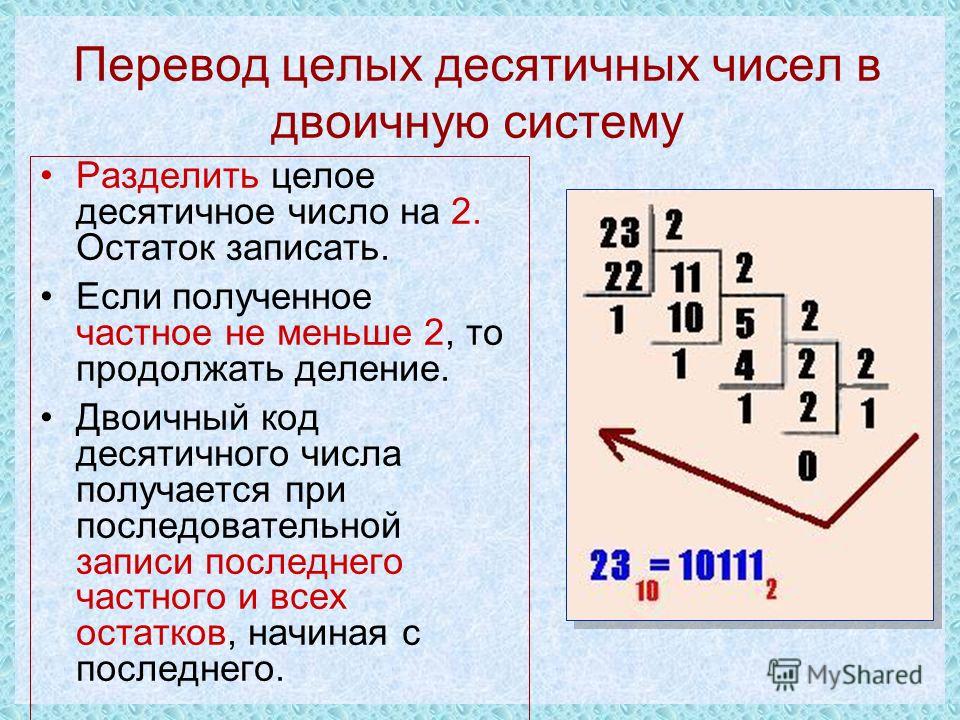
Например, переведем в привычный десятичный вид двоичное число 110001:
1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 49
Или то же самое чуть иначе:
1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49
Или так:
В современных вычислительных системах информация представлена не в виде непрерывного потока двоичных символов (условных нолей и единиц), а за единицу информации, как правило, принимается байт (byte).
Именно поэтому стандартные варианты разрядности кратны восьми. Например, для операционных систем это 32 или 64 разряда (или бита), а для цифрового звука: 8, 16, 24 и 32.
Важно не запутаться в трех основных значениях, которые определяются разрядностью числа: количество возможных значений, максимальное значение и значение старшего бита/разряда.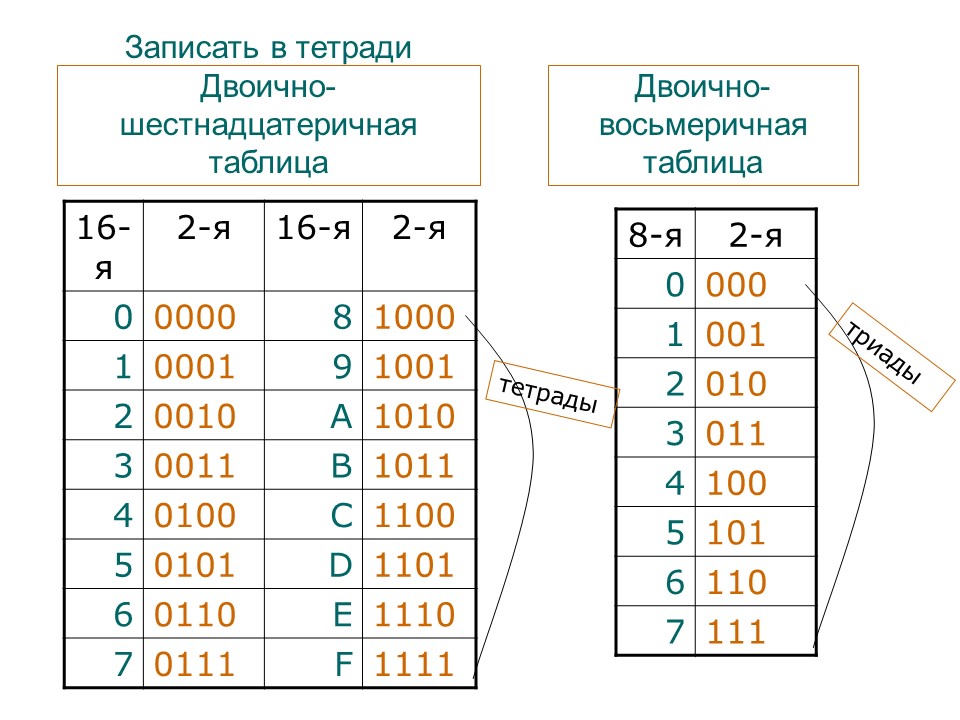
Например, для 8-разрядного числа количество возможных значений = 256 (0 — 255), максимальное значение = 255, а значение старшего бита = 128.
Двоичная система счисления | Encyclopedia.com
Двоичная система счисления, также называемая системой счисления с основанием 2 , представляет собой метод представления чисел, который считается путем использования комбинаций только двух цифр: нуля (0) и единицы (1). Компьютеры используют двоичную систему счисления для обработки и хранения всех своих данных, включая числа, слова, видео, графику и музыку.
Термин «бит», наименьшая единица цифровой технологии, расшифровывается как «двоичная цифра». Байт — это группа из восьми битов. Килобайт — это 1024 байта или 8,19.2 бита.
Используя двоичные числа, 1 + 1 = 10, потому что «2» не существует в этой системе. Другая система счисления, обычно используемая десятичная система счисления или система счисления с основанием 10 , считает с использованием 10 цифр (0,1,2,3,4,5,6,7,8,9), поэтому 1 + 1 = 2 и 7 + 7 = 14.
Другой системой счисления, используемой программистами, является шестнадцатеричная система с основанием 16 , в которой используется 16 символов (0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F), поэтому 1 + 1 = 2 и 7 + 7 = E. Системы счисления с основанием 10 и 16 более компактны, чем двоичная система. Программисты используют шестнадцатеричную систему счисления как удобный и более компактный способ представления двоичных чисел, поскольку ее очень легко преобразовать из двоичной в шестнадцатеричную и наоборот. Сложнее преобразовать из двоичного в десятичное и из десятичного в двоичное.
Преимуществом двоичной системы является ее простота. Вычислительное устройство может быть создано из всего, что имеет ряд переключателей, каждый из которых может переключаться между положением «включено» и положением «выключено». Эти переключатели могут быть электронными, биологическими или механическими, если их можно перемещать по команде из одного положения в другое. Большинство компьютеров имеют электронные переключатели.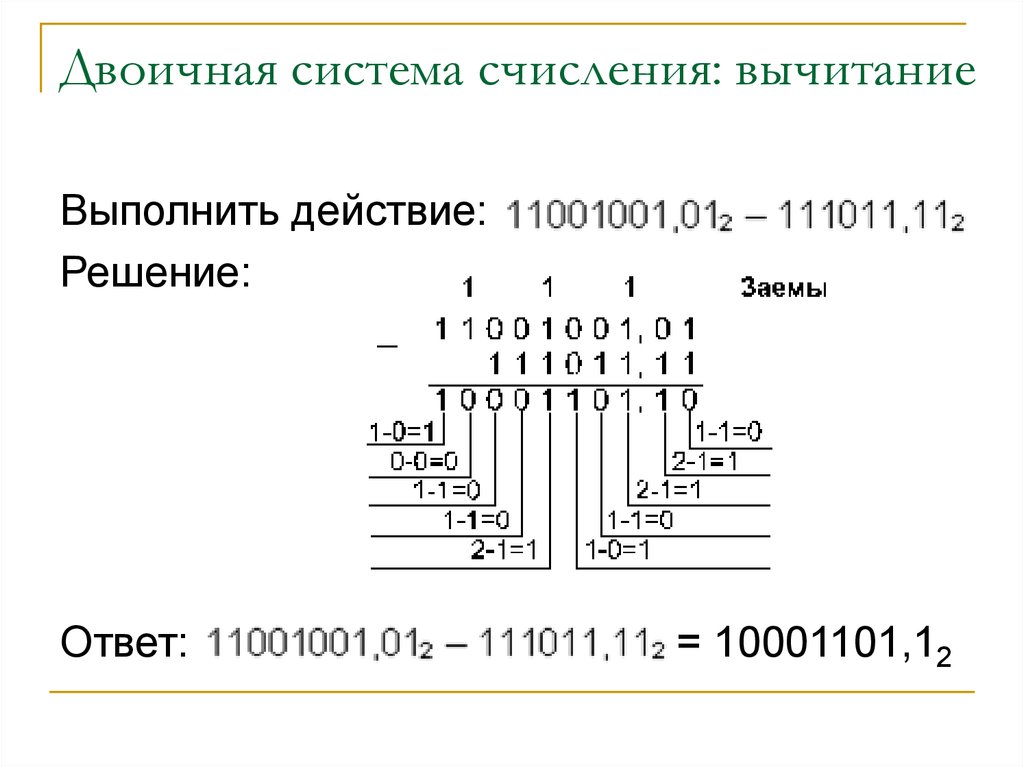
Когда переключатель находится в положении «включено», он представляет собой единицу, а когда переключатель находится в положении «выключено», он представляет собой нулевое значение. Цифровые устройства выполняют математические операции, включая и выключая двоичные переключатели. Чем быстрее компьютер может включать и выключать переключатели, тем быстрее он может выполнять свои вычисления.
| Binary | Decimal | Hexadecimal | ||
| Number | Number | Number | ||
| System | System | Система | ||
| 0 | 0 | 0 | ||
| 1 | 1 | |||
| 0020 | 10 | 2 | 2 | |
| 11 | 3 | 3 | ||
| 100 | 4 | 4 | ||
| 101 | 5 | 5 | ||
| 110 | 6 | 6 | ||
| 111 | 7 | 7 | ||
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | 10 | A | ||
| 1011 | 11 | B | ||
| 1100 | 12 | C | ||
| 1101 | 13 | D | ||
| 1110 | 14 | E | ||
| 1111 | 15 | F | ||
| 10000 | 16 | 10 |
по позиционированию.
Это называется позиционной записью. Это понятие также применимо к десятичным числам. Например, десятичное число 123 представляет десятичное значение 100 + 20 + 3. Число один представляет сотни, число два представляет десятки, а число три представляет единицы. Математическая формула для получения числа 123 может быть создана путем умножения числа в столбце сотен (1) на 100, или 10 2 ; умножение числа в столбец десятков (2) на 10 или 10 1 ; умножение числа в столбце единиц (3) на 1 или 10 0 ; а затем добавить продукты вместе. Формула: 1 × 10 2 + 2 × 10 1 + 3 × 10 0 = 123.
Это показывает, что каждое значение умножается на основание (10), возведенное в возрастающую степень. Значение степени начинается с нуля и увеличивается на единицу в каждой новой позиции формулы.
Эта концепция позиционной записи также применима к двоичным числам с той разницей, что основание равно 2. Например, чтобы найти десятичное значение двоичного числа 1101, формула имеет вид 1 × 2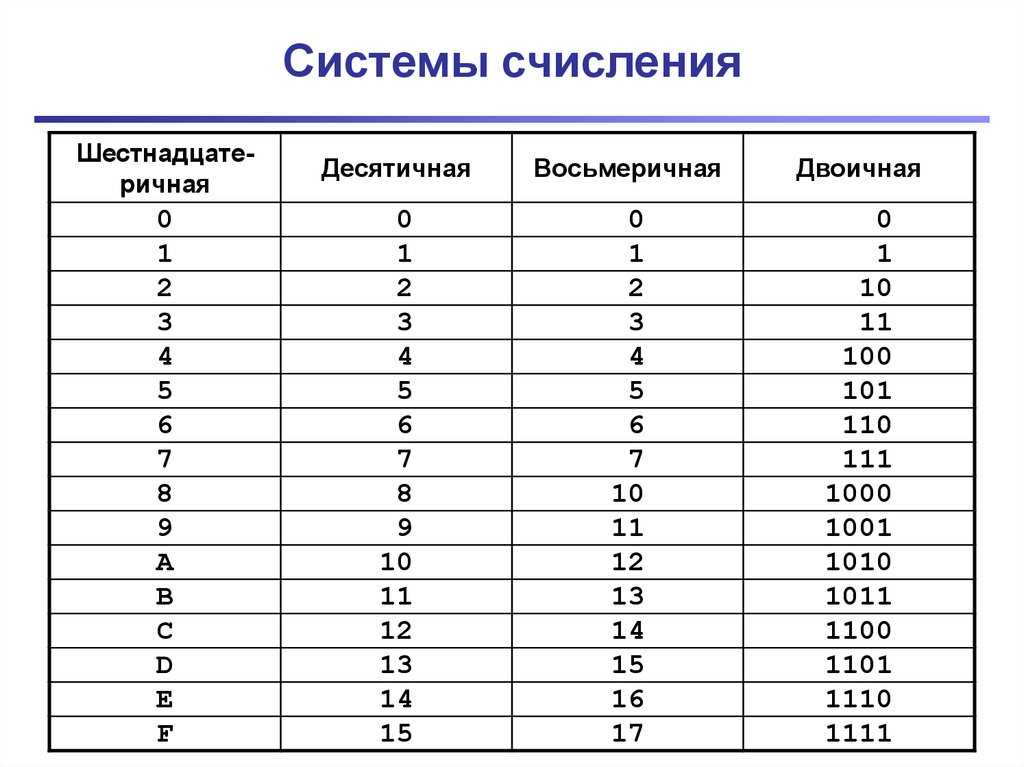 
Двоичные операции
Двоичные числа можно обрабатывать с помощью тех же операций, что и для вычисления десятичных чисел, но используя только нули и единицы. Чтобы сложить два числа, нужно запомнить только четыре правила:
Поэтому, чтобы решить следующую задачу на сложение, начните с крайнего правого столбца и прибавьте 1 + 1 = 10; запишите 0 и перенесите 1. Работая с каждым столбцом слева, продолжайте добавлять, пока проблема не будет решена.
Чтобы преобразовать двоичное число в десятичное, каждая цифра умножается на степень двойки. Затем продукты складываются. Например, чтобы преобразовать двоичное число 11010 в десятичное, формула будет следующей:
Чтобы преобразовать двоичное число в шестнадцатеричное, разделите двоичное число на группы по четыре, начиная справа, а затем переведите каждую группу в свою шестнадцатеричный эквивалент. Нули могут быть добавлены слева от двоичного числа, чтобы завершить группу из четырех. Например, чтобы перевести число 11010 в шестнадцатеричное, формула будет выглядеть так:
Цифровые данные
Биты являются фундаментальным элементом цифровых вычислений.
Термин «оцифровка» означает преобразование аналогового сигнала — диапазона напряжений — в цифровой сигнал,
или ряд чисел, представляющих напряжения. Музыкальное произведение можно оцифровать, взяв очень частые его сэмплы, называемые сэмплированием, и переведя их в дискретных числа, которые затем переводятся в нули и единицы. Если сэмплы берутся очень часто, музыка при воспроизведении звучит как непрерывный тон.
Черно-белую фотографию можно оцифровать, наложив на изображение мелкую сетку и вычислив количество серого на каждом пересечении сетки, называемое пикселем . Например, используя 8-битный код, чисто белая часть изображения может быть оцифрована как 11111111. Точно так же чисто черная часть может быть оцифрована как 00000000. Каждое из 254 чисел, попадающих между этими двумя крайними значениями (числа от 00000001 до 11111110) представляет собой оттенок серого. Когда пришло время реконструировать фотографию, используя ее набор двоичных цифр, компьютер декодирует изображение, присваивает правильный оттенок серого каждому пикселю, и изображение появляется.
Чтобы улучшить разрешение, можно использовать более мелкую сетку, чтобы изображение можно было увеличить до больших размеров без потери деталей.
Цветная фотография оцифровывается аналогичным образом, но требует гораздо больше битов для хранения цвета пикселя. Например, 8-битная система использует восемь битов, чтобы определить, какой из 256 цветов представлен каждым пикселем (2
см. также Первые компьютеры; Объем памяти.
Энн МакИвер Макхоуз
Библиография
Блиссмер, Роберт Х. Знакомство с компьютерными концепциями, системами и приложениями. Нью-Йорк: John Wiley & Sons, Inc., 1989.
Диллиган, Роберт Дж. Вычисления в эпоху Интернета: интерактивное веб-введение.
Нью-Йорк: Plenum Press, 1998.
Уайт, Рон. Как работают компьютеры: выпуск тысячелетия. Indianapolis: Que Corporation, 1999.
Что такое двоичный код?
Обновлено: 05.03.2023 автором Computer Hope
Двоичный может относиться к любому из следующих:
1. Двоичный — это система счисления с основанием 2 , изобретенная Готфридом Лейбницем и состоящая только из двух чисел или цифр: 0 (ноль) и 1 (единица). Эта система нумерации является основой для всего двоичного кода , который записывает цифровые данные, такие как инструкции компьютерного процессора, используемые с вашими устройствами каждый день.
- Как работает двоичный код?
- Почему компьютеры используют двоичные файлы.
- Как читать двоичные числа.
- Работа с числами больше 255 в двоичном виде.
- Использует ли двоичный файл больше памяти, чем десятичный?
- Как добавить в двоичный файл.
- Что такое сдвиг влево и вправо?
- Что такое префикс «0b»?
- Бинарный юмор.
- Преобразование текста в двоичный формат.
- Связанная информация.
Как работает двоичный код?
0 и 1 в двоичном коде означают ВЫКЛ или ВКЛ соответственно. В транзисторе «0» означает отсутствие потока электричества, а «1» означает, что поток электричества разрешен. Таким образом, числа физически представлены внутри вычислительного устройства, что позволяет выполнять вычисления. Эта концепция более подробно объясняется в нашем разделе о том, как читать двоичные числа.
Почему компьютеры используют двоичный код
- Простой и элегантный дизайн. Метод
- Binary 0 и 1 быстро определяет состояние электрического сигнала: выключено (ложно) или включено (истинно).
- Наличие в электрическом сигнале только двух состояний, расположенных далеко друг от друга, делает его менее восприимчивым к электрическим помехам.
- Положительные и отрицательные полюса магнитных сред быстро преобразуются в бинарные.
- Binary — наиболее эффективный способ управления логическими схемами.
- Переключатели, которые сегодня используются в современных компьютерах, могут надежно удерживать только два состояния (включено и выключено).
Примечание
В квантовых компьютерах используется кубит, который может принимать значения 0, 1 или оба значения одновременно.
Как читать двоичные числа
Поскольку система счисления поддерживает только «0» и «1», другие числа, такие как «2», должны быть представлены в двоичном формате путем включения и выключения каждого бита. В двоичном формате первый разряд равен «1», а второй — «2». Таким образом, чтобы получить значение «2», первый бит должен быть выключен, а второй бит должен быть включен для двоичного значения «10». С двоичным кодом важно понимать, что вы читаете справа налево. Если вы хотите, чтобы двоичное значение равнялось «3», первый и второй биты были бы включены для двоичного значения «11» (1 + 2 = 3).
| Позиция бита: | 1 | 0 |
| Значение: | 2 | 1 |
Примечание
Счет на компьютере часто начинается с «0» вместо «1».
Чтобы получить число больше «3», необходимо добавить дополнительные биты. По мере добавления битов их значение удваивается по сравнению с предыдущим битом. Итак, при добавлении третьего бита мы удваиваем предыдущее значение «2», чтобы получить «4». Каждый битовый столбец представляет собой число два, возведенное в степень (основание 2), при этом значение этой степени увеличивается на единицу при перемещении по каждой из восьми позиций. Таким образом, для представления «4» в двоичном формате будет «100» (0 + 0 + 4 = 4). Если все три бита были включены (111), это равно «7» (1+2+4=7).
| Позиция бита: | 2 | 1 | 0 |
| Показатель степени: | 2 2 | 2 1 | 2 0 |
| Значение: | 4 | 2 | 1 |
Если нам нужно число больше «7», необходимо добавить дополнительный бит.
Итак, удвоив «4» (предыдущий самый большой бит), наш следующий бит станет «8». Таким образом, для представления «8» в двоичном формате будет «1000». Если бы у нас было двоичное число «1100», у нас было бы «12» (0+0+4+8=12), поскольку включены только два из четырех битов.
| Позиция бита: | 3 | 2 | 1 | 0 |
| Показатель степени: | 2 3 | 2 2 | 2 1 | 2 0 |
| Значение: | 8 | 4 | 2 | 1 |
Кончик
В 4-битном режиме вы достигаете следующего измерения после бита, называемого полубайтом.
Чтобы представить символ или символ, мы начинаем с 8-битного байта. Следующая диаграмма иллюстрирует двоичное число 01101000. Чтобы получить итог этого примера, прочитайте диаграмму от справа налево и добавьте значение каждого столбца с «1» к предыдущему столбцу.
В следующей таблице это будет 0+0+0+8+0+32+64+0, что равно 104. Биты с 0 не учитываются, поскольку они «выключены».
| Позиция бита: | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Показатель степени: | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Значение: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ВКЛ/ВЫКЛ: | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
Следующий пример — 11111111 в двоичном формате с максимальным 8-битным значением 255.
Опять же, читая справа налево, мы имеем 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255.
| Значение: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ВКЛ/ВЫКЛ: | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Примечание
Поскольку счет начинается с «0» вместо «1», все включенные биты равны 255, но если вы считаете 0, их общее количество равно 256.
Когда у вас есть восемь бит, это равно одному байту. Если вы возьмете двоичный код из первого примера (01101000), который в сумме составляет «104», и поместите его в ASCII, получится строчная буква «h». Чтобы записать «привет», добавьте двоичный код к букве «i», которая равна 01101001 (105) в ASCII. Соединив эти два кода вместе, мы получим 0110100001101001 или 104 и 105, обозначающие «привет».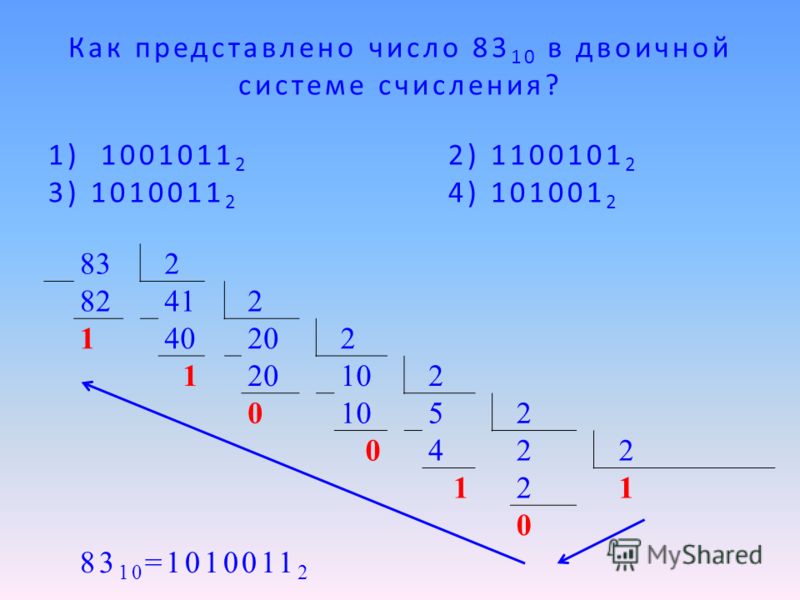
Дополнительную информацию о преобразовании двоичного кода в ASCII можно найти по следующей ссылке.
- Как компьютер преобразует текст в двоичный код или в 0 и 1?
Работа с числами больше 255 в двоичном формате
Для работы с числами больше 255 количество используемых битов удваивается. Например, если вы удвоите 8-битное число до 16-битного (2 16 ), у вас будет 65 536 комбинаций чисел. Увеличение до 32-битного (2 32 ) дает вам 4 294 967 296 комбинаций чисел. Увеличение до 64-битного (2 64 ) дает вам 18 446 744 073 709 551 616.
При сохранении (отображении) 8-битного двоичного числа, такого как «01101000» (104 в десятичной системе), как 16-битного оно становится «00000000 01101000», а как 32-битное — «00000000 00000000 00000000 01101000». Если вы имели дело с числом большим, чем 255, например «12 345», оно сохраняется как «00110000 00111001» (8192 + 4096 + 32 + 16 + 8 + 1) в 16-битном формате.
Кончик
См.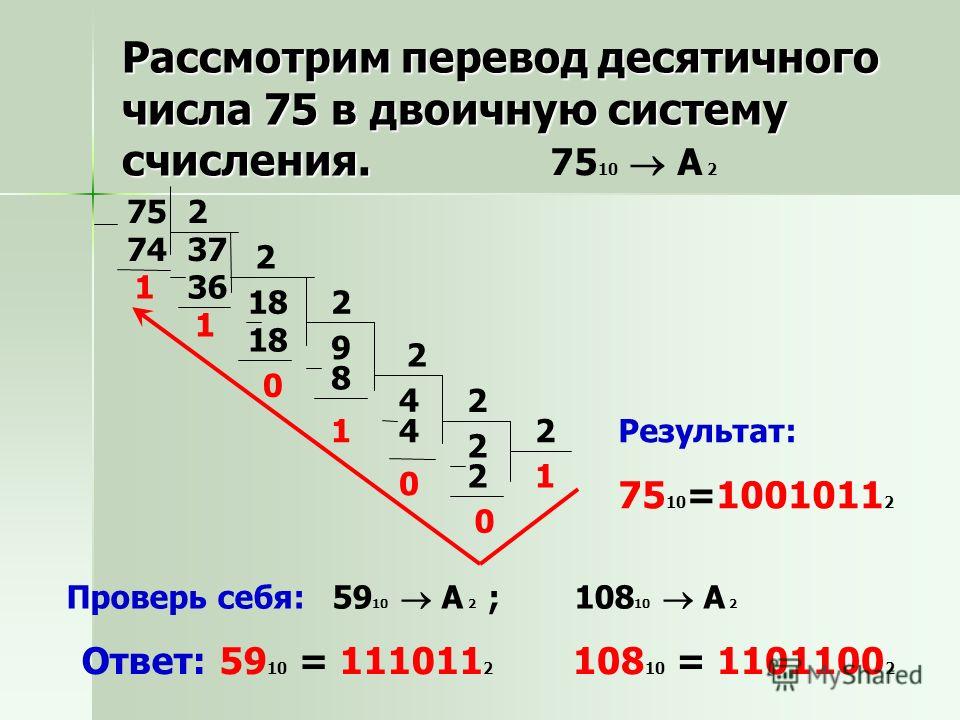
нашу 16-битную страницу для таблицы преобразования до 65 535.
Использует ли двоичный файл больше памяти, чем десятичный?
Длина десятичного числа (например, 234) меньше длины двоичного числа, равного 234 (11101010). Поэтому многие ошибочно полагают, что для хранения «234» вместо «11101010» потребуется меньше памяти.
Однако цифра «234», которую вы видите на экране, показана только для того, чтобы вам было легче читать. Когда компьютер хранит и передает какие-либо данные, все они двоичные. Увеличение основания числа обычно уменьшает его визуальную длину, но не меняет того, сколько места оно занимает на диске.
Как добавить в двоичный файл
Сложение в двоичном формате очень похоже на сложение в десятичном формате. Например, если бы у нас был двоичный файл 01101011 (107) и мы хотели добавить 10000111 (135), мы бы выполнили следующие шаги.
| + | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Начиная с правой стороны, мы должны добавить 1+1, чтобы получить «2».
Поскольку в двоичном формате нет числа два, мы будем использовать двоичное значение «10» и перенести «1» в следующий столбец.
В следующем столбце мы добавили бы «1», которую мы перенесли в следующий столбец, и добавили бы 1+1+1, чтобы получить «3». В двоичном формате нет числа «3», поэтому мы используем «11» (3 в двоичном формате), ставим 1 и переносим 1 в следующий столбец.
Затем мы снова добавляем «1», которая была перенесена, и добавляем 1+0+1, чтобы получить «10» (2 в двоичном формате).
| 0 | 1 | 0 |
Повторяем этот процесс для всех восьми цифр, чтобы получить результат 11110010 (242).
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
Что такое сдвиг влево и вправо?
А сдвиг влево — это когда каждый бит в двоичном числе сдвигается (перемещается) влево, чтобы удвоить двоичное значение или умножить на два.
Например, двоичное число «00000011» равно трем, а при сдвиге влево оно становится «00000110», что равно шести. Другой пример: двоичное число «00111110» равно 62, а сдвиг битов влево дает «01111100» или 124.
Сдвиг вправо похож на сдвиг влево, за исключением того, что биты сдвигаются вправо, чтобы разделить число на два. Например, двоичное число «00001010» равно десяти, а при сдвиге вправо оно становится «00000101» или пятью.
Что такое префикс «0b»?
Во избежание путаницы при записи двоичного числа оно может иметь префикс «0b» (ноль и b). Например, 0b0100 представляет «0100» в двоичном формате. Используя этот префикс, читатель знает, что это не «100» в десятичном виде.
Бинарный юмор
Изображение является примером бинарного юмора (шутки) с помощью известного высказывания на многих футболках гиков. Те, кто умеет читать в двоичном формате, понимают, что эта цитата гласит: «В мире есть только 90 265 двух 90 266 типов людей: те, кто понимает двоичный код, и те, кто не понимает».