Принцип формирования канального цифрового сигнала с ИКМ
Принцип формирования канального цифрового сигнала с ИКММатематическая теория сигналов |
Принцип формирования канального цифрового сигнала с ИКМ | назад | оглавление | вперёд |
3.1 Дискретизация во времени
Преобразование
непрерывного аналогового сигнала в дискретный может быть осуществлено в
соответствии с теоремой отсчетов, доказанной В.А. Котельниковым в 1933 г.:
любой непрерывный
сигнал с ограниченным частотой FМАКС спектром, может быть полностью представлен
в виде своих дискретных во времени отсчетов, взятых через интервал времени
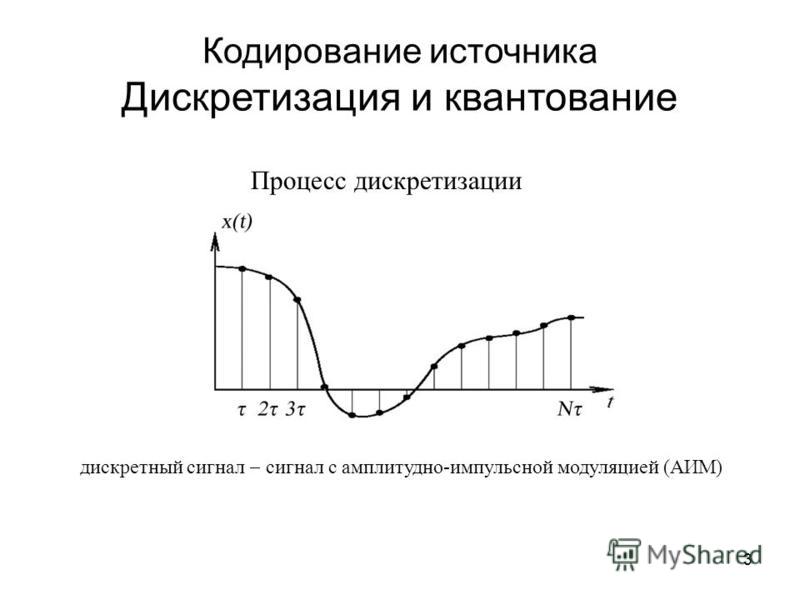
Т Технически операция дискретизации
по времени осуществляется при помощи ключевых схем путем получения сигналов
с амплитудно-импульсной модуляцией (АИМ). При АИМ амплитуда периодической
последовательности импульсов изменяется в соответствии с изменением амплитуды
модулирующего сигнала с(t) (например, телефонного сигнала). Различают
амплитудно-импульсную
модуляцию первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 амплитуда
отсчетов, следующих с частотой дискретизации, изменяется в соответствии с изменением
модулирующего сигнала с(t) на интервале времени передачи отсчета (и, а
при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего
сигнала в начальный момент отсчета. На рисунке 3.1 представлен исходный
модулирующий
сигнал с(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации двухуровневых
сигналов.Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму, а значит их частотные спектры G 1(f) и G2(f), определяемые преобразованием Фурье:
Технически операция дискретизации
по времени осуществляется при помощи ключевых схем путем получения сигналов
с амплитудно-импульсной модуляцией (АИМ). При АИМ амплитуда периодической
последовательности импульсов изменяется в соответствии с изменением амплитуды
модулирующего сигнала с(t) (например, телефонного сигнала). Различают
амплитудно-импульсную
модуляцию первого (АИМ-1) и второго (АИМ-2) рода. При АИМ-1 амплитуда
отсчетов, следующих с частотой дискретизации, изменяется в соответствии с изменением
модулирующего сигнала с(t) на интервале времени передачи отсчета (и, а
при АИМ-2 амплитуда каждого отсчета постоянна и равна значению модулирующего
сигнала в начальный момент отсчета. На рисунке 3.1 представлен исходный
модулирующий
сигнал с(t), а также сигналы АИМ-1 и АИМ-2 в случае дискретизации двухуровневых
сигналов.Сигналы АИМ-1 и АИМ-2 в общем случае имеют различную форму, а значит их частотные спектры G 1(f) и G2(f), определяемые преобразованием Фурье:
Рисунок 3. 1 — Формирование
АИМ сигнала.
1 — Формирование
АИМ сигнала.
также
имеют разный вид. Однако, если длительность АИМ отсчетов (и много меньше
периода дискретизации Тд >>и ,
т.е. скважность импульсной последовательности разница между сигналами АИМ-1
и АИМ-2 оказывается несущественной,
а их
частотные спектры практически совпадают: G1(f) = G2(f)
= G(f). Это условие выполняется
в ЦСП, так как длительность канальных импульсов (и выбирается из условия
где
а частотный спектр определяется следующим образом:
где G(f) спектр исходного сигнала ограниченный минимальной (FМИН) и максимальной (FМАКС) частотами.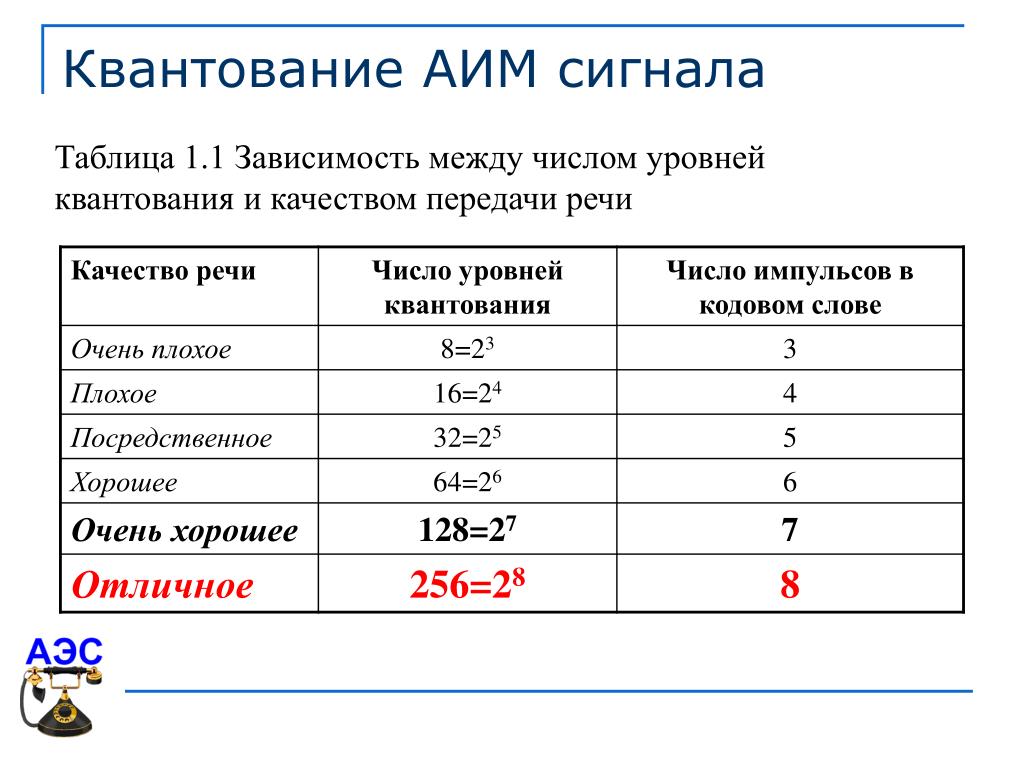 Вид частотного спектра
G(f) для АИМ сигнала при Тд >> ( приведен на рисунке 3.2.
Вид частотного спектра
G(f) для АИМ сигнала при Тд >> ( приведен на рисунке 3.2.
Рисунок 3.2 — Спектральный состав АИМ сигнала.
Частотный спектр модулированной последовательности при АИМ содержит:
- постоянную составляющую G0;
- составляющие с частотами исходного сигнала F МИН FМАКС;
- составляющие с частотой дискретизации Fд и ее гармоник к Fд;
- составляющие
боковых полос (верхней и нижней) при частоте дискретизации
Fд и ее гармоник к Fд (FМИН FМАКС).
При дискретизации двух полярных сигналов (телефонных, звукового вещания) в спектре АИМ сигнала практически отсутствуют постоянная составляющая и ее гармоники.Из рисунка
3.2 видно, что для восстановления исходного непрерывного сигнала из АИМ сигнала,
на приеме
достаточно поставить
ФНЧ (или фильтр-интерполятор) с частотой среза, равной FМАКС,
который выделит исходный сигнал. Поскольку при организации телефонного
канала FМАКС = 3,4
кГц, то F
Поскольку при организации телефонного
канала FМАКС = 3,4
кГц, то F
Fр = (Fд — FМАКС) — FМАКС = 1,2 кГц
и позволяет достаточно просто реализовывать канальные фильтры-интерполяторы. Кроме того, выбор Fд = 8 кГц обусловлен тем, что эта частота кратна 2, что позволяет существенно упростить оборудование ЦСП с ИКМ, передающих цифровые сигналы на основе двоичной системы счисления.Анализ спектрального состава АИМ сигнала, приведенного на рисунке 3.2, позволяет подтвердить правильность выводов теоремы отсчетов. Как видно из рисунка 3.2, для того, чтобы не возникло необратимых частотных искажений, в спектр непрерывного сигнала не должны попадать частотные составляющие нижней боковой полосы частот при F д, то есть:
Итак, при выполнении операции дискретизации во времени необходимо правильно выбрать частоту дискретизации, которая определяется параметром FМАКС непрерывного сигнала: Fд 2FМАКС. При передаче телефонных сигналов частота дискретизации стандартизирована во всем мире и равна Fд = 8 кГц.
При передаче телефонных сигналов частота дискретизации стандартизирована во всем мире и равна Fд = 8 кГц.
Выводы по разделу
Преобразование непрерывного аналогового сигнала в дискретный может быть осуществлено в соответствии с теоремой отсчётов, доказанной В.А. Котельниковым. Дискретизация по времени осуществляется путём получения сигналов с амплитудно-импульсной модуляцией (АИМ). АИМ различают первого (АИМ-1) и второго (АИМ-2) рода.При выполнении операции дискретизации во времени необходимо правильно выбрать частоту дискретизации, которая определяется параметром F
3.2 Квантование по уровню
Как видно из рисунка 3.2, АИМ-сигнал является дискретным во времени, но непрерывным по уровню, так как амплитуда отсчетов может принимать бесконечное множество значений. Однако любая аппаратура обработки сообщений и систем передачи имеет конечную разрешающую способность. Это связано как с ошибками, возникающими при обработке сигналов, так и с наличием шумов и искажений в аппаратуре и каналах передачи.В
связи с этим нет необходимости передавать все бесконечное множество амплитудных
значений непрерывных сигналов,
его можно ограничить конечным множеством, содержащим определенное, заранее
установленное, для того или иного вида сигналов, число «разрешенных» амплитудных значений. Эти «разрешенные» для
передачи амплитудные значения сигнала называются уровнями квантования;
выбор их количества определяет качество передачи сигналов.При квантовании
по уровню весь возможный динамический диапазон сигнала от U макс до
Uмин разбивается
на разрешенные
уровни (если электрический сигнал передается в виде АИМ напряжения непрерывного
сигнала: F(t) = U(t). Разность между двумя соседними разрешенными для
передачи уровнями называется шагом квантования .
Однако любая аппаратура обработки сообщений и систем передачи имеет конечную разрешающую способность. Это связано как с ошибками, возникающими при обработке сигналов, так и с наличием шумов и искажений в аппаратуре и каналах передачи.В
связи с этим нет необходимости передавать все бесконечное множество амплитудных
значений непрерывных сигналов,
его можно ограничить конечным множеством, содержащим определенное, заранее
установленное, для того или иного вида сигналов, число «разрешенных» амплитудных значений. Эти «разрешенные» для
передачи амплитудные значения сигнала называются уровнями квантования;
выбор их количества определяет качество передачи сигналов.При квантовании
по уровню весь возможный динамический диапазон сигнала от U макс до
Uмин разбивается
на разрешенные
уровни (если электрический сигнал передается в виде АИМ напряжения непрерывного
сигнала: F(t) = U(t). Разность между двумя соседними разрешенными для
передачи уровнями называется шагом квантования . Если амплитуда отсчета сигнала UАИМ(t)
в пределах двух соседних разрешенных значений превышает половину шага квантования
/2, ее значение увеличивается в большую сторону, если меньше половины
шага квантования — в меньшую сторону. Таким образом получается сигнал квантованный
по уровню — U
Если амплитуда отсчета сигнала UАИМ(t)
в пределах двух соседних разрешенных значений превышает половину шага квантования
/2, ее значение увеличивается в большую сторону, если меньше половины
шага квантования — в меньшую сторону. Таким образом получается сигнал квантованный
по уровню — U
Разность между истинным значением отсчета и его квантованным значением называется ошибкой, или шумом квантования, который определяется как Ш КВ(t) = UАИМ(t) — UКВ(t), при этом |Ш КВ (t)| /2
Произведя «нумерацию» уровней квантования можно передавать не сами уровни, а их значения по шкале уровней в двоичном коде. В этом случае на приеме восстановить квантованный по уровню сигнал достаточно просто:
UКВ(t)пр = li
Формула 3.1а
где li = (0, lМАКС)
— номер разрешенного уровня в десятичной системе счисления;
— шаг
квантования;
UКВ(t)МАКС= lМАКС
формула
3. 1б
1б
Указанные выше преобразования иллюстрируются рисунком 3.3.Выбор шага
квантования и количество уровней квантования lМАКС определяются, во-первых
параметрами преобразуемого
сигнала, в частности величиной UМАКС, а во-вторых допустимой
величиной помех, возникающих в канале, поскольку ошибки квантования при
передаче, например,
телефонного сигнала воспринимаются как специфический шум квантования, имеющий
некоторую мощность РШ КВ.Энергетический
спектр шумов квантования аналогичен энергетическому спектру «белого шума» и
имеет равномерный
характер в диапазонечастот:
-< f < .Плотность
распределения вероятности W(x) шума квантования в пределах одного шага квантования
в интервале от —
Рисунок
3.3 — Принципы квантования по уровню и формирования канального сигнала с
ИКМ.
Рисунок — 3.4 Плотность распределения вероятности шума квантования.
Средняя мощность случайного процесса с нулевым средним значением и одномерной плотностью распределения вероятности (каковым является шум квантования), определяется следующим образом:
Формула 3.2
где UKi = li — значение
i-го уровня квантования;
x —
случайная величина погрешности
квантования;
—
шаг квантования.
Так как погрешность квантования внутри каждого шага квантования имеет равномерный характер (рисунок 3.3) можно для простоты принять UKi = 0 и получить (из 3.2) выражение:
Формула 3.3
Мощность шума квантования не должна превышать допустимую норму на помехи на выходе канала, предназначенного для передачи различных аналоговых сигналов. Поскольку системы передачи с ИКМ плезиохронной цифровой иерархии (PDH) разрабатывались для передачи телефонных сообщений, далее определим минимально необходимое число уровней квантования при организации телефонного канала в ЦПС с ИКМ.Известно,
что согласно требованиям МСЭ-Т [8,9] суммарная допустимая мощность помех
Р на выходе канала тональной
частоты (ТЧ) эталонной цепи в точке нулевого относительного уровня (ТНОУ)
в час наибольшей нагрузки (ЧНН) не должна превышать величины Р10000
пВт псоф. В канале ТЧ ЦСП с ИКМ величина помехи определяется только шумом
квантования (при отсутствии ошибок при передаче двоичных символов по линейному
тракту): РШ КВдоп = Р = 10000 пВт псоф.При этом эффективное значение мощности шума квантования будет равно:
Поскольку системы передачи с ИКМ плезиохронной цифровой иерархии (PDH) разрабатывались для передачи телефонных сообщений, далее определим минимально необходимое число уровней квантования при организации телефонного канала в ЦПС с ИКМ.Известно,
что согласно требованиям МСЭ-Т [8,9] суммарная допустимая мощность помех
Р на выходе канала тональной
частоты (ТЧ) эталонной цепи в точке нулевого относительного уровня (ТНОУ)
в час наибольшей нагрузки (ЧНН) не должна превышать величины Р10000
пВт псоф. В канале ТЧ ЦСП с ИКМ величина помехи определяется только шумом
квантования (при отсутствии ошибок при передаче двоичных символов по линейному
тракту): РШ КВдоп = Р = 10000 пВт псоф.При этом эффективное значение мощности шума квантования будет равно:
где КПС = 0,75 псофометрический коэффициент, учитывающий чувствительность человеческого уха к различным частотным составляющим помех.
Наконец,
учтем то обстоятельство, что мощность квантования на выходе ФНЧ распределена
в полосе частот 0 fМАКС, где ,
. Тогда РШ КВ на 1 Гц полосы частот в общем
виде имеет выражение:
Тогда РШ КВ на 1 Гц полосы частот в общем
виде имеет выражение:
Формула 3.4
Для оценки
действия помех в каналах систем передачи пользуются параметром, который называется
защищенностью и
определяется следующим образом:
в относительных единицах, АЗ = 10 lg RМ, дБм или АЗ = 20 lg RН, дБм в логарифмических единицах, где РС, РП, UС, UП — мощности и напряжения сигнала и помехи соответственно.Величина средней мощности телефонного сигнала при передаче по каналу ТЧ известна и равна величине РСР ТФ = 32 мВт.Отсюда допустимая защищенность от шумов квантования
Средняя мощность на единичном сопротивлении равна .Телефонный (ТФ) сигнал имеет характеристику, называемую пик-фактором:
а UМАКС зависит от шага квантования и их числа (3. 3: lМАКС = 1080 1510
3: lМАКС = 1080 1510
Такое число уровней квантования оказывается чрезмерно большим, но его можно значительно снизить, принудительно уменьшая пик-фактор ТФ сигнала на передаче и восстанавливая его на приеме. Так, если уменьшить пик-фактор на передаче до величины q = 4,75 количество уровней квантования также резко уменьшится и составит величину lМАКС = 102.На практике изменение и восстановление пик-фактора сигнала (или динамического диапазона) осуществляется при помощи системы компандирования: на передающей стороне на входе АЦП включается устройство, которое называется компрессором (сжимателем) динамического диапазона, а на приеме на выходе ЦАП включается экспандер (расширитель) динамического диапазона. То есть в обощенную структурную схему рисунок 1.3 вводятся дополнительные блоки, как показано на рисунке 3.5.
Рисунок 3.5 — Система компандирования в ЦСП с ИКМ.
Для того, чтобы избежать искажений при передаче сигналов компрессор (К) и экспандер (Э) должны иметь взаимнообратные амплитудные характеристики, как показано на рисунке 3. 6.Здесь кривая 1 — амплитудная характеристика компрессора, кривая 2 — амплитудная характеристика экспандера, кривая 3 — результирующая амплитудная характеристика цепи компрессор-экспандер, которая должна быть линейной.Как видно из рисунка 3.6, значительно увеличивается амплитуда малых сигналов (отсчет 1) и мало меняется амплитуде больших сигналов (отсчет 2), то есть уменьшается как динамический диапазон сигнала так и пик-фактор .
6.Здесь кривая 1 — амплитудная характеристика компрессора, кривая 2 — амплитудная характеристика экспандера, кривая 3 — результирующая амплитудная характеристика цепи компрессор-экспандер, которая должна быть линейной.Как видно из рисунка 3.6, значительно увеличивается амплитуда малых сигналов (отсчет 1) и мало меняется амплитуде больших сигналов (отсчет 2), то есть уменьшается как динамический диапазон сигнала так и пик-фактор .
Рисунок 3.6 — Использование компандерных устройств для сжатия динамического диапазона:
а — амплитудные характеристики компандера;
б — сигнал на выходе компрессора.
Итак, отметим что операция квантования по уровню позволяет преобразовать бесконечное множество отсчетных значений аналогового сигнала в конечное множество разрешенных уровней, перенумеровать эти уровни и передавать информацию об амплитуде отсчета в виде двоичной кодовой комбинации с ИКМ. Для уменьшения числа разрешенных уровней квантования применяется нелинейная операция сжатия динамического диапазона сигнала.
Для уменьшения числа разрешенных уровней квантования применяется нелинейная операция сжатия динамического диапазона сигнала.
Выводы по разделу
Операция квантования по уровню позволяет преобразовать бесконечное множество отсчётных значений аналогового сигнала в конечное множество разрешённых уровней, перенумеровать эти уровни и передавать информацию об амплитуде отсчёта в виде двоичной кодовой комбинации с ИКМ. Для уменьшения числа разрешённых уровней квантования применяется нелинейная операция сжатия динамического диапазона сигнала.
3.3 Кодирование
Операция
кодирования заключается в преобразовании номера «разрешенного» уровня в кодовую комбинацию двоичной системы счисления, состоящую из m символов вида «0» и «1»,
где величина m называется разрядностью кода. Существует большое число двоичных
систем кодирования, однако в ЦСП с ИКМ нашли применение натуральный двоичный
код и его модификация — симметричный двоичный код.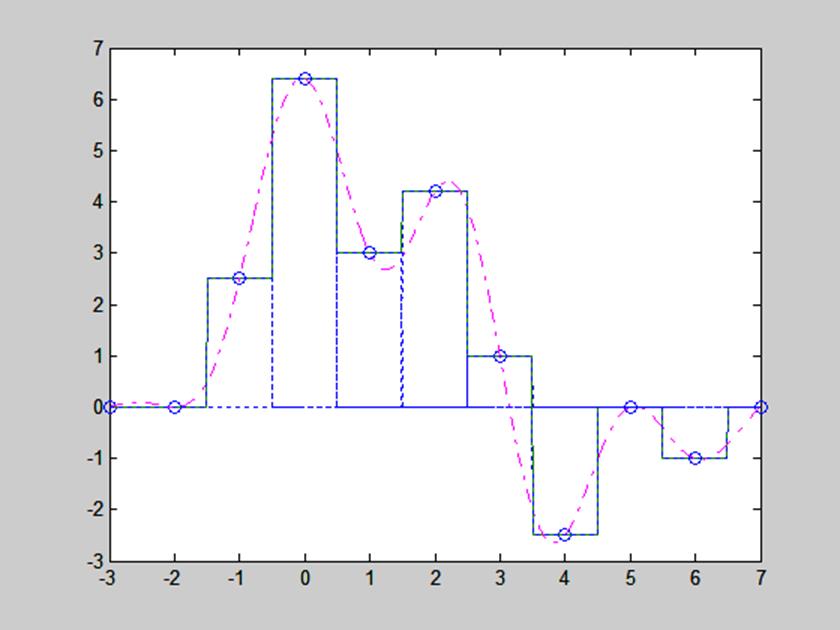 При использовании натурального кода любое положительное десятичное число li, не превышающее величины lМАКС (li = 0, lМАКС), может быть представлено в виде комбинации из m двоичных символов по следующему алгоритму:
При использовании натурального кода любое положительное десятичное число li, не превышающее величины lМАКС (li = 0, lМАКС), может быть представлено в виде комбинации из m двоичных символов по следующему алгоритму:
m — разрядность кода. Очевидно, что lМАКС определяется суммой весовых составляющих вида 2 m — j при значении всех коэффициентов аj = 1:
lМАКС = 2 m — 1,
а суммарное
число «разрешенных» уровней
квантования I = lМАКС + 1 = 2 m (учитывая,
что кодируется и ноль).Поскольку в при передаче телефонных сигналов в каналах ЦСП с ИКМ используется двухполярное кодирование (для устранения постоянной составляющей и гармонических частот вида kFд k=(0, ) в указанных ЦСП используется симметричный двоичный код, в котором 1 или 0 в старшем разряде определяют полярность кодируемого сигнала с АИМ.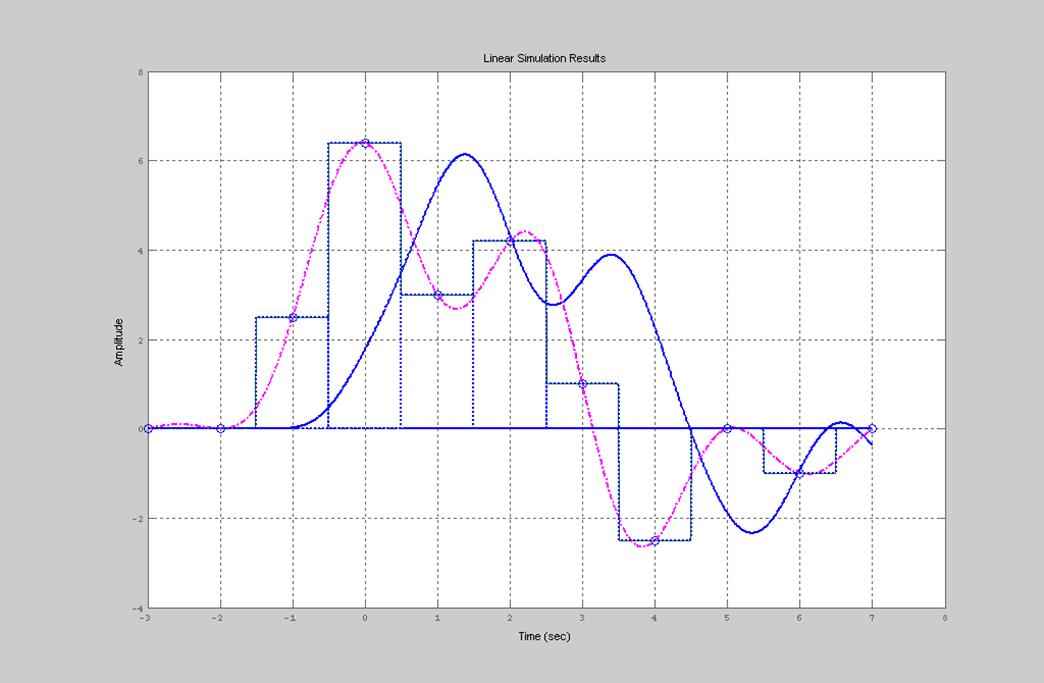 Проиллюстрируем процесс кодирования при помощи простейшего примера.Пусть разрядность натурального двоичного кода m = 4. Тогда образующий полином примет вид:
Проиллюстрируем процесс кодирования при помощи простейшего примера.Пусть разрядность натурального двоичного кода m = 4. Тогда образующий полином примет вид:
при этом lМАКС = 24 — 1 = 15, l? = 16, т.е. при помощи 4-х разрядной кодовой комбинации можно закодировать не более 16 «разрешенных» уровней с номерами от 0 до 15. Предположим, что номер «разрешенного» уровня li = 11, тогда двоичная комбинация в натуральном коде будет иметь вид:
При помощи симметричного двоичного кода первым символом кодовой комбинации кодируется знак отсчета:
li = +11=> 11011
li = -11=> 01011
В современных ЦСП с ИКМ операции квантования по уровню и кодирование на передаче реализуются в одном устройстве, называемом кодером: на его вход подается сигнал с АИМ-2, на выходе формируется цифровой двоичный сигнал с ИКМ. На приеме осуществляется обратное преобразование при помощи декодера. В общем случае двоичные коды по времени их появления разделяются на параллельные, если сигналы кодовой группы появляются одновременно, и последовательные, если сигналы кодовой группы появляются последовательно во времени, разряд за разрядом.
В общем случае двоичные коды по времени их появления разделяются на параллельные, если сигналы кодовой группы появляются одновременно, и последовательные, если сигналы кодовой группы появляются последовательно во времени, разряд за разрядом.
Выводы по разделу
Операция кодирования заключается в преобразовании номера «разрешённого» уровня в кодовую комбинацию двоичной системы счисления, состоящую из m символов вида «0» и «1», где величина m называется разрядностью кода. В ЦСП с ИКМ нашли применение натуральный двоичный код и его модификация — симметричный двоичный код.Двоичные коды по времени их появления разделяются на параллельные, если сигналы кодовой группы появляются одновременно, и последовательные, если сигналы кодовой группы появляются последовательно во времени, разряд за разрядом.
3.4 Амплитудные характеристики канала ЦСП с ИКМ
Амплитудные характеристики каналов, показывающие зависимость изменения UВЫХот UВХ,или
в нормированных единицах, а ЦСП с ИКМ бывают двух типов:
- с равномерной (линейной) шкалой квантования;
- с
неравномерной (нелинейной) шкалой квантования.

При линейном
квантовании как показано на рисунке 3.7 шаг квантования в зоне квантования
одинаков во всем рабочем динамическом диапазоне изменения входного сигнала
от UВХ МИН до UВХ МАКС, а амплитуда шума квантования
не превышает половины шага квантования:
При превышении UВХ некоторого UВХ МАКС, наступает режим ограничения:
, где lМАКС = 2 m — 1, определяется разрядностью кода m и при использовании кодов конечной разрядности, любой входной сигнал UВХ > UВХ МАКС будет передаваться в канале в виде сигнала UВЫХ = UВЫХ МАКС; при этом возникают шумы ограничения, величина которых значительно превышает шумы квантования: РШ ОГР > РШ КВ.
Рисунок
3. 7 — Линейное квантование
по уровню:
7 — Линейное квантование
по уровню:
а) амплитудная характеристика; б) шумы квантования.
Мощность шума квантования при равномерной шкале квантования является величиной постоянной:
PШ КВ=2/12 . При
динамическом диапазоне телефонного сигнала равном 40 дБ:
где PМАКСтф 0
Дб PМИНтф= -40 Дб норма на величину защищенности
от шумов квантования, равная АЗ Ш КВ доп =
10 lg
RШ КВ доп= 33 35 дБ (см. формулу 3.6), должна выполняться для всего динамического
диапазона ТФ сигнала.То есть
АЗ Ш КВ доп оказывается большей, чем величина АЗ Ш КВ МИН = РМИН ТФ — РШ
КВ = 35 дБ во всем динамическом
диапазоне ТФ сигнала, как показано на рисунке 3.8.Разрядность
кодовой комбинации,
при которой выполняется норма наАЗ Ш КВ доп можно определить из выражения (3. 6):
6):
Рисунок 3.8 — Защищенность от шумов квантования при линейном квантовании.
Пик-фактор Q речевого сигнала равен величине Q = 14 17 дБ, однако в каналах ЦСП с ИКМ передаются ТФ сигналы абонентской телефонной сети, причем для наиболее удаленных абонентов Q = 30 35
дБ, как показано на рисунке 3.8.Если требуется обеспечить защищенность от шумов квантования во всем динамическом диапазоне сигнала не менее, чем АЗ Ш КВ доп = 35 дБ, то потребуется m = 11 (из формулы 3.7), а с учетом двухполярного кодирования m = 12. При этом защищенность для сигналов с максимальной амплитудой (PМАКСтф) будет на 40 дБ превышать допустимое значение защищенности АЗ Ш КВ доп = 35 дБ.Большое число разрядов в коде (m = 12) при равномерном квантовании приводит к усложнению аппаратуры ЦСП с ИКМ и неоправданному увеличению частоты передачи кодовых импульсных комбинаций (тактовой частоты в канале).Устранить указанный существенный недостаток можно, осуществляя неравномерное (нелинейное) квантование, которое используется в современных ЦСП.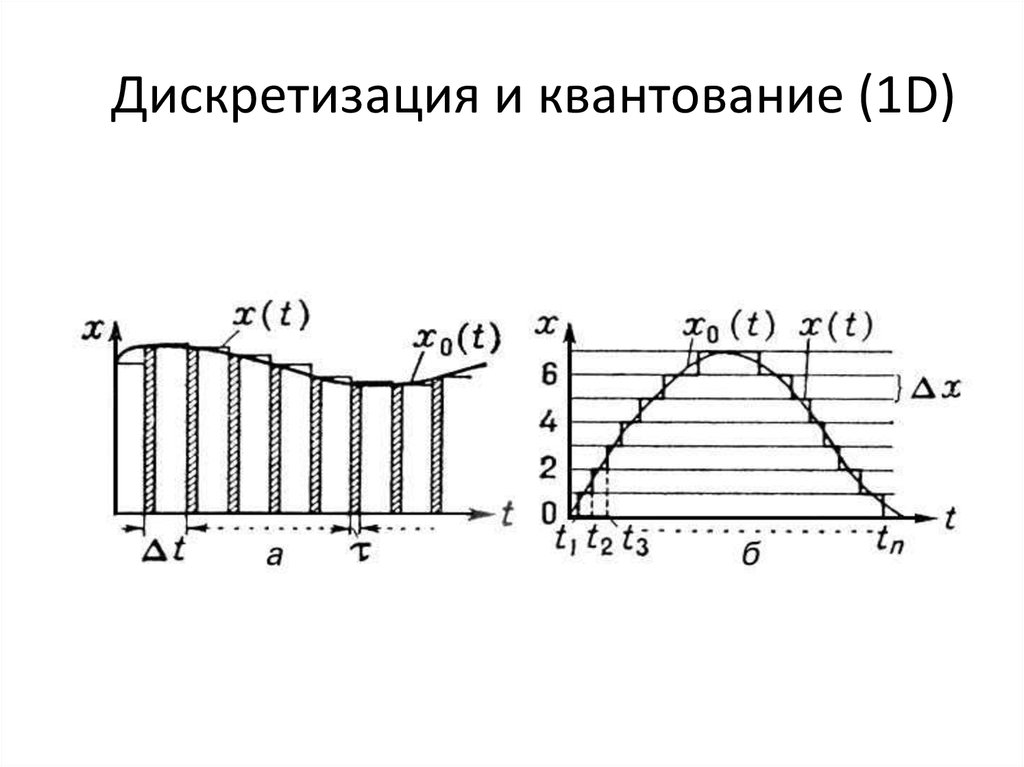 Сущность неравномерного квантования заключается в следующем. Для малых по амплитуде ТФ сигналов шаг квантования выбирается минимальным и постепенно увеличивается, достигая максимальных значений для больших по амплитуде ТФ сигналов, как показано на рисунке 3.9.При
этом РШ КВ возрастает с увеличение шага квантования для больших по мощности ТФ
сигналов, однако их отношение
Сущность неравномерного квантования заключается в следующем. Для малых по амплитуде ТФ сигналов шаг квантования выбирается минимальным и постепенно увеличивается, достигая максимальных значений для больших по амплитуде ТФ сигналов, как показано на рисунке 3.9.При
этом РШ КВ возрастает с увеличение шага квантования для больших по мощности ТФ
сигналов, однако их отношение
АЗ Ш КВ = 10 lg RШ КВ АЗ Ш КВ доп 35 дБ, как показано на рисунке 3.10.
Рисунок
3.9 — Нелинейное квантование по уровню:
а) амплитудная характеристика; б) шумы квантования.
При нелинейном квантовании общее число уровней квантования уменьшается по сравнению с линейным в том же динамическом диапазоне сигнала (рисунки 3. 7 и 3.9). В результате удается снизить разрядность кодовой канальной комбинации до m = 8 (l = 2 8 = 256). Во всех современных ЦСП с ИКМ (как PDH, так и SDH) канальные кодовые комбинации при передачи речи формируются при помощи нелинейного восьмиразрядного кодирования.
7 и 3.9). В результате удается снизить разрядность кодовой канальной комбинации до m = 8 (l = 2 8 = 256). Во всех современных ЦСП с ИКМ (как PDH, так и SDH) канальные кодовые комбинации при передачи речи формируются при помощи нелинейного восьмиразрядного кодирования.
Рисунок
3.10 — Защищенность от шумов квантования при нелинейном кодировании.
Эффект неравномерного квантования может быть получен путем сжатия динамического диапазона сигнала с последующим равномерным квантованием и обратным преобразованием на приеме при помощи системы компандирования, по алгоритму приведенному в разделе 3.2 (рисунок 3.5). Этот способ применялся в ЦСП с ИКМ первых выпусков (60 70-ые годы XX века).В настоящее время нелинейное кодирование осуществляется путем реализации логарифмической амплитудной характеристики, когда передается не эффективное напряжение ТФ сигнала, а его логарифмическое значение, что эквивалентно сжатию динамического диапазона. Используются две логарифмические характеристики типа А и (, которые удобно изображать и описывать в нормированном виде у = f (х), где
Используются две логарифмические характеристики типа А и (, которые удобно изображать и описывать в нормированном виде у = f (х), где
где А = 87,6 и = 255.
Процесс логарифмирования (сжатия (компрессии) динамического диапазона) и кодирования, а также обратная операция декодирования и расширения (экпандирования), реализуется в цифровом виде в нелинейных кодерах и декодерах (кодеки), алгоритмы работы которых и схемная реализация в данном разделе не рассматриваются.Характеристика компандирования типа А используется в ЦСП с ИКМ соответствующих европейской иерархии, а типа — в ЦСП с ИКМ, соответствующих совероамериканской иерархии.
Выводы по разделу
Амплитудные характеристики каналов бывают двух типов:
- С равномерной (линейной) шкалой квантования;
- С неравномерной (нелинейной) шкалой квантования.
При линейном квантовании шаг квантования в зоне квантования одинаков во всём рабочем динамическом диапазоне, а амплитуда шума квантования не превышает половины шага квантования.
Мощность шума квантования является величиной постоянной.
Большое число разрядов в коде (m =12) при равномерном квантовании приводит к усложнению аппаратуры ЦСП с ИКМ и неоправданному увеличению частоты передачи кодовых импульсных комбинаций.
Устранить этот недостаток можно, осуществляя неравномерное квантование, которое используется в современных ЦСП.
Сущность неравномерного квантования:
Для малых по амплитуде ТФ сигналов шаг квантования выбирается минимальным и постепенно увеличивается, достигая максимальных значений для больших по амплитуде ТФ сигналов.
При нелинейном квантовании общее число уровней квантования уменьшается по сравнению с линейным в том же динамическом диапазоне сигнала, в результате удаётся снизить разрядность кодовой канальной комбинации до m = 8.
Контрольные вопросы
- В чём суть кодирования квантованного по уровню сигнала?
- Какие существуют типы кодов?
- 3.
 Суть
операции квантования?
Суть
операции квантования? - Что такое уровень и шаг квантования?
- Что такое ошибка квантования, ошибка ограничения?
- Что такое защищённость и для чего ею пользуются?
- Сущность теоремы Котельникова?
- Что такое АИМ-1 и АИМ-2, как они получаются?
- Какой спектр имеют сигналы АИМ-1 и АИМ-2?
- Нарисовать различные типы амплитудных характеристик, указать достоинства и недостатки?
- Что такое неравномерная шкала квантования, необходимость её применения и способы её получения?
- Норма на величину защищённости от шумов квантования?
Примеры решения задач
Пример 1
Определить
относительную полосу расфильтровки, если известен спектр исходного сигнала
0,3 — 4,00 кГц и частота дискретизации FД = 10 кГц.
Решение:
1. Определяем абсолютную полосу расфильтровки:
Определяем абсолютную полосу расфильтровки:
FР = (FД — FМАКС) — FМАКС = FД — 2 FМАКС
FР = 10 — 2 * 4 = 2 кГц.
2. Определяем относительную полосу расфильтровки:
= FР/ f0 = FР / (FД / 2) = 2 / (10 / 2) = 0,4.
Ответ:= 0,4
Пример 2
Закодировать отсчет напряжения сигнала с помощью простого прямого кода, если UАИМ = 45,3 mB; = 1,0 mB; m = 7. Какова ошибка квантования(
Решение:
- Определяем квантованное значение сигнала UКВ= 45 mB.
- Определяем номер уровня квантования:
N = UКВ/, подставляем значения и получим N = 45/1 = 45. - Определяем коэффициенты двоичного кода:
N = 0 * 26 + 1 * 25 + 0 * 24 + 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 следовательно получим ответ: 0101101.
- Определяем ошибку квантования = UАИМ— UКВ = 45,3 45 = 0,3 mB.
Ответ: =0.3 mB, 0101101.
Пример 3
Определить число уровней квантования для минимально допустимого значения АКВ=25 дБ, если Q=35 дБ.
Решение:
- Определяем разрядность кода m = (АКВ + Q — 5.58) / 6 10.
- Определяем число уровней NКВ = 210 = 1024.
Ответ: N = 1024.
Пример 4
Закодировать отчеты напряжения аналогового сигнала с помощью симметричного кода, если UАИМ1 = -24,4 mB, UАИМ2 = 36,2 mB, = 0,5 mB,
m = 8.
Решение:
- 1. Определяем квантованное значение сигнала:
UКВ1 = (24,5 mB, UКВ2 = 36 mB. - 2.
 Определяем номер уровня квантования: N1 = (49, N2 = 72.
Определяем номер уровня квантования: N1 = (49, N2 = 72. - 3. Определяем коэффициенты двоичного кода.
Так как у нас код симметричный, то первый знак будет указывать положительный или отрицательный уровень квантования.
«0» ( отрицательный, а «1» ( положительный уровень.
N1 = 0*26 + 1*25 + 1*24 + 0*23 + 0*22 +0*21 + 1*20, получаем 0.0110001
N2 = 1*26 + 0*25 + 0*24 + 1*23 + 0*22 +0*21 + 0*20, получаем 1.1001000
Ответ: 0.0110001; 1.1001000.
Задачи для тестирования
Задача 1
Определить необходимую разрядность кода для кодирования второго отсчёта с использованием АДИКМ и ИКМ.
Ответ: При использовании ИКМ необходимая разрядность 28, а при использовании АДИКМ разрядность будет составлять 24 .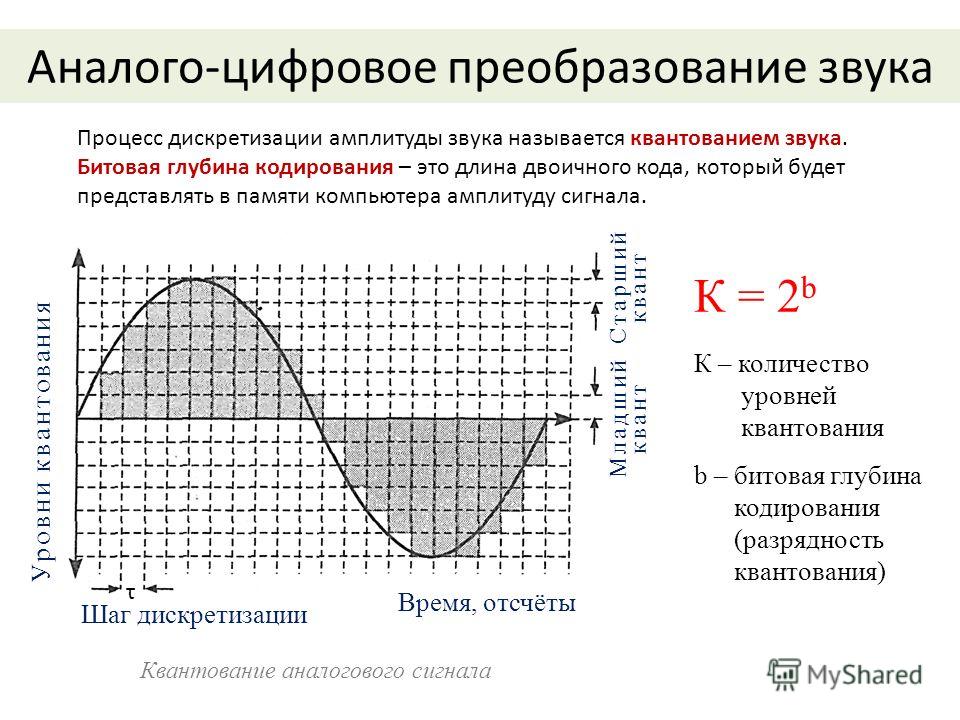
Задача 2
Определите напряжение шума квантования (перегрузки), при ДМ, если ?=0,05.
Ответ: Uпер=0,5.
назад I оглавление I вперед
Page 3 | Теория цифровой обработки видеоизображения | Обработка видео | Софт
Страница 3 из 5
Если потребовать, чтобы в процессе дискретизации не возникало искажений ТВ сигнала с граничной частотой, например, 6 МГц, то частота дискретизации должна быть не меньше 12 Мгц. Однако, чем ближе частота дискретизации к удвоенной граничной частоте сигнала, тем труднее создать фильтр нижних частот, который используется при восстановлении, а также при предварительной фильтрации исходного аналогового сигнала. Это объясняется тем, что при приближении частоты дискретизации к удвоенной граничной частоте дискретизируемого сигнала предъявляются все более жесткие требования к форме частотных характеристик восстанавливающих фильтров — она все точнее должна соответствовать прямоугольной характеристике.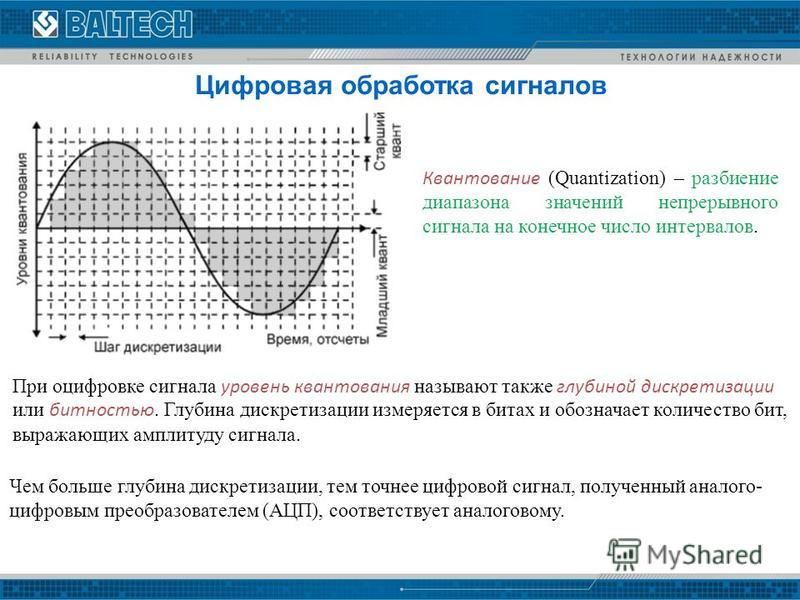 Следует подчеркнуть, что фильтр с прямоугольной характеристикой не может быть реализован физически. Такой фильтр, как показывает теория, должен вносить бесконечно большую задержку в пропускаемый сигнал. Поэтому на практике всегда существует некоторый интервал между удвоенной граничной частотой исходного сигнала и частотой дискретизации.
Следует подчеркнуть, что фильтр с прямоугольной характеристикой не может быть реализован физически. Такой фильтр, как показывает теория, должен вносить бесконечно большую задержку в пропускаемый сигнал. Поэтому на практике всегда существует некоторый интервал между удвоенной граничной частотой исходного сигнала и частотой дискретизации.
Квантование представляет собой замену величины отсчета сигнала ближайшим значением из набора фиксированных величин — уровней квантования. Другими словами, квантование — это округление величины отсчета. Уровни квантования делят весь диапазон возможного изменения значений сигнала на конечное число интервалов — шагов квантования. Расположение уровней квантования обусловлено шкалой квантования. Используются как равномерные, так и неравномерные шкалы. На рис. 3 показаны исходный аналоговый сигнал и его квантованная версия, полученная с использованием равномерной шкалы квантования, а также соответствующие сигналам изображения.
Рис. 3 Аналого-цифровое преобразование. Квантование.
3 Аналого-цифровое преобразование. Квантование.
Искажения сигнала, возникающие в процессе квантования, называют шумом квантования. При инструментальной оценке шума вычисляют разность между исходным сигналом и его квантованной копией, а в качестве объективных показателей шума принимают, например, среднеквадратичное значение этой разности. Временная диаграмма и изображение шума квантования также показаны на рис. 3 (изображение шума квантования показано на сером фоне). В отличие от флуктуационных шумов шум квантования коррелирован с сигналом, поэтому шум квантования не может быть устранен последующей фильтрацией. Шум квантования убывает с увеличением числа уровней квантования.
Рис.4, 5. Квантование.
На рис. 4 показаны изображение, квантованное на 4 уровня, и соответствующий такому числу уровней шум квантования, в котором нетрудно разглядеть сюжет исходного изображения. Изображение, показанное на рис. 5, получено с использованием 128 уровней. При таком уже сравнительно большом числе уровней шум квантования похож на обычный флуктуационный шум. Размах шума упал, поэтому пришлось при получении картинки шума квантования увеличить этот размах в 128 раз, чтобы шум был заметен. Еще несколько лет назад вполне достаточным казалось использовать 256 уровней для квантования телевизионного видеосигнала. Сейчас считается нормой квантовать видеосигнал на 1024 уровня. Число уровней квантования при формировании цифрового звукового сигнала намного больше: от десятков тысяч до миллионов.
При таком уже сравнительно большом числе уровней шум квантования похож на обычный флуктуационный шум. Размах шума упал, поэтому пришлось при получении картинки шума квантования увеличить этот размах в 128 раз, чтобы шум был заметен. Еще несколько лет назад вполне достаточным казалось использовать 256 уровней для квантования телевизионного видеосигнала. Сейчас считается нормой квантовать видеосигнал на 1024 уровня. Число уровней квантования при формировании цифрового звукового сигнала намного больше: от десятков тысяч до миллионов.
Цифровое кодирование.Квантованный сигнал, в отличие от исходного аналогового, может принимать только конечное число значений. Это позволяет представить его в пределах каждого интервала дискретизации числом, равным порядковому номеру уровня квантования. В свою очередь это число можно выразить комбинацией некоторых знаков или символов. Совокупность знаков (символов) и система правил, при помощи которых данные представляются в виде набора символов, называют кодом.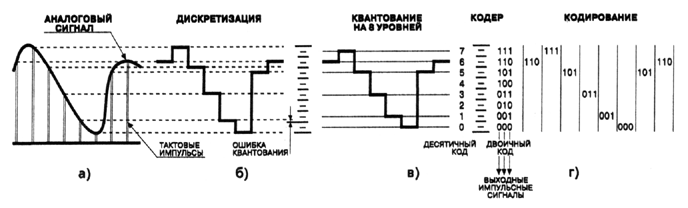 Конечная последовательность кодовых символов называется кодовым словом. Квантованный сигнал можно преобразовать в последовательность кодовых слов. Эта операция и называется кодированием. Каждое кодовое слово передается в пределах одного интервала дискретизации. Для кодирования сигналов звука и изображения широко применяют двоичный код. Если квантованный сигнал может принимать N значений, то число двоичных символов в каждом кодовом слове n >= log2N. Один разряд, или символ слова, представленного в двоичном коде, называют битом. Обычно число уровней квантования равно целой степени числа 2, т.е. N = 2n.
Конечная последовательность кодовых символов называется кодовым словом. Квантованный сигнал можно преобразовать в последовательность кодовых слов. Эта операция и называется кодированием. Каждое кодовое слово передается в пределах одного интервала дискретизации. Для кодирования сигналов звука и изображения широко применяют двоичный код. Если квантованный сигнал может принимать N значений, то число двоичных символов в каждом кодовом слове n >= log2N. Один разряд, или символ слова, представленного в двоичном коде, называют битом. Обычно число уровней квантования равно целой степени числа 2, т.е. N = 2n.
Рис.6 Аналого-цифровое преобразование.
Кодовые слова можно передавать в параллельной или последовательной формах (рис. 6). Для передачи в параллельной форме надо использовать n линий связи (в примере, показанном на рисунке, n = 4). Символы кодового слова одновременно передаются по линиям в пределах интервала дискретизации. Для передачи в последовательной форме интервал дискретизации надо разделить на n подинтервалов — тактов.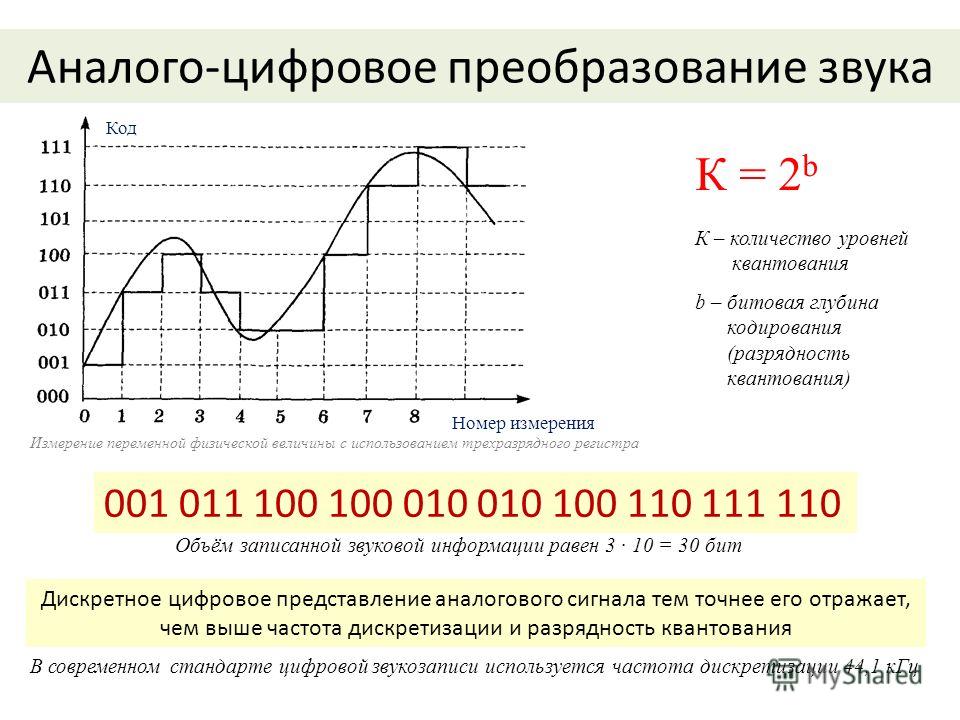 В этом случае символы слова передаются последовательно по одной линии, причем на передачу одного символа слова отводится один такт. Каждый символ слова передается с помощью одного или нескольких дискретных сигналов — импульсов. Преобразование аналогового сигнала в последовательность кодовых слов поэтому часто называют импульсно-кодовой модуляцией. Форма представления слов определенными сигналами определяется форматом кода. Можно, например, устанавливать в пределах такта высокий уровень сигнала, если в данном такте передается двоичный символ 1, и низкий — если передается двоичный символ 0 (такой способ представления, показанный на рис. 6, называют форматом БВН — Без Возвращения к Нулю). В примере рис. 6 используются 4-разрядные двоичные слова (это позволяет иметь 16 уровней квантования). В параллельном цифровом потоке по каждой линии в пределах интервала дискретизации передается 1 бит 4-разрядного слова. В последовательном потоке интервал дискретизации делится на 4 такта, в которых передаются (начиная со старшего) биты 4-разрядного слова.
В этом случае символы слова передаются последовательно по одной линии, причем на передачу одного символа слова отводится один такт. Каждый символ слова передается с помощью одного или нескольких дискретных сигналов — импульсов. Преобразование аналогового сигнала в последовательность кодовых слов поэтому часто называют импульсно-кодовой модуляцией. Форма представления слов определенными сигналами определяется форматом кода. Можно, например, устанавливать в пределах такта высокий уровень сигнала, если в данном такте передается двоичный символ 1, и низкий — если передается двоичный символ 0 (такой способ представления, показанный на рис. 6, называют форматом БВН — Без Возвращения к Нулю). В примере рис. 6 используются 4-разрядные двоичные слова (это позволяет иметь 16 уровней квантования). В параллельном цифровом потоке по каждой линии в пределах интервала дискретизации передается 1 бит 4-разрядного слова. В последовательном потоке интервал дискретизации делится на 4 такта, в которых передаются (начиная со старшего) биты 4-разрядного слова.
Операции, связанные с преобразованием аналогового сигнала в цифровую форму (дискретизация, квантование и кодирование), выполняются одним устройством — аналого-цифровым преобразователем (АЦП). Сейчас АЦП может быть просто интегральной микросхемой. Обратная процедура, т.е. восстановление аналогового сигнала из последовательности кодовых слов, производится в цифро-аналоговом преобразователе (ЦАП). Сейчас существуют технические возможности для реализации всех обработок сигналов звука и изображения, включая запись и излучение в эфир, в цифровой форме. Однако в качестве датчиков сигнала (например, микрофон, передающая ТВ трубка или прибор с зарядовой связью) и устройств воспроизведения звука и изображения (например, громкоговоритель, кинескоп) пока используются аналоговые устройства. Поэтому аналого-цифровые и цифро-аналоговые преобразователи являются неотъемлемой частью цифровых систем.
Цифровые сигналы можно описывать с помощью параметров, типичных для аналоговой техники, например таких, как полоса частот. Но их применимость в цифровой технике является ограниченной. Важным показателем, характеризующим цифровой поток, является скорость передачи данных. Если длина слова равна n, а частота дискретизации FD, то скорость передачи данных, выраженная в числе двоичных символов в единицу времени (бит/с), находится как произведение длины слова на частоту дискретизации: C = nFD .
Но их применимость в цифровой технике является ограниченной. Важным показателем, характеризующим цифровой поток, является скорость передачи данных. Если длина слова равна n, а частота дискретизации FD, то скорость передачи данных, выраженная в числе двоичных символов в единицу времени (бит/с), находится как произведение длины слова на частоту дискретизации: C = nFD .
7. Цифровое представление компонентного видеосигнала.
Компонентный телевизионный видеосигнал может быть представлен в цифровой форме в соответствии с Рекомендацией ITU-R 601. Эта рекомендация устанавливает правила раздельной дискретизации, квантования и кодирования сигнала яркости Y и двух цветоразностных сигналов R-Y (Cr) и B-Y (Cb). Частота дискретизации для яркостного сигнала Y установлена равной 13,5 МГц, для цветоразностных сигналов — 6,75 МГц, т.е. частота дискретизации яркостного сигнала в 2 раза больше частоты дискретизации цветоразностных сигналов. Если взять, как принято, в качестве условной (базовой для иерархии цифровых стандартов) единицы частоту 3,375 МГц, то частоты дискретизации яркостного и двух цветоразностных сигналов будут находиться в соотношении 4:2:2, которое и дает часто используемое название стандарта.
Рис.7 Кодирование компонентного видеосигнала (4:2:2).
При таких значениях частот дискретизации можно практически преобразовать без искажений в цифровую форму сигнал яркости в полосе до 5,75 МГц, а цветоразностные сигналы — в полосе до 2,75 МГц (надо помнить о запасном интервале между граничной частотой сигнала и половиной частоты дискретизации). Стандарт 4:2:2 используется в качестве базового при оценке других вариантов дискретизации, и на значение 5,75 МГц часто ссылаются как на границу полной полосы ТВ сигнала. Рис. 7 показывает дискретизацию компонентного телевизионного сигнала на примере сигнала цветных полос. Длина кодового слова — 10 двоичных разрядов — битов (в первоначальном варианте — 8 битов), что позволяет перенумеровать 1024 уровня квантования. Однако числа 0..3 и 1020..1023 резервируются для цифровых синхронизирующих сигналов. Для квантования яркостного сигнала выделяется 877 уровней (значение черного в видеосигнале соответствует уровню квантования 64, а номинальное значение белого — уровню 940). Для квантования цветоразностных сигналов выделяется 897 уровней, причем нулевому значению аналогового сигнала соответствует уровень квантования 512.Кодированию подлежат гамма-корректированные сигналы. Приведенные диапазоны уровней квантования часто используются при сравнении с другими вариантами квантования. В этом случае на них часто ссылаются как на показатели динамического диапазона или полного разрешения по уровню сигнала, поскольку число уровней квантования определяет шум квантования и, соответственно, динамический диапазон. В этом же смысле иногда говорят о 10-битном разрешении.
Для квантования цветоразностных сигналов выделяется 897 уровней, причем нулевому значению аналогового сигнала соответствует уровень квантования 512.Кодированию подлежат гамма-корректированные сигналы. Приведенные диапазоны уровней квантования часто используются при сравнении с другими вариантами квантования. В этом случае на них часто ссылаются как на показатели динамического диапазона или полного разрешения по уровню сигнала, поскольку число уровней квантования определяет шум квантования и, соответственно, динамический диапазон. В этом же смысле иногда говорят о 10-битном разрешении.
Рис.8 Кодирование компонентного видеосигнала (4:2:2). Структура дискретизации.
Частоты дискретизации представляют гармоники строчной частоты, что обеспечивает неподвижную ортогональную структуру отсчетов ТВ изображения (рис. 8). Величинам 13,5 и 6,75 МГц кратна, как частота строчной развертки стандарта телевизионного разложения 625/50, так и частота развертки стандарта 525/60.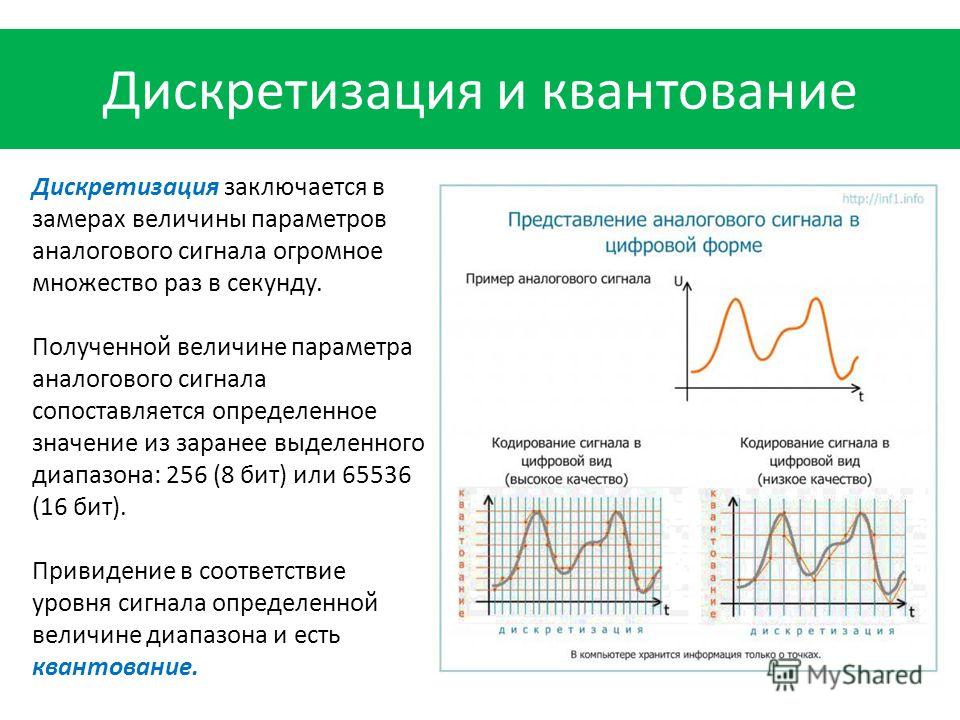 Собственно, выбор в качестве базовой именно частоты 3,375 МГц во многом связан с соображениями кратности с частотами строчной развертки двух мировых стандартов разложения. Это важно потому, что позволило ввести единый мировой стандарт цифрового кодирования компонентного видеосигнала, при котором в активной части строки содержится 720 отсчетов яркостного сигнала и по 360 — каждого цветоразностного. Различие в системах 625/50 и 525/60 заключается в разном числе строк и несколько отличающейся длительности интервала гашения. Полная скорость передачи цифрового компонентного видеосигнала составляет 10 х 13,5 + 10 х 6,75 + 10 х 6,75 = 270 Мбит/с.
Собственно, выбор в качестве базовой именно частоты 3,375 МГц во многом связан с соображениями кратности с частотами строчной развертки двух мировых стандартов разложения. Это важно потому, что позволило ввести единый мировой стандарт цифрового кодирования компонентного видеосигнала, при котором в активной части строки содержится 720 отсчетов яркостного сигнала и по 360 — каждого цветоразностного. Различие в системах 625/50 и 525/60 заключается в разном числе строк и несколько отличающейся длительности интервала гашения. Полная скорость передачи цифрового компонентного видеосигнала составляет 10 х 13,5 + 10 х 6,75 + 10 х 6,75 = 270 Мбит/с.
Рис.9 Кодирование компонентного видеосигнала (4:4:4).
- Назад
- Вперед
Количество — уровни — квантование
Cтраница 1
Количество уровней квантования определяется необходимой точностью вычисления гистограммы распределения. [1]
Количество уровней квантования 2, определяемое характеристикой АЦП, задает количество уровней анализа, а шаг квантования — ширину дифференциально го коридора.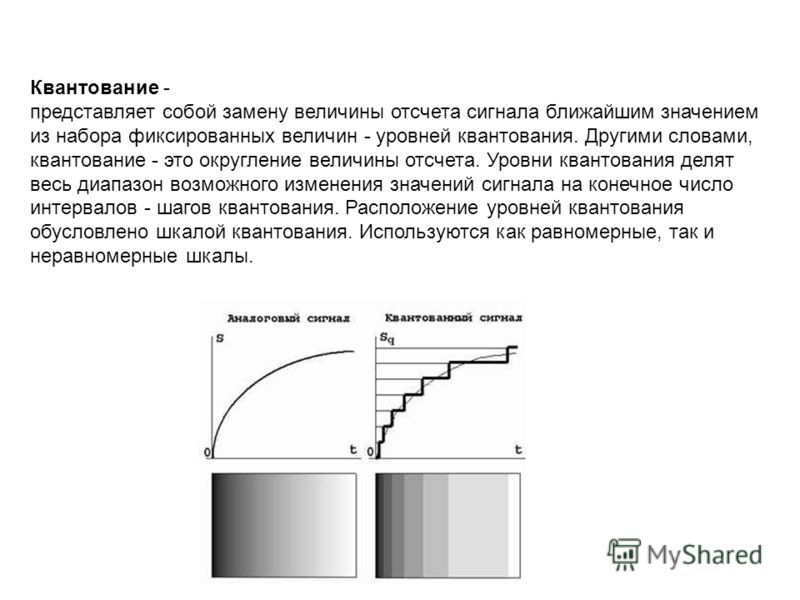 Если выполняется условие 7ь т9ь ь то это означает, что значение напряжения реализации х ( 1Т0) относится к &-му дифференциальному коридору, а в ячейке памяти, адрес которой соответствует номеру k, записывается единица. После истечения N выборок в п ячейках памяти накоплены числа, представляющие собой частости. По этим данным микропроцессор вычисляет значения плотности распределения вероятностей. Результаты вычислений отображаются дисплеем в цифровой форме или в виде графика.
[2]
Если выполняется условие 7ь т9ь ь то это означает, что значение напряжения реализации х ( 1Т0) относится к &-му дифференциальному коридору, а в ячейке памяти, адрес которой соответствует номеру k, записывается единица. После истечения N выборок в п ячейках памяти накоплены числа, представляющие собой частости. По этим данным микропроцессор вычисляет значения плотности распределения вероятностей. Результаты вычислений отображаются дисплеем в цифровой форме или в виде графика.
[2]
Количество уровней квантования определяем по табл. 4.1. Оно равно восьми. [3]
| Релейно-кон-тактный делитель напряжения. а — принципиальная схема. 6 — эквивалентная схема. [4] |
Погрешность рассматриваемого преобразователя определяется погрешностью дискретности, зависящей от количества уровней квантования, точностью подгонки сопротивлений компенсационной схемы, точностью установки рабочего тока / и его стабильностью во времени, а также чувствительностью и стабильностью нуль-органа. [5]
[5]
Как выбираются в системах И КМ период дискретизации и количество уровней квантования аналоговых сигналов. [6]
Этот параметр может также быть не вектором, а числом, в таком случае он задает лишь количество уровней квантования, а начальное приближение выбирается автоматически. [7]
Самый простой способ сокращения объема информации при оцифровке JNVKJ очевиден — нужно изменить параметры оцифровки, уменьшив частоту дискретизации и / или количество уровней квантования сигнала. Хот этот способ и самый прости, но он приводит к заметному ухудшению качеетна записанного звука. Ухудшение происходит из-за того, что при оцифровке отбрасываемся чаек, информации, которая, таким образом, безвозвратно потеряна. При уменьшении частоты дискретизации, имеющийся в аналоговой части звуковой карты адаптивный ( настраивающийся) фн и. При JTOM частотная характеристика деформируется таким образом, ч го частоты в спектре сигнала, лежащие иыше, чем половина выбранной частоты дискретизации, отбрасываю гея. Кроме того, уменьшение количеств уровней кнантонанпн не позволяет точно передать значение амплитуды. Все это приводит к тому, что при воспроизведении невозможно нос ста попить сигнал, лосшшчно полно лоиторяюшнн исходный, В приводимой ниже таблице показано, как влияют на качество зиука параметры оцифровки сигнала.
[8]
Кроме того, уменьшение количеств уровней кнантонанпн не позволяет точно передать значение амплитуды. Все это приводит к тому, что при воспроизведении невозможно нос ста попить сигнал, лосшшчно полно лоиторяюшнн исходный, В приводимой ниже таблице показано, как влияют на качество зиука параметры оцифровки сигнала.
[8]
Приведенные зависимости позволяют сделать вывод, что при указанных условиях преобразование измерительной информации с погрешностью, не превосходящй по абсолютной величине, например 1 %, в общем случае с наименьшими аппаратурными затратами обеспечивает вычислительная подсистема, в которой количество уровней квантования величин rmax. [9]
| Кодово-импульсная модуляция.. [10] |
Цифровая форма передачи информации, обусловливает характерную особенность систем с кодово-импульсной модуляцией: передаваемая величина квантуется не только по времени, но и амплитуде. Количество уровней квантования ( рис. 11.8) выбирается в соответствии с требуемой точностью воспроизведения данных. Каждому уровню квантования присваивается свое число.
[11]
Количество уровней квантования ( рис. 11.8) выбирается в соответствии с требуемой точностью воспроизведения данных. Каждому уровню квантования присваивается свое число.
[11]
Реальный сеанс связи длится время Г, в течение которого передается п слов. Используя весь массив полученной информации, получатель принимает некоторое практическое решение. Для данной задачи можно определить элементарный сеанс или как прием одного символа-при этом ансамбль сообщений ( и оценок) содержит два элемента, или как прием слова — ансамбль сообщений состоит из т элементов ( т — количество уровней квантования), или как прием блока, состоящего из k слов — ансамбль сообщений включает mk возможных комбинаций. В принципе возможен случай, когда число k равно п, при этом элементарный сеанс будет соответствовать реальному сеансу, а множество сообщений имеет т элементов. [12]
Основным преимуществом цифровых систем является наличие порогового эффекта. До тех пор пока отношение сигнал / шум на выходе приемника превышает некоторое значение, помехи и искажения радиосигнала в линии и аппаратуре системы практически не приводят к искажению принимаемого сообщения. Эти значения легко разделяются на приемной стороне. Поэтому точность цифровой передачи в основном определяется количеством уровней квантования непрерывного сообщения при его кодировании.
[13]
До тех пор пока отношение сигнал / шум на выходе приемника превышает некоторое значение, помехи и искажения радиосигнала в линии и аппаратуре системы практически не приводят к искажению принимаемого сообщения. Эти значения легко разделяются на приемной стороне. Поэтому точность цифровой передачи в основном определяется количеством уровней квантования непрерывного сообщения при его кодировании.
[13]
Страницы: 1
Что такое квантование и сэмплирование? Типы квантования
Содержание
Что такое квантование?Квантование — это процесс преобразования непрерывного амплитудного (аналогового) сигнала в дискретный амплитудный (цифровой) сигнал.
Аналоговый сигнал квантуется на счетные и дискретные уровни, известные как уровней квантования . Каждый из этих уровней представляет фиксированную входную амплитуду.
Во время квантования входная амплитуда округляется до ближайшего уровня квантования. Это округление известно как ошибка квантования . Ошибку квантования можно уменьшить, увеличив количество уровней квантования.
Это округление известно как ошибка квантования . Ошибку квантования можно уменьшить, увеличив количество уровней квантования.
Связанная запись: Что такое GSM и как он работает?
Пример квантованияНа рисунке ниже представлен аналоговый сигнал. Во время квантования амплитуда аналогового сигнала дискретизируется и дискретизируется до фиксированных уровней квантования.
В этом примере мы использовали 8 уровней квантования. Квантование приводит к потере информации . Пространство между двумя соседними уровнями известно как размер шага .
Размер шага = V ref /количество уровней.
V ref представляет максимальную амплитуду представленного.
Если размер шага большой, то ошибка квантования будет высокой. Другими словами, чем больше размер шага, тем больше потеря информации.
- Запись по теме: Что такое WiMAX? Разница между широкополосным WiMax и WiFi
Существует два типа квантования.
Равномерное квантованиеТип квантования, в котором уровни квантования равномерно разнесены , известен как равномерное квантование . При равномерном квантовании каждый размер шага представляет постоянных величин аналоговой амплитуды. он остается постоянным на протяжении всего сигнала.
Ниже приведен пример равномерного квантования .
В этом примере интервал между любыми двумя соседними шагами или уровнями соответствует амплитуде в 1 вольт.
Неравномерное квантование Тип квантования, в котором пространство между уровнями квантования является неравномерным и имеет логарифмическое отношение, называется неравномерным квантованием.
- Запись по теме: Знакомство с сигналами, типами, свойствами, работой и применением
В неравномерном квантовании аналоговый сигнал сначала проходит через компрессор . Компрессор применяет логарифмическую функцию к входному сигналу. Входной сигнал имеет большую разницу между низкой и высокой амплитудой. В выходном сигнале низкие амплитуды усиливаются, а высокие уровни амплитуды ослабляются, таким образом создавая сжатый сигнал.
Допустим, амплитуда входного сигнала м &m p — пиковая амплитуда сигнала. Y — выходной сигнал. Тогда график сжатия выглядит так:
Как видно из графика, малые входные уровни Δm отображаются на большие выходные уровни Δy . И более высокие входные уровни отображаются на меньшие выходные уровни.
- Запись по теме: Что такое промышленные коммуникационные сети? Обзор
Есть два закона сжатия
μ-закон μ закон — это алгоритм сжатия, используемый для неравномерного квантования . Выражением закона μ является и m — входная амплитуда и m p — пиковая амплитуда входного сигнала.
Выражением закона μ является и m — входная амплитуда и m p — пиковая амплитуда входного сигнала.
Когда μ=0 , тогда сжатия нет и квантование становится униформа . Характеристический график для μ Law приведен ниже:
Этот график показывает, что если параметр сжатия μ выше, то входной сигнал сжимается сильнее.
- Запись по теме: Интернет вещей (IOT) и его приложения в электроэнергетике
A-Law — еще один алгоритм сжатия аналогового сигнала для неравномерного квантования. Выражение для A-law :
Где A — параметр сжатия. Когда A=1 , тогда квантование равно однородному , потому что нет сжатия. График характеристик приведен ниже.
Оба закона применимы с некоторыми компромиссами.
- Запись по теме: Что такое система нечеткой логики — работа, примеры, преимущества и приложения
Отбор проб является важным этапом аналого-цифрового преобразования . Сбор или захват выборок входной аналоговой амплитуды называется выборкой .
Частота выборкиЧастота выборки — это количество выборок , сделанных в течение одной секунды. измеряется в герц или выборок в секунду . Непрерывно изменяющаяся амплитуда аналогового сигнала также непрерывна во времени. Таким образом, он должен быть выбран с фиксированной скоростью. Эта скорость называется частота дискретизации или частота дискретизации . Пример дискретизации:
Этот сигнал дискретизируется с частотой дискретизации 2 выборки в секунду или 2 Гц .
Частота дискретизации играет важную роль в идеальном преобразовании аналогового сигнала в цифровой и восстановлении аналогового сигнала из цифрового.
Частота дискретизации не должна быть очень низкой или очень высокой. В обоих случаях преобразованный сигнал — это не то, чего мы хотим добиться. Если частота дискретизации низкая, исходный сигнал уничтожается, а если частота дискретизации очень высока, то это экономически невыгодно.
- Связанная статья: Подводные кабели — конструкция, характеристики, прокладка кабелей и соединения
Если аналоговый сигнал дискретизирован на частоте ниже , чем требуемая скорость , то дискретизированный сигнал не будет похож на исходный сигнал. И реконструкция исходного сигнала становится невозможной. Такой случай называется псевдонимом , как показано на рисунке ниже.
В этом примере синусоидальный сигнал дискретизируется с частотой 3/4 его частоты. что значительно ниже требуемой нормы. Восстановленный сигнал (красный сигнал) восстанавливается из образца, который не похож на исходный сигнал.
что значительно ниже требуемой нормы. Восстановленный сигнал (красный сигнал) восстанавливается из образца, который не похож на исходный сигнал.
Частота дискретизации или частота дискретизации должна более чем в два раза превышать частоту входного сигнала. Теорема Найквиста предлагает минимальную частоту дискретизации для сигнала, который может быть идеально восстановлен из его выборок.
Related Posts
- Типы кабелей управления и связи
- Что такое промышленная автоматизация | Типы промышленной автоматизации
- Почему радиоволны выбирают для передачи на близкое расстояние?
- Последовательная связь с помощью Arduino
Показать полную статью
Связанные статьи
Кнопка «Вернуться к началу»
Квантование и шум квантования — DSPIllustrations.com
Квантизатор — это блок обработки сигналов, который преобразует непрерывную амплитуду в дискретную амплитуду. Выход квантователя является дискретным, то есть он может выводить только $Q$ различных значений. На практике квантователь представляет собой аналого-цифровой преобразователь, поскольку он отображает непрерывную входную амплитуду в цифровое представление этого значения. Формально квантованный выходной сигнал $Q[x]$ некоторого входного значения $x$ равен
Выход квантователя является дискретным, то есть он может выводить только $Q$ различных значений. На практике квантователь представляет собой аналого-цифровой преобразователь, поскольку он отображает непрерывную входную амплитуду в цифровое представление этого значения. Формально квантованный выходной сигнал $Q[x]$ некоторого входного значения $x$ равен
$$Q[x] = \arg \min_{l\in\mathcal{S}} |l-x|.$$
Здесь множество $\mathcal{S}$ содержит все возможные выходные значения квантователя, которые мы называем уровней квантования . Что это значит? Это означает, что для заданного входного значения $x$ квантизатор возвращает уровень квантования $l$, ближайший к входному значению. Следовательно, квантователь полностью определяется своим набором уровней квантования $\mathcal{S}$.
Предположим, что квантователь должен уметь квантовать значения между входными амплитудами $-U$ и $+U$, т.е. размах амплитуд равен $2U$. Кроме того, уровни квантования должны быть закодированы $b$ битами.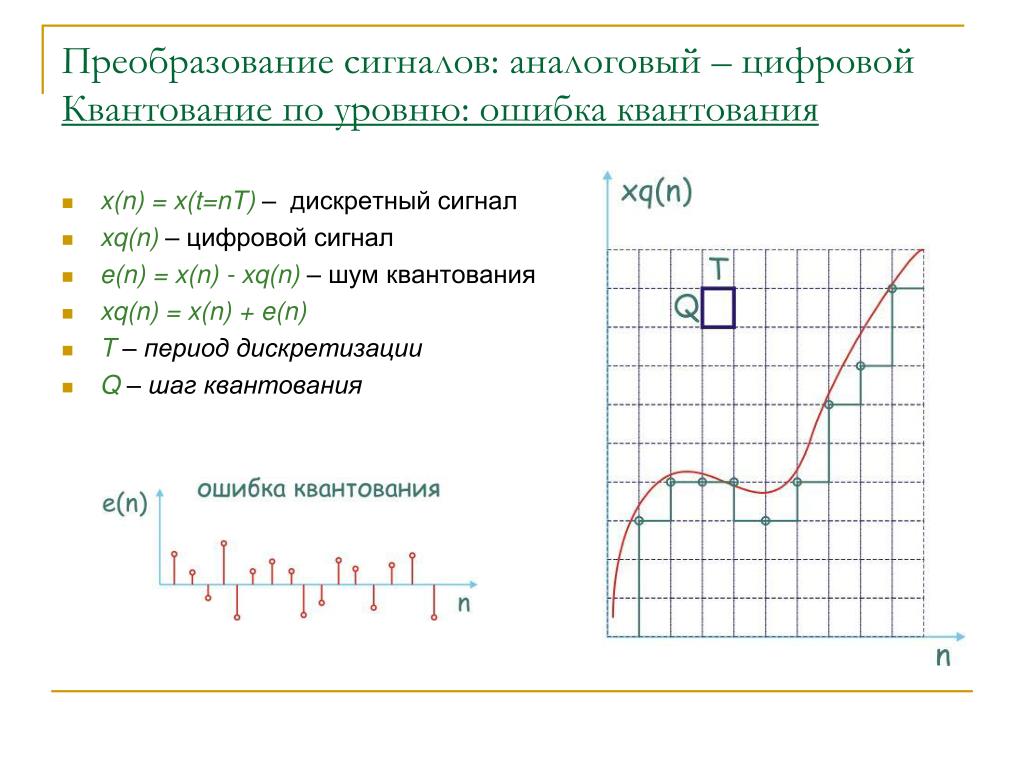 q$ различных уровней квантования в $\mathcal{S}$. Тогда логичным решением будет сделать расстояние $\Delta_s$ между уровнями квантования постоянным, равным
q$ различных уровней квантования в $\mathcal{S}$. Тогда логичным решением будет сделать расстояние $\Delta_s$ между уровнями квантования постоянным, равным
$$\Delta_s = \frac{2U}{q}.$$
Обычно используются два разных квантователя: со средним подъемом и со средним шагом . Они отличаются настройкой своих уровней: для среднего протектора мы имеем $0\in\mathcal{S}$, тогда как для среднего шага квантизатор мы имеем $0\neq\mathcal{S}$, т.е. квантователь среднего шага имеет уровень для нулевого выходного значения. Уровни квантования для обоих квантователей определяются
$$\begin{выравнивание}
\mathcal{S} &= \{-U+\frac{\Delta_s}{2}+\Delta_s\cdot(0,1,2,\dots, q-1)\}&\text{для средней высоты} \\
\mathcal{S} &= \{-U+\Delta_s\cdot(0,1,2,\dots, q-1)\}&\text{ для середины протектора}
\end{выравнивание}$$
9b=q$ — четное число, квантизатор среднего шага ни в коем случае не может быть симметричным.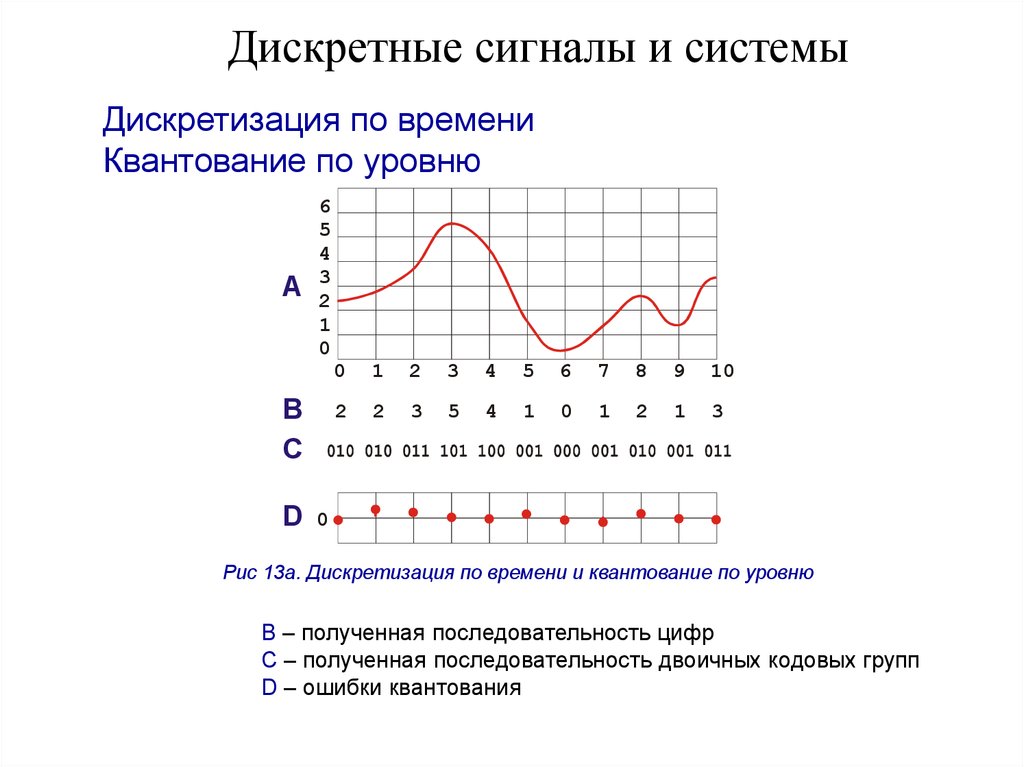 Далее мы сосредоточимся на квантизаторе среднего роста.
Далее мы сосредоточимся на квантизаторе среднего роста.
Операция квантования вносит ошибку, поскольку бесконечное количество различных входных амплитуд отображается на конечный набор дискретных уровней квантования. Ошибка между входом и выходом квантователя называется Шум квантования $n_q(t)$. При обозначении $s(t)$ входного сигнала и $s_q(t)$ выходного сигнала квантователя выполняется следующее соотношение:
$$\begin{выравнивание} s_q(t)&=Q[s(t)]&&\text{Операция квантования}\\ n_q(t)&=s(t)-s_q(t)&&\text{Выражение шума квантования}\\ s_q(t)&=s(t)-n_q(t) \end{align}.$$
Глядя на последнее уравнение, шум квантования действительно можно понимать как шум поверх сигнала с непрерывной амплитудой, отсюда и его название. Давайте создадим синусоидальную волну и пропустим ее через квантователь, и посмотрим на квантованный сигнал и шум квантования.
Сначала определим функцию удобства calcLevels , который вычисляет уровни квантования для данного количества битов b.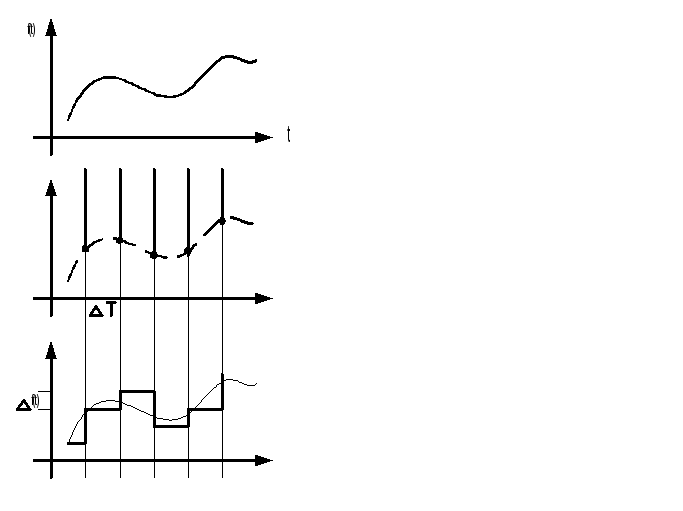
Теперь давайте сгенерируем синусоидальный сигнал и покажем результирующий шум квантования.
Как видите, с увеличением количества битов квантования ошибка квантования практически исчезает. Однако важной мерой является отношение сигнал/шум квантования (SNR), и мы собираемся его измерить. При достаточно большом количестве битов шум квантования примерно равномерно распределяется в пределах $\pm\frac{\Delta_s}{2}$. В литературе, например. Proakis: Digital Signal Processing, было показано, что SNR квантования для синусоидального сигнала с полным возбуждением (т.е. амплитуда синуса равна диапазону квантования) может быть определена как
$$SNR\приблизительно (1,76 + 6,02b)дБ,$$
, где $b$ — количество битов для квантования.
Напишем функцию для измерения этого шума квантования. Здесь мы напрямую конвертируем SNR в шкалу дБ.
Теперь мы можем построить график зависимости шума квантования от количества битов и сравнить его с теоретической кривой $1,76+6,02b$.
Как видим, приближение выполняется очень хорошо. Давайте теперь посмотрим, что происходит, когда мы уменьшаем амплитуду синуса:
Как мы видим, отношение SNR квантования ухудшается при уменьшении амплитуды синуса. Это разумно, так как шум квантования зависит только от количества битов квантования $b$ и, следовательно, не зависит от амплитуды сигнала и, следовательно, от мощности шума квантования. С другой стороны, мощность сигнала уменьшается при уменьшении амплитуды. Следовательно, мы видим деградацию SNR. Однако важным замечанием является то, что улучшение отношения сигнал-шум для каждого дополнительного бита остается на уровне $6$дБ, независимо от амплитуды сигнала.
Давайте теперь измерим SNR квантования для сигнала, который представляет собой просто гауссов шум:
Что здесь происходит? Отношение сигнал-шум квантования довольно низкое, несмотря на 14-битное разрешение? Глядя на исходный и квантованный сигнал, можно обнаружить проблему: квантизатор просто перегружен: входной сигнал выше, чем может вывести квантователь. Таким образом, он никогда не сможет достичь хорошего квантования. Давайте со временем уменьшим амплитуду шума и посмотрим, поможет ли это:
Таким образом, он никогда не сможет достичь хорошего квантования. Давайте со временем уменьшим амплитуду шума и посмотрим, поможет ли это:
Теперь мы видим, что отношение сигнал-шум квантования увеличивается на 6 дБ для каждого бита. Но, глядя на сигналы, мы видим еще одну важную вещь: хотя квантизатор мог бы выводить значения между $\pm 1$, большинство его значений сосредоточены в пределах $\pm 0,1$. Это связано с характером гауссовского шумового сигнала, который в основном концентрируется вокруг $s(t)=0$. Следовательно, для улучшения SNR имеет смысл увеличить разрешение на более низких уровнях квантования за счет более грубой дискретизации на более высоких амплитудах. Этот метод известен как нелинейные квантователи, но здесь он не рассматривается.
Квантование — javatpoint
следующий → ← предыдущая Квантование — это процесс преобразования непрерывного аналогового сигнала в последовательность дискретных значений . Квантизатор — это известное устройство, выполняющее процесс квантования. Сигналы при передаче на большие расстояния страдают от шумов и помех. Чтобы преодолеть это, процесс квантования создает сигнал, равный примерно равно сигналу сообщения . Он выбирает квантованный сигнал m q (t) со значениями, ближайшими к исходному аналоговому сигналу m(t). Процесс квантования выбирает значение и округляет эти значения до ближайшего стабилизированного значения. Квантованный сигнал m q (t) можно легко отделить от аддитивного шума. Рассмотрим пример аналогового сигнала, ограниченного диапазоном от V A до V B , как показано ниже: Квантование создает ряд дискретных значений из аналогового сигнала. Он разделяет аналоговый сигнал на N дискретных наборов. Каждый набор имеет равный размер S, который относится к размеру шага. Это дано: S = (V B — V A )/N Где, S — размер шага В В верхний предел данного аналогового сигнала В А — нижний предел данного аналогового сигнала N — количество наборов, на которые делится диапазон аналогового сигнала Здесь, Н = 8 Уровни квантования указаны в центре каждого шага, как показано ниже: Мы знаем, что квантованные сигналы выбираются для аппроксимации исходных сигналов. Уровни квантования разделены буквой «S», которая представляет собой размер шага. Но расстояние крайнего нижнего и верхнего уровня квантования от их ближайшего уровня составляет всего S/2. Пока мгновенная амплитуда квантованных сигналов меньше S/2, шум на выходе квантователя не появится. Из-за различных компонентов, подключенных к квантователю, таких как повторитель и усилитель, квантованный сигнал с выхода квантователя поступает с удаленным шумом. Вероятность возникновения ошибки квантования очень мала. Типы квантованияСуществует два типа квантования: однородное квантование и неравномерное квантование . Равномерное квантованиеКак следует из названия, уровни квантования в процессе равномерного квантования расположены на одинаковом расстоянии друг от друга. Равномерное квантование дополнительно классифицируется как равномерное квантование со средним подъемом и равномерное квантование со средним протектором. Оба процесса равномерного квантования симметричны относительно соответствующей оси. Униформа средней посадки Quantization Подъем относится к восходящей части. Источник дискретного квантованного сигнала находится в середине восходящей части ступенчатого графика, как показано ниже: Униформа со средним протектором Quantization Протекторотносится к плоской части . Источник дискретного квантованного сигнала находится в середине ступенчатой части ступенчатого графика, как показано ниже: Преимущества равномерного квантованияПреимущества равномерного квантования следующие:
Неравномерное квантованиеУровни квантования в процессе неравномерного квантования расположены неравномерно. Связь между таким квантованием обычно логарифмическая из-за нелинейной природы сигнала. Преимущества неравномерного квантованияПреимущества неравномерного квантования следующие:
Ошибка квантованияРазница во входном значении и квантованном значении сигнала известна как ошибка квантования . Квантованный сигнал (m q (t)) является сигналом аппроксимации сигнала сообщения (m(t)). Разница между сигналом сообщения и квантованным сигналом называется квантованным шумом. Это дано: Q e = m(t) — m q (t) Показывает, что результат процесса квантования или полученный сигнал не является точной копией сигнала сообщения. Ниже показан зашумленный квантованный сигнал: Тот же сигнал с удаленным шумом показан справа от зашумленного сигнала. Ретрансляторы помогают в передаче данных на большие расстояния за счет увеличения мощности сигнала. Мы можем уменьшить затухание квантованного сигнала, уменьшив расстояние между повторителями в канале связи. Найдем среднеквадратичную ошибку квантования, представленную как e 2 , где e — разность напряжений между входным и квантованным значением. Здесь будет использоваться та же концепция разделения сигнала на M уровней квантования. Разница между каждым уровнем известна как размер шага, представленный S, измеряемый в вольтах. е = m(t) — m qv Где, E = разница напряжений m(t) — сигнал входного сообщения m qv — выходной сигнал квантователя Чем выше уровни квантования, тем меньше будет размер шага. Среднеквадратическая ошибка квантования определяется как: e 2 = S 2 /12 Примеры квантованияУстройство, используемое для выполнения процесса квантования, называется квантователем. Давайте обсудим общий пример квантователя. Аналого-цифровой преобразователь аналого-цифровой или аналого-цифровой преобразователь состоит из сэмплер и квантователь . Для 8-битного числа уровней квантования 2 8 = 256 уровней. Для 16-битного числа уровней квантования 2 16 = 65 536 уровней. Для 64-битной системы количество уровней квантования равно 2 64 = 16,8 миллиона уровней. Шум квантования обратно пропорционален количеству уровней квантования. Чем выше уровни квантования, тем меньше будет шум квантования. Преимущества квантованияПреимущества квантования следующие:
Применение квантованияПомимо цифровой связи, процесс квантования также используется в различных областях, таких как обработка сигналов, системы управления, обработка изображений, наука и лингвистика.
КомпандированиеКомпандирование — это тип неравномерного квантования, который используется для увеличения мощности слабых сигналов. Он снижает скорость передачи данных входного сигнала за счет изменения промежутка между двумя соседними уровнями квантования. Неравномерный уровень квантования делает его похожим на процесс неравномерного квантования. Companding создается из комбинации двух слов, сжатия и расширения. Сигнал проходит через компрессор на передающей стороне и проходит через расширитель на принимающей стороне. |
 Функция квантизатора состоит в том, чтобы представить каждый уровень фиксированным дискретным конечным набором значений.
Функция квантизатора состоит в том, чтобы представить каждый уровень фиксированным дискретным конечным набором значений. Амплитуды дискретных квантованных уровней известны как уровни реконструкции . Эти уровни также называются уровнями представления. Как обсуждалось выше, расстояние между двумя соседними уровнями реконструкции определяется как размер шага . Его качество можно улучшить, уменьшив размер шага и увеличив количество уровней квантования. Телевизор с 64 уровнями обеспечивает удовлетворительное качество цвета, тогда как телевизор с 256 уровнями обеспечивает хорошее качество цвета.
Амплитуды дискретных квантованных уровней известны как уровни реконструкции . Эти уровни также называются уровнями представления. Как обсуждалось выше, расстояние между двумя соседними уровнями реконструкции определяется как размер шага . Его качество можно улучшить, уменьшив размер шага и увеличив количество уровней квантования. Телевизор с 64 уровнями обеспечивает удовлетворительное качество цвета, тогда как телевизор с 256 уровнями обеспечивает хорошее качество цвета.
 Следовательно, такой тип квантования имеет высокую аппроксимацию по сравнению с неравномерным квантованием.
Следовательно, такой тип квантования имеет высокую аппроксимацию по сравнению с неравномерным квантованием. Это связано с тем, что среднеквадратичное значение мощности квантованного шума пропорционально дискретизированному значению сигнала.
Это связано с тем, что среднеквадратичное значение мощности квантованного шума пропорционально дискретизированному значению сигнала. Это также снижает мощность шума и вероятность ошибки.
Это также снижает мощность шума и вероятность ошибки. Функция пробоотборника заключается в преобразовании непрерывного сигнала, изменяющегося во времени, в сигнал с дискретным временем. Процесс преобразования требует дискретизации и квантования для преобразования аналогового сигнала в цифровой сигнал. Функция квантизатора состоит в том, чтобы представлять каждый уровень фиксированным дискретным конечным набором значений. Существует ряд доступных битов квантования, таких как 8-битный, 16-битный и 64-битный. Количество уровней каждого бита можно вычислить по формуле (2n), где n относится к битам.
Функция пробоотборника заключается в преобразовании непрерывного сигнала, изменяющегося во времени, в сигнал с дискретным временем. Процесс преобразования требует дискретизации и квантования для преобразования аналогового сигнала в цифровой сигнал. Функция квантизатора состоит в том, чтобы представлять каждый уровень фиксированным дискретным конечным набором значений. Существует ряд доступных битов квантования, таких как 8-битный, 16-битный и 64-битный. Количество уровней каждого бита можно вычислить по формуле (2n), где n относится к битам. Кроме того, это приводит к уменьшению полосы пропускания, что имеет ряд других преимуществ, таких как низкая стоимость, повышенная надежность и эффективная передача.
Кроме того, это приводит к уменьшению полосы пропускания, что имеет ряд других преимуществ, таких как низкая стоимость, повышенная надежность и эффективная передача. Мы также можем сказать, что он сжимает входной сигнал и выдает сжатый сигнал на выходе. Например, уменьшение количества цветов, необходимых для представления цифрового изображения.
Мы также можем сказать, что он сжимает входной сигнал и выдает сжатый сигнал на выходе. Например, уменьшение количества цветов, необходимых для представления цифрового изображения.