Умножение в ассемблере
Используя наш сайт, вы подтверждаете, что прочитали и поняли политику о куки , политику конфиденциальности и пользовательское соглашение. Stack Overflow на русском — это сайт вопросов и ответов для программистов. Регистрация займёт не больше минуты. Аналогично сложению.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Разбираюсь с умножением в ассемблере, почему так работает, а так нет?
- Команда MUL
- Подписаться на ленту
- Оптимизация программ на ассемблере.
(Часть 2)
Умножение и деление в ассемблере. - 1. Регистры
- Арифметические операции. Умножение и деление
- Основы языка Assembler: Методические указания к лабораторным работам
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 0023 Инструкция LOOP
Разбираюсь с умножением в ассемблере, почему так работает, а так нет?
В предыдущей части мы обсуждали некоторые общие вопросы оптимизации, а затем поговорили о тех компромиссах, на которые приходится идти, оптимизируя быстродействие и размер программы. В этой и в следующей частях мы подробнее рассмотрим некоторые классические образцы «локальной» оптимизации.
Но важно помнить, что эти частные методики следует использовать только при определенных обстоятельствах — а именно: после того, как вы убедитесь, что применили правилные алгоритмы и структуры данных, что полностю отладили программу и что средства профилирования показали вам те самые фрагменты программы, которые ограничивают производительность. Операции умножения и деления требуют немалых усилий от почти любого ЦП, поскольку должны быть реализованы аппаратно или программно через сдвиги и сложения или сдвиги и вычитания соответственно.
Старинные 4- и 8-разрядные процесоры не содержали машинных команд для умножения или деления, так что эти операции приходилось реализовывать при помощи длинных подпрограмм, где явным образом выполнялись сдвиги и сложения или вычитания.
Первые разрядные микропроцессоры, такие, как и , действительно позволяли производить операции умножения и деления аппаратными средствами, но соответствующие процедуры были невероятно медленными: в процессоре , к примеру, для деления разрядного числа на разрядное требовалось примерно тактов.
Поэтому маленькие хитрости для ускорения или устранения операций умножения и деления были и пока остаются среди первых приемов, которые изучает любой программист, стремящийся к совершенству.
Большинство из этих хитростей относятся к категории, которую называют «отказ от универсальности». Под этим понимается замена рассчитанных на общий случай команд или вызовов соответствующих подпрограмм последовательностями сдвигов и сложений или вычитаний для случая конкретных операндов. Давайте сначала рассмотрим простейшую процедуру оптимизации умножения. Чтобы умножить число на степернь двойки, его достаточно просто сдвинуть влево на необходимое число двоичных битовых позиций.
Вот так, например, выглядит некотрая общая, но медленная последовательность команд при умножении значения переменной myvar на Если требуется сдвиг на одну или две позиции, то обычно проще всего выполнить эти операции над операндами в памяти. Если нужен сдвиг на многоо позиций, то повышенная скорость работы над регистровыми операндами вполне компенсирует дополнительную команду для загрузки числа в какой-либо регистр и извлечения его оттуда после сдвига.
Очередь команд в процессорах семейства 80×86, конкретная модель процессора, которая используется в вашем компьютере, и наличие или отсутствик кэш-памяти могут в совокупности сыграть самые причудливые шутки. В некотрых случаях и на некоторых моделях ЦП иногда соит использовать эту команду в варианте «сдвиг на указанное в CX число позиций»:. А в процессоре и более поздних имееется вариант «сдвиг на число позиций, заданное непосредственным операндом», что еще удобнее:. Если вам требуется умножать на степень двойки числа длиной более 16 разрядов, для организации операций над двумя и более регистрами используется флажок переноса.
Например, для умножения разрядного числа в DX:AX на 4 можно записать:. Творчески сочетая сдвиги и умножения, можног организовать быстрое умножение на почти любое конкретное значение. Следующий фрагмент производит умножение значения в регистре AX на Использование отказа от универсальности для деления несколько болле ограничено. Деление на степень двойки, конечно, очень просто. Вы просто сдвигаете число вправо, следя лишь за выбором родходящей команды сдвига для желаемого типа деления со знаком или без знака.
Деление на степень двойки, конечно, очень просто. Вы просто сдвигаете число вправо, следя лишь за выбором родходящей команды сдвига для желаемого типа деления со знаком или без знака.
Например, для выполнения деления без знака на 4 содержимого регистра AX можно написать:. Единственная разница между командой логического без знака сдвига SHR и командой арифметического со знаком сдвига SAR состоит в том, что SHR копирует старший знаковый разряд в следующий, а затем заменяет знаковый разряд нулем, тогда как SAR копирует знаковый разряд в следующий младший разряд, оставляя его исходное значение неизменным.
Выбор правильной команды сдвига для быстрого деления очень важен, особенно если вы имеете дело с адресами. Если вы случайно использовали арифметическое деление со знаком вместо деления без знака, которое предполагали сделать, последствия этого иногда проявляются сразу же, а иногда и нет — образовавшаяся «блоха» может до поры притаиться и укусить вас позже, когда какое-нибудь изменение размера или порядка компоновки прикладных программ выпустит ее на волю.
Между просим, не забывайте, что мнемообозначения SHL и SAL транслируются в одну и ту же машинную команду, и не без причины, не так ли? Деление на степени двойки со сдвигами может быть ваыполнено с помощью флага переноса, и оно ничуть не более сложно, чем умножение.
Например, для выполнения деления со знаком на 8 значения, в регистрах DX:AX можно использовать последовательность. Но, в отличие от операции умножения, использование сдвигов для быстрого деления на произволные числа, такие как 3 или 10, а не на степени двойки, на удивление хлопотно.
Обычно целесообразнее вместо этого обдумать всю ситуацию заново и преобразовать алгоритм или структуру данных так, чтобы избежать деления на «неудобные» числа. Прежде чем оставить эту тему и двигаться дальше, я должен упомянуть одну изящную оптимизацию, авторство которой приписывают Марку Збиковскому [Mark Zbikovski], одному из авторов версий 2. Приведенный нниже фрагмент делит значение в регистре AX на Теперь, когда вы увидели этот нетривиальный прием, у вас наверняка возникло множество идей о том, ка организовать умножение или деление на относительно большие степени двух: , и т.
Макаронные программы, изобилующие ветвлениями и переходами во всех направлениях, нежелательны во всех смыслах, а при работе с процессорами серии 80×86 — особенно. Можете считать это утверждение напутствием, цель которого — побудить программистов на ассемблере и тех, кто занимается оптимизацией компиляторов, должным образом структурировать программы. Тут есть свои проблемы, но прежде чем обсуждать оптимизацию переходовв и вызовов, давайте обсудим некоторые особенномти процессоров фирмы Intel.
Быстродействие этих процессоров в значительной мере определяется их архитектурой, основанной на простой конвейерной схеме, содержащей три компоненты: шинный интерфейс BIU — bus interface unit , очередь упереждающей выборки и исполнительный модуль EU — execution unit. Когда шина памяти находится в нерабочем состоянии например, прри выполнении команды из многих циклов, операнды которой находятся в регистрах , шинный интерфейс извлекает байты команд из памяти и помещает их в очередь упреждающей выборки, последовательно продвигаясь от текущего положения командного счетчика ЦП.
Когда исполнительный модуль завершает исполнение очередной команды, он в первую очередь ищет следующую команду в очереди упреждающей выборки: если она там действительно имеется, то к ее расшифровке можно приступить сразу же, не обращаясь лишний раз к памяти. Как же при такой реализации конвейерной обработки происходят переходы и вызовы подпрограмм? Всякий раз, когда исполнительный модуль расшифровывает команду перехода, он аннулирует текущее содержимое очереди упреждающей выборки и устанавливает новое содержимое счетчика команд.
После этого шинный интерфейс должен снова выбирать байты команд, теперь уже начиная с нового адреса, и заносить их в очередь. Кроме того, все обращения к памяти, которые требуются для исполнения команды перехода по новому адресу, также оказывают влияние на выборку следующих команд из памяти. Может пройти немалое время, прежде чем шина снова заполнит очередь упреждающей выборки так, чтобы исполнительный модуль мог работать с полной скоростью.
Он составляет всего 6 байтов в ранних моделях и 32 байта в компьютерах последних моделей. Это один из факторов, делающих крайне сложным предсказание времен исполнения для конкретных последовательностей команд исходя из количества тактов и длин в байтах. Кроме того, состояние очереди команд для разных типов ЦП зависит и от «выравнивания» команд. Шинный интерфейс должен выбирать команды в соответствии с разрядностью адресной и информационной частей шины.
Это один из факторов, делающих крайне сложным предсказание времен исполнения для конкретных последовательностей команд исходя из количества тактов и длин в байтах. Кроме того, состояние очереди команд для разных типов ЦП зависит и от «выравнивания» команд. Шинный интерфейс должен выбирать команды в соответствии с разрядностью адресной и информационной частей шины.
Поэтому производительность очереди команд может существенно ухудшиться из-за неудачных адресов вызовов или переходов. Например, в процессоре с разрядной шиной памяти выборка из памяти всегда происходит по 16 бит за один раз, так что если команда, на которую передается управление при вызове подпрограммы, начинается с нечетного адреса, половина первого обращения к памяти пропадает впустую.
Все это подталкивает нас к осознанию первого правила оптимизации переходов и вызовов: проверьте, что их точки назначения попадают в подходящие границы адресов для того типа процессора, на котором ваша программа будет исполняться чаще всего..jpg) Процессор имеет 8-разрядную внешнюю шину, так что он абсолютно нечувствителен к выравниванию.
Процессор имеет 8-разрядную внешнюю шину, так что он абсолютно нечувствителен к выравниванию.
Если потенциальными потребителями вашей программы являются пользователи компьютеров на процессоре , к выравниванию прибегать не стоит, поскольку оно лишь потребует дополнительной памяти, но не увеличит производительность. В то же время, если программе предстоит главным образом работать на компьютерах с процессорами или , следует произвести выравнивание в границах WORD, а если она рассчитана на процессоры DX, DX — используйте выравнивание DWORD. Для процессора , в котором есть внутренняя кэш-память, лучше, когда позиции лежат на байтовых границах, но тратить в среднем 8 байт на каждую метку мне кажется непозволительной роскошью.
Следующее эмпирическое правило, относящееся к переходам и вызовам, очень простое: избавляться от них везде, где только можно. По крайней мере в тех частях программы, где быстродействие определяется в основном процессором. Для этого организуйте программу так, чтобы она исполнялась прямым, последовательным образом, с минимальным числом точек принятия решения.
В результате очередь команд будет почти всегда заполнена, а вашу программу будет легче читать, сопровождать и отлаживать. После того, как вы улучшили программу насколько возможно за счет «хорошего» структурирования, следует решить, надо ли двигаться дальше, и постараться увеличить производительность введением в программу «плохой структуры», например, преобразовав переходы к общим точкам выхода из подпрограмм в множественные выходы.
В крайних случаях короткие подпрограммы можно преобразовать в макрокоманды, тогда команды процессора будут исполняться последовательно и дополнительных затрат времени на передачу и возврат управления не будет. Если в программе требуется условный переход, проанализируйте точку принятия решения и организуйте программу так, чтобы вероятность перехода была ниже, чем его отсутствия.
Таким образом вы уменьшите число сбросов очереди команд. Например, если программа производит проверку знака переменной, которая может быть отрицательной только в редких случаях, при особых обстоятельствах, то сделайте так, чтобы ваша прогамма «проскакивала» через точку разветвления при положительном значении переменной:. Аналогично, если разные значени некой переменной инициируют различные действия и вам требуется произвести множественные сравнения, за которыми следуют условные переходы, то попытайтесь переместить сравнения с наиболее вероятным значением ближе к началу цепочки:.
Аналогично, если разные значени некой переменной инициируют различные действия и вам требуется произвести множественные сравнения, за которыми следуют условные переходы, то попытайтесь переместить сравнения с наиболее вероятным значением ближе к началу цепочки:.
Если требуется произвести сравнения со многими значениями, разбросаннами по диапазону с больщими разрывами, реализовать множественные сравнения можно по принципу бинарного дерева, сначала сделав рассечение диапазона каким-нибудь одним значением из середины всего диапазона, а затем проверяя, в каком отношении к этому диапазону находится контролируемая переменная больше, меньше, равно , затем если переменная больше или меньше параметра сравнения деля оставшийся интервал другим значением, и так далее.
Такая стратегия чрезвычайно эффективна, если значения распределены более или менее однородно и редко. Если же они распределены плотно, то часто наилучшим решением является использование «таблицы переходов». Например, представьте, что в регистре AL находится значение переменной, являющейся ASCII-символом, и есть набор подпрограмм, запускаемых при некоторых определенных символах.
Сначала мы составим таблицу адресов подпрограмм в позициях, соответствующих численным значениям ASCII-кодов, затем реализуем разветвления через таблицу следующим образом:.
Есть еще две методики оптимизации, связанные с переходами и вызовами, которые требуют внесения определенной степени «деструктурированности» в во всем остальном верную программу и называются «сращиванием хвостов» и «устранением рекурсивных вызовов».
Каждая из них подразумевает преобразование вызовов в переходы: вызовы по самой своей природе требуют большего времени, чем переходы, поскольку помещают в стек адрес возврата и в результате требуют больше обращений к памяти.
Например, последовательность. Устранение рекурсивных вызовов очень похоже на сращивание хвостов. Когда программа последовательно вызывает сама себя и этот вызов расположен непосредственно перед командой RETURN в программе, вызов может быть преобразован в переход, что и увеличит скорость, и уменьщшит необходимый объем памяти в стеке.
Например, программа. Такая рекурсивная программа часто может быть еще оптимизирована за счет преобразования рекурсии в цикл. Все для программиста! Справочник функций. Ваш аккаунт Войти через:. Запомнить меня. Забыли пароль? Информацию о новых материалах можно получать и без регистрации:. Почтовая рассылка Подписаться. Подписчиков: -1 Последний выпуск : Чтобы оставить комментарий, необходимо авторизоваться.
Можно ввести логин и пароль, или авторизоваться через социальные сети. МНе нужна информация о ти разрядных однокристальных микропроцессорах Intel. Комментарий: можно использовать BB-коды Максимальная длина комментария — символов.
Команда MUL
Программирование — в обычном понимании, это процесс создания компьютерных программ. В узком смысле так называемое кодирование под программированием понимается написание инструкций — программ — на конкретном языке программирования часто по уже имеющемуся алгоритму — плану, методу решения поставленной задачи. Соответственно, люди, которые этим занимаются, называются программистами на профессиональном жаргоне — кодерами , а те, кто разрабатывает алгоритмы — алгоритмистами, специалистами предметной области, математиками. В более широком смысле под программированием понимают весь спектр деятельности, связанный с созданием и поддержанием в рабочем состоянии программ — программного обеспечения ЭВМ. Сюда входят анализ и постановка задачи, проектирование программы, построение алгоритмов, разработка структур данных, написание текстов программ, отладка и тестирование программы испытания программы , документирование, настройка конфигурирование , доработка и сопровождение. Команда IMUL выполняет умножение целого числа со знаком, находящегося в регистре AL в случае умножения на байт или АХ в случае умножения на слово , на операнд-источник целое число со знаком.
В более широком смысле под программированием понимают весь спектр деятельности, связанный с созданием и поддержанием в рабочем состоянии программ — программного обеспечения ЭВМ. Сюда входят анализ и постановка задачи, проектирование программы, построение алгоритмов, разработка структур данных, написание текстов программ, отладка и тестирование программы испытания программы , документирование, настройка конфигурирование , доработка и сопровождение. Команда IMUL выполняет умножение целого числа со знаком, находящегося в регистре AL в случае умножения на байт или АХ в случае умножения на слово , на операнд-источник целое число со знаком.
Онлайн учебники по программированию на языках Паскаль, Ассемблер, Си. Команда IMUL выполняет умножение целого числа со знаком.
Подписаться на ленту
Может быть тогда и инлайниться лучше будет. Очень интересная статья! Кстати, кроме как тем, что нужен свой формат хранения, матрички из GLM не такие же шустрые? Кажется, там была какая-то поддержка SIMD. Если бы! Вы вообще не поняли о чем я, видимо ни разу не использовали AVX. Я не про какие-то реализации каких-то процессоров, я про весь набор команд и их архитектуру. То есть нижние бит работают только с нижними битами, старшие со старшими — это больше похоже на два модуля SSE, чем на один модуль SSE, но в два раза больше.
Если бы! Вы вообще не поняли о чем я, видимо ни разу не использовали AVX. Я не про какие-то реализации каких-то процессоров, я про весь набор команд и их архитектуру. То есть нижние бит работают только с нижними битами, старшие со старшими — это больше похоже на два модуля SSE, чем на один модуль SSE, но в два раза больше.
Оптимизация программ на ассемблере. (Часть 2)
Команда MUL позволяет также производить вычисления в неупакованном двоично-десятичном формате неупакованный BCD-формат. SS 0 , если любая часть операнда в памяти находится вне допустимого пространства эффективных адресов в стековом сегменте SS. Intel … : PF Код ошибки при страничной ошибке. Intel … : AC 0 при невыровненной ссылке в память, если активирован контроль выравнивания CR0.
Замена деления умножением на Ассемблере Замена деления умножением на Ассемблере.
Умножение и деление в ассемблере.
В предыдущей части мы обсуждали некоторые общие вопросы оптимизации, а затем поговорили о тех компромиссах, на которые приходится идти, оптимизируя быстродействие и размер программы. В этой и в следующей частях мы подробнее рассмотрим некоторые классические образцы «локальной» оптимизации. Но важно помнить, что эти частные методики следует использовать только при определенных обстоятельствах — а именно: после того, как вы убедитесь, что применили правилные алгоритмы и структуры данных, что полностю отладили программу и что средства профилирования показали вам те самые фрагменты программы, которые ограничивают производительность. Операции умножения и деления требуют немалых усилий от почти любого ЦП, поскольку должны быть реализованы аппаратно или программно через сдвиги и сложения или сдвиги и вычитания соответственно. Старинные 4- и 8-разрядные процесоры не содержали машинных команд для умножения или деления, так что эти операции приходилось реализовывать при помощи длинных подпрограмм, где явным образом выполнялись сдвиги и сложения или вычитания. Первые разрядные микропроцессоры, такие, как и , действительно позволяли производить операции умножения и деления аппаратными средствами, но соответствующие процедуры были невероятно медленными: в процессоре , к примеру, для деления разрядного числа на разрядное требовалось примерно тактов.
В этой и в следующей частях мы подробнее рассмотрим некоторые классические образцы «локальной» оптимизации. Но важно помнить, что эти частные методики следует использовать только при определенных обстоятельствах — а именно: после того, как вы убедитесь, что применили правилные алгоритмы и структуры данных, что полностю отладили программу и что средства профилирования показали вам те самые фрагменты программы, которые ограничивают производительность. Операции умножения и деления требуют немалых усилий от почти любого ЦП, поскольку должны быть реализованы аппаратно или программно через сдвиги и сложения или сдвиги и вычитания соответственно. Старинные 4- и 8-разрядные процесоры не содержали машинных команд для умножения или деления, так что эти операции приходилось реализовывать при помощи длинных подпрограмм, где явным образом выполнялись сдвиги и сложения или вычитания. Первые разрядные микропроцессоры, такие, как и , действительно позволяли производить операции умножения и деления аппаратными средствами, но соответствующие процедуры были невероятно медленными: в процессоре , к примеру, для деления разрядного числа на разрядное требовалось примерно тактов.
1. Регистры
Все мы знаем со школы что такое умножение и деление и конечно же в ассемблере эти команды присутствуют, и я расскажу Вам о них. В ассемблере умножение и деление для положительных и отрицательных чисел выполняются по-разному. У этой команды только один операнд — второй множитель, который должен находиться в регистре или в памяти. Местоположение первого множителя и результата задаётся неявно и зависит от размера операнда:. Эта команда имеет три формы, различающиеся количеством операндов:. Деление целых двоичных чисел — это всегда деление с остатком.
Команды умножения MUL, IMUL умножение целых без знака mul операнд умножение целых со знаком imul операнд. Умножение байтов: AX:= AL * op.
Арифметические операции. Умножение и деление
Сложение и вычитание. ADD — команда для сложения двух чисел. Она работает как с числами со знаком, так и без знака.
Основы языка Assembler: Методические указания к лабораторным работам
Инструкция MUL в Ассемблере выполняет умножение без знака. Понять работу команды MUL несколько сложнее, чем это было для команд , рассмотренных ранее. Но, надеюсь, что я помогу вам в этом разобраться. Эта команда не работает с сегментными регистрами, а также не работает непосредственно с числами. То есть вот так. Вот такая немного сложноватая команда.
Понять работу команды MUL несколько сложнее, чем это было для команд , рассмотренных ранее. Но, надеюсь, что я помогу вам в этом разобраться. Эта команда не работает с сегментными регистрами, а также не работает непосредственно с числами. То есть вот так. Вот такая немного сложноватая команда.
Контакты: о проблемах с регистрацией, почтой и по другим вопросам пишите сюда — alarforum yandex.
В микроконтроллерах PIC16 отсутствует аппаратный блок умножения и деления чисел, но эти арифметические операции можно реализовать программным путем. Операцию умножения можно представить в виде многократного сложения, деление — многократным вычитанием. При этом результатом операции деления является количество вычитаний, но только без учета последнего вычитания, которое привело к отрицательному результату, так как я рассматриваю здесь только целочисленные операции без дробных частей. В данном примере после четырех вычитаний получаем -4, соответственно ответ равен 3, без учета последнего вычитания. Рассмотрим подпрограмму умножения однобайтных чисел, перед вызовом подпрограммы загружаем числа в регистры varLL и tmpLL число в varLL умножается на число в tmpLL , в подпрограмме первым делом очищаем регистр varLH, так как максимальный результат при перемножении однобайтных чисел равен , соответственно результат это двухбайтное число varLH, varLL. Далее проверяем перемножаемые числа на равенство нулю, если число в регистре varLL равно нулю, то выходим из подпрограммы с нулевым результатом, при обнаружении нуля в tmpLL, очищаем регистр varLL, также получая нулевой результат.
Рассмотрим подпрограмму умножения однобайтных чисел, перед вызовом подпрограммы загружаем числа в регистры varLL и tmpLL число в varLL умножается на число в tmpLL , в подпрограмме первым делом очищаем регистр varLH, так как максимальный результат при перемножении однобайтных чисел равен , соответственно результат это двухбайтное число varLH, varLL. Далее проверяем перемножаемые числа на равенство нулю, если число в регистре varLL равно нулю, то выходим из подпрограммы с нулевым результатом, при обнаружении нуля в tmpLL, очищаем регистр varLL, также получая нулевой результат.
У микроконтроллеров AVR, по сути, имеется два пути реализации умножения, разница между которыми заключается в форме представления произведения и, соответственно, в различии выполняемых арифметических операций. Первый оптимизирован для использования с командой однобайтового умножения, второй — использует только сложение и сдвиговые операции. Помимо этого существует особый случай умножения на целую степень 2. Как видно, коэффициенты xn числа X переместились на один разряд влево x 0 стал при 2 1 , x 1 стал при 2 2 и т.
Урок 11. Умножение и деление
Поход на рынок, как правило, заканчивается покупкой какого-либо товара. Если мы хотим купить несколько единиц товара одного наименования, то продавец посчитает нам итоговую сумму с использованием простейшего компьютера – микрокалькулятора. В аналогии с ассемблером при умножении товаров программа микрокалькулятора будет оперировать с числами без знака, поскольку нельзя купить минус три пури или минус пять круассанов. Чтобы есть и худеть, даже если очень бы хотелось
Умножение чисел без знака
Допустим, нам требуется сделать для нашего микрокалькулятора программу умножения количества товаров и цен. Применим команду ассемблера MUL для умножения беззнаковых чисел. Работать с этой командой просто, первый множитель по умолчанию хранится в регистре AL или AX, а второй множитель команде передаётся как единственный операнд – хранимый в регистре или в памяти.
| Размер операнда | Множитель | Результат |
| Байт | AL | AX |
| Слово | AX | DX:AX |
Как видно из таблицы, длина множителя (байт или слово) определяются по размеру переданного операнда. Если команда MUL перемножает два байтовых операнда, результатом будет слово, а если перемножаются двухбайтовые операнды, результатом будет двойное слово. При умножении в ассемблере разрядность результата будет ровно в 2 раза больше каждого из исходных значений. Говоря простым языком, если мы перемножаем числа одинаковой разрядности между собой, например 8 битное на 8 битное, то результат будет максимум из 16 бит.
Если команда MUL перемножает два байтовых операнда, результатом будет слово, а если перемножаются двухбайтовые операнды, результатом будет двойное слово. При умножении в ассемблере разрядность результата будет ровно в 2 раза больше каждого из исходных значений. Говоря простым языком, если мы перемножаем числа одинаковой разрядности между собой, например 8 битное на 8 битное, то результат будет максимум из 16 бит.
mul bl ;AX = AL * BL mul ax ;DX:AX = AX * AX
mul bl ;AX = AL * BL mul ax ;DX:AX = AX * AX |
Если умножаются два операнда размеров в байт, то результат умножения помещается в регистр AX, а при умножении двух слов, результат комбинируется в регистрах DX:AX, где старшее слово результата будет в DX, а младшее в AX. Не всегда результатом умножения двух байт будет слово или при умножением двух слов – двойное слово. Если старшая часть результата содержит ноль, то флаги CF и OF будут также равны нулю. Соответственно старшую часть результата умножения можно игнорировать, что может быть полезно в определенных случаях.
Соответственно старшую часть результата умножения можно игнорировать, что может быть полезно в определенных случаях.
Умножение чисел со знаком
Теперь переходим к миру математики, в котором знаковые числа перемножаются не реже беззнаковых. В ассемблере для таких операций есть команда IMUL. Инструкция имеет три формы, разнящиеся числом операндов:
Вызов с одним операндом – аналогично команде MUL. Передаваемым операндом может быть регистр или значение в памяти. Операнд умножается на значение в AL (операнд – байт) или AX (операнд – слово). Результат хранится в AX или комбинируется в DX:AX соответственно.
Вызов с двумя операндами – в этой форме перезаписываемый операнд назначения (первый множитель) умножается на передаваемый операнд — источник (второй множитель). В качестве перезаписываемого операнда должен указываться регистр общего назначения, а вторым операндом может быть непосредственное значение, регистр общего назначения или область памяти. Младшая часть результата помещается в перезаписываемый операнд, старшая часть (дважды от размера операнда – источника) отсекается.
Вызов с тремя операндами – в этой форме используется операнд назначения и два операнда -источника, содержащие первый и второй множители. Первый множитель, которым может быть регистр общего назначение или область памяти, умножается на второй множитель (непосредственное значение). Итоговое произведение операндов (дважды от размера первого операнда – источника) усекается и хранится в операнде назначения (регистр общего назначения).
Примеры использования команды IMUL:
imul bl ;AX = AL * BL imul cx ;DX:AX = AX * CX imul si,-13 ;SI = SI * -13 imul bx,si,123h ;BX = SI * 123h
imul bl ;AX = AL * BL imul cx ;DX:AX = AX * CX imul si,-13 ;SI = SI * -13 imul bx,si,123h ;BX = SI * 123h |
Для первой формы флаги CF = 0 и OF = 0 означают, что результат умножения поместился в младшей части, в то время как CF = OF = 1 для команды IMUL в форме с двумя или тремя операндами сигнализируют переполнение, то есть потерю старшей части результата.
Деление чисел без знака
Команда DIV используется для выполнения деления беззнаковых чисел с остатком. Если при умножении разрядность произведения всегда в два раза больше множителей, то при делении действует обратный принцип – большим разрядом является делимое, а частное всегда в два раза меньше делимого. Инструкция принимает единственный операнд – делитель, помещаемый в регистр общего назначения или в память. Размер делителя распределяет делимое, частное и остаток согласно таблице:
| Размер операнда (делителя) | Делимое | Частное | Остаток |
| Байт | AX | AL | AH |
| Слово | DX:AX | AX | DX |
Операция деления в ассемблере может вызывать прерывание (подробнее о прерываниях будет написано в одном из следующих уроков) в ряде случаев:
- При делении на ноль;
- Когда происходит переполнение частного, то есть результат не помещается в отведенную разрядность (например, если делимое – слово (1000), а делитель – байт (2), то результат (500) не поместится в байт).

Примеры:
div cl ;AL = AX / CL, остаток в AH div di ;AX = DX:AX / DI, остаток в DX
div cl ;AL = AX / CL, остаток в AH div di ;AX = DX:AX / DI, остаток в DX |
Деление чисел со знаком
Команда IDIV используется для деления чисел со знаком. Вызов аналогичен команде DIV – передаётся единственный аргумент – делитель, который неявно определяет размеры делимого, частного и остатка. Прерывание генерируется, если выполняется деление на ноль или частное превышает отведенную разрядность.
Программа к уроку
Применим полученные знания о командах деления и умножения для написания простой программы вычисления общего пройденного пути, имея исходные скорость, ускорение, время и расстояние:
s= s0+ v0t + at2/2
use16
org 100h
;===== Часть формулы: v0*t =====
mov al,[v] ;AL = v0
mov bl,[t] ;BL = t
mul bl ;AX = AL * BL
mov si,ax ;Произведение в SI
;===== Часть формулы: (a*t^2)/2 =====
mov al,[t] ;AL = t
mul bl ;AX = AL * BL = a*t
mov bl,[a] ;BX = a
mov bh,0 ;BX — второй множитель, поэтому прибираемся в BH
mul bx ;DX:AX = AX * BX = a*t^2
mov bx,2 ;BX = 2
div bx ;DX:AX / BX = a*t^2 / 2
;===== Складываем все вместе =====
add ax,si ;v0*t + (a*t^2)/2
add al,[s] ;|
adc ah,0 ;|. 2)/2
2)/2
add al,[s] ;|
adc ah,0 ;|… + s0
mov [r],ax ;Храним результат в [r]
mov ax,4C00h ;|
int 21h ;|Заверешение программы
;—————————————
s db 180
v db 7
a db 4
t db 41
r dw ?
В 8-й строке результат умножения сохраняется в регистре SI. В 14-й строке старшая часть регистра BX – BH выставляется в ноль, что корректно только для беззнаковых чисел. Попытка присвоить ноль старшей части регистра, хранящего число со знаком может привести к ошибке, если младшая часть регистра хранит отрицательное число. Обратите внимание на строках 21-22 прибавление байта из переменной [s0] к слову AX происходит в два этапа: прибавление числа к AL, и корректировкой на перенос прибавлением нуля к AH.
Упражнение к уроку (1):
z = a2 + 2ab + b2
Числа в формуле используйте 16 битные целые без знака.
Упражнение к уроку (2) (продвинутое):
Используя школьный курс сложения столбиком и команды MUL и ADD, напишите программу для умножения 32-битных чисел без знака. Результатом будет 64-битное число без знака.
Умножение чисел на ассемблере на микроконтроллерах ATtiny
Несмотря на то что в интернете можно найти команду MUL для умножения на микроконтроллерах AVR. В документациях на ATtiny2313 и ATtiny13 такой команды нет. Микроконтроллеры семейства «Tiny» имеют сокращенный набор команд. Но умножение может понадобиться даже на таких микроконтроллерах. Несмотря на скромные, относительно других современных микроконтроллеров вроде STM32, возможности, микроконтроллеры семейства Tiny всё равно могут выполнять сложные операции если бережно распоряжаться их ресурсами создавая программы для них на ассемблере. В среде WinAVR или AVR Studio на языке си можно использовать знак умножения но компилятор наверняка превратит конструкцию с умножением в большой кусок машинного кода. Который для какой нибудь ATtiny будет гораздо больше чем для какой нибудь ATmega. Одним из выходов может быть — стараться не использовать умножение там где без него можно обойтись. Если нужно умножить на 2,4,8,16,… и т.д. то умножение можно заменить побитовым сдвигом влево. Эта операция выполняется быстро однако подходит только для частных случаев. Самый простой и, при этом, являющийся определением умножения способ перемножить два числа между собой — это сложить первое число с самим собой столько раз сколько указывает второе число (далее первое число — это множимое, второе число — множитель). Например чтобы умножить 10 на 2 нужно 10 сложить с самим собой 2 раза т.е.
Который для какой нибудь ATtiny будет гораздо больше чем для какой нибудь ATmega. Одним из выходов может быть — стараться не использовать умножение там где без него можно обойтись. Если нужно умножить на 2,4,8,16,… и т.д. то умножение можно заменить побитовым сдвигом влево. Эта операция выполняется быстро однако подходит только для частных случаев. Самый простой и, при этом, являющийся определением умножения способ перемножить два числа между собой — это сложить первое число с самим собой столько раз сколько указывает второе число (далее первое число — это множимое, второе число — множитель). Например чтобы умножить 10 на 2 нужно 10 сложить с самим собой 2 раза т.е.
10*2=10+10=20
Операция умножения простых чисел обладает свойством коммутативности т.е. «от перемены мест множителей произведение (результат умножения) не меняется». Однако если сделать это в предыдущем примере то процессору будет нужно выполнить гораздо больше действий:
2*10=2+2+2+2+2+2+2+2+2+2=20
Отсюда видно что на производительность сильно влияет множитель а не множимое. Если множитель будет велик то будет велика и задержка на выполнение этой операции что может негативно сказаться на работе устройства. Например если микроконтроллер планируется использовать для векторного управления электродвигателем то этот микроконтроллер может не успевать умножать числа. Для ускорения можно использовать например таблицу умножения но для её хранения нужно некоторое количество памяти а например на ATtiny2313 flash памяти всего 2кб. Существует способ умножения не требующий большого количества памяти. Он известен как «умножение в столбик». Умножать этим способом учат в школах и, на листке бумаге, он выполняется (в большинстве случаев (если не надо умножать например на 2)) явно быстрее способа с использованием одного только сложения. Однако для данного способа необходимо знать таблицу умножения что может привести к мысли о том что микроконтроллер тоже должен её «знать» т.е. хранить во flash памяти. Однако, к счастью, таблица умножения в двоичном виде полностью совпадает с таблицей истинности логического «И».
Если множитель будет велик то будет велика и задержка на выполнение этой операции что может негативно сказаться на работе устройства. Например если микроконтроллер планируется использовать для векторного управления электродвигателем то этот микроконтроллер может не успевать умножать числа. Для ускорения можно использовать например таблицу умножения но для её хранения нужно некоторое количество памяти а например на ATtiny2313 flash памяти всего 2кб. Существует способ умножения не требующий большого количества памяти. Он известен как «умножение в столбик». Умножать этим способом учат в школах и, на листке бумаге, он выполняется (в большинстве случаев (если не надо умножать например на 2)) явно быстрее способа с использованием одного только сложения. Однако для данного способа необходимо знать таблицу умножения что может привести к мысли о том что микроконтроллер тоже должен её «знать» т.е. хранить во flash памяти. Однако, к счастью, таблица умножения в двоичном виде полностью совпадает с таблицей истинности логического «И». Ещё одним немаловажным упрощением является то что при применении логического «И» между 0 и множимым, по всем разрядам, получится 0. При применении логического «И» между 1 и множимым, по всем разрядам, получится множимое. Это упрощает написание кода т.к. с учетом этого нет необходимости проходиться по всем разрядам множимого во вложенном цикле. Однако по всем разрядам множителя всё рано придется пройтись. Отсутствие вложенного цикла также уменьшит количество операций для выполнения процессором что ускорит операцию умножения в целом. Чтобы проверить «такой облегченный алгоритм умножения столбиком» на микроконтроллере, можно например использовать UART. Т.к. произведение двух чисел имеет разрядов больше чем множитель то желательно не делать его большим чтобы произведение не вышло за пределы одного байта. Для этого можно послать по UARTу два числа в одном символе, после чего микроконтроллер их выделит, перемножит и пришлет результат. Так можно проверить работает ли алгоритм прежде чем начать использовать его для умножения.
Ещё одним немаловажным упрощением является то что при применении логического «И» между 0 и множимым, по всем разрядам, получится 0. При применении логического «И» между 1 и множимым, по всем разрядам, получится множимое. Это упрощает написание кода т.к. с учетом этого нет необходимости проходиться по всем разрядам множимого во вложенном цикле. Однако по всем разрядам множителя всё рано придется пройтись. Отсутствие вложенного цикла также уменьшит количество операций для выполнения процессором что ускорит операцию умножения в целом. Чтобы проверить «такой облегченный алгоритм умножения столбиком» на микроконтроллере, можно например использовать UART. Т.к. произведение двух чисел имеет разрядов больше чем множитель то желательно не делать его большим чтобы произведение не вышло за пределы одного байта. Для этого можно послать по UARTу два числа в одном символе, после чего микроконтроллер их выделит, перемножит и пришлет результат. Так можно проверить работает ли алгоритм прежде чем начать использовать его для умножения. При проверке, указанным способом, микроконтроллер должен будет выдать символ ‘8’ (без кавычек) при отправке ему символа ‘x’ (тоже без кавычек). Код программы для ATtiny2313:
При проверке, указанным способом, микроконтроллер должен будет выдать символ ‘8’ (без кавычек) при отправке ему символа ‘x’ (тоже без кавычек). Код программы для ATtiny2313:
.INCLUDE «tn2313def_for_avra.inc» ; загрузка предопределений
.CSEG ; начало сегмента кода
.ORG 0x0000
RJMP reset ; перепрыгиваем таблицу векторов
.ORG URXCaddr ; прерывание по завершению према
RJMP urx
reset:
;— инициализация стека —
LDI R16, Low(RAMEND) ; записать в регистр R16 адрес конца ОЗУ
OUT SPL, R16 ; записать в SPL значение из R16
;— инициализация uart —
;— установка скорости 9600 bps —
LDI R16, 12 ; стр.134 даташита Fosc=1MHz 9600bps U2X=1
OUT UBRRL, R16
;— установка удвоения скорости (так меньше ошибка стр.134) —
LDI R16, 0b00000010 ; U2X=1 стр.129
OUT UCSRA, R16
; — разрешение приема и прерывания по завершению према —
LDI R16, 0b10011000 ; разрешить прием (бит4) и передачу (3)
OUT UCSRB, R16 ; прерывание по завершению према (бит7)
; — установка колличества принимаемых бит
LDI R16, 0b00000110 ; принимать по 8 бит
OUT UCSRC, R16
; — включаем подтягивающий резистор —
LDI R16, 0b00010000
OUT PORTD, R16
SEI ; разрешить прерывания глобально
;— основной цикл программы —
loop:
SBIC PIND, 4 ; пропустить если кнопка на 4 пине порта D нажата
RJMP loop
L5: SBIS UCSRA,UDRE ; проверять пока регистр для
RJMP L5 ; отправки не будет свободен
OUT UDR, R21 ; отправить результат умножения по uart
RJMP loop
; — обработка прерывания по завершению према —
urx:
IN R16, UDR ; взять пришедший бит в R16
MOV R17, R16 ; скопировать R16 в R17
ANDI R16, 0b00001111 ; выделить младшую часть числа в R16
ANDI R17, 0b11110000 ; выделить старшую часть числа в R17
LSR R17 ; логически сдвинуть
LSR R17 ; вправо число в R17
LSR R17 ; 4 раза
LSR R17 ; R16-множимое, R17-множитель
; —умножение начало—
LDI R21, 0 ; сбросить R21 (R21 будет = R16 * R17)
LDI R18, 1 ; записать в R18 ед. в R18 разряд
L1:
MOV R19, R17 ; скопировать множитель в R19
AND R19, R18 ; выделить бит множителя текущего рзряда
CPI R19, 0 ; сравнить с нулем
BREQ L2 ; пропустить копирование можимого в R19
; если этот бит=0, далее в R19 будет 0
MOV R19, R16 ; скопировать множимое в R19 если этот бит=1
L2:
LDI R20, 1 ; записать 1 в R20 (R20 будет счетчик сдвига)
L3:
CP R20, R18 ; сравнить счетчик сдвига с текущим разрядом
BREQ L4 ; пропустить сдвиг если счетчик сдвига дстиг
; текущего разряда
LSL R20 ; сдвинуть вправо счетчик сдвига
LSL R19 ; сдвинуть вправо число для сложения
RJMP L3 ; попытаться повторить сдвиг
L4:
ADD R21, R19 ; сложить R21 c R19, результат поместить в R21
LSL R18 ; увеличить текущий разряд сдвигом влево
CPI R18, 0b00010000 ; сравнить текущий разряд с конечным
BRNE L1 ; перейти в начало если текущий
; разряд не достиг конца
; —умножение конец—
RETI ; вернуться из прерывания
в R18 разряд
L1:
MOV R19, R17 ; скопировать множитель в R19
AND R19, R18 ; выделить бит множителя текущего рзряда
CPI R19, 0 ; сравнить с нулем
BREQ L2 ; пропустить копирование можимого в R19
; если этот бит=0, далее в R19 будет 0
MOV R19, R16 ; скопировать множимое в R19 если этот бит=1
L2:
LDI R20, 1 ; записать 1 в R20 (R20 будет счетчик сдвига)
L3:
CP R20, R18 ; сравнить счетчик сдвига с текущим разрядом
BREQ L4 ; пропустить сдвиг если счетчик сдвига дстиг
; текущего разряда
LSL R20 ; сдвинуть вправо счетчик сдвига
LSL R19 ; сдвинуть вправо число для сложения
RJMP L3 ; попытаться повторить сдвиг
L4:
ADD R21, R19 ; сложить R21 c R19, результат поместить в R21
LSL R18 ; увеличить текущий разряд сдвигом влево
CPI R18, 0b00010000 ; сравнить текущий разряд с конечным
BRNE L1 ; перейти в начало если текущий
; разряд не достиг конца
; —умножение конец—
RETI ; вернуться из прерывания
К пину 4 порта D надо приделать кнопку которая делает 0В на этом пине при её нажатии. При нажатии на эту кнопку микроконтроллер присылает произведение по UARTу. Программа не идеальная но она нужна только для проверки алгоритма умножения. Вложенный цикл всё таки есть но он нужен для побитового сдвига на некоторое количество разрядов. Также можно заметить что 0 также будет сдвигаться в чем нет необходимости. Данную проблему можно решить перенеся цикл сдвига в пропускаемый участок кода перед меткой «L2». Возможно существуют и более быстрые и экономные способы умножения (о них можно написать в комментариях внизу или в комментариях к видео) однако данный тоже не плох по сравнению со способом на одном сложении.
При нажатии на эту кнопку микроконтроллер присылает произведение по UARTу. Программа не идеальная но она нужна только для проверки алгоритма умножения. Вложенный цикл всё таки есть но он нужен для побитового сдвига на некоторое количество разрядов. Также можно заметить что 0 также будет сдвигаться в чем нет необходимости. Данную проблему можно решить перенеся цикл сдвига в пропускаемый участок кода перед меткой «L2». Возможно существуют и более быстрые и экономные способы умножения (о них можно написать в комментариях внизу или в комментариях к видео) однако данный тоже не плох по сравнению со способом на одном сложении.
Видео по данной теме:
КАРТА БЛОГА (содержание)
Арифметические операции (1-ая часть) — презентация онлайн
Похожие презентации:
Арифметические и логические команды языка Ассемблер. Битовые команды
Основные команды ассемблера
Программирование на Ассемблере
Использование двоичной и шестнадцатеричной систем счисления
Программная модель микропроцессора INTEL 8080, регистры, форматы и системы команд, методы адресации
Основы языка Аssembler. Связь с программами на других языках
Связь с программами на других языках
Машинно-ориентированные языки, язык ассемблера. Занятие 2
Основные компоненты языка Ассемблер
Системное программирование
Архитектура ЭВМ и язык ассемблера. Лекция 3
1. Арифметические операции (1-ая часть)
2. План:
Обработка двоичных данныхБеззнаковые и знаковые данные
Умножение
Сдвиг регистровой пары DX: АХ
План:
3. Обработка двоичных данных
Сложение и вычитаниеПереполнение
Обработка двоичных данных
4. Сложение и вычитание
Команды ADD и SUB выполняют сложение ивычитание байтов или слов, содержащих
двоичные данные.
Пример:
MOV AX,WORDA
ADD AX,WORDB
MOV WORDB,AX
Сложение и вычитание
5. Переполнения
ADD AL,20HCBW ;Расширение AL до AX
ADD AX,20H
;Прибавить к AX
Переполнения
6. Беззнаковые и знаковые данные
Команды ADD и SUB не делают разницы междузнаковыми и беззнаковыми величинами, они
просто складывают и вычитают биты.

Беззнаковые и знаковые данные
Беззнаковое Знаковое
1111 1001 249 -7
+ +
+ +
0000 0010 2 +2
———————-1111 1011 251 -5
8. Умножение
Байт на байтСлово на слово
Беззнаковое умножение
Знаковое умножение
Повышение эффективности умножения
Многословное умножение
Умножение двойного слова на слово
Умножение двойного слова на двойное
слово
Умножение
Операция умножения для беззнаковых данных
выполняется командой MUL, а для знаковых — IMUL
Байт на байт Множимое находится в регистре AL, а
множитель в байте памяти или в однобайтовом
регистре. После умножения произведение находится в
регистре AX. Операция игнорирует и стиpает любые
данные, которые находились в регистре AH.
Слово на слово Множимое находится в регистре AX, а
множитель — в слове памяти или в регистре. После
умножения произведение находится в двойном слове,
для которого требуется два регистра: старшая (левая)
часть произведения находится в регистре DX, а
младшая (правая) часть в регистре AX.
 Операция
Операцияигнорирует и стирает любые данные, которые
находились в регистре DX.
MUL MULTR
MUL CL ;Байт-множитель: множимое в AL,
произвед. в AX
MUL BX ;Слово-множитель:множимое в AX,
произвед. в DX:AX
11. Беззнаковое умножение: Команда MUL
Команда MUL (MULtiplication — умножение)умножает беззнаковые числа.
Беззнаковое умножение: Команда MUL
12. Знаковое умножение: Команда IMUL
Команда IMUL (Integer MULtiplication умножение целых чисел) умножает знаковыечисла.
Знаковое умножение: Команда IMUL
13. Повышение эффективности умножения
Умножениена 2:
SHL AL,1
Умножение на 8:
MOV CL,3
SHL AX,CL
Повышение эффективности умножения
14. Многословное умножение
1365х
12
——2730
1365
——16380
Многословное умножение
13
х
12
—26
13
—156
65
х
12
—130
65
—780
15600
+
780
——16380
17. Умножение двойного слова на слово
Процедура E10XMUL умножает двойное слово наслово.
 Множимое, MULTCND, состоит из двух
Множимое, MULTCND, состоит из двухслов, содержащих соответственно шест.3206 и
шест.2521. Определение данных в виде двух слов
(DW) вместо двойного слова (DD) обусловлено
необходимостью правильной адресации для
команд MOV, пересылающих слова в регистр AX.
Множитель MULTPLR содержит шест.6400.
Умножение двойного слова на слово
Область для записи произведения, PRODUCT,
состоит из трех слов.
Первая команда MUL перемножает MULTPLR и
правое cлово поля MULTCND; произведение шест.0E80 E400 записывается в PRODUCT+2 и
PRODUCT+4.
Вторая команда MUL перемножает MULTPLR и
левое слово поля MULTCND, получая в
результате шест. 138A 5800.
Произведение 1: 00000E80E400
Произведение 2:
138A5800
—
Результат:
138A6680E400
20. Умножение двойного слова на двойное слово
слово2 слово 2
слово 2 слово 1
слово 1 слово 2
слово 1 слово 1
Каждое произведение в регистрах DX и AX
складывается с соответствующим словом в
окончательном результате.

Умножение двойного слова на двойное
слово
21. Сдвиг регистровой пары DX:AX
Сдвиг влево на 4 битаMOV CX,04 ;Инициализация на 4 цикла C20:
SHL DX,1 ;Сдвинуть DX на 1 бит влево
SHL AX,1 ;Сдвинуть AX на 1 бит влево
ADC DX,00 ;Прибавить значение переноса
LOOP C20 ;Повторить Сдвиг вправо на 4 бита
MOV CX,04 ;Инициализация на 4 цикла D20:
SHR AX,1 ;Сдвинуть AX на 1 бит вправо
SHR DX,1 ;Сдвинуть DX на 1 бит вправо
JNC D30 ;В случае, если есть перенос,
OR AH,10000000B ; то вставить 1 в AH D30:
LOOP D20 ;Повторить
Сдвиг регистровой пары DX:AX
MOV CL,04 ;Установить фактор сдвига
SHL DX,CL ;Сдвинуть DX влево на 4 бита
MOV BL,AH ;Сохранить AH в BL
SHL AX,CL ;Сдвинуть AX влево на 4 бита
SHL BL,CL ;Сдвинуть BL вправо на 4 бита
OR DL,BL ;Записать 4 бита из BL в DL
English Русский Правила
Программирование математических операций на Ассемблере в AVR Studio
Беззнаковые целые числа
Эта глава главным образом будет посвящена арифметическим операциям над большими беззнаковыми целыми числами (подробней о различных форматах чисел смотри в приложении Б). В приложениях на AVR-микроконтроллерах наиболее часто приходится использовать 16-разрядные вычисления, которые достаточно легко программируются. Двухбайтовые числа предоставляют достаточно широкий диапазон представления переменных. Однако, встречаются задачи в которых необходимо применение чисел и с большей разрядностью (счётчики импульсов, накопители суммы, промежуточные результаты вычислений и т.д.).
В приложениях на AVR-микроконтроллерах наиболее часто приходится использовать 16-разрядные вычисления, которые достаточно легко программируются. Двухбайтовые числа предоставляют достаточно широкий диапазон представления переменных. Однако, встречаются задачи в которых необходимо применение чисел и с большей разрядностью (счётчики импульсов, накопители суммы, промежуточные результаты вычислений и т.д.).
Сложение
Реализовать многобайтовое сложение очень просто. Для этого имеется специальная команда adc Rd,Rr, которая складывает содержимое двух регистров и добавляет к полученной сумме бит переноса C из регистре SREG (Rd <- Rd+Rr+С). Этот бит устанавливается всегда, когда в результате предыдущей операции сложения возникает переполнение (т.е. бит C всегда является 9-ым битом результата операции сложения). Так может выглядеть сложение двух 16-разрядных чисел R17:R16 и R19:R18 (сумма размещается на месте второго слагаемого R19:R18):
1 2 | add R18,R16 ;R18 <- R18 + R16 adc R19,R17 ;R19 <- R19 + R17 + C |
Необходимо помнить, что в результате сложения двух n-разрядных чисел возможно образование n+1-разрядной суммы. Например, в результате следующей операции сложения получим:
Например, в результате следующей операции сложения получим:
0xB2FF + 0xCC45 = 0x17F44 = 0x10000 + 0x7F44.
Сумма двухбайтовых слагаемых превысила максимальное 16-разрядное значение 0xFFFF = 65535 и вместо 0x17F44 = 98116 мы получили 0x7F44 = 32580. При этом должен установиться флаг C (17-тый разряд суммы), как признак того, что произошел перенос в старший разряд и к полученному результату необходимо добавить 0x10000 = 65536.
В регистре SREG имеется еще один бит непосредственно связанный с действием сложения. Это флаг половинного переноса H, который может использоваться в 4-разрядных вычислениях. Он носит тот же смысл, что и флаг C, но указывает на переполнение суммы младших полубайтов (т.е. перенос из третьего в четвертый разряды числа). Флаг H почти никогда не используется на практике.
Если для хранения результата вычисления не хватает РОНов, то сложение рационально производить с помощью косвенной адресации, а результат размещать в SRAM процессора. В этом случае разрядность слагаемых и вычисленной суммы будет ограничена только свободным местом в памяти данных.
Подпрограмма такого сложения:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | ; [YH:YL] = [YH:YL] + [XH:XL] ; [YH:YL] – первое слагаемое при входе и сумма при ; выходе (косвенно адресуется через YH:YL) ; [XH:XL] – второе слагаемое (косвенно адресуется через XH:XL) ; R16,R17,R18 – вспомогательные регистры ; composed1 – адрес 1-го слагаемого и ; полученной суммы в ОЗУ ; composed 2 – адрес 2-го слагаемого в ОЗУ ; SIZE – размер слагаемых в байтах ; на выходе в C находится старший разряд результата
add_indirect: ldi YH,high(composed1) ;заносим в указатель Y адрес ldi YL,low(composed1) ;первого слагаемого composed1 ldi XH,high(composed2) ;заносим в указатель Y адрес ldi XL,low(composed2) ;второго слагаемого composed2 ldi R16,SIZE clc ;при первом входе в цикл C=0 ad1: ld R17,X+ ld R18,Y ;поочерёдно складываем с учётом переноса adc R18,R17 ;все байты слагаемых и заносим результат st Y+,R18 ;по адресу первого слагаемого dec R16 brne ad1 ;повторяем сложение SIZE раз ret |
Вычитание
Подобно сложению с переносом в архитектуре AVR существует и команда вычитания с заемом sbc Rd,Rr. Для связи байтов в ней тоже участвует флаг C, который в этом случае обычно называется флагом заема. Бит C устанавливается каждый раз, когда результат предыдущей операции вычитания оказывается меньше нуля и автоматически вычитается из разности полученной после команды sbc Rd,Rr (Rd <- Rd-Rr-С). Ниже показан пример вычитания 16-разрядного числа R17:R16 из R19:R18 (разность помещается на место вычитаемого):
Для связи байтов в ней тоже участвует флаг C, который в этом случае обычно называется флагом заема. Бит C устанавливается каждый раз, когда результат предыдущей операции вычитания оказывается меньше нуля и автоматически вычитается из разности полученной после команды sbc Rd,Rr (Rd <- Rd-Rr-С). Ниже показан пример вычитания 16-разрядного числа R17:R16 из R19:R18 (разность помещается на место вычитаемого):
1 2 | sub R18,R16 ;R18 <- R18 — R16 sbc R19,R17 ;R19 <- R19 — R17 — C |
Разрядность разности при вычитании никогда не превысит разрядности делимого. Однако здесь возникает другая проблема, связанная с тем, что уменьшаемое может оказаться меньше вычитаемого. В результате такого действия мы получим установленный флаг C, как признак отрицательного результата. И хотя с точки зрения арифметики такая операция является вполне законной — она приводит к отрицательным числам, представленным в дополнительном коде, которые будут рассмотрены в следующем разделе.
Ниже приведена подпрограмма вычитания двух многобайтовых чисел, размещенных в SRAM.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | ; [YH:YL] = [YH:YL] — [XH:XL] ; [YH:YL] – уменьшаемое при входе и разность при ; выходе (косвенно адресуется через YH:YL) ; [XH:XL] – вычитаемое (косвенно адресуется через XH:XL) ; R16,R17,R18 – вспомогательные регистры ; reduced — адрес уменьшаемого и ; полученной разности в ОЗУ ; subtracted — адрес вычитаемого в ОЗУ ; SIZE – размер уменьшаемого и вычитаемого в байтах ; на выходе бит C=1 если [YH:YL] < [XH:XL]
sub_indirect: ldi YH, high(reduced) ;заносим в указатель Y адрес ldi YL, low(reduced) ;уменьшаемого reduced ldi XH, high(subtracted) ;заносим в указатель X адрес ldi XL, low(subtracted) ;вычитаемого subtracted ldi R16,SIZE clc ;при первом входе в цикл C=0 sb1: ld R17,X+ ld R18,Y ;поочерёдно вычитаем с учётом заёма из sbc R18,R17 ;уменьшаемого все байты вычитаемого и st Y+,R17 ;заносим результат по адресу уменьшаемого dec R16 brne sb1 ;повторяем вычитание SIZE раз ret |
Умножение
У микроконтроллеров AVR, по сути, имеется два пути реализации умножения, разница между которыми заключается в форме представления произведения и, соответственно, в различии выполняемых арифметических операций. Первый оптимизирован для использования с командой однобайтового умножения, второй – использует только сложение и сдвиговые операции. Для произведения n-разрядного множимого и m-разрядного множителя необходимо отводить n+m разрядов.
Первый оптимизирован для использования с командой однобайтового умножения, второй – использует только сложение и сдвиговые операции. Для произведения n-разрядного множимого и m-разрядного множителя необходимо отводить n+m разрядов.
Помимо этого существует особый случай умножения на целую степень 2. Всё дело в том, что 2 является основанием двоичной системы, а в любой позиционной системе операция умножения числа на основание системы приводит к увеличению веса каждого его разряда на порядок:
2*X = 2*(xn-1*2n-1 + xn-2*2n-2 + … + x1*21 + x0*20) = xn-1*2n + xn-2*2n-1 + … + x1*22 + x0*21.
Как видно, коэффициенты xn числа X переместились на один разряд влево (x0 стал при 21, x1 стал при 22 и т.д.). Итак, для умножения двоичного числа на 2n необходимо просто сдвинуть его на n разрядов влево. Так можно осуществить умножение на 2 двухбайтового числа в регистрах R17:R16 посредством сдвиговых операций:
1 2 | lsl R16 ;R16 <- R16 << 1 (LSB <- 0, флаг С <- MSB) rol R17 ;R17 <- R17 << 1 (LSB <- флаг С, флаг С <- MSB) |
Тот же результат можно получить, складывая число с самим собой:
1 2 | add R16, R16 adc R17, R17 |
Благодаря тому, что операции сдвига и сложения выполняются за одинаковое время (1 машинный цикл) оба примера равноценны.
Иногда встречаются операции умножения на число, которое близко к степени 2. В таких случаях намного проще заменить его суммой двух слагаемых, одно из которых кратно 2n, и использовать только операции сдвига и сложения (вычитания):
63*X = (26-1)*X = 26*X — X = X<<6 – X,
33*X = (25+1)*X = 25*X + X = X<<5 + X,
130*X = (27+2)*X = 27*X + 2*X = X<<7 + X<<2.
Для умножения 2-байтовых чисел (обозначим их как XH:XL = 28*XH + XL и YH:YL = 28*YH + YL) применяется следующая вычислительная схема:
XH:XL * YH:YL = (28*XH + XL)*(28*YH + YL) = 216*XH*YH + 28*(XH*YL + YH*XL) + XL*YL.
Рис.1 Вычислительная схема для умножения двухбайтовых чисел с использованием инструкции умножения
Отыскание 32-разрядного результата сводится к последовательности операций однобайтовых умножений и последующего сложения всех произведений с учётом сдвига слагаемых XH*YL, XL*YH на 1 байт и XH*YH на 2 байта, как показано на рис.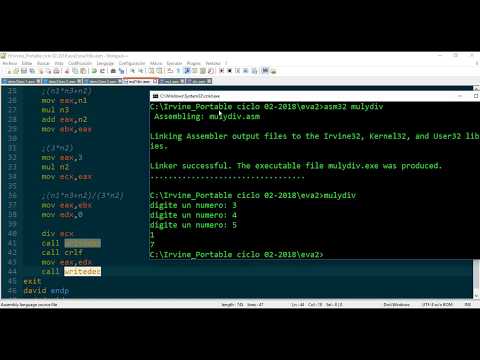 1. Подпрограмма, реализующая эти действия, приведена ниже. Напомним, что произведение двух однобайтовых множителей, полученное в результате выполнения команды mul Rd,Rr или любой другой команды умножения, всегда заносится в регистровую пару R1:R0.
1. Подпрограмма, реализующая эти действия, приведена ниже. Напомним, что произведение двух однобайтовых множителей, полученное в результате выполнения команды mul Rd,Rr или любой другой команды умножения, всегда заносится в регистровую пару R1:R0.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | ; R23:R22:R21:R20 = R17:R16 * R19:R18 ; R23:R22:R21:R20 — произведение ; R17:R16 – множимое ; R19:R18 – множитель ; R1,R0 – вспомогательные регистры
mul16_16: mul R16,R18 ;находим XL*YL = R16*R18 и заносим его в movw R20,R0 ;младшие байты произведения R21:R20 mul R17,R19 ;находим XH*YH = R17*R19 и заносим его в movw R22,R0 ;старшие байты произведения R23:R22 mul R17,R18 ;находим XH*YL = R17*R18 и прибавляем его к clr R17 ;байтам R23:R22:R21 произведения add R21,R0 adc R22,R1 adc R23,R17 mul R16,R19 ;находим YH*XL = R19*R16 и прибавляем его к add R21,R0 ;байтам R23:R22:R21 произведения adc R22,R1 adc R23,R17 ret |
Возвести двухбайтовое число в квадрат еще проще:
XH:XL * XH:XL = (28*XH + XL)*(28*XH + XL) = 216*XH*XH + 28*2*XH*XL + XL*XL.
Подпрограмма возведения в квадрат приведена ниже. Она является хорошим примером того, где может пригодиться инструкция fmul Rd,Rr, которая одним действием производит умножение двух однобайтовых чисел и сдвиг произведения на 1 разряд влево.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | ; R21:R20:R19:R18 = R17:R16 * R17:R16 ; R17:R16 – число, возводимое в квадрат ; R21:R20:R19:R18 – произведение ; R1,R0 – вспомогательные регистры
sqr16_16: mul R16,R16 ;находим XL*XL = R16*R16 и заносим его в movw R18,R0 ;младшие байты произведения R19:R18 mul R17,R17 ;находим XH*XH = R17*R17 и заносим его в movw R20,R0 ;старшие байты произведения R21:R20 fmul R17,R16 ;находим 2*XH*YL = R17*R18 и прибавляем его clr R17 ;к байтам R21:R20:R19 произведения rol R17 add R19,R0 adc R20,R1 adc R21,R17 ret |
Во многих случаях команда fmul Rd,Rr позволяет использовать аппаратный умножитель 8×8 фактически как умножитель 9×8 с получением 17-разрядного результата (MSB произведения размещается в C). Это бывает очень полезно, когда возникает необходимость умножить переменную на постоянный числовой коэффициент, который немного выходит за пределы 8-разрядной сетки. Так, допустим, можно умножить число из R16 на 500
Это бывает очень полезно, когда возникает необходимость умножить переменную на постоянный числовой коэффициент, который немного выходит за пределы 8-разрядной сетки. Так, допустим, можно умножить число из R16 на 500
1 2 | ldi R17,250 ;R1:R0 <- (250<<1)*R16 = 500*R16 fmul R17,R16 ; флаг С <- MSB |
или на 1000:
1 2 3 4 | ldi R17,250 ;R1:R0 <- (250<<2)*R16 = 1000*R16 fmul R17,R16 ;флаг С <- MSB lsl R0 rol R1 |
Ниже показан другой практически важный пример умножения, когда один из множителей (множитель X) однобайтовый.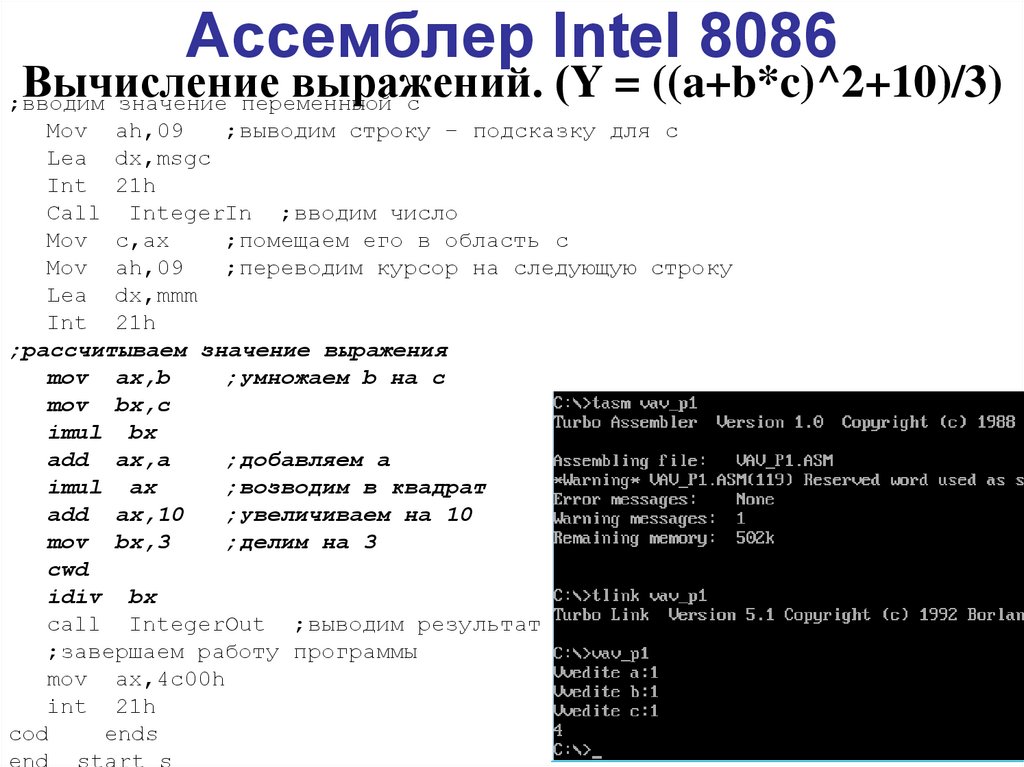 В основе подпрограммы лежит следующая вычислительная схема:
В основе подпрограммы лежит следующая вычислительная схема:
X * YH:YL = X*(28*YH + YL) = 28*X*YH + X*YL
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | ; R21:R20:R19 = R18 * R17:R16 ; R21:R20:R19 — произведение ; R18 – множимое ; R17:R16 – множитель ; R1,R0 – вспомогательные регистры
mul8_16: mul R18,R17 ;находим X*YH = R18*R17 и заносим его в movw R20,R0 ;старшие байты произведения R21:R20 mul R18,R16 ;находим X*YL = R18*R16 clr R18 add R19,R0 ;и прибавляем его add R20,R1 ;к произведению R21:R20:R19 adc R21,R18 ret |
Точно также могут быть разложены числа и с большей разрядностью. Однако с ростом их величины начинают резко возрастать и затраты ресурсов процессора. Так для умножения трёхбайтовых чисел понадобится по 9 операций однобайтовых умножений и двухбайтовых сложений; для четырёхбайтовых уже по 16 операций и т.д.
Однако с ростом их величины начинают резко возрастать и затраты ресурсов процессора. Так для умножения трёхбайтовых чисел понадобится по 9 операций однобайтовых умножений и двухбайтовых сложений; для четырёхбайтовых уже по 16 операций и т.д.
В подобных случаях необходимо использовать другой, наиболее общий алгоритм, который не использует команду mul Rd,Rr. А для микроконтроллеров семейства ATtiny, (а также для устаревшей линейки моделей Classic), у которых отсутствует аппаратный умножитель, он вообще является единственно возможным.
Для пояснения алгоритма, перепишем произведение Z двух произвольных двоичных чисел
Произведение X*yj называется частичным произведением (X*yj = X при yj =1 и X*yj = 0 при yj =0), а произведение (X*yj)*2j есть не что иное, как частичное произведение, сдвинутое на j разрядов влево. Итак, нахождение произведение X*Y сводится к нахождению суммы частичных произведений X*yj, каждое из которых в свою очередь сдвинуто на j разрядов влево соответственно. На этом принципе основан школьный метод умножения в столбик. Рассмотрим пример умножения двух 4-разрядных чисел:
На этом принципе основан школьный метод умножения в столбик. Рассмотрим пример умножения двух 4-разрядных чисел:
Как видим, для получения результата используются только операции сложения и сдвига. При этом в тех разрядах Y, где yj=0 и X*yj=0. И если предварительно анализировать значения yj/, то можно пропускать пустое сложение с 0 в соответствующих итерациях. Ниже приведена подпрограмма умножения двух трёхбайтовых чисел. В ней для получения суммы частичных произведений, сдвинутых каждое на j разрядов влево, производится сдвиг накопителя произведений m=24 раза вправо, а для экономии памяти младшие 3 байта произведения заносятся в те же регистры, где находился множитель.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | ; R24:R23:R22:R21:R20:R19 = R18:R17:R16 * R21:R20:R19 ; R24:R23:R22:R21:R20:R19 – произведение ; R18:R17:R16 – множимое ; R21:R20:R19 – множитель ; R25,R1,R0 – вспомогательный регистр
mul24_24: clr R22 ;очищаем регистры R22,R23,R24 clr R23 ;при входе в подпрограмму clr R24 ldi R25,24 ;инициализируем счётчик циклов сложения clc ;сдвинутых частичных произведений ml1: sbrs R19,0 ;если младший бит множителя 1, то rjmp ml2 add R22,R16 ;добавляем к накопителю очередное adc R23,R17 ;частичное произведение R18:R17:R16 adc R24,R18 ml2: ror R24 ;байтам R24:R23:R22 накопителя произведения ror R23 ;в ином случае пропускаем это действие ror R22 ;и переходим к очередному сдвигу множителя ror R21 ror R20 ror R19 clc dec R25 ;повторяем m=24 раз цикл сложения brne ml1 ;сдвинутых частичных произведений ret |
Деление
Из всех арифметических операций деление занимает особое место. По отношению к умножению деление является обратной операцией и не имеет конечной формулы для определения частного. Деление – единственная арифметическая операция ограниченной точности! Не смотря на это алгоритмы деления достаточно просты. Ниже будут показаны два таких алгоритма, которые используют только операции вычитания и сдвигов. Для того чтобы получить результат в виде целочисленных частного и остатка нужно предварительно убедиться в том, чтобы делимое было больше делителя и, конечно, исключить возникновение запрещённой операции деления на 0. При делении n-разрядного делимого на m-разрядный делитель под частное необходимо отвести n, а под остаток m разрядов.
По отношению к умножению деление является обратной операцией и не имеет конечной формулы для определения частного. Деление – единственная арифметическая операция ограниченной точности! Не смотря на это алгоритмы деления достаточно просты. Ниже будут показаны два таких алгоритма, которые используют только операции вычитания и сдвигов. Для того чтобы получить результат в виде целочисленных частного и остатка нужно предварительно убедиться в том, чтобы делимое было больше делителя и, конечно, исключить возникновение запрещённой операции деления на 0. При делении n-разрядного делимого на m-разрядный делитель под частное необходимо отвести n, а под остаток m разрядов.
Частным случаем является деление на целую степень 2:
X/2 = (x-1*2n-1 + xn-2*2n-2 + … + x1*21 + x0*20 )/2 = xn-1*2n-1 + xn-2*2n-2 + … + x1*20 + x0*1/21
Все коэффициенты xn двоичного числа X переместились на один разряд вправо (x0 стал при 1/21, x1 стал при 20 и т.д.). Таким образом для деления двоичного числа на 2n необходимо произвести сдвиг его содержимого на n разрядов в правую сторону.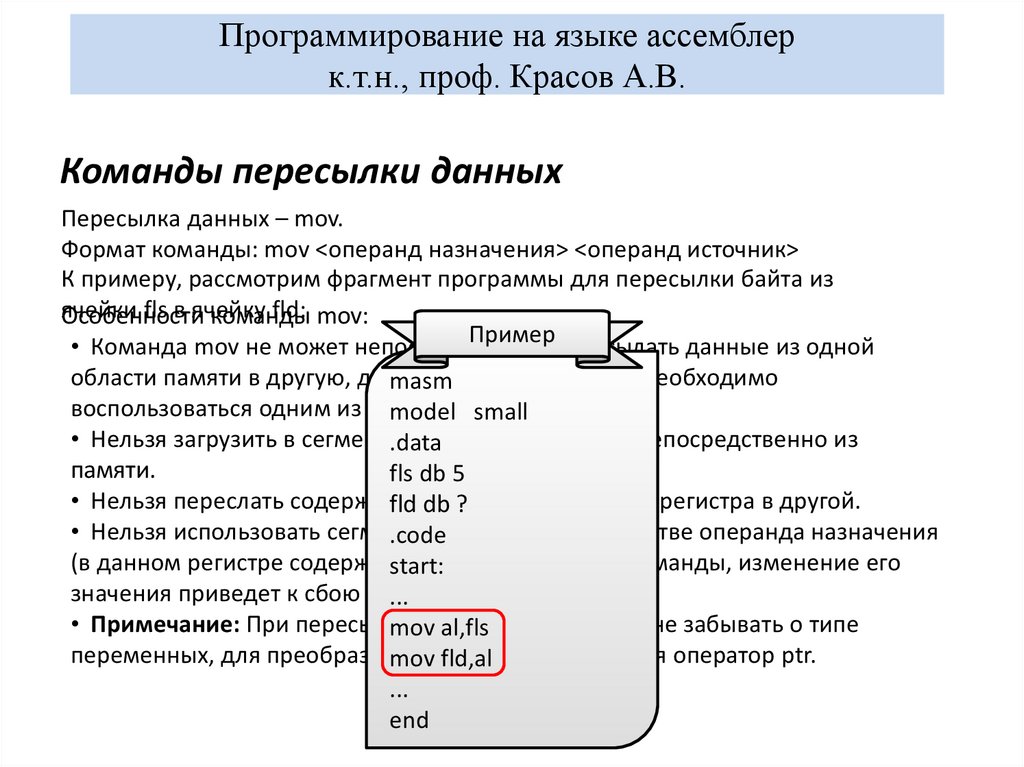 Так выглядит деление на 2 16-разрядного числа в регистрах R17:R16:
Так выглядит деление на 2 16-разрядного числа в регистрах R17:R16:
1 2 | lsr R17 ; R17 <- R17 >> 1 (MSB <- 0, флаг С <- LSB) ror R16 ; R16 <- R16 >> 1 (MSB <- С, флаг С <- LSB) |
Обратите внимание на то, что после сдвига вправо во флаге переноса С окажется целочисленный остаток (младший коэффициент x0) от деления на 2.
Для другого частного случая деления на 3 существует один очень интересный алгоритм, основанный на разложении дроби X/3 в ряд вида:
X/3 = X/2 — X/4 + X/8 — X/16 + X/32 — …
Каждый член ряда получается делением X на целую степень 2, что как было показано выше, легко реализуется сдвиговыми операциями. Ниже приведена подпрограмма деления на 3 16-разрядного числа.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | ; R19:R18 = R17:R16/3 ; R19:R18 – частное ; R17:R16 – делимое ; R20 – вспомогательный регистр
div16to3: clr R18 ;очищаем вспомогательные регистры R18,R19 clr R19 ;при входе в подпрограмму du1: rcall shft_right brne PC+2 ;если Z=1, ret ;то завершаем деление add R18,R16 ;в ином случае добавляем к накопителю adc R19,R17 ;очередной нечётный член ряда rcall shift_right brne PC+2 ;если Z=1, ret ;то завершаем деление sub R18,R16 ;в ином случае вычитаем из накопителя sbc R19,R17 ;очередной чётный член ряда rjmp du1
shft_right: lsr R17 ;производим деление R17:R16 / 2, ror R16 ;получая очередной член ряда mov R20,R17 ;если R20 = R17+R16 = 0 (т. or R20,R16 ;то выходим из подпрограммы с флагом Z=1 ret |
Этот пример очень эффективен. Его быстродействие ограничено только разрядностью делимого. Более того для делимого произвольной величины обрабатывается оптимальное число членов ряда (до 16), а результат автоматически округляется до ближайшего целого числа.
Естественно, что в тех случаях, когда необходимо разделить число на 6 можно совместно использовать приемы деления на 2 и 3:
X/6 = (X/2)/3 = (X >> 1)/3 = (X/3) >> 1
Для уменьшения погрешности деление чётных чисел следует начинать с деления на 2 (остаток 0) а, деление нечётных с деления на 3 (алгоритм этого вида деления учитывает остаток).
В общем случае самый естественный и простой способ разделить одно число на другое – это решить уравнение, вытекающее непосредственно из определения операции деления:
X = Z*Y + R,
R < Y, Y ≠ 0,
где X – делимое, Y – делитель, Z – частное, R – целочисленный остаток от деления.
Уравнение содержит два неизвестных параметра Z и R и поэтому не может быть явно разрешено. Для отыскания результата необходимо прибегнуть к итерационному методу: вычитать из делимого делитель до тех пор, пока остаток не окажется меньше делителя. Тогда число циклов вычитания численно даст частное Z, а остаток будет равен целочисленному остатку R от деления. Для примера, произведем следующее деление:
X = 213, Y = 10,
X — Z*Y = R, 213 – 21*10 = 3,
Z = 21, R = 3.
Мы 21 раз смогли вычесть из 213 по 10 пока не образовался остаток 3<10. Приведённый алгоритм имеет существенный недостаток – скорость его выполнения напрямую зависит от величины частного (числа итераций вычитания), что делает нежелательным его использование для деления больших чисел. Применяется он, в основном, в задачах ограниченных делением однобайтовых величин. Подпрограмма деления:
1 2 3 4 5 6 7 8 9 10 11 12 13 | ; [R18] + {R17} = R17 / R16 ; R18 – частное ; R17 – делимое при входе и целочисленный остаток на выходе ; R16 – делитель
div8_8: clr R18 ;очищаем R18 при входе sub R17,R16 ;производим вычитание R17-R16 inc R18 brcc PC-2 ;до тех пор пока разность R17-R16 > 0 dec R18 ;когда разность R17-R16 < 0 add R17,R16 ;восстанавливаем R17 и корректируем R18 ret |
Для чисел большей разрядности необходимо использовать способ деления, основанный на приведенной ниже вычислительной схеме. Для этого представим необходимо выражение операции деления в следующем виде:
Для этого представим необходимо выражение операции деления в следующем виде:
Нахождение частного сводится к отысканию его коэффициентов zi, которые определяются, согласно формуле, следующим образом: необходимо последовательно сравнивать X с произведениями Y*2i и если X > Y*2i, то в этом случае необходимо произвести вычитание Y*2i из X, а соответствующий разряд zi установить в 1; если X < Y*2i – вычитание пропускается и в этой итерации zi=0. Эта процедура продолжается до тех пор, пока не останется остаток Ri получаются простым сдвигом Y на i разрядов влево. Аналогично производится деление в любой позиционной системе (метод деления в столбик), но проще всего в двоичной из-за того, что в X может содержаться Y*2i максимум один раз (на что и указывает единица в соответствующем разряде). Рассмотрим пример деления:
Необходимо обратить внимание на то, что число итераций сравнения должно совпадать с числом значащих разрядов частного (в данном случае n=4 для определения z0…z3). Однако разрядность частного заранее никогда не известна и поэтому всегда необходимо знать максимально возможную разрядность результата деления. На практике чаще всего используют вычисления, в которых частное заведомо умещается в 8,16,24 бита (кратно одному байту) и т.д. При этом нужно использовать 8,16,24 итераций сравнения X с Y*2i, соответственно. С целочисленным остатком R проблем не возникает – его размер ограничен разрядностью Y (R < Y).
Однако разрядность частного заранее никогда не известна и поэтому всегда необходимо знать максимально возможную разрядность результата деления. На практике чаще всего используют вычисления, в которых частное заведомо умещается в 8,16,24 бита (кратно одному байту) и т.д. При этом нужно использовать 8,16,24 итераций сравнения X с Y*2i, соответственно. С целочисленным остатком R проблем не возникает – его размер ограничен разрядностью Y (R < Y).
Подпрограмма деления двухбайтового числа на однобайтовое приведена ниже. В ней для сравнения X с Y*2i (i ∈ {0,…,15}) вместо сдвига делителя Y на n разрядов вправо используется поочерёдный сдвиг делимого на n разрядов влево, а для экономии памяти частное записывается на тоже место, что и делимое. В начале программы осуществляется проверка условия Y ≠ 0, без которого деление не может быть корректно осуществлено.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | ; [R17:R16] + {R18} = R17:R16 / R20 ; R17:R16 – делимое при входе и частное на выходе ; R20 – делитель ; R18 – целочисленный остаток ; R21, R22 – вспомогательные регистры ; при выходе из подпрограммы в C находится признак ошибки ; если C = 1 – произошла ошибка (R20 = 0) ; если С = 0 – деление успешно выполнено
div16_8: tst R20 ;если R20=0 выходим из подпрограммы breq dv3 ;с признаком ошибки C=1 clr R18 ;очищаем регистры R18,R19,R21 при clr R19 ;входе в подпрограмму clr R21 ldi R22,16 ;инициализируем счётчик циклов dv1: lsl R16 ;сдвигаем делимое R17:R16 со rol R17 ;вспомогательными регистрами rol R18 ;R19,R18 на один разряд влево rol R19 sub R18,R20 ;осуществляем пробное вычитание sbc R19,R21 ;R19:R18 — R20 и если R19:R18 > R20, ori R16,0x01 ;то устанавливаем zi=1 brcc dv2 add R18,R20 ;в ином случае восстанавливаем делимое adc R19,R21 andi R16,0xFE ;и устанавливаем zi=0 dv2: dec R22 brne dv1 ;повторяем цикл n=16 раз clc ;успешно завершаем подпрограмму ret ;со флагом С=0 dv3: sec ;выходим из-за ошибки ret ;с флагом С=1 |
Ниже приведена еще одна важная подпрограмма, реализующая деление 4-хбайтового числа на двухбайтовое с получением 16-разрядных частного и остатка.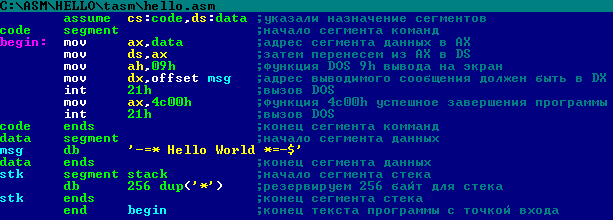 По своей структуре она аналогична предыдущей, кроме того, что при входе в подпрограмму производится проверка на переполнение результата и тем самым исключаются случаи, при которых частное может не умещаться в отведённых 2-х байтах (например, X = 0x51F356D, Y = 0x100, R = 0x6D, Z = 0x51F35 – имеет разрядность более 16 бит).
По своей структуре она аналогична предыдущей, кроме того, что при входе в подпрограмму производится проверка на переполнение результата и тем самым исключаются случаи, при которых частное может не умещаться в отведённых 2-х байтах (например, X = 0x51F356D, Y = 0x100, R = 0x6D, Z = 0x51F35 – имеет разрядность более 16 бит).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | ; [R17:R16] + {R21:R20} = R19:R18:R17:R16 / R23:R24 ; R17:R16 – частное ; R21:R20 — целочисленный остаток ; R19:R18:R17:R16 – делимое ; R23:R24– делитель ; R25,R26 – вспомогательный регистр ; при выходе из подпрограммы в C находится признак ошибки ; если C = 1 – произошла ошибка (R23:R24 = 0 или размер ; частного больше 2 байт) ; если С = 0 – деление успешно выполнено
div32_16: mov R20,R23 ;если R20 = R23 + R24 = 0 or R20,R24 ;(т. breq dv3 ;подпрограммы с признаком ошибки C=1 cp R18,R23 ;если R19:R18 < R24:R23 cpc R19,R24 ;(т.е.частное больше 2-х байт), то выходим brcc dv3 ;из подпрограммы с признаком ошибки C=1 clr R20 ;очищаем регистры R20,R21,R22,R25 clr R21 ;при входе в подпрограмму clr R22 clr R25 ldi R26,32 ;инициализируем счётчик циклов dv1: lsl R16 ;сдвигаем делимое R19:R18:R17:R16 со rol R17 ;вспомогательными регистрами R20, R21, R22 rol R18 ;на один разряд влево rol R19 rol R20 rol R21 rol R22 sub R20,R23 ;осуществляем пробное вычитание sbc R21,R24 ;R22:R21:R20 — R24:R23 и если sbc R22,R25 ;R22:R21:R20 > R24:R23, ori R16,0x01 ;то устанавливаем zi=1 brcc dv2 add R20,R23 ;в ином случае восстанавливаем делимое adc R21,R24 adc R22,R25 andi R16,0xFE ;и устанавливаем zi=0 dv2: dec R26 ;повторяем n=32 раза цикл brne dv1 ;сравнения R20:R19:R18 с R22:R21 clc ;успешно завершаем подпрограмму ret ;с флагом С=0 dv3: sec ;выходим из-за ошибки ret |
Формы представления частного в операциях деления
Все подпрограммы деления, приведенные в предыдущем разделе, возвращают на выходе результат в виде целочисленных частного Z и остатка R
X = 11, Y = 4,
X/Y = Z + R,
11/4 = [2] + {3}.
Однако при попытке продолжить деление, по аналогии с подобным действием в десятичной системе, что иногда бывает необходимо на практике, мы получим частное, представленное в форме дробного числа с фиксированной запятой
X = 11, Y = 4,
X/Y = Z + R,
11/4 = 0b10.11
Работа с такими числами ни чем не отличается от работы с неотрицательными целыми числами. Разница состоит лишь в том – где фиксируется дробная часть результата. Так результат деления 11/4 дал целую часть числа 2 и дробную (отделённые младшие два разряда) 0.75. Теперь если вам потребуется использовать этот результат в последующих арифметических операциях, то нужно просто запомнить где находится разделяющая запятая и соответственно определить веса каких разрядов 2n, а каких 1/2m. Тоже число 0b1011 может трактоваться по-разному в зависимости от того сколько разрядов отведено под целую и дробную части
0b1.011 = 1*20 + 0*(1/21) + 1*(1/22) + 1*(1/23) = 1.375 (формат (1.3)),
0b10.11 = 1*21 + 0*20 + 1*(1/21) + 1*(1/22) = 2. 750 (формат (2.2)),
750 (формат (2.2)),
0b101.1 = 1*22 + 0*21 + 1*20 + 1*(1/21) = 5.500 ( формат (3.1)) и т.д.
Рассмотрим как можно, например, сложить два дробных числа, предварительно приведя их к одному виду:
11/4 + 7/8 = 0b1011/0b0100 + 0b0111/0b1000 = 0b1011 >> 2 + 0b0111 >> 3 = 0b10.11 + 0b0.111 = 0b10.110 + 0b00.111 = 0b11.101 = 3.625
Дробные двоичные слагаемые 0b10.11 = 2.750 (формат (2.2)) и 0b0.111 = 0.875 (формата (1.3)) были приведены к единому формату представления (2.3) (0b10.110, 0b00.111), где целую и дробную части отделяют запятая между третьим и четвёртым разрядами. После этого мы их сложили, как два обыкновенных семизначных числа. Итак, дробные числа с фиксированной запятой – подчиняются всем тем же законам двоичной арифметики, что и целые числа.
В случае использования дробных чисел с фиксированной запятой в промежуточных вычислениях необходимо заранее ограничить разрядность дробной части результата. Это обусловлено тем, что при делении возможно образование бесконечных дробей, как допустим, 179/9 = 0b1001. 100001… = 10.515625….
100001… = 10.515625….
Округление двоичных чисел происходит точно так же, как и в десятичной системе исчисления. Если дробный остаток от деления ≥0.5 (т.е. если старший разряд в остатке, вес которого как раз 1/21, равен 1) или целочисленный остаток R≥0,5*Y , то частное Z округляется в большую сторону. Так при делении 9/2 = 0b100.1 = 4.5 необходимо учесть дробную часть 0.5 и округлить частное до 5, а, например, при делении 9/4 = 0b10.01 = 2.25 остаток 0.25 надо отбросить.
Другим способом произвести корректировку частного можно, если добавить к нему 1/2. Тогда можно будет свободно отбросить остаток, поскольку округление в большую сторону будет происходить каждый раз, когда R≥0,5. Добавление 1/2 к частному равносильно добавлению перед делением к делимому половины делителя
(X + Y/2) / Y = X/Y + 1/2 = Z + 1/2.
Подпрограмма, приведенная ниже вносит такую поправку перед делением 15-разрядного делимого на 8-разрядный делитель.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | ; R17:R16 + R18 / 2 = (2*R17:R16 + R18) / 2 ; R17:R16 – делимое, подлежащее корректировке ; R18 – делитель ; R19 – вспомогательный регистр
cor_div: clr R19 ;обнуляем R20 lsl R16 ;умножение 2*R17:R16 rol R17 add R16,R18 ;сложение 2*R17:R16 + R18 adc R17,R19 ror R17 ;деление (2*R17:R16 + R18)/2 ror R16 adc R16,R19 ;корректируем (2*R17:R16 + R18)/2 adc R17,R19 ;если остаток ≥0,5 ret |
Арифметические операции.
 Умножение и деление | RadioLaba.ru
Умножение и деление | RadioLaba.ru;Подпрограмма умножения однобайтных чисел (varLL)x(tmpLL)
;Первое число предварительно загружается в регистр varLL
;Второе число предварительно загружается в регистр tmpLL
;Результат умножения в регистре varHL, varLL, максимальный резултат
;составит 255х255=65025 (двухбайтное число)
;в подпрограмме используется дополнительный регистр regLL, для хранения константы
axb clrf varLH ;очистка регистра varLH (эквивалентно записи нуля)
movlw .0 ;побитное исключающее «или» числа ноль и числа лежащего в
xorwf varLL,W ;регистре varLL: это проверка равенства нулю числа лежащего
btfsc STATUS,Z ;в регистре varLL
return ;число в регистре varLL равно нулю: выход из подпрограммы
movlw .0 ;число в регистре varLL не равно нулю: проверка равенства
xorwf tmpLL,W ;нулю числа лежащего в регистре tmpLL
btfsc STATUS,Z ;
goto a1 ;число в регистре tmpLL равно нулю: переход на метку a1
movf varLL,W ;число в tmpLL не равно нулю: копирование числа из varLL
movwf regLL ;в регистр regLL, в качестве константы для дальнейшего сложения
a3 decfsz tmpLL,F ;декремент (с условием) регистра tmpLL, регистр tmpLL
;выступает в качестве счетчика сложений
goto a2 ;регистр tmpLL не равен нулю: переход на метку a2
return ;регистр tmpLL равен нулю: выход из подпрограммы
a2 movf regLL,W ;прибавление числа из регистра regLL к числу
addwf varLL,F ;в регистре varLL
btfsc STATUS,C ;проверка переполнения регистра varLL
incf varLH,F ;переполнение varLL: инкремент регистра varLH
goto a3 ;переход на метку a3
a1 clrf varLL ;очистка регистра varLL (эквивалентно записи нуля)
return ;выход из подпрограммы
;
;Подпрограмма умножения двухбайтного и однобайтного числа (varLH, varLL)x(tmpLL)
;Двухбайтное число предварительно загружается в регистры varLH (старший байт) и varLL (младший байт)
;Однобайтное число предварительно загружается в регистр tmpLL
;Результат умножения в регистрах varHL, varLH, varLL, максимальный резултат
;составит 65535х255=16 711 425 (трехбайтное число)
;в подпрограмме используются дополнительные регистры (regLL, regLH) для хранения константы
axb clrf varHL ;очистка регистра varHL (эквивалентно записи нуля)
movlw . 0 ;побитное исключающее «или» числа ноль и числа лежащего в
0 ;побитное исключающее «или» числа ноль и числа лежащего в
xorwf varLL,W ;регистре varLL: это проверка равенства нулю числа лежащего
btfss STATUS,Z ;в регистре varLL
goto a1 ;число в регистре varLL не равно нулю: переход на метку a1
movlw .0 ;число в регистре varLL равно нулю: проверка равенства
xorwf varLH,W ;нулю числа лежащего в регистре varLH
btfsc STATUS,Z ;
return ;число в регистре varLH равно нулю: выход из подпрограммы
a1 movlw .0 ;число в регистре varLH не равно нулю: проверка равенства
xorwf tmpLL,W ;нулю числа лежащего в регистре tmpLL
btfsc STATUS,Z ;
goto a2 ;число в регистре tmpLL равно нулю: переход на метку a2
movf varLL,W ;число в регистре tmpLL не равно нулю: копирование чисел из
movwf regLL ;из регистров varLL, varLH в регистры regLL, regLH в
movf varLH,W ;качечтве константы для дальнейшего сложения
movwf regLH
a4 decfsz tmpLL,F ;декремент (с условием) регистра tmpLL, регистр tmpLL
;выступает в качестве счетчика сложений
goto a3 ;регистр tmpLL не равен нулю: переход на метку a3
return ;регистр tmpLL равен нулю: выход из подпрограммы
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
a3 movf regLL,W ;
addwf varLL,F ;
btfss STATUS,C ;
goto a5 ;
incfsz varLH,F ;прибавление двухбайтного числа (regLH, regLL) к трехбайтному
goto a5 ;числу в регистрах varHL, varLH, varLL, то есть это операция
incf varHL,F ;сложения трехбайтного и двухбайтного числа
a5 movf regLH,W ;
addwf varLH,F ;
btfsc STATUS,C ;
incf varHL,F ;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
goto a4 ;переход на метку a4
a2 clrf varLL ;очистка регистров varLL, varLH (эквивалентно записи нуля)
clrf varLH
return ;выход из подпрограммы
;
;Подпрограмма умножения двухбайтных чисел (varLH, varLL)x(tmpLH, tmpLL)
;Первое число предварительно загружается в регистры varLH, varLL
;Второе число предварительно загружается в регистр tmpLH, tmpLL
;Результат умножения в регистрах varHH, varHL, varLH, varLL, максимальный резултат
;составит 65535х65535=4 294 836 225 (четырехбайтное число)
;в подпрограмме используются дополнительные регистры (regLL, regLH) для хранения константы
axb clrf varHL ;очистка регистров varHL, varHH (эквивалентно записи нуля)
clrf varHH ;
movlw .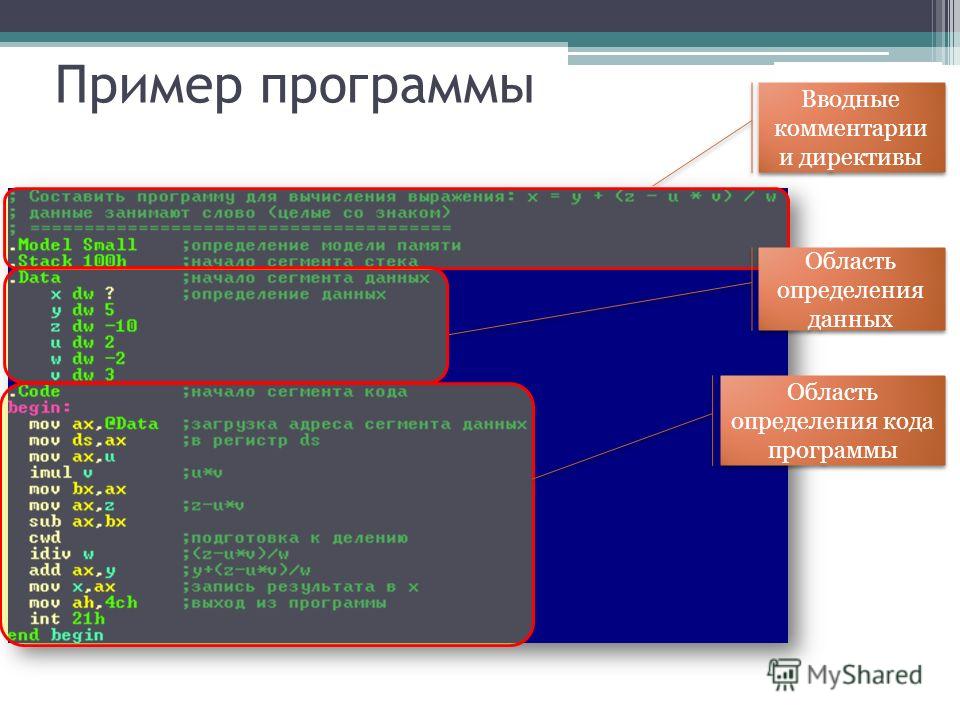 0 ;побитное исключающее «или» числа ноль и числа лежащего в
0 ;побитное исключающее «или» числа ноль и числа лежащего в
xorwf varLL,W ;регистре varLL: это проверка равенства нулю числа лежащего
btfss STATUS,Z ;в регистре varLL
goto a1 ;число в регистре varLL не равно нулю: переход на метку a1
movlw .0 ;число в регистре varLL равно нулю: проверка равенства
xorwf varLH,W ;нулю числа лежащего в регистре varLH
btfsc STATUS,Z ;
return ;число в регистре varLH равно нулю: выход из подпрограммы
a1 movlw .0 ;число в регистре varLH не равно нулю: проверка равенства
xorwf tmpLL,W ;нулю числа лежащего в регистре tmpLL
btfss STATUS,Z ;
goto a6 ;число в регистре tmpLL не равно нулю: переход на метку a6
movlw .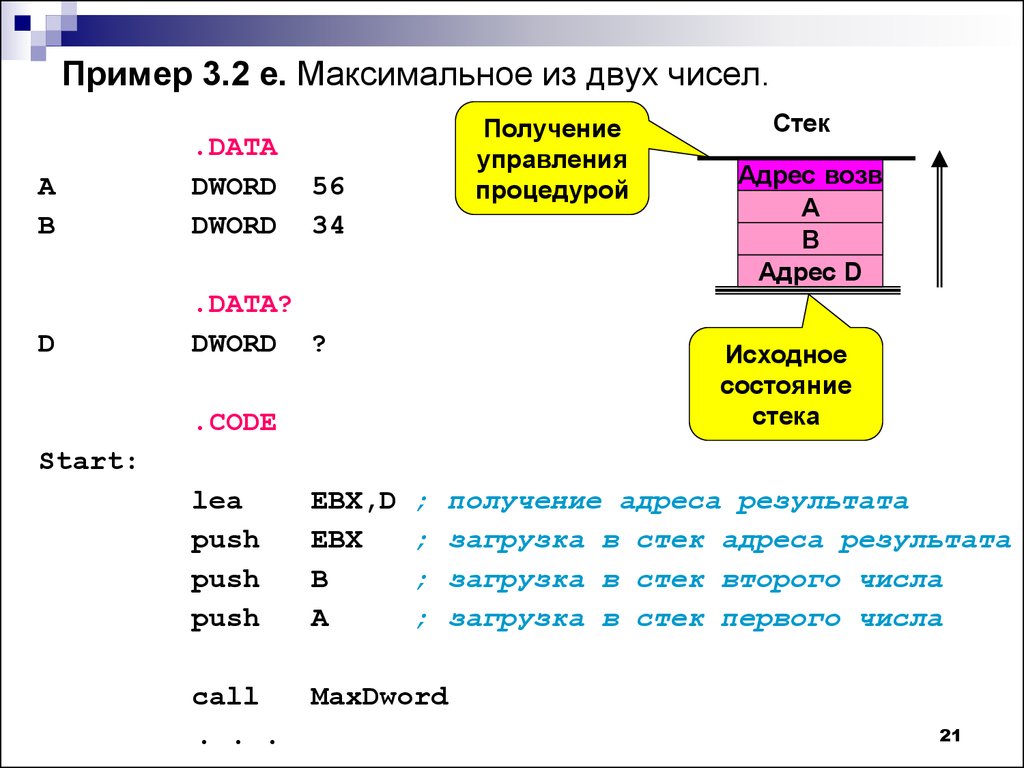 0 ;число в регистре varLH равно нулю: проверка равенства
0 ;число в регистре varLH равно нулю: проверка равенства
xorwf tmpLH,W ;нулю числа лежащего в регистре tmpLH
btfsc STATUS,Z ;
goto a2 ;число в регистре tmpLH равно нулю: переход на метку a2
a6 movf varLL,W ;число в регистре tmpLH не равно нулю: копирование чисел из
movwf regLL ;из регистров varLL, varLH в регистры regLL, regLH в
movf varLH,W ;качестве константы для дальнейшего сложения
movwf regLH ;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
a4 movlw .1 ;
subwf tmpLL,F ;
btfsc STATUS,C ;
goto a7 ;
decf tmpLH,F ;декремент двухбайтного числа в регистрах tmpLL, tmpLH
a7 movlw . 0 ;Регистры tmpLL, tmpLH выступают в качестве счетчика сложений
0 ;Регистры tmpLL, tmpLH выступают в качестве счетчика сложений
xorwf tmpLL,W ;
btfss STATUS,Z ;если значения регистров tmpLL, tmpLH не равны нулю то
goto a3 ;переходим на метку a3, если равны нулю выходим из подпрограммы
movlw .0 ;
xorwf tmpLH,W ;
btfsc STATUS,Z ;
return ;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
a3 movf regLL,W ;
addwf varLL,F ;
btfss STATUS,C ;
goto a5 ;
incfsz varLH,F ;прибавление двухбайтного числа (regLH, regLL) к четырехбайтному
goto a5 ;числу в регистрах varHH, varHL, varLH, varLL, то есть это
incfsz varHL,F ;операция сложения четырехбайтного и двухбайтного числа
goto a5 ;
incf varHH,F ;
a5 movf regLH,W ;
addwf varLH,F ;
btfss STATUS,C ;
goto a4 ;
incfsz varHL,F ;
goto a4 ;
incf varHH,F ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
goto a4 ;переход на метку a4
a2 clrf varLL ;очистка регистров varLL, varLH (эквивалентно записи нуля)
clrf varLH ;
return ;выход из подпрограммы
;
4 Умножение и деление
4 Умножение и делениеДалее: 5-битные манипуляции и Up: Лабораторное руководство для Предыдущий: 3 Реализация управляющих структур
Охватить операции SPARC, связанные с умножением и делением.
После выполнения этой лабораторной работы вы сможете писать на ассемблере программы, которые используют:
- Знаковые и беззнаковые операции умножения и деления,
В этой лабораторной работе мы рассматриваем операции SPARC, связанные с целыми числами. умножение и деление. Начнем с рассмотрения подписанного целочисленные операции умножения и деления.
Операции целочисленного умножения умножают два 32-битных источника. значения и получить 64-битный результат. Старшие 32 бита результат сохраняется в регистре Y (%y), а остальные 32 биты хранятся в одном из целочисленных регистров. Рисунок 4.1 иллюстрирует использование регистра Y во время умножения операция.
Рисунок 4.1: Целочисленное умножение
Операции целочисленного деления делят 32-битное значение на 64-битное.
значение и получить 32-битный результат. Регистр Y обеспечивает наиболее
значащие 32 бита 64-битного делимого. Одно из исходных значений
предоставляет младшие 32 бита, в то время как другой обеспечивает
32-битный делитель.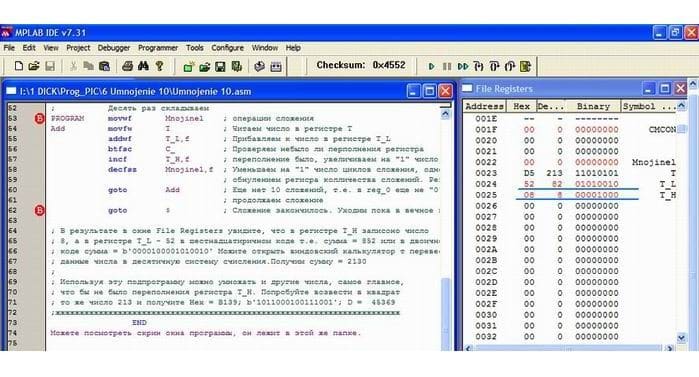 Реализация SPARC может дополнительно хранить
остаток в регистре Y. ISEM хранит остаток в , а не в .
в регистре Y, поэтому мы примем это соглашение в нашем
презентация. Рисунок 4.2 иллюстрирует использование Y
зарегистрироваться во время операции разделения.
Реализация SPARC может дополнительно хранить
остаток в регистре Y. ISEM хранит остаток в , а не в .
в регистре Y, поэтому мы примем это соглашение в нашем
презентация. Рисунок 4.2 иллюстрирует использование Y
зарегистрироваться во время операции разделения.
Рисунок 4.2: Целочисленное деление
В таблице 4.1 приведен синтаксис языка ассемблера для целочисленные операции умножения и деления, предоставляемые SPARC. Подобно операциям сложения и вычитания, умножение и операции деления имеют два формата языка ассемблера: один использует регистры для обоих исходных операндов и другой, который использует регистр и небольшое постоянное значение для исходных операндов.
Таблица 4.1: Форматы языка ассемблера для целочисленного умножения и
операции отдела
В Таблице 4.2 приведены имена для подписанных и неподписанных
целочисленные операции умножения и деления. Обратите внимание, что каждый
операция имеет две операции SPARC: одна, которая влияет на биты в
регистр кода состояния (например, smulcc) и другой, который не
(например, смул). Пример 4.1 иллюстрирует использование этих
операции.
Пример 4.1 иллюстрирует использование этих
операции.
Таблица 4.2: Умножение и деление целых чисел со знаком и без знака
операции
Пример: Напишите программу SPARC для вычисления оператора a = ( a * b )/ c . В при написании этого кода вы должны предположить, что a , b и c являются целочисленные значения со знаком и что все результаты могут быть представлены в 32 биты.
.данные
а: .слово 0x42
б: .слово 0x43
с: .слово 0x44
.текст
начало: установить a, %r1
лд [%r1], %r2
набор б, %r1
лд [%r1], %r3
набор с, %r1
лд [%r1], %r4
смул %r2, %r3, %r2 ! а* б --> %y, %r2
сдив %r2, %r4, %r2 ! %y, %r2 / c --> %r2
установить а, %r1
ст %r2, [%r1] ! %r2 --> а
конец: та 0
Подписанные и неподписанные операции отличаются тем, как они
интерпретировать их операнды. Подписанные операции интерпретируют свои
исходные операнды как целые числа со знаком и производят целые числа со знаком.
Беззнаковые операции интерпретируют свои исходные операнды как беззнаковые.
целые числа и производят целые числа без знака.
Подписанные операции интерпретируют свои
исходные операнды как целые числа со знаком и производят целые числа со знаком.
Беззнаковые операции интерпретируют свои исходные операнды как беззнаковые.
целые числа и производят целые числа без знака.
Операции с именами, оканчивающимися на «cc», обновляют биты в регистр кода состояния. Целочисленные операции умножения (smulcc и umulcc) всегда очищайте биты V (переполнение) и C (перенос) регистра кода состояния. Кроме того, эти операции обновляют биты N (отрицательный) и Z (нулевой) регистра кода состояния. Хотя операции умножения дают 64-битный результат, обновления флагов N и Z основаны только на наименее значимых 32 бита результата. Как и операции умножения, операции деления (sdivcc и udivcc) также очищают бит C в регистр кода состояния. Кроме того, обновление операций дивизии биты N, Z и V в регистре кода состояния в зависимости от значения 32-битного результата.
Обратите внимание, что код, представленный в примере 4. 1, не требует
проверить или установить значение в регистре Y. Умножение
устанавливает регистр Y, и деление использует значение, установленное
умножение. Во многих других случаях вам нужно будет изучить или установить
содержимое регистра Y. В частности, вам может понадобиться
проверить содержимое регистра Y после умножения или установки
содержимое регистра Y перед делением. Вы можете использовать
(синтетическая) операция mov, представленная в лабораторной работе 2 для копирования
содержимое регистра Y в целочисленный регистр или наоборот.
Вы также можете использовать операцию mov, чтобы установить содержимое Y
регистр. В Табл. 4.3 обобщена операция mov в том виде, в каком она
относится к регистру Y. Первый формат копирует содержимое
регистр Y в целочисленный регистр. Второй формат копирует
содержимое целочисленного регистра в регистр Y. Третий
Формат инструкции сохраняет маленькую целочисленную константу в Y
регистр.
1, не требует
проверить или установить значение в регистре Y. Умножение
устанавливает регистр Y, и деление использует значение, установленное
умножение. Во многих других случаях вам нужно будет изучить или установить
содержимое регистра Y. В частности, вам может понадобиться
проверить содержимое регистра Y после умножения или установки
содержимое регистра Y перед делением. Вы можете использовать
(синтетическая) операция mov, представленная в лабораторной работе 2 для копирования
содержимое регистра Y в целочисленный регистр или наоборот.
Вы также можете использовать операцию mov, чтобы установить содержимое Y
регистр. В Табл. 4.3 обобщена операция mov в том виде, в каком она
относится к регистру Y. Первый формат копирует содержимое
регистр Y в целочисленный регистр. Второй формат копирует
содержимое целочисленного регистра в регистр Y. Третий
Формат инструкции сохраняет маленькую целочисленную константу в Y
регистр.
Таблица 4.3: Операция перемещения применяется к регистру Y.
Когда вы сохраняете значение в регистре Y (используя инструкцию mov), требуется три командных цикла, прежде чем регистр Y будет фактически обновлено. Это означает, что вам нужно убедиться, что есть по крайней мере три инструкции между инструкцией, которая использует регистр Y как назначение и инструкция, которая использует значение, хранящееся в Y регистр.
Конвенция SPARC: Запись в регистр Y
Помните, всегда проверяйте наличие не менее трех инструкции между любой инструкцией, которая записывает в регистр %y и инструкция, которая использует значение в регистре %y.
Пример: Напишите фрагмент языка ассемблера SPARC для оценки оператора a = ( a + b ) / c . Опять же, вы должны предположить, что a , b и c являются целыми числами со знаком и что все результаты могут быть представлены в 32 биты.
.данные
а: .слово 0x42
б: .слово 0x43
с: .слово 0x44
. текст
начало: мов %r0, %y ! очистить регистр Y - ДОЛЖЕН БЫТЬ AT
! МИНИМУМ 3 ИНСТРУКЦИИ МЕЖДУ MOV И
! ИНСТРУКЦИЯ ПО СДВИВ
установить а, %r1
лд [%r1], %r2
набор б, %r1
лд [%r1], %r3
набор с, %r1
лд [%r1], %r4
текст
начало: мов %r0, %y ! очистить регистр Y - ДОЛЖЕН БЫТЬ AT
! МИНИМУМ 3 ИНСТРУКЦИИ МЕЖДУ MOV И
! ИНСТРУКЦИЯ ПО СДВИВ
установить а, %r1
лд [%r1], %r2
набор б, %r1
лд [%r1], %r3
набор с, %r1
лд [%r1], %r4
добавить %r2, %r3, %r2 ! а + б --> %r2
сдив %r2, %r4, %r2 ! %r2 / с --> %r2
установить а, %r1
ст %r2, [%r1] ! %r2 --> а
конец: та 0
До Версии 8 в SPARC не было целочисленного умножения или операции дивизии. Эти операции должны были выполняться с использованием более примитивные операции. Чтобы упростить целочисленное умножение, ранее версии SPARC обеспечивали многоступенчатую операцию «mulscc». Мы рассмотрим эту операцию в лабораторной работе 13, когда возьмем присмотритесь к целочисленной арифметике на SPARC.
В этой лабораторной работе мы рассмотрели целочисленное умножение и деление.
операций, предоставляемых SPARC. Как и в другой арифметике
операции (сложения и подстановки), есть варианты умножения и
операции деления, которые обновляют биты кода состояния и другие
операции умножения и деления, не меняющие условия
кодовые биты.
Как и в другой арифметике
операции (сложения и подстановки), есть варианты умножения и
операции деления, которые обновляют биты кода состояния и другие
операции умножения и деления, не меняющие условия
кодовые биты.
Все операции умножения и деления используют регистр специального назначения, регистр Y (%y). Вы можете использовать мов операция проверки и установки содержимого регистра Y.
- Как используется регистр Y при умножении целых чисел операции?
- Как используется регистр Y в операциях целочисленного деления?
Далее: 5-битные манипуляции и Up: Лабораторное руководство для Предыдущий: 3 Реализация управляющих структур Барни Маккейб
Пн, 2 сентября, 20:51:56 MDT 1996
2б. БАЗОВАЯ МАТЕМАТИКА — AVR ASM ВВЕДЕНИЕ
БАЗОВАЯ АРИФМЕТИКА AVR v1.7УМНОЖЕНИЕ, ДЕЛЕНИЕ, КВАДРАТНЫЙ И КУБИЧЕСКИЙ КОРЕНЬ от RetroDan@GMail.  Com ComСОДЕРЖИМОЕ:
1. УМНОЖЕНИЕ ДВУХ ОДНОБАЙТНЫХ ЧИСЕЛ С ПОМОЩЬЮ КОМАНДЫ MUL Если микросхема AVR поддерживает команду умножения (MUL), то умножение двух
цифры совсем простые. .DEF ANSL = R0 ;Для хранения младшего байта ответа
.DEF ANSH = R1 ;Для хранения старшего байта ответа
.DEF A = R16 ;для хранения множимого
.DEF B = R18 ;удерживать множитель
LDI A,42 ;Загрузить множимое в A
LDI B,10 ;Загрузить множитель в B
MUL A,B ;умножить содержимое A и B
;Результат 420 остался в ANSL и ANSH
2. УМНОЖЕНИЕ ОДНОБАЙТОВОГО ЧИСЛА НА СТЕПЕНЬ ДВОЙКИЕсли наш AVR не поддерживает аппаратную команду MUL, нам придется вычислять умножения вручную. Если нам нужно умножить на степень двойки, например 2,4,8 и т. Результата можно добиться сдвигом битов влево. Каждый сдвиг влево есть умножение на два. Команда логического сдвига влево (LSL) используется для младшего байта, поскольку она
сдвигает содержимое на один бит влево, ноль сдвигается в самый младший бит и
старший бит сдвигается во флаг переноса. 10101010 Carry [1] <-- 01010100 <--0 (LSL) Мы используем команду "Повернуть влево при переносе" (ROL) для старшего байта, потому что это также сдвигает содержимое на один бит влево, но при этом содержимое флага переноса сдвигается в самый младший бит. 00000000 Перенос [0] <-- 00000001 <--[1] Перенос (ROL) Каждый раз, когда мы сдвигаем множимое влево, мы умножаем его на два. Таким образом, чтобы умножить на восемь, мы просто сдвигаем множимое влево три раза. Процедура занимает около десяти циклов. .DEF ANSL = R0 ;Для хранения младшего байта ответа
.DEF ANSH = R1 ;Для хранения старшего байта ответа
.DEF AL = R16 ;Для хранения младшего байта множимого
.DEF AH = R17 ;Для хранения старшего байта множимого
LDI AL,LOW(42) ;Загрузить множимое в AH:AL
LDI AH, ВЫСОКИЙ (42) ;
МУЛ8:
MOV ANSL,AL ;копировать множимое в R1:R0
МОВ АНШ,АХ ;
LSL ANSL ;Умножить на 2
ROL ANSH ;Переключить перенос на R1
LSL ANSL ;Умножить на 2x2=4
ROL ANSH ;Переключить перенос на R1
LSL ANSL ;Умножить на 2x2x2=8
ROL ANSH ;Переключить перенос на R1
;Результат 42x8=336 осталось в ANSL и ANSH
3. УМНОЖЕНИЕ ДВУХ ОДНОБАЙТОВЫХ ЧИСЕЛ ВРУЧНУЮ УМНОЖЕНИЕ ДВУХ ОДНОБАЙТОВЫХ ЧИСЕЛ ВРУЧНУЮЧтобы выполнить стандартное умножение, мы исследуем, как достигается двоичное умножение, мы замечаем, что когда цифра в множителе равна единице, мы добавляем сдвинутую версию множимое к нашему результату. Когда цифра множителя равна нулю, нам нужно добавить ноль, значит ничего не делаем. 00101010 = 42 множимое
x00001010 = множитель 10
--------
00000000
00101010
00000000
00101010
00000000
00000000
00000000
00000000
----------------
0000000110100100 = 420 результат
================
Приведенная ниже процедура имитирует аппаратное умножение (MUL), оставляя множимое и
множитель не трогается, а результат появляется в регистровой паре R1 и R0. .DEF ANSL = R0 ;Для хранения младшего байта ответа
.DEF ANSH = R1 ;Для хранения старшего байта ответа
.DEF A = R16 ;для хранения множимого
.DEF B = R18 ;удерживать множитель
.DEF C = R20 ;Для хранения битового счетчика
LDI A,42 ;Загрузить множимое в A
LDI B,10 ;Загрузить множитель в B
МУЛ8x8:
LDI C,8 ;Загрузить битовый счетчик в C
CLR ANSH ;Очистить старший байт ответа
MOV ANSL,B ;копировать множитель в младший байт ответа
LSR ANSL ;Сдвинуть младший бит множителя в Carry
LOOP: BRCC SKIP ;Если перенос равен нулю, то сложение пропускается.
ADD ANSH,A ;Добавить множимое к ответу
SKIP: ROR ANSH ;Сдвиг младшего бита старшего байта
ROR ANSL ;ответа в младший байт
DEC C ;Уменьшить битовый счетчик
BRNE LOOP ;Проверить, выполнены ли все восемь битов
;Результат 420 остался в ANSL и ANSH
4. УМНОЖЕНИЕ ДВУХ 16-БИТНЫХ ЧИСЕЛ С ПОМОЩЬЮ КОМАНДЫ MUL УМНОЖЕНИЕ ДВУХ 16-БИТНЫХ ЧИСЕЛ С ПОМОЩЬЮ КОМАНДЫ MULУмножение двух 16-битных чисел может привести к четырем байтам. Мы используем команду аппаратного умножения (MUL) для создания всех четырех перекрестных произведений. и добавить их к 32-битному результату. Команда MUL каждый раз оставляет результаты в R1:R0, которые мы затем добавляем к нашему результату. Процедура занимает около двадцати циклов. .DEF ZERO = R2 ;удерживать ноль
.DEF AL = R16 ;Для хранения множимого
.DEF АХ = R17
.DEF BL = R18 ;удерживать множитель
.DEF ЧД = R19.DEF ANS1 = R20 ;Для хранения 32-битного ответа
.DEF ANS2 = R21
.DEF ANS3 = R22
.DEF ANS4 = R23
LDI AL,LOW(42) ;Загрузить множимое в AH:AL
LDI AH, ВЫСОКИЙ (42) ;
LDI BL,LOW(10) ;Загрузить множитель в BH:BL
LDI BH,ВЫСОКИЙ(10) ;
МУЛ16x16:
CLR ZERO ;Установить R2 в ноль
MUL AH,BH ;умножить старшие байты AHxBH
MOVW ANS4:ANS3,R1:R0 ;Переместить двухбайтовый результат в ответ
MUL AL,BL ;умножить младшие байты ALxBL
MOVW ANS2:ANS1,R1:R0 ;Переместить двухбайтовый результат в ответ
MUL AH,BL ;умножить AHxBL
ADD ANS2,R0 ;Добавить результат к ответу
АЦП ANS3,R1 ;
ADC ANS4,ZERO ;Добавить бит переноса
MUL BH,AL ;умножить BHxAL
ADD ANS2,R0 ;Добавить результат к ответу
АЦП ANS3,R1 ;
ADC ANS4,ZERO ;Добавить бит переноса
5. УМНОЖЕНИЕ ДВУХ 16-БИТНЫХ ЧИСЕЛ ВРУЧНУЮ УМНОЖЕНИЕ ДВУХ 16-БИТНЫХ ЧИСЕЛ ВРУЧНУЮУмножение двухбайтовых чисел может дать результат шириной четыре байта (32 бита). С помощью этой процедуры мы добавляем множимое к старшим байтам нашего результата для каждого, что появляется в нашем 16-битном множителе, затем сдвигаем результат в младшие байты нашего результата шестнадцать раз, один раз для каждого бита нашего множителя. Процедура занимает около 180 циклов. .DEF AL = R16 ;Для хранения множимого
.DEF АХ = R17
.DEF BL = R18 ;удерживать множитель
.DEF ЧД = R19.DEF ANS1 = R20 ;Для хранения 32-битного ответа
.DEF ANS2 = R21
.DEF ANS3 = R22
.DEF ANS4 = R23
.DEF C = R24 ;Счетчик битов
LDI AL,LOW(42) ;Загрузить множимое в AH:AL
LDI AH, ВЫСОКИЙ (42) ;
LDI BL,LOW(10) ;Загрузить множитель в BH:BL
LDI BH,ВЫСОКИЙ(10) ;
МУЛ16x16:
CLR ANS3 ;Установить старшие байты результата равными нулю
CLR ANS4 ;
LDI C,16 ;Счетчик битов
LOOP: LSR BH ;Сдвиг множителя вправо
ROR BL ;Сдвиг младшего бита в флаг переноса
BRCC SKIP ;Если перенос равен нулю, пропустить добавление
ADD ANS3,AL ;Добавить множимое в старшие байты
АЦП ANS4,AH ;результата
SKIP: ROR ANS4 ;Повернуть старшие байты результата в
ROR ANS3 ;младшие байты
РОР ОТВЕТ2 ;
РОР ОТВЕТ1 ;
DEC C ;Проверить, обработаны ли все 16 бит
BRNE LOOP ;Если нет, то цикл назад
6. УМНОЖЕНИЕ ДВУХ 32-БИТНЫХ ЧИСЕЛ ВРУЧНУЮ УМНОЖЕНИЕ ДВУХ 32-БИТНЫХ ЧИСЕЛ ВРУЧНУЮСледующая процедура умножает два 32-битных числа на 64-битный (8 байт) результат. Процедура занимает около 500 тактов. .DEF ANS1 = R0 ;64-битный ответ
.DEF ANS2 = R1 ;
.DEF ANS3 = R2 ;
.DEF ANS4 = R3 ;
.DEF ANS5 = R4 ;
.DEF ANS6 = R5 ;
.DEF ANS7 = R6 ;
.DEF ANS8 = R7 ;
.DEF A1 = R16 ;Множное
.DEF A2 = R17 ;
.DEF A3 = R18 ;
.DEF A4 = R19;
.DEF B1 = R20 ;Множитель
.DEF B2 = R21 ;
.DEF B3 = R22 ;
.DEF B4 = R23 ;
.DEF C = R24 ;Счетчик циклов
LDI A1, НИЗКИЙ ($FFFFFFFF)
LDI A2, BYTE2 ($FFFFFFFF)
LDI A3, BYTE3 ($FFFFFFFF)
LDI A4, BYTE4 ($FFFFFFFF)
LDI B1, НИЗКИЙ ($FFFFFFFF)
LDI B2, BYTE2 ($FFFFFFFF)
LDI B3, BYTE3 ($FFFFFFFF)
LDI B4, BYTE4 ($FFFFFFFF)
МУЛ3232:
CLR ANS1 ;Инициализировать Ответ на ноль
CLR ANS2 ;
CLR ANS3 ;
CLR ANS4 ;
CLR ANS5 ;
CLR ANS6 ;
CLR ANS7 ;
SUB ANS8,ANS8 ;очистить ANS8 и поставить флаг
MOV ANS1,B1 ;копировать множитель в ответ
ДВИГАТЕЛЬ ANS2,B2 ;
ДВИЖЕНИЕ ANS3,B3 ;
ДВИГАТЕЛЬ ANS4,B4 ;
LDI C,33 ;Установить счетчик циклов на 33
ПЕТЛЯ:
ROR ANS4 ;Сдвинуть множитель вправо
РОР ОТВЕТ3 ;
РОР ОТВЕТ2 ;
РОР ОТВЕТ1 ;
DEC C ;Уменьшение счетчика циклов
BREQ DONE ;Проверить, все ли биты обработаны
BRCC SKIP ; Если Carry Clear пропустить добавление
ADD ANS5,A1 ;Добавить множимое в ответ
АЦП ANS6,A2 ;
АЦП ANS7,A3 ;
АЦП ANS8,A4 ;
ПРОПУСКАТЬ:
ROR ANS8 ;Сдвинуть старшие байты ответа
РОР ОТВЕТ7 ;
РОР ОТВЕТ6 ;
РОР ОТВЕТ5 ;
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
7. ДЕЛЕНИЕ НА СТЕПЕНЬ ДВУХ ДЕЛЕНИЕ НА СТЕПЕНЬ ДВУХПоскольку аппаратной команды деления нет, нам придется делать это вручную. Если нам нужно разделить на степень двойки, например 2,4,8 и т. Результата можно добиться сдвигом битов вправо. Каждый сдвиг вправо — это деление на два. Команда логического сдвига вправо (LSR) используется для старшего байта, поскольку она сдвигает содержимое на один бит вправо, ноль сдвигается в старший бит, а младший бит сдвигается во флаг переноса. 01010101
0--> 00101010 -->[1] Перенос
Мы используем команду "Повернуть вправо при переносе" (ROR) для младшего байта, поскольку она также сдвинуть содержимое на один бит вправо, но при этом содержимое флага переноса будет смещено в самый старший бит. 00000000 Перенос [1] --> 10000000 -->[0] Перенос (ROL) Каждый раз, когда мы сдвигаем множимое вправо, мы делим его на два.
Таким образом, чтобы разделить на восемь, мы просто сдвигаем множимое вправо три раза.
Процедура занимает около десяти циклов. .DEF ANSL = R0 ;Для хранения младшего байта ответа
.DEF ANSH = R1 ;Для хранения старшего байта ответа
.DEF AL = R16 ;Для хранения младшего байта множимого
.DEF AH = R17 ;Для хранения старшего байта множимого
LDI AL,LOW(416) ;Загрузить множимое в A
LDI AH, ВЫСОКИЙ (416) ;
DIV8:
MOVW ANSH:ANSL,AH:AL ;копировать множимое в результат
LSR ANSH ;Делить на 2
ROR ANSL ;Сдвинуть флаг переноса на R0
LSR ANSH ;Деление на 4 (2x2)
ROR ANSL ;Перенести флаг переноса в R0
LSR ANSH ;Деление на 8 (2x2x2)
ROR ANSL ;Перенести флаг переноса в R0
;Результат 416/8=52 осталось в ANSL и ANSH
8. ДЕЛЕНИЕ ДВУХ ОДНОБАЙТОВЫХ ЧИСЕЛ Так же, как умножение может быть выполнено с помощью сдвига и сложения.
Деление может быть выполнено с помощью сдвига и вычитания.
Подпрограмма ниже пытается повторно вычесть делитель.
Если результат отрицательный, он отменяет процесс и сдвигает делимое влево, чтобы повторить попытку. .DEF ANS = R0 ;задержать ответ
.DEF REM = R2 ;Для удержания остатка
.DEF A = R16 ;для хранения дивидендов
.DEF B = R18 ;Для хранения делителя
.DEF C = R20 ;Счетчик битов
LDI A,255 ;Загрузить дивиденды в A
LDI B,5 ;Загрузить делитель в B
ДИВ88:
ЛДИ С,9;Загрузить счетчик битов
SUB REM,REM ;Очистить остаток и нести
MOV ANS,A ;Скопировать дивиденд в ответ
LOOP: ROL ANS ;Сдвиньте ответ влево
DEC C ;Уменьшение счетчика
BREQ DONE ;Выйти, если сделано восемь битов
ROL REM ;Сдвинуть остаток влево
SUB REM,B ;Попробовать вычесть делитель из остатка
BRCC SKIP ;Если результат отрицательный, то
ADD REM,B ;обратите вычитание, чтобы повторить попытку
CLC ;Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP ;цикл назад
SKIP: SEC ;Установить перенос флага на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
9. ДЕЛЕНИЕ ДВУХ 16-БИТНЫХ ЧИСЕЛ Предыдущую процедуру можно расширить для обработки деления двухбайтовых чисел в диапазоне от 0 до 65 535. .DEF ANSL = R0 ;Для хранения младшего байта ответа
.DEF ANSH = R1 ;Для хранения старшего байта ответа
.DEF REML = R2 ;Для хранения младшего байта остатка
.DEF REMH = R3 ;Для хранения старшего байта остатка
.DEF AL = R16 ;Для хранения младшего байта делимого
.DEF AH = R17 ;Для хранения старшего байта делимого
.DEF BL = R18 ;Для хранения младшего байта делителя
.DEF ЧД = R19;Для хранения старшего байта делителя
.DEF C = R20 ;Счетчик битов
LDI AL,LOW(420) ;Загрузить младший байт делимого в AL
LDI AH,HIGH(420) ;Загрузить старший байт делимого в AH
LDI BL,LOW(10) ;Загрузить младший байт делителя в BL
LDI BH,HIGH(10) ;Загрузить старший байт делителя в BH
ДИВ1616:
MOVW ANSH:ANSL,AH:AL ;Скопировать делимое в ответ
LDI C,17 ;Счетчик битов загрузки
SUB REML,REML ;Очистить остаток и перенести
КЛР РЕМХ ;
LOOP: ROL ANSL ;Сдвиньте ответ влево
РОЛ АНШ ;
DEC C ;Уменьшение счетчика
BREQ DONE ;Выйти, если сделано шестнадцать битов
ROL REML ;Сдвинуть остаток влево
РОЛ РЕМХ ;
SUB REML,BL ;Попробовать вычесть делитель из остатка
СБК РЭМХ,БХ
BRCC SKIP ;Если результат отрицательный, то
ADD REML,BL ;обратите вычитание, чтобы повторить попытку
АЦП REMH,BH ;
CLC ;Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP ;цикл назад
SKIP: SEC ;Установить перенос флага на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
10. ДЕЛЕНИЕ 32-БИТНОГО ЧИСЛА ДЕЛЕНИЕ 32-БИТНОГО ЧИСЛАПредыдущую процедуру можно расширить для обработки 32-битного числа, деленного на 16-битное число, Это означает, что числа в диапазоне от нуля до 4 294 967 295 (4,3 миллиарда) делятся на числа в диапазоне от 0 до 65 535. Процедура занимает около 700 циклов. .DEF ANS1 = R0 ;Для хранения младшего байта ответа .DEF ANS2 = R1 ;для хранения второго байта ответа .DEF ANS3 = R2 ;Для хранения третьего байта ответа .DEF ANS4 = R3 ;Для хранения четвертого байта ответа .DEF REM1 = R4 ;для хранения первого байта остатка .DEF REM2 = R5 ;для хранения второго байта остатка .DEF REM3 = R6 ;Для хранения третьего байта остатка .DEF REM4 = R7 ;для хранения четвертого байта остатка .DEF ZERO = R8 ;Чтобы сохранить нулевое значение .DEF A1 = R16 ;Для хранения младшего байта делимого .DEF A2 = R17 ;для хранения второго байта делимого .DEF A3 = R18 ;Для хранения третьего байта делимого .DEF A4 = R19;Для хранения четвертого байта делимого .DEF BL = R20 ;Для хранения младшего байта делителя . Если мы изучим приведенную выше таблицу, то заметим, что квадратный корень числа равен
количество нечетных чисел, которые мы просуммировали. .DEF ANS = R0 ;задержать ответ .DEF A = R16 ;удерживать квадрат .DEF B = R18 ;Сумма, рабочее пространство LDI A,100 ;Загрузить квадрат в A SQRT: ПЕТЛЯ: SUB A,B ;Вычесть B из квадрата BRCS DONE ;Если больше квадрата, мы закончили INC ANS ;увеличить ответ SUBI B,-2 ;Увеличить B на два ПЕТЛЯ RJMP 12. КВАДРАТНЫЙ КОРЕНЬ ИЗ 16-БИТНОГО ЧИСЛАМы могли бы расширить приведенную выше процедуру для обработки квадратного корня из шестнадцатибитного числа. но количество тактов может достигать 3750. Приведенная ниже процедура обрабатывает два бита за раз, начиная со старших битов и также обеспечивает остаток. Он использует около 160 тактовых циклов. .DEF ANSL = R0 ;Квадратный корень (ответ) .DEF ANSH = R1 ; .DEF REML = R2 ; Остаток .DEF REMH = R3 ; .DEF AL = R16 ;Квадрат для укоренения (ввод) .DEF AH = R17 ; . 13. КВАДРАТНЫЙ КОРЕНЬ ИЗ 32-БИТНОГО ЧИСЛА КВАДРАТНЫЙ КОРЕНЬ ИЗ 32-БИТНОГО ЧИСЛАМы можем расширить предыдущую процедуру для обработки 32-битных чисел. Для завершения требуется от 500 до 580 тактовых циклов. .DEF ANS1 = R0 ;Квадратный корень (ответ)
.DEF ANS2 = R1 ;
.DEF ANS3 = R2 ;
.DEF ANS4 = R3 ;
.DEF REM1 = R4 ;Остаток
.DEF REM2 = R5 ;
.DEF REM3 = R6 ;
.DEF REM4 = R7 ;
.DEF A1 = R16 ;Квадрат (ввод)
.DEF A2 = R17 ;
.DEF A3 = R18 ;
.DEF A4 = R19;
.DEF C = R20 ;Счетчик циклов
LDI A1, НИЗКИЙ ($FFFFFFFF)
LDI A2, BYTE2 ($FFFFFFFF)
LDI A3, BYTE3 ($FFFFFFFF)
LDI A4, BYTE4 ($FFFFFFFF)
кв16:
НАЖМИТЕ A1 ;Сохранить квадрат для последующего восстановления
НАЖМИТЕ A2 ;
НАЖМИТЕ A3 ;
НАЖМИТЕ A4 ;
CLR REM1 ;Инициализировать остаток до нуля
CLR REM2 ;
CLR REM3 ;
CLR REM4 ;
CLR ANS1 ;Инициализировать корень до нуля
CLR ANS2 ;
CLR ANS3 ;
CLR ANS4 ;
LDI C,16 ;Установить счетчик циклов на шестнадцать
ПЕТЛЯ:
LSL ANS1 ;Умножить корень на два
РОЛ АНС2 ;
РОЛ АН3 ;
РОЛ АНС4 ;
LSL A1 ;Сдвинуть два старших бита квадрата
ROL A2 ;в остаток
РОЛ А3 ;
РОЛ А4 ;
РОЛ РЕМ1 ;
РОЛ РЕМ2 ;
РОЛ РЕМ3 ;
РОЛ РЕМ3 ;
LSL A1 ;Сдвиг второго старшего бита Sqaure
ROL A2 ;в остаток
РОЛ А3 ;
РОЛ А4 ;
РОЛ РЕМ1 ;
РОЛ РЕМ2 ;
РОЛ РЕМ3 ;
РОЛ РЕМ4 ;
CP ANS1,REM1 ;Сравнить корень с остатком
КПК ANS2,REM2 ;
КПК ANS3,REM3 ;
КПК ANS4,REM4 ;
BRCC SKIP ;Если остаток меньше или равен корню
INC ANS1 ;Приращение корня
SUB REM1,ANS1 ;Вычесть корень из остатка
SBC REM2, ANS2 ;
SBC REM3, ANS3 ;
SBC REM4,ANS4 ;
INC ANS1 ;Приращение корня
ПРОПУСКАТЬ:
DEC C ;Уменьшение счетчика циклов
BRNE LOOP ;Проверить, все ли биты обработаны
LSR ANS4 ;Делить корень на два
РОР ОТВЕТ3 ;
РОР ОТВЕТ2 ;
РОР ОТВЕТ1 ;
POP A4 ;Восстановить исходный квадрат
ПОП А3
ПОП А2
ПОП А1
14. 3
МУЛЬ С, R0 ;
CP A,R0 ;Проверить, не зашло ли слишком далеко
BRCS FINI ;Если да, то Готово
MOV REM,A ;Вычислить остаток
СУБДРЕМ,R0 ;
INC C ;увеличить счетчик циклов
CPI C,7 ;Проверить выполнение
BRNE LOOP ;Вернуться назад
FINI: MOV ANS,C ;Ответ = Счетчик - 1
ДЕК ОТВЕТ
93
.DEF REMH = R3 ;
.DEF CUB1 = R4 ;ответ процедуры CUBE
.DEF CUB2 = R5 ;
.DEF CUB3 = R6 ;
.DEF TMP1 = R8 ;Временная рабочая область
.DEF TMP2 = R9 ;
.DEF ZERO = R10 ;Для удержания нулевого значения
.DEF ONE = R11 ;для сохранения значения One
.DEF LES = R12 ;Низкая оценка
.DEF HES = R13 ;высокая оценка
.DEF AVG = R14; средняя минимальная и максимальная оценка
.DEF AL = R16 ;Исходный куб
.DEF AH = R17 ;
.DEF B = R18 ;Общее назначение
LDI AL, LOW(1000) ;Загрузить исходный куб в AH:AL
LDI АХ,ВЫСОКИЙ(1000) ;
CLR REML ;Очистить остаток
КЛР РЕМХ ;
CLR ZERO ;Установить ноль
CLR ONE ; Установить один
ВКЛ ОДИН ;
CLR LES ;Начало нижней оценки с нуля
LDI B, 42 ; Старт высокой оценки в сорок два года
МОВ ГЭС,Б
ЦИКЛ: MOV AVG,LES ;AVG = (Низкий+Верхний+1)/2
ДОБАВИТЬ СРЕДНЕЕ,HES ;
АЦП СРЕДНИЙ, ОДИН ;
ЛСР СРЕДНИЙ;
MOV B,AVG ;Вычислить AVG^3
ВЫЗВАТЬ КУБ ;
CP CUB1,AL ;Сравнить AVG^3 с исходным CUBE
КПК CUB2,AH ;
цена за клик CUB3,НОЛЬ ;
BRNE SKIP1 ;Проверить, если AVG^3 = Исходный CUBE
MOV LES,AVG ;AVG^3 = CUBE, поэтому Low-Est = AVG (завершено)
RJMP FINI2 ;
SKIP1: BRCC ISHIGH ;
MOV LES,AVG ;AVG^3 < CUBE, поэтому Low-Est = AVG
ПРОПУСК 2 ;
ISHIGH: MOV HES,AVG ;AVG^3 > CUBE, поэтому High-Est = AVG
SKIP2: MOV B,HES ;B = HighEst - LowEst
SUB B,LES ;
BREQ FINI ;LowEst = HighEst, поэтому мы закончили
ИПЦ В,1;
BRNE LOOP ;Если HighEst-LowEst > 1, попробуйте еще раз
ФИНИ:
MOV B,LES ;Вычислить остаток
RCALL CUBE ; Остаток = Cube - LowEst^3
MOVW REMH:REML,AH:AL ;
SUB REML,CUB1 ;
SBC REMH,CUB2 ;
FINI2: MOV ANS,LES; Результат сохранения = LowEst
ВЫПОЛНЕНО: RJMP ВЫПОЛНЕНО
;---------------------------------------------------------;
; Вычисляет куб B ;
; Результаты в CUB3:CUB2:CUB1 ;
;---------------------------------------------------------;
КУБ:
МУЛЬЧ B,B ;Расч B*B
MOVW TMP2:TMP1,R1:R0 ;
MUL TMP1,B ;Расч B*B*B
MOVW КУБ2:КУБ1,R1:R0 ;
МУЛ ТМП2,Б ;
ДОБАВИТЬ КУБ2,R0 ;
CLR CUB3 ;
АЦП CUB3,R1 ;
РЕТ 3
МУЛЬ С, R0 ;
CP A,R0 ;Проверить, не зашло ли слишком далеко
BRCS FINI ;Если да, то Готово
MOV REM,A ;Вычислить остаток
СУБДРЕМ,R0 ;
INC C ;увеличить счетчик циклов
CPI C,7 ;Проверить выполнение
BRNE LOOP ;Вернуться назад
FINI: MOV ANS,C ;Ответ = Счетчик - 1
ДЕК ОТВЕТ
93
.DEF REMH = R3 ;
.DEF CUB1 = R4 ;ответ процедуры CUBE
.DEF CUB2 = R5 ;
.DEF CUB3 = R6 ;
.DEF TMP1 = R8 ;Временная рабочая область
.DEF TMP2 = R9 ;
.DEF ZERO = R10 ;Для удержания нулевого значения
.DEF ONE = R11 ;для сохранения значения One
.DEF LES = R12 ;Низкая оценка
.DEF HES = R13 ;высокая оценка
.DEF AVG = R14; средняя минимальная и максимальная оценка
.DEF AL = R16 ;Исходный куб
.DEF AH = R17 ;
.DEF B = R18 ;Общее назначение
LDI AL, LOW(1000) ;Загрузить исходный куб в AH:AL
LDI АХ,ВЫСОКИЙ(1000) ;
CLR REML ;Очистить остаток
КЛР РЕМХ ;
CLR ZERO ;Установить ноль
CLR ONE ; Установить один
ВКЛ ОДИН ;
CLR LES ;Начало нижней оценки с нуля
LDI B, 42 ; Старт высокой оценки в сорок два года
МОВ ГЭС,Б
ЦИКЛ: MOV AVG,LES ;AVG = (Низкий+Верхний+1)/2
ДОБАВИТЬ СРЕДНЕЕ,HES ;
АЦП СРЕДНИЙ, ОДИН ;
ЛСР СРЕДНИЙ;
MOV B,AVG ;Вычислить AVG^3
ВЫЗВАТЬ КУБ ;
CP CUB1,AL ;Сравнить AVG^3 с исходным CUBE
КПК CUB2,AH ;
цена за клик CUB3,НОЛЬ ;
BRNE SKIP1 ;Проверить, если AVG^3 = Исходный CUBE
MOV LES,AVG ;AVG^3 = CUBE, поэтому Low-Est = AVG (завершено)
RJMP FINI2 ;
SKIP1: BRCC ISHIGH ;
MOV LES,AVG ;AVG^3 < CUBE, поэтому Low-Est = AVG
ПРОПУСК 2 ;
ISHIGH: MOV HES,AVG ;AVG^3 > CUBE, поэтому High-Est = AVG
SKIP2: MOV B,HES ;B = HighEst - LowEst
SUB B,LES ;
BREQ FINI ;LowEst = HighEst, поэтому мы закончили
ИПЦ В,1;
BRNE LOOP ;Если HighEst-LowEst > 1, попробуйте еще раз
ФИНИ:
MOV B,LES ;Вычислить остаток
RCALL CUBE ; Остаток = Cube - LowEst^3
MOVW REMH:REML,AH:AL ;
SUB REML,CUB1 ;
SBC REMH,CUB2 ;
FINI2: MOV ANS,LES; Результат сохранения = LowEst
ВЫПОЛНЕНО: RJMP ВЫПОЛНЕНО
;---------------------------------------------------------;
; Вычисляет куб B ;
; Результаты в CUB3:CUB2:CUB1 ;
;---------------------------------------------------------;
КУБ:
МУЛЬЧ B,B ;Расч B*B
MOVW TMP2:TMP1,R1:R0 ;
MUL TMP1,B ;Расч B*B*B
MOVW КУБ2:КУБ1,R1:R0 ;
МУЛ ТМП2,Б ;
ДОБАВИТЬ КУБ2,R0 ;
CLR CUB3 ;
АЦП CUB3,R1 ;
РЕТ |
Умножения, деления и сдвиги
Поскольку Z80 не имеет встроенных инструкций умножения, когда программист хочет выполнить умножение, ему приходится делать это вручную.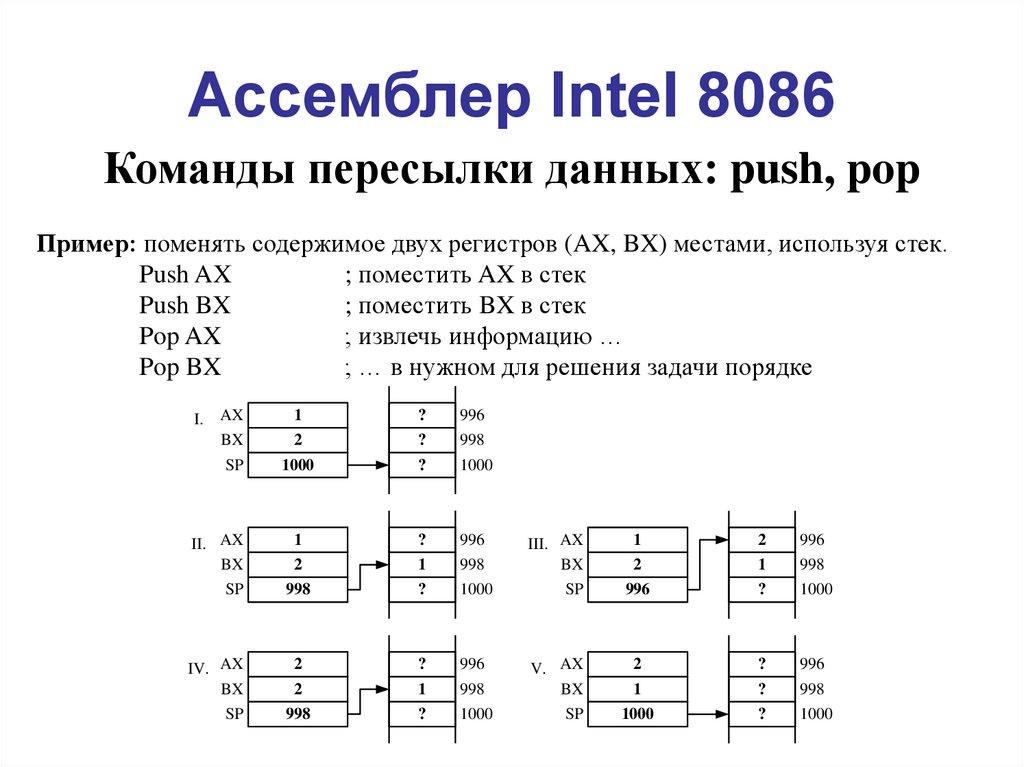 Программист может взять процедуру умножения из книги или журнала, которая не обязательно оптимизирована для конкретного случая (или вообще оптимизирована), или он может даже использовать процедуру, которая работает, добавляя одно и то же значение n раз, т. е. практически худшее решение проблемы.
Программист может взять процедуру умножения из книги или журнала, которая не обязательно оптимизирована для конкретного случая (или вообще оптимизирована), или он может даже использовать процедуру, которая работает, добавляя одно и то же значение n раз, т. е. практически худшее решение проблемы.
В этой статье представлены оптимизированные методы умножения. Во-первых, он знакомит вас с умножением с использованием сдвигов, которые выполняются очень быстро и могут использоваться, если один из параметров умножения является фиксированным числом. Затем он предоставляет ряд оптимизированных общих процедур умножения и деления для различной разрядности и даже процедуры извлечения квадратного корня.
- 8-битное умножение со сдвигом
- 8-битное деление с использованием сдвигов
- 16-битные сдвиги
- Быстрые общие процедуры умножения
- Умножение с вращением влево
- Умножение с вращением вправо
- Развернутое умножение с вращением влево
- Быстрые общие процедуры деления
- Деление на 9
- Процедура извлечения квадратного корня
8-битное умножение с использованием сдвигов
Когда вы сдвигаете регистр на 1 бит влево, вы умножаете значение регистра на 2. Этот сдвиг можно выполнить с помощью инструкции SLA r. Выполняя последовательно несколько сдвигов, вы можете очень легко умножить на любую степень двойки. Например:
Этот сдвиг можно выполнить с помощью инструкции SLA r. Выполняя последовательно несколько сдвигов, вы можете очень легко умножить на любую степень двойки. Например:
лд б,3 ; Умножь 3 на 4
сла б ; х4
сла б ; результат: б = 12
Если вы используете регистр A, вы можете умножать быстрее, используя инструкцию ADD A,A, которая составляет 5 T-состояний на инструкцию вместо 8. Таким образом, ADD A,A точно такой же, как SLA A, или умножение на два . Кстати, вместо использования ADD A,A вы также можете использовать RLCA, который фактически ведет себя так же.
ld a,15 ; Умножьте 15 на 8
добавить а, а ; х8
добавить а, а
добавить а, а ; результат: а = 120
При программировании умножения вы всегда должны убедиться, что результат никогда не превысит 255, другими словами, не может произойти перенос. В этом случае RLCA фактически действует иначе, чем SLA A или ADD A,A (в некоторых случаях более удобный, в некоторых менее удобный). Но, как правило, это не имеет значения, поскольку при переполнении регистра А результат, как правило, уже не будет иметь большого значения.
Если вы хотите умножить значение, отличное от степени двойки, вы почти всегда можете добиться желаемого результата, сохраняя промежуточные значения во время сдвига и добавляя или вычитая их впоследствии. Несколько примеров:
лд а,5 ; Умножьте 5 на 20 (= A x 16 + A x 4)
добавить а, а ; х16
добавить а, а
лд б, а ; Сохраните значение A x 4 в B
добавить а, а
добавить а, а
добавить а, б; Добавьте A x 4 к A x 16, результат: a = 100
Если вы хотите умножить на 22, вы также должны сохранить значение после первого сложения в регистре и впоследствии добавить его к сумме.
Иногда вы также можете использовать вычитания, чтобы быстрее достичь своих целей. Например, умножение А на 15. Это можно сделать описанным выше способом, однако в этом случае вам понадобятся 4 временных регистра, а потом четыре дополнительных сложения. Это может быть лучше сделано следующим образом, что требует еще 1 умножения, но использует только 1 временный регистр и 1 вычитание впоследствии:
лд а,3 ; Умножьте 3 на 15 (= A x 16 - A x 1)
лд б, а ; Сохраните значение A x 1 в B
добавить а, а ; х16
добавить а, а
добавить а, а
добавить а, а
суб б; результат: а = 45
8-битное деление с использованием сдвигов
Деление очень похоже на умножение. Если процедура умножения сложна, процедура деления еще сложнее. Однако, используя сдвиги, слишком легко делить в Assembly. Это делается простым сдвигом в другую сторону, вправо. Для этого следует использовать инструкцию SRL r. Пример:
Если процедура умножения сложна, процедура деления еще сложнее. Однако, используя сдвиги, слишком легко делить в Assembly. Это делается простым сдвигом в другую сторону, вправо. Для этого следует использовать инструкцию SRL r. Пример:
лд б,3 ; Разделите 18 на 4
ООО б ; х4
ООО б ; результат: b = 4 (остаток 2 потерян)
Нет реальной быстрой альтернативы сдвигу вправо при использовании регистра А. В качестве альтернативы вы можете использовать для этого RRCA. Однако при использовании RRCA необходимо следить за тем, чтобы не было пауз, иначе результат будет неверным. Это может быть достигнуто путем И исходного значения со значением, очищающим младшие биты (которые в противном случае были бы смещены), или убедившись, что вы используете значения, которые всегда кратны делителю.
л.д. а, 153 ; Разделите 153 на 8.
и %11111000 ; Очистить биты 0–2 (равно 256–8)
ррка ; /8
ррка
ррка ; результат: а = 19
Деление на значения, отличные от степеней двойки, сложнее и часто невозможно. Если вы хотите убедиться в этом сами, попробуйте создать процедуру, которая делит 100 на 20. Чтобы узнать, можно ли разделить значение, вы должны посмотреть на количество завершающих нулей в двоичном представлении этого значения. Максимальное количество RRCA, которое вы можете использовать, равно этому числу. Если вы посмотрите на ранее упомянутое значение 100 в двоичном формате (% 01100100), вы увидите два завершающих нуля. Таким образом, процедура деления может использовать только 2 RRCA, а для деления на 20 требуется 4 из них.
Если вы хотите убедиться в этом сами, попробуйте создать процедуру, которая делит 100 на 20. Чтобы узнать, можно ли разделить значение, вы должны посмотреть на количество завершающих нулей в двоичном представлении этого значения. Максимальное количество RRCA, которое вы можете использовать, равно этому числу. Если вы посмотрите на ранее упомянутое значение 100 в двоичном формате (% 01100100), вы увидите два завершающих нуля. Таким образом, процедура деления может использовать только 2 RRCA, а для деления на 20 требуется 4 из них.
Грубо говоря, если вы не имеете очень жесткого контроля над значениями, заданными в качестве параметра, вряд ли возможно разделить на значения, которые не являются степенью двойки. Используя метод, аналогичный умножению, деление на Например, 3, конечно, возможно, но только если все входные значения четны и все кратны 3. Если какое-либо из этих условий не выполняется, результат будет ошибочным.
16-битные сдвиги
Существуют также способы сдвига 16-битных регистров. Это делается с помощью 8-битного сдвига в сочетании с 8-битным поворотом и битом переноса. Для сдвига регистра DE на один бит влево следует использовать:
Это делается с помощью 8-битного сдвига в сочетании с 8-битным поворотом и битом переноса. Для сдвига регистра DE на один бит влево следует использовать:
список
рл д
Чтобы сдвинуть его на один бит вправо (теперь с BC в качестве примера), используйте:
srl b
рр с
К сожалению, обычно эти 16-битные сдвиги довольно медленные по сравнению с 8-битными сдвигами (которые чаще всего происходят в быстром регистре A, что делает их почти в 4 раза быстрее). Однако, как и в случае с 8-битными сдвигами, существует также возможность выполнять более быстрые 16-битные сдвиги влево с помощью инструкции ADD.
добавить гл, гл ; сдвиг HL 1 бит влево... hl = hl x 2
Таким образом, лучший способ умножения 16-битных значений — это использование регистра HL в сочетании с инструкциями ADD HL,HL.
Быстрые общие процедуры умножения
Вот и все, что можно рассказать о сдвиге и умножении/делении. Есть еще несколько мелких трюков, но на самом деле все, что я могу сказать по этому поводу, это просто проявить немного творчества.
Наконец, я дам вам самые быстрые общие процедуры умножения и деления, насколько я знаю. Вот процедуры, которые вы должны использовать, когда:
- оба параметра умножения/деления неизвестны,
- , если вы хотите разделить на другое значение, отличное от степени 2, или вам нужно остаточное значение,
- , если известное значение является таким значением, что его невозможно вычислить с помощью методов, описанных выше.
Вы также можете использовать их, если хотите, чтобы ваш код выглядел очень аккуратно и не особо заботился о скорости. Что касается их внутренней работы, то все, что я могу сказать о них, это то, что они работают так же, как вы учились решать умножение и деление в начальной школе. Но это действительно не имеет значения. Просто скопируйте их в свою программу как (развернутые) подпрограммы или, если вы хотите удалить любое понятие структурного программирования, как встроенный код или макрос.
О, и если у вас действительно очень низкие переменные коэффициенты умножения, вы можете использовать ужасный метод умножения путем сложения x циклов. Это наверное быстрее.
Это наверное быстрее.
Умножение с вращением влево
Это процедуры умножения с вращением влево. Их скорость в основном довольно постоянна, хотя в зависимости от количества единиц в первичном множителе может быть небольшая разница в скорости (1 обычно занимает на 7 состояний больше времени, чем 0).
;
; Умножение 8-битных значений
; В: Умножить H на E
; Out: HL = результат
;
Мульт8:
лд д,0
лд л, д
лд б,8
Mult8_Loop:
добавить хл, хл
младший нк, Mult8_NoAdd
добавить хл, де
Mult8_NoAdd:
DJ Mult8_Loop
рет
;
; Умножить 8-битное значение на 16-битное
; In: Умножить A на DE
; Out: HL = результат
;
Мульт12:
лд л,0
лд б,8
Mult12_Loop:
добавить хл, хл
добавить а, а
младший нк,Mult12_NoAdd
добавить хл, де
Mult12_NoAdd:
DJ Mult12_Loop
рет
;
; Умножение 16-битных значений (с 16-битным результатом)
; In: Умножить BC на DE
; Out: HL = результат
;
Мульт16:
лд а, б
лд б, 16
Mult16_Loop:
добавить хл, хл
сла с
рла
младший нк,Mult16_NoAdd
добавить хл, де
Mult16_NoAdd:
DJ Mult16_Loop
рет
;
; Умножение 16-битных значений (с 32-битным результатом)
; In: Умножить BC на DE
; Не сыграет: БХЛ = результат
;
Мульт32:
лд а, с
лд с, б
лд гл,0
лд б, 16
Mult32_Loop:
добавить хл, хл
рла
рл с
младший нк,Mult32_NoAdd
добавить хл, де
прил а,0
jp nc,Mult32_NoAdd
вкл с
Mult32_NoAdd:
DJ Mult32_Loop
лд б, в
лд с, а
рет
Умножение с вращением вправо
Умножение с вращением вправо в основном мало чем отличается от умножения с вращением влево. Они используют очень похожий процесс, и количество шагов в вычислении равно. Однако на Z80 умножение с вращением влево может быть закодировано намного быстрее и компактнее, поэтому все предыдущие подпрограммы использовали варианты с вращением влево.
Они используют очень похожий процесс, и количество шагов в вычислении равно. Однако на Z80 умножение с вращением влево может быть закодировано намного быстрее и компактнее, поэтому все предыдущие подпрограммы использовали варианты с вращением влево.
Однако у делений с вращением вправо есть одно довольно приятное преимущество, заключающееся в том, что он должен зацикливаться только до тех пор, пока не останется битов, после чего он может быть завершен без каких-либо дальнейших операций. Таким образом, если значение на самом деле использует только 4 бита (например, число 11), подпрограмма должна выполнить только 4 цикла, а затем может быть завершена с помощью быстрой условной проверки, поэтому для этого потенциально большого ускорения практически не требуется никаких дополнительных усилий.
Глядя на приведенную ниже таблицу с расчетами скорости подпрограммы Mult12R и учитывая тот факт, что Mult12 с оптимальным вращением влево (развернутый) принимает 268 T-состояний (состояния M1 включены, в основном это означает 1 дополнительное состояние для каждой инструкции), вы можете видеть, что в границе эффективности находится на уровне 4 бит. Кроме того, обычный Mult12 работает быстрее. Однако 4-битный Mult12, конечно же, снова будет быстрее, поэтому, чтобы воспользоваться этим преимуществом, большинство, но не все значения должны попадать в 4-битный диапазон.
Кроме того, обычный Mult12 работает быстрее. Однако 4-битный Mult12, конечно же, снова будет быстрее, поэтому, чтобы воспользоваться этим преимуществом, большинство, но не все значения должны попадать в 4-битный диапазон.
Сколько времени занимает n-битное умножение (в среднем):
1-бит: 78,5 Т-состояний
2-бит: 140 Т-состояний
3-бит: 201,5 Т-состояний
4-бит: 263 Т- состояния
5-бит: 324,5 Т-состояния
6-бит: 386 Т-состояния
7-бит: 447,5 Т-состояния
8-бит: 509 Т-состояния
Важно отметить, что это может показаться быстрым , но не забывайте, что количество битов и возможные значения связаны друг с другом в логарифмической шкале. Таким образом, если вы используете случайные байтовые значения, количество значений в 4-битном диапазоне составляет только 1 из каждых 16 значений. Чтобы немного лучше понять, что это значит, взгляните на следующую таблицу, в которой указана средняя скорость, которую вы можете ожидать для случайного значения в определенном домене.
Average speeds in the specified domain:
| <0,255> | 447.980 T-states |
| <0,127> | 386.961 T-states |
| <0,63> | 326.422 Т-государства |
| <0,31> | 266,844 Т-состояния |
| <0,15> | 209.188 T-States |
| 209,188 T-States | |
| 209.188 | |
| 209.1880318 | |
| <0,3> | 109,25 Т-состояния |
| <0,1> | 78,5 Т-состояния |
значения в основном меньше 6 бит, например, если ваши данные логарифмические, использование алгоритма вращения вправо будет самым быстрым выбором. Чтобы привести пример использования в реальном мире, эта процедура может быть применима, например, для вычислений в таблицах частот в музыкальном проигрывателе, которые установлены в логарифмической шкале. 9.
;
; Умножить 8-битное значение на 16-битное (вращение вправо)
; In: Умножить A на DE
; Поместите наименьшее значение в A для наиболее эффективного расчета
; Out: HL = результат
;
Мульти12Р:
лд гл,0
Mult12R_Loop:
ООО
младший нк,Mult12R_NoAdd
добавить хл, де
Mult12R_NoAdd:
сла э
рл д
или
jp nz,Mult12R_Loop
рет
Развернутое умножение с вращением влево
Для полноты картины здесь также приведен пример развернутой подпрограммы умножения с вращением влево. Это занимает немного больше места, но значительно быстрее. На самом деле он все еще достаточно компактен, всего 41 байт. Этот занимает в среднем 268 T-состояний (включая ожидания M1). Минимум — 235 состояний, максимум — 301 тик.
Это занимает немного больше места, но значительно быстрее. На самом деле он все еще достаточно компактен, всего 41 байт. Этот занимает в среднем 268 T-состояний (включая ожидания M1). Минимум — 235 состояний, максимум — 301 тик.
Между прочим, я рассматривал возможность использования той же техники, что и с умножением с вращением вправо в этой подпрограмме, это довольно легко сделать, поместив переходы между переходами в список добавления hl, hl. Тем не менее, потеря скорости, вызванная дополнительными прыжками, не перевешивает выигрыш, и в любом случае это вряд ли практично, поскольку это относится к nr. битов, используемых слева (число 128 будет использовать 1 бит, а 64 два).
;
; Умножить 8-битное значение на 16-битное (развернутое)
; In: Умножить A на DE
; Out: HL = результат
;
Мульти12У:
лд л,0
добавить а, а
младший нк,Mult12U_NoAdd0
добавить хл, де
Mult12U_NoAdd0:
добавить хл, хл
добавить а, а
младший нк,Mult12U_NoAdd1
добавить хл, де
Mult12U_NoAdd1:
добавить хл, хл
добавить а, а
младший нк,Mult12U_NoAdd2
добавить хл, де
Mult12U_NoAdd2:
добавить хл, хл
добавить а, а
младший нк,Mult12U_NoAdd3
добавить хл, де
Mult12U_NoAdd3:
добавить хл, хл
добавить а, а
младший нк,Mult12U_NoAdd4
добавить хл, де
Mult12U_NoAdd4:
добавить хл, хл
добавить а, а
младший нк,Mult12U_NoAdd5
добавить хл, де
Mult12U_NoAdd5:
добавить хл, хл
добавить а, а
младший нк,Mult12U_NoAdd6
добавить хл, де
Mult12U_NoAdd6:
добавить хл, хл
добавить а, а
рет нк
добавить хл, де
рет
Также стоит развернуть другие процедуры умножения. Например, для подпрограммы Mult8 она сохраняет в среднем 115 из 367 T-состояний, что на 31% быстрее, за счет всего 38 байтов (14 → 52).
Например, для подпрограммы Mult8 она сохраняет в среднем 115 из 367 T-состояний, что на 31% быстрее, за счет всего 38 байтов (14 → 52).
Быстрые общие процедуры деления
Прежде чем мы перейдем к фактическим процедурам деления, при делении вам не обязательно использовать (более медленные) процедуры деления. Не забывайте, что умножение и деление связаны. Если вы хотите разделить на 2, вы также можете умножить на 0,5. Преобразуя это в эти подпрограммы, чтобы разделить 8-битное значение на другое 8-битное значение (как это делает Div8), вы можете вызвать подпрограмму Mult8 с параметром 1 (1/первое 8-битное значение * 256) и параметром 2. являющееся другим 8-битным значением. Результирующее слово будет шестнадцатеричным значением с фиксированной точкой, с запятой, лежащей между старшим и младшим байтами.
Например, вычислить 55/11:
Ввод A: #18 (1/11*256 = 23,272727, округлено до 24)
Ввод B: #37 (55)
Вывод: #528 (#5,28 или 5,15625 десятичное число)
Обратите внимание, что вывод не не совсем правильное значение (которое должно было быть #500), это потому, что 1/11 на самом деле не очень хорошее число, как в десятичной записи (. 0), так и в шестнадцатеричной записи (#.1745D1). Если бы мы округлили значение не до #.18, а до #.17, что было бы правильным округлением, результат был бы #4F1. Это было бы более точным, чем текущий результат, однако наша цель состоит в том, чтобы написать оптимальный код, и получить правильно округленное целое число из этого результата (равного 5) было бы намного проще, когда в результате мы имеем # 528, потому что мы тогда можно было бы просто взять только старший байт. Кроме того, для «правильного округления» потребуется дополнительный код. Вот почему мы округлили значение.
0), так и в шестнадцатеричной записи (#.1745D1). Если бы мы округлили значение не до #.18, а до #.17, что было бы правильным округлением, результат был бы #4F1. Это было бы более точным, чем текущий результат, однако наша цель состоит в том, чтобы написать оптимальный код, и получить правильно округленное целое число из этого результата (равного 5) было бы намного проще, когда в результате мы имеем # 528, потому что мы тогда можно было бы просто взять только старший байт. Кроме того, для «правильного округления» потребуется дополнительный код. Вот почему мы округлили значение.
Если вы берете слишком большое базовое значение, ошибка накапливается. Если вы, например, попытаетесь разделить 2200 на 11, результатом будет 206, хотя должно было быть 200. Чтобы решить эту проблему, вы можете увеличить разрешение (используйте 16-битное значение деления (#.1746) и 24-битное значение деления). - или 32-битный результат) или разделить на значения, которые являются «аккуратными» в шестнадцатеричном представлении (степень числа 2). Однако также помните, что независимо от того, какое основание вы используете, будь то 10 или 16, у вас всегда будут деления, которые приводят к ошибкам. Значения, с которыми это происходит, различаются, но вам придется иметь дело с ограничениями разрешения и округлением.
Однако также помните, что независимо от того, какое основание вы используете, будь то 10 или 16, у вас всегда будут деления, которые приводят к ошибкам. Значения, с которыми это происходит, различаются, но вам придется иметь дело с ограничениями разрешения и округлением.
В любом случае. Это общие процедуры деления. Медленнее, чем подпрограммы умножения, но все же настолько быстрые, насколько это возможно, и, вероятно, очень полезные.
;
; Разделить 8-битные значения
; In: Разделите E на делитель C
; Out: A = результат, B = отдых
;
Раздел 8:
xor а
лд б,8
Div8_Loop:
рл э
рла
подраздел с
младший нк, Div8_NoAdd
добавить а, с
Div8_NoAdd:
DJ Div8_Loop
лд б, а
лд а, е
рла
капрал
рет
;
; Разделить 16-битные значения (с 16-битным результатом)
; In: Разделить BC на делитель DE
; Out: BC = результат, HL = отдых
;
Раздел 16:
лд гл,0
лд а, б
лд б,8
Div16_Loop1:
рла
прил гл, гл
sbc hl, де
младший нк, Div16_NoAdd1
добавить хл, де
Div16_NoAdd1:
DJ Div16_Loop1
рла
капрал
лд б, а
лд а, с
лд с, б
лд б,8
Div16_Loop2:
рла
прил гл, гл
sbc hl, де
младший нк, Div16_NoAdd2
добавить хл, де
Div16_NoAdd2:
DJ Div16_Loop2
рла
капрал
лд б, в
лд с, а
рет
Спасибо Flyguille за подпрограмму Div16, взятую из его исходного кода MNBIOS.
Процедуры деления также можно развернуть, чтобы получить хороший прирост скорости. Если вы возьмете, например, подпрограмму Div16, для ее завершения потребуется 1297 T-состояний. Однако при развертывании ему требуется всего 1070 T-состояний, что увеличивает скорость на 18%. Дополнительная стоимость в байтах составляет 146 (исходная процедура составляет 27 байт).
Деление на 9
Рикардо Биттенкур предоставил нам быструю процедуру деления на 9. Он построен для .dsk или подпрограммы Disk ROM. Это очень быстро, но работает только в диапазоне 0-1440.
;
; деление на девять
; введите HL = число от 0 до 1440
; выход А = HL/9
; уничтожить HL, DE
; Z80 R800
DIV9: ВКЛ. HL; 7 1
ЛД Д,Н ; 5 1
LD E, L ; 5 1
ДОБАВИТЬ HL, HL ; 12 1
ДОБАВИТЬ HL, HL ; 12 1
ДОБАВИТЬ HL, HL ; 12 1
SBC HL,DE ; 17 2
ЛД Е,0 ; 8 2
ЛД Д,Л ; 5 1
ЛД А,Н ; 5 1
ДОБАВИТЬ HL, HL ; 12 1
ДОБАВИТЬ HL, HL ; 12 1
ДОБАВИТЬ HL,DE ; 12 1
АЦП А,Е ; 5 1
Исключающее ИЛИ Н ; 5 1
И 03FH ; 8 2
Исключающее ИЛИ Н ; 5 1
РЛКА ; 5 1
РЛКА ; 5 1
РЕТ ; всего = 157 22
Процедура извлечения квадратного корня
Это более быстрая процедура извлечения квадратного корня, чем та, что была здесь ранее, результаты тестов говорят, что она на 26% быстрее. Это написано Рикардо Биттенкуртом, большое ему спасибо :).
Это написано Рикардо Биттенкуртом, большое ему спасибо :).
;
; Квадратный корень из 16-битного значения
; В: HL = значение
; Out: D = результат (округленный в меньшую сторону)
;
Кв.16:
лд де,#0040
лд а, л
лд л,ч
лд ч, д
или
лд б,8
Sqr16_Loop:
sbc hl, де
младший нк, Sqr16_Skip
добавить хл, де
Sqr16_Пропустить:
ccf
рл д
добавить а, а
прил гл, гл
добавить а, а
прил гл, гл
DJ Sqr16_Loop
рет
Вот и все. Спасибо, иди к мистеру. Rodnay Zaks 🙂 за написание книги «Программирование Z80», которая научила меня выполнять умножения на Z80 и послужила источником вдохновения для перечисленных здесь подпрограмм. Если у вас есть какие-либо предложения по улучшению скорости или вы знаете другой метод, который может быть быстрее при определенных условиях, сообщите мне об этом.
~Grauw
| ; Простой калькулятор умножения | |
| ; Курт Кайзер | |
ВКЛЮЧАЕТ Irvine32. inc inc | |
| ; .data используется для объявления и определения переменных | |
| .данные | |
| codeTitle BYTE " --------- Магия математического умножения --------- ", 0 | |
| направлений БАЙТ "Введите 2 числа.", 0 | |
| prompt1 BYTE "Первое число: ", 0 | |
| prompt2 BYTE "Второй номер: ", 0 | |
| равно БАЙТ "=", 0 | |
| раз БАЙТ "*", 0 | |
| число 1 DWORD ? | |
| число2 DWORD ? | |
| Всего | DWORD ? |
; . code для исполняемой части программы code для исполняемой части программы | |
| .код | |
| основной ПРОЦ | |
| ; Вывести название и автора | |
| mov edx, OFFSET codeTitle | |
| вызов WriteString | |
| звоните CrLf | |
| ; Подскажите первую цифру | |
| mov edx, OFFSET prompt1 | |
| вызов WriteString | |
| вызов ReadInt | |
| мов номер1, еах | |
| ; Подскажите второй номер | |
| mov edx, приглашение OFFSET2 | |
| вызов WriteString | |
| вызов ReadInt | |
| мов номер2, еах | |
| ; Умножьте два числа, используя реестр eax | .|
| mov eax, число1 | |
| mov ebx, число2 | |
| мул ebx | |
| Всего | мов, еакс |
| ; Вывести итог на консоль | |
| ; Распечатать номер1 | |
| mov eax, число1 | |
| вызов WriteDec | |
| ; Распечатать знак умножения | |
| mov edx, СМЕЩЕНИЕ раз | |
| вызов WriteString | |
| ; Распечатать номер2 | |
| mov eax, число2 | |
| вызов WriteDec | |
| ; Вывести знак равенства | |
| mov edx, СМЕЩЕНИЕ равно | |
| вызов WriteString | |
| ; Распечатайте общее количество | |
| движений по оси, всего | |
| вызов WriteDec | |
| звоните CrLf | |
| звонок CrLf | |
| выход | |
| главный ENDP | |
| КОНЕЦ основной |
Основы сборки — Эндрю Бланс
Bookclub Week 4
Наконец, после 3 недель работы в Книжном клубе, мы начнем писать код. Как мы увидим, мы пока не сможем скопировать и вставить его в ассемблер и заставить его работать. После сегодняшнего дня нам будет 90% пути туда. Мы рассмотрим два примера: простой и менее простой. Глядя на них, мы расширим наши знания о наборе инструкций 6502 и дадим нам лучшее понимание того, какие инструкции доступны. Кроме того, мы увидим, что наш ассемблерный код может быть украшен информацией, понятной ассемблеру. Это позволит нам сделать наш код более удобным для чтения и использования.
Как мы увидим, мы пока не сможем скопировать и вставить его в ассемблер и заставить его работать. После сегодняшнего дня нам будет 90% пути туда. Мы рассмотрим два примера: простой и менее простой. Глядя на них, мы расширим наши знания о наборе инструкций 6502 и дадим нам лучшее понимание того, какие инструкции доступны. Кроме того, мы увидим, что наш ассемблерный код может быть украшен информацией, понятной ассемблеру. Это позволит нам сделать наш код более удобным для чтения и использования.
Дополнение
Простейшим примером будет 1 + 2. Вот код:
ЛДА #01
АЦП №02
Стабильный $0402
Слева от каждой строки находится инструкция, а справа — данные или ячейка памяти, необходимые для выполнения инструкции. В этом стиле написана сборка. Давайте рассмотрим пример по одной строке за раз.
Строка 1 : LDA указывает 6502 загрузить следующую часть данных в аккумулятор. Здесь это #01 . Мы можем предварить наши данные символом, чтобы сообщить ассемблеру, какие данные мы ему передаем. В этом случае мы используем хэштег, который означает, что наши данные являются «буквальными» — мы буквально передаем им число. После этой строки содержимое A равно 1.
В этом случае мы используем хэштег, который означает, что наши данные являются «буквальными» — мы буквально передаем им число. После этой строки содержимое A равно 1.
Строка 2 : ADC означает добавление следующего значения к тому, что в данный момент находится в Аккумуляторе. «C» в инструкции говорит нам, что он будет отслеживать любые переносы, которые произошли в предыдущих вычислениях. Здесь мы предполагаем, что C = 0. Теперь значение в A равно 3,
Строка 3 : Инструкция STA отправит содержимое аккумулятора в место в памяти. В нашем примере это отправит значение 3 на адрес памяти $0402. Обратите внимание, мы не использовали # - это потому что это не литерал, это адрес. Кроме того, мы использовали $ , что говорит ассемблеру, что это значение в двоичном формате.
После этих трех инструкций мы успешно сделали 1+2 - молодцы! Если бы мы хотели просмотреть ответ, нам пришлось бы искать $0402 .
Адресация и флаги
На прошлой неделе мы обсуждали многочисленные регистры, которые могут быть установлены в 6502. Мы также упоминали выше, что ADC также добавит все, что было перенесено из последнего вычисления (т. е. все в регистре переноса). Мы должны быть осторожны, чтобы то, что происходит, было именно тем, чего мы хотим. Мы не хотим добавлять перенос, когда мы этого не хотим, и мы не хотим упустить его, если мы действительно этого хотим. Мы можем вручную сбросить флаги, чтобы гарантировать отсутствие неожиданных значений в нашей арифметике — лучше перестраховаться, чем потом сожалеть. Это то, что CLC (очистить флаг переноса) и CLD (очистить десятичный флаг) сделать.
В предыдущем примере мы напрямую ссылались на значения 1 и 2. Там все было в порядке, поскольку у нас есть только небольшое количество значений, которые нам нужно использовать в наших расчетах. Однако, если бы мы занимались чем-то более сложным, это бы утомляло. В Python вы можете вызвать переменную «x» или «y» и использовать их в своем коде. Что обычно делать, так это хранить ваши значения где-то в памяти, а затем в вашем коде указывать на это место в памяти. Это избавит нас от явной передачи значений. Например, значение 1 может храниться в ячейке 9.0923 $0400 и значение 2 в
В Python вы можете вызвать переменную «x» или «y» и использовать их в своем коде. Что обычно делать, так это хранить ваши значения где-то в памяти, а затем в вашем коде указывать на это место в памяти. Это избавит нас от явной передачи значений. Например, значение 1 может храниться в ячейке 9.0923 $0400 и значение 2 в $0401 . Теперь мы можем просто обратиться к ним и получить тот же результат, что и раньше.
Ниже приведен код с этими двумя внесенными изменениями.
КЛК
ХЛД
ЛДА $0400
АЦП $0401
Стабильный $0402
Помимо встроенных функций языка ассемблера, функциональность может исходить от выбранного вами ассемблера. Вот некоторые полезные функции, доступные в большинстве ассемблеров:
- Вы можете хранить значения в "переменной". Таким образом, вы могли бы сказать
ADR1 = $0400, и тогда всякий раз, когда вы вызывалиADR1, ассемблер понимал, что вы имели в виду адрес, содержащийся в . - Вы можете оставлять комментарии с помощью ";".
- Вы можете "называть" блоки кода. Это позволяет нам многократно ссылаться на него в нашей программе. Скоро мы увидим пример, где это может быть полезно.

Приведенный ниже код включает приведенные выше предложения:
ADR1 = 0400 долларов США
ADR2 = $0401
ADR3 = $0402
ЦЛК; очистить бит переноса
КЛД ; очистить десятичный бит
ДОБАВИТЬ LDA ADR1 ; загрузить содержимое ADR1 в аккумулятор
АЦП АДР2 ; добавить содержимое ADR2 в аккумулятор
СТА ADR3 ; сохранить результат в ADR3
Теперь наш простой код использует больше возможностей языка и ассемблеров. Мы надеемся, что его будет легче читать, и нам будет проще использовать и развивать его.
Обман малого отряда
Перед попыткой умножения мы кратко рассмотрим деление на 2. Это можно легко сделать, рассмотрев операции, которые мы можем выполнять с двоичными числами. Давайте посмотрим, что произойдет, если мы сдвинем двоичное число вправо. Число 15 (
Число 15 ( 0000 1110 ) становится 7 ( 0000 0111 ) и 55 ( 0011 0111 ) становится 27 ( 0001 1011 ). Я не эксперт, поэтому я не могу со 100% уверенностью сказать, что это работает в 100% случаев, но это обеспечивает простой способ половинного числа. По сравнению с «правильным» делением и умножением это значительно проще.
Такое переключение стало возможным благодаря многочисленным инструкциям, которые есть у 6502. Набор инструкций содержит 2 сдвига и 2 поворота. На следующем рисунке показан пример каждого из них:
Два примера инструкций сдвига в наборе инструкций 6502: ROL и LSR. Сделано с помощью draw.io ROL сдвигает число влево, при этом крайний левый бит попадает в регистр переноса, а старое содержимое C перемещается в крайний правый бит.
LSR сдвигает число вправо. Здесь правда, самый правый бит попадает в перенос, а самый левый заменяется на 0.
У этих двух инструкций есть эквиваленты, которые действуют и в противоположном направлении. А пока
А пока РОЛ и ЛСР понадобятся нам для выполнения умножения.
Умножение
Умножение сложнее, чем сложение. В первую очередь потому, что у нас нет ни одной инструкции, которая может это сделать — нам нужно прокладывать свой собственный путь. Это действительно хороший пример для изучения, поскольку в нем используется множество различных инструкций и методов. Мы начнем с рассмотрения того, как мы обычно делаем умножение, и построим его оттуда.
\[ \begin{выровнено} & \enspace\enspace\enspace\; 12\ & \подчеркивание{\enspace\enspace\times23} \\ & \enspace\enspace\enspace\; 36\\ & \подчеркивание{\enspace+240\enspace} \\ &=276\\ \end{выровнено} \]
Это (надеюсь) выглядит знакомо. Вот как мы можем умножать обычные десятичные числа. В дальнейшем мы будем называть верхнее число множителем (MPD), а нижнее — множителем (MPR). Итак, 12 — это наш MPD, а 23 — наш MPR. Чтобы сделать это умножение, мы должны:
- умножить 3 на 12, получится 36.

- , затем мы сдвигаем MPD (12) влево, что дает нам 120, а затем умножаем на 2. Это дает нам 240.
- , объединяя их, дает нам 276.
Это правильный результат. Для этого с двоичными числами проделать ту же процедуру:
\[ \begin{выровнено} & \enspace\enspace\enspace\enspace\; 101\\ & \underline{\enspace\enspace\enspace\times 011} \\ & \enspace\enspace\enspace\enspace\; 101\\ & \enspace+1010 \\ & \подчеркнуть{\enspace+00000\enspace} \\ & = 01111 \\ \end{выровнено} \]
В этом примере мы умножаем 5 на 3. 101 — это множимое (MPD), а 011 — это множитель (MPR)
- Берем первый бит MPR (011). Это 1. Мы умножаем MPD (101) на это. У нас остался 101
- Затем мы сдвигаем MPD влево, что дает нам 1010. Следующий бит MPR также равен 1, поэтому у нас остается 1010.
- Снова сдвигаем МУРЗ влево. В результате получается 10100. Последний бит MPR равен 0, что означает, что это дает нам 00000 .
- Если их сложить вместе, у нас останется 01110, то есть 15.

И снова правильный результат. Если старший бит MPR равен 1 (множитель), вы сохраняете результат. Затем сдвиньте исходную вещь (множимое - MPD). Вы повторяете эту процедуру до тех пор, пока не убедитесь, что все биты вашего числа были проверены.
Это можно показать на блок-схеме. Это полезно сделать до того, как дело дойдет до написания кода, так как это может помочь вам визуализировать проблему, которую вы решаете. Это хорошо, поскольку по сравнению с нашими хорошими современными языками высокого уровня сложнее просто пойти на это и написать функцию.
Блок-схема того, как будет работать двоичное умножение. Сделано с помощью draw.ioСначала это может сбить с толку, но на приведенном выше рисунке показана та же логика, которую мы должны были использовать для умножения двоичных чисел выше. Стоит подумать о графике и попытаться понять его. Наш следующий шаг — преобразовать это в код. Давайте быстро рассмотрим некоторые проблемы / крайние случаи, с которыми мы можем столкнуться при этом:
- Умножение двух 8-битных чисел может дать 16-битное.
 Чтобы обойти это, нам нужно будет сохранить результат в двух 8-битных ячейках. Один для младших битов и один для старших битов. Например, мы можем сохранить 326 в виде двух 8-битных чисел, таких как
Чтобы обойти это, нам нужно будет сохранить результат в двух 8-битных ячейках. Один для младших битов и один для старших битов. Например, мы можем сохранить 326 в виде двух 8-битных чисел, таких как 00000001и01000110, а затем прочитать их все вместе, например00000001 01000110. Вы можете проверить, это 326! - Для этого расчета нам нужно отслеживать большое количество информации. Мы будем вынуждены использовать больше, чем просто регистры 6502.
- Невозможно проверить и сравнить каждый бит числа сразу. Для этого мы должны по отдельности переместить биты в A или C и провести там наши сравнения.
Я просто представлю код, а затем, как и раньше, мы можем пройтись по нему построчно.
СТАРТ LDA #0 ; нулевой аккумулятор
СТА ТМП ; очистить адрес
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ ; Чисто
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ+1 ; Чисто
ЛДКС #8; х это счетчик
МУЛЬТ ЛСР МПР ; сдвинуть mpr вправо - немного нажать на C
СК НОАДД ; тестовый бит переноса
РЕЗУЛЬТАТ ЛДА; загрузить A с низкой частью результата
CLC
АЦП МПД ; добавить mpd в res
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ ; сохранить результат
РЕЗУЛЬТАТ ЛДА+1 ; добавить отдых от сдвинутого mpd
АЦП ТМП
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ+1
NOADD ASL MPD ; сдвиг mpd влево, готов к следующему «циклу»
РОЛ ТМП ; сохранить бит из mpd в temp
ДЕКС ; счетчик уменьшения
БНЭ МУЛЬТ; пройти еще раз, если счетчик 0
Теперь у нас есть несколько именованных блоков кода. Почему это полезно? Что ж, мы можем делать сравнения и переходить к этим блокам в зависимости от результата. Это то, что сделают
Почему это полезно? Что ж, мы можем делать сравнения и переходить к этим блокам в зависимости от результата. Это то, что сделают BCC и BNE . Если Carry = 0, BCC сделает прыжок. Инструкция BNE также может вызвать ответвление, если флаг Z не равен 0. Зная это, мы можем пройтись по нашему коду, стараясь при этом помнить о нарисованной нами блок-схеме.
ПУСК
СТАРТ LDA #0 ; нулевой аккумулятор
СТА ТМП ; очистить адрес
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ ; Чисто
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ+1 ; Чисто
ЛДКС #8; х это счетчик
Строка 1 : Мы загружаем Аккумулятор с 0, это будет использоваться для установки областей в памяти пустыми.
Строка 2/ 3/ 4 : Три ячейки памяти становятся пустыми путем переноса в них содержимого A. Эти места включают в себя область временного хранения значений (TMP) и два места, где мы будем хранить результат (одно для старших битов результата и одно для младших 8 бит).
Строка 5 : Регистр X загружается со значением 8. Это будет использоваться для подсчета того, сколько раз мы сдвинули наши значения влево. Мы можем увеличить X вниз, используя инструкцию ДЕКС .
МУЛЬТ
МУЛЬТ ЛСР МПР ; сдвиг мпр вправо
СК НОАДД ; тестовый бит переноса
РЕЗУЛЬТАТ ЛДА; загрузить с низким разрешением
CLC
АЦП МПД ; добавить mpd в res
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ ; сохранить результат
РЕЗУЛЬТАТ ЛДА+1 ; добавить отдых от сдвинутого mpd
АЦП ТМП
СТАТИСТИЧЕСКИЙ РЕЗУЛЬТАТ+1
Строка 1 : LSR — одна из смен, которые мы видели выше. Это приведет к тому, что значащий бит нашего множителя попадет в регистр переноса.
Строка 2 : BCC проверить содержимое переноса. Если это 1, мы продолжим со следующей строки. Однако, если это 0, мы перейдем к блоку кода, который мы назвали «NOADD». Это проигнорирует остальную часть блока MULT.
Строка 3 : Предполагая, что содержимое регистра переноса равно 1, теперь мы помещаем текущее содержимое нижней части нашего результата в аккумулятор.
Строка 4 : Поскольку нет необходимости что-либо переносить в нижнюю половину результата, мы можем сделать CLC . Однако в этом нет необходимости, если вы заботитесь о верхней половине битов - нам нужно знать, перенеслось ли что-то из нижней части в верхнюю.
Строка 5 : Поскольку MPR равен 1, мы можем включить MPD в результат. Здесь АЦП добавит множимое к результату.
Строка 6 : Теперь мы сохраняем нижний результат обратно в РЕЗУЛЬТАТ
Строка 7/8/9 : это делает то же самое, что и строки 3/5 и 6, но для старших битов.
НОАДД
NOADD ASL MPD ; сдвиг mpd влево
РОЛ ТМП ; сохранить бит из mpd
ДЕКС ; счетчик уменьшения
БНЭ МУЛЬТ; пройти еще раз, если счетчик 0
Сюда перейдет код из строки 2 MULT, если C = 0. Однако мы достигнем этого места и после строки 9 MULT.
Однако мы достигнем этого места и после строки 9 MULT.
Строка 1 : ASL сдвигает множимое влево. Это «противоположность» LSR . Это подготовит его к тому моменту, когда мы зациклимся и найдем следующий бит MPR.
Строка 2 : После Строки 1 что-то попадет в Carry. Это можно восстановить в TMP с помощью инструкции ROL , которая поместит содержимое регистра переноса в его самый правый бит. Это сделано для того, чтобы этот бит можно было включить в старшие биты результата (см. Строку 8 MULT)
Строка 3 : DEX уменьшает регистр X на 1.
Строка 4 : BNE ответвляется, если содержимое Z не равно 0. Z будет установлено в 1, когда Инструкция DEX в строке 3 устанавливает X в 0. Это произойдет после того, как все биты в MPR будут использованы.
Готово! Выполнение всей этой процедуры умножит 2 числа. Это немного сложно, правда? Тем не менее, он следует нашей блок-схеме, которая следует логике того, как мы делали умножение с самого начала. Это полезный пример, который стоит попытаться полностью понять, так как он содержит множество важных инструкций и идей, которые мы будем использовать для написания остального кода, который мы увидим.
Это полезный пример, который стоит попытаться полностью понять, так как он содержит множество важных инструкций и идей, которые мы будем использовать для написания остального кода, который мы увидим.
Набор инструкций
Теперь мы видели различные наборы инструкций 6502. Тем не менее, есть еще многое другое. Эти два примера показывают нам, какие инструкции доступны. В целом они относятся к следующим категориям:
- Обработка данных (ADC, DEX)
- Передача данных (LDA, STA, LDX)
- Смены (РОЛ, ЛСР, АСЛ)
- Тестирование и разветвление (BCC, BNE)
- Управление (CLC, CLD)
В каждой категории их гораздо больше. На этом этапе большинству ресурсов потребуется время (обычно около 100 страниц) для обсуждения каждой инструкции. Такой справочный материал может быть очень полезным и обеспечит подробное описание каждого аспекта инструкций. Тем не менее, я не собираюсь делать это здесь. Писать скучновато, а читать не очень интересно. Кроме того, все это вы без труда найдете в Интернете. Многие инструкции, которые мы сейчас не видели, являются вариациями тех, которые у нас есть (
Кроме того, все это вы без труда найдете в Интернете. Многие инструкции, которые мы сейчас не видели, являются вариациями тех, которые у нас есть ( DEY уменьшает регистр Y, SBC вычитает...). Лучший способ узнать, как все они работают, — это использовать их или посмотреть, как они используются в примерах. Именно так мы будем изучать остальные из них в течение следующих недель.
Заключение
Мы рассмотрели два полезных примера кода: сложение и умножение. Очевидно, вы можете выполнять вычитание и деление, но я просто не показал этого здесь. Эти примеры, в частности, умножение, дают нам ряд инструкций, которые будут полезны в будущем.
На следующей неделе мы сосредоточимся на том, чтобы заставить этот код действительно работать. Для этого нам потребуется установить ассемблер и эмулятор. Затем, после этого, мы вернемся к другим примерам использования набора инструкций и множеству методов доступа к областям памяти.
конец.
Как всегда, это в значительной степени основано на Zaks Programming the 6502
Программирование на языке ассемблера Информатика Языки программирования
4
Бит Манипуляции
4. 1. АЛГОРИТМ УМНОЖЕНИЯ
1. АЛГОРИТМ УМНОЖЕНИЯ
С важную способность принятие решений в нашем репертуаре мы переместить
на обсуждение алгоритма, который поможет нам раскрыть
важный набор инструкций в нашем процессоре используется для бит манипуляции.
Умножение это обычный процесс, который мы использовать, и мы были обучены сделать
в раннее школьное обучение. Запомнить умножение на цифру и затем поставив крест
и затем умножение на следующую цифру и поставить два кресты и тд
и тд суммирование промежуточных результатов в конец. Очень знакомо процесс но
мы никогда не рассматривал процесс как алгоритм, и нам нужно увидеть его как
алгоритм чтобы донести это до процессор.
Кому выделить важные дело в алгоритме мы пересмотреть его на два 4битных
бинарника числа. Цифры 1101 т.е. 13 и 0101 т. е. 5. Ответ
должен быть 65 или в двоичном формате 01000001. Соблюдайте что ответ дважды как
Соблюдайте что ответ дважды как
пока множитель и множимое. Умножение показано в
следующий рисунок.
1101 = 13
0101 = 5
-----
1101
0000x
1101xx
0000xxx
--------
01000001 = 65
Берем первая цифра номера множитель и умножить его на множимое
. Так как цифра одна ответ множимое сам. Итак, мы
место множимое под бар. Перед умножением на следующая цифра
крест размещается в самом правом разместить на следующей строке и результат
размещен сдвинулся на одну цифру влево. Однако, поскольку цифра ноль, результат нуль.
Следующий цифра единица, умножение на что, ответ 1101. Ставим две
кресты на следующей строке в правильное большинство позиций и поместите результат там
перешел два места левее. четвертая цифра равна нулю, поэтому ответ 0000 это
размещено с тремя крестами на своем Правильно.
Соблюдать красота бинарной базы, так как не нужно никакого реального умножения по телефону
уровень цифр. Если цифра 0 ответ равен 0 и если цифра 1 ответ
— это само множимое. Также заметить, что для каждого следующая цифра в множителе
ответ написан переместил еще на одно место слева. Без смещения
для первая цифра, один раз на второй, дважды для третьего и трижды за
четвертый один. Добавление всех промежуточные ответы на результат 01000001=65
как желанный. Кресты лечатся как ноль в этом добавление.
До формулировка алгоритма для этой задачи нам понадобится еще немного
инструкций который может сдвинуть число так что мы используем эту инструкцию для нашего множимого
смещение, а также каким-то образом чтобы проверить биты множитель
один на один.
4.2. ПЕРЕМЕЩЕНИЕ И ВРАЩЕНИЯ
набор сдвига и поворота инструкция является одним из самый полезный набор
любой набор инструкций процессора. Они упрощают действительно сложные задачи на очень
Они упрощают действительно сложные задачи на очень
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
чистый и лаконичный алгоритм. после смены и операции вращения
являются доступны в нашем процессоре.
Смена Логическое право (ШР)
сдвиг логического вправо операция вставляет ноль слева и ходов
каждый бит на одну позицию справа и копирует самый правый бит в нести
флаг. Представьте, что есть труба заполнен до отказа восемью яйца. Труба
открытая с обоих концов и есть корзина на правый конец держать что-нибудь
падает оттуда. Операция сдвиг логического права состоит в том, чтобы заставить белый
мяч с левого конца. Операция изображена на следующее иллюстрация.
0
1
0
1
1
0
1
0
0
C
Белый шарики представляют нулевые биты в то время как черные шары представляют один бит. Шестнадцать
Шестнадцать
бит переключение делается так же путь с трубой двойной вместимость.
Смена Логический левый (SHL) / сдвиг Арифметика слева (САЛ)
сдвиг логической операции влево является полной противоположностью сдвиг логического вправо. В
это операции нулевой бит вставляется справа и каждый бит движется одна позиция
слева от него наиболее значимый бит, попадающий в флаг переноса.
Смена арифметика слева просто другое название смены логично слева. Операция
снова проиллюстрировано следующим иллюстрация мяча и трубы.
C
1
0
1
1
0
1
0
0
0
Сдвиг. Арифметическое право (ЮАР)
А число со знаком содержит распишитесь в самом важном кусочек. Если бы этот бит был
один a логическое смещение вправо будет изменить знак этого число из-за
вставка нуля слева. Знак числа со знаком не должен
Знак числа со знаком не должен
изменяться из-за смещения.
операция сдвиговой арифметики поэтому правильно сместить каждый бит один
место справа с копией самый значимый бит слева не более
значимых место. Бит выпал из право застряло в нести
корзина. Знаковый бит сохраняется в эта операция. операция показана далее
ниже. С операция переключения влево есть в основном умножение на 2, в то время как правое
переключение операция деление на два. Однако для чисел со знаком деление на
две банки быть выполнено с помощью сдвига арифметическое право и нет сдвиг логического
вправо. Операция сдвига влево эквивалентно умножению, за исключением случаев, когда
важный бит выпадает из оставил. Флаг переполнения будет сигнализировать об этом
условии если это происходит и может быть проверено с Джо. Для деления на 2
подписано числовое логическое право переключение даст ошибку ответ на отрицательный номер
как ноль, вставленный из левая изменит свое знак. Чтобы сохранить знак
Чтобы сохранить знак
флаг и по-прежнему эффективно разделить смену на два арифметическое право
инструкция должен использоваться на подписанном числа.
44
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
Повернуть Справа (РОР)
В повернуть вправо каждый раз бит перемещается на одну позицию в право и
бит выпало справа вставляется слева. Этот бит также копируется
в флаг переноса. операцию можно понять представить, что
труба используется для переключения имеет был отлит таким образом, что оба конца совпадают. Сейчас
когда первый мяч вынужден двигаться вперед, каждый мяч перемещает на один шаг
вперед при входе последнего мяча труба от него другой конец, занимающий
первый старое положение мяча. корзина для переноски занимает снимок этого мяча оставив
один конец трубы и вход со стороны Другой. Вращение Слева (РОЛ)
Вращение Слева (РОЛ)
В операция поворота влево инструкция, самая значащий бит копируется
в нести флаг и вставляется справа, вызывая каждый бит, чтобы переместить один
позиция Слева. Это обратная сторона поворота вправо инструкция. Вращение
может быть из восьми или шестнадцати бит. Следующая иллюстрация будет сделать концепт
очистить с помощью того же труба и шарики пример.
С
1
0
1
1
0
1
0
0 0 0 Повернуть Через право переноса (RCR)В повернуть через перенос вправо инструкция, флаг переноса вставляется из
влево, каждый бит перемещается на один положение справа и самый правый бит
отброшен во флаге переноса. Фактически это девятибитный или семнадцать бит
вращение вместо восьми или шестнадцатибитное вращение, как в случай простого
оборотов.
Представьте себе круглая формованная труба, как используется в простых вращениях но это
время положение для переноски является частью круга между два конца трубы.
Толкание мяч для переноски из левые вызывают каждый мяч, чтобы переместиться на один шаг его
правильно и самый правый бит занимает переносное место. Идея дальше
иллюстрировано ниже. Вращение Через перенос влево (RCL)
полная противоположность вращения через право переноса инструкция - это повернуть
через выполнять левую инструкцию. В его работа флаг вставлен из
правильная причина, по которой каждый бит переместить одно место в его слева и самый
значимый бит, занимающий перенос флаг. Концепция показано ниже в
таким же образом, как и в прошлом пример.
C
1
0
1
1
0
1
0
0
45
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
CS401@vu. edu.pk
edu.pk
4.3. УМНОЖЕНИЕ В СБОРЕ ЯЗЫК
В обсужден алгоритм умножения выше мы пересмотрели способ мы
умножили число в младших классах и привел пример того метод по
бинарный числа. Мы делаем простой модификация традиционного алгоритм
до приступаем к формулировке его в сборке язык.
В традиционный алгоритм мы вычисляем все промежуточные ответы и затем
суммировать их в получить окончательный ответ. Если мы добавить все промежуточные ответ на
накопить результат, результат будет быть таким же в конце, за исключением что мы делаем
нет надо запомнить многое промежуточные ответы во время все
умножение. Умножение на новый показан алгоритм ниже.
1101 =
13
Накоплено Результат
0101 =
5
-----
0 (Исходный Значение)
1101 =
13
0 + 13
=
13
0000x =
0
13 + 0
=
13
1101xx =
52
13 + 52
=
65
0000xxx =
0
65 + 0
=
65 (Ответить)
Мы пытаемся определить шаги нашего алгоритма. Сначала мы устанавливаем результат нуль.
Сначала мы устанавливаем результат нуль.
Тогда мы проверьте правый бит множитель. Если это одно добавление
множимое к результату, и если он ноль не выполнять сложение. Сдвиньте влево множимое
перед следующим битом мультипликатор проверяется. сдвиг влево множимого
выполняется вне зависимости от значение множителя правый
самый кусочек. Так же, как кресты в традиционном умножении всегда ставится
отметить единицы, десятки, тысячи, места. Затем проверьте следующий бит и если
это один добавить сдвинутый значение множителя к результат. Повторить для как
много цифры, как есть в множитель, 4 в нашем примере. Формулировка
шагов алгоритма мы получить:
Shift множитель к Правильно.
Если CF=1 добавить множимое к результат.
Смена множимое к Правильно.
Повторить алгоритм 4 раз.
Для 8-битное умножение алгоритм повторится 8 раз а для
шестнадцать битовое умножение будет повторяться 16 раз, независимо от размера множитель
является.
алгоритм использует факт что смещение правых сил самый правый бит до
вставьте флаг переноса. Если мы проверим флаг переноса с помощью JC мы эффективно
тестирование самая правая часть множитель. Еще одно смещение будет вызвать
следующий немного заглянуть в следующий итерации и так далее. Итак, наш задача проверки бит
по одному человек удовлетворен использованием сменная операция. Есть многие другие
методы чтобы выполнить это битовое тестирование, однако мы проиллюстрируем один из методы
в этом примере.
В первой итерации нет смещается так же, как есть без креста в
традиционный умножение на первое проходить. Поэтому мы разместили слева
переключение множителя после шаг добавления. Однако правое смещение
Однако правое смещение
г. множитель должен стоять перед дополнение как дополнение выполнение шага
зависит по его результату.
Мы внедрить язык ассемблера программа для выполнения этого 4бит
умножение. Алгоритм расширяется до больше бит, но есть несколько
осложнения, что осталось обсудить потом. На данный момент мы делаем 4бит
умножение сохранить алгоритм просто.
Пример 4.1
01
; 4-битное умножение алгоритм
02
[орг. 0x100]
03
пмп начало
04
05
множимое: дб
13
; 4-битное множимое (8-битное пробел)
06
множитель:
дб
5
; 4 бит множитель
46
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
07
результат:
db
0
; 8 бит результат
08
09
старт:
мов
кл, 4
; инициализировать счетчик битов для четыре
10
mov
bl, [множимое] ; нагрузка множимое в бл
11
мов
дл, [множитель]
; множитель нагрузки в dl
12
13
контрольный бит:
shr
dl, 1
; двигаться вправо самый бит в переноске
14
jnc
пропустить
; пропустить добавление, если бит ноль
15
16
добавить
[результат], бл
; накапливать результат
17
18
пропуск:
шл
бл, 1
; сдвиг множителя левый
19
дек
кл
; бит декремента количество
20
джнз
контрольный бит
; повторить, если биты левый
21
22
мов
топор, 0x4c00
; прекращать программа
23
целое число
0x21
числа, которые нужно умножить, константы пока. Умножение
Умножение
04-06
четырехбитный, поэтому ответ хранится в 8-битном регистр.
Если операнды были 8-битными ответ будет 16-битным, и если
07
операнды были 16бит ответ будет 32 бит. С восьми биты могут входить
байт мы использовали 4bit умножение как наш первый пример.
С сложение нулевыми средствами ничего пропускаем дополнение шаг если
14-16
крайний правый бит множителя нуль. Если прыжок не взято
сдвинутое значение множимое прибавляется к результат.
множимое сдвинуто влево каждую итерацию независимо от множитель
18
кусочек.
DEC — новый инструкция, а ее действие должно быть сразу
19
понятно с полученными знаниями до сих пор. Это просто
вычитает один из синглов операнд.
JNZ инструкция вызывает алгоритм повторять до любого биты
20
множитель слева
Внутри отладчик наблюдает за работа ШР и ШЛ инструкции.
ШР инструкция эффективно разделяет его операнд на два и
остаток хранится во флаге переноса откуда мы это тестируем. Инструкция ШЛ
умножает свой операнд на два, поэтому что он добавлен в один место
больше влево в результат.
4.4. РАСШИРЕННЫЕ ОПЕРАЦИИ
Мы выполнил 4-битное умножение на объясните алгоритм однако
реальный Преимущество компьютера в том, что мы попросите его умножить большое номера,
номера чье умножение занимает в реальном времени. Если у нас есть 8-битное число, которое мы можем сделать
умножение в слове регистры, но мы ограничены слово
операций? Что, если мы хотим умножить 32-битные или еще большие цифры? Мы
конечно не ограничено. Только язык ассемблера предоставляет нам основные
здание блоки. Мы строим площадь из эти блоки, или здание, или
классический только архитектурный объект зависит от нашего воображения. С
С
наш логика, мы можем расширить эти алгоритмы столько, сколько мы хотим.
Наш следующим примером будет умножение 16-битные числа для производства
32 бита отвечать. Однако для 32-битной ответ нам нужен способ сместить 32 бит
номер и способ добавить 32bit числа. Мы не можем зависеть от 16 бит
сдвиг так как у нас есть 16 значащих битов в нашем множимое и сдвиг любой
бит слева может упасть ценный бит, вызывающий полностью неправильный результат.
ценный бит означает любой бит, который один. Отбрасывание нулевого бита не вызывает никаких
разница. Итак, мы размещаем число 16it в 32-битном пространстве с старшие 16 бит
обнулены так что шестнадцатая смена операции не вызывают ценный бит на
падение. Несмотря на то, что цифры были 16бит нам нужны 32бит операции до
умножить правильно.
Кому поясним эту необходимость, мы взять пример с числа 40000 или 9C40 в
шестнадцатеричном формате. В двоичном виде это представлено как 1001110001000000. Чтобы умножить
В двоичном виде это представлено как 1001110001000000. Чтобы умножить
47
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
через два мы сдвиньте его на одно место в оставил. Ответ, который мы получаем
0011100010000000 и самый левый один упал в переноске флаг.
ответ должно быть 17-битное число 0x13880, но это 0x3880, что
14464 в десятичном виде вместо ожидается 80000. Мы должны быть осторожно в этой ситуации
всякий раз, когда происходит смещение использовал.
Расширенный Переключение
Использование наше основное смещение и инструкции по вращению мы можем эффективно сдвинуть
32 бита число в памяти слово по слово. Мы не можем сместить целый номер
сразу поскольку наша архитектура ограничена словесные операции. алгоритм
используем состоит всего из двух инструкций и мы называем его расширенным смещение.
число1:
дд
40000
шл
слово [число1], 1
ркл
слово [число1+2], 1
ДД директива резервирует 32-битный место в памяти, однако значение мы
разместили там поместится 16бит. Итак, мы можно смело переключать число осталось 16 раз.
наименее значимое слово доступный по адресу num1 и самое значимое
слово доступен по адресу num1+2.
Два инструкции тщательно изготовлен таким образом, что первая смена
ниже слово слева и самый значимый бит этого слова
отброшено в переноске. Со следующим Инструкция, которую мы нажимаем упал немного в
минимум значащий бит следующего слово, эффективно присоединяющееся к два 16-битных слова.
окончательный перенос после вторая инструкция будет старший бит
высшее слово, которое для этого число всегда будет нуль.
следующая иллюстрация прояснит концепт. Труба на право
Труба на право
содержит нижняя половина и труба слева содержит верхнюю половину.
первый инструкция заставила ноль справа в нижняя половина и слева
большинство бит сохраняется в переносе, и оттуда вставляется верхняя половина
и верхняя половина смещена как Что ж.
C
10110100
0
Шаг 1
Шаг 2
C
10110100
Для смещение вправо точное однако делается наоборот необходимо соблюдать осторожность
смены правая верхняя половина сначала а потом повернуть через нести право нижняя
половина по понятным причинам. инструкции, как это сделать находятся.
число1:
дд
40000
шр
слово [число1+2], 1
rcr
слово [число1], 1
сработала та же логика. Смена поместила наименьший значащий бит верхний
половина в переносном флаге и его толкнули справа в нижний половина.
Для опаленная смена у нас была бы использовал арифметику сдвига правильная инструкция
вместосдвига логического вправо инструкция.
расширение, которое мы сделали, это не ограничивается 32 битами. Мы может сдвинуть число
любого размер скажем 1024 бит. Вторая инструкция будет повторил номер
из раз, и мы можем достичь желаемый эффект. С использованием две простые инструкции
у нас есть расширил возможности операция по эффективному неограниченный номер
бит. Фактический предел доступная память как даже сегмент
лимит можно угостить немного мысль.
Расширенное дополнение и вычитание
Мы также необходимо 32-битное дополнение для умножение 16-битных чисел.
идея расширение такое же здесь. Однако нам необходимо ввести новый
инструкция в этом месте. инструкция ADC или «добавить с переносом». Обычный
дополнение имеет два операнда и добавляется второй операнд первый
48
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
CS401@vu. edu.pk
edu.pk
операнд. Однако у ADC есть три операнды. Третий подразумевал операнд
перенос флаг. Инструкция АЦП специально для расширение возможностей
ДОБАВИТЬ. Цифры любого размера можно добавить с помощью правильная комбинация
ДОБАВИТЬ и АЦП. Все основные строительные блоки предоставляются для
сборка языковой программист и программист может расширить его
возможностей столько, сколько нужно, используя эти тонкие инструкции в
соответствующие комбинации.
Далее уточнение работы АЦП, рассмотрим инструкцию «ADC AX,
BX». Нормальное дополнение имело бы только что добавил BX в AX, однако ADC первые
добавляет флаг переноса в AX и затем добавляет BX к AX. Следовательно последний перенос
тоже включены в результат.
алгоритм должен быть очевиден в настоящее время. Нижние половины два номера
будут добавлены первыми с обычным дополнением. За верхняя
За верхняя
половинки нормальное дополнение потеряет след возможного переноса из нижней
половинки и ответ будет неправильный. Если перенос был сгенерирован, это должен идти
в верхняя половина. Следовательно верхние половины добавляются с дополнение с
носить инструкция.
С один операнд должен быть в регистре, ax привык читать снизу и
верхний половинки источника одна за другой один. Пункт назначения напрямую обновляется.
набор инструкций идет здесь.
DEST:
DD
40000
SRC:
DD
80000
MOV
AX, [SRC]
Добавить
Word] ax
mov
ax, [src+2]
adc
слово [dest+2], топор
К далее расширить его больше дополнение с переносами будет использоваться. Однако
нести от последнего добавления будет впустую, так как всегда будет предельный размер
где результаты и числа сохранены. Этот нести останется в
Этот нести останется в
нести флаг для проверки возможен перелив.
Для вычитание по той же логике будет использоваться и так же, как дополнение с
нести есть инструкция вычитать с заимствует под названием SBB. Занимать в
имя означает нести флаг и используется только для ясности. Или мы можем скажи
что флаг переноса держится перенос для добавления инструкции и одолжить
на инструкции по вычитанию. Также перенос генерируется в 17 бит и
заимствование также взято из 17-й бит. Также нет единого инструкция
что нужно брать и нести в их самостоятельные значения в то же время
. Поэтому логично использовать тот самый флаг для обе задачи.
Мы расширить вычитание с очень аналогичный алгоритм. Нижний половинки
должны быть вычитается нормально, пока верхние половины должны быть вычитается из
а вычесть с помощью команды заимствования, поэтому что если нижние половины нужен
займ, единица вычитается из верхние половинки. Алгоритм как
Алгоритм как
под.
DEST:
DD
40000
SRC:
DD
80000
MOV
AX, [SRC]
Sub
Word], Dest], топор
mov
топор, [источник+2]
sbb
слово [назначение+2], топор
Расширенный Умножение
Мы используем расширенное переключение и расширенное дополнение для формулировки нашего алгоритм
сделать расширенное умножение. множитель все еще хранится в 16 бит, так как мы только
нужно проверить его биты по одному. множимое однако не может быть сохранено
в 16 бит, иначе слева смещение его значительного биты могут получить потерял.
Поэтому он должен храниться в 32 битах и смещение и дополнение используется к
накапливается результат должен быть 32-битным, как Что ж.
Пример 4.2
49
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
CS401@vu. edu.pk
edu.pk
01
; 16 бит умножение
02
[орг. 0x0100]
03
пмп начало
04
05
множимое: дд
1300
; 16-битное множимое 32-битное пробел
06
множитель:
dw
500
; 16 бит множитель
07
результат:
дд
0
; 32 бит результат
08
09
старт:
мов
кл, 16
; инициализировать счетчик битов для 16
10
мов
дх, [множитель]
; множитель нагрузки в dx
11
12
контрольный бит:
shr
dx, 1
; двигаться вправо самый бит в переносе
13
jnc
пропуск
; пропустить добавление, если бит ноль
14
15
мов
топор, [множимое]
16
добавить
[результат], топор
; добавить меньше значащее слово
17
mov
топор, [множимое+2]
18
адк
[результат+2], топор
; добавлять старшее слово
19
20
пропустить:
шл
слово [множимое], 1
21
rcl
слово [множимое+2], 1 ; сдвиг множителя влево
22
dec
cl
; бит декремента count
23
jnz
контрольный бит
; повторить, если биты левый
24
25
мов
топор, 0x4c00
; прекращать программа
26
целое число
0x21
множимое и множитель хранится в 32-битное пространство, а
05-07
множитель хранится как слово.
10
множитель загружается в DX, где он будет сдвигаться по крупицам. Это
может быть непосредственно перемещается в памяти как Что ж.
15-18
множимое прибавляется к результат с использованием расширенного 32 бит
дополнение.
20-21
множимое сдвигается влево как 32-битное число с использованием расширенный
переключение операция.
множимое будет занимать пространство от 0103-0106, множитель займет
пробел от 0107-0108 и результат займет пространство от
0109-010C. Внутри отладчика наблюдайте изменения в этих память
ячеек в течение алгоритм. Расширенный переключение и
дополнение операции обеспечивают то же самое эффект, который был бы обеспечен, если бы там
были 32-битное сложение и сдвиг операции, доступные в Набор инструкций.
В конец алгоритма ячейки памяти результатов содержат значение
0009EB10 что составляет 65000 в десятичной форме; в желаемый ответ. Также обратите внимание что
Также обратите внимание что
число 00000514, которое составляет 1300 в десятичное, наше множимое,
стал 05140000 после ухода менялся 16 раз. Наш расширенный сдвиг имеет
дано такой же результат, как если бы 32-битное число сдвинуто влево 16 раз как единое целое.
Есть много других важных применения сдвига и вращения
операций в дополнение к этому примеру алгоритм умножения. Еще
примеров придет в ближайшие главы.
4.5. ПОБИТОВЫЙ ЛОГИЧЕСКИЙ ОПЕРАЦИИ
Процессор 8088 предоставляет нам несколько логических операций, которые работать
в битовый уровень. Логический операции такие же, как обсуждается в компьютерной логике
дизайн; однако наша точка зрения будет немного отличается. Четыре базовый
операций являются И, ИЛИ, исключающее ИЛИ, и не.
главное в этих операции заключается в том, что они побитовый. Это
Это
означает что если "и топор, бх" дается инструкция, затем применяется операция AND
на соответствующие биты AX и BX. Есть 16 операций И как
а результат; по одному на каждый бит АКС. Бит 0 регистра AX будет установлен, если оба его оригинал
значение и бит 0 BX установлены, бит 1 будет установить, если оба оригинала значение и
Бит 1 BX установлены и так далее для остальные биты. Эти операции
проведены параллельно на шестнадцати биты. Точно так же операции прочих
логических операции побитовые как Что ж.
50
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
И операция
И выполняет логическое побитовое и из два
X
Y
X и Y
операндов (байт или слово) и возвращает результат в пункт назначения
0
0
0
операнд. Немного в результате установить, если оба
Немного в результате установить, если оба
0
1
0
соответствующий биты оригинала устанавливаются операнды;
1
0
0
иначе бит очищается, как показано на таблица истинности.
1
1
1
Примеры являются «и топор, bx» и "и байт [mem], 5." Все
возможностей которые являются законными для дополнение также является законным для И операция.
другое дело - побитовое поведение этого операция.
ИЛИ операция
ИЛИ выполняет логическое побитовое "включительно или" из два
X
Y
X или Y
операндов (байт или слово) и возвращает результат в пункт назначения
0
0
0
операнд. Немного в результате установить, если либо или
0
1
1
оба соответствующие биты в исходные операнды набор
1
0
1
иначе бит результата очищается как показана правда
1
1
1
табл. Примеры: «или топор, bx». и "или байт [mem], 5".
Примеры: «или топор, bx». и "или байт [mem], 5".
Исключающее ИЛИ операция
Исключающее ИЛИ (Эксклюзивное или) выполняет логический побитовое
X
Y
X xor Y
"эксклюзивный или" из двух операндов и возвращает результат
0
0
0
в операнд назначения. Немного в результат устанавливается, если
0
1
1
соответствует биты оригинала операнды содержат
1
0
1
напротив значения (один установлен, другое очищается) иначе
1
1
0
бит результата очищается, как показано на таблица истинности. XOR
— это очень важная операция из-за к собственности, что это реверсивное
действие. Он используется во многих криптографических алгоритмы, обработка изображений, и
в операции рисования. Примеры являются «xor ax, bx» и "xor байт [память], 5".
НЕ операция
НЕ инвертирует биты (формирует дополнение) байт или слово
операнд. В отличие от других логических операций, это один операнд
инструкция, и не является чисто логическим операция в смысле другие,
но это до сих пор традиционно считается в тот же набор. Примеры "не топор" и
"не байт [память], 5".
4.6. ОПЕРАЦИИ ПО МАСКИРОВКЕ
Выборочный Очистка битов
Другое использование И заключается в том, чтобы сделать выборочным нулевые биты в его назначение
операнд. Исходный операнд загружается с маской, содержащей один на
позиций которые сохраняют свои старые значение и ноль в позициях которые должны быть
обнулено. Эффект применяя эту операцию к пункт назначения с маской
в источник, чтобы очистить нужные биты. Эта операция называется маскировкой.
Для пример, если нижний полубайт должен быть очищен, то операция может быть
применяется с F0 в исходнике. верхний полубайт сохранит свой старое значение и
верхний полубайт сохранит свой старое значение и
нижний клев будет очищено.
Селективный Установка бита
операцию можно использовать как операция маскирования для установки выборочные биты.
бит в маска очищена в должности, которые необходимо сохранить их значения и
ар установить в положения, которые должны быть установлен. Например, чтобы установить младший полубайт
операнд назначения, операцию следует проводить с маской 0F
в источник. Верхний откус сохранит свою ценность и будет установлен нижний полубайт
как результат.
51
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
Выборочно Битовая инверсия
XOR может также использовать в качестве маскировки операция инвертирования выборочного биты.
бит в маска очищена в должности, которые должны сохранить их значения,
и устанавливаются на позиции, которые подлежат инвертированию. За пример инвертировать
За пример инвертировать
ниже кусочек места назначения операнд, операнд должен применяться с
маской 0F в источник. Верхний nibble сохранит свое значение и
ниже в результате будет установлен nibble. Сравните это с НЕ которое инвертирует
все. XOR, с другой стороны, позволяет инвертирующий селективный биты.
Селективный Bit Testing
И может использоваться для проверки того, отдельные биты числа установлены или
нет. Раньше мы использовали сдвиг и JC для проверки битов один за другим один. Теперь мы
вводим другой способ проверить биты, который мощнее в смысле что
любой бит можно проверить в любое время и не обязательно по порядку. А ТАКЖЕ может быть
применяется в пункте назначения с 1 битом в желаемое положение и источник,
, который должен быть проверено. Если пункт назначения в результате ноль, что может проверить
с инструкцией JZ бит в желаемое положение в источник
был Чисто.
Однако операция И уничтожает маска назначения, которая может быть
нужно позже также. Следовательно Intel предоставила нам еще один инструкция
аналог CMP, который не разрушает вычитание. Это ТЕСТ
инструкция и является неразрушающей операцией И. Это не меняет пункт назначения
и устанавливает только флаги в соответствии с И операция. По
проверка флаги, мы можем видеть, если желаемый бит был установлен или очищено.
Мы изменить наш алгоритм умножения на использовать выборочное тестирование битов вместо
из проверка битов один за другим с помощью сдвига операции.
Пример 4.3
01
; 16-битное умножение с использованием тест для битового тестирования
02
[org 0x0100]
03
пмп старт
04
05
множимое: дд
1300
; 16-битное множимое 32-битное пробел
06
множитель:
dw
500
; 16 бит множитель
07
результат:
дд
0
; 32 бит результат
08
09
начало:
мов
кл, 16
; инициализировать счетчик битов для 16
10
мов
бх, 1
; бит инициализации маска
11
12
контрольный бит:
тест bx, [множитель]
; двигаться вправо самый бит в переносе
13
jz
пропустить
; пропустить добавление, если бит ноль
14
15
мов
топор, [множимое]
16
добавить
[результат], топор
; добавить меньше значащее слово
17
mov
топор, [множимое+2]
18
адк
[результат+2], топор
; добавлять старшее слово
19
20
пропустить:
шл
слово [кратное], 1
21
rcl
слово [множимое+2], 1 ; сдвиг множителя влево
22
шл
бх, 1
; сменная маска к следующему биту
23
dec
cl
; бит декремента count
24
jnz
контрольный бит
; повторить, если биты левый
25
26
мов
топор, 0x4c00
; прекращать программа
27
целое число
0x21
тестовая инструкция используется для битовое тестирование. BX держит маску и в
BX держит маску и в
12
каждый следующая итерация смещается слева, так как наш обеспокоенный бит теперь
следующий кусочек.
22-24
Можем делать в этом не считая пример. Мы можем остановиться, как только как
наша маска в BX становится нулем. Это маленькие хитрости что
в сборе позволяет нам делать и оптимизировать наши Код в результате.
52
Компьютер Архитектура и язык ассемблера Программирование
Курс Код: CS401
Внутри отладчик заметит, что оба места памяти и маску
BX сделать не измениться в результате Инструкция ТЕСТ. Также посмотрите, как выглядит наша маска
смещается влево так что следующий ТЕСТ инструкция тестирует
следующий кусочек. В итоге мы получаем тот же результат 0009EB10 как в предыдущем примере
.
УПРАЖНЕНИЯ
1. Напишите программу для замены каждая пара битов в AX регистр.
2. Дать значение регистра AX и флаг переноса после каждого из
следующих инструкции.
стк
мов
топор, <ваш rollnumber>
adc
ah, <первый символ вашего Название>
CMC
XOR
AH,
AL
MOV
CL,
4
SHR
AL,
CL
RCR
AH,
CL
3. Напишите программу для замены откусывает в каждом байте регистр АХ.
4. Подсчитайте число одного биты в BX и дополняют равно
номер младших значащих битов в АКС.
ПОДСКАЗКА: Используйте исключающее ИЛИ инструкция
5. Напишите программу для умножения двух 32-битные числа и хранилище ответ
в 64-битная локация.
6. Объявить 32-байтовый буфер содержащие случайные данные. Рассмотрим для этой проблемы
что биты в этих 32 байты нумеруются от 0 до 255.
Объявить другой байт, содержащий номер начального бита.
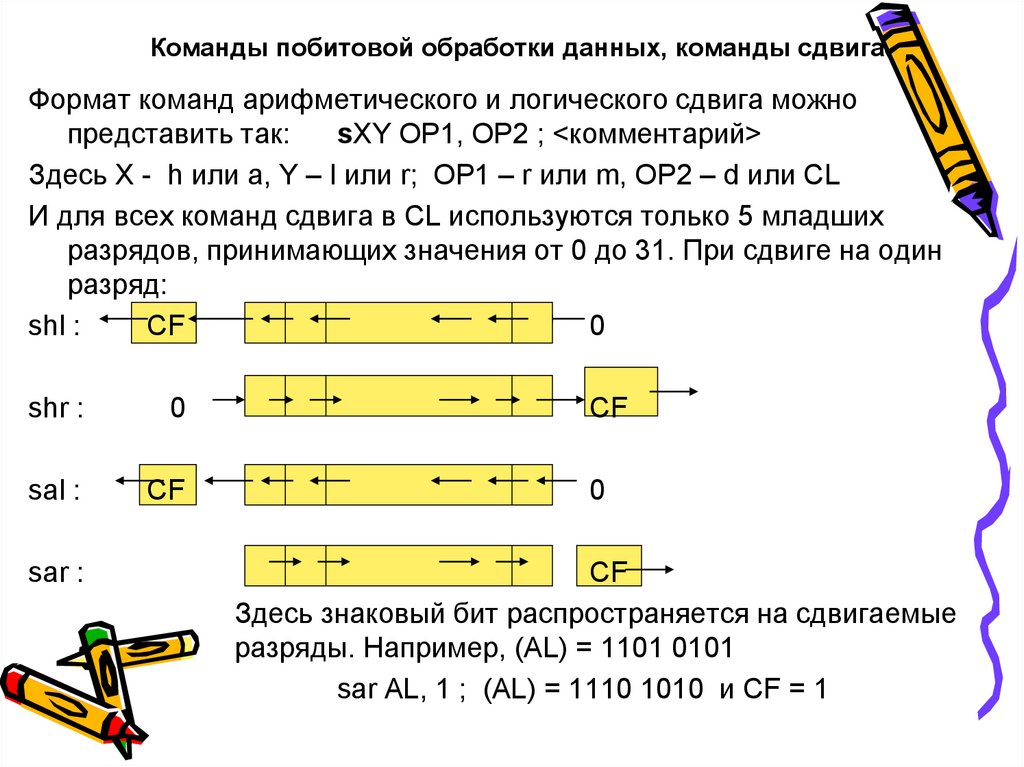 е. R17:R16=0),
е. R17:R16=0), е. R24:R23 = 0), то выходим из
е. R24:R23 = 0), то выходим из MUL будет работать со всеми 32 регистрами от R0 до R31 и оставит младший байт.
результата в R0 и старшего байта в R1.
Регистры множимого и множителя остаются без изменений.
Процедура занимает около трех циклов.
MUL будет работать со всеми 32 регистрами от R0 до R31 и оставит младший байт.
результата в R0 и старшего байта в R1.
Регистры множимого и множителя остаются без изменений.
Процедура занимает около трех циклов.
 Он сдвигает биты умножителя в бит переноса и использует содержимое переноса для
добавьте множимое, если оно равно единице, или пропустите его, если перенос равен нулю. Процедура занимает около шестидесяти циклов.
Он сдвигает биты умножителя в бит переноса и использует содержимое переноса для
добавьте множимое, если оно равно единице, или пропустите его, если перенос равен нулю. Процедура занимает около шестидесяти циклов.
 Процедура занимает около 90 циклов.
Процедура занимает около 90 циклов. Процедура занимает около 230 циклов.
Процедура занимает около 230 циклов. DEF BH = R21 ;Для хранения старшего байта делителя
.DEF C = R22 ;Счетчик битов
LDI A1,LOW(420) ;Загрузить младший байт делимого в A1
LDI A2,BYTE2(420) ;Загрузить второй байт делимого в A2
LDI A3,BYTE3(420) ;Загрузить третий байт делимого в A3
LDI A4,BYTE4(420) ;Загрузить четвертый байт делимого в A4
LDI BL,LOW(10) ;Загрузить младший байт делителя в BL
LDI BH,HIGH(10) ;Загрузить старший байт делителя в BH
ДИВ3216:
КЛР НОЛЬ
MOVW ANS2:ANS1,A2:A1 ;Копировать делимое в ответ
MOVW ANS4:ANS3,A4:A3 ;
LDI C,33 ;Счетчик битов загрузки
SUB REM1,REM1 ;Очистить остаток и перенести
CLR REM2 ;
CLR REM3 ;
CLR REM4 ;
LOOP: ROL ANS1 ;Сдвиньте ответ влево
РОЛ АНС2 ;
РОЛ АН3 ;
РОЛ АНС4 ;
DEC C ;Уменьшение счетчика
BREQ DONE ;Выход, если выполнено 32 бита
ROL REM1 ;Сдвиг остатка влево
РОЛ РЕМ2 ;
РОЛ РЕМ3 ;
РОЛ РЕМ4 ;
SUB REM1,BL ;Попробовать вычесть делитель из остатка
SBC REM2,BH ;
SBC REM3,НОЛЬ ;
SBC REM4,НОЛЬ ;
BRCC SKIP ;Если результат отрицательный, то
ADD REM1,BL ;обратите вычитание, чтобы повторить попытку
АЦП REM2,BH ;
АЦП REM3,НОЛЬ ;
АЦП REM4,НОЛЬ ;
CLC ;Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP ;цикл назад
SKIP: SEC ;Установить перенос флага на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
92 = 25
DEF BH = R21 ;Для хранения старшего байта делителя
.DEF C = R22 ;Счетчик битов
LDI A1,LOW(420) ;Загрузить младший байт делимого в A1
LDI A2,BYTE2(420) ;Загрузить второй байт делимого в A2
LDI A3,BYTE3(420) ;Загрузить третий байт делимого в A3
LDI A4,BYTE4(420) ;Загрузить четвертый байт делимого в A4
LDI BL,LOW(10) ;Загрузить младший байт делителя в BL
LDI BH,HIGH(10) ;Загрузить старший байт делителя в BH
ДИВ3216:
КЛР НОЛЬ
MOVW ANS2:ANS1,A2:A1 ;Копировать делимое в ответ
MOVW ANS4:ANS3,A4:A3 ;
LDI C,33 ;Счетчик битов загрузки
SUB REM1,REM1 ;Очистить остаток и перенести
CLR REM2 ;
CLR REM3 ;
CLR REM4 ;
LOOP: ROL ANS1 ;Сдвиньте ответ влево
РОЛ АНС2 ;
РОЛ АН3 ;
РОЛ АНС4 ;
DEC C ;Уменьшение счетчика
BREQ DONE ;Выход, если выполнено 32 бита
ROL REM1 ;Сдвиг остатка влево
РОЛ РЕМ2 ;
РОЛ РЕМ3 ;
РОЛ РЕМ4 ;
SUB REM1,BL ;Попробовать вычесть делитель из остатка
SBC REM2,BH ;
SBC REM3,НОЛЬ ;
SBC REM4,НОЛЬ ;
BRCC SKIP ;Если результат отрицательный, то
ADD REM1,BL ;обратите вычитание, чтобы повторить попытку
АЦП REM2,BH ;
АЦП REM3,НОЛЬ ;
АЦП REM4,НОЛЬ ;
CLC ;Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP ;цикл назад
SKIP: SEC ;Установить перенос флага на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
92 = 25
 Мы просто создаем процедуру, которая отслеживает общее количество вычтенных нечетных чисел.
Процедура занимает от пятнадцати до ста циклов.
Мы просто создаем процедуру, которая отслеживает общее количество вычтенных нечетных чисел.
Процедура занимает от пятнадцати до ста циклов.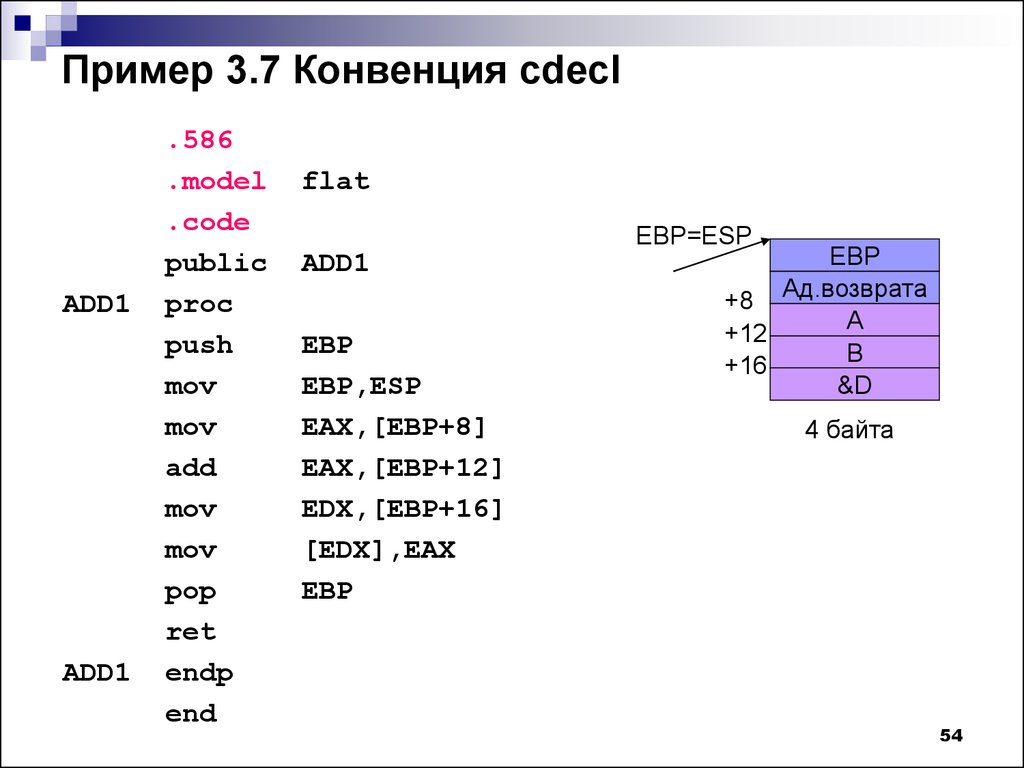 DEF C = R20 ;Счетчик циклов
LDI AL, НИЗКИЙ ($FFFF)
LDI AH, ВЫСОКИЙ ($ FFFF)
SQRT16:
PUSH AL ;Сохранить квадрат для последующего восстановления
НАЖМИТЕ АХ ;
CLR REML ;Инициализировать остаток до нуля
КЛР РЕМХ ;
CLR ANSL ;Инициализировать Root до нуля
КЛР АНШ ;
LDI C,8 ;Установить счетчик циклов на восемь
ПЕТЛЯ:
LSL ANSL ;Умножить корень на два
РОЛ АНШ ;
LSL AL ;Сдвинуть два старших бита Square
ROL AH ;в остаток
РОЛ РЕМЛ ;
РОЛ РЕМХ ;
LSL AL ;Сдвиг второго старшего бита Sqaure
ROL AH ;в остаток
РОЛ РЕМЛ ;
РОЛ РЕМХ ;
CP ANSL,REML ;Сравнить корень с остатком
КПК АНШ,РЕМХ ;
BRCC SKIP ;Если остаток меньше или равен корню
INC ANSL ;Приращение корня
SUB REML,ANSL ;Вычесть корень из остатка
СБК РЭМХ,АНШ ;
INC ANSL ;Приращение корня
ПРОПУСКАТЬ:
DEC C ;Уменьшение счетчика циклов
BRNE LOOP ;Проверить, все ли биты обработаны
LSR ANSH ;Делить корень на два
РОР АНСЛ ;
POP AH ;Восстановить исходный квадрат
POP AL
ПЕТЛЯ RJMP
DEF C = R20 ;Счетчик циклов
LDI AL, НИЗКИЙ ($FFFF)
LDI AH, ВЫСОКИЙ ($ FFFF)
SQRT16:
PUSH AL ;Сохранить квадрат для последующего восстановления
НАЖМИТЕ АХ ;
CLR REML ;Инициализировать остаток до нуля
КЛР РЕМХ ;
CLR ANSL ;Инициализировать Root до нуля
КЛР АНШ ;
LDI C,8 ;Установить счетчик циклов на восемь
ПЕТЛЯ:
LSL ANSL ;Умножить корень на два
РОЛ АНШ ;
LSL AL ;Сдвинуть два старших бита Square
ROL AH ;в остаток
РОЛ РЕМЛ ;
РОЛ РЕМХ ;
LSL AL ;Сдвиг второго старшего бита Sqaure
ROL AH ;в остаток
РОЛ РЕМЛ ;
РОЛ РЕМХ ;
CP ANSL,REML ;Сравнить корень с остатком
КПК АНШ,РЕМХ ;
BRCC SKIP ;Если остаток меньше или равен корню
INC ANSL ;Приращение корня
SUB REML,ANSL ;Вычесть корень из остатка
СБК РЭМХ,АНШ ;
INC ANSL ;Приращение корня
ПРОПУСКАТЬ:
DEC C ;Уменьшение счетчика циклов
BRNE LOOP ;Проверить, все ли биты обработаны
LSR ANSH ;Делить корень на два
РОР АНСЛ ;
POP AH ;Восстановить исходный квадрат
POP AL
ПЕТЛЯ RJMP