Транспортирование матриц: Транспонирование матриц в Excel

Транспонирование матриц в Excel

При работе с матрицами иногда нужно их транспонировать, то есть, говоря простыми словами, перевернуть. Конечно, можно перебить данные вручную, но Эксель предлагает несколько способов сделать это проще и быстрее. Давайте разберем их подробно.

Процесс транспонирования

Транспонирование матрицы – это процесс смены столбцов и строк местами. В программе Excel имеется две возможности проведения транспонирования: используя функцию ТРАНСП и при помощи инструмента специальной вставки. Рассмотрим каждый из этих вариантов более подробно.

Способ 1: оператор ТРАНСП

Функция ТРАНСП относится к категории операторов «Ссылки и массивы». Особенностью является то, что у неё, как и у других функций, работающих с массивами, результатом выдачи является не содержимое ячейки, а целый массив данных. Синтаксис функции довольно простой и выглядит следующим образом:

=ТРАНСП(массив)

То есть, единственным аргументом данного оператора является ссылка на массив, в нашем случае матрицу, который следует преобразовать.

Посмотрим, как эту функцию можно применить на примере с реальной матрицей.

1. Выделяем незаполненную ячейку на листе, планируемую сделать крайней верхней левой ячейкой преобразованной матрицы. Далее жмем на значок «Вставить функцию», который расположен вблизи строки формул.
2. Производится запуск Мастера функций. Открываем в нем категорию «Ссылки и массивы» или «Полный алфавитный перечень». После того, как отыскали наименование «ТРАНСП», производим его выделение и жмем на кнопку «OK».
3. Происходит запуск окна аргументов функции ТРАНСП. Единственному аргументу данного оператора соответствует поле «Массив». В него нужно внести координаты матрицы, которую следует перевернуть. Для этого устанавливаем курсор в поле и, зажав левую кнопку мыши, выделяем весь диапазон матрицы на листе. После того, как адрес области отобразился в окне аргументов, щелкаем по кнопке
   «OK».
4. Но, как видим, в ячейке, которая предназначена для вывода результата, отображается некорректное значение в

Матрица перевозок с применением метода северо-западного угла — Студопедия

Студопедия Категории Авто Автоматизация Архитектура Астрономия Аудит Биология Бухгалтерия Военное дело Генетика География Геология Государство Дом Журналистика и СМИ Изобретательство Иностранные языки Информатика Искусство История Компьютеры Кулинария Культура Лексикология Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлы и Сварка Механика Музыка Население Образование Охрана безопасности жизни Охрана Труда Педагогика Политика Право Программирование Производство Промышленность Психология Радио Регилия Связь Социология Спорт Стандартизация Строительство Технологии Торговля Туризм Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Эконометрика Экономика Электроника Юриспунденкция Предметы Авиадвигателестроения Административное право Административное право Беларусии Алгебра Архитектура Безопасность жизнедеятельности Введение в профессию «психолог» Введение в экономику культуры Высшая математика Геология Геоморфология Гидрология и гидрометрии Гидросистемы и гидромашины История Украины Культурология Культурология Логика Маркетинг Машиностроение Медицинская психология Менеджмент Металлы и сварка Методы и средства измерений
электрических величин Мировая экономика Начертательная геометрия Основы экономической теории Охрана труда Пожарная тактика Процессы и структуры мышления Профессиональная психология Психология Психология менеджмента Современные фундаментальные и
прикладные исследования
в приборостроении Социальная психология Социально-философская проблематика Социология Статистика Теоретические основы информатики Теория автоматического регулирования Теория вероятности Транспортное право Туроператор Уголовное право Уголовный процесс Управление современным производством Физика Физические явления Философия Холодильные установки Экология Экономика История экономики Основы экономики Экономика предприятия Экономическая история Экономическая теория Экономический анализ

Транспонировать матрицу в одну строку в Python

Транспонирование матрицы — это задача, которую все мы можем очень легко выполнить в python (используя вложенный цикл).

Но есть несколько интересных способов сделать то же самое в одной строке.
В Python мы можем реализовать матрицу как вложенный список (список внутри списка). Каждый элемент рассматривается как строка матрицы. Например, m = [[1, 2], [4, 5], [3, 6]] представляет собой матрицу из 3 строк и 2 столбцов.
Первый элемент списка — m [0] и элемент в первой строке, первый столбец — m [0] [0] .

1. Использование понимания вложенного списка: понимание вложенного списка используется для итерации каждого элемента в матрице. В данном примере мы выполняем итерацию по каждому элементу матрицы (m) в основном столбце и присваиваем результат рез-матрице, которая представляет собой транспонирование м.

   m = [[ 1,2],[3,4],[5,6]] for row in m :     print(row) rez = [[m[j][i] for j in range(len(m))] for i in range(len(m[0]))] print("\n") for row in rez:     print(row)

   Выход:

   [1, 2]
   [3, 4]
   [5, 6]
   
   
   [1, 3, 5]
   [2, 4, 6]
   

2. Использование zip: Zip возвращает итератор кортежей, где i-й кортеж содержит i-й элемент из каждой последовательности аргументов или итераций. В этом примере мы распаковываем наш массив, используя *, а затем упаковываем его, чтобы получить транспонирование.

   matrix=[(1,2,3),(4,5,6),(7,8,9),(10,11,12)] for row in matrix:     print(row) print ("\n") t_matrix = zip(*matrix) for row in t_matrix:     print(row)

   Выход:

   (1, 2, 3)
   (4, 5, 6)
   (7, 8, 9)
   (10, 11, 12)
   
   (1, 4, 7, 10)
   (2, 5, 8, 11)
   (3, 6, 9, 12)
   

   Примечание: — Если вы хотите, чтобы ваш результат был в форме [[1,4,7,10] [2,5,8,11] [3,6,9,12]], вы можете использовать t_matrix = map (list, застежка-молния (* матрица)).

3. Использование numpy: NumPy — это универсальный пакет обработки массивов, предназначенный для эффективной работы с большими многомерными массивами. Метод транспонирования возвращает транспонированное представление пройденной многомерной матрицы.

   import numpy  matrix=[[1,2,3],[4,5,6]] print(matrix) print("\n") print(numpy.transpose(matrix))

Эта статья пополняемая Mayank Равата Если вы любите GeeksforGeeks и хотела бы внести свой вклад, вы также можете написать статью с помощью contribute. geeksforgeeks.org или по почте статьи [email protected]. Смотрите свою статью, появляющуюся на главной странице GeeksforGeeks, и помогите другим вундеркиндам.

Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.

Рекомендуемые посты:

Транспонировать матрицу в одну строку в Python

0.00 (0%) 0 votes

линейная-алгебра / Умножение транспонированной матрицы / Математика

Матрицу B можно рассматривать как матрицу Грамма для базиса из столбцов матрицы A, поэтому линейное преобразование, определяемое матрицей, обратной к матрице A должно превращать матрицу B в единичную.

Рецепт такой

1) Преобразовать матрицу B в единичную, решив задачу на собственные значения и собственные векторы.

2) Обратить матрицу преобразования матрицы B в единичную. Это и будет искомая матрица A.

Пример. T \cdot A = \begin{pmatrix} 1/ \sqrt 5 & 2\sqrt {6/5} \\ -2/ \sqrt 5 & \sqrt {6/5} \end{pmatrix} \cdot \begin{pmatrix} 1/ \sqrt 5 & -2/ \sqrt 5 \\ 2\sqrt {6/5} & \sqrt {6/5} \end{pmatrix}= \begin{pmatrix} 1/5+24/5 & -2/5+12/5 \\ -2/5+12/5 & 4/5+6/5 \end{pmatrix}=B $$

Матрицы сложения и вычитания

Добавление и матриц вычитания Матрица сложена справедливо простой, и делается по входу. Добавьте следующие матрицы: Мне нужно добавить пары записей, а затем упростите для окончательного ответа: Итак, ответ: До сих пор вы были можете добавить любые две вещи, которые вам нравятся: числа, переменные, уравнения, и так далее. Но сложение не всегда работает с матрицами. Выполните указанные операции, или объясните, почему это невозможно. Так как матрицы складываются по умолчанию, я должен добавить 1 и 4, 2 и 5, 0 и 7, и 3 и 8. Но что мне добавить к 6 а к 9? В первой матрице нет соответствующих записей, которые можно добавить к этим элементам второй матрицы.Итак, ответ: Я не могу добавить эти матрицы, потому что они не одного размера . Это всегда так: Чтобы можно было добавить две матрицы, они должны быть одинакового размера. Если они разного размера (если у них разные «размеры»), тогда сложение «не определено» (не делает математических смысл). Вычитательные работы начальные, тоже.авторское право Элизабет Стапель 2003-2011 Все права защищены Учитывая следующее матрицы, найти A B и А С , или объяснить почему нельзя. А и B одинакового размера, по 2 3 матрицы, так что я могу вычесть, рабочий начальный: Однако A и C не одинакового размера, так как A 2 3 и C равно 2 2.Итак, это вычитание не определено. А К не определено, потому что A и C не одинакового размера. Сложение и вычитание матриц, где определено (то есть, где матрицы одинакового размера, поэтому сложение и вычитание имеет смысл), можно превратить в домашние задания. Найдите значения x и y дано следующее уравнение: Во-первых, упрощу левую часть немного, добавив по записи: Поскольку матричное равенство работает по умолчанию, Я могу сравнивать записи и составлять простые уравнения, которые я могу решить. В этом случае 1,2-записи скажите мне, что x + 6 = 7, а 2,1-элементы скажи мне, что 2 л 3 = 5. Решая, я получаю: х + 6 = 7 х = 1 2 y 3 = 5 2 y = 2 л = 1 Верх | Вернуться к индексу Цитируйте эту статью как: Стапель, Елизавета.«Сложение и вычитание матриц». Purplemath . Доступно по номеру https://www.purplemath.com/modules/mtrxadd.htm . Доступ [дата] [месяц] 2016

Матрицы на ACT — Как решить задачи матрицы экзамена ACT по математике

Матрицы по матричным задачам ACT -5

Инструкции: Вы увидите как минимум один вопрос по матрицам на ACT. Решите задачи матрицы ACT, указанные ниже. Ответы представлены в следующем разделе. Вы можете просмотреть примеры и пояснения в последнем разделе этой страницы, прежде чем попробовать это упражнение.

1) Что такое матрица A + матрица B?

2) Что такое Матрица P — Матрица Q?

3) Решите следующее:

=?

4) Каков определитель следующей матрицы?

5) Каков определитель следующей матрицы?

Матрицы на СПО — ответы на матричные задачи

Ответ 1

1) Добавьте числа из матрицы A к числам в той же позиции в матрице B, как показано ниже.

=

=

Ответ 2

Вычтите числа из матрицы Q из чисел в той же позиции в матрице P, как показано ниже.

=

=

Ответ 3

Умножьте каждое число на 3 и решите:

= =

Ответ 4

Чтобы найти определитель, нужно умножить крестиком, чтобы получить два произведения. Затем вычтите эти два продукта, чтобы получить определитель.

(2 × 24) — (4 × 16) = 48 — 64 = -16

Ответ 5

Будьте осторожны с отрицательными числами при умножении и сложении.

(-5 × 9) — (-6 × 4) = -45 — -24 = -21

Что такое матрицы?

Матрицы, которые вы увидите на экзамене по математике ACT, обычно имеют формат два на два, как показано ниже.

Это означает, что эти типы матриц представлены в виде прямоугольника, состоящего из 4 чисел.

Два числа будут в верхней части матрицы, а два числа будут непосредственно под ними в нижней части матрицы.

Выполнение операций с матрицами — примеры

Пример 1 — Добавление матриц в ACT

1) Два сложить две матрицы вместе, вам нужно добавить числа из первой матрицы к числам в той же позиции во второй матрице

=

=

Пример 2 — Вычитание матриц в ACT

Вычтите числа во второй матрице из чисел в той же позиции в матрице forst, как показано ниже.

=

=

Пример 3 — Умножение матрицы на целое число

Для этих типов задач матрицы ACT необходимо каждое число в матрице умножить на целое число:

=

Что такое матрица в математике? (Введение, типы и операции с матрицами)

Матрица — важная тема в математике. В этом посте мы обсудим эти моменты.

В 1858 году британский математик Артур Кэли впервые разработал «Теорию матриц». Артур Кэли был также организатором Современной британской школы чистой математики.

В детстве он любил решать сложные математические задачи для удовольствия и блестяще изучал французский, немецкий, итальянский, греческий языки и математику в Тринити-колледже Кембриджа.

Что такое матрица?

Обычно он представляет собой набор информации, хранящейся в упорядоченном виде. Математически он представляет собой набор чисел, переменных или функций, упорядоченных по строкам и столбцам. Матрицы представлены заглавными буквами английского алфавита, например A, B, C …… и т. Д.

Например,

В приведенном выше примере матрица A имеет 3 строки и 3 столбца.

Применение матриц

Матрицы используются в различных отраслях наука, некоторые из ее приложений:

1. Кому решать систему линейных уравнений
2. Компьютер Графика
3. Физика
4. Криптография
5. График Теория

Порядок матрицы

Определяется количеством строк и столбцов в матрице.

Порядок матрицы = количество строк × количество столбцов

В В приведенном выше примере количество строк равно 3, а количество столбцов также равно 3, следовательно,

Порядок матрицы A — 3 × 3.

Типы матриц

1. Матрица строк

Если матрица имеет только одну строку, тогда она называется матрицей-строкой. Например,

Это матрица-строка порядка 1 на 3.

2. Матрица столбцов

Если матрица имеет только один столбец, она называется матрицей столбцов.Например,

Это матрица столбцов порядка 3 на 1.

3. Нулевая или нулевая матрица

Если все элементы матрицы равны нулю, то она называется Null или нулевая матрица. Например,

Это нулевая матрица порядка 2 на 2. Нулевая или нулевая матрица обозначается «O».

4. Квадратная матрица

В матрице, если количество строк равно количеству столбцов, то она называется квадратной матрицей.Например, если матрица имеет 2 строки и 2 столбца, то она называется квадратной матрицей, как указано ниже

.

5. Прямоугольная матрица

В матрице, если количество строк не равно количеству столбцов, то она называется прямоугольной матрицей. Например, если матрица имеет 2 строки и 3 столбца, то она называется прямоугольной матрицей, как указано ниже.

6. Диагональная матрица

Если все элементы квадратной матрицы равны нулю, за исключением элементов на главной диагонали, то она называется диагональной матрицей.Однако некоторые элементы главной диагонали могут быть нулевыми, но не все элементы. Например,

7. Скалярная матрица

Если все диагональные элементы диагональной матрицы одинаковы, то она называется скалярной матрицей. Например,

8. Матрица единиц измерения или идентичности

Если каждый диагональный элемент диагональной матрицы равен 1, то он называется единичной матрицей или матрицей идентичности. Например,

9.Негатив матрицы

Отрицательная матрица получается заменой знаков во всех ее элементах. Рассмотрим матрицу A и заменим ее на отрицательную матрицу –A as,

, если

, затем

10. Транспонирование матрицы

Транспонирование матрицы достигается перестановкой всех ее строк на столбцы или столбцов на строки. Обозначается он

или. Например,

Если

, затем

11.Симметричная матрица

Квадратная матрица называется симметричной, если она равна своему транспонированию. Например,

Если

, затем

Следовательно, A симметрична.

Если

, то

Следовательно, B не симметричен.

12. Кососимметричная матрица

Квадратная матрица называется кососимметричной, если ее транспонирование равно отрицательному значению этой матрицы, то есть

. Например,

Если

, затем

Следовательно, матрица A кососимметрична.

Операции с матрицами

Добавление матриц:

Добавление к двум матрицам A и B приведет к возможно, если у них одинаковые заказы. Сложение двух матриц A и B есть обозначается A + B. Например,

Если

и

Затем,

Вычитание матриц:

Вычитание одной матрицы из другой матрица будет возможна, если у них будут одинаковые заказы. Вычитание двух матрицы A и B обозначим A — B.Например,

Если

и

Затем,

Продукт матриц:

Произведение двух матриц A и B будет быть возможным, если количество столбцов матрицы A равно количеству строк другой Матрицы Б. Например,

Если

и

Затем,

Транспонирование и соединение матриц — MathsTips.com

Транспонирование матрицы

Матрица, полученная из данной матрицы A путем перестановки ее строк и столбцов, называется транспонированием матрицы A.Транспонирование A обозначается A ’или. Если A имеет порядок m * n, то A ’имеет порядок n * m. Ясно, что транспонирование транспонированной матрицы A — это сама матрица A, т.е. (A ’)’ = A.

Рассмотрим матрицу Если A = || порядка m * n, тогда = || порядка n * m. Так, .

Пример 1: Рассмотрим матрицу. Сделайте транспонирование матрицы.

Решение: Это заказ 2 * 3. Записав другую матрицу B из A, записав строки A как столбцы B. Мы имеем:. Матрица B называется транспонированной матрицей A.

Пример 2: Рассмотрим матрицу. Сделайте транспонирование матрицы.

Решение: Транспонирование матрицы A путем перестановки строк и столбцов равно.

Свойства транспонирования

1. Транспонирование транспонированной матрицы состоит в том, что сама матрица = = A
2. Транспонирование сложения 2-х матриц аналогично сумме их транспонирования =
3. Когда скалярная матрица умножается на матрицу, порядок транспонирования не имеет значения =
4. Транспонирование произведения матриц 2 аналогично произведению их перемещений в обратном порядке =

Присоединение к матрице

Для квадратной матрицы A транспонированная матрица кофактора A называется присоединенной к A и обозначается adj A.Сопряженная матрица также называется сопряженной матрицей.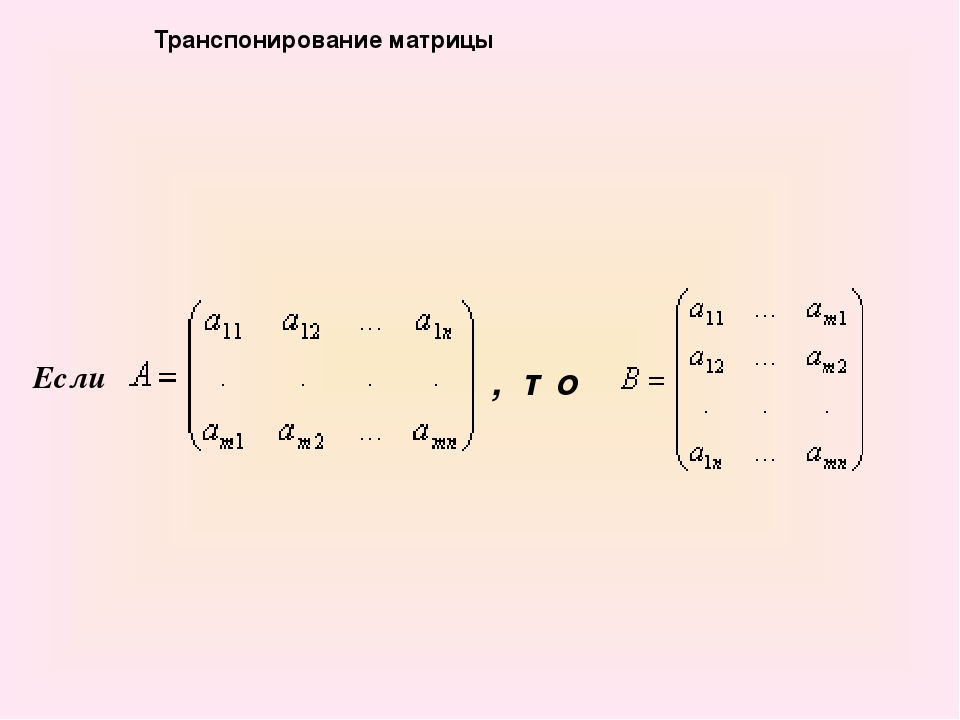 Другими словами, мы можем сказать, что матрица A — это другая матрица, сформированная заменой каждого элемента текущей матрицы его соответствующим кофактором и последующим транспонированием новой сформированной матрицы.

Предположим, тогда Adj A =

Пример 1: Рассмотрим матрицу Найдите Adj of A.

Решение: Сначала нужно выяснить минор и сомножитель матрицы: = 2 = 2, = 2 = -2, = -1 = +1, = 5 = 5.

Матрица сомножителей = и Adj A =

Пример 2: Рассмотрим матрицу Найдите Adj of A.

Решение: = 7 = 7, = 18 = -18, = 30 = 30, = 1 = -1, = 6 = 6, = 10 = -10, = 1 = 1, = 8 = -8, = 26 = 26,

Матрица сомножителей = и Adj A =.

Упражнение

1. Найдите сопряженный к матрице.
2. Найдите сопряженный к матрице.
3. Найдите сопряженный к матрице.
4. Найдите сопряженный к матрице.
5. Найдите сопряженный к матрице.

Стоимость поездки | WMATA

Тарифы Metrorail рассчитываются на основе (1) времени суток и дня недели, когда совершается поездка (классифицируются как пиковые или внепиковые) и (2) расстояния, пройденного между станциями отправления и назначения. Дополнительная информация о стоимости поездки и пропусках находится внизу этой страницы. Чтобы рассчитать стоимость проезда, используйте Планировщик поездок.

Оплата за поездку

Metrorail	Стоимость поездки
Пик тариф *	$ 2.25–6,00 долл. США
Тариф вне пиковой нагрузки *	2,00–3,85 долл. США
Метробус	Стоимость поездки
Регулярные маршруты	$ 2,00
Экспресс-маршруты	4,25
Airport Express Routes	$ 7.50
Льготный тариф — Обычный	1,00 $
Льготный тариф — Экспресс	$ 2,10
Сниженный тариф — Airport Express	$ 3,75

Пропуска

Metrorail и Metrobus	Стоимость поездки
Билет на 1 день	13 долларов США. 00
3-дневный абонемент	28,00 $
Билет на 7 дней	58,00
Короткая поездка на 7 дней	38,00
Ежемесячный абонемент	72–216 долл. США
Проездной на региональный автобус
Билет на 7 дней	15 долларов США.00

* Пиковые тарифы применяются во время AM Rush и PM Rush часов указано на текущем Расписание поездов. В остальное время действуют тарифы вне часов пик.

Как купить

SmarTrip® и тарифы можно приобрести по следующему адресу:

Оплата за поездку

Metrorail

Метробус

• Осуществлять безналичный расчет с использованием SmarTrip Mobile или пластиковые карты SmarTrip
• Наличные платежи принимаются на большинстве маршрутов, но должны производиться с точной сдачей — операторы автобусов не носят наличные (Примечание: на маршруте 79 MetroExtra не принимаются наличные платежи).
• Льготные тарифы доступны для соответствующих требованиям пожилых людей и людей с ограниченными возможностями

Переводы

• Metrobus — Metrobus: Бесплатные неограниченные трансферы в течение 2 часов
• Metrobus до Metrorail / Metrorail до Metrobus: 0 долларов.Скидка 50 за 2 часа
• Перекресток Фаррагут: Бесплатный проезд между красной линией и оранжевой, серебряной и синей линиями при выезде и въезде через Фаррагут-Уэст и Фаррагут-Север.

Использование продукта Pass не дает права на перевод средств.

Дети

• До двух детей (в возрасте 4 лет и младше) могут ездить бесплатно на каждого взрослого, оплачивающего проезд
• Дети от 5 лет по стандартному тарифу
Маршрут
• Metrorail и Metrobus бесплатный для учащихся округа Колумбия, которые посещают государственные, частные, чартерные или приходские школы через DC Kids Ride Бесплатная программа

Региональные транзитные партнеры

Пасс

• Платите меньше за поездку с неограниченным пропуском
• Доступны проездные на Metrorail и Metrobus
.