16.Теорема о проецировании прямого угла.
Ответ:
Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.
Док-во:
Дан прямой угол АВС, у которого по условию прямая ВС АВ и ВС || плоскости проекций П1. По построению прямая ВС к проецирующему лучу ВВ1. Следовательно, прямая ВС к плоскости b (АВхВВ1), т. к. она к двум пересекающимся прямым , лежащим в этой плоскости. По условию прямая В1С1 || ВС, поэтому тоже к плоскости b, т. е. и прямой А1В1 этой плоскости. Следовательно, угол между прямыми А1В1 и В1С1 равен 90°, что и требовалось доказать.
17.Какая задача считается основной позиционной задачей.
Под позиционными задачами будем понимать задачи по определению общих элементов геометрических фигур. К ним относятся задачи на принадлежность и задачи на пересечение геометрических фигур.
Задачами на
принадлежность являются задачи на
построение проекций: точек на линии или
поверхности, линий на поверхности, линий
и поверхностей, проходящих через заданные
точки и линии.
ПЕРВАЯ ПОЗИЦИОННАЯ ЗАДАЧА
(ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ЛИНИИ И ПОВЕРХНОСТИ)
18.Как располагаются проекции плоскостей в разных случаях.
Плоскость частного положения — плоскость проходящая через проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью. Существует три вида проецирующих плоскостей:
Горизонтально-проецирующая плоскость — перпендикулярна к П1. И поэтому проецируется на нее как прямая.
Фронтально-проецирующая плоскость — перпендикулярна к П2. И поэтому проецируется на нее как прямая.
Профильно-проецирующая плоскость — перпендикулярна к П3. И поэтому проецируется на нее как прямая. На обычном ортогональном чертеже, когда плоскость П3 не используется, профильно-проецирующая плоскость выглядит как плоскость общего положения.
Если плоскость перпендикулярна к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций. Существует три вида плоскостей уровня:
Горизонтальная плоскость уровня — || П1.
Фронтальная плоскость уровня — || П2.
Профильная плоскость уровня — || П3.
.Что такое особые прямые плоскости.
Прямые уровня — это прямые, принадлежащие плоскости и параллельные какай — либо плоскости проекций. Эти прямые называют прямыми уровня, так как они принадлежат плоскости уровня. Существует три вида прямых уровня:
h — горизонталь плоскости — прямая принадлежащая данной плоскости и || П1;
f — фронталь плоскости — прямая принадлежащая данной плоскости и || П2;
w — профильная прямая плоскости — прямая принадлежащая данной плоскости и || П3.
20. Как на основе теории о проекции прямого угла можно строить эпюры двух перпендикулярных между собой прямых, либо прямой и плоскости или двух плоскостей.
Точки. Линии. Теорема о частном случае проецирования прямого угла (Рабочая тетрадь по начертательной геометрии), страница 2
Математика \ Начертательная геометрия
Приведем простой пример. Пусть у нас есть прямая a, и точка А, лежащая на этой прямой(см. рис.) Построим АВ так, чтобы и.в. АВ была равна, скажем, 15. Для этого берем произвольную точку 1 и находим ту самую гипотенузу (т. е. делаем вид, что мы ищем и. в. А-1, но доделываем только до того момента, когда мы построили эту гипотенузу). Гипотенуза и есть линия истинных величин отрезка. Отмеряем на этой прямой заданное расстояние (равное 15), и строим, строим, строим… Желаю удачи. (мне в лом писать дальше, это и так видно из рисунка.)
Нетрудно
догадаться, что если нам даны две из трех величин (например, ∆Z и и.
Теорема о частном случае проецирования прямого угла.
Собственно, теорема звучит так:
Если одна из сторон угла параллельна плоскости проекций, а другая не перпендикулярна этой плоскости, то угол проецируется на эту плоскость в истинную величину. (см. Гордон, стр. 38, рис. 89)
Никогда не следует забывать про вторую часть теоремы про «другая не перпендикулярна этой плоскости».
В общем можно сказать, что если у нас прямая частного положения(горизонталь или фронталь), то теорема будет справедлива, правда, с учетом некоторых оговорок.(подумайте, каких).
Итак, приступим. С задачей 2,1 вам все должно быть ясно (не зря же я старался, примеры приводил!). Едем дальше.
2,2 Вертолет, летит… Тьфу! Нехорошая (хотя, для кого как) задача, и в условие сразу не въедешь… Был засечен. Локатором. В точке. Угол места, расстояние до локатора… Найти положение.
Короче.
И. в.
СА дано, угол дан. Находим |С’A’|. Ползадачи есть.
На прямой l’ отмечаем А’ так, чтобы С’A’ было равно тому катету(указан стрелкой). (на рисунках размеры не сверять, указан только принцип) Внимание опечатка: на рисунке перепутано С’ и C’’, читать наоборот!
Едем дальше.
Продолжаем линию связи от А’. Под углом 30 градусов проводим линию из точки C’’. Получаем А’’ . Задача решена.
3. Плоскость
Рис 2 |
Рис. 3 |
Необходимая теория.
Плоскость можно задать
по-разному, в том числе и следами. Следы плоскости – линии пересечения
плоскости с плоскостями проекций. На рис. 2 плоскость α задана следами: горизонтальным h0α и фронтальным f0α.
Рис. 5 |
Рис 4 |
Пусть некоторая точка лежит в плоскости, заданной следами. Запомните правило: фронтальная проекция точки на фронтальном следе – горизонтальная проекция на оси(и наоборот: если штрих на оси, то два штриха на следе), горизонтальная проекция на горизонтальном следе – вторая проекция на оси(и наоборот).(рис. 3)
Точка лежит в плоскости, если она
лежит в какой-нибудь прямой этой плоскости. Это условие нам понадобится, чтобы
построить вторую проекцию точки. Если плоскость задана следами, то
горизонтальная проекция любой горизонтали, лежащей в этой плоскости, будет
параллельна горизонтальному следу, а фронтальная фронтали – фронтальному
(простите за каламбур)(рис.
4). Таким образом, если дана одна проекция точки,
принадлежащей плоскости, заданной следами, мы всегда можем провести горизонталь
или фронталь и построить вторую (рис. 5). На рисунке 5 была дана A’’. Мы провели проекцию горизонтали h’’
через эту точку. По правилу « “ 1’’ ” на следе -> “ 1‘ “ на оси» построили точку 1. Через
эту точку провели h’ || h0α. Продолжили
линию связи, построили А’’. С точкой B
– аналогично.
При выполнении задачи 3.1 помните, что если плоскость задана прямой и точкой, или двумя параллельными прямыми, или следами, мы всегда можем перезадать ее двумя пересекающимися прямыми, просто проведя оные. Это очень удобно для построения недостающих проекций точек. Алгоритм такой: строим прямую через точку, с помощью точек пересечения этой прямой с двумя прямыми, которыми задана плоскость, строим вторую проекцию этой прямой. Вторые проекции точек будут лежать на только что построенной проекцией прямой.
Скачать файл
Видео с вопросом: Нахождение длины проекции стороны прямоугольного треугольника на прямую, несущую другую сторону, с помощью теоремы Пифагора
Учитывая, что 𝐴𝐵 = 29, 𝐶𝐵 = 20 и 𝐶𝐷 = 35, вычислите длину проекции отрезка 𝐶𝐷 на прямую 𝐴𝐷.
Стенограмма видео
Учитывая, что 𝐴𝐵 равно 29, 𝐶𝐵 равно 20, а 𝐶𝐷 равно 35, вычислить длину проекции линии отрезок 𝐶𝐷 на линии 𝐴𝐷.
Прежде чем мы сможем вычислить длину этой проекции, нам нужно увидеть, к какому сегменту линии относится эта проекция. Линия 𝐴𝐷 — наша целевая линия. Это линия, на которой проекция упадет. А 𝐶𝐷 — это отрезок, который мы будем использовать для создания нашей проекции. Но для того, чтобы создать проекции, нам понадобятся перпендикулярные линии к нашей целевой линии. Потому что мы знаем эту строчку 𝐵𝐶 и прямые 𝐴𝐷 параллельны, угол 𝐵𝐶𝐴 является внутренним углом, противолежащим углу 𝐶𝐴𝐷, что означает, что отрезок 𝐴𝐶 перпендикулярен отрезку 𝐴𝐷.
Как только мы представим источник света как
множество всех перпендикулярных линий к нашей целевой линии, мы можем найти конечные точки
нашей проекции.
Во-первых, мы знаем, что 𝐴𝐵 имеет
мера 29 и 𝐶𝐵 имеет меру 20 и 𝐶𝐷 имеет меру 35. На нашем рисунке есть два
отдельные прямоугольные треугольники, составляющие этот четырехугольник. И поэтому мы помним, что можем найти
длины сторон в прямоугольных треугольниках по теореме Пифагора, где 𝑎 и 𝑏
представляют две меньшие стороны, а 𝑐 представляет гипотенузу. 𝑎 в квадрате плюс 𝑏 в квадрате равно
𝑐 в квадрате. Чтобы использовать теорему Пифагора, вы
нужно как минимум две длины. Так как мы не знаем длину
𝐴𝐶, мы не можем найти длину 𝐴𝐷.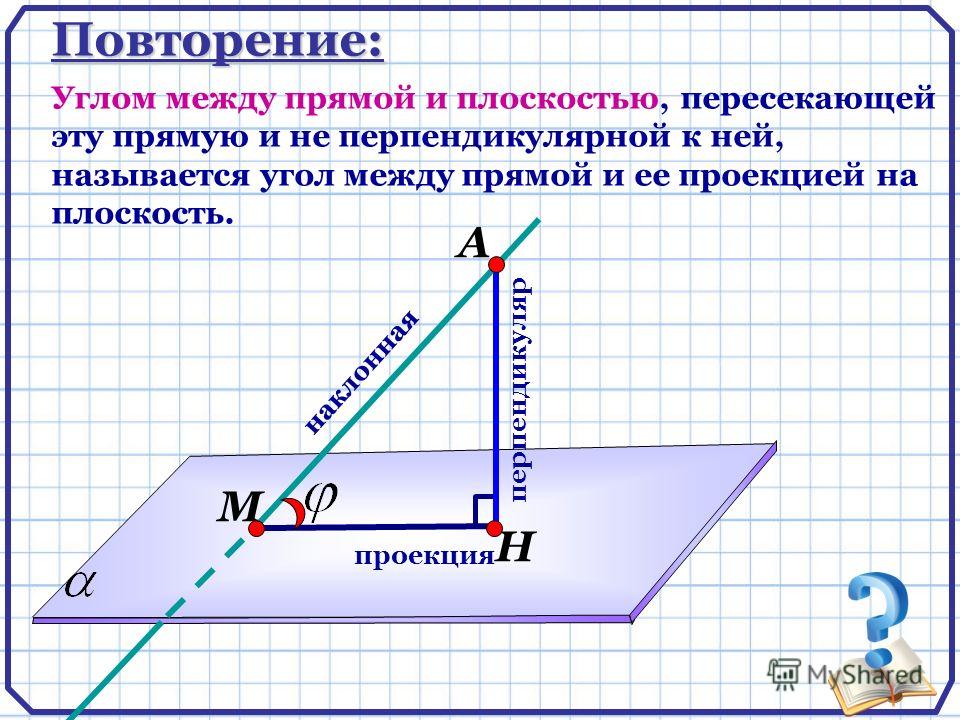
Когда мы подключаем то, что знаем, мы получить 20 в квадрате плюс 𝐴𝐶 в квадрате равно 29 в квадрате. 400 плюс 𝐴𝐶 в квадрате равно 841. Итак, мы вычтем 400 из обоих стороны уравнения, и мы получим 𝐴𝐶 в квадрате равно 441. После этого возьмем квадрат корень с обеих сторон. Нас интересует только положительный квадратный корень, так как мы имеем дело с расстоянием, и поэтому мы видим, что 𝐴𝐶 равно 21. Теперь, когда мы знаем, что 𝐴𝐶 равно 21, мы знаем два расстояния в нашем прямоугольном треугольнике и мы сможем найти сторону длина нашего третьего расстояния 𝐴𝐷. Но нам нужно настроить Теорема Пифагора во второй раз.
На этот раз у нас будет 21 в квадрате
плюс 𝐴𝐷 в квадрате равно 35 в квадрате. 441 плюс 80 в квадрате равно
1225.
Итак, из обоих вычитаем 441.
стороны, и мы получим 𝐴𝐷 в квадрате равно 784. Итак, мы берем квадратный корень из обоих
стороны. Опять же, нас интересует только
положительный квадратный корень из 784, что равно 28. Отрезок 𝐴𝐷 будет равен
до 28. Отрезок 𝐴𝐷 — это
проекция отрезка 𝐶𝐷 на прямую 𝐴𝐷 и имеет меру 28,
Первый угол против третьего угла — ортогональные виды
Ортогональные виды позволяют нам представлять 3D-объект в 2D на чертеже. Ортографические виды могут показать нам объект, рассматриваемый с каждого направления. Расположение видов на чертеже зависит от того, используется ли угловая проекция 3 rd или 1 st . Вы можете сказать, какая угловая проекция используется символом, показанным на чертеже.
Проекция под третьим углом
Проекцию под третьим углом можно визуализировать, «развернув коробку», как если бы сам объект разворачивался, чтобы показать виды с каждой стороны.
На рис. 1 показаны виды куба, представленные проекцией под третьим углом.
Виды в проекции под третьим углом интуитивно понятны, так как они позволяют вам смотреть на объект с соответствующей стороны. Вид спереди всегда отображается в центре. Вид объекта справа показан справа от вида спереди, вид объекта слева показан слева от вида спереди, а виды сверху и снизу показаны выше и ниже вида спереди , соответственно. Если бы нам нужно было показать вид сзади, вид сзади был бы размещен под видом снизу.
Краткая заметка о представлении символа для третьего угла. На самом деле существует четыре способа представления проекции под третьим углом на отпечатке, и все они приемлемы (рис. 2). Главный вывод здесь заключается в том, что не имеет значения, находится ли «боковой» вид «конуса» справа или слева . Для проекции под третьим углом «заостренный» конец бокового вида конуса в символе всегда указывает вперед/на «круг», как показано на Рисунке 2 ниже.
Все четыре варианта вполне приемлемы для третьего угла:
Проекция под первым углом
Представления под первым углом менее интуитивно понятны. Их можно визуализировать, «опрокинув коробку». На рис. 2 показаны виды куба, представленные проекцией первого угла.
Рис. 3. Виды в проекции под первым углом Вид спереди показан в центре, как и в проекции под третьим углом. Чтобы разместить вид на правую сторону, вы должны наклонить коробку так, чтобы правая сторона была обращена к вам. Для этого коробку нужно наклонить влево. Это приводит к тому, что вид справа на объект располагается слева от вида спереди. Повернув коробку лицевой стороной к себе еще раз, наклоните коробку вправо, и левая сторона будет обращена к вам. Таким образом, вид слева будет расположен справа от вида спереди. Этот же метод используется для просмотра сверху и снизу. Повернув перед собой объект, наклоните куб вниз.
Теперь у вас есть верхняя сторона, обращенная к вам, при этом вид сверху расположен под видом спереди на чертеже. Если наклонить вид спереди вверх, вид снизу объекта будет обращен к вам, а вид снизу расположен над видом спереди.
Снова часто возникает путаница в представлении символов для проекта First Angle. Существует четыре способа представления проекции первого угла на отпечатке (рис. 4), и все они приемлемы. Главный вывод здесь заключается в том, что не имеет значения, находится ли «боковой» вид «конуса» справа или слева . Для первого угла «заостренный» конец бокового вида конуса в символе всегда направлен в сторону от передней части/«круга», как показано на рисунке 4 ниже. Все четыре из них вполне приемлемы для Первого Угла.
Рисунок 4: Допустимые представления символа проекции первого углаТретий угол и ортогональные виды первого угла
Как видно из рисунков 1 и 2, ортогональные виды первого и третьего угла противоположны в том, что касается размещения проекций каждой стороны вид расположен на чертеже.
Если человек не знает, какая угловая проекция используется на чертеже, это может привести к путанице. Важно не забывать искать символ проекции и понимать, относится ли символ к третьему или первому виду проекции.
Чтобы помочь вам вспомнить, какой символ относится к какому представлению, давайте посмотрим на символ для каждого из них. Символ третьего угла показан в верхнем левом углу Рисунка 1. Символ первого угла показан в левом верхнем углу Рисунка 2.
Каждый символ представляет виды конуса с этого углового вида. Символы третьего и первого угла показывают круговой вид конуса сверху и вид конуса справа. Разница в символах заключается в том, где находится правый вид конуса.
Символ третьего угла показан на рис. 1. Он представлен круговым видом конуса сверху с правым видом конуса справа от него. На виде справа узкий конец конуса направлен в сторону вида сверху.
Символ первого угла, показанный на Рисунке 2, представляет собой круговой вид конуса сверху с правым видом конуса слева от него.