Сводная таблица переводов целых чисел из одной системы счисления в другую
Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:
На этом рисунке использованы следующие обозначения:
в кружках записаны основания систем счисления;
стрелки указывают направление перевода;
номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице
Например: означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.
Сводная таблица переводов целых чисел
Арифметические операции в позиционных системах счисления
Сложение
Сложение в 16-ричной системе
Сложение в 8-ричной системе
При
сложении цифры суммируются по разрядам,
и если при этом возникает избыток, то
он переносится влево.
Пример. Сложим числа 15 и 6 в различных системах счисления.
Шестнадцатеричная: F16+616 | Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2.81 + 5.80 = 16 + 5 = 21, 1516 = 1.161 + 5.160 = 16+5 = 21. |
Вычитание
Пример. Вычтем единицу из чисел 102, 108 и 1016
Умножение
Выполняя
умножение многозначных чисел в различных
позиционных системах счисления, можно
использовать обычный алгоритм перемножения
чисел в столбик, но при этом результаты
перемножения и сложения однозначных
чисел необходимо заимствовать из
соответствующих рассматриваемой системе
таблиц умножения и сложения.
Умножение в двоичной системе | Умножение в восьмеричной системе |
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример. Перемножим числа 5 и 6.
Ответ: 5.6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду: 111102 = 24 + 23 + 22 + 21 = 30;
368 = 381 + 680 = 30.
Деление
Деление
в любой позиционной системе счисления
производится по тем же правилам, как и
деление углом в десятичной системе. В
двоичной системе деление выполняется
особенно просто, ведь очередная цифра
частного может быть только нулем или
единицей.
Пример
9. Разделим число 30 на число 6.
В
двоичной системе деление выполняется
особенно просто, ведь очередная цифра
частного может быть только нулем или
единицей.
Пример
9. Разделим число 30 на число 6.
Ответ: 30 : 6 = 510 = 1012 = 58.
Контрольные вопросы
Что такое система счисления?
Каким требованиям должна удовлетворять система счисления?
Какие бывают системы счисления?
Чем отличаются позиционные системы счисления от непозиционных? Приведите примеры.
Как можно записать любое десятичное число в общем виде?
Что такое вес разряда?
Чему равно основание системы счисления?
Какие системы счисления используются в вычислительной технике?
Каковы достоинства и недостатки 2-ной, 8-ной, 16-ной систем счисления?
Почему в вычислительной технике применяются системы счисления с основаниями 2, 8, 16?
Правило перевода целого числа из 10-ой системы в любую другую систему счисления
Арифметические операции в позиционных системах счисления
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Системы представления чисел — десятичная, двоичная, восьмеричная и шестнадцатеричная — x-engineer.org
В этой статье мы обсудим различные системы представления чисел, где они используются и почему они полезны. Вкратце мы рассмотрим десятичное , двоичное , восьмеричное и шестнадцатеричное числовое представление.
Десятичный (с основанием 10)
Наиболее распространенной системой представления чисел является десятичный . Все используют его. Это настолько распространено, что большинство людей должно полагать, что это единственное. Он используется в финансах, технике и биологии почти везде, где мы видим и используем числа.
Если кто-то попросит вас думать о числе, вы наверняка будете думать о десятичном числе. Если вы думаете в двоичном или шестнадцатеричном формате, вы должны быть очень увлечены арифметикой или программным обеспечением/программированием.
Если вы думаете в двоичном или шестнадцатеричном формате, вы должны быть очень увлечены арифметикой или программным обеспечением/программированием.
Как следует из названия, в десятичной системе счисления используется 10 символов/символов. В латинском языке 10 — это «decem», поэтому десятичная дробь может быть связана с латинским словом.
| Десятичные символы | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9002 9
Как видите, есть 10 символов от 0 до 9 . С помощью этих символов мы можем построить все числа в десятичной системе.
Все числа в десятичной системе можно построить, используя вышеупомянутые символы ( 0 … 9 ), умноженные на степень 10. Степень десятки дает нам единицы, десятки, сотни, тысячи и так далее.
| 10 к | … | 10 5 | 10 4 | 10 3 | 10 2 | 10 1 | 10 0 |
| N | … | 100000 | 10000 | 1000 | 100 | 10 | 9003 1 1
В приведенном ниже примере десятичное число 9 разбивается на части. 0055 67049 в степени 10, умноженные на числа от
0055 67049 в степени 10, умноженные на числа от 0 до 9 . Это просто для того, чтобы показать, что любое число в десятичной системе можно разложить на сумму слагаемых, состоящую из произведения степени 10 и символов 0 … 9 .
| 67049 | |||||||
| 10 7 | 10 6 | 10 5 | 10 4 | 10 3 | 10 2 | 10 1 | 10 0 |
| 0 | 0 9 0028 | 0 | 6 | 7 | 0 | 4 | 9 |
| 67049 = 6 ⋅ 10 4 + 7 ⋅ 10 3 + 0 ⋅ 10 2 + 4 ⋅ 10 1 + 9 ⋅ 10 0 = 6 0000 + 7000 + 0 + 40 + 9 | |||||||
То же Метод будет применяться к двоичной, восьмеричной и шестнадцатеричной системам счисления, являясь по сути методом преобразования числа из десятичной системы в другой формат (базу).
Мы можем помнить следующие характеристики десятичной системы счисления:
- использует 10 символов
- может быть разложена на множители, содержащие степени 10
- это наиболее распространенная система представления чисел
)
А теперь давайте перейдем к компьютерным играм.
Другой системой представления чисел является двоичная . Как следует из названия и по аналогии с десятичной системой, мы можем сказать, что двоичная система использует только 2 символа/символа:
| Двоичные символы | |
| 0 | 1 |
В двоичном представлении мы используем только 0 (нули) и 1 (единицы) для представления чисел.
Двоичная система используется везде, где требуется хранить информацию в электронном формате. Все известные вам компьютеры, интеллектуальные устройства, все, что связано с электроникой и микроконтроллерами, используют двоичную систему.
В электронике (цифровой) все операции выполняются с использованием двух уровней напряжения: высокого и низкого. Каждому уровню напряжения присваивается значение/символ: HIGH для 1 и LOW для 0. Для микроконтроллера, на который подается напряжение +5 В, 1 (высокий) будет представлен +5 В, а 0 (низкий) 0 В.
Грубо говоря, мы можем сказать, что используется двоичная система, потому что ее можно перевести в электронный сигнал.
Все десятичные числа, которые мы можем представить, могут быть представлены в виде двоичных символов. Мы делаем это, используя сумму между членами степени 2, умноженной на 0 или 1.
| 2 k | … | 2 7 | 9003 1 2 62 5 | 2 4 | 2 3 | 2 2 | 900 31 2 12 0 | ||
| N | … | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
В качестве примера мы будем использовать число 149 (десятичное представление) и преобразовать его в двоичное представление.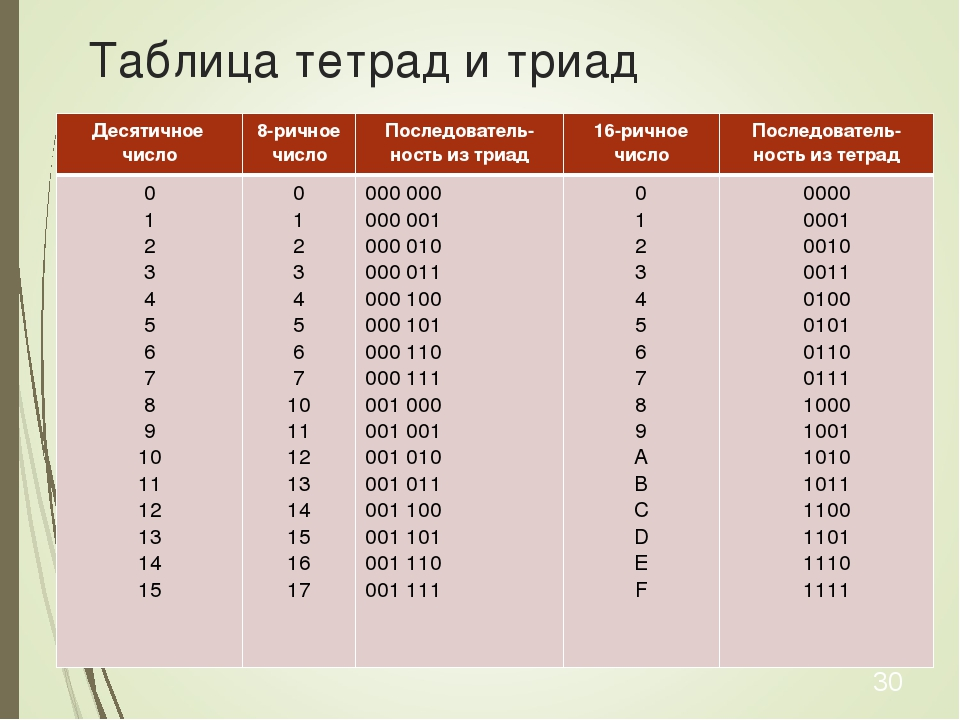 Мы могли бы использовать любое число, но если оно окажется слишком большим, оно превратится в длинную строку нулей и единиц.
Мы могли бы использовать любое число, но если оно окажется слишком большим, оно превратится в длинную строку нулей и единиц.
| 149 | |||||||
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 149 = 1 ⋅ 2 7 + 0 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 0 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 128 + 0 + 0 + 16 + 0 + 4 + 0 + 1 | |||||||
Как видите, десятичное число 149 представлено в двоичной системе последовательностью нулей и единиц ( 10010101 ). Обычно, чтобы различать десятичное или двоичное число, мы должны указать основание, на которое мы ссылаемся. Основание описывается как нижний индекс после последнего символа числа 9.0011
Основание описывается как нижний индекс после последнего символа числа 9.0011
Пример:
| Десятичный (по основанию 10) | Двоичный (по основанию 2) |
| 149 10 | 9 0031 10010101 2
Указав основание числа, мы исключаем вероятность путаницы, потому что одно и то же представление (например, 11) может означать разные вещи для разных оснований.
| 11 2 ≠ 11 10 |
Другой способ избежать путаницы — использовать специальную запись (префикс) для двоичных чисел. Это потому что 1100 может представлять одиннадцать сотен в десятичной системе или десятичные двенадцать в двоичной системе. Поэтому, если вы хотите указать двоичное число, мы используем префикс 0b . Пример: 0b1100 .
Кратко характеристики двоичной системы:
- использует 2 символа
- может быть разложена на множители, содержащие степень 2
- используется в компьютерах, микроконтроллерах
Восьмеричное (основание 8) 90 013
Все числа в восьмеричной системе представлены с использованием 8 символов/символов, от 0 до 7 . Причина использования восьмеричной системы вместо десятичной может быть разной. Один из них заключается в том, что вместо того, чтобы считать пальцами, мы используем промежутки между пальцами.
Причина использования восьмеричной системы вместо десятичной может быть разной. Один из них заключается в том, что вместо того, чтобы считать пальцами, мы используем промежутки между пальцами.
У человека 4 промежутка между пальцами одной руки; всего у нас будет 8 пробелов, для обеих рук. В этом случае имеет смысл использовать восьмеричную систему представления чисел вместо десятичной. Недостатком является то, что для более высоких чисел потребуется больше символов по сравнению с десятичным числом.
| Восьмеричные символы | |||||||
| 0 | 1 | 2 | 3 | 4 90 028 | 5 | 6 | 7 |
Чтобы преобразовать десятичное число в восьмеричную систему, мы разделим в степени 8:
| 8 k | … | 8 5 | 8 4 900 69 | 8 3 | 8 2 | 8 1 | 8 0 |
| N | … | 32768 | 4096 | 512 | 64 | 8 | 1 |
В качестве Например, мы собираемся представить десятичное число 67049 в восьмеричной системе счисления:
| 67049 | |||||
| 8 5 | 8 4 | 8 3 | 8 2 | 8 1 | 8 0 |
| 2 | 0 | 2 | 7 | 5 | 1 |
| 67049 = 2 ⋅ 8 5 + 0 ⋅ 8 4 + 2 ⋅ 8 3 + 7 ⋅ 8 2 + 5 ⋅ 8 1 + 1 ⋅ 8 0 = 65535 + 0 + 1024 + 448 + 40 + 1 | |||||
Шестнадцатеричный (основание 16)
Шестнадцатеричный 9Система представления чисел 0004 использует 16 символов/символов для определения чисел. Он используется в информатике в основном потому, что может представлять большие десятичные числа с меньшим количеством символов.
Он используется в информатике в основном потому, что может представлять большие десятичные числа с меньшим количеством символов.
| Шестнадцатеричные символы | |||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | Д | Е | F |
По сравнению с десятичной системой также используются числовые символы от 0 до 9. Кроме того, используются буквенно-цифровые символы от A до F для значений от 10 до 15.
| 16 9006 8 к | … | 16 5 | 16 4 | 16 3 | 16 2 | 16 1 | 16 0 |
| С | … | 1048576 | 65535 | 4096 | 256 | 16 | 1 |
Чтобы представить десятичное число в шестнадцатеричном формате, мы разбиваем десятичное число на сумму членов.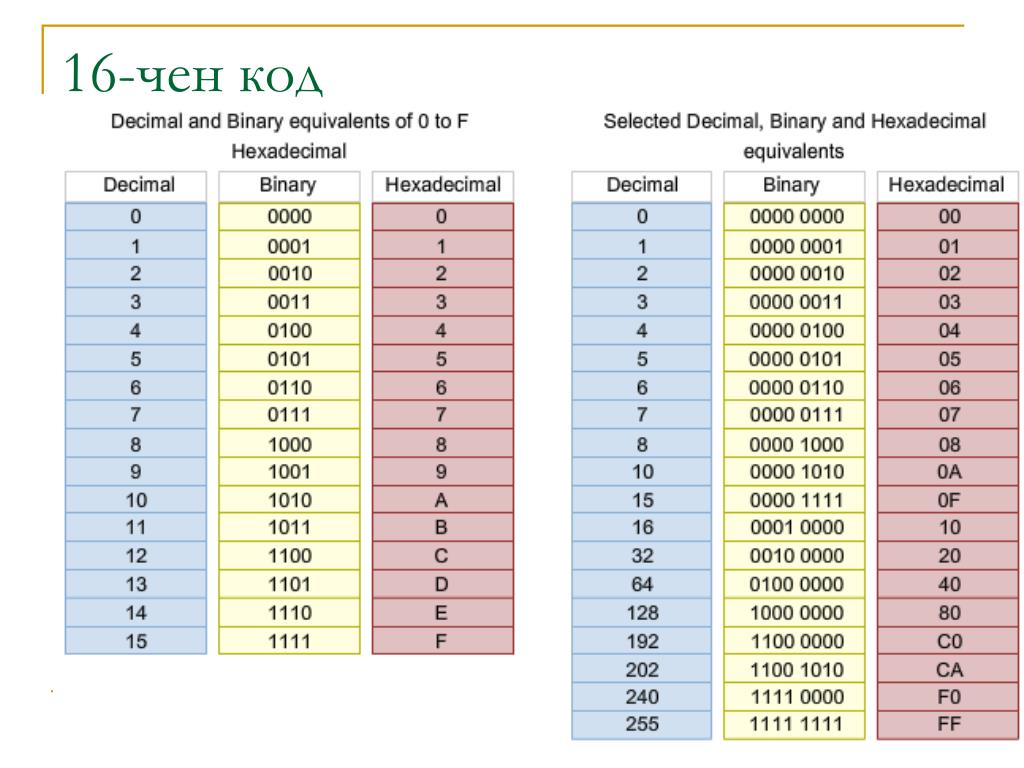 Каждый член представляет собой произведение шестнадцатеричного символа на степень числа 16.
Каждый член представляет собой произведение шестнадцатеричного символа на степень числа 16.
| 67049 | ||||
| 16 4 | 16 3 | 16 2 | 16 1 | 16 0 |
| 1 | 0 | 5 | E | 9 |
| 67049 = 1 ⋅ 16 4 + 0 ⋅ 16 3 + 5 ⋅ 16 2 + E ⋅ 16 1 + 9 ⋅ 16 0 = 65536 + 0 + 1280 + 224 + 9 | ||||
Представление десятичного числа 6704 9 в шестнадцатеричном формате равно 105E9 . Подобно двоичной системе, обычной практикой является использование префикса «9».0055 0x », чтобы отличить от десятичной системы счисления. Пример: 0x105E9 .
Кратко характеристики шестнадцатеричной системы представления чисел:
- использует 16 символов
- может быть разложен на множители, содержащие степени 16
- используется в компьютерах, микроконтроллерах
Таблица ниже приведены характеристики вышеупомянутые системы представления чисел.
| Система | Количество символов | Символы | Префикс | Пример 9000 4 |
| Десятичный | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | Нет | 147 |
| Двоичный | 2 | 0, 1 | 0b | 0b10010011 |
| Шестнадцатеричный | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F | 0x | 0x93 |
| Восьмеричный | 8 | 0, 1, 2, 3, 4, 5, 6, 7 9 0028 | Нет | 41 |
Как восьмеричная, так и шестнадцатеричная системы представления чисел связаны с компьютерной системой, в основном с процессорами и микроконтроллерами. Например, если микропроцессор использует 8-битные данные, то для интерфейса данных подходит восьмеричная система. Если микропроцессор использует 16 бит, то для представления данных подходит шестнадцатеричная система.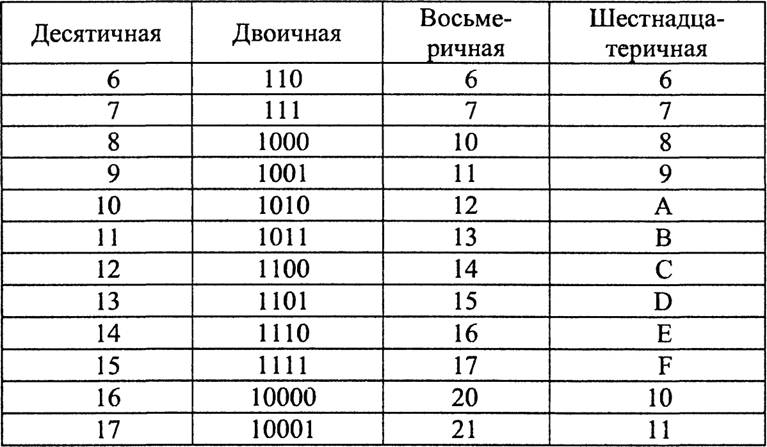
Система счисления | Двоичное, восьмеричное, десятичное, шестнадцатеричное число
В конце этого урока-
1. Вы сможете описать историю числа.
2. Вы сможете различать числа и цифры.
3. Вы сможете описать типы системы счисления.
4. Вы сможете различать различные типы систем счисления.
Что такое число ?
Число — это строка из одной или нескольких цифр, которая используется для подсчета, количественной оценки и измерения чего-либо. Например, в классе 20 учеников; Здесь 20 – это число.
Что такое цифра?
Цифра — это одиночный числовой символ числа или наименьшие символы чисел. Все цифры являются числами, но все числа не являются цифрами. Например, 243 — это трехзначное число, состоящее из 2, 4 и 3 отдельных трех цифр. Каждый из них представляет собой отдельный номер.
Значение каждой цифры в числе можно определить с помощью –
- Цифра
- Позиция цифры в числе
- Основание системы счисления
Что такое Система счисления?
Техника представления чисел и работы с ними называется системой счисления.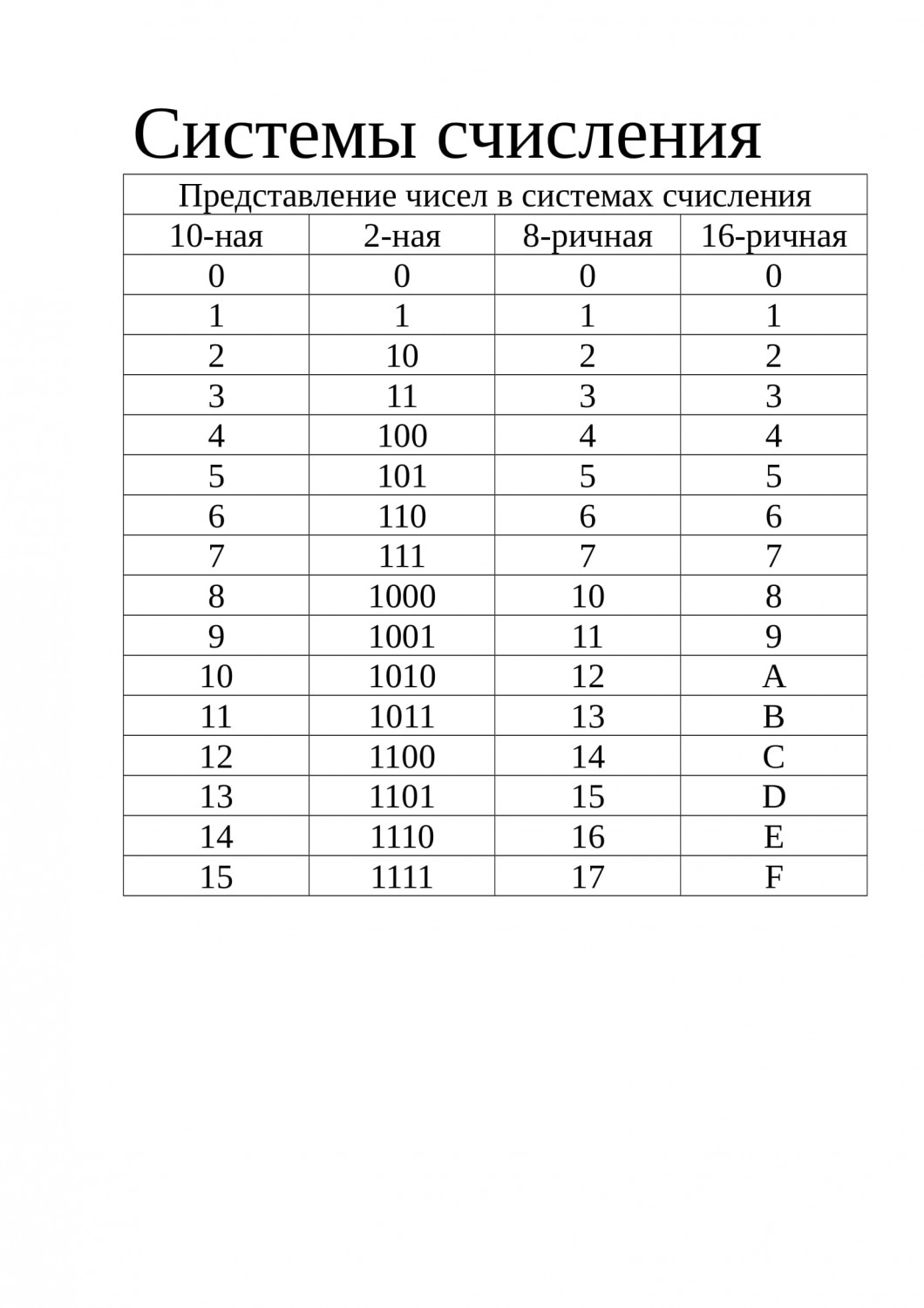 Десятичная система счисления является наиболее распространенной системой счисления.
Десятичная система счисления является наиболее распространенной системой счисления.
Система счисления состоит из следующих элементов. As-
- Некоторые символы- Например- 1,2,3 …
- Некоторые операторы. Например – +, -, ×, ÷ и т. д.
- Некоторые правила. Например, правила сложения, вычитания, умножения, деления и т. д.
Типы системы счисления:
Система счисления классифицируется двумя способами в зависимости от положения цифр в числе. Они:
- Непозиционная система счисления
- Позиционная система счисления
Непозиционная система счисления:
В непозиционной системе счисления каждый символ представляет одно и то же значение независимо от его положения.
Система счисления, в которой значение цифры не зависит от положения цифры, используемой в числе, называется непозиционной системой счисления. В этой системе положение символов или цифр не имеет значения. В результате цифры не имеют локального значения. На основании собственной стоимости производится расчет кем. Иероглифы майя и римляне, использовавшиеся в древности, являются примером непозиционной системы счисления.
В результате цифры не имеют локального значения. На основании собственной стоимости производится расчет кем. Иероглифы майя и римляне, использовавшиеся в древности, являются примером непозиционной системы счисления.
Рис. Иероглифическая система счисления
Рис. В системе каждый символ представляет разное значение в зависимости от позиции, которую он занимает в числе.
Система счисления, в которой значение цифры зависит от положения цифры, используемой в числе, называется позиционной системой счисления. В этой системе счисления значение числа вычисляется с использованием локального значения цифр, позиционного значения цифр и базы системы счисления. В этой системе каждое число делится на целое и дробное с точкой счисления ( . ). Например: (126,34) 10 .
В любой позиционной системе счисления
Позиционное значение цифры в числе = (основание числа) позиция цифры .
позиция цифр целого числа начинается с 0 (справа налево), а позиция цифр дробного числа начинается с -1 (слева направо). Например, номер (126,34) 10 ; позиционное значение цифры 2 равно (10) 1 = 10 и позиционное значение цифры 1 равно (10) 2 = 100.
Различные части числа в позиционной системе счисления- 9 1018
Типы позиционной системы счисления:
Позиционная система счисления бывает четырех типов. Они:
- Двоичный
- Восьмеричный
- Десятичный
- Шестнадцатеричный
В двоичной системе счисления есть только две цифры, равные 9.0931 0 и 1 . Каждое число (значение) представляет собой 0 и 1 в этой системе счисления. Основание двоичной системы счисления равно 2, потому что в нем всего две цифры.
Его также называют системой счисления с основанием 2. Самый простой способ варьировать инструкции с помощью электрических сигналов — система с двумя состояниями — включено и выключено.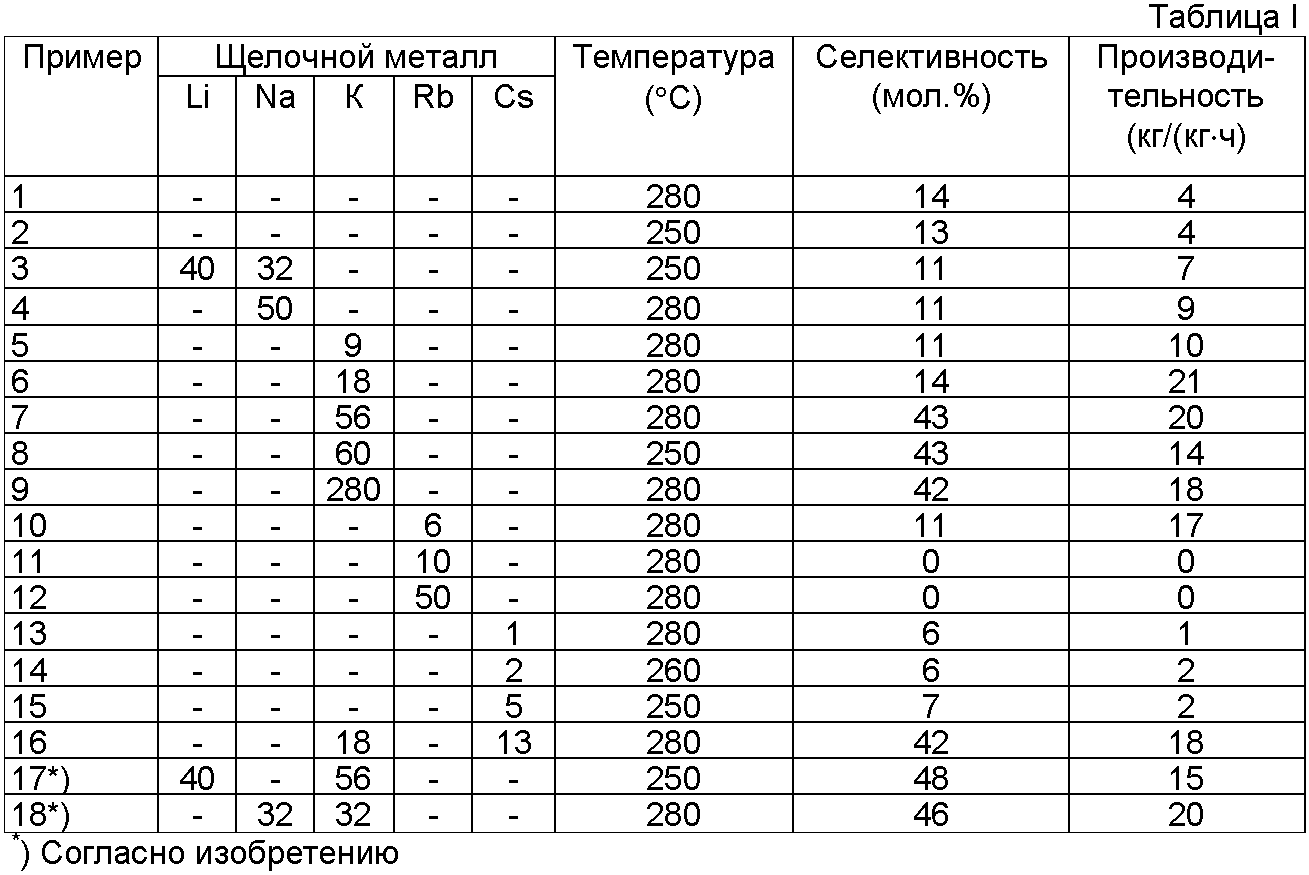 ON представлен как 1, а OFF как 0, хотя 0 на самом деле не сигнал, а сигнал при более низком напряжении.
ON представлен как 1, а OFF как 0, хотя 0 на самом деле не сигнал, а сигнал при более низком напряжении.
Каждая двоичная цифра также называется бит . Двоичная система счисления также является позиционной системой счисления, где каждая цифра имеет значение, выраженное в степени 2.
В любом двоичном числе самая правая цифра называется младший значащий бит (LSB) , а самая левая цифра называется старший значащий бит (MSB) .
Память компьютера измеряется количеством битов, которые она может хранить. Вот диаграмма преобразования объема памяти.
- 1 байт (B) = 8 бит
- 1 килобайт (КБ) = 1024 байта
- 1 мегабайт (МБ) = 1024 КБ
- 1 гигабайт (ГБ) = 1024 МБ 9 0207 1 терабайт (ТБ) = 1024 ГБ
- 1 экзабайт (EB) = 1024 PB
- 1 зеттабайт = 1024 EB
- 1 йоттабайт (YB) = 1024 ZB
Восьмеричная система счисления: 90 891
Восьмеричная система счисления имеет только восемь (8) цифр от от 0 до 7 .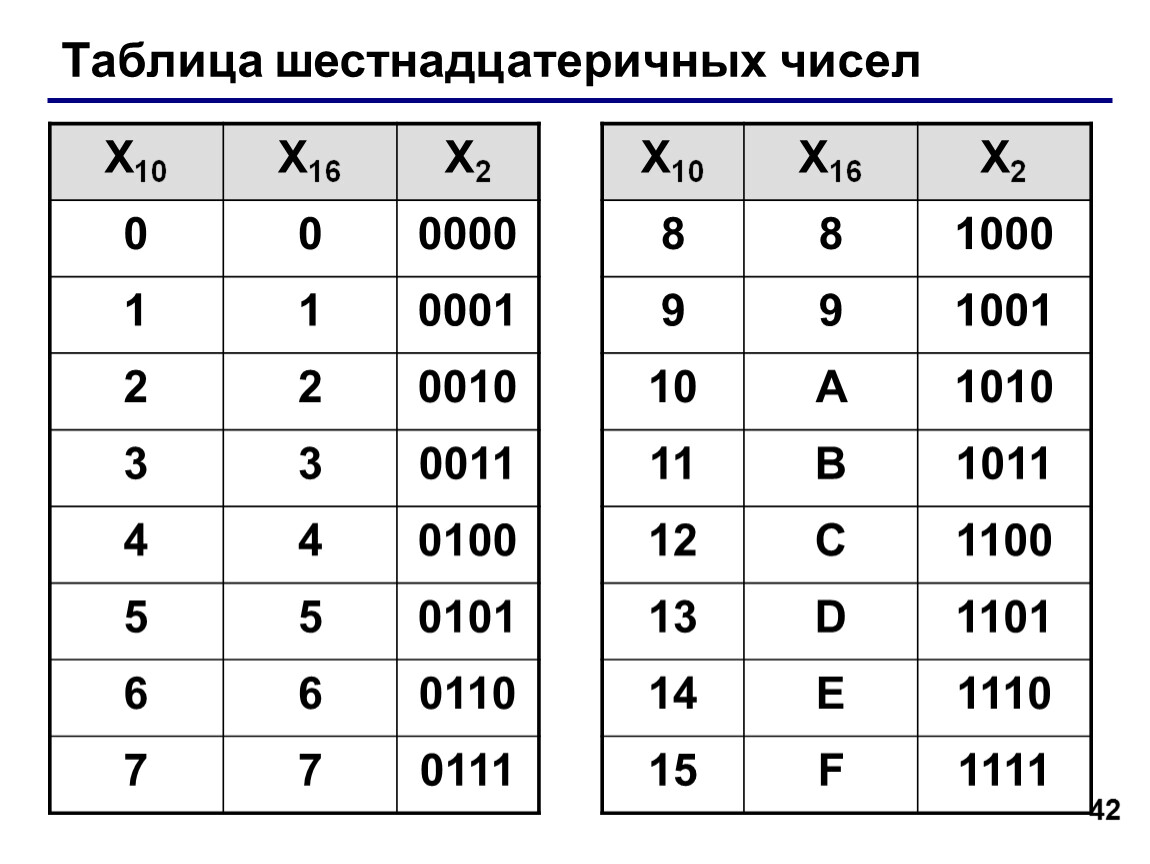 Каждое число (значение) представляет собой 0,1,2,3,4,5,6 и 7 в этой системе счисления. Основание восьмеричной системы счисления равно 8, потому что в ней всего 8 цифр.
Каждое число (значение) представляет собой 0,1,2,3,4,5,6 и 7 в этой системе счисления. Основание восьмеричной системы счисления равно 8, потому что в ней всего 8 цифр.
Восьмеричная система счисления также является позиционной системой счисления, в которой каждая цифра имеет свое значение, выраженное в степени 8. Она также называется системой счисления с основанием 8.
Десятичная система счисления:
В десятичной системе счисления всего десять (10) цифр от 0 до 9 . Каждое число (значение) представляет собой 0,1,2,3,4,5,6, 7,8 и 9 в этой системе счисления. Основание десятичной системы счисления равно 10, потому что в ней всего 10 цифр.
Десятичная система счисления также является позиционной системой счисления. Это означает, что значение цифр будет зависеть от их положения.
Шестнадцатеричная система счисления:
Шестнадцатеричная система счисления имеет шестнадцать (16) буквенно-цифровых значений от 0 до 9 и от A до F .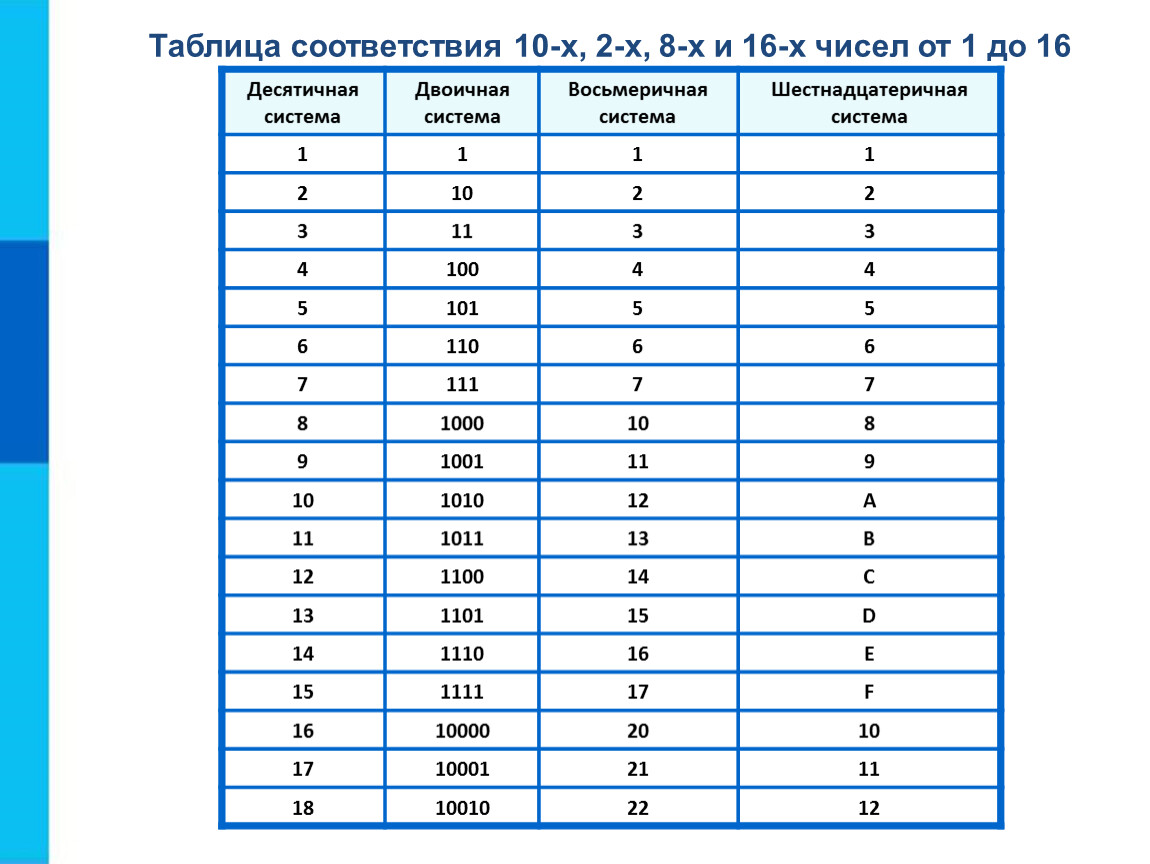 Каждое число (значение) представляет собой 0,1,2,3,4,5,6, 7,8,9,A,B,C,D,E и F в этой системе счисления. Основание шестнадцатеричной системы счисления равно 16, потому что оно имеет 16 буквенно-цифровых значений.
Каждое число (значение) представляет собой 0,1,2,3,4,5,6, 7,8,9,A,B,C,D,E и F в этой системе счисления. Основание шестнадцатеричной системы счисления равно 16, потому что оно имеет 16 буквенно-цифровых значений.
Здесь A равно 10, B равно 11, C равно 12, D равно 13, E равно 14 и F равно 15.
Шестнадцатеричная система счисления также является позиционной системой счисления где каждая цифра имеет свое значение, выраженное в степенях числа 16.
Эта система счисления используется для цветового кода и адреса памяти.
Что такое Основа системы счисления?
- Основание системы счисления — это общее количество цифр, используемых в этой системе счисления.
- База используется как нижний индекс числа.
- Система счисления с основанием «b» имеет цифры в диапазоне [0 , b-1].
- Также называется основанием системы счисления.
Таблица систем счисления с основанием, используемые цифры, представление:
Оценка урока –
Вопросы на основе знаний:
a. Что такое число?
Что такое число?
а. Что такое цифра?
а. Что такое бит/байт?
а. Что такое система счисления?
а. Что такое позиционная система счисления?
а. Что такое точка радикса?
а. Что такое позиционное значение?
а. Что такое непозиционная система счисления?
а. Что такое двоичная система счисления?
а. Что такое десятичная система счисления?
а. Что такое восьмеричная система счисления?а. Что такое шестнадцатеричная система счисления?
а. Что лежит в основе системы счисления?
Перейти к ответу
Вопросы на понимание:
b. «Все цифры — числа, но не все числа — цифры» — объясните.
б. «Подсчитайте непозиционную систему счисления» – Объясните.
б. Почему основание шестнадцатеричной системы счисления равно 16? Объяснять.
б. Что понимают под основанием системы счисления? Объясни это.
б. Почему число ( 11 ) 10 называется позиционным?
б.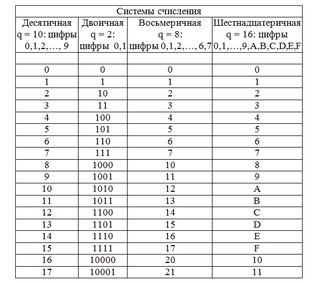 Объясните позиционное значение десятичной системы счисления.
Объясните позиционное значение десятичной системы счисления.
б. Какой тип числа 10101 в системе счисления? Объяснять.
б. Что такое число 988 в системе счисления? Объяснять.
б. Какой тип числа является 3D? Объяснять.
б. Объясните трехмерную систему счисления.
б. (298) 8 действительный номер? -Объяснять.
б. Двоичная система счисления аналогична функциям внутренних частей компьютера. Объяснять.
б. Почему цифровой сигнал важен в компьютерной системе? Объяснять.
б. Запишите причины использования двоичной системы счисления в компьютерном дизайне.
б. Компьютер не понимает (169) 10 Объясните.
б. Как вы будете различать десятичную и шестнадцатеричную системы счисления?
б. «Восьмеричная система счисления называется 3-разрядным кодом» -Объясните.
б. «Шестнадцатеричная система счисления называется 4-разрядным кодом» — Объясните.
Перейти к ответу
Творческие вопросы:
Вопросы с несколькими вариантами ответов:
9000 2 1.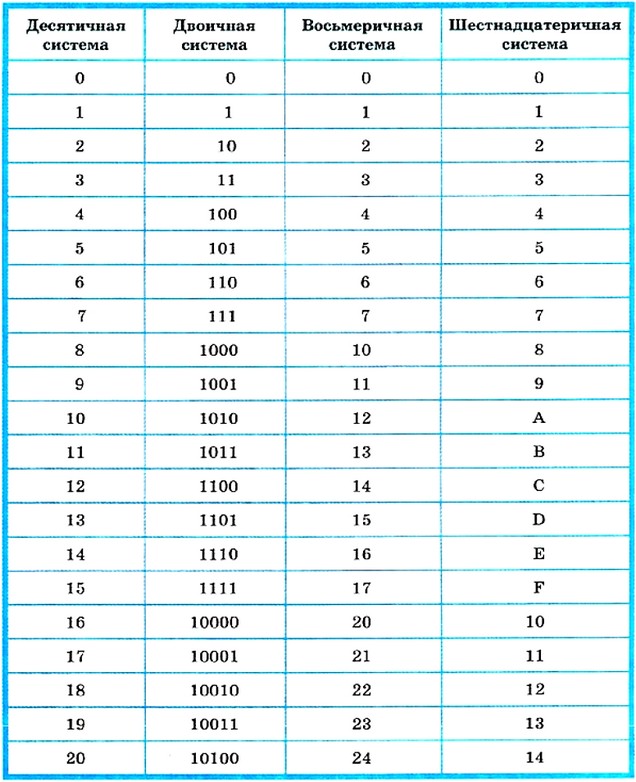 Какая из них является непозиционной системой счисления?
Какая из них является непозиционной системой счисления?а) Двоичная б) Иероглифическая в) Десятичная г) Восьмеричная
2. Какую систему счисления обычно использует компьютер?
a) Двоичная b) Восьмеричная c) Десятичная d) Шестнадцатеричная
3. Сколько цифр в шестнадцатеричной системе счисления?
а) 6 б) 8 в) 10 г) 16
4. Что такое основание шестнадцатеричной системы счисления?
а) 6 б) 8 в) 10 г) 16
5. Что является основой десятичной системы счисления?
а) 6 б) 8 в) 10 г) 16
6. Что является основой двоичной системы счисления?
а) 2 б) 8 в) 10 г) 16
7. Какой тип числа является A68B в системе счисления?
a) Двоичная b) Восьмеричная c) Десятичная d) Шестнадцатеричная
8. Сколько типов системы счисления основано на позиционном значении?
Сколько типов системы счисления основано на позиционном значении?
a) 2 b) 4 c) 10 d) 16
9. Какая единица измерения памяти является наименьшей?
a) Бит b) Байт c) Килобайт d) Мегабайт
10. Какой тип числа 101B в системе счисления?
a) Двоичный b) Восьмеричный c) Десятичный d) Шестнадцатеричный
11. Что обозначается 0 в (1110) 2 ?
a) BOS b) BCD c) LSB d) MSB
12. Сколько бит в числе 1011?
а) 2 б) 3 в) 4 г) 10
13. Какой тип числа 2BAD.8C в системе счисления?
a) Двоичный b) Восьмеричный c) Десятичный d) Шестнадцатеричный
14. Для определения значения позиционного числа необходимо –
i. Основание числа ii. Локальное значение цифр iii. Позиционное значение цифр
Какой из них правильный?
a) i & ii b) i & iii c) ii & iii d) i,ii & iii
15.
 Способы представления чисел в ЭВМ — Теория — 1.2 Перевод чисел из одной системы счисления в другую
Способы представления чисел в ЭВМ — Теория — 1.2 Перевод чисел из одной системы счисления в другую
 Для перевода числа Nисх с основанием исходной системы счисления в число с новым основанием системы счисления в данном случа используется метод деления.
Для перевода числа Nисх с основанием исходной системы счисления в число с новым основанием системы счисления в данном случа используется метод деления. Этот метод заключается в сложении результатов произведений разрядов исходного числа на основание исходной системы счисления возведенное в степень соответствующую позиции данного разряда, вычисленных в десятичной системе счисления. Для перевода числа с основанием исходной системы счисления в число с новым основанием системы счисления в данном случае используется метод умножения.
Этот метод заключается в сложении результатов произведений разрядов исходного числа на основание исходной системы счисления возведенное в степень соответствующую позиции данного разряда, вычисленных в десятичной системе счисления. Для перевода числа с основанием исходной системы счисления в число с новым основанием системы счисления в данном случае используется метод умножения. Перевод
Перевод
 19 ⋅ 2 = 0.38
19 ⋅ 2 = 0.38 16
16
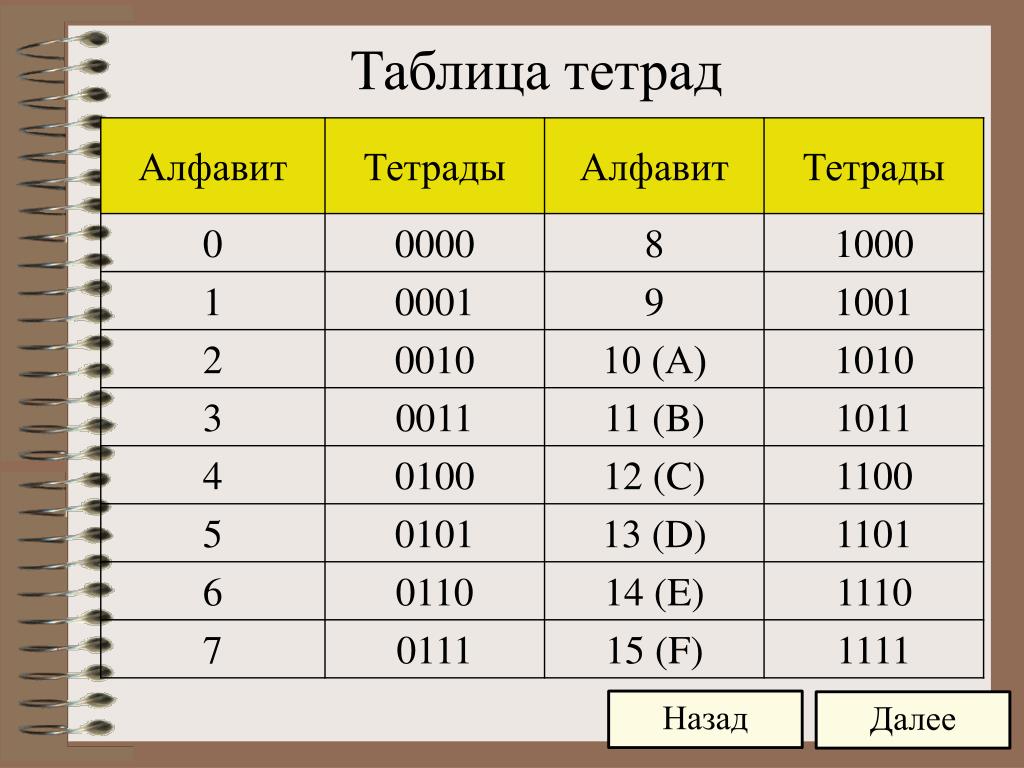 Но недостатком является то, что размер таблицы и занимаемый ею объём памяти очень большой, что технически неприемлемо.
Но недостатком является то, что размер таблицы и занимаемый ею объём памяти очень большой, что технически неприемлемо.