Таблицы сложного процента: Таблицы сложных процентов

Таблицы сложных процентов

Таблицы сложных процентов – шесть функции денежной единицы типа Б

6%

Начисление процентов – ежегодное

	Будущая	Накопление	Фактор	Текущая	Текущая	Взнос
Ãîä	стоимость	единицы	фонда	стоимость	стоимость	çà àìîð-
	единицы	за период	возмещения	единицы	единичного	тизацию
					аннуитета	единицы
1	1,06000	1,00000	1,00000	0,94340	0,94340	1,06000
2	1,12360	2,06000	0,48544	0,89000	1,83339	0,54544
3	1,19102	3,18360	0,31411	0,83962	2,67301	0,37411
4	1,26248	4,37462	0,22859	0,79209	3,46511	0,28859
5	1,33823	5,63709	0,17740	0,74726	4,21236	0,23740
6	1,41852	6,97532	0,14336	0,70496	4,91732	0,20336
7	1,50363	8,39384	0,11914	0,66506	5,58238	0,17914
8	1,59385	9,89747	0,10104	0,62741	6,20979	0,16104
9	1,68948	11,49132	0,08702	0,59190	6,80169	0,14702
10	1,79085	13,18079	0,07587	0,55839	7,36009	0,13587
11	1,89830	14,97164	0,06679	0,52679	7,88687	0,12679
12	2,01220	16,86994	0,05928	0,49697	8,38384	0,11928
13	2,13293	18,88214	0,05296	0,46884	8,85268	0,11296
14	2,26090	21,01507	0,04758	0,44230	9,29498	0,10758
15	2,39656	23,27597	0,04296	0,41727	9,71225	0,10296
16	2,54035	25,67253	0,03895	0,39365	10,10590	0,09895
17	2,69277	28,21288	0,03544	0,37136	10,47726	0,09544
18	2,85434	30,90565	0,03236	0,35034	10,82760	0,09236
19	3,02560	33,75999	0,02962	0,33051	11,15812	0,08962
20	3,20714	36,78559	0,02718	0,31180	11,46992	0,08718
21	3,39956	39,99273	0,02500	0,29416	11,76408	0,08500
22	3,60354	43,39229	0,02305	0,27751	12,04158	0,08305
23	3,81975	46,99583	0,02128	0,26180	12,30338	0,08128
24	4,04893	50,81558	0,01968	0,24698	12,55036	0,07968
25	4,29187	54,86451	0,01823	0,23300	12,78336	0,07823
26	4,54938	59,15638	0,01690	0,21981	13,00317	0,07690
27	4,82235	63,70576	0,01570	0,20737	13,21053	0,07570
28	5,11169	68,52811	0,01459	0,19563	13,40616	0,07459
29	5,41839	73,63980	0,01358	0,18456	13,59072	0,07358
30	5,74349	79,05818	0,01265	0,17411	13,76483	0,07265
31	6,08810	84,80168	0,01179	0,16425	13,92909	0,07179
32	6,45339	90,88978	0,01100	0,15496	14,08404	0,07100
33	6,84059	97,34316	0,01027	0,14619	14,23023	0,07027
34	7,25102	104,18375	0,00960	0,13791	14,36814	0,06960
35	7,68609	111,43478	0,00897	0,13011	14,49825	0,06897
36	8,14725	119,12087	0,00839	0,12274	14,62099	0,06839
37	8,63609	127,26812	0,00786	0,11579	14,73678	0,06786
38	9,15425	135,90421	0,00736	0,10924	14,84602	0,06736
39	9,70351	145,05846	0,00689	0,10306	14,94907	0,06689
40	10,28572	154,76197	0,00646	0,09722	15,04630	0,06646

7%

Начисление процентов – ежегодное

	Будущая	Накопление	Фактор	Текущая	Текущая	Взнос
Ãîä	стоимость	единицы	фонда	стоимость	стоимость	çà àìîð-
	единицы	за период	возмещения	единицы	единичного	тизацию
					аннуитета	единицы
1	1,07000	1,00000	1,00000	0,93458	0,93458	1,07000
2	1,14490	2,07000	0,48309	0,87344	1,80802	0,55309
3	1,22504	3,21490	0,31105	0,81630	2,62432	0,38105
4	1,31080	4,43994	0,22523	0,76290	3,38721	0,29523
5	1,40255	5,75074	0,17389	0,71299	4,10020	0,24389
6	1,50073	7,15329	0,13980	0,66634	4,76654	0,20980
7	1,60578	8,65402	0,11555	0,62275	5,38929	0,18555
8	1,71819	10,25980	0,09747	0,58201	5,97130	0,16747
9	1,83846	11,97799	0,08349	0,54393	6,51523	0,15349
10	1,96715	13,81645	0,07238	0,50835	7,02358	0,14238
11	2,10485	15,78360	0,06336	0,47509	7,49867	0,13336
12	2,25219	17,88845	0,05590	0,44401	7,94269	0,12590
13	2,40985	20,14064	0,04965	0,41496	8,35765	0,11965
14	2,57853	22,55049	0,04434	0,38782	8,74547	0,11434
15	2,75903	25,12902	0,03979	0,36245	9,10791	0,10979
16	2,95216	27,88805	0,03586	0,33873	9,44665	0,10586
17	3,15882	30,84022	0,03243	0,31657	9,76322	0,10243
18	3,37993	33,99903	0,02941	0,29586	10,05909	0,09941
19	3,61653	37,37896	0,02675	0,27651	10,33560	0,09675
20	3,86968	40,99549	0,02439	0,25842	10,59401	0,09439
21	4,14056	44,86518	0,02229	0,24151	10,83553	0,09229
22	4,43040	49,00574	0,02041	0,22571	11,06124	0,09041
23	4,74053	53,43614	0,01871	0,21095	11,27219	0,08871
24	5,07237	58,17667	0,01719	0,19715	11,46933	0,08719
25	5,42743	63,24904	0,01581	0,18425	11,65358	0,08581
26	5,80735	68,67647	0,01456	0,17220	11,82578	0,08456
27	6,21387	74,48382	0,01343	0,16093	11,98671	0,08343
28	6,64884	80,69769	0,01239	0,15040	12,13711	0,08239
29	7,11426	87,34653	0,01145	0,14056	12,27767	0,08145
30	7,61226	94,46079	0,01059	0,13137	12,40904	0,08059
31	8,14511	102,07304	0,00980	0,12277	12,53181	0,07980
32	8,71527	110,21815	0,00907	0,11474	12,64656	0,07907
33	9,32534	118,93343	0,00841	0,10723	12,75379	0,07841
34	9,97811	128,25877	0,00780	0,10022	12,85401	0,07780
35	10,67658	138,23688	0,00723	0,09366	12,94767	0,07723
36	11,42394	148,91346	0,00672	0,08754	13,03521	0,07672
37	12,22362	160,33740	0,00624	0,08181	13,11702	0,07624
38	13,07927	172,56102	0,00580	0,07646	13,19347	0,07580
39	13,99482	185,64029	0,00539	0,07146	13,26493	0,07539
40	14,97446	199,63511	0,00501	0,06678	13,33171	0,07501

8%

Начисление процентов – ежегодное

	Будущая	Накопление	Фактор	Текущая	Текущая	Взнос
Ãîä	стоимость	единицы	фонда	стоимость	стоимость	çà àìîð-
	единицы	за период	возмещения	единицы	единичного	тизацию
					аннуитета	единицы
1	1,08000	1,00000	1,00000	0,92593	0,92593	1,08000
2	1,16640	2,08000	0,48077	0,85734	1,78326	0,56077
3	1,25971	3,24640	0,30803	0,79383	2,57710	0,38803
4	1,36049	4,50611	0,22192	0,73503	3,31213	0,30192
5	1,46933	5,86660	0,17046	0,68058	3,99271	0,25046
6	1,58687	7,33593	0,13632	0,63017	4,62288	0,21632
7	1,71382	8,92280	0,11207	0,58349	5,20637	0,19207
8	1,85093	10,63663	0,09401	0,54027	5,74664	0,17401
9	1,99900	12,48756	0,08008	0,50025	6,24689	0,16008
10	2,15892	14,48656	0,06903	0,46319	6,71008	0,14903
11	2,33164	16,64549	0,06008	0,42888	7,13896	0,14008
12	2,51817	18,97713	0,05270	0,39711	7,53608	0,13270
13	2,71962	21,49530	0,04652	0,36770	7,90378	0,12652
14	2,93719	24,21492	0,04130	0,34046	8,24424	0,12130
15	3,17217	27,15211	0,03683	0,31524	8,55948	0,11683
16	3,42594	30,32428	0,03298	0,29189	8,85137	0,11298
17	3,70002	33,75023	0,02963	0,27027	9,12164	0,10963
18	3,99602	37,45024	0,02670	0,25025	9,37189	0,10670
19	4,31570	41,44626	0,02413	0,23171	9,60360	0,10413
20	4,66096	45,76196	0,02185	0,21455	9,81815	0,10185
21	5,03383	50,42292	0,01983	0,19866	10,01680	0,09983
22	5,43654	55,45675	0,01803	0,18394	10,20074	0,09803
23	5,87146	60,89329	0,01642	0,17032	10,37106	0,09642
24	6,34118	66,76476	0,01498	0,15770	10,52876	0,09498
25	6,84847	73,10594	0,01368	0,14602	10,67478	0,09368
26	7,39635	79,95441	0,01251	0,13520	10,80998	0,09251
27	7,98806	87,35077	0,01145	0,12519	10,93516	0,09145
28	8,62711	95,33883	0,01049	0,11591	11,05108	0,09049
29	9,31727	103,96593	0,00962	0,10733	11,15841	0,08962
30	10,06266	113,28321	0,00883	0,09938	11,25778	0,08883
31	10,86767	123,34586	0,00811	0,09202	11,34980	0,08811
32	11,73708	134,21353	0,00745	0,08520	11,43500	0,08745
33	12,67605	145,95062	0,00685	0,07889	11,51389	0,08685
34	13,69013	158,62666	0,00630	0,07305	11,58693	0,08630
35	14,78534	172,31680	0,00580	0,06763	11,65457	0,08580
36	15,96817	187,10215	0,00534	0,06262	11,71719	0,08534
37	17,24562	203,07032	0,00492	0,05799	11,77518	0,08492
38	18,62527	220,31595	0,00454	0,05369	11,82887	0,08454
39	20,11530	238,94122	0,00419	0,04971	11,87858	0,08419
40	21,72452	259,05652	0,00386	0,04603	11,92461	0,08386

9%

Начисление процентов – ежегодное

	Будущая	Накопление	Фактор	Текущая	Текущая	Взнос
Ãîä	стоимость	единицы	фонда	стоимость	стоимость	çà àìîð-
	единицы	за период	возмещения	единицы	единичного	тизацию
					аннуитета	единицы
1	1,09000	1,00000	1,00000	0,91743	0,91743	1,09000
2	1,18810	2,09000	0,47847	0,84168	1,75911	0,56847
3	1,29503	3,27810	0,30505	0,77218	2,53129	0,39505
4	1,41158	4,57313	0,21867	0,70843	3,23972	0,30867
5	1,53862	5,98471	0,16709	0,64993	3,88965	0,25709
6	1,67710	7,52333	0,13292	0,59627	4,48592	0,22292
7	1,82804	9,20043	0,10869	0,54703	5,03295	0,19869
8	1,99256	11,02847	0,09067	0,50187	5,53482	0,18067
9	2,17189	13,02104	0,07680	0,46043	5,99525	0,16680
10	2,36736	15,19293	0,06582	0,42241	6,41766	0,15582
11	2,58043	17,56029	0,05695	0,38753	6,80519	0,14695
12	2,81266	20,14072	0,04965	0,35553	7,16073	0,13965
13	3,06580	22,95339	0,04357	0,32618	7,48690	0,13357
14	3,34173	26,01919	0,03843	0,29925	7,78615	0,12843
15	3,64248	29,36092	0,03406	0,27454	8,06069	0,12406
16	3,97031	33,00340	0,03030	0,25187	8,31256	0,12030
17	4,32763	36,97371	0,02705	0,23107	8,54363	0,11705
18	4,71712	41,30134	0,02421	0,21199	8,75562	0,11421
19	5,14166	46,01846	0,02173	0,19449	8,95011	0,11173
20	5,60441	51,16012	0,01955	0,17843	9,12855	0,10955
21	6,10881	56,76453	0,01762	0,16370	9,29224	0,10762
22	6,65860	62,87334	0,01590	0,15018	9,44243	0,10590
23	7,25788	69,53194	0,01438	0,13778	9,58021	0,10438
24	7,91108	76,78982	0,01302	0,12640	9,70661	0,10302
25	8,62308	84,70090	0,01181	0,11597	9,82258	0,10181
26	9,39916	93,32398	0,01072	0,10639	9,92897	0,10072
27	10,24508	102,72314	0,00973	0,09761	10,02658	0,09973
28	11,16714	112,96822	0,00885	0,08955	10,11613	0,09885
29	12,17218	124,13536	0,00806	0,08215	10,19828	0,09806
30	13,26768	136,30754	0,00734	0,07537	10,27365	0,09734
31	14,46177	149,57522	0,00669	0,06915	10,34280	0,09669
32	15,76333	164,03699	0,00610	0,06344	10,40624	0,09610
33	17,18203	179,80032	0,00556	0,05820	10,46444	0,09556
34	18,72841	196,98234	0,00508	0,05339	10,51784	0,09508
35	20,41397	215,71076	0,00464	0,04899	10,56682	0,09464
36	22,25123	236,12472	0,00424	0,04494	10,61176	0,09424
37	24,25384	258,37595	0,00387	0,04123	10,65299	0,09387
38	26,43668	282,62978	0,00354	0,03783	10,69082	0,09354
39	28,81599	309,06646	0,00324	0,03470	10,72552	0,09324
40	31,40942	337,88245	0,00296	0,03184	10,75736	0,09296

Расчёт сложных процентов в Excel

Уроки MS Excel

Работая с таблицами Excel, иногда возникает необходимость в распределении информации из одного столбца по

Уроки MS Excel

Тем людям, которые регулярно работают с таблицами Excel, нужно часто выполнять одни и те

Уроки MS Excel

Нередко пользователям приходится перенести часть информации с документа Microsoft Word в Excel формат, чтобы

Уроки MS Excel

Огромное преимущество электронных таблиц Excel заключается в том, что пользователю доступна работа как с

Уроки MS Excel

Пользователю Excel нередко приходится сталкиваться с тем, чтобы определять, сколько строк содержит таблица. Чтобы

Уроки MS Excel

Excel – одна из лучших программ для аналитика данных. А почти каждому человеку на

Уроки MS Excel

Время от времени при работе с электронными таблицами появляется необходимость изменить положение нескольких рядов

Уроки MS Excel

Excel – удивительная программа, дающая возможность не только числовые данные обрабатывать. С ее помощью

Уроки MS Excel

Сейчас век информации. Количество данных, которые людям приходится обрабатывать каждый день, растет все больше

Уроки MS Excel

Определение процента от числа – довольно частая задача, с которой приходится сталкиваться пользователю Ecxel,

Уроки MS Excel

Excel – невероятно функциональная программа. Она может использоваться и в качестве некого подобия среды

Уроки MS Excel

Excel – невероятно функциональная программа, позволяющая не просто записывать данные в табличном виде, но

Уроки MS Excel

Стандартное обозначение строк в Excel – цифровое. Если же речь идет о столбцах, то

Уроки MS Excel

Набор функций у программы Excel, конечно, поистине огромный. В том числе, можно в определенной

Уроки MS Excel

При работе с Excel могут возникать различные ситуации, такие как сбои в поставках электроэнергии,

Уроки MS Excel

Важно понимать, что Excel – это не только программа для создания баз данных, но

Сложные проценты с ежемесячным внесением платежа

Выполняем просьбу пользователя frouzen, который просил написать Финансовый калькулятор. — рассчитывающий наращенную сумму при использовании сложных процентов и довложении средств ежемесячно равными платежами. Начисление процентов предполагается тоже ежемесячное (самый выгодный случай).

Чтобы не отвлекать пользователя от калькулятора, ниже идет сам калькулятор, а немного теории и формул надо смотреть под ним, кому не лень.

Калькулятор

Сложные проценты с ежемесячным вложением равной суммы

Точность вычисления

Знаков после запятой: 2

Наращенная сумма

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

content_copy Ссылка save Сохранить extension Виджет

Формула сложных процентов, начисляемых несколько раз в течении года
, где m в нашем случае равно 12, а n — срок вклада в годах

Это простейший случай при внесении вклада сразу, и без дальнейшего его пополнения.

Теперь займемся более сложным случаем — пополнением вклада одинаковыми платежами ежемесячно.
Заметим, что множитель степени mn не что иное, как число периодов начисления процентов.

Таким образом, для самого первого вклада за несколько лет наращенная сумма будет равна

Для вклада, который был внесен в конце первого месяца, число периодов начисления процентов на один меньше, и формула будет выглядеть так
,
для третьего вклада — так
,
…
и для последнего вклада, то есть внесенного за месяц до окончания срока — так
,

Интересующий нас результат равен сумме всех этих выражений. И эти выражения кое-что роднит — все они члены геометрической прогрессии, в которой первый член равен , а знаменатель прогрессии равен .

Про геометрическую прогрессию смотри Геометрическая прогрессия

Таким образом, искомая сумма по формуле суммы геометрической прогрессии равна

Вот и все на сегодня.

Обновление

По просьбе пользователя добавлена возможность отдельного указания размера первого взноса. (C$1-$A2))-1)

• Столбец А является датой депозита
• Колонка B — сумма депозита
• Ячейка С1 — сегодняшняя дата
• Ячейка D1 — годовая процентная ставка

Большинство сберегательных счетов, о которых я знаю, составляют сложные проценты ежедневно и кредитные проценты ежемесячно , поэтому реально приведенная выше формула будет верна на сегодняшний день, даже если некоторые проценты вам еще не зачислены.

Вы также можете пропустить фактическую формулу сложного процента и просто использовать встроенную формулу будущей стоимости:

 =FV(D$1/360,C$1-$A2,0,-B2)-B2 

---

Чтобы углубиться в изучение только составления ежемесячно, вам нужно начать играть с настройкой дат …

Вы можете начать с взятия двух дат и подсчета количества прошедших месяцев с помощью функции DATEDIF (), например:

 =DATEDIF(A2,C$1,"M") 

Но вам придется скорректировать две даты, потому что простой DATEDIFF между сегодняшней датой и ячейками A3 и A4 будет возвращать 2, что не совсем правильно. (DATEDIF(EOMONTH($A2,0)+1,DATE(YEAR(C$1),MONTH(C$1),1),»M»)))-1)

Но это не совсем правильно, потому что он не начинает накапливать проценты до первого месяца, следующего за депозитом. Вы также можете получить приблизительное количество месяцев, вычтя две даты и разделив на 30 дней.

Вы можете сделать это более сложным, чтобы рассчитать количество дней в течение первого месяца + полный ежемесячный процент сверх этого, но это сделает формулу намного длиннее, потому что у вас будет

 First month in days interest + monthly interest beyond that 

Чтобы получить дни, оставшиеся в месяце, вы должны сделать что-то вроде:

 =EOMONTH($A2,0) - $A2 

Таким образом, чтобы получить долю оставшегося месяца, который вы делаете (количество дней, произошедших в месяце, деленное на количество дней в месяце):

 =(EOMONTH($A2,0) - $A2) / DAY(EOMONTH($A2,0)) 

Затем умножьте вышеупомянутое значение на месячную процентную ставку, умноженную на принцип, чтобы получить неполный месяц, затем добавьте ежемесячный процент выше. (DATEDIF(EOMONTH($A2,0)+1,DATE(YEAR(C$1),MONTH(C$1),1),»M»)))-1))

На данный момент вы действительно раскалываетесь, потому что это разница в 1,74327 долл. США по сравнению с 1,74331 долл. США, если учесть проценты основного долга в первые месяцы за оставшиеся месяцы. Это отличается от $ 1,85 в ячейке C2 выше, потому что вы еще не были зачислены в течение первых 10 дней в августе. Во многих случаях мелкие различия в рецептуре будут иметь значение только для больших чисел, и даже тогда … Если бы у вас было в принципе 10 000 000 долларов, разница в рецептуре изменилась бы с 0,00004 до 4 долларов. Для большинства целей первая формула более чем достаточна (и, вероятно, та, которую я на самом деле использовал бы во всех случаях, потому что практическая разница в сложении дневных и месячных просто незначительна).

Иллюстрированный самоучитель по Microsoft Excel 2002 › От таблицы умножения к элементарным расчетам денежных потоков › Модуль расчета сложного процента на сумму вклада [страница — 62] | Самоучители по офисным пакетам

Модуль расчета сложного процента на сумму вклада

Зачем нам нужна такая большая таблица для расчета суммы начисленного процента? Ведь если деньги будут положены в банк на год, то для отображения результатов нам потребуется 365 строк. (B2 - B1)

Здесь производится умножение первоначальной суммы депозита (ячейка В3) на индекс депозита (единица плюс значение в ячейке В4), возведенный в степень, равную количеству дней размещения (значение в ячейке В2 минус значение в ячейке В1).

Рис. 3.32. Модуль для расчета сложного процента на сумму вклада при периоде капитализации 1 день (с формулами)

Рис. 3.33. Модуль для расчета сложного процента на сумму вклада при периоде капитализации 1 день (с числовыми данными)

Резюме

На практике часто приходится сталкиваться с задачами, для решения которых требуется выполнить однотипные расчеты для разных наборов входных данных. Простейший пример – составление таблицы умножения. При решении таких задач оперируют наборами однородных входных данных и одинаковыми математическими формулами. Для быстрого выполнения подобных расчетов средствами Excel необходимо уметь создавать наборы данных и формулы с абсолютными и смешанными ссылками. Другими словами, сначала вы должны быстро определить, при помощи какой формулы или прогрессии создать набор входных данных, и составить формулу для расчета, а затем назначить ссылки в формуле таким образом, чтобы ее можно было разместить в области вычислений путем копирования.

Таблицы для расчета станут более гибкими, если все их управляющие параметры будут размещены в специальной области ввода. Создавая ее, мы научились перемещать таблицы и объединять ячейки.

На базе таблицы умножения мы создали таблицы, которые позволяют определить проценты по вкладу, реальную стоимость денег, рассчитать сложный процент.

В этой главе вы познакомились и с модулями. В более сложных расчетных схемах модули могут применяться в виде отдельных элементов. Благодаря своей простоте и наглядности они очень удобны в использовании.

Сложный процент

Как работает «сложный процент»?

Сила сложения

Что такое «сложение»? Говоря попросту, это процент, на который зарабатывается новый процент. Почему он столь значителен? Потому что при проценте, заработанном на основном капитале, основной капитал увеличивается, увеличивая следующий процент, что приводит к росту вашего счета скорее в геометрической прогрессии, чем в арифметической. Чем выше ставка процента, тем круче кривая прироста всего капитала.

Приведем простой пример. Два инвестора инвестируют $1,000 долларов в год каждый в фонд доверия оставляя дивиденды под сложенный интерес. У инвестора А фонд обеспечивает 4% годового возврата, у инвестора В — 8%. Процент интереса роста у инвестора В всего в два раза больше, но что произошло через 10 лет и 20 лет.

		10 лет	20 лет
	Инвестор А —	20. 1%	48.9%
	Инвестор B —	44,9%	128.8%

Таким образом, сложный процент плюс время начинают работать на Вас с предельной активностью даже при «скромной» процентой ставке и порой при немного падающей рыночной стоимости самой ценной бумаги.

Три способа заставить работать на Вас сложный процент

► Реивестируйте дивиденды. Вместо того, чтобы забирать доходы из фонда, проинструктируйте фонд, чтобы на полученные дивиденды были приобретены дополнительные доли фонда. Большинство фондов взаимного доверия допускают это без дополнительной оплаты за покупку.
► Инвестируйте регулярно. Придерживайтесь и не нарушайте правила вносить дополнительные инвестиции на Ваш счет с определенной периодичностью (год, полгода, квартал). Инвестируя систематически, вы используете преимущество стратегии называемой усреднение стоимости доллара. Но помните, регулярное инвестирование не защищает Вас дополнительно от рыночных потерь.
► Заставьте время работать на Вас.Чем дольше Ваши деньги работают на Вас, тем лучше эффект сложения. Просмотрите следующую ситуацию: При одноразовом инвестировании всего $1000 под 8% вы зарабатываете $80 за год. Но уже на 10 год вы будете получать прирост $160, на 25 год — $507, на 40 год — $1607 — и это из $1000.

Как скоро вложенные деньги увеличатся вдвое

Правило 72 подсказывает, сколько нужно времени. При изучении таблиц сложного процента, можно обнаружить, что при умножении количества лет, которые нужны, чтобы $1. 00 дорос до $2.00, на процентную ставку прироста, результат примерно равен 72. Зная этот трюк, получивший название — Правило 72, Вы можете примерно рассчитать количество лет, когда ваши инвестиции удвоятся. Или ставку процента, под которую Вы хотите инвестировать средства на определенное время. Чтобы определить количество лет, просто разделите 72 на ставку. А чтобы найти ставку, разделите 72 на количество лет. Однако следует помнить, что все инвестиции, а фонды взаимного доверия в особенности, не прирастают при постоянной ставке интереса. Поэтому это правило можно применять только при долгосрочных вложениях и только для примерной оценки ситуации.

Узнайте разницу между простым и сложным процентом в Excel

Процентная ставка, используемая в самых различных финансовых приложениях, — это сумма, необходимая для получения данного кредита. Его можно рассчитать двумя способами: простой процент и сложный процент. Его база расчета определяется месячными, квартальными, полугодовыми или годовыми ставками в большинстве переговоров, и в статье мы увидим некоторые применения обоих.

Вы знаете разницу между ними? У вас есть идея правильной формулы, которая будет использоваться в Excel? Посмотрите ниже разницу между простым и сложным процентом в Excel

Разница между простым и сложным процентом в Excel

Простыми процентами сумма получается из первоначальной стоимости (заемного капитала) в определенный период времени, и нет никакого накопления процентов. Таким образом, независимо от того, насколько ваши деньги ценят с течением времени, сумма всегда рассчитывается по первоначальной стоимости или добавляется. Хотя более практичные, простые процентные ставки не используются в реальной жизни. Например, если вы подаете заявку на кредит или вкладываете свои деньги, расчеты всегда выполняются с учетом сложных процентов.

В отношении сложных процентов сумма получается из накопления процентов по первоначальной стоимости (заемному капиталу) в определенный период времени. Например, если я делаю инвестиции R $ 100, для 3 лет, со сложным процентом 10% в год, каков будет мой окончательный доход?

• Год 1 = R $ 100 x 1,1 = R $ 110
• Год 2 = R $ 110 x 1,1 = R $ 121
• Год 3 = R $ 121 x 1,1 = R $ 133,1

Доходность 33,1 реала. Если бы мы проводили эти расчеты с использованием только простых процентов, доход составил бы 30 реалов. Это может показаться небольшим, но это процент, который может быть очень положительным или отрицательным в случае более длительных периодов, больших сумм или более высоких процентных ставок. Вот почему мы говорим, что и для простых процентов, и для сложных процентов требуются три фактора: заемный (или инвестированный) капитал, срок платежа и процентная ставка, подлежащая начислению.

Простой интерес к Excel

Математическая формула для вычисления простого интереса:

J = cin

c = заемный капитал (начальная стоимость)

i = процентная ставка (ежемесячно, ежеквартально, полугодовая, годовая, среди прочих, должна учитываться для правильного расчета)

n = крайний срок для оплаты (также учитывайте период времени для проведения правильного расчета)

Давайте посмотрим на пример расчета простого процента в Excel:

В приведенной выше таблице есть ячейки 3, где пользователь вводит значения и ячейки 4, которые выполняют вычисления на основе введенных данных. Все это как способ иллюстрировать для вас расчет простых интересов.

В ячейке A4 будет заполнена суммой заемных средств, то есть начальным капиталом. Уже ячейка B4 представляет собой процентную ставку, установленную в 2% ежемесячно в этом примере. Наконец, член ячейки C4 относится к месячному периоду оплаты, в случае 10 месяцев.

Формула, вставленная в ячейку D4 é = A4 * B4 и представляет собой сумму ежемесячных уплаченных процентов.

Кроме того, клеточная формула E4 é = A4 / C4 + D4 и относится к выплаченной ежемесячной сумме.

Формула = A4 * B4 * C4 постоянный в объединенных ячейках B6, C6, D6 и E6 представляет собой общий процент, уплаченный по кредиту.

И формула =A4 + B6 объединенных ячеек B7, C7, D7 и E7 общая сумма, уплаченная за кредит.

Составной интерес в Excel

Математическая формула для расчета сложных процентов:

М = с * (1 + я)^t

M = сумма

c = заемный капитал (начальная стоимость)

i = процентная ставка (ежемесячный, квартальный, полугодовой, годовой период, среди прочего, необходимо учитывать для выполнения правильного расчета)

t = крайний срок платежа (также следует учитывать период времени для правильного расчета)

Давайте посмотрим на пример в Excel:

Мы используем те же данные из простой таблицы интересов: R $ 20. A13

Интерес

• C4 CELL    = B4- $ B $ 1
• C5 CELL   = B5- $ B $ 1
• C6 CELL   = B6- $ B $ 1
• C7 CELL    = B7- $ B $ 1
• C8 CELL    = B8- $ B $ 1
• C9 CELL    = B9- $ B $ 1
• C10 CELL  = B10- $ B $ 1
• C11 CELL  = B11- $ B $ 1
• C12 CELL  = B12- $ B $ 1
• C13 CELL  = B13- $ B $ 1

Таким образом, анализируя клетки B13 e C13 которые представляют соответственно общую накопленную сумму и сумму уплаченных процентов, мы можем отметить резкую разницу значений по отношению к простым процентам, имея в качестве параметра тот же капитал, вложенный, такую ​​же процентную ставку и тот же период времени.

Несколько более простой способ — использовать функцию PGTO в самом Excel, что позволяет использовать этот тип вычислений.

Разница между простым и сложным интересом в Excel и реальной жизни

Я считаю, что самое главное знать о сложном и простом интересе к Excel заключается в том, что это не так сложно делать, если вы понимаете логику накопления сложных процентов. Уже в реальной жизни эта логика еще важнее, потому что именно она может поглотить вас долгами или хорошим доходом.

Если вы хотите узнать больше о Excel, проверьте наши курсы для начинающих и промежуточных или продвинутых курсов на нашей платформе, Воспользуйтесь также, чтобы убрать свои сомнения в наших форум об Excel или здесь, в комментариях!

Таблицы сложных процентов

Таблицы сложных процентов

Engineering ToolBox — ресурсы, инструменты и базовая информация для проектирования и разработки технических приложений!

– поиск — самый эффективный способ навигации по Engineering ToolBox!

Таблицы сложных процентов — процентные ставки от 0,25 до 60%

Единовременный платеж

• Коэффициент совокупной суммы
• Фактор текущей стоимости

Серия арифметических градиентов

• Серия с равномерным градиентом
• Серийная стоимость градиента

Серия унифицированных выплат

• Коэффициент возврата капитала
• Коэффициент сложного дохода
• Фактор текущей стоимости

Связанные темы

Связанные документы

Поиск по тегам

• ru: таблицы сложных процентов

Перевести эту страницу на

О Engineering ToolBox!

Мы не собираем информацию от наших пользователей. В нашем архиве хранятся только письма и ответы. Файлы cookie используются в браузере только для улучшения взаимодействия с пользователем.

Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложений на локальном компьютере. Эти приложения — из-за ограничений браузера — будут отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.

Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочтите Условия использования Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.

AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочтите AddThis Privacy для получения дополнительной информации.

Цитирование

Эту страницу можно цитировать как

• Engineering ToolBox, (2010). Таблицы сложных процентов . [онлайн] Доступно по адресу: https://www. engineeringtoolbox.com/compound-interest-tables-d_1649.html [день доступа в месяц, год].

Изменить дату доступа.

. .

закрыть

Научный онлайн-калькулятор

5 7

.

Формулы сложных процентов II | EME 460: Оценка георесурсов и инвестиционный анализ

3. Коэффициент совокупной суммы для унифицированной серии

Третья категория проблем в Таблице 1-5 демонстрирует ситуацию, когда равные суммы денег, A , инвестируются в каждый период времени для n периодов времени с процентной ставкой i (приведенная информация A , n, и i ) и будущую стоимость (стоимость) этих сумм необходимо рассчитать.Этот набор проблем можно обозначить как F / Ai, n. На следующем графике показана сумма. Подумайте об этом как о следующем примере: вы можете вкладывать долларов каждый год (в конце года, начиная с первого года) на воображаемый банковский счет, который дает вам — процентов, и вы можете повторить это для n года (внесение австралийских долларов в конце года).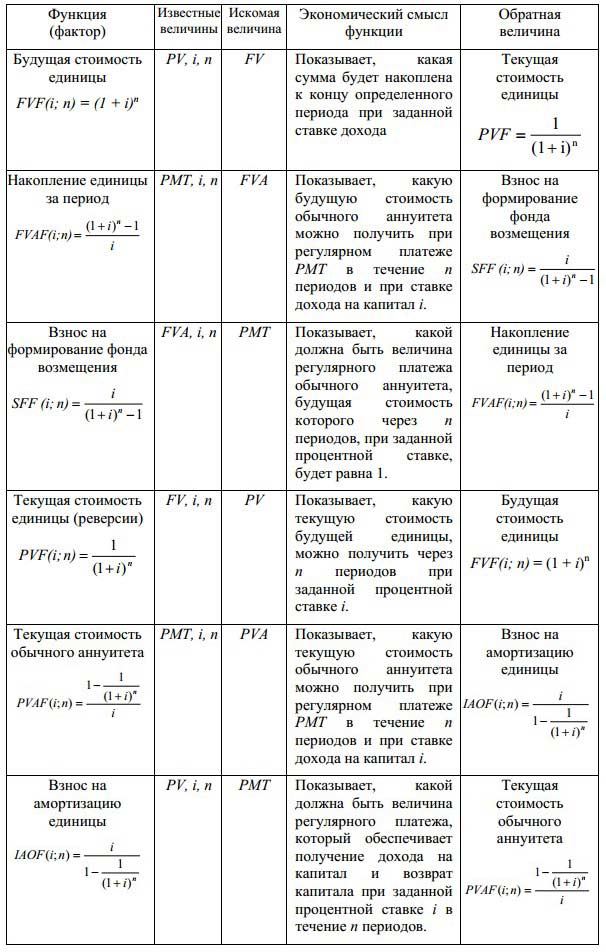 Вы хотите знать, сколько у вас будет в конце года n ^th .

0		A	A		A	A	F =?
	0	1	2	…	н-1	n

Рис. 1-4: Uniform Series коэффициент количества соединения, F / Ai, n

В этом случае использование уравнения 1-2 может помочь нам рассчитать будущую стоимость каждой отдельной инвестиции, а затем совокупную будущую стоимость этих равных инвестиций.

Будущая стоимость первой инвестиции, произошедшей в период времени 1, равна A (1 + i) n − 1
Обратите внимание, что первая инвестиция произошла в период времени 1 (один период после настоящего времени), поэтому это n-1 период до n ^-го , а затем мощность н-1.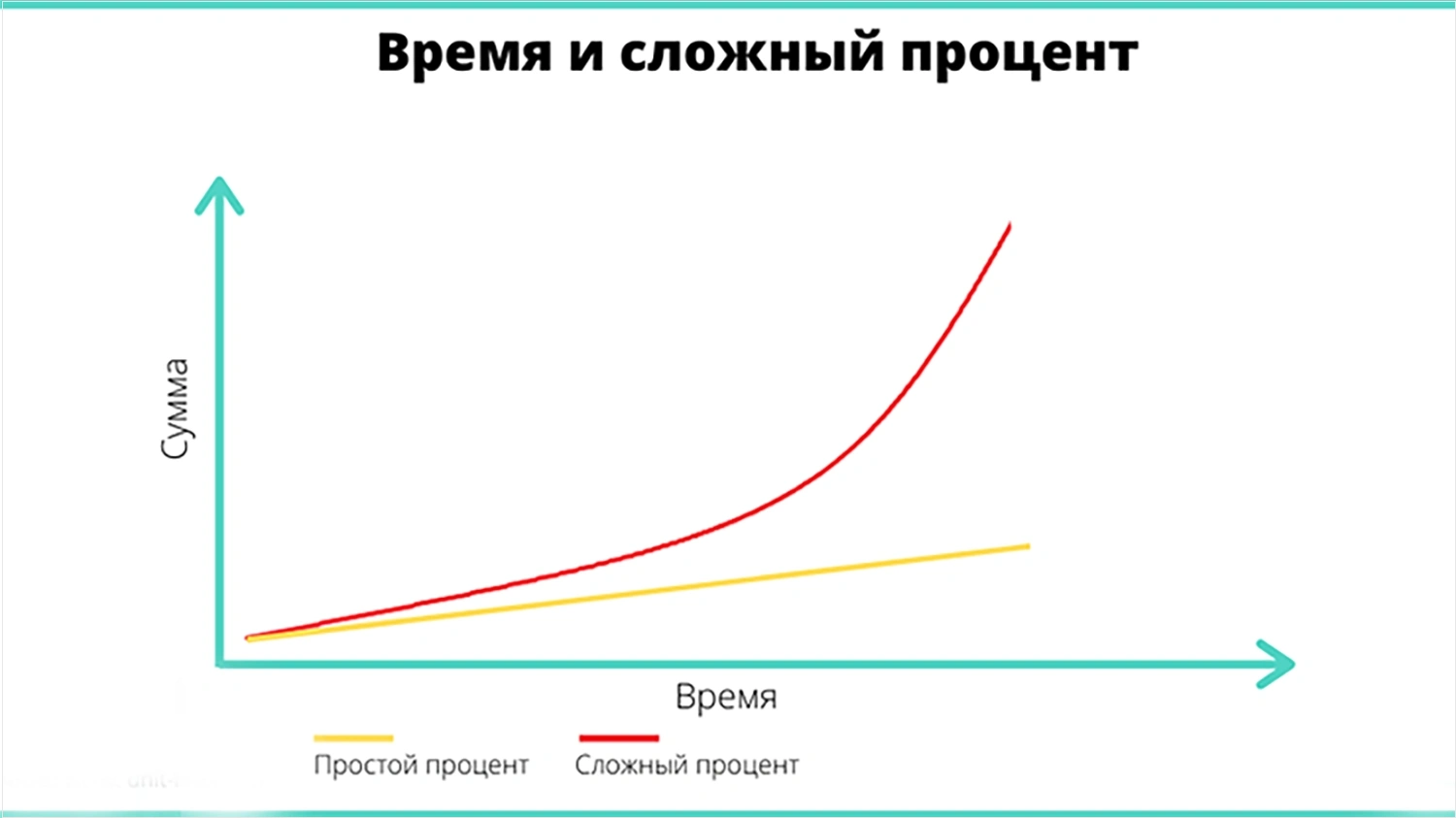

И аналогично:
Будущая стоимость второй инвестиции произошла в период времени 2: A (1 + i) n − 2
Будущая стоимость третьей инвестиции произошла в период времени 3: A (1 + i) n − 3
Будущая стоимость последняя инвестиция произошла в период времени n: A (1 + i) n − n = A
Обратите внимание, что последний платеж происходит одновременно с F .

Итак, сумма всех будущих значений равна
F = A (1 + i) n − 1 + A (1 + i) n − 2 + A (1 + i) n − 3 +… + A

Умножив обе части на (1 + i), , мы получим
F (1 + i) = A (1 + i) n + A (1 + i) n − 1 + A (1 + i) n− 2 +… + A (1 + i)

Вычитая первое уравнение из второго, мы получим
F (1 + i) –F = A (1 + i) n + A (1 + i) n − 1 + A (1 + i) n − 2 +… + A (1 + i) — [A (1 + i) n − 1 + A (1 + i) n − 2 + A (1 + i) n − 3 +… + A] F + Fi – F = A (1 + i) n + A (1 + i) n − 1 + A (1 + i) n − 2 +… + A (1 + i) — A (1 + i) n − 1− A (1+ i) n − 2− A (1 + i) n − 3−… −A

, который становится:
Fi = A (1 + i) n – A

, затем

F = A [(1 + i) n − 1] / i

Уравнение 1-3

Следовательно, уравнение 1-3 может определять будущую стоимость однородного ряда равных инвестиций как F = A [(1 + i) n − 1] / i. Что также может быть записано относительно обозначений Таблицы 1-5 как: F = A * F / Ai, n. Тогда F / Ai, n = [(1 + i) n − 1] / i.
Фактор [(1 + i) n − 1] / i называется «равномерным последовательным коэффициентом суммы сложного соединения» и обозначается F / A _{i, n} . Этот коэффициент используется для расчета будущей единой суммы «F», которая эквивалентна однородному ряду равных платежей в конце периода «A».

Обратите внимание, что n — это количество периодов времени, в течение которых происходят равные серии платежей.

Пожалуйста, просмотрите следующее видео, Коэффициент количества соединения для унифицированной серии (3:42).

Суммарный коэффициент однородной серии

Щелкните, чтобы увидеть стенограмму видеоролика «Коэффициент сложного соединения Uniform Series».

ВЕДУЩИЙ: В третьей категории перечислены равные суммы денег, которые A должны получать в каждый период времени в течение n периодов времени. n может быть годами или месяцами, а процентная ставка — i. И вопрос просит вас рассчитать будущую стоимость этих платежей, единую денежную сумму, которая эквивалентна всем этим сериям платежей A.Здесь заданная информация — это A, n и i. А F — неизвестный параметр. Эти наборы проблем могут отображаться с косой чертой F фактора A или F / A. Опять же, левая часть этого знака косой черты — это неизвестный параметр F, а правая часть — заданная переменная, которая равна A.

Здесь вы можете увидеть уравнение для вычисления F из A, i и n. Математическое доказательство этого уравнения простое, и они объясняют его в первом уроке. Мы можем написать это уравнение относительно обозначения множителя: F равно A умножить множитель.Этот коэффициент называется коэффициентом составного количества однородной серии. И он используется для расчета будущей единой суммы F, которая эквивалентна однородному ряду равных выплат в конце периода A.

Давайте поработаем на примере, чтобы увидеть, как можно использовать этот коэффициент. Предположим, вы экономите 4000 долларов в год и вкладываете их в конце года на воображаемый сберегательный счет или в какое-либо другое вложение, которое дает вам 6% годовых, усугубляемых ежегодно, в течение 20 лет, начиная с 1 года по 20 год. .И вы хотите знать, сколько денег у вас будет в конце 20-го года.

Сначала мы рисуем временную шкалу. Левая часть — настоящее время. У нас там ничего нет. Обратите внимание, что ваши инвестиции начинаются с 1 по 20 год. Если в вопросе нет дополнительной информации, а в вопросе говорится, что вы инвестируете в течение 20 лет, вы должны принять свои инвестиции, они начинаются с первого года. Таким образом, в настоящее время или нулевой год выплаты отсутствуют.

Правая часть — будущее время, которое представляет собой будущую стоимость одной суммы, и оно неизвестно.Ваши инвестиции занимают 20 лет, поэтому n равно 20. И выше каждый год вы должны писать 4000 долларов, потому что у вас есть платеж в размере 4000 долларов в конце каждого года. Итак, A равно 4000 долларов, n количество лет равно 20, i процентная ставка 6%, и F необходимо рассчитать.

И F равно A, умноженному на коэффициент F / A. В этом множителе i составляет 6% и 20. И мы используем уравнение для вычисления F. И мы находим ответ. Итак, если вы инвестируете 4000 долларов в год на 20 лет под 6% процентной ставки, у вас будет около 147000 долларов в конце 20-го года.

Кредит: Фарид Тайари

Пример 1-3:

Предположим, вы экономите 4000 долларов в год и вкладываете их в конце года на воображаемый сберегательный счет (или какое-либо другое вложение), который дает вам 6% -ную процентную ставку (ежегодно усугубляемую) на 20 лет. Сколько у вас будет денег в конце 20-го года?

0		$ 4000	$ 4000		$ 4000	$ 4000	F =?
	0	1	2	. ..	19	20

Итак,
A = 4000 долларов США
n = 20
i = 6%
F =?

Обратите внимание, что n — это количество равных платежей.

Используя уравнение 1-3, мы получим
F = A * F / Ai, n = A [(1 + i) n − 1] / iF = A * F / A6%, 20 = 4000 * [(1+ 0,06) 20−1] /0.06F=4000*36.78559 = 147142,4

Итак, на 20-й год у вас будет 147 142,4 доллара.

Таблица 1-8 : Коэффициент количества соединения для унифицированной серии

Фактор	Имя	Формула	Запрошенная переменная	Заданные переменные
F / A i, n	Коэффициент количества соединения для унифицированной серии	[(1 + i) n − 1] / i	F: Будущая стоимость однородных серий равных инвестиций	A: равномерный ряд равных инвестиций n: количество периодов времени i: процентная ставка

4.

Депозитный коэффициент погашения

Четвертая группа в Таблице 1-5 аналогична третьей группе, но вместо A как дано и F в качестве неизвестных параметров задается F и необходимо вычислить A . Эта группа иллюстрирует набор задач, которые просят вас рассчитать единый ряд равных платежей (или инвестиций), A , который будет инвестирован на n периодов времени с процентной ставкой i и накопленной будущей стоимостью всех выплаты равны F .Такие проблемы можно обозначить как A / Fi, n и отобразить на следующем графике. Подумайте об этом как о следующем примере: вы планируете иметь франков долларов в течение n лет, и есть сберегательный счет, который может дать вам i процентов. Вы хотите знать, сколько вы должны вкладывать каждый год (в конце года, начиная с года 1), чтобы иметь возможность иметь F долларов через n лет.

0		А =?	А =?		А =?	А =?	F
	0	1	2	. ..	н-1	n

Рисунок 1-5: Коэффициент депозита фонда погашения, A / Fi, n

Уравнение 1-3 можно переписать для A (как неизвестное), чтобы решить эти проблемы:

A = F {i / [(1 + i) n − 1]}

Уравнение 1-4

Уравнение 1-4 может определять однородный ряд равных инвестиций, A , учитывая накопленную будущую стоимость, F , номер инвестиционного периода, n , и процентную ставку i .Таблица 1-5 отмечает эти проблемы как: A = F * A / Fi, n. Тогда A / Fi, n = i / [(1 + i) n − 1]. T Фактор i / [(1 + i) n − 1] называется «фактором депозита фонда погашения» и обозначается A / Fi, n. Коэффициент используется для расчета однородного ряда равных платежей в конце периода A, которые эквивалентны будущей сумме F.

Обратите внимание, что n — это количество периодов времени, в течение которых происходят равные серии платежей.

Посмотрите следующее видео: Фактор депозита фонда погашения (4:42).

Фактор депозита фонда погашения

Щелкните, чтобы увидеть стенограмму видео «Фактор депозита погашаемых средств».

ВЕДУЩИЙ: Четвертая группа похожа на третью. Но A — неизвестное, а F — заданная переменная. Этот набор задач предлагает вам рассчитать однородную серию равных платежей A, которые будут инвестированы в течение n периодов времени с процентной ставкой i. А накопленная будущая стоимость всех платежей или эквивалентная будущая стоимость равна F.

Этот набор проблем можно суммировать с множителем A над F или наклонной чертой F. Левая часть этого последнего знака — неизвестный параметр. Здесь это A. А правая часть — заданная переменная, то есть F.

Уравнение 1-3 для количественного коэффициента соединения однородной серии может быть переписано для A как неизвестное, чтобы решить эти проблемы, что дает уравнение 1-4. Уравнение 1-4 может определять однородный ряд равных инвестиций, A, для накопленной будущей стоимости, F, номера инвестиционного периода n и процентной ставки i.

Мы можем записать это уравнение в соответствии с обозначением факторов: A равно F, умноженному на множитель A над F. Этот коэффициент называется фактором депозита фонда погашения. И это отображается с помощью косой черты F. Коэффициент используется для расчета однородного ряда равных платежей в конце периода, A, которые эквивалентны будущей сумме F.

Например, ссылаясь на пример 1-7 в предыдущем видео, предположим, что вы планируете получить 200 000 долларов через 20 лет. И вам предлагают инвестицию, которая может быть воображаемым сберегательным счетом, которая дает вам 6% годовых по сложным процентным ставкам.И вы хотите знать, сколько денег равных выплат вам нужно откладывать каждый год или инвестировать — вносить депозит на свой счет в конце каждого года.

Итак, вы хотите иметь 200 000 долларов через 20 лет.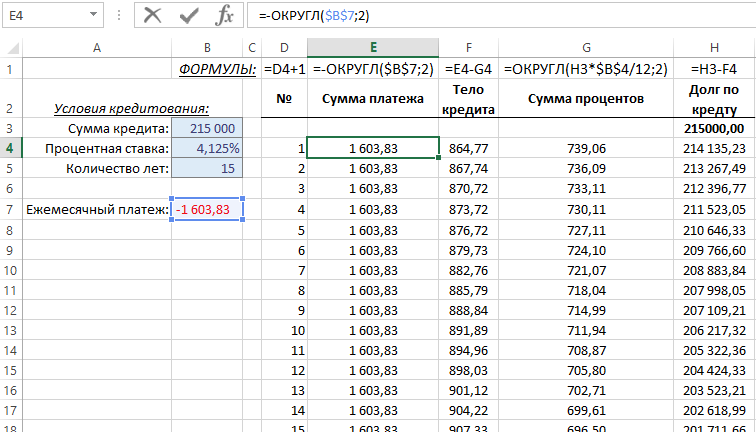 И вы можете вложить свои деньги под 6% годовых. Вопрос в том, сколько нужно вкладывать в год?

Опять же, первый шаг — это рисование временной шкалы. Левая часть — настоящее время. У нас не будет оплаты. Таким образом, в настоящее время или в нулевое время выплаты отсутствуют.Правая сторона — будущее. И вы хотите иметь единую сумму в 200000 долларов. Итак, вы пишете 200 000 долларов в 20-м году или в конце правой части временной шкалы.

Обратите внимание, что 200 000 долларов имеют то же временное измерение, что и последний платеж, A. Оба относятся к 20-му году. Ваши инвестиции занимают 20 лет, поэтому n равно 20. И выше каждый год вы должны писать A, который неизвестен и должен быть рассчитан.

So F равняется 200000 долларов. n количество лет — 20. i, процентная ставка — 6%.И необходимо вычислить A.

Мы можем использовать обозначение множителей, чтобы резюмировать уравнение. В этом множителе i равно 6%, n равно 20, дано F, и необходимо вычислить A. И рассчитываем результат. Итак, если вы хотите иметь 200 000 долларов через 20 лет с 6% процентной ставкой, вам нужно будет инвестировать равные суммы в 5 437 долларов в год в конце каждого года в течение 20 лет, начиная с первого года.

Кредит: Фарид Тайари

, пример 1-4:

Обращаясь к примеру 1-3, предположим, что вы планируете иметь 200 000 долларов через 20 лет, и вам предлагается инвестиция (воображаемый сберегательный счет), которая дает вам 6% годовых по сложной процентной ставке.Сколько денег (равных выплат) вам нужно откладывать каждый год и вкладывать (вносить на свой счет) в конце каждого года?

0		А =?	А =?		А =?	А =?	F = 200 000
	0	1	2	…	19	20

Итак,
F = 200 000 долларов США
n = 20
i = 6%
A =?

Используя уравнение 1-4, мы получим
A = F * A / Fi, n = F {i / [(1 + i) n − 1]} A = F * A / F6%, 20 = 200 000 * 0 . 06 / [(1 + 0,06) 20−1] A = 200 000 * 0,027185 = 5436,912

Итак, чтобы иметь 200 000 долларов на 20-й год, вы должны инвестировать 5 436,9 долларов в конце каждого года в течение 20 лет с годовой сложной процентной ставкой 6%.

Таблица 1-9 : Фактор депозита обратного фонда

Фактор	Имя	Формула	Запрошенная переменная	Данные переменные
A / Fi, n	Фактор депозита обратного фонда	i / [(1 + i) n − 1]	A: Единая серия равных платежей в конце периода	F: накопленная будущая стоимость инвестиций n: количество периодов времени i: процентная ставка

Обратите внимание, что i / [(1 + i) n − 1]

Калькулятор сложных процентов [с формулой]

Этот калькулятор сложных процентов — инструмент, который поможет вам оценить, сколько денег вы заработаете на своем депозите. Чтобы принимать разумные финансовые решения, нужно уметь предвидеть конечный результат. Вот почему стоит знать, как рассчитывать сложные проценты. Наиболее распространенное применение формулы сложных процентов в реальной жизни — это регулярный расчет сбережений.

Прочтите, чтобы найти ответы на следующие вопросы:

• Что такое определение процентной ставки?
• Что такое определение сложных процентов и какова формула сложных процентов?
• В чем разница между простой и сложной процентной ставкой?
• Как рассчитать сложные проценты?
• Каковы наиболее распространенные частоты начисления процентов?

Вы также можете воспользоваться нашим калькулятором студенческой ссуды, где вы можете сделать прогноз своих расходов и изучить влияние различных вариантов студенческой ссуды на ваш бюджет.

Определение процентной ставки

В финансах процентная ставка определяется как сумма , взимаемая кредитором с заемщика за использование актива . Итак, для заемщика процентная ставка — это стоимость долга, а для кредитора — это норма прибыли.

Обратите внимание, что в случае, когда вы делаете вклад в банк (например, кладете деньги на свой сберегательный счет), с финансовой точки зрения вы ссужаете деньги банку. В таком случае процентная ставка отражает вашу прибыль.

Процентная ставка обычно выражается в процентах от основной суммы (непогашенной ссуды или суммы депозита). Обычно он представляется на годовой основе, которая известна как годовая процентная доходность (APY) или эффективная годовая ставка (EAR).

Что такое определение сложных процентов?

Как правило, сложные проценты определяются как проценты , которые начисляются не только на первоначальную вложенную сумму, но и на любые последующие проценты . Другими словами, сложные проценты — это проценты как на первоначальную основную сумму , так и на проценты, накопленные по этому принципу до сих пор.Эта концепция добавления балансовой стоимости заставляет депозит или ссуду расти более быстрыми темпами.

Вы можете использовать уравнение сложных процентов, чтобы найти стоимость инвестиции через определенный период времени или оценить ставку, которую вы заработали при покупке и продаже некоторых инвестиций. Это также позволяет вам ответить на некоторые другие вопросы, например, сколько времени потребуется, чтобы удвоить ваши инвестиции.

Мы ответим на эти вопросы в приведенных ниже примерах.

Простые и сложные проценты

Вы должны знать, что простой процент отличается от сложного процента .Он рассчитывается только на начальную сумму денег. С другой стороны, сложные проценты — это проценты на первоначальную основную сумму плюс накопленные проценты.

Частота добавления

Большинство финансовых консультантов скажут вам, что сложная частота — это периоды начисления сложных процентов в году. Но если вы не уверены, что такое начисление сложных процентов, это определение будет для вас бессмысленным… Чтобы понять этот термин, вы должны знать, что частота начисления сложных процентов является ответом на вопрос Как часто процент добавляется к основной сумме процентов каждый год? Другими словами, частота начисления процентов — это период времени, по истечении которого проценты будут начисляться сверх начальной суммы .

Например:

• годовое (1 / год) начисление сложных процентов имеет частоту начисления один ,
• ежеквартально (4 / год) компаундирование имеет частоту начисления четыре ,
• ежемесячно (12 / год) компаундирования имеет частоту начисления двенадцать .

Обратите внимание, что чем выше частота начисления сложных процентов, тем больше окончательный баланс. Однако, даже если частота необычно высока, окончательное значение не может превысить определенный предел.Чтобы понять математику, стоящую за этим, воспользуйтесь нашим калькулятором натурального логарифма.

Поскольку основное внимание в калькуляторе уделяется механизму начисления сложных процентов, мы разработали диаграмму, на которой вы можете визуально следить за ходом годового процентного баланса. Если вы выберете более высокую частоту начисления сложных процентов, чем годовая, на диаграмме отобразится полученная дополнительная или дополнительная часть процента, полученная за годовое начисление с более высокой частотой . Таким образом, вы можете легко увидеть реальную силу сложения.mt

Где:

• FV — будущая стоимость инвестиции, в нашем калькуляторе это окончательный баланс
• П — первоначальное сальдо (стоимость вложения)
• р — годовая процентная ставка (в десятичной системе)
• m — количество начислений процентов в год ( частота начисления процентов )
• т — чисел года вложено денег на

Стоит знать, что когда период начисления сложных процентов равен единице ( м = 1 ), тогда процентная ставка ( r ) называется CAGR (сложный годовой темп роста).

Как рассчитать сложные проценты

На самом деле, вам не нужно запоминать формулу сложных процентов из предыдущего раздела, чтобы оценить будущую стоимость ваших инвестиций. Фактически, вам даже не нужно знать, как рассчитывать сложные проценты! Благодаря нашему калькулятору сложных процентов вы можете сделать это всего за несколько секунд, когда и где захотите. (NB: Вы уже пробовали мобильную версию наших калькуляторов?)

С помощью нашего интеллектуального калькулятора все, что вам нужно для расчета будущей стоимости ваших инвестиций, — это заполнить соответствующие поля:

1. Начальный баланс — сумма денег, которую вы собираетесь вложить или внести.
2. Процентная ставка — процентная ставка, выраженная на годовой основе.
3. Срок — сроки, в которые вы собираетесь вложить деньги.
4. Частота начисления процентов — в этом поле вы должны выбрать, как часто начисление начислений применяется к вашему весу. Обычно проценты добавляются к основному остатку ежедневно, еженедельно, ежемесячно, ежеквартально, раз в полгода или ежегодно. Но вы также можете установить его как непрерывное начисление процентов, что является теоретическим пределом частоты начисления процентов.В этом случае количество периодов, когда происходит начисление процентов, бесконечно.

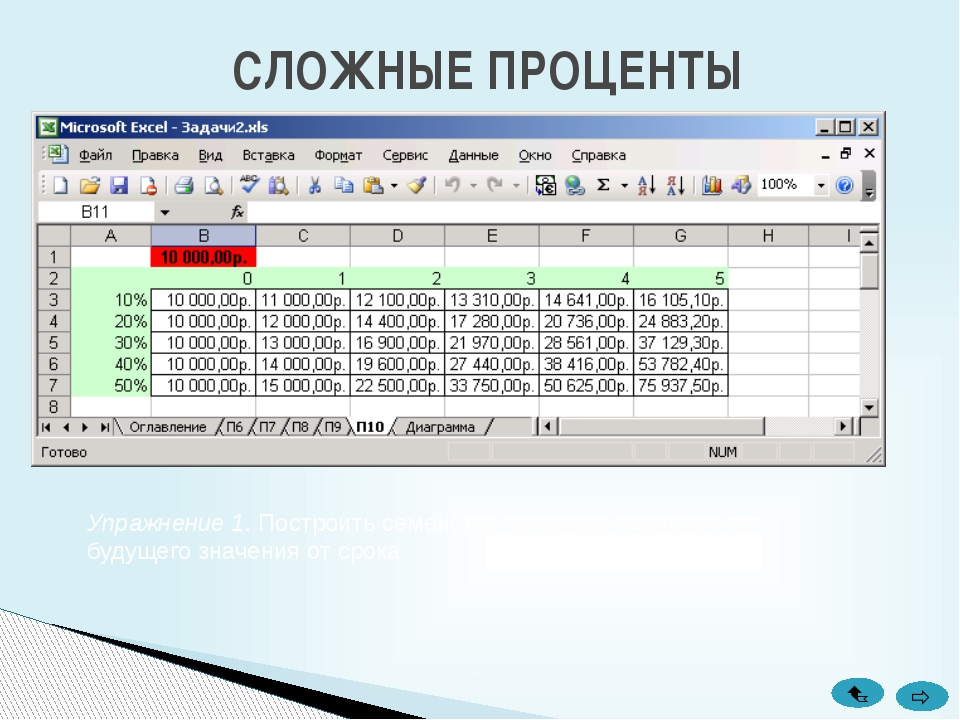
1. Сколько — сумма, которую вы планируете положить на счет.
2. Как часто — здесь вы можете выбрать периодичность пополнения.
3. При — следует выбрать сроки транзакции дополнительного депозита. В частности, вы можете поместить деньги на счет в начале или в конце периодов.
4. Скорость роста депозита — опция позволяет установить скорость роста дополнительного депозита. Этот вариант может быть особенно полезен в долгосрочной перспективе, когда ваш доход может возрасти, например, из-за инфляции и / или рекламных акций.

Вот и все! Наш калькулятор сложных процентов мгновенно выполнит все необходимые вычисления и предоставит вам результаты.

Два основных результата:

• окончательный баланс , то есть общая сумма денег, которую вы получите после указанного периода, и
• — общая сумма процентов , — общая сумма начисленных процентов.

В случае, если вы задали поле дополнительного депозита, мы предоставили вам результаты для составленного начального баланса и сложного дополнительного баланса .

Кроме того, мы также показываем вам их вклад в общую сумму процентов, а именно процентов на начальный остаток и процентов на дополнительный депозит .

Примеры сложных процентов

• Хотите понять уравнение сложных процентов?
• Вам интересно узнать подробности того, как рассчитать сложную процентную ставку?
• Вам интересно, как работает наш калькулятор?
• Вам нужно знать, как интерпретировать результаты расчета сложных процентов?
• Вас интересуют все возможные варианты использования формулы сложных процентов?

Следующие ниже примеры помогут вам ответить на эти вопросы.Мы уверены, что после их изучения у вас не возникнет проблем с пониманием и практической реализацией сложных процентов.

Пример 1 — базовый расчет стоимости инвестиции

Первый пример — самый простой, в котором мы вычисляем будущую стоимость первоначальных инвестиций.

Вопрос

Вы инвестируете 10 000 долларов США на 10 лет под 5% годовых. Процентная ставка начисляется ежегодно. Какова будет стоимость ваших инвестиций через 10 лет?

Решение

Во-первых, давайте определим, какие значения даны и что нам нужно найти.Мы знаем, что вы собираетесь инвестировать 10 000 долларов — это ваш начальный баланс P , а количество лет, в течение которых вы собираетесь инвестировать деньги, составляет 10 . Кроме того, процентная ставка r равна 5% , а проценты начисляются ежегодно, поэтому m в формуле сложных процентов равно 1 .

Мы хотим рассчитать сумму денег, которую вы получите от этой инвестиции, то есть мы хотим найти будущую стоимость FV ваших инвестиций.(10 * 1) = 10 000 * 1,628895 = 16 288,95

Ответ

Стоимость ваших инвестиций через 10 лет составит 16 288,95 долларов США.

Ваша прибыль составит FV - P . Это 16 288,95 долларов - 10 000,00 долларов = 6 288,95 долларов США .

Обратите внимание, что при выполнении расчетов вы должны быть очень осторожны с округлением. Не стоит делать слишком много до самого конца. В противном случае ваш ответ может быть неверным. Точность зависит от вычисляемых значений.Для стандартных расчетов должно быть достаточно шести цифр после десятичной точки.

Пример 2 — комплексный расчет стоимости инвестиции

Во втором примере мы вычисляем будущую стоимость первоначальной инвестиции, по которой ежемесячно начисляются проценты.

Вопрос

Вы инвестируете 10 000 долларов США под 5% годовых. Процентная ставка начисляется ежемесячно. Какова будет стоимость ваших инвестиций через 10 лет?

Решение

Как и в первом примере, мы должны сначала определить значения.120 = 10 000 * 1,647009 = 16 470,09

Ответ

Стоимость ваших инвестиций через 10 лет составит 16 470,09 долларов США.

Ваша прибыль составит FV - P . Это 16 470,09 долларов - 10 000,00 долларов = 6 470,09 долларов .

Вы заметили, что этот пример очень похож на первый? Собственно, разница только в частоте начисления сложных процентов. Обратите внимание, что только благодаря более частому начислению сложных процентов на этот раз вы заработаете на 181,14 доллара больше за тот же период! ( 6470 долларов.09 - 6 288,95 долларов США = 181,14 доллара США )

Пример 3 — Расчет процентной ставки инвестиции с использованием формулы сложных процентов

Теперь давайте попробуем вопрос другого типа, на который можно ответить, используя формулу сложных процентов. На этот раз потребуются некоторые базовые преобразования алгебры. В этом примере мы рассмотрим ситуацию, в которой мы знаем начальный баланс, окончательный баланс, количество лет и частоту начисления сложных процентов, но нас просят рассчитать процентную ставку.Этот тип расчета может применяться в ситуации, когда вы хотите определить ставку, полученную при покупке и продаже актива (например, собственности), который вы используете в качестве инвестиции.

Данные и вопрос Вы купили оригинальную картину за 2000 долларов. Шесть лет спустя вы продали эту картину за 3000 долларов. Если предположить, что картина рассматривается как инвестиция, какой годовой доход вы получали?

Решение Во-первых, давайте определимся с данными значениями.0,166667 — 1 = 1,069913 — 1 = 0,069913 = 6,9913%

Ответ

В этом примере вы заработали 1000 долларов из первоначальных инвестиций в размере 2000 долларов в течение шести лет, что означает, что ваша годовая ставка была равна 6,9913%.

Как видите, на этот раз формула не очень проста и требует большого количества вычислений. Вот почему стоит протестировать наш калькулятор сложных процентов, который мгновенно решает те же уравнения, экономя ваше время и усилия.

Пример 4 — Расчет времени удвоения инвестиции с использованием формулы сложных процентов

Вы когда-нибудь задумывались, сколько лет потребуется, чтобы ваши инвестиции удвоили их стоимость? Помимо других возможностей, наш калькулятор может помочь вам ответить на этот вопрос.Чтобы понять, как это происходит, давайте взглянем на следующий пример.

Данные и вопрос

Вы положили 1000 долларов на свой сберегательный счет. Предполагается, что процентная ставка равна 4% и начисляется ежегодно. Найдите количество лет, по истечении которого первоначальный баланс удвоится.

Решение

Приведены следующие значения: начальное сальдо P составляет 1000 долларов , а окончательное сальдо FV составляет 2 * 1000 долларов = 2000 долларов , а процентная ставка r составляет 4%.т

Чтобы найти t, вам нужно взять натуральное логарифм (ln) с обеих сторон:

ln (2) = t * ln (1,04)

Так

t = ln (2) / ln (1,04) = 0,6 / 0,039221 = 17,67

Ответ

В нашем примере требуется 18 лет (18 — ближайшее целое число, которое больше 17,67), чтобы удвоить первоначальные инвестиции.

Вы заметили, что в приведенном выше решении нам даже не нужно было знать начальный и конечный сальдо инвестиций? Это благодаря упрощению, которое мы сделали на третьем этапе ( Разделите обе стороны на P ).Однако при использовании нашего калькулятора сложных процентных ставок вам необходимо будет указать эту информацию в соответствующих полях. Не волнуйтесь, если вы просто хотите узнать время, в течение которого данная процентная ставка удвоит ваши инвестиции, просто введите любые числа (например, 1 и 2 ).

Также стоит знать, что точно такие же вычисления можно использовать для вычисления того, когда инвестиции утроятся (или фактически умножатся на любое число). Все, что вам нужно сделать, это просто использовать другое кратное P на втором шаге приведенного выше примера.Вы также можете сделать это с помощью нашего калькулятора.

Таблица сложных процентов

Таблицы сложных процентов использовались каждый день, до эры калькуляторов, персональных компьютеров, электронных таблиц и невероятных решений, предоставляемых Omni Calculator 😂. Таблицы были разработаны, чтобы упростить и ускорить финансовые расчеты (да, действительно…). Они включены во многие старые учебники по финансам в качестве приложений.

Ниже вы можете увидеть, как выглядит таблица сложных процентов.

Используя данные, представленные в таблице сложных процентов, вы можете рассчитать окончательный баланс ваших инвестиций.t для соответствующей процентной ставки (первая строка) и t (первый столбец). Итак, чтобы рассчитать окончательный баланс инвестиций, вам необходимо умножить начальный баланс на соответствующее значение из таблицы.

Обратите внимание, что значения из столбца Фактор текущей стоимости используются для вычисления текущей стоимости инвестиций, когда вы знаете их будущую стоимость.

Очевидно, это только базовый пример таблицы сложных процентов. Фактически, они обычно намного больше, поскольку содержат больше периодов t , различные процентные ставки r и разные частоты начисления процентов m … Вам пришлось пролистать десятки страниц, чтобы найти подходящее значение сложного коэффициента суммы или коэффициента текущей стоимости.

Вам понравился наш инструмент с новыми знаниями о том, как выглядел мир финансовых расчетов до Omni Calculator? Почему бы не поделиться этим с друзьями? Сообщите им об Omni! Если вы хотите быть финансово грамотным, вы также можете попробовать другие наши финансовые калькуляторы.

Дополнительная информация

Теперь, когда вы знаете, как рассчитывать сложные проценты, самое время найти другие приложения, которые помогут вам получить максимальную прибыль от ваших инвестиций:

Чтобы сравнить предложения банков с разными периодами начисления сложных процентов, нам необходимо рассчитать годовой процентный доход, также называемый эффективной годовой ставкой (EAR).Это значение говорит нам, какую прибыль мы получим в течение года. Самый удобный способ выяснить это — использовать калькулятор APY, который рассчитывает EAR по процентной ставке и частоте начисления сложных процентов.

Если вы хотите узнать, сколько времени потребуется, чтобы что-то увеличилось на n%, вы можете использовать наш калькулятор с правилом 72. Этот инструмент позволяет вам проверить, сколько времени вам нужно, чтобы удвоить ваши инвестиции, даже быстрее, чем калькулятор сложных процентных ставок.

Вас также может заинтересовать калькулятор выплат по кредитной карте, который позволяет оценить, сколько времени потребуется, чтобы полностью освободиться от долгов.

Еще один интересный калькулятор — наш калькулятор капитальной ставки, который определяет норму прибыли от покупки недвижимости.

Мы также предлагаем вам попробовать калькулятор аренды, который поможет вам определить ежемесячные и общие платежи по аренде.

Если вы хотите профинансировать покупку нового жилого автомобиля (RV), наш калькулятор ссуды RV позволяет легко определить, какое предложение будет для вас наиболее выгодным.

Калькулятор амортизации позволяет использовать три различных метода для оценки того, насколько быстро стоимость вашего актива снижается с течением времени.

И, наконец, почему бы не попробовать калькулятор нашей мечты. что отвечает на вопрос: сколько нужно копить, чтобы реализовать свою мечту?

Определение сложных процентов, формула, расчет

Что такое сложный процент?

Сложные проценты (или сложные проценты) — это проценты по ссуде или депозиту, рассчитываемые как на основе первоначальной основной суммы, так и накопленных процентов за предыдущие периоды. Считается, что сложный процент зародился в Италии 17-го века, сложный процент можно рассматривать как «процент на процент», и он заставляет сумму расти быстрее, чем простой процент, который рассчитывается только на основную сумму.

Ставка, по которой начисляются сложные проценты, зависит от частоты начисления сложных процентов, так что чем больше количество периодов начисления сложных процентов, тем больше сложный процент. Таким образом, сумма сложных процентов, начисленных на 100 долларов США с начислением 10% годовых, будет ниже, чем сумма сложных процентов на 100 долларов США с начислением 5% годовых в течение того же периода времени. Поскольку эффект процентной ставки может приносить все более положительную прибыль на основе первоначальной основной суммы, ее иногда называют «чудом сложных процентов».»

Ключевые выводы

• Сложные проценты (или сложные проценты) — это проценты, начисляемые на первоначальную основную сумму, которая также включает все накопленные проценты за предыдущие периоды по депозиту или ссуде.
• Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная до количества составных периодов минус один.
• Проценты могут начисляться по любому заданному графику периодичности, от непрерывного до ежедневного или ежегодного.
• При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение.

Общие сведения о сложных процентах

Расчет сложных процентов

Сложные проценты рассчитываются путем умножения первоначальной основной суммы на единицу плюс годовая процентная ставка, повышенная на количество составных периодов минус один. Затем из полученной стоимости вычитается общая начальная сумма ссуды.

Кэти Керпель {Copyright} Investopedia, 2019.

Формула расчета сложных процентов:

• Сложные проценты = общая сумма основной суммы долга и процентов в будущем (или будущая стоимость) минус текущая сумма основного долга (или приведенная стоимость)

= [P (1 + i ) ⁿ ] — P

= P [(1 + i ) ⁿ — 1]

Где:

P = основной

i = номинальная годовая процентная ставка в процентах

n = количество периодов начисления сложных процентов

Возьмите трехлетний заем в размере 10 000 долларов США под 5% годовых.Какая будет сумма процентов? В этом случае это будет:

10 000 долл. США [(1 + 0,05) ³ — 1] = 10 000 [1,157625 — 1] = 1 576,25 доллара

Рост сложных процентов

Используя приведенный выше пример, поскольку сложные проценты также учитывают накопленные проценты за предыдущие периоды, сумма процентов не будет одинаковой для всех трех лет, как это было бы с простыми процентами. В то время как общая сумма процентов, подлежащих выплате за трехлетний период по этой ссуде, составляет 1576 долларов.25, проценты, подлежащие выплате в конце каждого года, показаны в таблице ниже.

Периоды начисления процентов

При расчете сложных процентов количество периодов начисления сложных процентов имеет большое значение. Основное правило состоит в том, что чем больше количество периодов начисления сложных процентов, тем больше сумма сложных процентов.

Следующая таблица демонстрирует разницу, которую может составить количество периодов начисления сложных процентов для ссуды в размере 10 000 долларов США с годовой процентной ставкой 10% в течение 10-летнего периода.

Сложные проценты могут значительно повысить доходность инвестиций в долгосрочной перспективе. В то время как депозит в размере 100 000 долларов, который получает 5% простых годовых процентов, принесет 50 000 долларов в виде общих процентов за 10 лет, годовые сложные проценты в размере 5% на 10 000 долларов составят 62 889,46 долларов за тот же период. Если бы период начисления сложных процентов вместо этого выплачивался ежемесячно в течение того же 10-летнего периода под 5% сложных процентов, общая сумма процентов вырастала бы до 64 700,95 долларов.

Расчет компаундирования в Excel

Если с тех пор, как вы учились в математике, прошло некоторое время, не бойтесь: есть удобные инструменты, которые помогут сложить числа.Многие калькуляторы (как карманные, так и компьютерные) имеют функции экспоненты, которые можно использовать для этих целей. Если возникают более сложные сложные задачи, они могут быть выполнены с помощью Microsoft Excel тремя различными способами.

1. Первый способ расчета сложных процентов — это умножение нового баланса каждого года на процентную ставку. Предположим, вы вкладываете 1000 долларов на сберегательный счет с годовой процентной ставкой 5% и хотите рассчитать остаток через пять лет.В Microsoft Excel введите «Год» в ячейку A1 и «Баланс» в ячейку B1. Введите годы от 0 до 5 в ячейки с A2 по A7. Баланс за год 0 составляет 1000 долларов, поэтому вы должны ввести «1000» в ячейку B2. Затем введите «= B2 * 1,05» в ячейку B3. Затем введите «= B3 * 1.05» в ячейку B4 и продолжайте делать это, пока не дойдете до ячейки B7. В ячейке B7 вычисление будет «= B6 * 1,05». Наконец, вычисленное значение в ячейке B7 — 1276,28 доллара — это остаток на вашем сберегательном счете через пять лет. Чтобы найти значение сложных процентов, вычтите 1000 долларов из 1276 долларов.n) — P. »В третьей строке модуля введите« Конечная функция ». Вы создали макрос функции для расчета сложной процентной ставки. Продолжая с той же таблицы Excel выше, введите« Сложный процент »в ячейку A6 и введите «= Compound_Interest (B1, B2, B3).» Это даст вам значение 276,28 доллара США, что согласуется с первыми двумя значениями.

Использование других калькуляторов

Как упоминалось выше, в Интернете предлагается ряд бесплатных калькуляторов сложных процентов, и многие портативные калькуляторы также могут выполнять эти задачи.

• Бесплатный калькулятор сложных процентов, предлагаемый на сайте Financial-Calculators.com, прост в использовании и предлагает выбор частоты от дня до года. Он включает в себя возможность выбора непрерывного начисления процентов, а также позволяет вводить фактические календарные даты начала и окончания. После ввода необходимых данных расчета результаты показывают заработанные проценты, будущую стоимость, годовой процентный доход (APY), который является мерой, включающей начисление сложных процентов и ежедневные проценты.
• Investor.gov, веб-сайт, управляемый Комиссией по ценным бумагам и биржам США (SEC), предлагает бесплатный онлайн-калькулятор сложных процентов. Калькулятор довольно прост, но он позволяет вводить ежемесячные дополнительные депозиты основному лицу, что полезно для расчета доходов, когда вкладываются дополнительные ежемесячные сбережения.
• Бесплатный онлайн-калькулятор процентов с несколькими дополнительными функциями доступен на TheCalculatorSite.com. Этот калькулятор позволяет производить расчеты для различных валют, учитывать ежемесячные депозиты или снятия, а также автоматически рассчитывать ежемесячные депозиты или снятия с поправкой на инфляцию.

Частота смешивания

Проценты могут быть увеличены по любому заданному графику периодичности, от ежедневного до ежегодного. Существуют стандартные графики частоты начисления сложных процентов, которые обычно применяются к финансовым инструментам.

Обычно для сберегательного счета в банке используется ежедневный график начисления сложных процентов. Для компакт-диска типичные графики частоты начисления сложных процентов — ежедневно, ежемесячно или раз в полгода; для счетов денежного рынка — часто ежедневно. Для жилищных ипотечных ссуд, ссуд под залог недвижимости, ссуд для личного бизнеса или счетов по кредитным картам обычно применяется ежемесячный график начисления сложных процентов.

Также могут быть разные временные рамки, в течение которых начисленные проценты фактически зачисляются на существующий баланс. Проценты по счету могут начисляться ежедневно, но только ежемесячно. Только когда проценты фактически зачисляются или добавляются к существующему балансу, они начинают приносить дополнительные проценты на счет.

Некоторые банки также предлагают так называемое непрерывное начисление сложных процентов, которое увеличивает процентную ставку к основной сумме в каждый возможный момент.Для практических целей это не намного больше, чем ежедневное начисление сложных процентов, если только вы не хотите вкладывать деньги и снимать их в тот же день.

Более частое начисление сложных процентов выгодно инвестору или кредитору. Для заемщика все наоборот.

Временная стоимость денег Возмещение

Понимание временной стоимости денег и экспоненциального роста, создаваемого сложным капиталом, важно для инвесторов, стремящихся оптимизировать свои доходы и распределение богатства.

Формула для получения будущей стоимости (FV) и текущей стоимости (PV) выглядит следующим образом:

FV = PV (1 + i) ⁿ и PV = FV / (1 + i) ⁿ

Например, будущая стоимость 10 000 долларов США составит 5% годовых в течение трех лет:

= 10 000 долларов США (1 + 0,05) ³

= 10 000 долл. США (1 157 625 долл. США)

= 11 576,25 долл. США

Приведенная стоимость 11 576,25 долларов США со скидкой 5% на три года:

= 11 576 долларов США.25 / (1 + 0,05) ³

= 11 576,25 долл. США / 1 157 625 долл. США

= 10 000 долл. США

Обратное значение 1,157625, равное 0,8638376, в данном случае является коэффициентом дисконтирования.

Рассмотрение по «Правилу 72»

Так называемое Правило 72 рассчитывает приблизительное время, в течение которого инвестиции удвоятся при заданной норме прибыли или процентах «i», и определяется выражением (72 / i). Его можно использовать только для годового начисления процентов.

Например, инвестиция с годовой доходностью 6% удвоится через 12 лет.Таким образом, инвестиции с годовой доходностью 8% за девять лет увеличатся вдвое.

Совокупный годовой темп роста (CAGR)

Совокупный годовой темп роста (CAGR) используется для большинства финансовых приложений, которые требуют расчета единого темпа роста за период времени.

Допустим, ваш инвестиционный портфель вырос с 10 000 до 16 000 долларов за пять лет; что такое CAGR? По сути, это означает, что PV = — 10 000 долларов США, FV = 16 000 долларов США и nt = 5, поэтому переменная «i» должна быть вычислена.Используя финансовый калькулятор или Excel, можно показать, что i = 9,86%.

В соответствии с соглашением о движении денежных средств ваши первоначальные инвестиции (PV) в размере 10 000 долларов отображаются со знаком минус, поскольку они представляют собой отток средств. Чтобы найти «i» в приведенном выше уравнении, PV и FV обязательно должны иметь противоположные знаки.

CAGR Реальные приложения

CAGR широко используется для расчета доходности за периоды времени для акций, паевых инвестиционных фондов и инвестиционных портфелей.CAGR также используется для определения того, превышал ли управляющий паевым инвестиционным фондом или управляющий портфелем рыночную норму прибыли в течение определенного периода времени. Если, например, рыночный индекс обеспечил общую доходность 10% за пятилетний период, но управляющий фондом получил только 9% годовой прибыли за тот же период, это означает, что этот менеджер отстал от рынка.

CAGR также можно использовать для расчета ожидаемых темпов роста инвестиционных портфелей в течение длительных периодов времени, что полезно для таких целей, как накопление средств на пенсию.Рассмотрим следующие примеры:

Пример 1: Не склонный к риску инвестор доволен скромной 3% годовой доходностью своего портфеля. Таким образом, ее нынешний портфель в 100 000 долларов через 20 лет вырастет до 180 611 долларов. Напротив, толерантный к риску инвестор, ожидающий годовой доходности своего портфеля в размере 6%, через 20 лет увидит, что 100 000 долларов США вырастут до 320 714 долларов США.

Пример 2: CAGR можно использовать для оценки того, сколько нужно убрать, чтобы сэкономить для конкретной цели.Пара, которая хотела бы сэкономить 50 000 долларов в течение 10 лет на первоначальный взнос за кондоминиум, должна будет экономить 4 165 долларов в год, если они предполагают, что годовой доход (CAGR) составит 4% от своих сбережений. Если они готовы пойти на небольшой дополнительный риск и рассчитывать на среднегодовой темп роста 5%, им нужно будет экономить 3 975 долларов в год.

Пример 3: CAGR также можно использовать для демонстрации преимуществ инвестирования в более раннем, чем в более позднем возрасте. Если цель состоит в том, чтобы сэкономить 1 миллион долларов к выходу на пенсию в возрасте 65 лет, исходя из среднегодового роста в 6%, 25-летнему человеку нужно будет откладывать 6 462 доллара в год для достижения этой цели.С другой стороны, 40-летнему человеку нужно будет сэкономить 18 227 долларов, или почти в три раза больше, чтобы достичь той же цели.

• CAGR также часто встречается в экономических данных. Вот пример: ВВП Китая на душу населения увеличился с 193 долларов в 1980 году до 6091 долларов в 2012 году. Каков годовой рост ВВП на душу населения за этот 32-летний период? Темп роста «i» в данном случае составляет впечатляющие 11,4%.

Плюсы и минусы компаундирования

Хотя магия сложного капитала привела к апокрифической истории о том, что Альберт Эйнштейн назвал его восьмым чудом света или величайшим изобретением человека, сложный процесс также может работать против потребителей, у которых есть ссуды с очень высокими процентными ставками, например, задолженность по кредитной карте.Баланс кредитной карты в размере 20 000 долларов США с ежемесячной процентной ставкой 20% приведет к общей сумме сложных процентов в размере 4 388 долларов США за год или около 365 долларов США в месяц.

С положительной стороны, магия начисления сложных процентов может работать вам на пользу, когда дело касается ваших инвестиций, и может быть мощным фактором создания богатства. Экспоненциальный рост за счет сложных процентов также важен для смягчения факторов, разрушающих благосостояние, таких как рост стоимости жизни, инфляция и снижение покупательной способности.

Паевые инвестиционные фонды предлагают инвесторам один из самых простых способов воспользоваться преимуществами сложных процентов. Если вы решите реинвестировать дивиденды, полученные от взаимного фонда, вы приобретете больше акций фонда. Со временем накапливается больше сложных процентов, и цикл покупки большего количества акций будет продолжать способствовать росту стоимости инвестиций в фонд.

Рассмотрим инвестиционный паевой инвестиционный фонд, открытый с начальными 5000 долларов и ежегодным приростом в 2400 долларов. При средней годовой доходности 12% за 30 лет будущая стоимость фонда составляет 798 500 долларов.Сложный процент — это разница между денежными средствами, внесенными в инвестиции, и фактической будущей стоимостью инвестиций. В этом случае при внесении 77 000 долларов США или совокупного взноса в размере всего 200 долларов США в месяц в течение 30 лет сложные проценты составляют 721 500 долларов США от будущего баланса.

Конечно, доходы от сложных процентов подлежат налогообложению, если только деньги не находятся на счете, защищенном от налогов; обычно он облагается налогом по стандартной ставке, соответствующей налоговой категории налогоплательщика.

Инвестиции со сложными процентами

Инвестор, который выбирает план реинвестирования в рамках брокерского счета, по сути, использует возможность начисления сложных процентов во все, что он инвестирует.Инвесторы также могут получить сложный процент при покупке облигации с нулевым купоном. Традиционные выпуски облигаций обеспечивают инвесторам периодические выплаты процентов на основе первоначальных условий выпуска облигаций, и, поскольку они выплачиваются инвестору в форме чека, проценты не складываются.

Бескупонные облигации не высылают инвесторам процентные чеки; вместо этого облигации этого типа приобретаются со скидкой по сравнению с их первоначальной стоимостью и со временем растут. Эмитенты бескупонных облигаций используют возможность начисления сложных процентов для увеличения стоимости облигации, чтобы она достигла своей полной цены к моменту погашения.

Компаундирование также может работать на вас при выплате кредита. Например, если вы будете выплачивать половину ипотечного платежа дважды в месяц вместо того, чтобы вносить полный платеж один раз в месяц, это сократит ваш период амортизации и сэкономит вам значительную сумму процентов.

Кстати о займах…

Определение начисления процентов

Закон о правде в кредитовании (TILA) требует, чтобы кредиторы раскрывали потенциальным заемщикам условия займа, включая общую сумму процентов в долларах, подлежащую выплате в течение срока займа, а также то, начисляются ли проценты простым или сложным образом.

Другой метод — сравнить процентную ставку по ссуде с ее годовой процентной ставкой (APR), которую TILA также требует от кредиторов. Годовая процентная ставка конвертирует финансовые расходы по вашему кредиту, которые включают все проценты и комиссии, в простую процентную ставку. Существенная разница между процентной ставкой и годовой процентной ставкой означает один или оба из двух сценариев: в вашем ссуде используются сложные проценты или в дополнение к процентам он включает огромные комиссии по ссуде. Даже когда речь идет о ссуде одного и того же типа, диапазон годовых может сильно различаться между кредиторами в зависимости от комиссий финансового учреждения и других расходов.

Вы заметите, что процентная ставка, которую вы взимаете, также зависит от вашего кредита. Ссуды, предлагаемые тем, у кого есть отличная кредитоспособность, имеют значительно более низкие процентные ставки, чем те, которые взимаются с лиц с плохой кредитной историей.

Часто задаваемые вопросы

Что такое простое определение сложных процентов?

Сложные проценты относятся к явлению, при котором проценты, связанные с банковским счетом, ссудой или инвестициями, со временем растут экспоненциально, а не линейно.Ключом к пониманию концепции является слово «составной». Предположим, вы инвестируете 100 долларов в бизнес, который ежегодно выплачивает вам 10% дивидендов. У вас есть выбор: вложить эти дивиденды в наличные или реинвестировать эти выплаты в дополнительные акции. Если вы выберете второй вариант, реинвестируя дивиденды и сложив их вместе с вашими первоначальными инвестициями в 100 долларов, то получаемая вами прибыль со временем начнет расти.

Кому выгодны сложные проценты?

Проще говоря, сложные проценты приносят пользу инвесторам, но значение слова «инвесторы» может быть довольно широким.Банки, например, получают выгоду от сложных процентов, когда ссужают деньги и реинвестируют полученные проценты в выдачу дополнительных ссуд. Вкладчики также извлекают выгоду из сложных процентов, когда они получают проценты по своим банковским счетам, облигациям или другим инвестициям. Важно отметить, что, хотя термин «сложные проценты» включает слово «проценты», эта концепция применяется за пределами ситуаций, в которых обычно используется слово «проценты», таких как банковские счета и ссуды.

Могут ли сложные проценты сделать вас богатым?

Да.Фактически, сложные проценты, возможно, являются самой мощной из когда-либо задуманных сил для создания богатства. Есть записи о купцах, кредиторах и различных бизнесменах, которые использовали сложные проценты, чтобы разбогатеть буквально на тысячи лет. Например, в древнем городе Вавилон глиняные таблички использовались более 4000 лет назад для обучения студентов математике сложных процентов.

В наше время Уоррен Баффет стал одним из самых богатых людей в мире благодаря бизнес-стратегии, которая включала в себя старательно и терпеливо увеличивать доходность его инвестиций в течение длительных периодов времени.Вполне вероятно, что в той или иной форме люди будут использовать сложные проценты для создания богатства в обозримом будущем.

Таблица сложных процентов

9109 2,50% Годы Проценты Заработано Итого 1000,00 долл. США 1 1 3 26 долларов США.27 $ 1,076.89 4 $ 26,92 $ 1,103.81 5 $ 27,60 $ 1,131.41 6 $ 28,29 $ 1,159.69 7 $ 28,99 $ 1,188.69 8 29,72 долл. США 1218,40 долл. США 9 30,46 долл. США 1 248,86 долл. США 10 31 долл. США.22 $ 1,280.08 11 $ 32,00 $ 1,312.09 12 $ 32.80 $ 1,344.89 13 $ 33,62 $ 1,378.51 14 $ 34,46 $ 1,412.97 15 35,32 долл. США 1448,30 долл. США 16 36,21 долл. США 1 484,51 долл. США 17 37 долл. США.11 $ 1,521,62 18 $ 38,04 $ 1,559,66 19 $ 38,99 1598,65 20 20 20 Годы Проценты Заработано Итого 1000,00 долларов США 1 45 долларов США.00 $ 1,045.00 2 $ 47,02 $ 1,092.03 3 $ 49,14 $ 1,141.17 4 $ 51,35 $ 1,192.52 5 $ 53,66 $ 1,246.18 6 56,08 долл. США 1302,26 долл. США 7 58,60 долл. США 1 360,86 долл. США 8 61 долл. США24 $ 1,422.10 9 $ 63,99 $ 1,486.10 10 $ 66,87 $ 1,552.97 11 $ 69,88 $ 1,622.85 12 $ 73,03 $ 1,695.88 13 76,31 долл. США 1772,20 долл. 14 79,75 долл. США 1851,94 долл. США 15 долл. США 83.34 $ 1,935.28 16 $ 87,09 $ 2,022.37 17 $ 91,01 $ 2,113.38 18 $ 95,10 $ 2,208.48 19 $ 99.38 $ 2,307.86 20 103,85 долл. США 2411,71 долл. США Заработано 00 6,50% Годы Проценты 1 65,00 долл. США 1 065,00 долл. США 2 долл. США 69,22 долл. США 1,134,23 3 83,62 долл. США 1370,09 долл. США 6 89,06 долл. США 1,459,14 долл. США 7 94,84 долл. США долл. США 1553 долл. США.99 8 $ 101,01 $ 1,655,00 9 $ 107,57 $ 1,762,57 10 10 $ 114,57 9111 $ 114,57 $ 114,57 $ 114,57 129,94 долл. 2 129,10 долл. США 13 138,39 долл. США 2267,49 долл. США 14 147,39 долл. США 2414 долл. США.87 15 $ 156,97 $ 2,571.84 16 $ 167,17 $ 2,739.01 17 $ 178,04 $ 2,917.05 18 $ 189,61 $ 3,106.65 19 $ 201,93 $ 3308,59 20 $ 215,06 $ 3,523,65

3.00% Годы Проценты Заработано Итого 1000,00 долл. 31,83 долл. США 1092,73 долл. США 4 32,78 долл. США 1 125,51 долл. США 5 33,77 долл. США 1 159,27 долл. США 6137378 $ 1,194.05 7 $ 35,82 $ 1,229.87 8 $ 36,90 $ 1,266.77 9 $ 38,00 $ 1,304.77 10 $ 39,14 $ 1,343.92 11 40,32 долл. США 1384,23 долл. США 12 41,53 долл. США 1 425,76 долл. США 13 42 долл. США.77 $ 1,468.53 14 $ 44,06 $ 1,512.59 15 $ 45.38 $ 1,557.97 16 $ 46.74 $ 1,604.71 17 $ 48,14 $ 1,652.85 18 49,59 долл. США 1 702,43 долл. США 19 51,07 долл. США 1753,51 долл. США 20 52 долл. США.61 $ 1806,11 103 103 103 5,00% Годы Проценты 9011 9011 9011 Итого 2 52,50 долл. США 1 102,50 долл. США 3 55,13 долл. США 1 157,63 долл. США 4 57 долл. США.88 $ 1,215.51 5 $ 60,78 $ 1,276.28 6 $ 63,81 $ 1,340.10 7 $ 67,00 $ 1,407.10 8 $ 70,36 $ 1,477.46 9 73,87 долл. США 1551,33 долл. США 10 77,57 долл. США 1628,89 долл. США 11 81 долл. США44 $ 1,710.34 12 $ 85,52 $ 1,795.86 13 $ 89.79 $ 1,885.65 14 $ 94.28 $ 1,979.93 15 $ 99.00 $ 2,078.93 16 103,95 долл. США 2182,87 долл. США 17 109,14 долл. США 2292,02 долл. США 18 114 долл. США.60 $ 2,406,62 19 $ 120,33 $ 2,526,95 20 $ 126,35 $ 2,653,30 Итого 1 000,00 долл. 1 75,00 долл. США 1 075,00 долл. США 2 80 долл. США.63 $ 1,155.63 3 $ 86,67 $ 1,242.30 4 $ 93,17 $ 1,335.47 5 $ 100,16 $ 1,435.63 6 $ 107,67 $ 1,543.30 7 115,75 долл. США 1 659,05 долл. США 8 124,43 долл. США 1783,48 долл. США 9 133 долл. США.76 $ 1,917.24 10 $ 143,79 $ 2,061.03 11 $ 154,58 $ 2,215.61 12 $ 166,17 $ 2,381.78 13 $ 178,63 $ 2,560.41 14 192,03 долл. США 2,752,44 долл. США 15 206,43 долл. США 2 958,88 долл. США 16 221 долл. США.92 $ 3,180.79 17 $ 238,56 $ 3,419.35 18 $ 256,45 $ 3,675.80 19 $ 275,69 $ 3,951.49 20 $ 296,36 $ 4,247.85

3,50% Годы Проценты Заработано Итого 1000 долларов.00 1 35,00 долл. США 1 035,00 долл. США 2 долл. США 36,22 долл. США 40,16 долл. США 1 187,69 долл. США 6 41,57 долл. США 1229,26 долл. США 7 43,02 долл. США 1272 долл. США.28 8 44,53 долл. США 1316,81 долл. США 9 46,09 долл. США 1362,90 долл. США 10 51,10 долл. 1 511,07 долл. США 13 52,89 долл. США 1 563,96 долл. США 14 54,74 долл. США 1 618 долл. США.69 15 $ 56,65 $ 1,675.35 16 $ 58,64 $ 1,733.99 17 $ 60,69 $ 1,794.68 18 $ 62,81 $ 1,857.49 19 65,01 долл. США 1 922,50 долл. США 20 67,29 долл. США 1 989,79 долл. США 5.50% Годы Проценты Заработано Итого 1000,00 долл. 61,22 долл. США 1,174,24 долл. США 4 64,58 долл. США 1 238,82 долл. США 5 68,14 долл. США 1 306,96 долл. США 88 $ 1,378.84 7 $ 75,84 $ 1,454.68 8 $ 80,01 $ 1,534.69 9 $ 84,41 $ 1,619.09 10 $ 89,05 $ 1,708.14 11 93,95 долл. США 1 802,09 долл. США 12 99,12 долл. США 1 901,21 долл. США 13 104 долл. США.57 $ 2,005.77 14 $ 110,32 $ 2,116.09 15 $ 116.39 $ 2,232.48 16 $ 122,79 $ 2,355.26 17 $ 129,54 $ 2,484.80 18 136,66 долл. США 2 621,47 долл. США 19 144,18 долл. США 2 765,65 долл. США 20 152 долл. США.11 $ 2,917,76 7,50% Годы 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 9011 2 80,63 долл. США 1,155,63 долл. США 3 долл. США 86,67 1,242,30 долл. США 4 93 долл. США.17 $ 1,335.47 5 $ 100,16 $ 1,435.63 6 $ 107.67 $ 1,543.30 7 $ 115,75 $ 1,659.05 8 $ 124.43 $ 1,783.48 9 133,76 долл. США 1 917,24 долл. США 10 143,79 долл. США 2 061,03 долл. США 11 154 долл. США.58 $ 2,215.61 12 $ 166,17 $ 2,381.78 13 $ 178,63 $ 2,560.41 14 $ 192,03 $ 2,752.44 15 $ 206,43 $ 2,958.88 16 221,92 долл. США 3180,79 долл. США 17 238,56 долл. США 3,419,35 долл. США 18 256 долл. США.45 3 675,80 долл. США 19 275,69 долл. США 3 951,49 долл. США 20 296,36 долл. США 4 247,85 долл. США 125119 125119 4,00% Годы Проценты Заработанные Итого 1000,00 долларов США 1 40,00 долларов США долларов США.00 2 $ 41,60 $ 1,081.60 3 $ 43,26 $ 1,124.86 4 $ 44,99 $ 1,169.86 5 $ 46,79 $ 1,216.65 6 48,67 долл. 1 265,32 долл. США 7 50,61 долл. США 1315,93 долл. США 8 52,64 долл. США 1368 долл. США.57 9 $ 54,74 $ 1,423,31 10 $ 56,93 $ 1,480,24 11 $ 59,21 $ 59,21 64,04 долл.94 16 $ 72,04 $ 1,872.98 17 $ 74,92 $ 1,947.90 18 $ 77,92 $ 2,025.82 19 $ 81,03 $ 2,106.85 20 84,27 долл. США 2191,12 долл. США 6,00% Годы Проценты Заработано 1 000 долл.00 1 60,00 долл. США 1 060,00 долл. США 2 долл. США 63,60 1,123,60 долл. США 3 9119 9119 75,75 долл. 1338,23 долл. США 6 80,29 долл. США 1418,52 долл. США 7 85,11 долл. США 1 503 долл. США.63 8 90,22 долл. США 1 593,85 долл. США 9 95,63 долл. США 1 689,48 долл. США 10 9107 9109 113,90 долл. США 2,012,20 долл. США 13 120,73 долл. США 2132,93 долл. США 14 127,98 долл. США 2260 долл. США.90 15 $ 135,65 $ 2,396.56 16 $ 143,79 $ 2,540.35 17 $ 152,42 $ 2,692.77 18 $ 161,57 $ 2,854.34 19 171,26 доллара 3025,60 доллара 20 181,54 доллара 3,207,14 доллара 8.00% Годы Проценты Заработано Итого 1000,00 долл. 93,31 долл. США 1259,71 долл. США 4 100,78 долл. США 1360,49 долл. США 5 108,84 долл. США 1 469 долл. США.33 6 $ 117,55 $ 1,586.87 7 $ 126,95 $ 1,713.82 8 $ 137,11 $ 1,850.93 9 $ 148,07 $ 1,999.00 10 159,92 долларов 2158,92 долларов 11 172,71 долларов 2331,64 долларов 12 186,53 2518 долларов.17 13 $ 201,45 $ 2,719.62 14 $ 217,57 $ 2,937.19 15 $ 234,98 $ 3,172.17 16 $ 253,77 $ 3,425.94 17 274,08 долл. 3,700,02 долл. США 18 296,00 долл. США 3,996,02 долл. США 19 319,68 долл. США 4 315 долл. США.70 20 $ 345,26 $ 4 660,96 Факторы будущей стоимости | AccountingCoach Математика для расчета будущей стоимости одной суммы в размере 10 000 долларов с доходом 8% в год , составляемой ежеквартально в течение двух лет , отображается в левом столбце следующей таблицы. В правом столбце находится формула, в которой используется коэффициент будущей стоимости. Коэффициенты будущей стоимости доступны в таблицах будущих значений, например в сокращенной версии, показанной здесь: Мы выделили фактор, использованный в наших вычислениях.Как видите, коэффициент будущей стоимости 1,172 находится там, где n = 8, а i = 2%. Наше будущее значение 1 таблицы уникально тем, что у нас есть дополнительная строка: n = 0. Большинство FV из 1 таблиц пропускают строку для n = 0 и начинаются со строки n = 1. Не должно быть никаких различий в коэффициентах БС, кроме незначительных различий в округлении. Чтобы оценить полезность FV 1 таблицы, сосредоточьтесь на столбце с заголовком i = 10%. В этом столбце указано, что текущая стоимость 1.000 равна 1.000 в период времени 0 — настоящее время. При перемещении вниз по столбцу 10% следующая строка (где n = 1) показывает, что будущее значение увеличится на 10% до 1,100. Продолжая движение вниз по столбцу 10%, вы видите, что в конце двух периодов (n = 2) будущее значение равно 1,210, увеличиваясь на 0,110 (1,100 x 10%). Следующая цифра вниз указывает на то, что в конце трех периодов будущее значение составляет 1,331, что представляет собой увеличение на 0,121 (1,331 — 1,210; и 1,210 x 10%). Таблица FV 1 представляет будущие суммы по сложным процентам для единой суммы 1.000 по разным процентным ставкам. Эти факторы должны сделать будущие вычисления немного проще, чем вычисления с использованием экспонент. Столбец 10% таблицы будущей стоимости может использоваться для определения будущей стоимости одного доллара, инвестированного сегодня под 10% годовых, начисленных на год. Единая сумма в 1 доллар вырастет до 3,138 доллара по прошествии 12 лет. Таблица FV также дает некоторое представление о будущей стоимости предметов, которые, как ожидается, будут расти с постоянной скоростью. Например, если чашка кофе сейчас стоит 1 доллар.00, и ожидается, что стоимость будет увеличиваться на 10% в год, усугубляемая ежегодно, тогда чашка кофе будет стоить 3,138 доллара за чашку в конце 12 лет. Мы также можем использовать коэффициенты для сумм, превышающих 1 доллар. Например, если ежемесячная стоимость семейного плана медицинского страхования составляет 1000 долларов в настоящее время и ожидается, что она будет увеличиваться на 10% в год в совокупности ежегодно, то ежемесячные расходы по истечении 12 лет будут составлять 3138 долларов. В оставшейся части этого раздела мы будем использовать более полную таблицу будущего значения 1: Щелкните здесь, чтобы открыть таблицу FV 1 Сложные проценты и приведенная стоимость Есть выражение «время — деньги».«При составлении бюджета капиталовложений эта концепция фактически измеряется и используется в процессе принятия решений. Основная идея заключается в том, что доллар, полученный сегодня, стоит больше, чем доллар, который будет получен в будущем. Этот результат происходит потому, что доллар, который есть сегодня в наличии, можно инвестировать для получения дополнительных немедленных доходов. В контексте составления бюджета капиталовложений предположим, что две альтернативные инвестиции имеют одинаковую первоначальную стоимость. Инвестиционная Альфа приносит 100 долларов в год в течение каждого из следующих 5 лет.Инвестиционная бета-версия приносит 50 долларов в год в течение каждого из следующих 10 лет. Основываясь исключительно на этой информации, следует сделать вывод, что альфа-версия предпочтительнее бета-версии. Хотя общие денежные доходы одинаковы, временная стоимость денег лучше для Alpha, чем для Beta. С Alpha деньги возвращаются раньше, что расширяет возможности реинвестирования. Конечно, очень немногие варианты капитальных затрат столь же однозначны, как альфа и бета. Поэтому бухгалтеры полагаются на точные математические методы для количественной оценки временной стоимости денег. Сложные проценты Отправной точкой для понимания временной стоимости денег является понимание сложных процентов. Цитируется высказывание Альберта Эйнштейна: «Самая мощная сила во Вселенной — это сложные проценты». Проще говоря, деньги можно вкладывать, чтобы заработать деньги. В этом контексте учтите, что когда кто-то тратит доллар на безалкогольный напиток, этот человек фактически отказывается от 0,10 доллара в год до конца своей жизни (при 10% -ной процентной ставке).И, как будет показано, эта ежегодная экономия увеличивается до гораздо большего из-за процентов, полученных с процентов. Расчеты сложных процентов можно использовать для вычисления суммы, до которой вырастут инвестиции в будущем. Сложный процент также называется , будущая стоимость . Если кто-то инвестирует 1 доллар на один год под 10% годовых, сколько он или она будет иметь в конце года? Ответ, конечно же, 1,10 доллара. Он рассчитывается путем умножения 1 доллара на 10% (1 доллар X 10% = 0 долларов.10) и прибавив 0,10 доллара к начальному доллару. Если полученные 1,10 доллара инвестировать еще на год под 10%, они вырастут до 1,21 доллара. То есть 1,10 доллара на 110%. Этот процесс будет продолжаться из года в год. Годовая процентная ставка каждый год больше, чем годом ранее, из-за «начисления сложных процентов». Компаундирование просто означает, что инвестиции растут за счет накопленных процентов и получения процентов от ранее начисленных процентов, которые становятся частью общего инвестиционного пула.Эта формула выражает основную математику сложных процентов: (1 + я) № Где «i» — процентная ставка за период, а «n» — количество периодов Будущая стоимость паушальной суммы Насколько вырастет 1 доллар через 25 лет при 10% -ной процентной ставке? Ответ можно определить, взяв 1,10 в 25-й степени [(1.10) 25 ], и ответ будет 10,83 доллара. Таблицы будущих значений предоставляют заранее определенные значения для множества таких вычислений (полный набор таблиц см. На сопутствующем веб-сайте).Чтобы поэкспериментировать с таблицей будущих значений, определите, насколько вырастет 1 доллар за 10 периодов при 5% за период. Ответ на этот вопрос составляет 1,63 доллара США, и его можно найти, указав значение в «5% столбце / 10-периодной строке». Если бы первоначальные инвестиции составляли 5000 долларов (вместо 1 доллара), они вырастут до 8 144,45 долларов (5000 долларов X 1,62889). При использовании таблиц обязательно обратите внимание на то, что процентная ставка — это ставка за период. «Периодом» могут быть годы, кварталы, месяцы и т. Д. Все зависит от того, как часто будут начисляться проценты.Например, годовая процентная ставка 12% с ежемесячным начислением сложных процентов в течение двух лет потребует ссылки на столбец 1% (годовая ставка 12% соответствует месячной ставке 1%) и строку с 24 периодами (2 года равны 24. месяцы). Если та же самая инвестиция включала годовое начисление сложных процентов, то можно было бы сослаться на столбец 12% и строку с двумя периодами. Частота начисления сложных процентов влияет на накопленную сумму. В данном примере ежемесячное начисление сложных процентов дает 1,26973, а годовое — только 1.25440. Будущая стоимость аннуитетов Аннуитеты — это ровные потоки платежей. Каждый платеж имеет одинаковую сумму и происходит через равные промежутки времени. Аннуитеты — обычное дело в бизнесе. Они могут возникать в ссудах, пенсионных планах, аренде, страховых расчетах, налоговых расчетах и ​​т. Д. Иногда может быть любопытно узнать, до какой степени вырастет повторяющийся поток платежей через несколько периодов. Это называется будущей стоимостью аннуитета. Аннуитетный платеж Аннуитет к уплате (также известный как аннуитет вперед) включает в себя поток платежей уровня, причем платежи производятся в начале каждого периода времени. Например, возможно, кто-то планирует откладывать на пенсию, инвестируя 5000 долларов в начале каждого года в течение следующих пяти лет. Если годовая процентная ставка составляет 10% годовых, сколько накопится к концу 5-летнего периода? На следующем рисунке показано, как будет расти каждый из пяти отдельных платежей, а общая сумма составит 33 578 долларов США: Хотя рисунок представляет собой полезный пояснительный инструмент, его довольно сложно реализовать.К такому же выводу можно прийти, ссылаясь на будущую стоимость таблицы причитающихся аннуитетов. Таблица показывает значение 6,71561 (10% столбец / 5-периодная строка). Умножение ежегодного платежа в размере 5000 долларов на этот коэффициент дает 33 578 долларов (5000 долларов X 6,71561). Это означает, что аннуитет вырастет до 33 578 долларов. Обыкновенная рента Иногда аннуитет будет основываться на выплатах «в конце периода». Эти аннуитеты называются обычными аннуитетами (также известными как аннуитеты с просрочкой).На следующем рисунке изображена 5-летняя 10% -ная обычная рента, включающая выплаты уровня в 5000 долларов каждая. Обратите внимание на сходство с предыдущим рисунком, за исключением того, что ежегодная выплата переносится на конец года. Это означает, что каждый платеж будет накапливать проценты за год меньше, а последний платеж не будет накапливать проценты! Обязательно обратите внимание на разительную разницу между накопленной суммой по аннуитету и по обычному аннуитету (33 578 долларов против 30 526 долларов). Существуют также таблицы, отражающие будущую стоимость обычного аннуитета.Просмотрите таблицу, чтобы убедиться в сумме 30 526 долларов (5 000 долларов X 6,10510). Текущая стоимость Расчеты будущей стоимости предоставляют полезные инструменты для финансового планирования. Но многие решения и бухгалтерские измерения будут основаны на взаимной концепции, известной как приведенная стоимость . Приведенная стоимость (также известная как дисконтирование) определяет текущую стоимость денежных средств, которые будут получены в будущем. Например, сколько человек готов взять сегодня вместо 1 доллара в год? Если процентная ставка составляет 10%, вероятно, он или она примет сумму, которая вырастет до 1 доллара в год, если бы она была инвестирована под 10%.Это будет 0, доллара. Другими словами, инвестируйте 90,9 цента в год под 10%, и он вырастет до 1 доллара (0, доллара х 1,1 = 1 доллар). Таким образом, расчеты текущей стоимости — это просто обратная величина для расчетов будущей стоимости. В терминах формулы это будет 1 / (1 + i) n . Таблица приведенной стоимости 1 доллара показывает заранее определенные значения для расчета приведенной стоимости 1 доллара на основе альтернативных предположений о процентных ставках и временных периодах. Единовременная выплата в размере 25000 долларов США, которая должна быть получена в конце 10 лет под 8% годовых с полугодовым начислением сложных процентов, будет иметь приведенную стоимость 11410 долларов США (вспомните предыдущее обсуждение и используйте столбец 4% / 20-периодную строку: 25000 долларов X 0.45639). Аннуитетный платеж Расчет приведенной стоимости также применим к аннуитетам. Возможно, кто-то рассматривает возможность покупки инвестиции, приносящей доход в 5000 долларов в год в течение пяти лет с немедленным получением первого платежа. Чем должны быть оплачены эти вложения, если целевая доходность 10%? Этот сценарий относится к приведенной стоимости аннуитета: . На графике показано, что приведенная стоимость аннуитета составляет 20 849 долларов.Конечно, существует приведенная стоимость таблицы причитающихся аннуитетов, чтобы облегчить бремя этого расчета (5000 долларов X 4,16897 = 20 849 долларов). Обыкновенная рента Часто первый платеж аннуитета происходит в конце каждого периода. Приведенная стоимость обычной аннуитетной таблицы обеспечивает необходимый фактор для определения того, что 5000 долларов, которые должны быть получены в конце каждого года в течение 5-летнего периода, стоят всего 18 954 доллара при 10% -ной процентной ставке (5000 долларов X 3,79079 = 18 954 доллара).Следующий рисунок подтверждает этот вывод: Электронная таблица Имейте в виду, что большинство электронных таблиц также включают функции для расчета сумм текущей и будущей стоимости путем простого выполнения набора заранее определенных запросов. Эти функции электронных таблиц могут оказаться очень эффективными при выполнении вычислений, проиллюстрированных в этой главе. Вызовы Многие сценарии представляют собой комбинацию единовременной выплаты и суммы аннуитетного денежного потока.Для таких сценариев существует множество подходов к расчету будущей или текущей стоимости. Возможно, самый безопасный подход — составить схему ожидаемых денежных потоков и применить логические манипуляции. Для иллюстрации предположим, что Markum Real Estate рассматривает возможность покупки офисного здания. Пока идет ремонт, здание пустует два года. Затем он будет приносить годовую арендную плату в размере 100 000 долларов США в начале каждого из следующих трех лет. Здание будет продано через пять лет за 700 тысяч долларов.Маркум желает знать текущую стоимость ожидаемого притока денежных средств, предполагая, что годовая процентная ставка составляет 5%. Поток аренды имеет приведенную стоимость 285 941 доллар на начало третьего года. Эта стоимость дисконтируется до значения начала первого года (259 357 долларов), рассматривая его как единовременную выплату. Цена продажи отдельно дисконтируется до ее приведенной стоимости в 548 471 доллар США. Приведенная стоимость арендной платы и продажной цены объединяются для получения общей приведенной стоимости всех денежных поступлений (807 828 долларов США).Этот тип манипулирования денежными потоками довольно распространен при расчете приведенной стоимости многих инвестиционных решений. Альтернативный способ оценки потока аренды — вычесть стоимость двухлетнего аннуитета из стоимости пятилетнего (4,54595 — 1,95238 = 2,59357; 100 000 долларов США X 2,59357 = 259 357 долларов США). Этот результат возникает потому, что он предполагает пятилетний аннуитет и вычитает сумму, относящуюся к первым двум годам, оставляя только последние три года в итоговом коэффициенте приведенной стоимости. Вы узнали? Что означает «временная стоимость денег»? Уметь рассчитывать сложные проценты. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт