Таблица восьмеричный код: Таблица перевода двоичных, восьмеричных, десятичных (от 1 до 255) и шестнадцатеричных чисел. Binary, Octal and Hexadecimal Numbers vs Decimal Numbers

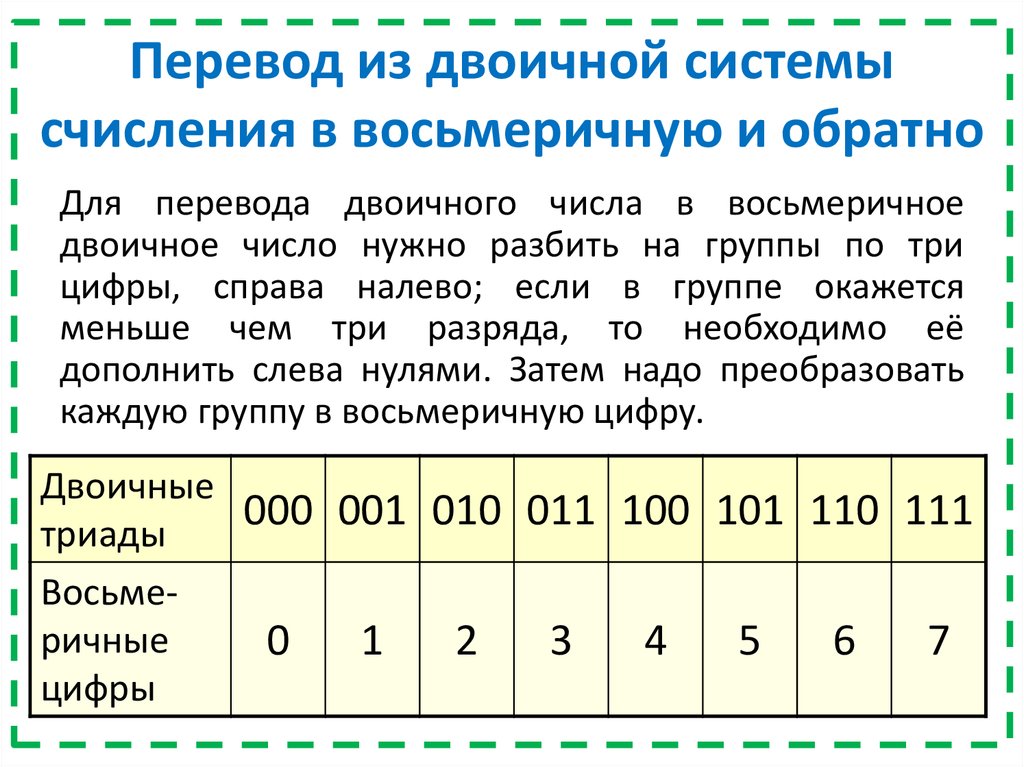
Двоично-восьмеричная таблица

8	2
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Пример 4. Перевести смешанное число 1011101,1O111₂ в восьмеричную систему.

Решение. Группы по три двоичных знака выделяются от запятой как влево, так и вправо. Затем производится перекодировка по таб­лице:

1011101, 10111₂ => 001 01l 101, 101 110 => 135,56₈.

Для записи одного и того же значения в различных системах счисления требуется разное число позиций или разрядов (разная длина числа). Например, 96₁₀= 140₈ = 1100000₂. Чем меньше основание системы, тем больше длина числа. Если длина разрядной сетки задана, например N, то это ограничивает максимальное по абсолютному значению число, которое можно записать:

A_(q)max=q^N—1.

Интервал числовой оси, заключенный между максимальным и минимальным числами, называют диапазоном представления (ДП) чисел в данной системе счисления для заданного ограничения на длину разрядной сетки.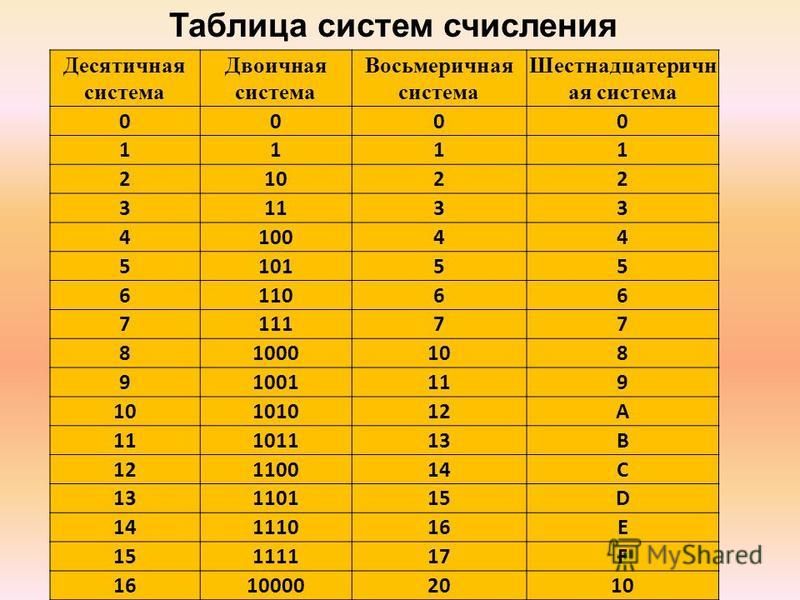

Существуют различные способы кодировки символов. В коде обмена информацией ASCII (American Standard Code for Information Interchange), как и во многих других, символы (латинские буквы и цифры, русские буквы, знаки препинания и арифметических операций и другие) обычно кодируются последовательностями из 8 нулей и единиц, т.е. байтами. С помощью байта из 8 нулей и единиц можно закодировать 256 различных символов (2⁸ = 256).

В международном стандарте Unicode на каждый символ отводится два байта. С помощью двух байт можно закодировать 2¹⁶ = 65 536 различных символов.

Рассмотрим код обмена информацией ASCII. Кодовая таблица ASCII состоит из 256 символов.

Таблица стандартной части кода ASCII

32	20		56	38	8	80	50	P	104	68	h
33	21	!	57	39	9	81	51	Q	105	69	i
34	22	“	58	3A	:	82	52	R	106	6A	j
35	23	#	59	3B	;	83	53	S	107	6B	k
36	24	$	60	3C	<	84	54	T	108	6C	l
37	25	%	61	3D	=	85	55	U	109	6D	m
38	26	&	62	3E	>	86	56	V	110	6E	n
39	27	‘	63	3F	?	87	57	W	111	6F	o
40	28	(	64	40	@	88	58	X	112	70	p
41	29	)	65	41	A	89	59	Y	113	71	q
42	2A	*	66	42	B	90	5A	Z	114	72	r
43	2B	+	67	43	C	91	5B	[	115	73	s
44	2C	,	68	44	D	92	5C	\	116	74	t
45	2D	—	69	45	E	93	5D	]	117	75	u
46	2E	.	118	76	v
47	2F	/	71	47	G	95	5F	_	119	77	w
48	30	0	72	48	H	96	60	‘	120	78	x
49	31	1	73	49	I	97	61	a	121	79	y
50	32	2	74	4A	J	98	62	b	122	7A	z
51	33	3	75	4B	K	99	63	c	123	7B	{
52	34	4	76	4C	L	100	64	d	124	7C	|
53	35	5	77	4D	M	101	65	e	125	7D	}
54	36	6	78	4E	N	102	66	f	126	7E	~
55	37	7	79	4F	O	103	67	g	127	7F

Первая половина таблицы с кодами от 0 до 127 соответствует стандартному интернациональному коду. Символы с кодами от 0 до 31 являются управляющими. Они используются для управления принтером и других специальных целей.

Символы с кодами от 32 до 127 используются для представления знаков пунктуации и арифметических операций, цифр, прописных и строчных букв латинского алфавита.

Вторая половина таблицы с кодами от 128 до 255 называется кодовой страницей и предназначена для представления символов псевдографики, букв национальных алфавитов и других специальных символов.

Таблица альтернативной части кода ASCII (фрагмент с русскими буквами)

128	80	А	144	90	Р	160	A0	а	224	E0	р
129	81	Б	145	91	С	161	A1	б	225	E1	с
130	82	В	146	92	Т	162	A2	в	226	E2	т
131	83	Г	147	93	У	163	A3	г	227	E3	у
132	84	Д	148	94	Ф	164	A4	д	228	E4	ф
133	85	Е	149	95	Х	165	A5	е	229	E5	х
134	86	Ж	150	96	Ц	166	A6	ж	230	E6	ц
135	87	З	151	97	Ч	167	A7	з	231	E7	ч
136	88	И	152	98	Ш	168	A8	и	232	E8	ш
137	89	Й	153	99	Щ	169	A9	й	233	E9	щ
138	8A	К	154	9A	Ъ	170	AA	к	234	EA	ъ
139	8B	Л	155	9B	Ы	171	AB	л	235	EB	ы
140	8C	М	156	9C	Ь	172	AC	м	236	EC	ь
141	8D	Н	157	9D	Э	173	AD	н	237	ED	э
142	8E	О	158	9E	Ю	174	AE	о	238	EE	ю
143	8F	П	159	9F	Я	175	AF	п	239	EF	я

Здесь 1, 4, 7 и 10-й столбцы – десятичные, 2, 5, 8 и 11-й – шестнадцатеричные коды соответствующих символов, расположенных в 3, 6, 9 и 12-м столбцах.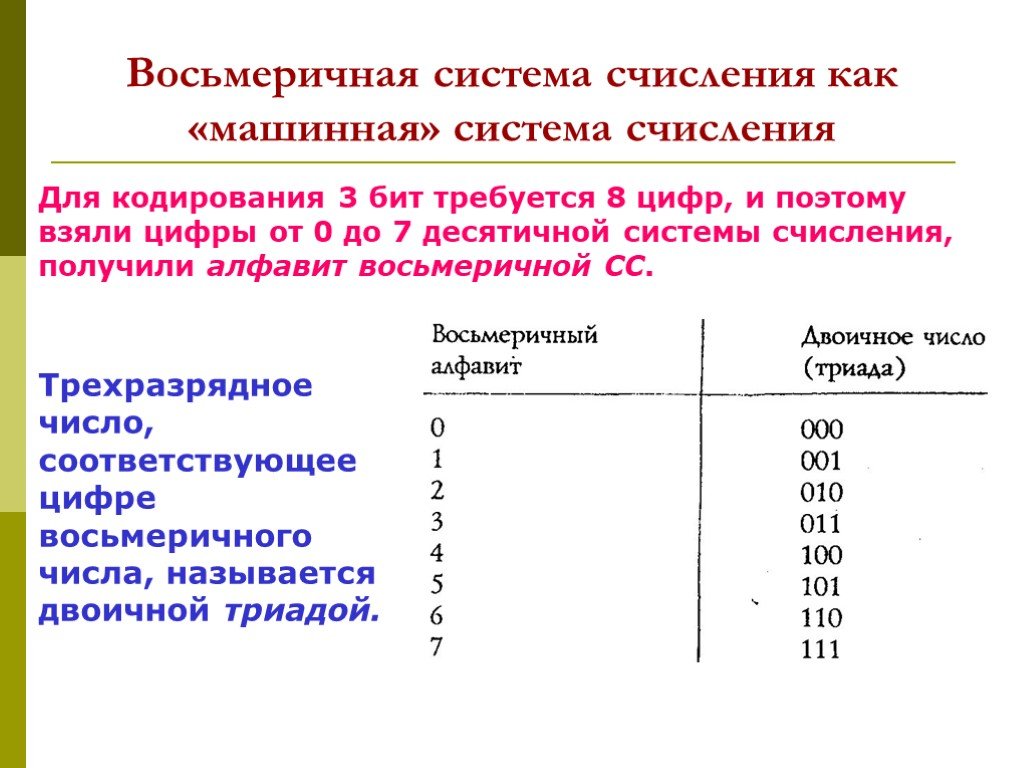

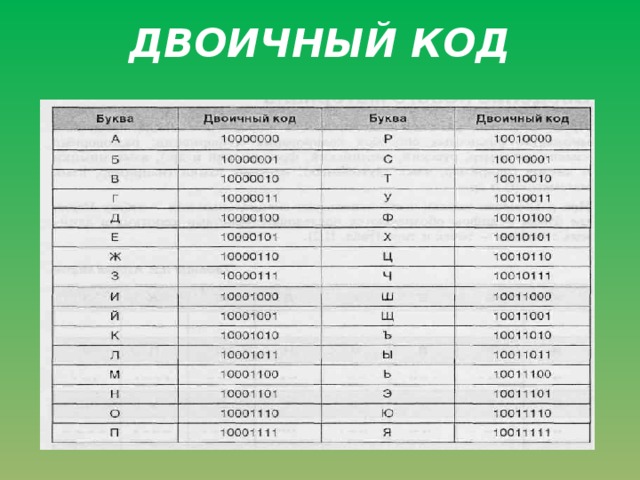
Пример использования таблицы кодировки для записи слова «Лук» в двоичной форме. Ищем в таблице букву «Л», слева от неё – шестнадцатеричный код этой буквы 8B, аналогично находим коды остальных букв:

8 B E 3 A A

1000 1011

1110 0011

1010 1010

Л у к

Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.

Автор материалов — Лада Борисовна Есакова.

Кодирование – это перевод информации, представленной символами первичного алфавита, в последовательность кодов.

Декодирование (операция, обратная кодированию) – перевод кодов в набор символов первичного алфавита.

Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.

Код называется однозначно декодируемым, если любое сообщение, составленное из кодовых слов, можно декодировать единственным способом.

Равномерное кодирование всегда однозначно декодируемо.

Для неравномерных кодов существует следующее достаточное (но не необходимое) условие однозначного декодирования:

Сообщение однозначно декодируемо с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова.

Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.

 

Кодирование в различных системах счисления

Пример 1.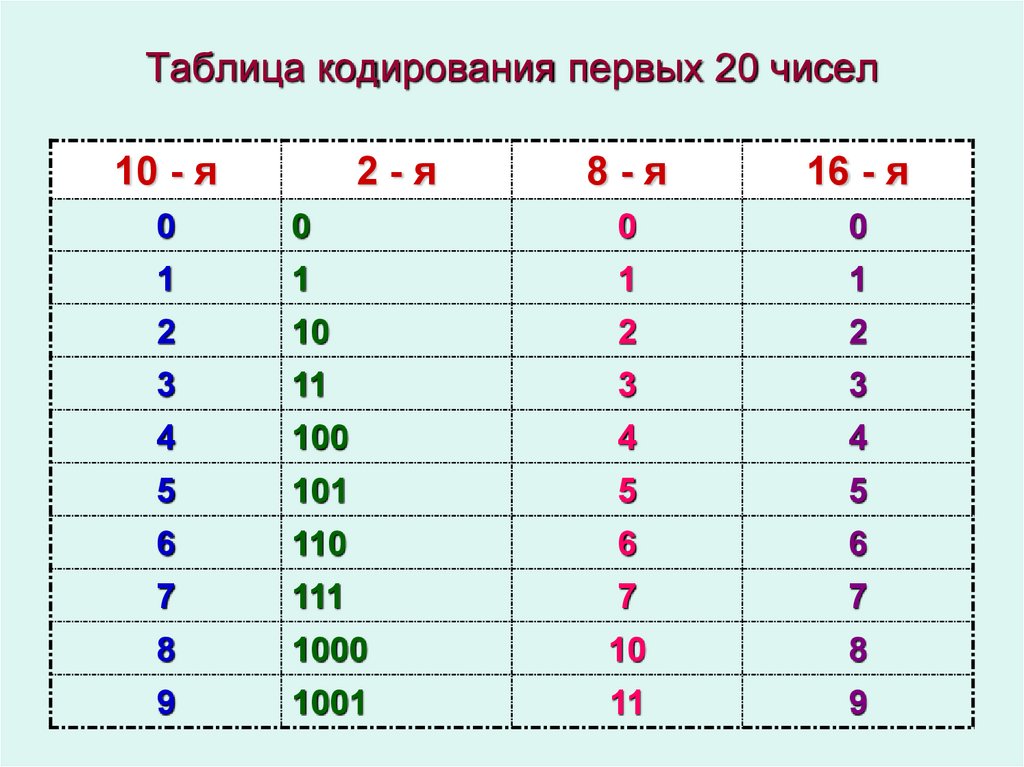

Для кодирования букв О, В, Д, П, А решили использовать двоичное представление

чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится

1) 22162

2) 1020342

3) 2131453

4) 34017

Решение:

Представим коды указанных букв в дво­ич­ном коде, добавив незначащий нуль для одноразрядных чисел:

О	В	Д	П	А
0	1	2	3	4
00	01	10	11	100

Закодируем по­сле­до­ва­тель­ность букв: ВО­ДО­ПАД — 010010001110010.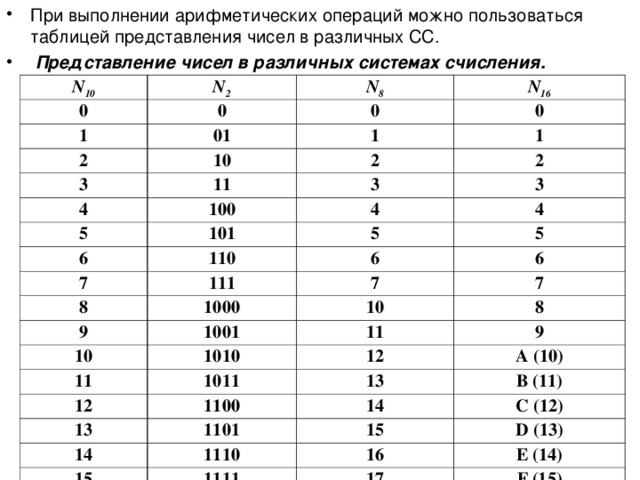

Разобьём это пред­став­ле­ние на трой­ки спра­ва на­ле­во и пе­ре­ведём каждую тройку в восьмеричное число.

010 010 001 110 010 — 22162.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

Пример 2.

Для пе­ре­да­чи по ка­на­лу связи со­об­ще­ния, со­сто­я­ще­го толь­ко из сим­во­лов А, Б, В и Г, ис­поль­зу­ет­ся по­сим­воль­ное ко­ди­ро­ва­ние: А-10, Б-11, В-110, Г-0. Через канал связи пе­ре­даётся со­об­ще­ние: ВАГ­БА­А­ГВ. За­ко­ди­руй­те со­об­ще­ние дан­ным кодом. По­лу­чен­ное дво­ич­ное число пе­ре­ве­ди­те в шест­на­дца­те­рич­ный вид.

            1) D3A6

2) 62032206

3) 6A3D

4) CADBAADC

 

Решение:

За­ко­ди­ру­ем по­сле­до­ва­тель­ность букв: ВАГ­БА­А­ГВ — 1101001110100110. Разобьем это пред­став­ле­ние на четвёрки спра­ва на­ле­во и пе­ре­ведём каждую четверку в шестнадцатеричное число:

 

1101 0011 1010 0110₂ = D3A6₁₆

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

Расшифровка сообщений

Пример 3.

Для 5 букв ла­тин­ско­го ал­фа­ви­та за­да­ны их дво­ич­ные коды (для не­ко­то­рых букв – из двух бит, для не­ко­то­рых – из трех). Эти коды пред­став­ле­ны в таб­ли­це:

 

a	b	c	d	e
100	110	011	01	10

Опре­де­ли­те, какой набор букв за­ко­ди­ро­ван дво­ич­ной стро­кой 1000110110110, если из­вест­но, что все буквы в по­сле­до­ва­тель­но­сти – раз­ные:

1) cbade

2) acdeb

3) acbed

4) bacde

 

Решение:

Мы видим, что усло­вия Фано и об­рат­ное усло­вие Фано не вы­пол­ня­ют­ся, зна­чит код можно рас­ко­ди­ро­вать не­од­но­знач­но.

Значит, будем перебирать варианты, пока не получим подходящее слово :

1) 100 011 01 10 110

Пер­вая буква опре­де­ля­ет­ся од­но­знач­но, её код 100: a.

Пусть вто­рая буква — с, тогда сле­ду­ю­щая буква — d, потом — e и b.

Такой ва­ри­ант удо­вле­тво­ряет усло­вию, зна­чит, окон­ча­тель­но по­лу­чи­ли ответ: acdeb.

 

Ответ: 2

Пример 4.

Для пе­ре­да­чи дан­ных по ка­на­лу связи ис­поль­зу­ет­ся 5-би­то­вый код. Со­об­ще­ние со­дер­жит толь­ко буквы А, Б и В, ко­то­рые ко­ди­ру­ют­ся сле­ду­ю­щи­ми ко­до­вы­ми сло­ва­ми: А — 11010, Б — 10111, В — 01101.

При пе­ре­да­че воз­мож­ны по­ме­хи. Од­на­ко не­ко­то­рые ошиб­ки можно по­пы­тать­ся ис­пра­вить. Любые два из этих трёх ко­до­вых слов от­ли­ча­ют­ся друг от друга не менее чем в трёх по­зи­ци­ях. По­это­му если при пе­ре­да­че слова про­изо­шла ошиб­ка не более чем в одной по­зи­ции, то можно сде­лать обос­но­ван­ное пред­по­ло­же­ние о том, какая буква пе­ре­да­ва­лась. (Го­во­рят, что «код ис­прав­ля­ет одну ошиб­ку».) На­при­мер, если по­лу­че­но ко­до­вое слово 10110, счи­та­ет­ся, что пе­ре­да­ва­лась буква Б. (От­ли­чие от ко­до­во­го слова для Б толь­ко в одной по­зи­ции, для осталь­ных ко­до­вых слов от­ли­чий боль­ше.) Если при­ня­тое ко­до­вое слово от­ли­ча­ет­ся от ко­до­вых слов для букв А, Б, В более чем в одной по­зи­ции, то счи­та­ет­ся, что про­изо­шла ошиб­ка (она обо­зна­ча­ет­ся ‘х’).

 

По­лу­че­но со­об­ще­ние 11000 11101 10001 11111. Де­ко­ди­руй­те это со­об­ще­ние — вы­бе­ри­те пра­виль­ный ва­ри­ант.

 

1) АххБ

2) АВхБ

3) хххх

4) АВББ

 

Решение:

Де­ко­ди­ру­ем каж­дое слово со­об­ще­ния. Пер­вое слово: 11000 от­ли­ча­ет­ся от буквы А толь­ко одной по­зи­ци­ей. Вто­рое слово: 11101 от­ли­ча­ет­ся от буквы В толь­ко одной по­зи­ци­ей. Тре­тье слово: 10001 от­ли­ча­ет­ся от любой буквы более чем одной по­зи­ци­ей. Четвёртое слово: 11111 от­ли­ча­ет­ся от буквы Б толь­ко одной по­зи­ци­ей.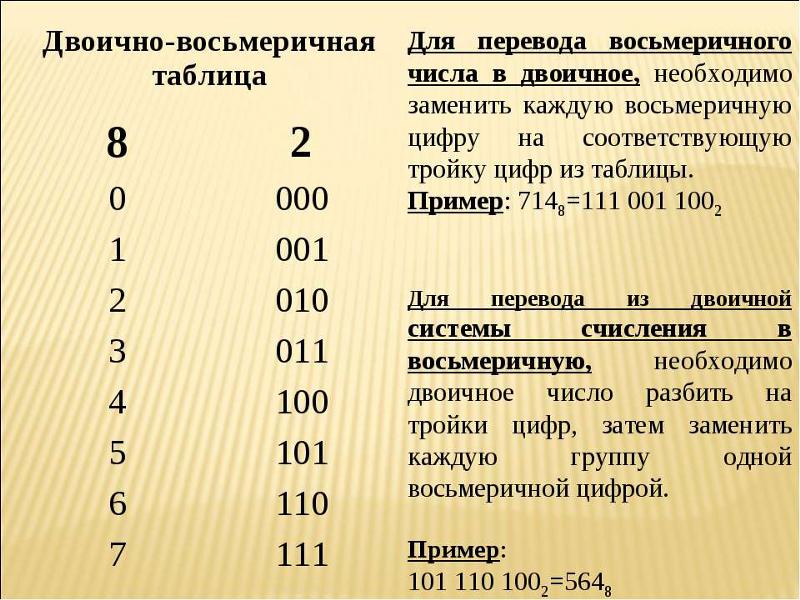

Таким об­ра­зом, ответ: АВхБ.

Ответ: 2

Однозначное кодирование

Пример 5.

Для пе­ре­да­чи по ка­на­лу связи со­об­ще­ния, со­сто­я­ще­го толь­ко из букв А, Б, В, Г, ре­ши­ли ис­поль­зо­вать не­рав­но­мер­ный по длине код: A=1, Б=01, В=001. Как нужно за­ко­ди­ро­вать букву Г, чтобы длина кода была ми­ни­маль­ной и до­пус­ка­лось од­но­знач­ное раз­би­е­ние ко­ди­ро­ван­но­го со­об­ще­ния на буквы?

1) 0001

2) 000

3) 11

4) 101

 

Решение:

Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:

 

Видим, что ближайший от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.

Ответ: 2

Пример 6.

Для ко­ди­ро­ва­ния не­ко­то­рой по­сле­до­ва­тель­но­сти, со­сто­я­щей из букв У, Ч, Е, Н, И и К, ис­поль­зу­ет­ся не­рав­но­мер­ный дво­ич­ный пре­фикс­ный код. Вот этот код: У — 000, Ч — 001, Е — 010, Н — 100, И — 011, К — 11. Можно ли со­кра­тить для одной из букв длину ко­до­во­го слова так, чтобы код по-преж­не­му остал­ся пре­фикс­ным? Коды осталь­ных букв ме­нять­ся не долж­ны.

Вы­бе­ри­те пра­виль­ный ва­ри­ант от­ве­та.

При­ме­ча­ние. Пре­фикс­ный код — это код, в ко­то­ром ни одно ко­до­вое слово не яв­ля­ет­ся на­ча­лом дру­го­го; такие коды поз­во­ля­ют од­но­знач­но де­ко­ди­ро­вать по­лу­чен­ную дво­ич­ную по­сле­до­ва­тель­ность.

1) ко­до­вое слово для буквы Е можно со­кра­тить до 01

2) ко­до­вое слово для буквы К можно со­кра­тить до 1

3) ко­до­вое слово для буквы Н можно со­кра­тить до 10

4) это не­воз­мож­но

 

Решение:

Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:

 

Легко заметить, что если букву Н перенести в вершину 10, она останется листом.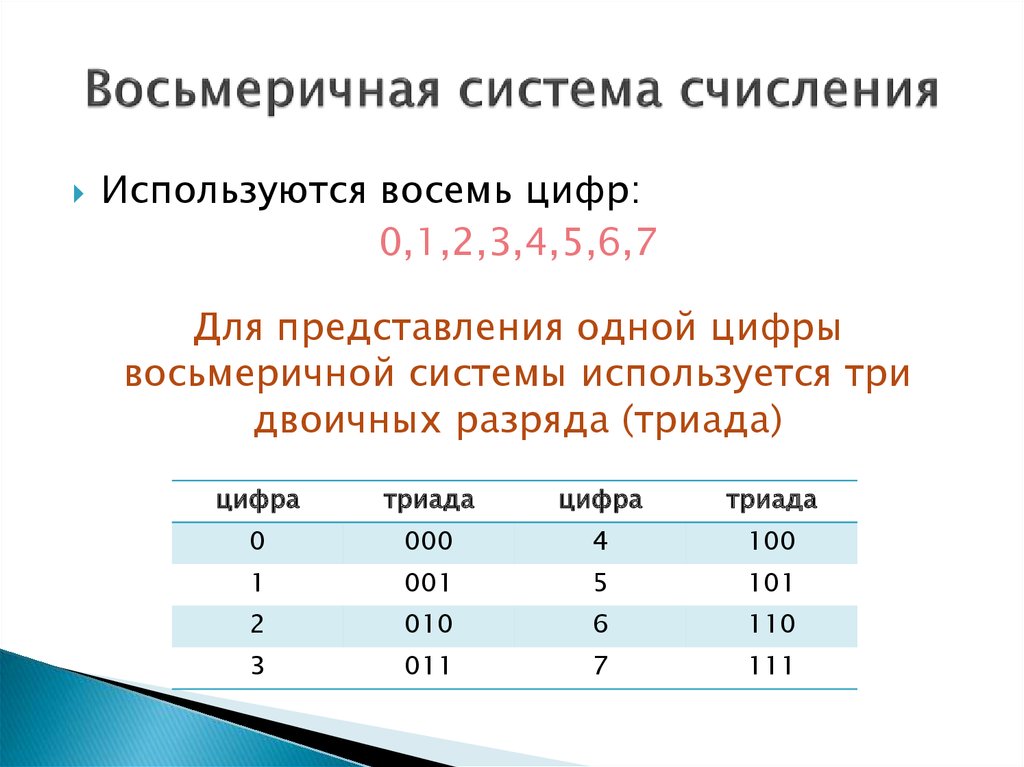 Т.е. ко­до­вое слово для буквы Н можно со­кра­тить до 10.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 06.02.2023

Таблица ASCII

       Десятичное восьмеричное шестнадцатеричное двоичное значение
       ------- ----- --- ------ -----
         000 000 000 00000000 NUL (Нулевой символ)
         001 001 001 00000001 SOH (начало заголовка)
         002 002 002 00000010 STX (начало текста)
         003 003 003 00000011 ETX (конец текста)
         004 004 004 00000100 EOT (конец передачи)
         005 005 005 00000101 ENQ (Запрос)
         006 006 006 00000110 ACK (Подтверждение)
         007 007 007 00000111 БЕЛ (Колокол)
         008 010 008 00001000 БС (Backspace)
         009011 009 00001001 HT (горизонтальная вкладка)
         010 012 00A 00001010 LF (перевод строки)
         011 013 00B 00001011 VT (вертикальная вкладка)
         012 014 00C 00001100 FF (подача листа)
         013 015 00D 00001101 CR (возврат каретки)
         014 016 00E 00001110 SO (Выход из смены)
         015 017 00F 00001111 СИ (Сдвиг В)
         016 020 010 00010000 DLE (выход канала передачи данных)
         017 021 011 00010001 DC1 (XON) (Управление устройством 1)
         018 022 012 00010010 DC2 (Управление устройством 2)
         019023 013 00010011 DC3 (XOFF)(Управление устройством 3)
         020 024 014 00010100 DC4 (Управление устройством 4)
         021 025 015 00010101 NAK (отрицательное подтверждение)
         022 026 016 00010110 SYN (синхронный холостой ход)
         023 027 017 00010111 ETB (конец блока передачи)
         024 030 018 00011000 CAN (Отмена)
         025 031 019 00011001 EM (конец среды)
         026 032 01A 00011010 SUB (заменитель)
         027 033 01B 00011011 ESC (выход)
         028 034 01C 00011100 FS (разделитель файлов)
         029035 01D 00011101 ГС (разделитель групп)
         030 036 01E 00011110 RS (запрос на отправку) (разделитель записей)
         031 037 01F 00011111 США (разделитель блоков)
         032 040 020 00100000 СП (Космос)
         033 041 021 00100001 ! (восклицательный знак)
         034 042 022 00100010 "(двойные кавычки)
         035 043 023 00100011 # (цифровой знак)
         036 044 024 00100100 $ (знак доллара)
         037 045 025 00100101 % (проценты)
         038 046 026 00100110 & (амперсанд)
         039047 027 00100111 '(одинарная кавычка)
         040 050 028 00101000 ( (левая/открывающая скобка)
         041 051 029 00101001 ) (правая/закрывающая скобка)
         042 052 02А 00101010 * (звездочка)
         043 053 02В 00101011 + (плюс)
         044 054 02C 00101100 , (одинарная кавычка)
         045 055 02D 00101101 - (минус или тире)
         046 056 02E 00101110 .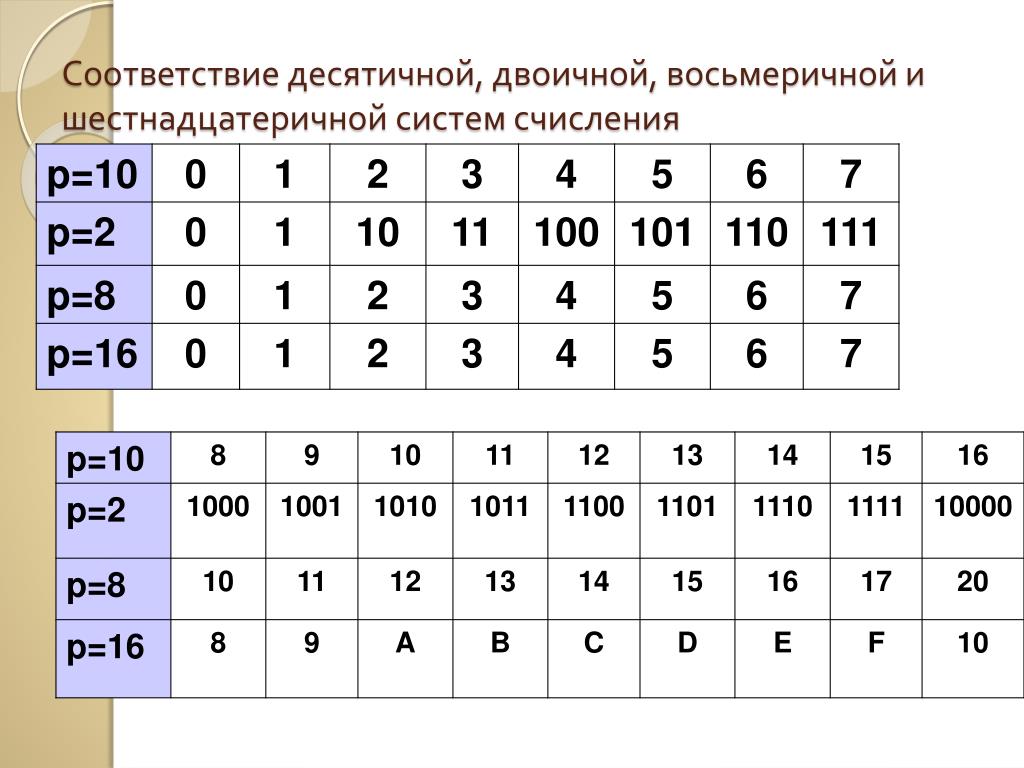  (точка)
         047 057 02F 00101111 / (косая черта)
         048 060 030 00110000 0
         049061 031 00110001 1
         050 062 032 00110010 2
         051 063 033 00110011 3
         052 064 034 00110100 4
         053 065 035 00110101 5
         054 066 036 00110110 6
         055 067 037 00110111 7
         056 070 038 00111000 8
         057 071 039 00111001 9
         058 072 03A 00111010 : (двоеточие)
         059073 03Б 00111011 ; (точка с запятой)
         060 074 03C 00111100 < (меньше чем)
         061 075 03D 00111101 = (знак равенства)
         062 076 03E 00111110 > (больше)
         063 077 03F 00111111 ? (вопросительный знак)
         064 100 040 01000000 @ (символ АТ)
         065 101 041 01000001 А
         066 102 042 01000010 Б
         067 103 043 01000011 С
         068 104 044 01000100 Д
         069105 045 01000101 Э
         070 106 046 01000110 Ф
         071 107 047 01000111 Г
         072 110 048 01001000 Ч
         073 111 049 01001001 Я
         074 112 04А 01001010 Дж
         075 113 04Б 01001011 К
         076 114 04C 01001100 л
         077 115 04Д 01001101 М
         078 116 04Е 01001110 Н
         079 117 04Ф 01001111 О
         080 120 050 01010000 Р
         081 121 051 01010001 В
         082 122 052 01010010 Р
         083 123 053 01010011 С
         084 124 054 01010100 Т
         085 125 055 01010101 У
         086 126 056 01010110 В
         087 127 057 01010111 Вт
         088 130 058 01011000 Х
         089(карет/цирумфлекс)
         095 137 05F 01011111 _ (подчеркивание)
         096 140 060 01100000`
         097 141 061 01100001 а
         098 142 062 01100010 б
         099 143 063 01100011 с
         100 144 064 01100100 д
         101 145 065 01100101 е
         102 146 066 01100110 ф
         103 147 067 01100111 г
         104 150 068 01101000 ч
         105 151 061001 я
         106 152 06А 01101010 ж
         107 153 06Б 01101011 к
         108 154 06С 01101100 л
         109 155 06Д 01101101 м
         110 156 06Е 01101110 н
         111 157 06Ф 01101111 о
         112 160 070 01110000 р
         113 161 071 01110001 q
         114 162 072 01110010 р
         115 163 073 01110011 с
         116 164 074 01110100 т
         117 165 075 01110101 у
         118 166 076 01110110 в
         119167 077 01110111 ш
         120 170 078 01111000 х
         121 171 079 01111001 г
         122 172 07А 01111010 з
         123 173 07B 01111011 { (левая/открывающая скобка)
         124 174 07С 01111100 | (вертикальная полоса)
         125 175 07D 01111101 } (правая/закрывающая скобка)
         126 176 07E 01111110 ~ (тильда)
         127 177 07F 01111111 ДЕЛ (удалить)
 

Вернуться к началу

Ссылки по теме

• ASCII-диаграмма (Джим Прайс)
• ASCII-код (Эрик Остергаард)
• Краткая история кодов символов (Стивен Сирл)
• Как появился ASCII (от Боба Бемера)
• 1963: Дебют ASCII (от Мэри Брандел)
• Американский национальный институт стандартов (Ansi. org)
• Коды Ascii для Visual Studio (от Microsoft)
• Таблица ASCII — ISO 8859-1 (Latin-1) с именами объектов HTML (от bbsinc)
• Таблица Ascii, расширенные коды Ascii и IBM Scancodes (от RPI)
• Десятичный код Ascii для HTML (с сайта efn.org)
• Расширенная диаграмма Ascii (с qc.ca)
• Коды Ascii и HTML (из ascii.cl)
• Домашняя страница Юникода
• Asciitable.com
• Многоязычный Интернет (от Гейба Бокора)

Двоичный/десятичный/шестнадцатеричный/восьмеричный преобразователь

Двоичный/десятичный/шестнадцатеричный/восьмеричный преобразователь

Главная›Преобразование›Преобразование чисел›Шестнадцатиричный/десятичный/восьмеричный/двоичный преобразователь

Числовой формат NumberSigned 8-bitSigned 16-bitSigned 32-bitSigned 64-bit

Биты переключения

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Двоичный

Десятичный

* Числа со знаком являются дополнением до 2.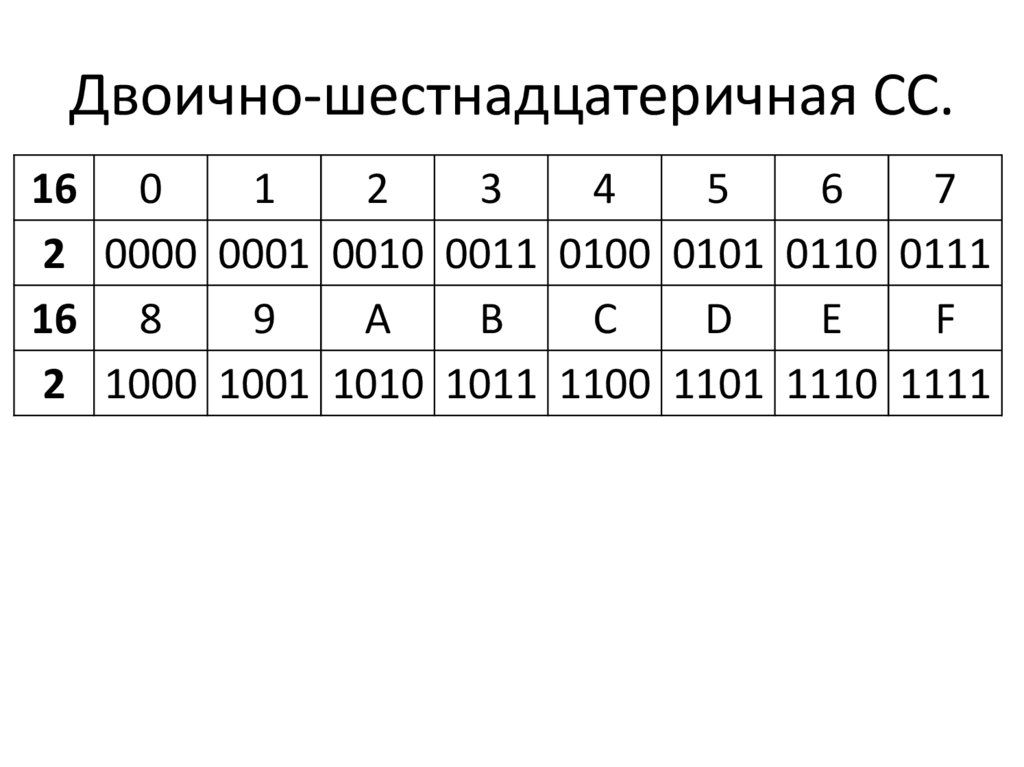

ASCII, шестнадцатеричный, двоичный, десятичный преобразователь ►

Таблица преобразования шестнадцатеричного / десятичного / восьмеричного / двоичного числа

Шестнадцатеричный	Десятичный	Восьмеричный	Двоичный
0	0	0	0
1	1	1	1
2	2	2	10
3	3	3	11
4	4	4	100
5	5	5	101
6	6	6	110
7	7	7	111
8	8	10	1000
9	9	11	1001
А	10	12	1010
Б	11	13	1011
С	12	14	1100
Д	13	15	1101
Е	14	16	1110
Ф	15	17	1111
10	16	20	10000
20	32	40	100000
40	64	100	1000000
80	128	200	10000000
100	256	400	100000000
200	512	1000	1000000000
400	1024	2000	10000000000

 

Базовый преобразователь ►

 

---

См.