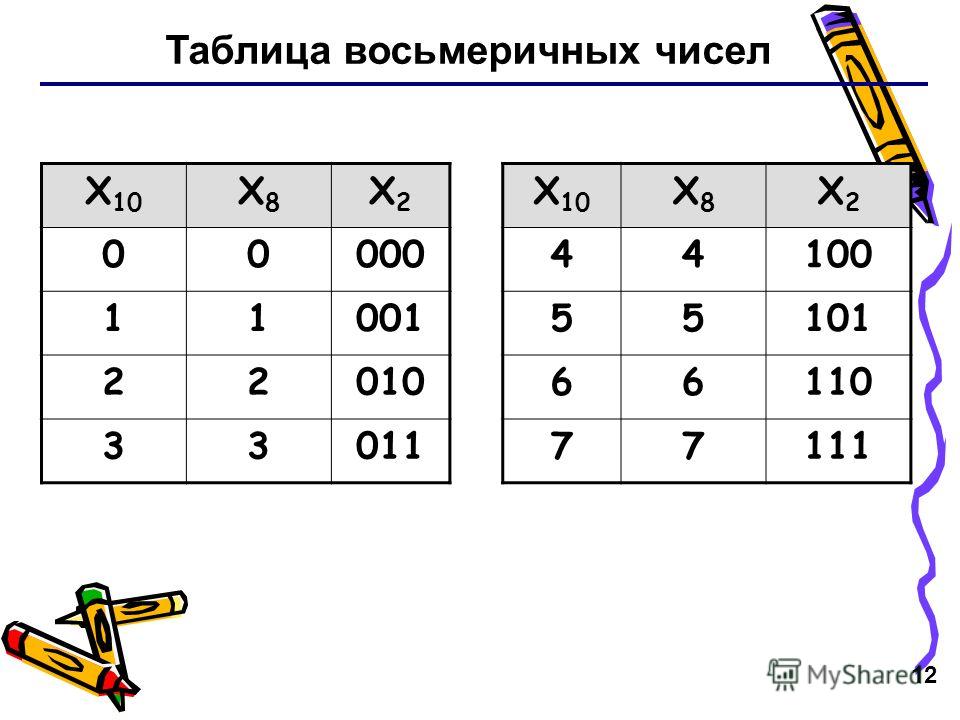
Таблица восьмеричных чисел: Таблица перевода двоичных, восьмеричных, десятичных (от 1 до 255) и шестнадцатеричных чисел. Binary, Octal and Hexadecimal Numbers vs Decimal Numbers

Таблица восьмеричных чисел от 0 до 128

Таблица восьмеричных чисел от 0 до 128

Главная > ч >

десят. число	восьмеричное число
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	10
9	11
10	12
11	13
12	14
13	15
14	16
15	17
16	20
17	21
18	22
19	23
20	24
21	25
22	26
23	27
24	30
25	31
26	32
27	33
28	34
29	35
30	36
31	37
32	40
33	41
34	42
35	43
36	44
37	45
38	46
39	47
40	50
41	51
42	52
43	53
44	54
45	55
46	56
47	57
48	60
49	61
50	62
51	63
52	64
53	65
54	66
55	67
56	70
57	71
58	72
59	73
60	74
61	75
62	76
63	77
64	100
65	101
66	102
67	103
68	104
69	105
70	106
71	107
72	110
73	111
74	112
75	113
76	114
77	115
78	116
79	117
80	120
81	121
82	122
83	123
84	124
85	125
86	126
87	127
88	130
89	131
90	132
91	133
92	134
93	135
94	136
95	137
96	140
97	141
98	142
99	143
100	144
101	145
102	146
103	147
104	150
105	151
106	152
107	153
108	154
109	155
110	156
111	157
112	160
113	161
114	162
115	163
116	164
117	165
118	166
119	167
120	170
121	171
122	172
123	173
124	174
125	175
126	176
127	177
128	200

Ряд восьмеричных чисел от 0 до 128

0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 24, 25, 26, 27, 30, 31, 32, 33, 34, 35, 36, 37, 40, 41, 42, 43, 44, 45, 46, 47, 50, 51, 52, 53, 54, 55, 56, 57, 60, 61, 62, 63, 64, 65, 66, 67, 70, 71, 72, 73, 74, 75, 76, 77, 100, 101, 102, 103, 104, 105, 106, 107, 110, 111, 112, 113, 114, 115, 116, 117, 120, 121, 122, 123, 124, 125, 126, 127, 130, 131, 132, 133, 134, 135, 136, 137, 140, 141, 142, 143, 144, 145, 146, 147, 150, 151, 152, 153, 154, 155, 156, 157, 160, 161, 162, 163, 164, 165, 166, 167, 170, 171, 172, 173, 174, 175, 176, 177, 200

 

Информатика.

Таблица перевода шестнадцатеричных чисел в двоичные — Студопедия

Поделись  

Таблица перевода шестнадцатеричных чисел в двоичные

Таблица перевода восьмеричных чисел в двоичные

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратный перевод чисел.

Перевод чисел из одной системы счисления в другую

Операция сдвига по разрядной сетке

В компьютерах, кроме операции алгебраического суммирования двоичных чисел, к которой относятся операции сложения и вычитания, выполняется операция сдвига числа по разрядной сетке влево и вправо, осуществляющая, фактически, умножение и деление двоичных чисел.

В случае сдвига влево осуществляется умножение двоичного числа на 2^j, а при сдвиге вправо – деление на 2^j, где j – количество разрядов, на которое сдвигается двоичное число.

Например, осуществить сдвиг на 2 разряда

1) 000011₂ = 3₁₀ влево

001100₂ = 12₁₀

т. е. 3 х 4(2²) = 12₁₀

2) 001000₂ = 8₁₀ вправо

000010₂ = 2₁₀

т. е. 8 : 4(2²) = 2₁₀

В компьютерах часто используется циклический сдвиг, при выполнении которого разрядная сетка, отведенная для операнда (числа, над которым производится действие), представляется замкнутой в кольцо. Тогда при сдвиге влево содержимое старшего разряда попадает в младший разряд операнда, а при сдвиге вправо содержимое младшего разряда попадает в старший разряд операнда.

Правила перевода чисел из двоичной системы в восьмеричную, шестнадцатеричную и обратно достаточно просты, поскольку основания восьмеричной и шестнадцатеричной систем счисления выражаются целой степенью двойки: 8 = 2

3, 16 = 2⁴.

восьмеричное число	двоичное число

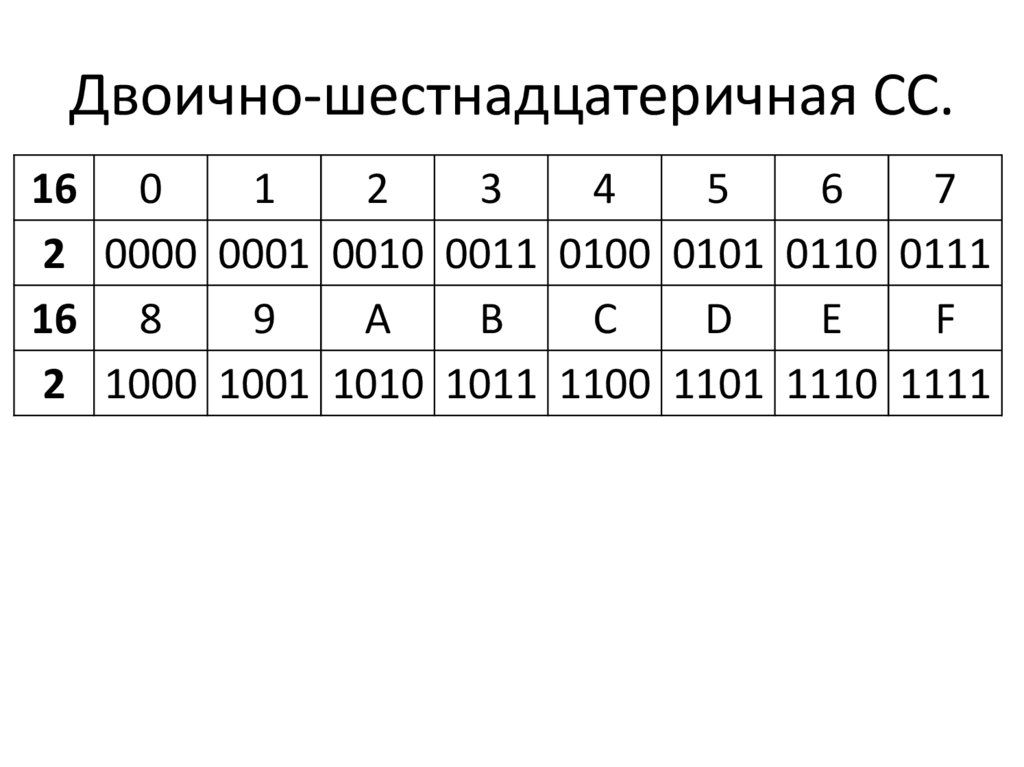
шестнадцатеричное число	двоичное число
A (10)
B (11)
C (12)
D (13)
E (14)
F (15)

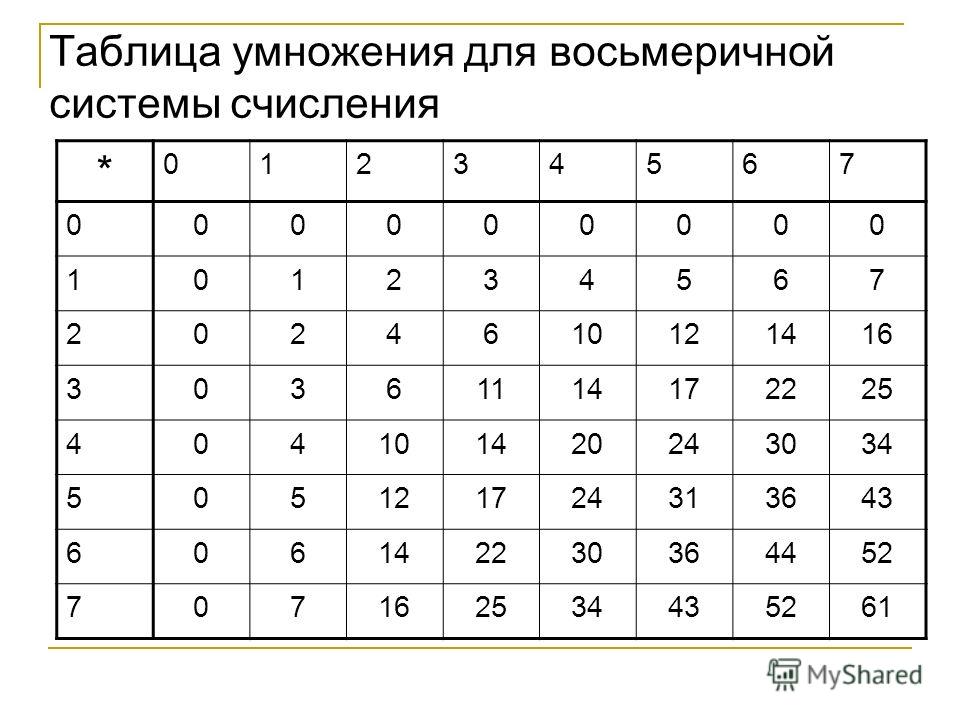
4. 1.1. Перевод чисел из восьмеричной системы счисления в двоичнуюосуществляется представлением каждой цифры восьмеричного числа трехразрядным двоичным числом – триадой.

762,35₈ = 111 110 010, 011 101₂

4.1.2. Перевод шестнадцатеричных чисел в двоичную систему счисления

осуществляется представлением каждой цифры шестнадцатеричного числа четырехразрядными двоичными числами – тетрадами.

A7B,C7₁₆ = 1010 0111 1011, 1100 0111₂

Перевести в двоичную систему счисления:

_1. 27,23435₈ = 010 111, 010 011 100 011 101₂

_2. 302,673₈ = 011 000 010, 110 111 011₂

_3. 23А4,09C7₁₆ = 0010 0011 1010 0100, 0000 1001 1100 0111₂

_4. 177,246₈ = 001 111 111, 010 100 110₂

_5. 732,075₈ = 111 011 010, 000 111 101₂

_6. ССА8,9А3₁₆ = 1100 1100 1010 1000, 1001 1010 0011₂

_7. 7F01,ВA6E₁₆ = 0111 1111 0000 0001, 1011 1010 0110 1110₂

4.1.3. Перевод чисел из двоичной системы счисления в восьмеричную или шестнадцатеричную систему

осуществляется представлением разрядов двоичного числа, которые разбиваются на группы по три разряда при переводе в восьмеричную систему или по четыре разряда при переводе в шестнадцатеричную систему, отсчитывая от запятой влево и вправо; неполные крайние группы дополняются нулями; затем каждая двоичная группа представляется цифрой той системы счисления, в которую переводится число.

001 111, 101 010₂ = 17,52₈

0101 1100, 1011 011₂ = 5C,B6₁₆

Перевести в восьмеричную:

_1. 10111, 010011100011101₂ = 010 111, 010 011 100 011 101₂ = 27,23435₈

2. 11000010, 110111011₂ = 011 000 010, 110 111 011₂ = 302,673₈

_3. 1111, 110100110011110011₂ = 001 111, 110 100 110 011 110 011

2 = 17,646363₈

4. 1011010010, 00101101₂ = 001 011 010 010, 001 011 010₂ = 1322,132₈

Перевести в шестнадцатеричную:

_1. 10001110100100, 0000100111000111₂ = 0010 0011 1010 0100, 0000 1001 1100 0111₂ = 23А4,09C7₁₆

_2. 1010111101010110, 0011000100011011₂ = 1010 1111 0101 0110, 0011 0001 0001 1011₂ = АF56,311В₁₆

_3. 11001110110100, 0010011100111₂ = 0011 0011 1011 0100, 1010 0111 0011 1000₂ = 33B4,A738₁₆

4. 10111110101110, 0010001000101₂ = 0010 1111 1010 1110, 0010 0010 0010 1000₂ = 2FAE,2228₁₆



Решенные примеры восьмеричного умножения

Поиск в этом блоге

Примеры решения карты Карно (K-Map с тремя, четырьмя и пятью переменными)

Примеры решенных карт Karnaugh Примеры решенных карт SOP и POS K Map: в этом руководстве есть несколько решенных примеров сопоставления стандартных и нестандартных выражений POS и SOP с K-Map. Я постарался сделать это как можно проще. Сопоставление стандартного POS и SOP с картой Карно: Пример 1: Сопоставьте выражение SOP с тремя переменными: \[\bar A \bar B \bar C+ A \bar B C + \bar ABC+AB \bar C\] Для трех переменных , карта k имеет сетку из 8 ячеек (4×2 или 2×4). Никакое упрощение невозможно. Пример 2: Сопоставьте стандартное выражение SOP с тремя переменными: \[\bar A \bar B \bar C+ \bar AB \bar C+AB \bar C\] Дано другое простое выражение SOP. Непосредственно сопоставьте это. Упрощенное выражение: \[\bar A \bar C+B\bar C\] Пример 3: Сопоставьте выражение POS: \[(A+B+C)(\bar A +\bar B + \bar C)( A +\bar B +C)\] В этом примере задано стандартное выражение POS. Нанесите на карту напрямую. Упрощенное выражение: \[(A+C)(\bar A +\bar B + \bar C)\]   Отображение нестандартного

Примеры решения восьмеричного умножения

• Получить ссылку
• Фейсбук
• Твиттер
• Пинтерест
• Электронная почта
• Другие приложения

Решенные примеры восьмеричного умножения

Это моя третья статья о восьмеричной арифметике. В этой статье я собираюсь объяснить умножение восьмеричных чисел. Я также буду обсуждать умножение с использованием восьмеричной таблицы умножения. Есть мои сообщения о восьмеричном сложении и восьмеричном вычитании.

Ключевые вопросы:

• Как выполнить восьмеричное умножение?

• Как выполнить дробное умножение восьмеричных чисел?

• Обсудить восьмеричную таблицу умножения

Восьмеричная таблица умножения:

X		1	2	3	4	5	6	7
1		1	2	3	4	5	6	7
2		2	4	6	10	12	14	16
3		3	6	11	14	17	22	25
4		4	10	14	20	24	30	34
5		5	12	17	24	31	36	43
6		6	14	22	30	36	44	52
7		7	16	25	34	43	52	61

Примеры восьмеричного умножения:

Процесс умножения восьмеричных чисел такой же, как и в других системах счисления.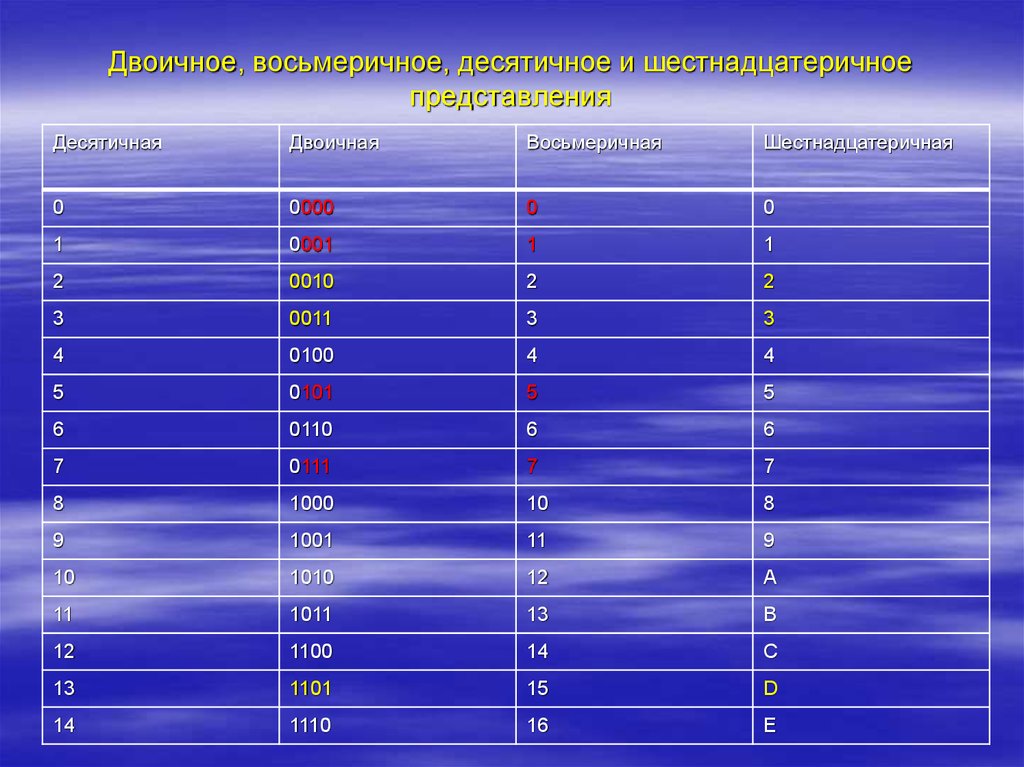 Вы можете проверить свой результат с помощью этого онлайн-конвертера. Моменты, которые вы должны учитывать при умножении восьмеричных чисел:

• Если сумма превышает 7 (0,1,2,3,4,5,6,7), необходимо вычислить эквивалентное восьмеричное значение.

• Разделите число на 8 и найдите эквивалентное восьмеричное число. Частное переносится, а остаток принимается как сумма

  .

Например, 5) 8*6) 8 = 30) 10

5

*6

36) 8

3 ← Коэффициент переноски

8⟌30

24

6 ← Остальная сумма

   

---

Пример № 01: 777) 8*33) 8

2 2 ← Перенесия

7 7 7

*33

1 1 1 ← Перенесия

2 7 7 5

2 7 7 5 x

.

3 2 7 4 5

	6 Десятичное число	Восьмеричный эквивалент	Сумма/остаток	Перенос/частное
7*3	21	21÷8=25	5	2
7*3	21+2	23÷8=27	7	2
7*3	21+2	23÷8=27	7	2
7+5	12	12÷8=14	4	1
7+7+1	15	15÷8=17	7	1
2+7+1	10	10÷8=12	2	1

Ответ: 32745) 8

---

Пример № 02: 466,4) 8*2,7) 8

1 1 1

5 5 3

4 6 6. 4

            *2 . 7

1

4 1 7 5 4

1 1 5 5 0 x

1 5 7 4. 5 4

0059

	Десятичный	Восьмеричный эквивалент	Сумма/остаток	Перенос/частное
7*4	28	28÷8=24	4	2
7*6	42+3	45÷8=5	5	5
7*6	42+5	47÷8=47	7	4
7*4	28+5	33÷8=41	1	4
2*4	8	8÷8=10		1
2*6	12+1	13÷8=15	5	1
2*6	12+1	13÷8=15	5	1
2*4	8+1	9÷8=11	1	1
7+5	12	12÷8=14	6	1

Ответ:1574. 54)8

---

Example#03:3636)8*741)8

Давайте попробуем решить пример с восьмеричной таблицей умножения.

X=3636

Y=741

1*6 найти пересечение 3 и 6. Что равно 6. Аналогично для всех продуктов см. таблицу.

5 3 5

3 1 3

3 6 3 6

*7 4 1

1 1

3 6 3 6

1 7 1 7 0 x

3 2 2 2 2 x

3 4  4 7 7 3 6

Ответ: 3447736)8

Вывод:

Это все об умножении восьмеричных чисел. Я проверил и проверил все ответы и решения. Если вы все же обнаружите какую-либо логическую или типографскую ошибку, пожалуйста, сообщите мне. Если вы считаете этот пост полезным, ставьте лайк.

Рекомендуемые книги

Мои любимые книги моих любимых авторов. Вы можете получить все концепции цифровой электроники в этой книге. Множество примеров, иллюстраций, упражнений, приложений. Эта книга очень проста для понимания от начального до среднего уровня.

• Получить ссылку
• Фейсбук
• Твиттер
• Пинтерест
• Электронная почта
• Другие приложения

популярные посты

Примеры решения восьмеричного сложения

Примеры сложения восьмеричных чисел Это моя первая статья о восьмеричной арифметике. В этом посте я собираюсь объяснить два разных метода сложения восьмеричных чисел. Ключевые вопросы: Как выполнить восьмеричное сложение? Как выполнить сложение дробных восьмеричных чисел? Нарисуйте таблицу восьмеричного сложения. Обсудите два метода восьмеричного сложения. Техника сложения восьмеричных чисел. Существует два метода сложения восьмеричных чисел. Я буду решать каждый пример, используя методы для лучшего понимания. Вы можете проверить свои результаты, используя этот онлайн-калькулятор восьмеричного сложения. Метод № 1: В этом методе вы должны помнить следующие моменты: Думайте о каждом числе как о десятичном числе и добавляйте их как десятичные числа.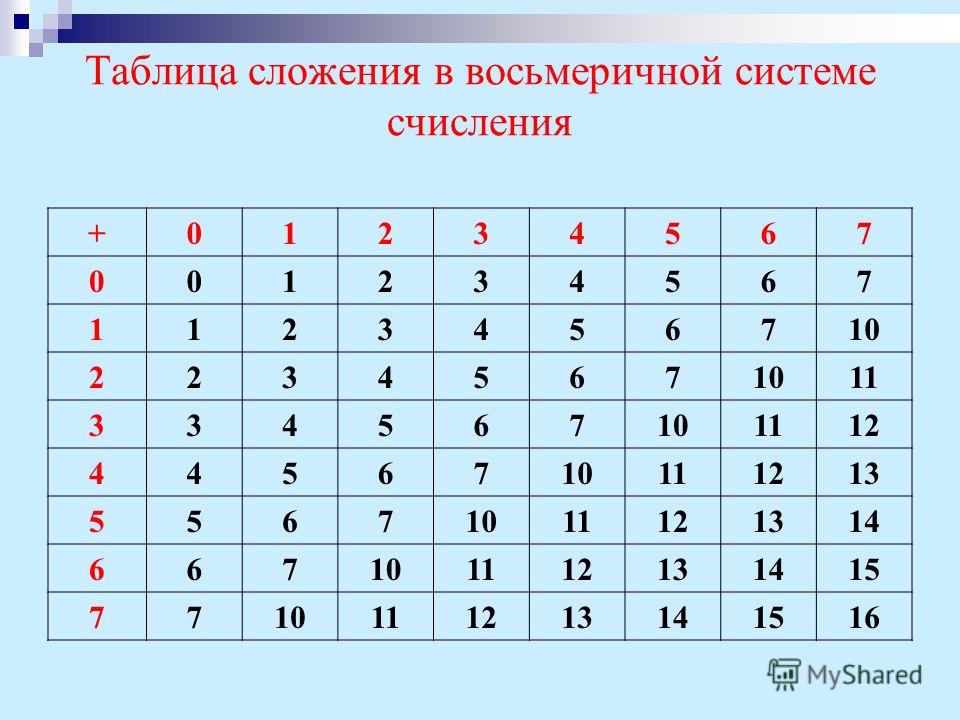 После добавления каждого столбца, если сумма столбца превышает 7, разделите результат на 8, чтобы оценить эквивалентное восьмеричное значение. Остаток будет частью ответа (подсумма), а частное станет переносом. Пример № 01: 167) 8 +765) 8   

Читать далее

Двойственность в электрических цепях

Принцип двойственности в электрических цепях Интересно знать, как системы соотносятся друг с другом. Как механическую систему можно смоделировать как электрическую систему и наблюдать. Понятие двойственности в электрических цепях имеет большое значение. Два явления называются двойственными, если они могут быть выражены одной и той же формой математических уравнений. Эта тема обычно рассматривается в топологии сети или теории графов. Ключевые вопросы: Что такое принцип двойственности в электрических цепях? Список двойных пар и их объяснение. Формирование двойных сетей. Принцип двойственности: принцип двойственности в контексте электрических сетей гласит, что двойственная связь — это связь, в которой ток и напряжение взаимозаменяемы. Две сети двойственны друг другу, если одна из них имеет сетку. уравнение, численно идентичное другим уравнениям узла Список двойных пар: Для оценки двойной сети вы должны следовать следующим пунктам Количество ячеек в

Читать далее

Решенные примеры вычитания восьмеричных чисел

Примеры восьмеричного вычитания Это моя вторая статья о восьмеричной арифметике. В этом посте я объясню вычитание восьмеричных чисел. Вы можете проверить мою статью о восьмеричном сложении. Ключевые вопросы Как выполнить восьмеричное вычитание? Как выполнить дробное восьмеричное вычитание? Как выполнить восьмеричное вычитание, используя дополнение до 8? Примеры восьмеричного вычитания: Метод №1: Уменьшаемое>Вычитаемое Это метод, который мы использовали в элементарной математике. Все правила, которым мы следуем, остаются такими же, как и в других системах счисления. Заем равен основанию системы счисления. Если вы работаете с основанием 2, вы заимствуете 2. Если вы работаете с основанием 8, вы заимствуете 8. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора. Пример#01: 345) 8 -146) 8               8         2     3    8      3 4 5     -1 4 6      1 7 7 1-й столбец (столбец единиц) вычитания. 5-6 Это невозможно. Вы должны заимствовать из столбца десятков. Число

Читать далее

Примеры шестнадцатеричных делений

Примеры шестнадцатеричных делений Это моя четвертая и последняя статья о шестнадцатеричной арифметике. В этом посте я решу несколько примеров по делению шестнадцатеричных чисел. Прежде чем приступить к этой теме, вы должны знать, как умножать шестнадцатеричные числа. Вот моя статья об умножении шестнадцатеричных чисел. Ключевые вопросы: Как выполнить шестнадцатеричное деление? Как выполнить деление на дробные шестнадцатеричные числа? Примеры шестнадцатеричных делений: Деление шестнадцатеричных чисел такое же, как деление в других системах счисления. Все правила и принципы одинаковы. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора. 5÷6  здесь 5 — делимое, а 6 — делитель. Я рассмотрю три случая с помощью трех примеров. В первом случае делимое и делитель являются целыми числами. Во втором случае делимое имеет дробную часть, а делитель — целое число. В третьем случае и делимое, и делитель имеют дробные части. Пример

Читать далее

Примеры шестнадцатеричных умножений

Шестнадцатеричное умножение Это моя третья статья о шестнадцатеричной арифметике. В этом посте я объясню, как умножить два шестнадцатеричных числа. Это так же, как мы умножаем числа в других системах счисления. Прежде чем начать шестнадцатеричное умножение, вы должны знать шестнадцатеричное сложение. Вот мои статьи о шестнадцатеричном сложении и шестнадцатеричном вычитании. Ключевые вопросы: Как выполнить шестнадцатеричное умножение? Как выполнить дробное умножение шестнадцатеричных чисел? Шестнадцатеричная таблица умножения: X 0 1 2 3 4 5 6 7 8 9A B C D E F 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 7 8 9 A B C D E F 2 0 2 4 6 8 A C E 10 12 14 16 18 1A 1C 1E 3 0 3 6 9 C F 12 15 18 1B 1F 21 24 27 2A 2D 4 0 4 8 C 10 14 18 1C 20 24 28 2C 30 34 38 3C 5

Читать далее

Примеры решения восьмеричного деления

Примеры решения восьмеричного деления Это моя четвертая статья о восьмеричной арифметике. В этой статье я собираюсь решить несколько примеров на восьмеричное деление. Это очень простая задача, а принципы и правила деления остаются прежними. Вот статьи о сложении восьмеричных чисел, вычитании восьмеричных чисел и умножении восьмеричных чисел. Ключевые вопросы: Как выполнить деление восьмеричных чисел? Как выполнить дробное деление восьмеричных чисел Примеры восьмеричного деления: Чтобы решить примеры деления, вы должны знать, как выполнять умножение восьмеричных чисел. Буду решать примеры по каждому случаю. Первый случай, когда делимое и делитель являются целыми числами. Второй случай, когда у делимого есть восьмеричная точка, а делитель — целое число. Третий случай, когда и делимое, и делитель имеют числа с плавающей запятой. Вы можете проверить свои результаты с помощью этого онлайн-конвертера. Example#01:6573) 8 ÷16) 8 Сначала мы делаем таблицу для 16 и их кратных чисел. Десятичный восьмеричный

Читать далее

Анализ линии нагрузки (диоды)

В этом руководстве рассматриваются следующие понятия. Описание: Что такое грузовая линия? Как нарисовать линию нагрузки? Что такое характеристическая кривая? Как найти характеристическую кривую? Что такое точка Q? Как узнать его стоимость? Линия нагрузки – прямая. Из этой строки мы можем найти точные значения тока и напряжения диода. Изменяя значение сопротивления и значение приложенного напряжения (это параметры схемы), мы можем перемещать точку Q вверх и вниз по оси Y. Эта прямая линия называется линией нагрузки. При изменении нагрузки изменяется наклон линии нагрузки. Характеристическая кривая или кривая V-I или график напряжение-ток показывают зависимость тока диода от напряжения. Прикладываемое напряжение является независимой переменной и откладывается по оси x, а ток является зависимой переменной и откладывается по оси y. Ниже приведен график V-I диода. Кривая представляет собой ток диода, который быстро увеличивается, когда напряжение приближается к 0,7 В. прямая линия является линией нагрузки.

Читать далее

Матрица набора галстуков | Основная матрица контура — график электрической сети

Это моя третья статья о графах электрических сетей.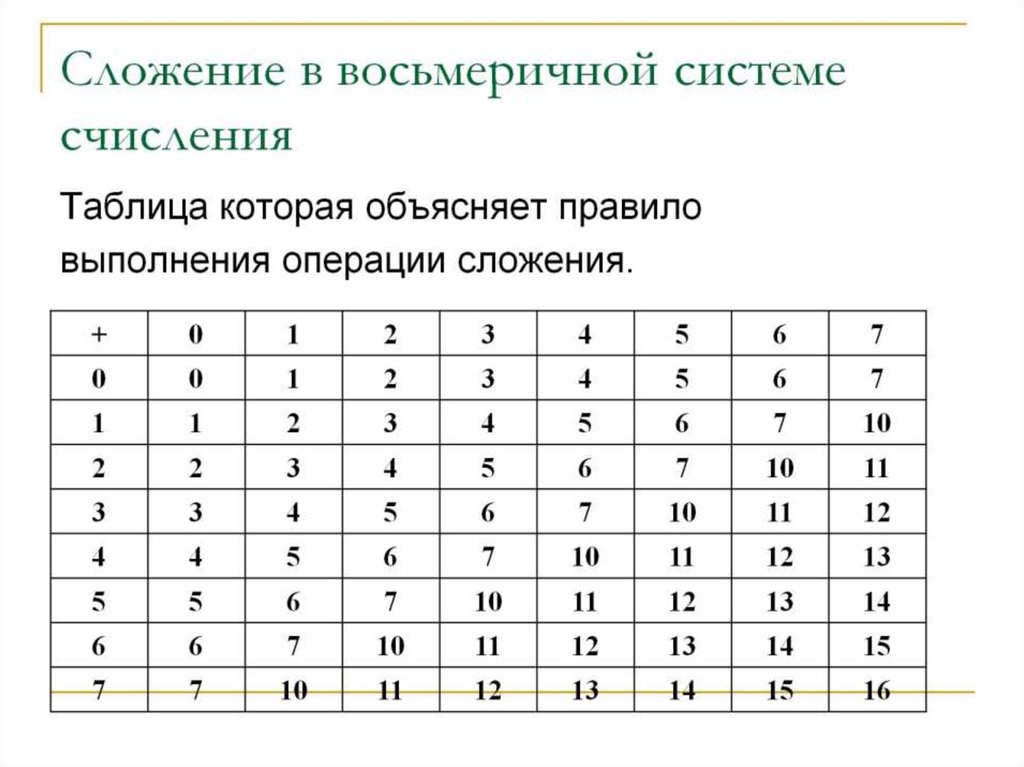 В этой статье я собираюсь объяснить матрицу набора галстуков. Матрица набора связей также известна как матрица фундаментальной петли, матрица цепи и обозначается буквой B. Это набор ветвей, который дает нам замкнутый путь. Это помогает нам определить токи ветвей. Ключевые вопросы: Объясните набор связей или основную петлю Объясните матрицу наборов связей Процедура написания матрицы наборов связей Оцените напряжения ответвлений с помощью матрицы наборов связей, используя KVL Оцените токи ответвлений с помощью матрицы наборов связей, используя KCL Матрица наборов связей и контурные токи: Нарисуйте график вышеприведенной схемы. Связующий набор. Связующий набор – это набор ветвей, содержащихся в цикле. Каждая петля состоит из дерева и звена или хорды. Как известно, в дереве нет ни одного замкнутого пути или петли. Ссылка добавляется в дерево, чтобы соединить два узла и сформировать замкнутый путь. Этот замкнутый путь называется основной петлей. См. рис. 1. Рис. 1 График, т

Читать далее

Шестнадцатеричное вычитание 16 в дополнении

Шестнадцатеричное вычитание Это моя вторая статья о шестнадцатеричной арифметике.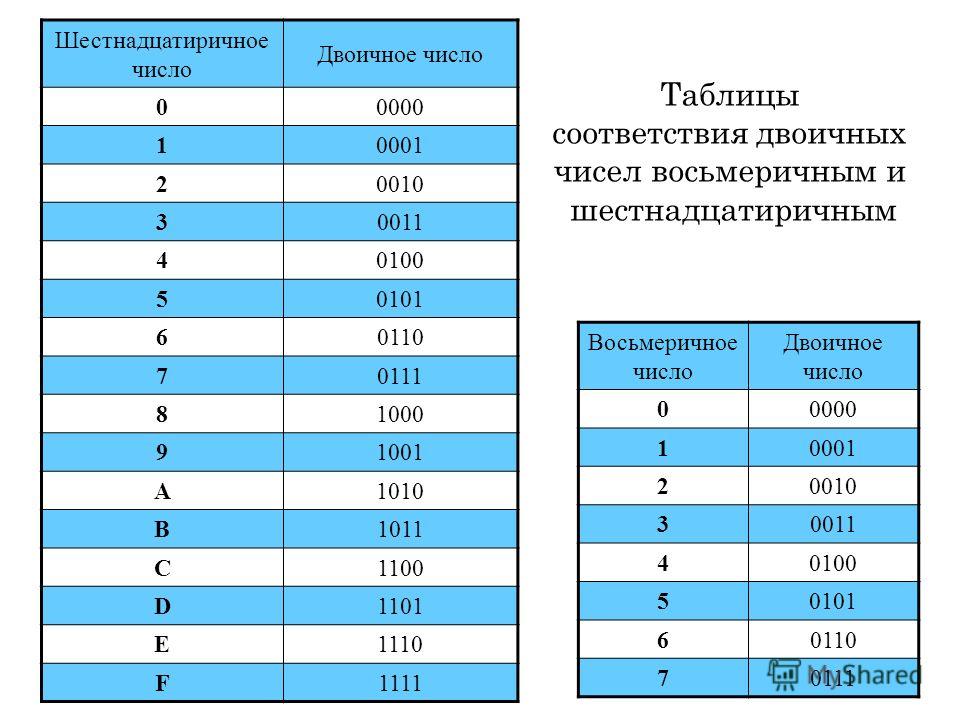 В этой статье я объясню вычитание шестнадцатеричных чисел. Ключевые вопросы: Как выполнить шестнадцатеричное вычитание? Как выполнить вычитание дробных шестнадцатеричных чисел? Как выполнить шестнадцатеричное вычитание с использованием дополнения до 16 Шестнадцатеричный 0 1 2 3 4 5 6 7 8 9A B C D E F Десятичный 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Примеры шестнадцатеричного вычитания: Вычитание шестнадцатеричных чисел такое же, как вычитание в других системах счисления. Правила и принципы точно такие же, как мы учили в начальных классах. Имейте в виду, что при работе с двоичными числами вы заимствуете 2. При работе с восьмеричными числами вы заимствуете 8. При работе с шестнадцатеричными числами вы заимствуете 16 . Вы можете изменить свои результаты, используя этот онлайн-калькулятор. Давайте начнем. Пример#01:578) 16 -34

Читать далее

Восьмеричная система счисления

и преобразование

в

Шриджита Хришикесана • 26 октября 2018 г.

Восьмеричная система счисления:  

В восьмеричной системе счисления основание или основание равно 8, а в качестве основных элементов используются цифры от 0 до 7. Например, 127 — допустимое восьмеричное число. Но 128 — недопустимое число в восьмеричной системе.

Преобразование десятичного числа в эквивалентное ему восьмеричное число

Пример 7: Преобразование десятичного числа 83 в эквивалентное восьмеричное число .

Решение: Мы подготовим таблицу десятично-восьмеричного преобразования, как показано в таблице 1.6, на основе обсуждений в разделе 1.4.2.

Из таблицы 1.6 мы получаем

(83) ₁₀ = (123) ₈

Обращение октального числа в эквивалентный бинарный номер

0873

Чтобы преобразовать восьмеричное число в двоичное, мы сначала преобразуем его в эквивалентное ему десятичное число, которое затем преобразуется в эквивалентное ему двоичное число. Эта процедура проиллюстрирована на примере 8.

Пример 8: Рассмотрим восьмеричное число (123) ₈ . Его десятичное эквивалентное число было получено в примере 6 как (83) ₁₀ . Мы можем преобразовать (83) ₁₀ в двоичный код, как описано в разделе 1.4.2. Однако мы можем выполнить преобразование, используя еще один более простой метод. В этом процессе мы делим 83 на сумму набора десятичных чисел, которые являются степенями числа 2. Например, мы видели, что 2 ⁰ = 1, 2 ¹ = 2, 2 ³ = 8 и так далее. Используя этот принцип, теперь мы размещаем 83 на полномочия 2 следующим образом:

83 = 64 + 16 + 2 + 1

Теперь очень легко преобразовать эти уничтоженные числа в эквивалентный бинар. Таким образом,

           ( 83) ₁₀ = 1 ´ 2 ⁶ + 1 ´ 2 ⁴ + 1 ´ 2 ¹ +1 ´ 2 ⁰ = (1010011) ₂

The above procedure is lengthy and кропотливый. Существует простой и быстрый способ преобразования восьмеричных чисел в двоичные. Для этого сначала подготовим таблицу восьмерично-двоичного преобразования, табл. 1.7, как показано ниже. Восьмеричное число затем вводится в самые верхние ячейки таблицы. Тогда это 9В ячейки второй строки таблицы записывается 1060 3-битных двоичных эквивалентов . Наконец, мы удаляем барьеры в ячейках таблицы и записываем объединенные биты в третью строку таблицы 1.7, как показано, что дает желаемый ответ. Запятые используются в последней строке для обозначения бинарных групп.

Восьмеричное число
Двоичные эквиваленты0094
(123) 8	(001 010 011) 2

From Table 1.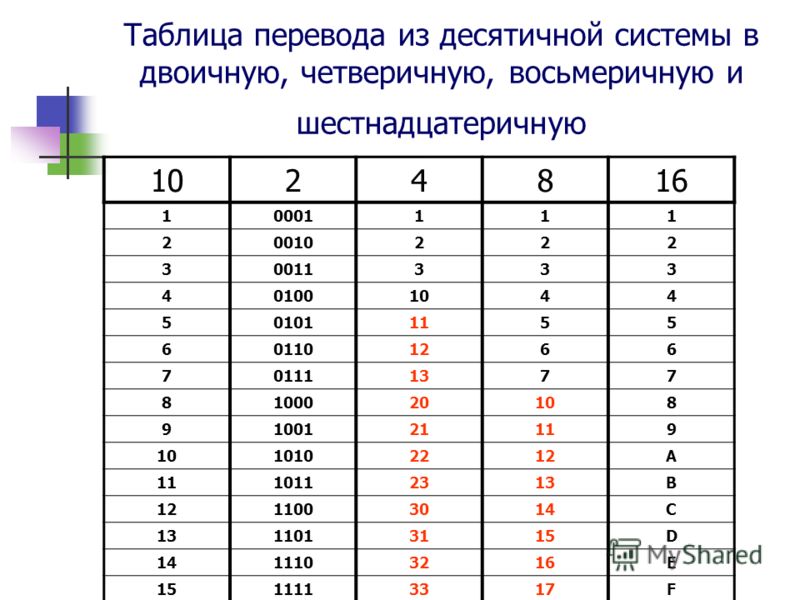 7, we get the desired answer as

   (123) ₈ = (001010011) ₂ = (1010011) ₂

Из примера 8 видно, что очень легко преобразовать восьмеричное число в двоичное. Аналогично, обратный процесс тоже очень быстрый. Для этого мы разделим двоичных чисел на группы по 3 бита в каждой, начиная с самого правого бита, а затем запишем соответствующее десятичное число под этими группами. Окончательный ответ будет восьмеричным эквивалентом двоичного.

Пример 9: Найдите восьмеричный эквивалент (11110100010) ₂ .

Решение: Действуя, как описано выше, мы сначала подготовим таблицу преобразования двоичных чисел в восьмеричные, обозначенную как Таблица 1.8. Чтобы нарисовать столбцы этой таблицы, мы сначала подсчитываем количество битов в данном двоичном числе, а затем делим его на 3.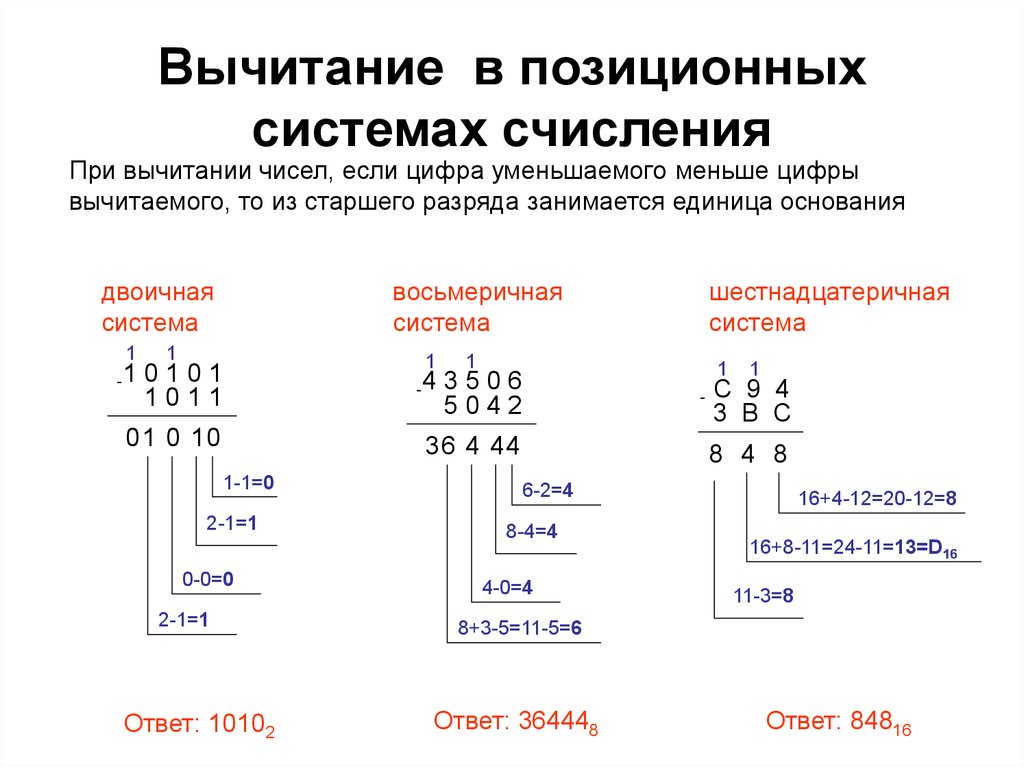 В данной задаче у нас есть 11 бит. Это означает, что имеется три группы по 3 бита в каждой. Оставшиеся два бита образуют четвертую группу. Можно заметить, что процесс группирования начинается с самых правых трех битов и продолжается в левом направлении. Мы можем разделить группы с помощью запятых, как показано ниже:

                                                         11, 110, 100,010

После того, как мы определили группы и их элементы, как показано в таблице 1, нарисуем ее. Сначала вводим заданное двоичное число в первую строку таблицы 1.8. Во второй строке мы делаем записи групп в соответствующих ячейках. Можно заметить, что первая ячейка в этой строке содержит только два бита. Чтобы превратить его в 3-битную группу, мы добавляем 0 (выделено жирным шрифтом) в качестве начального бита, так что данное двоичное число теперь читается как  0 11, 110, 100 010. Понятно, что это 0 не имеет значения; он добавляется только как бит заполнения для формирования 3-битной группы.

Заполнив записи во второй строке таблицы 1.8, переходим к выполнению записей в ячейках третьей строки. В ячейках этой строки мы записываем десятичное число , эквивалентное , под каждой 3-битной группой второй строки. Таким образом, под самой правой группой 010 мы вводим в третью строку ее десятичный эквивалент 2. Продолжая эту операцию, мы вводим 4 под группой 100, 6 под 110 и 3 под 011, как показано. В четвертой строке таблицы 1.2 мы объединяем цифры строки 3, чтобы получить восьмеричное число 3642, эквивалентное двоичному числу 11110100010.

Следует отметить, что приведенное выше объяснение довольно длинное; однако можно заметить, что его реализация выполняется очень быстро, поскольку нет необходимости в каких-либо длинных пояснениях к рисунку таблицы 1.8. Когда принципы понятны, составить таблицу 1.8 несложно.

Таблица 1.8 Двоина-октальное преобразование

Указано двоичное число, разделенное на 3-битные группы	011,110,100,010
Bits in groups
Corresponding octal numbers
Octal equivalent of the given binary number

From Table 1.