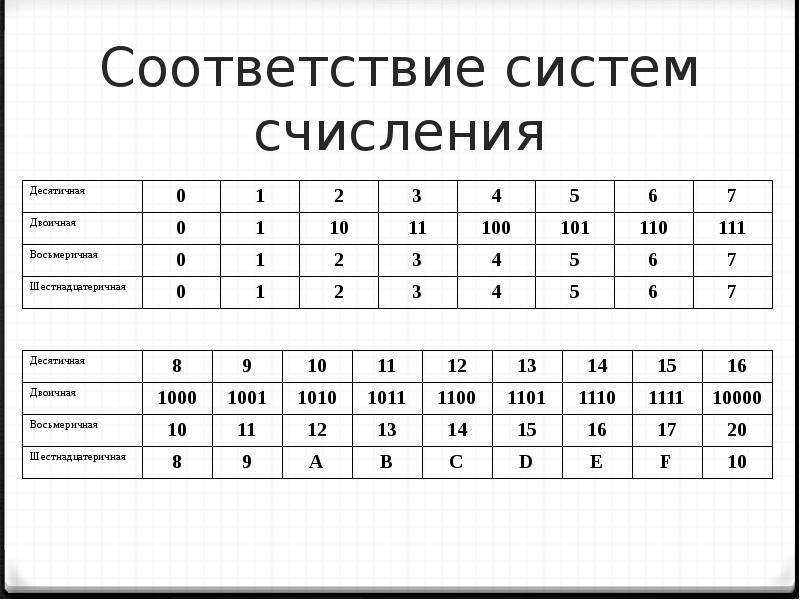
как перевести из 2 в 16
Возникли какие-то трудности и недопонимания с преобразованием чисел из двоичной в шестнадцатеричную систему счисления? Записывайтесь ко мне на индивидуальные уроки по информатике и ИКТ. На своих частных уроках мы с учениками разбираем не только теоретическую часть, но также решаем колоссальное количество различных тематических упражнений.
Нужно знать, что такое двоичная или бинарная система счисления
Прежде чем размышлять о том, как перевести число из 2 в 16, необходимо хорошо понимать, что собою представляют числа в двоичной системе счисления. Напомню, что алфавит бинарной системы счисления состоит из двух допустимых элементов – 0 и 1. Это означает, что абсолютно любое число, записанное в двоичном виде, будет состоять из набора нулей и единиц. Вот примеры чисел, записанных в бинарном представлении: 10010, 100, 111101010110, 1000001.
Нужно знать, что такое шестнадцатеричная система счисления
С бинарной системой мы разобрались, вспомнили базовые моменты, сейчас поговорим о 16-ричной системе. Алфавит 16-ричной системы счисления состоит из шестнадцати различных знаков: 10 арабских цифр (от 0 до 9) и 6 первых заглавных латинских букв (от ‘А’ до ‘F’). Это означает, что абсолютно любое число, записанное в шестнадцатеричном виде, будет состоять из знаков вышеприведенного алфавита. Вот примеры чисел, записанных в 16-ричном представлении:
Алфавит 16-ричной системы счисления состоит из шестнадцати различных знаков: 10 арабских цифр (от 0 до 9) и 6 первых заглавных латинских букв (от ‘А’ до ‘F’). Это означает, что абсолютно любое число, записанное в шестнадцатеричном виде, будет состоять из знаков вышеприведенного алфавита. Вот примеры чисел, записанных в 16-ричном представлении:
| 810A | FCDF | 198303 | 100FFF0 |
Поговорим об алгоритме преобразования числа из 2-ной в 16-ричную систему счисления
Нам потребуется в обязательном порядке рассмотреть кодировочную таблицу Тетрад. Без применения данной таблицы будет довольно затруднительно оперативно осуществлять перевод чисел из 2 в 16 систему.
Назначение кодировочной таблицы Тетрад: однозначно сопоставить символы двоичной системы счисления и 16-ричной системы счисления.
Таблица Тетрад имеет следующую структуру:
Таблица Тетрад | |||||||
0000 — 0 | 0001 — 1 | 0010 — 2 | 0011 — 3 | 0100 — 4 | 0101 — 5 | 0110 — 6 | 0111 — 7 |
1000 — 8 | 1001 — 9 | 1010 — A | 1011 — B | 1100 — C | 1101 — D | 1110 — E | 1111 — F |
Допустим нам требуется преобразовать число 1010111110010102 в 16-ричную систему.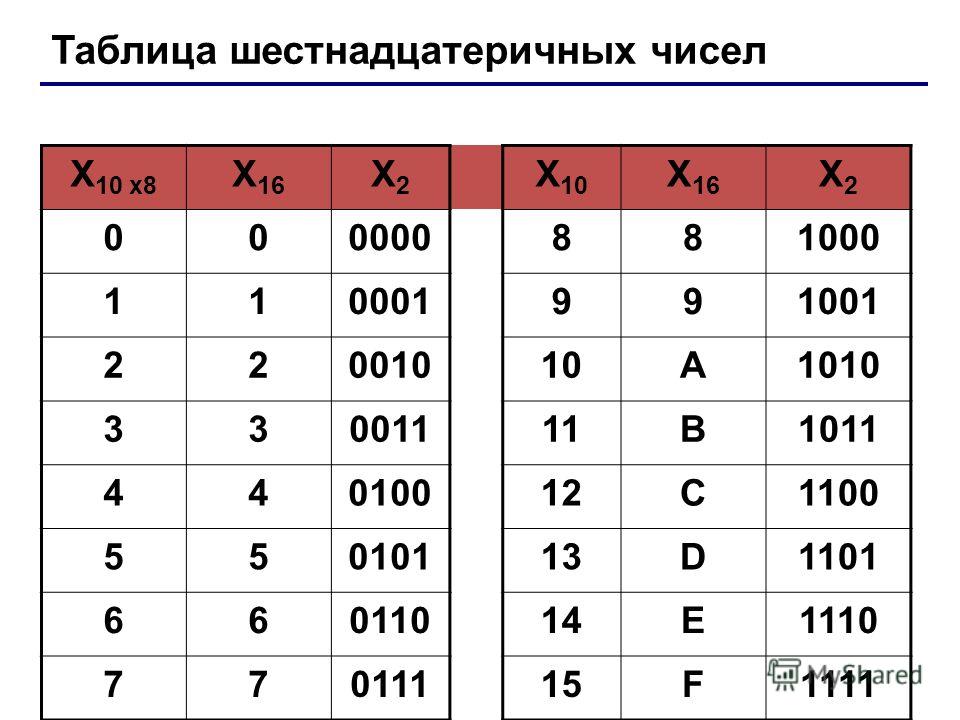 В первую очередь необходимо исходный бинарный код разбить на группы по четыре разряда, причем, что очень важно, разбиение в обязательном порядке следует начинать справа налево.
В первую очередь необходимо исходный бинарный код разбить на группы по четыре разряда, причем, что очень важно, разбиение в обязательном порядке следует начинать справа налево.
101 . 0111 . 1100 . 1010
После разбиения мы получили четыре группы: 101, 0111, 1100 и 1010. Особого внимания требует самый левый сегмент, то есть сегмент 101. Как видно, его длина составляет 3 разряда, а необходимо, чтобы его длина равнялась четырем, следовательно, дополним данный сегмент ведущим незначащим нулем:
101 -> 0101.
Вы скажите, а собственно на каком основании мы дописываем слева от числа какой-то 0? Все дело в том, что добавление незначащих нулей не оказывает никакого влияния на значение исходного числа. Следовательно, мы имеем полное право дописать слева от бинарного числа не только один ноль, а в принципе любое количество нулей и получить число нужной длины.
На заключительном этапе преобразования необходимо каждую из полученных бинарных групп перевести в соответствующее значение по кодировочной таблице Тетрад.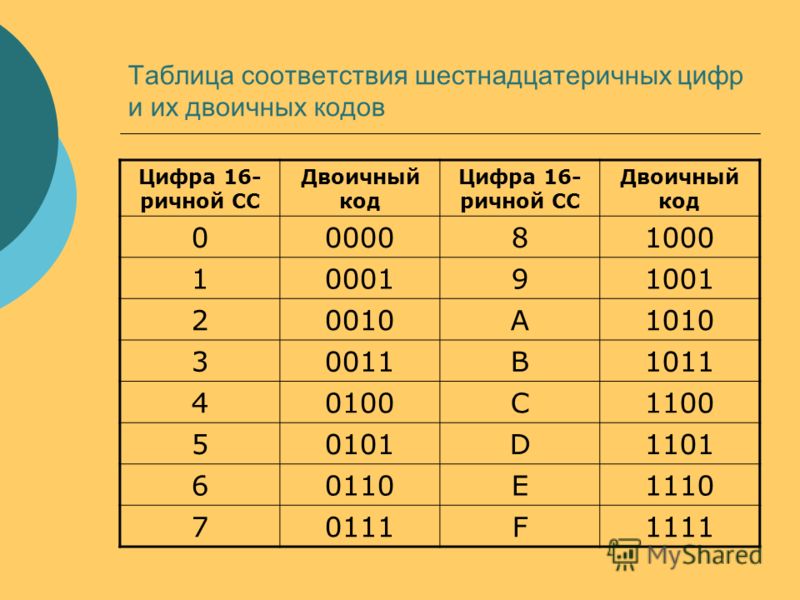
| 0101 -> 5 | 0111 -> 7 | 1100 -> C | 1010 -> A |
1010111110010102 = 57СА16
А сейчас я вам предлагаю ознакомиться с мультимединым решением, в котором показано как неравномерный код преобразуется из бинарного состояния в 16-ричное состояние:
Краткие выводы
В данной небольшой статье мы разобрали тему «Системы счисления: как перевести из 2 в 16». Если у вас остались какие-либо вопросы, недопонимания, то звоните и записывайтесь на мои индивидуальные уроки по информатике и программированию. Я предложу вам решить не один десяток подобных упражнений и у вас не останется ни одного вопроса. Вообще, системы счисления – чрезвычайно важная тема, которая образует фундамент, используемый на протяжении всего курса информатики.
Функция ОСНОВАНИЕ в Excel переводит число в систему счисления
Функция ОСНОВАНИЕ выполняет преобразование числового значение в указанную систему счисления (двоичная, восьмеричная, шестнадцатеричная и т. д.) и возвращает соответствующий результат в виде текстовой строки.
д.) и возвращает соответствующий результат в виде текстовой строки.
Примеры использования функции ОСНОВАНИЕ в Excel
Пример 1. Для хранения чисел в БД удобно использовать их представление в двоичной системе счисления. Выполнить преобразование представленных значений.
Исходная таблица:
Для преобразования используем формулу:
Описание аргументов:
- B2 – число, которое требуется преобразовать;
- 2 – указатель вида системы счисления.
Выполним преобразование для всех чисел. Полученный результат:
Ошибка #ЧИСЛО! Возникла потому, что -56 находится вне диапазона допустимых значений (отрицательное число). Результат вычисления формулы =ОСНОВАНИЕ(0,9;2) эквивалентен результату =ОСНОВАНИЕ(0;2), поскольку рассматриваемая функция усекает дробные значения аргумента число до целых значений.
Перевод числа из одной системы счисления в другую в Excel
Пример 2. Преобразовать числа, записанные в шестнадцатеричной системе счисления в двоичную систему с длиной полученной строки не менее 20 символов.
Таблица значений:
В Excel предусмотрена формула ШЕСТН.В.ДВ, однако она поддерживает значения из диапазона от FFFFFFFE00 до 1FF. Поэтому выполним промежуточное преобразование в десятичную систему и воспользуемся функцией ОСНОВАНИЕ для перевода в двоичную:
Описание аргументов:
- ШЕСТН.В.ДЕС(A2) – исходное число, преобразованное в десятичную систему счисления;
- 2 – указание на вид системы счисления;
- 20 – минимальное количество символов в возвращаемой строке.
Результаты расчетов:
Сложение чисел в разных системах счисления в Excel
Пример 3. Отобразить результаты сложения двух чисел, записанных в двоичной системе, в виде чисел в десяти- и тридцатидвухричных системах счисления.
Исходная таблица:
В ячейке A6 запишем следующую формулу:
Функция ДВ.В.ДЕС преобразует числа из двоичной в десятеричную систему.
В ячейке B6 запишем формулу:
В данном способе выполняется преобразование в понятную многим десятичную систему счисления, в которой и выполняется операция сложения чисел (вместо, например, алгоритма сложения в столбик в двоичной системе, где необходимо учитывать правила: 0+0=0, 1+1=10 и т.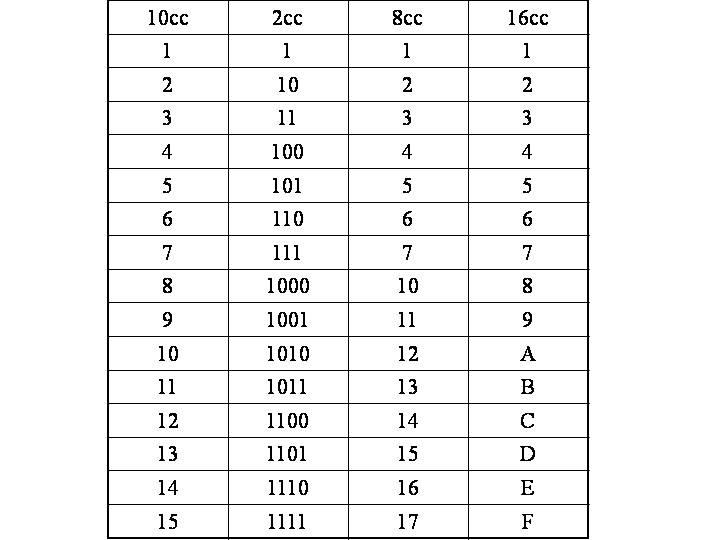 д.). Функцией ОСНОВАНИЕ выполняется преобразование результата в требуемые системы исчисления. Пример расчета:
д.). Функцией ОСНОВАНИЕ выполняется преобразование результата в требуемые системы исчисления. Пример расчета:
Особенности использования функции ОСНОВАНИЕ в Excel
Функция имеет следующую синтаксическую запись:
=ОСНОВАНИЕ(число;основание;[минимальная_длина])
Описание аргументов:
- число – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 0 до 253, которое требуется преобразовать к указанной системе счисления.
- основание – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 2 до 36, которое является основанием требуемой системы исчисления.
- [минимальная_длина] – необязательный аргумент, характеризующий числовое значение из диапазона от 0 до 255, определяющее минимальную длину в символах возвращаемой текстовой строки.
Примечания:
- Функция возвращает код ошибки #ЧИСЛО!, если любой из ее аргументов является числовым значением, выходящим за пределы допустимых для данного аргумента значений.
- Если один или несколько аргументов являются текстовой строкой, рассматриваемая функция вернет код ошибки #ЗНАЧ!.
- Функция доступна только в новых версиях программы (Excel 2013 и более поздних).
- В отличие, например, от функции ДЕС.В.ДВ, которая выполняет преобразование чисел из диапазона от -512 до 511, функция ОСНОВАНИЕ выполняет преобразование чисел от 0 до 2
- При явном указании аргумента [минимальная_длина] возможны следующие ситуации:
- длина полученного значения меньше, чем регламентируется аргументом [минимальная_длина]. В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины;
- длина рассчитанного значения больше, чем регламентируемая. Функция ОСНОВАНИЕ вернет полученный результат, не урезая его. Например, функция с аргументами (12345;2;20) вернет значение «00000011000000111001», а функция с аргументами (12345;2;2) вернет «11000000111001».
Что такое Система счисления? Определение, типы, примеры, факты
Десятичная система счисления состоит из 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 и является наиболее часто используемой системой счисления. Мы используем комбинацию этих 10 цифр для формирования всех остальных чисел. Значение цифры в числе зависит от ее положения в числе. Таблица разрядов для десятичной системы счисления выглядит следующим образом:
Мы используем комбинацию этих 10 цифр для формирования всех остальных чисел. Значение цифры в числе зависит от ее положения в числе. Таблица разрядов для десятичной системы счисления выглядит следующим образом:
Каждый разряд слева в десять раз больше разряда справа от него, то есть при движении справа налево разрядность увеличивается в десять раз с каждое место.
В двоичной системе счисления мы используем только две цифры 0 и 1. Это означает двойную систему счисления.
Каждая цифра двоичного числа называется битом. Итак, двоичное число 101 имеет 3 бита. 499787080
Компьютеры и другие цифровые устройства используют двоичную систему. В двоичной системе счисления используется основание 2.
Слово шестнадцатеричное происходит от Hexa, означающего 6, и десятичного, означающего 10. Итак, в шестнадцатеричной системе счисления 16 цифр. Он состоит из цифр от 0 до 9, а затем имеет первые 5 букв алфавита как:
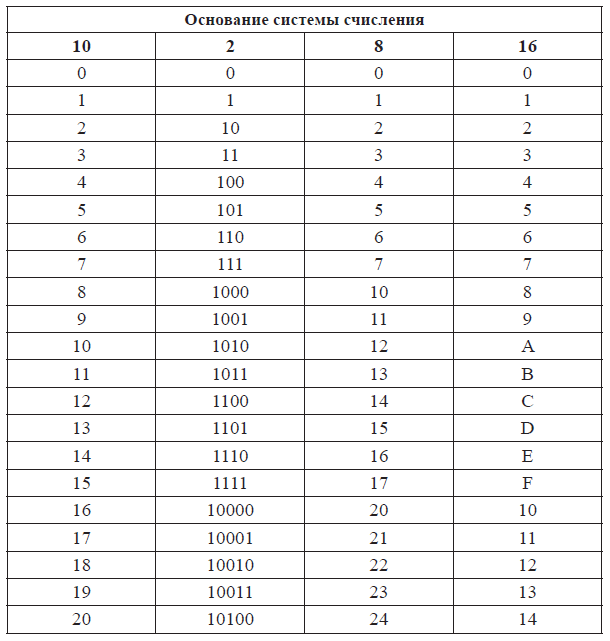
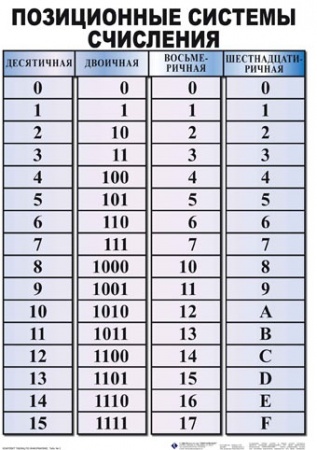
В таблице ниже показаны числа от 1 до 20 с использованием десятичных, двоичных и шестнадцатеричных чисел.
1 Какое число из десятичной системы счисления представляет буква А в шестнадцатеричной системе счисления?15 12 11 10 Правильный ответ: 10 2 Что из следующего НЕ используется для представления чисел в шестнадцатеричной системе счисления?A B M F Правильный ответ: M 3 Сколько уникальных цифр содержит десятичное число система использует для представления всех чисел?10 2 10 16 Правильный ответ: 10 4 Какие два числа из десятичной системы используются в двоичной системе счисления?1 и 2 0 и 1 0 и 9 A и 1 Правильный ответ: 0 и 1 другие числа. |
Какая система счисления используется чаще всего?
Наиболее часто используемой системой счисления является десятичная позиционная система счисления.
Какие системы счисления используют компьютеры?
В компьютерах используются десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
В какой системе счисления используются буквы?
Шестнадцатеричная система счисления использует 6 букв (A, B, C, D, E и F) в дополнение к 10 цифрам от 0 до 9..
Что является основанием шестнадцатеричной системы счисления?
Основание шестнадцатеричной системы счисления 16.
404: Страница не найдена
Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы приносим свои извинения за доставленные неудобства.
Обычно это результат плохой или устаревшей ссылки. Мы приносим свои извинения за доставленные неудобства.
Что я могу сделать сейчас?
Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:
Поиск- Узнайте последние новости.
- Наша домашняя страница содержит самую свежую информацию о Java-разработке.
- Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, TheServerSide.com.
- Если вам нужно, свяжитесь с нами, мы будем рады услышать от вас.
Просмотр по категории
Архитектура приложения
- Учебник по основным концепциям структуры команды разработчиков
Чтобы установить правильный размер команды разработчиков, менеджеры должны учитывать обязанности каждого члена и пути коммуникации, как …
- 10 учебных курсов для подготовки к сертификации по микросервисам
Хотя получить сертификат по архитектуре микросервисов не всегда просто, существует множество курсов, которые вы можете пройти, чтобы .

- Признаки антипаттерна «Золотой молот» и 5 способов его избежать
Антипаттерн «Золотой молот» может подкрасться к команде разработчиков, но есть способы его обнаружить. Изучайте знаки, а также некоторые…
Качество ПО
- 10 основных навыков Скрам-мастера
Скрам-мастера помогают разработчикам Agile, владельцам продуктов и другим членам команды выполнять задачи, начиная от планирования спринта и заканчивая лидерством на службе…
- Salesforce DevOps Center поставляется для обуздания приложений с низким кодом
Salesforce DevOps Center развернут с функциями, предназначенными для обновления пользовательских приложений с низким и профессиональным кодом на его платформе CRM…
- Уязвимости сайта Lego выявляют бреши в безопасности API
Старое снова стало новым: сайт Lego BrickLink был признан уязвимым для межсайтового скриптинга и других хорошо изученных типов .
 ..
..
Облачные вычисления
- Интерпретация и применение рекомендаций AWS Compute Optimizer
Трудно найти правильный баланс между производительностью, доступностью и стоимостью. Узнайте, как включить и применить AWS Compute…
- Взвесьте преимущества и недостатки гибридного хранилища данных
Помимо прочих преимуществ, гибридное облачное хранилище данных может предложить повышенную гибкость и масштабируемость, а также доступ по требованию …
- AWS запускает новые инстансы EC2 на выставке re:Invent 2022
Неправильный тип экземпляра может повлиять на производительность рабочей нагрузки и даже увеличить затраты. В этом году на выставке re:Invent AWS выпустила новый EC2 …
Безопасность
- Вредоносный пакет Python в PyPI выдает себя за SentinelOne SDK
На сегодняшний день не зарегистрировано ни одной атаки, вызванной вредоносным пакетом Python.
 Однако, по данным PyPI, более 1000…
Однако, по данным PyPI, более 1000… - Что такое атаки перечислением и как их предотвратить
Веб-приложения могут быть уязвимы для атак с перечислением пользователей. Узнайте, как работают эти атаки грубой силы и как предотвратить …
- 20 компаний, пострадавших от крупных атак программ-вымогателей в 2021 году Между огромными требованиями выкупа, серьезными сбоями и утечками данных, 2021 год был отмечен большой активностью программ-вымогателей среди компаний и …
ПоискAWS
- AWS Control Tower стремится упростить управление несколькими учетными записями
Многие организации изо всех сил пытаются управлять своей огромной коллекцией учетных записей AWS, но Control Tower может помочь. Услуга автоматизирует…
- Разбираем модель ценообразования Amazon EKS
В модели ценообразования Amazon EKS есть несколько важных переменных.