Перевод систем счисления – таблица, правила, формулы
В решении определенного класса задач иногда удобно записывать числовые значения в разных системах счисления. Разработан ряд унифицированных правил перевода чисел между системами. О том, как выполняется перевод систем счисления, рассказано в статье.
Что такое перевод систем счисления
Основанием системы счисления является величина, определяющая количество символов для записи числового значения. Например, основанием двоичной системы является число 2, пятеричной, соответственно – 5.
Рис. 1. Таблица: основание и алфавит различных систем счисления.Число 15 в десятичной системе при переводе в пятеричную равно 30, а в восьмеричной будет равно 17. Шестнадцатеричный эквивалент пятнадцати представляет собой букву F. Как так получается?
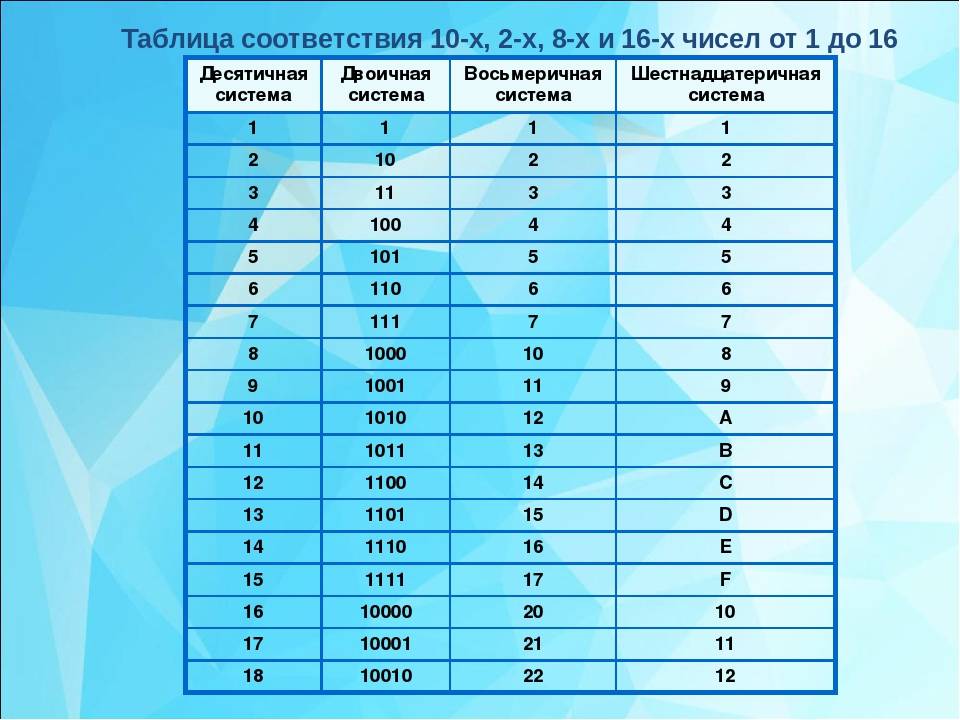
Рис. 2. Таблица соответствия десятичных и шестнадцатеричных чисел.Перевод чисел с участием десятичной системы счисления
В преобразовании чисел с участием десятичной системы приняты три строгих правила перевода.
1. Пересчет числового значения из десятичного формата в эквивалент другой системы счисления заключается в делении целой части и полученных частных, на величину основания будущей системы счисления. При этом остатки от деления записываются начиная с последнего.
Например, 15 из десятичной системы в восьмеричную переводится так: 15 / 8 = 1 (в остатке 7). Записываем итог, начиная с конечного и в данном случае единственного частного, и затем остаток. Получим 17.
Еще один пример: десятичное 125 в восьмеричной системе: 125 / 8 = 15 (5). Полученное частное больше, чем основание 8.
Продолжаем делить: 15 / 8 = 1 (7). Ответ записывается с последнего частного, а затем остатки от деления: 175.
Следует запомнить, что запись результата всегда начинает с последнего частного и остатков от деления в обратном порядке.
2. Преобразование части десятичного числа, записанной после запятой, выполняется с помощью обратной процедуры, то есть умножения, вычисляя одно за другим произведения дробных частей на основание будущей системы счисления и записывая последовательно цифры, полученные в целой части.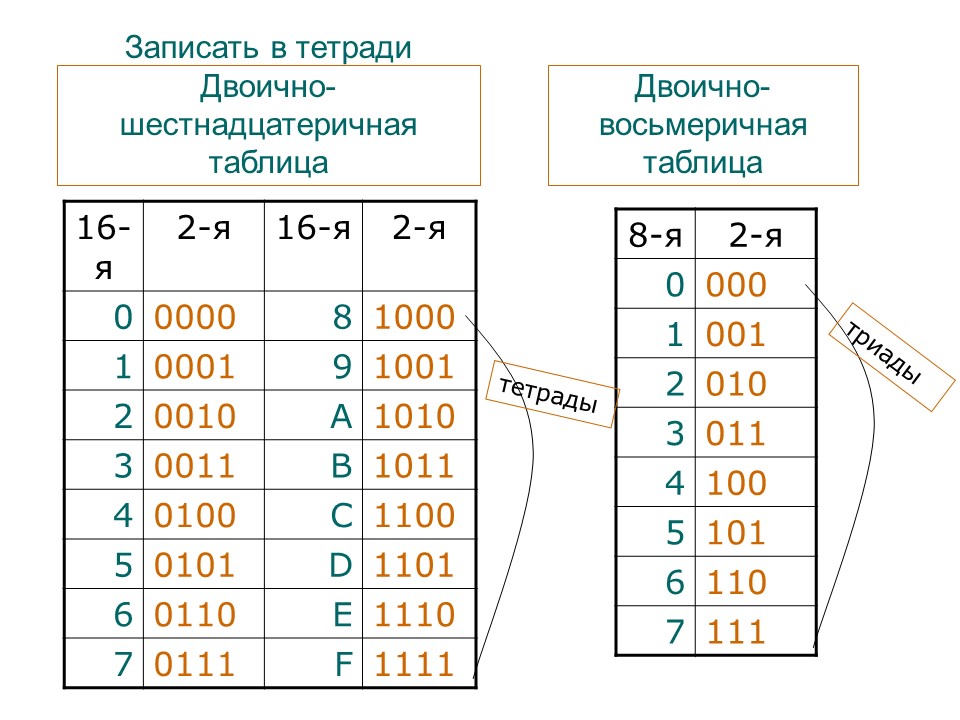
Каждое восьмеричное число представляется триадой (тремя элементами) двоичных знаков, каждое шестнадцатеричное – двоичной тетрадой (четыре элемента).
Например, 8 → 2: 134 ⇔ 001011100
16 → 2: 8F ⇔ 10001111
2 → 8: 110101 ⇔ 65
2 → 16: 11011000 ⇔ D8
Что мы узнали?
Переход между различными системами счисления выполняется по строго определенным правилам. Десятичные числа преобразуются в другие системы путем последовательного деления целой части и умножения дробной, обратный перевод выполняется с помощью полинома. Перевод между 2-, 8- и 16-ми системами выполняется по таблице.
Оценка статьи
Перевод чисел в различные системы счисления в Excel — TutorExcel.Ru
Перевод чисел в различные системы счисления в Excel
Изучим стандартные способы перевода чисел в различные системы счисления в Excel: двоичную, восьмеричную, десятичную и шестнадцатеричную.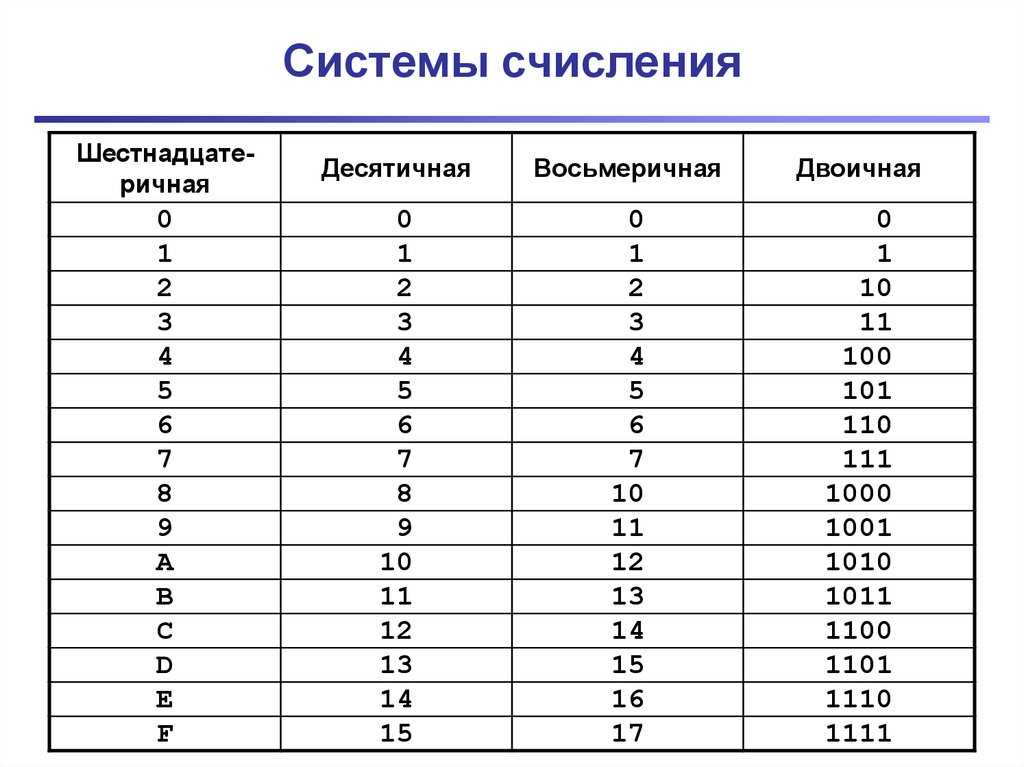
Помимо повсеместно распространенной и всем нам хорошо известной десятичной системы счисления также используются и системы с другими основаниями (отличными от 10), например, двоичная, троичная, восьмеричная и т.д.
Большинство из них имеют достаточно широкое применение практически во всех современных электронных устройствах, в программировании или компьютерной документации.
Системы счисления в Excel
В Excel есть возможность стандартными средствами переводить данные в четырех системах счисления:
Давайте подробно остановимся на основных вариантах преобразования данных.
Перевод числа из десятичной в двоичную систему в Excel
Для преобразования данных в двоичную запись в Excel существует стандартная функция ДЕС.В.ДВ (имя функции получается как первые буквы от слов ДЕСятичное В ДВоичное, дополнительно разделенное точками):
ДЕС.В.ДВ(число; [разрядность])
Преобразует десятичное число в двоичное.
- Число (обязательный аргумент) — десятичное целое число, которое требуется преобразовать;
- Разрядность (необязательный аргумент) — количество знаков для использования в записи. Данный аргумент необходим если нужно приписать к двоичной записи данных ведущие нули. К примеру, число 1101 с разрядностью 7 будет иметь вид 0001101.
Обратите внимание, что Excel накладывает определенные ограничения на размер преобразуемых данных.
Двоичная запись не должна занимать более 10 знаков, поэтому десятичное число, соответственно, не должно быть больше 511 или меньше -512, иначе в качестве значения функция ДЕС.В.ДВ вернет ошибку.
Перевод числа из двоичной в десятичную систему в Excel
Для осуществления обратного перевода можно воспользоваться функцией ДВ.В.ДЕС:
ДВ.В.ДЕС(число)
Преобразует двоичное число в десятичное.
- Число (обязательный аргумент) — двоичное число, которое требуется преобразовать.
При этом разрядность в качестве аргумента функции для десятичной записи не используется.
Как и в случае с функцией ДЕС.В.ДВ при использовании ДВ.В.ДЕС существует ограничение на размер преобразуемых данных — не более 10 знаков в записи, в ином случае функция вернет значение ошибки.
Перевод в других системах счисления
Для других систем счисления (восьмеричной, шестнадцатеричной) также определен набор стандартных формул.
Для удобства мы составили таблицу со схемой выбора формулы для преобразования данных (в левом столбце указано откуда переводим данные, в верхней строчке — куда переводим):
Как и в примерах выше имена функций образуются по достаточно простому правилу — берутся первые буквы от названий систем в которых преобразуются данные и разделяются точками (ВОСЬМеричное В ШЕСТНадцатеричное и пр.)
Арифметические операции с данными
Операции в Excel осуществляются в десятичной системе счисления, поэтому при применении арифметических действий (сложение, вычитание и т.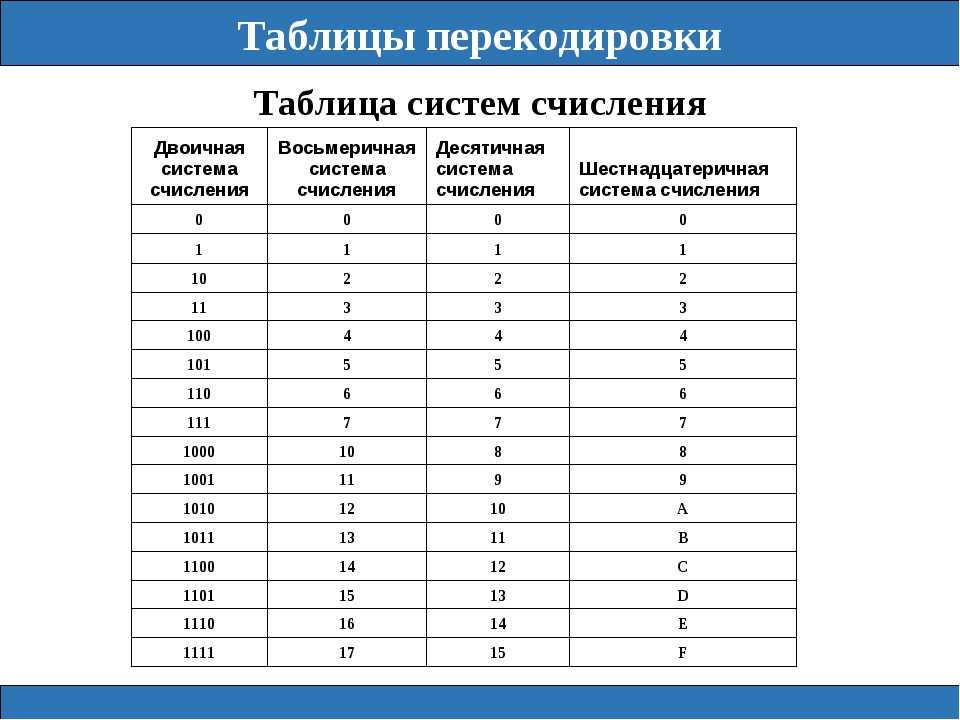
д.) для преобразованных данных учитывайте, что конечный результат также будет записан в десятичной записи:
Чтобы избежать подобной проблемы, необходимо сначала перевести все данные в десятичный вид, произвести требуемые вычисления, а уже затем вновь преобразовать полученный результат в исходную систему счисления:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Математика,Функции
- ← Пузырьковая диаграмма в Excel
- Фильтр и сортировка ячеек по цвету в Excel →
№ 2535: Таблицы умножения
Компьютерам легче всего работать с двумя цифрами — нулем и единицей. Эти двоичные числа называются битами. Чтобы записать возраст Вселенной, требуется тридцать четыре бита. Это больше, чем одиннадцать в нашей десятичной системе, но у компьютера гораздо более простая таблица умножения: ноль умножить на ноль, ноль умножить на один и один умножить на один.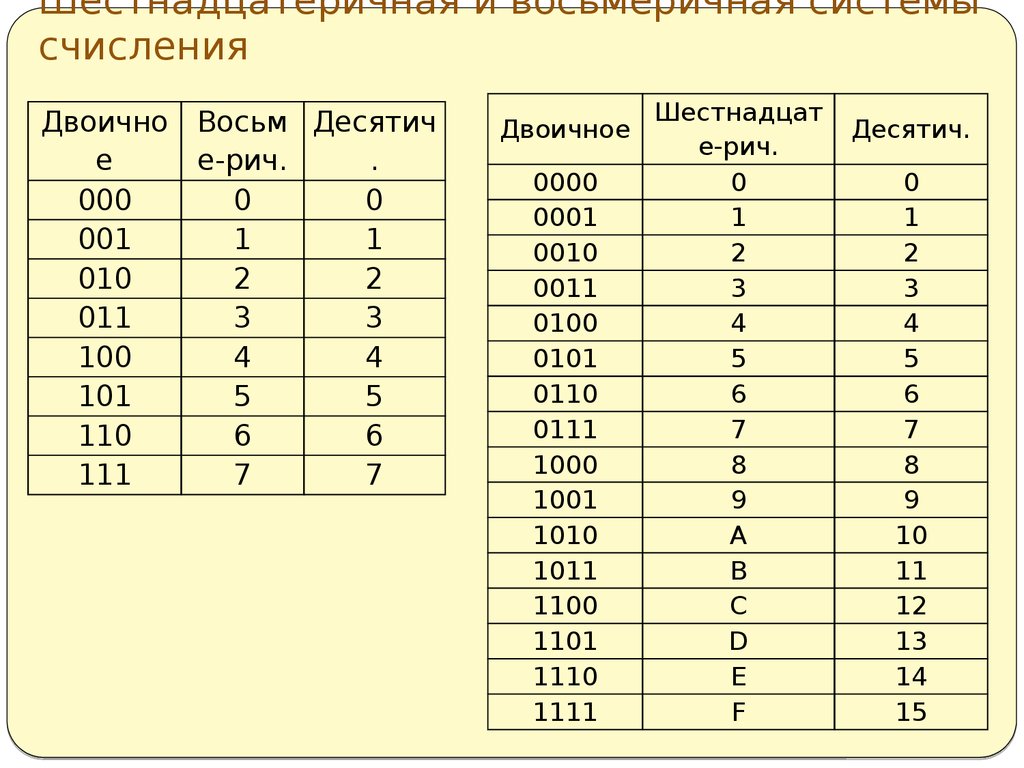
Вот и все!
Широко распространено мнение, что мы используем десять цифр, потому что столько у нас пальцев. Это более чем необходимо для хорошей, работоспособной системы счисления. Я бы предпочел восьмерку. Но я просто рад, что мы не родились с двадцатью пальцами. Я так и не разобрался со своей таблицей умножения.
Я Энди Бойд из Университета Хьюстона, где интересовался тем, как работают изобретательные умы.
[аудио: три — магическое число]
Чтобы узнать о связанных эпизодах, см. БОЛЬШИЕ ЦИФРЫ и НОЛЬ среди многих других.
Системы счисления, обсуждаемые в этом выпуске, известны как позиционные системы . Позиционные системы счисления работают путем выбора базы , которая равна количеству цифр в системе. Положение цифры в строке цифр соответствует степени основания.
Например, в нашей стандартной десятичной системе счисления мы имеем
52 907 (с основанием десять) =
5 x 10 4 + 2 x 10 3 + 9 x 10 2 + 0 x 10 1 + 7 x 10 0
В базе восемь у нас есть
147 253 (с основанием восемь) =
1 x 8 5 + 4 x 8 4 + 7 x 8 3 + 2 x 8 2 + 5 x 8 1 + 3 x 8 0 .
Заметьте, что оба эти числа, 52 907 (с основанием десять) и 147 253 (с основанием восемь), представляют одно и то же количество; они просто выражены в двух разных системах счисления.
Таблицы времени для двоичной (с основанием два), четверичной (с основанием четыре), восьмеричной (с основанием восемь) и десятичной (с основанием десять) систем счисления показаны ниже. Обратите внимание, что нужно запомнить только немногим более половины значений в этих таблицах, поскольку изменение порядка умножения на обратный не меняет результат (например, 6 x 8 = 8 x 6).
Следует отметить, что однозначные дополнительные таблицы, подобные таблицам умножения, также необходимы для овладения базовой арифметикой, но не обсуждаются в этом эпизоде. Большинство людей осваивают эти таблицы без особых проблем.
Для получения дополнительной информации о позиционных системах счисления см., например, http://en.wikipedia.
org/wiki/Positional_notation.
Изображения таблиц умножения взяты с веб-сайта http://www.cut-the-knot.org/blue/SysTable.shtml.
Двигатели нашей изобретательности Copyright © 1988-2009 Джон Х. Линхард.
Предыдущий Эпизод | Индекс | Дом | Далее Эпизод
Системы счисления — десятичная, двоичная, восьмеричная и шестнадцатеричная | Рукшани Атапату | Уголок кодера
Изображение предоставлено: Pexels Давайте рассмотрим несколько различных систем счисления, которые используются сегодня, и посмотрим, как с помощью трех простых правил мы можем построить любую систему счисления, какую захотим.
В математике «база» или «основание» — это количество различных цифр или комбинация цифр и букв, которые система счета использует для представления чисел. ~Wiki~
Например,
- Основание 10 ( Десятичное) — Представление любого числа с использованием 10 цифр [0–9]
- База 2 ( Двоичный ) — Представление любого числа с использованием 2 цифр [0–1]
- База 8 ( Восьмеричное ) — Представление любого числа с использованием 8 цифр [0–7] ) — Представление любого числа с помощью 10 цифр и 6 символов [0–9, A, B, C, D, E, F]
В любой из упомянутых выше систем счисления ноль очень важен как заполнитель ценность. Возьмем число 1005. Как нам написать это число, чтобы мы знали, что в нем нет десятков и сотен? Мы не можем записать его как 15, потому что это другое число, и как мы напишем миллион (1 000 000) или миллиард (1 000 000 000) без нулей? Вы понимаете его значение?
Сначала мы посмотрим, как устроена десятичная система счисления, а затем применим те же правила и к другим системам счисления.
Все мы умеем писать числа до 9, не так ли? Что тогда? Ну, это действительно просто. Когда вы израсходовали все свои символы, вы делаете следующее:
- вы добавляете еще одну цифру слева и делаете правую цифру 0.
- Затем снова идите вверх, пока не закончите все свои символы с правой стороны. и когда вы нажмете последний символ, увеличьте цифру слева на 1.
- Когда вы израсходуете все символы как правой, так и левой цифры, сделайте их оба 0 и добавьте еще 1 слева, и так далее и так далее.
Если вы используете 3 вышеуказанных правила в десятичной системе,
- Напишите числа 0–9.
- Как только вы достигнете 9, сделайте крайнюю правую цифру 0 и добавьте 1 слева, что означает 10.
- Затем на правой цифре мы увеличиваем до 9, и когда мы достигаем 19, мы используем 0 на правой цифре и добавляем 1 к влево, поэтому получаем 20.
- Аналогичным образом, когда мы достигаем 99, мы используем 0 на обоих местах этих цифр и добавляем 1 слева, что дает нам 100.
Итак, вы видите, когда у нас есть десять разных символов, когда мы добавляем цифры слева стороне числа каждая позиция будет стоить в 10 раз больше, чем предыдущая.
Возьмем ту же десятичную систему счисления. На самом деле правил всего два.
- У вас есть символ для представления количества [0–9]
- Тогда значение цифры зависит от ее положения — давайте немного проясним это.
Возьмем однозначное число «8». Это просто означает 8, другими словами, это именно то, что он представляет. А 24? В случае двух цифр правая цифра говорит то, что она означает, а левая цифра означает в десять раз больше, чем она говорит. То есть 4 равно 4, 2 равно 20. В сумме получается 24.
Если мы возьмем трехзначное число, крайняя правая цифра означает то, что она говорит, средняя цифра в десять раз больше, а самая левая цифра в 100 раз больше, чем она говорит. Просто если мы возьмем число 546, то это будет 6 + (10 * 4) + (5 * 100) = 546.
В двоичном формате у нас есть только две цифры для представления числа, 0 и 1, и у нас уже нет символов.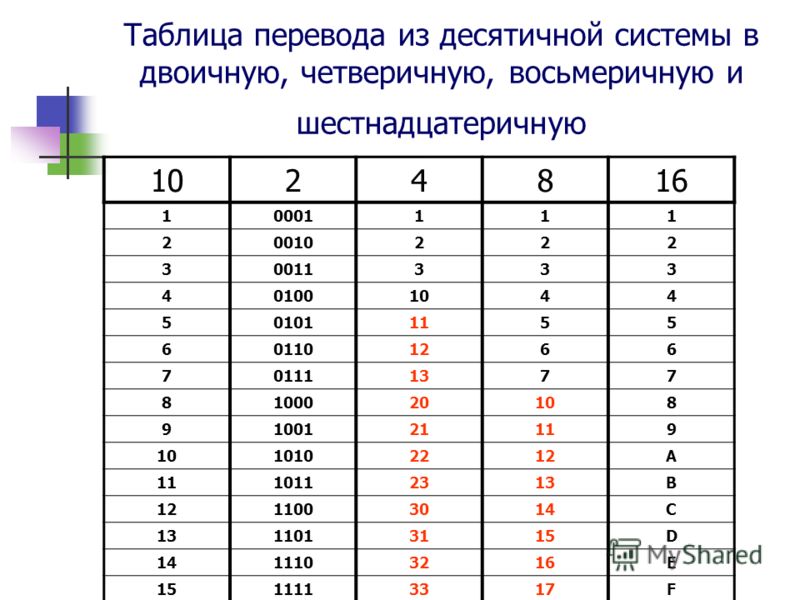
Так что же нам делать? Давайте применим те же правила, которые мы использовали в десятичной системе.
Делаем правую цифру 0 и прибавляем 1 к левой, то есть наше следующее число — «10». Затем мы поднимаемся вверх, пока не израсходуем все наши символы с правой стороны. Итак, следующее число в строке — 11.
После «11» мы ставим 0 в обоих этих местах и добавляем 1 слева, и мы получаем 100.
Затем 101, 110, 111, затем 1000 …
Эта двоичная система счисления основана на двух цифрах, и каждая позиция стоит в два раза больше, чем предыдущая позиция.
Чтение двоичного числа почти такое же, как чтение десятичного. Правая цифра говорит, что она означает, следующая означает в два раза больше предыдущей, после этого в 4 раза и т. д.
Таким образом, 101 означает 5 в десятичном виде.
Эти же правила применимы к восьмеричной и шестнадцатеричной системам счисления. В восьмеричном формате у нас есть только 8 цифр для представления чисел, поэтому, как только мы дойдем до 7, следующим числом будет 10, а в шестнадцатеричном формате у нас будет 10 цифр и 6 букв для представления чисел.