Таблица шестнадцатиричных чисел: Таблица перевода двоичных, восьмеричных, десятичных (от 1 до 255) и шестнадцатеричных чисел. Binary, Octal and Hexadecimal Numbers vs Decimal Numbers

Таблица шестнадцатеричных чисел от 0 до 128

Таблица шестнадцатеричных чисел от 0 до 128

Главная > ш >

десят. число	шестнадц. число
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	A
11	B
12	C
13	D
14	E
15	F
16	10
17	11
18	12
19	13
20	14
21	15
22	16
23	17
24	18
25	19
26	1A
27	1B
28	1C
29	1D
30	1E
31	1F
32	20
33	21
34	22
35	23
36	24
37	25
38	26
39	27
40	28
41	29
42	2A
43	2B
44	2C
45	2D
46	2E
47	2F
48	30
49	31
50	32
51	33
52	34
53	35
54	36
55	37
56	38
57	39
58	3A
59	3B
60	3C
61	3D
62	3E
63	3F
64	40
65	41
66	42
67	43
68	44
69	45
70	46
71	47
72	48
73	49
74	4A
75	4B
76	4C
77	4D
78	4E
79	4F
80	50
81	51
82	52
83	53
84	54
85	55
86	56
87	57
88	58
89	59
90	5A
91	5B
92	5C
93	5D
94	5E
95	5F
96	60
97	61
98	62
99	63
100	64
101	65
102	66
103	67
104	68
105	69
106	6A
107	6B
108	6C
109	6D
110	6E
111	6F
112	70
113	71
114	72
115	73
116	74
117	75
118	76
119	77
120	78
121	79
122	7A
123	7B
124	7C
125	7D
126	7E
127	7F
128	80

Ряд шестнадцатеричных чисел от 0 до 128

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 2A, 2B, 2C, 2D, 2E, 2F, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 3A, 3B, 3C, 3D, 3E, 3F, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 4A, 4B, 4C, 4D, 4E, 4F, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 5A, 5B, 5C, 5D, 5E, 5F, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 6A, 6B, 6C, 6D, 6E, 6F, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 7A, 7B, 7C, 7D, 7E, 7F, 80

 

1.

2. Преобразование чисел из одной системысчисления в другую

Программное обеспечение вычислительной техники и автоматизированных систем / Аппаратные и программные средства систем управления / 1.2. Преобразование чисел из одной системысчисления в другую

Основания восьмеричной и шестнадцатеричной систем счисления выражаются целой степенью числа два (8 = 2³, 16 = 2⁴).  Этим объясняется простота преобразования чисел, представленных в этих системах счисления, в двоичную систему счисления и обратно.

Для перевода чисел из восьмеричной системы счисления в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом. Например:

.

В табл. 1.1 приведены эквиваленты десятичных, восьмеричных и двоичных чисел.

Перевод шестнадцатеричных чисел в двоичную систему счисления достигается пред­ставлением цифр шестнадцатеричного числа четырехразрядными двоичными числами. Например:

.

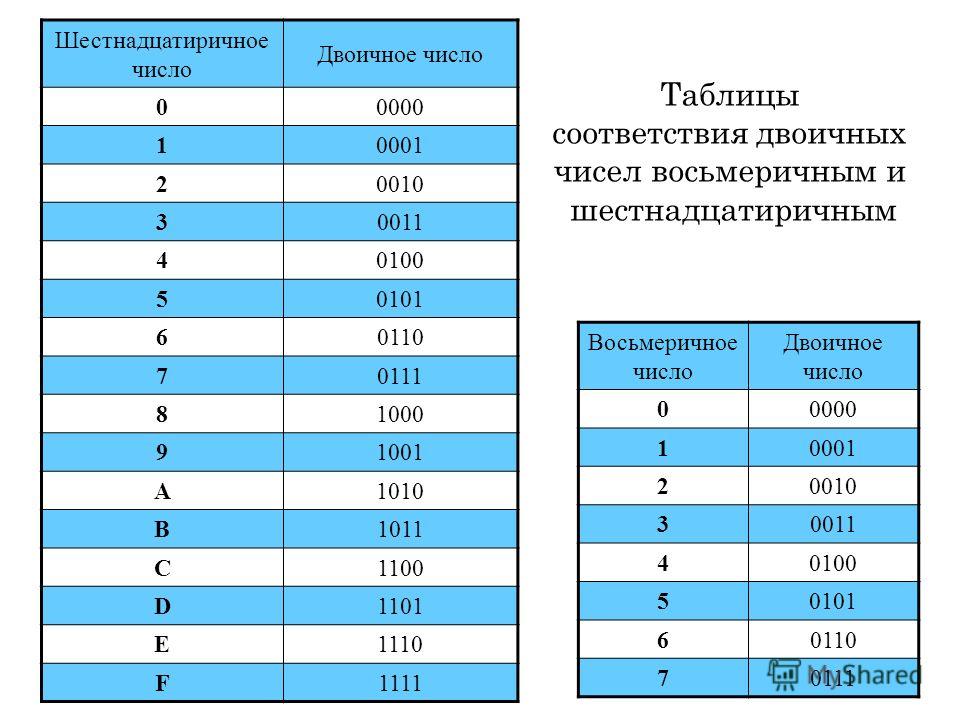
При обратном переводе чисел из двоичной системы в восьмеричную или шестнадцатеричную систему счисления необходимо разряды двоичного числа разбить на группы по три разряда в случае перевода в восьмеричную систему или на группы по четыре разряда в случае перевода в шестнадцатеричную систему счисления. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представ­ляется цифрой той системы счисления, в которую переводится число. Например:

;

Большую сложность представляет перевод чисел из десятичной системы в двоичную и обратно.  Рассмотрим пример перевода числа 155₁₀ в двоичную систему счисления, процедура перевода приведена на рис.

1.1.

Десятичное число 155 сначала делится на 2, что дает нам частное 77 и остаток 1. Этот остаток становится значением младшего разряда двоичного числа и помещается в крайнюю справа позицию. Затем частное (77) перемещается, как показывает стрелка, и становится следующим делимым.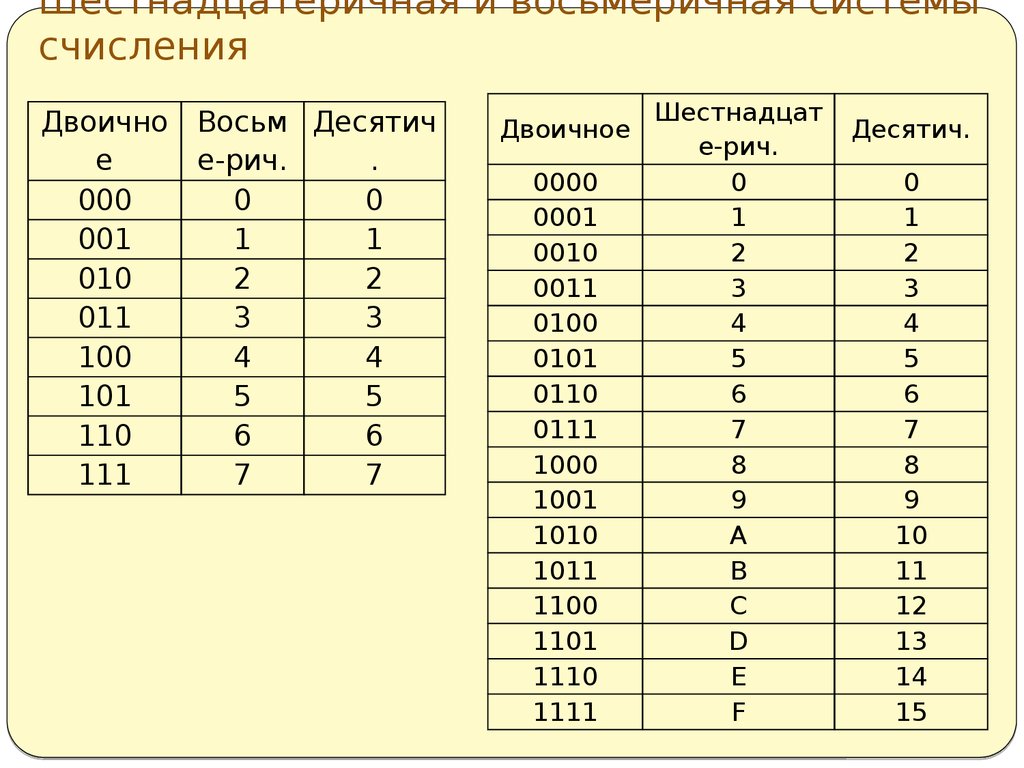

Затем каждое частное последовательно делится на 2 до тех пор, пока не получится частное, равное 0 и остаток, равный 1 (см. рис. 1.1). Последняя строка на рис. 1.1 дает нам результат 155₁₀ = 10011011₂.

Для преобразования десятичных чисел в восьмеричную и шестнадцатеричную системы счисления используют аналогичные алгоритмы.

На рис. 1.2 представлена процедура перевода числа 3336₁₀ в его восьмеричный эквивалент.

В первую очередь число 3336₁₀ разделим на 8, что дает частное 417 и остаток 0₁₀, причем 0₁₀ = 0₈, восьмеричный 0 становится значением младшего разряда восьмеричного числа. Первое частное (417) становится делимым и снова делится на 8 (вторая строка), что дает частное 52 и остаток 1₁₀ = 1₈, который становится второй цифрой восьмеричного числа. В третьей строке частное (52) становится делимым и деление его на 8 дает частное 6 и остаток 4

10 =4₈.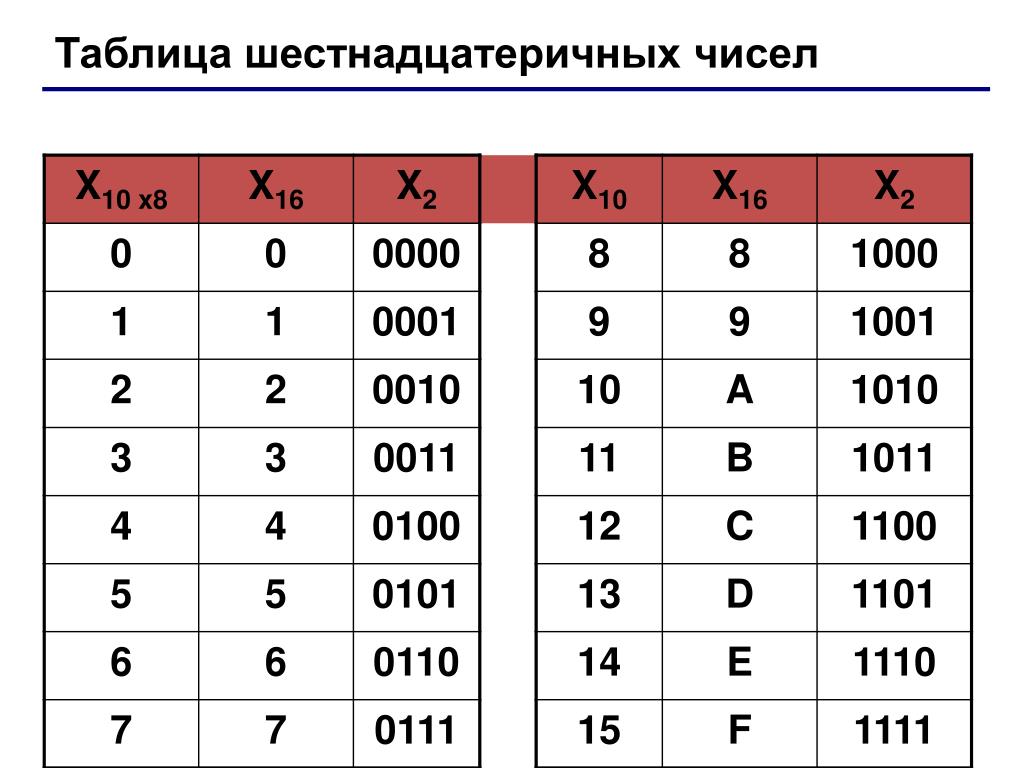 В четвертой строке частное 6 разделено на 8 с частным 0 и остатком 6₁₀ = 6₈. Теперь счет закончен последним частным 0. Цифра 6₈ становится значением старшего разряда восьмеричного числа, и мы можем видеть на рис. 1.2, что 3336₁₀ = 6410₈.

На рис. 1.3 показана последовательность действий по переводу десятичного числа 15797 в шестнадцатеричное.

В первой строке 15797₁₀ делится на 16, что дает частное 987₁₀ и остаток 5₁₀, который преобразуется потом в свой шестнадцатеричный эквивалент (5₁₀ = 5₁₆) и становится цифрой младшего разряда шестнадцатеричного числа. Первое частное (987) становится делимым во второй строке и сно­ва делится на 16, что дает частное 61 и остаток 11₁₀ или шестнадцатеричное B. В третьей строке 61 делится на 16, дает частное 3 и остаток 13

10 или D₁₆, а в четвертой строке делимое 3 делится на 16, дает частное 0 и остаток 3₁₀ или 3₁₆. Когда частное равно 0 (см. четвертую строку рис. 1.3), преоб­разование заканчивается. 3₁₆ становится цифрой старшего разряда результата, т.е. 3DB5₁₆.

Шестнадцатеричные

Шестнадцатеричное число основано на числе 16

16 различных значений

Есть 16 Шестнадцатеричные цифры. Они совпадают с десятичными цифрами до 9, но вместо десятичных цифр от 10 до 15 стоят буквы A, B, C, D, E и F:

.

Шестнадцатеричный:	0	1	2	3	4	5	6	7	8	9	А	Б	С	Д	Э	Ф
Десятичный:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

Таким образом, одна шестнадцатеричная цифра может отображать 16 различных значений вместо обычных 10.

Подсчет

Выберите «Шестнадцатеричный» ниже и посмотрите, как он подсчитает:

После заполнения позиции «Единицы» (после F ) единицы начинаются с 0 , и мы добавляем 1 к следующей позиции слева (чтобы показать 1 лот из 16).

И после эта позиция достигает F , мы делаем то же самое и так далее.

Когда мы движемся влево, каждый разряд равен 16 раз больше .

Пример: Каково десятичное значение шестнадцатеричного числа «D1CE»

(Проверьте это в конвертере двоичных и десятичных чисел в шестнадцатеричные.)

Суть!

Пример: 2E6.A3

Это 2×16×16 + 14×16 + 6 + 10/16 + 3/(16×16)
= 742,63671875 в десятичном формате
Читайте ниже, чтобы узнать, почему 9005

Цифры можно размещать слева или справа от точки, чтобы показать значения больше единицы или меньше одного:

•		Число слева от точки является целым числом. 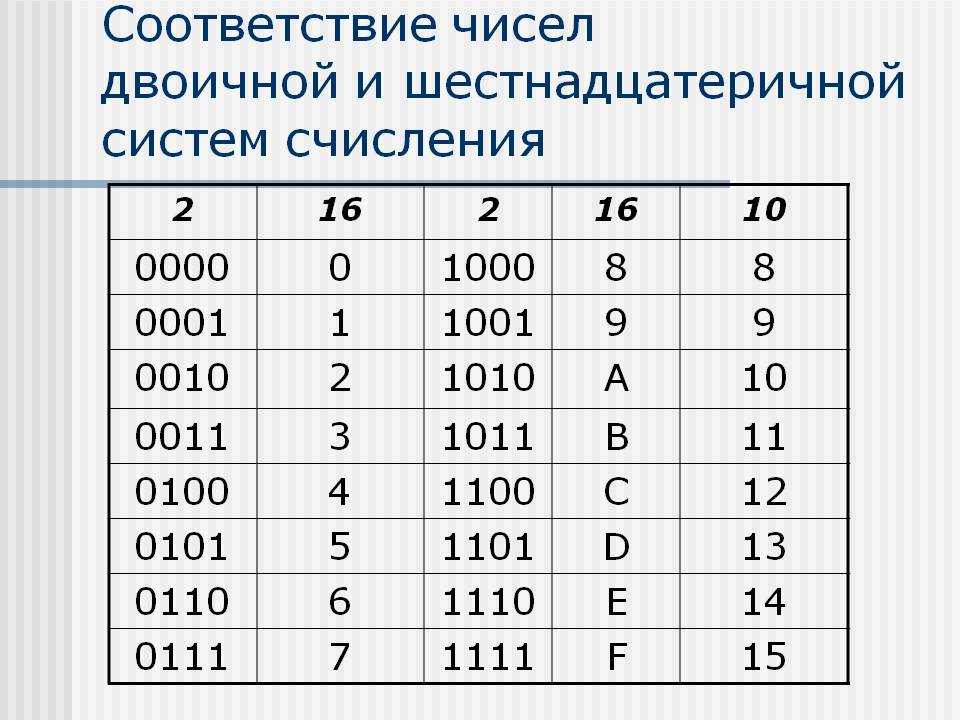Переезжаем оставляем каждый разряд в 16 раз больше.
•		Первая цифра справа от точки означает шестнадцатые доли (1/16). Перемещение вправо каждый разряд числа в 16 раз меньше (на одну шестнадцатую больше).

Дополнительные примеры

Пример 1: Что такое 4B5 (шестнадцатеричный)?

• «4» стоит в позиции «16×16», значит, это означает 4×16×16
• «B» (11) находится в позиции «16», значит, 11 × 16
• «5» стоит в позиции «1», значит 5.
• Ответ: 4B5 = 4×16×16 + 11×16 + 5 (=1205) в десятичной системе счисления

Пример 2: Что такое 2,3 (шестнадцатеричное число)?

• Слева «2», то есть целое число часть.
• 3 находится в позиции «шестнадцатых», что означает «3 шестнадцатые», или 3/16
• Таким образом, 2,3 — это «2 и 3 шестнадцатых» (= 2,1875 в десятичной системе счисления)

Собаки

Собакам было бы легко понять шестнадцатеричные числа: просто посчитайте на пальцах ног!

Слово «Шестнадцатеричный»

Слово «шестнадцатеричный» означает «на основе 16».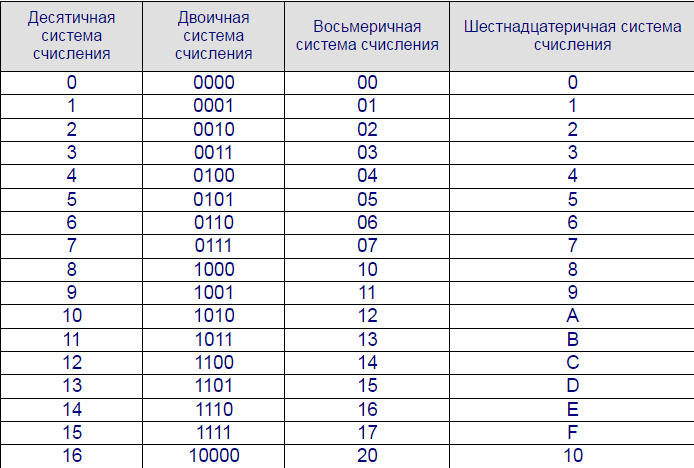 (от греческого гекса: «шесть» и латинское десятичное число : «десятая часть» ).

2016, 2017, 2018, 2019, 2020, 2021, 3595, 3596, 3597, 3598

Шестнадцатеричная система счисления 1 — 100

Шестнадцатеричная система счисления — это система счисления с основанием 16. Представляет числовые значения с помощью шестнадцати символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F.

В таблице ниже представлены шестнадцатеричные числа от 1 до 64, эквивалентные десятичным числам от 1 до 100.

Hexadecimal	Decimal	Hexadecimal	Decimal
1	1	33	51
2	2	34	52
3	3	35	53
4	4	36	54
5	5	37	55
6	6	38	56
7	7	39	57
8	8	3A	58
9	9	3B	59
A	10	3C	60
B	11	3D	61
C	12	3E	62
D	13	3F	63
E	14	40	64
F ​​	15	41	65
10	16	42	66
11	17	43	67
12	18	44	68
13	19	45	69
14	20	46	70
15	21	47	71
16	22	48	72
17	23	49	73
18	24	4A	74
19	25	4B	75
1A	26	4C	76
1B	27	4D	77
1C	28	4E	78
1D	29	4F	79
1E	30	50	80
1F	31	51	81
20	32	52	82
21	33	53	83
22	34	54	84
23	35	55	85
24	36	56	86
25	37	57	87
26	38	58	88
27	39	59	89
28	40	5A	90
29	41	5B	91
2A	42	5C	92
2B	43	5D	93
2C	44	5E	94
2D	45	5F	95
2E	46	60	96
2F	47	61	97
30	48	62	98
31	49	.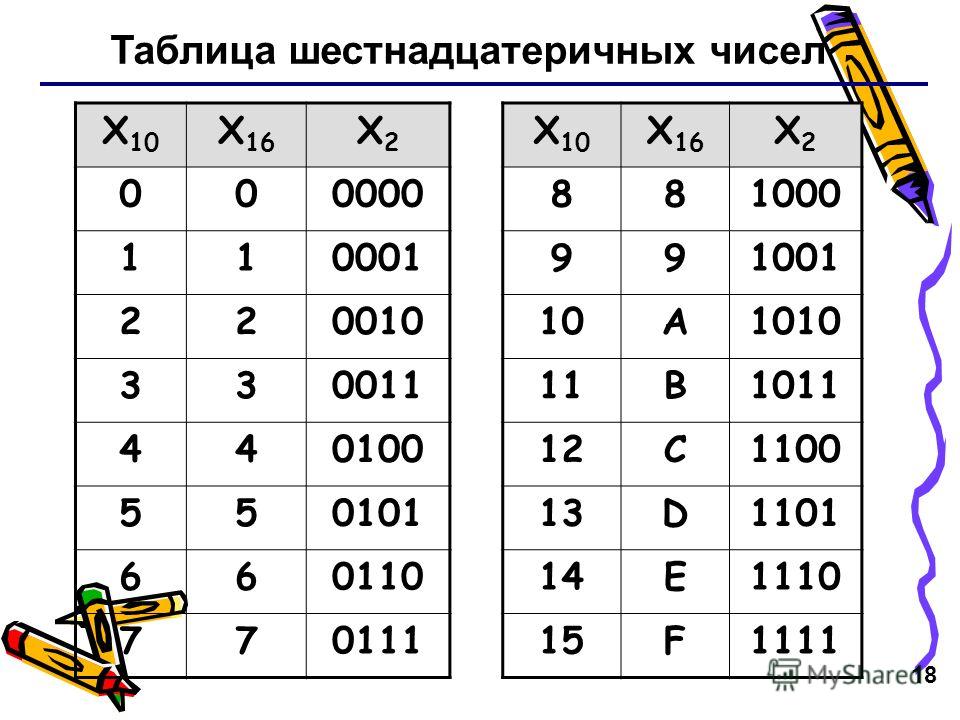 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт