Разное

Таблица пирсона хи квадрат: Таблица распределения хи-квадрат

Таблица критических точек распределения Пирсона хи-квадрат

Таблица критических точек распределения Пирсона «хи-квадрат»)

k /α0,010,0250,050,950,9750,99
16,634905,023893,841460,003930,000980,00016
29,210347,377765,991460,102590,050640,02010
311,344879,348407,814730,351850,215800,11483
413,276711,143299,487730,710720,484420,29711
515,0862712,832511,07051,145480,831210,55430
616,8118914,4493812,591591,635381,237340,87209
718,4753116,0127614,067142,167351,689871,23904
820,0902417,5345515,507312,732642,179731,64650
921,6659919,0227716,918983,325112,700392,08790
1023,20925 20,4831818,307043,940303,246972,55821
1124,7249721,9200519,675144,574813,815753,05348
1226,2169723,3366621,026075,226034,403793,57057
1327,6882524,735622,362035,891865,008754,10692
1429,1412426,1189523,684796,570635,628734,66043
1530,5779127,4883924,995797,260946,262145,22935
1631,9999328,8453526,296237,961656,907665,81221
1733,4086630,1910127,587118,671767,564196,40776
1834,8053131,5263828,869309,390468,230757,01491
1936,1908732,8523330,1435310,117018,906527,63273
2037,5662334,1696131,41043 10,850819,590788,26040
2138,9321735,4788832,6705711,5913110,28298,89720
2240,2893636,7807133,9244412,3380110,982329,54249
2341,6384038,0756335,1724613,0905111,6885510,19572
2442,9798239,3640836,4150313,8484312,4011510,85636
2544,3141040,6464737,65248
14,61141		13,1197211,52398
2645,6416841,9231738,8851415,3791613,8439112,19815
2746,9629443,1945140,1132716,1514014,5733812,87850
2848,2782444,4607941,3371416,9278815,3078613,56471
2949,5878845,7222942,5569717,7083716,0470714,25645
3050,8921846,9792443,7729718,49266 16,7907714,95346
3152,1913948,2318944,9853419,2805717,5387415,65546
3253,4857749,4804446,1942620,0719118,2907616,36222
3354,7755450,7250847,3998820,8665319,0466617,07351
3456,0609151,9660048,6023721,6642819,8062517,78915
3557,3420753,2033549,8018522,46502
20,56938		18,50893
3658,6192154,4372950,9984623,2686121,3358819,23268
3759,8925055,6679752,1923224,0749422,1056319,96023
3861,1620956,8955253,3835424,883922,8784820,69144
3962,4281258,1200654,5722325,6953923,6543221,42616
4063,6907459,3417155,7584826,509324,43304
22,16426
4164,9500760,5605756,9423927,3255525,2145222,90561
4266,2062461,7767658,1240428,1440525,9986623,65009
4367,4593562,9903659,3035128,9647226,7853724,39760
4468,7095164,2014660,4808929,7874827,5745725,14803
4569,9568365,4101661,6562330,6122628,3661525,90127
4671,2014066,6165362,8296231,4390029,1600526,65724
4772,4433167,8206564,0011132,2676229,9562027,41585
4873,6826469,0225965,1707733,0980830,7545128,17701
4974,9194770,2224166,3386533,9303131,5549228,94065
5076,1538971,4202067,5048134,7642532,3573629,70668


Обычно такая точность (5 знаков после запятой) не требуется. 2) = \alpha $$0,250,10,050,0250,010,0050,00111,322,713,845,026,637,8810,822,774,615,997,389,2110,613,834,116,25

7,819,3511,312,816,345,397,789,4911,113,314,918,556,639,2411,112,815,116,720,567,8410,612,614,416,818,522,579,041214,11618,520,324,3810,213,415,517,520,12226,1911,414,716,91921,723,627,91012,51618,320,523,225,229,61113,717,319,721,924,726,831,31214,818,52123,326,228,332,9131619,822,424,727,729,834,51417,121,123,726,129,131,336,11518,222,32527,530,632,837,71619,423,526,328,83234,339,31720,524,827,630,233,435,740,81821,62628,931,534,837,242,31922,727,230,132,936,238,643,82023,828,431,434,237,64045,32124,929,632,735,538,941,446,8222630,833,936,840,342,848,32327,13235,238,141,644,249,72428,233,236,439,44345,651,22529,334,437,740,644,346,952,62630,435,638,941,945,648,354,12731,536,740,143,24749,655,52832,637,941,344,548,35156,92933,739,142,645,749,652,358,33034,840,343,84750,953,759,7

Значения χ2 критерия Пирсона — таблица

k

$$P({\chi ^2} > \chi _{}^2) = \alpha $$

0,9950,990,9750,950,90,750,5
10,0000390,000160,000980,00390,0160,1020,455
20,010,020,0510,1030,2110,5751,39
30,0720,1150,2160,3520,5841,212,37
40,2070,2970,4840,7111,061,923,36
50,4120,5540,8311,151,612,674,35
60,6760,8721,241,642,23,455,35
70,9891,241,692,172,834,256,35
81,341,652,182,733,495,077,34
91,732,092,73,334,175,98,34
102,162,563,253,944,876,749,34
112,63,053,824,575,587,5810,3
123,073,574,45,236,38,4411,3
133,574,115,015,897,049,312,3
144,074,665,636,577,7910,213,3
154,65,236,267,268,551114,3
165,145,816,917,969,3111,915,3
175,76,417,568,6710,112,816,3
186,267,018,239,3910,913,717,3
196,847,638,9110,111,714,618,3
207,438,269,5910,912,415,519,3
218,038,910,311,613,216,320,3
228,649,5411,012,314,017,221,3
239,2610,211,713,114,818,122,3
249,8910,912,413,815,719,023,3
2510,511,513,114,616,519,924,3
2611,212,213,815,417,320,825,3
2711,812,914,616,218,121,726,3
2812,513,615,316,918,922,727,3
2913,114,316,017,719,823,628,3
3013,81516,818,520,624,529,3
k$$P({\chi ^2} > \chi _{}^2) = \alpha $$
0,9950,990,9750,950,90,750,5
10,0000390,000160,000980,00390,0160,1020,455
20,010,020,0510,1030,2110,5751,39
30,0720,1150,2160,3520,5841,212,37
40,2070,2970,4840,7111,061,923,36
50,4120,5540,8311,151,612,674,35
60,6760,8721,241,642,23,455,35
70,9891,241,692,172,834,256,35
81,341,652,182,733,495,077,34
91,732,092,73,334,175,98,34
102,162,563,253,944,876,749,34
112,63,053,824,575,587,5810,3
123,073,574,45,236,38,4411,3
133,574,115,015,897,049,312,3
144,074,665,636,577,7910,213,3
154,65,236,267,268,551114,3
165,145,816,917,969,3111,915,3
175,76,417,568,6710,112,816,3
186,267,018,239,3910,913,717,3
196,847,638,9110,111,714,618,3
207,438,269,5910,912,415,519,3
218,038,910,311,613,216,320,3
228,649,5411,012,314,017,221,3
239,2610,211,713,114,818,122,3
249,8910,912,413,815,719,023,3
2510,511,513,114,616,519,924,3
2611,212,213,815,417,320,825,3
2711,812,914,616,218,121,726,3
2812,513,615,316,918,922,727,3
2913,114,316,017,719,823,628,3
3013,81516,818,520,624,529,3

Как пользоваться таблицей Пирсона

k — число степеней свободы, определяется по формуле:

k=n−r−1

где
m — количество признаков; 
r — количество оцениваемых параметров распределения случайной величины.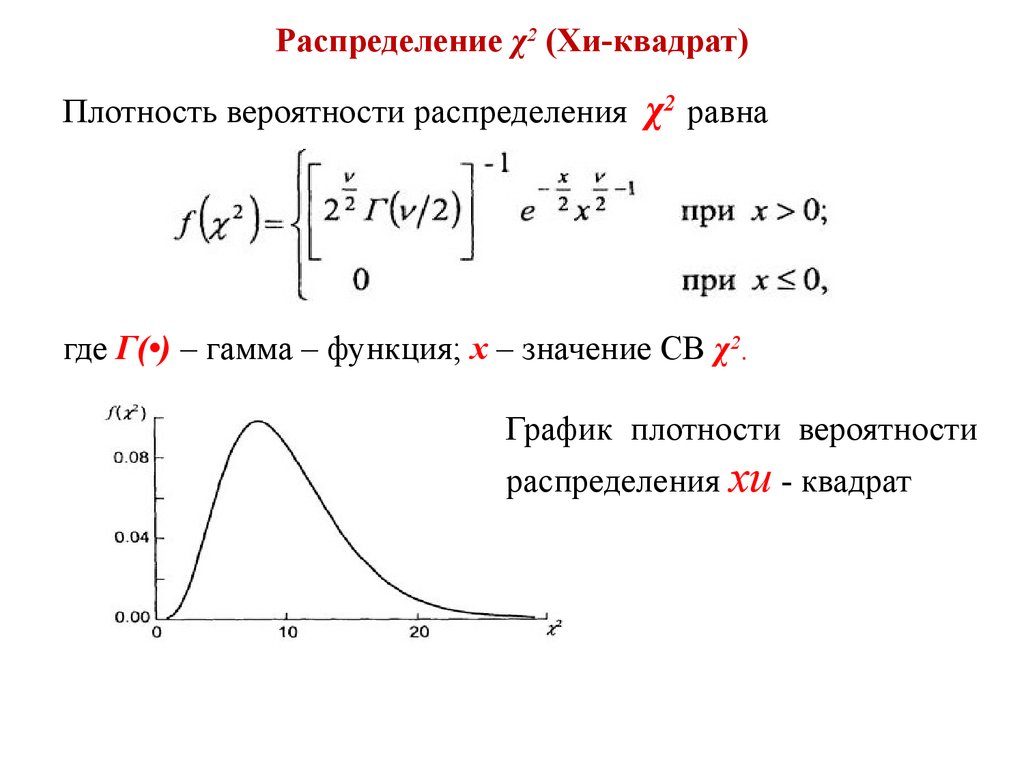
Для нормального распределения число степеней свободы находится по формуле

k=ι−3

Уровень значимости α берется из условия задачи.
Например α=0,01, k=12, тогда

Получаем значение Fтабл=26,2

7810

15.9 — Таблица хи-квадрат

Один из основных способов взаимодействия с распределением хи-квадрат, в первую очередь позже в Статистике 415, заключается в необходимости знать значение хи-квадрат или вероятность хи-квадрата для завершения статистического анализа. По этой причине мы теперь рассмотрим, как использовать типичную таблицу хи-квадрат для поиска значений хи-квадрата и/или вероятностей хи-квадрата. Начнем с двух определений. 92_{1-\alpha} (r)\) есть \(1-\alpha\):

x α 1 — α = P(x ≥ χ21-α(r) ) χ 21-α(r)

С этими Определения остались позади, а теперь давайте взглянем на таблицу хи-квадрат в конце вашего учебника.

Решение

Таким образом, вот шаги, которые вы должны использовать при использовании таблицы хи-квадрат, чтобы найти значение хи-квадрат:

  1. Найдите строку, соответствующую соответствующим степеням свободы, \(r \) .
  2. Найдите столбец, возглавляемый интересующей вероятностью… будь то 0,01 , 0,025 , 0,05 , 0,10 , 0,90 , 0,95 , 0,975 , или 0,99 .
  3. Определите значение хи-квадрат в точке пересечения строки \(r\) и столбца вероятности.

Теперь, по крайней мере теоретически, вы также можете использовать таблицу хи-квадрат, чтобы найти вероятность, связанную с конкретным значением хи-квадрат. Но, как видите, таблица довольно ограничена в этом направлении. Например, если у вас есть случайная величина хи-квадрат с 5 степенями свободы, вы можете найти только вероятности, связанные со значениями хи-квадрат 0,554, 0,831, 1,145, 1,610, 9.236, 11.07, 12.83 и 15.09:

P ( X ≤ x )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) х 2 0,975 ( р ) x 2 0,95 ( r ) x 2 0,90 ( r ) x 2 0,10 ( r ) x 2 0,05 ( r ) x 2 0,025 ( r ) х 2 0,01 ( р )
1 0,000 0,001 0,004 0,016 2,706 3,841 5.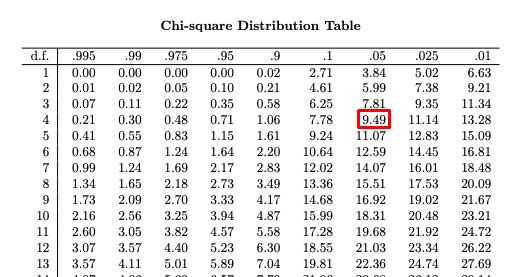 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9.488 11.14 13,28
5 0,554 0,831 1,145 1,610 9.236 11.07 12,83 15.09

 

Что бы вы сделали, если бы захотели найти вероятность того, что случайная величина хи-квадрат с 5 степенями свободы меньше, скажем, 6,2? Что ж, ответ, конечно… статистическое программное обеспечение, такое как SAS или Minitab! Для того, что мы будем делать в Stat 414 и 415, таблица хи-квадрат будет (в основном) служить нашей цели. Теперь давайте немного попрактикуемся, используя таблицу хи-квадрат.

Пусть \(X\) — случайная величина хи-квадрат с 10 степенями свободы. Что такое верхний пятый процентиль?

Решение

Верхний пятый процентиль — это значение хи-квадрат x , такое, что вероятность справа от \(x\) равна 0,05, и, следовательно, вероятность слева от \(x\) равна 0,95. Чтобы найти x с помощью таблицы хи-квадрат, мы:

  1. Найдите \(r=10\) в первом столбце слева.
  2. Найти столбец, возглавляемый \(P(X\le x)=0,95\).

Теперь все, что нам нужно сделать, это прочитать значение хи-квадрат, где пересекаются строка \(r=10\) и столбец \(P(X\le x)=0,95\). Что вы получаете?

P ( X ≤ x )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) x 2 0,975 ( r ) x 2 0,95 ( r ) x 2 0,90 ( r ) x 2 0,10 ( r ) x 2 0,05 ( r ) x 2 0,025 ( r ) x 2 0,01 ( r )
1 0,000 0,001 0,004 0,016 2,706 3,841 5.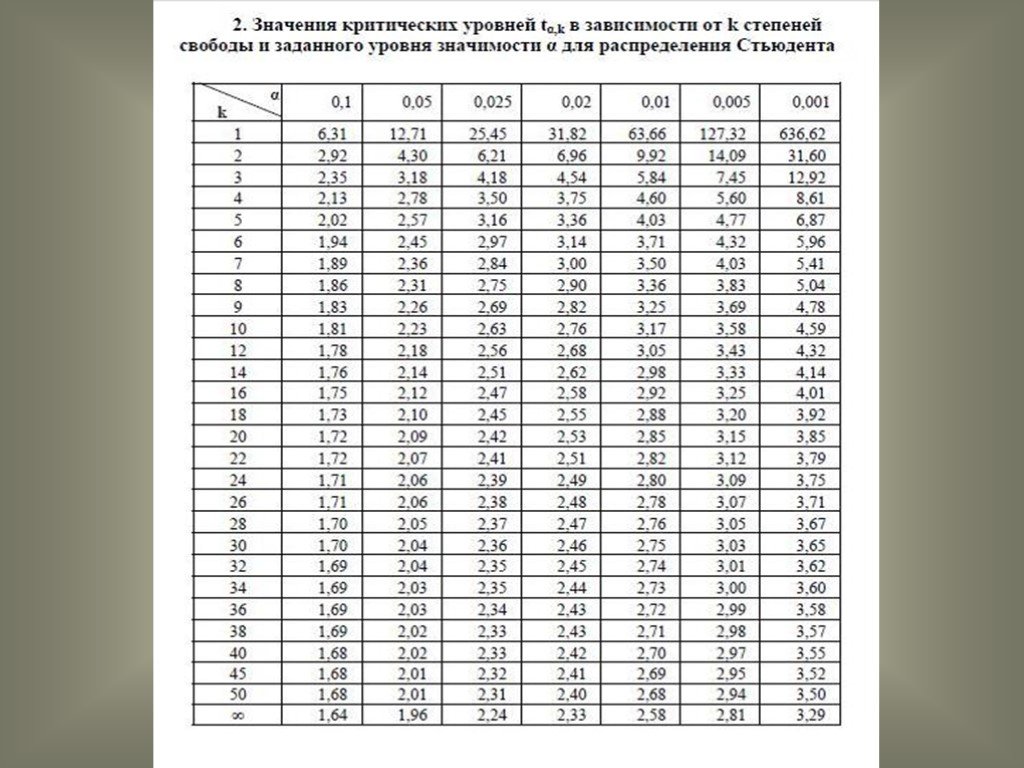 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9.488 11,14 13,28
5 0,554 0,831 1,145 1,610 9.236 11.07 12,83 15.09
6 0,872 1,237 1,635 2,204 10,64 12,59 14,45 16,81
7 1,239 1,690 2,167 2,833 12.02 14.07 16.01 18,48
8 1,646 2,180 2,733 3,490 13,36 15,51 17,54 20. 09
9 2,088 2.700 3,325 4,168 14,68 16,92 19.02 21,67
10 2,558 3,247 3,940 4,865 15,99 18,31 20,48 23.21

P ( X ≤ x )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) x 2 0,975 ( r ) x 2 0,95 ( r ) х 2 0,90 ( р ) x 2 0,10 ( r ) x 2 0,05 ( r ) x 2 0,025 ( r ) x 2 0,01 ( r )
1 0,000 0,001 0,004 0,016 2,706 3,841 5.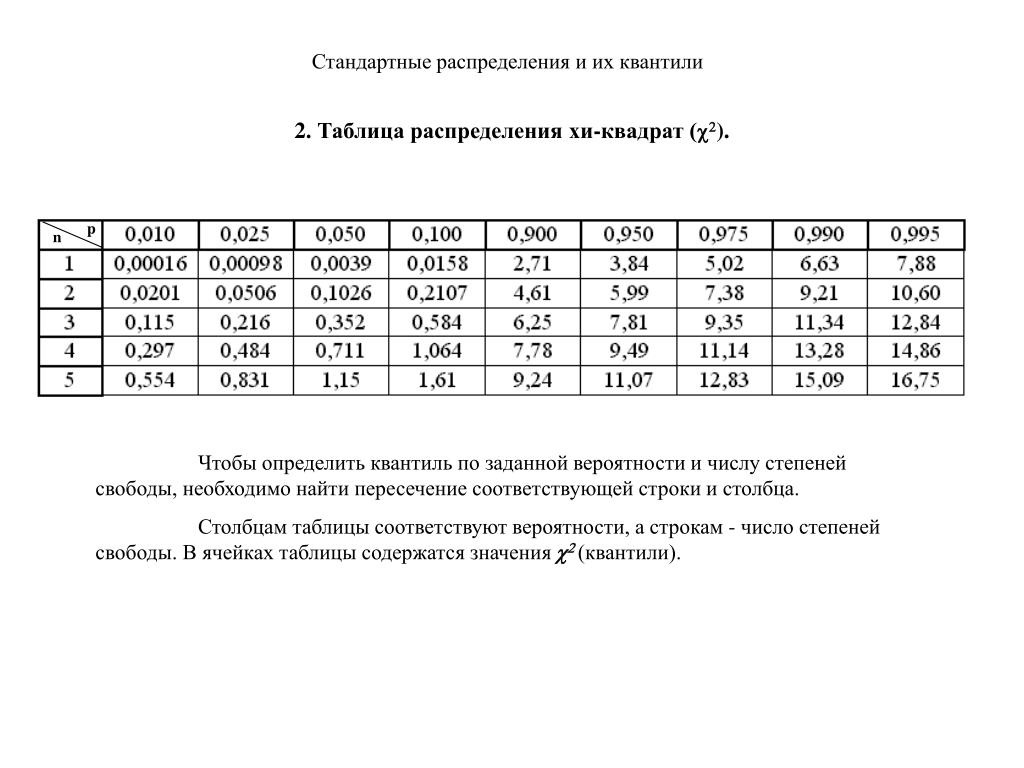 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9,488 11.14 13,28
5 0,554 0,831 1,145 1,610 9.236 11.07 12,83 15.09
6 0,872 1,237 1,635 2,204 10,64 12,59 14,45 16,81
7 1,239 1,690 2,167 2,833 1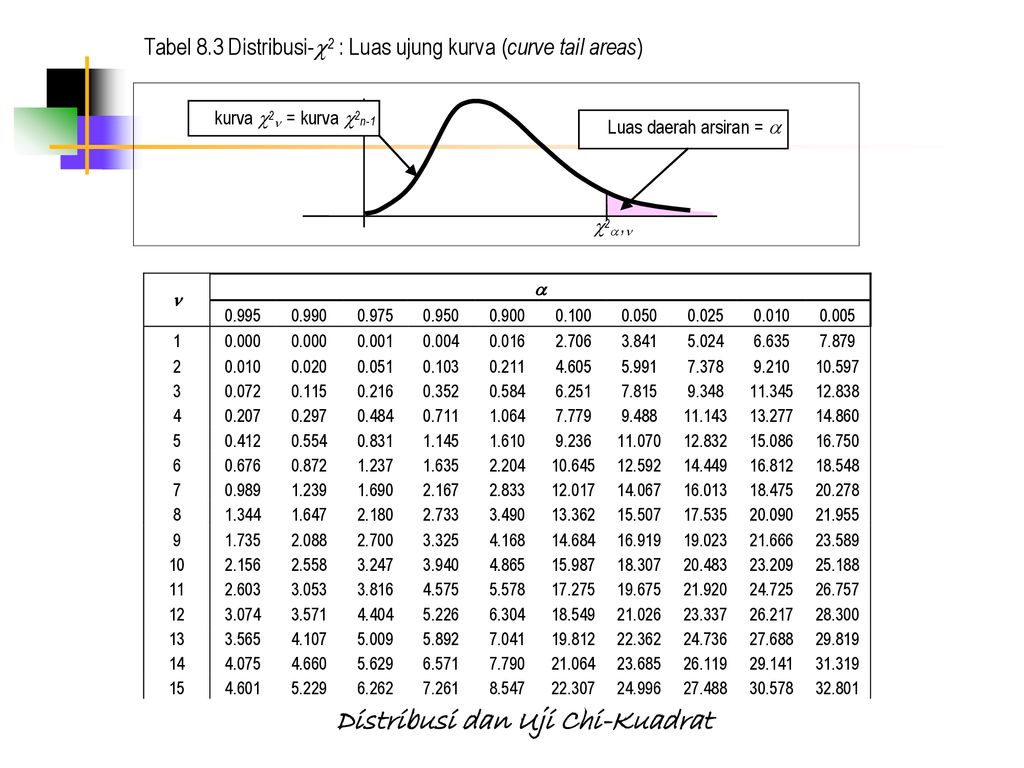2. 02 14.07 16.01 18,48
8 1,646 2,180 2,733 3,490 13,36 15,51 17,54 20.09
9 2,088 2.700 3,325 4,168 14,68 16,92 19.02 21,67
10 2,558 3,247 3,940 4,865 15,99 18,31 20,48 23,21

 

Из таблицы видно, что верхний пятый процентиль случайной величины хи-квадрат с 10 степенями свободы равен 18,31.

Что такое десятый процентиль?

Решение

Десятый процентиль — это значение хи-квадрат \(x\), такое, что вероятность слева от \(x\) равна 0,10. Чтобы найти x с помощью таблицы хи-квадрат, мы:

  1. Найдите \(r=10\) в первом столбце слева.
  2. Найдите столбец, возглавляемый \(P(X\le x)=0,10\).

Теперь все, что нам нужно сделать, это прочитать значение хи-квадрат, где пересекаются строка \(r=10\) и столбец \(P(X\le x)=0,10\). Что вы получаете?

P ( X ≤ x )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) x 2 0,975 ( r ) x 2 0,95 ( r ) x 2 0,90 ( r ) x 2 0,10 ( r ) x 2 0,05 ( r ) x 2 0,025 ( r ) x 2 0,01 ( r )
1 0,000 0,001 0,004 0,016 2,706 3,841 5. 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9.488 11.14 13,28
5 0,554 0,831 1,145 1,610 9.236 11.07 12,83 15.09
6 0,872 1,237 1,635 2,204 10,64 12,59 14,45 16,81
7 1,239 1,690 2,167 2,833 12.02 14.07 16.01 18,48
8 1,646 2,180 2,733 3,490 13,36 15,51 17,54 20. 09
9 2,088 2.700 3,325 4,168 14,68 16,92 19.02 21,67
10 2,558 3,247 3,940 4,865 15,99 18,31 20,48 23.21

P ( X ≤ x )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) x 2 0,975 ( r ) x 2 0,95 ( r ) x 2 0,90 ( р ) x 2 0,10 ( r ) x 2 0,05 ( r ) x 2 0,025 ( r ) x 2 0,01 ( r )
1 0,000 0,001 0,004 0,016 2,706 3,841 5. 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9.488 11.14 13,28
5 0,554 0,831 1,145 1,610 9.236 11.07 12,83 15.09
6 0,872 1,237 1,635 2,204 10,64 12,59 14,45 16,81
7 1,239 1,690 2,167 2,833 1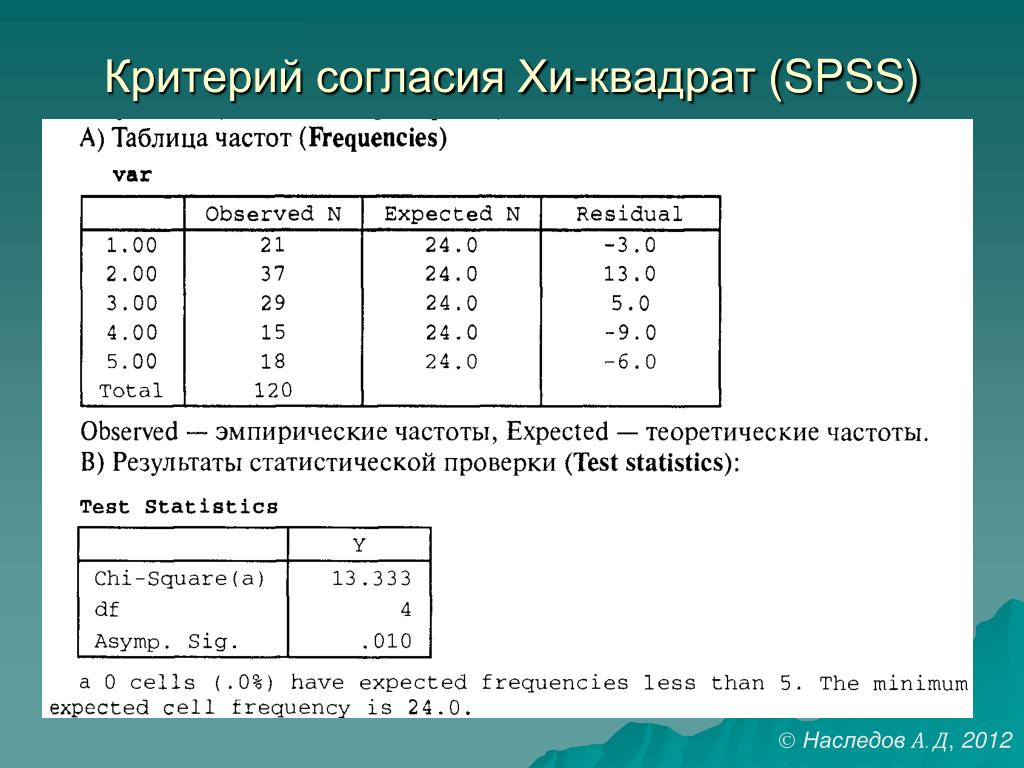2. 02 14.07 16.01 18,48
8 1,646 2,180 2,733 3,490 13,36 15,51 17,54 20.09
9 2,088 2.700 3,325 4,168 14,68 16,92 19.02 21,67
10 2,558 3,247 3,940 4,865 15,99 18,31 20,48 23,21

Из таблицы видно, что десятый процентиль случайной величины хи-квадрат с 10 степенями свободы равен 4,865.

Какова вероятность того, что случайная величина хи-квадрат с 10 степенями свободы больше 15,99?

Решение

Ну вот… минуту назад я сказал, что таблица хи-квадрат не очень помогает в определении вероятностей, затем я поворачиваюсь и прошу вас использовать таблицу, чтобы найти вероятность! Выполнение этого хотя бы один раз поможет нам убедиться, что мы полностью понимаем таблицу. В этом случае нам нужно будет прочитать таблицу «назад». Чтобы найти вероятность, мы:

  1. Найдите \(r=10\) в первом столбце слева.
  2. Найдите значение 15,99 в строке \(r=10\).
  3. Прочитайте вероятность, возглавляемую столбцом, в который попадает 15,99.

Что вы получаете?

P ( X ≤ x )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) x 2 0,975 ( r ) x 2 0,95 ( r ) x 2 0,90 ( r ) x 2 0,10 ( р ) x 2 0,05 ( r ) x 2 0,025 ( r ) x 2 0,01 ( r )
1 0,000 0,001 0,004 0,016 2,706 3,841 5. 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9.488 11.14 13,28
5 0,554 0,831 1,145 1,610 9.236 11.07 12,83 15.09
6 0,872 1,237 1,635 2,204 10,64 12,59 14,45 16,81
7 1,239 1,690 2,167 2,833 12.02 14.07 16.01 18,48
8 1,646 2,180 2,733 3,490 13,36 15,51 17,54 20. 09
9 2,088 2.700 3,325 4,168 14,68 16,92 19.02 21,67
10 2,558 3,247 3,940 4,865 15,99 18,31 20,48 23.21

P ( X ≤ х )
  0,010 0,025 0,050 0,100 0,900 0,950 0,975 0,990
р x 2 0,99 ( r ) x 2 0,975 ( r ) х 2 0,95 ( р ) x 2 0,90 ( r ) x 2 0,10 ( r ) x 2 0,05 ( r ) x 2 0,025 ( r ) x 2 0,01 ( r )
1 0,000 0,001 0,004 0,016 2,706 3,841 5. 042 6,635
2 0,020 0,051 0,103 0,211 4,605 ​​ 5,991 7,378 9.210
3 0,115 0,216 0,352 0,584 6.251 7,815 9,348 11,34
4 0,297 0,484 0,711 1,046 7,779 9.488 11.14 13,28
5 0,554 0,831 1,145 1,610 9,236 11.07 12,83 15.09
6 0,872 1,237 1,635 2,204 10,64 12,59 14,45 16,81
7 1,239 1,690 2,167 2,833 12. 02 14.07 16.01 18,48
8 1,646 2,180 2,733 3,490 13,36 15,51 17,54 20.09
9 2,088 2.700 3,325 4,168 14,68 16,92 19.02 21,67
10 2,558 3,247 3,940 4,865 15,99 18,31 20,48 23,21

Таблица говорит нам, что вероятность того, что случайная величина хи-квадрат с 10 степенями свободы будет на меньше чем 15,99, равна 0,90. Следовательно, вероятность того, что случайная величина хи-квадрат с 10 степенями свободы на 90 281 больше, чем 15,99, на 90 282 равна 1–0,90, или 0,10.

Шаг 5 — Интерпретация результатов | Хи-квадрат критерия согласия в примере селекции растений

Теперь мы готовы к последнему шагу, интерпретации результатов нашего вычисления хи-квадрата. Для этого нам нужно обратиться к таблице распределения хи-квадрат. Это таблица вероятностей выбранных значений X 2  (таблица 3).

Таблица 3: Таблица распределения хи-квадрат.

Статистики рассчитывают определенные возможности появления (значения P) для значения X 2 в зависимости от степеней свободы. Степени свободы — это просто количество классов, которые могут варьироваться независимо друг от друга, минус один (n-1). В этом случае степени свободы = 1, потому что у нас есть 2 класса фенотипов: устойчивые и восприимчивые.

Рассчитанное значение X 2  на основе наших результатов можно сравнить со значениями в таблице в соответствии с конкретными степенями свободы, которые у нас есть. Это покажет нам вероятность того, что отклонения (между тем, что мы ожидали увидеть, и тем, что мы действительно видели) вызваны исключительно случайностью, и наша гипотеза или модель могут быть подтверждены.

В нашем примере значение X 2  1,2335 и степень свободы 1 связаны со значением P меньше 0,50, но больше 0,25 (следуйте синей пунктирной линии и стрелкам на рис. 5). Это означает, что такое большое или большее значение хи-квадрата (или такое или большее различие между ожидаемыми и наблюдаемыми числами) будет возникать просто случайно в 25–50 % случаев. По соглашению биологи часто используют значение 5,0% (p<0,05), чтобы определить, являются ли наблюдаемые отклонения значительными. Любые отклонения, превышающие этот уровень, заставят нас отвергнуть нашу гипотезу и предположить, что дело не в случайности. (см. красный кружок на рис. 5.) Если вычисленное вами значение хи-квадрат больше критического значения хи-квадрат, вы отвергаете свою нулевую гипотезу. Если вычисленное вами значение хи-квадрат меньше критического значения хи-квадрат, то вы «не сможете отвергнуть» свою нулевую гипотезу.

Рис. 5 : Нахождение значения вероятности для хи-квадрата 1,2335 с 1 степенью свободы. Сначала прочитайте столбец 1 вниз, чтобы найти строку с 1 степенью свободы, а затем перейдите вправо, где должно быть 1,2335. Это соответствует вероятности меньше 0,5, но больше 0,25, как показано синими стрелками.

Таким образом, в нашем примере селекции томатов мы не смогли опровергнуть нашу гипотезу о том, что устойчивость к бактериальной пятнистости в этом наборе скрещиваний обусловлена ​​одним доминантно наследуемым геном (Rx-4). Мы можем предположить, что наблюдаемые нами отклонения между тем, что мы ожидали, и фактически наблюдаемыми с точки зрения количества устойчивых и восприимчивых растений, могли быть вызваны чистой случайностью. Мы можем продолжить работу с нашей текущей гипотезой. Помните, мы еще не «доказали» нашу гипотезу на данный момент. Дальнейшее тестирование в других скрещиваниях и популяциях будет использовано для получения дополнительных доказательств того, что наша гипотеза точно объясняет способ наследования Rx-4.

Запустите приведенный ниже видеоучебник, показывающий, как использовать диаграмму распределения хи-квадрат, используя этот пример селекции помидоров.

Далее мы рассмотрим пример генотипирования, или вы пропустите этот урок к обсуждению компьютерных программ, доступных при наличии обширных данных, а также сильных и слабых сторон теста хи-квадрат.

Вопрос

В BC 2 S 4  Популяция IBC (инбредное обратное скрещивание) с 197 линий томата, вы наблюдали следующие фенотипические данные в отношении бактериальной пятнистости. Рассчитайте значение хи-квадрат для гипотезы о преимущественной наследственности резистентности. Вы бы отвергли или не смогли бы отвергнуть эту гипотезу?

169 чувствительны к бактериальной пятнистости

6 устойчивы к бактериальной пятнистости

Отклонять

ОТВЕТ: Для IBC поколения BC2S4 мы ожидаем 7 восприимчивых линий к 1 устойчивой, или 153 восприимчивых линии и 22 устойчивых.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *