Таблица хи квадрат пирсона: Таблица распределения хи-квадрат

Справочник по прикладной статистике. Том 1

Ллойд Э., Ледерман У. (ред.). Справочник по прикладной статистике. Том 1. М.: Финансы и статистика, 1989. — 510 с. В справочнике освещены основные математико-статистические методы. Том 1 включает введение в статистику, вопросы, связанные с выборочным распределением, точечным и интервальным оцениванием, общую теорию статистических критериев, дисперсионный анализ, планирование эксперимента. Для широкой аудитории специалистов, разрабатывающих и использующих статистические методы. Оглавление ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ Глава I. ВВЕДЕНИЕ В СТАТИСТИКУ 1.1. СМЫСЛ ПОНЯТИЯ «СТАТИСТИКА» 1.2. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ, СТАТИСТИКА, ОЦЕНКА 1.3. ТЕМА ЭТОЙ КНИГИ 1.4. СОГЛАШЕНИЯ И ОБОЗНАЧЕНИЯ Глава 2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ 2.1. МОМЕНТЫ И ДРУГИЕ СТАТИСТИКИ 2.1.2. МОМЕНТЫ 2.2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ: ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ 2.3. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАТИСТИК 2.3.1. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ СРЕДНЕГО ЗНАЧЕНИЯ ВЫБОРКИ 2.3.2. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ ДИСПЕРСИИ ВЫБОРКИ 2.3.3. ВЫБОРОЧНАЯ КОВАРИАЦИЯ МЕЖДУ СРЕДНИМ ЗНАЧЕНИЕМ ВЫБОРКИ x И ДИСПЕРСИЕЙ ВЫБОРКИ v 2.3.4. ВЫБОРОЧНЫЕ МОМЕНТЫ ДЛЯ МОМЕНТОВ ВЫБОРКИ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ 2.3.5. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАНДАРТНОГО ОТКЛОНЕНИЙ ВЫБОРКИ 2.3.6. ВЫБОРОЧНЫЕ МОМЕНТЫ КОЭФФИЦИЕНТА АСИММЕТРИИ ВЫБОРКИ 2.4. РАСПРЕДЕЛЕНИЯ СУММ НЕЗАВИСИМЫХ ОДИНАКОВО РАСПРЕДЕЛЕННЫХ ПЕРЕМЕННЫХ 2.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ 2.5.2. РЕЗУЛЬТАТ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СТАНДАРТИЗАЦИЯ 2.5.3. ЛИНЕЙНЫЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ 2.5.4. КВАДРАТИЧЕСКИЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ 2.5.5. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА (t-распределение) 2.5.6. РАСПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ДИСПЕРСИЙ (F-распределение) 2. 5.7. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ВЫБОРКИ 2.5.8. НЕЗАВИСИМОСТЬ КВАДРАТИЧНЫХ ФОРМ. ТЕОРЕМА ФИШЕРА—КОКРЕНА. ТЕОРЕМА КРЕЙГА 2.5.9. РАЗМАХ И СТЬЮДЕНТИЗИРОВАННЫЙ РАЗМАХ 2.6. АССИМПТОТИЧЕСКОЕ ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ х И НЕЛИНЕЙНЫХ ФУНКЦИЙ ОТ х 2.7. ПРИБЛИЖЕНИЕ ВЫБОРОЧНЫХ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ НЕЛИНЕЙНЫХ СТАТИСТИК. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ 2.7.1. АППРОКСИМАЦИЯ 2.7.2. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ 2.7.3. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ 2.7.4. ПРЕОБРАЗОВАНИЯ, ВЫПРЯМЛЯЮЩИЕ ЗАВИСИМОСТЬ 2.7.5. ПРЕОБРАЗОВАНИЕ ВЫБОРОЧНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПРИ r=0 В СТЬЮДЕНТОВУ ВЕЛИЧИНУ 2.7.6. ПРЕОБРАЗОВАНИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПЕРЕМЕННОЙ В «хи-квадрат»-ПЕРЕМЕННУЮ 2.8. НЕЦЕНТРАЛЬНЫЕ ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ 2.8.1. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ 2.8.2. НЕЦЕНТРАЛЬНОЕ F-РАСПРЕДЕЛЕНИЕ 2.8.3. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА 2.9. ПОЛИНОМИАЛЬНОЕ (МУЛЬТИНОМИАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ В ТЕОРИИ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ 2. 9.1. БИНОМИАЛЬНОЕ, ТРИНОМИАЛЬНОЕ И МУЛЬТИНОМИАЛЬНОЕ (ПОРЯДКА m) РАСПРЕДЕЛЕНИЯ 2.9.2. СВОЙСТВА ПОЛИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ 2.9.3. ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК УСЛОВНОЕ ОТ СОВМЕСТНОГО РАСПРЕДЕЛЕНИЯ НЕЗАВИСИМЫХ ПУАССОНОВСКИХ ПЕРЕМЕННЫХ 2.9.4. ТАБЛИЦЫ ЧАСТОТ 2.10. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ Глава 3. ОЦЕНИВАНИЕ. ВВОДНОЕ ОБОЗРЕНИЕ 3.1. ЗАДАЧА ОЦЕНИВАНИЯ 3.2. ИНТУИТИВНЫЕ ПРЕДСТАВЛЕНИЯ И ГРАФИЧЕСКИЙ МЕТОД 3.2.2. ЧАСТОТНЫЕ ТАБЛИЦЫ, ГИСТОГРАММЫ И ЭМПИРИЧЕСКАЯ ф.р. 3.3. НЕКОТОРЫЕ ОБЩИЕ КОНЦЕПЦИИ И КРИТЕРИИ ОЦЕНОК 3.3.1. ВВЕДЕНИЕ. РАЗМЕРНОСТЬ, ЗАМЕНЯЕМОСТЬ, СОСТОЯТЕЛЬНОСТЬ, КОНЦЕНТРАЦИЯ 3.3.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ И НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ 3.3.3. ЭФФЕКТИВНОСТЬ. ГРАНИЦА КРАМЕРА—РАО 3.4. ДОСТАТОЧНОСТЬ 3.4.2. КРИТЕРИЙ ФАКТОРИЗАЦИИ И ЭКСПОНЕНЦИАЛЬНОЕ СЕМЕЙСТВО 3.4.3. ДОСТАТОЧНОСТЬ И НЕСМЕЩЕННАЯ МИНИМАЛЬНО ДИСПЕРСНАЯ ОЦЕНКА 3.4.4. ДОСТАТОЧНОСТЬ В СЛУЧАЕ МНОГИХ ПАРАМЕТРОВ 3.5. ПРАКТИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ ОЦЕНОК. 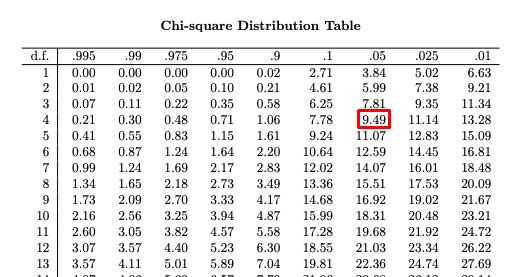ВВЕДЕНИЕ 3.5.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 3.5.3. МЕТОД МОМЕНТОВ 3.5.4. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 3.5.5. НОРМАЛЬНЫЕ ЛИНЕЙНЫЕ МОДЕЛИ, В КОТОРЫХ ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ И НАИМЕНЬШИХ КВАДРАТОВ СОВПАДАЮТ Глава 4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ 4.1.2. СТАНДАРТНОЕ ОТКЛОНЕНИЕ 4.1.3. ИНТЕРВАЛЫ ВЕРОЯТНОСТИ 4.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ 4.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА С ПОМОЩЬЮ ОПОРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 4.4. ИСТОЛКОВАНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА КАК МЕРЫ ТОЧНОСТИ ОЦЕНКИ НЕИЗВЕСТНОГО ПАРАМЕТРА 4.5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ПРИ НЕСКОЛЬКИХ ПАРАМЕТРАХ 4.5.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ФУНКЦИЙ ДВУХ ПАРАМЕТРОВ, ВКЛЮЧАЮЩИХ ОТНОШЕНИЕ ПАРАМЕТРОВ И ИХ РАЗНОСТЬ (ТЕОРЕМА ФЕЛЛЕРА) 4.6. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ БЕЗ ИСПОЛЬЗОВАНИЯ ОПОРНОЙ ПЕРЕМЕННОЙ 4.7. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ ДЛЯ ПАРАМЕТРОВ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ 4.8. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ КВАНТИЛЕЙ, НЕ ЗАВИСЯЩИЕ ОТ ИСХОДНОГО РАСПРЕДЕЛЕНИЯ (РАСПРЕДЕЛЕННЫЕ СВОБОДНО) 4. 9. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ МНОГОМЕРНОГО ПАРАМЕТРА 4.9.2. ЭЛЛИПТИЧЕСКИЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ВЕКТОРА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДВУМЕРНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ. ПРИБЛИЖЕННЫЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ОЦЕНОК НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ 4.10. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ НА ОСНОВЕ БОЛЬШИХ ВЫБОРОК С ИСПОЛЬЗОВАНИЕМ ФУНКЦИИ ПРАВДОПОДОБИЯ 4.10.2. ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ ПРОИЗВОДНОЙ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ ПРАВДОПОДОБИЯ 4.10.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ (ПРИБЛИЖЕННО) НОРМАЛИЗУЮЩЕГО ПРЕОБРАЗОВАНИЯ 4.11. ДОВЕРИТЕЛЬНАЯ ПОЛОСА ДЛЯ НЕИЗВЕСТНОЙ НЕПРЕРЫВНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 4.11.2. РАССТОЯНИЕ КОЛМОГОРОВА—СМИРНОВА МЕЖДУ ИСТИННОЙ (ТЕОРЕТИЧЕСКОЙ) И ЭМПИРИЧЕСКОЙ ФУНКЦИЯМИ РАСПРЕДЕЛЕНИЯ 4.11.3. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СТАТИСТИКИ КОЛМОГОРОВА—СМИРНОВА. ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 4.12. ТОЛЕРАНТНЫЕ ИНТЕРВАЛЫ 4.13. ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ 4.13.2. ПРАВДОПОДОБНЫЕ ЗНАЧЕНИЯ И ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ 4. 13.3. СИТУАЦИЯ С ДВУМЯ ПАРАМЕТРАМИ 4.14. БАЙЕСОВСКИЕ ИНТЕРВАЛЫ Глава 5. СТАТИСТИЧЕСКИЕ КРИТЕРИИ 5.2.1. ДВУХСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ. СОСТАВНЫЕ ЧАСТИ, ПРОЦЕДУРА И ИНТЕРПРЕТАЦИЯ 5.2.2. ТРАДИЦИОННАЯ ИНТЕРПРЕТАЦИЯ УРОВНЕЙ ЗНАЧИМОСТИ; ИСПОЛЬЗУЕМЫЕ НА ПРАКТИКЕ УРОВНИ ЗНАЧИМОСТИ; КРИТИЧЕСКАЯ ОБЛАСТЬ 5.2.3. ОДНОСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ 5.2.4. КРИТЕРИИ О РАСПРЕДЕЛЕНИИ ПУАССОНА 5.2.5. КРИТЕРИИ ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ 5.2.6. ВЫБОР СТАТИСТИКИ КРИТЕРИЯ 5.3. КРИТЕРИИ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ 5.3.2. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ОДНОСТОРОННЕГО КРИТЕРИЯ ДЛЯ ВЫБОРКИ ИЗ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ, КОГДА ЗНАЧЕНИЕ «сигма» НЕИЗВЕСТНО 5.3.3. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ДВУХСТОРОННЕГО КРИТЕРИЯ 5.4. КРИТЕРИИ ДЛЯ СЛОЖНЫХ НУЛЕВЫХ ГИПОТЕЗ 5.4.2. КРИТЕРИИ НЕЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ 2×2. ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА 5.5. КРИТЕРИИ, СОДЕРЖАЩИЕ БОЛЕЕ ОДНОГО ПАРАМЕТРА. ОБОБЩЕННЫЕ КРИТЕРИИ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ 5.6. АППРОКСИМАЦИЯ УРОВНЯ ЗНАЧИМОСТИ КРИТЕРИЯ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ ДЛЯ БОЛЬШИХ ВЫБОРОК 5. 7. КРИТЕРИИ РАНДОМИЗАЦИИ 5.8. СТАНДАРТНЫЕ КРИТЕРИИ ДЛЯ МОДЕЛИ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ 5.8.2. ЗНАЧИМОСТЬ СРЕДНЕГО, КОГДА ДИСПЕРСИЯ НЕИЗВЕСТНА. t-КРИТЕРИЙ СТЬЮДЕНТА 5.8.3. КРИТЕРИЙ ФИШЕРА-БЕРЕНСА ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ 5.8.4. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ (КОГДА ДИСПЕРСИИ РАВНЫ) 5.8.5. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА РЕГРЕССИИ В ПРОСТОЙ ЛИНЕЙНОЙ МОДЕЛИ 5.8.6. КРИТЕРИЙ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ 5.8.7 ПРОВЕРКА РАВЕНСТВА НЕКОТОРЫХ СРЕДНИХ. ВВЕДЕНИЕ В ДИСПЕРСИОННЫЙ АНАЛИЗ 5.9. ПРОВЕРКА НОРМАЛЬНОСТИ 5.10. ПРОВЕРКА РАВЕНСТВА к ДИСПЕРСИЙ (КРИТЕРИЙ БАРТЛЕТТА) 5.11. СОЧЕТАНИЕ РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ КРИТЕРИЕВ 5.12. ТЕОРИЯ НЕЙМАНА—ПИРСОНА 5.12.2. ТЕОРИЯ НЕЙМАНА-ПИРСОНА ПРОВЕРКИ ГИПОТЕЗ Глава 6. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 6.2. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 6.2.2. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 6.2.3. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ИНТУИТИВНАЯ АРГУМЕНТАЦИЯ 6. 2.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ТИПЫ МАКСИМУМОВ 6.2.5. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ. СВОЙСТВА ФУНКЦИИ ПРАВДОПОДОБИЯ 6.2.6. ОЦЕНИВАНИЕ ФУНКЦИИ ПАРАМЕТРА «тетта». СВОЙСТВО ИНВАРИАНТНОСТИ 6.3. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ В ОДНОПАРАМЕТРИЧЕСКОЙ СИТУАЦИИ 6.4. ПРИМЕРЫ О.М.П. В МНОГОПАРАМЕТРИЧЕСКИХ СЛУЧАЯХ 6.5. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ 6.5.2. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ЛИНЕЙНОЙ РЕГРЕССИИ С ВЕСАМИ 6.5.3. ЛИНЕЙНАЯ РЕГРЕССИЯ С ОДИНАКОВЫМИ ВЕСАМИ 6.6. ОЦЕНИВАНИЕ ЗАВИСИМОСТИ ТОКСИЧНОСТИ ИНСЕКТИЦИДА ОТ УРОВНЯ ДОЗИРОВКИ 6.6.2. ВЕРОЯТНОСТНАЯ МОДЕЛЬ 6.6.3. ИССЛЕДОВАНИЕ ПОВЕРХНОСТИ ФУНКЦИИ ПРАВДОПОДОБИЯ 6.6.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ 6.6.5. ТОЧНОСТЬ ОЦЕНОК 6.6.6. ДОЗА, НЕОБХОДИМАЯ ДЛЯ ЗАДАННОГО ЗНАЧЕНИЯ ОТКЛИКА 6.7. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПО ГРУППИРОВАННЫМ, ЦЕНЗУРИРОВАННЫМ И УСЕЧЕННЫМ ДАННЫМ 6.7.2. НЕПРЕРЫВНЫЕ ДАННЫЕ И ГРУППИРОВКА. ПОПРАВКА ШЕППАРДА ГЛАВА 7. СТАТИСТИКА ХИ-КВАДРАТ. КРИТЕРИИ СОГЛАСИЯ, НЕЗАВИСИМОСТИ И ОДНОРОДНОСТИ 7.1.2. АДЕКВАТНОСТЬ ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ 7.2. РАССТОЯНИЕ К. ПИРСОНА: КРИТЕРИЙ «хи-квадрат» 7.3. ОБЪЕДИНЕНИЕ ЯЧЕЕК С НИЗКИМИ ЧАСТОТАМИ. КРИТЕРИЙ У. КОКРЕНА 7.4. КРИТЕРИЙ «хи-квадрат» ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ 7.5. ТАБЛИЦЫ ЧАСТОТ ПЕРЕКРЕСТНОЙ КЛАССИФИКАЦИИ (ТАБЛИЦЫ СОПРЯЖЕННОСТИ). КРИТЕРИИ НЕЗАВИСИМОСТИ 7.5.2. ТАБЛИЦЫ k x m 7.6. ИНДЕКС РАССЕЯНИЯ 7.6.1. ИНДЕКС РАССЕЯНИЯ ДЛЯ ВЫБОРКИ ИЗ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ 7.6.2. ИНДЕКС РАССЕЯНИЯ ДЛЯ ПУАССОНОВСКИХ ВЫБОРОК Глава 8. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ И ДИСПЕРСИОННЫЙ АНАЛИЗ 8.1. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ МОДЕЛЕЙ ОБЩЕГО ВИДА 8.2. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ЛИНЕЙНЫХ МОДЕЛЕЙ ПОЛНОГО РАНГА. НОРМАЛЬНЫЕ УРАВНЕНИЯ. ТЕОРЕМА ГАУССА—МАРКОВА 8.2.1. ПРИМЕРЫ ОЦЕНИВАНИЯ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ 8.2.2. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ МОДЕЛЕЙ 8. 2.3. СВОЙСТВА ОЦЕНОК МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ 8.2.4. ОСТАТКИ 8.2.5. ОРТОГОНАЛЬНЫЕ ПЛАНЫ И ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ 8.2.6. МОДИФИКАЦИИ ДЛЯ НЕРАВНОТОЧНЫХ НАБЛЮДЕНИЙ; ВЗВЕШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 8.2.7. МОДИФИКАЦИИ ДЛЯ НЕ НЕЗАВИСИМЫХ НАБЛЮДЕНИЙ 8.3. ДИСПЕРСИОННЫЙ АНАЛИЗ И ПРОВЕРКА ГИПОТЕЗ ДЛЯ ПЛАНОВ ПОЛНОГО РАНГА 8.3.2. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ 8.2 3. ПРОВЕРКА ГИПОТЕЗ 8.3.4. ОСНОВНЫЕ ТОЖДЕСТВА 8.3.5. ПРОВЕРКИ ГИПОТЕЗ В ОРТОГОНАЛЬНЫХ ПЛАНАХ 8.3.6. ПРОВЕРКА ГИПОТЕЗ ДЛЯ НЕ ОРТОГОНАЛЬНЫХ ПЛАНОВ 8.3.7 ГРУППОВАЯ ОРТОГОНАЛЬНОСТЬ 8.3.8. ОБЩИЕ ЛИНЕЙНЫЕ ГИПОТЕЗЫ Глава 9. ПЛАНИРОВАНИЕ СРАВНИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ 9.3. БОЛЕЕ СЛОЖНЫЙ ПРИМЕР: ЭКСПЕРИМЕНТ ДАРВИНА 9.4. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЕ БЛОЧНЫЕ ПЛАНЫ 9.5. ОБРАБОТКИ НА ОДНОМ И НА НЕСКОЛЬКИХ УРОВНЯХ 9.6. ПОТРЕБНОСТЬ В РАЗРАБОТКАХ ПО УМЕНЬШЕНИЮ РАЗМЕРОВ БЛОКОВ 9.7. СБАЛАНСИРОВАННЫЕ НЕПОЛНЫЕ БЛОКИ ДЛЯ СРАВНЕНИЯ ОДНОУРОВНЕВЫХ ОБРАБОТОК 9.8. ПОЛНЫЙ ФАКТОРНЫЙ ПЛАН 9.8. j 9.9. НЕПОЛНЫЕ БЛОКИ: СМЕШИВАНИЕ 9.10. ЧАСТИЧНОЕ СМЕШИВАНИЕ 9.11. ФАКТОРЫ НА ТРЕХ И БОЛЕЕ УРОВНЯХ 9.11.2. ГРЕКО-ЛАТИНСКИЙ КВАДРАТ Глава 10. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И АНАЛИЗ СТАТИСТИЧЕСКИХ ЭКСПЕРИМЕНТОВ: ВЫРОЖДЕННЫЕ МОДЕЛИ, МНОЖЕСТВЕННЫЕ КРИТЕРИИ 10.1.2. ОЦЕНИВАНИЕ. ФУНКЦИИ, ДОПУСКАЮЩИЕ ОЦЕНКУ 10.1.3. ПРОВЕРКА ГИПОТЕЗ 10.1.4. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ИЕРАРХИЧЕСКАЯ КЛАССИФИКАЦИЯ 10.1.5. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ПЕРЕКРЕСТНАЯ КЛАССИФИКАЦИЯ 10.1.6. КЛАССИФИКАЦИИ БОЛЕЕ ВЫСОКОГО ПОРЯДКА 10.1.7. КОВАРИАЦИОННЫЙ АНАЛИЗ 10.2. МНОЖЕСТВЕННЫЕ КРИТЕРИИ И СРАВНЕНИЯ 10.2.2. КОМБИНАЦИИ ПРОВЕРОК И ОБЩИЙ РАЗМЕР КРИТЕРИЯ 10.2.3. МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ 10.3. ПРЕДПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ОШИБОК 10.3.2. АНАЛИЗ ОСТАТКОВ

Хи квадрат-распределение. Распределение Пирсона. Квантили хи-квадрат распределения

		Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. / / Хи квадрат-распределение. Распределение Пирсона. Квантили хи-квадрат распределения Поделиться:    -распределение. Распределение Пирсона. В таблице приведены значения квантилей Χ21-α(m) в зависимости от числа степеней свободы m и вероятности α m/α 0,99 0,98 0,95 0,90 0,80 0,20 0,10 0,05 0,02 0,01 0,001 1 0,00016 0,00063 0,00393 0,0158 0,0642 1,642 2,706 3,841 5,412 6,635 10,827 2 0,0201 0,0404 0,103 0,211 0,446 3,219 4,605 5,991 7,824 9,210 13,815 3 0,115 0,185 0,352 0,584 1,005 4,642 6,251 7,815 9,837 11,341 16,268 4 0,297 0,429 0,711 1,064 1,649 5,989 7,779 9,488 11,668 13,277 18,465 5 0,554 0,752 1,145 1,610 2,343 7,289 9,236 11,070 13,388 15,086 20,517 6 0,872 1,134 1,635 2,204 3,070 8,558 10,645 12,592 15,033 16,812 22,457 7 1,239 1,564 2,167 2,833 3,822 9,803 12,017 14,067 16,622 18,475 24,322 8 1,646 2,032 2,733 3,490 4,594 11,030 13,362 15,507 18,679 20,090 26,125 9 2,088 2,532 3,325 4,168 5,380 12,242 14,684 16,919 19,679 21,666 27,877 10 2,588 3,059 3,940 4,865 6,179 13,442 15,987 18,307 21,161 23,209 29,588 11 3,053 3,609 4,575 5,578 6,989 14,631 17,275 19,675 22,618 24,725 31,264 12 3,571 4,178 5,226 6,304 7,807 15,812 18,549 21,026 24,054 26,217 32,909 13 4,107 4,765 5,892 7,042 8,634 16,985 19,812 22,362 25,472 27,688 34,528 14 4,660 5,368 6,571 7,790 9,467 18,151 21,064 23,685 26,873 29,141 36,123 15 5,229 5,985 7,262 8,547 10,307 19,311 22,307 24,996 28,259 30,578 37,697 16 5,812 6,614 7,962 9,312 11,152 20,465 23,542 26,296 29,633 32,000 39,252 17 6,408 7,255 8,672 10,085 12,002 21,615 24,769 27,587 30,995 33,409 40,790 18 7,015 7,906 9,390 10,865 12,857 22,760 25,989 28,869 32,346 34,805 42,312 19 7,633 8,567 10,117 11,651 13,716 23,900 27,204 30,144 33,687 36,191 43,820 20 8,260 9,237 10,851 12,443 14,578 25,038 28,412 31,410 35,020 37,566 45,315 21 8,897 9,915 11,591 13,240 15,445 26,171 29,615 32,671 36,343 38,932 46,797 22 9,542 10,600 12,338 14,041 16,314 27,301 30,813 33,924 37,659 40,289 48,268 23 10,196 11,298 13,091 14,848 17,187 28,429 32,007 35,172 38,968 41,638 49,728 24 10,856 11,992 13,848 15,659 18,062 29,553 33,196 36,415 40,270 42,980 51,179 25 11,542 12,697 14,611 16,473 18,940 30,675 34,382 37,652 41,566 44,314 52,620 26 12,198 13,409 15,379 17,292 19,820 31,795 35,563 38,885 42,856 45,642 54,052 27 12,879 14,125 16,151 18,114 20,703 32,912 86,741 40,113 44,140 46,963 55,476 28 13,565 14,847 16,928 18,939 21,588 34,027 37,916 41,337 45,419 48,278 56,893 29 14,256 15,574 17,708 19,768 22,475 35,139 39,087 42,557 46,693 49,588 58,302 30 14,953 16,306 18,493 20,599 23,364 36,250 40,256 43,773 47,962 50,892 59,703 Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Критерий независимости Пирсона хи-квадрат: использование и неправильное использование

(независимость результата, парные выборки, кластерная выборка, объединение нескольких таблиц, коррекция непрерывности Йейтса)

Курсы по статистике, особенно для биологов, предполагают, что формулы = понимание и учат, как делать статистику, но в значительной степени игнорируют то, что предполагают эти процедуры, и то, как их результаты вводят в заблуждение, когда эти предположения необоснованны. В результате неправильное использование, скажем так, предсказуемо…

Использование и неправильное использование

Этот тест соперничает с t-критерием за то, что он является наиболее часто используемым статистическим тестом практически во всех дисциплинах. Различные авторы (в частности, Сокал и Рхольф) выступали за его замену критерием отношения правдоподобия G. Такие просьбы в значительной степени остались без внимания (по крайней мере, для анализа 2 2 таблиц), хотя мы включили пару примеров его использования. Возможно, из-за того, что критерий хи-квадрат Пирсона так широко используется, он также является одной из самых неправильно применяемых статистических процедур. Применительно к результатам кластерных рандомизированных исследований он может привести к самым ошибочным выводам, которые можно найти в литературе.

Отсутствие независимости результатов является наиболее распространенным фактором, делающим тест недействительным. Это может возникнуть несколькими способами. Если образцы являются парными (либо в исследованиях «до-после», либо в сопоставленных образцах), то хи-квадрат Пирсона не является подходящим тестом. Мы приводим примеры такого неправильного использования в исследовании «до и после» заболеваемости малярией и присутствия/отсутствия двух видов лягушек в соответствующих парах естественных и искусственных прудов. Другой причиной не независимости результатов является использование кластерной выборки. Приведены примеры отбора свиней на фермах и отбора барвинков с использованием квадратов. В экспериментах частоты в таблице непредвиденных обстоятельств должны применяться к тому количеству единиц, которые были распределены случайным образом — изменение экспериментальной единицы после рандомизации недопустимо. Мы приводим примеры, когда это делалось при испытаниях вакцины против холеры и противомоскитных сеток, пропитанных инсектицидами. Та же проблема возникает, если матери распределяются случайным образом, но тест применяется к потомству, будь то свиньи или паразитоиды.

Связанная проблема связана с объединением частот из нескольких таблиц 2 2. Это может вводить в заблуждение, если образцы не являются однородными, и в любом случае отбрасывает данные о изменчивости между повторами. Мы приводим несколько примеров, включая заражение свиней ленточными червями и заражение белок вирусом. Несколько таблиц следует анализировать с использованием методов Мантеля-Хензеля. Другой тип объединения состоит в том, чтобы сделать это между категориями таблицы непредвиденных обстоятельств, скажем, путем свертывания, скажем, таблицы 3 2 в три таблицы 2 2. При этом необходимо проявлять большую осторожность, чтобы в процессе не создавались бессмысленные категории.

Существует реальная проблема, как справиться с очень малыми ожидаемыми частотами. Поправка на непрерывность Йейтса делает тест слишком консервативным. До недавнего времени считалось, что следует использовать точный критерий Фишера, даже если модель (фиксированные предельные суммы) неверна. Мы показываем в основном тексте, что точный критерий Монте-Карло гораздо предпочтительнее. Различия во мнениях среди статистиков вносят предвзятость, потому что можно выбирать, какой тест использовать — приведенные примеры включают, питаются ли паразитоиды преимущественно паразитированными хозяевами, и факторы, влияющие на заражение лошадиным гриппом. Наконец, поскольку критерий хи-квадрат Пирсона часто используется в качестве критерия ассоциации, следует подчеркнуть, что связь никогда не может доказать причинно-следственную связь, какой бы сильной она ни была. Мы приводим пример, который ставит вопрос о том, делает ли плохой статус витамина D человека более восприимчивым к туберкулезу, или же туберкулез является причиной наблюдаемого дефицита витамина D.

Что говорят статистики

Agresti (2002) подробно описывает критерий хи-квадрат Пирсона в главе 3. Armitage & Berry (2002) охватывают материал, представленный здесь в главах 4 и 15, тогда как Woodward (2004) рассматривает ту же тему в главе 3. Флейсс и др. (2003) рассматривает широкий спектр статистических методов, доступных для показателей и долей. Коновер (1999) рассматривает анализ таблиц непредвиденных обстоятельств в главе 4, в то время как Эверит (1992) весь текст посвящает анализу таблиц сопряженности. Sokal & Rohlf (1995) и Zar (1999) охватывают большую часть (но не все) одного и того же материала.

Ludbrook (2008) решает проблему соответствия теста экспериментальному плану для таблицы 2×2. Кэмпбелл (2007) отдает предпочтение критерию хи-квадрат «n — 1», за исключением случаев, когда любая ожидаемая частота меньше единицы. Агрести (2001) рассмотрел продолжающиеся разногласия по поводу использования точного вывода для категориальных данных. Рид (2004) рассматривает использование скорректированной статистики хи-квадрат для анализа кластеризованных двоичных данных. Йейтс (1984) рассматривает (бесконечные) споры о том, как анализировать таблицы 2 × 2 до 1984 года. Плакетт (1983) исследует историю разработки Карлом Пирсоном критерия хи-квадрат. Cochran (1954) и Armitage (1955) предложили критерий хи-квадрат для тренда. Барнард (1947) первым определил различные используемые модели, которые генерируют таблицы 2 × 2.

Кремер и др. (2004) не рекомендует использовать взвешенную каппу для оценки согласия. Greenland & Robins (1985) продемонстрировали, что коэффициент риска Мантела-Хензеля является беспристрастным, даже когда некоторые категории имеют небольшую частоту. Пето (1978) критикует вводящий в заблуждение анализ выживания, в котором учитывалось только распределение времени смерти тех, кто умер.

В Википедии есть разделы, посвященные критерию хи-квадрат Пирсона, поправке Йейтса на непрерывность, G-критерию, критерию хи-квадрат для тренда и методам Кохрана-Мантела-Хензеля (недостаточно освещенные). Справочник по биологической статистике также описывает критерий хи-квадрат Пирсона и G-критерий независимости. Электронный справочник по статистике NIST/SEMATECH содержит полезный общий раздел, посвященный тестам отношения правдоподобия.

Дэвид С. Хауэлл предлагает простое введение в использование критерия хи-квадрат Пирсона для анализа таблиц непредвиденных обстоятельств. Ян Кэмпбелл дает справочную информацию о выборе тестов для таблиц два на два. Брюс Уивер резюмирует некоторые материалы, подготовленные Яном Кэмпбеллом. Сотрудник Университета Альберты дает код R для логарифмических тестов правдоподобия независимости и согласия с поправками Уильямса и Йейтса или без них (хотя он также предоставляется в пакете Deducer в R).

Хи-квадрат (расширение)

• карта
|
• <
|
• >
|
• дом

Как только вы узнаете степени свободы (или df), вы можете использовать таблицу хи-квадрат, как та, что справа (иногда книги имеют более сложная таблица, о которой мы поговорим внизу страницы). Хотя эта таблица основана на математической функции (называемой хи-квадрат дистрибутив, пойди разберись!) для наших целей вы можете в основном обращаться с ним так, как он есть появился волшебным образом. Первое, что вам нужно знать, это степени свободы вашего теста. Как мы говорили о на последней странице, это то же самое, что количество строк в вашей таблице минус 1. Используйте свой df, чтобы найти критическое значение критерия хи-квадрат, также называемого критом хи-квадрат. Итак, для теста с 1 df (степень свободы) «критическое» значение статистика хи-квадрат равна 3,84. Что означает критическое значение? По сути, , если рассчитанный вами хи-квадрат больше , чем критическое значение в таблице, то данные не подошли модели, а значит надо отвергнуть нулевую гипотезу. С другой стороны, , если рассчитанный вами хи-квадрат меньше , чем критическое значение, то данные соответствуют модели, вы не можете отвергнуть нулевую гипотезу и пойти на вечеринку*. (*Предполагая, что вы не хотите отклонять нуль. Что вы обычно не надо)

Как вы думаете, почему хи-квадрат-крит увеличивается с увеличением степеней свободы?

 

(Чтобы сделать эту задачу интерактивной, включите JavaScript!)

• Мне нужна подсказка… : Если у вас есть, скажем, 15 степеней свободы,
  сколько строк в вашей таблице?
• …еще одна подсказка… : Для каждой строки в таблице нужно вычислить другое отклонение.

Думаю, у меня есть ответ: с большим количеством степеней свободы,

у вас много строк в таблице. Поэтому вы добавляете
больше чисел вместе, чтобы получить ваш окончательный хи-квадрат.
Поэтому имеет смысл, что критическое значение также увеличивается.

Мелкий шрифт: в некоторых таблицах много столбцов, по одному для каждого интересующего вас p-значения. В этом случае вам сначала нужно найти p-значение 0,05 (или любое другое запрашиваемое вами p-значение), а затем df, то хи-квадрат-крит.