Критерий Фридмана
Определение
Вычисление
Пример: ранговый дисперсионный анализ Фридмана и конкордация
Определение
Критерий Фридмана — это непараметрический аналог дисперсионного анализа повторных измерений, применяется для анализа повторных измерений, связанных с одним и тем же индивидуумом. Логика критерия очень проста. Каждый больной ровно один раз подвергается каждому методу лечения (или наблюдается в фиксированные моменты времени). Результаты наблюдения у каждого больного упорядочиваются.
Причем мы отдельно упорядочиваем значения у каждого больного независимо от всех остальных. Таким образом получается столько упорядоченных рядов, сколько больных участвует в исследовании. Далее, для каждого метода лечения вычисляется сумма рангов. Если разброс сумм велик — различия статистически значимы.
Вычисление
Для применения этого критерия столбцы таблицы данных отражают различные значения переменной эффекта, а строки соответствуют повторным измерениям одного и того же субъекта.
Процедура состоит в упорядочивании (ранжировании) значений в каждой строке (при этом ранги в каждой строке принимают значения от 1 до m — число сравниваемых методов лечения), суммировании полученных рангов по каждому столбцу и вычислении статистики Хи-квадрат.
Рассчитанная статистика Хи-квадрат имеет такое же распределение, что и Хи-квадрат при (m-1) степенях свободы. Если соответствующее значение превзойдет критическое значение (для выбранного уровня значимости и соответствующего числа степеней свобод), то нулевая гипотеза отклоняется.
Этот критерий может применяться и в случае, когда вместо отдельных пациентов сравниваются однородные группы (рандомизированный блочный план исследования).
Пример: ранговый дисперсионный анализ Фридмана и конкордация
Фридмана ранговая ANOVA альтернативна дисперсионному анализу с одним внутригрупповым фактором с повторными измерениями.
Этот критерий сравнивает переменные в зависимых выборках. Коэффициент конкордации Кендалла, по существу, представляет усредненную ранговую корреляцию.
Следующий пример основан на данных, представленных Siegel (1956, стр. 233). 20 матерей и их глухих детей присутствовали на семинаре, обучающему уходу за детьми с данным видом дефекта. В конце семинара 13 экспертов ранжировали 20 матерей в соответствии с тем, насколько, по их мнению, они будут способствовать развитию своих детей.
Рис. 1. Пример исходных данных.
Цель анализа
Анализ преследовал следующие цели:
(1) Определить, можно ли на основании оценок экспертов сделать вывод о значимых различиях между матерями относительно их способностей воспитывать детей с данным дефектом. Этот вопрос может быть решен с помощью рангового дисперсионного анализа (ANOVA) Фридмана.
(2) Можно ли доверять экспертам? Иными словами, согласованы ли их рейтинги, выставленные матерям (зависимы ли они)? Если нет, то вы, очевидно, не можете доверять их оценкам относительно способностей матерей.
Эту гипотезу (эксперты согласованы в большей степени, чем можно бы ожидать из-за чисто случайных совпадений их мнений) можно проверить с помощью коэффициента конкордации Кендалла.
Результаты
Между матерями имеются высоко значимые различия. Дополнительно также видно, что эксперты, выставившие оценки, согласованы друг с другом — конкордация Кендалла равна 0,57 (среднее ранговых корреляций равно .53).
Рис. 2. Результаты рангового анализа и конкордации в виде таблицы.
Для визуализации результатов можно построить диаграмму размаха.
Рис. 3. Результаты рангового анализа и конкордации в виде диаграммы.
Если бы вы знали имена матерей, принявших участие в семинаре, то, используя график, могли бы сказать, кто, по мнению экспертов, наиболее успешно будет воспитывать своего глухого ребенка.
Связанные определения:
Непараметрические статистические методы
Свободный от распределения критерий
В начало
Содержание портала
Критерий Фридмана | это.
.. Что такое Критерий Фридмана?Критерий Фридмана[1] (англ. Friedman test) — непараметрический статистический тест, разработанный американским экономистом Милтоном Фридманом. Является обобщением критерия Уилкоксона и применяется для сопоставления условий измерения () для объектов (испытуемых) с ранжированием по индивидуальным значениям измерений[2]. Непараметрический аналог дисперсионного анализа с повторными измерениями ANOVA.
Содержание
|
Задача
Дана выборка из измерений для каждого из испытуемых, которую можно представить в виде таблицы[2][3]:
| Условия | ||||
|---|---|---|---|---|
| № объекта | ||||
В качестве нулевой гипотезы рассматривается следующая: «между полученными в разных условиях измерениями имеются лишь случайные различия»[2].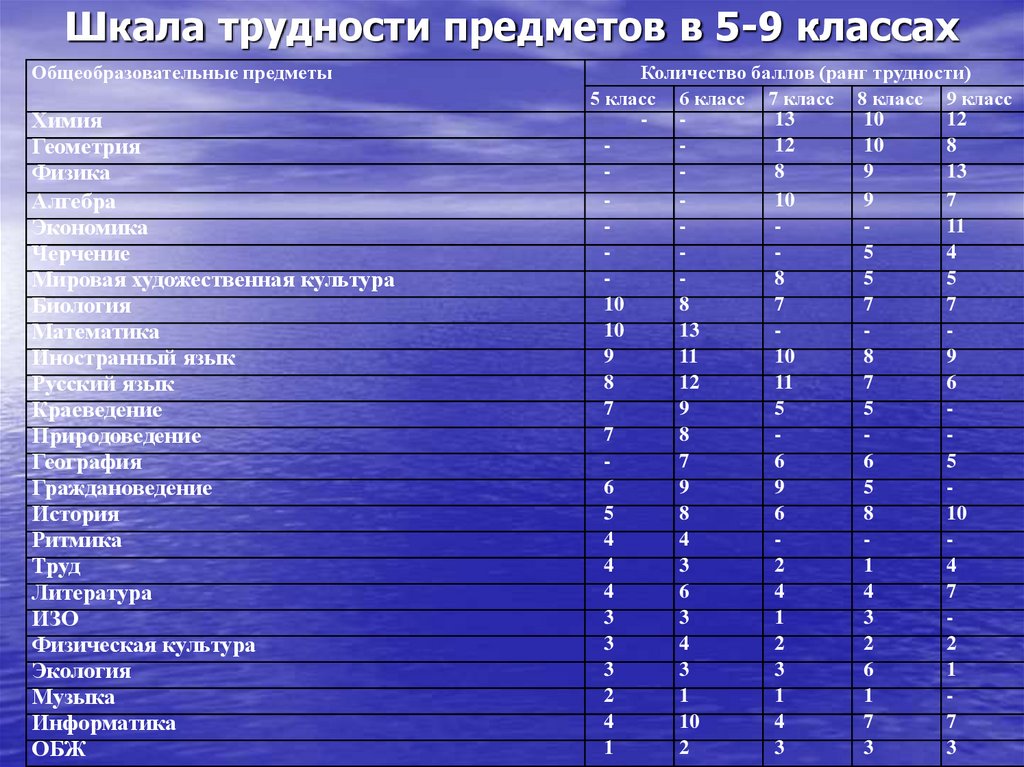
Выбирается уровень значимости , например, (вероятность ошибочно отклонить нулевую гипотезу).
Проверка гипотезы
Для начала получим таблицу рангов по строкам, при котором получаем ранги объекта при ранжировке [3]:
| Ранги | ||||
|---|---|---|---|---|
| № объекта | ||||
Получим суммы рангов и введём другие обозначения:
Для проверки гипотезы будем использовать эмпирическое значение критерия — статистику:
- ,
которую можно записать также в виде:
Нулевая гипотеза принимается, если критическое значение критерия превосходит эмпирическое:
Для малых значений и для критического значения Фридмана существуют таблицы для разных значений уровня значимости (или доверительной вероятности[3]).
При и применима аппроксимация — -квантиль распределения хи-квадрат с степенями свободы[3]:
Для некоторых малых значений статистику можно преобразовать для аппроксимации -квантилью распределения Фишера или применить статистику Имана-Давенпорта
Примеры
Классические примеры применения:
- дегустаторов оценивают различные сорта вин. Имеют ли вина значимые отличия?
- Сварные швы, сделанные сварщиками с использованием сварочных горелок, были оценены по качеству. Есть ли отличия в качестве у какой-либо из горелок?
Апостериорный анализ
Апостериорный анализ (англ. post-hoc analysis) был предложен Шайхом и Хамерли (1984)[4], а также Коновер (1971, 1980)[5] для определения того, какие условия существенно отличаются друг от друга, на основании различия их средних рангов[6].
Программная реализация
Тест Фридмана содержится во многих пакетах программ для статистической обработки данных (SPSS, R[7] и других[8]).
Не все статистические пакеты поддерживают апостериорный анализ для теста Фридмана, но программный код можно найти, например, для SPSS[9] и R[10].
Примечания
- ↑ Кобзарь А. И. («Прикладная математическая статистика») называет этот критерий критерием Фридмена-Кендалла-Бэбингтона Смита
- ↑ 1 2 3 Афанасьев, Сивов, 2010
- ↑ 1 2 3 4 5 Кобзарь, 2006
- ↑ Schaich, E. & Hamerle, A. (1984). Verteilungsfreie statistische Prüfverfahren. Berlin: Springer. ISBN 3-540-13776-9.
- ↑ Conover, W. J. (1971, 1980). Practical nonparametric statistics. New York: Wiley. ISBN 0-471-16851-3.
- ↑ Bortz, J., Lienert, G. & Boehnke, K. (2000). Verteilungsfreie Methoden in der Biostatistik. Berlin: Springer.
ISBN 3-540-67590-6. - ↑ Friedman Rank Sum Test
- ↑ Friedman’s test
- ↑ Post-hoc comparisons for Friedman test
- ↑ Post hoc analysis for Friedman’s Test (R code)
ISBN 3-540-67590-6.Литература
- Афанасьев В. В., Сивов М. А. Математическая статистика в педагогике. — Ярославль: Издательство ЯГПУ, 2010. — С. 63-65. — 76 с. — ISBN 978-5-87555-366-0
- Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: Физматлит, 2006. — С. 484-486. — 816 с. — ISBN 5-9221-0707-0
- Myles Hollander, Douglas A. Wolfe Nonparametric Statistical Methods. — New York: John Wiley & Sons, 1973. — 503 с. — P. 139–146. — ISBN 9780471406358
- Friedman, Milton (December 1937). «The use of ranks to avoid the assumption of normality implicit in the analysis of variance». Journal of the American Statistical Association (American Statistical Association) 32 (200): 675–701. DOI:10.2307/2279372.
- Friedman, Milton (March 1939). «A correction: The use of ranks to avoid the assumption of normality implicit in the analysis of variance». Journal of the American Statistical Association (American Statistical Association) 34 (205): 109. DOI:10.2307/2279169.
- Friedman, Milton (March 1940). «A comparison of alternative tests of significance for the problem of m rankings». The Annals of Mathematical Statistics 11 (1): 86–92. DOI:10.1214/aoms/1177731944.
DOI:10.2307/2279372.Критерий Фридмана / Двусторонний дисперсионный анализ по рангам
Определения статистики > Критерий Фридмана
Что такое критерий Фридмана?
Критерий Фридмана — это непараметрический тест для выявления различий в лечении при нескольких попытках. Непараметрический означает, что тест не предполагает, что ваши данные получены из определенного распределения (например, из нормального распределения).
По сути, он используется вместо теста ANOVA, когда вы не знаете распределения ваших данных.
Критерий Фридмана является расширением знакового теста, используемого при многократном лечении. На самом деле, если есть только два лечения, два теста идентичны.
Выполнение теста
Ваши данные должны соответствовать следующим требованиям:
- Данные должны быть порядковыми (например, по шкале Лайкерта) или непрерывными,
- Данные получены из одной группы, измеренные как минимум в трех разных случаях,
- Выборка создана методом случайной выборки,
- Блоки взаимно независимы (т.е. все пары независимы — один не влияет на другой),
- Наблюдения ранжированы в блоках без совпадений.
Нулевая гипотеза теста состоит в том, что все виды лечения имеют одинаковый эффект или что образцы каким-то образом отличаются. Например, у них разные центры, развороты или формы. Альтернативная гипотеза состоит в том, что лечение действительно имеет разные эффекты.
1. Подготовьте данные для теста.
Шаг 1: Сортируйте данные по блокам (столбцам в электронной таблице). В этом примере у нас есть 12 пациентов, получающих три разных лечения.
Шаг 2: Ранжируйте каждый столбец отдельно. Наименьший балл должен получить ранг 1. Здесь я ранжирую ряды, поэтому каждый пациент получает ранг 1, 2 или 3 для каждого лечения.
Шаг 3: Суммируйте ранги (найдите сумму для каждого столбца).
2. Запустите тест
Примечание . Этот тест обычно не запускается вручную, так как вычисления требуют много времени и труда. Почти все популярные пакеты статистического программного обеспечения могут выполнять этот тест. Тем не менее, я включаю ручные шаги здесь для справки.
Шаг 4. Рассчитайте статистику теста. Вам понадобится:
- n: количество предметов (12)
- к: количество процедур (3)
- R: Сумма рангов для каждого из трех столбцов (32, 27, 13).
Вставьте их в следующую формулу и решите:
Шаг 5: Найдите критическое значение FM из таблицы критических значений для Фридмана (см.
таблицу ниже).
Используйте таблицу k=3 (поскольку именно столько процедур у нас есть) и уровень альфа 5%. Вы можете выбрать более высокий или более низкий альфа-уровень, но 5%, если это довольно распространено — поэтому используйте таблицу 5%, если вы не знаете свой альфа-уровень.
Просматривая n-12 в этой таблице, мы находим критическое значение FM, равное 6,17.
Шаг 6: Сравните рассчитанную статистику теста FM (Шаг 4) с критическим значением FM (Шаг 5). Отклоните нулевую гипотезу, если вычисленное значение F больше критического значения FM.:
- Расчетная статистика теста FM = 15,526.
- FM Критическое значение из таблицы = 6,17.
Вычисленная статистика FM больше, поэтому вы отвергаете нулевую гипотезу.
Дисперсионный анализ Фридмана по рангам Таблица критических значений
Три таблицы по «k».
Если ваш k больше 5 или n больше 13, используйте таблицу критического значения хи-квадрат на шаге 5, чтобы получить критическое значение.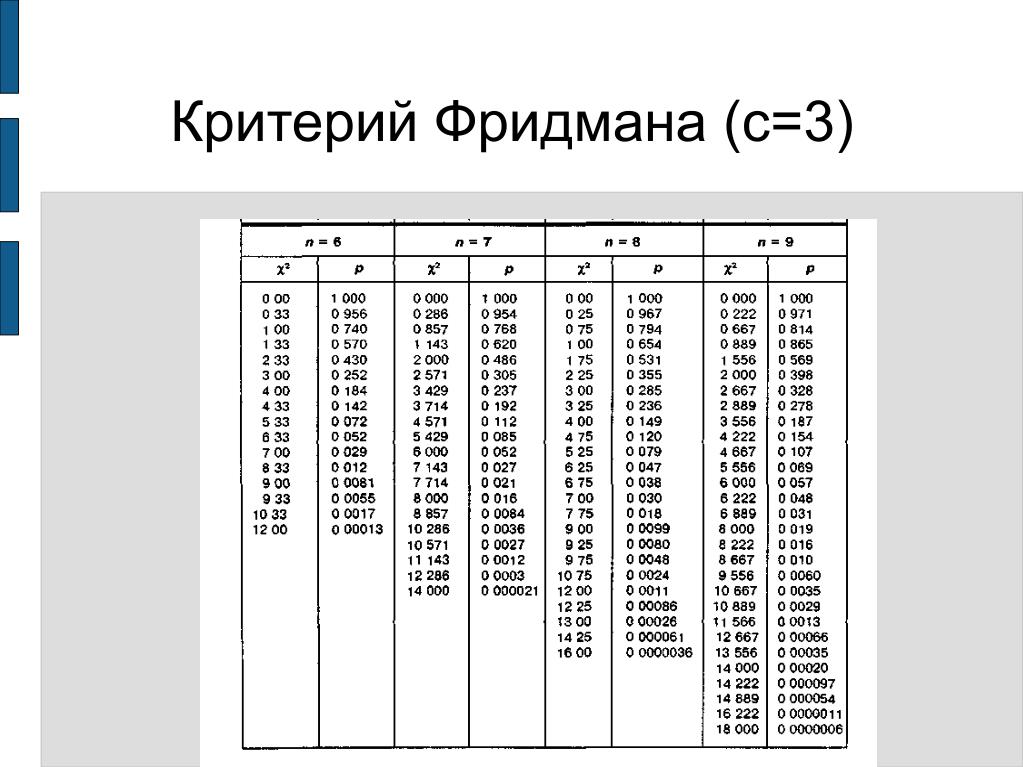
k=3
| С | α <0,10 | α ≤ 0,05 | α <.01 |
| 3 | 6,00 | 6,00 | — |
| 4 | 6.00 | 6,50 | 8,00 |
| 5 | 5,20 | 6,40 | 8,40 |
| 6 | 5,33 | 7,00 | 9,00 |
| 7 | 5,43 | 7,14 | 8,86 |
| 8 | 5,25 | 6,25 | 9,00 |
| 9 | 5,56 | 6,22 | 8,67 |
| 10 | 5,00 | 6,20 | 9,60 |
| 11 | 4,91 | 6,54 | 8,91 |
| 12 | 5,17 | 6,17 | 8,67 |
| 13 | 4,77 | 6,00 | 9,39 |
| ∞ | 4,61 | 5,99 | 9,21 |
к=4
| Н | α <0,10 | α ≤ 0,05 | α <. 01 |
| 2 | 6,00 | 6,00 | — |
| 3 | 6,60 | 7,40 | 8,60 |
| 4 | 6,30 | 7,80 | 9,60 |
| 5 | 6,36 | 7,80 | 9,96 |
| 6 | 6,40 | 7,60 | 10.00 |
| 7 | 6,26 | 7,80 | 10,37 |
| 8 | 6,30 | 7,50 | 10,35 |
| ∞ | 6,25 | 7,82 | 11,34 |
к=4
| Н | α <0,10 | α ≤ 0,05 | α <.01 |
| 3 | 7,47 | 8,53 | 10.13 | 4 | 7,60 | 8,80 | 11.00 | 5 | 7,68 | 8,96 | 11,52 | ∞ | 7,78 | 9,49 | 13,28 |
Ссылка :
Двусторонний дисперсионный анализ Фридмана по рангам — анализ данных внутри группы k с переменной количественного отклика
.
Получено 17 июля 2016 г. с: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
ЦИФЕРТИРУЙТЕ ЭТО КАК:
Стефани Глен . «Тест Фридмана / Двусторонний анализ дисперсии по рангам» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/friedmans-test/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Непараметрический тест гипотезы Фридмана
Непараметрический тест гипотезы Фридмана является альтернативой однофакторному ANOVA с повторными измерениями.
Тест Фридмана был разработан американским экономистом Милтоном Фридманом.
Проверка непараметрической гипотезы Фридмана предназначена для проверки различий между группами (тремя или более парными группами), когда зависимая переменная имеет по крайней мере порядковый номер. Тест Фридмана предпочтительнее по сравнению с другими непараметрическими тестами в ситуации, когда один и тот же параметр был измерен в разных условиях у одного и того же субъекта. Пример: Мониторинг содержания сыворотки пациента до лечения, через один месяц и через три месяца лечения.
Критерий Фридмана аналогичен критерию Крускала-Уоллиса, а также является расширением критерия знаков. Этот статистический тест лучше всего использовать для экспериментов с повторяющимися измерениями, чтобы определить, оказывает ли влияние тот или иной фактор.
Критерий Фридмана предназначен для проверки k парных выборок (k>2) размера n из одной и той же совокупности или выборок из совокупностей, имеющих схожие свойства, с учетом параметра положения.
- Группа представляет собой случайную выборку из генеральной совокупности
- Нет взаимодействия между блоками (строками) и уровнями лечения (столбцами)
- Одна группа, которая измеряется в трех или более различных случаях
- Данные должны быть не ниже порядкового номера или непрерывный
- Образцы не должны быть нормально распределены
- Ранжируйте каждую строку (блок) вместе и независимо от других строк. При наличии связей средние ранги наблюдений.
- Суммируйте ранги для каждого столбца (обработки), а затем просуммируйте квадрат столбцов
- Вычислите статистику теста
- Определите критическое значение из таблицы распределения хи-квадрат с k-1 степенями свободы
- Формулируйте решение и заключение
Тест статика критерия Фридмана равна
, где R j — сумма рангов для выборки j.
н это количество независимых блоков
к количество групп или уровней лечения
DF= количество групп -1 (k-1)
- Нулевые гипотезы H 0 : Медианные эффекты лечения для всей популяции одинаковы
- Альтернативные гипотезы H 1 : Есть разница в лечебных эффектах.
Пример проверки непараметрической гипотезы Фридмана
Департамент общественного здравоохранения и безопасности следит за тем, чтобы меры, предпринятые для очистки питьевой воды, были эффективными. Сравнение тригалометанов (ТГМ) в питьевой воде в 12 округах до очистки, через 1 неделю и через 2 недели после очистки.
- Нуль Гипотеза H 0 = система очистки не повлияла на ТГМ
- Альтернатива Гипотеза h2= система очистки повлияла на ТГМ
Значение уровень α=0,05
Рассчитать R j
Q=20,16
Для значений независимых блоков (n) больше 20 и/или значений групп (k) больше 6 используйте таблицу χ 2 с k-1 степенями свободы в противном случае используйте таблицу Фридмана
Расчетное значение Q равно
больше критического значения Q для уровня значимости 0,05.