Таблица двоичных чисел от 0 до 100
Таблица двоичных чисел от 0 до 100Главная > ч >
| десят. число | двоичное число |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 33 | 100001 |
| 34 | 100010 |
| 35 | 100011 |
| 36 | 100100 |
| 37 | 100101 |
| 38 | 100110 |
| 39 | 100111 |
| 40 | 101000 |
| 41 | 101001 |
| 42 | 101010 |
| 43 | 101011 |
| 44 | 101100 |
| 45 | 101101 |
| 46 | 101110 |
| 47 | 101111 |
| 48 | 110000 |
| 49 | 110001 |
| 50 | 110010 |
| 51 | 110011 |
| 52 | 110100 |
| 53 | 110101 |
| 54 | 110110 |
| 55 | 110111 |
| 56 | 111000 |
| 57 | 111001 |
| 58 | 111010 |
| 59 | 111011 |
| 60 | 111100 |
| 61 | 111101 |
| 62 | 111110 |
| 63 | 111111 |
| 64 | 1000000 |
| 65 | 1000001 |
| 66 | 1000010 |
| 67 | 1000011 |
| 68 | 1000100 |
| 69 | 1000101 |
| 70 | 1000110 |
| 71 | 1000111 |
| 72 | 1001000 |
| 73 | 1001001 |
| 74 | 1001010 |
| 75 | 1001011 |
| 76 | 1001100 |
| 77 | 1001101 |
| 78 | 1001110 |
| 79 | 1001111 |
| 80 | 1010000 |
| 81 | 1010001 |
| 82 | 1010010 |
| 83 | 1010011 |
| 84 | 1010100 |
| 85 | 1010101 |
| 86 | 1010110 |
| 87 | 1010111 |
| 88 | 1011000 |
| 89 | 1011001 |
| 90 | 1011010 |
| 91 | 1011011 |
| 92 | 1011100 |
| 93 | 1011101 |
| 94 | 1011110 |
| 95 | 1011111 |
| 96 | 1100000 |
| 97 | 1100001 |
| 98 | 1100010 |
| 99 | 1100011 |
| 100 | 1100100 |
Ряд двоичных чисел от 0 до 100
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, 10010, 10011, 10100, 10101, 10110, 10111, 11000, 11001, 11010, 11011, 11100, 11101, 11110, 11111, 100000, 100001, 100010, 100011, 100100, 100101, 100110, 100111, 101000, 101001, 101010, 101011, 101100, 101101, 101110, 101111, 110000, 110001, 110010, 110011, 110100, 110101, 110110, 110111, 111000, 111001, 111010, 111011, 111100, 111101, 111110, 111111, 1000000, 1000001, 1000010, 1000011, 1000100, 1000101, 1000110, 1000111, 1001000, 1001001, 1001010, 1001011, 1001100, 1001101, 1001110, 1001111, 1010000, 1010001, 1010010, 1010011, 1010100, 1010101, 1010110, 1010111, 1011000, 1011001, 1011010, 1011011, 1011100, 1011101, 1011110, 1011111, 1100000, 1100001, 1100010, 1100011, 1100100
|
Перевод десятичных чисел в двоичные онлайн Перевод двоичных чисел в десятичные онлайн
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Двоичный конвертер
Создано Bogna Szyk и Philip Maus
Отзыв Стивена Вудинга
Последнее обновление: 02 февраля 2023 г.
- Что такое двоичная система?
- Преобразование десятичных чисел в двоичные
- Преобразование двоичных чисел в десятичные
- Преобразование отрицательных чисел
- Как использовать двоичный преобразователь?
Двоичный конвертер — это удобный инструмент, который позволит вам быстро выполнить преобразование чисел. Вы сможете использовать его как двоично-десятичный преобразователь и десятичный в двоичный калькулятор. Читайте дальше, чтобы узнать, что такое двоичная система, как преобразовать числа и как использовать этот калькулятор для получения правильных результатов.
И не забудьте проверить наш конвертер чисел майя, чтобы понять систему счисления майя и узнать, как преобразовать любое число в числа майя!
Что такое двоичная система?
Обычно мы работаем в десятичной системе. Это означает, что мы используем десять различных цифр от 0 до 9.3 = 81×23=8).
Сложив все эти числа, получим 1+2+4+8=151+2+4+8=151+2+4+8=15.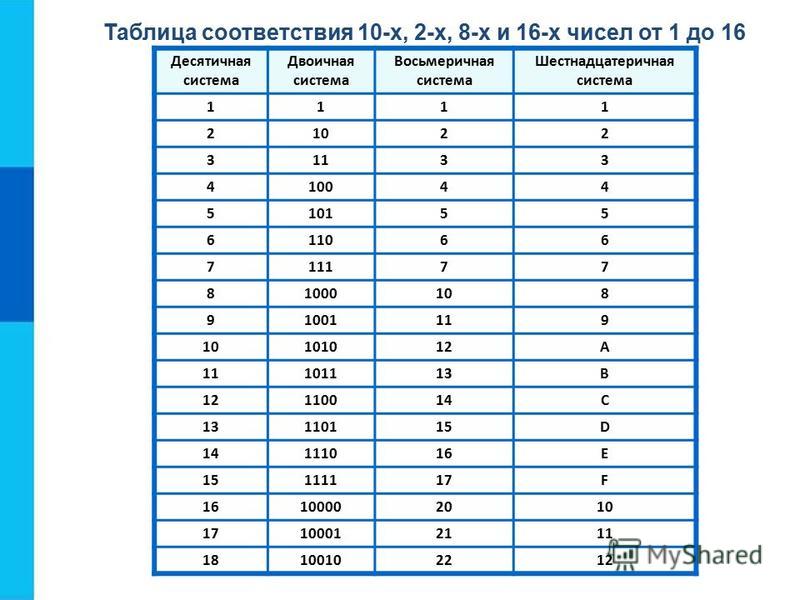
Число 111111111111 в двоичной системе соответствует 151515 в десятичной системе.
Преобразование десятичной системы в двоичную
Вы можете использовать очень простой и эффективный алгоритм для преобразования чисел из десятичной системы в двоичную.
- Возьмите свой первоначальный номер. Разделите на 222.
- Запишите остаток. Он будет равен 000 или 111. Это будет последняя цифра двоичного числа (самая правая).
- Возьмите частное . Это ваш новый «начальный номер».
- Продолжайте повторять вышеуказанные шаги, каждый раз добавляя остаток слева от ранее полученных цифр.
Например, для числа 191919 у нас будут следующие шаги:
- 19/219/219/2 = 999, остаток 111
- 29.09.29.2 = 444, остаток 111
- 24/4/24/2 = 222, остаток 000
- 2/22/22/2 = 111, остаток 000
- 21/21/2 = 000, остаток 111
Читая снизу вверх, 191919 соответствует 100111001110011 в двоичной системе.
Проверьте этот результат с помощью двоичного конвертера!
Преобразование из двоичного в десятичное
Это так же просто — все, что вам нужно сделать, это обратить алгоритм, описанный выше:
- Возьмите крайнюю левую цифру вашего исходного числа. Умножьте на 222.
- Добавьте к следующей цифре двоичного числа. Сумма будет вашим новым «начальным числом».
- Продолжайте повторять эти шаги, каждый раз сначала умножая на 222, а затем добавляя последнюю цифру.
Например, для двоичного числа 110011110011110011 у нас были бы следующие шаги:
- 1×2=21 \times 2 = 21×2=2
- (2+1)×2=6(2+1) \умножить на 2 = 6(2+1)×2=6
- (6+0)×2=12(6+0) \умножить на 2 = 12(6+0)×2=12
- (12+0)×2=24(12+0) х 2 = 24(12+0)×2=24
- (24+1)×2=50(24+1) х 2 = 50(24+1)×2=50
- 50+1=5150 + 1 = 5150+1=51
110011110011110011 соответствует 515151 в десятичной системе.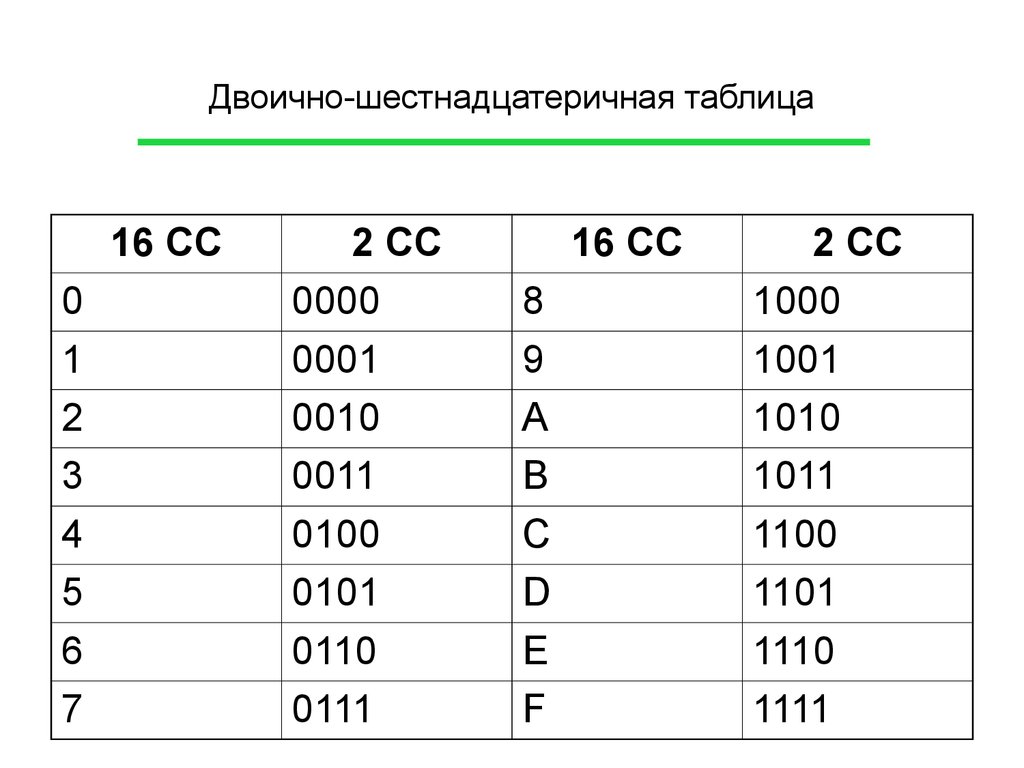
Проверьте этот результат с помощью двоичного конвертера!
Преобразование отрицательных чисел
Мы привыкли просто добавлять знак минус перед числом, если мы хотим выразить отрицательное число в десятичной системе. Но двоичная система не позволяет использовать символ минус . Итак, как мы можем представить отрицательные числа в двоичном формате?
Общая концепция для выражения отрицательных чисел в двоичной системе — это подписано обозначение . Это означает, что первый бит указывает на знак числа: 000 означает положительное значение, 111 — отрицательное значение . Знаковая нотация имеет два представления:
Дополнение до единицы отрицательного числа в двоичном виде достигается путем переключения всех цифр противоположного положительного числа на противоположные битовые значения .
Дополнение до двух отрицательного числа в двоичном коде достигается с помощью переключение всех цифр противоположного положительного числа на противоположные битовые значения и добавление 1 к числу .
Давайте рассмотрим пример, чтобы лучше понять дополнение до единицы и до двух. Мы хотим преобразовать число −87-87−87 в десятичной системе в 8-битную двоичную систему.
- Найти двоичное представление положительного числа 878787 в десятичной системе: 0101 01110101\ 01110101 0111.
- Переключить все цифры на противоположные : 1010 10001010\ 10001010 1000. Это дополнение .
- Добавьте 111 к дополнению до единицы, чтобы получить дополнение до до 2 : 1010 10011010\ 10011010 1001.
С этими представлениями вы можете без проблем создавать такие приложения, как двоичное вычитание. Чтобы узнать больше, вы можете посетить калькулятор двоичного вычитания или двоичный калькулятор.
Однако для преобразования дробных чисел вы не можете применить те же рассуждения: узнайте, как это сделать с помощью нашего конвертера двоичных дробей!
Как использовать двоичный конвертер?
Наконец, мы можем поговорить о , как использовать двоичный преобразователь .
Например, мы преобразуем число -87 из десятичной системы в двоичную.
Выберите количество битов . В нашем примере хорошим выбором будет 8 бит, поскольку они позволяют использовать диапазон от −128-128−128 до 127127127.
Введите свое десятичное значение в поле ввода в разделе десятичного преобразования в двоичное . Калькулятор выводит результат:
- Двоичное значение положительной противоположности нашему числу, то есть 878787, равно: 0101 01110101\ 01110101 0111.
- Дополнение до единицы: 1010 10001010\ 10001010 1000.
- Дополнение до двух: 1010 10011010\ 10011010 1001.
Дополнение до единицы и до двух вычисляется, как описано выше, переворачивая все цифры для противоположного числа и добавляя 111 для дополнения до двух.
Преобразователь также позволяет выполнять обратное преобразование из двоичной системы в десятичную.
Просто введите свое двоичное число в соответствующее поле и посмотрите результат в десятичном формате, показанном ниже.
Богна Шик и Филип Маус
Двоичное представление
Преобразование десятичного числа в двоичное
Вы можете ввести десятичное число от -128 до 127. 8 цифр. Вам не нужно вводить лидирующие нули.
Двоичная
Посмотрите 5 похожих преобразователей систем счисления 🧮
Двоичная в шестнадцатеричнаяДвоичная в восьмеричнаяДесятичная в шестнадцатеричную… Еще 2
Двоичная | Интерактивный | Компьютеры
Это бесплатный интерактивный ресурс, который показывает, как представлять числа в двоичном формате и преобразовывать между двоичным и десятичным, как того требуют требования Национальной учебной программы KS3 для курсов Computing и GCSE Computer Science. Для более подробного обсуждения числовых оснований, включая двоичные, см.
9Страница 0245 Основы счисления в разделе Математика .
Вы также можете посмотреть введение в двоичные файлы и примеры того, как компьютеры используют двоичные файлы, на канале Advanced ICT YouTube .
Что такое двоичный код?
Двоичный код — это просто метод записи (т. е. хранения) чисел. Возможно, вы уже знакомы с другими методами, например. 4 (цифры), четыре (английский), quatre (французский), vier (немецкий), IV (римский Цифры). Это все одно и то же; все они на единицу больше трех и на единицу меньше пяти.
На уроках математики мы используем систему под названием денариев , которая основана на десятках. Некоторые люди думают, что наша система счисления основана на десятках, потому что у нас десять пальцев, и мы используем их для счета. Однако у компьютеров нет пальцев — у них есть электрические цепи,
а электрические цепи имеют два состояния: на или на . Поэтому компьютеры используют систему счисления, основанную на двойках — это называется двоичным (и также известно как 9).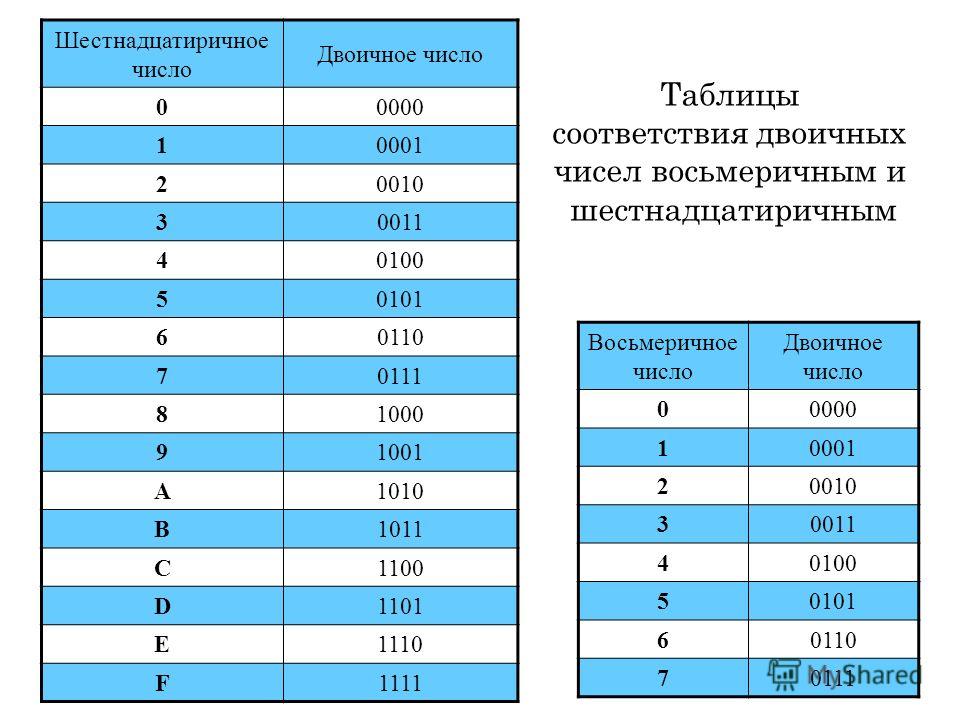
0245 база 2 ).
У этих двух систем много общего. В системе счисления, основанной на десять с, часто называемой динарием , каждый столбец (единицы, десятки, сотни и т. д.) имеет десять раз больше значения столбца справа от него, и каждый столбец может содержать одно из десяти значений (1-9 и 0). В системе счисления, основанной на два , каждый заголовок столбца имеет два , умноженных на единицу справа от него, и может быть два возможных значения в каждой позиции.
Ниже представлено двоичное число (с добавленными заголовками столбцов) и его Денарный эквивалент:
Щелкните цифру для переключения между 0 и 1. Преобразование двоичного значения в десятичное просто требует, чтобы вы сложили заголовки столбцов, содержащих единицу. Например, 00001010 будет означать, что у нас есть один 16 и один 2, что дает 00010010, что дает десятикратное значение 18.
Вот и все!
Расследовать
Нажмите на цифры, чтобы составить несколько цифр и проверить свое понимание. Вы можете сделать 100? Существует ли только одна комбинация нулей и единиц, составляющих каждое число? Последовательность из восьми битов (0 или 1), подобная показанной выше, называется байт . Какое максимальное число может содержать байт магазин? Если бы вы использовали свои 10 пальцев для счета в двоичном формате, вы могли бы сосчитать до 1023! Для альтернативного представления двоичного кода вы можете попробовать использовать счеты в базе 2. Если вам интересно, как мы можем представлять числа, которые не являются положительными целыми числами, взгляните на страницы, посвященные двоичным дробям или нормализованным двоичным числам с плавающей запятой.
Как только вы научитесь конвертировать в двоичные файлы и из них, почему бы не попрактиковаться в игре Binary Breakout?
Использование двоичного кода и дополнительное чтение
Мы можем воспользоваться тем фактом, что есть только один способ сделать каждое число с помощью так называемых двоичных флагов .