Перевод чисел в различных системах счисления
Перевод чисел в различных системах счисленияПеревод чисел в различных системах счисления.
Для перевода числа из десятичной системы счисления в систему счисления с другим основанием поступают следующим образом:
а) Для перевода целой части числа его делят нацело на основание системы, фиксируя остаток. Если неполное частное не равно нулю продолжают делить его нацело. Если равно нулю остатки записываются в обратном порядке.
б) Для перевода дробной части числа ее умножают на основание системы счисления, фиксируя при этом целые части полученных произведений. Целые части в дальнейшем умножении не участвуют. Умножение производиться до получения 0 в дробной части произведения или до заданной точности вычисления.
в) Ответ записывают в виде сложения переведенной целой и переведенной
дробной части числа.
Пример: перевод чисел из десятичной системы счисления в двоичную систему счисления.
Перевести число 75,375 в двоичную систему счисления.
а) переведем в двоичную систему целую часть — 75
75 : 2 = 37 ( 1 )
37 : 2 = 18 ( 1 )
18 : 2 = 9 ( 0 )
9 : 2 = 4 ( 1 )
4 : 2 = 2 ( 0 )
2 : 2 = 1 ( 0 )
1 : 2 = 0 ( 1 )
Закончив деление, запишем остатки в обратном порядке, и получим искомый результат:
75=1001011 2
б) переведем в двоичную систему дробную часть — 0,375
0,375
2
0,750
2
1,500
2
1,000
Выделенные числа запишем в естественном порядке и получим дробное число в двоичной системе счисления:
0,375 = 0,0112
в) получив целую и дробную части числа в двоичном виде (75=10010112 и 0,375 = 0,0112 ) можем сделать вывод:
75,375=75+0,375 = 10010112+0,0112=1001011,0112, значит 75,375=1001011,0112
Пример:
Представить десятичное число 157,23 в шестнадцатеричной системе счисления. Целая часть числа равна 157, дробная — 0,23.
а) переведем в двоичную систему целую часть — 157
157 : 16 = 9 (13 или D)
9 : 16 = 0 ( 9 )
Закончив деление, запишем остатки в обратном порядке, и получим искомый результат:
157=9D 16
а) переведем в двоичную систему дробную часть — 0,23.
Результат умножения 0,23 на 16 равен 3,68. Целая часть этого числа равна
3, значит первый коэффициент дробной части равен 3. Дробная часть равна 0,68.
Снова умножим ее на основание системы: 0,68*16=10,88. Целая часть равна 10 или в
шестнадцатеричной системе А. Дробная часть равна 0,88, она опять
умножается на 16 и так далее.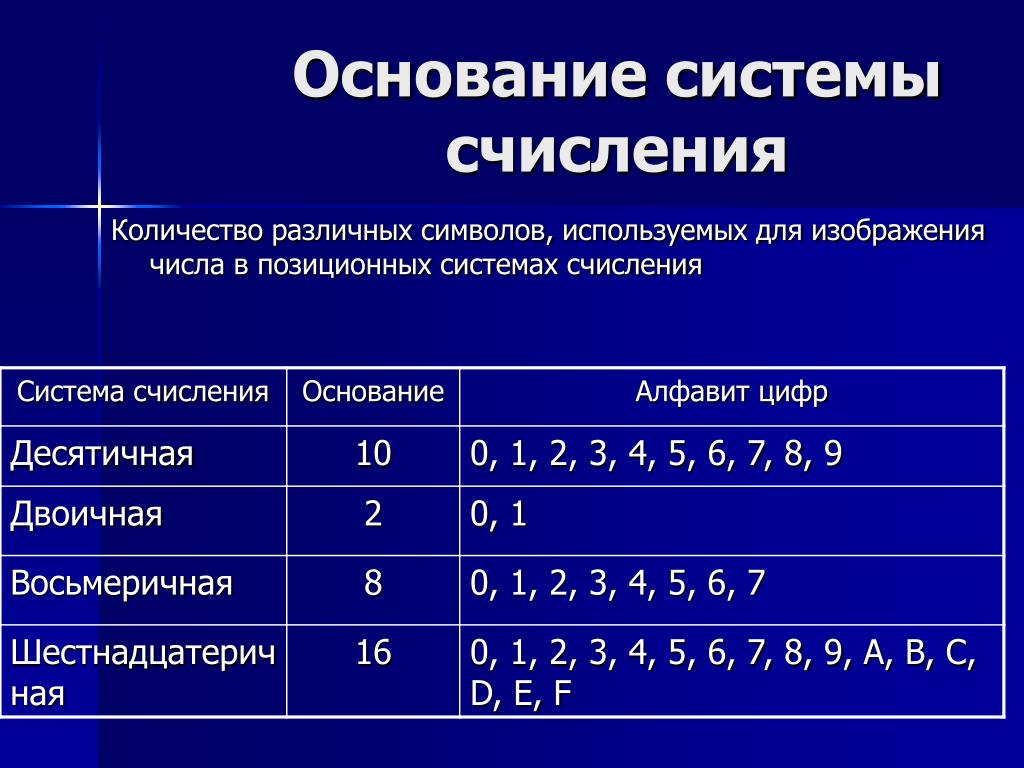
Выпишем весь процесс:
0,23 * 16 = 3,68 ( 3 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
0,08 * 16 = 1,28 ( 1 )
0,28 * 16 = 4,48 ( 4 )
0,48 * 16 = 7,68 ( 7 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
0,08 * 16 = 1,28 ( 1 )
0,28 * 16 =
0,48 * 16 = 7,68 ( 7 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
Замечаем, что последовательность чисел 0,68; 0,88; 0,08; 0,28; 0,48 повторилась
уже 2 раза и начинается в третий раз. Получается бесконечная шестнадцатеричная
дробь в которой период (бесконечно повторяемая последовательность цифр)
заключен в скобки:
Получается бесконечная шестнадцатеричная
дробь в которой период (бесконечно повторяемая последовательность цифр)
заключен в скобки:
157,23=9D,3(АЕ147)16
Для перевода числа в десятичную систему счисления из системы счисления с другим основанием каждый коэффициент переводимого числа умножается на основание системы в степени соответствующей этому коэффициенту и полученные результаты складываются.
Пример: перевод чисел из двоичной системы счисления в десятичную систему счисления
Перевести число 1001011,0112 в десятичную систему счисления
1001011,0112 = 1*26+0*25+0*24+1*23+0*22+1*21+1*20+0*2-1+1*2-2+1*2-3 =64+8+2+1+0,25+0,125=75,375
Двоичная система проста, так как использует две цифры, но громоздка. В
десятичной хранить числа в памяти возможно, но сложен перевод из десятичной в
двоичную и обратно и занимает много времени. Необходима система счисления
компактнее двоичной, но с более простым переводом.
В
десятичной хранить числа в памяти возможно, но сложен перевод из десятичной в
двоичную и обратно и занимает много времени. Необходима система счисления
компактнее двоичной, но с более простым переводом.
23 = 8 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода из двоичной системы счисления в восьмеричную необходимо разбить данное двоичное число вправо и влево от запятой на триада ( три цифры ) и представить каждую триаду соответствующим восьмеричным кодом. При невозможности разбиения на триады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру восьмеричного числа представляют соответствующей триадой двоичного кода.
|
Десятичная система счисления |
Двоичная система счисления |
Восьмеричная система счисления |
Шестнадцатеричная система счисления |
|
|
Триады (0-7) |
Тетрады (0-15) |
|||
|
0 |
000 |
0000 |
00 |
0 |
|
1 |
001 |
0001 |
|
1 |
|
2 |
010 |
0010 |
02 |
2 |
|
3 |
011 |
0011 |
03 |
3 |
|
4 |
100 |
0100 |
04 |
4 |
|
5 |
101 |
0101 |
05 |
5 |
|
6 |
110 |
0110 |
06 |
6 |
|
7 |
111 |
0111 |
07 |
7 |
|
8 |
|
1000 |
10 |
8 |
|
9 |
|
1001 |
11 |
9 |
|
10 |
|
1010 |
12 |
A |
|
11 |
|
1011 |
13 |
B |
|
12 |
|
1100 |
14 |
C |
|
13 |
|
1101 |
15 |
D |
|
14 |
|
1110 |
16 |
E |
|
15 |
|
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
|
Пример:
перевод чисел из двоичной системы счисления в восьмеричную систему
счисления.
Переведем число 1001011,0112 в восьмеричную систему счисления. Разобьем данное число на триады, приписав слева недостающие нули:
001 001 011 , 011
1 1 3 , 3
и заменим каждую триаду соответствующим восьмеричным кодом (см. таблицу). Можем сделать вывод:
1001011,0112 = 113,38
Пример: перевод чисел из восьмеричной системы счисления в двоичную систему счисления.
Переведем число 347,258 в двоичную систему счисления. Каждую цифру восьмеричного числа заменим соответствующей триадой (см. таблицу).
3 4 7 , 2 5
011 100 111 , 010 101
Запишем ответ, удалив нули слева в записи числа:
347,258 = 11100111,0101012
Восьмеричная система компактнее двоичной и с более простым переводом чисел,
однако, современные требования к ЭВМ заставили создавать шестнадцатеричную
систему счисления.
24 = 16 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Правило перевода из двоичной системы счисления в шестнадцатеричную: разбить двоичное число вправо и влево от запятой на тетрады ( по 4 цифры ) и представить каждую тетраду соответствующим шестнадцатеричным кодом. При невозможности разбиения на тетрады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру шестнадцатеричного числа представляют тетрадой двоичного кода.
Пример: перевод чисел из двоичной системы счисления в шестнадцатеричную систему счисления.
Переведем число 1001011,0112 в шестнадцатеричную систему счисления. Разобьем данное число на тетрады, приписав слева в целой части, и справа в
дробной части недостающие нули:
Разобьем данное число на тетрады, приписав слева в целой части, и справа в
дробной части недостающие нули:
0100 1011, 0110
4 В , 6
и заменим каждую тетраду соответствующим шестнадцатеричным кодом (см. таблицу). Можем сделать вывод:
1001011,0112 = 4В,616
Пример: перевод чисел из шестнадцатеричной системы счисления в двоичную систему счисления.
Переведем число А4F,C516 в двоичную систему счисления. Каждую цифру шестнадцатеричного числа заменим соответствующей тетрадой (см. таблицу).
A 4 F , C 5
1010 0100 1111 , 1100 0101
Запишем ответ, удалив нули слева в записи числа:
A4F,C516 = 101001001111,110001012
В МЕНЮ
Используются технологии uCoz
Переводы из различных систем счисления.
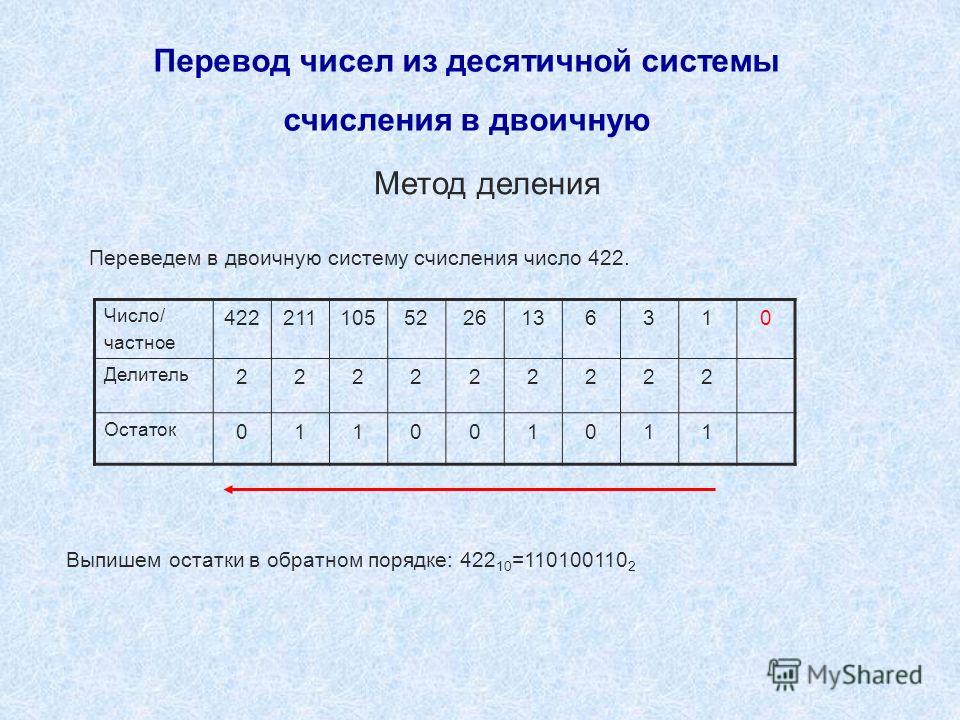 Таблица соответствия систем. Переводы из различных систем счисления. Таблица соответствия систем.
Таблица соответствия систем. Переводы из различных систем счисления. Таблица соответствия систем.Содержание
Перевод из десятичной в двоичную систему счисления.
[youtube fLv4gs9EnJs nolink]
Перевод из двоичной в десятичную систему счисления и наоборот.
[youtube C0ai9-3GHJY nolink]
Перевод чисел из двоичной системы счисления в восьмеричную и наоборот.
[youtube x1bx7o2uESg nolink]
Перевод чисел из двоичной системы счисления в шестнадцатеричную. Сложение двоичных чисел.
[youtube rToqA6rEUQ8 nolink]
Перевод чисел в десятичную систему счисления. Полиномы.
[youtube eSviqB6Db7A nolink]
Краткая таблица соответствия – двоичная система в восьмеричную (8СС) и шестнадцатеричная (16СС) системы:
Таблица соответствия десятеричного от 1 до 255 (Decimal), двоичного (Binary) и шестнадцатеричного (Hexadecimal) представлений чисел.Dec – десятеричная система;
Hex – шестнадцатеричная система;
Bin – двоичная система.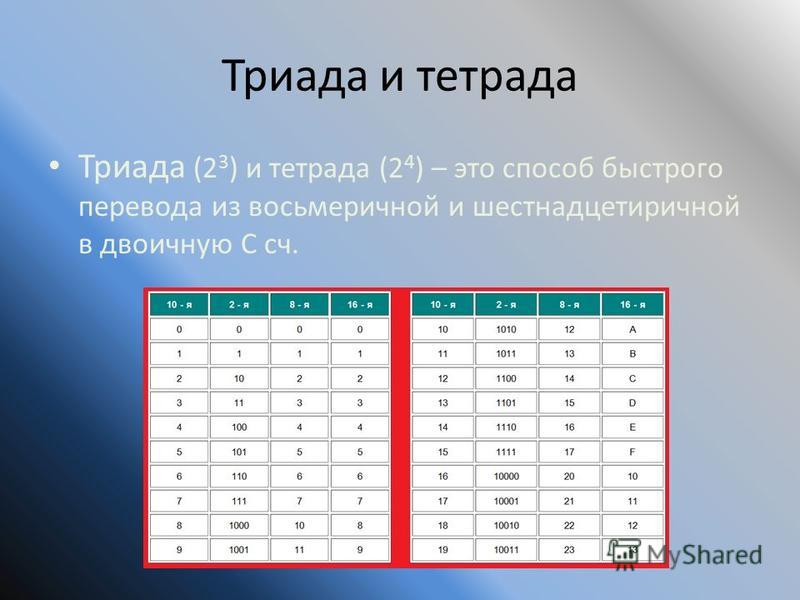
| Dec | Hex | Bin | Dec | Hex | Bin | Dec | Hex | Bin | Dec | Hex | Bin |
| 0 | 0 | 0 | 64 | 40 | 1000000 | 128 | 80 | 10000000 | 192 | c0 | 11000000 |
| 1 | 1 | 1 | 65 | 41 | 1000001 | 129 | 81 | 10000001 | 193 | c1 | 11000001 |
| 2 | 2 | 10 | 66 | 42 | 1000010 | 130 | 82 | 10000010 | 194 | c2 | 11000010 |
| 3 | 3 | 11 | 67 | 43 | 1000011 | 131 | 83 | 10000011 | 195 | c3 | 11000011 |
| 4 | 4 | 100 | 68 | 44 | 1000100 | 132 | 84 | 10000100 | 196 | c4 | 11000100 |
| 5 | 5 | 101 | 69 | 45 | 1000101 | 133 | 85 | 10000101 | 197 | c5 | 11000101 |
| 6 | 6 | 110 | 70 | 46 | 1000110 | 134 | 86 | 10000110 | 198 | c6 | 11000110 |
| 7 | 7 | 111 | 71 | 47 | 1000111 | 135 | 87 | 10000111 | 199 | c7 | 11000111 |
| 8 | 8 | 1000 | 72 | 48 | 1001000 | 136 | 88 | 10001000 | 200 | c8 | 11001000 |
| 9 | 9 | 1001 | 73 | 49 | 1001001 | 137 | 89 | 10001001 | 201 | c9 | 11001001 |
| 10 | a | 1010 | 74 | 4a | 1001010 | 138 | 8a | 10001010 | 202 | ca | 11001010 |
| 11 | b | 1011 | 75 | 4b | 1001011 | 139 | 8b | 10001011 | 203 | cb | 11001011 |
| 12 | c | 1100 | 76 | 4c | 1001100 | 140 | 8c | 10001100 | 204 | cc | 11001100 |
| 13 | d | 1101 | 77 | 4d | 1001101 | 141 | 8d | 10001101 | 205 | cd | 11001101 |
| 14 | e | 1110 | 78 | 4e | 1001110 | 142 | 8e | 10001110 | 206 | ce | 11001110 |
| 15 | f | 1111 | 79 | 4f | 1001111 | 143 | 8f | 10001111 | 207 | cf | 11001111 |
| 16 | 10 | 10000 | 80 | 50 | 1010000 | 144 | 90 | 10010000 | 208 | d0 | 11010000 |
| 17 | 11 | 10001 | 81 | 51 | 1010001 | 145 | 91 | 10010001 | 209 | d1 | 11010001 |
| 18 | 12 | 10010 | 82 | 52 | 1010010 | 146 | 92 | 10010010 | 210 | d2 | 11010010 |
| 19 | 13 | 10011 | 83 | 53 | 1010011 | 147 | 93 | 10010011 | 211 | d3 | 11010011 |
| 20 | 14 | 10100 | 84 | 54 | 1010100 | 148 | 94 | 10010100 | 212 | d4 | 11010100 |
| 21 | 15 | 10101 | 85 | 55 | 1010101 | 149 | 95 | 10010101 | 213 | d5 | 11010101 |
| 22 | 16 | 10110 | 86 | 56 | 1010110 | 150 | 96 | 10010110 | 214 | d6 | 11010110 |
| 23 | 17 | 10111 | 87 | 57 | 1010111 | 151 | 97 | 10010111 | 215 | d7 | 11010111 |
| 24 | 18 | 11000 | 88 | 58 | 1011000 | 152 | 98 | 10011000 | 216 | d8 | 11011000 |
| 25 | 19 | 11001 | 89 | 59 | 1011001 | 153 | 99 | 10011001 | 217 | d9 | 11011001 |
| 26 | 1a | 11010 | 90 | 5a | 1011010 | 154 | 9a | 10011010 | 218 | da | 11011010 |
| 27 | 1b | 11011 | 91 | 5b | 1011011 | 155 | 9b | 10011011 | 219 | db | 11011011 |
| 28 | 1c | 11100 | 92 | 5c | 1011100 | 156 | 9c | 10011100 | 220 | dc | 11011100 |
| 29 | 1d | 11101 | 93 | 5d | 1011101 | 157 | 9d | 10011101 | 221 | dd | 11011101 |
| 30 | 1e | 11110 | 94 | 5e | 1011110 | 158 | 9e | 10011110 | 222 | de | 11011110 |
| 31 | 1f | 11111 | 95 | 5f | 1011111 | 159 | 9f | 10011111 | 223 | df | 11011111 |
| 32 | 20 | 100000 | 96 | 60 | 1100000 | 160 | a0 | 10100000 | 224 | e0 | 11100000 |
| 33 | 21 | 100001 | 97 | 61 | 1100001 | 161 | a1 | 10100001 | 225 | e1 | 11100001 |
| 34 | 22 | 100010 | 98 | 62 | 1100010 | 162 | a2 | 10100010 | 226 | e2 | 11100010 |
| 35 | 23 | 100011 | 99 | 63 | 1100011 | 163 | a3 | 10100011 | 227 | e3 | 11100011 |
| 36 | 24 | 100100 | 100 | 64 | 1100100 | 164 | a4 | 10100100 | 228 | e4 | 11100100 |
| 37 | 25 | 100101 | 101 | 65 | 1100101 | 165 | a5 | 10100101 | 229 | e5 | 11100101 |
| 38 | 26 | 100110 | 102 | 66 | 1100110 | 166 | a6 | 10100110 | 230 | e6 | 11100110 |
| 39 | 27 | 100111 | 103 | 67 | 1100111 | 167 | a7 | 10100111 | 231 | e7 | 11100111 |
| 40 | 28 | 101000 | 104 | 68 | 1101000 | 168 | a8 | 10101000 | 232 | e8 | 11101000 |
| 41 | 29 | 101001 | 105 | 69 | 1101001 | 169 | a9 | 10101001 | 233 | e9 | 11101001 |
| 42 | 2a | 101010 | 106 | 6a | 1101010 | 170 | aa | 10101010 | 234 | ea | 11101010 |
| 43 | 2b | 101011 | 107 | 6b | 1101011 | 171 | ab | 10101011 | 235 | eb | 11101011 |
| 44 | 2c | 101100 | 108 | 6c | 1101100 | 172 | ac | 10101100 | 236 | ec | 11101100 |
| 45 | 2d | 101101 | 109 | 6d | 1101101 | 173 | ad | 10101101 | 237 | ed | 11101101 |
| 46 | 2e | 101110 | 110 | 6e | 1101110 | 174 | ae | 10101110 | 238 | ee | 11101110 |
| 47 | 2f | 101111 | 111 | 6f | 1101111 | 175 | af | 10101111 | 239 | ef | 11101111 |
| 48 | 30 | 110000 | 112 | 70 | 1110000 | 176 | b0 | 10110000 | 240 | f0 | 11110000 |
| 49 | 31 | 110001 | 113 | 71 | 1110001 | 177 | b1 | 10110001 | 241 | f1 | 11110001 |
| 50 | 32 | 110010 | 114 | 72 | 1110010 | 178 | b2 | 10110010 | 242 | f2 | 11110010 |
| 51 | 33 | 110011 | 115 | 73 | 1110011 | 179 | b3 | 10110011 | 243 | f3 | 11110011 |
| 52 | 34 | 110100 | 116 | 74 | 1110100 | 180 | b4 | 10110100 | 244 | f4 | 11110100 |
| 53 | 35 | 110101 | 117 | 75 | 1110101 | 181 | b5 | 10110101 | 245 | f5 | 11110101 |
| 54 | 36 | 110110 | 118 | 76 | 1110110 | 182 | b6 | 10110110 | 246 | f6 | 11110110 |
| 55 | 37 | 110111 | 119 | 77 | 1110111 | 183 | b7 | 10110111 | 247 | f7 | 11110111 |
| 56 | 38 | 111000 | 120 | 78 | 1111000 | 184 | b8 | 10111000 | 248 | f8 | 11111000 |
| 57 | 39 | 111001 | 121 | 79 | 1111001 | 185 | b9 | 10111001 | 249 | f9 | 11111001 |
| 58 | 3a | 111010 | 122 | 7a | 1111010 | 186 | ba | 10111010 | 250 | fa | 11111010 |
| 59 | 3b | 111011 | 123 | 7b | 1111011 | 187 | bb | 10111011 | 251 | fb | 11111011 |
| 60 | 3c | 111100 | 124 | 7c | 1111100 | 188 | bc | 10111100 | 252 | fc | 11111100 |
| 61 | 3d | 111101 | 125 | 7d | 1111101 | 189 | bd | 10111101 | 253 | fd | 11111101 |
| 62 | 3e | 111110 | 126 | 7e | 1111110 | 190 | be | 10111110 | 254 | fe | 11111110 |
| 63 | 3f | 111111 | 127 | 7f | 1111111 | 191 | bf | 10111111 | 255 | ff | 11111111 |
И, напоследок – удобный online-калькулятор систем счисления тут>>>.
Раздел: HOWTO’s Разное
Мови блога
Загрузка …
More results…
Exact matches only
Exact matches only
Search in title
Search in title
Search in content
Search in content
Search in excerpt
Hidden
Hidden
Navigation
aСамое читаемое
- CentOS: установка, настройка Zabbix-agent и добавление нового хоста в мониторинг — 507 141 views
- MySQL/MariaDB: наиболее используемые команды, примеры — 289 181 views
- BASH: описание циклов for, while, until и примеры использования — 152 189 views
- Команда find и её опции в примерах — 139 575 views
- Карта сайта — 127 518 views
Архив месяца
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | ||||||
Архивы по годам
Архивы по годам Выберите месяц Сентябрь 2022 (1) Июнь 2022 (1) Май 2022 (1) Апрель 2022 (1) Март 2022 (2) Январь 2022 (1) Декабрь 2021 (3) Ноябрь 2021 (8) Октябрь 2021 (4) Сентябрь 2021 (5) Август 2021 (5) Июль 2021 (6) Июнь 2021 (6) Май 2021 (6) Апрель 2021 (11) Март 2021 (8) Февраль 2021 (6) Январь 2021 (1) Декабрь 2020 (1) Ноябрь 2020 (9) Октябрь 2020 (9) Сентябрь 2020 (4) Август 2020 (8) Июль 2020 (4) Июнь 2020 (3) Май 2020 (5) Апрель 2020 (9) Март 2020 (8) Февраль 2020 (9) Январь 2020 (2) Декабрь 2019 (9) Ноябрь 2019 (9) Октябрь 2019 (11) Сентябрь 2019 (11) Август 2019 (10) Июль 2019 (2) Июнь 2019 (4) Май 2019 (9) Апрель 2019 (13) Март 2019 (32) Февраль 2019 (20) Январь 2019 (10) Декабрь 2018 (9) Ноябрь 2018 (12) Октябрь 2018 (15) Сентябрь 2018 (12) Август 2018 (14) Июль 2018 (17) Июнь 2018 (18) Май 2018 (21) Апрель 2018 (6) Март 2018 (18) Февраль 2018 (7) Январь 2018 (13) Декабрь 2017 (14) Ноябрь 2017 (6) Октябрь 2017 (24) Сентябрь 2017 (13) Август 2017 (15) Июль 2017 (11) Июнь 2017 (11) Май 2017 (11) Апрель 2017 (7) Март 2017 (18) Февраль 2017 (13) Январь 2017 (14) Декабрь 2016 (12) Ноябрь 2016 (15) Октябрь 2016 (13) Сентябрь 2016 (21) Август 2016 (19) Июль 2016 (14) Июнь 2016 (8) Май 2016 (24) Апрель 2016 (15) Март 2016 (19) Февраль 2016 (21) Январь 2016 (19) Декабрь 2015 (17) Ноябрь 2015 (17) Октябрь 2015 (14) Сентябрь 2015 (13) Август 2015 (1) Июль 2015 (20) Июнь 2015 (23) Май 2015 (26) Апрель 2015 (28) Март 2015 (30) Февраль 2015 (26) Январь 2015 (24) Декабрь 2014 (31) Ноябрь 2014 (21) Октябрь 2014 (28) Сентябрь 2014 (23) Август 2014 (31) Июль 2014 (23) Июнь 2014 (11) Май 2014 (14) Апрель 2014 (8) Март 2014 (11) Февраль 2014 (11) Январь 2014 (11) Декабрь 2013 (12) Ноябрь 2013 (23) Октябрь 2013 (20) Сентябрь 2013 (30) Август 2013 (20) Июль 2013 (6) Июнь 2013 (9) Май 2013 (5) Апрель 2013 (13) Март 2013 (22) Февраль 2013 (36) Январь 2013 (10) Декабрь 2012 (4) Ноябрь 2012 (8) Октябрь 2012 (13) Сентябрь 2012 (29) Август 2012 (24) Июль 2012 (18) Июнь 2012 (2) Май 2012 (4) Март 2012 (5) Февраль 2012 (5) Январь 2012 (25) Декабрь 2011 (15) Ноябрь 2011 (6) Август 2011 (13)Iconic One Theme | Powered by WordPress
Таблицы сложения и умножения
Таблицы сложения и умноженияДвоичная система счисления
| 1+0=1 | 1*0=0 |
| 1+1=10 | 1*1=1 |
Троичная система счисления
| Таблица сложения | Таблица умножения | ||
| 1+1=2 | 1*1=1 | ||
| 1+2=10 | 2+2=11 | 1*2=2 | 2*2=11 |
Восьмеричная система счисления
| Таблица сложения | ||||||
| 1+1=2 | ||||||
| 1+2=3 | 2+2=4 | |||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=10 | |||
| 1+5=6 | 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | ||
| 1+6=7 | 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | |
| 1+7=10 | 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
| Таблица умножения | ||||||
| 1*1=2 | ||||||
| 1*2=2 | 2*2=4 | |||||
| 1*3=3 | 2*3=6 | 3*3=11 | ||||
| 1*4=4 | 2*4=10 | 3*4=14 | 4*4=20 | |||
| 1*5=5 | 2*5=12 | 3*5=17 | 4*5=24 | 5*5=31 | ||
| 1*6=6 | 2*6=14 | 3*6=22 | 4*6=30 | 5*6=36 | 6*6=44 | |
| 1*7=7 | 2*7=16 | 3*7=25 | 4*7=34 | 5*7=43 | 6*7=52 | 7*7=61 |
Шестнадцатеричная система счисления
| Таблица сложения | ||||||||||||||
| 1+1=2 | ||||||||||||||
| 1+2=3 | 2+2=4 | |||||||||||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||||||||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=8 | |||||||||||
| 1+5=6 | 2+5=7 | 3+5=8 | 4+5=9 | 5+5=A | ||||||||||
| 1+6=7 | 2+6=8 | 3+6=9 | 4+6=A | 5+6=B | 6+6=C | |||||||||
| 1+7=8 | 2+7=9 | 3+7=A | 4+7=B | 5+7=C | 6+7=D | 7+7=E | ||||||||
| 1+8=9 | 2+8=A | 3+8=B | 4+8=C | 5+8=D | 6+8=E | 7+8=F | 8+8=10 | |||||||
| 1+9=A | 2+9=B | 3+9=C | 4+9=D | 5+9=E | 6+9=F | 7+9=10 | 8+9=11 | 9+9=12 | ||||||
| 1+A=B | 2+A=C | 3+A=D | 4+A=E | 5+A=F | 6+A=10 | 7+A=11 | 8+A=12 | 9+A=13 | A+A=14 | |||||
| 1+B=C | 2+B=D | 3+B=E | 4+B=F | 5+B=10 | 6+B=11 | 7+B=12 | 8+B=13 | 9+B=14 | A+B=15 | B+B=16 | ||||
| 1+C=D | 2+C=E | 3+C=F | 4+C=10 | 5+C=11 | 6+C=12 | 7+C=13 | 8+C=14 | 9+C=15 | A+C=16 | B+C=17 | C+C=18 | |||
| 1+D=E | 2+D=F | 3+D=10 | 4+D=11 | 5+D=12 | 6+D=13 | 7+D=14 | 8+D=15 | 9+D=16 | A+D=17 | B+D=18 | C+D=19 | D+D=1A | ||
| 1+E=F | 2+E=10 | 3+E=11 | 4+E=12 | 5+E=13 | 6+E=14 | 7+E=15 | 8+E=16 | 9+E=17 | A+E=18 | B+E=19 | C+E=1A | D+E=1B | E+E=1C | |
| 1+F=10 | 2+F=11 | 3+F=12 | 4+F=13 | 5+F=14 | 6+F=15 | 7+F=16 | 8+F=17 | 9+F=18 | A+F=19 | B+F=1A | C+F=1B | D+F=1C | E+F=1D | F+F=1E |
| Таблица умножения | ||||||||||||||
| 1*1=1 | ||||||||||||||
| 1*2=2 | 2*2=4 | |||||||||||||
| 1*3=3 | 2*3=6 | 3*3=9 | ||||||||||||
| 1*4=4 | 2*4=8 | 3*4=C | 4*4=10 | |||||||||||
| 1*5=5 | 2*5=A | 3*5=F | 4*5=14 | 5*5=19 | ||||||||||
| 1*6=6 | 2*6=C | 3*6=12 | 4*6=18 | 5*6=1E | 6*6=24 | |||||||||
| 1*7=7 | 2*7=E | 3*7=15 | 4*7=1C | 5*7=23 | 6*7=2A | 7*7=31 | ||||||||
| 1*8=8 | 2*8=10 | 3*8=18 | 4*8=20 | 5*8=28 | 6*8=30 | 7*8=38 | 8*8=40 | |||||||
| 1*9=9 | 2*9=12 | 3*9=1B | 4*9=24 | 5*9=2D | 6*9=36 | 7*9=3F | 8*9=48 | 9*9=51 | ||||||
| 1*A=A | 2*A=14 | 3*A=1E | 4*A=28 | 5*A=32 | 6*A=3C | 7*A=46 | 8*A=50 | 9*A=5A | A*A=64 | |||||
| 1*B=B | 2*B=16 | 3*B=21 | 4*B=2C | 5*B=37 | 6*B=42 | 7*B=4D | 8*B=58 | 9*B=63 | A*B=6E | B*B=79 | ||||
| 1*C=C | 2*C=18 | 3*C=24 | 4*C=30 | 5*C=3C | 6*C=48 | 7*C=54 | 8*C=60 | 9*C=6C | A*C=78 | B*C=84 | C*C=90 | |||
| 1*D=D | 2*D=1A | 3*D=27 | 4*D=34 | 5*D=41 | 6*D=4E | 7*D=5B | 8*D=68 | 9*D=75 | A*D=82 | B*D=8F | C*D=9C | D*D=A9 | ||
| 1*E=E | 2*E=1C | 3*E=2A | 4*E=38 | 5*E=46 | 6*E=54 | 7*E=62 | 8*E=70 | 9*E=7E | A*E=8C | B*E=9A | C*E=A8 | D*E=B6 | E*E=C4 | |
| 1*F=F | 2*F=1E | 3*F=2D | 4*F=3C | 5*F=4B | 6*F=5A | 7*F=69 | 8*F=78 | 9*F=87 | A*F=96 | B*F=A5 | C*F=B4 | D*F=C3 | E*F=D2 | F*F=E1 |
Задачи
Контрольная работа
К оглавлению
Таблица перевода в десятичную систему счисления
Skip to content
Содержание:
- 0.
 0.1 Предупреждение
0.1 Предупреждение
- 0.
- 1 Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
- 2 Перевод чисел из одной системы счисления в другую
- 3 Перевод чисел из любой системы счисления в десятичную систему счисления
- 4 Перевод чисел из десятичной системы счисления в другую систему счисления
| Поставить LIKE | и поделиться ссылкой |
Ура. Вам стало интересно как получилось данное число Вы ввели число: в системе счисления и хотите перевести его в .
Калькулятор перевода чисел имеет одно поле для ввода. После этого Вам обязательно нужно указать в какой системе счисления Вы его ввели. Для этого под полем ввода есть графа «Его система счисления». Если Вы не нашли своей системы, то выберите графу «другая» и появится поле ввода . В это поле необходимо вписать основание системы одним числом без пробелов. После нажмите кнопку «ПЕРЕВЕСТИ» и результат появится в соответствующем поле. Если Вы хотите получить подробный ход решения, то нажмите на соответствующую ссылку. Научиться переводить число из одной системы счисления в другую очень просто. Любое число может быть легко переведено в десятичную систему по следующему алгоритму: Каждая цифра числа должна быть умножена на основание системы счисления этого числа возведенное в степень равное позиции текущей цифры в числе справа налево, причём счёт начинается с 0. С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже. ПредупреждениеПеревод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решенияСуществуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля: |
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 |
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
где Цn-целое число в позиции n, Д-k— дробное число в позиции (-k), s — система счисления.
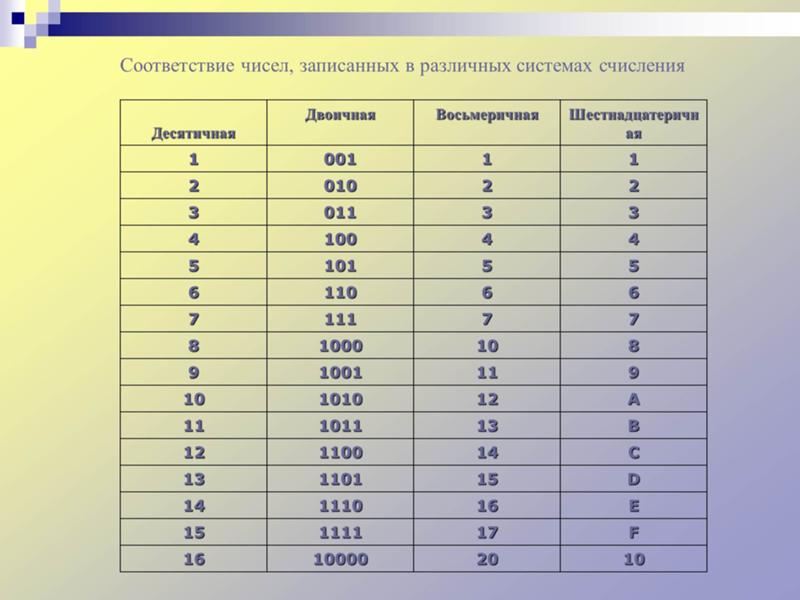
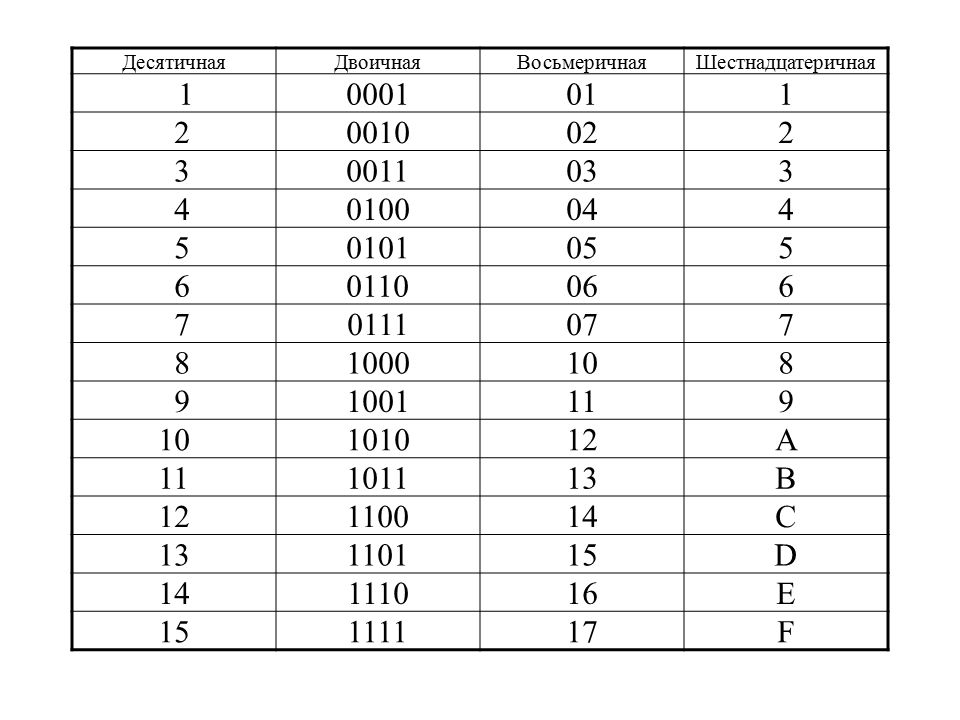
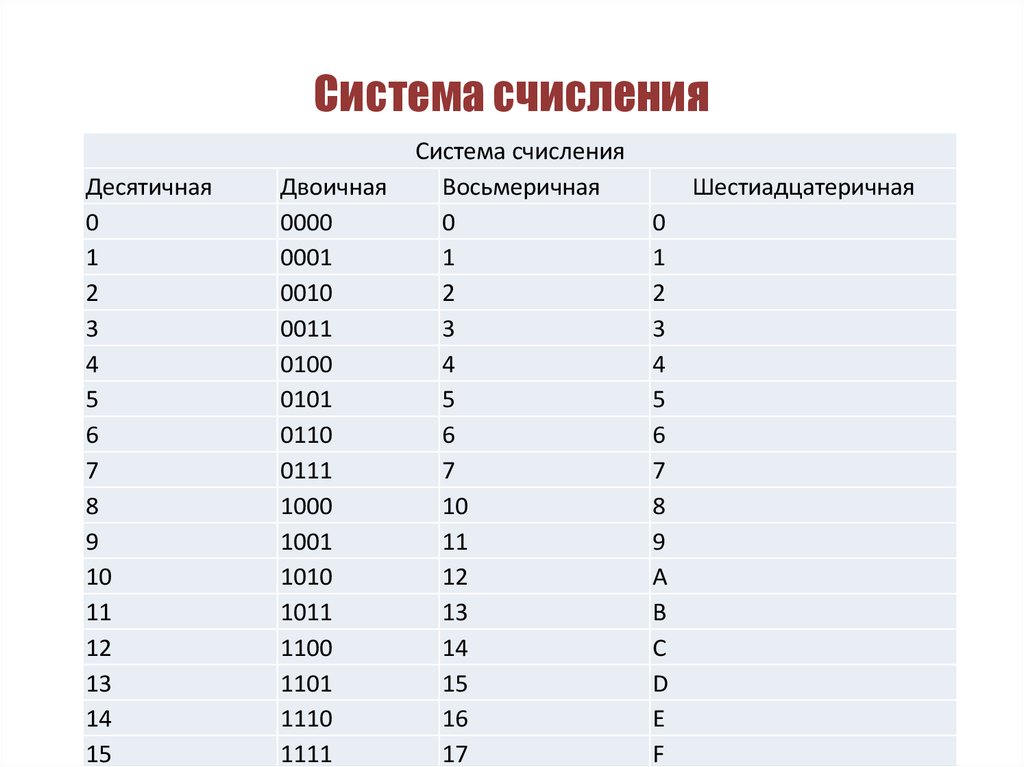
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр <0,1,2,3,4,5,6,7,8,9>, в восьмеричной системе счисления — из множества цифр <0,1,2,3,4,5,6,7>, в двоичной системе счисления — из множества цифр <0,1>, в шестнадцатеричной системе счисления — из множества цифр <0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F>, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.
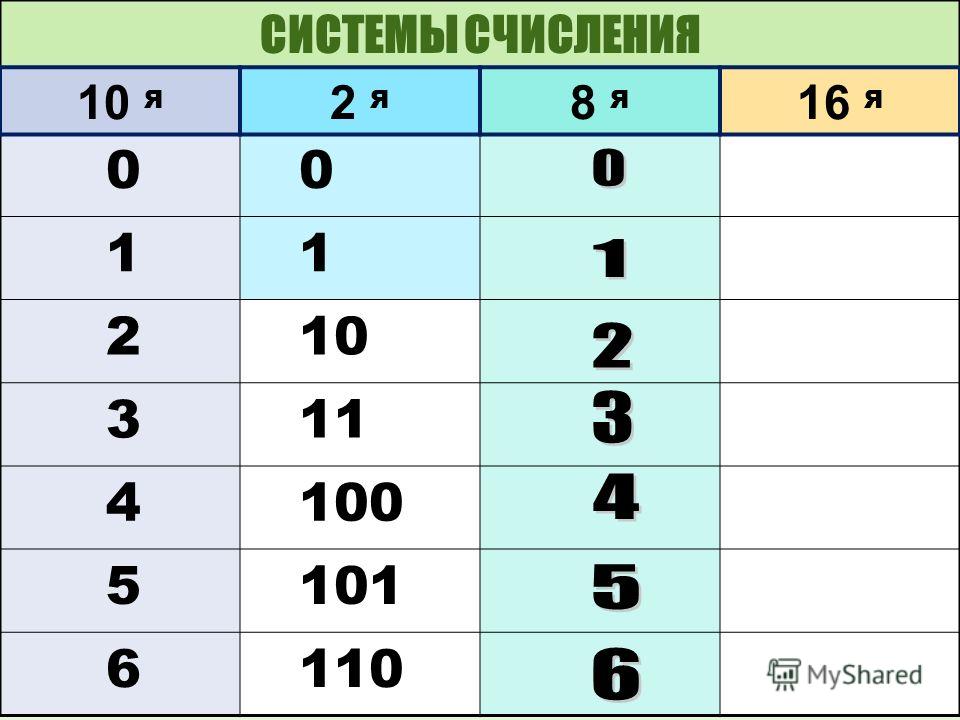
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.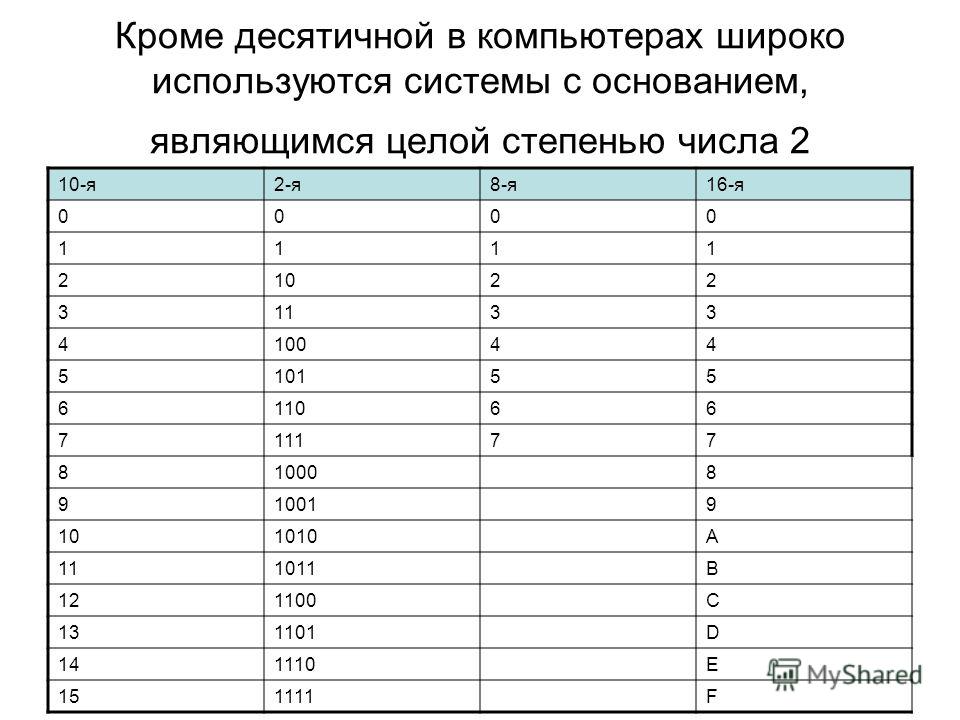
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1·2 6 + 0 ·2 5 + 1·2 4 + 1·2 3 + 1·2 2 + 0·2 1 + 1·2 0 + 0·2 -1 + 0·2 -2 + 1·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C- на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т. д.) до получения целого остатка, меньше, чем основание СС.
д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||
| 158 | 79 | 2 | |
| 1 | 78 | 39 | 2 |
| 1 | 38 | 19 | 2 |
| 1 | 18 | 9 | 2 |
| 1 | 8 | 4 | 2 |
| 1 | 4 | 2 | 2 |
| 2 | 1 | ||
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8.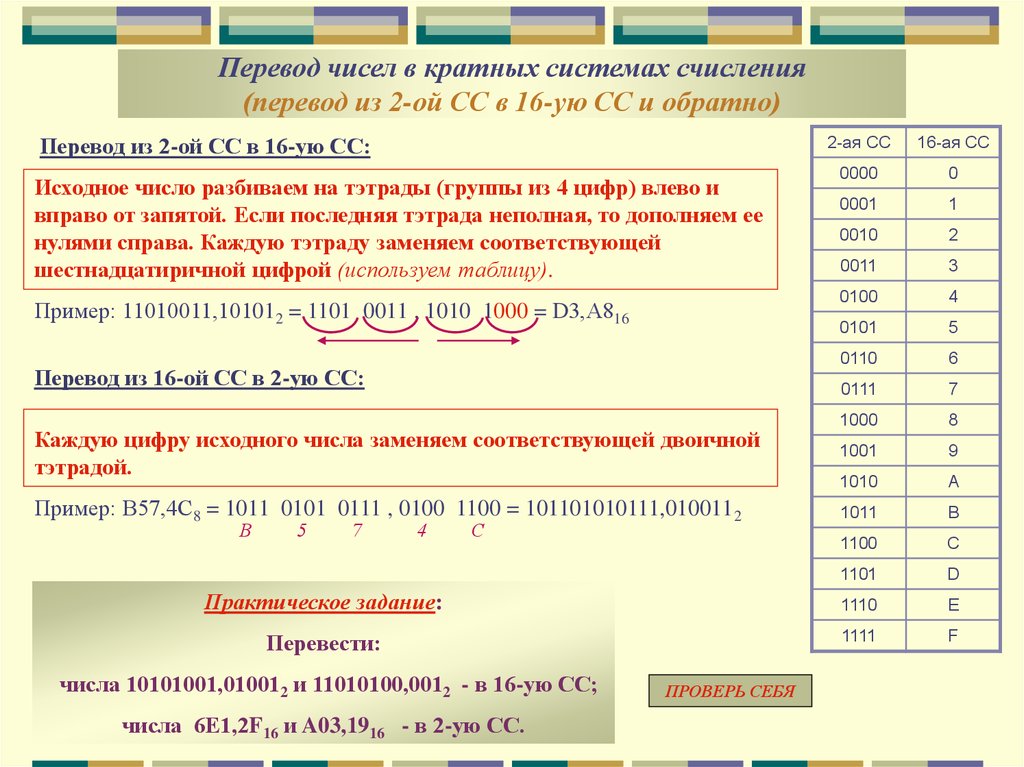 В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | |
| x | 2 |
| 0.428 | |
| x | 2 |
| 0.856 | |
| x | 2 |
| 1 | 0.712 |
| x | 2 |
| 1 | 0.424 |
| x | 2 |
| 0.848 | |
| x | 2 |
| 1 | 0.696 |
| x | 2 |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | |
| x | 2 |
| 0.25 | |
| x | 2 |
| 0.5 | |
| x | 2 |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
0. 214 214 | |
| x | 16 |
| 3 | 0.424 |
| x | 16 |
| 6 | 0.784 |
| x | 16 |
| 12 | 0.544 |
| x | 16 |
| 8 | 0.704 |
| x | 16 |
| 11 | 0.264 |
| x | 16 |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | |
| x | 8 |
| 4 | 0.096 |
| x | 8 |
| 0.768 | |
| x | 8 |
| 6 | 0.144 |
| x | 8 |
| 1 | 0.152 |
| x | 8 |
| 1 | 0.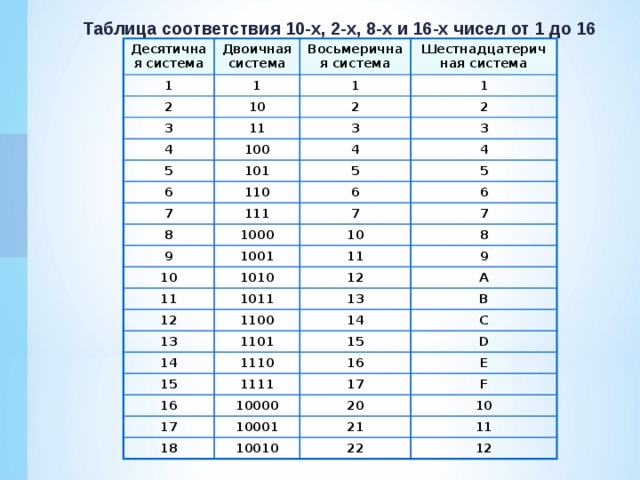 216 216 |
| x | 8 |
| 1 | 0.728 |
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Таблица соответствия десятеричного от 1 до 255 (decimal), двоичного (binary) и шестнадцатеричного (hexadecimal) представлений чисел.
Рубрики
- Без рубрики
- Дримкаст аксессуары
- Дримкаст игры
- Дримкаст прохождения
- Дримкаст эмуляторы
- История
- Компьютеры
- Помощь
- Приставки
Adblock
detector
Персональный сайт — Системы счисления
1.
 Позиционные и непозиционные системы счисления
Позиционные и непозиционные системы счисления1.1. Основные определения
Для записи информации о количестве объектов мы пользуемся числами. Числа записываются при помощи особых знаковых систем, называемых системами счисления. Система счисления — совокупность правил для записи чисел из символов исходного алфавита. Алфавит — конечный набор (множество) символов. Элементы алфавита мы будем называть цифрами. Можно составить любую комбинацию из символов исходного алфавита. Здесь и далее мы будем предполагать, что мы можем представить любое число, используя символы алфавита системы счисления. Системы счисления бывают позиционные и непозиционные. В позиционной системе счисления позиция цифры в числе влияет на ее значение, в непозиционных, соответственно, не влияет.
1.2. Непозиционные системы счисления
Примером непозиционной системы счисления является унарная (единичная) система счисления. Основное ее применение — обучение детей счету.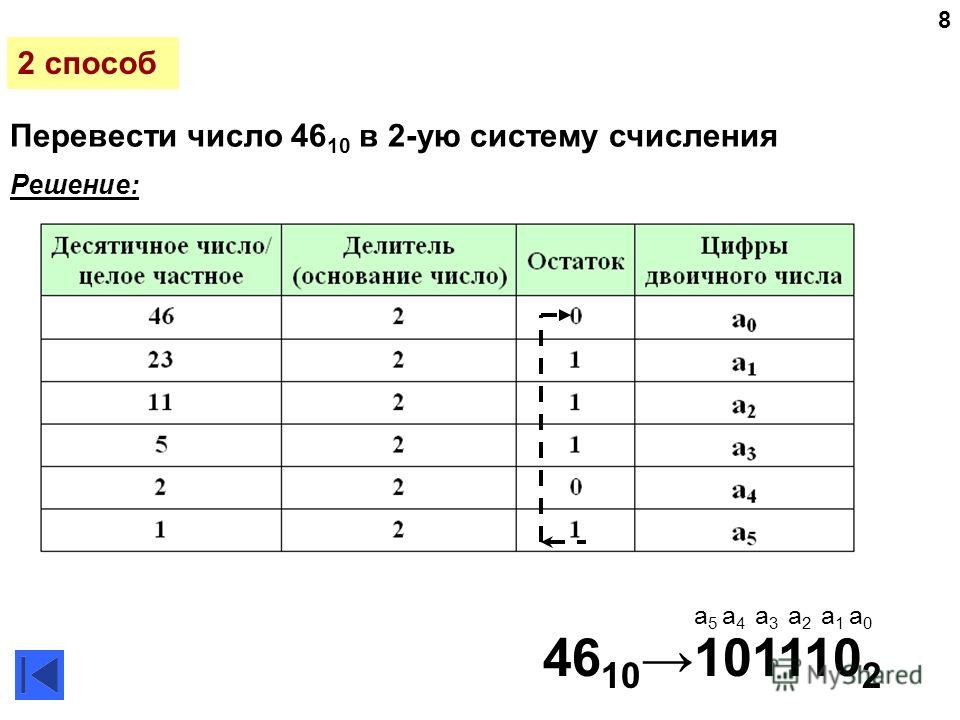 В ее алфавит входит единственная цифра — 1, а количество единиц соответствует количеству объектов. Так, число 111 в унарной системе счисления обозначает число 3 в десятичной. В числе 111 встречаются три цифры 1, и каждая из них обозначает одну величину — число “один”.
В ее алфавит входит единственная цифра — 1, а количество единиц соответствует количеству объектов. Так, число 111 в унарной системе счисления обозначает число 3 в десятичной. В числе 111 встречаются три цифры 1, и каждая из них обозначает одну величину — число “один”.
Еще одним классическим примером непозиционной системы счисления является римская система счисления (использовалась в Древнем Риме). Несмотря на то, что Римская империя рухнула многие сотни лет назад, римская система счисления применяется до сих пор, например, в нумерации глав. Ее алфавит состоит из следующего набора цифр (здесь и далее в скобках указаны соответствующие цифры десятичной системы счисления):
{I(1),V(5), X(10), L(50),C(100), D(500), M(1000)}.
Число составляется по следующим правилам:
- Если меньшая цифра стоит слева от большей, то меньшая цифра вычитается из большей.
- Если меньшая цифра стоит справа от большей, то обе цифры складываются. Одинаковые цифры так же складываются.

Примеры:
- IX = 9.
- MMXI = 1000 + 1000 +10 + 1 = 2011.
- MCMXCVIII = 1000 +(-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1999.
Очевидным недостатком непозиционных систем счисления является трудность записи больших чисел, они слишком длинные и при их записи легко допустить ошибку. Для простоты обозначения больших чисел постоянно вводились новые цифры. Кроме того, в той же самой римской системе счисления трудно совершать арифметические операции, т.к. не существует четких алгоритмов их вычисления. Запись дробных и отрицательных чисел невозможна.
1.3. Позиционные системы счисления
Вышеперечисленные недостатки решают позиционные системы счисления. Классическим примером позиционной системы счисления является десятичная (арабская) система счисления. В позиционных системах счисления количественное значение цифры зависит от того, какую позицию в числе она занимает. Основание позиционной системы счисления показывает, сколько чисел в алфавите системы счисления, а также определяет, во сколько раз различаются значения одинаковых цифр в соседних позициях числа.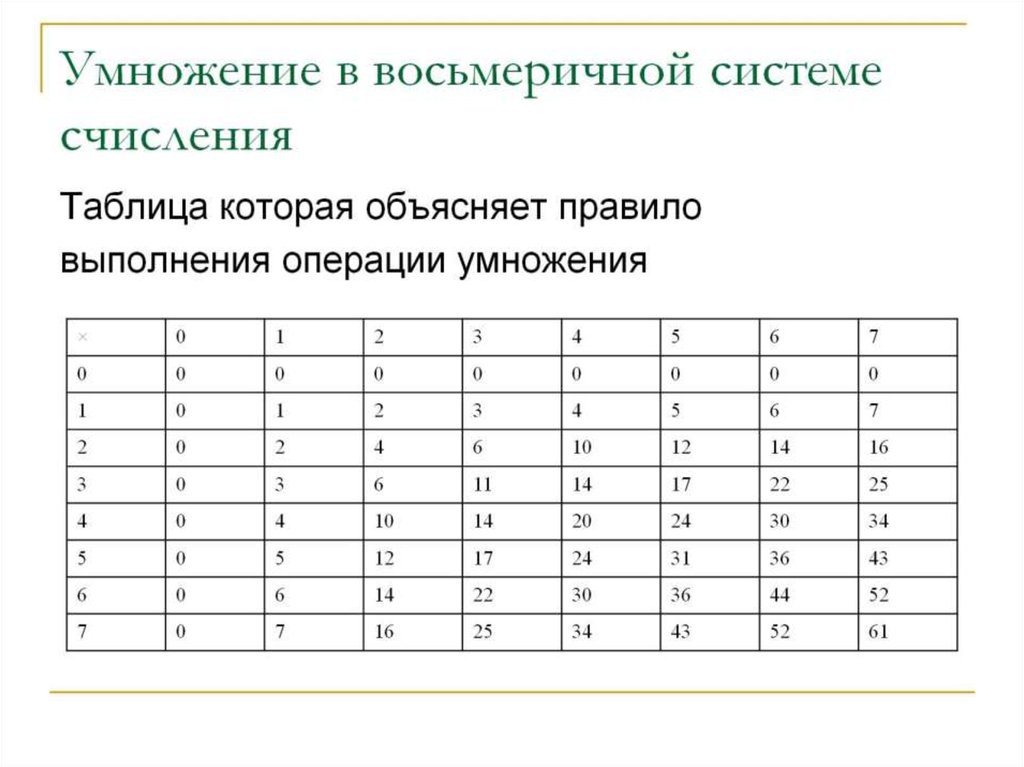 Основание системы счисления записывают нижним индексом рядом с числом. К примеру, число 1110, 123, А16. Позиционную систему счисления с основанием P принято называть P-ичной. Примерами позиционной системы счисления могут служить двоичная, троичная, восьмеричная, шестнадцатеричная и т.д (табл. 1).
Основание системы счисления записывают нижним индексом рядом с числом. К примеру, число 1110, 123, А16. Позиционную систему счисления с основанием P принято называть P-ичной. Примерами позиционной системы счисления могут служить двоичная, троичная, восьмеричная, шестнадцатеричная и т.д (табл. 1).
Таблица SEQ Таблица \* ARABIC 1. Примеры позиционных систем счисления.
Позиционная система счисления | Основание | Алфавит |
Двоичная | 2 | 0, 1 |
Троичная | 3 | 0, 1, 2 |
Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15) |
Позиция цифры в числе называется разрядом.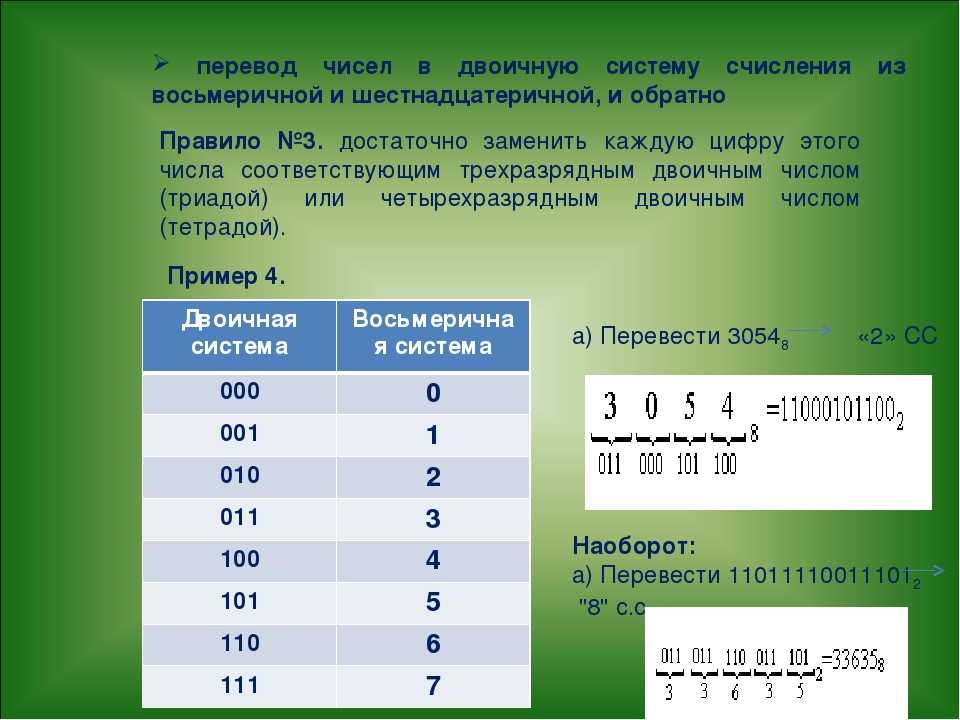 Для целых чисел разряды нумеруются справа налево, началом отсчета является 0.
Для целых чисел разряды нумеруются справа налево, началом отсчета является 0.
Например, для числа 571004910 разряды нумеруются следующим образом:
Цифра | 5 | 7 | 1 | 0 | 0 | 4 | 9 |
Разряд | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Различают свернутую и развернутую форму записи числа. В нашем примере запись 571004910 является свернутой формой записи. В развернутой форме число запишется следующим образом:
571004910 = 5 * 106 + 7 * 105 + 1 * 104 + 0 * 103 + 0 * 102 + 4 * 101 + 9 * 100
Т. е. для того, чтобы определить количественное значение цифры, мы умножаем ее на число, равное основанию системы счисления в степени, равной разряду рассматриваемой цифры. Это правило действует и для дробей. Счет разряда дробной части ведется слева направо, начиная от запятой. Для развернутой формы записи дробных частей используются отрицательные значения степеней.
е. для того, чтобы определить количественное значение цифры, мы умножаем ее на число, равное основанию системы счисления в степени, равной разряду рассматриваемой цифры. Это правило действует и для дробей. Счет разряда дробной части ведется слева направо, начиная от запятой. Для развернутой формы записи дробных частей используются отрицательные значения степеней.
Пример:
Число 45,36710
Цифра | 4 | 5 | 3 | 6 | 7 |
Разряд | 1 | 0 | -1 | -2 | -3 |
45,36710 = 4 * 101 + 5 * 100 + 3 * 10-1 + 6 * 10-2 + 7 * 10-3
В общем виде свернутая и развернутая запись числа AР с n целых разрядов и m дробных выглядят следующим образом:
AP=i=-mn-1ai∙ Pi=an-1∙Pn-1+⋯+a0∙P0+a-1 ∙P-1+⋯+a-m∙P-m
Примеры:
1012 = 1 * 22 + 0 * 21 + 1 * 20
0,2223 = 0 * 30 + 2 * 3-1 + 2 * 3-2 + 2 * -3
347,48 = 3 * 82+ 4 * 81 + 7 * 80 + 4 * 8-1
3A,B716 = 3 * 161 +10 * 160 + 11 * 16-1 +7 * 16-2
Очень часто позиционные системы разделяются на однородные (P-ичные) и смешанные.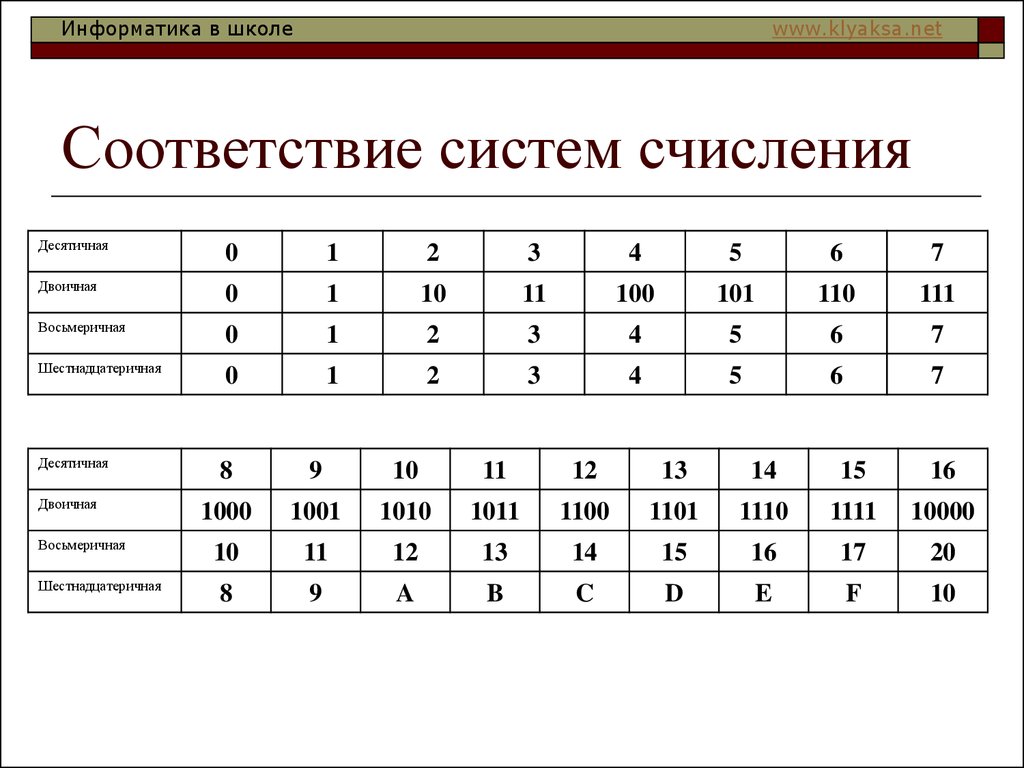
2. Единственность представления чисел в Р-ичных системах счисления
Пусть Р – произвольное натуральное число, большее 1. Существует и единственно представление любого натурального числа А в виде:
А=an∙Pn+an-1∙Pn-1+⋯+a0,
Где 0≤ai<P, 0<i<n, an≠0
Доказательство:
Существование.В качестве доказательства приведем алгоритм построения с пояснениями. Числа Р0, Р1, Р2… образуют монотонную возрастающую числовую последовательность. Из этого следует, что найдется такое число n, что
Pn≤A≤Pn+1,
Рассмотрим интервал [Pn,Pn+1). Для начала разделим его на (P-1) равных частей. Получим интервалы [Pn,2∙Pn), [2∙Pn,3∙Pn), [3∙Pn,4∙Pn), …,[(P-1)∙Pn,P∙Pn). Длина каждого из этих интервалов равна P.
Для начала разделим его на (P-1) равных частей. Получим интервалы [Pn,2∙Pn), [2∙Pn,3∙Pn), [3∙Pn,4∙Pn), …,[(P-1)∙Pn,P∙Pn). Длина каждого из этих интервалов равна P.
Из того, что
Pn≤A≤Pn+1,
Следует, что существует такое m, что
mPn≤A<(m+1)Pn+1,
Тогда положим an = m. an≠0 по построению. Для нахождения an-1 повторим описанные выше действия для числа (A — an∙Pn). Найдем коэффициент an-1.
A’ = (A – anPn) Если это число меньше либо равно P, то an-1 = A’ и процесс останавливается. Если же нет, то находим ah по описанной выше схеме, а затем применяем алгоритм уже к числу
Если же нет, то находим ah по описанной выше схеме, а затем применяем алгоритм уже к числу
A”=(A’ – ahPh)
Для тех номеров, которые находятся между n и h (h<i<n), полагаем ai= 0. Процесс завершится, т.к. каждый раз мы рассматриваем число меньшее, чем было изначально, а именно, когда
А-an∙Pn—an-1∙Pn-1-⋯-a0=0,
Единственность. Рассмотрим получившееся разложение
А=an∙Pn+an-1∙Pn-1+⋯+a0,
Пусть существует еще одно разложение числа А
А=a‘k∙Pk+a’k-1∙Pk-1+⋯+a’0,
В первую очередь докажем, что n=k. Пусть это не так, и n>k. Оценим разложение
Пусть это не так, и n>k. Оценим разложение
А=an∙Pn+an-1∙Pn-1+⋯+a0,
Снизу наименьшим возможным числом (старший разряд an = 1, остальные — 0).
A≥Pn
Разложение
А=a‘k∙Pk+a’k-1∙Pk-1+⋯+a’0,
Оценим сверху максимально возможным числом (все разряды равны P-1).
А≤P-1∙Pk+P-1∙Pk-1+⋯+P-1=Pk+1— 1<Pk+1
Т.к. у нас n≥(k+1), то Pn≤A<Pk+1 . Из чего и из n>k следует, что n=k.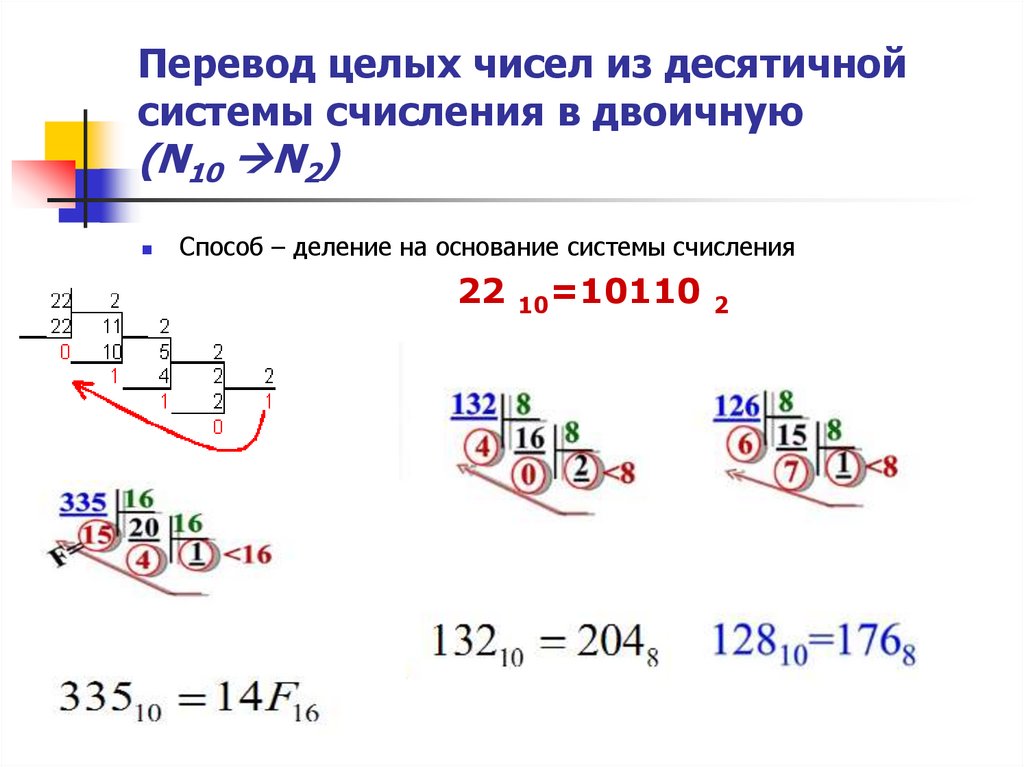 Т.е. второе разложение имеет вид
Т.е. второе разложение имеет вид
А=a‘n∙Pn+a’n-1∙Pn-1+⋯+a’0,
Теперь докажем, что все коэффициенты a’i=ai, для любого 0≤i≤n.Пусть в некотором разряде j (0≤j≤n)это не так, а для j<i≤n равенство выполняется. Рассмотрим числа
B=A- an∙Pn-…-aj+1∙Pj+1=aj∙Pj+aj-1∙Pj-1+⋯+a0,
B’=A- a’n∙Pn-…-a’j+1∙Pj+1=a’j∙Pj+a’j-1∙Pj-1+⋯+a’0,
Причем B=B’ при aj≠a’j. Это невозможно. Даже если aj=a’j+1, а aj-1=…=а0 = P-1, мы все равно не получим равенство. А если В≠В’, то и разложения на самом деле не равны одному числу. Получаем противоречие с утверждением о том, что число А представляется двумя разными разложениями.
Это невозможно. Даже если aj=a’j+1, а aj-1=…=а0 = P-1, мы все равно не получим равенство. А если В≠В’, то и разложения на самом деле не равны одному числу. Получаем противоречие с утверждением о том, что число А представляется двумя разными разложениями.
3. Арифметические операции в Р-ичных системах счисления
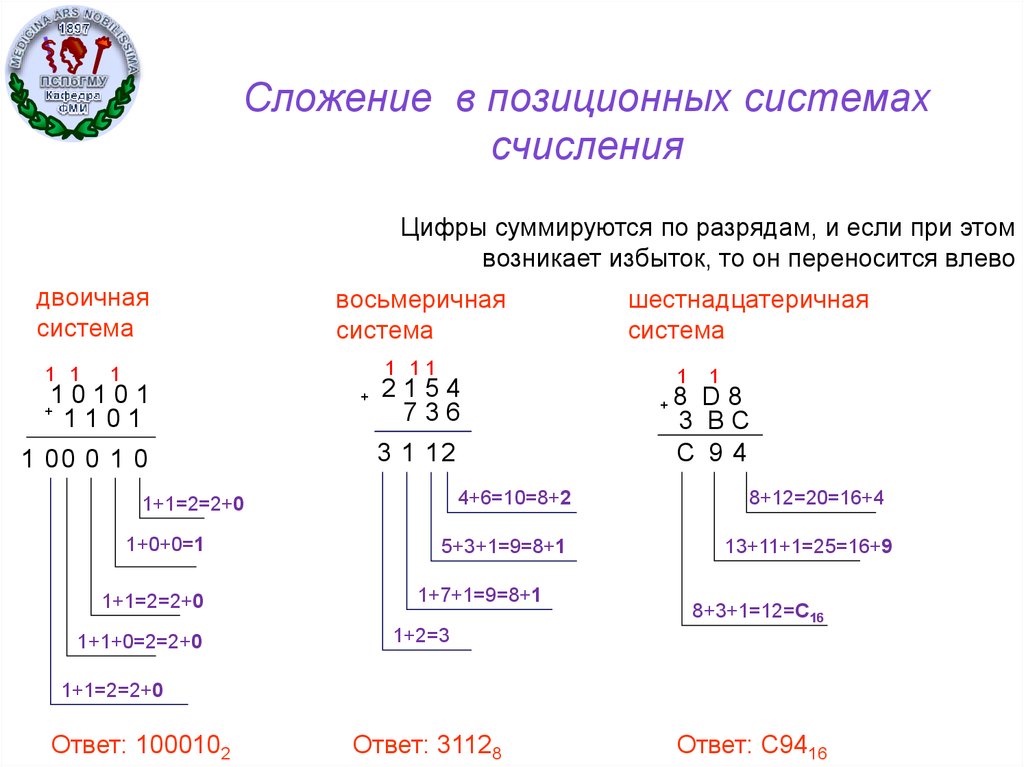
3.1. Сложение
Для выполнения этой операции используют таблицы сложения. По вертикали и по горизонтали откладываем числа алфавита. На пересечении строки и столбца получаем результат операции. При сложении двух чисел P-ичной системы счисления мы не можем перенести в старший разряд больше 1. Действительно, максимальная сумма, которую мы можем получить, будет результатом сложения двух максимальных цифр алфавита (P — 1) + (P — 1) = 2(P — 1) = 2P — 2 = P + P — 2 = 1[P — 2]. Число “десятков” — 1, число “единиц” — P-2.
Примеры:
+1010111200001012 10111002 +1011,0121000,112 10100,002 +538478 1228 +46,02812,108 60,128
3.2. Вычитание
Для вычитания также используется таблица сложения. Предположим, мы вычитаем цифру b из числа a.
- Ищем строку, именованную цифрой b.
- В этой строке ищем цифру a.
- Смотрим, какой цифрой именован столбец, на пересечении которого с цифрой получаем результат a.
Эта схема работает, если у нас a≥b. В противном случае, мы занимаем единицу старшего разряда и по вышеописанной схеме решаем 1a — b.
Примеры:
—10012 01102 00112 —100,102 01,002 11,002 —43,508 11,448 32,048
3.
 3. Умножение
3. УмножениеПо сути, это то же самое умножение столбиком, которые мы привыкли применять в десятичной системе счисления. Единственное отличие — для проведения этой операции в P-ичной системе нам необходимо использовать таблицы сложения для этой P-инчной системы счисления.
Примеры:
×10111012 1012+10111012 10111012 1110100012 ×101,012 101,12+ 101012 101012 000002 101012 11100,1112
3.4. Деление
Делим также “столбиком”, однако, как и в случае умножения, используем таблицы умножения и сложения для P-ичной системы счисления.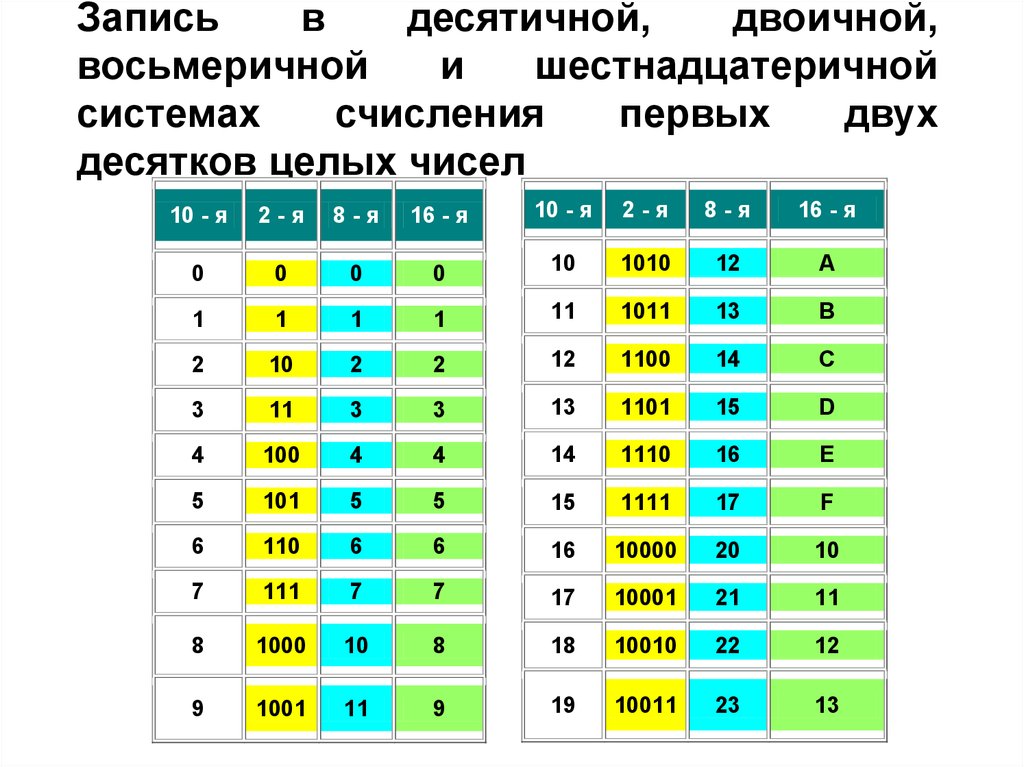 В качестве примера приведем деление 69 на 3 в двоичной и восьмеричной системах счисления.
В качестве примера приведем деление 69 на 3 в двоичной и восьмеричной системах счисления.
10001012|112101112-11 0101 -11 100 -11 011 -11 01058|38278-6 25 -25 0
Можно выделить и другой подход. Перед началом выполнения операций можно перевести все слагаемые в десятичную систему счисления, выполнить в привычной форме необходимые расчеты, а результат перевести обратно в системы с основанием P. Вопрос о том, как переводить из одной системы счисления в другую, подробно рассмотрен в следующих главах.
3.5. Таблицы сложения и умножения (двоичная и восьмеричная система счисления)
Таблица SEQ Таблица \* ARABIC 2.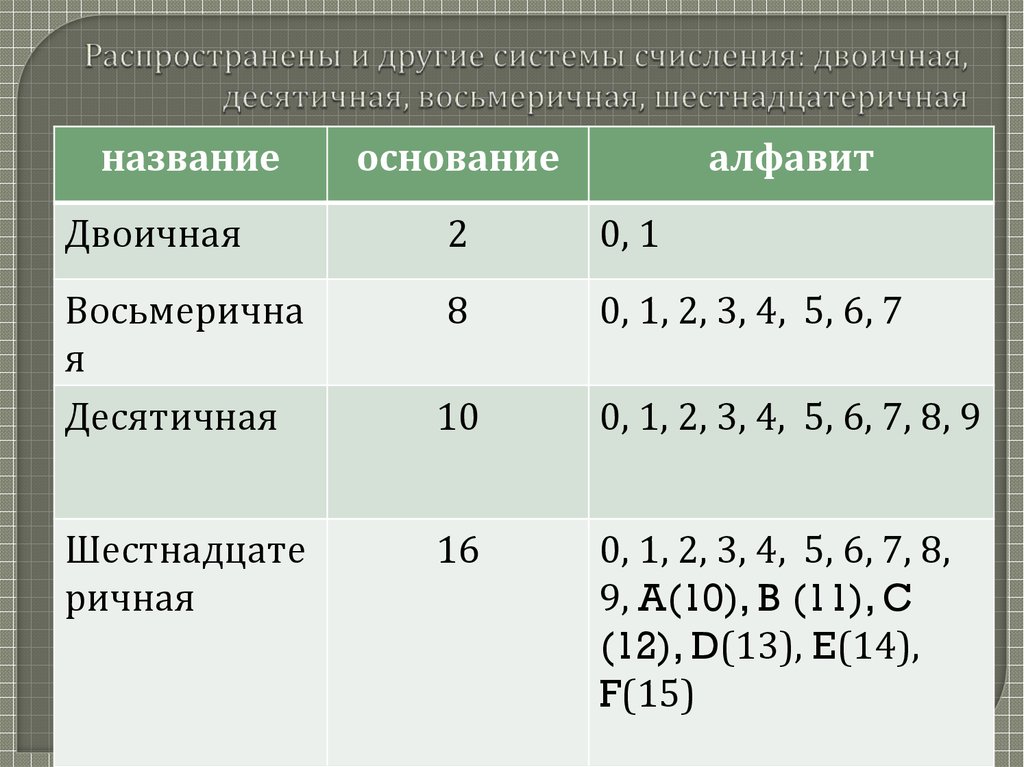 Таблица сложения в двоичной системе счисления.
Таблица сложения в двоичной системе счисления.
+ | 0 | 1 |
0 | 0 | 1 |
1 | 1 | 10 |
Таблица SEQ Таблица \* ARABIC 3. Таблица умножения в двоичной системе счисления.
* | 0 | 1 |
0 | 0 | 0 |
1 | 0 | 1 |
ы
Таблица 4. Таблица сложения в восьмеричной системе счисления.
Таблица сложения в восьмеричной системе счисления.
+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Таблица 5. Таблица умножения в восьмеричной системе счисления.
Таблица умножения в восьмеричной системе счисления.
* | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
Вы и сами можете составить таблицу умножения или сложения для любого основания.
- В крайних левом вертикальном и верхнем горизонтальном записываете алфавит (цифры записываются по возрастанию). В ячейке, основанной на пересечении i строчки и j столбца будет записан результат операции.
- Считаем i * j или i + j как бы мы считали в обычной десятичной системе. Переводим результат в систему счисления с исходным основанием.
В качестве упражнения можете составить таблицы умножения и сложения для троичной и шестнадцатеричной систем счисления.
4. Перевод чисел из Р-ичной системы счисления в десятичную
Алгоритм:
1)Записываем исходное число в развернутой форме.
2) Считаем полученную сумму.
Примеры:
1012 = 1 * 22 + 0 * 21 + 1 * 20 = 510
0,2223 = 0 * 30 + 2 * 3-1 + 2 * 3-2 + 2 * 3-3 = 0,(962)10
347,48 = 3 * 82 + 4 * 81 + 7 * 80 + 4 * 8-1 = 231,510
3A,B716 = 3 * 161 +10 * 160 + 11 * 16-1 +7 * 16-2= 58, 7148437510
5.
 Перевод чисел из десятичной системы счисления в Р-ичную
Перевод чисел из десятичной системы счисления в Р-ичную5.1. Перевод целой части числа
Алгоритм перевода рассмотрим на примере перевода из десятичной системы счисления в двоичную. Пусть необходимо перевести число 2710 в двоичную систему счисления.
- Разделим 27 на 2. Получим 13 и остаток 1. Значит, последняя цифра в двоичной системе счисления будет 1.
- 13 /2 = 6 (остаток 1)
- 6 /2 = 3 (остаток 0)
- 3 / 2 = 1 (остаток 1)
Следовательно, 2710 = 110112
Проверка:
1101110 = 1 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 = 16 + 8 + 0 + 2 + 1 = 2710
Для других оснований аналогично. Переведем то же число в троичную систему счисления.
- 27 / 3 = 9 (остаток 0)
- 9 / 3 = 3 (остаток 0)
- 3 / 3 = 1 (остаток 0)
Следовательно, 2710 = 10003
Проверка:
10003 = 1 * 33 + 0 + 0 + 0 + 0 = 2710
Пусть теперь необходимо перевести число 2710 в восьмеричную систему счисления.
1)27 \8 = 3 (остаток 3)
2710 = 338
Проверка :
338 = 3 * 8 + 3 = 2710
Перевести 2710 в шестнадцатеричную систему счисления.
1) 27/16 = 1(остаток 11)
2710 = 1B16
Проверка :
1B16 = 1 * 16 + 11 = 2710
5.2. Перевод дробной части числа
Необходимо производить умножение на основание системы до тех пор, пока не останется дробной части или не будет достигнута необходимая степень точности.
Примеры:
- 0,2510
- 0,25 * 2 = 0,5 (целая часть 0)
- 0,5 * 2 = 1,0 (целая часть1)
- 0,25 = 0, 01
- 0,72510
- 0,725 * 2 = 1,45 (целая часть1)
- 0,45 * 2 = 0,9 (целая часть0)
- 0.9 * 2 = 1,8 (целая часть1)
- 0,8 * 2 = 1,6 (целая часть1)
- 0.6 * 2 = 1,2 (целая часть1)
- 0,2 * 2 = 0,4 (целая часть0)
- 0.
 4 * 2 =0,8 (целая часть0)
4 * 2 =0,8 (целая часть0) - 0,8 * 2 = 1,6 (целая часть1)
- 0,725 = 0.101(1100)
Упражнение: проделать самостоятельно для остальных систем счисления
6. Перевод из двоичной в родственные системы счисления и обратно
6.1. Перевод целой части числа
Для выполнения этой операции удобно воспользоваться таблицей соответствия чисел в двоичной системе счисления числам в другой.
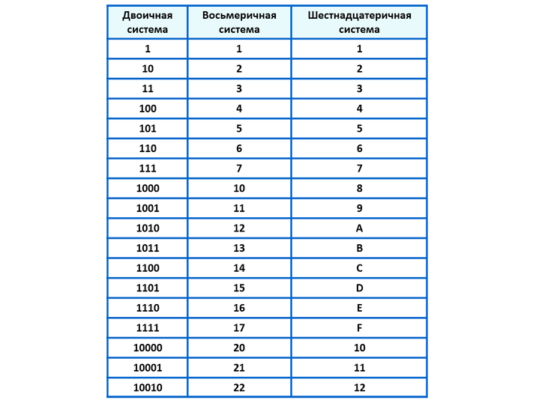
Таблица 6. Перевод из двоичной системы счисления в восьмеричную.
основание 2 | основание 8 |
000 | 0 |
001 | 1 |
010 | 2 |
011 | 3 |
100 | 4 |
101 | 5 |
110 | 6 |
111 | 7 |
Таблица 7. Перевод из двоичной системы счисления в шестнадцатеричную.
Перевод из двоичной системы счисления в шестнадцатеричную.
основание 2 | основание 16 |
0000 | 0 |
0001 | 1 |
0010 | 2 |
0011 | 3 |
0100 | 4 |
0101 | 5 |
0110 | 6 |
0111 | 7 |
1000 | 8 |
1001 | 9 |
1010 | A |
1011 | B |
1100 | C |
1101 | D |
1110 | E |
1111 | F |
Рассмотрим пример перевода из двоичной системы счисления в восьмеричную числа 11101010000011011012.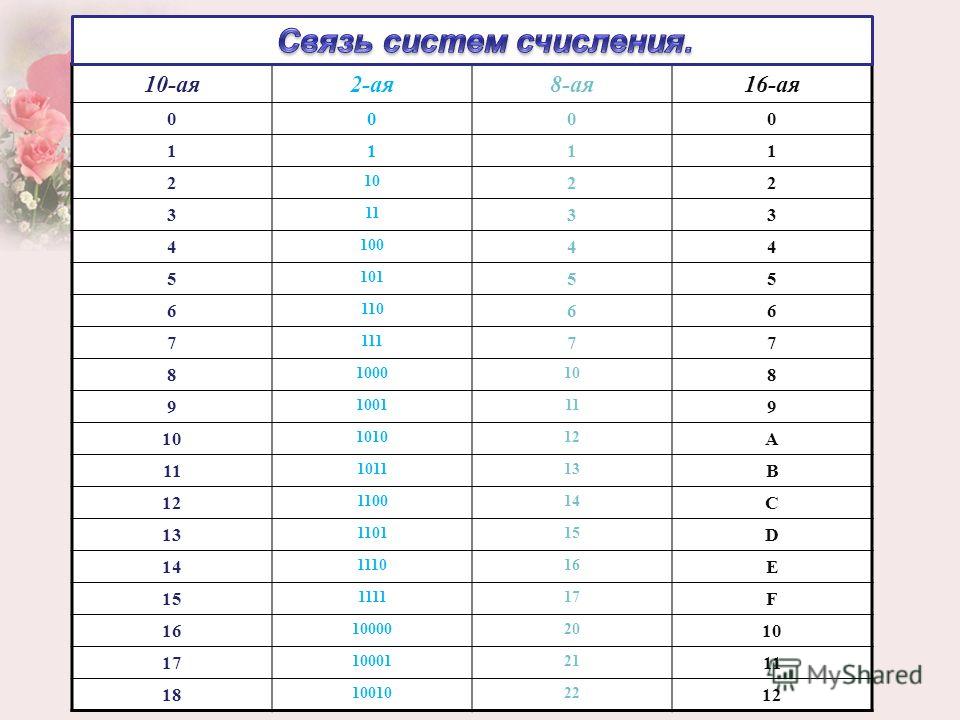 Первым делом разбиваем число на триады, начиная с правого конца 1 110 101 000 001 101 1012. Нам необходимо целое число триад, потому дописываем слева недостающие нули 001 110 101 000 001 101 1012. Далее смотрим по таблице перевода, какому числу соответствует очередная триада в восьмеричной системе счисления 001 110 101 000 001 101 1012 = 16501558.
Первым делом разбиваем число на триады, начиная с правого конца 1 110 101 000 001 101 1012. Нам необходимо целое число триад, потому дописываем слева недостающие нули 001 110 101 000 001 101 1012. Далее смотрим по таблице перевода, какому числу соответствует очередная триада в восьмеричной системе счисления 001 110 101 000 001 101 1012 = 16501558.
Переведем то же самое число в шестнадцатеричную систему счисления. Записываем число, разбиваем его на группы по 4 с правого конца, если необходимо, дописываем слева недостающие нули. 0111 0101 0000 0110 11012. Далее действуем как и в случае с восьмеричной системой — ищем соответствующее число в таблице перевода.
0111 0101 0000 0110 11012 = 7506D16
6.2. Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
Для этого переведем число из восьмеричной системы счисления в двоичную, а уже из двоичной — в шестнадцатеричную. Обратно перевод производится аналогично.
Обратно перевод производится аналогично.
Примеры.
462137328 = 100 110 010 001 011 111 011 0102 = 1001 1001 0001 0111 1101 10102 = 9917DA16
Перевод дробной части:
0,2510 = 0,01002 = 0,28 = 0,416
Совет: для выполнения арифметических операций в двоичной системе счисления, бывает удобнее перевести число в шестнадцатеричную, выполнить соответствующие действия в ней, а результат перевести обратно в двоичную. Заметим, что ЭВМ используют этот же принцип, только все арифметические операции выполняются в двоичной системе счисления, а уже результат переводится в десятичную.
7. Смешанные системы счисления
В отличие от P-ичных систем счисления, в смешанных системах счисления количество символов алфавита может меняться в зависимости от разряда числа. Классическим примером смешанных систем счисления является система измерения времени, где мы используем часы, минуты, секунды.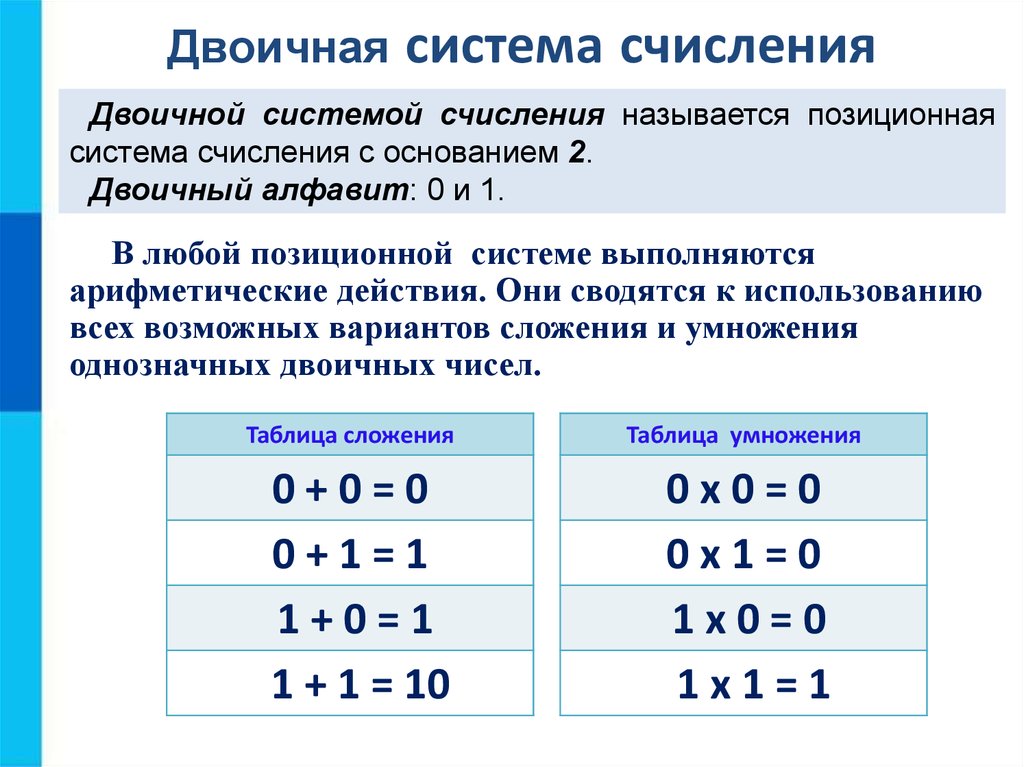
Существует также факториальная
АQ=k=1ndkk!, 0≤dk≤k
и фиббоначиева
AQ=k=0nfkFk,
системы счисления. При записи числа в фиббоначиевой системе счисления Fk – числа Фиббоначи, коэффициенты fk принимают значения 0 или 1, и в последовательности коэффициентовfnfn-1…f0нет двух подряд идущих единиц.
8. Литература
- С. Б. Гашков. Системы счисления и их применение. М.: МЦНМО, 2004. — 52 с.: ил.
- Игорь Н. Бекман. Компьютеры в информатике. Лекция 4: Кодирование в информатике. [http://profbeckman.narod.ru/Komp.files/Lec4.pdf]
- В. М. Казиев. Введение в информатику. [http://www.intuit.ru/department/informatics/intinfo/4/1.
 html]
html]
Е. А. Роганов. Практическая информатика. [http://www.intuit.ru/department/se/pinform/1/4.html
Таблица перевода из 16 в 2 систему. Перевод чисел из одной системы счисления в другую онлайн
Результат уже получен!
Системы счисления
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.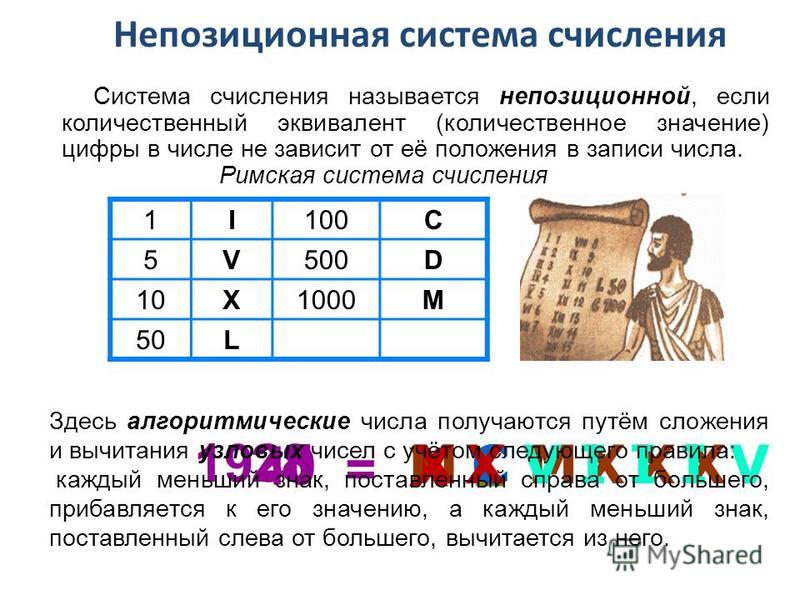 923 можно представить в виде:
923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +…+Д -k ·s -k
где Ц n -целое число в позиции n , Д -k — дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.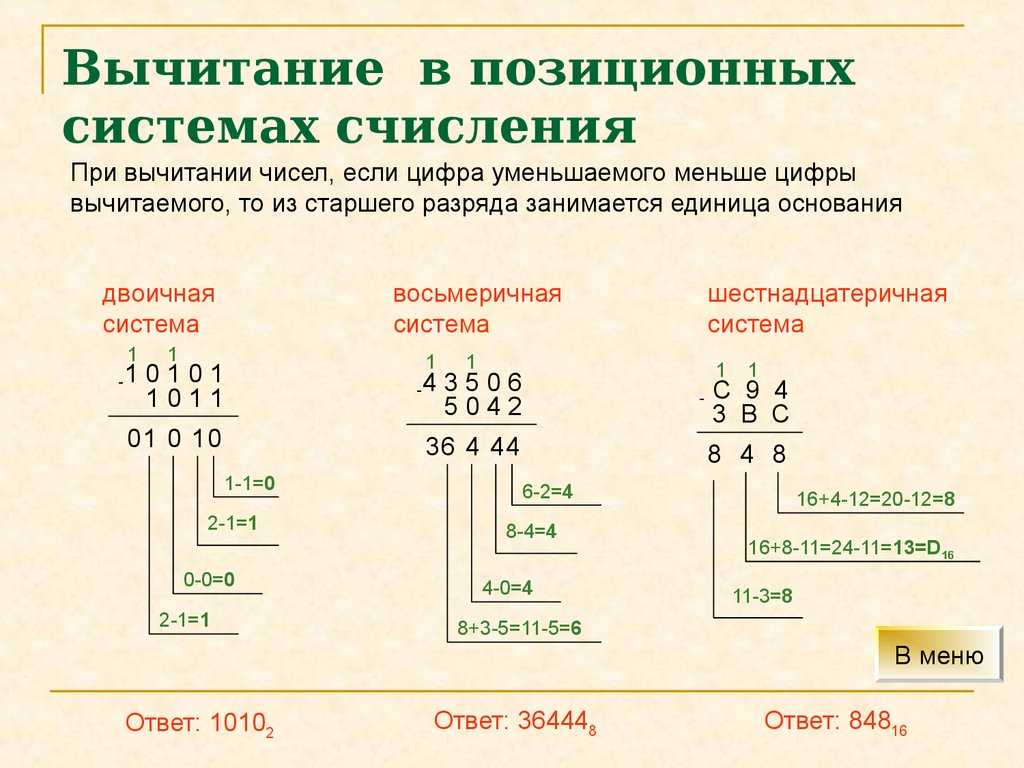
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.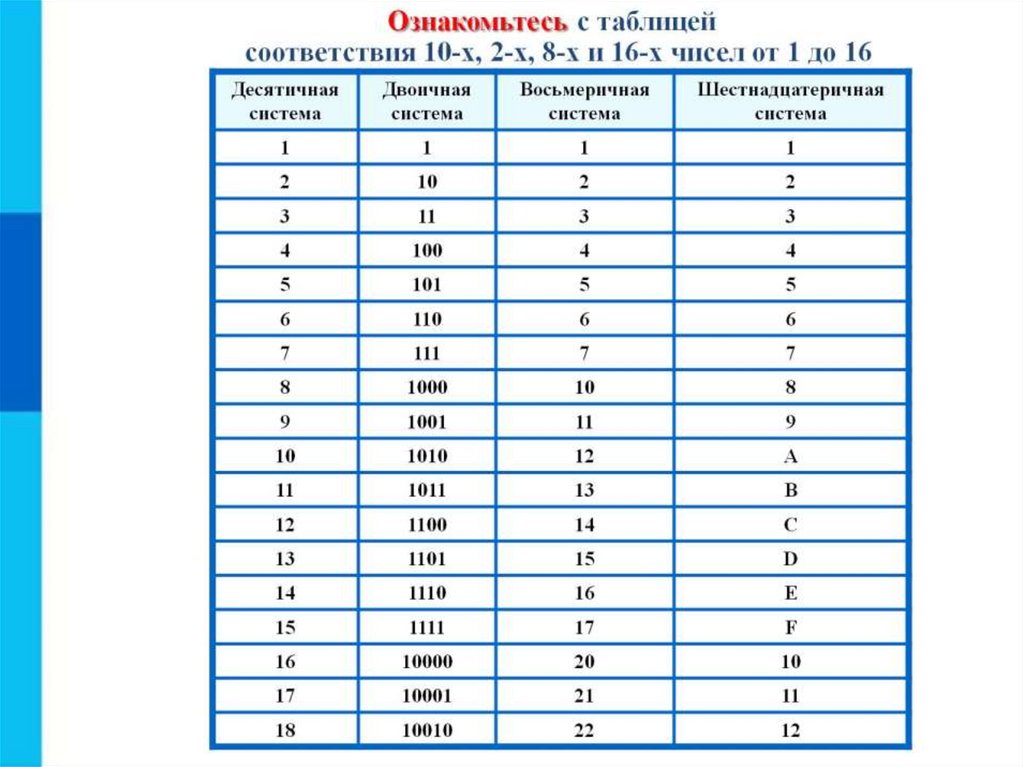
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис.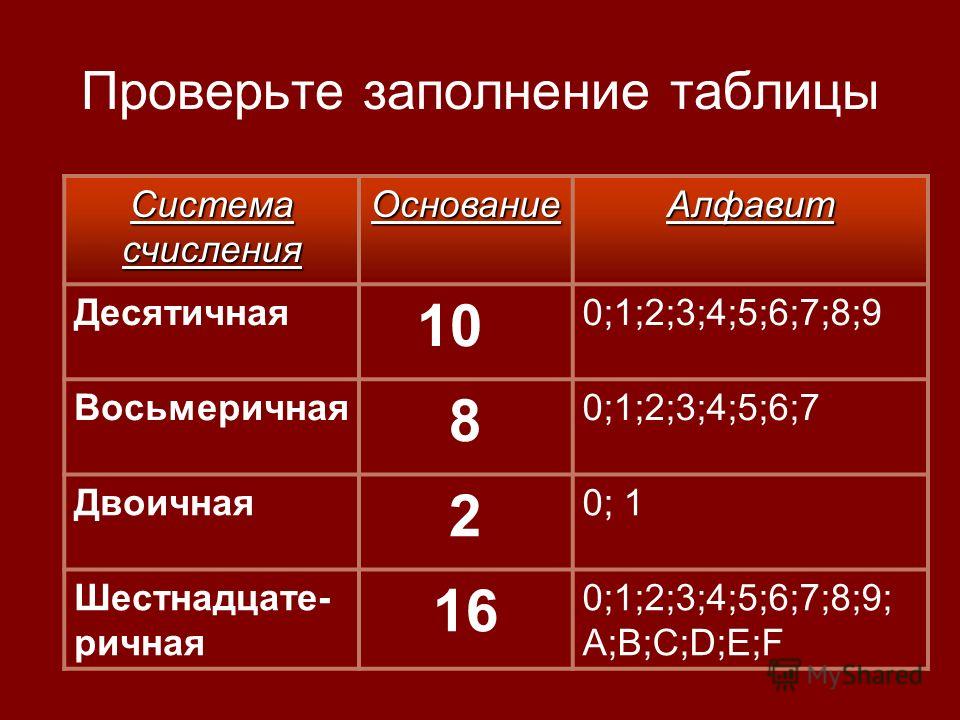 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .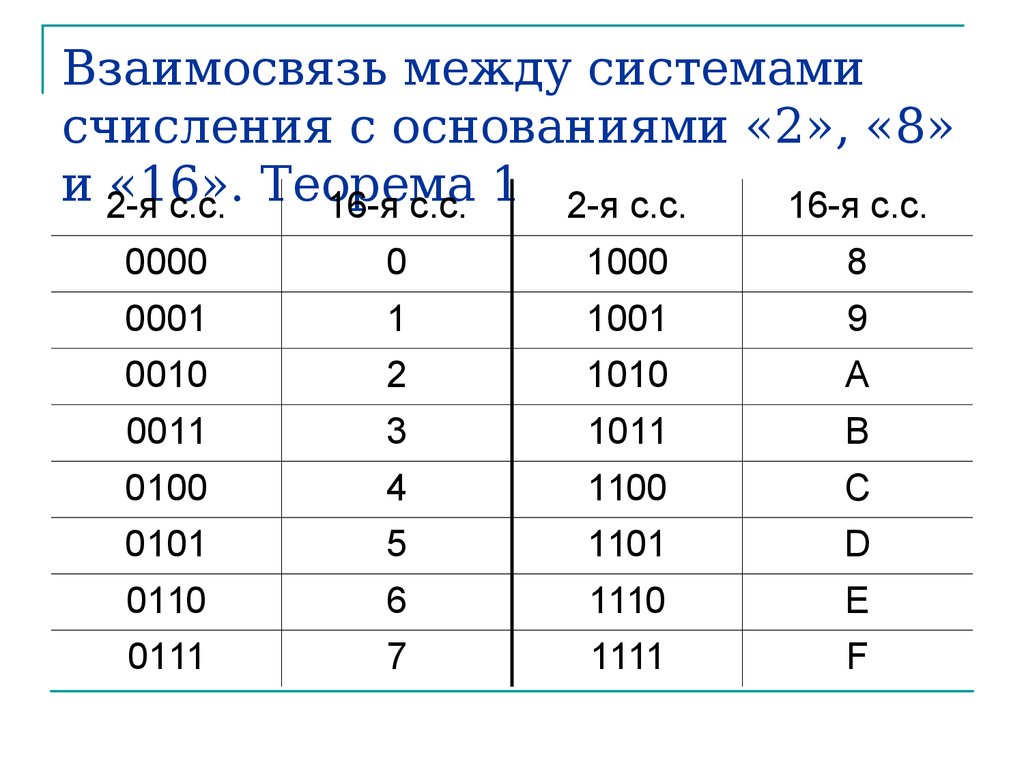
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Следовательно, получился следующий результат:
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
0. 214 10 =0.36C8B4 16 .
214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример 11 . Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8).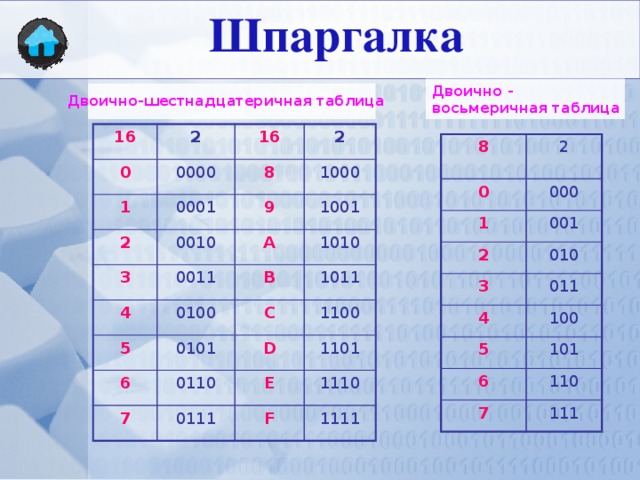 Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
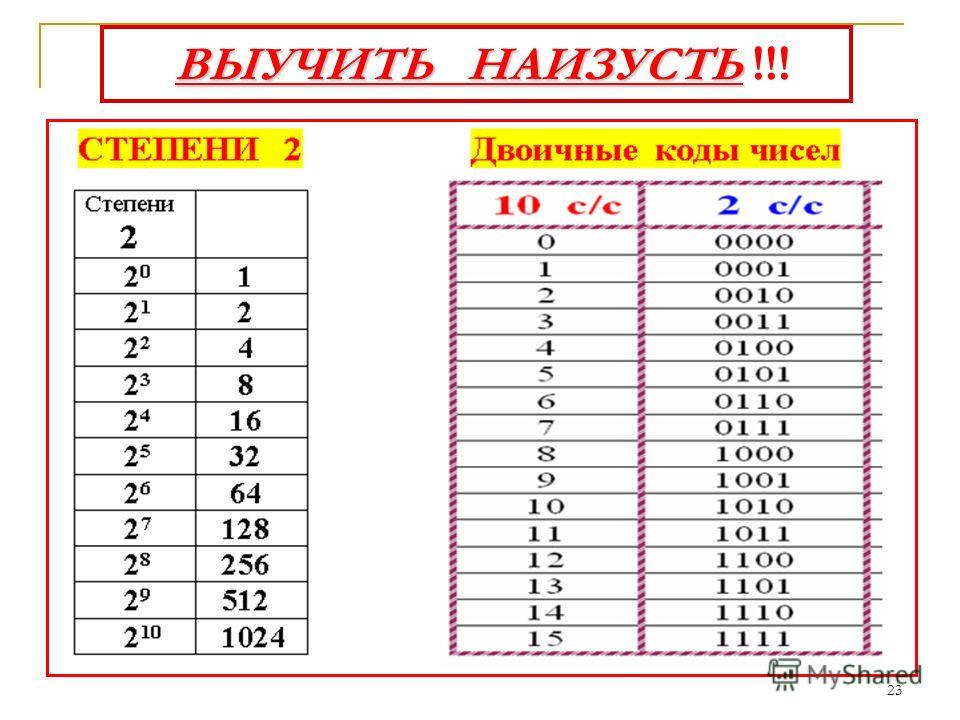
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
n (степень) | |||||||||||
Пример.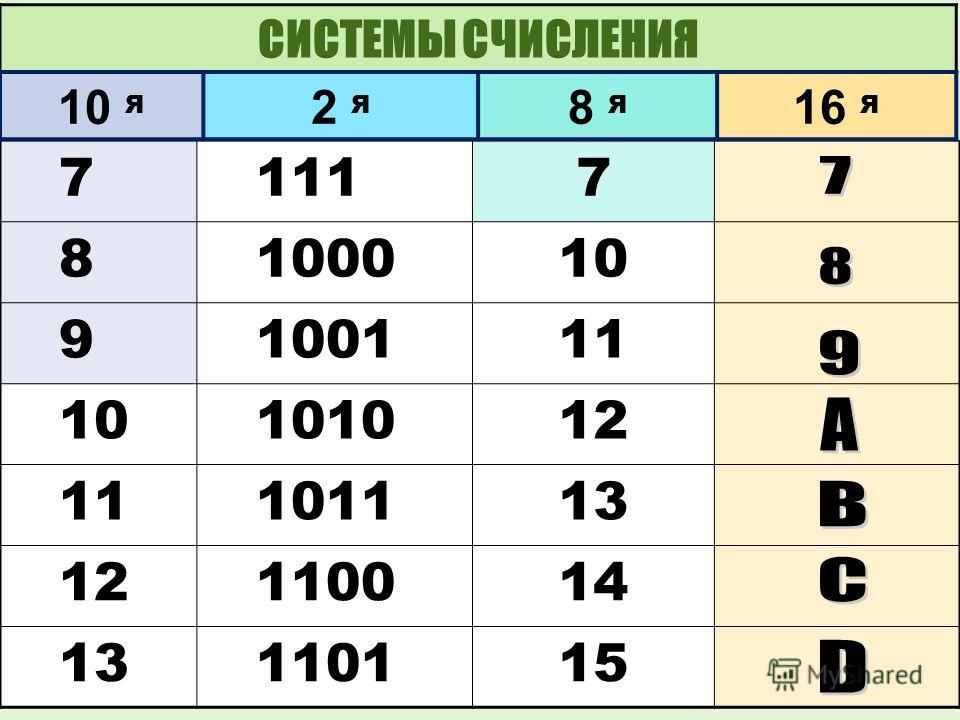
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
n (степень) | |||||||
Пример. Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6.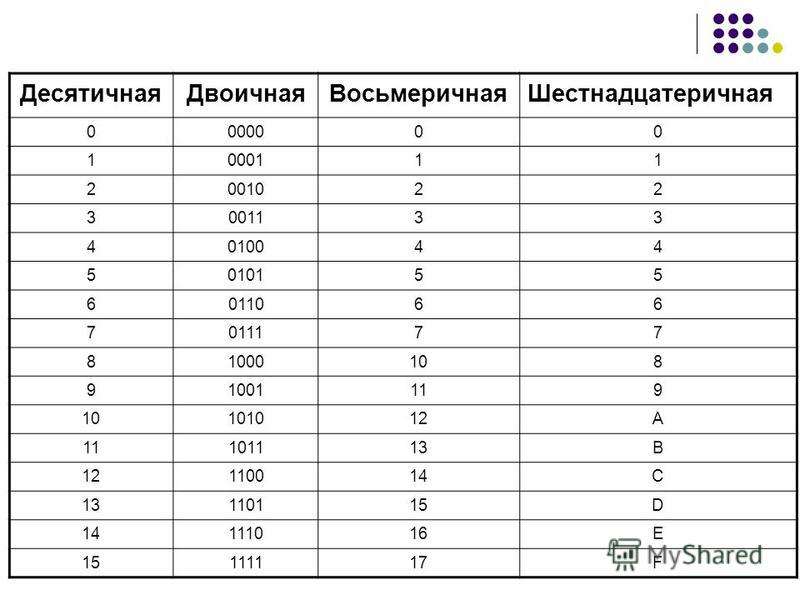 Степени числа 16
Степени числа 16
n (степень) | |||||||
Пример. Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
Сдающим ЕГЭ и не только…
Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую. Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке.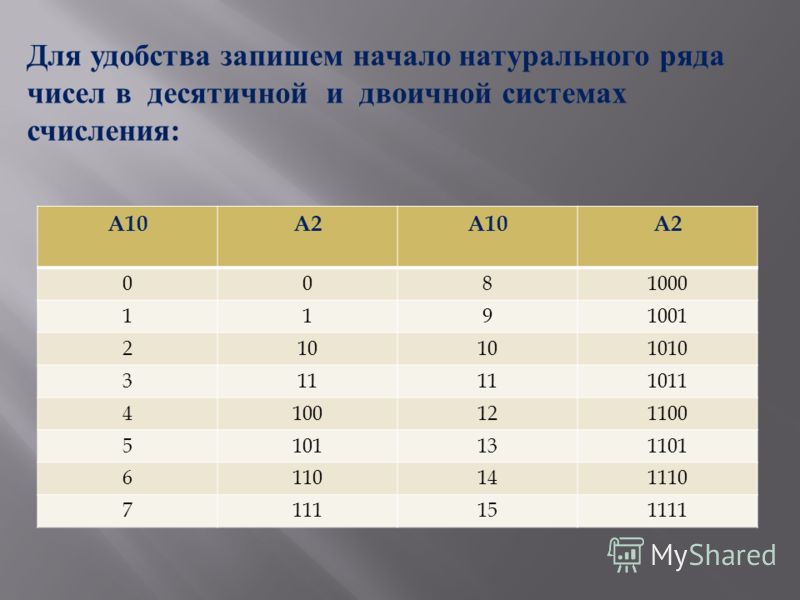
Например, нужно перевести число 810 10 в двоичную систему:
Результат записываем в обратном порядке снизу вверх. Получается 81010 = 11001010102
Если нужно переводить в двоичную систему довольно большие числа, то лестница делений приобретает размер многоэтажного дома. И как тут собрать все единички с нулями и ни одной не пропустить?
В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.
Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.
Таблица степеней числа 2:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 | 2 8 | 2 9 | 2 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Она легко получается умножением предыдущего числа на 2. Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.
Перевод целых чисел
Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 810 10 . Нам нужно разложить это число на слагаемые, равные степеням двойки.
- Ищем ближайшую к 810 степень двойки, не превосходящую его. Это 2 9 = 512.
- Вычитаем 512 из 810, получаем 298.
- Повторим шаги 1 и 2, пока не останется 1 или 0.
- У нас получилось так: 810 = 512 + 256 + 32 + 8 + 2 = 2 9 + 2 8 + 2 5 + 2 3 + 2 1 .
Далее есть два способа, можно использовать любой из них. Как легко увидеть, что в любой системе счисления её основание всегда 10. Квадрат основания всегда будет 100, куб 1000. То есть степень основания системы счисления — это 1 (единица), и за ней столько нулей, какова степень.
Способ 1 : Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Итак, мы получили двоичное представление числа 810 10 = 1100101010 2
. Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Способ 2 : Распишем слагаемые как степени двойки друг под другом, начиная с большего.
810 =
А теперь сложим эти ступеньки вместе, как складывают веер: 1100101010 .
Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».
Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.
Теперь пример попроще.
Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 (квадрат 5). Куб (125) будет уже много. То есть 63 лежит между квадратом 5 и кубом. Тогда подберем коэффициент для 5 2 . Это 2.
Получаем 63 10 = 50 + 13 = 50 + 10 + 3 = 2 * 5 2 + 2 * 5 + 3 = 223 5 .
Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Переведем в двоичную систему число 547 8 .
| 547 8 = | 101 | 100 | 111 |
| 5 | 4 | 7 |
Ещё одно, например 7D6A 16 .
| 7D6A 16 = | (0)111 | 1101 | 0110 | 1010 |
| 7 | D | 6 | A |
Переведем в 16-ричную систему число 7368. Сначала цифры запишем тройками, а потом поделим их на четверки с конца:
736 8 = 111 011 110 = 1 1101 1110 = 1DE 16
.
Переведем в 8-ричную систему число C25 16 . Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца:
C25 16 = 1100 0010 0101 = 110 000 100 101 = 6045 8
. Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
E68 16 = 14 * 16 2 + 6 * 16 + 8 = 3688
.
732 8 = 7 * 8 2 + 3*8 + 2 = 474
.
Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
E68 16 = 14 * 16 2 + 6 * 16 + 8 = 3688
.
732 8 = 7 * 8 2 + 3*8 + 2 = 474
.
Перевод отрицательных чисел
Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.
Затем прибавить к результату 1.
Итак, переведем число -79 в двоичную систему. Число займёт у нас один байт.
Переводим 79 в двоичную систему, 79 = 1001111. Дополним слева нулями до размера байта, 8 разрядов, получаем 01001111. Меняем 1 на 0 и 0 на 1. Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001 . Попутно отвечаем на вопрос ЕГЭ «сколько единиц в двоичном представлении числа -79?». Ответ — 4.
Прибавление 1 к инверсии числа позволяет устранить разницу между представлениями +0 = 00000000 и -0 = 11111111. В дополнительном коде они будут записаны одинаково 00000000.
Перевод дробных чисел
Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.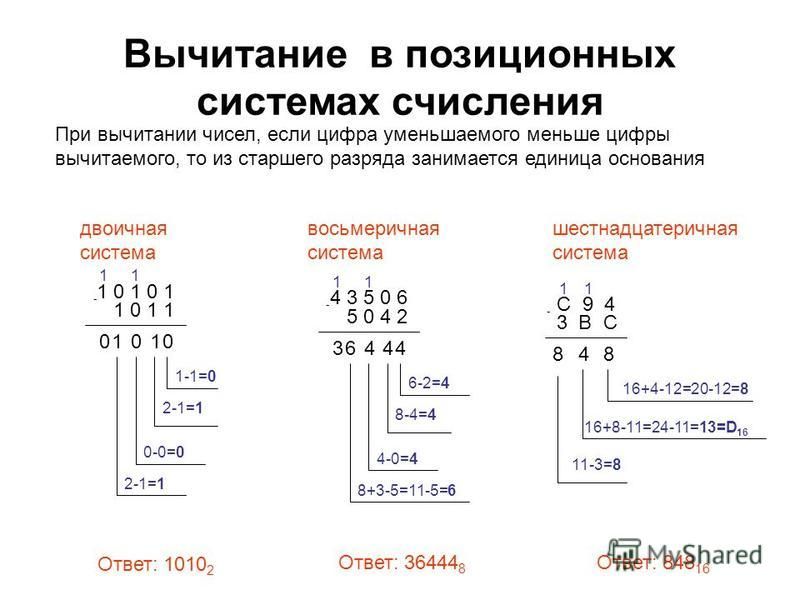
Переведем число 0,6752 в двоичную систему.
| 0 | ,6752 |
| *2 | |
| 1 | ,3504 |
| *2 | |
| 0 | ,7008 |
| *2 | |
| 1 | ,4016 |
| *2 | |
| 0 | ,8032 |
| *2 | |
| 1 | ,6064 |
| *2 | |
| 1 | ,2128 |
Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.
Получается 0,6752 = 0,101011 .
Если число было 5,6752, то в двоичном виде оно будет 101,101011 .
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ.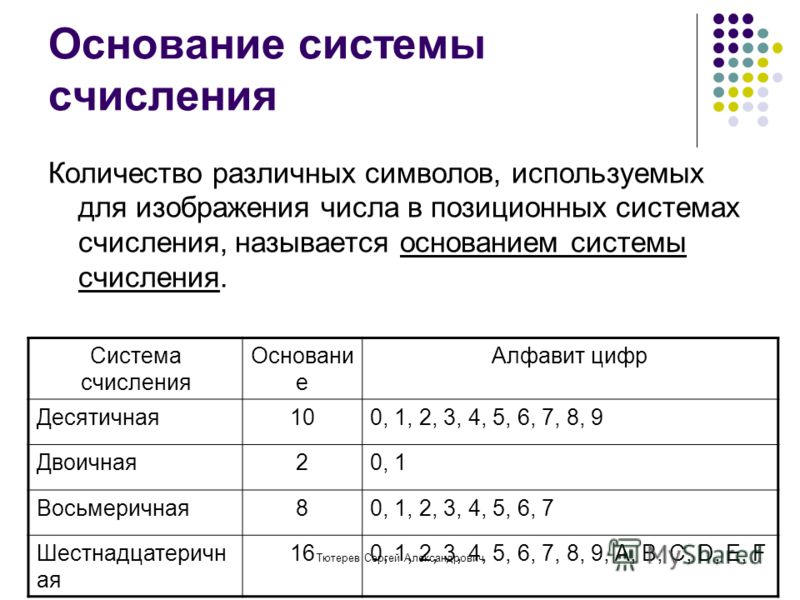 hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.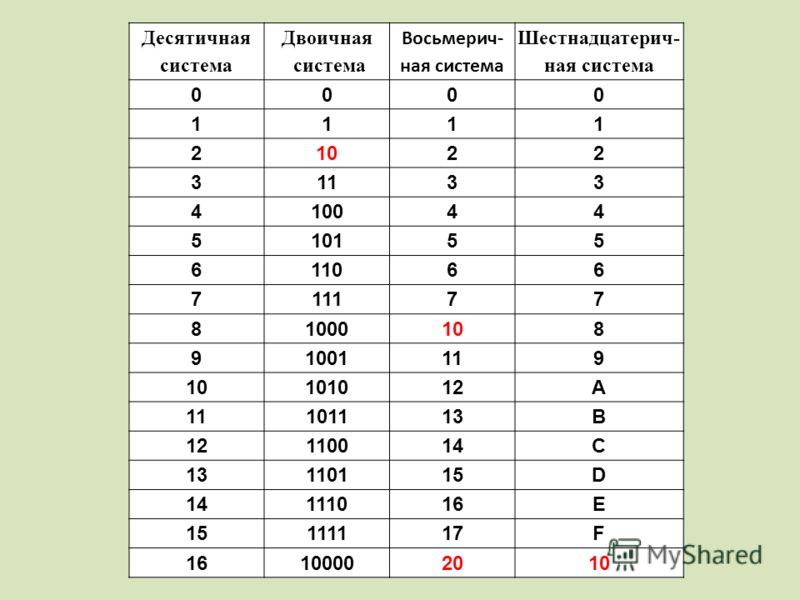
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Двоичная СС | шестнадцатеричная СС |
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры.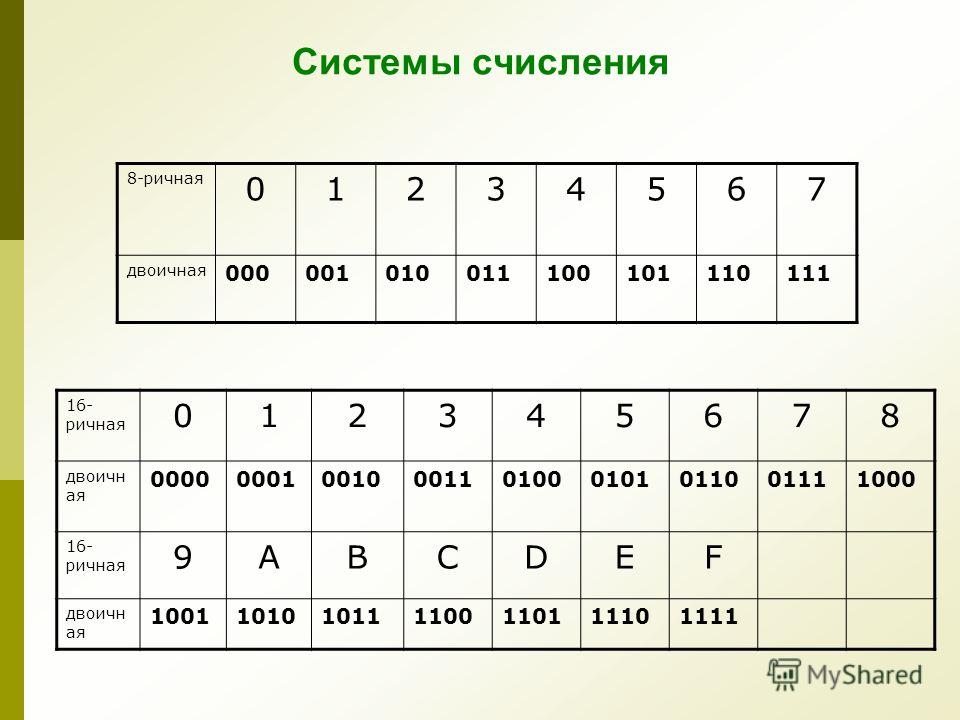 Используя правило, запишем его в виде суммы степеней с основанием 16:
Используя правило, запишем его в виде суммы степеней с основанием 16:
A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
Двоичная СС | Восьмеричная СС |
Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2
Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.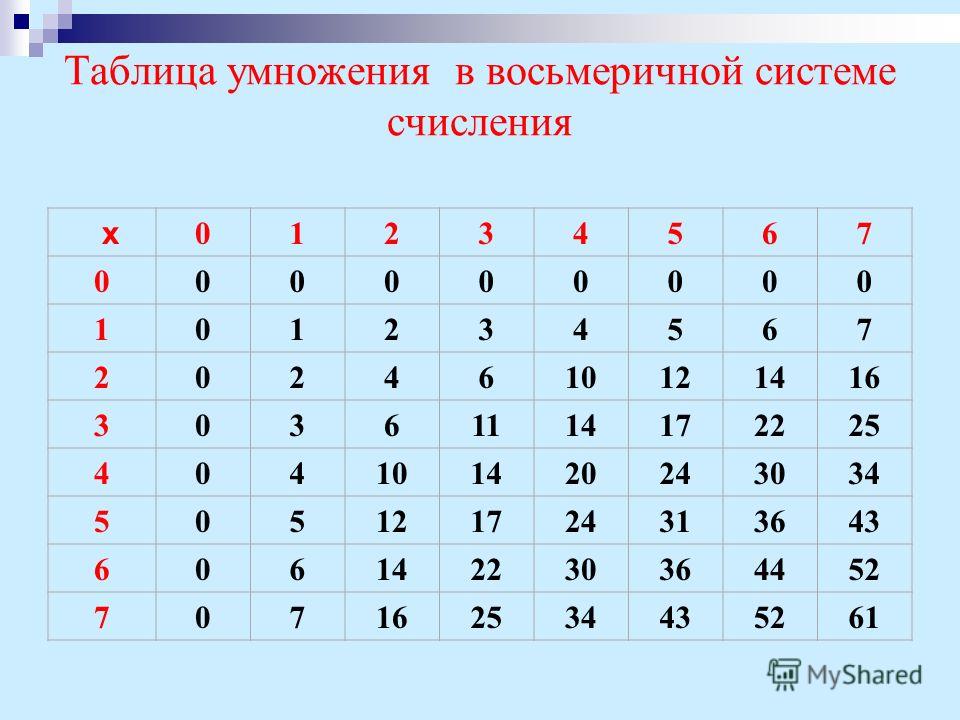
Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.
Системы счисления
Обзор
[Вернитесь к началу страницы]
Эта страница посвящена системам счисления. Вы уже знакомы по крайней мере с одной системой счисления — десятичной системой счисления, которую мы используем каждый день — на работе или когда ходим по магазинам — даже во время отдыха (подумайте о многих играх и спортивных мероприятиях, которые включают хронометраж или подсчет очков). ). На протяжении всей письменной истории возникло множество различных систем счисления. Нас в первую очередь интересуют те, с которыми мы столкнемся в контексте математики, науки и техники.
). На протяжении всей письменной истории возникло множество различных систем счисления. Нас в первую очередь интересуют те, с которыми мы столкнемся в контексте математики, науки и техники.
Существует множество различных систем счисления, основное различие между которыми заключается в количестве используемых символов (называемых основанием или основанием системы счисления). Десятичные числа имеют основание десять , двоичные числа (которые очень важны в вычислениях) имеют основание два , восьмеричные числа имеют основание восемь , а шестнадцатеричные числа имеют основание шестнадцать .
В вычислениях используются двоичные, восьмеричные и шестнадцатеричные числа. Шестнадцатеричные числа особенно важны в области вычислительной техники, потому что они обеспечивают удобный способ выражения двоичных значений. Каждая шестнадцатеричная цифра может использоваться для представления группы из четырех двоичных цифр (или бит ), а пара шестнадцатеричных цифр может использоваться для представления байт (группа из восьми двоичных цифр).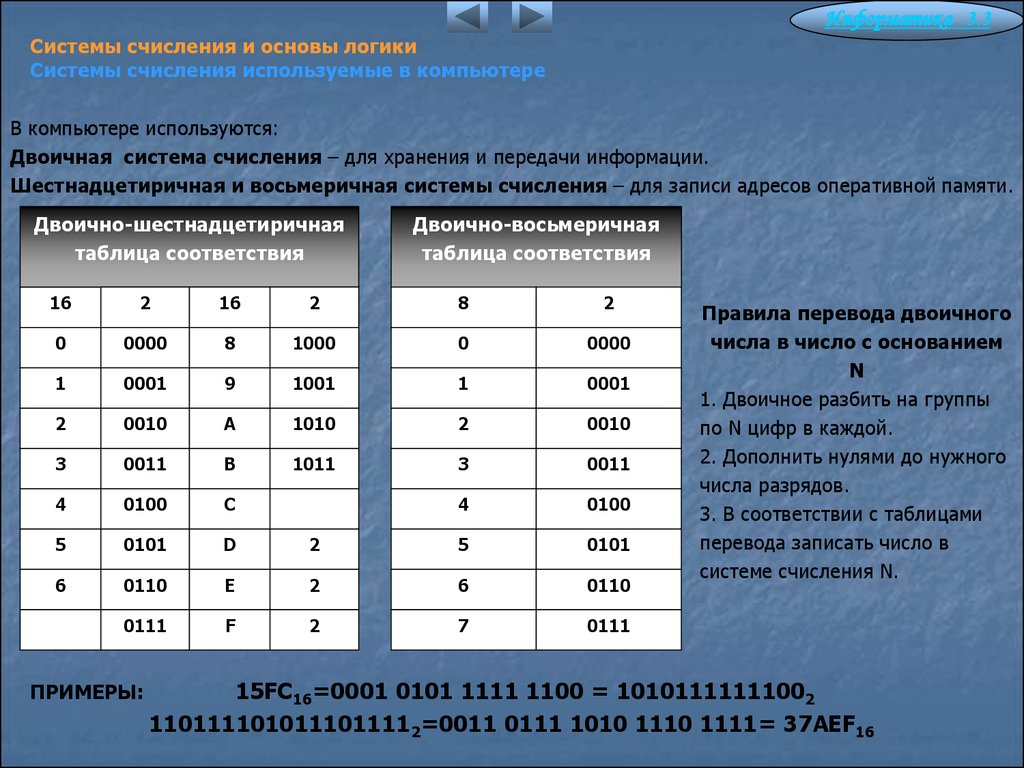
Символы, используемые в большей части западного мира для выражения числовых значений, являются версией индийско-арабской системы счисления, позиционной десятичной системы счисления, разработанной индусскими и индийскими математиками в девятом веке, позже принятой арабскими математиками и распространенной их во многие части Европы. Система имеет десять символов, каждый из которых представляет одно из десяти целых чисел от 0 до 9..
Символы, используемые для представления чисел, важны только в том смысле, что они обеспечивают способ идентификации различных числовых значений для целей передачи их другим. Свойства данной системы счисления зависят только от количества различных используемых символов и от того, является ли система счисления позиционной.
Цифры, используемые в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления, приведены ниже. Обратите внимание, что шестнадцатеричная система счисления использует первые шесть букв алфавита (A-F) для представления чисел 9от 0009 десять до пятнадцать (10-15).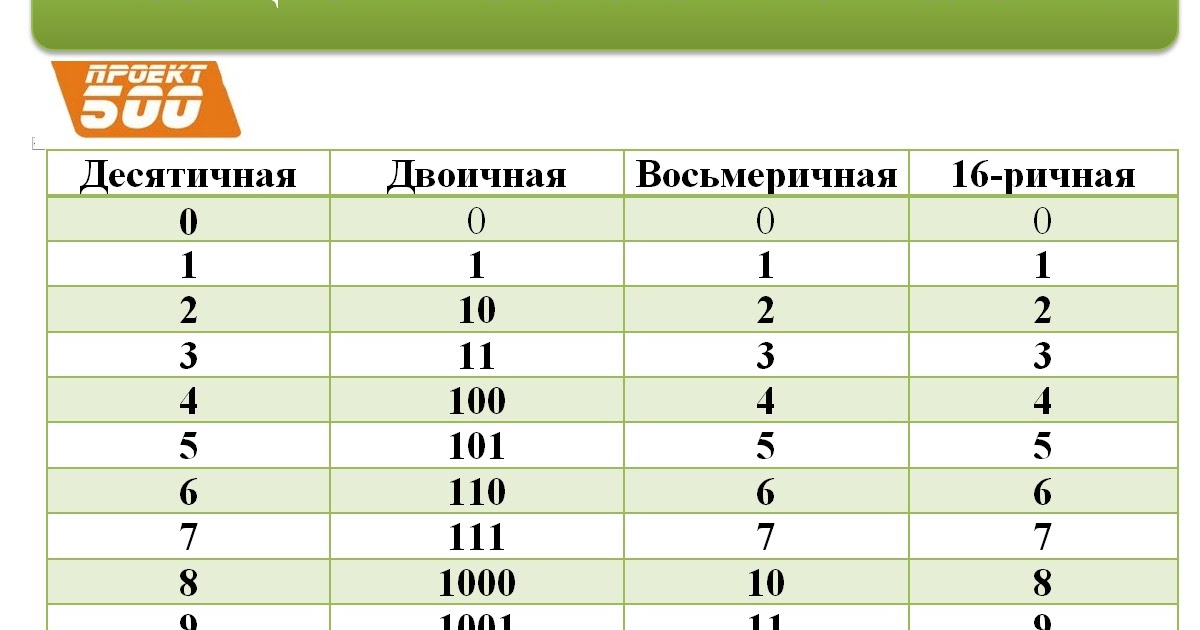
| Система счисления | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Двоичный | 1 | 0 | ||||||||||||||
| Восьмеричный | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||||
| Десятичный | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||
| Десятичный | Ф | Э | Д | С | Б | А | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Десятичные числа
[Вернитесь к началу страницы]
Принято считать, что использование системы счисления, основанной на десяти символах (десятичная система счисления ), основано на том факте, что древний человек сначала научился считать, используя пальцы обеих рук, что позволило им считать до десять с относительной легкостью.
Интересующие нас системы счисления (включая знакомую большинству из нас десятичную систему счисления) являются позиционными системами. Рассмотрим в качестве примера число 123,456. Число число с плавающей запятой , т. е. оно имеет дробную часть, представленную цифрами, которые появляются справа от десятичной точки (термин «с плавающей запятой» просто означает, что десятичная точка (или точка счисления ) может быть размещена где угодно относительно до значащих цифр числа).
Цифра в первой позиции перед запятой (3) представляет собой значение 3×10 0 (три умножить на десять в нулевой степени), что равняется трем, поскольку любое число в нулевой степени равно единице. Цифра во второй позиции слева от десятичной точки (2) представляет значение 2×10 1 , или 20 (любое число в степени единицы само по себе). Число в третьей позиции слева от десятичной точки (1) представляет значение 1×10 2 , или сто.
Каждое числительное в десятичном числе должно быть умножено на десять в степени, которая зависит от положения числительного в числе относительно десятичной точки, отделяющей целую часть числа от дробной части (если она есть). Позиция важна, потому что она указывает величина значения, представленного каждой цифрой. Три цифры справа от запятой в приведенном выше примере (4, 5 и 6) представляют значения 4×10 -1 , 5×10 -2 и 6×10 -3 соответственно.
Восьмеричные числа
[Вернитесь к началу страницы]
Восьмеричная система счисления, как следует из названия, имеет основание восемь (8). В нем используются те же первые восемь цифр, что и в десятичной системе счисления (от 0 до 7). Восьмеричная система счисления больше не используется широко в вычислительной технике (или где-либо еще в этом отношении), но когда-то она была популярна, потому что все восьмеричные цифры можно было представить с помощью всего трех битов.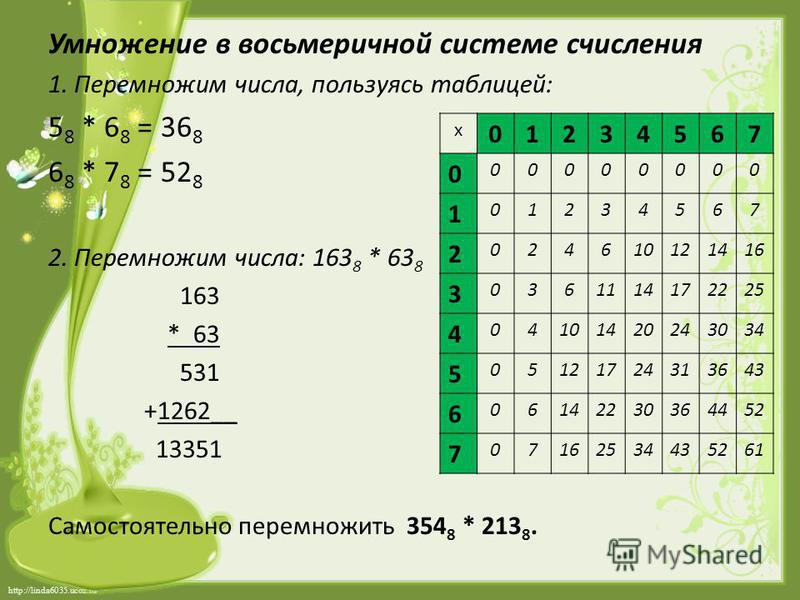
Некоторые ранние системы мэйнфреймов и миникомпьютеров были построены на базе тридцатишестибитной архитектуры. Восьмеричное число часто использовалось для хранения цифровой информации, потому что группы из трех битов довольно хорошо вписывались в 36-битное слово. Восьмеричные цифры и их двоичные представления показаны ниже.
0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111
Подобно шестнадцатеричной и двоичной системам счисления, используемым в современных компьютерах, восьмеричные числа часто требовались для представления десятичных значений. Выше мы видели, что представляет собой число 123,456 в десятичной системе счисления. Каждая цифра представляет собой степень, кратную десяти, в зависимости от ее положения относительно точки счисления. Что представляла бы та же самая последовательность чисел, если бы вместо десятичной системы счисления мы использовали восьмеричную систему счисления? Давай выясним.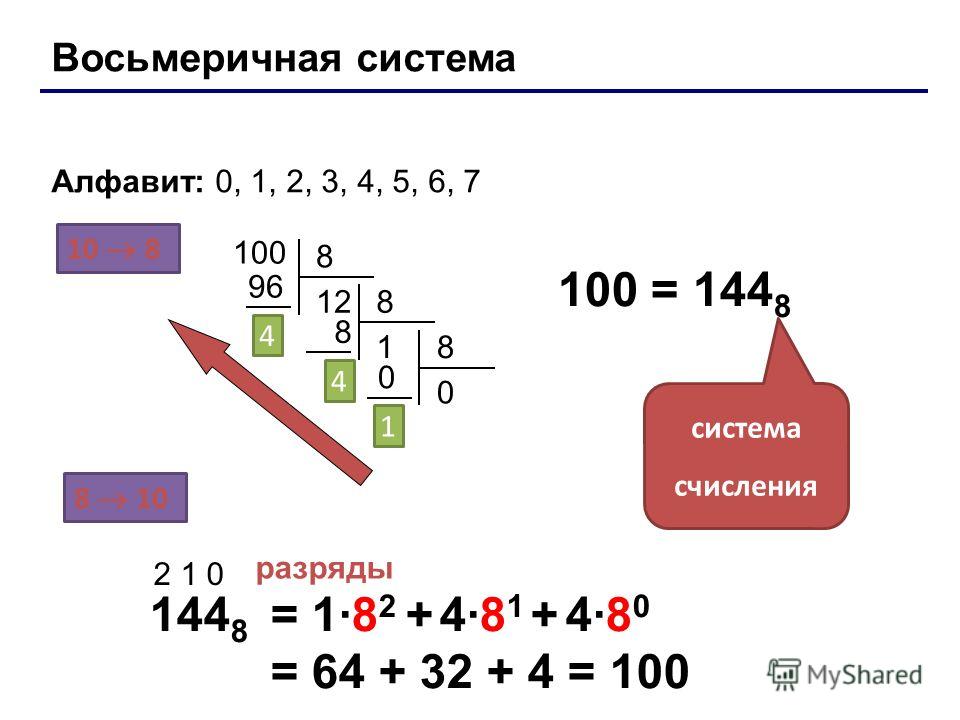
Чтобы преобразовать это значение в его десятичный эквивалент, нам нужно сложить значения цифр:
123.456 8 = 1 × 8 2 + 2 × 8 1 + 3 × 8 0 + 4 × 8 -1 + 5 × 8 -2 + 6 × 8 -3
123,456 8 = 64 + 16 + 3 + 0,5 + 0,078125 + 0,01171875
Как видите, эта последовательность цифр представляет совсем другое значение в восьмеричной системе. Обратите внимание, что когда мы пишем десятичное число, мы обычно не указываем явно, что это десятичное число. Однако при записи чисел в других системах счисления иногда рекомендуется указывать используемую систему счисления, чтобы избежать путаницы. Мы можем сделать это, добавив индекс после числа следующим образом:
123,456 8
Мы видели, что преобразование чисел из восьмеричных в десятичные относительно просто.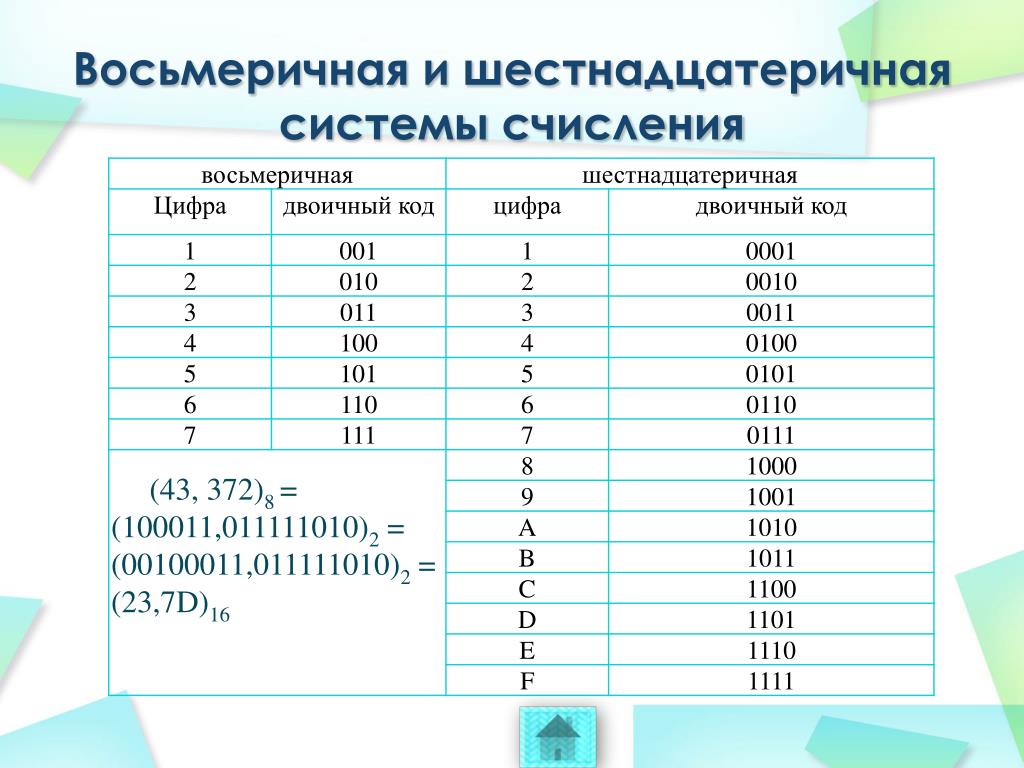 Преобразование чисел из восьмеричных в двоичные еще проще. Мы видели, что каждая цифра восьмеричного числа умножается на степень восьмерки, а восемь равняется двум в степени три:
Преобразование чисел из восьмеричных в двоичные еще проще. Мы видели, что каждая цифра восьмеричного числа умножается на степень восьмерки, а восемь равняется двум в степени три:
8 = 2 3
Каждая дополнительная цифра при движении справа налево в двоичном числе представляет собой последовательную степень двойки. Точно так же каждая дополнительная цифра при движении справа налево в восьмеричном числе представляет собой последовательную степень числа восемь. Это означает, что сдвиг на одну позицию влево в восьмеричном числе эквивалентен сдвигу на три позиции влево в двоичном числе.
Значение может быть неочевидным сразу — возможно, вам придется подумать об этом некоторое время. Важно понимать, что для преобразования восьмеричного числа в его двоичный эквивалент мы просто заменяем каждую восьмеричную цифру тремя двоичными цифрами, которые ее представляют (мы видели их в списке выше). Преобразуем восьмеричное число 123. 456 в двоичное:
456 в двоичное:
Следовательно:
123,456 8 = 1010011.10010111 2
Обратите внимание, что мы удалили два начальных нуля и последний ноль из двоичного результата. Вы должны увидеть, что обратный процесс (преобразование двоичных чисел в их восьмеричное представление) — это просто замена каждой группы из трех двоичных цифр ее восьмеричным представлением. Преобразуем двоичное число 111110101.10001101 в восьмеричное:
Следовательно:
111110101.10001101 2 = 765,432 8
Единственное, с чем вам нужно быть осторожным, — это убедиться, что вы разбиваете двоичное число на правильные группы из трех цифр (при необходимости добавьте начальные или конечные нули, чтобы завершить левую и крайнюю правую группы двоичных цифр.
Преобразование восьмеричных чисел в шестнадцатеричные не может быть выполнено напрямую — это двухэтапный процесс.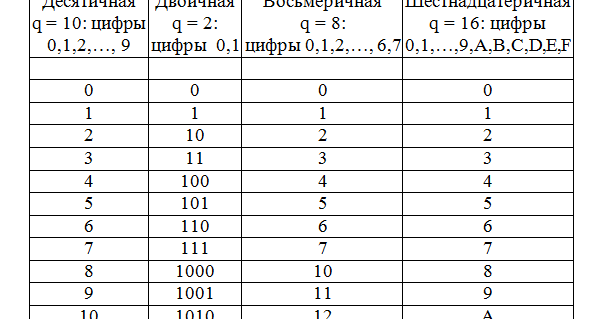 Первым шагом является преобразование восьмеричного числа в его десятичный эквивалент, как показано выше. Второй шаг — преобразовать полученное десятичное число в шестнадцатеричное (см. ниже).
Первым шагом является преобразование восьмеричного числа в его десятичный эквивалент, как показано выше. Второй шаг — преобразовать полученное десятичное число в шестнадцатеричное (см. ниже).
Шестнадцатеричные числа
[Вернитесь к началу страницы]
Шестнадцатеричная система счисления (или основание шестнадцать) представляет собой позиционную систему счисления, которая представляет числовые значения с использованием шестнадцати символов — от 0 до 9 для значений от нуля до девяти и A, B, C, D, E и F для представления чисел. от десяти до пятнадцати. По этой причине говорят, что его основание равно шестнадцати. Шестнадцатеричные числа выражаются в виде последовательности из одной или нескольких шестнадцатеричных цифр, за которыми следует строчная буква «h» или иногда нижний индекс 16, чтобы указать, что они на самом деле являются шестнадцатеричными (с основанием шестнадцать) числами. Вот десятичное число сто шестьдесят пять (165) в виде шестнадцатеричного числа:
A5h
Подобно десятичной системе, с которой мы знакомы, положение каждой цифры в шестнадцатеричном числе определяет его значение.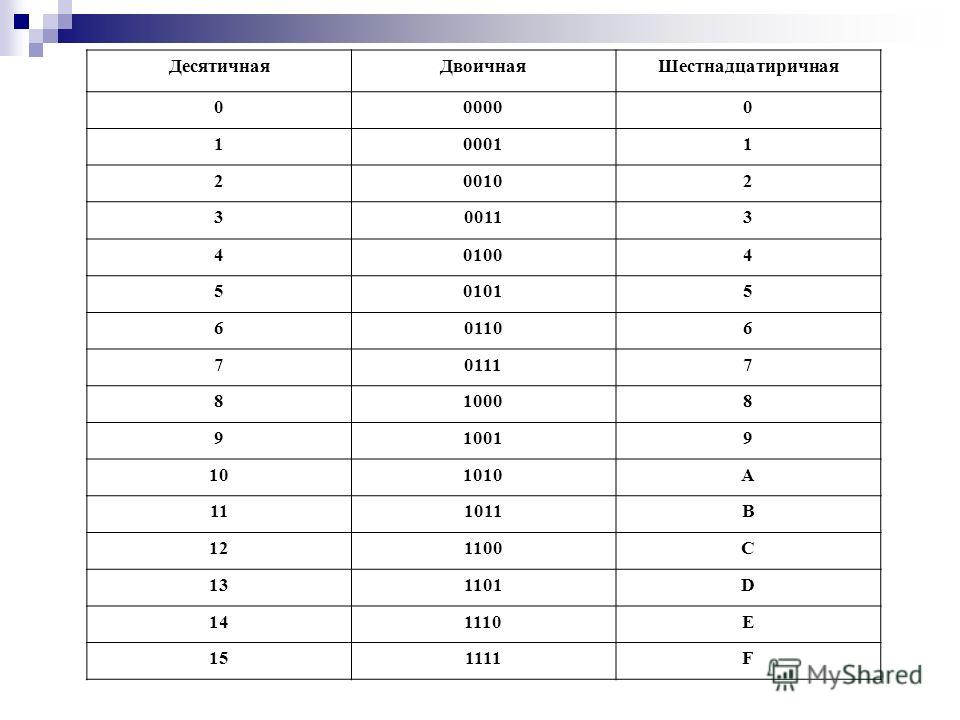 В то время как каждая позиция в десятичном числе представляет некоторую степень числа десять, каждая позиция в шестнадцатеричном числе представляет степень шестнадцати. В таблице ниже показаны числа от 0 до 63 (с основанием десять) в виде шестнадцатеричных чисел.
В то время как каждая позиция в десятичном числе представляет некоторую степень числа десять, каждая позиция в шестнадцатеричном числе представляет степень шестнадцати. В таблице ниже показаны числа от 0 до 63 (с основанием десять) в виде шестнадцатеричных чисел.
| Шестигранник | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Э | Ф |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Декабрь | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Шестигранник | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1А | 1Б | 1С | 1Д | 1Е | 1F |
| Декабрь | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| Шестигранник | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 2А | 2Б | 2С | 2D | 2Э | 2F |
| Декабрь | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| Шестигранник | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 3А | 3Б | 3С | 3D | 3Е | 3F |
| Декабрь | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
Таким образом, десятичное число тридцать девять (39), выраженное в виде шестнадцатеричного числа (27h), равно:
2 × 16 1 + 7 × 16 0 = 32 + 7 = 39
Шестнадцатеричная цифра в самой правой позиции любого шестнадцатеричного целого числа содержит наименьшее значение (с максимальным значением пятнадцать).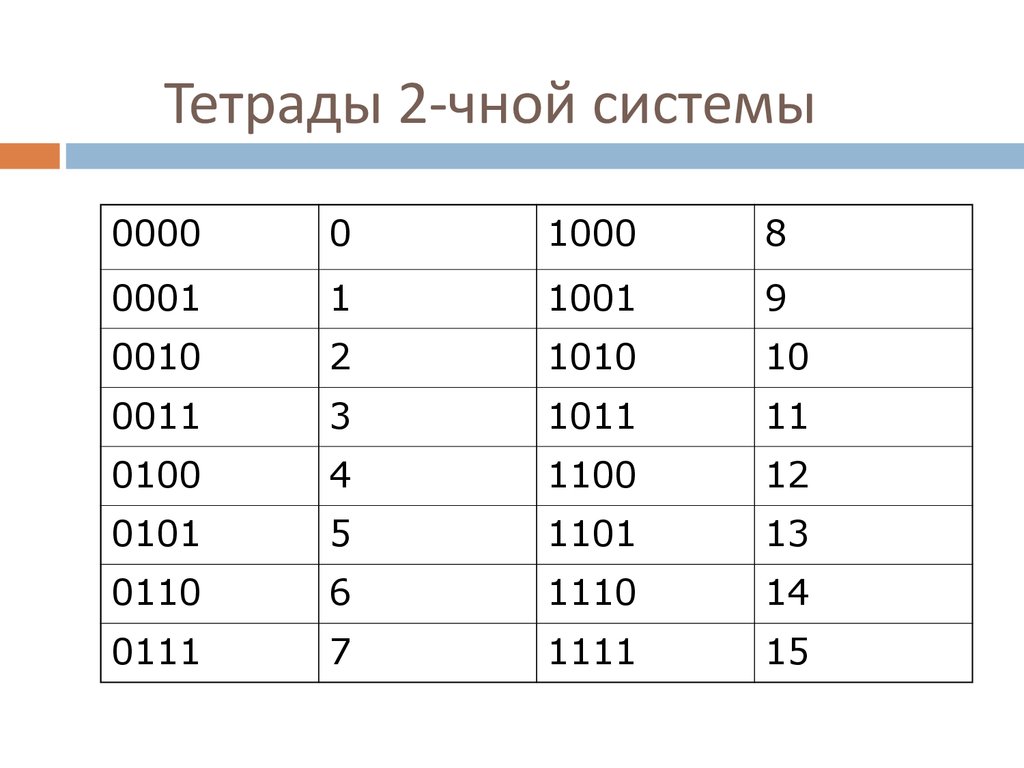 Крайняя левая шестнадцатеричная цифра имеет максимальное значение, отражающее ее позицию относительно самой правой цифры, и будет кратна некоторой степени шестнадцати больше нуля. Значение самой левой шестнадцатеричной цифры (при условии, что мы игнорируем начальные нули) всегда превышает общее значение всех цифр справа от нее. По этой причине общая Величина шестнадцатеричного числа всегда определяется положением самой левой цифры.
Крайняя левая шестнадцатеричная цифра имеет максимальное значение, отражающее ее позицию относительно самой правой цифры, и будет кратна некоторой степени шестнадцати больше нуля. Значение самой левой шестнадцатеричной цифры (при условии, что мы игнорируем начальные нули) всегда превышает общее значение всех цифр справа от нее. По этой причине общая Величина шестнадцатеричного числа всегда определяется положением самой левой цифры.
Дроби также могут быть представлены с помощью шестнадцатеричных цифр, как и действительные (дробные) числа. Как и действительные числа с основанием десять, дробная часть шестнадцатеричного числа следует за точкой. В десятичной системе счисления мы называем это десятичной точкой. В шестнадцатеричной системе счисления мы называем это шестнадцатеричной точкой .
В десятичной системе число, стоящее в первой позиции после запятой, умножается на 10 9.0217 -1 (0,1), цифра во втором разряде после запятой умножается на 10 -2 (0,01) и так далее. Дробная часть шестнадцатеричного числа работает по тому же принципу, за исключением того, что цифра в первой позиции после двоичной точки умножается на 16 -1 (0,0625 по основанию десяти), цифра во второй позиции после двоичной точки умножается на 16 -2 (0,003 с основанием десять) и так далее.
Дробная часть шестнадцатеричного числа работает по тому же принципу, за исключением того, что цифра в первой позиции после двоичной точки умножается на 16 -1 (0,0625 по основанию десяти), цифра во второй позиции после двоичной точки умножается на 16 -2 (0,003 с основанием десять) и так далее.
Обратите внимание, что в то время как каждая последующая положительная степень числа шестнадцать имеет в шестнадцать раз большее значение предыдущей, каждая последующая отрицательная степень числа шестнадцать имеет один шестнадцатый значение своего предшественника. Анатомия реального шестнадцатеричного числа показана ниже.
Анатомия реального шестнадцатеричного числа
Поскольку так легко представить группы из четырех двоичных цифр с помощью шестнадцатеричных цифр, шестнадцатеричная система счисления часто используется для представления двоичных значений в области вычислительной техники и цифровой электроники.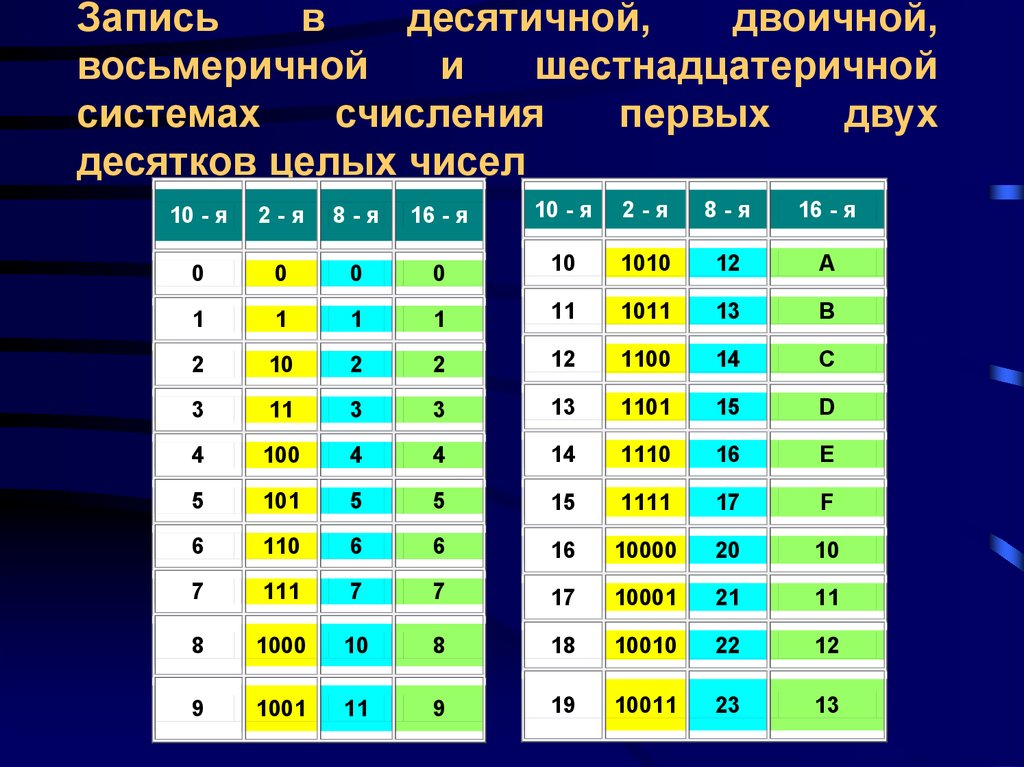 Значения байтов, которые могут представлять десятичные числа в диапазоне от 0 до 255, часто выражаются с помощью пары шестнадцатеричных цифр в диапазоне от 00h до FFh. Шестнадцатеричные числа также обычно используются для представления адресов памяти в программах на ассемблере.
Значения байтов, которые могут представлять десятичные числа в диапазоне от 0 до 255, часто выражаются с помощью пары шестнадцатеричных цифр в диапазоне от 00h до FFh. Шестнадцатеричные числа также обычно используются для представления адресов памяти в программах на ассемблере.
Двоичные числа
[Вернитесь к началу страницы]
Важность двоичной системы счисления, которая, как следует из названия, имеет только два символа (0 и 1), заключается в том, что это единственная система счисления, которую современные цифровые компьютеры действительно «понимают». Следует помнить, что в основе этих устройств лежит центральный процессор (ЦП), который по сути является конечным автоматом, состоящим из транзисторов и микросхем, который обеспечивает сотни миллионов взаимосвязанных высокоскоростных переключателей. Состояние каждого отдельного переключателя может быть включено или выключено, поэтому каждый переключатель может представлять только единицу или ноль.
Хотя компьютеры могут обрабатывать огромные объемы данных и выполнять миллионы вычислений в секунду, базовые машинные операции, обеспечивающие это, основаны на манипулировании двоичными значениями с использованием различных типов логических схем. Даже данные, хранящиеся в оперативной памяти (ОЗУ) и на магнитных или оптических дисках, физически хранятся в виде двоичных данных — миллиардов отдельных двоичных цифр («битов»), имеющих значение 0 или 1.
В то время как целые значения в других системах счисления могут быть точно представлены с помощью двоичной системы счисления, многие действительные числа (с дробными значениями) не могут. Таким образом, такие значения аппроксимируются, хотя достигаемая степень точности увеличивается с количеством битов, используемых в их представлении, за счет увеличения объема памяти в рабочей памяти или на диске.
Поскольку двоичная (или с основанием два) система счисления представляет числовые значения, используя всего два символа (0 и 1), говорят, что она имеет основание из двух.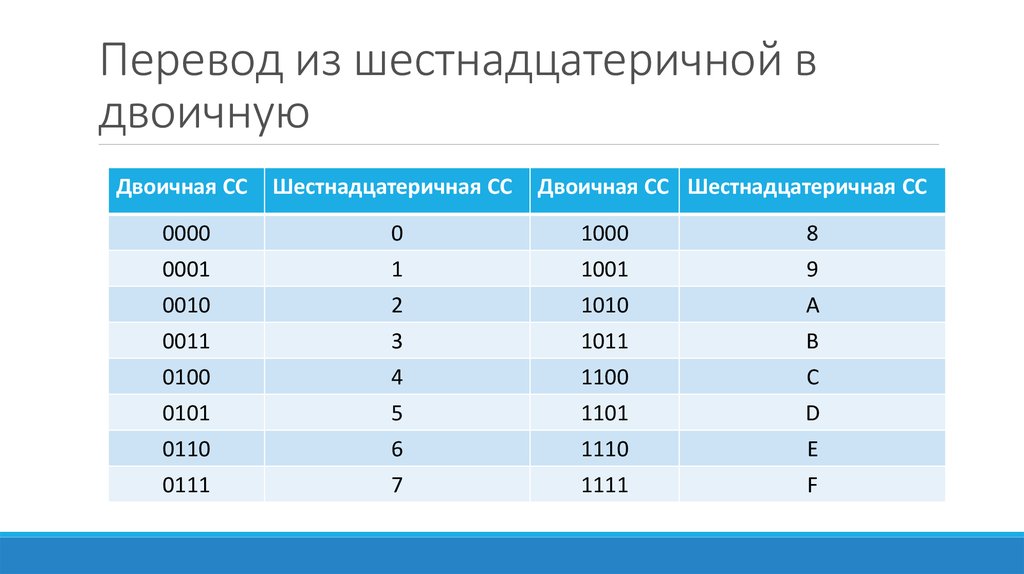 Двоичные числа выражаются в виде последовательности двоичных цифр, за которыми иногда следует цифра 2 в нижнем индексе, чтобы указать, что они на самом деле являются двоичными числами. Вот десятичное число сто семьдесят (170) в виде двоичного числа:
Двоичные числа выражаются в виде последовательности двоичных цифр, за которыми иногда следует цифра 2 в нижнем индексе, чтобы указать, что они на самом деле являются двоичными числами. Вот десятичное число сто семьдесят (170) в виде двоичного числа:
10101010 2
Подобно десятичной системе, с которой мы знакомы, положение каждой цифры в двоичном числе определяет его значение. В то время как каждая позиция в десятичном числе представляет некоторую степень числа десять, каждая позиция в двоичном числе представляет степень двойки. В таблице ниже показаны числа от 0 до 15 (с основанием десять) в виде 4-битных двоичных чисел (пятнадцать — это наибольшее число, которое может быть выражено четырьмя двоичными цифрами).
| Двоичный | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Декабрь | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| Двоичный | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | ||||||||
| Декабрь | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||||||
Десятичное число 13 будет выражено в виде двоичного числа следующим образом:
1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 8 + 4 + 0 + 1 = 13
Двоичная цифра в самой правой позиции любого двоичного целого числа имеет наименьшее значение (с максимальным значением, равным единице) и иногда называется младшим значащим битом (LSB).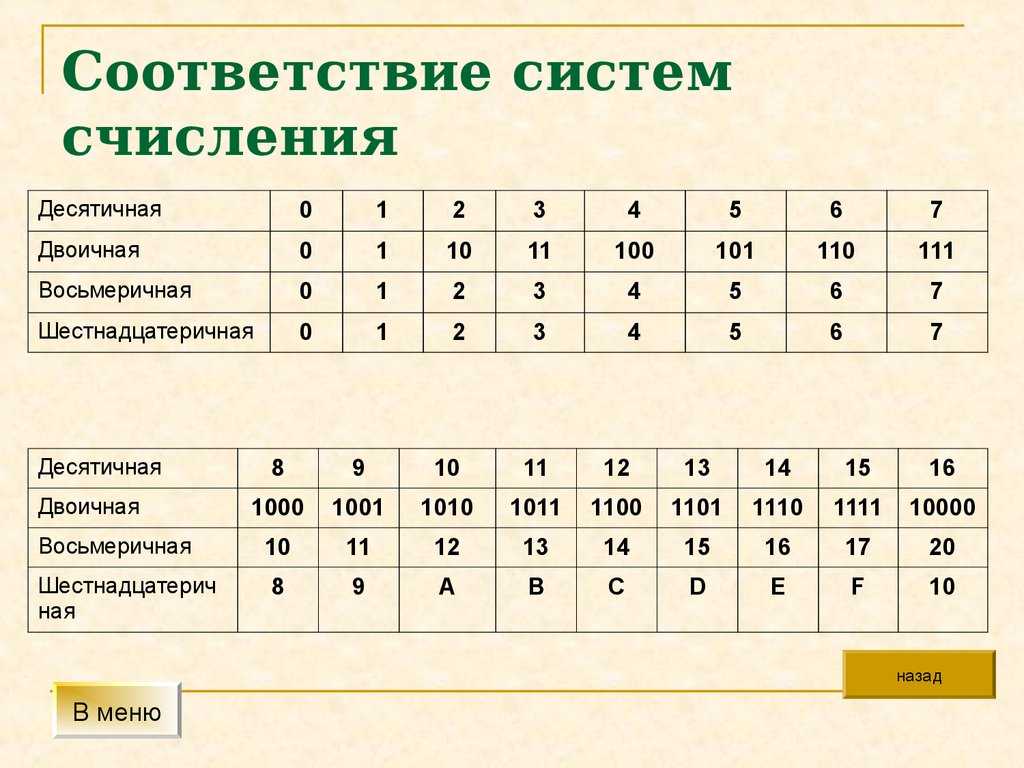 Крайняя левая двоичная цифра имеет максимальное значение, отражающее ее положение относительно младшего бита, и будет иметь степень двойки, большую нуля.
Крайняя левая двоичная цифра имеет максимальное значение, отражающее ее положение относительно младшего бита, и будет иметь степень двойки, большую нуля.
Самая левая двоичная цифра (при условии, что мы игнорируем начальные нули) иногда называют старшим битом (MSB), и ее значение всегда превышает объединенное значение всех битов справа от нее. По этой причине общая величина двоичного числа всегда определяется положением самого левого (ненулевого) бита.
Дроби также могут быть представлены с помощью двоичных цифр, как и действительные (дробные) числа. Как и действительные числа с основанием десять, дробная часть двоичного числа следует за точкой счисления. В десятичной системе счисления мы называем это десятичной точкой, но в двоичной системе счисления мы называем это 9.0009 двоичная точка .
В десятичной системе число в первой позиции после запятой умножается на 10 -1 (0,1), цифра во второй позиции после запятой умножается на 10 -2 (0,01) и скоро. Дробная часть двоичного числа работает по тому же принципу, за исключением того, что цифра в первой позиции после двоичной точки умножается на 2 -1 (0,5 по основанию десяти), цифра во второй позиции после двоичной точки умножается на 2 -2 (0,25 по основанию десяти) и так далее.
Дробная часть двоичного числа работает по тому же принципу, за исключением того, что цифра в первой позиции после двоичной точки умножается на 2 -1 (0,5 по основанию десяти), цифра во второй позиции после двоичной точки умножается на 2 -2 (0,25 по основанию десяти) и так далее.
Обратите внимание, что, хотя каждая последующая положительная степень двойки имеет удвоенное значение предыдущей, каждая последующая отрицательная степень двойки имеет половину значения предыдущей. Анатомия реального двоичного числа показана ниже.
Анатомия реального двоичного числа
Из вышеизложенного видно, что преобразовать двоичные числа в десятичные относительно просто. Просто сложите степени двойки, представленные каждой двоичной цифрой (это работает для двоичных целых чисел, дробей и действительных чисел).
Почти столь же очевидным, если подумать, является тот факт, что точность, с которой действительные числа и дроби (с основанием десять) могут быть преобразованы в двоичные, часто зависит от количества битов, доступных для представления дробной части числа.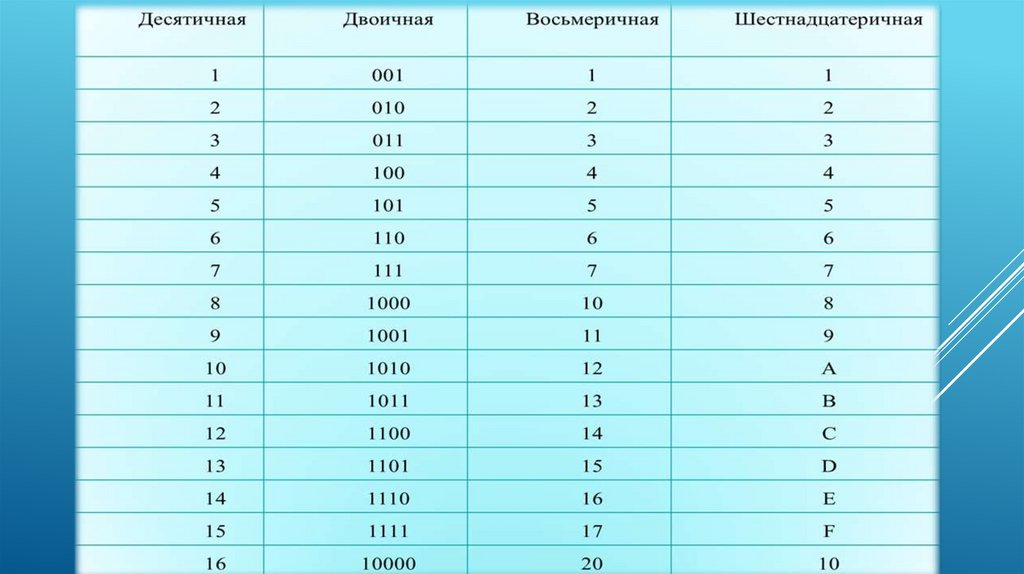 Чем больше количество используемых битов, тем более точным будет результат (с точки зрения вычислений, большая точность соответствует большему объему памяти, необходимому для хранения результата).
Чем больше количество используемых битов, тем более точным будет результат (с точки зрения вычислений, большая точность соответствует большему объему памяти, необходимому для хранения результата).
Преобразование двоичных чисел в шестнадцатеричные еще проще и позволяет нам представлять двоичные значения гораздо более удобным для человека способом. Мы уже видели таблицу, содержащую десятичные целые (целые числа) значения от нуля до пятнадцати (0–15) и их двоичные эквиваленты. Давайте теперь посмотрим на двоичные эквиваленты шестнадцати цифр, используемых в шестнадцатеричной системе счисления (0–9)., А–Ф):
| Двоичный | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестигранник | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| Двоичный | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | ||||||||
| Шестигранник | 8 | 9 | А | Б | С | Д | Э | Ф | ||||||||
Мы видели, что каждая цифра в шестнадцатеричном числе умножается на шестнадцатую степень, а шестнадцать равна двум в степени четыре:
16 = 2 4
Каждая дополнительная цифра при движении справа налево в двоичном числе представляет собой последовательную степень двойки. Точно так же каждая дополнительная цифра при движении справа налево в шестнадцатеричном числе представляет собой последовательную степень шестнадцати. Это означает, что сдвиг на одну позицию влево в шестнадцатеричном числе эквивалентен сдвигу на четыре позиции влево в двоичном числе.
Точно так же каждая дополнительная цифра при движении справа налево в шестнадцатеричном числе представляет собой последовательную степень шестнадцати. Это означает, что сдвиг на одну позицию влево в шестнадцатеричном числе эквивалентен сдвигу на четыре позиции влево в двоичном числе.
Значение может быть неочевидным сразу — возможно, вам придется подумать об этом некоторое время. Важно понимать, что для преобразования двоичного числа в его шестнадцатеричный эквивалент достаточно просто заменить каждую группу из четырех двоичных цифр ее шестнадцатеричным представлением. Преобразуем двоичное число 110111110101.100011010011 в шестнадцатеричное:
Следовательно:
110111110101.100011010011 2 = DF5.8D3h
Единственное, с чем вам нужно быть осторожным, — это убедиться, что вы разбиваете двоичное число на правильные группы из четырех цифр (при необходимости добавьте начальные или конечные нули, чтобы завершить левую и крайнюю правую группы двоичных цифр. Кстати). , если вы хотите проверить любой из примеров преобразования, приведенных на этой странице, вы можете найти удобный онлайн-инструмент преобразования здесь:
Кстати). , если вы хотите проверить любой из примеров преобразования, приведенных на этой странице, вы можете найти удобный онлайн-инструмент преобразования здесь:
Coder’s Toolbox – Преобразование чисел
Преобразование из шестнадцатеричного в двоичное — это просто обратный процесс. Другими словами, мы просто заменяем каждую цифру в шестнадцатеричном числе четырьмя двоичными цифрами, которые ее представляют. После того, как мы выполнили преобразование, мы можем безопасно удалить все нули в начале или в конце. Преобразуем шестнадцатеричное число F08.7A5h в двоичное:
Следовательно:
F08.7A5h = 111100001000.011110100101 2
Десятичное в восьмеричное преобразование
[Вернитесь к началу страницы]
Один из методов, который можно использовать для преобразования десятичного числа в его восьмеричный эквивалент, заключается в выполнении целочисленного деления с использованием восьмерки в качестве делителя.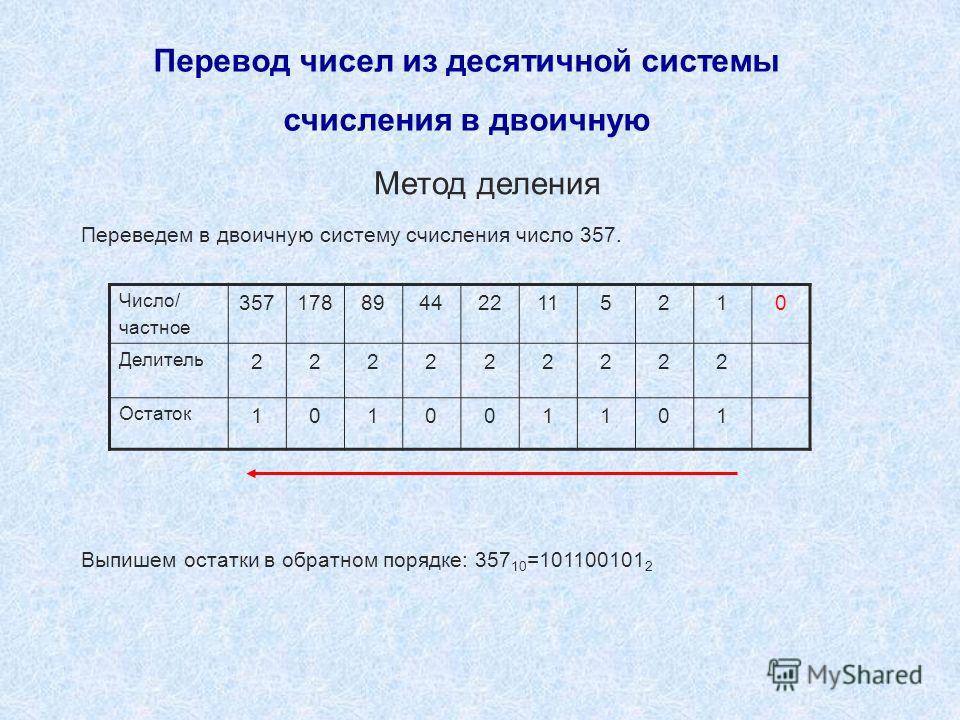 Преобразуемое число делится на восемь, а остаток записывается в крайнем правом положении (в виде восьмеричной цифры). Затем целочисленный результат деления снова делится на восемь, а остаток записывается (снова в виде восьмеричной цифры) слева от восьмеричной цифры, полученной на предыдущем шаге. Этот процесс повторяется до тех пор, пока целочисленный результат деления не станет равным нулю. Пример послужит иллюстрацией процесса. Чтобы преобразовать десятичное число 16,895 в восьмеричное, действуйте следующим образом:
Преобразуемое число делится на восемь, а остаток записывается в крайнем правом положении (в виде восьмеричной цифры). Затем целочисленный результат деления снова делится на восемь, а остаток записывается (снова в виде восьмеричной цифры) слева от восьмеричной цифры, полученной на предыдущем шаге. Этот процесс повторяется до тех пор, пока целочисленный результат деления не станет равным нулю. Пример послужит иллюстрацией процесса. Чтобы преобразовать десятичное число 16,895 в восьмеричное, действуйте следующим образом:
| Integer division | Integer result | Remainder | Octal |
|---|---|---|---|
| 16,895 ÷ 8 | 2,111 | 7 | 7 8 |
| 2,111 ÷ 8 | 263 | 7 | 7 8 |
| 263 ÷ 8 | 32 | 7 | 7 8 |
| 32 ÷ 8 | 4 | 0 | 0 8 |
| 4 ÷ 8 | 0 | 4 | 4 8 |
Следовательно:
16 895 10 = 40777 8
Мы можем выполнить относительно простой процесс — тот, который мы уже видели, — преобразовать число обратно в десятичное (и в то же время подтвердить, что полученный ответ правильный).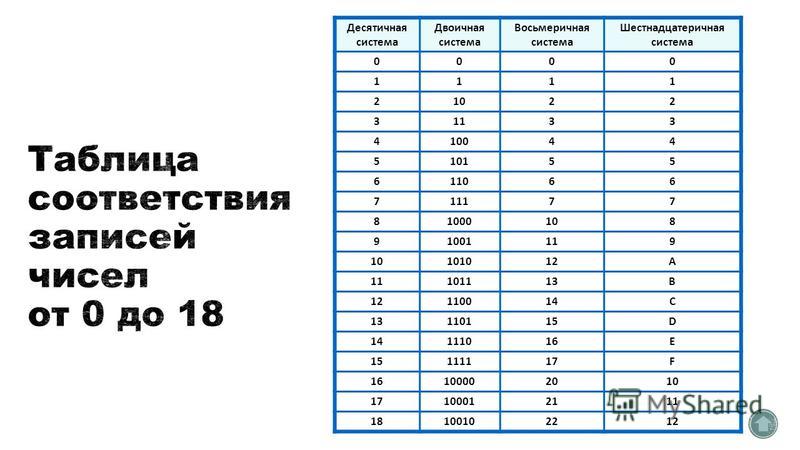 Просто умножьте каждую шестнадцатеричную цифру на соответствующую степень шестнадцати и сложите полученные десятичные значения вместе следующим образом:
Просто умножьте каждую шестнадцатеричную цифру на соответствующую степень шестнадцати и сложите полученные десятичные значения вместе следующим образом:
4 × 8 4 + 0 × 8 3 + 7 × 8 2 + 7 × 8 1 + 7 × 8 0
= 4 × 4,096 + 0 × 512 + 7065
= 4 × 4,096 + 0 × 512 + 7 × 64. × 8 + 7 × 1
= 16 384 + 0 + 448 + 56 + 7
= 16 895 10
Десятичное в шестнадцатеричное преобразование
[Вернитесь к началу страницы]
Один из методов, который можно использовать для преобразования десятичного числа в его шестнадцатеричный эквивалент, заключается в выполнении целочисленного деления с использованием шестнадцати в качестве делителя. Преобразуемое число делится на шестнадцать, а остаток записывается в самой правой позиции (в виде шестнадцатеричной цифры). Затем целочисленный результат деления снова делится на шестнадцать, а остаток записывается (снова в виде шестнадцатеричной цифры) слева от шестнадцатеричной цифры, полученной на предыдущем шаге. Этот процесс повторяется до тех пор, пока целочисленный результат деления не станет равным нулю. Пример послужит иллюстрацией процесса. Чтобы преобразовать десятичное число 13 337 в шестнадцатеричное, выполните следующие действия:
Этот процесс повторяется до тех пор, пока целочисленный результат деления не станет равным нулю. Пример послужит иллюстрацией процесса. Чтобы преобразовать десятичное число 13 337 в шестнадцатеричное, выполните следующие действия:
| Integer division | Integer result | Remainder | Hex |
|---|---|---|---|
| 13,337 ÷ 16 | 833 | 9 | 9h |
| 833 ÷ 16 | 52 | 1 | 1h |
| 52 ÷ 16 | 3 | 4 | 4h |
| 3 ÷ 16 | 0 | 3 | 3 часа |
Следовательно:
13 337 10 = 3419 ч
Мы можем выполнить относительно простой процесс — тот, который мы уже видели, — преобразовать число обратно в десятичное (и в то же время подтвердить, что полученный ответ правильный).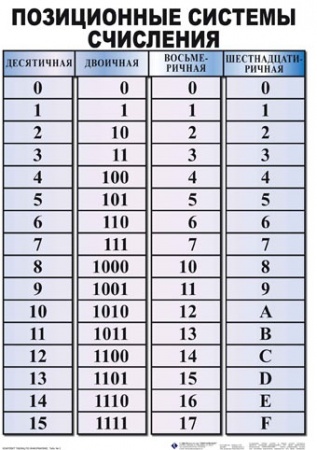 Просто умножьте каждую шестнадцатеричную цифру на соответствующую степень шестнадцати и сложите полученные десятичные значения вместе следующим образом:
Просто умножьте каждую шестнадцатеричную цифру на соответствующую степень шестнадцати и сложите полученные десятичные значения вместе следующим образом:
3 × 16 3 + 4 × 16 2 + 1 × 16 1 + 9 × 16 0
= 3 × 4096 + 4 × 256 + 1 × 16 + 9 × 1 0005
= 1288 + + + + + + 1 × 1024 + 16 + 9
= 13 337 10
Преобразование десятичного числа в двоичное
[Вернитесь к началу страницы]
Преобразование десятичных чисел в двоичные не так просто, но и не так уж сложно. Чтобы упростить задачу, мы будем иметь дело с целыми числами и дробями (или целым числом и дробными частями действительных чисел) отдельно. Начнем с двоичных целых чисел («целое» — это имя, которое мы используем для целого числа). Описанный здесь метод — один из нескольких, которые можно использовать, но, вероятно, он самый простой. Чтобы преобразовать десятичное число n в двоичный, действуйте следующим образом:
- Разделите n на два и запишите остаток (ноль или единицу).
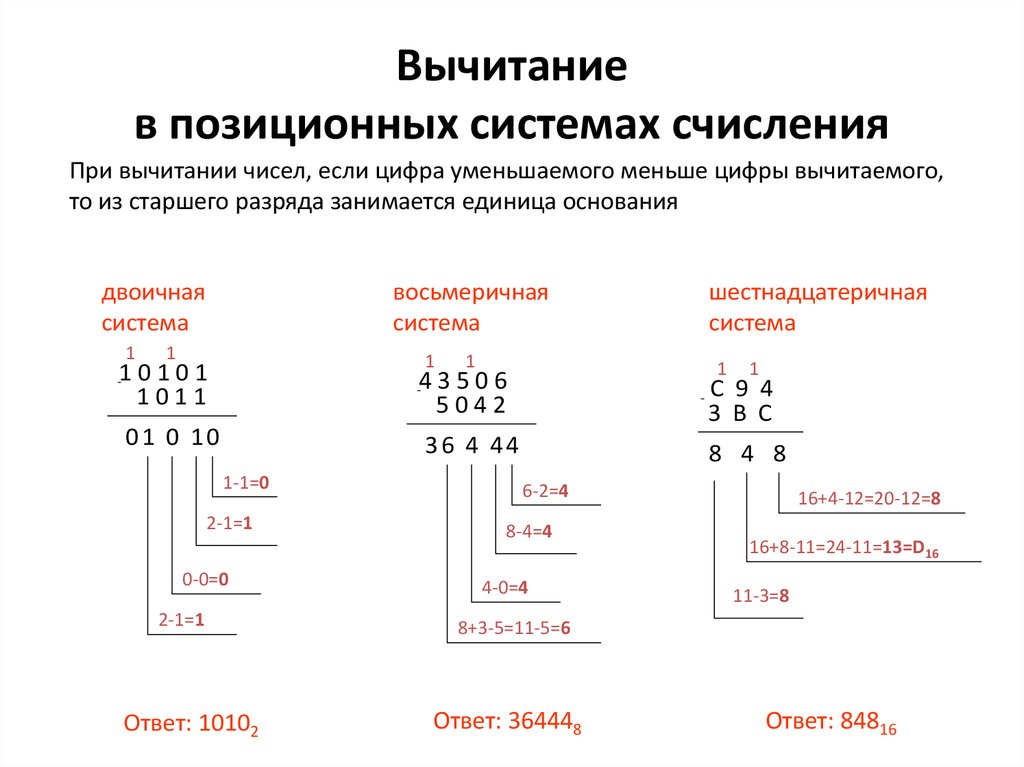
- Если результат предыдущего шага больше нуля, разделите его на два и запишите остаток. В противном случае перейдите к шагу 4.
- Повторить шаг 2.
- Запишите последовательность остаточных значений в обратном порядке.
Следующий пример должен прояснить этот процесс. Мы собираемся преобразовать десятичное число сто шестьдесят девять (169) в его двоичном эквиваленте.
| Integer division | Integer result | Remainder | Bit | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 169 ÷ 2 | 84 | 1 | LSB | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 ÷ 2 | 42 | 0 | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 ÷ 2 | 21 | 0 | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 ÷ 2 | 10 | 1 | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 ÷ 2 | 5 | 0 | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 ÷ 2 | 2 | 1 | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 ÷ 2 | 1 | 0 | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 ÷ 2 | 0 | 1 | 444. | 1 | 4444444. | 1 | 444444444444444444444. | 1 | 4444444444. | 1 | . Двоичное число считывается из остатка столбца, начиная с самого нижнего бита (9).0009 старший бит или MSB) и заканчивается самым старшим битом ( младший бит или LSB), что дает нам двоичное значение: |
| Дробь × 2 | Результат | <1 или >1 ? | Binary fraction |
|---|---|---|---|
| 1 / 3 × 2 | 2 / 3 | <1 (add 0) | 0.0 |
| 2 / 3 × 2 | 1 1 / 3 | >1 (добавить 1) | 0,01 |
| 22 7 3 3 × 3 1 0085 | 2 / 3 | <1 (add 0) | 0. 010 010 |
| 2 / 3 × 2 | 1 1 / 3 | >1 (add 1 ) | 0.0101 |
| 1 / 3 × 2 | 2 / 3 | <1 (add 0) | 0.010 |
| 2 / 3 × 2 | 1 1 / 3 | >1 (добавить 1) | 0,0101 |
Должно быстро стать очевидным, что преобразуемая десятичная дробь в данном случае представлена повторяющимся двоичным образцом . Таким образом, точность преобразования будет зависеть от того, сколько битов доступно для хранения дробного значения. В этом случае мы разрешили шесть битов справа от двоичной точки, что дало нам двоичное значение:
0,010101 2
Обратите внимание, что 1 / 3 , выраженное в виде десятичной дроби, равно 0,333, и поэтому точность десятичного представления зависит от количества двоичных цифр, стоящих после точки счисления.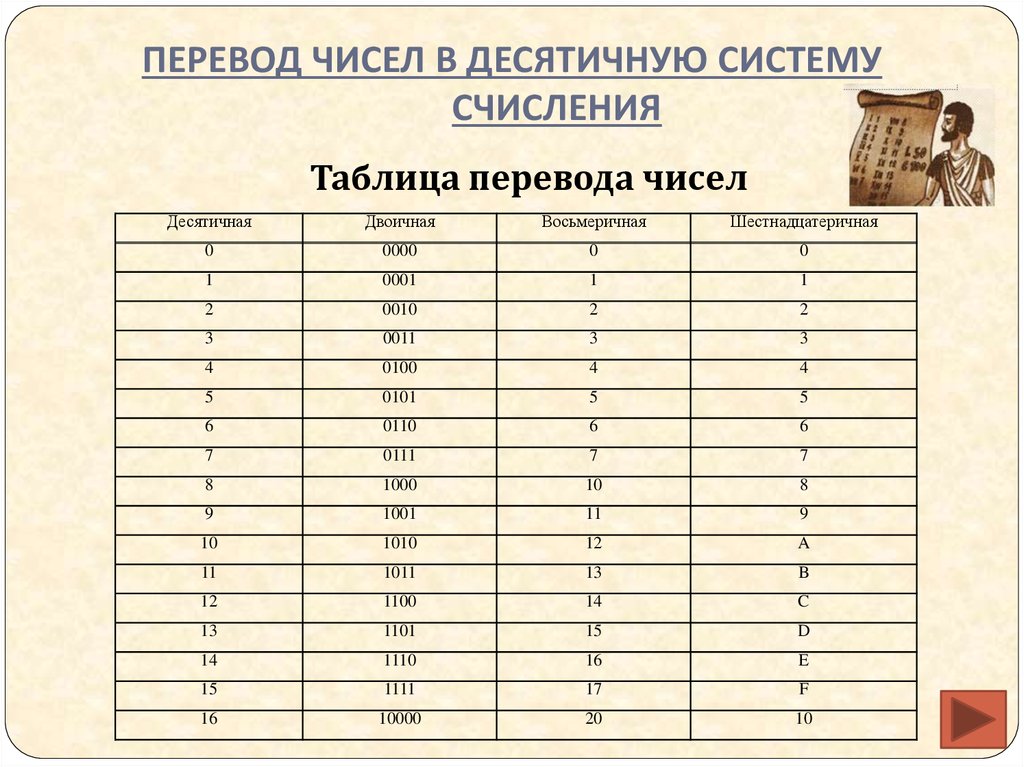 Поэтому при выполнении расчетов с дробными значениями всегда полезно определить степень точности, требуемую для ответа. Для двоичных вычислений обычно существует некоторый верхний предел количества битов, доступных для дробной части результата.
Поэтому при выполнении расчетов с дробными значениями всегда полезно определить степень точности, требуемую для ответа. Для двоичных вычислений обычно существует некоторый верхний предел количества битов, доступных для дробной части результата.
[Вернитесь к началу страницы]
10 Альтернативные численные и численные системы
BY: Марк Зегарелли и
Обновлено: 03-26-2016
Общие сердечные стандарты для родителей для твиков
. числа и цифры тонкие, но важные. Число — это идея, которая выражает сколько или сколько. Числительное – это письменный знак, который выражает число. Вот десять способов представления чисел, которые отличаются от индийско-арабской (десятичной) системы.
Учетные отметки
Числа — это абстракции, обозначающие реальные вещи. Первые известные числа появились с ростом торговли и коммерции — людям нужно было отслеживать такие товары, как животные, собранный урожай или инструменты.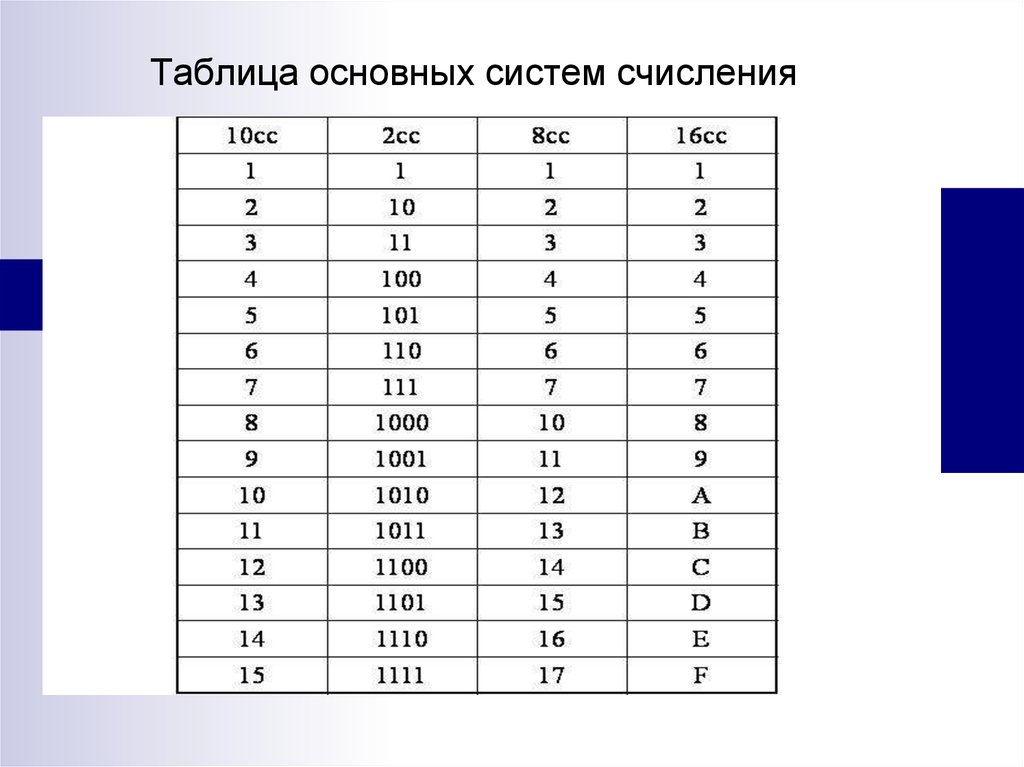 Сначала торговцы использовали глиняные или каменные жетоны, чтобы упростить работу по подсчету. Со временем жетоны заменили счетные метки, выцарапанные на кости или на глине.
Сначала торговцы использовали глиняные или каменные жетоны, чтобы упростить работу по подсчету. Со временем жетоны заменили счетные метки, выцарапанные на кости или на глине.
Учетные марки в комплекте
По мере того, как ранние люди привыкали к тому, что метки для подсчета обозначают объекты реального мира, следующим шагом в развитии чисел, вероятно, стали метки для подсчета, нацарапанные в связок по 5 (пальцы одной руки), 10 (пальцы обеих рук) или 20 (пальцы рук и ног). Объединение предоставило простой способ более легкого подсчета больших чисел.
Конечно, эту систему гораздо легче читать, чем несвязанные скретчи — можно легко умножить или посчитать на пять, чтобы получить сумму. Даже сегодня люди отслеживают очки в играх, используя такие пакеты.
Египетские цифры
Древнеегипетские цифры — одна из старейших систем счисления, используемых до сих пор. Египетские цифры используют семь символов.
| Номер | Символ |
|---|---|
| 1 | Ход |
| 10 | Хомут |
| 100 | Катушка веревки |
| 1000 | Лотос |
| 10 000 | Палец |
| 100 000 | Лягушка |
| 1 000 000 | Мужчина с поднятыми руками |
Числа формируются путем накопления достаточного количества символов, которые вам нужны. Например,
Например,
7 = 7 ходов
24 = 2 скобы, 4 такта
1,536 = 1 лотос, 5 мотков веревки, 3 ярма, 6 ударов
Вавилонские цифры
Вавилонские цифры, появившиеся около 4000 лет назад, используют два символа:
.1 = Д
10 = <
Для чисел меньше 60 числа формируются путем накопления достаточного количества необходимых вам символов. Например,
6 = ГГГГГГ
34 = <<Для чисел от 60 и выше вавилонские цифры используют разрядное значение, основанное на числе 60.
61 = Г Д (один 60 и один 1) 124 = ГГ ГГГГ (две 60 и четыре единицы) 611 = < (десять 60 и одиннадцать единиц) Древнегреческие цифры
Древнегреческие цифры были основаны на греческих буквах.
Цифры от 1 до 999 были сформированы с использованием показанных символов:
Римские цифры
Хотя римским цифрам более 2000 лет, люди все еще используют их сегодня либо в декоративных целях (например, на часах, краеугольных камнях и памятных вещах Суперкубка), либо когда необходимы цифры, отличные от десятичных чисел (например, в контурах). Римские цифры используют семь символов, все из которых являются заглавными буквами латинского алфавита (который также является английским алфавитом):
Я = 1 В = 5 Х = 10 Д = 50 С = 100 Д = 500 М = 1000 Цифры майя
Цифры майя появились в Южной Америке примерно в тот же период, что и римские цифры в Европе. Цифры майя используют два символа: точки и горизонтальные полосы. Полоса равна 5, а точка равна 1. Числа от 1 до 19 образуются путем накопления точек и полос. Например,
3 = 3 точки7 = 2 точки на 1 полосе19 = 4 точки на 3 полосахЧисла от 20 до 399 формируются из тех же комбинаций, но подняты вверх для обозначения разрядности.
Например,
21 = поднятая 1 точка, 1 точка (одна 20 + одна 1)399 = поднятые 4 точки над 3 полосами, 4 точки над 3 полосами (девятнадцать 20 + три пятерки + четыре единицы)Базовые 2 (двоичные) числа
Двоичные числа используют только два символа: 0 и 1. Эта простота делает двоичные числа полезными в качестве системы счисления, которую компьютеры используют для хранения данных и вычислений.
Как и в знакомой вам десятичной системе, в двоичных числах используется разрядное значение. В отличие от десятичной системы, двоичная разрядность основана не на степенях десяти (1, 10, 100, 1000 и т. д.), а на степенях двойки (20, 21, 22, 23, 24, 25, 26, 27, 28, 29 и т. д.), как показано здесь:
.
Двоичные разрядные значения 512с 256с 128с 64с 32 с 16 с 8 с 4с 2 с 1с Числа с основанием 16 (шестнадцатеричные)
Первым языком компьютера являются двоичные числа.
Но на практике люди находят двоичные числа любой значительной длины практически не поддающимися расшифровке. Шестнадцатеричные числа, однако, удобочитаемы для человека и по-прежнему легко переводятся в двоичные числа, поэтому программисты используют шестнадцатеричные числа как своего рода общий язык при взаимодействии с компьютерами на самом глубоком уровне, на уровне аппаратного и программного обеспечения.
В шестнадцатеричной системе счисления используются все десять цифр от 0 до 9 из десятичной системы счисления. Кроме того, он использует еще шесть символов:
.
А = 10 Б = 11 С = 12 Д = 13 Е = 14 Ф = 15 Шестнадцатеричная система счисления, основанная на степенях числа 16.
Шестнадцатеричные разрядные значения 1 048 576 с 65 536 с 4096 с 256с 16 с 1с Как видите, каждое число в таблице ровно в 16 раз больше числа, стоящего справа от него.
Числа, основанные на простых числах
Одним из дурацких способов представления чисел, в отличие от других, являются числа, основанные на простых числах. Числа, основанные на простых числах, аналогичны десятичным, двоичным и шестнадцатеричным числам в том, что они используют разрядное значение для определения значения цифр. Но в отличие от этих других систем счисления, простые числа основаны не на сложении, а на умножении.
Значения места на основе простых чисел 31с 29 с 23 с 19 с 17 с 13 с 11с 7 с 5с 3 с 2 с Вы можете использовать таблицу, чтобы найти десятичное значение числа на основе простого числа.
Об этой статье
Эту статью можно найти в категории:
- Предварительная алгебра,
номеров
номеров Это объяснение довольно сложное. Остальная часть сайта проще!
Остальная часть сайта проще!
Вот анализ того, как работают различные системы на этом сайте. См. ниже таблицу, суммирующую существенные различия, но сначала описание различных типов.
Описание : Системы счисления делятся на категории. Унарные и позиционные описаны ниже. Римские числа описываются как модифицированные унарные, так как они имеют странную концепцию вычитания, поэтому IV означает единицу 9.1512 меньше чем 5. Некоторые системы основаны на счетах. Китайская стандартная система на самом деле представляет собой систему слов, а не цифр, очень похожую на наши собственные слова для чисел. Греческая система использует греческий алфавит для представления чисел. Это довольно распространено — евреи и арабы поступали так же. Как система она отличается как от унарной, так и от позиционной систем.
Основание : Все системы счисления имеют основание, в котором числа ниже обрабатываются иначе, чем числа выше. Несколько систем имеют более одной базы.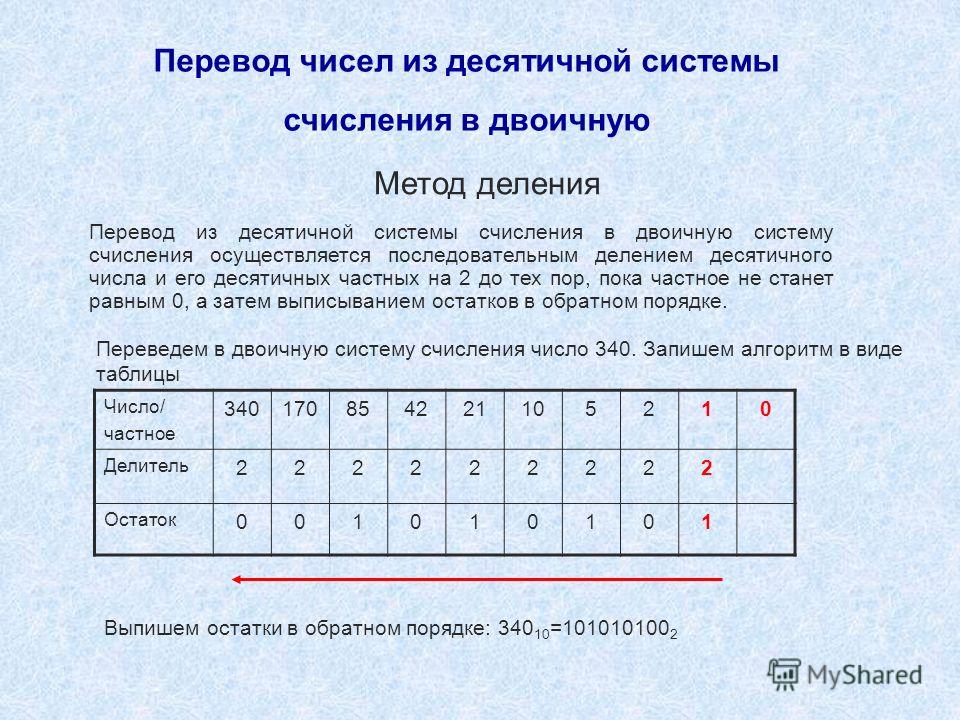 Например, римские числа используют несколько единиц для 1, 2, 3, но другой символ для 5 и снова для 10. (Есть и другие сложности, но это основной принцип). Некоторые системы не только имеют двойную базу, но и по-разному трактуют разные базы. Например, у вавилонских чисел есть унарная система с основанием 10, пока они не достигнут 60. Затем у них есть позиционная система для кратных и шестидесятикратных степеней.
Например, римские числа используют несколько единиц для 1, 2, 3, но другой символ для 5 и снова для 10. (Есть и другие сложности, но это основной принцип). Некоторые системы не только имеют двойную базу, но и по-разному трактуют разные базы. Например, у вавилонских чисел есть унарная система с основанием 10, пока они не достигнут 60. Затем у них есть позиционная система для кратных и шестидесятикратных степеней.
Унарный : Самые старые системы счисления были унарными. Один представлен одним символом, два представлены двумя такими символами и так далее. Через некоторое время им это надоедает, и они вводят новый символ, обычно на 5 или 10, а затем комбинируют эти новые символы со старыми. Особенностью унарных систем является то, что они имеют тенденцию исчерпать символы и вынуждены постоянно изобретать новые. Это означает, что они ограничены и не могут выражать любое число, каким бы большим оно ни было. Некоторые системы преодолевают эту проблему, принимая двойную унарную/позиционную систему, например майя.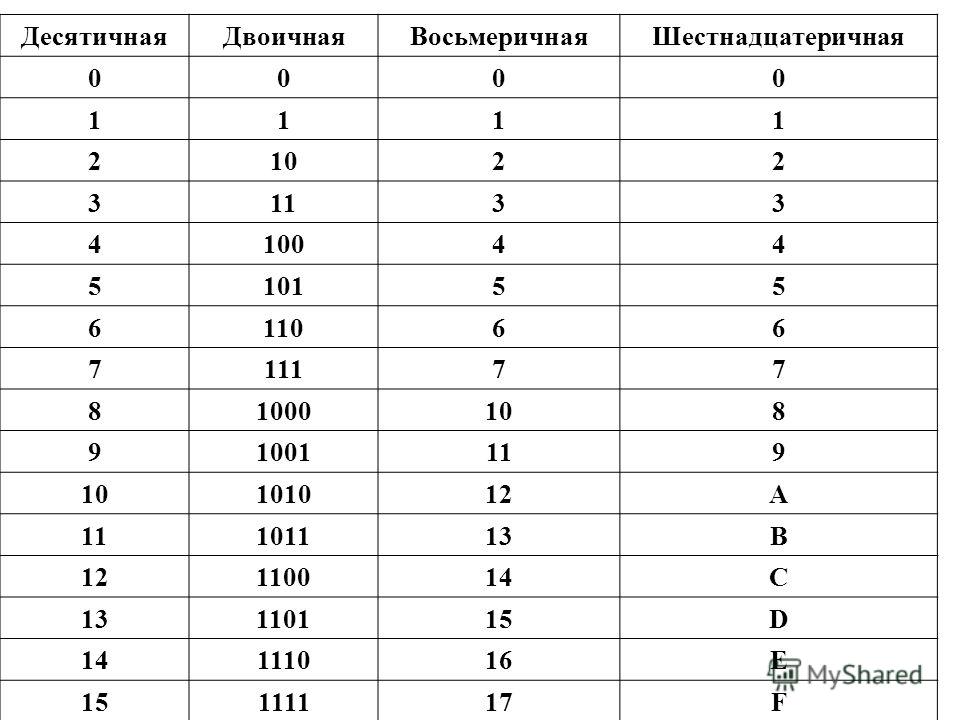 Счета — простейшая из унарных систем. Я назвал это основанием 5, но оно еще проще. Там конечно есть символ для 5, но это повторяется до бесконечности. Для больших чисел нет дополнительного символа. Таким образом, вы можете выразить любое число, но оно получится довольно длинным.
Счета — простейшая из унарных систем. Я назвал это основанием 5, но оно еще проще. Там конечно есть символ для 5, но это повторяется до бесконечности. Для больших чисел нет дополнительного символа. Таким образом, вы можете выразить любое число, но оно получится довольно длинным.
Позиционное : Счеты естественно позиционные. Количество бисеринок в одном столбце представляет собой другое число по сравнению с тем же количеством бисерин в другом. Некоторые системы счисления также делают это. Они имеют ограниченное количество символов и выражают большие числа тем, где эти символы появляются в числе. Его преимущество в том, что вы можете представить любое число, независимо от того, насколько оно велико. Арифметика тоже проще. Системы слов, как и наши собственные слова для чисел, на самом деле не являются позиционными. Они используют слова от одного до девяти по всему числу, но также имеют слова для степеней десяти, чтобы определить, насколько велико число.
Ноль : Ноль выполняет две функции в системе счисления.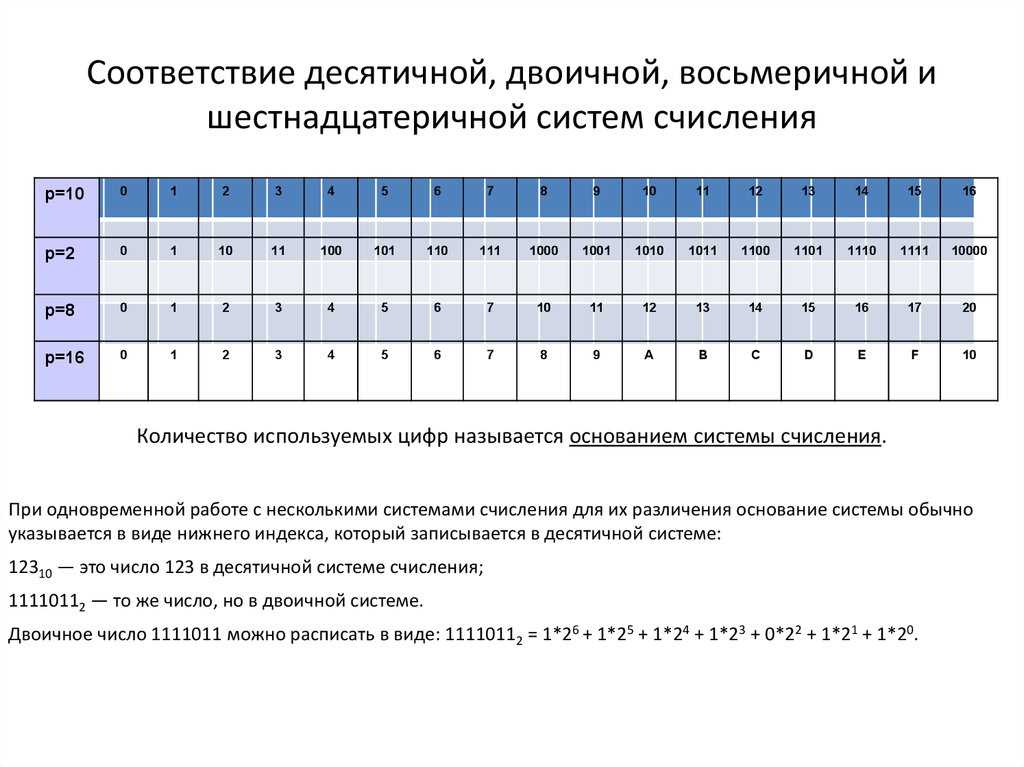 Вы можете использовать его, чтобы вообще ничего не выражать. Во всех культурах должен был быть способ сказать это, даже если они использовали для этого слова. (Тем не менее, это важное математическое понятие, и наличие символа для него жизненно важно.) Однако вам нужен ноль в позиционной системе, и вы получите проблемы, если у вас его нет. Вам нужен способ сказать «нет значения в этом конкретном столбце». В счетах нет четок, и это не имеет значения. Но в письменной системе счисления без нуля вы должны оставить пробел, который может быть пропущен по ошибке или неверно истолкован. Позиционные системы постепенно приобретали нули, но, казалось, использовали их с перерывами. Именно постоянное использование нуля в арабской системе вместе с использованием нескольких символов, а не двойной унарной/позиционной системы, сделало ее такой хорошей системой. Я сказал, что ноль не используется в «Числах как словах». Звучит глупо — есть слово — ноль! Но мы не используем ноль в середине числа. Я также сказал, что на счетах нет нулей.
Вы можете использовать его, чтобы вообще ничего не выражать. Во всех культурах должен был быть способ сказать это, даже если они использовали для этого слова. (Тем не менее, это важное математическое понятие, и наличие символа для него жизненно важно.) Однако вам нужен ноль в позиционной системе, и вы получите проблемы, если у вас его нет. Вам нужен способ сказать «нет значения в этом конкретном столбце». В счетах нет четок, и это не имеет значения. Но в письменной системе счисления без нуля вы должны оставить пробел, который может быть пропущен по ошибке или неверно истолкован. Позиционные системы постепенно приобретали нули, но, казалось, использовали их с перерывами. Именно постоянное использование нуля в арабской системе вместе с использованием нескольких символов, а не двойной унарной/позиционной системы, сделало ее такой хорошей системой. Я сказал, что ноль не используется в «Числах как словах». Звучит глупо — есть слово — ноль! Но мы не используем ноль в середине числа. Я также сказал, что на счетах нет нулей.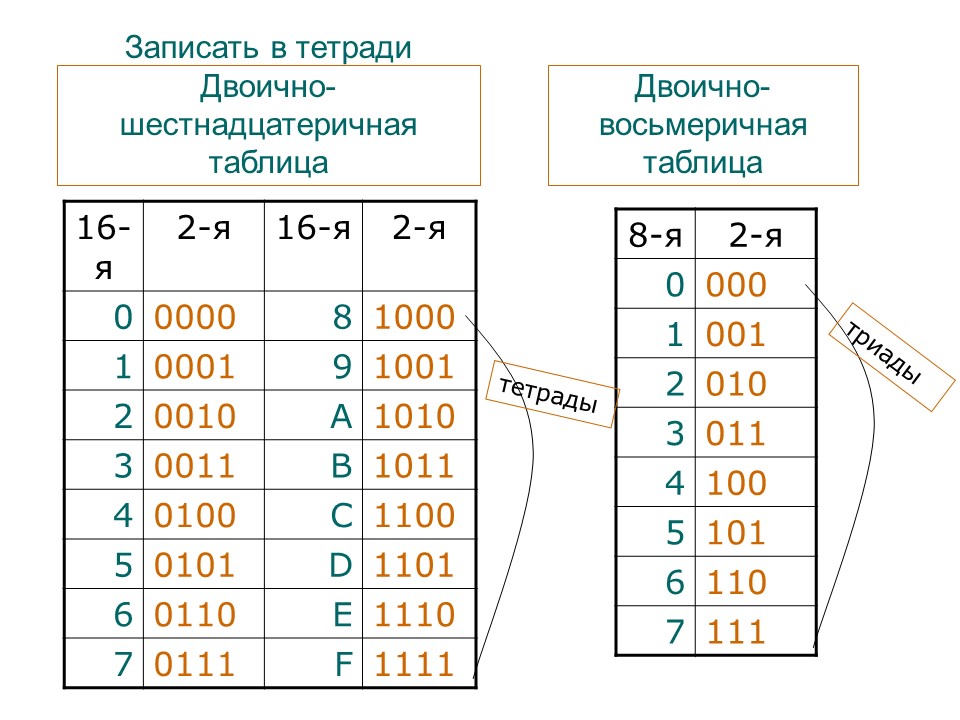 Пустой столбец представляет ноль. Но пробел представляет ноль в некоторых позиционных системах без нуля. Для этого типа нуля, известного как заполнитель, вам нужен определенный символ, а не его отсутствие.
Пустой столбец представляет ноль. Но пробел представляет ноль в некоторых позиционных системах без нуля. Для этого типа нуля, известного как заполнитель, вам нужен определенный символ, а не его отсутствие.
Обязательный порядок : Одно из преимуществ чисто унарных систем состоит в том, что не имеет значения, в каком порядке следуют цифры. У них был обычный порядок, но это было необязательно. Позиционные системы требуют порядка, так как положение цифр определяет их значение. 123 означает нечто иное, чем 321. Однако некоторые непозиционные системы также должны быть в правильном порядке. У римлян была модифицированная унарная система, и IX означает нечто отличное от XI. Когда мы используем числа как слова, двести три означают нечто отличное от триста два.
Все еще используется : Все эти системы использовались для счета или вычислений в прошлом, даже если некоторые из них были настолько сложными, что для серьезных вещей требовались счеты! Сейчас арабские числа используются во всем мире для расчетов.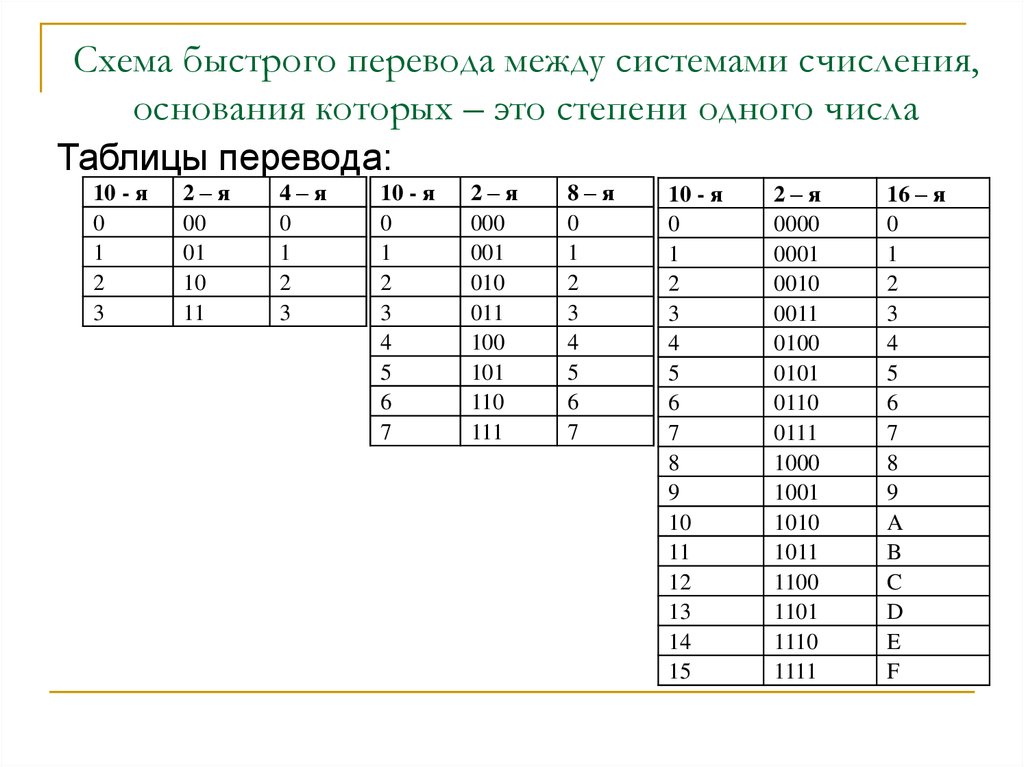 Компьютеры используют двоичный код, а программисты иногда используют шестнадцатеричный формат для сокращения двоичного кода. Счета используются для подсчета. Восточные счеты используются как машина для счета. Другие системы имеют более формальное применение.
Компьютеры используют двоичный код, а программисты иногда используют шестнадцатеричный формат для сокращения двоичного кода. Счета используются для подсчета. Восточные счеты используются как машина для счета. Другие системы имеют более формальное применение.
Легко/сложно : Это мое личное мнение! Это зависит от того, встречались ли вы с системой раньше или уже знаете символы. Я назвал греческий и китайский языки средними. Это простые системы, но они используют множество символов, которые могут сбить вас с толку, если вы не встречались с ними раньше. Вообще говоря, я говорю, что система сложнее, если в ней используется основание, отличное от 10, или двойное основание, особенно если они работают по-разному.
| Система | Описание | Основание | Унарный | Позиционный | Нулевой | Необходимый порядок | Все еще используется | Простой/сложный | |
|---|---|---|---|---|---|---|---|---|---|
| Египетский | Унарный | 100да | нет | нет | нет | нет | |||
| вавилонский | двойное основание, одинарное/позиционное| да | да | периодически | да | нет | | |||
| китайский стандарт | слова | 10 | нет | нет | периодически | да | да | ||
| Китайская палочка | счеты | 50/да | да | нет | да | да | |||
| Греческий | буквы | 10 | нет | нет | нет | нет | да | ||
| Роман | модифицированный одинарный | 0/185 | да | нет | нет | да | да | ||
| майя | двойное основание, одинарное/позиционное | 5 5 9020 | да | да | да | да | нет | ||
| арабский | позиционный | 10 | нет | да | да | да | да | ||
| Бинарный | позиционный | нет | да | да | да | да | |||
| шестнадцатеричный | позиционный | 169084 8нет | да | да | да | да | |||
| Чизенбоп | счеты | 5/10 | да | да | нет | да | да | ||
| Счеты простые | да | да | нет | да | нет | ||||
| Восточные счеты | счеты | 5/10 | да | да | нет | да | да | ||
| слов | слов | 8 10 | нет | нет | нет | да | да | ||
| счетчики | простые унарные | 5 | да | нет | нет | нет | да | ||
| Система | Основание | Одинарный | Позиционный | Нулевой | Необходимый заказ | Все еще используется | Простой/сложный |
© Джо Эдкинс, 2007 – Вернуться к индексу Numbers
История и эволюция чисел
Содержание
История чисел.
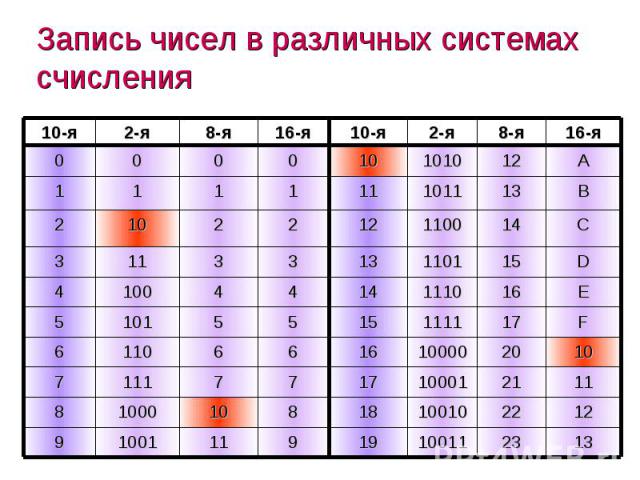 0004 Индо-арабская история чисел
0004 Индо-арабская история чиселИстория чисел майя
История чисел: Заключение эссе
Процитированные работы
Мы напишем
сочинение на заказ
специально для вас
всего за 16,05 долларов 11 долларов за страницу
308 сертифицированных авторов онлайн
Узнать больше
История чисел: введение в эссе , майя, римляне и современные американские системы счисления. История развития счета основана на математической эволюции, которая, как полагают, существовала до появления систем счета (Завлацкий 124).
История математики в счете началась с идей формулирования методов измерения, которыми пользовались вавилоняне и египтяне, введения распознавания образов при счете чисел в доисторическое время, организации понятий различной формы, размеры и числа доисторических людей, а также наблюдение за природными явлениями и поведение во вселенной. В этой статье будет освещена история развития счета у египтян/вавилонян, римлян, индо-арабских систем счета и систем счета майя. Кроме того, в статье будут изложены причины, по которым в настоящее время широко используются западные системы счета.
В этой статье будет освещена история развития счета у египтян/вавилонян, римлян, индо-арабских систем счета и систем счета майя. Кроме того, в статье будут изложены причины, по которым в настоящее время широко используются западные системы счета.
Египтяне/Вавилоняне История чисел
Потребность в счете возникла из-за того, что древние люди признавали измерения с точки зрения большего или меньшего. Несмотря на то, что предположение о числах основывалось на археологических свидетельствах около 50 000 лет назад, система счета развивалась на основе древнего распознавания большего и меньшего во время рутинной деятельности (Higgins 87). Более того, потребность в простом счете у древних людей в истории выработала нечетные или четные, более или менее, и другие формы систем счисления, которые эволюционировали до нынешних систем счета. Потребность в подсчете возникла из-за того, что людям нужен был способ подсчета групп людей за счет прироста населения по рождению. Кроме того, Меннингер утверждает, что повседневная деятельность доисторических людей, такая как разведение крупного рогатого скота и бартерная торговля, приводила к необходимости подсчета и определения стоимости (105).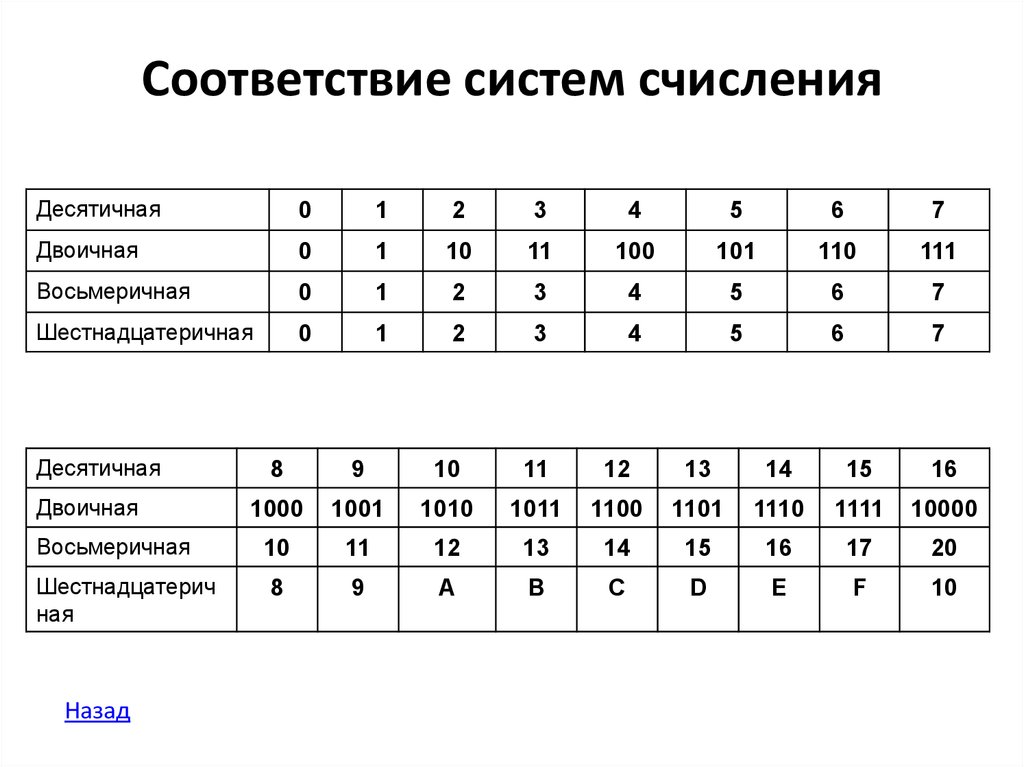
Например, чтобы считать коров, доисторические люди использовали палки. Сбор и раздача палочек для подсчета животных помогли определить общее количество присутствующих животных. Математическая история развилась из маркировки рядов на костях, подсчета и распознавания образов, что привело к введению чисел. Кости и древесина были отмечены, как показано ниже.
Рис.1: Резьба по дереву и камню. (Ифра и Белло198). Более того, развитие чисел произошло от произносимых доисторическими людьми слов. Однако закономерность чисел от одного до десяти было трудно проследить. К счастью, любой набор чисел после десяти можно распознать и легко отследить. Например, одиннадцать произошли от 9.0009 ein lifon , которое доисторические люди использовали для обозначения «оставшегося». Двенадцать развились из жизни, , что означало «два остатка» (Higgins143). Кроме того, тринадцать было выведено из трех, а четыре — из четырнадцати, и эта закономерность продолжалась до девятнадцати. Сто происходит от слова «десять раз» (Ифра и Белло, 147). Кроме того, письменные слова, используемые древними людьми, такие как насечки на резьбе по дереву, резьба по камню и узлы для счета, дали прочную основу для эволюции счета.
Сто происходит от слова «десять раз» (Ифра и Белло, 147). Кроме того, письменные слова, используемые древними людьми, такие как насечки на резьбе по дереву, резьба по камню и узлы для счета, дали прочную основу для эволюции счета.
Подсчет досок широко использовался инками для ведения учета. Инки использовали «шутку», которая помогала доисторическим людям записывать свои предметы в своей повседневной жизни. Счетные доски были окрашены тремя разными цветовыми уровнями. Это была самая темная область, которая представляла самые высокие числа, более светлая часть представляла вторые по величине уровни, а белые части представляли отсеки для камней (Havil 127). Кроме того, остроумие использовалось для быстрых математических вычислений (Завлацкий 154). Как правило, в остроте использовались узлы на шнурах, которые были расположены определенным образом для передачи определенной числовой информации. Однако шутливые системы ведения записей и информации были связаны с несколькими тайнами, которые до сих пор не раскрыты. Примеры того, как выглядели узлы, показаны ниже
Примеры того, как выглядели узлы, показаны ниже
Получите ваш
100% оригинал статьи
по любой теме
всего за
3 часа
Подробнее
Рис.2: Узлы и шнуры, использовавшиеся вавилонянами (Havil 187).Индо-арабская история чисел
Эта форма является общей системой счета и чисел, используемой в 21 веке. В Индии Аль-Брахми ввел числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 (Меннингер 175). Цифры Брахми со временем менялись. Например, в 4-6 веках цифры были такими, как показано ниже.
Рис.3 Численное развитие на протяжении столетий (Хиггинс 189). Наконец, со временем цифры были преобразованы в 1,2,3,4,5,6,7,8,9. Самая ранняя система использования нуля была разработана в Камбодже. Эволюция десятичных точек возникла в эпоху саков, когда были введены три цифры и точка между ними (Hays and Schmandt-Besserat 198). Вавилоняне ввели позиционную систему, посредством которой было установлено позиционное значение числовых систем.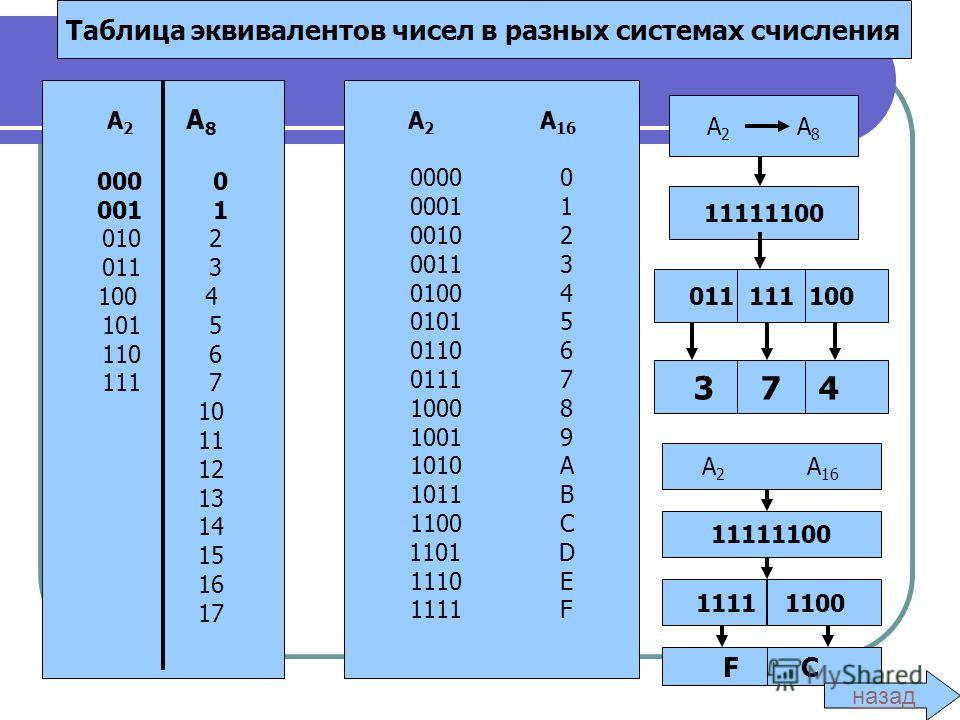 Более того, позиционная система вавилонян развила основные системы до числовых, а индийцы позже развили ее дальше. Числа Брахми развивались в разных воплощениях, что привело к нынешней системе счисления (Хиггинс 204).
Более того, позиционная система вавилонян развила основные системы до числовых, а индийцы позже развили ее дальше. Числа Брахми развивались в разных воплощениях, что привело к нынешней системе счисления (Хиггинс 204).
Числа Гупта были одним из процессов, которые прошли индийско-арабскую систему счисления, чтобы стать широко используемой американской версией счисления. В настоящее время теории о формировании и развитии числительных Гупта остаются спорными для исследователей.
Кроме того, европейцы переняли индийско-арабскую систему через торговлю, согласно которой путешественники использовали Средиземное море для торговых взаимодействий (Havil 190). Использование счетов и пифагорейцев доминировало в эволюции европейских чисел. Пифагорейцы использовали «священные числа», хотя через некоторое время эти две системы уменьшились. Со временем европейцы заимствовали индийско-арабскую систему счисления, чтобы изобрести свои математические системы счисления (Ifrah and Bello 207). Однако процесс, посредством которого европейцы приняли индийско-арабскую систему, не установлен полностью. Считается, что европейцы приняли индийско-арабскую систему счисления, в значительной степени полагаясь на нее при построении своих нынешних сильных числительных (Higgins 210). Например, область применения системы позиционных оснований довольно велика, что связано с преобразованием различных оснований с использованием числового числа 10.
Однако процесс, посредством которого европейцы приняли индийско-арабскую систему, не установлен полностью. Считается, что европейцы приняли индийско-арабскую систему счисления, в значительной степени полагаясь на нее при построении своих нынешних сильных числительных (Higgins 210). Например, область применения системы позиционных оснований довольно велика, что связано с преобразованием различных оснований с использованием числового числа 10.
История чисел майя
Цивилизация счета и числовых систем майя развивалась в Мексике посредством ритуальных систем. Ритуалы представляли собой календарные расчеты, в которых участвовали две ритуальные системы, а именно. один для священников, а другой для простых гражданских лиц (Higgins 217). Например, в жреческом календарном счете использовались смешанные базовые системы, в которых использовались числовые кратные числа. Системы счисления майя составляют основу математических знаний. Кроме того, в системе чисел майя использовалось расположение чисел для определения разрядности объединенных цифр (Havil 223).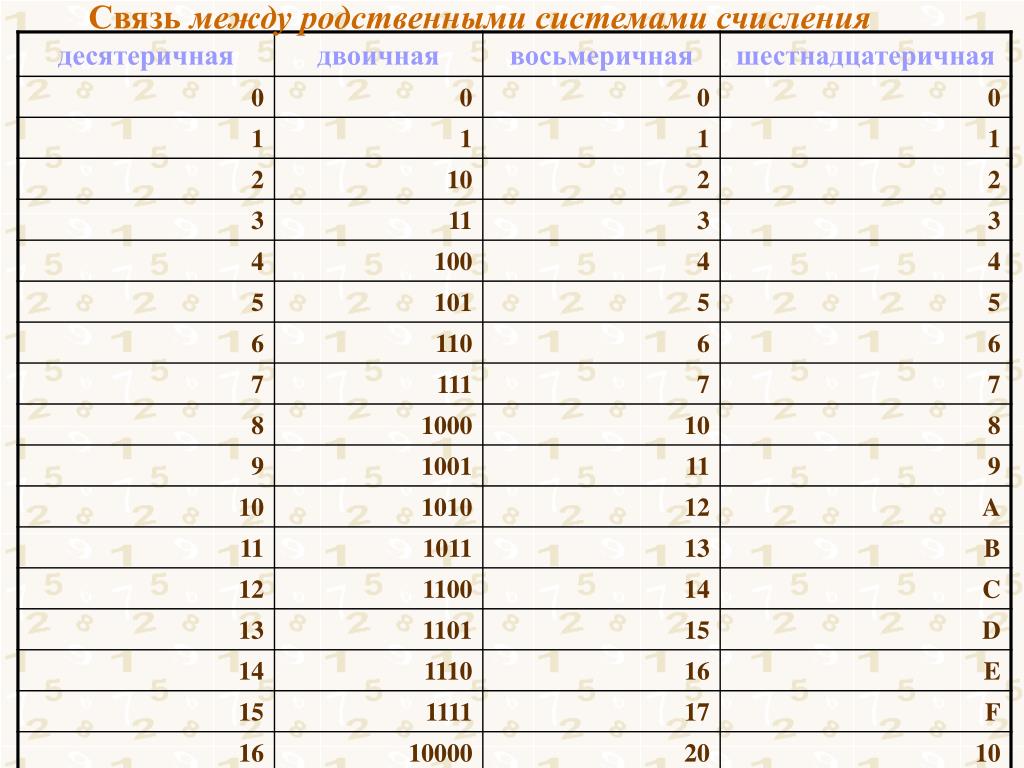
Майя использовали разрядность числовых чисел, которые были представлены в виде таблиц для сложения и умножения чисел. В конечном счете, индо-арабская система счисления и система счисления майя внесли большой вклад в эволюцию чисел, в отличие от систем счисления египтян/вавилонян (Menninger 199). Тем не менее, западная система счисления и математики вобрала в себя сильные черты всех других эволюций, чтобы получить стандартную твердую систему счисления. Например, в американской системе, которая обычно используется в большинстве стран, используются десятичные точки, разрядное значение, основные значения и римские числа от 1 до 10 (Ифра и Белло 225). На рисунке ниже представлен набросок табличных цифр майя.
Рис. 4: Таблица математических значений, используемых майя для расчетов (Havil 234). Американская версия чисел и счета использовала все особенности развития майя, вавилонян, инков, египтян и индо-арабских систем для разработки надежной и общепринятой системы счисления (Hays and Schmandt-Besserat 214). Этот аспект выдающийся, поскольку он выделяет американскую систему из всех систем счисления и счета. Тем не менее, нельзя недооценивать похвальную работу майя, вавилонян, египтян и индийцев, поскольку без них исторический след системы счета и счисления был бы невозможен.
Этот аспект выдающийся, поскольку он выделяет американскую систему из всех систем счисления и счета. Тем не менее, нельзя недооценивать похвальную работу майя, вавилонян, египтян и индийцев, поскольку без них исторический след системы счета и счисления был бы невозможен.
Мы напишем заказные
сочинения
специально для вас
!
Получите свою первую статью с
СКИДКА 15%
Узнать больше
История чисел: Заключение эссе
Исторические следы систем счисления и счета охватывают широкий спектр доисторических археологических свидетельств. Прослеживание древних времен исследователями представляет собой серьезную проблему в попытке установить систему счета и счисления. Исследования по теме систем счисления и счета еще не решены на фактическом источнике информации для доказательства. В конечном счете, наиболее эффективными системами счисления, которые привели к нынешней доминирующей западной системе счисления, являются системы майя, индуизма и вавилонян, основанные на разработках инков.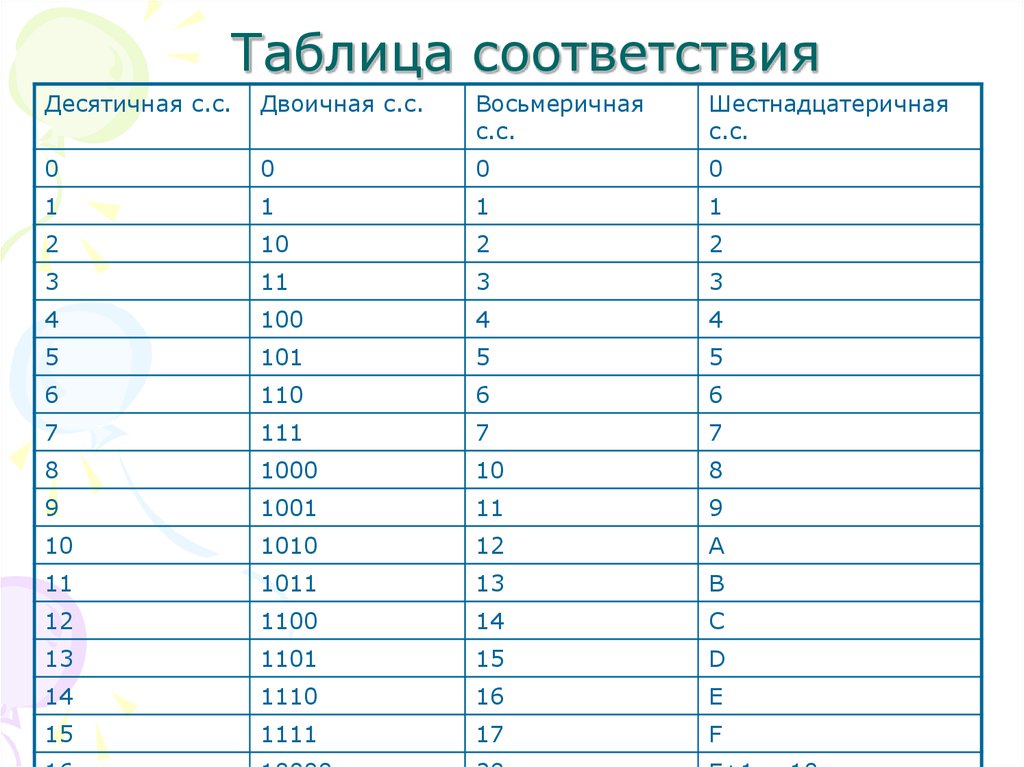 Доисторические останки оставили математические доказательства в виде камней и резьбы по дереву, что привело к эволюции счета, а следовательно, и к развитию математических методологий. Методология исследования и аргументы варьируются в зависимости от эволюции чисел. Следовательно, не существует общепризнанных результатов исследований эволюции математических и числовых систем.
Доисторические останки оставили математические доказательства в виде камней и резьбы по дереву, что привело к эволюции счета, а следовательно, и к развитию математических методологий. Методология исследования и аргументы варьируются в зависимости от эволюции чисел. Следовательно, не существует общепризнанных результатов исследований эволюции математических и числовых систем.
Процитированные работы
Хэвил, Джулиан. Иррациональные идеи : История чисел, на которые нельзя рассчитывать, Принстон: Princeton University Press, 2014. Печать.
Хейс, Майкл и Дениз Шмандт-Бессера. История подсчета , Бродвей: HarperCollins, 1999. Печать.
Хиггинс, Питер. История чисел : от подсчета к криптографии, Геттинген: Коперник, 2008. Печать.
Ифра, Жорж и Дэвид Белло. Универсальная история чисел: от предыстории до изобретения компьютера , Hoboken: Wiley, 2000. Печать.
Меннингер, Карл. Числовые слова и числовые символы; Культурная история чисел, Минеола: Dover Publications, 2011.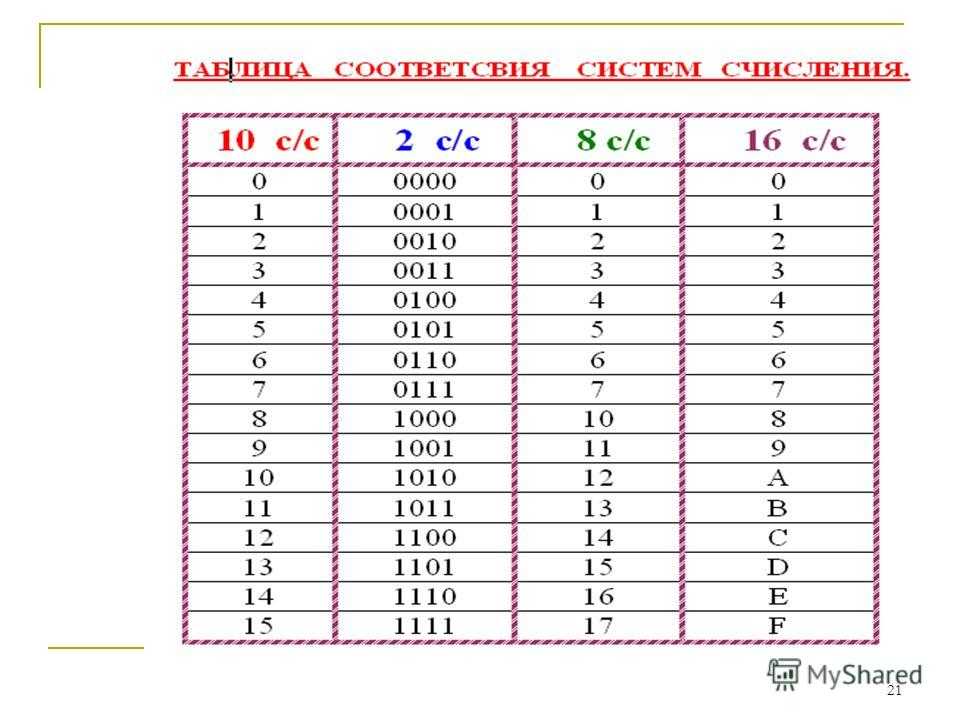 Печать.
Печать.
Завлацкая Клавдия. Африка графов; Число и образец в африканских культурах, , Чикаго: Chicago Review Press, 1999. Печать.
Системы счисления – Математика для учителей начальных классов
Разрядное значение
Наша система счисления является западной адаптацией индийско-арабской системы счисления, разработанной где-то между первым и четвертым веками нашей эры. Однако на протяжении всей истории числа записывались с подсчетными отметками. Кость Ишанго [1] из Африки имеет возраст около 25 000 лет. Это кость голени бабуина, на ней есть отметки. Мы знаем, что метки использовались для подсчета, потому что они появляются отдельными группами.
Этот рог северного оленя [2] из Франции имеет возраст около 15 000 лет и также имеет четко сгруппированные учетные отметки.
Конечно, мы и сегодня используем счетные метки! [3]
Числа с основанием 10 (те, которыми вы, вероятно, пользовались всю свою жизнь) и числа с основанием b (о которых вы узнали в этой главе) являются позиционными системами счисления.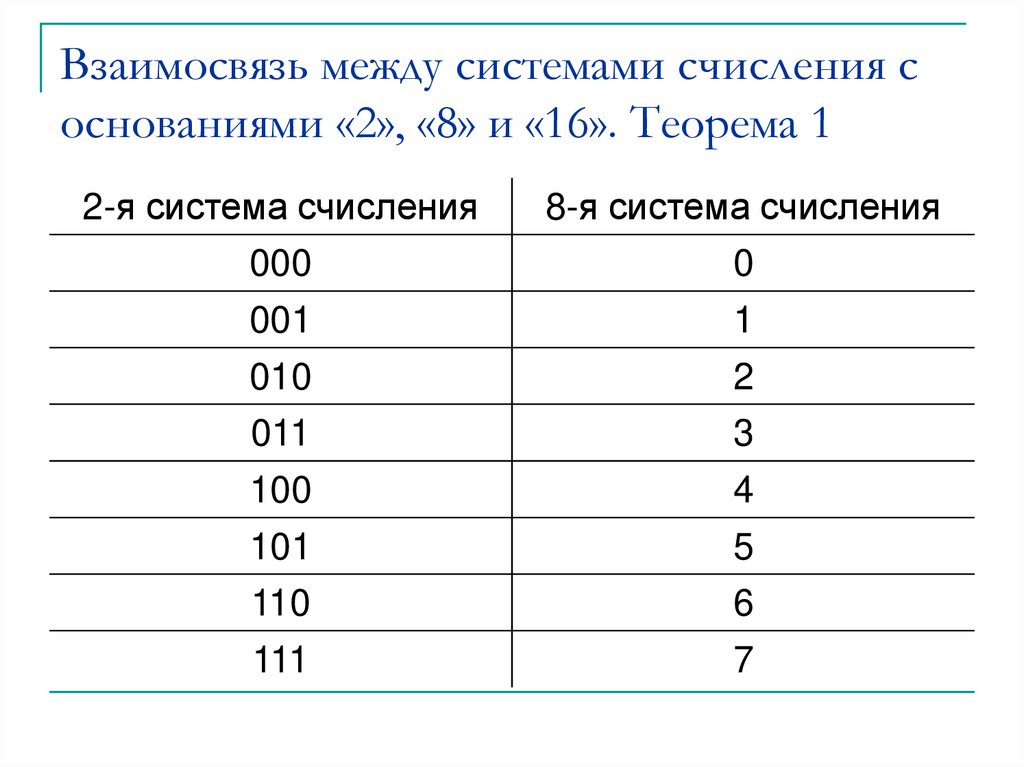
Определение
A позиционная система счисления — это один из способов записи чисел. Он имеет уникальные символы от 1 до b – 1, где b — это основа системы. Современные позиционные системы счисления также включают символ 0.
Позиционное значение каждого символа зависит от его позиции в числе:
- Позиционное значение символа в первой позиции является просто его номиналом.
- Позиционное значение символа во второй позиции в b раз больше его значения.
- Позиционное значение символа в третьей позиции умножено на его значение.
- И так далее.
Значение числа представляет собой сумму позиционных значений его цифр.
Определение
В аддитивной системе счисления значение записанного числа представляет собой сумму номиналов символов, составляющих число. Единственный символ, необходимый для аддитивной системы счисления, — это символ 1, однако многие аддитивные системы счисления содержат другие символы.
Единственный символ, необходимый для аддитивной системы счисления, — это символ 1, однако многие аддитивные системы счисления содержат другие символы.
Древние римляне использовали вариант аддитивной системы счисления. Римляне представляли числа так:
.| номер | Римская цифра |
| 1 | я |
| 5 | В |
| 10 | х |
| 50 | л |
| 100 | С |
| 500 | Д |
| 1000 | М |
Таким образом, число 2013 будет представлено как MMXIII. Это читается как 2000 (две М), одна десятка (один Х) и три единицы (три И).
Для любой аддитивной системы счисления записывать очень большие числа становится непрактично. Чтобы представить число один миллион римскими цифрами, потребуется тысяча М!
Однако у римских цифр было одно преимущество: порядок символов имел значение. Если символ слева был меньше символа справа, он будет вычтен, а не добавлен. Так, например, девять представлены как IX, а не как VIIII.
Если символ слева был меньше символа справа, он будет вычтен, а не добавлен. Так, например, девять представлены как IX, а не как VIIII.
Подумай / Соедини / Поделись
Если вы еще не знаете, как использовать римские цифры, немного изучите это. Тогда ответьте на эти вопросы.
- Напишите числа 1–20 римскими цифрами.
- Какое максимальное количество символов необходимо для записи любого числа от 1 до 1000 римскими цифрами? Обосновать ответ.
Самые ранние позиционные системы счисления приписываются вавилонянам (основание 60) и майя (основание 20). Обе эти позиционные системы были разработаны до того, как у них появился символ или четкая концепция нуля. Вместо использования 0 для обозначения пропуска определенного разряда использовалось пустое место. Это может привести к двусмысленности.
Предположим, у нас не было символа 0, и кто-то написал число
Было бы невозможно сказать, означают ли они 23, 203, 2003 или, может быть, два отдельных числа (два и три).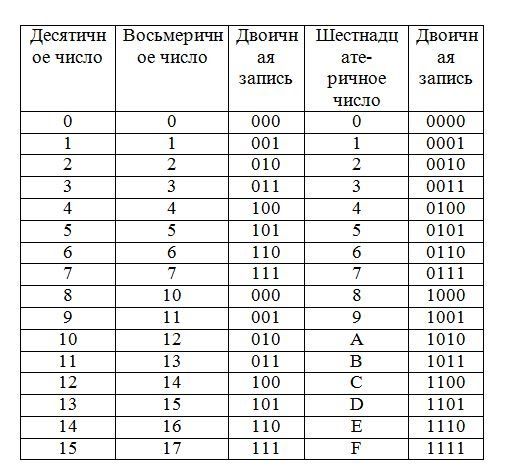
Леонардо Пизано Биголло, более известный как Фибоначчи [4] , сыграл ключевую роль в том, чтобы вывести Европу из долгого периода, когда важность и развитие математики находились в заметном упадке. Он родился в Италии около 1170 г. н.э. в семье Гульельмо Боначчи, успешного купца. Гульельмо привез с собой сына на территорию нынешнего Алжира, и Леонардо получил там математическое образование.
ФибоначчиВ то время в Европе господствовали римские цифры, а официальным средством расчетов были счеты. Мухаммад ибн Муса аль-Хорезми [5] описал использование индийско-арабской системы в своей книге «О расчетах с помощью индуистских цифр » в 825 г. н.э., но она не была широко известна в Европе.
Статуя аль-Хорезми в Технологическом университете Амиркабир Книга Фибоначчи Liber Abaci описывала индийско-арабскую систему и ее бизнес-приложения для европейских читателей. Его книга была хорошо принята во всей Европе и положила начало возрождению европейской математики.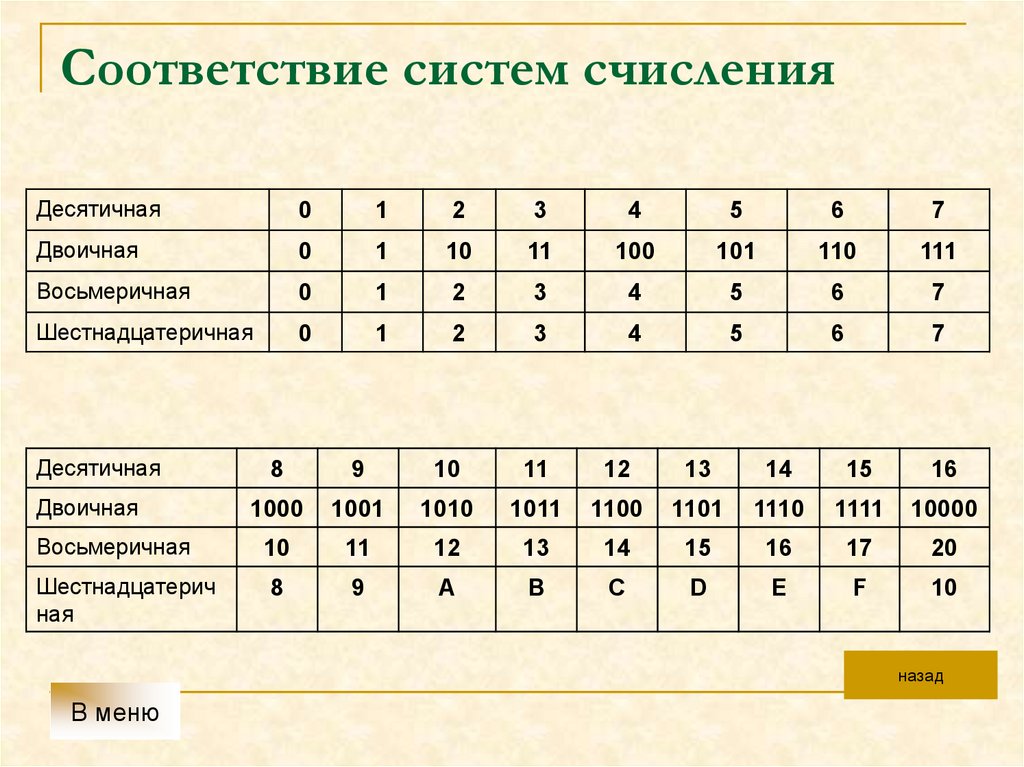
Индо-арабская система счисления в настоящее время используется почти исключительно во всем мире. Но у многих культур были свои собственные системы счисления до того, как контакты и торговля с другими странами распространили работу аль-Хорезми по всему миру.
Есть свидетельства того, что гавайцы до контакта фактически использовали две разные системы счисления. В зависимости от того, что они считали, они могли вместо этого использовать систему счисления с основанием 4 (или смешанную систему счисления с основанием 10 и 4). Одна из теорий состоит в том, что некоторые предметы (рыба, таро и т. д.) часто складывались в связки по 4 штуки, поэтому было естественнее считать по 4, а не по 10. Число четыре также имело духовное значение в гавайской культуре.
У людей по 5 пальцев на каждой руке [6] , что делает десятый естественным выбором для счета. Но между пальцами есть 4 промежутка, а это означает, что рука может нести четыре рыбы, растения таро или подобные предметы, что делает основание четыре естественным выбором для некоторых культур.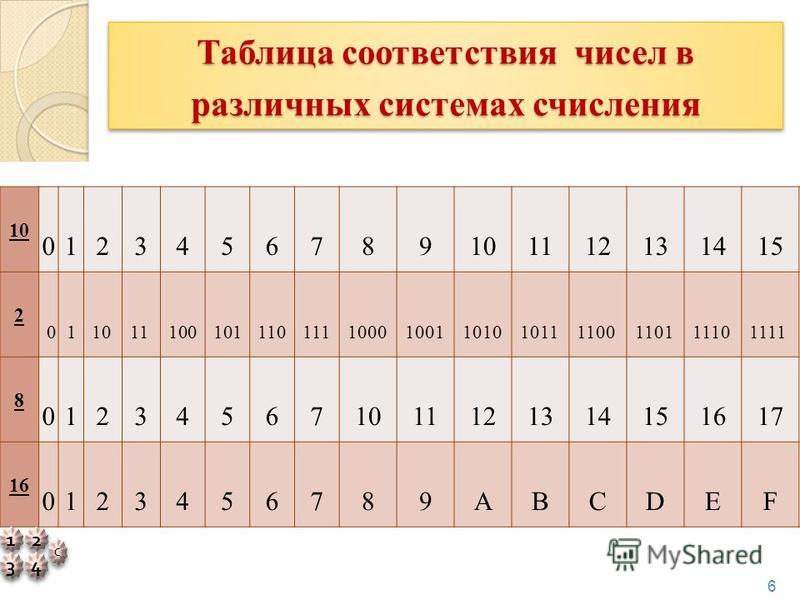 |
В смешанной системе счисления вместо степеней 10 числа разбиваются на суммы чисел, которые выглядят как 4-кратная степень 10 (40, 400, 4000 и т. д.).
| 1 | ‘экахи |
| 2 | ‘элуа |
| 3 | эколу |
| 4 | ‘эха (или кауна) |
| 5 | Элима |
| 6 | ‘эоно |
| 7 | ‘эхику |
| 8 | ‘эвалу |
| 9 | ‘эйва |
| 10 | ‘уми |
| 11–19 | ‘уми кумама {кахи, луа, колу, ха и т. д.} |
| 20 | Ивакалуа |
| 21–29 | Ивакалуа кумама {кахи, луа, колу, ха и т. д.} |
| 30 | канаколу |
| 31–39 | канаколу кумама {кахи, луа и т. д.} |
| 40 | канаха |
| 400 | или |
| 4000 | мано |
| 40 000 | кино |
| 400 000 | леху |
Вот несколько примеров (обратитесь к таблице выше для гавайских названий номеров):
Пример
‘ekolu kini, ‘ewalu lau me ‘ekahi
переводится как три 40 000, восемь 400 и один;
3 ⋅ 40000 + 8 ⋅ 400 + 1 = 123201
Пример
5207 = 1 ⋅ 4000 + 3 ⋅ 400 + 7
будет ‘ekahi mano, ‘ekolu lau me ‘ehiku
Самостоятельно
Выполните следующие упражнения самостоятельно или с партнером.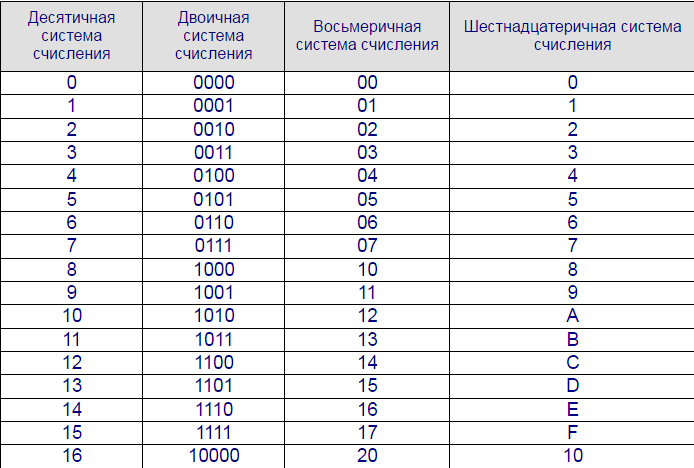
1. Переведите это гавайское число на английский язык, а затем запишите его в десятичной системе счисления.
‘экахи канаха ме канаколу кумамаива
2. Переведите это десятичное число на гавайский язык.
1 573
Подумай / Соедини / Поделись
В чем ценность изучения различных систем счисления (включая представление чисел в разных системах счисления) для вас как будущего учителя?
- Изображение кости Ишанго от Ben2 (собственная работа), CC-BY-SA-3.0 или CC BY-SA 2.5-2.0-1.0], через Викисклад. ↵
- Изображение рога. Автор: Райан Сомма из Оккокуана, США [CC BY-SA 2.0], через Викисклад -3.0], через Викисклад. ↵
- Изображение Фибоначчи из Викисклада, в свободном доступе. ↵
- Изображение статуи аль-Хорезми работы М. Томчака [CC BY-SA 3.0], через Wikimedia Commons. ↵
- Изображение руки с сайта https://pixabay.com, лицензия CC0 Creative Commons.
 ↵
↵
Преобразование системы счисления — Таблица преобразования системы счисления и часто задаваемые вопросы
Что такое система счисления?
Проще говоря, систему счисления можно описать как систему, представляющую числа. В математике существуют различные типы систем счисления, включая двоичные системы счисления и десятичные системы счисления.
В этой статье читатели смогут понять концепцию системы счисления. Они также смогут изучить метод решения вопросов преобразования системы счисления. Существует таблица преобразования чисел для лучшего понимания этих понятий.
Как упоминалось выше, система счисления может быть объяснена как система письма, выражающая числа. Его также можно определить как математическую запись для представления различных чисел данного набора. Это делается с помощью очень последовательного использования цифр или других символов. Студенты должны использовать эти знания для работы над преобразованием системы счисления с решениями.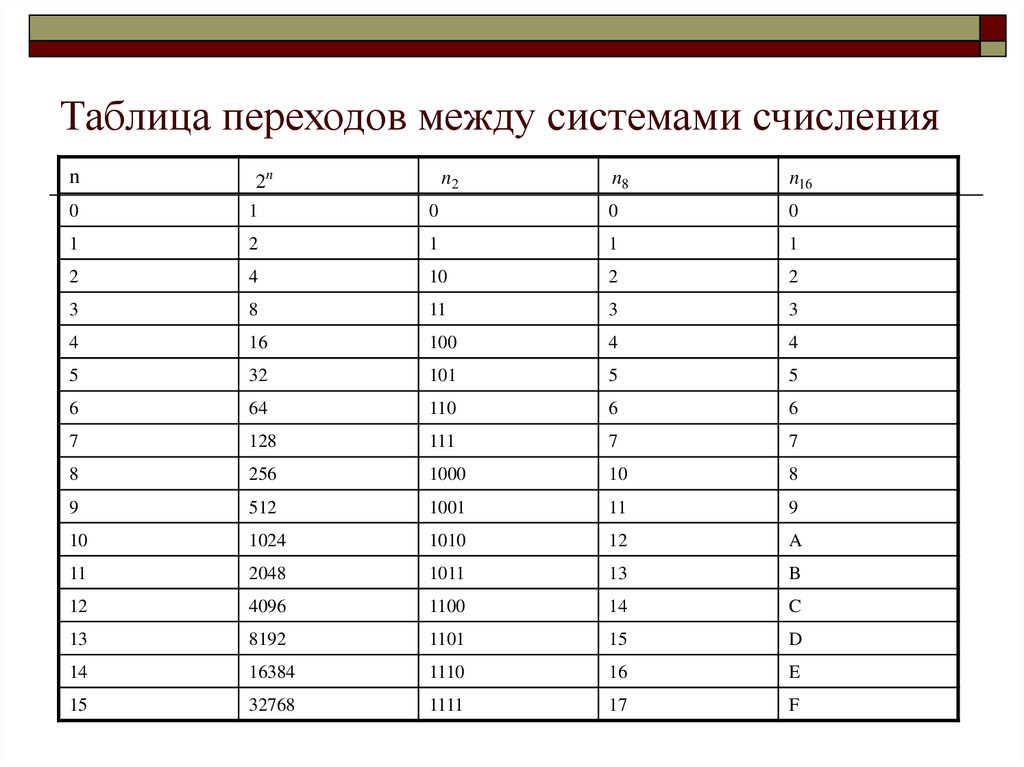
Следует отметить, что преобразование системы счисления онлайн также обеспечивает уникальное представление каждого отдельного числа. Он также представлял арифметические и алгебраические структуры фигур. Это также позволяет человеку выполнять различные арифметические операции, такие как вычитание, сложение и деление.
Если учащемуся предстоит решать вопросы, связанные с переводом какого-либо основания в десятичное, то ему следует знать, что значение любой цифры в числе также можно определить по:
Типам систем счисления
Существует множество различных типы систем счисления. В этом разделе читатели узнают об этих различных типах систем счисления. Это обсуждение проводится ниже.
Десятичная система счисления характеризуется наличием основания 10. Это связано с тем, что в этой системе счисления используются десять цифр от 0 до 9.. Кроме того, позиции слева от десятичной точки представляют единицы, десятки, сотни, тысячи и другие числа.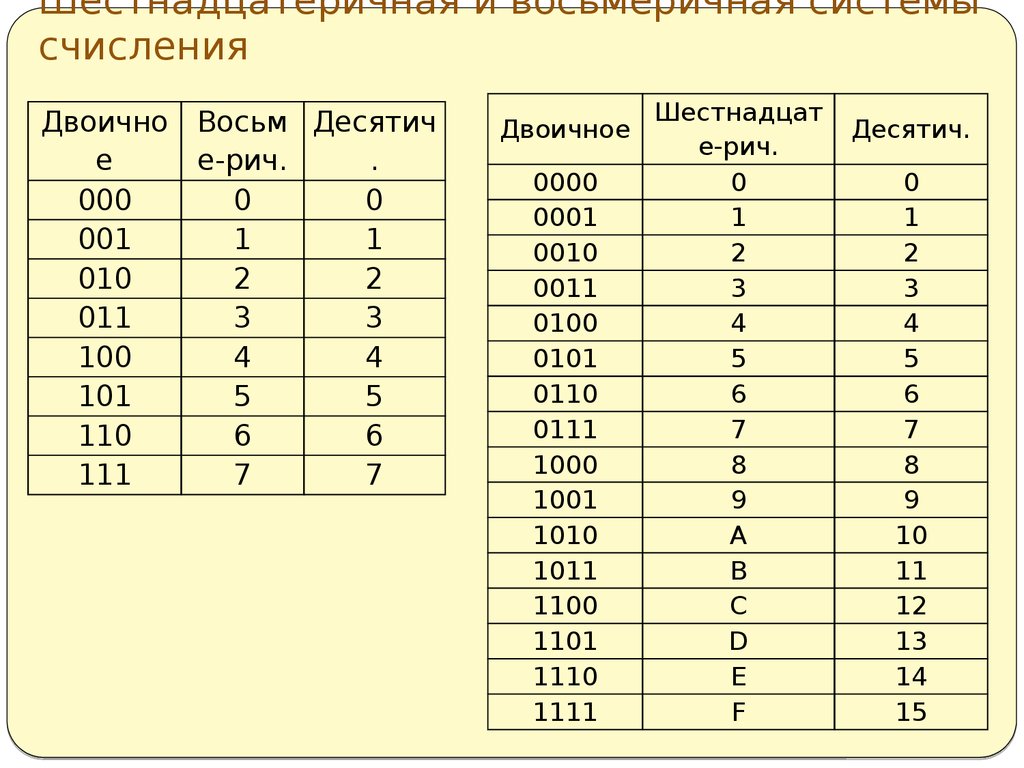 Эта система может быть описана в терминах десятичных чисел.
Эта система может быть описана в терминах десятичных чисел.
Каждая позиция в десятичной системе счисления используется для выделения определенной степени основания (1). Например, десятичное число 1457 состоит из цифры 7 в разряде единиц, 5 в разряде десятков, 4 в разряде сотен и 1 в разряде тысяч. Это значение также может быть записано как:
(1 x 103) + (4 x 102) + (5 x 101) + (7 x 100)
(1 x 1000) + (4 x 100) + (5 x 10) + (7 x 1)
1000 + 400 + 50 + 7
= 1457
Двоичная система счисления или система счисления с основанием 2 имеет только две двоичные цифры, включая 0 и 1. Следует отметить, что обычное основание 2 является основанием 2. Цифры, описываемые в двоичной системе счисления, известны просто как двоичные числа, представляющие собой комбинации 0 и 1. Например, 101001110 — это двоичное число. Любую систему счисления можно преобразовать в двоичную. Это также верно и наоборот.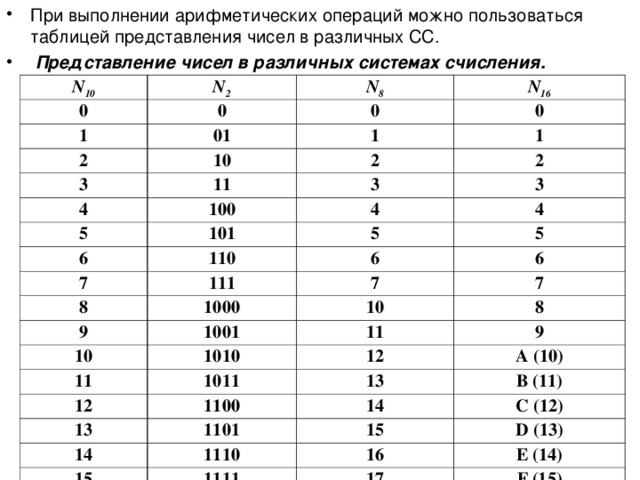
В системе счисления с основанием 8 или восьмеричной системе счисления числа от 0 до 7 используются для представления чисел. Студенты должны помнить, что восьмеричные числа обычно используются в компьютерных приложениях. Кроме того, преобразование восьмеричного числа в десятичное аналогично преобразованию десятичной системы счисления. Чтобы понять это более четко, давайте посмотрим на пример, который приведен ниже.
Преобразовать 2158 в десятичное число.
2158 = 2 х 82 + 1 х 81 + 5 х 80
= 2 х 64 + 1 х 8 + 5 х 1,
= 128 + 8 + 5
= 14110
Как видно из названия, шестнадцатеричная система счисления представлена или записана с основанием 16. В этой системе счисления числа обычно представляются так же, как десятичная система, которая от 0 до 9. После этого числа представляются с использованием алфавитов от A до F.
Чтобы подвести итог всему этому, учащиеся должны пройти через таблицу системы счисления.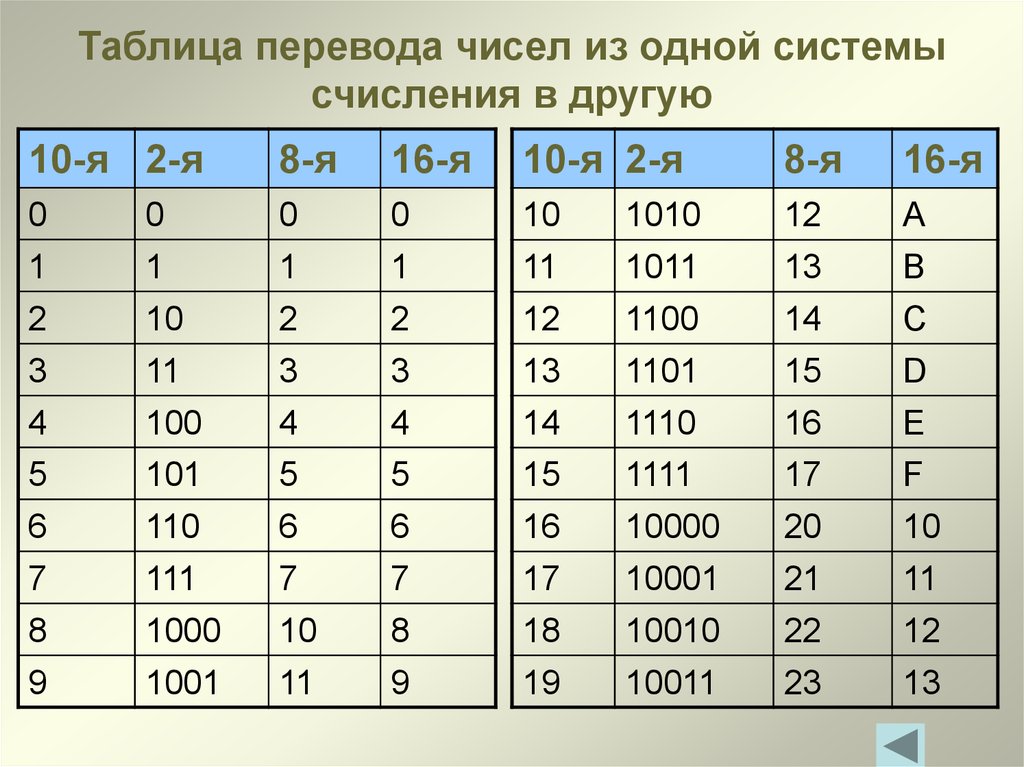 К счастью, мы составили аналогичную диаграмму и прикрепляем ее ниже.
К счастью, мы составили аналогичную диаграмму и прикрепляем ее ниже.
Number System | Base Value | Set of Digits | Examples | ||
Base 3 | 3 | 0 , 1, 2 | (121) 3 | ||
Основание 4 | 4 | 0, 1, 3 9008 | 0, 1, 3 9008 | .0084 (232) 4 | |
Base 5 | 5 | 0, 1, 2, 3, 4 | (324) 5 | ||
Base 6 | 6 | 0, 1, 2, 3, 4, 5 | (542) 6 | ||
Base 7 | 7 | 0 , 1, 2, 3, 4, 5, 6 | (635) 7 | ||
Base 8 | 8 | 0, 1, 2, 3, 4, 5, 6, 7 | (752) 8 | ||
Base 9 | 9 | 0, 1, 2, 3, 4, 5, 6, 7, 8 | (863) 9 | ||
Основание 10 | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | (975) 10 |
Преобразование системы счисления
Как было сказано ранее, любое число, представленное в системе счисления, может быть преобразовано в ряд других систем счисления. Существует несколько методов, которые можно использовать для решения подобных вопросов. Кроме того, студенты могут также обратиться к таблице преобразования системы счисления.
Существует несколько методов, которые можно использовать для решения подобных вопросов. Кроме того, студенты могут также обратиться к таблице преобразования системы счисления.
Использование таблицы преобразования системы счисления может быть очень полезным. Имея это в виду, мы упомянули аналогичную таблицу ниже. Студенты должны пройти через эту таблицу, чтобы решить вопросы, связанные с преобразованием системы счисления.
Binary Numbers | Octal Numbers | Decimal Numbers | Hexadecimal Numbers |
0000 | 0 | 0 | 0 |
0001 | 1 | 1 | |
0010 | 2 | 2 | 2 |
0011 | 3 | 3 | 3 |
0100 | 4 | 4 | 4 |
0101 | 5 | 5 | 5 |
0110 | 6 | 6 | 6 |
0111 | 7 | 7 | 7 |
1000 | 10 | 8 | 8 |
| 9979797 100975 | |||
| 7 595 | |||
| 7 | |||
9 | 9 | ||
1010 | 12 | 10 | A |
1011 | 13 | 11 | B |
1100 | 14 | 12 | C |
1101 | 15 | 13 | D |
1110 | 16 | 14 | E |
1111 | 17 | 15 | F |
Теперь давайте рассмотрим другие методы преобразования чисел в другие системы. Это делается на основе базы чисел. Например, если человек хочет изменить десятичное число с основанием 10 на двоичное число с основанием 2, то мы должны начать с базового представления преобразования основания системы счисления. Общая форма любого основного числа:
Это делается на основе базы чисел. Например, если человек хочет изменить десятичное число с основанием 10 на двоичное число с основанием 2, то мы должны начать с базового представления преобразования основания системы счисления. Общая форма любого основного числа:
(Номер) b = d n — 1 , d n — 2 , —, d 1 d 0 . D -1 d -2 —- d -m
В этом выражении d n -1 d n -2 — d 1 3 d 0 значения целой части, а d -1 d -2 — d m представляет собой дробную часть уравнения.
Кроме того, d n-1 также известен как старший значащий бит (MSB), а dm — младший значащий бит (LSB). Перейдем к конкретным случаям преобразования системы счисления. Эти конкретные случаи обсуждаются в списке ниже.
Для преобразования десятичного числа в какое-либо другое основание мы должны разделить десятичное число после преобразования значения нового основания.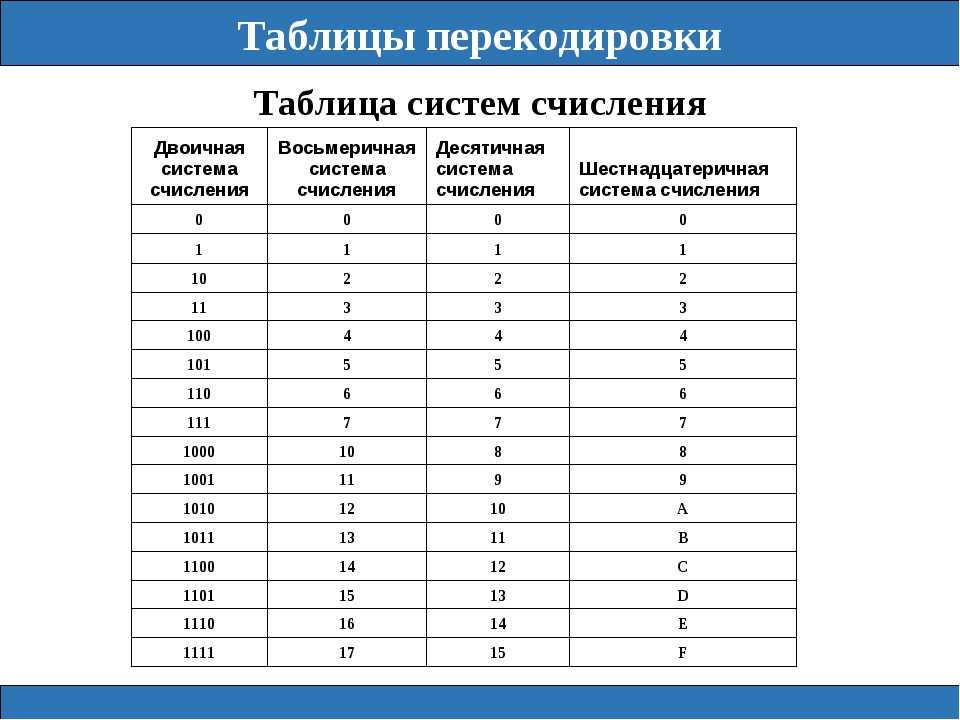 Это может показаться сложным, но это довольно просто. Предположим, что если нам нужно перевести десятичную систему счисления в двоичную, то нужно разделить десятичное число на 2. Например, попробуем преобразовать (25) 10 в двоичную систему счисления.
Это может показаться сложным, но это довольно просто. Предположим, что если нам нужно перевести десятичную систему счисления в двоичную, то нужно разделить десятичное число на 2. Например, попробуем преобразовать (25) 10 в двоичную систему счисления.
Чтобы лучше понять ответ, рассмотрим ответ в виде таблицы. Эта таблица упоминается ниже.
Operation | Output | Remainder | |||||||||||||||||||||||
25/2 | 12 | 1 (MSB) | |||||||||||||||||||||||
12/2 | 6 | 0 | |||||||||||||||||||||||
6/2 | 3 | 0 9008 | 0 9005 | 80808080895950 9008 | 80 9008 | 80 9008 | 80 9008 | 87. | 1 | 1 | |||||||||||||||
1/2 | 0 | 0 | 0 | 0 | 0 | 79999999999999999999999999999999999999999999999999999999999999999999999999998 | . можно сделать вывод, что (25) 10 = (11001) 2 Если вы хотите преобразовать десятичное число в восьмеричное, то нам нужно начать с деления данного исходного числа на 8. Это должно быть сделано в таким образом, чтобы основание 10 изменилось на основание 8. Например, если нам нужно преобразовать (128) 10 в восьмеричное число, то мы можем прийти к ответу с помощью таблицы, которая указана ниже.
. |
 В это поле необходимо ввести число которое Вы хотите перевести.
В это поле необходимо ввести число которое Вы хотите перевести.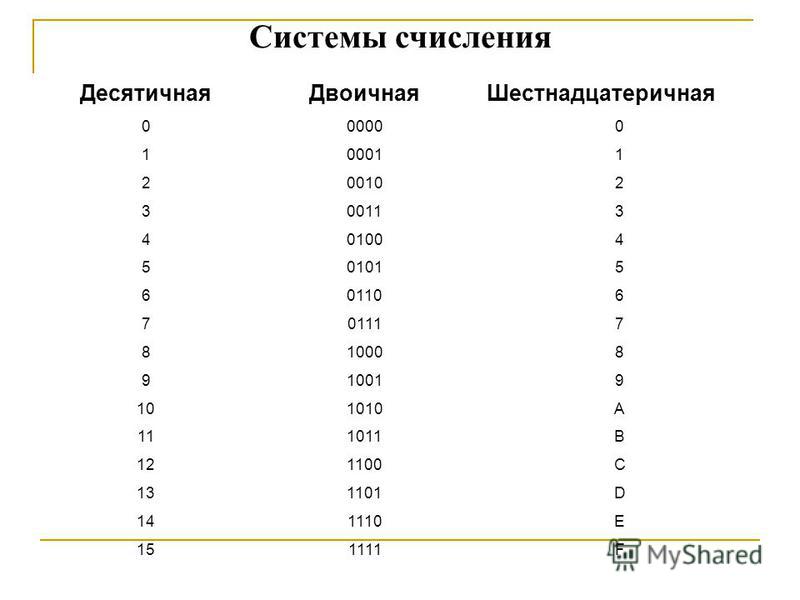
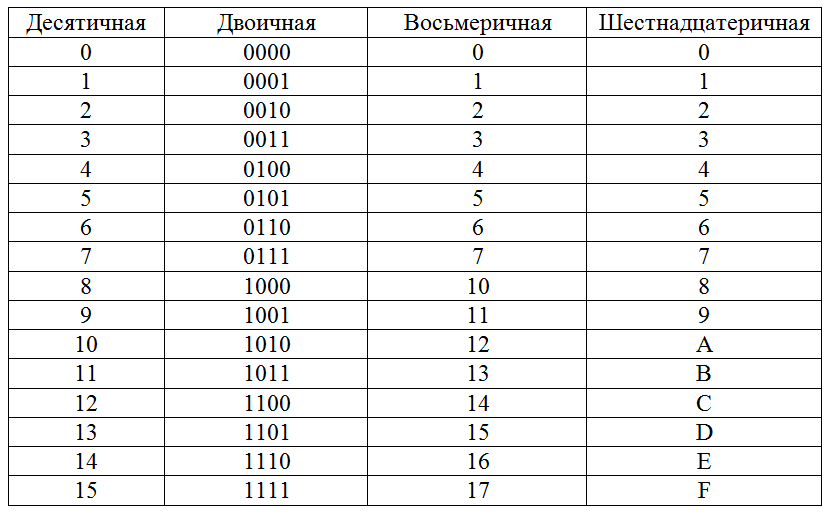
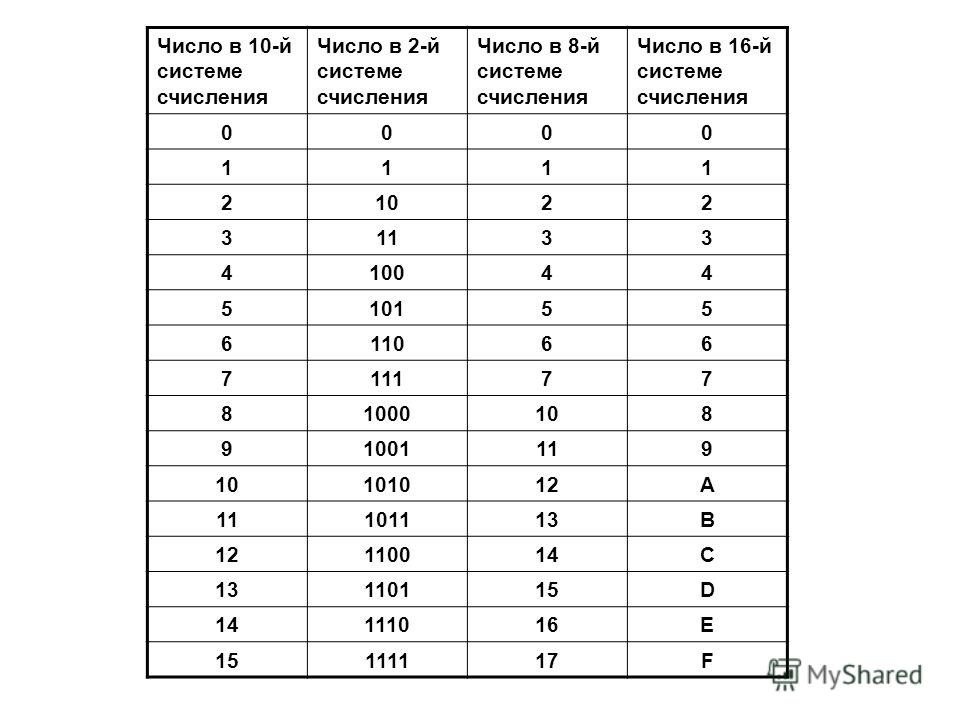
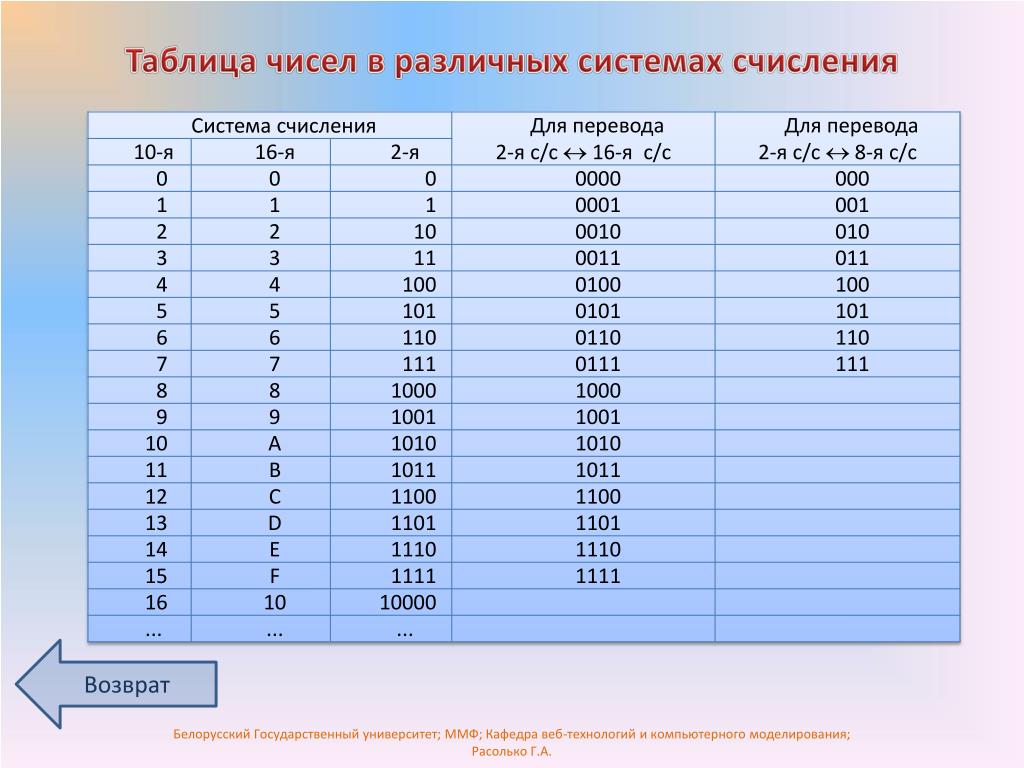 0084
0084