Таблица чисел в разных системах счисления – Таблица соответствия чисел между разными системами счисления — Системы счисления — Общая теоретическая справка — Основы дискретной математики — ДонНТУ — Статьи

Таблица перевода двоичных, восьмеричных, десятичных (от 1 до 255) и шестнадцатеричных чисел. Binary, Octal and Hexadecimal Numbers vs Decimal Numbers

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 1 2 3 4 5 6 7 8 9 A B C D E F	000 001 002 003 004 005 006 007 010 011 012 013 014 015 016 017	00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31	10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F	020 021 022 023 024 025 026 027 030 031 032 033 034 035 036 037	00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47	20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F	040 041 042 043 044 045 046 047 050 051 052 053 054 055 056 057	00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63	30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F	060 061 062 063 064 065 066 067 070 071 072 073 074 075 076 077	00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79	40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F	100 101 102 103 104 105 106 107 110 111 112 113 114 115 116 117	01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111

dpva.ru

Соответствие чисел в различных системах счисления

10 Dec	2 Bin	8 Oct	16 Hex
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Таблица 3.3.

Арифметические операции с двоичными числами

Сложение`	Вычитание	Умножение
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (перенос 1 в старший разряд)	0 — 0 = 0 0 — 1 = -1 1 — 0 = 1 1 — 1 = 0	0 * 0 = 0 1 * 0 = 0 0 * 1 = 0 1 * 1 = 1

2. Двоичное кодирование чисел

Кодирование целого числа осуществляют его простым переводом в двоичную систему счисления.

Для кодирования действительного числа и сохранения его в памяти ЭВМ каждое число R преобразуют следующим образом:

• переводят в нормализованную форму и представляют как произведение мантиссы m на основание системы счисления n в целой степени p, (р называют порядком или характеристикой): R = m _*n ^p;

• полученные значения мантиссы и порядка переводят в двоичный код;

• двоичный код разбивают на группы, в каждой из которых оставляют четыре разряда.

Последовательность преобразования в двоичную форму показана в табл. 3.4, на примере числа 12,34. Из таблицы видно, в каком виде указанное число сохраняется в ячейках памяти ЭВМ.

Таблица 3.4

Порядок перевода числа в двоичный машинный код

Представление	Число
десятичное	12,34
десятичное нормализованное	0,1234*102
двоичное	10011010010 10
двоичное машинное	0100 1101 0010 0010

3. Двоичное кодирование текста

Кодирование текста построено на системе двоичного представления каждого символа алфавита.

Алфавит – множество символов, используемых для записи текста.

Кодирование алфавита осуществляется на основе восьмибитового байта, который может принимать 256 вариантов двоичного кода (от 0 до 255). Каждому варианту двоичного кода противопоставляется один символ, таким образом, в одном байте можно закодировать 256 символов.

В основу системы кодирования алфавита положены следующие принципы:

• 256 возможных вариантов двоичного кода разделяются на две группы, первая из которых относится к базовой таблице и включает значения от 0 до 127, а вторая – к расширенной со значениями от 128 до 255;

• в первой группе путем последовательного перебора кодируются буквы латинского алфавита, цифры, математические знаки, знаки препинания и другие символы, размещенные на стандартной клавиатуре компьютера; кодировка первой группы символов выполнена Институтом стандартизации США, закреплена международным стандартом в виде кодовой таблицы ASCII и применяется на каждом компьютере;

• вторая расширенная группа используются для кодировки букв национальных алфавитов, в том числе, для кодировки русского алфавита – кириллицы.

studfiles.net

Переводы из различных систем счисления. Таблица соответствия систем.

Перевод из десятичной в двоичную систему счисления.

[youtube fLv4gs9EnJs nolink]

Перевод из двоичной в десятичную систему счисления и наоборот.

[youtube C0ai9-3GHJY nolink]

Перевод чисел из двоичной системы счисления в восьмеричную и наоборот.

[youtube x1bx7o2uESg nolink]

Перевод чисел из двоичной системы счисления в шестнадцатеричную. Сложение двоичных чисел.

[youtube rToqA6rEUQ8 nolink]

Перевод чисел в десятичную систему счисления. Полиномы.

[youtube eSviqB6Db7A nolink]

Краткая таблица соответствия — двоичная система в восьмеричную (8СС) и шестнадцатеричная (16СС) системы:

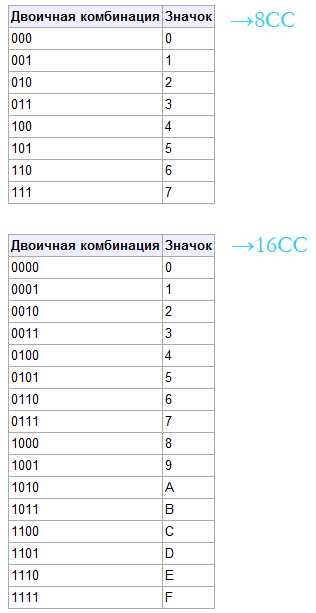
Таблица соответствия десятеричного от 1 до 255 (Decimal), двоичного (Binary) и шестнадцатеричного (Hexadecimal) представлений чисел.

Dec — десятеричная система;

Hex — шестнадцатеричная система;

Bin — двоичная система.

Dec	Hex	Bin	Dec	Hex	Bin	Dec	Hex	Bin	Dec	Hex	Bin
0	0	0	64	40	1000000	128	80	10000000	192	c0	11000000
1	1	1	65	41	1000001	129	81	10000001	193	c1	11000001
2	2	10	66	42	1000010	130	82	10000010	194	c2	11000010
3	3	11	67	43	1000011	131	83	10000011	195	c3	11000011
4	4	100	68	44	1000100	132	84	10000100	196	c4	11000100
5	5	101	69	45	1000101	133	85	10000101	197	c5	11000101
6	6	110	70	46	1000110	134	86	10000110	198	c6	11000110
7	7	111	71	47	1000111	135	87	10000111	199	c7	11000111
8	8	1000	72	48	1001000	136	88	10001000	200	c8	11001000
9	9	1001	73	49	1001001	137	89	10001001	201	c9	11001001
10	a	1010	74	4a	1001010	138	8a	10001010	202	ca	11001010
11	b	1011	75	4b	1001011	139	8b	10001011	203	cb	11001011
12	c	1100	76	4c	1001100	140	8c	10001100	204	cc	11001100
13	d	1101	77	4d	1001101	141	8d	10001101	205	cd	11001101
14	e	1110	78	4e	1001110	142	8e	10001110	206	ce	11001110
15	f	1111	79	4f	1001111	143	8f	10001111	207	cf	11001111
16	10	10000	80	50	1010000	144	90	10010000	208	d0	11010000
17	11	10001	81	51	1010001	145	91	10010001	209	d1	11010001
18	12	10010	82	52	1010010	146	92	10010010	210	d2	11010010
19	13	10011	83	53	1010011	147	93	10010011	211	d3	11010011
20	14	10100	84	54	1010100	148	94	10010100	212	d4	11010100
21	15	10101	85	55	1010101	149	95	10010101	213	d5	11010101
22	16	10110	86	56	1010110	150	96	10010110	214	d6	11010110
23	17	10111	87	57	1010111	151	97	10010111	215	d7	11010111
24	18	11000	88	58	1011000	152	98	10011000	216	d8	11011000
25	19	11001	89	59	1011001	153	99	10011001	217	d9	11011001
26	1a	11010	90	5a	1011010	154	9a	10011010	218	da	11011010
27	1b	11011	91	5b	1011011	155	9b	10011011	219	db	11011011
28	1c	11100	92	5c	1011100	156	9c	10011100	220	dc	11011100
29	1d	11101	93	5d	1011101	157	9d	10011101	221	dd	11011101
30	1e	11110	94	5e	1011110	158	9e	10011110	222	de	11011110
31	1f	11111	95	5f	1011111	159	9f	10011111	223	df	11011111
32	20	100000	96	60	1100000	160	a0	10100000	224	e0	11100000
33	21	100001	97	61	1100001	161	a1	10100001	225	e1	11100001
34	22	100010	98	62	1100010	162	a2	10100010	226	e2	11100010
35	23	100011	99	63	1100011	163	a3	10100011	227	e3	11100011
36	24	100100	100	64	1100100	164	a4	10100100	228	e4	11100100
37	25	100101	101	65	1100101	165	a5	10100101	229	e5	11100101
38	26	100110	102	66	1100110	166	a6	10100110	230	e6	11100110
39	27	100111	103	67	1100111	167	a7	10100111	231	e7	11100111
40	28	101000	104	68	1101000	168	a8	10101000	232	e8	11101000
41	29	101001	105	69	1101001	169	a9	10101001	233	e9	11101001
42	2a	101010	106	6a	1101010	170	aa	10101010	234	ea	11101010
43	2b	101011	107	6b	1101011	171	ab	10101011	235	eb	11101011
44	2c	101100	108	6c	1101100	172	ac	10101100	236	ec	11101100
45	2d	101101	109	6d	1101101	173	ad	10101101	237	ed	11101101
46	2e	101110	110	6e	1101110	174	ae	10101110	238	ee	11101110
47	2f	101111	111	6f	1101111	175	af	10101111	239	ef	11101111
48	30	110000	112	70	1110000	176	b0	10110000	240	f0	11110000
49	31	110001	113	71	1110001	177	b1	10110001	241	f1	11110001
50	32	110010	114	72	1110010	178	b2	10110010	242	f2	11110010
51	33	110011	115	73	1110011	179	b3	10110011	243	f3	11110011
52	34	110100	116	74	1110100	180	b4	10110100	244	f4	11110100
53	35	110101	117	75	1110101	181	b5	10110101	245	f5	11110101
54	36	110110	118	76	1110110	182	b6	10110110	246	f6	11110110
55	37	110111	119	77	1110111	183	b7	10110111	247	f7	11110111
56	38	111000	120	78	1111000	184	b8	10111000	248	f8	11111000
57	39	111001	121	79	1111001	185	b9	10111001	249	f9	11111001
58	3a	111010	122	7a	1111010	186	ba	10111010	250	fa	11111010
59	3b	111011	123	7b	1111011	187	bb	10111011	251	fb	11111011
60	3c	111100	124	7c	1111100	188	bc	10111100	252	fc	11111100
61	3d	111101	125	7d	1111101	189	bd	10111101	253	fd	11111101
62	3e	111110	126	7e	1111110	190	be	10111110	254	fe	11111110
63	3f	111111	127	7f	1111111	191	bf	10111111	255	ff	11111111

 

И, напоследок — удобный online-калькулятор систем счисления тут>>>.

Раздел: HOWTO’s Разное

rtfm.co.ua

Таблицы сложения и умножения

Таблицы сложения и умножения

Таблицы сложения и умножения в различных системах счисления

Двоичная система счисления

Троичная система счисления

Таблица сложения		Таблица умножения
1+1=2		1*1=1
1+2=10	2+2=11	1*2=2	2*2=11

Восьмеричная система счисления

Таблица сложения
1+1=2
1+2=3	2+2=4
1+3=4	2+3=5	3+3=6
1+4=5	2+4=6	3+4=7	4+4=10
1+5=6	2+5=7	3+5=10	4+5=11	5+5=12
1+6=7	2+6=10	3+6=11	4+6=12	5+6=13	6+6=14
1+7=10	2+7=11	3+7=12	4+7=13	5+7=14	6+7=15	7+7=16

Таблица умножения
1*1=2
1*2=2	2*2=4
1*3=3	2*3=6	3*3=11
1*4=4	2*4=10	3*4=14	4*4=20
1*5=5	2*5=12	3*5=17	4*5=24	5*5=31
1*6=6	2*6=14	3*6=22	4*6=30	5*6=36	6*6=44
1*7=7	2*7=16	3*7=25	4*7=34	5*7=43	6*7=52	7*7=61

Шестнадцатеричная система счисления

Таблица сложения

1+1=2

1+2=3

2+2=4

1+3=4

2+3=5

3+3=6

1+4=5

2+4=6

3+4=7

4+4=8

1+5=6

2+5=7

3+5=8

4+5=9

5+5=A

1+6=7

2+6=8

3+6=9

4+6=A

5+6=B

6+6=C

1+7=8

2+7=9

3+7=A

4+7=B

5+7=C

6+7=D

7+7=E

1+8=9

2+8=A

3+8=B

4+8=C

5+8=D

6+8=E

7+8=F

8+8=10

1+9=A

2+9=B

3+9=C

4+9=D

5+9=E

6+9=F

7+9=10

8+9=11

9+9=12

1+A=B

2+A=C

3+A=D

4+A=E

5+A=F

6+A=10

7+A=11

8+A=12

9+A=13

A+A=14

1+B=C

2+B=D

3+B=E

4+B=F

5+B=10

6+B=11

7+B=12

8+B=13

9+B=14

A+B=15

B+B=16

1+C=D

2+C=E

3+C=F

4+C=10

5+C=11

6+C=12

7+C=13

8+C=14

9+C=15

A+C=16

B+C=17

C+C=18

1+D=E

2+D=F

3+D=10

4+D=11

5+D=12

6+D=13

7+D=14

8+D=15

9+D=16

A+D=17

B+D=18

C+D=19

D+D=1A

1+E=F

2+E=10

3+E=11

4+E=12

5+E=13

6+E=14

7+E=15

8+E=16

9+E=17

A+E=18

B+E=19

C+E=1A

D+E=1B

E+E=1C

1+F=10

2+F=11

3+F=12

4+F=13

5+F=14

6+F=15

7+F=16

8+F=17

9+F=18

A+F=19

B+F=1A

C+F=1B

D+F=1C

E+F=1D

F+F=1E

Таблица умножения

1*1=1

1*2=2

2*2=4

1*3=3

2*3=6

3*3=9

1*4=4

2*4=8

3*4=C

4*4=10

1*5=5

2*5=A

3*5=F

4*5=14

5*5=19

1*6=6

2*6=C

3*6=12

4*6=18

5*6=1E

6*6=24

1*7=7

2*7=E

3*7=15

4*7=1C

5*7=23

6*7=2A

7*7=31

1*8=8

2*8=10

3*8=18

4*8=20

5*8=28

6*8=30

7*8=38

8*8=40

1*9=9

2*9=12

3*9=1B

4*9=24

5*9=2D

6*9=36

7*9=3F

8*9=48

9*9=51

1*A=A

2*A=14

3*A=1E

4*A=28

5*A=32

6*A=3C

7*A=46

8*A=50

9*A=5A

A*A=64

1*B=B

2*B=16

3*B=21

4*B=2C

5*B=37

6*B=42

7*B=4D

8*B=58

9*B=63

A*B=6E

B*B=79

1*C=C

2*C=18

3*C=24

4*C=30

5*C=3C

6*C=48

7*C=54

8*C=60

9*C=6C

A*C=78

B*C=84

C*C=90

1*D=D

2*D=1A

3*D=27

4*D=34

5*D=41

6*D=4E

7*D=5B

8*D=68

9*D=75

A*D=82

B*D=8F

C*D=9C

D*D=A9

1*E=E

2*E=1C

3*E=2A

4*E=38

5*E=46

6*E=54

7*E=62

8*E=70

9*E=7E

A*E=8C

B*E=9A

C*E=A8

D*E=B6

E*E=C4

1*F=F

2*F=1E

3*F=2D

4*F=3C

5*F=4B

6*F=5A

7*F=69

8*F=78

9*F=87

A*F=96

B*F=A5

C*F=B4

D*F=C3

E*F=D2

F*F=E1

Задачи
Контрольная работа
К оглавлению

slbazhenova.narod.ru

Различные типы позиционных систем счисления двоичная система счисления

Произвольное число Х в двоичной системе представляется в виде полинома

, (5)

где каждый коэффициент a_i может быть либо 0, либо 1.

Примеры изображения чисел в двоичной ПСС:

1₁₀ = 1₂ 2₁₀ = 10₂

3₁₀ = 11₂ 4₁₀ = 100₂

5₁₀ = 101₂ 6₁₀ = 110₂

7₁₀ = 111₂ 8₁₀ = 1000₂

9₁₀ = 1001₂ 10₁₀ = 10102

11₁₀ = 1011₂ 12₁₀ = 1100₂

13₁₀ = 1101₂ 14₁₀ = 1110₂

15₁₀ = 1111₂ 16₁₀ = 10000₂

0.5₁₀ = 0.1₂ 0.25₁₀ = 0.01₂

Таблица сложения чисел в двоичной ПСС имеет вид:

0+0=0 1+0=1 (6)

0+1=1 1+1=10

Таблица умножения в двоичной ПСС имеет вид:

0·0=0 1·0=0 (7)

0·1=0 1·1=1

Шестнадцатеричная система счисления

В этой ПСС базисными являются числа от нуля до пятнадцати. Так как арабских цифр не хватает для обозначения всех базисных чисел, то пришлось ввести в употребление новые символы. Таким образом, для обозначения базисных чисел в шестнадцатеричной ПСС используется ряд символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f. Например, десятичное число 175.5 в шестнадцатеричной ПСС будет записываться в виде af.8₁₆. Действительно, согласно формуле (4):

af.8₁₆ =1016¹ + 1516⁰ + 816^-1 = 160 + 15 + 8/16 = 175.5

Шестнадцатеричная ПСС, как правило, используется для более компактной записи двоичных чисел.

Представление чисел в различных системах счисления

Из формулы (4) следует, что любое число можно записать в любой допустимой ПСС. Вид числа при этом (коэффициенты a_i в (2) или (4)) зависит от основания ПСС – K. Например, ниже приведено представление ряда натуральных чисел в трёх различных ПСС.

Соответствие между представлением натуральных чисел в различных псс

Число в 10-ой ПСС	Число в 16-ой ПСС	Число в 2-ой ПСС
1	1	1
2	2	10
3	3	11
4	4	100
5	5	101
6	6	110
7	7	111
8	8	1000
9	9	1001
10	А	1010

Выполнение арифметических операций в двоичной системе счисления

Арифметические действия над числами в любой ПСС производятся по тем же правилам, что и в десятичной ПСС. Это связано с тем, что правила выполнения арифметических операций основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые имеют место для ПСС с основанием К. В этом разделе мы покажем примеры выполнения арифметических операций для двоичной ПСС.

Сложение

При сложении числа записываются столбиком (разряд под разрядом), затем цифры суммируются по разрядам. Если результат больше или равен основанию ПСС (2), то возникает единица переноса в соседний левый разряд, а в текущем разряде записываем остаток от деления результата на 2. В следующих примерах точка над разрядом будет означать единицу переноса из соседнего правого разряда.

Пример 1. Сложим числа 15 и 6 в различных системах счисления.

Десятичная:15₁₀ + 6₁₀ Двоичная: 1111₂ + 110₂

_{. . . .}

15 1111

⁺ 6 + 110

21 10101

5+6 =11=10+1 1+0 = 1

1+1=2 1+1 = 2 = 2 + 0

1+1+1 = 3 =2+1

1+1 = 2 = 2+ 0

Пример 2. Сложим три числа 15, 7 и 3.

Десятичная:15₁₀ +7₁₀+3₁₀ Двоичная: 1111₂ + 111₂ +11₂

. . .. .. .

1 5 1 1 1 1

⁺ 7 ⁺ 1 1 1

3 1 1

2 5 1 1 0 0 1

5+7+3 =15 = 10+5 1+1+1=3=2+1

1+1=2 1+1+1+1=4=2+2+0

1+1+1+1 =4=2+2+0

1+1+1=3=2+1

Пример 3. Сложим числа 141.5 и 59.75.

Десятичная:141.5₁₀ + 59.75₁₀ Двоичная: 10001101.1₂ + 111011.11₂

. . . . . . . . . .

141.5 10001101.1

⁺ 59.75 ⁺ 111011.11

201.25 11001001.01

1+1=2 0+5=5 1+0=1 1+1=2+0

5+7=12=10+2 1+1=2=2+0 1+1+1=3=2+1

1+9+1=11=10+1 1+1=2=2+0 1+1=2=2+0

4+5+1=10=10+0 1+1+1=3=2+1 1+1=2=2+0

studfiles.net

Представление чисел в различных системах счисления

Десятичная, основание 10 (Dec)	Римская	Двоичная, основание 2 (Bin)	Восьмеричная, основание 8 (Oct)	Двоичная (триады)	Шестнадцатеричная, основание 16 (Hex)	Двоичная (тетрады)
0		0	0	000	0	0000
1	I	1	1	001	1	0001
2	II	10	2	010	2	0010
3	III	11	3	011	3	0011
4	IV	100	4	100	4	0100
5	V	101	5	101	5	0101
6	VI	110	6	110	6	0110
7	VII	111	7	111	7	0111
8	VIII	1000	10	001 000	8	1000
9	IX	1001	11	001 001	9	1001
10	X	1010	12	001 010	A	1010
11	XI	1011	13	001 011	B	1011
12	XII	1100	14	001 100	C	1100
13	XIII	1101	15	001 101	D	1101
14	XIV	1110	16	001 110	E	1110
15	XV	1111	17	001 111	F	1111
16	XVI	10000	20	010 000	10	0001 0000
17	XVII	10001	21	010 001	11	0001 0001

Перевод из восьмеричной в шестнадцатеричную систему и обратно удобно осуществлять через двоичную систему с помощью триад и тетрад.

4. Двоичная арифметика

Правила выполнения арифметических действий над двоичными числами такие же, как и в десятичной системе, и задаются таблицами двоичного сложения, вычитания и умножения (табл. 2). Таблицы для восьмеричной и шестнадцатеричной систем счисления приведены в приложении к пособию [9].

Таблица 2

Арифметические действия над двоичными числами

Таблица двоичного сложения	Таблица двоичного вычитания	Таблица двоичного умножения
0+0=0 0+1=1 1+0=1 1+1=10	0-0=0 1-0=1 1-1=0 10-1=1	0×0=0 0×1=0 1×0=0 1×1=1

При сложении двоичных чисел производится сложение цифр слагаемых в каждом разряде и единиц переноса из соседнего младшего разряда, если они имеются. При этом необходимо учитывать, что в двоичной системе переполнение разряда наступает при количестве единиц, больше либо равным двум. В случае переполнения нужно вычесть из текущего разряда число, равное основанию системы (в данном случае – двойку), и добавить единицу переноса в следующий старший разряд.

При вычитании двоичных чисел, аналогично вычитанию десятичных, может возникнуть необходимость займа единицы из предыдущего старшего разряда. Эта занимаемая единица переносится в текущий разряд как двойка (количество единиц, равное основанию).

Операции умножения и деления в двоичной системе счисления аппаратно реализовать проще, чем в десятичной системе. Их выполнение сводится к операциям сложения (вычитания) и сдвигу.

5. Представление чисел в эвм

В цифровых ЭВМ числовая информация представляется в двух формах:

При представлении чисел с фиксированной точкой подразумевается, что положение точки, разделяющей число на целую и дробную части, неизменно для всех чисел. Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях. В современных ЭВМ естественная форма используется, например, для представления целых чисел (дробная часть числа всегда отсутствует), денежных сумм (дробная часть всегда составляет четыре знака).

Представление с плавающей точкой любого числа Nв общем виде описывается следующей формулой:

N =  M  p^k, (3.3)

где M– мантисса (дробная часть) числа;p– основание системы счисления;k – порядок (целое число), при этом положительный знак мантиссы и порядка может опускаться, а при указании порядка в десятичной системе принято использовать символЕ. Например, десятичное число с фиксированной точкой 123,45 может быть представлено в форме с плавающей точкой как 0,1234510³, или, как это принято, 1,2345Е+02. Такая форма представления имеет огромный диапазон отображения чисел и является основной в современных ЭВМ.

Для представления положительных и отрицательных чисел в машинах используются специальные коды: прямой, обратныйидополнительный.Причём два последних позволяют заменить неудобную для ЭВМ операцию вычитания на операцию сложения с отрицательным числом; дополнительный код обеспечивает более быстрое выполнение операций при помощи сумматора, поэтому в ЭВМ применяется чаще именно он. Рассмотрим правила кодирования на примере целых чисел.

Для перевода числа в прямой кодзнак числа опускается, а в старший (знаковый) разряд ставится 0, если число положительное, и 1 – если число отрицательное. Младшие разряды кода являются двоичным представлением модуля числа. Оставшиеся разряды кода заполняются нулями. Отметим, что перевод положительных чисел в прямой, обратный и дополнительный код не изменяет изображения этих чисел (табл. 3).

Для перевода отрицательного числа в обратный коднеобходимо все разряды прямого кода, кроме знакового, инвертировать (заменить нули единицами, а единицы – нулями).

Для перевода отрицательного числа в дополнительный коднеобходимо к младшему разряду его обратного кода прибавить единицу.

Перевод отрицательного числа из дополнительного кода в прямой осуществляется в обратной последовательности: сначала вычитается единица, затем инвертируются разряды. Отметим, что положительное число (0 в старшем разряде) обратному переводу не подвергается, и имеет одинаковую запись как в прямом коде, так и в дополнительном.

Таблица 3

studfiles.net

Перевод чисел в различные системы счисления с решением | Онлайн калькулятор

Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую. Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку «Получить запись».

Исходное число записано в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.

Хочу получить запись числа в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.

Получить запись

---

=

Выполнено переводов: 1776794

Также может быть интересно:

Системы счисления

Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.

Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:

Число:	5	9	2	1
Позиция:	3	2	1	0

Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 = 5·103+9·102+2·101+1·100. Число 10 является характеристикой, определяющей систему счисления. В качестве степеней взяты значения позиции данного числа.

Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:

Число:	1	2	3	4	5	6	7
Позиция:	3	2	1	0	-1	-2	-3

Число 1234.567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·103+2·102+3·101+4·100+5·10-1+6·10-2+7·10-3.

Перевод чисел из одной системы счисления в другую

Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:

1. Перевести число 1001101.11012 в десятичную систему счисления.
Решение: 10011.11012 = 1·24+0·23+0·22+1·21+1·20+1·2-1+1·2-2+0·2-3+1·2-4 = 16+2+1+0.5+0.25+0.0625 = 19.812510
Ответ: 10011.11012 = 19.812510

2. Перевести число E8F.2D16 в десятичную систему счисления.
Решение: E8F.2D16 = 14·162+8·161+15·160+2·16-1+13·16-2 = 3584+128+15+0.125+0.05078125 = 3727.1757812510
Ответ: E8F.2D16 = 3727.1757812510

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.

Перевод целой части числа из десятичной системы счисления в другую систему счисления

Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.

3. Перевести число 27310 в восьмиричную систему счисления.
Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421
Проверка: 4·82+2·81+1·80 = 256+16+1 = 273 = 273, результат совпал. Значит перевод выполнен правильно.
Ответ: 27310 = 4218

Рассмотрим перевод правильных десятичных дробей в различные системы счисления.

Перевод дробной части числа из десятичной системы счисления в другую систему счисления

Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.

4. Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 — целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 — вторая цифра результата), 0.5·2 = 1.0 (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
Ответ: 0.12510 = 0.0012

programforyou.ru