Связь систем счисления таблица: Урок 32. Перевод чисел между системами счисления

§9. Восьмеричная система счисления | Связь с двоичной системой счисления

Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень) | §9. Восьмеричная система счисления

Содержание урока

Восьмеричная система счисления

Связь с двоичной системой счисления

Алгоритм перевода восьмеричного числа в двоичную систему счисления

Алгоритм перевода двоичного числа в восьмеричную систему счисления

Арифметические действия

Применение восьмеричной системы

Выводы. Интеллект-карта

Вопросы и задания

Более интересен перевод из восьмеричной системы в двоичную и обратно. Конечно, можно перевести число сначала в десятичную систему, а потом — в двоичную, но для больших чисел этот способ требует достаточно сложных вычислений и может приводить к ошибкам.

Переведите число 15₈ в десятичную систему счисления, а потом — из десятичной в двоичную.

Оказывается, можно сделать перевод из восьмеричной системы в двоичную напрямую, используя тесную связь между этими системами: их основания связаны равенством 2

3 = 8. Покажем это на примере восьмеричного числа 753₈. Запишем его в развёрнутой форме:

753₈ = 7 • 8² + 5 • 8¹ + 3-8^° = 7 — 2⁶ + 5 — 2³ + 3 — 2^°.

Теперь переведём отдельно каждую цифру в двоичную систему и также запишем в развёрнутой форме:

7 = 111₂ = 1 • 2² + 1 • 2¹ + 1-2^°, 5 = 101₂ = 1-2² + 1-2^°, 3 = 11₂ = 1 • 2¹ + 1^°.

Подставим эти выражения в предыдущее равенство:

753₈ = (1 • 2² + 1 • 2¹ + 1 • 2^°) • 2⁶ + (1 • 2² + 1 • 2^°) • 2³ + (1 • 2¹

+ 1 • 2^°) • 2^°.

Раскрывая скобки, мы получим разложение исходного числа по степеням двойки, т. е. его развёрнутую запись в двоичной системе счисления (здесь для отсутствующих степеней числа 2 добавлены нулевые слагаемые):

Таким образом, 753₈= 111 101 011₂. Двоичная запись разбита на триады (группы из трех цифр), каждая триада — это двоичная запись одной цифры исходного восьмеричного числа. Фактически мы каждую восьмеричную цифру отдельно переводим в двоичную систему (табл. 2.2).

Таблица 2.2

Следующая страница Алгоритм перевода восьмеричного числа в двоичную систему счисления

Cкачать материалы урока

Системы счисления — презентация онлайн

1.

Системы счисления

2. Что такое система счисления?

Система счисления – это совокупность
правил записи чисел с помощью
определенного набора символов.
Для записи чисел могут использоваться
не только цифры, но и буквы.

3. Что такое система счисления?

Системы счисления
позиционные
непозиционные
Значение каждой
цифры числа зависит
от того, в каком
месте (позиции или
разряде) цифра
записана
Цифры не изменяют
своего значения при
изменении их
расположения в числе
Десятичная СС
Римская СС

4. Не позиционные системы счисления

Римская система счисления
• Является непозиционной, т.к. каждый символ
обозначает всегда одно и тоже число;
• Цифры обозначаются латинскими буквами:
I, V, X, L, C,
D,
M
(1, 5, 10, 50, 100, 500, 1000)
Например: XXX – 30; XLI — 41

5. Позиционные системы счисления

Основание ПСС – это количество цифр, используемое
для представления чисел;
Алфавит – набор символов, используемый для
обозначения цифр.
• Значение цифры зависит от ее позиции, т.е. одна и та
же цифра соответствует разным значениям в
зависимости от того, в какой позиции числа она стоит;
Например: 888: 800; 80; 8
• Любое позиционное число можно представить в виде
суммы степеней основания системы.

6. Позиционные системы счисления

Десятичная СС
• Основание системы – число 10;
• Алфавит (10 цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
• Любое десятичное число можно
представить в виде суммы степеней числа
10 – основания системы;
234510 2 10 3 10 4 10 5 10
3
2
1
0

7. Позиционные системы счисления

Двоичная СС
• Основание системы – 2;
• Алфавит (2 цифры): 0; 1;
• Любое двоичное число можно
представить в виде суммы степеней
числа 2 – основания системы;
101012 1 2 0 2 1 2 0 2 1 2
4
3
2
1
0

8. Позиционные системы счисления

Восьмеричная СС
8
• Основание системы –
0, 1, 2, 3, 4, 5, 6, 7
• Алфавит ( 8 цифр):
• Любое восьмеричное число можно
представить в виде суммы степеней числа 8
– основания системы;
23458 2 8 3 8 4 8 5 8
3
2
1
0

9.

Позиционные системы счисленияШестнадцатеричная СС
16
• Основание системы –
• Алфавит (16 цифр):
0, 1 ,2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• Любое шестнадцатеричное число можно
представить в виде суммы степеней числа 16
– основания системы;
A 163 16
D 16
23416AD
216 16
4 16
2
1
1
0
0

10. 1. Перевод чисел из любой системы счисления в десятичную.

Для перехода из любой системы
счисления в десятичную необходимо
число представить в виде суммы
степеней основания системы счисления
и найти его десятичное значение.

11. Перевод чисел из двоичной системы счисления в десятичную.

Для перехода из двоичной системы
счисления в десятичную необходимо
двоичное число представить в виде
суммы степеней двойки и найти его
десятичное значение.
Пример:
111012 = 1*2 4 + 1*2 3+ 1*2 2 + 0*2 1 + 1*2 0 =
= 16 + 8 + 4 + 0 + 1 = 2910

12. Перевод двоичных чисел в десятичную систему ?2?10

Перевод двоичных чисел в десятичную
систему
?2 ?10
Примеры:
102 = 1*2 1 + 0*2 0 = 2 + 0 =
1002 = 2 2 = 4
10002 = 2 3 = 8
100002 = 2 4 = 16
101112 = 2 4 +
22+
21+
= 16 + 4 + 2 + 1 = 2310
210
20=

13.

Задание № 1:?2 ?10
Двоичные числа
1011001,
11110,
11011011
перевести в десятичную систему.
проверка

14. 2. Перевод чисел из десятичной системы счисления в любую другую

• Разделить десятичное число на основание
системы счисления. Получится частное и
остаток.
• Выполнять деление до тех пор, пока последнее
частное не станет меньше основания новой
системы счисления.
• Записать последнее частное и все остатки в
обратном порядке. Полученное число и будет
двоичной записью исходного десятичного
числа.

15. 2. Перевод чисел из десятичной системы счисления в двоичною.

• Разделить десятичное число на 2. Получится
частное и остаток.
• Частное опять разделить на 2. Получится
частное и остаток.
• Выполнять деление до тех пор, пока последнее
частное не станет меньшим 2.
• Записать последнее частное и все остатки в
обратном порядке. Полученное число и будет
двоичной записью исходного десятичного
числа.

16. Перевод ?10 ?2

Перевод ?10 ?2
Примеры:
27 2
1 13 2
1 6
0
2710 =
2
3 2
1 1
2

17. Задание № 2:

?10 ?2
Для десятичных чисел
341; 125; 1024
выполни перевод в двоичную систему
счисления.
проверка

18. Восьмеричная СС

• Основание системы – 8;
• Содержит 8 цифр: 0; 1; 2; 3; 4; 5; 6; 7;
• Любое восьмеричное число можно
представить в виде суммы степеней
числа 8 – основания системы;
• Примеры восьмеричных чисел: 2105;
73461;

19. Правило перевода из десятичной системы счисления в восьмеричную

• Разделить десятичное число на 8. Получится
частное и остаток.
• Частное опять разделить на 8. Получится
частное и остаток.
• Выполнять деление до тех пор, пока
последнее частное не станет меньшим 8.
• Записать последнее частное и все остатки в
обратном порядке. Полученное число и будет
восьмеричной записью исходного
десятичного числа.

20.

Перевод ?10 ?8Перевод ?10 ?8
132 8
4 16
0
13210 =
8
2
8

21. Задание № 3:

?10 ?8
Десятичные числа
421, 5473, 1061
перевести в восьмеричную систему.
проверка

22. Правило перехода из восьмеричной системы счисления в десятичную.

Для перехода из восьмеричной системы
счисления в десятичную необходимо
восьмеричное число представить в виде
суммы степеней восьмерки и найти ее
десятичное значение.
2158 = 2*82 + 1*81+ 5*80 =
= 128 + 8 + 5 = 14110

23. Задание № 4:

?8 ?10
Восьмеричные числа
41,
520,
306
перевести в десятичную систему.
проверка

24. Шестнадцатеричная СС

• Основание системы – 16;
• Содержит 16 цифр: от 0 до 9; A; B; C; D;
E; F;
• Любое шестнадцатеричное число можно
представить в виде суммы степеней
числа 16 – основания системы;
• Примеры шестнадцатеричных чисел:
21AF3; B09D;

25. Правило перехода из десятичной системы счисления в шестнадцатеричную

• Разделить десятичное число на 16. Получится
частное и остаток.
• Частное опять разделить на 16. Получится
частное и остаток.
• Выполнять деление до тех пор, пока
последнее частное не станет меньшим 16.
• Записать последнее частное и все остатки в
обратном порядке. Полученное число и будет
шестнадцатеричной записью исходного
десятичного числа.

26. Примеры:

?10 ?16
335 16
15 20
4
33510 =
16
1
F 16

27. Задание № 5:

?10 ?16
Десятичные числа
512,
302, 2045
перевести в шестнадцатеричную
систему.
проверка

28. Правило перехода из шестнадцатеричной системы счисления в десятичную.

Для перехода из шестнадцатеричной
системы счисления в десятичную
необходимо шестнадцатеричное число
представить в виде суммы степеней
шестнадцати и найти ее десятичное
значение.
A1416 = 10*162 +1*161 + 4*160 =
= 10*256 + 16 + 4 = 258010

29. Задание № 6:

?16 ?10
Шестнадцатеричные числа
B5, A28,
CD
перевести в десятичную систему.
проверка

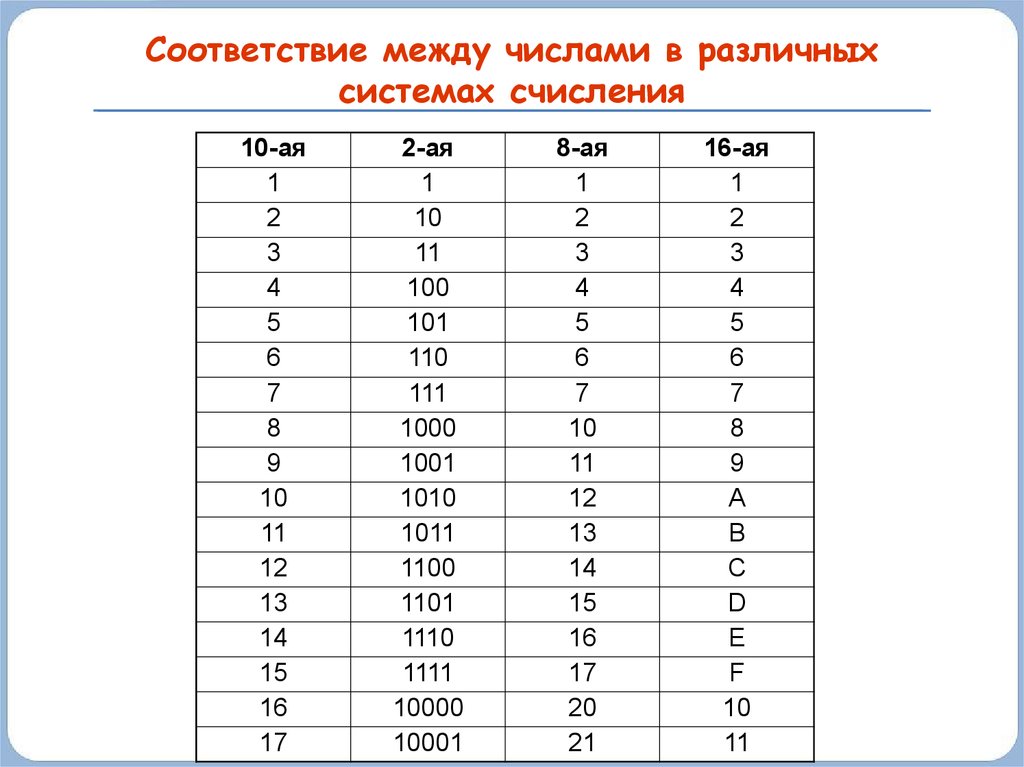
30. Связь систем счисления

10-ая
2-ая
8-ая
16-ая
0
0
0
0
1
1
1
1
2
0010
2
2
3
0011
3
3
4
0100
4
4
5
0101
5
5
6
0110
6
6
7
0111
7
7
8
1000
8
9
1001
9
10
1010
A
11
1011
B
12
1100
C
13
1101
D
14
1110
E
15
1111
F
возврат

31. Правило перехода из двоичной системы счисления в восьмеричную

Разбить двоичное число на классы справа
налево по три цифры в каждом.
Заменить каждый класс
соответствующей восьмеричной
цифрой.
11101011002 = 11101011002
16548

32. Задание № 7:

?2 ?8
Двоичные числа 10101111, 11001100110
перевести в восьмеричную систему
проверка

33. Правило перехода из восьмеричной системы счисления в двоичную

?8 ?2
Каждую восьмеричную цифру заменить
двоичным классом по три цифры в
каждом
25718 = 10101111 0012
таблица

34.

Задание № 8:?8 ?2
Восьмеричные числа 26, 702, 4017
перевести в двоичную систему.
проверка

35. Правило перехода из двоичной системы счисления в шестнадцатеричную

?2 ?16
Разбить двоичное число на классы справа
налево по четыре цифры в каждом. Заменить
каждый класс соответствующей
шестнадцатеричной цифрой.
1 1 0 1 1 1 0 0 0 1 1 0 12 = 1 B 8 D 16
таблица

36. Задание № 9:

?2 ?10
Двоичные числа 10101111,
11001100110 перевести в
шестнадцатеричную систему
проверка

37. Правило перехода из шестнадцатеричной системы счисления в двоичную

?16 ?2
Каждую шестнадцатеричную цифру
заменить двоичным классом по четыре
цифры в каждом
F54D016 = 1111 01010100110100002
таблица

38. Задание № 10:

?16 ?2
Шестнадцатеричные числа C3,
B096,
E38 перевести в двоичную систему.
проверка

39. Задания для домашней работы

1. Для каждого из чисел: 12310, 45610
выполнить перевод: 10 2, 10 8, 10 16.
2. Для каждого из чисел: 1000112, 1010010112,
11100100012 выполнить перевод: 2 10, 2
8, 2 16.
3. Для чисел: 543218, 545258, 7778, 1AB16,
A1B16, E2E416, E7E516 выполнить
соответствующий перевод: 8 2, 16 2.

40. Ответы к заданию № 1

10110012 8910
111102 3010
110110112 21910

41. Ответы к заданию №2

34110 1010101012
12510 11111012
102410 10000000000 2
409510 1111111111112

42. Ответы к заданию №3

42110 6458
547310 125418
106110 20458

43. Ответы к заданию №4

418 3310
5208 33610
3068 19810

44. Ответы к заданию №5

51210 20016
30210 12 E16
204510 7 FD16

45. Ответы к заданию №6

B516 18110
A2816 260010
CD16 20510

46. Ответы к заданию №7

101011112 2578
110011001102 31468

47. Ответы к заданию №8

268 10.1102
7028 111.000.0102
40178 100.000.001.1112

48. Ответы к заданию №9

101011112 AF16
110011001102 66616

49.

Ответы к заданию №10C 316 1100.00112
B09616 1011.0000.1001.0110 2
E 3816 1110.0011.1000 2

50. Связь систем счисления

10-ая
2-ая
8-ая
16-ая
0
0
0
0
1
1
1
1
2
0010
2
2
3
0011
3
3
4
0100
4
4
5
0101
5
5
6
0110
6
6
7
0111
7
7
8
1000
8
9
1001
9
10
1010
A
11
1011
B
12
1100
C
13
1101
D
14
1110
E
15
1111
F
возврат

51. Связь систем счисления

10-ая
2-ая
8-ая
16-ая
0
0
0
0
1
1
1
1
2
0010
2
2
3
0011
3
3
4
0100
4
4
5
0101
5
5
6
0110
6
6
7
0111
7
7
8
1000
8
9
1001
9
10
1010
A
11
1011
B
12
1100
C
13
1101
D
14
1110
E
15
1111
F
возврат

52.

Задания для домашней работы1. Для каждого из чисел: 12310, 45610
выполнить перевод: 10 2, 10 8, 10 16.
2. Для каждого из чисел: 1000112, 1010010112,
11100100012 выполнить перевод: 2 10, 2
8, 2 16.
3. Для чисел: 543218, 545258, 7778, 1AB16,
A1B16, E2E416, E7E516 выполнить
соответствующий перевод: 8 2, 16 2.

Двоичный учебник — Понимание и управление двоичными числами

Системы счисления!

Теория чисел и принцип работы двоичных чисел.

Введение

Числа окружают нас повсюду, и по большей части мы принимаем их как должное. Если бы я предложил вам 1337 долларов, вы были бы счастливы, потому что знаете, что это довольно разумная сумма. Система счисления — это средство представления количества вещей. Десятичная система счисления — это всего лишь одна из нескольких систем счисления, а другие, особенно двоичные, важны для понимания в различных областях, особенно в вычислительной технике.

В нашем введении для начинающих в двоичные, шестнадцатеричные и восьмеричные числа вы изучите двоичные преобразования и арифметику с интерактивными демонстрациями и подробными объяснениями.

Outline

Этот двоичный учебник разделен на 3 раздела. В общем, я рекомендую вам работать с ними по порядку, но если вы пришли сюда только для того, чтобы узнать о конкретной теме, то кто я такой, чтобы замедлять вас, просто идите прямо дальше.

1. Системы счисления. Читайте ниже, чтобы узнать о теории чисел.
2. Преобразования — Как преобразовать между двоичным и десятичным, шестнадцатеричным и восьмеричным.
3. Арифметика. Узнайте, как выполнять различные арифметические операции с двоичными числами.
4. Отрицательные числа — Узнайте, как управлять отрицательными числами в двоичном формате.
5. Плавающая точка и дроби. Узнайте, как преобразовывать десятичные числа в двоичные дроби и числа с плавающей запятой.

Шаблоны и ярлыки

При работе с системами счисления есть много сокращений, которые можно использовать:

• облегчают работу с ними.
• поможет проверить вашу работу / выявить глупые ошибки, которые вы могли допустить.

Я укажу на некоторые из них по мере работы с материалом, но вы всегда должны сами их искать (не только в работе с числами, но и в других областях).

В общем, вы хотите следить за шаблонами, а затем думать о том, как вы можете использовать эти шаблоны для своей выгоды. С практикой вы научитесь их замечать.

Десятичная система счисления

Десятичная система счисления нам наиболее знакома, мы используем ее каждый день. Десятичная система счисления — это то, что мы называем позиционной системой счисления. То есть положение цифр придает значение значению, которое они представляют. Другие системы счисления (двоичная, шестнадцатеричная и восьмеричная) также являются позиционными, поэтому, как только мы поймем основную теорию десятичной системы счисления, мы сможем легко применить ее для понимания других систем.

Рассмотрим пример:

Если у меня есть число 31415, то это на самом деле означает:

30 000 + 1 000 + 400 + 10 + 5

Или, точнее:

8

3 * 10 4	30 000
1 * 10 3	1000
4 * 10 2	400
1 * 10 1	10
5 * 10 0	5

Десятичное число равно по основанию 10 . Это означает, что у нас есть 10 символов для представления значений (0-9). По мере того, как мы перемещаемся по каждой позиции, мы умножаем это число на 10 в степени этой позиции (начиная с 0 в крайнем правом углу).

Помните: все, что в степени 0, всегда равно 1

Десятичная система удобна как система счисления, так как каждый раз, когда мы увеличиваем степень, все, что нам нужно сделать, это добавить еще один 0. К каждой цифре в числе добавить количество 0 требуется для позиции, и у вас есть ее позиционное значение. Затем каждая цифра естественным образом выстраивается в общее число.

Двоичный

Двоичный соответствует тому же шаблону, что и Десятичный, за исключением того, что вместо 10 используется с основанием 2 . Вместо 10 символов для представления значений у нас есть два (0 и 1).

Итак, Decimal — это система счисления с основанием 10, у нас есть 10 символов и умножение на степени 10. Отсюда следует, что Binary — это система счисления с основанием 2, у нас есть два символа и умножение на степени 2.

Давайте посмотрим на пример:

Если у меня есть двоичное число 101010, это преобразуется в десятичное как:

32 + 0 + 8 + 0 + 2 + 0 = 42

Или:

1 * 2 5	32
0 * 2 4	0
1 * 2 3	8
0 * 2 2	0
1 * 2 1	2
0 * 2 0	0

Как видно из этого примера, двоичная система не так удобна для чтения и работы, как десятичная. Итак, вы можете спросить, зачем тогда возиться с двоичным кодом? Ответ заключается в том, что это более простой формат для работы с компьютерами. Его также можно использовать в других областях в качестве ярлыка для представления настроек.

Поскольку все степени двойки, кроме 0, дают четное число, единственный способ получить нечетное число — это сделать так, чтобы самая правая цифра была равна 1. Это можно использовать в качестве быстрой проверки при выполнении преобразований, которые вы еще не выполняли. совершил глупую ошибку.

Шестнадцатеричная и восьмеричная

Две другие системы счисления, которые обычно используются в вычислениях, — шестнадцатеричная и восьмеричная. Обе они также являются базовыми системами счисления.

• Шестнадцатеричное основание 16
• Восьмеричное основание 8

Оба тесно связаны с двоичным кодом. Вы заметите, что:

• 16 равно 2 ⁴
• 8 равно 2 ³

Это не относится к десятичным числам (нет степени двойки, равной 10). Это дает шестнадцатеричные и восьмеричные характеристики по отношению к двоичному, которых нет у десятичного. Мы рассмотрим их в следующем разделе, конверсии.

Для шестнадцатеричных чисел мы увеличиваем число до 15 (помните, что мы начинаем с 0). Как только мы доберемся до 9, мы добавим буквы алфавита от A до F, чтобы представить 10-15 (см. справочную таблицу ниже).

Возьмем десятичное число 27.

В шестнадцатеричном виде это будет 1B, что в десятичном виде будет:

1 * 16 ¹ + 11 * 16 ⁰ = 16 + 11

5 В восьмеричном будет 33, что в десятичной форме означает:

3 * 8 ¹ + 3 * 8 ⁰ = 24 + 3

Префиксы

Как видно из приведенных выше примеров, числа потенциально могут выглядеть одинаково независимо от того, являются ли они двоичными, десятичными, восьмеричными или шестнадцатеричными. Если бы я дал вам число 2F7, вы бы сразу поняли, что оно шестнадцатеричное, но если бы я дал вам число 101, то это:

• 101 в двоичном формате и 5 в десятичном
• 101 в десятичном формате
• 101 в шестнадцатеричном формате и 257 в десятичном формате
• 101 в восьмеричном и 65 в десятичном

??

Как видите, количество, которое представляет 101, сильно различается в зависимости от используемой базы. Чтобы избежать этой двусмысленности, мы добавляем префиксы к числам, чтобы идентифицировать их основу.

• Десятичное число не имеет префикса.
• Шестнадцатеричный код имеет префикс Ox, например: Ox1B
• Octal имеет префикс O, например: O421
• Двоичный файл имеет префикс Ob, например: Ob1101

Некоторые люди вместо этого используют суффикс, но они не так популярны:

• Десятичное число не имеет суффикса.
• Шестнадцатеричный код имеет суффикс H, например: 1BH
• Octal имеет суффикс O, например: 421O
• Двоичный файл имеет суффикс B, например: 1101B

Примечание: для префиксов и суффиксов выше это заглавная буква, а не ноль.

В большей части этого урока я не буду использовать префиксы, а укажу базу напрямую, чтобы было понятнее.

Справочная таблица

Вот справочная таблица для различных систем счисления.

Десятичный	Двоичный	Восьмеричный	Шестнадцатеричный
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	А
11	1011	13	Б
12	1100	14	С
13	1101	15	Д
14	1110	16	Е
15	1111	17	Ф

Вы заметите, что в двоичном файле есть шаблон. Крайний правый столбец чередуется между 0 и единицей. Следующий столбец делает то же самое, но по 2 за раз. Третий столбец делает то же самое, но по 4 за раз. Крайний левый столбец делает то же самое, но по 8 за раз. Этот шаблон упрощает проверку правильности написания.

Если вы сдаете экзамен по двоичному коду, вам часто не разрешают сдавать материал, но ничто не мешает вам самостоятельно нарисовать эту таблицу после начала экзамена. Это может быть хорошим справочным материалом, особенно для конверсий, которые мы рассмотрим в следующем разделе.

Совет

Это может быть немного сложно понять. Если чтение материала утомляет вас, вот что я предлагаю:

• Работайте с примерами на бумаге. Изучение двоичного кода похоже на езду на велосипеде. Лучший способ — просто сделать это.
• Оставьте это на день или два, затем вернитесь и попробуйте еще раз.

Шестнадцатеричная система: Объяснение системы счисления

В то время как десятичная система и ее десять цифр глубоко укоренились в нашей повседневной жизни, информатика и обработка данных в значительной степени зависят от двоичной системы, или двоичного кода . Двоичная система позволяет представлять сложные ситуации всего двумя состояниями: 0 и 1. Однако большие двоичные числа быстро запутываются. Вот где шестнадцатеричная система может помочь. Информация, выраженная с помощью восьми цифр в двоичной системе, может быть выражена с помощью всего двух шестнадцатеричных чисел.

Содержание

1. Какая шестнадцатеричная система?
2. Для чего используется шестнадцатеричная система?
3. Шестнадцатеричная система: как ее записывать
4. Связь между шестнадцатеричными и двоичными числами
5. Шестнадцатеричная таблица преобразования в десятичные и двоичные числа
6. Подсчет с помощью шестнадцатеричных чисел
7. Сводка

Доменные имена за 1 доллар

Зарегистрируйте отличные TLD менее чем за 1 доллар в первый год.

Зачем ждать? Получите свое любимое доменное имя сегодня!

Соответствующий адрес электронной почты

Сертификат SSL

Поддержка 24/7/365

Что такое шестнадцатеричная система?

Слово шестнадцатеричное состоит из терминов шестнадцатеричное и десятичное число . Hexa происходит от греческого и означает «шесть», тогда как decem — это латинское слово, означающее «десять». Шестнадцатеричная система, таким образом, является системой позиционных значений, которая представляет числа с использованием основания 16. Это означает, что шестнадцатеричная система использует 16 различных цифр. Другими словами, существует 16 возможных цифр, в отличие от двух в двоичной системе (0 и 1) и десяти в десятичной системе (от 0 до 9). Но какова цель системы?

Для чего используется шестнадцатеричная система?

Шестнадцатеричная система используется в компьютерных технологиях и делает большие числа и длинные битовые последовательности более удобочитаемыми. Они группируются в разделы по четыре бита, а затем преобразуются в шестнадцатеричные числа. В результате длинная последовательность единиц и нулей превращается в более короткие шестнадцатеричные числа, которые, в свою очередь, можно разделить на группы по два или четыре. Таким образом, шестнадцатеричные числа представляют собой более компактный способ представления битовых последовательностей. Система используется, например, для адресов источника и получателя в интернет-протоколах (IP), в кодах ASCII или для описания цветовых кодов в веб-дизайне с помощью языка таблиц стилей CSS.

Шестнадцатеричная система: как писать

Как упоминалось выше, шестнадцатеричная система использует 16 цифр. Здесь мы сталкиваемся с потенциальной проблемой. В нашем традиционном способе записи чисел мы используем десятичные числа 10, 11, 12, 13, 14 и 15, которые состоят из двух символов, сложенных вместе. Поэтому, если бы вы использовали число 10 в шестнадцатеричной системе счисления, было бы неясно, что вы имеете в виду.

Чтобы избежать этой проблемы, буквы от A до F используются для представления чисел от десяти до 15 в шестнадцатеричной системе счисления. Итак, всего чисел 9.0456 от 0 до 9 и от A до F используются для представления эквивалентов двоичных и десятичных чисел. There are various notations available for distinguishing hexadecimal numbers from decimal numbers:

• 73 ₁₆
• 73 _hex
• 73h
• 73H
• 73H
• 0x73
• $73
• #73
• «73
• X’73’

Префикс 0x и суффикс h особенно распространены в программировании, а префикс доллара $ часто используется в некоторых семействах процессоров на языке ассемблера.

Связь между шестнадцатеричными и двоичными числами

Когда дело доходит до представления сложных состояний, битовые последовательности и двоичные строки могут быть очень длинными. В ежедневном использовании десятичной системы мы используем группы из трех цифр, чтобы сделать больших чисел, таких как миллионы, миллиарды и триллионы, более удобочитаемыми. То же самое и с цифровыми системами. Чтобы сделать битовые последовательности, такие как 1111010111001111 ₂ легче читать, они обычно делятся на группы по четыре. Итак, наш пример будет выглядеть так: 1111 0101 1100 1111 ₂ . Читать становится еще легче, когда двоичные числа преобразуются в шестнадцатеричную систему.

Поскольку шестнадцать — это четвертая степень числа два (2 ⁴ ), существует прямая связь между числами два и шестнадцать: одна шестнадцатеричная цифра соответствует четырем двоичным цифрам . Это означает, что вы можете представить четырьмя цифрами 9.0457 из двоичного числа с одной шестнадцатеричной цифрой . Это делает преобразование между двоичными и шестнадцатеричными числами относительно простым, и большие двоичные числа могут быть записаны в шестнадцатеричной системе с меньшим количеством цифр.

Шестнадцатеричная таблица преобразования в десятичные и двоичные числа

Шестнадцатеричная система более сложна, чем двоичная и десятичная системы, и часто используется в связи с адресами памяти. Двоичные числа делятся на группы по четыре бита, и каждая группа битов имеет значение от «0000» до «1111». Это приводит к 16 различным комбинациям чисел от 0 до 15. Обратите внимание, что «0» также является допустимой цифрой.

4 7

9 7

4 7

4 7

0004 1100

959959959959959959959959959959959959959959959959 9005

Decimal number	4 bit binary number	Hexadecimal number
0	0000	0
1	0001	1
2	0010	2	0010	2	0005
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	01111159	0111115	0111115	0111115	0111159
7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12
12 999
12
C
13	1101	D
14	1110	E
15	1111	F
16	0001 0000	10 (1+0)
9 9 (1+0)
9 9000 4. 0004 17	0001 0001	11 (1+1)
18	0001 0010	12 (1+2)
19	0001 0011	13 (1+3)
20	0001 010095	14 (1+4) 999	14 (1+4). последовательность двоичных чисел 1111 0101 1100 1111 2 в шестнадцатеричной системе будет выглядеть так: F5CF . Это число намного легче читать, чем длинную последовательность битов. Шестнадцатеричная система может быть использована для записи цифрового кода с меньшим количеством цифр и, таким образом, меньше шансов сделать ошибку . Преобразование шестнадцатеричных чисел обратно в двоичные можно сделать так же просто, используя ту же шестнадцатеричную таблицу, что и выше. Чтобы было понятно, что число является шестнадцатеричным числом, мы можем записать его следующим образом: F5CF 16 , $F5CF или #F5CF . Последнее обозначение, также называемое хеш-значением, используется для цифрового цветового кодирования, поскольку дизайнеры и разработчики используют шестнадцатеричные цвета в веб-дизайне. Шестнадцатеричные цвета представлены шестизначной комбинацией цифр и букв, определяемой смесью красного, зеленого и синего цветов (RGB). #000000 обозначает черный цвет, а #FFFFFF — белый. Счет с помощью шестнадцатеричных чисел Теперь вы знаете, как преобразовывать двоичные числа в шестнадцатеричные числа. Если вы работаете с более чем четырьмя двоичными цифрами, просто начните сначала или продолжите со следующего набора из четырех битов. С двумя шестнадцатеричными цифрами вы можете считать до FF, что соответствует десятичному числу 255. Добавление дополнительных шестнадцатеричных цифр для преобразования двоичного числа в шестнадцатеричное очень просто, если у вас есть четыре, восемь, двенадцать или шестнадцать цифр. Но вы также можете добавить «0» или «00» слева от старшего бита, даже если количество двоичных разрядов больше не кратно четырем. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт