Статистика хи квадрат: что у них под капотом и какие выбрать для сравнения воронок — Gamedev на DTF

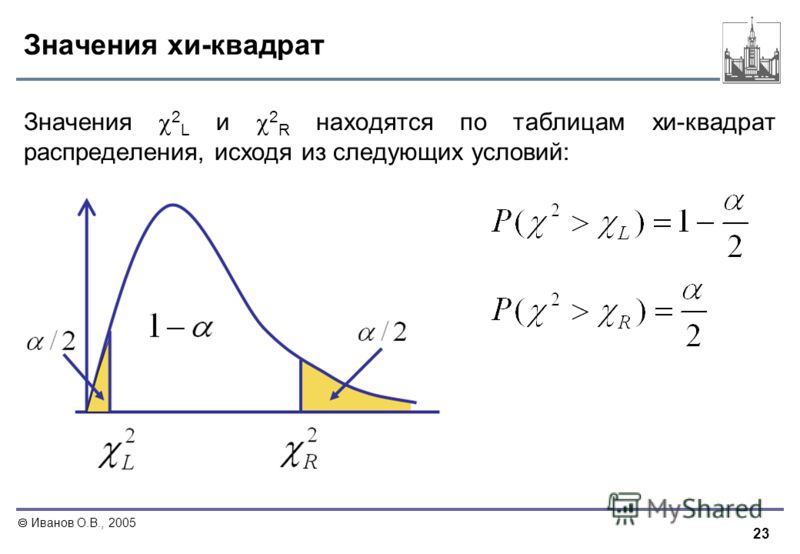
понимание гипотезы с использованием критерия хи-квадрат

Дата публикации Jul 11, 2019

ЦСИ

Как инженер по науке о данных, крайне важно, чтобы набор выборочных данных, который вы выбираете из данных о населении, был надежным, чистым и хорошо проверенным на предмет его пригодности для построения моделей машинного обучения.

Так как ты это делаешь?Ну, у нас есть несколько статистических методов, таких как описательная статистика, где мы измеряем центральное значение данных, как они распределяются по среднему значению / медиане. Это нормально распределено или в разбросе данных есть перекос. Пожалуйста, обратитесь к моей предыдущей статье на том же для большей ясности.

Основы описательной статистики для аспирантов по науке о данных

Прикладная статистика фундаментальная для аспирантов Data Science

towardsdatascience.com

Первым делом мы визуализируем данные с использованием различных методов визуализации данных, чтобы на ранних этапах осознать любую асимметрию или несоответствие данных, чтобы идентифицировать любые виды взаимосвязей между переменными набора данных.

Данные имеют так много, чтобы сказать, и мы, инженер данных, даем им право высказывать и описывать себя, используя описательные статистические методы.

Но для того, чтобы делать какие-либо прогнозы или делать какие-то выводы, помимо данных, чтобы найти скрытую вероятность, мы полагаемся на методы логической статистики.

Инференциальная статистика касается выводов, основанных на отношениях, найденных в выборке, на отношениях в популяции. Инференциальная статистика помогает нам, например, решить, достаточно ли сильны различия между группами, которые мы видим в наших данных, чтобы поддержать нашу гипотезу о том, что групповые различия существуют в целом по всему населению.

Сегодня мы рассмотрим один из логически выведенных статистических механизмов для понимания концепции проверки гипотез с использованием популярного теста хи-квадрат.

Помни об этом,

Это логический статистический тест, который работает с категориальными данными.

Тест хи-квадрат представляет собой статистический тест гипотезы, который предполагает (нулевая гипотеза), что наблюдаемые частоты для категориальной переменной соответствуют ожидаемым частотам для категориальной переменной. Тест вычисляет статистику, которая имеет распределение хи-квадрат, названное в честь греческой заглавной буквы Chi (X), произносится как «ки», как в кайте.

Мы пытаемся проверить вероятность тестовых данных (данных выборки), чтобы выяснить, является ли наблюдаемое распределение набора данных статистической случайностью (случайно) или нет.Статистика доброты соответствияв тесте хи-квадрат измеряет, насколько хорошо наблюдаемое распределение данных соответствует распределению, которое ожидается, если переменные являются независимыми.

Как работает Chi-Square?

Как правило, мы пытаемся установить связь между данной категориальной переменной в этом тесте. Хи-квадрат оценивает, являются ли данные переменные в наборе данных (выборке) независимыми, называемымиТест Независимости.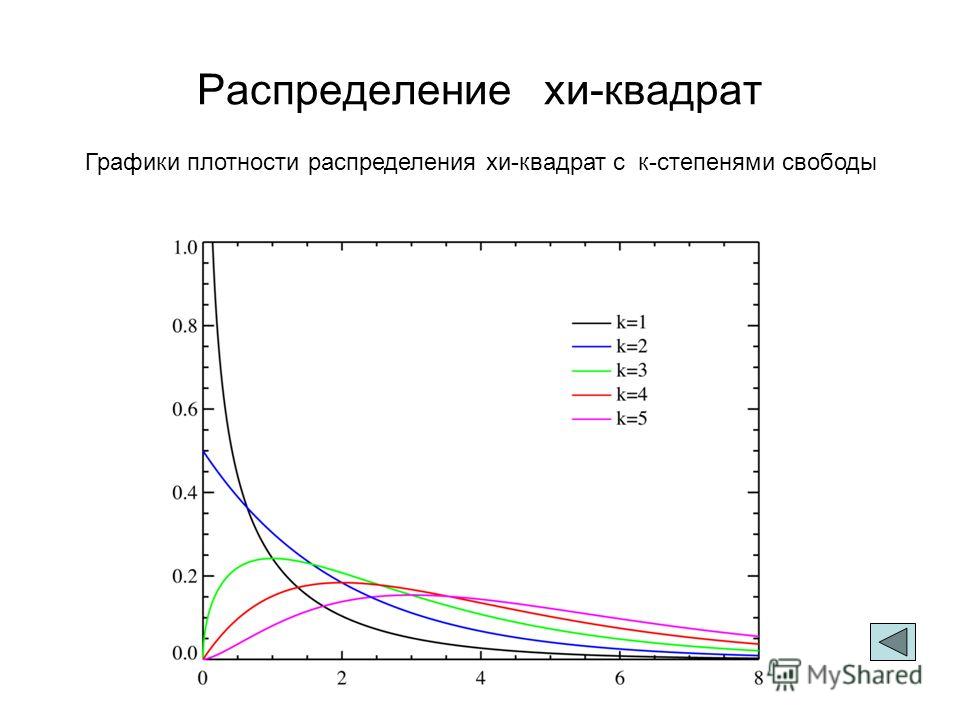 Критерии хи-квадрат используются для проверки гипотез об одной или двух категориальных переменных иуместно, когда данные могут быть обобщены путем подсчета в таблице, Переменные могут иметь несколько категорий.

Тип теста хи-квадрат:

Для одной категориальной переменной мы выполняем

• Тест Хи-квадрат

Проверка на соответствие критерия хи-квадрат начинается с предположения, что распределение переменной ведет себя определенным образом. Например, чтобы определить ежедневные кадровые потребности магазина розничной торговли, менеджер может пожелать узнать, существует ли равное количество покупателей каждый день недели.

Для двух категориальных переменных мы выполняем

• Тест хи-квадрат для ассоциации

Другой способ описать критерий хи-квадрат заключается в следующем:

Он проверяет нулевую гипотезу о том, что переменные являются независимыми.

Тест сравнивает наблюдаемые данные с моделью, которая распределяет данные в соответствии с ожиданием того, что переменные являются независимыми. В тех случаях, когда наблюдаемые данные не соответствуют модели, вероятность того, что переменные являются зависимыми, возрастает, что доказывает ошибочную гипотезу!

Гипотеза в хи-квадрат:

Прежде чем выполнять какие-либо дифференциальные статистические тесты, такие как Chi-Square, вы должны установить в качестве инженера данных.

• H0: нулевая гипотеза
• h2: альтернативный гипотез

Для одной категориальной переменной:

• Нулевая гипотеза: Пропорции соответствуют предполагаемому набору пропорций
• Альтернативная гипотеза: По крайней мере одна категория имеет другую пропорцию. •

Для двух категориальных переменных:

• Нулевая гипотеза: Нет никакой связи между двумя переменными
• Альтернативная гипотеза: Существует связь между двумя переменными

Прежде чем мы начнем понимать, как работает хи-квадрат на примере, нам необходимо понять, что такое распределение хи-квадрат и некоторые другие связанные понятия Это распределение хи-квадрат — это то, что мы будем анализировать в дальнейшем. хи-квадратилиχ2 теста.

распределение хи-квадрат(такжехи-квадратилиχ2-распределение) сКСтепени свободы это распределение суммы квадратовКнезависимые стандартные нормальные случайные величины.

Это одно из наиболее широко используемых распределений вероятностей в логической статистике, особенно при проверке гипотез или построении доверительных интервалов.

Основной причиной того, что распределение хи-квадрат широко используется при проверке гипотез, является его связь с нормальным распределением. Дополнительная причина, по которой широко используется распределение хи-квадрат, состоит в том, что он является членом класса тестов отношения правдоподобия (LRT). У LRT есть несколько желательных свойств; в частности, LRT обычно предоставляют высочайшую силу, чтобы отвергнуть нулевую гипотезу.

Степень свободы в распределении Чи в квадрате:

Степени свободы в распределении хи-квадрат равны числу суммируемых стандартных нормальных отклонений. Среднее значение распределения хи-квадрат — это его степени свободы. Говорят, что распределение хи-квадрат, построенное путем возведения в квадрат единственного стандартного нормального распределения, имеет 1 степень свободы

степени свободы(Д.Ф.илиd) скажу, сколько чисел в вашей сеткена самом деленезависимый. Для сетки хи-квадрат можно сказать, что степенью свободы является количество ячеек, которые необходимо заполнить до этого, учитывая итоги в полях, вы можете заполнить оставшуюся часть сетки, используя формулу.

Степени свободы для сетки хи-квадрат равны числу строк минус один раз, а число столбцов минус один: то есть (R-1) * (C-1).

Помнить!

По мере того как степень свободы (df) увеличивается, распределение хи-квадрат приближается к нормальному распределению

Формула для статистики хи-квадрат, используемая в тесте хи-квадрат:

Индекс «сВот степени свободы. «ОЭто ваша наблюдаемая ценность иЕваше ожидаемое значение Символ суммирования означает, что вам придется выполнять вычисления для каждого отдельного элемента данных в вашем наборе данных.

E = (общее количество строк × общее количество столбцов) / размер выборки

Статистика хи-квадрат может использоваться только для чисел. Они не могут быть использованы для процентов, пропорций, средних или аналогичных статистических значений. Например, если у вас 10 процентов из 200 человек, вам нужно преобразовать это число (20), прежде чем вы сможете запустить тестовую статистику.

Тест хи-квадрат включает в себя вычисление метрики, называемой статистикой хи-квадрат, упомянутой выше, которая следует за распределением хи-квадрат.

Давайте рассмотрим пример, чтобы получить ясность по всем вышеупомянутым темам, связанным с хи-квадрат:

P-значение:

Нулевая гипотеза обеспечивает вероятностную структуру, с которой можно сравнивать наши данные. В частности, с помощью предложенной статистической модели нулевая гипотеза может быть представлена ​​распределением вероятностей, называемымР-значение, который дает вероятность всех возможных результатов, если нулевая гипотеза верна;

Это вероятностное представление наших ожиданий при нулевой гипотезе.

Мы рассмотрим следующие важные шаги в нашем путешествии по тесту Chi_square для независимости двух переменных.

1. Государство Гипотеза
2. Сформулировать план анализа данных
3. Анализировать данные Smaple
4. Интерпретировать результат

Проблема: эта проблема была получена изstarttrek

Опрос общественного мнения опросил простую случайную выборку из 1000 избирателей. Респонденты были классифицированы по полу (мужчина или женщина) и по избирательному предпочтению (республиканец, демократ или независимый). Результаты показаны в таблице непредвиденных расходов ниже.

Мы должны сделать вывод, есть ли гендерный разрыв? Значительно ли отличаются предпочтения мужчин при голосовании? Используйте уровень значимости 0,05.

Давайте попробуем решить эту проблему, используя критерий хи-квадрат, чтобы узнать значение P.

Вот тип теста, который мы будем использовать:

Тест хи-квадрат на независимость.

Итак, начнем с того, что сначала изложим нашу гипотезу.

Шаг 1: сформулируйте гипотезу:

Здесь нам нужно начать с установления нулевой гипотезы и контр-гипотезы (альтернативной гипотезы), как указано ниже.

Нулевая гипотеза:

Хо: Пол и избирательные предпочтения независимы.

Альтернативная гипотеза:

h2: Пол и предпочтения голосования не являются независимыми.

Шаг 2: Давайте создадим наш план анализа данных:

Здесь мы попытаемся выяснить значение P и сравнить его с уровнем значимости. Давайте возьмем стандарт и принялиуровень значимости должен быть 0,05. Учитывая пример данных в таблице выше, давайте попробуем использоватьТест хи-квадрат на независимость и вывести значение вероятности

Шаг 3: Давайте сделаем анализ образца:

Здесь мы проанализируем данные образца для вычисления

• Степень свободы
• Ожидаемая частота отсчета переменной образца
• Рассчитать статическое значение критерия хи-квадрат

Все вышеперечисленные значения помогут нам найтиР-значение,

Степень свободы расчета:Давайте вычислим df = (r — 1) * (c — 1), поэтому в данной таблице r (строки) = 2 и c (столбец) = 3

df = (2–1) * (3–1) = 1 * 2 = 2;

Расчет ожидаемой частоты:

Пусть Eij, представляет ожидаемые значения двух переменных, не зависящих друг от друга.

Eij = ih (итоговая строка X итоговая сумма в столбце) / итоговая сумма

Давайте вычислим ожидаемое значение для каждой данной строки и значения столбца, используя вышеупомянутую формулу.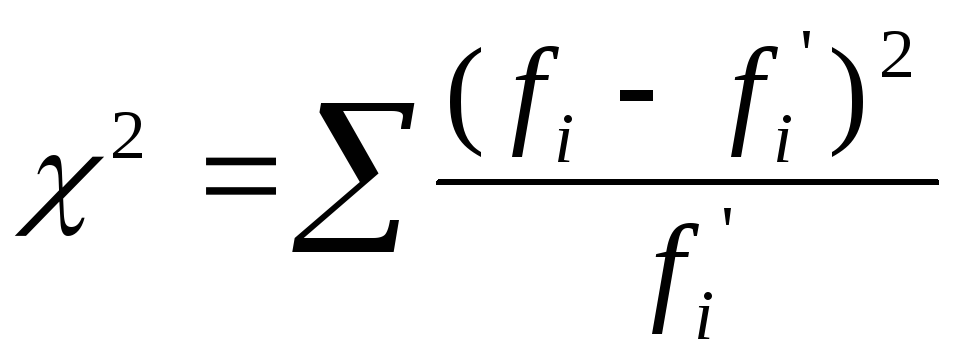 Позвольте мне снова скопировать изображение таблицы ниже, чтобы помочь вам сделать расчет легко,

Здесь общее значение строки 1 = 400, общее значение для column1 = 450, общий размер выборки = 1000,

Так ,

E1,1 = (400 * 450) / 1000 = 180000/1000 = 180

Аналогично, давайте рассчитаем другие ожидаемые значения, как показано ниже,

E1,2 = (400 * 450) / 1000 = 180000/1000 = 180
E1,3 = (400 * 100) / 1000 = 40000/1000 = 40
E2,1 = (600 * 450) / 1000 = 270000/1000 = 270
E2,2 = (600 * 450) / 1000 = 270000/1000 = 270
E2,3 = (600 * 100) / 1000 = 60000/1000 = 60

Время для вычисления хи-квадратов для каждого вычисленного ожидаемого значения выше по формуле:

Расчет Chi-Sqaures:

Как уже обсуждалось выше, формула для расчета статистики хи-квадрат

Статистическая формула хи-квадрат

Индекс «сВот степени свободы. «О”- ваше наблюдаемое значение (фактические значения приведены в таблице выше) иЕваше ожидаемое значение (которое мы только что рассчитали). Символ суммирования означает, что вам придется выполнять вычисления для каждого отдельного элемента данных в вашем наборе данных.

Χ² = Σ [(Oi, j — Ei, j) ² / Ei, j]

Используя приведенную выше формулу, наши значения хи-квадрат получаются такими, как указано ниже,

Χ² = (200–180) ² / 180 + (150–180) ² / 180 + (50–40) ² / 40 + (250–270) ² / 270 + (300–270) ² / 270 + (50– 60) ² / 60
Χ² = 400/180 + 900/180 + 100/40 + 400/270 + 900/270 + 100/60

Итак, наше окончательное значение статистики хи-квадрат,

Χ² = 2,22 + 5,00 + 2,50 + 1,48 + 3,33 + 1,67 = 16,2

Рассчитав значение хи-квадрат и степени свободы, мы просматриваем таблицу хи-квадрат, чтобы проверить, превышает ли статистика хи-квадрат 16,2 критическое значение для распределения хи-квадрат. Цель состоит в том, чтобы найтиЗначение P, которое является вероятностью того, что статистика хи-квадрат, имеющая 2 степени свободы, является более экстремальной, чем 16,2.

Как рассчитать P-значение?

Учитывая степень свободы = 2 и значение статистики хи-квадрат = 16,2, мы можем легко найти P-значение, используя это

Калькулятор хи-квадратссылку, просто введите статистическое значение хи-квадрат и степень свободы в качестве входных данных, а также сохраните свой уровень значимости как 0,05, вы найдете результат, как показано ниже,

Значение P =. 000304. Результат значим при р <0,05.

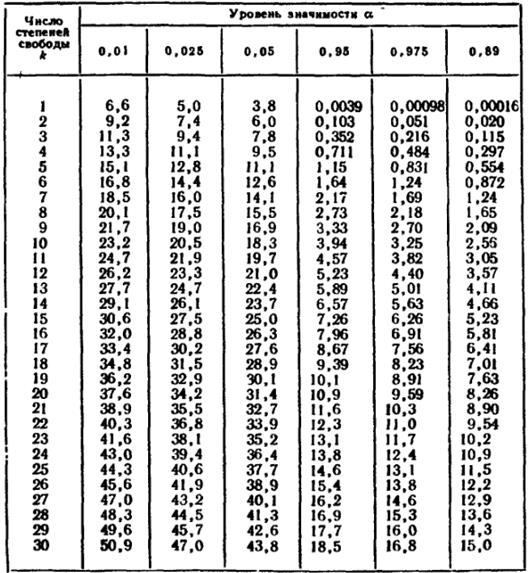
Вы также можете найти P-значение, используя таблицу хи-квадрат, приведенную ниже, вы можете получить эту таблицу из этогоисточник

Хи-квадрат стол

Рассчитав значение хи-квадрат равным 16,2, а степень свободы — 2, мы просматриваем приведенную выше таблицу хи-квадрат, чтобы проверить, превышает ли статистика хи-квадрат 16,2 критическое значение для распределения хи-квадрат.Критическое значение для альфа 0,05 (95% достоверности) для df = 2 получается 5,99

Шаг 4: Интерпретация результата

A: Вывод из P-значения:

Так как мы получили P-значение 0,000304, мы можем интерпретировать результат, где это означает, что

Поскольку значение P (0,000304) меньше уровня значимости (0,05),

Таким образом, мы должны отклонить приведенное ниже

Нулевая гипотеза, который говорит, гНастройки ender и голосования независимы.

и принятьАльтернативная гипотеза:

Что говорит, гендерные и избирательные предпочтения не являются независимыми.

Отсюда можно сделать вывод, что

Существует связь между полом и предпочтениями при голосовании.

B: Интерпретация из таблицы хи-квадрат:

Поскольку критическое значение для альфа 0,05 (достоверность 95%) для df = 2 составляет 5,99, а наше статистическое значение хи-квадрат 16,3 намного больше 5,99, у нас есть достаточно доказательств, чтобы отвергнуть нашу гипотезу Null, которую мы рассмотрели выше.

Итак, мы принимаем альтернативную гипотезу:

Что говорит, гендерные и избирательные предпочтения не являются независимыми.

Отсюда мы заключаем, что

Существует связь между полом и предпочтениями при голосовании

Мы поймем, как выполнить тест Chi-Square с использованием ноутбука Python & Jupyter во второй части этой серии статей.Инференциальная статистика: проверка гипотез с использованием хи-квадрати буду дальше исследовать

• Нормальный тест Devitate Z:
• Два образца T-теста
• Тест ANOVA

& также представит одну из ключевых тем: «Сила статистического теста »

Сила любого теста статистической значимости определяется как вероятность того, что он отвергнет ложную нулевую гипотезу.

Подводя итог этой части, с очень полезной инфографикой, которая поможет вам выбрать тип проверки гипотезы:

Кредит: Скотт Муни

Поэтому выбирайте свои тестовые данные с умом и убедитесь, что вы правильно интерпретируете выборочные данные, чтобы вы могли продолжить разработку моделей ML с необходимой точностью и уверенностью.

Ваша способность быть эффективным исследователем данных в значительной степени станет реальностью только в том случае, если вы знаете, как анализировать данные выборки с минимальным отклонением. Чем больше вы обрабатываете данные с необходимой точностью и очищаете их на предварительной стадии EDA, тем более надежными и продуктивными будут ваши усилия по построению модели.

Спасибо, что всегда были там и вдохновляли меня писать больше …

Оригинальная статья

Тест независимости хи-квадрат — MathCracker.com

Решатели Статистика

---

Инструкции: Этот калькулятор выполняет проверку независимости по критерию хи-квадрат. Пожалуйста, сначала укажите количество столбцов и строк для перекрестной таблицы. Затем введите данные таблицы, уровень значимости и, при необходимости, имя строк и столбцов, и результаты теста хи-квадрат будут представлены вам ниже:

Num. Rows = Num. Cols =   

---

Хи-квадрат независимости — это тест, используемый для категориальных переменных, чтобы оценить степень связи между двумя переменными. Иногда критерий независимости хи-квадрат называют критерием хи-квадрат на однородность дисперсий, но они математически эквивалентны. Идея теста состоит в том, чтобы сравнить информацию об образце (наблюдаемые данные) со значениями, которые можно было бы ожидать, если бы две переменные действительно были независимыми. Основные свойства теста независимости хи-квадрат:

• Распределение тестовой статистики — это распределение хи-квадрат с \((r-1)\times(c-1)\) степенями свободы, где r — количество строк, а c — количество столбцов.
  2 }{E_{ij} }\]

  Одно из наиболее распространенных применений этого теста — оценить, связаны ли две категориальные переменные в значительной степени или нет.

  Обычно критерий хи-квадрат на независимость упоминается как 2-сторонняя перекрестная таблица тестовое задание. Если у вас есть односторонняя перекрестная таблица, вам следует использовать Проверка согласия по критерию хи-квадрат .

  Что делать, если у вас есть парные данные?

  Если у вас есть парные данные, вместо использования калькулятора хи-квадрат вам следует использовать этот Калькулятор теста Макнемара .

  ---

  Базовый пакет статистики О Square Test Статистика хи-квадрат Хи-квадрат тест независимости Проверка гипотез Статистический тест Статистический решатель

  Таблица хи-квадрата (правый хвост)

  
  
  

  Таблица хи-квадрата

  Приведенная ниже таблица хи-квадрата используется для проверки гипотез. Это поможет вам решить, принять или отклонить нулевую гипотезу. В следующей таблице хи-квадрата приведены наиболее распространенные значения хи-квадрата. Вы можете найти

  точных цифр с помощью Excel (как вычислить значение хи-квадрат p в Excel), SPSS (как выполнить хи-квадрат в SPSS) или другой технологии. Однако в подавляющем большинстве случаев таблица хи-квадрат даст вам нужное значение.

  Посмотрите видео, показывающее, как читать критические значения в таблице хи-квадрат. Видео включает в себя примеры задач со случайными величинами хи-квадрат.

  Как читать значения таблицы критических значений хи-квадрат

  Посмотрите это видео на YouTube.

  Видео не видно? Кликните сюда.

  Таблица хи-квадрат

  Правые хвостовые области для

  Хи-квадрат Распределение

  df\area	.995	.990	.975	.950	.900	.750	. 500	.250	.100	.050	.025	.010	.005
  1	0,00004	0,00016	0,00098	0,00393	0,01579	0,10153	0,45494	1.32330	2.70554	3,84146	5.02389	6,63490	7,87944
  2	0,01003	0,02010	0,05064	0,10259	0,21072	0,57536	1.38629	2,77259	4.60517	5,99146	7.37776	9.21034	10,59663
  3	0,07172	0,11483	0,21580	0,35185	0,58437	1.21253	2,36597	4.10834	6.25139	7,81473	9.34840	11.34487	12.83816
  4	0,20699	0,29711	0,48442	0,71072	1. 06362	1,92256	3,35669	5.38527	7,77944	9.48773	11.14329	13.27670	14.86026
  5	0,41174	0,55430	0,83121	1.14548	1.61031	2,67460	4.35146	6.62568	9.23636	11.07050	12.83250	15.08627	16.74960
  6	0,67573	0,87209	1.23734	1,63538	2.20413	3.45460	5.34812	7.84080	10.64464	12.59159	14.44938	16.81189	18.54758
  7	0,98926	1.23904	1,68987	2.16735	2.83311	4.25485	6.34581	9.03715	12.01704	14.06714	16.01276	18. 47531	20.27774
  8	1.34441	1,64650	2.17973	2,73264	3.48954	5.07064	7.34412	10.21885	13.36157	15.50731	17.53455	20.09024	21.95495
  9	1.73493	2.08790	2.70039	3.32511	4.16816	5.89883	8.34283	11.38875	14.68366	16.91898	19.02277	21.66599	23.58935
  10	2.15586	2,55821	3,24697	3.94030	4.86518	6.73720	9.34182	12.54886	15.98718	18.30704	20.48318	23.20925	25.18818
  11	2.60322	3.05348	3,81575	4.57481	5,57778	7. 58414	10.34100	13.70069	17.27501	19.67514	21.92005	24.72497	26.75685
  12	3.07382	3,57057	4.40379	5.22603	6.30380	8.43842	11.34032	14.84540	18.54935	21.02607	23.33666	26.21697	28.29952
  13	3,56503	4.10692	5.00875	5.89186	7.04150	9.29907	12.33976	15.98391	19.81193	22.36203	24.73560	27.68825	29.81947
  14	4.07467	4.66043	5.62873	6.57063	7,78953	10.16531	13.33927	17.11693	21.06414	23.68479	26.11895	29. 14124	31.31935
  15	4.60092	5.22935	6.26214	7.26094	8.54676	11.03654	14.33886	18.24509	22.30713	24.99579	27.48839	30.57791	32.80132
  16	5.14221	5.81221	6.	7,96165	9.31224	11.91222	15.33850	19.36886	23.54183	26.29623	28.84535	31,99993	34.26719
  17	5.69722	6.40776	7,56419	8.67176	10.08519	12.79193	16.33818	20.48868	24.76904	27.58711	30.19101	33.40866	35.71847
  18	6.26480	7.01491	8.23075	9. 39046	10.86494	13.67529	17.33790	21.60489	25.98942	28.86930	31.52638	34.80531	37.15645
  19	6.84397	7,63273	8.	10.11701	11.65091	14.56200	18.33765	22.71781	27.20357	30.14353	32.85233	36.19087	38.58226
  20	7.43384	8.26040	9.59078	10.85081	12.44261	15.45177	19.33743	23.82769	28.41198	31.41043	34.16961	37.56623	39,99685
  21	8.03365	8.89720	10.28290	11.59131	13.23960	16.34438	20.33723	24.93478	29.61509	32. 67057	35.47888	38.93217	41.40106
  22	8.64272	9.54249	10,98232	12.33801	14.04149	17.23962	21.33704	26.03927	30.81328	33.92444	36.78071	40.28936	42.79565
  23	9.26042	10.19572	11.68855	13.09051	14.84796	18.13730	22.33688	27.14134	32.00690	35.17246	38.07563	41.63840	44.18128
  24	9.88623	10.85636	12.40115	13.84843	15.65868	19.03725	23.33673	28.24115	33.19624	36.41503	39.36408	42.97982	45.55851
  25	10. 51965	11.52398	13.11972	14.61141	16.47341	19.93934	24.33659	29.33885	34.38159	37.65248	40.64647	44.31410	46.92789
  26	11.16024	12.19815	13.84390	15.37916	17.29188	20.84343	25.33646	30.43457	35.56317	38.88514	41.92317	45.64168	48.28988
  27	11.80759	12.87850	14.57338	16.15140	18.11390	21.74940	26.33634	31.52841	36.74122	40.11327	43.19451	46.96294	49.64492
  28	12.46134	13.56471	15.30786	16.92788	18.93924	22. 65716	27.33623	32.62049	37.91592	41.33714	44.46079	48.27824	50,99338
  29	13.12115	14.25645	16.04707	17.70837	19.76774	23.56659	28.33613	33.71091	39.08747	42.55697	45.72229	49.58788	52.33562
  30	13.78672	14.95346	16.79077	18.49266	20.59923	24.47761	29.33603	34.79974	40.25602	43.77297	46.97924	50.89218	53.67196

  
  

  Пример задачи с использованием таблицы хи-квадрат

  Пример вопроса: : Вы работаете на производителя семян. Вы хотите выяснить, есть ли связь между гибридными растениями и сколько отклонений (т. е. нежелательных растений) возникает. Кукуруза бывает двух видов: синяя и желтая. Вероятность того, что отклонения произойдут случайно, составляет около 5%. Найдите критическое значение хи-квадрат, используя таблицу хи-квадрат.

  Шаг 1: Вычтите 1 из числа категорий, чтобы получить степени свободы. Категории — синяя кукуруза и желтая кукуруза, поэтому df = 2-1 = 1,

  Шаг 2: Найдите свои степени свободы и вероятность в таблице хи-квадрат. Вероятность указана вам в вопросе (5% или 0,05).

  Одна степень свободы и 5-процентная вероятность составляют 3,84 в таблице хи-квадрат. Это ваше критическое значение хи-квадрат.

  
  Поиск df=1 и вероятности 5% в таблице хи-квадрат.

  Совет: Небольшое значение из таблицы хи-квадрат означает, что между двумя переменными нет большой связи. Большее значение указывает на большую взаимосвязь между двумя вашими переменными.

  Ссылки

  Бейер, В. (2017). Справочник таблиц вероятностей и статистики, 2-е издание. КПР Пресс.

  УКАЗЫВАЙТЕ ЭТО КАК:
  Стефани Глен . «Таблица хи в квадрате (правый хвост)» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/tables/chi-squared-table-right-tail/

  ————————————————— ————————-

  Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

  Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

  
  

  Проверка пригодности: определение

  
  

  Статистические определения > Проверка пригодности

  Проверка пригодности показывает, представляют ли данные вашей выборки данные, которые вы ожидаете найти в реальной совокупности. В частности, он используется для проверки того, соответствуют ли выборочные данные распределению определенной совокупности (т. е. совокупности с нормальным распределением или совокупности с распределением Вейбулла).

  Критерии согласия, обычно используемые в статистике:

  
  
  
  1. Хи-квадрат.
  2. Колмогоров-Смирнов.
  3. Андерсон-Дарлинг.
  4. Шапиро-Вилк.

  Тест хи-квадрат является наиболее распространенным из тестов на пригодность, и именно его вы встретите в статистике AP или элементарной статистике. Хи-квадрат можно использовать для дискретных распределений, таких как биномиальное распределение и распределение Пуассона, в то время как тесты согласия Колмогорова-Смирнова и Андерсона-Дарлинга можно использовать только для непрерывных распределений.

  Формула хи-квадрат.

  Посмотрите видео с обзором тестов хи-квадрат:
  

  Тест хи-квадрат Введение

  Посмотрите это видео на YouTube.

  Видео не видно? Кликните сюда.

  Два возможных недостатка метода хи-квадрат:

  1. Тест хи-квадрат можно использовать только для данных, помещенных в классы (бины). Если у вас есть данные, не объединенные в бины, вам нужно будет сделать таблицу частот или гистограмму перед выполнением теста.
  2. Другим недостатком теста хи-квадрат является то, что он требует достаточного размера выборки, чтобы аппроксимация хи-квадрат была достоверной.

  Существует еще один тип критерия хи-квадрат, который называется критерием хи-квадрат для независимости. Их иногда путают, но они совершенно разные.

  • Тест хи-квадрат на независимость сравнивает два набора данных, чтобы определить, существует ли взаимосвязь.
  • Хи-квадрат Правильность подгонки состоит в том, чтобы подобрать одну категориальную переменную к распределению.

  Оба теста используют статистику хи-квадрат и распределение. Для получения дополнительной информации о расчете статистики хи-квадрат см. :
  Статистика теста хи-квадрат (включает расчеты): Что такое статистика хи-квадрат?

  
  

  Выполнение теста

  Обычно этот тест выполняется с помощью программного обеспечения. Нулевая гипотеза для критерия согласия хи-квадрат состоит в том, что данные поступают из определенного распределения. Альтернативная гипотеза состоит в том, что данные не поступают из определенного распределения.

  Для интерпретации теста вам необходимо выбрать альфа-уровень (обычно 1%, 5% и 10%). Тест хи-квадрат вернет p-значение. Если p-значение мало (меньше уровня значимости), можно отклонить нулевую гипотезу о том, что данные получены из указанного распределения.

  Хотя Колмогорова-Смирнова называют тестом на нормальность, он на самом деле не говорит вам, вероятно ли, что конкретная выборка была получена из нормальной популяции. Вместо этого он сообщит вам, когда маловероятно, что у вас нормальное распределение. Одним из преимуществ этого теста является то, что он не делает никаких предположений о распределении данных. Выборку можно сравнить с распределением, используя одновыборочный критерий K – S или двухвыборочный критерий K – S. Тест обычно выполняется с помощью программного обеспечения (например, SPSS), потому что критические значения должны быть рассчитаны для каждого распределения, а найти таблицы критических значений — непростая задача. Тест обычно рекомендуется для больших выборок более 2000. Для меньших выборок используйте Шапиро-Уилка.

  Андерсон-Дарлинг — модификация Колмогорова-Смирнова. Он более чувствителен к отклонениям в хвостах распределения. Как и тест Колмогорова-Смирнова, этот тест покажет вам, когда маловероятно, что у вас нормальное распределение, и обычно выполняется с использованием статистического программного обеспечения.

  Тест Шапиро-Уилка вычисляет значение W, которое покажет вам, была ли случайная выборка получена из нормально распределенной совокупности. Тест рекомендуется для образцов до n = 2000.

  Литература

  Beyer, WH Стандартные математические таблицы CRC, 31-е изд.