Сравнение матрицы фотоаппаратов: Какую матрицу в камере выбрать – что будет лучшим?

Матрицы и камеры

Производителей цифровых камер больше, чем тех кто «умеет» делать матрицы. Схем используемых объективов не много. Но споры о том, чьи фотографии лучше не прекращаются. Алгоритмы преобразования сигнала с матрицы «в файл», дизайн и пользовательские функции — то, над чем собственно и могут потрудиться «фирменные» конструкторы.

И все же интересно — много ли зависит от матрицы и могут ли камеры с близкими по характеристикам CCD/CMOS (или даже идентичными) сильно отличаться по фотографическим возможностям и изображению.

Для сравнения были взяты экземпляры распространенных и очень удачных цифровых камер «полупрофессионального» уровня. Все они уже были испытаны ранее и описаны. Технические характеристики и описания: Canon Power Shot G2, Olympus C-5050ZOOM, Casio QV4000 и здесь, Casio QV5700, Nikon Coolpix 5000. Данные о матрицах взяты из этих же материалов, а так же статей о матрицах и итогах года. В прочем SONY и Panasonic не держат секретов об уже выпущенных светочувствительных чипах и найти их описание можно через любую поисковую систему в сети. Труднее установить, что же конкретно установлено в цифровой фотоаппарат.

Отобранные для сравнения аппараты интересны тем, что два из них практически идентичны по конструкции, но имеют матрицы разных производителей и разрешения (Casio), Canon G2 и Casio QV4000 собраны на одинаковых матрицах и объективах, но различны по конструкции и используемым алгоритмам «оцифровки», 5-ти мегапиксельные аппараты собраны на матрицах разных производителей и размеров. Так что есть, что сравнить.

То, что дизайнеры могут по разному использовать ресурсы матриц хорошо видно на примере Canon G2 и Casio QV4000. При одной и той же матрице и объективе, аппараты отличаются максимальным форматом кадра, диапазоном возможных светочувствительностей (у Casio вообще единственное базовое значение ISO) и наличием RAW (у Casio формально RAW нет). Возможно, что такая «искусственная скромность» Casio результат «рыночного соглашения». И это вполне вероятно — ведь множество функций Casio QV4000 скрыты от «рядового пользователя» (смотри здесь) но все же существуют. Прямой конкурент Casio QV5700 с 1/1,8″ матрицей Panasonic — Olympus C-5050 с такой же по размеру и разрешению матрицей от Sony. В Nikon Coolpix 5000 установлена 5 мегапиксельная и в 2/3″ — большая матрица с наибольшим размером отдельного чувствительного элемента — 3,4 микрона. При таком «большом» элементе и матрице максимальная диафрагма в F/8 и то только для широкого угла выглядит скромной в сравнении с F/10 у Olympus с его меньшей матрицей.

камера	Canon PowerShot G2	Olympus С-5050 Zoom	Casio QV4000	Casio QV5700	Nikon 5000
матрица	Sony ICX406AQ	Sony ICX452	Sony ICX406AQ	Panasonic MN39594PH-L	Sony ICX282
матрица, размер	1/1,8″	1/1,8″	1/1,8″	1/1,8″	2/3″
матрица, эффективных элементов млн	3,9	4,92	3,98	4,92	4,92
Размер элемента мкм	3,12×3,12	2,775×2,775	3,12×3,12	2,7×2,7	3,4×3,4
чувствительность	50, 100, 200, 400	100, 200, 400	64 (100)	50, 100, 200, 400, 800	100, 200, 400, 800
кадр	2272×1704	2560×1920	2240×1680	2560×1920	2560×1920
диафрагма	F/2,0 — F/2,5 -F/8	F/1,8 — F/10	F/2,0 — F/2,5 -F/8	F/2,0 — F/2,5 -F/8	W F/2,8 — F/8 T F/4,8 — F/7,6

Одной из ключевых характеристик цифрового фотоаппарата является его «шумность». Она и была использована для сравнения камер. Про методики определения и оценки шум можно посмотреть здесь и здесь. «Мерой шумности для цифровой фотографии можно считать стандартное отклонение — среднеквадратичное отклонение от среднего, которое выводит Photoshop для всей картинки или выделенной ее области в меню «Гистограмма» (можно смотреть значение среднего и отклонения для яркости L или любого из цветов выбранного цветового пространства RGB, HSB, LAB)».

При испытаниях на световой столик укладывалась молочная пленка, запечатанная черными чернилами различной плотности в четырех отдельных зонах. Камера устанавливалась на штатив и производилась съемка с максимальной и минимальной возможной для камеры чувствительностью. Для сглаживания неоднородностей тестового объекта объектив камеры расфокусировался, а диафрагма устанавливалась максимально открытой. Баланс белого устанавливался вручную, экспозиция по экспонометру и с вилкой ±1 ступень выдержки. Съемка производилась в TIFF или RAW. Из снимка вырезались 4 квадратика различной оптической плотности размером 150×150 пикс. Таким образом для каждого фотоаппарата было получено по набору однородных квадратиков для максимальной и минимальной чувствительности. С помощью Photoshop можно определить для каждого из квадратиков значение яркости L и стандартного отклонения яркости dL. Далее не составит труда построить зависимость шума от яркости L. Величиной, характеризующей шум традиционно считается 20хLg(dL/L). Исходные данные в Excel можно посмотреть здесь. Зависимость шума от яркости для каждой камеры представлена в фильме Shockwave Flash:Для удобства сравнения можно «включить» только необходимые камеры и величины светочувствительности.

Лучший результат при минимальной чувствительности у Nikon 5000. И это не удивительно — его чувствительный элемент наибольший, а система фильтров C-Y-G-M теоретически использует свет более эффективно, чем G-R-G-B. Так же вполне логично и то, что Canon G2 и Casio QV4000 шумят почти одинаково. 5-ти мегапиксельная матрица SONY 1/1,8″ (Olympus C-5050) шумит чуть сильнее конкурента от Panasonic (Casio QV5700). На максимальной чувствительности Nikon 5000 с его ISO 800 уступает только Olympus C-5050 с ISO 400 и лучше других аппаратов с ISO 400 и 800. Так что размер отдельной ячейки все еще важен.

Дополнительно для визуальной оценки «шумности» приведены фрагменты квадратиков близкой яркости для минимальной возможной чувствительности и разных камер (яркость некоторых фрагментов немного изменена для «удобства» сравнения, у фрагмента Casio QV4000 цвета приведены к «серому», так как ручной баланс «сработал» некорректно):

Olympus C5050ZOOM ISO64 1/100 c F/2,6
Nikon Coolpix 5000 ISO100 1/37 c F/4,8
Canon PS G2 ISO50 1/8 c F/2,5
Casio QV4000 ISO 64 (100) 1/139 c F/2
Casio QV5700 ISO 50 1/93 c F/2

Выводы:

1.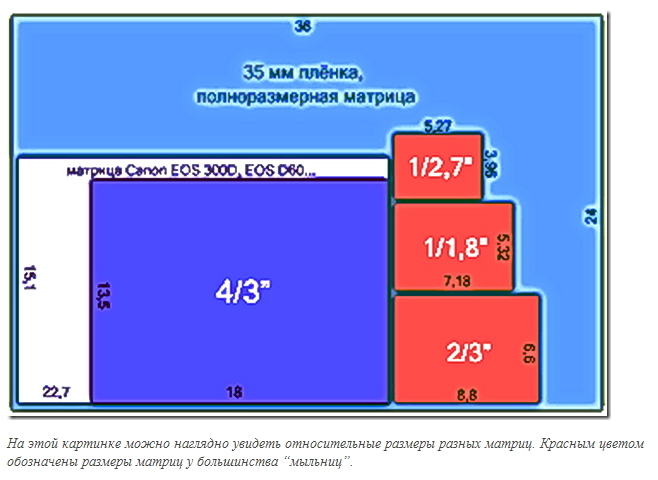 Большая матрица с большим светочувствительным элементом шумит меньше.

2. Шумы Canon G2 и Casio QV4000 очень похожи и если предположить, что у этих аппаратов с одинаковыми матрицами и объективами алгоритмы оцифровки разные, то надеяться на «всесилие математики» в борьбе с шумами пока рано и главное все же матрица.

3. Так как камеры собраны на базе близких по характеристикам матриц (или вообще одних и тех же), то как и в случае с пленкой выбирать следует (в одном классе) тот фотоаппарат, который устраивает вас функционально и просто вам «по душе».

Камеры предоставлены компанией «Компьютер для любителей фото»

4 июля 2003 Г.

Сергей Щербаков

Новости

• Fujifilm прощается со 100-мегапиксельной среднеформатной камерой GFX 100

  5 марта 2023

• Опубликованы изображения портретного объектива Sony FE 50mm F/1.4 GM

  12 февраля 2023

• Fujifilm готовит новую камеру линейки X. Премьера Fujifilm X-S20 ожидается в апреле

  29 января 2023

Раздел новостей >

Полнокадровая технология — Sony Pro

• Профессиональные камеры
• Вещательные и студийные камеры
• Цифровые кинокамеры
• Камкордеры
• Роботизированные и PTZ-камеры

• Вещание и видеопроизводство
• Профессиональные мониторы
• Деки и рекордеры
• Микшеры и системы для прямых трансляций
• Профессиональные носители

• Архивирование и управление медиаресурсами
• Архивирование данных на базе оптических дисков
• Управление медиаресурсами
• Оцифровка и консолидация

• Аудио
• Профессиональный звук

• Медицина
• Мониторы
• Принтеры и носители для печати

---

• Просмотреть все >

• Кинематограф

• Вещание и видеопроизводство

• Спорт

• Развлечения

• Образование

• Бизнес

• Intelligent Media Services

---

• Просмотреть все >

• Профессиональные камеры

• Вещание и видеопроизводство

• Проекторы

• Профессиональные дисплеи

• Архивирование и управление медиаресурсами

• Аудио

• Системы сетевых камер

• Медицина

• Видеосистемы безопасности

• Сервисы и поддержка

• Ресурсы по продукту

• Мероприятия

• Авторизованные сервисные центры

• Что такое полнокадровая матрица?
• Преимущества
• Почему именно Sony
• Продукты

Что такое полнокадровая матрица?

Полнокадровая матрица отличается от других своим размером — 36 мм на 24 мм — и техническими характеристиками, благодаря которым получаются невероятно красивые кадры. По сравнению с матрицей Super 35, полнокадровая почти вдвое больше, что позволяет увеличить угол обзора и снизить глубину резкости. 
Полнокадровые матрицы вне всяких сомнений являются самыми большими и популярными сенсорами сегодня. Сами по себе они обладают улучшенными функциями, а также используют инновационные технологии, что делает эти матрицы идеальным решением для реализации творческих возможностей в сфере цифровой кинематографии.

Loading video…

Безграничные возможности полного кадра: как снимают камкордеры FX9 и VENICE

История создания полнокадровой матрицы

Почему полнокадровая матрица такого размера? В начале 1900-х гг. в сфере кинематографии стали использовать 35-миллиметровую пленку в качестве универсального стандартного решения. Позже для фотосъемки начали производить кассеты тип-135. Во время создания фильмов традиционным способом пленка в камере движется в вертикальном направлении, что позволяет снимать в различных форматах изображения.

Например, в формате Super 35, при котором шаг кадра в 3 перфорации равен отдельному широкоформатному кадру 24,89 х14 мм. В фотокамере пленка движется в горизонтальном направлении, при этом размер кадра — 36 х 24 мм, а шаг кадра — 8 перфораций. Это самый большой и популярный формат изображения для съемки на 35-миллиметровую пленку, который обычно называют полнокадровым форматом.

В начале XXI века появились цифровые камеры с матрицами Super 35, включая инновационную модель F35 от Sony, которые снимали не хуже, чем кинокамеры. Так началась цифровая революция в мире кино. Однако производители кинокамер продолжали разрабатывать новые технологии и начали выпускать модели с матрицами больше, чем Super 35. Намного больше.

Loading video…

Известный режиссер Алистер Чапман изучает возможности и преимущества полнокадровой съемки

Преимущества полнокадровых матриц

Размер кадра при съемке на полнокадровую камеру такой же, как у 35-миллиметровых фотокамер. Это позволяет использовать объективы и узлы крепления от старых кинокамер для оснащения новых цифровых моделей, а также обеспечивает те же параметры кадрирования, фокуса, глубины резкости и принципы съемки. В результате вы получаете знакомую и удобную конструкцию с улучшенными возможностями. Более того, полнокадровые модели поддерживают Super 35 и другие форматы изображения.

Более широкий угол обзора

Полнокадровая матрица больше, чем матрица Super 35, что позволяет делать широкоформатные снимки. Поэтому во время съемки на полнокадровую камеру вам не нужно менять объектив и отходить дальше, чтобы захватить в кадр всю сцену. Изучите изображения ниже, чтобы увидеть разницу.

Полный кадр (16:9)

Super 35 (16:9)

Эффектные кадры с разной глубиной резкости

Полнокадровые матрицы обеспечивают небольшую глубину резкости, что позволяет эффективно использовать все функции объективов с большой апертурой. Благодаря этому камера, оснащенная таким объективом и матрицей, может сфокусироваться на определенном объекте и выделить его среди других, заставляя зрителей на подсознательном уровне обратить на него внимание, чтобы передать суть происходящего на экране.

Небольшая глубина резкости

Большая глубина резкости

Больше форматов благодаря полнокадровой матрице

Благодаря своей полнокадровой матрице с разрешением в 6K камера поддерживает много различных форматов в соответствии с разными зонами развертки. Полнокадровая матрица 6K обеспечивает исходное разрешение 4K при съемке на объективы Super 35, а также во множестве анаморфотных режимов*¹, включая режим Open Gate для 35-миллиметровых объективов. Это значит, что матрица позволяет вести съемку как на специальные полнокадровые объективы, так и на традиционные кинообъективы Super 35 и анаморфотные модели. При съемке в 4K с разверткой Super 35 камера будет прекрасно работать в сравнении с традиционными камерами 4K, имеющими объективы Super 35. Пользователи камеры Venice от Sony могут выбирать нужный из множества режимов сенсора и форматов изображения. Также в камере FX9 поддерживается съемка в 2K с режимом развертки Super 16*².

*¹ Во встроенном ПО версии 3. 0 будет поддерживаться вывод разжатого изображения на видоискатель и отображение межкадрового поля при съемке на анаморфотный объектив
*² Во встроенном ПО версии 3.0 будет поддерживаться съемка в 2K с режимом развертки Super 16.

Четкость и передискретизация благодаря высокому разрешению

Большой размер полнокадровой матрицы означает, что можно вести съемку с более высоким разрешением (с увеличенным количеством светочувствительных элементов) или повышенной чувствительностью (с более крупными светочувствительными элементами) либо, как это часто бывает, использовать оба метода. Также можно снимать в высоком разрешении с передискретизацией: когда матрица обрабатывает больше пикселей, чем это требуется, чтобы получить финальный кадр, но при этом задействует улучшенную функцию обработки изображения, доступную в камере, чтобы повысить четкость и сохранить детали, которые могли бы быть утеряны в случае использования небольшой матрицы с низким разрешением.

Светочувствительные элементы матриц с одинаковым разрешением

Воспроизведение высокодетализированных изображений, начиная от картинок в 6K с помощью фильтра Байера

Изображения слева направо: схема размещения пикселей фильтра Байера, байеризация, цветное дебайеризированное изображение.​

Полнокадровая передискретизация для потрясающих изображений в 4K, UHD и HD

Шум от наложения спектров возникает, когда частотный компонент входного сигнала выше ½ частоты дискретизации (частоты Найквиста) во время настройки параметров сигнала. При снижении разрешения может возникнуть шум от наложения спектров. При съемке в 4K на камеру с полнокадровой матрицей 6K шум от наложения спектров снижается, а изображение становится более четким и резким.

Широкий выбор объективов

Полнокадровая матрица позволяет вести съемку на множество моделей из ряда полнокадровых объективов, а также фото- и кинообъективов Super 35.

Полнокадровые матрицы и новые технологии

Помимо улучшенных функций самих полнокадровых матриц, в таких камерах используются дополнительные технологии, которые повышают производительность и обеспечивают широкие творческие возможности.

Динамический диапазон и технология Exmor R 

Динамический диапазон обычно измеряется в ступенях. Это единица измерения апертуры или диафрагмы объектива. Качественная матрица может различать больше ступеней серого между черным и белым цветом. Например, динамический диапазон человеческого глаза составляет приблизительно 10–15 ступеней. 

Полнокадровые матрицы обеспечивают улучшенный динамический диапазон благодаря светочувствительным элементам большего размера и продуманной конструкции. Чтобы улучшить эти характеристики, инженеры Sony разработали технологию Exmor R, которая используется в камкордере FX9. С ее помощью, как показано ниже, была полностью изменена структура пикселей. В результате полнокадровые матрицы от Sony могут использовать динамические диапазоны, как у человеческого глаза, и даже недостижимые для него. 

Матрица Exmor CMOS

Традиционная матрица с передней подсветкой, используемой в камере FS7II

CMOS-матрица Exmor R

Матрица с тыльной подсветкой, используемой в камере FX9

Два стандартных параметра ISO

Для эффективной работы цифрового датчика изображения необходимо использовать базовое значение ISO. Благодаря ему вы обеспечите максимально низкий уровень шума, оптимальное соотношение «сигнал — шум» и наиболее расширенный динамический диапазон. Это возможно, так как при использовании базовых настроек ISO на сигнал, исходящий от матрицы, не действует коэффициент усиления напряжения. Довольно часто при повышении этого коэффициента, например чтобы увеличить значение ISO или сделать изображение ярче, на картинке появляются шумы и снижается динамический диапазон. Ваше изображение действительно будет в два раза ярче, но при этом так же увеличится соотношение «сигнал — шум», а качество снимка значительно снизится. Если зернистый кадр, снятый на аналоговую пленку, например ASA 400, может выглядеть интересно и уникально, то шум на цифровом изображении свидетельствует о его низком качестве.

Поэтому в настройках полнокадровой матрицы, встроенной в камеры VENICE и FX9, доступны два базовых значения ISO, с помощью которых можно отрегулировать показатели чувствительности датчика изображения. Они имеют лишь небольшую разницу в качестве изображения. Цветопередача и динамический диапазон остаются практически идентичными, что можно сказать и об уровне шумов.

В камере VENICE используется базовое значение ISO 500, что обеспечивает оптимальный баланс динамического диапазона при стандартном освещении на съемочной площадке. Вспомогательное высокое базовое значение ISO равняется 2500 и отлично подходит для съемки в расширенном динамическом диапазоне в условиях низкой освещенности. Камера FX9 с чувствительностью ISO 800 обеспечивает оптимальный динамический диапазон для съемки как на улице, так и в ярко освещенных помещениях. Вспомогательное высокое базовое значение чувствительности ISO равняется 4000 и отлично подходит для работы в условиях низкой освещенности. Вы можете подобрать базовое значение ISO под свой уровень освещенности и менять его, не снижая качество изображения и не прерывая рабочий процесс.

Низкое базовое значение ISO

Высокое базовое значение ISO

Творческая съемка с помощью электронного нейтрального фильтра переменной плотности и полнокадровой матрицы 

FX9 — это первый в мире полнокадровый камкордер с электронным нейтральным светофильтром, который значительно упрощает работу, а также избавляет от необходимости заряжать неперестраиваемые фильтры и менять их вручную. Это огромное преимущество, ведь с помощью полнокадровой матрицы, объектива с большой апертурой и автоматической диафрагмой, а также электронного нейтрального светофильтра можно создать невероятно красивые кадры. При изменении настроек нейтрального светофильтра во время съемки диафрагма автоматически регулирует глубину резкости изображения, чтобы обеспечить нужную экспозицию. Объектив не поддерживает режим автоматической регулировки диафрагмы? Это не проблема! Чтобы создать подобный эффект, переключите электронный нейтральный светофильтр в автоматический режим и скорректируйте работу диафрагмы во время съемки. Ознакомьтесь с Техническим руководством по использованию электронного нейтрального светофильтра, чтобы узнать, как он работает.

 

Loading video…

Улучшенная автофокусировка от Sony для полнокадровых камер

Во время работы с полнокадровыми камерами можно получить красивую картинку с небольшой глубиной резкости. Однако сохранение точного фокуса на объекте съемки требует большого мастерства от оператора. Обычно при использовании таких высококачественных кинокамер, как VENICE, ассистент оператора вручную регулирует фокус и следит, чтобы не было расфокусировки. Такой метод работы не подходит для создания документальных фильмов и новостных сюжетов.

Часто операторы камер скептически относятся к использованию систем автофокусировки и считают, что они не обладают всеми нужными функциями и не могут обеспечить точный фокус на объекте. Инженеры Sony решили опровергнуть этот стереотип и встроили в полнокадровую камеру FX9 улучшенную систему автофокусировки, создав таким образом первый в мире профессиональный камкордер такого уровня. Эта система обеспечивает невероятно маленькую глубину резкости и широкий выбор опций для регулировки скорости и отслеживания, а также предоставляет целый набор дополнительных инструментов, с помощью которых оператор может эффективно использовать преимущества полнокадровой камеры, например снимать в режиме замедленной или ускоренной съемки для создания исторических драм или динамичных спортивных сюжетов.

 

Loading video…

Профессиональные полнокадровые камеры от Sony

Серия VENICE

Новое поколение кинокамер с непревзойденной цветопередачей, удобным управлением и поддержкой полнокадровых матриц 8K и 6K. Два стандартных параметра ISO и встроенная 8-ступенчатая система нейтральных светофильтров обеспечивают исключительную гибкость съемки.

Подробнее >

 

PXW-FX9

Камера FX9 оснащена полнокадровой матрицей 6K, которая позволяет записывать в высоком качестве в разрешениях DCI 4K*, Ultra HD и HD. Мощная обработка изображения с дебайеризацией и передискретизацией обеспечивает лучшее качество изображения по сравнению с традиционными матрицами Super 35 мм. Это первый в мире полнокадровый камкордер с электронным нейтральным фильтром переменной плотности, быстрой гибридной автофокусировкой и двумя базовыми значениями ISO 800 / ISO 4000.

* Для съемки в разрешении DCI 4K (4096 x 2160 с соотношением сторон 17:9) требуется встроенное ПО версии 2.0 и выше.

Подробнее >

FX6

В ILME-FX6 используется технология одной из лучших в отрасли кинокамер — VENICE от Sony, а также инновационное решение беззеркальной камеры Sony Alpha. В камкордере установлена полнокадровая матрица с тыловой подсветкой Exmor R™ CMOS на 10,2 МП, которая обеспечивает 15 ступеней широкого динамического диапазона с высокой чувствительностью и низким уровнем шума. Камкордер ILME-FX6 обладает той самой технологией цветопередачи, что и VENICE, поэтому при производстве можно легко использовать материалы, отснятые на другие камеры серии Cinema Line.

Подробнее >

FX3

В ILME-FX3 используется технология одной из лучших в отрасли кинокамер — VENICE от Sony, а также инновационное решение, задействованное в беззеркальной камере Sony Alpha. В камкордере установлена полнокадровая CMOS-матрица с тыловой подсветкой Exmor R™ на 10,2 МП, которая обеспечивает более 15 ступеней широкого динамического диапазона с высокой чувствительностью и низким уровнем шума. Камкордер ILME-FX6 обладает той самой технологией цветопередачи, что и VENICE, поэтому при производстве можно легко использовать материалы, отснятые на другие камеры серии Cinema Line.

Подробнее >

🎈 Общественная лаборатория: Матрица экспозиции камеры

MaggPi была награждена Basic Barnstar компанией xose за свою работу в этой исследовательской заметке.

В этой исследовательской заметке приведены примеры матрицы оптимизации или цифрового контактного листа, которые позволяют пользователю визуализировать влияние различных настроек камеры.

Введение: Несколько приложений цифровых камер, таких как спектроскопия или инфракрасное изображение, выигрывают от ручной настройки экспозиции по сравнению с автоматической. Хотя ручные режимы могут повысить производительность приложений, для поиска правильных настроек часто требуется метод проб и ошибок. В этой исследовательской заметке описывается программное обеспечение для сбора изображений, которое создает матрицу, которая сравнивает два параметра камеры.

В идеале матрица сравнения позволяет пользователю сузить количество вариантов и определить наилучшие настройки коллекции изображений.

Чтобы продемонстрировать, как можно использовать матрицу оптимизации, с помощью камеры Raspberry Pi NoIR были собраны изображения с различными настройками ISO в зависимости от времени экспозиции. Приведены два разных примера: получение изображений в ночное время и спектроскопия.

Настройки камеры Raspberry: Ручные настройки камер Raspberry Pi описаны в https://picamera.readthedocs.io/en/release-1.13/fov.html. Некоторые основные настройки управления экспозицией для камеры V2 перечислены ниже:

• Shutter_speed — управляет временем выдержки, максимальная длина 10 секунд. Относится к частоте кадров

• ISO — ISO управляет чувствительностью камеры (регулируя аналоговое_усиление и цифровое_усиление). Значения находятся в диапазоне от 0 (авто) до 1600. Фактическое значение, используемое при явном задании iso, будет одним из следующих значений (в зависимости от того, что ближе): 100, 200, 320, 400, 500, 640, 800.

• AWB — автоматический баланс белого контролирует усиление (красный, синий) и «балансирует» цвет.

Описание матрицы экспозиции: На картинке ниже показан макет матрицы экспозиции. Матрица предназначена для отображения самой низкой части диапазона экспозиции в верхнем левом углу и самой высокой части в правом нижнем углу. Каждое изображение пронумеровано и может быть отслежено до настроек экспозиции, сохраненных в отдельном файле/распечатке. .

Спектроскопия Пример: На картинке ниже показана экспонирующая матрица со спектром светодиода белого света. Настройка камеры/решетки была описана в примечании к спектральной лестнице: https://publiclab.org/notes/MaggPi/06-17-2018/how-can-you-use-computer-vision-to-reduce-spectral-overlap сравнивались настройки ISO (от 100 до 900) и выдержкой (от 0,1 до 1 с) при 1 кадре в секунду (кадров в секунду).

Оценка матрицы экспозиции светодиодов белого света описана ниже:

Можно настроить дополнительные параметры или выбрать альтернативные диапазоны экспозиции. На левом изображении ниже показана та же сцена, что и выше, но с отключенным балансом белого. На правом изображении показаны те же настройки, что и выше, но с выдержками затвора, установленными от 1 до 10 секунд. Частота кадров была неправильно установлена ​​слишком высокой (1/6 кадров в секунду) для выдержки изображения более 6 секунд. На правом рисунке показано, как матрица экспозиции может помочь обнаружить неправильные настройки.

Пример ночного видения: На картинке ниже показано другое изображение, наблюдаемое с использованием матрицы экспозиции. Изображение представляет собой ночное дерево без освещения (кроме звездного света/света, рассеянного уличными фонарями). Автоматические настройки не могут отображать дерево, но более высокие настройки ISO могут. Обратите внимание, что условия освещения могли измениться во время длительной выдержки, и движение листьев может привести к размытию изображений.

Резюме: Два примера демонстрируют, как матрица экспозиции помогает оптимизировать работу камеры. Первый пример (спектроскопия) показывает, что выдержка позволяет увидеть второй/третий спектральный порядок. Второй пример показывает, что высокие настройки ISO позволяют снимать в ночное время с малой выдержкой.

Я все еще разрабатываю программное обеспечение и ищу лучший способ ввести настройки экспозиции, отрегулировать диапазон настроек и представить сравнительные изображения. Цель состоит в том, чтобы предоставить инструменты, которые «брекетируют» настройки экспозиции для лучшей ручной экспозиции. Если у вас есть какие-либо предложения, прокомментируйте….. Код программного обеспечения размещен по адресу: https://github.com/MargaretAN9

@warren, @icarito, @amirberAgain

Калибровка камеры с примером на Python | Нирадж Кришна

Часть 5 обширной серии руководств по формированию изображения и калибровке камеры в Python матрица камеры, отвечающая за трансформацию проекции. Затем мы можем спроецировать любую точку мира на изображение, используя эту матрицу.

В этой статье мы увидим, как выполнить калибровку камеры.

Перед этим давайте рассмотрим внешние и внутренние компоненты камеры.

Внешняя матрица камеры

Во второй части серии мы видели, что внешняя матрица камеры представляет собой изменение базовой матрицы, которое преобразует координаты точки из мировой системы координат в систему координат камеры. Это позволяет нам смотреть на мир с точки зрения камеры. Мы также видели, что это комбинация матрицы вращения и матрицы перемещения — матрица вращения ориентирует камеру, а матрица перемещения перемещает камеру. Итак, учитывая координаты точки в мире, мы можем применить внешнюю матрицу камеры, чтобы изменить ее координаты относительно камеры, как показано ниже:0006

Здесь используются следующие обозначения:

Здесь точки представлены как однородные координаты, что существенно добавляет дополнительное измерение к исходным координатам.

Последняя строка внешней матрицы камеры состоит только из нулей и единиц, и они не добавляют значения к преобразованию, поэтому мы можем безопасно удалить последнюю строку и переписать уравнение следующим образом:

Обратите внимание на форму вывода здесь 3×1, а раньше было 4×1. Это означает, что точка здесь представлена ​​в евклидовой форме, и это хорошо, так как нам не нужен дополнительный шаг для обратного преобразования из однородных координат; также внутренняя матрица камеры, следующая в конвейере, принимает входную форму 3×1, как мы увидим дальше.

Подводя итог, можно сказать, что, учитывая координаты точки в мировой системе координат, внешняя матрица камеры преобразует координаты в систему координат камеры. Преобразование может быть представлено как:

Внутренняя матрица камеры

Теперь, когда мы получили координаты точки относительно камеры, используя внешнюю матрицу камеры, следующим шагом является проецирование этой точки на плоскость изображения камеры и сформировать образ. Это работа встроенной матрицы камеры. Собственная матрица камеры подробно обсуждалась в части 3 этой серии, но подведем итог: внутренняя матрица камеры проецирует точки, координаты которых заданы относительно камеры, на плоскость изображения камеры. По сути, мы можем получить расположение точек на изображении в пикселях, используя внутреннюю матрицу камеры. Это показано ниже:

Обозначения:

Результатом будет проекция в однородной форме. Чтобы преобразовать его в евклидову форму, мы просто делим на последнюю координату и отбрасываем последнее измерение, как показано ниже:

Здесь (u, v) — это положение точки P в пикселях на изображении. Внутренняя матрица камеры представлена ​​как 𝜅, а преобразование может быть представлено как:

Комбинируя внутреннюю матрицу камеры и внешнюю матрицу, мы можем построить конвейер, который принимает точку в мировой системе координат в качестве входных данных и вычисляет ее проекцию на изображение. формируется камерой. Это можно представить как:

Кроме того, используя матричные композиции, мы можем объединить обе матрицы в одну матрицу M , как показано ниже:

Эта матрица M формы 3×4 содержит всю необходимую информацию.

Собираем все вместе

Используя матрицу M , мы можем представить весь конвейер в виде: внешняя матрица имеет в совокупности 11 степеней свободы (6 от внешней матрицы и 5 от внутренней матрицы). Итак, в числе 9 один элемент.0088 M , который зависит от других элементов.

Предположим, что последний элемент M(3, 4) является зависимым элементом. Это означает, что если мы разделим матрицу M на этот элемент, информация внутри M не пострадает, потому что это зависимый элемент.

В приведенном выше уравнении мы делим матрицу M на последний элемент M(3, 4) , чтобы получить новую матрицу. Здесь важно отметить, что вывод или проекция будут одинаковыми в обоих случаях, несмотря на операцию. Это свойство матрицы M называется масштабной инвариантностью , что означает, что мы можем масштабировать матрицу M на любой коэффициент, и это не повлияет на результат.

Обычно в реальных приложениях матрица M неизвестна, и цель калибровки камеры — найти ее по набору известных точек и их проекций.

Мы можем найти координаты изображения (ui, vi) из приведенного выше матричного умножения как:

Мы можем переписать это уравнение как:

Мы можем еще больше упростить это как:

Если вы заметили, приведенные выше уравнения выглядят как однородная система линейных уравнений в м ⃗, которая обычно имеет вид:

Теперь можно представить однородную систему линейных уравнений В форме матрицы как A 𝑥⃗ = 0 ⃗ , где A — M × N Матрица, 𝑥⃗ — вектор колонны с N , а также 0 e -eperies — 0 ye -eperies — 0 ye -eperies — 0 ye -eperies, а 0 o — 0 o — 0 o — . с м записей.

Итак, теперь мы можем представлять наше уравнение в форме матрицы как AM ⃗ = 0 ⃗:

AM ⃗ = 0 ⃗

Приведенное выше уравнение представляет утра ⃗ = 0 ⃗ . Здесь m ⃗ — сглаженная матрица M в векторной форме. Помните, наша цель — найти коэффициенты матрицы M , что равносильно решению этой однородной системы. Теперь каждая однородная система имеет по крайней мере одно решение, известное как нулевое решение, которое получается путем присваивания нулевого значения каждому из элементов. Но это не то решение, которое мы ищем. Как же найти ненулевое решение этой однородной системы?

Что ж, вместо того, чтобы найти точное решение, в существовании которого мы не уверены, мы могли бы найти приблизительное решение.

Математически это означает, что вместо нахождения точного решения Am ⃗ =0 ⃗ , мы можем найти m ⃗ такое, что |Am ⃗ | будет минимум. По сути, мы пытаемся минимизировать здесь алгебраическую ошибку .

Более того, мы можем нормализовать м ⃗, чтобы он стал единичным вектором. Помните, что матрица M не зависит от масштаба, и мы можем выбрать коэффициент масштабирования, равный величине, чтобы нормализовать ее. Опять же, m ⃗ просто сглажено M в векторной форме.

Итак, теперь наша задача — найти минимальное значение |Am ⃗ | при условии |m ⃗ |= 1. В части 4 серии мы видели, что |𝐴𝑥⃗| будет минимальным, если единичный вектор 𝑥⃗ совпадает с наименьшим собственным вектором 𝐴⊺𝐴.

Давайте сначала посмотрим на матрицу A :

Идея состоит в том, что мы найдем несколько точек в мире, представленных (Xi, Yi, Zi), , и найдем их соответствующие проекции на изображении, представленном (ui , vi), , и тогда мы можем вычислить матрицу A. Этот процесс маркировки должен выполняться вручную. Теперь, если мы разметим n точек, форма матрицы A будет 2n×12, а форма m ⃗ останется фиксированной и будет равна 12×1. Форма нулевого вектора будет 2n×1.

Вот вам вопрос: сколько точек нам нужно пометить, чтобы решить приведенную выше однородную систему? Размер м ⃗ равен 12, что означает, что имеется 12 неизвестных, поэтому нам нужно решить 12 независимых уравнений, чтобы найти эти 12 неизвестных. Таким образом, мы требуем, чтобы n было , по крайней мере, 6, что означает, что мы должны пометить не менее 6 независимых точек, чтобы найти m ⃗ . Мы могли бы также пометить больше точек, и вообще, чем больше точек, тем лучше; но 6 это минимум. Ударение здесь делается на слове «независимый», что означает, что никакие три точки не должны лежать на одной прямой.

Собираем все вместе

Итак, план состоит в том, чтобы пометить как минимум 6 точек и вычислить матрицу A. Затем мы можем вычислить 𝐴⊺𝐴 и m ⃗ будет его собственным вектором с минимальным собственным значением. Наконец, мы можем изменить форму вектора m ⃗ обратно в матрицу 3×4 M , которая будет нашей калиброванной матрицей камеры. Используя M, , мы можем найти проекцию любой точки мира на изображении.

Давайте посмотрим на это в действии на примере.

Настройка

Репозиторий GitHub со всем кодом можно найти здесь.

Предполагая, что вы не настраивали среду ранее, вы можете сделать это сейчас, выполнив следующие команды:

 # создать виртуальную среду в anaconda 
 conda create -n camera-calibation-python python=3.6 anaconda 
 conda активировать камера-калибровка-python# клонировать репозиторий и установить зависимости0296 cd Формирование изображения и калибровка камеры 
 pip install -r requirements.txt 

Примечание: Предполагается, что у вас установлена ​​Anaconda.

Мы будем использовать две основные библиотеки:

• pytransform3d: Эта библиотека имеет отличные функции для визуализации и преобразования в трехмерном пространстве.
• ipympl: Это меняет правила игры. Это делает график matplotlib интерактивным, позволяя нам выполнять панорамирование, масштабирование и вращение в режиме реального времени в ноутбуке, что полезно при работе с 3D-графиками.

Пример Интуиция

Чтобы выполнить калибровку камеры, нам сначала нужно подготовить наземную истину, которая по существу представляет собой набор точек в мире и их соответствующих проекций на изображении. В реальном мире мы вручную измеряем расстояние точек от камеры и находим соответствующие им пиксели на изображении. Однако на компьютере мы можем смоделировать этот процесс — мы можем создать внешнюю матрицу камеры и внутреннюю матрицу и построить конвейер для вычисления проекций мировых точек. Мы уже видели, как создавать матрицы в части 2 и части 3 серии. Когда у нас есть основная истина, мы можем использовать ее для построения алгебраической матрицы

A , а затем найти его транспонирование и вычислить 𝐴⊺𝐴, и, наконец, мы можем взять собственный вектор 𝐴⊺𝐴 с наименьшим собственным значением и изменить его форму, чтобы получить калиброванную матрицу камеры M .

Ниже приведен блокнот Jupyter с кодом:

Код представляет собой просто математические уравнения, которые мы обсуждали выше. Давайте шаг за шагом пройдемся по блокноту и поймем, что происходит:

• Сначала мы определим необходимые параметры и создадим внешнюю матрицу камеры и внутреннюю матрицу. Они необходимы для построения трубопровода и подготовки достоверной информации. Затем мы генерируем n случайных точек мира (здесь я выбрал n=12). Вот сюжет нашего мирового пространства с камерой и случайными точками. Сюжет интерактивен в Jupyter Notebook благодаря ipympl.

Установка

• Мы можем вычислить проекции этих точек и сформировать изображение. Во-первых, мы должны применить внешнюю матрицу для представления точек относительно системы координат камеры, а затем мы можем применить внутреннюю матрицу для получения проекций, и, наконец, мы можем нанести эти проекции на изображение, как показано ниже.

проекции n точек на изображении

• Теперь у нас есть готовая исходная информация, которая по существу представляет собой точки мира (Xi, Yi, Zi) и соответствующие им проекции на изображении (ui, vi) . Используя их, мы можем вычислить алгебраическую матрицу A. Это матрица A , если вы помните:

Алгебраическая матрица A

• После вычисления матрицы A мы можем вычислить 𝐴⊺𝐴 и выбрать его собственный вектор с наименьшее собственное значение. Это даст нам вектор m ⃗ размера 12. Наконец, мы можем преобразовать m ⃗ в 3×4, чтобы получить калиброванную матрицу
  M , которую мы ищем.
• Мы можем использовать матрицу M непосредственно для вычисления проекций мировых точек на изображении. В нем есть вся необходимая информация. Давайте применим матрицу M к n случайным точкам, которые мы сгенерировали; таким образом, мы можем сравнить проекции нашей калиброванной матрицы M с истинной реальностью. На рисунке ниже показано сравнение.

наземная правда против прогнозов

• Ну… проекции из нашей калиброванной матрицы M — назовем их прогнозами — не совсем точны. Что-то близко к истине, что-то далеко, но в целом не очень хорошо. В следующем разделе мы обсудим, что могло произойти и что мы можем сделать для улучшения.

рисунок, показывающий, как прогнозы сравниваются с реальными данными

Метод, который мы обсуждали выше, называется прямой линейной калибровкой. Одна из причин, по которой это не очень хорошо, заключается в том, что мы пытались свести к минимуму

алгебраическая ошибка — мы, по сути, пытались найти значение m ⃗, которое хорошо вписывается в алгебраическое уравнение Am ⃗ = 0 ⃗ . Проблема с такого рода линейной оптимизацией заключается в том, что когда в камеру проникают нелинейные ошибки и неопределенности, такие как радиальное искажение, что часто происходит в реальном мире, алгоритм ужасно дает сбой. Мы должны оптимизировать для правильного типа ошибки.

Ошибка, на которую мы должны обратить внимание, называется геометрической ошибкой. Геометрическая ошибка, по сути, дает оценку того, насколько далеки предсказания от реальной истины. Это достигается путем измерения расстояния между предсказанной проекцией точки и ее истинной проекцией. Когда мы минимизируем геометрическую ошибку, мы, по сути, минимизируем расстояние между предсказаниями и истинной реальностью.

Геометрическая погрешность определяется по формуле:

Здесь d — это метрика расстояния, и мы обычно используем евклидово расстояние. В нашем случае прогноз 𝑥′𝑖 задается как MXi , где M — наша калиброванная матрица камеры, а Xi — точка в мировой системе координат. Таким образом, мы можем переписать уравнение как:

Геометрическая ошибка

Итак, идея состоит в том, чтобы выполнить некоторую нелинейную оптимизацию и обновить веса матрицы M , чтобы минимизировать геометрическую ошибку. Этот подход интуитивно похож на машинное обучение, когда мы обновляем модель, используя алгоритм градиентного спуска, чтобы минимизировать потери. К счастью, нам не нужно самим писать алгоритм оптимизации. scipy предоставляет десятки алгоритмов оптимизации в модуле scipy. optimize .

Давайте посмотрим, как это сделать в коде:

В приведенном выше коде сначала мы определяем нашу геометрическую функцию ошибки. Эта функция принимает в качестве аргумента вектор

м ⃗ и наземная истина, которая представляет собой набор мировых точек и соответствующих им проекций на изображении. Он вычисляет предсказания, используя формулу, которую мы обсуждали выше:

Наконец, мы вычисляем евклидово расстояние между предсказанными проекциями и фактическими проекциями по всем точкам и вычисляем геометрическую ошибку.

Функция минимизировать из модуля scipy.optimize принимает два важных аргумента — функцию ошибок и начальные веса. Мы можем пройти геометрическая_ошибка функция, которую мы определили выше в качестве первого аргумента, а в качестве второго аргумента мы можем передать любой 12-мерный вектор в качестве начального состояния — однако, поскольку мы уже вычислили значение m ⃗ из прямого линейный метод калибровки, мы можем передать его в качестве начального состояния вместо некоторого случайного вектора. В качестве третьего аргумента мы можем передать кортеж, содержащий аргументы функции ошибки.

После выполнения функции минимизировать она запускается и завершает процесс оптимизации и возвращает объект, содержащий результат. Мы можем получить доступ к окончательным обновленным весам этого объекта через 9Атрибут 0415 x . Затем мы можем преобразовать этот 12-мерный вектор весов в матрицу 3 × 4 и вычислить прогнозы. Ниже приведен рисунок, сравнивающий прогнозы, полученные с помощью этого метода, с проекциями наземной истины:

наземных истин и прогнозов — они перекрываются!

Как мы видим, предсказания и правда совпадают! Это означает, что мы точно откалибровали матрицу камеры. На рисунке выше трудно увидеть перекрытие, поэтому на рисунке ниже я их разделил:

Еще одним преимуществом этого метода является то, что он может моделировать камеру, даже если преобразование проекции нелинейно. Это происходит в реальном мире, поскольку мы не используем камеру-обскуру, и в нее вкрадываются ошибки и неопределенности, такие как радиальное искажение.