Способы записи чисел: развернутая запись чисел

сайт школы №127 — Системы счисления_1

Основные достоинства любой позиционной системы счисления:

1. Возможность записи произвольного числа при помощи ограниченного количества символов;
2. Простота выполнений арифметических операций.

Разряд — позиция цифры в числе.
Основание (базис) позиционной системы счисления — это количество цифр или других знаков, используемых для записи чисел в данной системе счисления.

Развернутая запись числа a=±(a_n-1P^n-1+a_n-2P^n-2+…+a₀P⁰+a_-1P^-1+a_-2P^-2+…+a_-mP^-m)

Здесь:
a — само число;
P — основание системы счисления;
a_i — цифры данной системы счисления;
n — число разрядов целой части числа;
m — число разрядов дробной части числа.

Свернутая запись числа — запись числа в виде а=a_n-1a_n-2…a₀,a_-1а-₂. ..a_-mP^-m
Позиционных систем счисления очень много, так как за основание системы счисления можно принять любое число не меньшее 2. На уроках информатики мы подробно изучим 10-ю, 2-ю, 8-ю, 16-ю системы счисления.

10-я система счисления

Основание: 10
Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Пример:

а₁₀ = 2012 — свернутая форма записи
а₁₀ = 2·10³+2·10²+2·10¹+2·10⁰ — развернутая форма записи

2-я система счисления

Основание: 2
Цифры: 0, 1

Пример:

а₂ = 1011 — свернутая форма записи
а₂ = 1·2³+0·2²+1·2¹+1·2⁰ — развернутая форма записи

8-я система счисления

Основание: 8
Цифры: 0, 1, 2, 3, 4, 5, 6, 7

Пример:

а₈ = 3752 — свернутая форма записи
а₈ = 3·8

3+7·8²+5·8¹+2·8⁰ — развернутая форма записи

16-я система счисления

Основание: 16
Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Пример:

а₁₆ = 2A9E — свернутая форма записи
а₁₆ = 2·16³+A·16²+9·16¹+E·16⁰ — развернутая форма записи

 

Способ — запись — число

Способ — запись — число

Cтраница 1

Способ записи чисел цифровыми символами определяется системой счисления. В современных ЭЦВМ находят применение десятичная и двоичная, а в качестве промежуточных — восьмеричная и шестнадцатиричная системы счисления.  [1]

Этим способом записи чисел мы подчеркиваем ограниченную точность наших знаний — мы опускаем все цифры, в которых у нас нет достаточной уверенности. Например, когда речь идет о радиусе Земли и мы указываем, что он равен 6 37 — 10е м, а не 6 374 — 10 м или 6 370 — 10 м, то мы тем самым говорим, что вполне уверены в третьей значащей цифре, но не в четвертой. Число цифр, в которых мы вполне уверены, называется числом достоверных цифр.  [2]

Системой счисления называется способ записи чисел при помощи цифр. Различают позиционные и непозиционные системы счисления. В позиционной системе значение каждой цифры, входящей в запись числа, зависит от ее положения ( позиции) в ряду цифр, изображающих число. Наиболее распространенная десятичная система счисления является позиционной. Изменение позиции цифры на один разряд вправо или влево изменяет ее значение в 10 раз. Число 10 определяет структуру десятичной системы и называется ее основанием. Примером непозиционной системы может служить запись числа римскими цифрами.  [3]

Под системой счисления понимают способ записи чисел цифровыми знаками. Информация, характеризующая цифровую программу, может быть задана в различных системах счисления — десятичной, двоичной и двоично-десятичной.  [4]

ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при к-ром один и тот же знак ( цифра) из десяти: О, 1, 2, 3, 4, 5, 6, 7, 8, 9 имеет разл.  [5]

Наиболее распространенный в настоящее время способом записи чисел является позиционный способ, согласно которому один и тот же символ ( цифра) имеет различное значение в зависимости от занимаемого места в записи числа. Этот способ используется и в привычной для нас десятичной системе счисления.  [6]

Этот метод основывается на еще одном способе записи чисел, соответствующих ключам.  [7]

ПЛАВАЮЩАЯ ЗАПЯТАЯ, п р е д-ставление чисел с плавающей запя-той, — способ записи чисел в позиционной системе счисления с основанием R, при котором число JV представляется в виде N np-q, где р — целое число, называемое порядком числа N, а q — правильная дробь ( — g — 9l), называемая мантиссой числа N.  [8]

Существует третий вид погрешностей, не зависящий ни от погрешностей исходных данных, ни от способа записи чисел, ни от точности вычислений.  [9]

Способ записи чисел называют нумерацией или по-другому системой счисления.  [10]

Для преобразования числа в ДДК необходимо преобразовать в двоичную систему счисления каждую цифру десятичного числа, сохранив при этом их порядок следования.

Преимущество такого способа записи чисел состоит в том, что для преобразования чисел из одного представления в другое не требуются сложные расчеты.  [11]

СТЕПЕННОЕ ПРЕДСТАВЛЕНИЕ ЧИСЛЕННЫХ ВЕЛИЧИН Представление численных величин в степенной форме позволяет избежать недоразумений при определении количества значащих цифр, а также избавляет от необходимости записывать большое количество нулей для очень малых или, наоборот, очень больших чисел. Многочисленные примеры помогают убедиться в удобстве такого способа записи чисел.  [12]

Ранняя греческая система счисления была десятичной и аддитивной, как египетская и римская. В александрийскую эпоху, а может быть и раньше, появляется способ записи чисел

, которым пятнадцать веков пользовались не только ученые, на и купцы и чиновники. Три архаичные буквы были добавлены к 24 буквам греческого алфавита, чтобы получить необходимые 27 знаков. С помощью такой системы любое число меньше 1000 можно было записать не более чем тремя знаками, например 14 как i6, так как i10, 6 4; числа, большие 1000, можно было выразить с помощью простого расширения такой системы. Архимеда, Ге-рона и всех других классических авторов. Имеются археологические данные о том, что этой системе обучали в школах. Такое отсутствие позиционности и использование не менее чем 27 знаков иной раз рассматривались как доказательство несовершенства системы. Но то, как легко ею пользовались математики древности, и то, что греческие купцы применяли ее даже при очень сложных расчетах — в Восточной Римской империи вплоть до ее гибели в 1453 г. — указывает, по-видимому, на наличие некоторых преимуществ. При известном опыте вычислений при такой системе мы действительно убеждаемся, что четыре основных действия можно выполнять достаточно легко, если твердо знать символы. Действия с дробями при подходящих обозначениях тоже просты, но греки не были при этом последовательны, так как у них не было единой системы: они пользовались египетскими основными дробями, вавилонскими шестиде-сятичнымн дробями и записью — дробей, напоминающей нашу. Десятичные дроби не были введены, это великое усовершенствование в Европе появляется в эпоху позднего Ренессанса, когда вычислительный аппарат был развит значительно больше, чем когда бы то ни было в древности. Но даже в этих условиях десятичные дроби не были приняты во многих школах до восемнадцатого и девятнадцатого столетия.  [13]

Качественный материал этой главы может быть проработан за короткий срок. Точно так же немного времени займет и ознакомление с количественными методами измерения промежутков времени. Способ записи чисел с помощью числа десять в какой-то степени будет применяться на протяжении всего курса, и если он окажется незнакомым учащимся, следует на него обратить самое серьезное внимание. Определение порядка величин очень полезно, но иногда трудно для начинающих, и поэтому вначале не следует увлекаться этим. По мере того как на протяжении всего курса учащиеся будут решать задачи, они на практике оценят удобства этого метода оценки величин.  [14]

Страницы:      1    2

4.1. Что такое система счисления?

Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7•10² + 5•10¹ + 7•10⁰ + 7•10^-1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1 q^n-1 + a_n-2 q^n-2+ . .. + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 + … + a_-m q^-m,

где a_i — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно.

Например:

Позиционные системы счисления система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр)

Позиционные системы счисления

Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).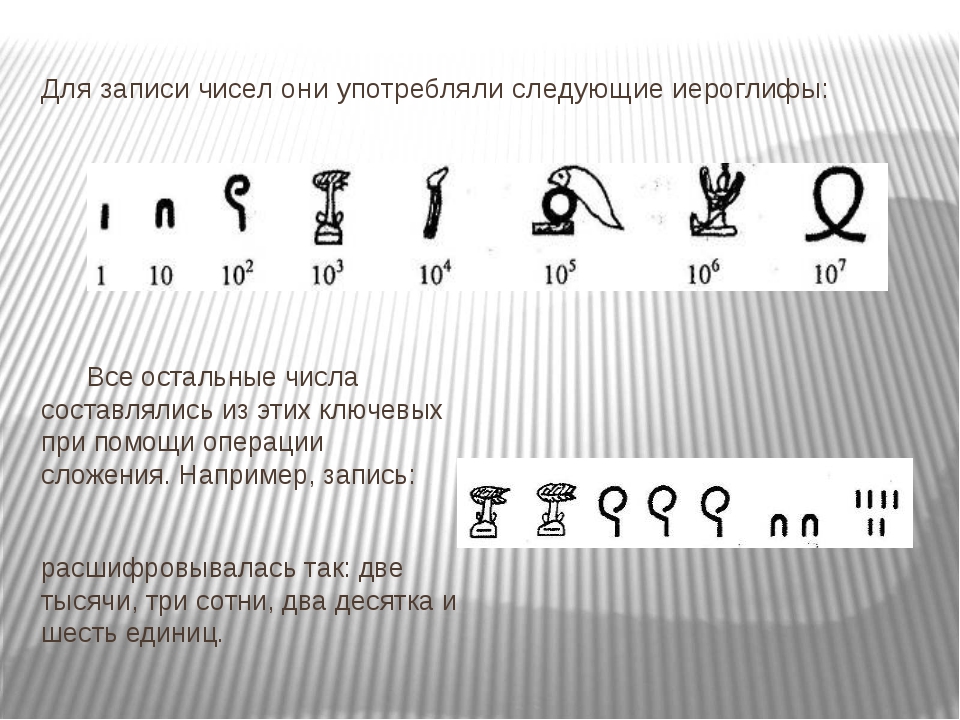

Существуют системы позиционные и непозиционные.
В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.
Любая позиционная сиситема характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.
За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т.д. Следовательно, возможно бесконечное множество позиционных систем.

Десятичная система счисления.

Пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т.д.

Двоичная система счисления.

В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.

Восьмеричная система счисления.

В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмиричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.

Шестнадцатиричная система счисления.

Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем — 16 (десятичное), в следующем — 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогочно тому, как это делается для восьмеричной системы.

Вопрос: Почему люди пользуются десятичной системой счисления, а ЭВМ — двоичной?

По материалам газеты «Информатика» 1998 N24 и книги Л.З.Шауцуковой, «Основы информатики в вопросах и ответах», Издательский центр «Эль-Фа», Нальчик, 1994.

Перевод чисел в позиционных системах счисления_8 класс_Урок информатики

Главная / 8 класс / Конспект

Перевод чисел в позиционных системах счисления

В древние времена, когда люди начали считать, появилась потребность в записи чисел.

Количество предметов изображалось нанесением черточек или засечек на какой-либо твёрдой поверхности: камне, дереве, глине. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища).

Для записи информации о количестве объектов используются числа. Числа заключают в себе количественную информацию. Числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Система счисления (СС) — способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.

Алфавит – это набор цифр, используемый в записи числа в данной СС.

Различают СС позиционные и непозиционные.

Позиционные — количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра. (В числе 252 – первая двойка означает количество сотен, последняя – количество единиц)

Непозиционные — количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.

Пример позиционной системы счисления — арабская (современная десятичная), непозиционной — римская.

К непозиционным системам исчисления можно отнести системы счисления древности: старославянскую, древнеегипетскую, китайскую, ацтеков, майя …

Недостатки: Очень сложно выполнять математические расчеты и  необходимо большого числа различных знаков для записи чисел, особенно больших

Приведем пример самой распространенной из непозиционных систем счисления является римская. В качестве цифр используются следующие латинские буквы:

I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000.

Величина числа определяется как сумма или разность цифр в числе.

444=400+40+4=(D-С)+(L-X)+(V-I)=CDXLIV

Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр. (До сих пор считаем, час — 60 минут, минута — 60 секунд, окружность — 360о).

В позиционных СС количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды возрастают справа налево (единицы, десятки, сотни и т.д.).

Основанием СС — количество различных символов (цифр), используемых для изображения числа в позиционных системах счисления, называется .  (Например, 32245 число записано в пятеричной СС, читается «три-два-два-четыре в пятеричной СС»)

Например, в десятичной системе счисления, которой мы пользуемся, алфавит состоит из  десяти цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, соответственно основание равно 10.

Четверичная СС. Основание — 4. Алфавит — 0, 1, 2, 3.

Семеричная СС. Основание — 7. Алфавит — 0, 1, 2, 3, 4, 5, 6.

Шестнадцатеричная СС. Основание — 16. Алфавит — 0 … 9, A, B, C, D, E, F. (Например 2D616 «два-д-шесть в шестнадцатеричной СС, цифре А соотв. 10 в десятичной СС, B — 11, C — 12, D — 13, E — 14, F — 15)

В современной информатике используются в основном двоичная, восьмеричная, шестнадцатеричная СС. Двоичная система счисления используется для кодирования дискретного сигнала в вычислительной технике, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1.

Перевод чисел из любой позиционной СС в десятичную

Мы пользуемся свернутой формой записи числа, но мы знаем, что, например, число 352 = 3*100+5*10+2.

В развернутой форме производится умножение цифр числа на степень основания, т.е. 352=3*102+5*101+2*100.

Т.о. любое число в позиционной СС можно записать в развернутой форме и перевести в десятичную СС.

В памяти компьютера числа представлены в двоичной СС, поэтому в информатике часто возникает необходимость перевода чисел из двоичной системы в десятичную и обратно. Приведем пример перевода двоичного числа:

Пример 1:

5 4 3 2 1 0 1101012 = 1*25 + 1*24 + 0*23 + 1*22 + 0*21 + 1*20 = 32 + 16 + 0 + 4 + 0 + 1 = 5310.

Двоичное число с дробной частью:

Пример 2:

3210-1-2 1001,112 = 1*23 + 0*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = 8 + 1 + 1/2 + 1/4 = 9+ 0,75 = 9,7510.

По такому же принципу можно переводить числа в десятичную СС из других позиционных СС.

Пример 3:

32114 =  3*43 + 2*42 + 1*41 + 1*10 = 3*64 + 2*16 + 1*4 + 1*1 = 192 + 32 + 4 + 1 = 22910

Пример 4:

2148 = 4 * 80 + 1 * 81 + 2 * 82 = 4 + 8 + 128 = 14010

Пример 5:

2 1 0 2AF16 =  2*162 + 10*161 + 15*160 = 2*256 + 10*16 + 15*1 = 512 + 160 + 15 = 68710

В записи числа в шестнадцатеричной системе счисления А=10 и F=15.

Пример 6:

1D316 = 3 * 160 + 13 * 161 + 1* 162 = 3 + 208 + 256 = 46710

В записи числа в шестнадцатеричной системе счисления D=13.

Перевод чисел из десятичной СС в любую позиционную систему счисления.

Существует алгоритм перевода целого десятичного числа в двоичное:

Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание СС (на 2) до тех пор, пока частное от деления не окажется меньше основания СС (<2). Записать полученные остатки в обратной последовательности, начиная с последнего результата.

2510 = 110012

Для перевода дробных десятичных чисел существует тоже алгоритм. Для этого необходимо  отдельно перевести целую и дробную часть.

26, 7510 = 26 + 0,75 = 11010+0,11 = 11010,112

Целую часть переведем как указано выше, а дробную часть переведем по следующему алгоритму:

последовательно умножать исходную и получаемые дробные части на основание системы до тех пор, пока не получим нулевую дробную часть. Записать полученные целые части произведений в прямой последовательности.

0, 75   *2 Ô 1, 5   *2   1, 0   Поучаем 0,7510 = 0,112

Используя данный алгоритм можно перевести десятичное число в позиционную систему с любым основанием.

18010 = B416

Результат 158 79 39 19 9 4 2 1 Остаток 0 1 1 1 1 0 0 1

15810 = 100111102

Результат 467 58 7 Остаток 3 2 7

46710 = 7238

./diz/line-r.gif»>

10 правил написания чисел и цифр

Майкл

Как вы выражаете числа в письме? Когда вы используете цифры (цифры), а когда записываете число словами (буквами)? То есть когда вы пишете 9 , а когда девять ?

1. Число в сравнении с числом . Перво-наперво, в чем разница между числом и цифрой? Число — это абстрактное понятие, а цифра — это символ, используемый для выражения этого числа. «Три», «3» и «III» — все символы, используемые для обозначения одного и того же числа (или концепции «тройственности»). Можно сказать, что разница между числом и его цифрами подобна разнице между человеком и ее именем.

2. Введите маленькие числа по буквам . Маленькие числа, такие как целые числа меньше десяти, следует писать по буквам. Это одно правило, на которое можно положиться. Если вы не набираете числа по буквам, это будет выглядеть так, как будто вы отправляете мгновенное сообщение, и вы хотите быть более формальным, чем это, в своем письме.

3. Других стандартных правил нет. : Эксперты не всегда соглашаются с другими правилами. Некоторые специалисты говорят, что любое число из одного слова нужно записывать. Двухсловные числа следует выражать цифрами. То есть, говорят, нужно выписать двенадцать или двадцать . Но не 24 .

4. Использование запятой . В английском языке запятая используется как разделитель тысяч (и точка как десятичный разделитель), чтобы было легче читать большие числа. Поэтому запишите размер Аляски как 571951 квадратную милю вместо 571951 квадратных миль. В континентальной Европе все наоборот: точки используются для разделения больших чисел, а запятая используется для десятичных дробей. Наконец, Международная система единиц (СИ) рекомендует использовать пробел для разделения групп из трех цифр, а запятую и точку следует использовать только для обозначения десятичных знаков, например $ 13 200,50 (запятая часть бардак… знаю).

5. Не начинайте предложение с цифры .Сделайте «Четыре очка и семь лет назад», а не «4 очка и 7 лет назад». Это означает, что вам, возможно, придется переписать некоторые предложения: «Поклонники купили 400 000 копий в первый день» вместо «400 000 копий были проданы в первый день».

6. Следует указать века и десятилетия . Используйте восьмидесятых или девятнадцатого века .

7. Проценты и рецепты . В повседневном письме и рецептах вы можете использовать цифры, например «4% детей» или «Добавьте 2 чашки коричневого риса. Однако в формальном письме вы должны указать процентное соотношение как «12 процентов игроков» (или «двенадцать процентов игроков», в зависимости от ваших предпочтений, как объяснено в пункте 3).

8. Если число округлено или оценено, укажите его по буквам . Округлые числа более миллиона записываются как цифра плюс слово. Используйте «Около 400 миллионов человек изначально говорят на испанском» вместо «Около 400000000 человек говорят на испанском ». Если вы используете точный номер, вы, конечно, его запишите.

9. Два числа рядом друг с другом . Если вы напишете «7 13-летних», это может сбить с толку, поэтому напишите один из них цифрой, например «семь 13-летних». Выберите номер с наименьшим количеством букв.

10. Порядковые номера и последовательность . Не говорите «Он был моей первой настоящей любовью», а скорее «Он был моей первой настоящей любовью». Будьте последовательны в одном предложении. Если у моего учителя 23 начинающих ученика, у нее также 18 продвинутых учеников, а не восемнадцать продвинутых учеников.

Обзор видео

Хотите улучшить свой английский за пять минут в день? Оформите подписку и начните получать наши ежедневные советы и упражнения по написанию!

Продолжайте учиться! Просмотрите категорию «Грамматика», просмотрите наши популярные публикации или выберите соответствующую публикацию ниже:

Хватит делать эти досадные ошибки! Подпишитесь на Daily Writing Tips уже сегодня!

• Вы будете улучшать свой английский всего за 5 минут в день, гарантировано!
• Подписчики получают доступ к нашим архивам с более чем 800 интерактивными упражнениями!
• Вы также получите три бонусные электронные книги совершенно бесплатно!

Попробовать бесплатно

Стандартная, расширенная и словесная форма

Преобразование чисел из их обычной формы в письменную и расширенную формы — один из способов начать понимать значение разряда. Девять цифр в разрядах сотен сильно отличается от девяти цифр в разрядах единиц, и эти понятия иногда трудно уловить. Рабочие листы на этой странице практикуют преобразование чисел между стандартными, расширенными и словесными формами, чтобы помочь в построении этих концепций, и включают в себя рабочие листы с особыми крайними случаями, которые часто сбивают с толку учеников начальной школы, только начинающих исследовать значение места.

Записывайте числа в форме слова

---

52 Рабочие листы в стандартной, расширенной и словесной формах

Практические рабочие листы для преобразования чисел из стандартных числовых обозначений в письменные (словоформы).Написание чисел в форме слова аналогично письменной форме слова, используемой для заполнения проверок, и некоторые из этих рабочих листов словоформы включают варианты с десятичными знаками, подходящими для этой темы.

Напишите числа в форме слова

Записать слово из в стандартной форме

---

48 Рабочих листов в стандартных, расширенных и словесных формах

Практические рабочие листы для преобразования чисел из письменных обозначений (словоформ) в стандартные числовые обозначения.

Написать слово в стандартной форме

Ввод чисел в форме расширенного числового значения

---

48 Рабочих листов стандартных, расширенных и словесных форм

Практикуйте рабочие листы расширенной формы для преобразования чисел из стандартной числовой записи в расширенную форму числового значения.Рабочие листы в расширенной форме помогут учащимся понять концепции разряда и лучше понять пробелы в преобразовании длинных чисел с нулевыми разрядами в словоформу или другие представления.

Ввод чисел в развернутой форме разметки

Запишите расширенную форму разметки в стандартной форме

---

Рабочие листы в расширенной форме

---

48 Рабочие листы в стандартной, расширенной и словесной формах

Это рабочие листы в расширенной форме для преобразования чисел из стандартной цифровой записи в обычную расширенную форму, в которой множитель разряда и цифра объединены.

Рабочие листы расширенной формы

Запись номеров развернутой формы в стандартной форме

---

Преобразование чисел между формами

Когда мы записываем числа в стандартной числовой форме, мы делаем много предположений, которые младшим школьникам необходимо усвоить в явном виде. Хороший пример — когда мы произносим числовую выгрузку (в «словоформе»), мы пропускаем значения мест, в которых есть нули. Этот тонкий разрыв — это то, что может легко сбить с толку студентов, которые все еще борются с числовой ценностью, и вы можете увидеть числа вроде «четыре тысячи шесть», написанные как «46» в качестве ответа.Ой!

Печатные листы на этой странице практикуют преобразование чисел как в развернутую, так и в словоформу. Это помогает студентам сосредоточиться на разрядах отдельных цифр, а также лучше понять, как мы произносим числа. На листах есть проблемы разной длины (больше цифр!), Конвертировать в разные направления. Каждый отдельный тип рабочего листа преобразования чисел и когда вы можете захотеть его применить, более подробно обсуждаются ниже.

Использование расширенной формы Рабочие листы

Рабочие листы на этой странице требуют, чтобы учащийся писал числа в развернутой форме, записывал числа в стандартной форме и переписывал числа в форме слова. Сами числа имеют особое значение, которое представляет собой точное количество объектов, к которым относится число. Существует несколько способов выражения числа, и каждый играет свою роль. Однако, когда вы начинаете понимать значение разряда, умение преобразовывать числа в развернутую форму или обратно — очень полезный навык.

Рабочие листы в развернутой форме на этой странице — отличная практика для студентов, которые узнают о разрядах и числах с большими цифрами.

Что такое расширенная форма?

Расширенная форма — это способ записи числа таким образом, чтобы все компоненты числового значения числа были разделены.

Когда мы пишем число в развернутой форме, каждая цифра вырезается и умножается на ее разряд, так что сумма всех значений равна исходному числу.

Запись чисел в развернутой форме

Самый простой способ визуализировать запись числа в развернутой форме — это увидеть пример. Рассмотрим число 1234. Это число состоит из трех цифр, поэтому представление числа в развернутой форме будет состоять из трех компонентов.

1,234 = 1000 + 200 + 30 + 4

Когда число записано в развернутой форме, легче понять точную величину каждой цифры.В этом примере, даже несмотря на то, что «1» в разряде тысяч численно меньше, чем «4» в разряде единиц, нотация в развернутой форме дает понять, что разрядное значение означает гораздо большее значение, даже если сама цифра меньше. .

Числа в форме слова

Числа в форме слова записываются так, как если бы вы читали значение слова вслух. Для меньших чисел числовая словоформа — это то, с чем большинство студентов знакомо, и это легко понять…

123 в форме слова — это «сто двадцать три»

Сложность возникает, когда вводятся точки (мы не говорим здесь о десятичных дробях). Точка в числовой форме — это группа из трех цифр, обозначающая основные разрядные значения групп чисел. Обычно это тысячи, миллионы, миллиарды и тому подобные суммы, которые разделены на группы по трехзначным числам либо десятичными знаками (или, в некоторых странах, запятыми). Так, например, рассмотрим это число …

123,123,123

Словоформа этого числа — «сто двадцать три миллиона сто двадцать три тысячи сто двадцать три».Вы заметите, что типичная группировка чисел соответствует тому месту, где мы вводим слова «миллионы» и тому подобное. Цель рабочих листов словоформ здесь — развить уровень комфорта с этими группировками по периодам.

Обратите внимание, что когда вы пишете числа в форме слова (или произносите числа, если на то пошло), использование слова «и» является очень конкретным показателем того, что весь компонент рассматриваемого числа был полностью описан и что десятичный разряд начинается. Так например…

4 321,5 = «четыре тысячи триста двадцать одна и пять десятых».

Слово «и» здесь говорит нам, где находится десятичный разряд и где мы собираемся начать описание словоформы дробной или десятичной составляющей числа. Это важно не только при написании чисел в словесной форме, но и при написании числового описания суммы в долларах при написании чека или другого юридического описания денег. Там часть после «и» обычно обозначается как центы.

В любом случае, не делайте ошибки, используя слово «и» где-либо при написании словоформы целого!

Преподавание значения разряда с помощью рабочих листов в расширенной форме

Рабочие листы с расширенными формами усиливают концепцию разряда, побуждая учащихся рассматривать фактическое значение, присвоенное каждой цифре в числе. Несмотря на то, что процесс кажется упрощенным, практикуя преобразование в развернутую форму и обратно, ваши ученики развивают более врожденное чувство числа, будучи вынуждены учитывать не только абсолютное значение цифры, но и ее соответствие ее положению во всем числе.

Хорошее место для начала — это либо более ранние рабочие листы в Рабочих листах расширенной формы с указанием стоимости, либо рабочие листы в обычной расширенной форме, а затем постепенно работать над ними, включая упражнения в расширенной форме с десятичными знаками, если вы затронули эти темы.

Разложение чисел в развернутую форму несколько более процедурно, чем переход к другим формам, но как только этот навык освоен, любое из обратных чисел из рабочих листов расширенной формы укрепит концепцию.

Вы можете изменять сложность назначаемой работы, выбирая рабочие листы в развернутой форме с более длинными цифрами или десятичными значениями, или просто смешивать эти рабочие листы в качестве заданий периодического обзора, особенно со студентами, которые, похоже, испытывают трудности с базовыми операциями, задействованными в нескольких -цифровые проблемы.

Независимо от того, какой подход вы выберете, все рабочие листы на этой странице, включая рабочие листы с развернутой формой, помогут конвертировать между различными формами чисел и обучать разряду.Также обязательно ознакомьтесь с таблицей с числовой стоимостью, чтобы определить периоды и другие тонкости определения числовой стоимости!

Таблица значений разряда

---

Когда числа становятся длиннее, диаграмма значений разряда может помочь учащимся научиться читать числа и различать меньшие и большие значения даже при использовании десятичных знаков.

Таблица значений мест

Знайте, когда их произносить по буквам

Числа появляются не только в математических заданиях, но и в повседневном письме. Как и во многих других аспектах английского языка, существуют правила написания чисел. Некоторые числа пишутся буквами, а другие — только цифрами. Вы, вероятно, встречали больше, чем ваша изрядная доля в топ-10 списков; почему он не входит в первую десятку? Научившись писать числа на английском, вы узнаете ответ!

Правила для прописанных чисел

Хотите знать, когда писать числа? Есть несколько ситуаций, в которых следует произносить числовые слова.Конечно, как это часто бывает с английским языком, есть некоторые исключения из правил, изложенных ниже. Как и в случае с другими правилами грамматики, правила написания чисел меняются в соответствии с определенными руководствами по стилю (например, Chicago Manual of Style, AP, MLA и т. Д.). Откройте для себя несколько общих правил написания чисел.

Число заклинаний меньше 10

При написании в предложении чисел до 10 их следует писать по буквам. Это верно независимо от того, где они находятся в предложении.

• У Мартина две младшие сестры и пять старших братьев .
• Мэри прочитала на прошлой неделе четыре новых книг и семь газетных статей.

Числа заклинаний, начинающиеся с предложений

Всякий раз, когда в начале предложения стоят числа. эти числа должны быть записаны.

• Шестьдесят детей приехали на экскурсию в прошлом году, а в этом году их было 80 .
• Двенадцать кредитных часов считаются дневной учебной нагрузкой в ​​колледже.
  

Переносы по буквам номера соединений

При написании составных чисел, например, в начале предложения, они всегда должны переноситься через дефис.

• Пятьдесят две миль — это все, что ей оставалось на пути в Шотландию.
• В городе проживает 49 процентов учителей.

Дроби, прописанные через дефис

Дроби в начале предложения должны быть написаны по буквам. В предложении они могут быть выражены цифрами или словами. При написании они должны быть расставлены через дефис.

• O Третья группы родом из Китая.
• Она наполнила свой бензобак двумя третями галлона.

Рекомендации для чисел, требующих использования цифр

Часть обучения тому, как писать числа на английском языке, требует изучения ситуаций, в которых числа не должны быть написаны по буквам. Вместо этого они должны быть представлены в виде цифр.Конечно, все эти правила использования цифр предполагают, что число не находится в самом начале предложения или вопроса.

Используйте цифры в заголовках и заголовках

Когда вы включаете число в заголовок или заголовок, лучше использовать число, а не писать слово по буквам. Вот почему вы увидите «10 лучших» в заголовках статей, а не «десятку лучших». Это правило верно даже тогда, когда число является первым словом заголовка.

• Назовите статью « 15 Лучшие рестораны Сан-Франциско» вместо того, чтобы перечислять пятнадцать.
• Для названия или заголовка в статье напишите «6 главных правил, которые необходимо запомнить», а не перечисляйте шесть.

Используйте цифры для чисел 10 и более

Когда вы включаете в предложения числа 10 или больше, их следует выражать цифрами, если только они не находятся в самом начале предложения.

• Я планирую отправиться в круиз по Карибскому морю с 10 моих самых близких друзей.
• Она купила около 12 пар обуви и 16 платьев за последние три месяца.

Используйте числа для смешанных фракций

Хотя дроби обычно записываются, есть исключение из этого правила для смешанных дробей. Смешанная дробь объединяет целое число и дробь. Для них требуются цифры, если они не находятся в начале предложения.

• Рецепт предусматривает 2½ стаканов орехов.
• Наш классный арт-проект требует 1¼ чашек с блестками.

Используйте числа для дней месяца

Даты следует выражать числами.Есть несколько специальных правил для правильного написания дат. При написании только дня месяца вы можете использовать кардинальное (4) или порядковое (4-е) число. Оба верны.

• Вы придете в игру 21 мая года?
• Ее день рождения — г. 2 октября г.

Используйте числа для полной даты

При написании полной даты вы можете использовать числа для месяца, дня и года. Или вы можете указать месяц по буквам, указав день и год.

• Присоединяйтесь к нашей жуткой вечеринке в честь Хэллоуина: 31.10.2018 .
• Спектакль находится на 23 марта 2010 года .

Обратите внимание, что использовать порядковые номера (1-й, 2-й, 3-й) с полными датами неправильно. Было бы неверно указать « 23 марта 2010 г. .» Существуют особые правила для записи даты в военном формате.

Используйте числа для процентов

При написании процентов используйте числа в паре со знаком%.

• Согласно последнему опросу , 52%, учителей проживают в городе.
• Приятно знать, что только 7% американцев говорят, что они недовольны.

Слово «процент» обычно следует использовать только при написании процентов словами, что вы делаете только в начале предложения.

Используйте числа для десятичных знаков

Десятичные знаки следует записывать цифрами.

• В прошлом месяце выпало 3,73 дюймов дождя.
• На горе сегодня накопилось 8,98 дюймов снега.

Лучше не начинать предложение с десятичной дроби, так как эти типы чисел было бы неудобно читать, если бы вам пришлось их писать по буквам. Часто вы можете перефразировать то, что хотите сказать, поставив фразу «Всего» перед десятичной дробью, чтобы не начинать предложение с десятичной дроби.

Правила написания чисел и денег

Когда дело доходит до денег, числа следуют своим собственным правилам.Деньги обычно записываются цифрами, но их можно выписать, если сумма нечеткая или округленная — «это стоит два или три доллара».

Наиболее важные рекомендации, о которых следует помнить:

• Символы валюты следует размещать перед числом без пробелов.
  Пример: она заработала $ 2750 за этот проект.
• Тысячи следует разделять запятыми.
  Пример: Марси унаследовала $ 35 000 от своего покойного дяди.
• Десятичные дроби следует разделять точками.
  Пример: Шеймус потратил всего 149,99 долларов на новый смарт-телевизор.
• Когда вы достигнете больших чисел в миллионы и миллиарды, выпишите все слово (вместо всех этих нулей).
  Пример: эта новая компания заработала 10 миллионов долларов в 2018 году.
• Не записывайте валюту, если вы уже указали сумму с символом валюты.
  Пример: на моем текущем счете осталось $ 895 . (Было бы излишне говорить «895 долларов»)

Особые случаи: несколько правил и исключений

Есть некоторые особые случаи, когда числа могут быть записаны разными способами.

Избегайте смешивания числовых слов и цифр в списках

Когда числа находятся в списке, обычно идеально поддерживать согласованность всех чисел в списке, даже если некоторые числа меньше 10, а некоторые больше. Однако, если вы следуете руководству по стилю, которое предписывает всегда писать числа меньше десяти (например, AP), вы должны следовать правилам, даже если это приведет к непоследовательному списку. В противном случае лучше всего подходит последовательность.

• несовместимо: У нее четыре брата в возрасте лет семь , девять , 12 и 15 .
• соответствует : У нее четыре брата в возрасте 7 , 9 , 12 и 15 .

• непоследовательно : Мэри посетила три европейских стран и 14 безлюдных островов.
• соответствует : Мэри посетила 3 европейских стран и 14 безлюдных островов.

Изменить формат с двумя соседними номерами

Когда вы пишете предложение, в котором рядом расположены два числа, которые не являются частью связанного списка, вам необходимо изменить текст для ясности.В этом случае лучше всего записать одно число словом, а другое — цифрой.

• лучшее: В эти выходные у меня будет 12 десять -летних детей.
• сбивает с толку: В эти выходные у меня дома будут 12 10 -летних детей.
• менее запутанно, но не идеально : В эти выходные у меня дома будут 12, 10 -летних детей.
  

Другой вариант — переставить предложение, чтобы разделить числа. Вы можете сказать: «В эти выходные у меня дома будет 12 детей, которым по 10 лет».

Запись цифр на чеках

Когда вы выписываете чек, который будет использоваться для снятия средств на банковский счет или получения наличных по кредитной карте, применяется особое правило. В этом случае вам нужно будет указать сумму численно в обозначенном месте рядом со знаком доллара. Затем вам нужно будет объяснить это. Вы можете использовать слова для обозначения долларов и центов или выразить центы как дробную часть из 100, поскольку для получения доллара требуется 100 центов.Не забудьте поставить слово «и» между долларами и центами.

• При выписке чека на 1 044,12 доллара полный текст должен быть записан как одна тысяча сорок четыре доллара и 12/100.
• Если вы выписываете чек на 182,40 доллара, вы можете написать сто восемьдесят два доллара пятьдесят центов или сто восемьдесят два доллара 50/100 .
• Если вы выписываете чек даже на 79 долларов, в тексте может быть написано семьдесят девять долларов и 00/100 , семьдесят девять долларов и не будет центов или долларов ивентов девять долларов только .

Правила обращения к десятилетиям

Когда речь идет об определенном десятилетии, есть несколько разных вариантов. Вы можете использовать слово, полную дату или сокращенную дату.

• Она жила в Сан-Франциско в восьмидесятых .
• В течение 1980-х она жила в Сан-Франциско.
• Она жила в Сан-Франциско в 80-х .

Указания по времени написания (утра / вечера)

При записи времени вместе с.м. обозначить утро или вечер чтобы обозначить вечер, используйте цифру для обозначения времени. Чтобы получить точное время, добавьте минуты после двоеточия (20:22). Если речь идет о четном часе, просто укажите час, вместо того, чтобы указывать нулевые минуты (используйте 2 часа ночи вместо 2 часов ночи). Не используйте слова для обозначения времени, когда говорите утро или вечер. (если время не является первым словом в предложении).

• правильно : авария произошла в 20:22 по московскому времени. прошлой ночью.
  
• правильно : Они не покидали партию до 2 а.м.
• неверно : Они не покинули вечеринку до два утра

Как указать время с часами

Фраза o’clock означает «часы», хотя эта точная фраза не используется в стандартном английском языке. Однако, когда вы говорите о равномерном приращении времени, можно использовать часы. Его не следует использовать с утра или вечера. Вместо этого вы можете указать «утром», «вечером» или «ночью», чтобы прояснить значение.При использовании часов вы можете использовать цифры или слова для обозначения времени, соблюдая правила любого руководства по стилю, которому вы следуете (если применимо).

• Мы должны вставать в , 6 часов, утра, чтобы успеть в школу.
• Мы должны вставать в , шесть часов, , чтобы успеть в школу.
• Она возвращается домой около восемь 9:14 вечера.

Правила для полуночи и полудня

Обычно вместо 12 п. Пишут полдень и полночь.м. и 12 часов утра, хотя любой из этих вариантов верен. Однако не стоит совмещать оба варианта.

• правильно : Мы пришли домой около , полночь, и проспали до , полдень следующего дня.
• правильно : Спал до 12 часов. а потом снова лег спать в 00:00
• неверно : Мне нужно быть дома к 00:00, полночь .
• неверно : Она приносит мне обед в 12 полудня .

Когда сомневаешься, объясни по буквам

Если вы сомневаетесь, следует ли писать число по буквам или по буквам, обычно лучше всего написать его. Однако для больших чисел вы всегда можете ошибиться в числовой форме.

• В прошлом году издательство продало 10 миллионов экземпляров моей книги.
• На этом свадебном платье 1 500 блесток!

Мастер как писать числа на английском языке

Теперь, когда вы знаете, когда писать числа по буквам, найдите время, чтобы узнать еще несколько правил написания чисел. Например, изучите правила использования запятых в числах. Затем вы можете захотеть еще глубже погрузиться в числа и изучить те, которые можно выразить как частное, просмотрев эти примеры рациональных чисел.

Цифры, цифры и цифры

Число

Число — это счетчик или измерение, которое на самом деле является идеей в нашем сознании.

Мы пишем или говорим о числах, используя цифр , например, «4» или «четыре».

Но мы также можем поднять 4 пальца или 4 раза постучать по земле.

Это разные способы обозначения одного и того же номера.

Существуют также специальные числа (например, π (Пи)), которые нельзя записать точно, но они все еще являются числами, потому что мы знаем, что за ними стоит идея .

Цифра

Цифра — это символ или имя , обозначающее число.

Примеры: 3 , 49 и двенадцать — все числа.

Итак, число — это идея, а число — это то, как мы его записываем.

Цифра

Цифра — это одиночный символ , используемый для составления цифр.

0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — десять цифр, которые мы используем в повседневных числах.

Пример: цифра 153 состоит из 3 цифр («1», «5» и «3»).

Пример: цифра 46 состоит из 2 цифр («4» и «6»).

Пример: цифра 9 состоит из 1 цифры («9»). Таким образом, одна цифра также может быть цифрой

.

Мы можем использовать и другие символы, например, в шестнадцатеричном формате также используются некоторые буквы!

Цифры -> Цифры -> Цифры

Таким образом, цифры составляют цифры, а цифры соответствуют идее числа.

Также как буквы составляют слова, а слова обозначают идею предмета.

Номер вместо цифры

Но часто люди (включая меня) говорят «Число», хотя им действительно следует сказать «Числовое»… не имеет значения, если вы это сделаете, потому что другие люди вас понимают.

Но попробуйте использовать «цифру» только когда говорите об отдельных символах, составляющих цифры, хорошо?

Цифры и цифры других типов

Мы все привыкли использовать такие числа, как «237» и «99», но римляне использовали римские цифры, и на протяжении всей истории использовалось много других цифр и цифр.

Научная запись

Научная нотация (также называемая Стандартной формой в Великобритании) — это особый способ записи чисел:

Как это:
Или это:

Позволяет легко использовать большие и маленькие значения.

Хорошо, как это работает?

Пример: 700

Почему 700 записывается как 7 × 10 ² в научной нотации?

700 = 7 × 100

, поэтому 700 = 7 × 10 ²

И 700 , и 7 × 10 ² имеют одинаковое значение, но показаны по-разному.

Пример: 4 900 000 000

1,000,000,000 = 10 ⁹ ,
, поэтому 4,900,000,000 = 4.9 × 10 ⁹ в научной нотации

Число записывается в виде из двух частей :

• Всего цифр с десятичной запятой после первой цифры, за которой следует
• × 10 в степень , которая помещает десятичную точку там, где она должна быть
  (т.е. показывает, на сколько мест нужно переместить десятичную точку).

В этом примере 5326,6 записывается как 5,3266 × 10 ³ ,
потому что 5326.4 = 3 × 10 × 10 × 10 × 10 = 30 000

Калькуляторы часто используют «E» или «e», например:

Пример: 6E + 5 совпадает с 6 × 10 ⁵

• 6E + 5 = 6 × 10 × 10 × 10 × 10 × 10 = 600000

Пример: 3.12E4 то же самое, что 3.12 × 10 ⁴

• 3.12E4 = 3,12 × 10 × 10 × 10 × 10 = 31 200

Как это сделать

Чтобы вычислить степень 10, подумайте: «На сколько раз переставить десятичную запятую?»

	Когда число 10 или больше, десятичная точка должна переместиться на влево на , а степень 10 равна положительному значению .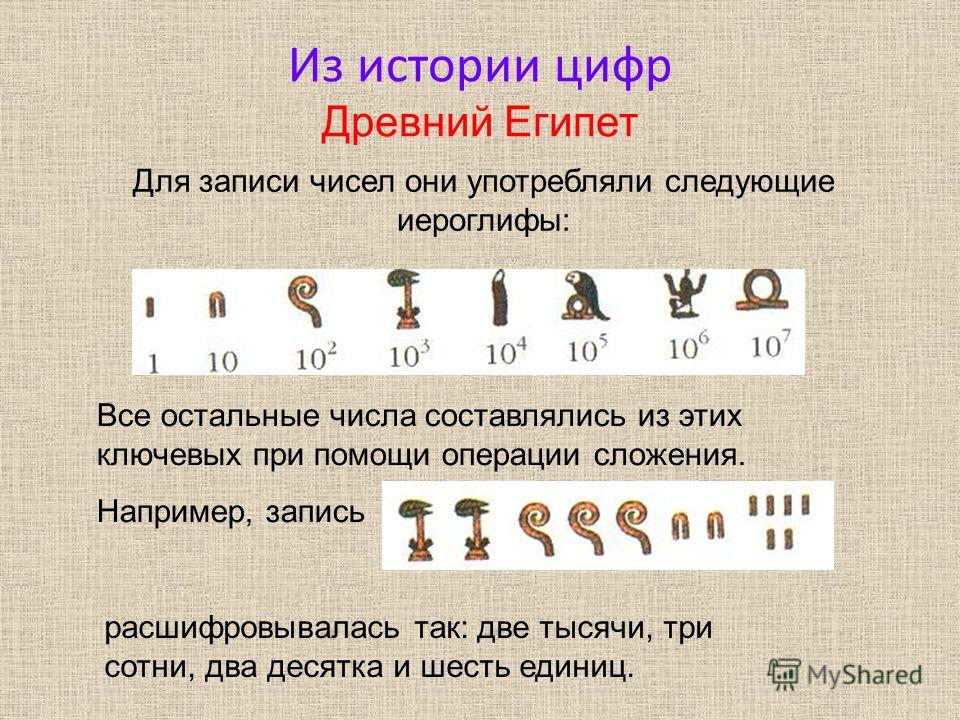
	Когда число меньше 1, десятичная точка должна сместиться на вправо на , поэтому степень 10 будет равна отрицательному значению .

Пример: записано 0,0055

5,5 × 10 ^-3

Потому что 0,0055 = 5,5 × 0,001 = 5,5 × 10 ^-3

Пример: записано 3.2

3.2 × 10 ⁰

Нам вообще не нужно было перемещать десятичную точку, поэтому степень равна 10 ⁰

Но теперь в научной нотации

Проверить!

После ввода числа в научную нотацию просто проверьте, что:

• Цифры от 1 до 10 (может быть 1, но не 10)
• «Степенная» часть показывает, на сколько раз переместить десятичную запятую.

Зачем это нужно?

Потому что это упрощает работу с очень большими или очень маленькими числами, которые часто встречаются в научной и инженерной работе.

Пример: проще писать (и читать) 1,3 × 10 ^-9 , чем 0,0000000013

Он также может упростить вычисления, как в этом примере:

Пример: крошечное пространство внутри компьютерной микросхемы было измерено как 0,00000256 м в ширину, 0,00000014 м в длину и 0,000275 м в высоту.

Каков его объем?

Давайте сначала преобразуем три длины в экспоненциальное представление:

• ширина: 0.000 002 56m = 2,56 × 10 ^-6
• длина: 0,000 000 14м = 1,4 × 10 ^-7
• высота: 0,000 275 м = 2,75 × 10 ^-4

Затем умножьте цифры (игнорируя × 10):

2,56 × 1,4 × 2,75 = 9,856

Наконец, умножаем на 10:

10 ^-6 × 10 ^-7 × 10 ^-4 = 10 ^-17 (проще, чем кажется, просто сложите вместе −6, −4 и −7 )

Результат: 9.856 × 10 ^-17 м ³

Много используется в науке:

Пример: Солнца, Луны и планеты

Солнце имеет массу 1,988 × 10 ³⁰ кг.

Легче, чем писать 1,988,000,000,000,000,000,000,000,000,000 кг
(и это число дает ложное представление о точности многих цифр).

Это также может сэкономить место! Вот что происходит, когда вы удваиваете на каждом поле шахматной доски:

Значения округлены, поэтому 53,6870,912 отображается как 5 × 10 ⁸

Последнее значение, показанное как 9 × 10 ¹⁸ , на самом деле 9 223 372 036 854 775 808

Инженерное обозначение

Engineering Notation похожа на Scientific Notation, за исключением того, что мы используем только те степени десяти, которые кратны 3 (например, 10 ³ , 10 ^-3 , 10 ¹² и т. Д.).

Примеры:

• Записано 2700 2,7 × 10 ³
• 27000 записано 27 × 10 ³
• 270,000 записано 270 × 10 ³
• 2,700,000 записано 2,7 × 10 ⁶

Пример: записано 0,00012

120 × 10 ^-6

Обратите внимание, что часть «цифры» теперь может быть от 1 до 1000 (это может быть 1, но никогда не 1000).

Преимущество состоит в том, что мы можем заменить × 10 с метрическими числами. Таким образом, мы можем использовать стандартные слова (например, тысяча или миллион), префиксы (например, кило, мега) или символ (k, M и т. Д.)

Пример: записано 19 300 метров 19,3 × 10 ³ м, или 19,3 км

Пример: записано 0,00012 секунд 120 × 10 ^-6 с или 120 микросекунд

Расширенная запись — способ расширения чисел

Что означает расширенная запись?

Расширенное представление можно определить как способ выражения чисел путем отображения значения каждой цифры.Запись числа в развернутой форме — это не то же самое, что запись числа в развернутой форме.

В расширенной записи число представлено как сумма каждой цифры, умноженной на ее разрядное значение, тогда как в развернутой форме сложение используется только между числами разрядного значения. Например:

234 в развернутой форме:

= 200 + 30 + 4

, а 234 в развернутой форме:

= (2 x 100) + (3 x 10) + (4 x 1)

Исходный Форма числа «234» называется стандартной формой.

Как сделать расширенную нотацию?

Чтобы раскрыть конкретное число (из его стандартной формы), нам нужно расширить его до суммы каждой цифры, умноженной на соответствующее ей разрядное значение (единицы, десятки, сотни и т. Д.).

Эти методы записи числа в развернутой нотации и формах проиллюстрированы в примерах ниже.

Пример 1

Записать 4981 в развернутом виде?

Решение

Число 4981 можно записать в развернутой форме как:

4981 = 4000 + 900 + 80 + 1
В этом методе каждое число, следующее после цифры, заменяется нулями.Например, 4 и 9 в номере представлены как 4000 и 900 соответственно.

Пример 2

Записать 15 807 в развернутом виде?

Решение

15 807 в развернутой форме представлено как:

15 807 = 10 000 + 5 000 + 800 + 7
В этом примере значение разряда 0 в числе равно нулю; следовательно, значение в разряде десятков не отображается, потому что нет десятков.

Запись числа в расширенной системе счисления влечет за собой указание места числа в экспоненциальной степени десяти.

Пример 3

Запишите расширенное обозначение: 4,981

Решение

4,981 = (4 x 1,000) + (9 x 100) + (8 x 10) + (1 x 1)

= (4 x 10 ³ ) + (9 x 10 ² ) + (8 x 10 ¹ ) + (1 x 10 ⁰ )

Пример 4

Запишите 15,807 в развернутом формате ?

Решение

15 807 = (1 x 10 000) + (5 x 1000) + (8 x 100) + (7 x 1)

= (1 x 10 ⁴ ) + (5 x 10 ³ ) + (8 x 10 ² ) + (7 x 10 ⁰ )

Пример 5

Запишите тысячи, сотни, десятки и единицы для каждого из следующих чисел:

a.945

945 = 9 сотен + 4 десятков + 7 единиц

= 900 + 40 + 5

б. 458

458 = 4 сотни + 5 десятков + 8 единиц

= 400 + 50 + 8

c. 5973

5973 = 5 тысяч + 9 сотен + 7 десятков + 3 единицы

= 5000 + 900 + 70 + 3

г. 333

333 = 3 сотни + 3 десятки + 3 единицы

= 300 + 30 + 3

e. 789

789 = 7 сотен + 8 десятков + 9 единиц

= 700 + 80 + 9

Расширенная запись с десятичными знаками

Десятичные числа также могут быть записаны в расширенной записи с использованием экспоненциальной степени десяти.

Пример 5

Записать 96.24 в развернутой нотации?

Решение

96,24 = 90 + 6 + 0,2 + 0,04
(9 x 10) + (6 x 1) + (3 x 10 ^-1 ) + (4 x 10 ^-2 )

Пример 6

Запишите десятичное число 536.072 в развернутой записи.

Решение

536,072 = 500 + 30 + 6 + 0,07 + 0,002
(5 x 10 ² ) + (3 x 10 ¹ ) + (6 x 10 ⁰ ) + (7 x 10 ^-2 ) + (2 x 10 ^-3 )

Практические вопросы

I. Запишите в развернутом виде следующие числа:

2. 6587
3. 1234
4. 29012
5. 49500
6. 4007

II. Ниже представлены развернутые формы разных чисел. Напишите числа в стандартной форме.

1. 50000 + 7000 + 900 + 60 + 1
2. 6000 + 500 + 30 + 7
3. 20000 + 1000 + 200 + 70 + 9
4. 50000 + 7000 + 10 + 8
5. 400000 + 80 + 8
6. 70000 + 7000 + 10 + 1

III.Напишите развернутые формы чисел ниже:

(i) 1749, …………., ……………., ……………., …………… .., ……………. .
(ii) 5605, …………., ……………., ……………., …………… .., ……………. .
(iii) 43453, …………., ……………., ……………., …………… .., ……………. .
(iv) 76125, …………., ……………., ……………., …………… .., ……………. .

IV. Заполните пропуски:
(i) 56371 = …… десять тысяч + …… тысяча + …… сотня + …… десятки + …… единицы
(ii) 937032 = …… сто + …… тысячи + …… единицы
( iii) 59278 = (…… x 10000) + (9 x ……) + (…… x 100) + (2 x ……) + (…… x 8)
(iv) 33602 = 30000 + …… +… … + 2

Предыдущий урок | Главная страница | Следующий урок

Пять упражнений по написанию чисел для учащихся младшего возраста

Это задание является частью моих ресурсов «Учимся писать числа». Не забудьте щелкнуть мышью, чтобы получить все интересные распечатки и идеи.

В моем доме появилась новая навязчивая идея. У нас есть совершенно новый писатель чисел, и он все о некоторой практике написания чисел . Он любит учиться писать числа, а вы сами пишете числа.

«Мама, пиши бесплатно. Мам, напиши шестьдесят два. Мам, напиши cero, cero, семь. Когда ему нравится, мы могли сидеть и писать числа долгое время.

К счастью, я хорошо подготовлен к новым числам.Наше число, пишущее стихи и печатные издания, по-прежнему очень популярно на их прыжковой площадке. И они по-прежнему идеальны — для новичков в числах или для детей постарше, которые все еще борются с переворотами.

Но, знаете, иногда нужно немного разнообразия. Итак, вот еще несколько занятий, которые помогут детям — маленьким и старшим — попрактиковаться в написании чисел.

Практика написания чисел

1. Запись номера лотка для соли

На сайте

Learn with Play at Home есть отличная статья о том, как использовать солонку для написания чисел.Вы можете использовать карточки и посчитать их, как показано, или просто сделать так, чтобы они скопировали номерную сторону карточки. Мне нравится, что это самоконтроль, и что у Дебс есть потрясающие идеи для расширения деятельности.

Не так много соли? Вы также можете заменить песок, сахар, муку или кукурузный крахмал. Если у вас нет необычного подноса, подойдет любой плоский контейнер с низкими стенками. А для тех, кто беспокоится о беспорядке и хранении, Джули из Nurturing Learners нашла для себя большую коробочку с крышкой.

2. Играть в калькулятор

Еще одна идея от «Учись с игрой дома»; это требует немного большей подготовки, но какой забавный вариант. Сделайте свой собственный калькулятор на крышке бутылки, и дети смогут играть, нажимая числа, а затем записывая их на бумажной полоске в области отображения. И снова Дебс предлагает множество вариантов расширения этой деятельности для дошкольной и детской возрастной группы.

3. Отличное применение для старых календарей

Discover, Explore, Learn делится фантастическим использованием старых календарей! Годовые календари дадут вам много практики письма, а старые так легко найти бесплатно.

4. Гонка за следом

Ой, детям НРАВИТСЯ эта игра. Он по-прежнему слишком быстр для Томаса, но большие игроки любят играть в него. Вы можете увидеть исходную идею примерно на полпути вниз в этом списке идей математического центра Шари Слоан.

Вы играете, бросая кубик, а затем отслеживая число на странице. Игра развивается быстро, так как у каждого игрока есть свой собственный кубик, и он быстро бросает кубики. Игрок, проследивший все свои номера первым, выигрывает.

Мы помещаем наши в защитные пленки и используем маркеры для сухого стирания. Это помогает Джону закрепить его числовое образование, а Оливия работает над этими надоедливыми переворотами. И они никогда не устают играть.

5. Рабочие тетради Kumon

По мере того, как ваш писатель чисел приобретает способность управлять мелкой моторикой и хочет или нуждается в дополнительной практике, Кумон предлагает Моя книга чисел 1-30 . Кумон — наша любимая рабочая тетрадь, и в эту книгу входит не только практика письма, но также счет и распознавание чисел.

А как насчет вас? Есть ли у вас какие-нибудь любимые упражнения по написанию чисел, которые помогут маленьким математикам с практикой написания чисел?

Пэм является автором The Your Morning Basket Guide и Plan Your Year: Homeschool Planning for Purpose and Peace .Она также является ведущей трех популярных подкастов — The Homeschool Snapshots Podcast , Your Morning Basket и The Homeschool Solutions Show .