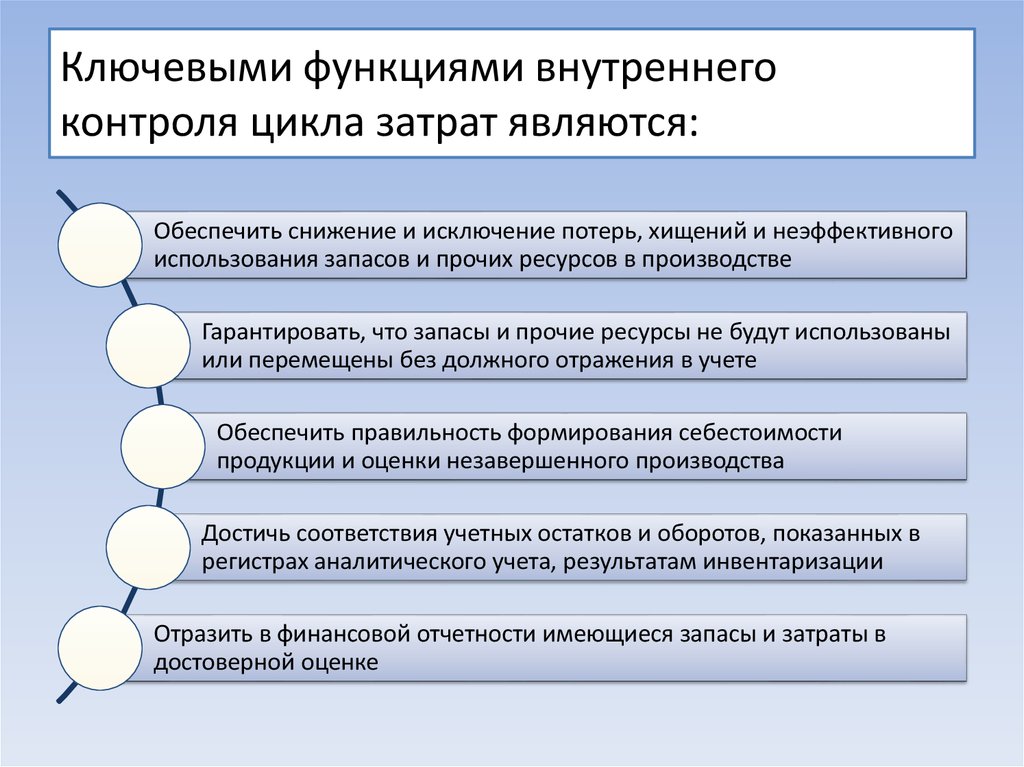
Использование стандартных функций. — Информатика, информационные технологии
Функции — заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Например, функция СУММ суммирует значения в диапазоне ячеек.
Список аргументов может состоять из чисел, текста, логических величин (например, ИСТИНА или ЛОЖЬ), массивов, значений ошибок (например #Н/Д) или ссылок. Необходимо следить за соответствием типов аргументов. Кроме того, аргументы могут быть как константами, так и формулами.
Структура функции начинается с указания имени функции, затем вводится открывающая скобка, указываются аргументы (Рис.102), отделяющиеся точками с запятыми, а затем — закрывающая скобка.
Если написание формулы начинается с функции, перед именем функции вводится знак равенства «=».
Рис. 102. Функция вычисления среднего значения.
Копирование и перемещение формулы.
При копировании и перемещении формулы относительные адреса в ссылках автоматически изменяются в соответствии с относительным расположением исходной ячейки и создаваемой копией. Используемые в формуле абсолютные адреса ссылок при копировании и перемещении формулы не изменяются.
Используемые в формуле абсолютные адреса ссылок при копировании и перемещении формулы не изменяются.
Форматирование.
Установка параметров форматирования текста и чисел выполняется в диалоговом окне (Рис.103), отображаемом после выполнения команд меню Формат/Ячейки.
Рис. 103.Диалоговое окно Формат ячеек.
Кроме форматирования шрифта (Вкладка Шрифт) здесь же можно настроить форматы данных (Вкладка Число), размещение данных внутри ячейки (Вкладка Выравнивание), оформление границ (Вкладка Граница), оформление заливки (Вкладка Вид), защиту данных и скрытие формул (Вкладка Защита).
Часть настроек вынесены на панель инструментов Форматирование.
Объединение/разъединение выделенных ячеек можно выполнять как при помощи диалогового окна Формат ячеек, так и при помощи кнопки Объединить и поместить в центре .
Добавление, удаление, переименование листов.
Добавление, удаление, перемещение, переименование листов можно выполнить вызвав контекстное меню кликом по имени листа (Рис.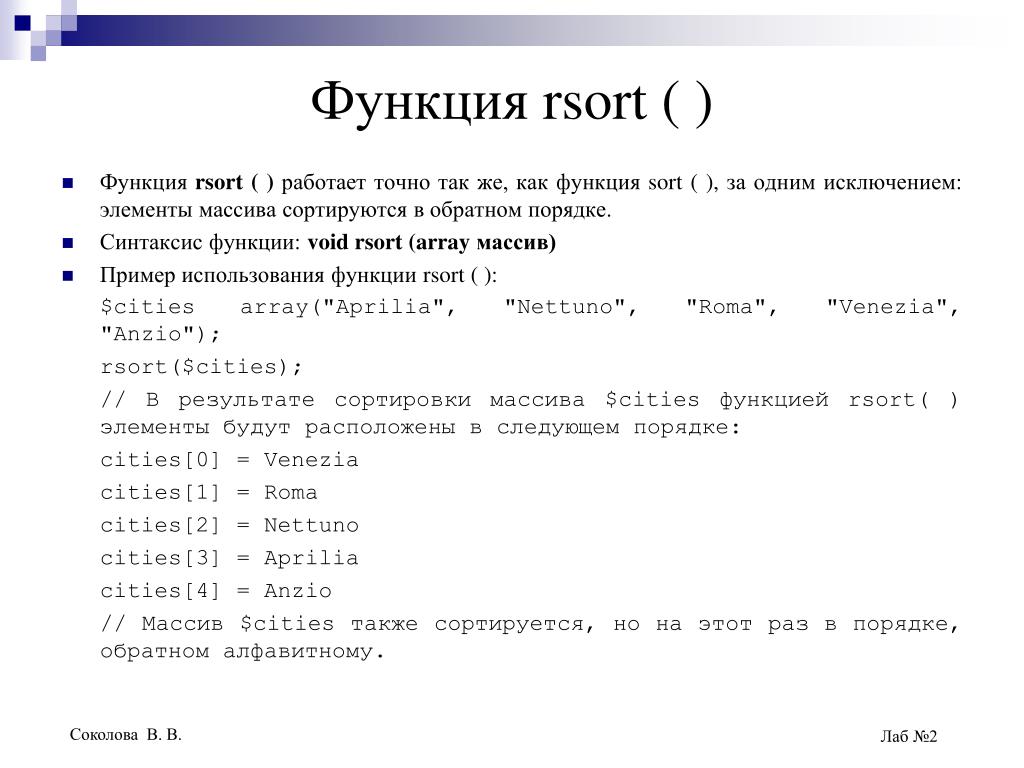 104).
104).
Рис. 104.Контекстное меню работы с листом.
Задание для выполнения лабораторной работы № 8.
Создание, форматирование и оформление электронных таблиц.
Использование функций и арифметических действий.
1. Откройте электронную таблицу Microsoft Excel.
2. Создайте новую книгу, если его окно не отобразилось автоматически.
3. Сохраните новую книгу в папке MSExcel с именем Задание8.xls.
4. Откройте файл Задание5 .doc, находящийся в папке MSWord.
5. Установив табличный курсор в ячейку А1 на Листе 1 и скопируйте 2 и 3 строки заголовка таблицы «Крупнейшие банки …» в файл Задание8.xls (Рис.105) .
Рис. 105. Результат выполнения п.5
6. Включите предварительный просмотр , закройте его кнопкой . После чего на листе пунктирной линией будут отображаться границы страниц.
7. Установите все поля по 1 см (Файл/ Параметры страницы/Поля).
8. Установите альбомную ориентацию (Файл/ Параметры страницы/ Страница/ Ориентация/ Альбомная).
9. Добавьте столбцы «Всего за 2005-6» для «Числа выданных кредитов» и «Объема выданных кредитов…» (Вставка / Столбец) (Рис.106)
Рис. 106. Результат выполнения п.9
10. Справа от таблицы добавьте столбцы Средний объем кредита (2005 (тыс.$), 2006 (тыс.$), Всего за 2005-6)
11. Преобразуйте заголовок к следующему виду (Форматирование шрифта :Times New Roman, 12 , Ж. Выравнивание в ячейке: По вертикали — по центру, По горизонтали – по центру, Отображение — переносить по словам). Обратите внимание на то, чтобы заголовок занимал ширину страницы полностью (Рис.107).
Рис. 107. Результат выполнения п.11
12. Добавьте пустую строку над строкой 1 (Вставка/Строка).
13. Объедините ячейки A1:N1 (Выделить, нажать кнопку «Объединить» ).
14. В полученную ячейку введите название таблицы (Рис.108).
Рис. 108. Результат выполнения п.14
15. Заполните ячейки A4: A56 данными , начиная с номера 1 по 53 при помощи функции «Прогрессия». Для этого :
Для этого :
a. Установите табличный курсор в ячейку А4 напечатайте начальное значение (1) и нажмите Enter
b. Снова установите табличный курсор в ячейку А4 и заполните остальные номера с помощью Прогрессии (Правка/ Заполнить/ Прогрессия/ Расположение – по столбцам, Шаг – 1, Тип – арифметическая, Предельное значение — 53)
16. Перейдите в файл Задание5.doc.
17. Скопируйте и вставьте имеющиеся данные в соответствующие столбцы файла Задание8.xls (Рис.109).
Рис. 109. Результат выполнения п.17
18. Рассчитайте данные по формулам в столбцах (Рис.110):
a. Число выданных кредитов – Всего ( и далее используйте Маркер заполнения)
b. Объем выданных кредитов – Всего (аналогично пункту а)
c. Средний объем выданных кредитов – 2005 ( и далее используйте Маркер заполнения)
d. Средний объем выданных кредитов – 2006 (аналогично пункту с)
e. Средний объем выданных кредитов – Всего (аналогично пункту а)
Рис. 110. Результат выполнения п. 18
18
Если в результате расчетов получилось «#ЗНАЧ» — проверьте – нет ли пробела в числовых данных. Для двух банков данные за 2005 год отсутствуют (Номос- банк и БФГ – Кредит – н.д. ), поэтому для них рассчитать итог нельзя. (Выделим строки этих банков – красным цветом).
Если в результате получилось значение «#ДЕЛ/0!» — замените это значение нулем.
19. Рассчитайте значение ИТОГО для следующих столбцов (Рис.111):
a. Число выданных кредитов – 2005 год
b. Число выданных кредитов – 2006 год
c. Объем выданных кредитов – 2005 год
d. Объем выданных кредитов – 2006 год
(Выделите все значения столбца и нажмите знак Автосумма )
Рис. 111. Результат выполнения п.19
Если в результате получилось значение «######» — число не умещается в поле – уменьшите размер шрифта.
20. Отформатируйте таблицу указанным способом при помощи панели Форматирование (Рис.112).
Рис. 112. Результат выполнения п.20
а.Шрифт : Arial, 9, выравнивание текста – по левому краю, выравнивание числовых данных – по правому краю.
b.Обрамление по контуру таблицы и заголовка — сплошная толстая линия, внутри таблицы – тонкая линия.
c.Заливка отдельных столбцов цветом.
21. Переименуйте Лист 1 в лист Таблица (Рис.113) (правой кнопкой мыши по «Лист»/ Переименовать).
Рис. 113. Результат выполнения п.21
22. Сохраните изменения в файле Задание8.xls.
Статьи к прочтению:
- Использование стека для передачи параметров
- Использование трансляторов и интерпретаторов на разных уровнях
Урок 28Использование стандартных функций
Похожие статьи:
Iv использование логических функций
Логические функции предназначены для проверки выполнения условия или для проверки нескольких условий. Функция ЕСЛИ позволяет определить, выполняется ли…
Использование встроенных функций excel
Excel содержит набор функций, сгруппированным по категориям.
 Ввод функции удобно осуществлять с использованием Мастера функций. Прежде всего, следует…
Ввод функции удобно осуществлять с использованием Мастера функций. Прежде всего, следует…
Использование функций и вложенных функций в формулах Excel
Excel для Microsoft 365 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления. Все функции Excel можно найти на вкладке «формулы» на ленте.
-
Синтаксис функции Excel
В приведенном ниже примере функции ОКРУГЛ , округленной на число в ячейке A10, показан синтаксис функции.
1. Structure. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающую круглую скобку, аргументы функции, разделенные запятыми, и закрывающая круглая скобка.
2. имя функции. Чтобы просмотреть список доступных функций, щелкните ячейку и нажмите клавиши SHIFT + F3, чтобы открыть диалоговое окно Вставка функции .
3. аргументы. Аргументы могут быть числами, текстом, логическими значениями, такими как Истина или ложь, массивами, значениями ошибок, например #N/a или ссылками на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Примечание:
Вам не нужно вводить функции во все прописные буквы, например = «ОКРУГЛИТЬ», так как Excel автоматически заполнит ввод имени функции после нажатия кнопки «Добавить». Если вы неправильно наводите имя функции, например = СУМА (a1: A10), а не = сумм (a1: A10), Excel вернет #NAME? Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
Если вы неправильно наводите имя функции, например = СУМА (a1: A10), а не = сумм (a1: A10), Excel вернет #NAME? Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
-
Ввод функций Excel
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. После выбора функции в диалоговом окне Вставка функции Excel запустит мастер функций, который выведет на экран имя функции, каждый из ее аргументов, описание функции и каждый аргумент, текущий результат функции и текущий результат всей формулы.
Для упрощения создания и редактирования формул, а также для минимизации ошибок ввода и синтаксиса используйте Автозаполнение формул.
 После ввода знака = (знак равенства) и начальных букв функции Excel отобразит динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих этим буквам. Затем вы можете выбрать один из раскрывающегося списка, и приложение Excel введет его автоматически.
После ввода знака = (знак равенства) и начальных букв функции Excel отобразит динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих этим буквам. Затем вы можете выбрать один из раскрывающегося списка, и приложение Excel введет его автоматически. -
Вложение функций Excel
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в следующей формуле используется вложенная функция СРЗНАЧ , а результат сравнивается со значением 50.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных.
 Например, если аргумент должен быть логическим, т. е. иметь значение ИСТИНА либо ЛОЖЬ, вложенная функция также должна возвращать логическое значение (ИСТИНА или ЛОЖЬ). В противном случае Excel выдаст ошибку «#ЗНАЧ!».
Например, если аргумент должен быть логическим, т. е. иметь значение ИСТИНА либо ЛОЖЬ, вложенная функция также должна возвращать логическое значение (ИСТИНА или ЛОЖЬ). В противном случае Excel выдаст ошибку «#ЗНАЧ!».<c0>Предельное количество уровней вложенности функций</c0>.
|
⇐ ПредыдущаяСтр 6 из 13Следующая ⇒ Функция в составе формулы вызывается по имени, после которого в круглых скобках указываются один или несколько аргументов, разделенных точкой с запятой. Пример 2: вычислить значения функции на отрезке xÎ[0;0,5] с шагом h = 0,1 и определить среди найденных величин количество отрицательных и сумму положительных значений функции.
Рис. 4.3. Ввод исходных данных: аргументов функции (а) и ее значений (б)
Для нахождения количества отрицательных значений функции организуем справа дополнительный столбец признаков. Каждая ячейка столбца признаков будет содержать 1, если значение функции в этой строке больше нуля и 0 в противном случае. Просуммировав в дальнейшем эти ячейки, мы получим количество отрицательных значений функции.
Рис. 4. Вычисление количества отрицательных (а) и суммы положительных (б) значений функции
Установить требуемые значения в ячейках столбца можно с помощью функции ЕСЛИ. Эта функция возвращает одно из двух значений, в зависимости от истинности логического выражения. Установим указатель в ячейку C2 и вызовем Мастер функций. В категории Логические выберем функцию ЕСЛИ. На следующем шаге в поле Лог_выражение введем B2<0, а в поля Значение_если_истина и Значение_если_ложь значения 1 и 0 соответственно. Заполним созданной формулой диапазон C3:C7. Далее нажмем кнопку с символом “∑” (автосумма) и в ячейке C8 получим искомое значение (рис. 4.4, Для вычисления суммы положительных значений будем использовать функцию СУММЕСЛИ, которая суммирует содержимое тех ячеек заданного диапазона, которые удовлетворяют некоторому критерию. Сделаем активной ячейку C9 и вызовем Мастер функций.
Построение диаграмм Диаграммы позволяют в наглядной форме представить данные, расположенные на рабочих листах и визуально оценить соотношение между их значениями. Наиболее просто можно построить диаграмму выделив на листе диапазон с данными и выполнив команду Вставка | Диаграмма. Запускается Мастер диаграмм, который предлагает за четыре шага настроить вид создаваемой диаграммы. На первом шаге необходимо выбрать тип диаграммы. Для перехода к следующему шагу нажимается кнопка Далее. Нажатие кнопки Готово прервет работу Мастера диаграмм и приведет к немедленной вставке диаграммы на текущий лист. При этом те параметры, которые настраиваются на последующих шагах, будут иметь значения, установленные по умолчанию. На втором шаге при необходимости уточняется диапазон с данными и способ размещения рядов данных (если их несколько) внутри этого диапазона: в строках или столбцах. Кроме того, каждому из рядов данных на вкладке Ряд можно присвоить свое имя. Третий шаг позволяет указать заголовки диаграммы и осей, включить или отключить линии сетки, добавить легенду, а также произвести другие настройки. На четвертом шаге выбирается место размещения диаграммы: на отдельном листе (специальном листе диаграмм) или текущем листе с данными. Если диаграмма расположена на листе данных, то после построения ее размеры можно изменять, как и у любого графического объекта. Также можно изменять любые параметры диаграммы, установленные при ее создании: тип, диапазон исходных данных, параметры и место размещения. Для этого необходимо вызвать контекстное меню диаграммы и выбрать соответствующую команду.
Работа со списками данных Большинство таблиц, создаваемых в Excel, являются какими-либо списками. — верхняя строка таблицы должна содержать уникальные заголовки столбцов, содержимое которых располагается ниже; — каждый столбец должен содержать однородные данные; — каждая строка имеет одинаковую структуру; — в таблице не должно быть пустых строк и столбцов. Если на листе имеется несколько списков, то они должны отделяться друг от друга как минимум одной пустой строкой или столбцом. Основными операциями, производимыми со списками, являются сортировка и фильтрация. Для выполнения сортировки необходимо установить указатель в любую ячейку списка и выполнить команду Данные | Сортировка. В диалоговом окне команды выбирается нужный столбец списка и направление сортировки: по возрастанию или по убыванию. Причем если список соответствует изложенным выше требованиям, то программа может идентифицировать столбцы по их заголовкам. Фильтрация позволяет временно скрыть те строки списка, в которых значения в одном или нескольких столбцах не удовлетворяют заданным критериям. При этом с видимой после наложения фильтра частью списка можно производить те же действия, что и с любым другим фрагментом рабочего листа. В Excel существует два варианта наложения фильтра: автофильтрация и расширенный фильтр. Первый обычно используется для установки простых условий отбора, второй – для фильтрации с применением более сложных критериев. Наиболее просто в Excel производится автофильтрация. Для ее применения необходимо сделать активной любую ячейку списка и выполнить команду Данные | Фильтр| Автофильтр.
Рис. 4.5. Вид списка после включения режима автофильтрации
Щелкнув на значке в том столбце, по содержимому которого будет производиться фильтрация, можно выбрать один из нескольких вариантов отбора. Для того чтобы оставить видимыми строки с одним конкретным значением, его необходимо выбрать из списка вариантов фильтрации. Выбрав команду Первые 10 можно указать сколько наибольших (наименьших) значений останется после наложения фильтра. Более сложные критерии отбора можно установить, выбрав команду Условие. В диалоговом окне можно установить два условия, объединив их логической связкой «И» или «ИЛИ». Для примера произведем отбор тех записей, у которых должностной оклад больше 2000 р. и меньше 6000 р. (рис. 4.6, а). Введем каждое из условий в соответствующие строки диалогового окна (рис. 6, а) и нажмем ОК. Результат фильтрации показан на рис.
Рис. 6. Диалоговое окно ввода условий фильтрации (а) и ее результаты (б)
При необходимости, после фильтрации списка по содержимому одного столбца, можно повторить операцию с другим столбцом и отфильтровать уже оставшуюся часть таблицы. Для отключения режима автофильтрации и показа всех скрытых записей, необходимо повторно выполнить команду Данные | Фильтр| Автофильтр.
Контрольные задания. 1. Запустите приложение Microsoft Excel и создайте с его помощью файл с именем Lab.xls. 2. Переименуйте листы книги MS Excel: первый в «Задание», второй лист в «Данные», третий лист – «График». 3. Выберите из таблицы вариант задания соответственно номеру в журнале группы. Варианты задания
4. На листе «Задание» объедините несколько ячеек. Используя шрифт Times New Roman, размер шрифта 12, горизонтальное и вертикальное выравнивание в ячейкепо центру, наберите следующую информацию:
Вариант №__ (укажите номер варианта выполняемого задания) Выполнили студенты группы (укажите группу) ФИО (перечислите фамилии студентов, выполняющих данное задание) Функция (приведите вид функции у = f(x,a) для Вашего варианта) Значение параметраа (в отдельной ячейке укажите первое значение параметра а) Начальное значение аргумента (в отдельной ячейке укажите начальное значение аргумента) Шаг приращения аргумента (в отдельной ячейке укажите шаг приращения аргумента). 5. На листе «Данные» для табулирования функции y = f(x,a) создайте таблицу №1 по шаблону, приведенному на рис. 4.7. 6. Заполните столбец значений аргумента х. Обязательно используйте ссылку на ячейки с начальным значением аргумента х и шагом приращения аргумента х, расположенные на листе «Задание». 7. Заполните столбец значений функции y. Обязательно используйте ссылку на ячейку со значением параметра а, расположенную на листе «Задание». 8. В четвертом столбце укажите критерий отбора значений функции для вашего варианта: например, y>2 – для первого варианта,
Рис. 7. Пример оформления таблицы
9. Под табл. 1 выведите количество значений функции, удовлетворяющих критерию отбора (см. рис. 7). Для этого используйте автосуммирование (кнопка с символом “∑”). 10. На третьем листе постройте график: по оси абсцисс должны располагаться значения аргумента х, по оси ординат – значения функции у. 11. Вставьте в рабочую книгу новый лист и назовите его «Сортировка». Выделите табл. 1 на листе «Данные» и скопируйте ее в буфер обмена. Перейдите на лист «Сортировка», вызовите диалоговое окно команды Правка | Специальная вставка, поставьте переключатель в положение «Вставить значения». Произведите вставку значений табл. 1. Произведите сортировку значений функции упо убыванию. 12. Скопируйте лист «Данные» в конец книги. Назовите появившийся лист «Фильтрация», а скопированную таблицу — «Таблица № 2». 13. Замените первое значение параметра а на листе «Задание» сначала вторым его значением, а затем третьим (см. седьмой и восьмой столбцы в таблице вариантов задания). Проследите, изменяются ли значения функции, вид графика, представление данных на листах «Сортировка» и «Фильтрация». 14. Напишите краткий отчет о ваших действиях, произведенных при выполнении каждого пункта лабораторной работы. Обязательно приведите примеры использованных вами формул, три строки табл. 1, схематичный рисунок графика функции. 15. Сделайте вывод о проделанной работе, о преимуществах и недостатках программы Microsoft Excelдля обработки различного рода информации: текстовой, числовой, графической. 16. Продемонстрируйте результаты выполнения работы и отчет преподавателю.
ЛАБОРАТОРНАЯ РАБОТА №8. ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: |
Правильное округление данных Excel для получения правильных сумм :: think-cell
При компиляции данных для отчета или презентации PowerPoint округление сумм в Excel часто вызывает проблемы. Во многих случаях требуется, чтобы округленные итоговые значения совпадали с итоговыми значениями округленных слагаемых, но этого сложно достичь. Для примера рассмотрим следующую таблицу:
Если значения округляются до целых чисел с помощью функции форматирования ячеек Excel, результатом будет следующая таблица. Итоговые значения, вычисленные «неправильно», выделены полужирным шрифтом:
Аналогично при использовании стандартных функций округления итоговые значения округленных значений вычисляются правильно, однако ошибки округления накапливаются, из-за чего результаты часто существенно отличаются от фактических сумм исходных значений. В следующей таблице показан результат
В следующей таблице показан результат =ROUND(x,0) примера выше. Суммы, которые отличаются от исходного значения на 1 и более, выделены полужирным шрифтом:
Используя округление think-cell, можно получить согласованные округленные суммы с минимальными изменениями. Хотя большинство значений округляются до ближайшего целого числа, некоторые значения округляются в противоположном направлении, что гарантирует правильное вычисления без накопления ошибки округления. Так как существует много способов получения правильных округленных сумм за счет изменения значений, think-cell выбирает решение, для которого требуется изменить минимальное число значений и минимальное отклонение от точных значений. Например, округление 10,5 до 10 будет предпочтительнее, чем округление 3,7 до 3. В следующей таблице показано оптимальное решение для примера выше, при этом измененные значения выделены полужирным шрифтом:
Чтобы получить такой же результат в собственных вычислениях, просто выберите соответствующий диапазон ячеек Excel. Затем нажмите кнопку на вкладке Формулы и, при необходимости, измените точность округления, используя раскрывающийся список на панели инструментов.
Затем нажмите кнопку на вкладке Формулы и, при необходимости, измените точность округления, используя раскрывающийся список на панели инструментов.
- 22.1
- Использование округления think-cell
- 22.2
- Ограничения округления think-cell
- 22.3
- Устранение неполадок с формулами TCROUND
22.1 Использование округления think-cell
Округление think-cell полностью интегрируется с Microsoft Excel и предоставляет набор функций, которые похожи на стандартные функции округления Excel. Вы легко можете применять эти функции к собственным данным, используя кнопки на панели инструментов на вкладке Формулы в think-cell.
22.1.1 Параметры округления
Как и функции Excel, функции округления think-cell принимают два параметра.
- x
- Значение, которое необходимо округлить. Это может быть константа, формула или ссылка на другую ячейку.
- n
- Точность округления.
 Значение этого параметра зависит от используемой функции. Параметры функций think-cell эквивалентны параметрам соответствующих функций Excel. Примеры см. в таблице ниже.
Значение этого параметра зависит от используемой функции. Параметры функций think-cell эквивалентны параметрам соответствующих функций Excel. Примеры см. в таблице ниже.
Округление think-cell позволяет округлять значения не только до целых чисел, но и до любых кратных чисел. Например, если вы хотите представить данные в последовательности 5-10-15…, просто округляйте значения до чисел, кратных пяти. Используя раскрывающееся меню на панели инструментов think-cell, просто введите или выберите нужную точность округления. Затем think-cell выберет требуемые функцию и параметры. В следующей таблице представлен ряд примеров округления определенных значений x с использованием панели инструментов вместе с соответствующим параметром n.
x = n = | 100 | 50 | 2 | 1 | 0,01 |
|---|---|---|---|---|---|
| 1,018 | 0 | 0 | 2 | 1 | 1,02 |
| 17 | 0 | 0 | 18 | 17 | 17,00 |
| 54,6 | 100 | 50 | 55 | 54 | 54,60 |
| 1234,1234 | 1200 | 1250 | 1234 | 1234 | 1234,12 |
| 8776,54321 | 8800 | 8800 | 8776 | 8777 | 8776. 54 54 |
Если значения отображаются не так, как вы ожидаете, убедитесь, что в параметрах формата ячейки Excel выбрано значение Общий, а столбцы достаточно широкие для отображения всех знаков после запятой.
| Кнопка | Формула | Описание |
|---|---|---|
TCROUND(x, n) | Позволить think-cell определять ближайшее кратное число для округления, чтобы минимизировать ошибку округления. | |
TCROUNDUP(x, n) | Принудительное округление x от нуля. | |
TCROUNDDOWN(x, n) | Принудительное округление x к нулю. | |
TCROUNDNEAR(x, n) | Принудительное округление x к ближайшему кратному числу с требуемой точностью.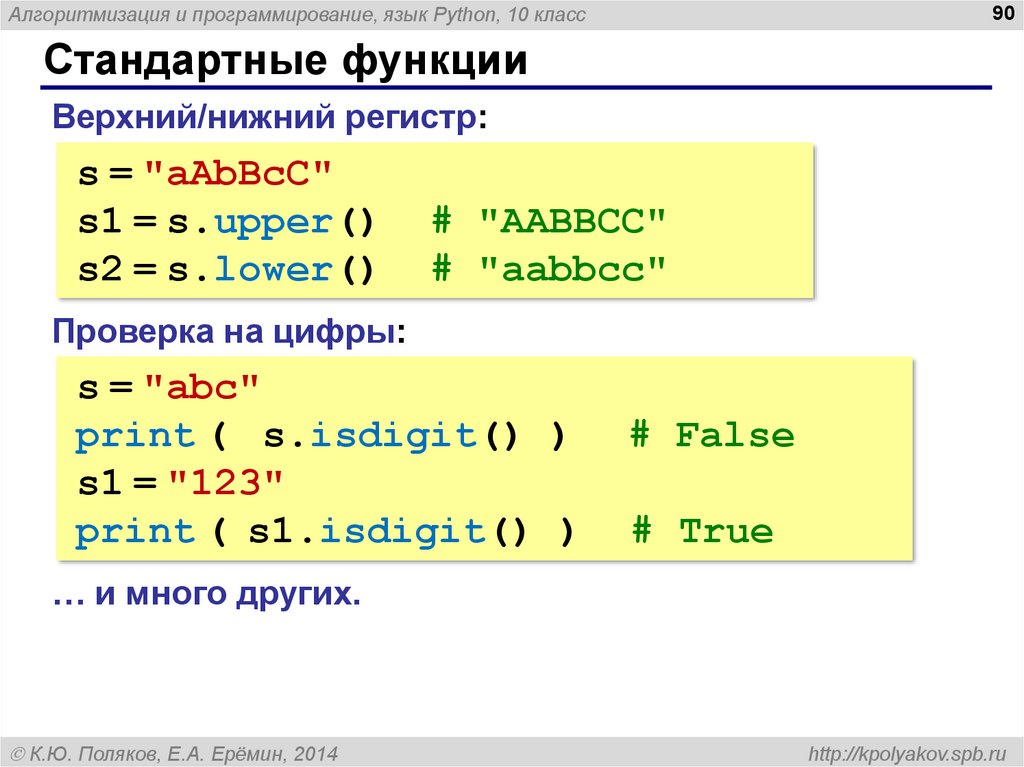 | |
| Удалить все функции округления think-cell из выбранных ячеек. | ||
| Выберите или введите требуемое кратное число для округления. | ||
| Выделить все ячейки, которые надстройка think-cell решила округлить до наиболее отдаленного из двух кратных чисел вместо наиболее близкого числа. | ||
| Вращающееся колесико означает, что функция округления think-cell применяется. |
Для получения оптимальных результатов и минимального отклонения от базовых значений, следует использовать TCROUND, когда это возможно. Используйте более ограничительные функции TCROUNDDOWN, TCROUNDUP или TCROUNDNEAR, только если это необходимо.
Внимание! Не следует использовать недетерминированные функции, такие как RAND(), с какими-либо формулами TCROUND. Если функции возвращают разные значения при каждом вычислении, округление think-cell будет совершать ошибки при вычислении значений.
Если функции возвращают разные значения при каждом вычислении, округление think-cell будет совершать ошибки при вычислении значений.
22.1.2 Макет вычисления
Прямоугольный макет примера выше приведен исключительно для демонстрации. Вы можете использовать функции TCROUND, чтобы настроить отображение произвольных сумм на листе Excel. Трехмерные ссылки Excel на другие листы и ссылки на другие файлы также работают.
22.1.3 Размещение функций TCROUND
Так как функции TCROUND предназначены для управления выходными данными ячейки, они должны быть крайними функциями:
| Неправильно: | =TCROUND(A1, 1)+TCROUND( SUM(B1:E1), 1 ) |
| Правильно: | =TCROUND( A1+SUM(B1:E1), 1 ) |
| Неправильно: | =3*TCROUNDDOWN(A1, 1) |
| Правильно: | =TCROUNDDOWN(3*A1, 1) |
Если вы введете что-то в строках неправильных примеров, think-cell уведомит вас о значении ошибки Excel #VALUE!.
22.2 Ограничения округления think-cell
Округление think-cell всегда ищет решение для произвольных сумм с промежуточными итогами и итоговыми значениями. Округление think-cell также предоставляет подходящие решения для других вычислений, использующих умножение и числовые функции. Однако в математических целях существование согласованного округляемого решения не может гарантироваться, если используются операторы, отличные от +, — и SUM.
22.2.1 Умножение на константу
Во многих случаях округление think-cell дает хорошие результаты, если используется умножение на константу, то есть если хотя бы один из коэффициентов основан на результате другой функции TCROUND. Рассмотрим следующий пример:
Точный результат вычисления для ячейки C1: 3×1,3+1,4=5,3. Чтобы получить этот результат, можно округлить значение 1,4 до 2:
Однако округление think-cell может только изменить значение, округлив его до большего или меньшего значения. Большее отклонение от исходных значений не поддерживается. Поэтому для определенных сочетаний входных значений невозможно найти согласованное решение для округления. В этом случае функция
Большее отклонение от исходных значений не поддерживается. Поэтому для определенных сочетаний входных значений невозможно найти согласованное решение для округления. В этом случае функция TCROUND предоставляет значение ошибки Excel #NUM!. В следующем примере показана нерешаемая задача:
Точный результат вычисления для ячейки C1: 6×1,3+1,4=9,2. Округление ячеек A1 и B1 даст следующий результат: 6×1+2=8 или 6×2+1=13. Фактический результат нельзя округлить до 8 или 13, а выходные данные округления think-cell будут выглядеть следующим образом:
Примечание. Функция AVERAGE Excel интерпретируется округлением think-cell как комбинация суммирования и умножения на константу. Кроме того, сумма, в которой одно слагаемое используется несколько раз, математически эквивалентно умножению на константу, и существование решения не гарантируется.
22.2.2 Общее умножение и другие функции
Если функции TCROUND используются для соответствующих ячеек и промежуточные результаты связаны только операторами +, -, SUM и AVERAGE, слагаемые и (промежуточные) итоговые значения объединяются в одной задаче округления. В этих случаях округление think-cell найдет решение, которое обеспечивает согласованность для всех связанных ячеек, если такое решение существует.
В этих случаях округление think-cell найдет решение, которое обеспечивает согласованность для всех связанных ячеек, если такое решение существует.
Так как TCROUND — обычная функция Excel, ее можно объединить с любыми функциями и операторами. Но если вы используете функции, отличные от указанных выше, для соединения результатов операторов TCROUND, округление think-cell не может объединить компоненты в одной общей задаче. Вместо этого компоненты формулы будут считаться отдельными задачами, каждая из которых будет решаться независимо друг от друга. Затем результаты будут использоваться как входные данные для других формул.
Во многих случаях результаты округления think-cell по-прежнему будут рациональными. Однако в некоторых случаях использование операторов, отличных от +, -, SUM и AVERAGE, приводит к получению округленных результатов, которые существенно отличаются от вычисления без округления. Рассмотрим следующий пример:
Точный результат вычисления для ячейки C1 в этом случае: 8,6×1,7=14,62. Так как ячейки A1 и B1 связаны умножением, округление think-cell не сможет объединить формулы из этих ячеек в общую задачу. Вместо этого после обнаружения ячейки A1 как допустимых входных данных, ячейка B1 будет вычислена независимо, а результат будет считаться константой для оставшейся задачи. Так как других ограничений нет, значение 1,7 из ячейки B1 округляется до ближайшего целого числа (2).
Так как ячейки A1 и B1 связаны умножением, округление think-cell не сможет объединить формулы из этих ячеек в общую задачу. Вместо этого после обнаружения ячейки A1 как допустимых входных данных, ячейка B1 будет вычислена независимо, а результат будет считаться константой для оставшейся задачи. Так как других ограничений нет, значение 1,7 из ячейки B1 округляется до ближайшего целого числа (2).
«Точный» результат вычисления для ячейки C1 в этом случае: 8,6×2=17,2. Теперь эту задачу попытается решить функция округления think-cell. Существует согласованное решение, для которого необходимо округлить 17,2 до 18. Результат будет выглядеть следующим образом:
Обратите внимание, что округленное значение в ячейке C1, которое равно 18, сильно отличается от исходного значения 14,62.
22.3 Устранение неполадок с формулами TCROUND
При использовании округления think-cell вы можете столкнуться с двумя ошибками: #VALUE! и #NUM!.
22.3.
 1 #VALUE!
1 #VALUE! Ошибка #VALUE! указывает на синтаксические проблемы, такие как неправильно введенные формулы или недопустимые параметры. Например, второй параметр TCROUND должен быть целым числом. Кроме того, уделите внимание правильному использованию разделителей. Например, в международной версии Excel формула выглядит так: =TCROUND(1.7, 0), а в немецкой версии Excel ее следует записать следующим образом: =TCROUND(1,7; 0).
Еще одна ошибка, связанная с округлением think-cell, — это размещение вызова функции TCROUND: нельзя использовать функцию TCROUND с другой формулой. Убедитесь, что TCROUND — это крайняя функция в формуле ячейки. (См. раздел Размещение функций TCROUND.)
22.3.2 #NUM!
Ошибка #NUM! возникает из-за числовых проблем. Если результат функции TCROUND равен #NUM!, это значит, что задача, определенная данным набором формул, не имеет математического решения. (См. раздел Ограничения округления think-cell.)
(См. раздел Ограничения округления think-cell.)
Если формулы, окруженные функциями TCROUND, содержат только операторы +, — и SUM и для всех операторов TCROUND используется одинаковая точность (второй параметр), решение будет гарантированно существовать и будет найдено округлением think-cell. Однако в следующих случаях существование согласованного округленного решения не гарантируется.
- Формулы содержат другие операции, такие как умножение или числовые функции. Кроме того, суммы, в которых одно слагаемое используется несколько раз, математически эквивалентны умножению.
- Вы должны использовать разные точности во втором параметре функции
TCROUND. - Вы часто используете функции
TCROUNDDOWN,TCROUNDUPиTCROUNDNEAR.
Вы можете заново сформулировать задачу, чтобы получить согласованное решение. Попробуйте следующее:
- Используйте более высокую точность для некоторых или всех операторов
TCROUND.
- Не используйте
TCROUNDс умножением или числовыми функциями, отличными от +, — иSUM. - Используйте одинаковую точность (второй параметр) для всех операторов
TCROUND. - Используйте
TCROUNDвместо функцийTCROUNDDOWN,TCROUNDUPиTCROUNDNEAR, где это возможно.
Возведение в степень в Microsoft Excel
Возведение в степень – одна из самых популярных математических задач, применяемая во время работы с электронными таблицами в Excel. При помощи встроенной функциональности программы вы можете реализовать данный вид операции всего в несколько кликов, выбрав наиболее подходящий метод. Кроме того, можно записать число как текст, если нужно только обозначить степень, но не считать ее.
Обо всем этом и пойдет речь в следующих разделах статьи.
Способ 1: Использование специального символа
Самый простой метод возведения в степень в Excel – использование записи специального символа, обозначающего этот вид операции. и вторую цифру, обозначающую степень. После нажатия клавиши Enter произойдет расчет, и в ячейке отобразится итоговое число возведения.
и вторую цифру, обозначающую степень. После нажатия клавиши Enter произойдет расчет, и в ячейке отобразится итоговое число возведения.
То же самое можно сделать, если необходимо посчитать степень числа, стоящего в конкретной ячейке. Число может измениться во время редактирования таблицы, но сама математическая операция останется. В таком случае оптимально записать в формуле номер ячейки, а затем указать, в какую степень следует возвести число, стоящее в ней. Используйте ту же методику записи, что показана в предыдущем абзаце.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Способ 2: Добавление функции степени
Одна из стандартных функций Excel позволяет вычислить степень числа, предварительно используя все входные данные. Использование данной формулы актуально в тех случаях, когда приведенный выше метод записи не подходит или само действие уже является частью обширной формулы. Вы можете использовать ручную запись или графическое окно добавления функции, которое мы и рассмотрим в качестве примера.
Вы можете использовать ручную запись или графическое окно добавления функции, которое мы и рассмотрим в качестве примера.
-
Активируйте ячейку для расположения функции, кликнув по ней левой кнопкой мыши. Затем нажмите по значку fx для открытия соответствующего окна.
-
В нем выберите категорию, отображающую полный перечень функций. Отыщите «СТЕПЕНЬ» и дважды кликните по этой строке.
-
В отдельном поле задайте число, а ниже укажите степень, в которую необходимо возвести число. В качестве числа можете использовать ячейку, имеющую определенное значение.
-
Примените изменения и вернитесь к таблице, чтобы ознакомиться с результатом. На следующем скриншоте вы видите, какую запись имеет эта функция, поэтому можете использовать ее для ручного ввода, если так будет проще.
Способ 3: Обозначение возведения в степень
Два рассмотренных выше способа подразумевают обязательное возведение числа в степень с отображением результата. Узнать, какая степень ему присвоена, не получится без нажатия по строке для отображения функции. Не всем пользователям подходит такая методика, поскольку некоторые заинтересованы в обычном отображении числа с обозначением, показывающим степень. Для реализации подобной задачи формат ячейки необходимо перевести в текстовый, а затем произвести запись с изменением символа.
Узнать, какая степень ему присвоена, не получится без нажатия по строке для отображения функции. Не всем пользователям подходит такая методика, поскольку некоторые заинтересованы в обычном отображении числа с обозначением, показывающим степень. Для реализации подобной задачи формат ячейки необходимо перевести в текстовый, а затем произвести запись с изменением символа.
-
Активируйте курсор на строке для ввода числа и на главной вкладке разверните список «Число», из которого выберите пункт «Текстовый».
-
Напишите два числа рядом: первое будет выступать основой, а второе – степенью.
-
Выделите то, которое является степенью, и щелкните по нему правой кнопкой мыши. Из контекстного меню выберите пункт «Формат ячеек».
-
Отметьте галочкой «Надстрочный» и примените изменения.
-
Вернитесь в таблицу и убедитесь в том, что результат отображается корректно, то есть так, как это показано на изображении ниже.

Вкратце разберем другой способ добавления желаемого символа без ручного изменения формата ячеек и перехода в меню редактирования. Для этого используйте специальную вставку.
-
Перейдите на вкладку с соответствующим названием и вызовите окно «Символы».
-
В нем укажите набор «Верхние и нижние индексы», после чего отыщите подходящий символ, который и будет выступать степенью.
Остается вставить его в ячейку рядом с уже написанным основанием. К слову, саму степень можно копировать и добавлять к другим ячейкам, если это потребуется.
Учитывайте, что подобные методы обозначения степени без ее возведения сразу конвертируют ячейку в текстовую и делают невозможными любые математические операции. Используйте подобное редактирование исключительно для визуального обозначения, а для подсчетов – Способ 1 и Способ 2.
run, with, let, also и apply
Некоторые стандартные функции Kotlin настолько похожи, что мы не уверены, какую из них использовать. Здесь я представлю простой способ, чтобы четко их различать и выбирать, какую использовать.
Здесь я представлю простой способ, чтобы четко их различать и выбирать, какую использовать.
Функции скоупа
Функции, на которых я сконцентрируюсь, это run, with, T.run, T.let, T.also и T.apply. Я называю их функциями скоупа (видимости), поскольку я вижу их основную функциональность в том, что они поставляют внутреннюю область для вызывающей стороны.
Самый простой способ проиллюстрировать определение скоупа, это функция run
fun test() {
var mood = «I am sad»
run {
val mood = «I am happy»
println(mood) // I am happy
}
println(mood) // I am sad
}
Logcat:
I/System.out: I am happy
I/System.out: I am sad
Благодаря этому, внутри функции test вы можете получить отдельный изолированный скоуп, в котором mood переопределен, чтобы напечатать «I am happy».
Эта функция скоупа сама по себе кажется не очень полезной. Но есть и еще один приятный момент, помимо скоупа; он возвращает что-то, то есть последний объект в области видимости.
Следовательно, мы можем «красиво» применить show() к одному из view, не вызывая его дважды:
run {
if (firstTimeView) introView else normalView
}.show()
3 атрибута скоуп функции
Чтобы сделать функции обзора более интересными, позвольте мне классифицировать их поведение по 3 атрибутам. Я буду использовать эти атрибуты, чтобы отличать их друг от друга.
1. Нормальная функция VS функции расширения
Если мы посмотрим на with и T.run, обе функции на самом деле очень похожи. Ниже делается одно и тоже.
with(webview.settings) {
javaScriptEnabled = true
databaseEnabled = true
}
// тоже самое что и
webview.settings.run {
javaScriptEnabled = true
databaseEnabled = true
}
Их отличает лишь то, что одна из них — нормальная функция with, тогда как другая — функция расширения T.run
В чем же преимущество каждого?
Представьте, что webview. settings может принимать значение NULL, тогда эти две функции выглядеть так:
settings может принимать значение NULL, тогда эти две функции выглядеть так:
// Ужас!
with(webview.settings) {
this?.javaScriptEnabled = true
this?.databaseEnabled = true
}
// Норм
webview.settings?.run {
javaScriptEnabled = true
databaseEnabled = true
}
В этом случае очевидно, что функция расширения T.run лучше, поскольку мы могли бы применить проверку на null перед ее использованием.
2. this VS it
Если мы посмотрим на T.run и T.let, обе функции похожи, за исключением способа, которым они принимают аргумент. Ниже показана одинаковая логика для обеих функций.
stringVariable?.run {
println(«The length of this String is $length»)
}
// тоже самое что и
stringVariable?.let {
println(«The length of this String is ${it.length}»)
}
Если вы проверите сигнатуру функции T. run, вы заметите, что T.run сделан просто как функция расширения, вызывающая блок T.().
run, вы заметите, что T.run сделан просто как функция расширения, вызывающая блок T.().
Следовательно, все в пределах скоупа, T может быть обозначено как this.
В программировании this может быть пропущено в большинстве случаев. Поэтому в нашем примере выше мы могли бы использовать $length в выражении println вместо ${this.length}. Я называю это отправкой this в качестве аргумента.
Однако для сигнатуры функции T.let вы заметите, что T.let отправляет себя в функцию, т.е. в блок: (T). Следовательно, это похоже на лямбда-аргумент. Это можно отнести к функции скоупа как есть. Поэтому я называю это отправкой в качестве аргумента.
Из вышесказанного кажется, что T.run лучше, чем T.let, так как он неявен, но есть некоторые тонкие преимущества функции T.let, как показано ниже:
- T.let обеспечивает более четкое разграничение использования данной переменной функции/члена по сравнению с функцией/членом внешнего класса
- Если this нельзя пропустить, например, когда оно отправляется в качестве параметра функции, ее запись короче и понятнее
- T.
 let позволяет лучше именовать преобразованную используемую переменную, то есть вы можете преобразовать ее в другое имя.
let позволяет лучше именовать преобразованную используемую переменную, то есть вы можете преобразовать ее в другое имя.
stringVariable?.let {
nonNullString ->
println(«The non null string is $nonNullString»)
}
3. Возвращение this VS другие типы
Теперь давайте посмотрим на T.let и T.also, оба они идентичны, если мы посмотрим на их внутренний скоуп.
stringVariable?.let {
println(«The length of this String is ${it.length}»)
}
// Точно тоже самое что и
stringVariable?.also {
println(«The length of this String is ${it.length}»)
}
Однако их главное отличие — вот что они возвращают. T.let возвращает значение другого типа, в то время как T.also возвращает сам T, то есть this.
Оба полезны для цепочки функций, где помощь T.let позволяет вам расширить операцию, а T.also позволяет вам использовать ту же самую переменную (т. е. this) в следующем обработчике.
е. this) в следующем обработчике.
Простая иллюстрация ниже
val original = «abc»
// Обрабатываем значение и отправляем в следующий обработчик
original.let {
println(«The original String is $it«) // «abc»
it.reversed() // evolve it as parameter to send to next let
}.let {
println(«The reverse String is $it«) // «cba»
it.length // can be evolve to other type
}.let {
println(«The length of the String is $it») // 3
}
// Неправильно
// Тоже самое значение в следующий обработчик (печатает неправильный ответ)
original.also {
println(«The original String is $it«) // «abc»
it.reversed() // even if we evolve it, it is useless
}.also {
println(«The reverse String is ${it}») // «abc»
it.length // even if we evolve it, it is useless
}.also {
println(«The length of the String is ${it}») // «abc»
}
// Исправленный вариант also (т. е. манипуляции с исходной строкой)
е. манипуляции с исходной строкой)
// Тоже самое значение отправляется в следующий обработчик
original.also {
println(«The original String is $it«) // «abc»
}.also {
println(«The reverse String is ${it.reversed()}») // «cba»
}.also {
println(«The length of the String is ${it.length}») // 3
}
T.also может показаться бессмысленным выше, так как мы могли бы легко объединить их в единый блок функций. Но если хорошо продумать, у него есть несколько хороших преимуществ:
- Можно очень четко разделить процесс обработки объекта на маленькие функциональные участки
- Подход очень мощный для манипуляций со значениями перед использованием, мы создаем цепочку Builder
Когда два действия объединяются в цепь, т.е. сначала вычисляется одно значение, другое действие ждет, это становится очень мощным подходом, например, ниже:
// Нормальный подход
fun makeDir(path: String): File {
val result = File(path)
result.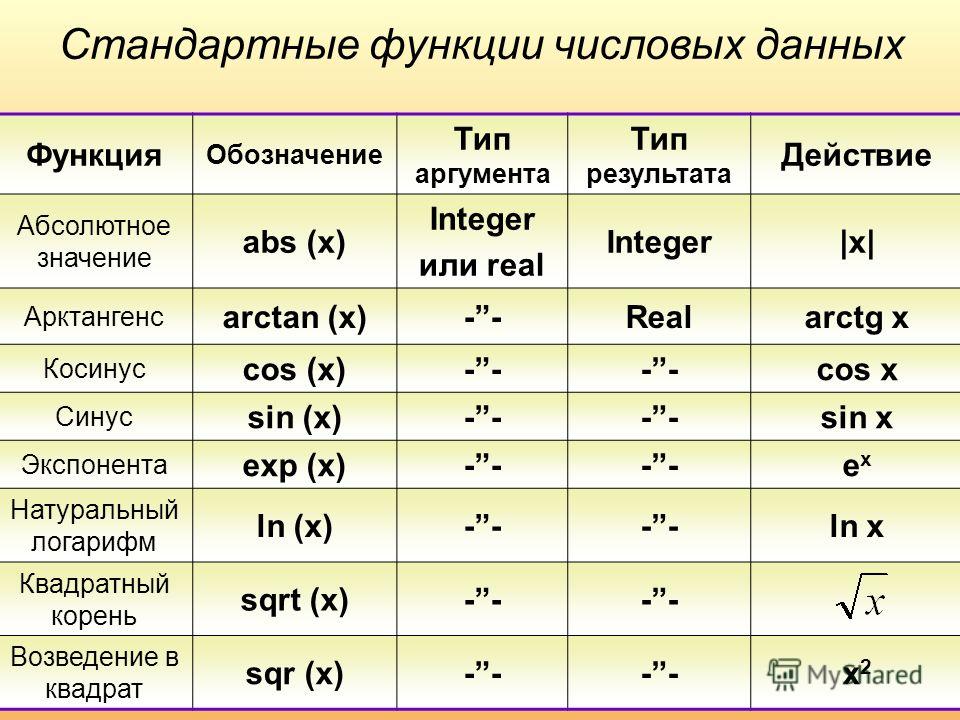 mkdirs()
mkdirs()
return result
}
// Улучшенный подход
fun makeDir(path: String) = path.let{ File(it) }.also{ it.mkdirs() }
Обзор всех свойств
Посмотрев на 3 свойства, мы в значительной степени знать поведение функции. Позвольте мне проиллюстрировать функцию T.apply, так как она не упоминалась выше. 3 атрибута T.apply, как показано ниже:
1. функция расширения
2. посылает this как аргумент
3 возвращает this (то есть само себя)
Следовательно, можно представить, что его можно использовать следующим образом:
// Нормальный подход
fun createInstance(args: Bundle) : MyFragment {
val fragment = MyFragment()
fragment.arguments = args
return fragment
}
// Улучшенный подход
fun createInstance(args: Bundle)
= MyFragment().apply { arguments = args }
Или мы могли бы также сделать цепочку создания объектов:
// Normal approach
fun createIntent(intentData: String, intentAction: String): Intent {
val intent = Intent()
intent. action = intentAction
action = intentAction
intent.data=Uri.parse(intentData)
return intent
}
// Improved approach, chaining
fun createIntent(intentData: String, intentAction: String) =
Intent().apply { action = intentAction }
.apply { data = Uri.parse(intentData) }
Выбор функций
Отсюда ясно, что с помощью 3 атрибутов мы теперь можем классифицировать функции. И на основании этого мы могли бы сформировать дерево решений ниже, которое могло бы помочь решить, какую функцию мы хотим использовать, ожидая того, что нам нужно.
Надеюсь что эта блок-схема проясняет функции, а также упрощает процесс принятия решений, позволяя вам надлежащим образом освоить использование этих функций.
Как использовать функцию СТАНДАРТИЗАЦИЯ
- Главная
- Функции
- Формулы
- Функции
Основы Excel Таблица Excel Расширенный фильтр Проверка данных Выпадающие списки Именованные диапазоны Решатель
- Графики
- Условное форматирование
- Сводная таблица
- VBA
Функции VBA Методы Характеристики Заявления Макросы Пользовательские функции Файлы и папки Флажки
- Архив
Все статьи отсортированы по дате Категории Товары Расширенный курс Excel
- Контакт
Обо мне Блоги, которые я прочитал
Автор: Оскар Кронквист Последнее обновление статьи: 11 мая 2022 г.
Формула в ячейке C5:
=СТАНДАРТ(C2, C3, C4)
Синтаксис функций Excel
STANDARDIZE( x , означает , стандартное_устройство )
Аргументы
| x | Обязательно. Значение, которое вы хотите нормализовать. |
| Среднее | Обязательно. Среднее арифметическое распределения. |
| Standard_dev | Обязательно. Стандартное отклонение распределения. |
Функции в этом артикуле
СТАНДАРТИЗАЦИЯ
Функции в категории «Статистические»
Функция «СТАНДАРТИЗАЦИЯ» является одной из многих функций в категории «Статистические».
Функция AVEDEV
Вычисляет среднее значение абсолютных отклонений точек данных от их среднего значения.
Функция СРЗНАЧ
Вычисляет среднее число чисел в диапазоне ячеек.
Функция AVERAGEA
Возвращает среднее значение группы значений. Текстовое и логическое значение FALSE равно 0. TRUE равно 1.
Функция СРЗНАЧЕСЛИ
Возвращает среднее значение ячеек, допустимых для данного условия.
Функция СРЗНАЧЕСЛИМН
Возвращает среднее значение ячеек, которое оценивается как ИСТИНА для нескольких критериев.
Функция БЕТА.РАСП
Вычисляет бета-распределение.
Функция БЕТА.ОБР
Вычисляет обратное значение кумулятивного бета-распределения.
Функция БИНОМ.РАСП
Вычисляет вероятность биномиального распределения отдельного термина.
Функция БИНОМ.ОБР
Вычисляет минимальное значение, для которого биномиальное распределение равно или превышает заданное пороговое значение.
Функция ХИ.РАСП.
Вычисляет вероятность распределения хи-квадрат, кумулятивного распределения или плотности вероятности.
Функция CHISQ.DIST.RT
Вычисляет правостороннюю вероятность распределения хи-квадрат.
Функция ХИ.ОБР.
Вычисляет обратную левостороннюю вероятность распределения хи-квадрат.
Функция CHISQ.INV.RT
Вычисляет обратную правостороннюю вероятность распределения хи-квадрат.
Функция CHISQ.TEST
Вычисляет критерий независимости, значение, полученное из статистического распределения хи-квадрат, и правильные степени свободы. Используйте эту функцию, чтобы проверить, верны ли предполагаемые результаты.
Функция ДОВЕРИТЕЛЬНОСТЬ.НОРМ
Вычисляет доверительный интервал для среднего значения генеральной совокупности.
УВЕРЕННОСТЬ.Функция
Вычисляет доверительный интервал для среднего значения генеральной совокупности с использованием распределения Стьюдента.
Функция КОРРЕЛ
Вычисляет корреляцию между двумя группами чисел.
Функция COUNT
Подсчитывает все числовые значения в аргументе.
Функция COUNTA
Подсчитывает непустые или пустые ячейки в диапазоне ячеек.
Функция СЧИТАТЬПУСТОТЫ
Подсчитывает пустые или пустые ячейки в диапазоне.
Функция СЧЁТЕСЛИ
Вычисляет количество ячеек, соответствующих условию.
Функция COUNTIFS
Вычисляет количество ячеек в нескольких диапазонах, соответствующих всем заданным условиям.
Функция COVARIANCE.P
Вычисляет ковариацию, означающую среднее значение произведений отклонений для каждой пары в двух разных наборах данных.
Функция COVARIANCE.S
Вычисляет выборочную ковариацию, означающую среднее значение произведений отклонений для каждой пары в двух разных наборах данных.
Функция EXPON.DIST
Вычисляет экспоненциальное распределение, представляющее результат в форме вероятности.
Функция F.РАСП
Вычисляет вероятность F для двух тестов.
Функция F.DIST.RT
Вычисляет правостороннюю F-вероятность для двух тестов.
Функция F.TEST
Вычисляет двустороннюю вероятность из F-теста
Функция FORECAST. LINEAR
LINEAR
Вычисляет значение на основе существующих значений x и y с использованием линейной регрессии.
Функция ЧАСТОТА
Вычисляет, как часто значения встречаются в диапазоне значений, а затем возвращает вертикальный массив чисел.
Функция ГАММА
Вычисляет значение ГАММА.
Функция ГАММА.РАСП
Вычисляет гамму, часто используемую в анализе очередей (статистика вероятностей), которая может иметь искаженное распределение.
Функция GEOMEAN
Вычисляет среднее геометрическое.
Функция РОСТА
Возвращает предполагаемый экспоненциальный рост на основе заданных данных.
Функция INTERCEPT
Возвращает значение, представляющее значение y, где линия пересекает ось y.
Функция НАИБОЛЬШИЙ
Вычисляет k-е наибольшее значение из массива чисел.
Функция ЛИНЕЙН
Возвращает массив значений, представляющих параметры прямой линии на основе метода наименьших квадратов.
Функция ЛИНЕЙН
Возвращает массив значений, представляющих параметры экспоненциальной кривой, соответствующей вашим данным, на основе метода наименьших квадратов.
Функция ЛОГНОРМ.РАСП
Вычисляет логнормальное распределение аргумента x на основе нормально распределенного ln(x) с аргументами среднее значение и стандартное_отклонение.
Функция MAX
Вычислить наибольшее число в диапазоне ячеек.
Функция MAXIFS
Вычисляет наибольшее значение на основе условия или критериев.
Функция МЕДИАНА
Вычисляет медиану на основе группы чисел. Медиана — это среднее число группы чисел.
Функция MIN
Возвращает наименьшее число в диапазоне ячеек.
Функция MINA
Возвращает наименьшее число. Текстовые значения и пробелы игнорируются, логическое значение TRUE оценивается как 1, а FALSE как 0 (ноль).
Функция MINIFS
Вычисляет наименьшее значение на основе заданного набора критериев.
Функция MODE.MULT
Возвращает наиболее часто встречающееся число в диапазоне ячеек. Он вернет несколько чисел, если они встречаются одинаково часто.
Функция MODE. SNGL
SNGL
Вычисляет наиболее часто встречающееся значение в массиве или диапазоне данных.
Функция НОРМ.РАСП
Вычисляет нормальное распределение для данного среднего значения и стандартного отклонения.
Функция НОРМ.ОБР
Вычисляет обратное значение нормального кумулятивного распределения для заданного среднего значения и стандартного отклонения.
Функция PERCENTRANK.EXC
Вычисляет процент ранга заданного числа в наборе данных.
PERCENTRANK.INC функция
Вычисляет процент ранга заданного числа по сравнению со всем набором данных.
Функция ПЕРЕСТАВКА
Возвращает количество перестановок для набора элементов, которые можно выбрать из большего числа элементов.
PERMUTATIONA function
Возвращает количество перестановок для определенного количества элементов, которые можно выбрать из большей группы элементов.
Функция PHI
Вычисляет число функции плотности для стандартного нормального распределения.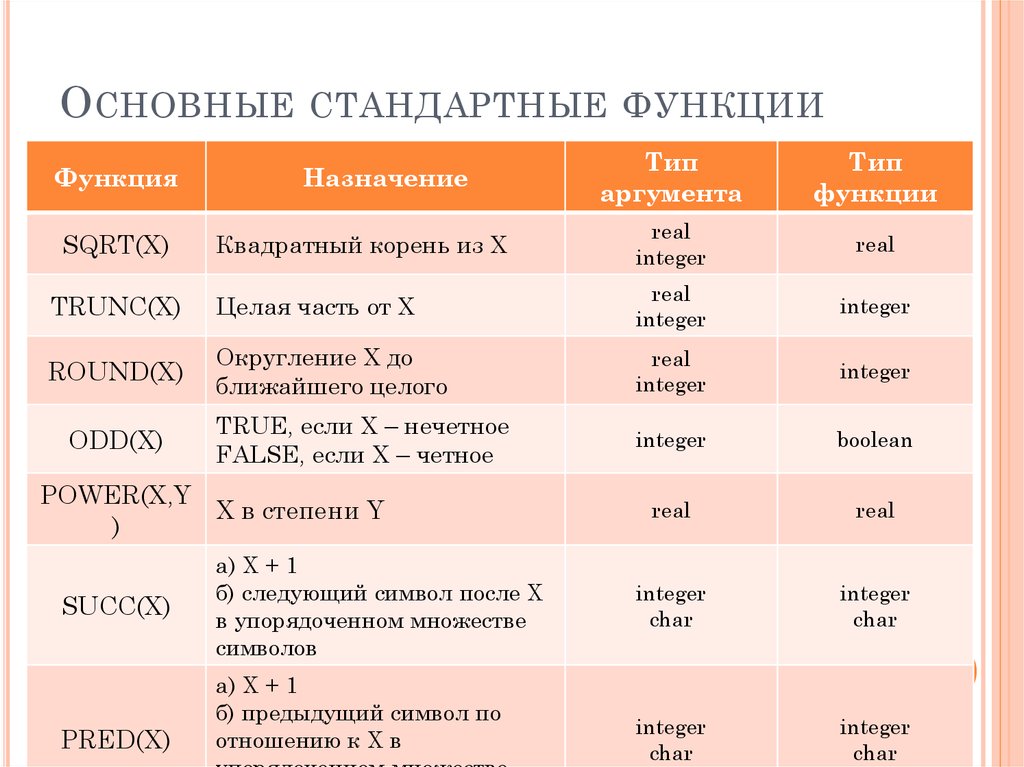
Функция PROB
Вычисляет вероятность того, что значения в диапазоне находятся между заданным нижним и верхним пределом.
Функция QUARTILE.EXC
Возвращает квартиль набора данных.
Функция QUARTILE.INC
Возвращает квартиль набора данных на основе значений процентилей от 0 до 1 включительно.
Функция RANK.AVG
Возвращает ранг числа из списка чисел.
Функция RANK.EQ
Вычисляет ранг числа в списке чисел на основе его позиции, если список был отсортирован.
Функция SKEW
Вычисляет асимметрию группы значений.
Функция НАКЛОН
Вычисляет наклон линии линейной регрессии через координаты.
Функция МАЛЕНЬКИЙ
Возвращает k-е наименьшее значение из группы чисел.
Функция СТАНДАРТИЗАЦИЯ
Вычисляет нормализованное значение из распределения, характеризуемого средним значением и стандартным_отклонением.
Функция STDEV.P
Возвращает стандартное отклонение на основе всей совокупности.
Функция СТАНДОТКЛОН.С
Возвращает стандартное отклонение на основе выборки всей совокупности.
Функция STDEVA
Оценивает стандартное отклонение по выборке значений.
Функция STDEVPA
Возвращает стандартное отклонение на основе всей совокупности, включая текстовые и логические значения.
Функция TREND
Вычисляет значения по линейному тренду.
Функция ОБРЕЗАТЬСРЕДНЕЕ
Вычисляет среднее значение внутренней части набора данных.
Функция VAR.P
Возвращает дисперсию на основе всей совокупности. Функция игнорирует логические и текстовые значения.
Функция VAR.S
Функция VAR.S пытается оценить дисперсию на основе выборки генеральной совокупности. Функция игнорирует логические и текстовые значения.
Категории функций Excel
Манипуляции с массивами
Функции Excel, позволяющие изменять размер, комбинировать и формировать массивы.
Совместимость
Функции обратной совместимости с более ранними версиями Excel. Функции совместимости заменены более новыми функциями с повышенной точностью. Используйте новые функции, если совместимость не требуется.
Функции совместимости заменены более новыми функциями с повышенной точностью. Используйте новые функции, если совместимость не требуется.
База данных
Выполнение основных операций со структурой, подобной базе данных.
Дата и время
Функции, позволяющие выполнять вычисления со значениями даты и времени в Excel.
Инженерное дело
Позволяет работать с двоичными числами, преобразовывать значения между различными системами счисления и вычислять мнимые числа.
Финансы
Расчет текущей стоимости, процентов, накопленных процентов, основной суммы, накопленной основной суммы, амортизации, платежей, цен, роста, доходности по ценным бумагам и других финансовых расчетов.
Информация
Функции, позволяющие получать информацию из ячейки, форматирования, формулы, листа, книги, пути к файлу и других объектов.
Логический
Функции, позволяющие возвращать логические значения и управлять ими, а также управлять расчетами формул на основе логических выражений.
Поиск и ссылка
Эти функции позволяют сортировать, искать, получать внешние данные, такие как котировки акций, фильтровать значения на основе условий или критериев и получать относительное положение заданного значения в определенном диапазоне ячеек. Они также позволяют вычислять строки, столбцы и другие свойства ссылок на ячейки.
Математика и тригонометрия
В этой категории вы найдете функции, которые вычисляют случайные значения, округляют числовые значения, создают последовательные числа, выполняют тригонометрию и многое другое.
Статистический
Расчет распределений, биномиальных распределений, экспоненциального распределения, вероятностей, дисперсии, ковариации, доверительного интервала, частоты, среднего геометрического, стандартного отклонения, среднего, медианы и других статистических показателей.
Текст
Функции, которые позволяют вам манипулировать текстовыми значениями, заменять строки, находить строку в значении, извлекать подстроку в строке, преобразовывать символы в код ANSI среди других функций.
Web
Получение данных из Интернета, извлечение данных из строки XML и многое другое.
Категории Excel
Домашняя страница
Последние обновленные статьи.
Функции Excel
Более 300 функций Excel с подробной информацией, включая синтаксис, аргументы, возвращаемые значения и примеры для большинства функций, используемых в формулах Excel.
Формулы Excel
Более 1300 формул, организованных в подкатегории.
Таблицы Excel
Таблицы Excel упрощают работу с данными, добавляя или удаляя данные, фильтруя, суммируя, сортируя, улучшая читаемость с помощью форматирования ячеек, ссылок на ячейки, формул и многого другого.
Расширенный фильтр
Позволяет фильтровать данные на основе выбранного значения, заданного текста или других критериев. Он также позволяет фильтровать существующие данные или перемещать отфильтрованные значения в новое место.
Проверка данных
Позволяет контролировать, что пользователь может вводить в ячейку. Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.
Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.
Раскрывающийся список
Позволяет пользователю работать более эффективно, отображая список, из которого пользователь может выбрать значение. Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.
Именованные диапазоны
Позволяет дать имя одной или нескольким ячейкам, это упрощает поиск ячеек с помощью поля Имя, чтение и понимание формул, содержащих имена вместо ссылок на ячейки.
Excel Solver
Excel Solver — это бесплатная надстройка, которая использует целевые ячейки, ограничения, основанные на формулах на листе, для выполнения анализа «что, если» и других проблем принятия решений, таких как перестановки и комбинации.
Диаграммы
Функция Excel, позволяющая визуализировать данные в виде графика.
Условное форматирование
Форматирование ячеек или значений ячеек на основе условия или критерия. Существует множество встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.
Существует множество встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.
Сводные таблицы
Позволяет быстро суммировать большие объемы данных в удобной для пользователя форме. Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.
VBA
VBA означает Visual Basic для приложений и представляет собой язык программирования, разработанный Microsoft. Он позволяет автоматизировать трудоемкие задачи и создавать пользовательские функции.
Макросы
Программа или подпрограмма, встроенная в VBA, которую может создать любой. Используйте средство записи макросов, чтобы быстро создавать собственные макросы VBA.
UDF
UDF расшифровывается как User Defined Functions и представляет собой настраиваемые функции, которые может создать каждый.
Архив
Список всех опубликованных статей.
Стандартные функции
Использование
Значения элементов или атрибутов сообщения XML (полезной нагрузки) технически представляют собой строку. Поэтому все стандартные функции, работающие со значениями поля, ожидают строк аргументов и вернуть строка значение. Тем не менее, передаваемое значение, конечно, может иметь другой семантический тип данных, а именно тот, который вы указали при определении схемы полезной нагрузки для поля. Стандартные функции демонстрируют следующее стандартное поведение:
В зависимости от стандартной функции используются преобразования типов данных, чтобы гарантировать, что значения передаются в формате, подходящем для функции (с использованием отливка ). Если значение не может быть интерпретировано, среда выполнения сопоставления вызывает исключение Java.
Операторы if оценивают условия, которые возвращают логические значения.
 Стандартные функции, возвращающие логические значения, возвращают строку правда или ложно . Стандартные функции, которые ожидают логических значений, интерпретируют значения «1» и «истина» (не
с учетом регистра) как true и все остальные значения как ложно .
Стандартные функции, возвращающие логические значения, возвращают строку правда или ложно . Стандартные функции, которые ожидают логических значений, интерпретируют значения «1» и «истина» (не
с учетом регистра) как true и все остальные значения как ложно .
Дополнительная информация: Поведение во время выполнения
Обзор функций
Объекты потока данных для стандартных функций имеют следующую структуру:
Большинство объектов потока данных имеют два или три входящих канала с левой стороны и один исходящий канал с правой стороны.
If-функции имеют форму ромбов или треугольников.
Существуют также функции преобразования с одним входящим и исходящим каналом и функции, возвращающие значение без каких-либо входных данных.

Стандартные функции, требующие дополнительных спецификаций, отмечены звездочкой. Чтобы вызвать диалог для Параметры функции дважды щелкните объект потока данных.
На следующем рисунке представлен обзор всех различных форм объектов потока данных:
Рисунок 1: Объекты потока данных
Чтобы проиллюстрировать, как используются отдельные функции, поля ввода на рисунке выше содержат переменные х , И , Z или I , а результирующая переменная либо Р или О .
Все стандартные функции в таблицах ниже описываются с использованием этих входных и выходных переменных. В редакторе потока данных другие объекты потока данных, подключенные к функциям с помощью соединительных полей, либо возвращают входные значения, либо получают результат операции. Вы можете комбинировать функции
любым способом, который вам требуется (при условии, что значения, переданные в функцию, могут быть интерпретированы).
Категория функции: Арифметика
Для этой категории можно вводить только числовые значения (включая значения с цифрами после запятой). Если значение нельзя интерпретировать как цифру, система инициирует исключение Java. В противном случае все вычисления выполняются с точностью типа данных Java. плавать . Формат значения результата зависит от результата:
Если результатом является значение с цифрами после запятой, они остаются неизменными.
Исключение: если за десятичной точкой следует нуль, то она обрезается. Это означает, что результат расчета 4,2 - 0,2 это 4 и не 4,0 .
Также обратите внимание, что значения Java типа
float конвертируются во вторую систему перед расчетом. Результат вычисляется там, а затем этот результат преобразуется обратно в десятичный формат. Преобразование может привести к десятичным разрядам в диадическом формате, которые
периодически повторяется, а затем автоматически отключается. В десятичной системе это может привести к неточным результатам (пример: 2,11 + 22,11 = 24,220001). Если количество позиций после запятой должно быть ограничено двумя, например, в случае значений для валюты, вы можете отформатировать значения
после расчета с помощью стандартной функции Номер Формата .
Результат вычисляется там, а затем этот результат преобразуется обратно в десятичный формат. Преобразование может привести к десятичным разрядам в диадическом формате, которые
периодически повторяется, а затем автоматически отключается. В десятичной системе это может привести к неточным результатам (пример: 2,11 + 22,11 = 24,220001). Если количество позиций после запятой должно быть ограничено двумя, например, в случае значений для валюты, вы можете отформатировать значения
после расчета с помощью стандартной функции Номер Формата .
Если в конкретном случае использования требуются более подробные результаты, можно также выбрать десятичную систему в качестве основы для расчетов. Класс Java BigDecimal используется для внутренних целей. Дополнительные сведения см. в SAP-ноте 958486.
Имя функции | Функция |
добавить | Р = Х + У |
вычесть | Р = Х — У |
равноA | Р = true , если значение X равно значению Д , иначе Р = ложно . |
абс | O = Абсолютное значение я |
кв | R — квадратный корень из х |
кв | R – площадь х |
знак | R = 1 , когда х это положительное число R = 0 , когда х равно 0 R = 1 , когда X это отрицательное число |
отрицательный | Р = -Х |
1/х | R является обратной величиной х |
мощность | Р = Х Д |
меньше | верно , когда х < Y , иначе ложь |
больше | верно , когда х > Y , иначе ложь |
умножить | Р = Х * У |
разделить | Р = Х/У |
макс | R = Максимум значений х и Д |
мин | R = Минимум значений х и Д |
потолок | O = Наименьшее возможное целочисленное значение (до минус «бесконечность»), которое не меньше аргумента я . |
этаж | O = максимально возможное целочисленное значение, не превышающее аргумент я . Соответствует функции Java java.lang.Math.floor() . |
круглый | O = Целочисленное значение, ближайшее к значению аргумента я . |
счетчик | O = Количество вызовов для этого сопоставления целевого поля, где вы указываете начальное значение и приращение счетчика в параметрах функции. |
Номер Формата | конвертирует I в соответствии с шаблоном, который вы определяете с помощью параметров функции. |
Категория функции: Логическая
Все функции в этой категории предполагают логические входные значения (см. выше).
Имя функции | Функция |
и | Р есть верно если х и Y имеют значение верно . |
или | Р есть верно если х или Y имеют значение верно . В противном случае, Р есть ложно . |
Не | |
равно | Сравнивает оба логических значения х и Y и возвращается true , если оба равны, иначе ложно . Используйте функции равно S или сравните с Текст категории для сравнения строк. |
не равно | R = Нет (равно (X, Y)) |
если | |
еслиБезЭльсе | Если условие X удовлетворяется (возвращает правда ): Р = Y . |
Категория функции: константы
Поскольку эти функции не имеют входных значений, они производящие функции.
Функция | Использовать |
Константа | O получает любую строковую константу, которую можно ввести в диалоге параметров функции. |
Копивалуе | Для часто встречающегося элемента копирует значение в определенной позиции в исходной структуре в назначенное целевое поле. |
отправитель | O получает имя бизнес-системы отправителя. Test_Sender_System выводится при тестировании сопоставления сообщений в Integration Builder. |
приемник | O возвращает имя бизнес-системы получателя. |
Категория функции: Преобразования
Функция | Использовать |
FixValues | Выполняет сопоставление значений с использованием таблицы фиксированных значений, которую вы заполняете с помощью параметров функции. |
Преобразование значений | Выполняет сопоставление значения для значения Я ввел. В параметрах функции назначьте оба входных значения I и исходное значение O к представлению в таблице сопоставления значений. Таким образом, вы можете назначить источник
и целевые поля структуры для представления. Вы заполняете таблицу сопоставления значений на экране обслуживания конфигурации в Integration Builder. Поскольку эти записи недоступны во время разработки, результат сопоставления является лишь оценкой при тестировании сопоставления сообщений. Примечание В XI 3.0 интерфейс среды выполнения для сопоставления значений изменился. Однако сопоставления сообщений XI 2.0, вызывающие Функция Value Mapping по-прежнему работает с использованием старого интерфейса среды выполнения. Чтобы использовать параметры функции в новом интерфейсе среды выполнения, выберите XI 3.0 Интерфейс. В свойствах функции для стандартной функции Сопоставление значений , в полях
Агентство и
Schema введите ключ исходного или целевого значения. Эти значения могут иметь любые значения. Однако вы также можете
обратитесь к полям
отправитель,
ОтправительСервис ,
ПолучательСторона или
РесиверСервис. Среда выполнения сопоставления заменяет эти значения во время выполнения значениями из соответствующих полей.
в заголовке сообщения, для которого выполняется сопоставление значений. Примечание В поле Агентство вы также можете ввести имя бизнес-системы. При переносе сопоставлений значений из одного Каталога интеграции в другой Построитель интеграции определяет, вошли ли вы в бизнес-систему в качестве агентства, и преобразует ее во время переноса. |
Категория функции: Дата
Следующие функции позволяют определить формат даты для исходного или целевого формата с помощью диалогового окна параметров функции.
Примечание
Формат соответствует соглашению, определенному в стандартном классе Java. java.util.SimpleDateFormat . В диалоговом окне параметров функции есть мастер, который можно использовать для ввода наиболее часто используемых форматов даты.
Функция | Использовать |
текущая дата | Возвращает текущую дату, используя О . |
DateTrans | Преобразует формат даты I в другой формат даты О . |
Дата до | Р = true , когда дата X предшествует дате Y, иначе ложь |
ДатаПосле | Р = правда , когда дата X идет после даты Y, иначе ложь |
Сравнение дат | R = 1 , когда дата X после даты Д R = 0 , когда дата X совпадает с датой Д R = -1 , когда свидание X до даты Д |
Расширенные настройки
Не только форматы даты зависят от страны; количество рабочих дней и календарных недель также зависит от страны. Вы можете указать соответствующие соглашения для них в параметрах функции:
Вы можете указать соответствующие соглашения для них в параметрах функции:
Первый день недели Указывает, какой день недели записывается как первый день недели. Например, в США первый рабочий день — воскресенье, а во Франции — понедельник. Счетчик начинается с 1. Среда выполнения сопоставления устанавливает этот атрибут с помощью Java метод setFirstDayOfWeek() . Для получения дополнительной информации см. документацию по Java в разделе http://java.sun.com/j2se/1.4.2/docs/api/java/util/Calendar.html .
Минимальное количество дней, необходимое в первую неделю Указывает, сколько дней должна быть первая неделя года, чтобы считаться первой календарной неделей. Среда выполнения сопоставления устанавливает этот атрибут с помощью метода Java. setMinimalDaysInFirstWeek() . Для получения дополнительной информации см.
 документацию по Java в разделе
http://java.sun.com/j2se/1.4.2/docs/api/java/util/Calendar.html
.
документацию по Java в разделе
http://java.sun.com/j2se/1.4.2/docs/api/java/util/Calendar.html
.
Использование флажка Календарь мягкий, вы можете контролировать, вызывают ли неверные даты исключения или нет. Если этот флажок установлен, среда выполнения сопоставления допускает дату, такую как февраль 1942 г. 1996 г., которая затем интерпретируется как 941-й день после 1 февраля 1996 года. Исключение не запускается. Среда выполнения сопоставления устанавливает этот атрибут с помощью метода Java. setLenient() . Для получения дополнительной информации см. документацию по Java в разделе http://java.sun.com/j2se/1.4.2/docs/api/java/util/Calendar.html.
Категория функции: функции узла
Функция | Использовать |
создатьесли | Если в целевой структуре есть элементы структурирования, которых нет в исходной структуре, вставьте их с помощью этой функции. |
удалитьконтексты | Удаляет все высокоуровневые контексты исходного поля. Таким образом, вы можете удалить все уровни иерархии и создать список. |
заменить значение | Заменяет значение I со значением, которое можно определить в диалоговом окне для параметров функции. |
существуют | О = true , если исходное поле назначено входящему каналу I существует в экземпляре XML. В противном случае, ложно . |
Разделить по значению | Вставки изменение контекста для элемента. |
свернутьКонтексты | Удаляет все значения из всех контекстов из входящей очереди, кроме первого значения. |
использоватьOneAsMany | Реплицирует значение поля, встречающееся один раз, чтобы связать его как запись со значениями поля, встречающимися более одного раза. |
сорт | Сортирует все значения многократно встречающегося входящего поля I в существующем или заданном контексте. |
сортировка по ключу | Нравится sort , но с двумя входящими параметрами для сортировки пар (ключ/значение). Процесс сортировки можно сравнить с таблицей с двумя столбцами.
|
карта с дефолтом | Заменяет пустые контексты во входящей очереди значением по умолчанию, которое вы указываете в параметрах функции. Пример: если «По умолчанию» является значением по умолчанию и А|В1,В2| |С| |D — входящая очередь, mapWithDefault возвращает следующую исходящую очередь: А | В1, В2 | По умолчанию | С | По умолчанию |D . Функция соответствует следующей комбинации стандартных функций: Если ([] поле, существует ([] поле), константа ([значение = по умолчанию])) |
formatByExample | Эта функция имеет две входящие очереди, обе из которых должны иметь одинаковое количество значений. |
Категория функции: Статистика
Функции этой категории функций предназначены для исходных полей, которые встречаются в исходной структуре более одного раза (maxOccurs = i > 1).
Функция | Использовать |
сумма | R = Сумма значений х 1 Си контекста. |
средний | R = Среднее значение х 1 по х и контекста |
количество | R = Количество полей в контексте ( и ) |
индекс | R = Индекс и из х и . |
Категория функции: Текст
Примечание
В спецификации позиции позиция 0 соответствует первому символу в строке.
Функция | Использовать |
подстрока | Возвращает подстроку O для строки я . |
конкат | Р = Связывание строк х и Y (без пробелов). Пример: Х = «миссис» ; Y = «Миллер» ; R = «Миссис Миллер» . Используйте диалог свойств функции, чтобы вставить разделитель в строку. |
равноS | Р = true , если строка X равно строке Д , иначе Р = ложно . |
indexOf (2 входных параметра) | Р = первая позиция, в которой строка Y находится в X и -1, если Y вообще не встречается. |
indexOf (3 входных параметра) | R = первая позиция от позиции Z, в которой строка Y находится в X и -1, если Y вообще не встречается. |
lastIndexOf (2 входных параметра) | R = последняя позиция, в которой строка Y находится в X и -1, если Y вообще не встречается. |
lastIndexOf (3 входных параметра) | R = последняя позиция с позиции z, в которой строка Y находится в X и -1, если Y вообще не встречается. |
сравнить | Сравнивает строку X со строкой Д : Р = 0 , когда строки равны Р = положительное число i, когда X лексикографически больше, чем Y R = отрицательное число i, когда X лексикографически меньше, чем Y i определяет разницу между двумя строками лексикографически. Функция действует так же, как
http://java. |
заменить строку | X : Строка, в которой нужно что-то заменить Y : Заменить строку в X Z : Строка для замены Y R = Строка, в которой каждое вхождение Y в X заменено на Z. Пример X = «спарринг с фиолетовой морской свинкой» Д = «р» Z = «т» R = «в главной роли с черепахой-черепахой» |
длина | О = Длина строки |
заканчивается | R = верно , когда Y — последняя строка в х ; в противном случае ложно . |
начинается с (2 входных параметра) | R = верно , когда Y — первая строка в х ; в противном случае ложно . |
startWith (3 входных параметра) | R = верно , когда Y спички X от позиции Z ; в противном случае ложно . |
в верхний регистр | Преобразует все строчные буквы в I в верхний регистр. |
отделка | Удаляет все пробельные символы (пробелы, табуляции, возвраты) в начале и в конце строки. Действует так же, как http://java.sun.com/j2se/1.3/docs/api/java/lang/String.html. |
в нижний регистр | Преобразует все прописные буквы I в строчные. |
Стандартное отклонение в Excel: функции и примеры формул
В учебнике объясняется сущность стандартного отклонения и стандартной ошибки среднего, а также какая формула лучше всего используется для расчета стандартного отклонения в Excel.
В описательной статистике среднее арифметическое (также называемое средним) и стандартное отклонение являются двумя тесно связанными понятиями. Но если первое понятно большинству, то второе понимают немногие. Цель этого руководства — пролить свет на то, что на самом деле представляет собой стандартное отклонение и как его рассчитать в Excel.
- Что такое стандартное отклонение?
- Как найти стандартное отклонение в Excel
- Функции для расчета стандартного отклонения выборки
- Функции для получения стандартного отклонения генеральной совокупности
- Примеры формул для расчета стандартного отклонения в Excel
- Как рассчитать стандартную ошибку среднего в Excel
- Как добавить столбцы стандартного отклонения в Excel
Что такое стандартное отклонение?
стандартное отклонение — это мера, показывающая, насколько значения набора данных отклоняются (разбросаны) от среднего значения. Другими словами, стандартное отклонение показывает, близки ли ваши данные к среднему значению или сильно колеблются.
Другими словами, стандартное отклонение показывает, близки ли ваши данные к среднему значению или сильно колеблются.
Стандартное отклонение предназначено для того, чтобы помочь вам понять, действительно ли среднее значение возвращает «типичные» данные. Чем ближе стандартное отклонение к нулю, тем ниже изменчивость данных и тем надежнее среднее значение. Стандартное отклонение, равное 0, указывает на то, что каждое значение в наборе данных точно равно среднему значению. Чем выше стандартное отклонение, тем больше вариаций в данных и тем менее точным является среднее значение.
Чтобы лучше понять, как это работает, взгляните на следующие данные:
Для биологии стандартное отклонение равно 5 (округлено до целого числа), что говорит нам о том, что большинство оценок не более более чем на 5 баллов от среднего. Это хорошо? Что ж, да, это указывает на то, что оценки студентов по биологии довольно постоянны.
Для математики стандартное отклонение равно 23. Это показывает, что существует огромная дисперсия (разброс) в оценках, а это означает, что некоторые учащиеся справились намного лучше, а некоторые намного хуже, чем в среднем.
Это показывает, что существует огромная дисперсия (разброс) в оценках, а это означает, что некоторые учащиеся справились намного лучше, а некоторые намного хуже, чем в среднем.
На практике стандартное отклонение часто используется бизнес-аналитиками в качестве меры инвестиционного риска: чем выше стандартное отклонение, тем выше волатильность доходности.
Стандартное отклонение выборки в сравнении со стандартным отклонением совокупности
В отношении стандартного отклонения вы часто можете слышать термины «выборка» и «совокупность», которые относятся к полноте данных, с которыми вы работаете. Основное отличие состоит в следующем:
- Население включает все элементы из набора данных.
- Выборка представляет собой подмножество данных, которое включает один или несколько элементов генеральной совокупности.
Исследователи и аналитики оперируют стандартным отклонением выборки и генеральной совокупности в различных ситуациях. Например, при подведении итогов экзаменов класса учащихся учитель будет использовать стандартное отклонение совокупности. Статистики, рассчитывающие средний балл SAT по стране, будут использовать стандартное отклонение выборки, потому что им представлены данные только выборки, а не всего населения.
Например, при подведении итогов экзаменов класса учащихся учитель будет использовать стандартное отклонение совокупности. Статистики, рассчитывающие средний балл SAT по стране, будут использовать стандартное отклонение выборки, потому что им представлены данные только выборки, а не всего населения.
Понимание формулы стандартного отклонения
Причина, по которой характер данных имеет значение, заключается в том, что стандартное отклонение генеральной совокупности и стандартное отклонение выборки рассчитываются по немного отличающимся формулам:
Стандартное отклонение выборки | Стандартное отклонение населения |
Где:
- x i являются отдельными значениями в наборе данных
- x — среднее значение всех значений x
- n — общее количество x значений в наборе данных
Возникли трудности с пониманием формул? Разбивка их на простые шаги может помочь. Но сначала давайте поработаем над некоторыми примерами данных:
Но сначала давайте поработаем над некоторыми примерами данных:
1. Вычислите среднее (среднее)
Сначала вы найдете среднее значение всех значений в наборе данных ( x в формулах выше). При расчете вручную вы складываете числа, а затем делите сумму на количество этих чисел, например:
(1+2+4+5+6+8+9)/7=5
Чтобы найти означает в Excel, используйте функцию СРЗНАЧ, например. =СРЗНАЧ(A2:G2)
2. Для каждого числа вычтите среднее значение и возведите результат в квадрат
Это часть формулы стандартного отклонения, которая гласит: ( x i — x) 2
Чтобы представить себе, что происходит на самом деле, взгляните на следующие изображения.
В этом примере среднее значение равно 5, поэтому мы вычисляем разницу между каждой точкой данных и 5.
Затем вы возводите в квадрат различия, превращая их все в положительные числа:
3. Складываем квадраты разностей
Чтобы сказать «суммировать» в математике, вы используете сигму Σ. Итак, что мы делаем сейчас, так это складываем квадраты разностей, чтобы закончить эту часть формулы: Σ( x i — x) 2
Итак, что мы делаем сейчас, так это складываем квадраты разностей, чтобы закончить эту часть формулы: Σ( x i — x) 2
16 + 9 + 1 + 1 + 9 + 16 = 52
4. Разделите сумму квадратов разностей на количество значений
До сих пор формулы стандартного отклонения выборки и стандартного отклонения генеральной совокупности были идентичными. На данный момент они разные.
Для стандартного отклонения выборки вы получите дисперсию выборки путем деления общих квадратов разностей на размер выборки минус 1:
52 / (7-1) = 8,67
, вы найдете среднее квадратов разностей путем деления суммы квадратов разностей на их количество:
52 / 7 = 7,43
Почему такая разница в формулах? Потому что в формуле выборочного стандартного отклонения вам нужно скорректировать смещение в оценке среднего значения выборки вместо истинного среднего значения генеральной совокупности. И вы делаете это, используя n — 1 вместо n , что называется поправкой Бесселя.
5. Извлеките квадратный корень
Наконец, извлеките квадратный корень из приведенных выше чисел, и вы получите стандартное отклонение (в приведенных ниже уравнениях, округленное до 2 знаков после запятой):
| Стандартное отклонение выборки | Стандартное отклонение населения |
| √8,67 = 2,94 | √7,43 = 2,73 |
В Microsoft Excel стандартное отклонение вычисляется таким же образом, но все вышеперечисленные вычисления выполняются скрыто. Ключевым моментом для вас является выбор правильной функции стандартного отклонения, о чем следующий раздел даст вам некоторые подсказки.
Как рассчитать стандартное отклонение в Excel
Всего существует шесть различных функций для определения стандартного отклонения в Excel. Какой из них использовать, зависит в первую очередь от характера данных, с которыми вы работаете — будь то вся совокупность или выборка.
Функции для расчета стандартного отклонения выборки в Excel
Для расчета стандартного отклонения на основе выборки используйте одну из следующих формул (все они основаны на описанном выше методе «n-1»).
Функция Excel СТАНДОТКЛОН
СТАНДОТКЛОН(число1,[число2],…) — это самая старая функция Excel для оценки стандартного отклонения на основе выборки, и она доступна во всех версиях Excel с 2003 по 2019.
В Excel 2007 и более поздних версиях стандартное отклонение может принимать до 255 аргументов, которые могут быть представлены числами, массивами, именованными диапазонами или ссылками на ячейки, содержащие числа. В Excel 2003 функция может принимать не более 30 аргументов.
Подсчитываются логические значения и текстовые представления чисел, указанные непосредственно в списке аргументов. В массивах и ссылках учитываются только числа; пустые ячейки, логические значения ИСТИНА и ЛОЖЬ, текстовые и ошибочные значения игнорируются.
Примечание. СТАНДОТКЛОН Excel — это устаревшая функция, которая сохраняется в более новых версиях Excel только для обратной совместимости. Однако Microsoft не дает никаких обещаний относительно будущих версий. Поэтому в Excel 2010 и более поздних версиях рекомендуется использовать СТАНДОТКЛОН.С вместо СТАНДОТКЛОН.
Функция Excel СТАНДОТКЛОН.С
СТАНДОТКЛОН.С(число1,[число2],…) — это улучшенная версия СТАНДОТКЛОН, представленная в Excel 2010.
Как и СТАНДОТКЛОН, функция СТАНДОТКЛОН.С вычисляет выборочное стандартное отклонение набора значений на основе классической формулы выборочного стандартного отклонения, рассмотренной в предыдущем разделе.
Функция Excel СТАНДОТКЛОН
СТАНДОТКЛОН (значение1, [значение2], …) — еще одна функция для расчета стандартного отклонения выборки в Excel. Он отличается от двух предыдущих только способом обработки логических и текстовых значений:
- Подсчитываются все логические значения , независимо от того, содержатся ли они в массивах или ссылках или введены непосредственно в список аргументов (ИСТИНА оценивается как 1 , FALSE оценивается как 0).

- Текстовые значения в массивах или ссылочных аргументах считаются равными 0, включая пустые строки («»), текстовые представления чисел и любой другой текст. Текстовые представления чисел, указанные непосредственно в списке аргументов, учитываются как числа, которые они представляют (вот пример формулы).
- Пустые ячейки игнорируются.
Примечание. Чтобы образец формулы стандартного отклонения работал правильно, предоставленные аргументы должны содержать не менее двух числовых значений, в противном случае #DIV/0! возвращается ошибка.
Функции для расчета стандартного отклонения совокупности в Excel
Если вы имеете дело со всей совокупностью, используйте одну из следующих функций для расчета стандартного отклонения в Excel. Эти функции основаны на методе «n».
Функция Excel STDEVP
СТАНДОТКЛОН(число1,[число2],…) — это старая функция Excel для нахождения стандартного отклонения совокупности.
В новых версиях Excel 2010, 2013, 2016 и 2019 она заменена улучшенной функцией СТАНДОТКЛОН. П, но сохранена для обратной совместимости.
П, но сохранена для обратной совместимости.
Функция Excel СТАНДОТКЛОН.П
СТАНДОТКЛОН.П(число1,[число2],…) — это современная версия функции СТАНДОТКЛОН, обеспечивающая повышенную точность. Он доступен в Excel 2010 и более поздних версиях.
Как и их аналогичные образцы стандартного отклонения, в массивах или ссылочных аргументах функции СТАНДОТКЛОН и СТАНДОТКЛОН.P считают только числа. В списке аргументов также учитываются логические значения и текстовые представления чисел.
Функция Excel СТАНДОТКЛОНПА
СТАНДОТКЛОНПА(значение1, [значение2], …) вычисляет стандартное отклонение совокупности, включая текстовые и логические значения. Что касается нечисловых значений, СТАНДОТКЛОНПА работает точно так же, как функция СТАНДОТКЛОН.
Примечание. Какую бы формулу стандартного отклонения Excel вы ни использовали, она вернет ошибку, если один или несколько аргументов содержат значение ошибки, возвращаемое другой функцией или текстом, который нельзя интерпретировать как число.
Какую функцию стандартного отклонения Excel использовать?
Различные функции стандартного отклонения в Excel определенно могут вызвать путаницу, особенно у неопытных пользователей. Чтобы выбрать правильную формулу стандартного отклонения для конкретной задачи, просто ответьте на следующие 3 вопроса:
- Вы рассчитываете стандартное отклонение выборки или генеральной совокупности?
- Какую версию Excel вы используете?
- Включает ли ваш набор данных только числа или логические значения и текст?
Чтобы вычислить стандартное отклонение на основе числовой выборки , используйте функцию СТАНДОТКЛОН.С в Excel 2010 и более поздних версиях; СТАНДОТКЛОН в Excel 2007 и более ранних версиях.
Чтобы найти стандартное отклонение совокупности , используйте функцию СТАНДОТКЛОН.П в Excel 2010 и более поздних версиях; STDEVP в Excel 2007 и более ранних версиях.
Если вы хотите включить в расчет логических или текстовых значений, используйте либо СТАНДОТКЛОН (выборочное стандартное отклонение), либо СТАНДОТКЛОНПА (стандартное отклонение генеральной совокупности). Хотя я не могу придумать ни одного сценария, в котором любая функция может быть полезна сама по себе, они могут пригодиться в более крупных формулах, где один или несколько аргументов возвращаются другими функциями в виде логических значений или текстовых представлений чисел.
Хотя я не могу придумать ни одного сценария, в котором любая функция может быть полезна сама по себе, они могут пригодиться в более крупных формулах, где один или несколько аргументов возвращаются другими функциями в виде логических значений или текстовых представлений чисел.
Чтобы помочь вам решить, какая из функций стандартного отклонения Excel лучше всего подходит для ваших нужд, просмотрите следующую таблицу, в которой обобщается уже изученная вами информация.
| СТАНДОТКЛОН | СТАНДОТКЛОН.S | СТАНДАРТ | СТАНДОТКЛОН.P | СТДЕВА | СТДЕВПА | |
| Версия Excel | 2003 — 2019 | 2010 — 2019 | 2003 — 2019 | 2010 — 2019 | 2003 — 2019 | 2003 — 2019 |
| Образец | ✓ | ✓ | ✓ | |||
| Население | ✓ | ✓ | ✓ | |||
| Логические значения в массивах или ссылках | Игнорируется | Оценено (ИСТИНА=1, ЛОЖЬ=0) | ||||
| Текст в массивах или ссылках | Игнорируется | Оценивается как ноль | ||||
| Логические значения и «текстовые числа» в списке аргументов | Оценено (ИСТИНА=1, ЛОЖЬ=0) | |||||
| Пустые ячейки | Игнорируется | |||||
Примеры формулы стандартного отклонения Excel
После того, как вы выбрали функцию, соответствующую вашему типу данных, сложностей с написанием формулы возникнуть не должно — синтаксис настолько прост и прозрачен, что не оставляет места для ошибок 🙂 Следующие примеры демонстрируют пару формул стандартного отклонения Excel в действии.
Расчет стандартного отклонения выборки и генеральной совокупности
В зависимости от характера ваших данных используйте одну из следующих формул:
- Для вычисления стандартного отклонения на основе всей совокупности , т. .P функция:
=СТАНДОТКЛОН.П(B2:B50) - Чтобы найти стандартное отклонение на основе выборки , которая составляет часть или подмножество генеральной совокупности (в данном примере B2:B10), используйте функцию СТАНДОТКЛОН.С:
=СТАНДОТКЛОН.С(B2:B10)
Как вы можете видеть на снимке экрана ниже, формулы возвращают несколько разные числа (чем меньше выборка, тем больше разница):
В Excel 2007 и более ранних версиях вместо этого следует использовать функции СТАНДОТКЛОН и СТАНДОТКЛОН:
- Чтобы получить стандартное отклонение населения:
=СТАНДОТКЛОН(B2:B50) - Для расчета стандартного отклонения выборки:
=СТАНДОТКЛОН(B2:B10)
Вычисление стандартного отклонения для текстового представления чисел
При обсуждении различных функций для вычисления стандартного отклонения в Excel мы иногда упоминали «текстовое представление чисел», и вам может быть любопытно узнать, что это на самом деле означает.
В этом контексте «текстовые представления чисел» — это просто числа, отформатированные как текст. Как такие числа могут появиться в ваших рабочих листах? Чаще всего они экспортируются из внешних источников. Или, возвращаемые так называемыми текстовыми функциями, предназначенными для манипулирования текстовыми строками, например. TEXT, MID, RIGHT, LEFT и т. д. Некоторые из этих функций могут работать и с числами, но их вывод всегда является текстом, даже если он очень похож на число.
Чтобы лучше проиллюстрировать это, рассмотрим следующий пример. Предположим, у вас есть столбец кодов товаров, например «Джинсы-105», где цифры после дефиса обозначают количество. Ваша цель — извлечь количество каждого элемента, а затем найти стандартное отклонение извлеченных чисел.
Вытащить количество в другой столбец не проблема:
=ВПРАВО(A2,ДЛСТР(A2)-ПОИСК("-",A2,1))
Проблема в том, что при использовании формулы стандартного отклонения Excel для извлеченных чисел возвращает либо #DIV/0! или 0, как показано на скриншоте ниже:
Почему такие странные результаты? Как упоминалось выше, выходом функции ПРАВИЛЬНО всегда является текстовая строка. Но ни STDEV.S, ни STDEVA не могут обрабатывать числа, отформатированные как текст в ссылках (первый просто игнорирует их, а второй считает нулями). Чтобы получить стандартное отклонение таких «текстовых чисел», вам нужно указать их непосредственно в списке аргументов, что можно сделать, встроив все ПРАВИЛЬНЫЕ функции в вашу формулу СТАНДОТКЛОН.С или СТАНДОТКЛОН:
Но ни STDEV.S, ни STDEVA не могут обрабатывать числа, отформатированные как текст в ссылках (первый просто игнорирует их, а второй считает нулями). Чтобы получить стандартное отклонение таких «текстовых чисел», вам нужно указать их непосредственно в списке аргументов, что можно сделать, встроив все ПРАВИЛЬНЫЕ функции в вашу формулу СТАНДОТКЛОН.С или СТАНДОТКЛОН:
=СТАНДОТКЛОН.С (ПРАВО(A2,ДЛСТР(A2)-ПОИСК("-",A2,1)), ПРАВО(A3,ДЛСТР(A3)-ПОИСК("-",A3,1)), ПРАВО(A4,ДЛСТР(A4 )-ПОИСК("-",A4,1)), ВПРАВО(A5,ДЛСТР(A5)-ПОИСК("-",A5,1)))
=СТАНДАРТ(ПРАВО(A2,ДЛСТР(A2)-ПОИСК("-",A2,1)), ПРАВО(A3,ДЛСТР(A3)-ПОИСК("-",A3,1)), ПРАВО (A4,ДЛСТР(A4)-ПОИСК("-",A4,1)), ВПРАВО(A5,ДЛСТР(A5)-ПОИСК("-",A5,1)))
Формулы немного громоздко, но это может быть рабочим решением для небольшой выборки. Для большего, не говоря уже о всем населении, это точно не вариант. В этом случае более элегантным решением было бы использование функции VALUE для преобразования «текстовых чисел» в числа, которые может понять любая формула стандартного отклонения (обратите внимание на числа, выровненные по правому краю на снимке экрана ниже, в отличие от текстовых строк, выровненных по левому краю). на скриншоте выше):
на скриншоте выше):
Как вычислить стандартную ошибку среднего в Excel
В статистике есть еще одна мера для оценки изменчивости данных — стандартная ошибка среднего , которую иногда сокращают (хотя и некорректно) до просто «стандартная ошибка «. Стандартное отклонение и стандартная ошибка среднего — это два тесно связанных понятия, но не одно и то же.
В то время как стандартное отклонение измеряет изменчивость набора данных от среднего, стандартная ошибка среднего (SEM) оценивает, насколько вероятно, что среднее значение выборки будет отличаться от истинного среднего значения генеральной совокупности. Другими словами, если вы взяли несколько выборок из одной и той же совокупности, стандартная ошибка среднего показала бы дисперсию между этими средними выборками. Поскольку обычно мы вычисляем только одно среднее для набора данных, а не несколько средних, стандартная ошибка среднего оценивается, а не измеряется.
В математике стандартная ошибка среднего рассчитывается по следующей формуле:
Где SD — стандартное отклонение, а n — размер выборки (количество значений в выборке).
На листах Excel вы можете использовать функцию СЧЕТ, чтобы получить количество значений в выборке, КОРЕНЬ, чтобы извлечь квадратный корень из этого числа, и СТАНДОТКЛОН.С, чтобы вычислить стандартное отклонение выборки.
Сложив все это вместе, вы получите стандартную ошибку формулы среднего в Excel:
СТАНДОТКЛОН.С( диапазон )/КОР.КОР.(СЧЁТ( диапазон ))
Предполагая, что данные выборки находятся в B2:B10, наша формула SEM будет выглядеть следующим образом:
=СТАНДОТКЛОН.S(B2: B10)/SQRT(COUNT(B2:B10))
И результат может быть похож на этот:
Как добавить столбцы стандартного отклонения в Excel
Чтобы визуально отобразить границу стандартного отклонения, вы можете добавить бары стандартного отклонения к вашей диаграмме Excel. Вот как:
- Создайте график обычным способом ( Вставка вкладка > группа Диаграммы ).
- Щелкните в любом месте графика, чтобы выбрать его, затем нажмите кнопку Элементы диаграммы .

- Щелкните стрелку рядом с Столбики ошибок и выберите Стандартное отклонение .
При этом будут вставлены одни и те же столбцы стандартного отклонения для всех точек данных.
Вот как сделать стандартное отклонение в Excel. Я надеюсь, что вы найдете эту информацию полезной. В любом случае, я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе.
Вас также может заинтересовать
Стандартное отклонение в Excel (формула, примеры)
Стандартное отклонение в Excel (оглавление)
- Стандартное отклонение в Excel
- Формула стандартного отклонения в Excel
- Как использовать стандартное отклонение в Excel?
Стандартное отклонение показывает, насколько вся совокупность из выбранной области отличается от средней точки выбранных значений. Это помогает найти и классифицировать значения по среднему значению. Мы можем рассчитать стандартное отклонение в Excel с помощью трех функций: STD, STD. P и STD.S, где STD недоступно в последней версии Excel, STD.P используется, когда мы хотим рассмотреть все население, и STD.S используется, когда мы хотим рассмотреть только выборочные данные.
P и STD.S, где STD недоступно в последней версии Excel, STD.P используется, когда мы хотим рассмотреть все население, и STD.S используется, когда мы хотим рассмотреть только выборочные данные.
Образец (STDEV.S) Стандартное отклонение в Excel
- Функция стандартного отклонения может использоваться как функция рабочего листа, а также может применяться с помощью кода VBA.
- Инвесторы чаще всего используют его для измерения риска акций (показатель волатильности акций за определенный период времени). Финансовый аналитик часто использует его для измерения и управления рисками для конкретного портфеля или фонда.
- Он также используется в предвыборных опросах и результатах опросов (т.е. кто победит на выборах) и в прогнозах погоды.
Определение
Стандартное отклонение — это расчет, который определяет, насколько ваши значения или наборы данных отклоняются (разбросаны) от СРЕДНЕГО или СРЕДНЕГО значения.
Этот Excel показывает, близки ли ваши данные к среднему (среднему) значению или нет.
Три возможных сценария с уравнением стандартного отклонения:
- Если стандартное отклонение выше, то в данных больше вариаций, и это указывает на то, что среднее или среднее значение менее точно.
- Если стандартное отклонение равно 0, это означает, что каждое значение в наборе данных точно равно среднему или среднему значению.
- Если стандартное отклонение близко к нулю, то изменчивость данных меньше, а среднее или среднее значение более надежно.
Формула стандартного отклонения в Excel
Ниже приведена формула стандартного отклонения в Excel:
Формула стандартного отклонения в Excel имеет следующие аргументы:
- номер 1: (Обязательный или обязательный аргумент) Это первый элемент выборки населения.
- [число2]: (необязательный аргумент): существует ряд аргументов от 2 до 254, соответствующих выборке населения.

Примечание. Если вы уже охватили все данные выборки по всему диапазону в аргументе number1, то этот аргумент вводить не нужно.
Примечание: Функция в Excel игнорирует логические значения и текстовые данные в образце.
Функция СТАНДОТКЛОН Excel может принимать до 255 аргументов, где она может быть представлена либо именованными диапазонами, либо числами, либо массивами, либо ссылками на ячейки, содержащие числа.
Если в Excel 2016 ввести =std или =dstd , появятся 8 типов формул стандартного отклонения.
Здесь 8 типов стандартного отклонения разделены на две группы.
а) S, STDEVA, STDEV, DSTDEV относятся к выборке.
Принимая во внимание, что b) STDEV.P, STDEVP, STDEVPA, DSTDEVP будут подпадать под Население.
Основное различие между выборкой и совокупностью составляет
Население ( STDEV.P ) : Где «P» означает «Население», оно включает все элементы из набора данных в Населении (N).
Образец ( STDEV.S ): где «S» означает «Образец», из всего набора данных (N-1) рассматривается только образец набора данных.
Примечание: Здесь «Выборка» означает, что из большой совокупности взяты только несколько элементов.
Выбор формулы стандартного отклонения для конкретной задачи основан на логических или текстовых значениях, присутствующих в наборах данных. Приведенная ниже таблица поможет вам.
Как использовать стандартное отклонение в Excel?
Он очень прост и удобен в использовании. Давайте разберемся с работой стандартного отклонения в Excel на примере формулы стандартного отклонения.
Вы можете скачать этот шаблон Excel со стандартным отклонением здесь — Шаблон Excel со стандартным отклонением
Пример № 1. Расчет стандартного отклонения данных о высоте
В приведенной ниже таблице он содержит три столбца: серийный номер в столбце B (от B8 до B20), имя в столбце C (от C8 до C20) и высоту человека в столбце D (от D8 до D20).
Мне нужно узнать стандартное отклонение роста человека.
Перед расчетом стандартного отклонения в Excel нам необходимо рассчитать сумму и среднее (среднее) значение для наборов данных.
Где значение суммы рассчитывается с помощью формулы суммы, т.е. =СУММ (D8:D20) в ячейке G10.
Результат:
И Среднее (Среднее) вычисляется с помощью формулы Среднее, т.е. = СРЗНАЧ (D8:D20 ) в ячейке G11.
Результат:
Давайте применим функцию стандартного отклонения в ячейке «G14». Выберите ячейку «G14», к которой необходимо применить функцию стандартного отклонения.
Нажмите кнопку функции вставки (fx) под панелью инструментов формулы; появится диалоговое окно, введите ключевое слово «Стандартное отклонение» в поле поиска функции; 6 типов формул стандартного отклонения появятся в поле выбора функции.
Здесь мы вычисляем стандартное отклонение только для выборки набора данных, взятого из большой совокупности; поэтому нам нужно выбрать любой из них, т. е. STDEV.S или STDEV. Давайте STDEV.S (для примера) из категории Statistical. Дважды щелкните STDEV.S в Excel.
е. STDEV.S или STDEV. Давайте STDEV.S (для примера) из категории Statistical. Дважды щелкните STDEV.S в Excel.
Появится диалоговое окно, в котором необходимо заполнить или ввести аргументы для функции стандартного отклонения, т.е. D20) Здесь данные высоты представлены в диапазоне D8:D20.
Чтобы ввести аргумент Number 1 , , щелкните внутри ячейки D8, и вы увидите выбранную ячейку, затем выберите ячейки до D20. Таким образом, этот диапазон столбцов будет выбран, то есть D8: D20.
[число2] Здесь мы уже охватили весь пример данных через диапазон в аргументе число1, поэтому вводить этот аргумент не нужно. Нажмите «ОК» после ввода аргументов стандартного отклонения.
=СТАНДОТКЛОН.С(D8:D20), т. е. в результате возвращает значение стандартного отклонения 1,12.
Значение стандартного отклонения 1,12 указывает, что большинство людей в группе будут иметь рост 174,61 (со стандартным отклонением +1,12 или -1,12)
Здесь стандартное отклонение близко к нулю ; следовательно, это указывает на более низкую изменчивость данных и более надежное среднее или среднее значение.
Примечание: Когда мы применим формулу к большим наборам данных, мы увидим большую разницу.
Что следует помнить
- Число Аргументы должны содержать не менее двух числовых значений для расчета стандартного отклонения в Excel.
- В большинстве случаев мы используем формулу S для расчета стандартного отклонения в Excel, потому что мы рассматриваем только выборку набора данных из всего набора данных (N-1).
- #ДЕЛ/0! ошибка Происходит, если в числовом аргументе функции стандартного отклонения (S) меньше двух числовых значений.
- #ЗНАЧ Ошибка возникает, если любое из заданных значений в числовом аргументе является текстовым значением в S & STDEV.P. ( Примечание: Если функция стандартного отклонения не может интерпретировать текстовое значение как числовое, возникает ошибка #ЗНАЧ) Функция
- S & STDEV.P может применяться к нескольким диапазонам или группам.

Рекомендуемые статьи
Это руководство по стандартному отклонению в Excel. Здесь мы обсуждаем формулу стандартного отклонения в Excel и способы использования стандартного отклонения в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете ознакомиться с другими нашими рекомендуемыми статьями –
- Функция СУММ в Excel
- Функция Excel СРЕДНИЙ
- СУММЕСЛИ в Excel
- Функция Excel БОЛЬШОЙ
Когда использовать стандартные функции Kotlin
Kotlin поставляется с несколькими высокоуровневыми универсальными стандартными функциями, которые применяются к любому объекту: let() , run() , with() , apply() , и также() .
Если вы новичок в Kotlin, вам может быть интересно, когда их использовать. Они довольно непостижимы; источник показывает шведский стол из дженериков, лямбда-выражений и приемников. Существует множество статей (1, 2, 3 и т. д.) и шпаргалок (1, 2) о том, как различать их, несмотря на их тонкие различия.
д.) и шпаргалок (1, 2) о том, как различать их, несмотря на их тонкие различия.
Вот мой противоречивый совет для новичков в Kotlin: Не используйте их. Пока что.
Слишком легко запутаться со стандартными функциями и создать беспорядок. Говорю из личного опыта, много раз видел (и делал) с ними кавардак. Кроме того, они никоим образом не нужны; все они просто сокращения для (немного) более длинных фрагментов кода. Если они вас смущают или создают беспорядок, то они бесполезны!
В этой статье я расскажу о нескольких способах злоупотребления стандартными функциями. Затем я расскажу о том, что они вам не нужны, когда вы все равно начинаете, и почему вы должны сначала изучить другие части Kotlin.
Из-за их общего характера можно использовать несколько стандартных функций для одной и той же цели. Эта взаимозаменяемость на самом деле является недостатком, поскольку приводит к непоследовательному и запутанному коду.
Одним из основных примеров использования стандартных функций является работа с ненулевой версией переменной, допускающей значение NULL:
nullableVar?.let { /* здесь больше не null */ }
Но на самом деле этот паттерн можно использовать с кучей других функций
// Во всех этих лямбда-выражениях переменная, допускающая значение NULL, больше не является нулевой
nullableVar?.run { }
nullableVar?.apply {}
nullableVar?.also {}
Какая разница между всем этим? Что ж, в конце концов вы это поймете… но если вы не можете с ходу назвать разницу, то этот код может быстро запутаться при чтении.
Для тех, кто увлекается функциональным программированием, заманчиво попробовать написать Kotlin, не используя ни одной императивной строки кода. Но это может быстро привести к пирамиде лямбда-стеков:
значение1?.let { значение1NonNull ->
значение2?.let { значение2NonNull ->
значение3?.let { значение3NonNull ->
// ...Выполнить код...
}
}
}
Я разрешаю вам использовать оператор if для упрощения кода:
если (значение1 != null && значение2 != null && значение3 != null) {
// . ..Выполнить код...
}
..Выполнить код...
}
Лично я нахожу последний более легким для понимания и , он позволяет избежать глубокой вложенности.
Kotlin позволяет вам изменить приемник внутри лямбда-функции. Этот паттерн отлично подходит для создания безопасных по типу компоновщиков, но он потенциально может создать запутанный код:
класс MyClass {
весело foo(бар: Бар) {
println(toString()) // Печатает MyClass.toString()
бар.применить {
println(toString()) // Печатает Bar.toString()
}
}
}
Какой toString() вызывается здесь? Легко ошибиться!
Иногда люди испытывают искушение использовать функцию определения области действия, чтобы уменьшить количество подробностей кода. Но это не всегда так. Я действительно видел такой код:
с (someVar) {
фу()
бар()
}
Но сравните это с кодом смены не получателя:
некотораяVar.foo() someVar.bar()
Нестандартная версия функции — меньше строк кода!
Маленький секрет: все эти функции — просто сокращения для немного более длинного кода.
Как упоминалось ранее, один прием заключается в использовании значения ?.let { } для выполнения некоторого кода, если значение не равно нулю. Я думаю, что это один из немногих случаев, когда раннее использование стандартных функций на самом деле имеет смысл, так как это своего рода обратная сторона медали foo?.bar() .
Но на самом деле это просто сокращение:
val значение = someNullableVar
если (значение != ноль) {
// Делаем что-то с ненулевым значением
}
Простой val плюс оператор if ! Да, это немного более многословно, но на самом деле это не так уж и плохо.
Давайте рассмотрим пример с , применим :
значение х = StringBuilder (). применить {
добавить (var1)
добавить("\п")
добавить (var2)
}
И без применить :
значение х = StringBuilder()
x.append(var1)
х.добавить("\n")
x.append(var2)
В этом случае альтернативой является меньшее количество строк кода!
Я мог бы продолжить с остальными, но идея та же: обычно вы экономите себе только пару строк кода и/или символов, используя их.
Я просто не думаю, что эти функции стоят душевных страданий, когда вы впервые изучаете Kotlin. Существует множество других особенностей языка Kotlin, идиом и лучших практик, которые вам лучше изучить в первую очередь.
Для ясности: я , а не , предлагаю навсегда отказаться от этих функций. Я сам использую их сейчас, и они могут быть весьма полезными!
Что я am говорю, так это то, что они не нужны для написания кода на Kotlin, так что не зацикливайтесь на них. Сначала изучите, как работает остальная часть языка, а затем вернитесь к этим функциям. Будет намного легче понять их правильное использование в этот момент и когда они действительно смогут улучшить ваш код.
Введение в функции нормального распределения Excel
(Скачать рабочую тетрадь.)
Когда посетитель спросил меня, как сгенерировать случайное число из нормального распределения , она заставила меня задуматься о создании статистики в Excel.
Многие из нас познакомились со статистикой в школе, а затем забыли то немногое, что узнали… часто в течение нескольких секунд после выпускного экзамена.
Кроме того, когда мы собирали статистику, многих из нас не учили, как использовать ее в Excel. Это печально, потому что в бизнесе часто бывает полезно иметь некоторое представление об этой теме.
По всем этим причинам я подумал, что было бы полезно кратко изучить нормальные — или «колоколообразные» — кривые в Excel. Это широко используемая область статистики, для которой Excel предоставляет несколько полезных функций.
Одна интересная особенность нормальной кривой заключается в том, что она часто встречается в самых разных условиях:
- Рост каждого пола в популяции распределяется нормально.
- Показатели холестерина ЛПНП у взрослых обычно распределяются.
- Ширина полос на зебре считается нормально распределенной.
- Предполагается, что большинство ошибок измерения имеют нормальное распределение.
- Многие расчеты по методу «шесть сигм» предполагают нормальное распределение.
- И т. д.
В качестве последнего примера, вот удивительное проявление нормальной кривой: возьмем любую популяцию, независимо от того, распределена она нормально или нет. Случайным образом выберите не менее 30 членов из этой совокупности, измерьте их по какой-либо характеристике, а затем найдите среднее значение этих показателей. Это среднее значение является одной точкой данных. Теперь выберите другую случайную выборку того же числа и найдите среднее значение 9.0033 их мер. Делайте то же самое снова и снова. Центральная предельная теорема утверждает, что эти средние имеют тенденцию к нормальному распределению.
Случайным образом выберите не менее 30 членов из этой совокупности, измерьте их по какой-либо характеристике, а затем найдите среднее значение этих показателей. Это среднее значение является одной точкой данных. Теперь выберите другую случайную выборку того же числа и найдите среднее значение 9.0033 их мер. Делайте то же самое снова и снова. Центральная предельная теорема утверждает, что эти средние имеют тенденцию к нормальному распределению.
Нормальные распределения окружают нас повсюду. Поэтому максимально безболезненно давайте подробнее рассмотрим, как мы с ними работаем с помощью Excel.
Краткие определения
Каждое число на колоколообразной кривой этой диаграммы Excel является значением z.Нам нужно получить несколько кратких определений, чтобы мы могли начать описывать данные с помощью функций Excel.
Нормальное распределение вероятностей от холестерина до полосок зебры описывает долю населения, имеющую определенный диапазон значений атрибута. У большинства членов есть суммы, близкие к среднему; некоторые имеют суммы, которые далеки от среднего; а некоторые имеют суммы, чрезвычайно далекие от среднего.
У большинства членов есть суммы, близкие к среднему; некоторые имеют суммы, которые далеки от среднего; а некоторые имеют суммы, чрезвычайно далекие от среднего.
Например, популяция может состоять из всех полосатых зебр в мире. Нормальная кривая будет показывать пропорцию полос различной ширины.
стандартное отклонение выборки – это мера разброса выборки от ее среднего значения. (Конечно, мы берем в «выборку» множество элементов, а не только один элемент.) В нормальном распределении около 68% выборки находится в пределах одного стандартного отклонения от среднего. Около 95% находится в пределах двух стандартных отклонений. И около 99,7% находится в пределах трех стандартных отклонений. Цифры на рисунке выше обозначают стандартные отклонения от среднего значения.
Значение z – это расстояние между значением и средним значением с точки зрения стандартных отклонений. На рисунке выше каждое число представляет собой значение z.
Расчет или оценка стандартного отклонения
Для некоторых из следующих функций требуется значение стандартного отклонения. Есть как минимум два способа найти это значение.
Есть как минимум два способа найти это значение.
Во-первых, если у вас есть образец данных, Excel изначально предлагал функцию СТАНДОТКЛОН. Но в Excel 2010 это было заменено функцией СТАНДОТКЛОН.С:
=СТАНДОТКЛОН.С(диапазон_значений)
С другой стороны, если вы работаете со всей совокупностью, вы вычисляете стандартное отклонение с помощью функции СТАНДОТКЛОН.П:
=СТАНДОТКЛОН.П(диапазон_значений)
Однако, если вы работаете с приблизительными оценками, вы должны использовать другой подход, потому что у вас нет фактических данных, подтверждающих ваши оценки.
В этом случае сначала вычислите диапазон . Это наименьшее вероятное значение, вычитаемое из наибольшего вероятного значения. К 9 0033 скорее всего , давайте предположим, что все возможные значения будут находиться в этом диапазоне примерно в 95% случаев.
Помните, что около 95 % выборки находится в пределах двух стандартных отклонений по обе стороны от среднего значения. (Это, конечно, всего четыре стандартных отклонения.) Поэтому, если мы разделим диапазон на четыре, мы должны получить приблизительное стандартное отклонение.
(Это, конечно, всего четыре стандартных отклонения.) Поэтому, если мы разделим диапазон на четыре, мы должны получить приблизительное стандартное отклонение.
Простое деление диапазона на четыре может показаться небрежным подходом. Но подумайте, как часто используется этот расчет.
Предположим, вы прогнозируете продажи на следующий год. Вы думаете, что объем продаж составит около 1000, но это число может достигать 1200 и меньше 800. Имея эту информацию, вы можете построить нормальную кривую вокруг предполагаемых продаж и начать генерировать различные прогнозы прибыли и денежного потока. .
Чтобы подчеркнуть, эти цифры являются лишь вашими приблизительными оценками. Таким образом, использование оценочного стандартного отклонения не кажется таким небрежным, как могло бы быть в противном случае.
Основываясь на этих оценках, ваш средний объем продаж составит около 1000, а стандартное отклонение будет около (1200 – 800) / 4 = 100. С помощью этой информации вы можете использовать следующую функцию для выполнения многих необходимых вам расчетов. в вашем анализе.
в вашем анализе.
НОРМ.РАСП(x, среднее, стандартное_отклонение, кумулятивное)
Функция НОРМ.РАСП дает вероятность того, что число окажется равным или ниже заданного значения нормального распределения.
- x — значение, которое вы хотите проверить.
- mean — Среднее значение распределения.
- standard_dev — Стандартное отклонение распределения.
- кумулятивный — Если FALSE или ноль, возвращает вероятность появления x; если TRUE или не ноль, возвращает вероятность того, что значение будет меньше или равно x.
Пример: Распределение роста американских женщин в возрасте от 18 до 24 лет примерно нормальное распределение со средним значением 65,5 дюймов (166,37 см) и стандартным отклонением 2,5 дюйма (6,35 см). Какой процент этих женщин выше 5 футов 8 дюймов, то есть 68 дюймов (172,72 см)?
Процент женщин ростом менее 68 дюймов составляет:
=НОРМ. РАСП(68, 65,5, 2,5, ИСТИНА) = 84,13%
РАСП(68, 65,5, 2,5, ИСТИНА) = 84,13%
Следовательно, процент женщин выше 68 дюймов составляет 1–84,13% или примерно 15,87%. Это значение представлено заштрихованной областью на приведенной выше диаграмме.
НОРМ.СТРАСП(z, совокупный)
Функция НОРМ.СТРАСП переводит количество стандартных отклонений (z) в кумулятивные вероятности.
- z — Значение, для которого требуется распределение.
- кумулятивный — кумулятивный — это логическое значение, определяющее вид функции. Если кумулятивный параметр имеет значение ИСТИНА, функция НОРМ.СТ.РАСП возвращает кумулятивную функцию распределения; если FALSE, возвращается функция массы вероятности .
(Функция массы вероятности, PMF, дает вероятность того, что дискретная, то есть прерывистая, случайная величина точно равна некоторому значению.)
Для иллюстрации:
=НОРМ.СТ.РАСП(1, ИСТИНА) = 84,13%
=НОРМ.СТ.РАСП(-1, ИСТИНА) = 15,87%
Следовательно, вероятность того, что значение находится в пределах одного стандартного отклонения от среднего, равна разнице между этими значениями, или 68,27%. Этот диапазон представлен заштрихованной областью диаграммы.
Этот диапазон представлен заштрихованной областью диаграммы.
(Вы можете скачать файлы для этой статьи здесь.)
НОРМ.ОБР(вероятность, среднее, стандартное_отклонение)
Функция НОРМ.ОБР является обратной функцией НОРМ.РАСП. Он вычисляет переменную x с учетом вероятности.
В качестве иллюстрации рассмотрим рост американок, использованный на иллюстрации функции НОРМ.РАСП выше. Насколько высокой должна быть женщина, если она хочет войти в число 75% самых высоких американок?
Используя НОРМ.ОБР, она узнает, что ее рост должен быть не менее 63,81 дюйма, как показывает эта формула:
=НОРМ.ОБР(0,25, 65,5, 2,5) = 63,81 дюйма
На рисунке показана площадь, представленная 25% американских женщин, которые ниже этого роста.
НОРМ.СТ.ОБР(вероятность)
Функция НОРМ.СТ.ОБР является обратной по отношению к функции НОРМ.СТ.РАСП. Учитывая вероятность того, что переменная находится в пределах определенного расстояния от среднего значения, она находит значение z.
Для иллюстрации предположим, что вам нужна половина выборки, ближайшая к среднему значению. То есть вы хотите, чтобы значения z, обозначающие границу, были на 25 % меньше среднего и на 25 % больше среднего.
Следующие две формулы определяют границы -,674 и +,674, как показано на рисунке.
=НОРМ.С.ОБР(0,25)
=НОРМ.С.ОБР(0,75)
СТАНДАРТ(x, среднее, стандартное_отклонение)
Функция СТАНДАРТ возвращает значение z для указанного значения, среднего значения и стандартного отклонения .
Чтобы проиллюстрировать это, в приведенном выше примере NORM.INV мы обнаружили, что женщина должна быть ростом не менее 63,81 дюйма, чтобы избежать нижних 25% населения по росту. Функция СТАНДАРТИЗАЦИЯ сообщает нам, что значение z для 63,81 дюйма равно:
=СТАНДАРТ(63,81, 65,5, 2,5) = -0,6745
Мы можем проверить это число с помощью функции НОРМ.СТ.РАСП:
=НОРМ.СТ.РАСП(-0,6745, ИСТИНА) = 25%
То есть значение z, равное -0,6745, имеет вероятность 25%.
Как вычислить случайное число из нормального распределения
Помните, что функция НОРМ.ОБР возвращает значение с заданной вероятностью. В Excel 2007 и более поздних версиях используется следующий синтаксис:
НОРМ.ОБР(вероятность, среднее, стандартное_отклонение)
Также помните, что функция СЛЧИС возвращает случайное число от 0 до 1. То есть СЛЧИС генерирует случайные вероятности. Таким образом, вы можете использовать функцию НОРМ.ОБР для вычисления случайного числа из нормального распределения, используя эту формулу в Excel 2007 и более поздних версиях…
=НОРМ.ОБР(СЛЧИС(), среднее, стандартное_отклонение)
Связанные статьи пользователя Excel
Я создал все рисунки для этой статьи в Excel. Если вы хотите узнать, как это сделать, см. Как создавать нормальные кривые с затененными областями в Excel.
Для некоторых анализов требуются случайные числа из нормального распределения, о которых вы можете узнать здесь: Как получить случайные числа из нормального распределения для ваших прогнозов Excel статистика в экселе.
 В случае отсутствия у функции аргументов, скобки после ее имени остаются пустыми. Аргументами функции могут быть константы, ссылки или выражения. Зная синтаксис функции можно ввести ее в формулу вручную. Но, как правило, для вставки функции используют Мастер функций. Для его вызова можно выполнить команду Вставка | Функция или щелкнуть по кнопке в строке формул с надписью fx. После этого появляется диалоговое окно 1-го шага Мастера функций, в котором необходимо выбрать нужную категорию (математические, финансовые, логические и т.д.) и требуемую функцию в этой категории. Причем если активная ячейка не содержала в себе формулу, то знак равенства вставляется в нее автоматически. После выбора функции и нажатия кнопки ОК, появляется диалоговое окно, в котором необходимо ввести аргументы функции. Закончив ввод аргументов, нужно нажать кнопку ОК и вставка функции будет завершена.
В случае отсутствия у функции аргументов, скобки после ее имени остаются пустыми. Аргументами функции могут быть константы, ссылки или выражения. Зная синтаксис функции можно ввести ее в формулу вручную. Но, как правило, для вставки функции используют Мастер функций. Для его вызова можно выполнить команду Вставка | Функция или щелкнуть по кнопке в строке формул с надписью fx. После этого появляется диалоговое окно 1-го шага Мастера функций, в котором необходимо выбрать нужную категорию (математические, финансовые, логические и т.д.) и требуемую функцию в этой категории. Причем если активная ячейка не содержала в себе формулу, то знак равенства вставляется в нее автоматически. После выбора функции и нажатия кнопки ОК, появляется диалоговое окно, в котором необходимо ввести аргументы функции. Закончив ввод аргументов, нужно нажать кнопку ОК и вставка функции будет завершена.

 В категории Математические выберем функцию СУММЕСЛИ. Далее в поле Диапазон введем B2:B7, а в поле Критерий выражение >0. После ввода аргументов нажмем ОК и получим требуемое значение (рис. 4, б).
В категории Математические выберем функцию СУММЕСЛИ. Далее в поле Диапазон введем B2:B7, а в поле Критерий выражение >0. После ввода аргументов нажмем ОК и получим требуемое значение (рис. 4, б).
 Для большей эффективности при работе со списком, его структура должна соответствовать следующим правилам:
Для большей эффективности при работе со списком, его структура должна соответствовать следующим правилам: Однократно сортировку списка можно произвести по содержимому одного, двух или трех столбцов. В случае множественной сортировки, строки, у которых совпадают значения в первом столбце, между собой сортируются по содержимому второго столбца и т.д. Для сортировки по четырем и более столбцам, описанная выше процедура повторяется многократно.
Однократно сортировку списка можно произвести по содержимому одного, двух или трех столбцов. В случае множественной сортировки, строки, у которых совпадают значения в первом столбце, между собой сортируются по содержимому второго столбца и т.д. Для сортировки по четырем и более столбцам, описанная выше процедура повторяется многократно. В заголовке каждого столбца появится значок раскрывающегося списка (рис. 5).
В заголовке каждого столбца появится значок раскрывающегося списка (рис. 5). 6, б.
6, б. 5
5

 рис. 7). Произвести автозаполнение ячеек данного столбца.
рис. 7). Произвести автозаполнение ячеек данного столбца. Используя автофильтрацию, оставьте в табл. 2 только те строки, значения функции ув которых удовлетворяют критерию отбора.
Используя автофильтрацию, оставьте в табл. 2 только те строки, значения функции ув которых удовлетворяют критерию отбора.
 Значения интерпретируются численно, поэтому значение 1,5 есть
такой же как 1,50 .
Значения интерпретируются численно, поэтому значение 1,5 есть
такой же как 1,50 . Соответствует функции Java java.lang.Math.ceil() .
Соответствует функции Java java.lang.Math.ceil() . Соответствует функции Java java.lang.Math.round() .
Соответствует функции Java java.lang.Math.round() . Возможные схемы такие же, как и в
http://java.sun.com/j2se/1.3/docs/api/java/text/DecimalFormat.html.
Возможные схемы такие же, как и в
http://java.sun.com/j2se/1.3/docs/api/java/text/DecimalFormat.html. В противном случае, Р есть ложно .
В противном случае, Р есть ложно .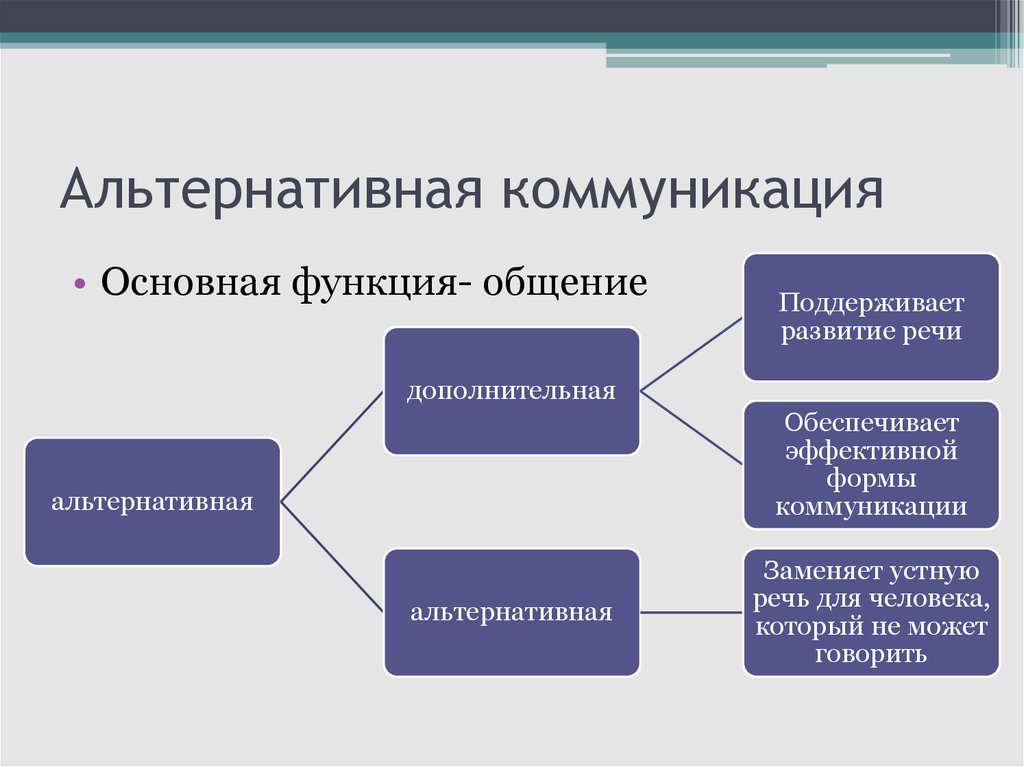 Небулевы значения интерпретируются как ложные (см. выше).
Небулевы значения интерпретируются как ложные (см. выше). Какое значение Else должна возвращать функция, зависит от различных факторов (см. подробную документацию).
Какое значение Else должна возвращать функция, зависит от различных факторов (см. подробную документацию).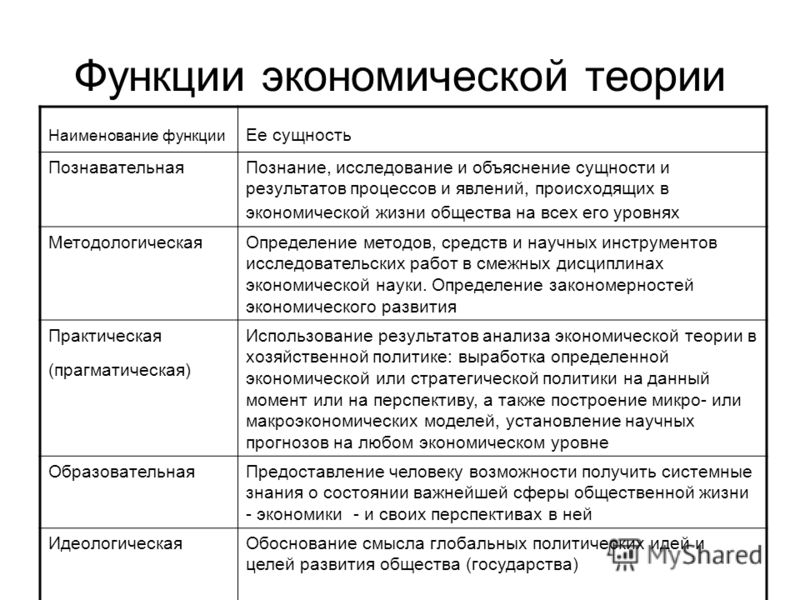
 Test_Receiver_System выводится при тестировании сопоставления сообщений в Integration Builder.
Test_Receiver_System выводится при тестировании сопоставления сообщений в Integration Builder. Таблица сохраняется вместе с самым последним сопоставлением сообщений и может использоваться только один раз.
Таблица сохраняется вместе с самым последним сопоставлением сообщений и может использоваться только один раз.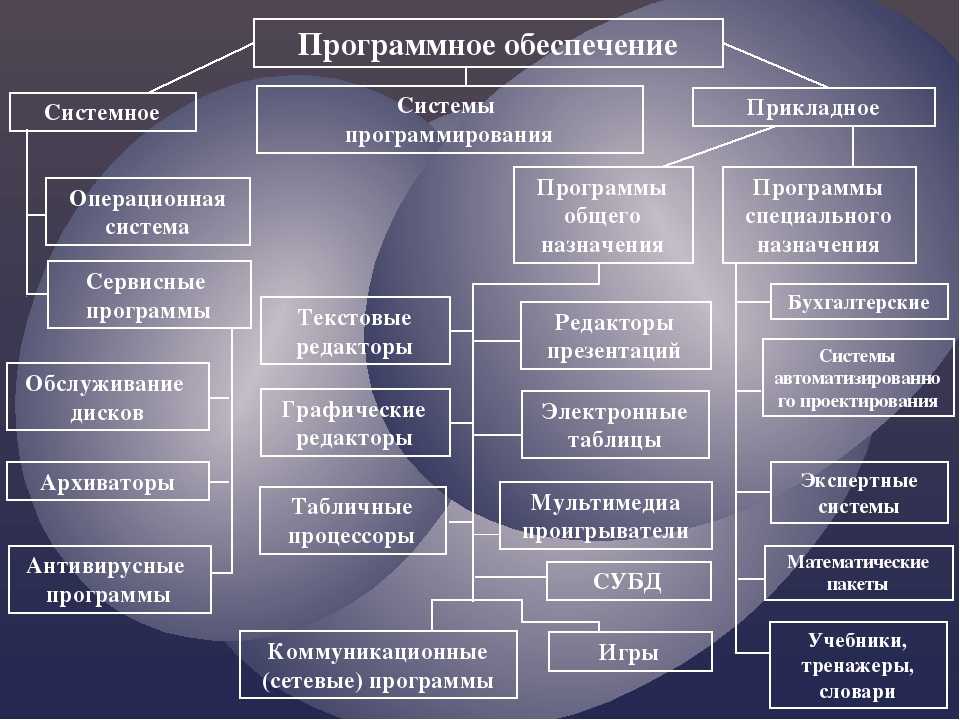

 Эта функция является
производящая функция.
Эта функция является
производящая функция. Использование условия I вы можете контролировать, вставлен ли элемент или нет. Вы соединяете элемент в целевой структуре, используя
О.
Использование условия I вы можете контролировать, вставлен ли элемент или нет. Вы соединяете элемент в целевой структуре, используя
О.
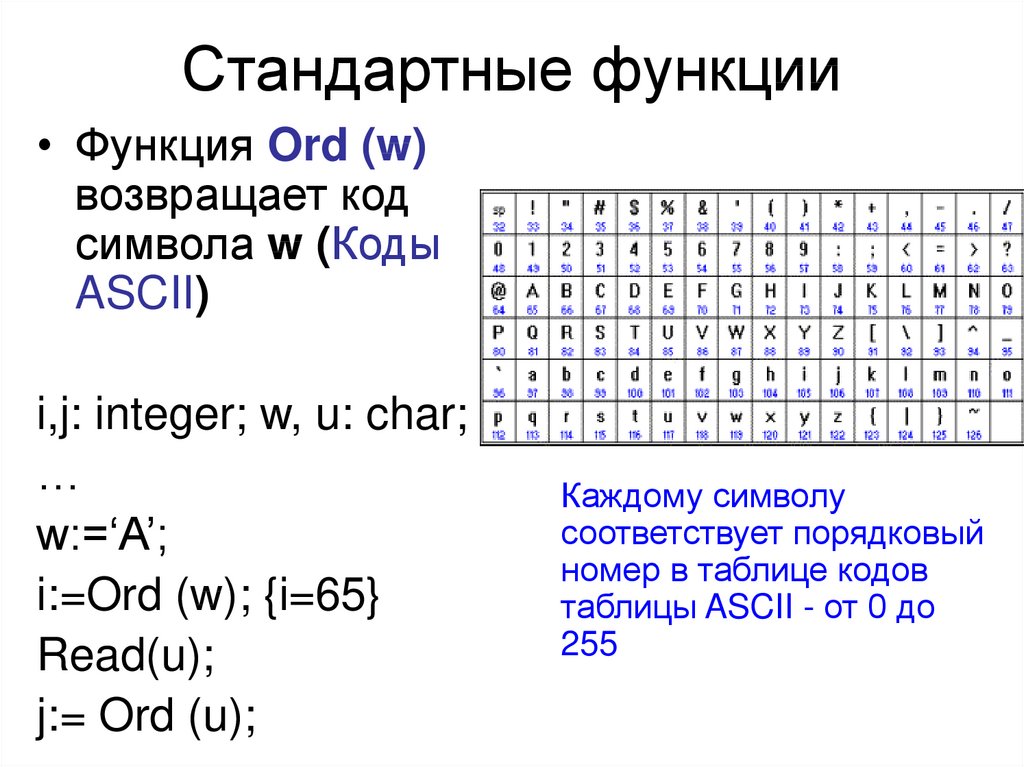 Пустые контексты (= ResultList.SUPPRESS) заменяются пустыми строками. Остается только одна очередь, состоящая из контекстов, каждый из которых содержит только одно значение. Наконец, все изменения внутреннего контекста удаляются,
чтобы все значения принадлежали одному и тому же контексту.
Пустые контексты (= ResultList.SUPPRESS) заменяются пустыми строками. Остается только одна очередь, состоящая из контекстов, каждый из которых содержит только одно значение. Наконец, все изменения внутреннего контекста удаляются,
чтобы все значения принадлежали одному и тому же контексту. Процесс сортировки стабилен (порядок одинаковых элементов не меняется) и сортирует значения за O(n*log(n)) шагов. Используя параметры функции, вы
может указать, должны ли значения сортироваться в числовом или лексикографическом порядке (с учетом или без учета регистра) и в порядке возрастания или убывания.
Процесс сортировки стабилен (порядок одинаковых элементов не меняется) и сортирует значения за O(n*log(n)) шагов. Используя параметры функции, вы
может указать, должны ли значения сортироваться в числовом или лексикографическом порядке (с учетом или без учета регистра) и в порядке возрастания или убывания. Если вы классифицировали ключевые значения как числовые в параметрах функции, они не должны быть равны константе ResultList.SUPPRESS. Смотрите также:
Объект списка результатов
Если вы классифицировали ключевые значения как числовые в параметрах функции, они не должны быть равны константе ResultList.SUPPRESS. Смотрите также:
Объект списка результатов
 Для создания очереди результатов функция берет значения из первой очереди и объединяет их с изменениями контекста из второй очереди.
Для создания очереди результатов функция берет значения из первой очереди и объединяет их с изменениями контекста из второй очереди.
 В параметрах функции вы указываете следующее: начальное значение i , приращение и должно ли значение индекса
быть повторно инициализирован в начале каждого нового контекста или должен иметь одно и то же значение для всей исходной структуры.
В параметрах функции вы указываете следующее: начальное значение i , приращение и должно ли значение индекса
быть повторно инициализирован в начале каждого нового контекста или должен иметь одно и то же значение для всей исходной структуры. Используйте диалог свойств функции, чтобы указать положение подстроки. Пример: substring(«Hello», 0,1) = «H», означает, что подстрока от Startindex 0 до Endindex 1 (
не включая должность
1).
Используйте диалог свойств функции, чтобы указать положение подстроки. Пример: substring(«Hello», 0,1) = «H», означает, что подстрока от Startindex 0 до Endindex 1 (
не включая должность
1).