Способом замены плоскостей проекций определить натуральную величину: Метод замены плоскостей проекций

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Содержание

1. Замена одной плоскости проекции
2. Замена двух плоскостей проекций
3. Использование метода замены при решении задач

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Пример 1.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл.  П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Пример 2.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис.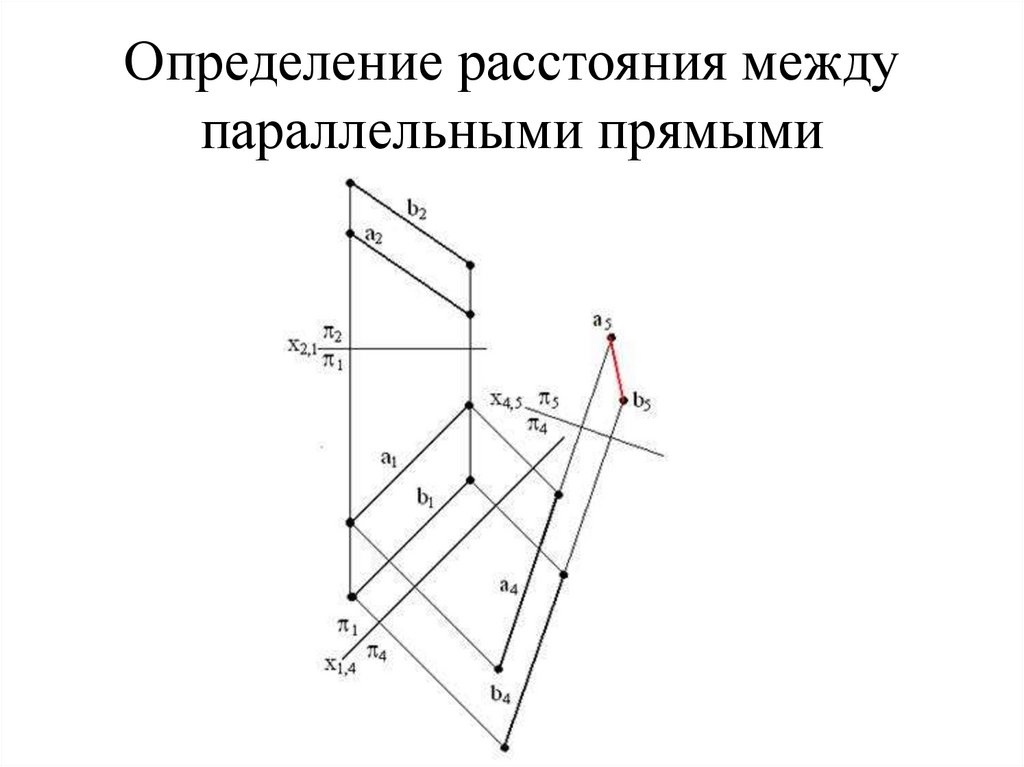 ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл.  П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Метод замены плоскостей найти натуральную величину отрезка. Способы преобразования комплексного чертежа. Определение расстояния между параллельными плоскостями

Л Е К Ц И Я 10

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

1. Сушность способа замены плоскостей

2. Применение способа замены плоскостей к отрезку прямой

3. Применение способа замены плоскостей к плоской фигуре

1. Сушность способа замены плоскостей

Этот способ заключается в том, что заданную систему плос­костей проек­ций заменяют новой системой так, что предмет (прямая или плоскость), не изменяя своего положения в про­странстве, оказывается в частном положении относительно новой системы плоскостей проекций. Плоскости проекций обра­зуют новую ортогональную систему.

В зависимости от условий задачи приходится заменять либо одну из заданных плоскостей проекций, либо обе, если заменой одной плоскости проекций не удается получить необходимого расположения проецируемого предмета относительно плоско­сти проекций.

Возьмем в системе плоскостей проекций Н и V произвольную точку А и построим ее прямоугольные проекции а и а» (рис. 60). Заменим фронтальную плоскость V новой плос­костью V 1 , перпендикулярной плоскости Н, т. е. от системы плоскостей color:black»> перейдем к системе с новой осью jx 1 . Спроеци-

ровав точку А на плоскость V 1 получим новую проекцию а1″. Горизонтальная проекция а точки А принадлежит обеим систе­мам плоскостей проекций. Из построений видно, что a 1 » aXi = Aa = a » ax = zA , т. е. при замене плоскости V плоскостью V 1 , пер­пендикулярной плоскости Н, координата проецируемой точки остается без изменения.

Для получения чертежа совмещаем все три плоскости –

Н, V к V 1 – в одну плоскость (рис. 60). В новой системе проекции a и a » находятся на линии проекционной связи, пер­пендикулярной к новой оси x 1 . При этом расстояние aXi a 1 » = axa «= zA .

Заменив горизонтальную плоскость проекций Н новой плос­костью H 1 , перпендикулярной плоскости V, от системы плоскостей проекций font-size:14.0pt;color:black»> переходят к новой системе (рис. 61).

Построив проекции точки А в обеих системах, замечаем, что координата у остается неизменной. На чертеже отрезок oXla 1 = axa = yA , что и позволяет строить новую проекцию а1 заданной точки А на перпендикуляре, проведенном из

а» к но­вой оси о x 1 .

Последовательная замена двух плоскостей проекций показа­на на рис. 62. Сначала плоскость V заменена плоскостью V 1 перпендикулярной плоскости H , и построена новая проекция а1 точки А. Затем плоскость Н заменена плоскостью Н1 перпен­дикулярной плоскости V 1 , и построена новая проекция а1.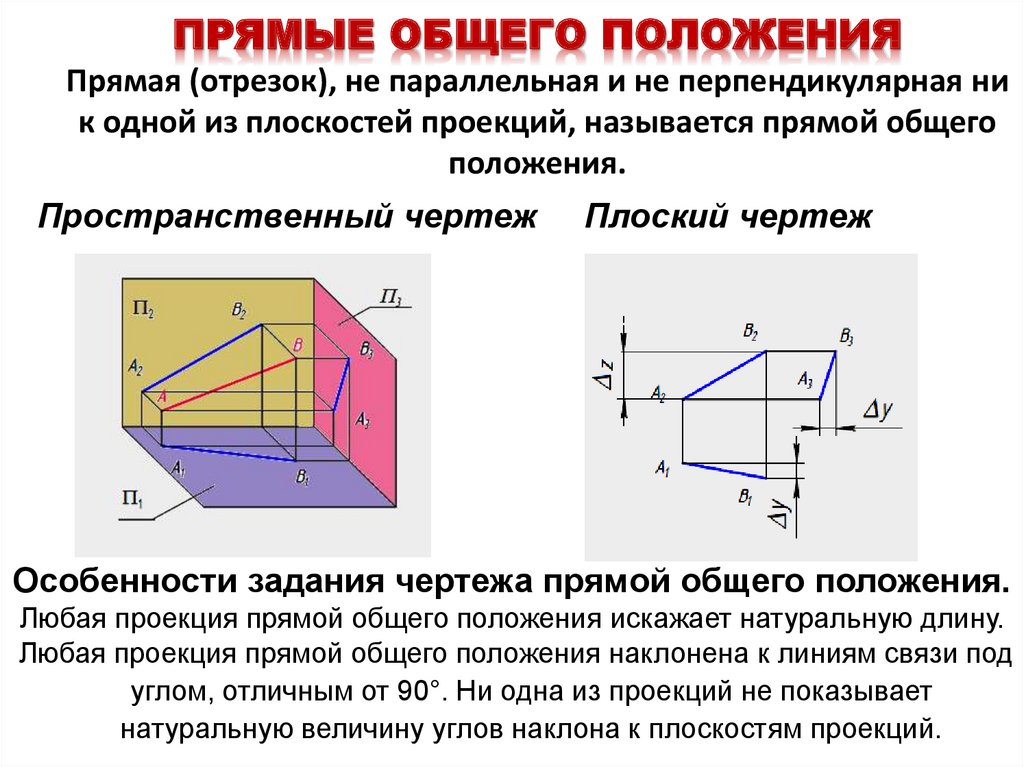 Та­ким образом совершен последовательный переход от системы плоскостей проекций к системе, а затем к системе.

position:relative; z-index:-10″>

В системе плоскостей проекциями точки А будут а{ и а1″, после­довательное построение которых определяется неизменностью координаты z в системе плоскостей и координаты y 1 в системе плоскостей

Решение задач данным методом рассмотрим на двух при­мерах.

2. Применение способа замены плоскостей

к отрезку прямой

Пример 1. Определить длину отрезка АВ прямой по его проекциям ab и а»Ь» (рис. 63).

Задача решается путем замены одной из заданных плоско­стей проекций новой плоскостью проекций, параллельной отрез­ку АВ. На новую плоскость отрезок проецируется в истинную величину.

При замене плоскости V плоскостью V 1 , параллельной отрез­ку АВ, новую ось ох1 проводят параллельно горизонтальной про­екции ab (рис. 63 а). Опустив из точек а и b перпендикуляры на ось ох1 и отложив на них aXla 1 «= axa » и bXib 1 » = bxb «, получа­ют новую проекцию а1″ b «1, равную отрезку АВ, а также угол

ан, равный углу наклона прямой к плоскости Н.

На рис. 63 б дано решение той же задачи путем замены плоскости Н плоскостью Н1, параллельной отрезку АВ. В этом случае ось ох1 располагаем параллельно фронтальной проек­ции a » b » и аналогично предыдущему получаем проекцию а1 b 1 равному заданному отрезку, и угол α v , раный углу наклона прямой к плоскости V .

3. Применение способа замены плоскостей

к плоской фигуре

Пример 2. Определить величину и форму треугольника АВС по его проекциям abc и а» b «с» (рис. 64).

Треугольник прое­циру­ет­ся без искажения на па­рал­лельную ему плос­кость про­екций.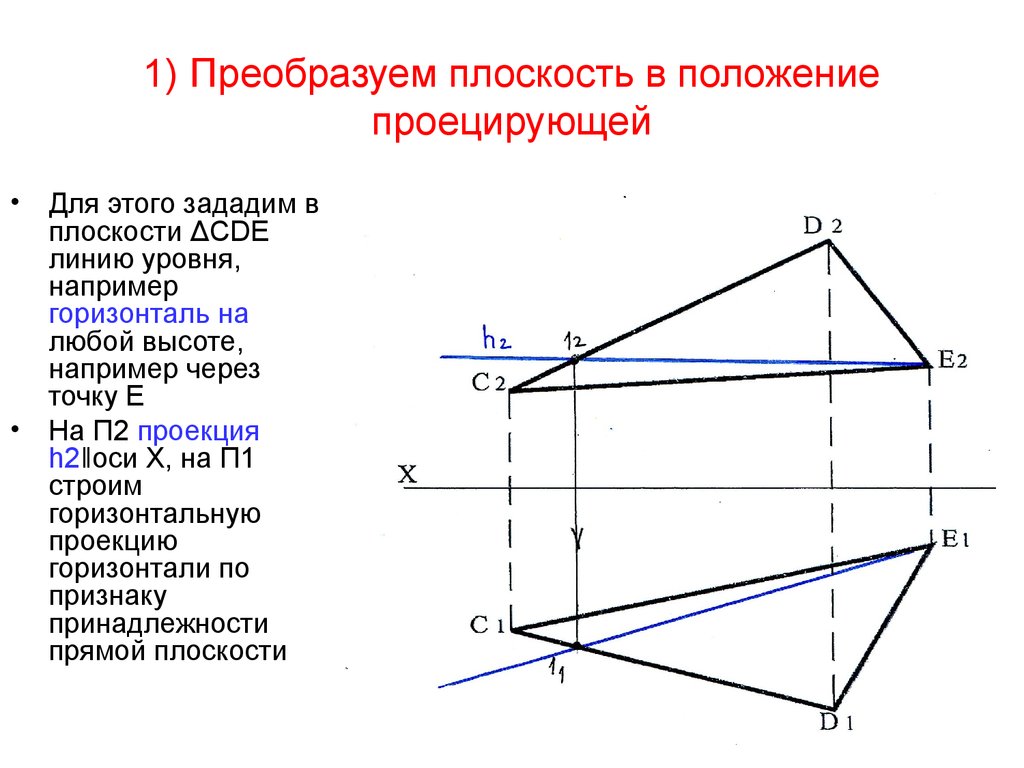 В общем случае од­ной заменой плос­костей проек­ций этого добиться невоз­можно, поэто­му после­дова­тель­но заменяют две плос­кости проек­ций.

Сначала заменяют плос-кость V плоскостью V 1 пер-пен­ди­ку­­лярной плоскости треу­гольника. Для этого в плоскости тре­уголь­ни­ка проводят горизонталь AD и пер­пендикулярно к ней рас­пола­га­ют плоскость V 1 . На чертеже построение сводится к прове­де­нию оси х1, перпендикулярной горизонтальной проек­ции ad горизонтали. Горизонталь AD проецируется на плос­кость V 1 в точку a 1 » ≡ d 1 , а треугольник — в отрезок b 1 c 1 .

Затем заменяют плоскость Н плоскостью Н1 параллельной плоскости треугольника ABC . Ось ох2 будет параллельна проек­ции b 1 «а1″с1», а проекция b 1 а1с1 отобразит истинную величину треугольника.

Сущность способа замены плоскостей проекций состоит в том, что заданную систему плоскостей проекций заменяют новой системой так, что геометрические фигуры оказываются в частном положении относительно новой системы плоскостей проекций.

Проследим, как изменятся проекции точки B , если плоскость V заменить на новую плоскость проекций V 1 (рис. 5.1, а ). Плоскость V 1 проводим перпендикулярно плоскости Н , положение которой остается без изменения. Плоскости Н и V 1 пересекутся по прямой 0х 1 , определяющей новую ось проекций. В новой системе плоскостей проекций вместо проекций b и b» получим новые проекции b и b 1 ′ . Легко убедиться, что расстояние от новой проекции точки b 1 ′ до новой оси 0х 1 (координата Z ) равно расстоянию от заменяемой проекции b» до заменяемой оси 0х . Чтобы перейти от пространственного чертежа к эпюру, нужно совместить плоскость

V 1 с плоскостью Н . На эпюре (рис. 5.1, 6 ) для построения новой проекции b 1 ′ используем неизменность координаты Z точки B . Для этого достаточно из горизонтальной проекции b провести перпендикуляр к новой оси 0х 1 и от точки b X 1 отложить координату Z , определяемую расстоянием b»b x (Z B ) в прежней системе.

Замена горизонтальной плоскости Н новой плоскостью Н 1 (рис. 5.1, в ) производится аналогично, с той лишь разницей, что теперь не изменяется фронтальная проекция точки b» , для построения новой горизонтальной проекции b 1 необходимо из сохраняемой фронтальной проекции b» провести линию связи к новой оси 0х 1 и отложить от новой оси расстояние, равное расстоянию от заменяемой проекции b

до заменяемой оси 0х .

Замена плоскостей проекций может осуществляться только последовательно, нельзя менять обе плоскости сразу.

Рассмотрим на примерах, как производится замена плоскостей проекций и строятся новые проекции фигур.

Задача 1. Определить длину отрезка прямой АВ общего положения.

Заменяем плоскость V плоскостью V 1 , параллельной отрезку АВ (рис. 5.2, а ). Проводим новую ось Х 1 параллельно ab и на перпендикулярах, проведенных к ней из точек а и b, откладываем а X 1 а 1 ′ = а x а» и b X 1 b 1 ′ = b x b». Получаем новую проекцию a 1 ′b 1 ′ = AB и одновременно угол α наклона прямой к плоскости Н.

Если плоскость Н заменим плоскостью H 1 параллельной отрезку АВ (рис. 5.2,

б ), то получим а 1 b 1 = АВ и угол β наклона прямой к плоскости V.

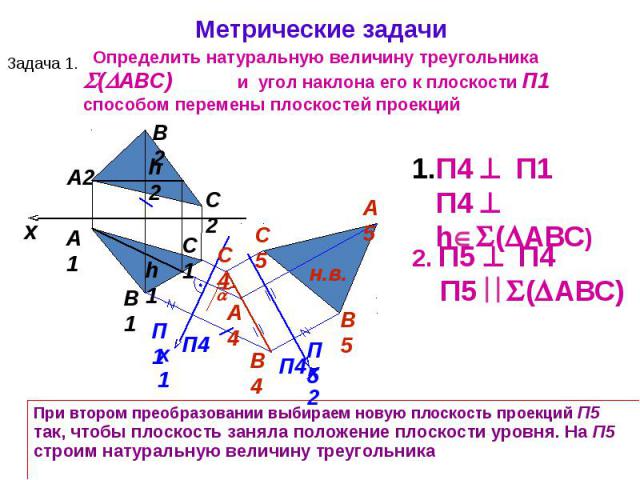
Задача 2. Определить натуральную величину и форму треугольника ABC .

Задача решается последовательной заменой двух плоскостей проекций.

Сначала плоскость V заменяем плоскостью V 1 , перпендикулярной к плоскости треугольника (рис. 5.3). Для этого в плоскости треугольника проводим горизонталь AD (ad, a»d») и новую ось Х 1 располагаем перпендикулярно к ad. На новой плоскости проекций треугольник спроецируется в прямую b 1 ′а 1 ′с 1 . На втором этапе плоскость Н заменяем плоскостью Н 1 , параллельной плоскости треугольника, располагая ось Х 2 параллельно прямой b 1 ′а 1 ′с 1 ′. Построенная проекция a 1 b 1 с 1 определяет натуральную величину и форму треугольника ABC.

Сущность способа состоит в том, что положение изображаемой фигуры в пространстве остаётся неизменным, а исходная система плоскостей проекций, относительно которой задана фигура, заменяется новой.

При выборе новой плоскости проекций должен быть выполнен основной принцип ортогонального проецирования (метода Монжа) – взаимной перпендикулярности плоскостей проекций, т.е. новую плоскость проекций необходимо обязательно располагать перпендикулярно одной из основных исходных плоскостей проекций.

Пусть задана система плоскостей проекций П 1 и П 2 (в дальнейшем будем обозначать сокращенно ). Спроецируем какую-либо точку А на эти плоскости и найдем ее проекции А 2 и А 1 (рис. 9.5).

Предположим, что при решении какой-либо задачи мы нашли целесообразным заменить плоскость П 2 другой фронтальной плоскостью П 4 , перпендикулярной к плоскости П 1 . Линия пересечения плоскостей проекций П 1 и П 4 называется новой осью проекций и обозначается Х 1 . Построим ортогональные проекции точки А в системе . Так как, плоскость П 1 осталась прежней, то и проекция точки А на эту плоскость на изменит своего положения.

Для получения новой фронтальной проекции точки на новую плоскость П 4 опускаем перпендикуляр из А на плоскость П 4 . Основание А 4 этого перпендикуляра определяет искомую фронтальную проекцию точки А .

Установим, какая связь существует между проекциями А(А 1 , А 2) и А(А 1 А 4) одной и той же точки в обеих системах.

Горизонтальная проекция у них общая и так как расстояние точки А от плоскости П 1 не изменилось, то /АА 1 /=/А 2 А x /=/А 4 А x1 ¹ /, т. е. расстояние новой фронтальной проекции до новой оси равно расстоянию заменяемой проекции до предыдущей оси.

Чтобы перейти к эпюру, повернём плоскость П 4 вокруг оси Х 1 и совместим с плоскостью П 1 . Тогда и новая фронтальная проекция А 4 совместится с плоскостью П 1 и при этом окажется на одном перпендикуляре к оси х 1 с проекцией А 1 .

На рис. 9.6 показаны те построения, которые надо произвести на эпюре, Чтобы от проекций (А 1 , А 2) точки А в системе перейти к проекциям A 1 А 4) той же точки в системе , необходимо: провести новую ось проекций Х 1 , которая определяет положение горизонтально-проецирующей плоскости П 4 , затем из горизонтальной проекции точки А 1 Х 1 . На построенном перпендикуляре отложить (от новой оси) отрезок А x А 4 =А x А 2 . Полученная таким образом точка А 4 является проекцией точки А на плоскость П 4 .

Замена горизонтальной плоскости П 1 новой плоскостью П 4 и построение новых проекций точки А в системе осуществляется аналогично рассмотренному случаю, с той лишь разницей, что теперь остается без изменения фронтальная проекция точки, а для нахождения новой горизонтальной проекции А 4 точки А необходимо из фронтальной проекции точки А 2 опустить перпендикуляр на новую ось Х 1 и отложить на нем от точки пересечения с осью Х 1 отрезок А 4 А x ¹ , равный расстоянию старой горизонтальной проекции от старой оси А 1 А х (рис. 9.7).

Рассмотренные примеры позволяют установить следующее общее правило: для того, чтобы построить проекцию точки в новой системе плоскостей проекций, необходимо из неизменяемой проекции точки опустить перпендикуляр на новую ось проекций и отложить на нем от новой оси до новой проекции расстояние, равное расстоянию от заменяемой проекции до предыдущей оси.

Назначение способов преобразования чертежа состоит в том, чтобы геометрическую фигуру общего положения расположить в частное положение относительно плоскостей проекций с целью использования свойств ее проекций. Например, преобразование плоскости общего положения в плоскость уровня позволит определить по соответствующей проекции ее натуральную величину.

Способы преобразования комплексного чертежа разделяют на две группы по признаку, определяющему положение фигуры и плоскостей проекций друг относительно друга или направление проецирования:

1. Изменяют положение плоскостей проекций или направление проецирования так, чтобы неподвижная в пространстве фигура оказалась в частном положении. К этой группе относят:

способ замены плоскостей проекций;

способ дополнительного проецирования.

2. Изменяют положение геометрической фигуры в пространстве так, чтобы она оказалась в частном положении относительно фиксированной системы плоскостей проекций. В эту группу включают:

способ вращения.

Задачи, решаемые с помощью способов преобразования комплексного чертежа, сводятся к следующим основным задачам, в которых необходимо преобразовать:

прямую (плоскость, цилиндрическую или призматическую поверхности) в проецирующую фигуру;

Рассмотрим последовательно все способы преобразования, за исключением способа дополнительного проецирования, с которым рекомендуется ознакомиться самостоятельно по учебнику .

Сущность способа состоит в замене первоначальной системы взаимно перпендикулярных плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций при неизменном положении геометрической фигуры в пространстве.

Для решения конкретной задачи выполняют одно или два последовательных преобразования способом замены, например, Π 1 Π 2 →Π 1 Π 4 илиΠ 1 Π 2 →Π 1 Π 4 →Π 5 Π 4 . Во втором случае преобразование называют композицией преобразований. При каждом шаге в данном способе заменяется только одна плоскость проекций, а другая остается общей для двух систем.

Рассмотрим механизм и особенности способа замены плоскостей проекций на примере преобразования комплексного чертежа точки (рис. 28).

При замене, например, фронтальной плоскости проекций Π 2 новой вертикальной плоскостьюΠ 4 горизонтальная плоскостьΠ 1 в данном случае является общей для двух систем плоскостей проекций, вследствие чего проекцияА 1 точкиА на эту плоскость является также общей для этих систем. При этом сохраняется неизменной величина расстояния (АА 1 ) от заданной точки до этой плоскости проекций и, как следствие, равенство ее проекций на плоскостиΠ 2 иΠ 4 , т. е.АА 1 =А 2 А 12 =А 4 А 14 , что позволяет выполнять на комплексном чертеже построение новой проекцииА 4 заданной точки (см рис. 28).

Еще одна особенность способа замены плоскостей проекций заключается в том, что комплексный чертеж образуется совмещением плоскостей проекций с той плоскостью, которая является общей для двух систем. В рассматриваемом на рис. 28 примере такой плоскостью является горизонтальная плоскость проекций.

В качестве примера рассмотрим задачу преобразования прямой общего положения в проецирующую. Для достижения конечного результата необходимо провести замену двух плоскостей проекций, используя композицию преобразований, т. е. два последовательных преобразования (рис. 29).

Замена одной плоскости проекций, например, Π 2 наΠ 4 позволяет преобразовать прямую общего положения только в прямую уровня, так как невозможно сразу расположить новую вертикальную плоскость проекцийΠ 4 перпендикулярно заданной прямой. Далее, заменяя последовательно вторую плоскость проекцийΠ 1 наΠ 5 и располагая ее перпендикулярно прямойАВ , получаем конечный результат (см. рис. 29).

ОБЩИЕ ПОЛОЖЕНИЯ

СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

Лекция 4

Решение ряда задач в начертательной геометрии значительно упрощается, когда геометрические фигуры занимают частное положение относительно плоскостей проекций. Задачи на определение взаимного положения фигур и метрические задачи (определение натуральных величин плоскостей, отрезков и т.д.). Для этого существуют различные способы преобразования комплексного чертежа. Каждый из них основан на одном из следующих принципов:

1. на изменении положения плоскостей проекций относительно неподвижных геометрических фигур;

2. на изменении положения заданных геометрических фигур относительно неподвижных плоскостей проекций;

Рассмотрим некоторые из них.

Сущность способа состоит в том, что заданные геометрические фигуры неподвижны в заданной системе плоскостей проекций (П 1 , П 2 ). Последовательно вводятся новые плоскости проекций (П 4 , П 5 ), относительно которых геометрические фигуры займут частное положение. Новая плоскость проекций выбирается с таким расчетом, чтобы она была перпендикулярной к незаменяемой плоскости проекций.

Большинство задач решается с применением одного или двух последовательных преобразований исходной системы плоскостей проекций. Одновременно можно заменять только одну плоскость проекций П 1 (или П 2 ), другая плоскость П 2 (или П 1 ) должна оставаться неизменной.
На рисунке 1 представлено наглядное изображение метода замены плоскостей проекций. Фронтальная плоскость П 2 заменяется на новую фронтальную плоскость П 4 . Новые проекции точки А (А 1 А 4 ), при этом, как видно из рисунка, высота точки А осталась прежней.

Необходимо запомнить правило построения новых проекций точек при методе замены:

1. линии связи всегда перпендикулярны новым осям проекций;
2. расстояние от новой оси проекций до новой проекции точки всегда берется с той плоскости, которую заменяют.

Рисунок 1.Наглядное изображение метода замены плоскостей проекций.

Рисунок 2.Изображение метода замены плоскостей проекций на эпюре.

Большинство задач в начертательной геометрии решаются на базе четырех задач:

1. Преобразовать прямую общего положения в прямую уровня;
2. Преобразовать прямую общего положения в проецирующую прямую;
3. Преобразовать плоскость общего положения в проецирующую плоскость;
4. Преобразовать плоскость общего положения в плоскость уровня .

Задача №1

Рассмотрим решение задачи №1 . Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рис.3). Для этого вводим новую фронтальную плоскость проекций П 4 , ось Х 1,4 проводим параллельно А 1 В 1 АВ – А 4 В 4. В новой системе плоскостей проекций прямая АВ – фронталь.

Рисунок 3.

Преобразование прямой общего положения в прямую уровня (фронталь)

Задача №2

Дана прямая АВ – общего положения, преобразуем ее в проецирующую прямую (рис. 4). Для решения этой задачи необходимо выполнить последовательно два преобразования:

1. Преобразовать прямую общего положения в прямую уровня, то есть решить сначала задачу №1;
2. Преобразовать прямую уровня в проецирующую прямую.

Вычертить условие задачи №1, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П 5 Х 4 , 5 перпендикулярно проекции А 4 В 4 и строим новую проекцию прямой А 5 В 5. В системе плоскостей П 4 ,П 5 , прямая АВ является горизонтально проецирующей прямой.

На базе задач №1 и №2 решаются следующие задачи:

1. определение расстояния от точки до прямой;

2. определение расстояния между параллельными и скрещивающимися прямыми;

3. определение натуральной величины прямой;

4. определение величины двугранного угла.

Рисунок 4.

Преобразование прямой общего положения в проецирующую прямую.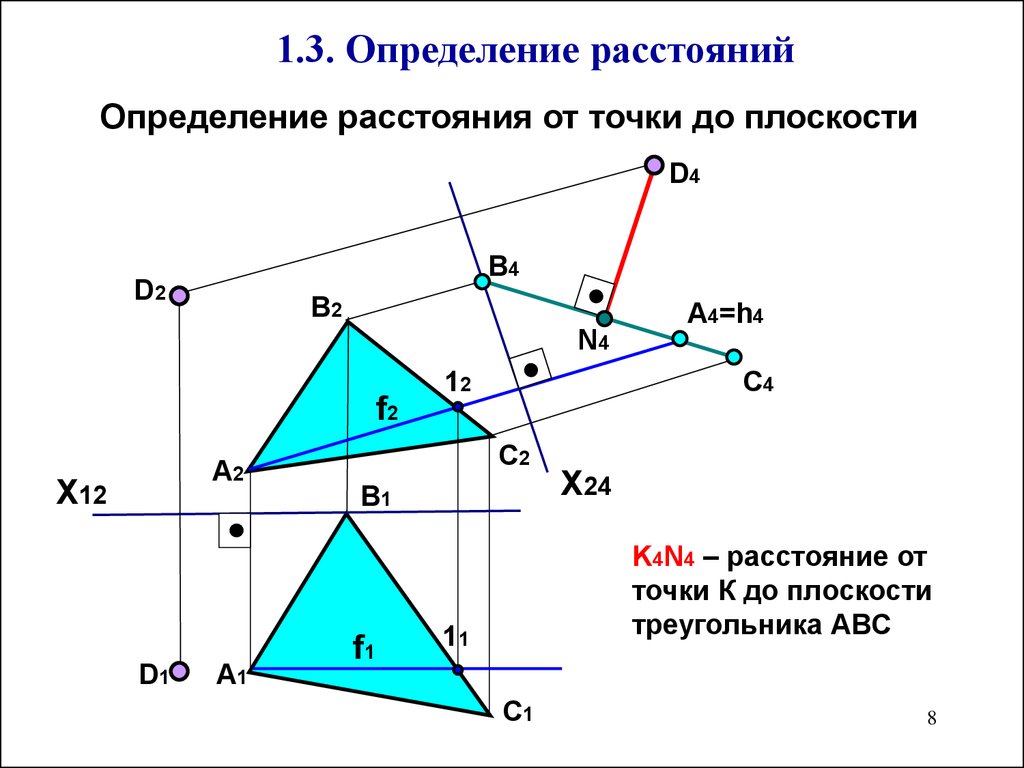

Задача №3.

Дана плоскость АВС – общего положения, преобразуем ее в проецирующую плоскость (рис.5). Для решения этой задачи необходимо в плоскости провести линию уровня, если такая отсутствует. Новую ось проекций проводим перпендикулярно лини уровня. В треугольнике АВС проводим горизонталь h. Ось проекций Х 14 проводим перпендикулярно h 1 , новую проекцию плоскости А 4 В 4 С 4 , строим по правилам, разобранным в предыдущих задачах.

В системе плоскостей проекций П 1 ,П 4, плоскость треугольника является фронтально-проецирующей плоскостью.

Рисунок 5.

Преобразование плоскости общего положения в проецирующую плоскость.

Задача №4.

Рисунок 6.

Преобразование плоскости общего положения в плоскость уровня.

Дана плоскость АВС – общего положения, преобразуем ее в плоскость уровня (рис.6). Для решения этой задачи необходимо выполнить последовательно два преобразования:

1. Преобразовать плоскость общего положения в проецирующую плоскость, то есть решить сначала задачу №3;
2. Преобразовать проецирующую плоскость в плоскость уровня.

Вычертить условие задачи №3, самостоятельно решить ее, затем приступить к выполнению второго преобразования. Вводим новую горизонтальную плоскость проекций П 5 , для этого проводим новую ось проекций Х 4 , 5 параллельно проекции А 4 В 4 С 4 и строим новую проекцию треугольника А 5 В 5 С 5. В системе плоскостей П 4 ,П 5 , треугольник АВС является горизонтальной плоскостью уровня.

На базе задач №3 и №4 решаются следующие задачи:

1. определение расстояния от точки до плоскости;

2. определение расстояния между параллельными плоскостями;

3. определение натуральных (истинных) величин геометрических фигур;

определение углов наклона плоскости к плоскостям проекций

Метод плоскопараллельного перемещения

Все вышерассмотренные задачи можно решить используя метод плоско-параллельного перемещения, при котором плоскости проекций остаются на месте, а проекция фигуры перемещается (рис. 7).

Рисунок 7. Определение натуральной величины отрезка методом плоско-параллельного перемещения.

Дана прямая АВ – общего положения, преобразуем ее в прямую уровня (рис.7). Для этого перемещаем проекцию А 1 В 1 параллельно оси Х . Строим новую проекцию прямой АВ – А 2 ` В 2 ` , которая будетявляться— натуральной величиной отрезка. Этот метод используется для определения натуральных величин ребер многогранников при построении развертки.

Метод вращения

Частным случаем плоско-параллельного перемещения является метод вращения вокруг проецирующих прямых и прямых уровня.

Метод замены плоскостей заключается в нахождении фактического размера отрезка прямой. Способы преобразования сложного рисунка. Определение расстояния между параллельными плоскостями

Л Е С И З 10

МЕТОД ЗАМЕНЫ ПРОЕКЦИОННЫХ ПЛОСКОСТЕЙ

1. Сухость пути замены плоскостей

2. Применение метода замены плоскостей к отрезку

3. Применение метода замены плоскостей к плоской фигуре

1. Сухость пути замены плоскостей

Этот метод заключается в замене данной системы плоскостей проекций новой системой таким образом, чтобы объект (прямая или плоскость), не меняя своего положения в пространстве, оказывался в том или ином положении относительно новой системы плоскостей проекций. Плоскости проекций образуют новую ортогональную систему.

В зависимости от условий задачи необходимо заменить либо одну из заданных плоскостей проекций, либо обе, если заменой одной плоскости проекций не удается получить требуемое положение проецируемого объекта относительно плоскости проекций.

Возьмите в системе плоскостей проекций Н и V произвольную точку А и постройте ее прямоугольные проекции а и а» (рис. 60). Замените фронтальную плоскость V новой плоскостью V 1 перпендикулярно плоскости H, т. е. из системы planescolor:black»> перейдем в систему с новой осью j x 1 . Проект

попадание в точку А на самолете V 1 получаем новую проекцию а1″. Горизонтальная проекция а точек А принадлежит обеим системам проекционных плоскостей. Из построений видно, что а 1″ aXi = Аа = а» ах = zA, т.е. при замене плоскости V плоскость V 1, перпендикулярная плоскость H, координата проецируемой точки остается неизменной05.

Для получения чертежа объединяем все три плоскости — Г, В до В 1 — в одной плоскости (рис. 60). В новой проекционной системе а и а» находятся на линии соединения проекций, перпендикулярной новой оси х 1. В этом случае расстояние а Xi а 1 «= аха «= zA

Замена плоскости горизонтальной проекции H новая плоскость Н 1 , перпендикулярно плоскости V, из системы проекционных плоскостей, размер шрифта: 14.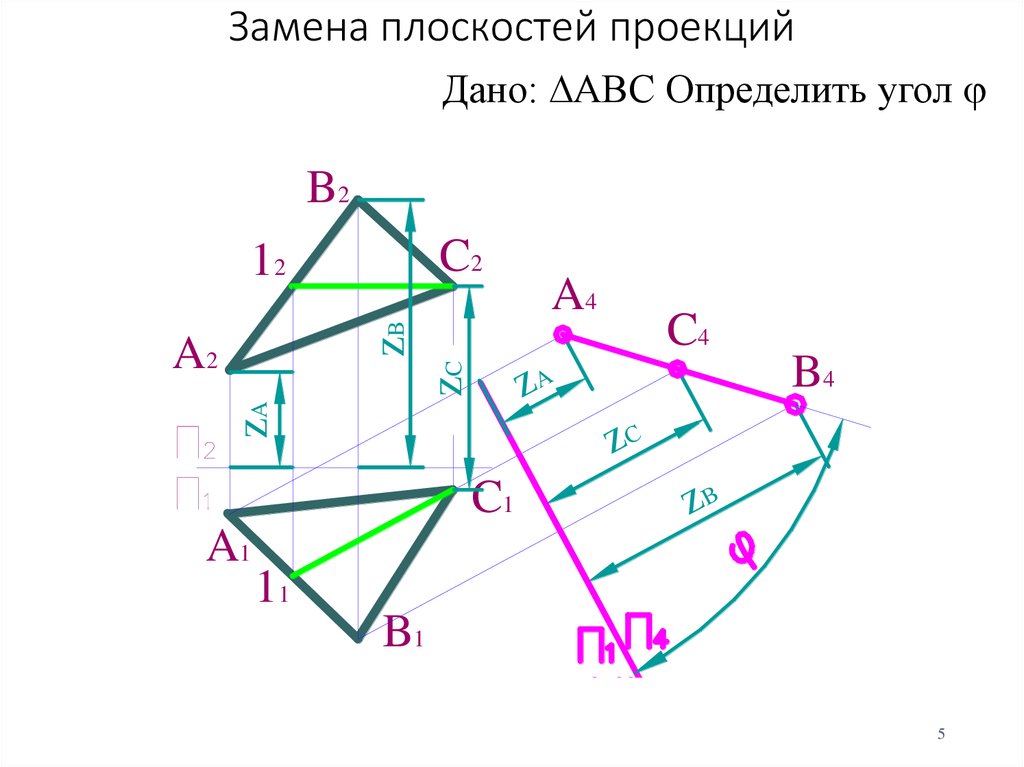 0pt; цвет: черный «> переход на новую систему (рис. 61).

Построив проекции точки А в обеих системах, заметим, что координата в точке остается неизменной. На чертеже отрезок oXla 1 = axa = yA, который позволяет построить новую проекцию a1 set point A на перпендикуляре, проведенном от а» к новой оси o x 1 .

Последовательная замена двух проекционных плоскостей показана на рис. 62. Плоскость первая V заменена плоскостью V 1 перпендикулярная плоскость H , и строится новая проекция a1 точек A. Затем плоскость H заменяется плоскостью h2 перпендикулярной плоскостью V 1 , и построена новая проекция а1. Таким образом, осуществляется последовательный переход от системы плоскостей проекций к системе, а затем к системе.

позиция: относительная; z-индекс: -10 «>

В системе плоскостей проекциями точки А будут а( и а1″, последовательное построение которых определяется неизменностью координат z в системе плоскостей и координат у 1 в системе самолета

Решение задач этим методом рассмотрим на двух примерах.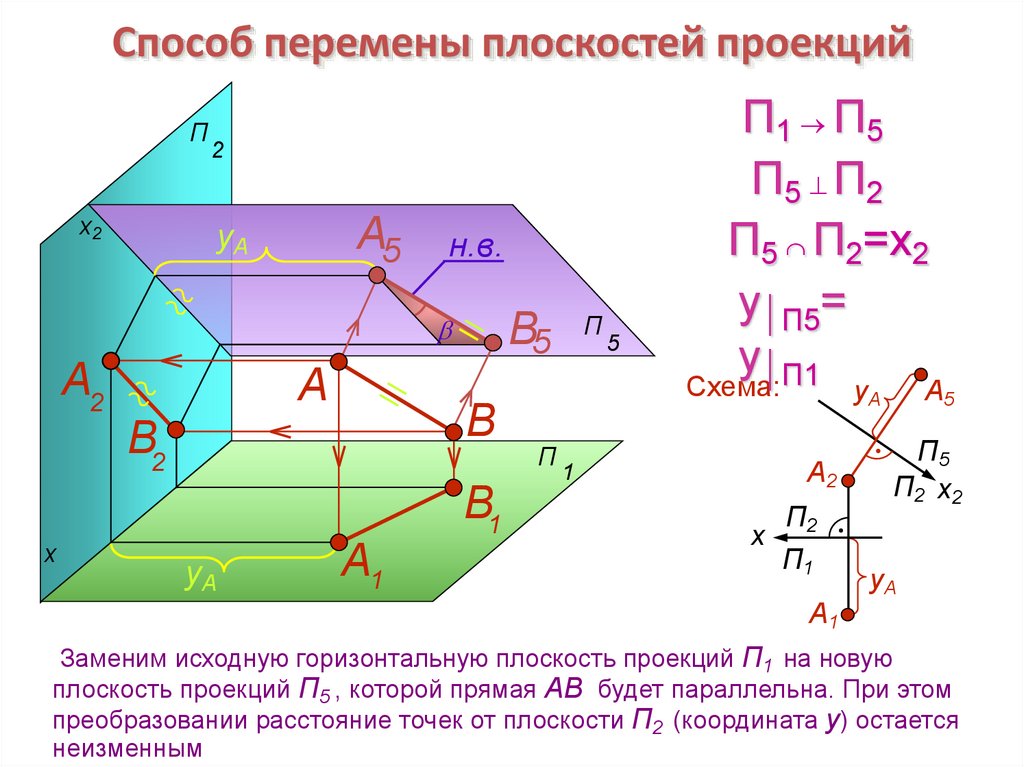

2. Применение метода замены плоскостей

на отрезок прямой

Пример 1. Определить длину отрезка АВ прямой на его проекции аб и а «б» (рис. 63).

Задача решается заменой одной из заданных плоскостей проекций на новую плоскость проекций, параллельную отрезку АБ. Сегмент проецируется на новую плоскость до своего истинного значения.

При смене плоскости V плоскость V 1, параллельна линии AB, новая ось o x1 проводится параллельно горизонтальной проекции ab (рис.63 a ). Отбрасывая точки a и b перпендикуляры к оси о x1 и откладывая для них aXla 1 «= axa » и bXib 1 «= bxb», получить новую проекцию а1″ б»1, равен отрезку АВ, а также угол ан, равен углу наклона прямой к плоскости Н.

На рис. 63 б решение той же задачи дано заменой плоскости Н на плоскостью h2, параллельно линии АВ. В данном случае ось х1 располагаем параллельно фронтальной проекции а» б» и аналогично предыдущей получаем проекцию а1 b 1 равен заданному отрезку, а угол α v , равен углу наклона прямой к плоскости V.

3. Применение метода замены плоскостей

до плоской цифры

Пример 2. Определить размер и форму треугольника ABC согласно его прогнозам abc и а» б «с» (рис. 64).

Треугольник проецируется без искажения на параллельную ему плоскость проекции. В общем случае этого нельзя добиться заменой только плоскостей проекций, поэтому последовательно заменяют две плоскости проекций.

Плоскость-кость заменяется первой V плоскостью V 1 перпендикулярно плоскости треугольника. Для этого проведите горизонтальную линию в плоскости треугольника AD и перпендикулярно к ней размещена плоскость V 1. На чертеже построение сводится к нанесению оси x1, перпендикулярно горизонтальной проекции ad горизонтально. Горизонталь AD в проекции на плоскость V 1 точно a 1 » ≡ d 1 , а треугольник — в отрезок b 1 c 1 .

Затем заменить плоскость H плоскостью h2 параллельно плоскости треугольника азбука. Ось o x2 будет параллельна проекции b 1″a1″c1″, и проекция b 1 а1с1 отобразит истинный размер треугольника.

Суть метода замены плоскостей проекций состоит в том, что данная система плоскостей проекций заменяется новой системой так, чтобы геометрические фигуры находились в определенном положении относительно новой системы плоскостей проекций.

Посмотрим, как изменятся проекции точки B если плоскость V заменить новой проекционной плоскостью V 1 (рис. 5.1, a ). Плоскость V 1 проводим перпендикулярно плоскости H , положение которой остается неизменным. Плоскости H и V 1 пересекаются по прямой линии 0x 1 , определяющей новую ось проекции. В новой системе плоскостей проекции вместо проекций b и b» получаем новые проекции b и b 1 ′ … Легко проверить, что расстояние от новой проекции точки b 1 ′ до новой оси 0x 1 (координата Z ) равно расстоянию от заменяемая проекция b» на заменяемую ось 0x … Для перехода от пространственного чертежа к сюжетному необходимо совместить плоскость V 1 с плоскостью H … На схеме (Рис.5.1, 6 ) построить новую проекцию b 1 ′ используем неизменность координаты Z точек B … Для этого достаточно из горизонтальной проекции b провести перпендикуляр к новой оси 0x 1 и из точки b X 1 координата переноса Z определяется расстоянием b»b x ( Z B ) в старой системе.

Замена горизонтальной плоскости Н новой плоскостью Н 1 (рис. 5.1, v ) выполняется аналогично, с той лишь разницей, что теперь фронтальная проекция точки не изменяется b» , для построения новой горизонтальной проекции b 1 необходимо из сохраненной фронтальной проекции b » провести линию связи до новой оси 0x 1 и отложить от новой оси расстояние равное расстоянию от заменяемого выступа b до заменяемой оси 0x .

Замена плоскостей проекций может производиться только последовательно, менять обе плоскости сразу нельзя.

Рассмотрим на примерах, как заменяются плоскости проекций и строятся новые проекции фигур.

Задача 1. Определить длину отрезка AB Общее положение.

Заменить плоскость V плоскостью V 1, параллельно линии AB (рис.5.2, a ). Проводим новую ось X 1 параллельно ab и по перпендикулярам, ​​проведенным к ней из точек a и b, откладываем a X 1 a 1′ = a x a» и b X 1 b 1 ′ = б х б «. Получаем новую проекцию a 1 ′ b 1 ′ = AB и в то же время угол α наклон прямой к плоскости Н.

Если плоскость H заменить на плоскость H 1 , параллельную линии AB (рис.5.2, b ), то получим a 1 b 1 = AB и угол β наклон прямой к плоскости В.

Задача 2. Определить реальный размер и форму треугольника ABC .

Проблема решается последовательной заменой двух проекционных плоскостей.

Плоскость первую V замените на плоскость V 1 , перпендикулярную плоскости треугольника (рис.5.3). Для этого начертите горизонтальную линию в плоскости треугольника AD (ad, a «d») и новую ось X 1 в положении , перпендикулярном ad. На новую плоскость проекции треугольник проецируется на прямую b 1 ′ a 1 ′ c 1, На втором этапе плоскость H заменить плоскостью H 1 , параллельной плоскости треугольника, расположив оси X 2 параллельно прямой b 1 ′ и 1 ′ c 1 ′. Построенная проекция a 1 b 1 c 1 определяет реальный размер и форму треугольника ABC.

Суть метода заключается в том, что положение изображаемой фигуры в пространстве остается неизменным, а исходная система проекционных плоскостей, относительно которой дана фигура, заменяется новой.

При выборе новой плоскости проекций должен выполняться основной принцип ортогонального проецирования (метод Монжа) — взаимная перпендикулярность плоскостей проекций, т.е. новая плоскость проекций должна располагаться перпендикулярно одной из основных исходных плоскостей проекций.

. Пусть задана система проекционных плоскостей P 1 и P 2 (в дальнейшем мы будем обозначать ее сокращенно). Спроецируем на эти плоскости некоторую точку A и найдем ее проекции А 2 и А 1 (рис. 9.5).

Предположим, что при решении какой-то задачи мы сочли целесообразным заменить плоскость P 2 другой фронтальной плоскостью P 4 , перпендикулярной плоскости P 1 . .. Линия пересечения плоскостей проекций P 1 и P 4 называется новой осью проекции и обозначается X 1. Построим ортогональные проекции точки A в системе . Так как самолет P 1 осталась прежней, то проекция точки А на эту плоскость не изменит своего положения.

Для получения новой фронтальной проекции точки на новую плоскость P 4 опустите перпендикуляр из A на плоскость P 4 … Основание A 4 этот перпендикуляр определяет желаемую фронтальную проекцию точки А .

Выясним, какая связь существует между проекциями A (A 1, A 2) и A (A 1 A 4) одинаковая точка в обеих системах.

Имеют общую горизонтальную проекцию и так как расстояние точки А от плоскости Р 1 не изменилось, то / АА 1 / = / А 2 А x / = / А 4 А x1 ¹ / , , то есть расстояние новой фронтальной проекции до новой оси равно расстоянию замененной проекции до предыдущей оси.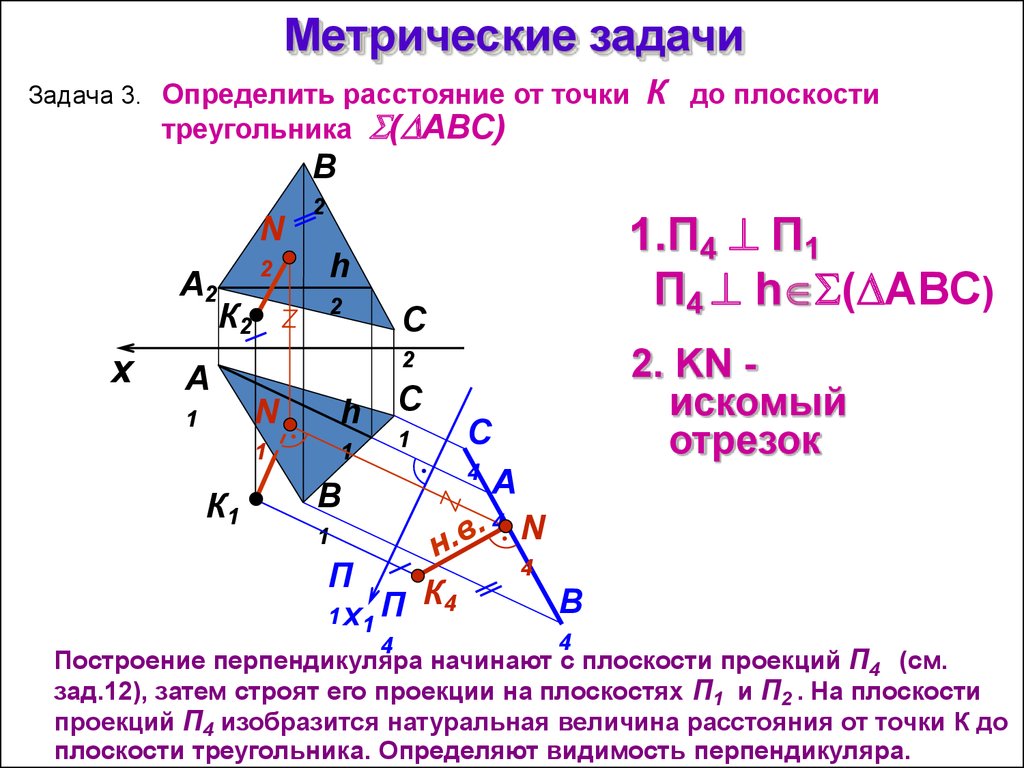

Чтобы перейти к сюжету, поверните самолет. P 4 вокруг оси X 1 и совместима с плоскостью P 1. Тогда новая фронтальная проекция A 4 совместится с плоскостью P 1 и при этом окажется на том же перпендикуляре к оси x 1 с выступом A 1 .

На рис. 9.6 показаны построения, которые необходимо сделать на схеме, чтобы от проекций (А 1, А 2) точек А перейти к проекциям в системе А 1 А 4) той же точки в системе, необходимо: нарисовать новую ось проекции X 1 , определяющая положение горизонтально проецирующей плоскости P 4 , затем от горизонтальной проекции точки A 1 X 1 … На построенный перпендикуляр откладываем (от новой оси) отрезок A x A 4 = A x A 2. Полученная таким образом точка A 4 является проекцией точки A на плоскость P 4 .

Замена горизонтальной плоскости P 1 новая плоскость P 4 и построение новых проекций точки А в системе осуществляется аналогично рассмотренному случаю, с той лишь разницей, что теперь фронтальная проекция точки остается неизменной, а найти новую горизонтальную проекцию А 4 точек А необходимо из фронтальной проекции точки А 2 опустить перпендикуляр на новую ось Х 1 и отложить на нее от точки пересечения с осью Х 1 сечение A 4 A x ¹, равно расстоянию старой горизонтальной проекции от старой оси A 1 A x (рис. 9.7).

Рассмотренные примеры позволяют установить следующее общее правило: чтобы построить проекцию точки в новой системе проекционных плоскостей, необходимо опустить перпендикуляр из неизменной проекции точки на новую ось проекции и установить расстояние от новой оси до новой проекции на нее, равное расстоянию от замененной проекции до предыдущей оси.

Целью методов преобразования чертежа является размещение геометрической фигуры в общем положении в определенном положении относительно плоскостей проекций с целью использования свойств ее проекций. Например, преобразование плоскости общего положения в плоскость уровня позволит определить ее реальный размер по соответствующей проекции.

Способы преобразования сложного рисунка делятся на две группы по признаку, определяющему положение фигуры и плоскостей проекции друг относительно друга или направление проекции:

1. Изменить положение плоскостей проекции или направление проекции так, чтобы фигура, зафиксированная в пространстве, находилась в определенном положении. В эту группу входят:

способ замены проекционных плоскостей;

метод дополнительной проекции.

2. Изменить положение геометрической фигуры в пространстве так, чтобы она находилась в определенном положении относительно неподвижной системы плоскостей проекций. В эту группу входят:

способ вращения.

Задачи, решаемые методами преобразования сложного чертежа, сводятся к следующим основным задачам, в которых необходимо преобразовать:

прямую (плоскую, цилиндрическую или призматическую поверхность) в проецирующую фигуру;

Давайте последовательно рассмотрим все методы трансформации, за исключением метода дополнительной проекции, с которым рекомендуется ознакомиться с туториалом самостоятельно.

Суть метода заключается в замене исходной системы взаимно перпендикулярных плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций с постоянным положением геометрической фигуры в пространстве.

Для решения конкретной задачи выполняется одно или два последовательных преобразования методом замены, например, Π 1  Π 2 → Π 1  Π 4 или Π 1  Π 2 → Π 1 Π 4 → Π 5  Π 4 … Во втором случае преобразование называется композицией преобразований. На каждом шаге этого метода заменяется только одна плоскость проекций, а другая остается общей для двух систем.

Рассмотрим механизм и особенности метода замены плоскостей проекций на примере преобразования сложного рисунка точки (рис. 28).

При замене, например, плоскости лобовой проекции Π 2 новая вертикальная плоскость Π 4 горизонтальная плоскость Π 1 в данном случае является общим для двух систем плоскостей проекций, в результате чего проекция А 1 точек А на этой плоскости также является общим для этих систем. При этом значение расстояния остается неизменным ( AA 1 ) из данной точки на эту плоскость проекций и, как следствие, равенство ее проекций на плоскость Π 2 и Π 4 , т.е. АА 1 = А 2 А 12 = А 4 А 14 , который позволяет создавать новую проекцию на сложном чертеже A 4 уставка (см. рис. 28).

Еще одной особенностью метода замены плоскостей проекций является то, что сложный чертеж формируется путем совмещения плоскостей проекций с общей для двух систем плоскостью. В случае, рассмотренном на рис. В примере такой плоскостью является горизонтальная плоскость проекции.

В качестве примера рассмотрим задачу о преобразовании прямой линии общего положения в проектирующую. Для достижения конечного результата необходимо заменить две проекционные плоскости с помощью композиции преобразований, то есть двух последовательных преобразований (рис. 29).

Замена одной проекционной плоскости, например, Π 2 на Π 4 позволяет преобразовать прямую общего положения только в прямую линию уровня, так как невозможно сразу поставить новую вертикальную плоскость проекции Π 4 перпендикулярно данной прямой. Далее, заменяя последовательно вторую проекционную плоскость Π 1 на Π 5 и расположив ее перпендикулярно прямой АВ , получим окончательный результат (см. рис. 29).

ОБЩИЕ ПОЛОЖЕНИЯ

МЕТОДЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

Лекция 4

Решение ряда задач начертательной геометрии значительно упрощается, когда геометрические фигуры занимают определенное положение относительно плоскостей проекций. Задачи на определение взаимного положения фигур и метрические задачи (определение натуральных значений плоскостей, отрезков и др.). Для этого существуют различные способы преобразования сложного рисунка. Каждый из них основан на одном из следующих принципов:

1. на изменение положения плоскостей проекций относительно неподвижных геометрических фигур;

2. об изменении положения заданных геометрических фигур относительно неподвижных плоскостей проекций;

Давайте посмотрим на некоторые из них.

Суть метода заключается в том, что заданные геометрические фигуры неподвижны в заданной системе проекционных плоскостей ( P 1 , P 2 ). Новые проекционные плоскости ( P 4 , F 5 ), относительно которых геометрические фигуры будут занимать то или иное положение. Новая плоскость проекции выбирается так, чтобы она была перпендикулярна несменной плоскости проекции.

Большинство задач решается с помощью одного-двух последовательных преобразований исходной системы проекционных плоскостей. Одновременно может быть заменена только одна плоскость проекции P 1 (или P 2 ), другая плоскость P 2 (или P 1 ) должна оставаться неизменной.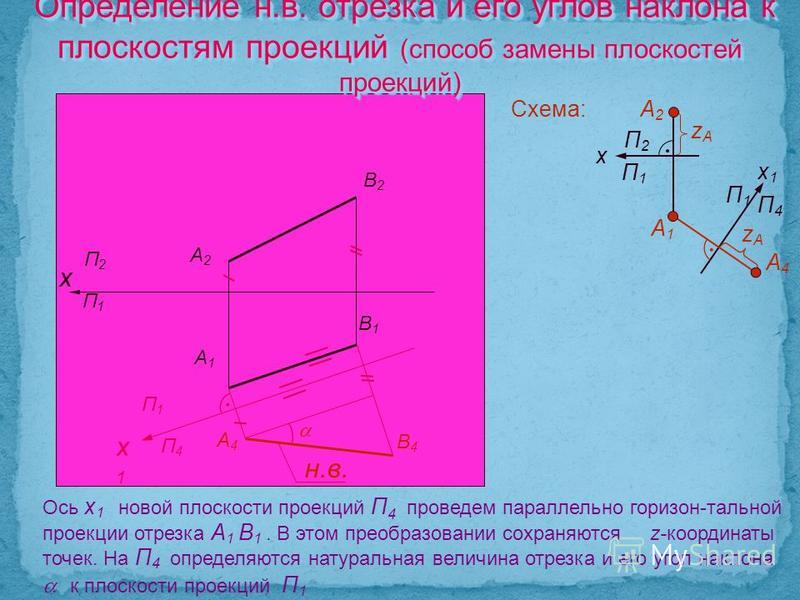
На рис. 1 показано визуальное представление метода замены проекционных плоскостей. Фронтальная плоскость P 2 заменяется на новую фронтальную плоскость P 4 … Новые точечные проекции A ( A 1 A 4 ), при этом, как видно из рисунка, высота точки A осталась прежней тем же.

Необходимо запомнить правило построения новых проекций точек методом замены:

1. линии связи всегда перпендикулярны новым осям проекций;
2. расстояние от оси новой проекции до новой проекции точки всегда берется от заменяемой плоскости.

Рис. 1. Наглядное представление метода замены плоскости проекции.

Рисунок 2: Изображение метода замены плоскостей проекций на графике.

Большинство задач начертательной геометрии решаются на основе четырех задач:

1. Преобразование прямой общего положения в прямую уровня;
2. Преобразование прямой линии общего положения в проекционную линию;
3. Преобразование общей плоскости в плоскость проекции;
4. Преобразование общей плоскости в плоскость уровня .

Проблема номер 1

Рассмотрим решение задание №1 … Дана прямая АВ — в общем положении, преобразуем ее в прямую линию уровня (рис. 3). Для этого введем новую плоскость фронтальной проекции P 4 , ось X 1.4 параллель A 1 B 1 AB – A 4 B 4. В новой системе плоскостей проекции прямая AB – фронтальная.

Рисунок 3.

Преобразование генеральной линии в горизонтальную (фронтальную)

Проблема номер 2

Дана прямая АВ — в общем положении преобразуем ее в проекционную (рис. 4). Для решения этой задачи необходимо выполнить два последовательных преобразования:

1. Прямую общего положения преобразовать в прямую уровня, то есть сначала решить задачу №1;
2. Преобразование линии уровня в линию проекции.

Нарисуйте условие задачи №1, решите ее самостоятельно, затем приступайте ко второму преобразованию.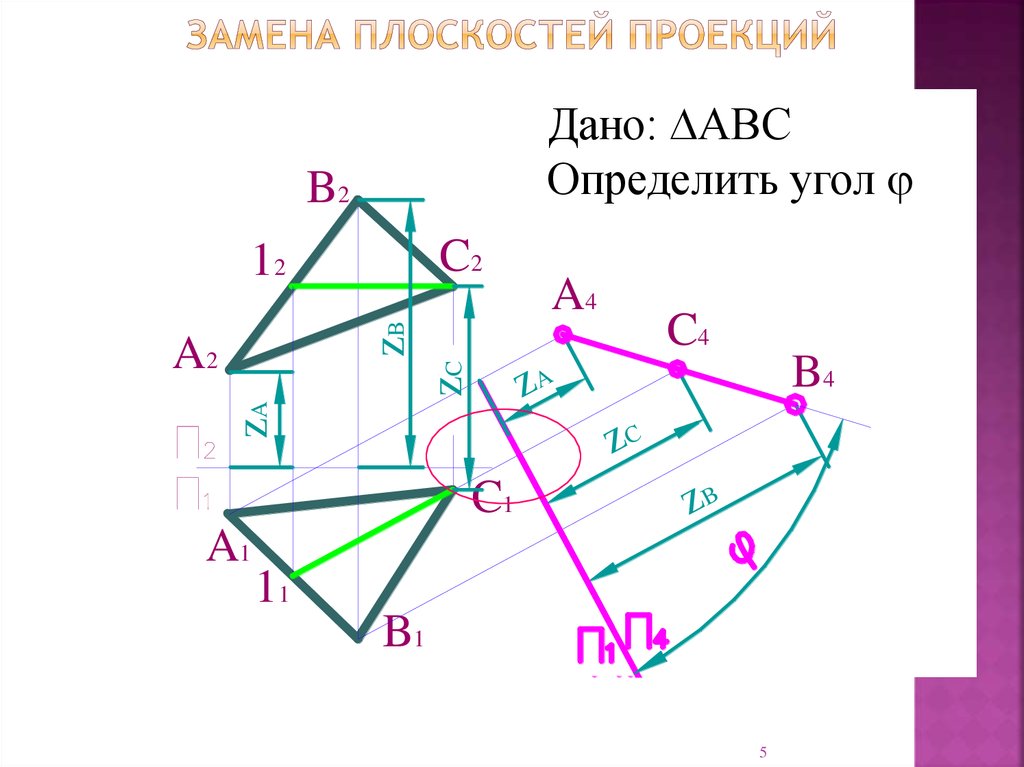 Ввести новую горизонтальную плоскость проекции F 5 X 4, 5 перпендикулярно проекции A 4 B 4 и построить новую проекцию линии A 5 B 5. В системе плоскостей P 4, P 5 прямая AB — горизонтально проецирующая линия.

На основании задач №1 и №2 решаются следующие задачи:

1. определение расстояния от точки до прямой;

2. определение расстояния между параллельными и пересекающимися линиями;

3. определение натурального размера прямой;

4. определение величины двугранного угла.

Рисунок 4.

Преобразование прямой линии общего положения в проекционную линию.

Задача №3.

Дана плоскость ABC — в общем положении преобразуем ее в плоскость проекций (рис. 5). Для решения этой задачи необходимо провести на плоскости линию уровня, если такой линии нет. Нарисуйте новую ось проекции перпендикулярно линии уровня. В треугольнике ABC проведите горизонтальную линию час. Проекция оси Х 14 рисуем перпендикулярно h 1, новую плоскую проекцию A 4 B 4 C 4 , строим по правилам рассмотренным в предыдущих заданиях.

В системе плоскостей проекций П 1, П 4, плоскость треугольника является плоскостью фронтальной проекции.

Рисунок 5.

Преобразование общей плоскости в плоскость проекции.

Задача №4.

Рисунок 6.

Преобразование общей плоскости в плоскость уровня.

Дана плоскость ABC — в общем положении, преобразуем ее в плоскость уровня (рис. 6). Для решения этой задачи необходимо выполнить два последовательных преобразования:

1. Преобразовать плоскость общего положения в плоскость проекции, т. е. сначала решить задачу №3;
2. Преобразование плоскости проекции в плоскость уровня.

Нарисуйте условие задачи №3, решите ее самостоятельно, затем приступайте ко второму преобразованию. Представляем новую горизонтальную проекционную плоскость F 5 , для этого проводим новую ось проекции X 4, 5 параллельную проекцию A 4 B 4 C 4 и строим новую проекцию треугольника A 5 B 5 C 5. В системе плоскости P 4, P 5 , треугольник ABC — горизонтальная плоскость уровня.

На основании задач №3 и №4 решаются следующие задачи:

1.определение расстояния от точки до плоскости;

2. определение расстояния между параллельными плоскостями;

3. определение натуральных (истинных) значений геометрических фигур;

определение углов наклона плоскости к плоскостям проекций

Метод плоскопараллельного перемещения

Все вышеперечисленные задачи можно решить с помощью метода плоскопараллельного движения, при котором плоскости проекций остаются на месте, а проекция фигуры перемещается (рис. 7).

Рис. 7. Определение фактического размера сегмента методом плоскопараллельного перемещения.

Дана прямая АВ — в общем положении преобразуем ее в прямую линию уровня (рис. 7). Для этого перемещаем проекцию A 1 B 1 параллельно оси NS . .. Строим новую проекцию линии AB – A 2`B 2`, которая будет — реальный размер сегмента. Этот метод используется для определения натуральных значений ребер многогранников при построении развертки.

Метод вращения

Частным случаем плоскопараллельного движения является способ вращения вокруг выступающих прямых и прямых линий уровня.

Методы иллюстрации — чертежи самолетов

Геометрия — раздел математики, изучающий линии, углы, фигуры и определенные предполагаемые свойства пространства. Прикладная геометрия, используемая в чертежах, использует эти свойства для точного и правильного графического представления объектов. В прошлом рисовальщики использовали различные инструменты с различными масштабами, формами и кривыми для создания своих рисунков. Сегодня компьютерные графические программы отображают рисунки практически в любом масштабе, форме и кривой, какие только можно вообразить, что избавляет от необходимости в дополнительных инструментах.

Для графического изображения объектов используется несколько методов. Наиболее распространенными являются орфографические проекции, графические рисунки, диаграммы и блок-схемы.

Чертежи в ортогональной проекции

Чтобы показать точные размеры и форму всех частей сложных объектов, необходимо несколько видов. Это система, используемая в орфографической проекции.

В орфографической проекции существует шесть возможных видов объекта, поскольку все объекты имеют шесть сторон — переднюю, верхнюю, нижнюю, заднюю, правую и левую стороны. На рис. 1А показан объект, помещенный в прозрачную коробку, шарнирно закрепленную по краям. Проекции по бокам коробки — это виды, которые видны прямо на объекте с каждой стороны. Если контуры объекта нарисованы на каждой поверхности коробки, а затем коробка открыта [Рисунок 1B] для плоской укладки [Рисунок 1C], результатом будет ортогональная проекция с шестью видами.

Рис. 1. Орфографическая проекция

Редко требуется показывать все шесть видов, чтобы четко изобразить объект; поэтому рисуются только те виды, которые необходимы для иллюстрации требуемых характеристик объекта. Наиболее распространены одно-, двух- и трехракурсные чертежи. Независимо от количества используемых видов, расположение в целом такое, как показано на рисунке 1, с видом спереди в качестве основного вида. Если показан вид справа, он будет справа от вида спереди. Если показан вид слева, он будет слева от вида спереди. Виды сверху и снизу, если они включены, будут показаны в соответствующих положениях относительно вида спереди.

Чертежи с одним видом обычно используются для объектов одинаковой толщины, таких как прокладки, прокладки и пластины. В примечании к размерам указана толщина, как показано на рисунке 2. Чертежи с одним видом также обычно используются для цилиндрических, сферических или квадратных деталей, если все необходимые размеры могут быть правильно показаны на одном виде. Когда пространство ограничено и необходимо показать два вида, симметричные объекты часто представляют половинными видами, как показано на рисунке 3.

Figure 2. One-view drawing

Figure 3. Symmetrical object with exterior half view

Aircraft drawings seldom show more than two principal or complete views объекта. Вместо этого обычно будет один полный вид и один или несколько подробных видов или видов в разрезе.

Детальный вид

Детальный вид показывает только часть объекта, но более подробно и в большем масштабе, чем основной вид. Деталь, подробно показанная в другом месте на чертеже, обычно обведена толстой линией на главном виде. [Рисунок 4] Основной вид показывает весь объект, а детальный вид представляет собой увеличенный рисунок части объекта.

Рис. 4. Детальный вид

Графические рисунки

Графический рисунок подобен фотографии. [Рисунок 5] Он показывает объект таким, каким он кажется глазу, но не подходит для отображения сложных форм и форм. Графические рисунки полезны для демонстрации общего вида объекта и широко используются с чертежами ортогональной проекции. Наглядные рисунки используются в руководствах по техническому обслуживанию самолетов (AMM), руководствах по ремонту конструкций (SRM) и иллюстрированных каталогах деталей (IPC). Авиаинженеры и техники часто используют три типа графических рисунков: перспективный, изометрический, наклонный и в разобранном виде.

Рис. 5. Графический рисунок

Чертежи в перспективе

Вид в перспективе показывает объект таким, каким он кажется наблюдателю. [Рисунок 6A] Это больше всего похоже на то, как объект будет выглядеть на фотографии. Из-за перспективы некоторые линии объекта не параллельны, и поэтому фактические углы и размеры не точны.

Рис. 6. (A) перспективный, (B) изометрический и (C) наклонный чертежи

изометрические чертежи

Изометрический вид использует комбинацию видов ортогональной проекции и наклоняет объект вперед так, что части всех трех видов можно увидеть в одном представлении. [Рисунок 6B] Это дает наблюдателю трехмерное изображение объекта. В отличие от чертежа в перспективе, где линии сходятся, а размеры неверны, линии в изометрическом чертеже параллельны и имеют размеры, как в ортогональной проекции.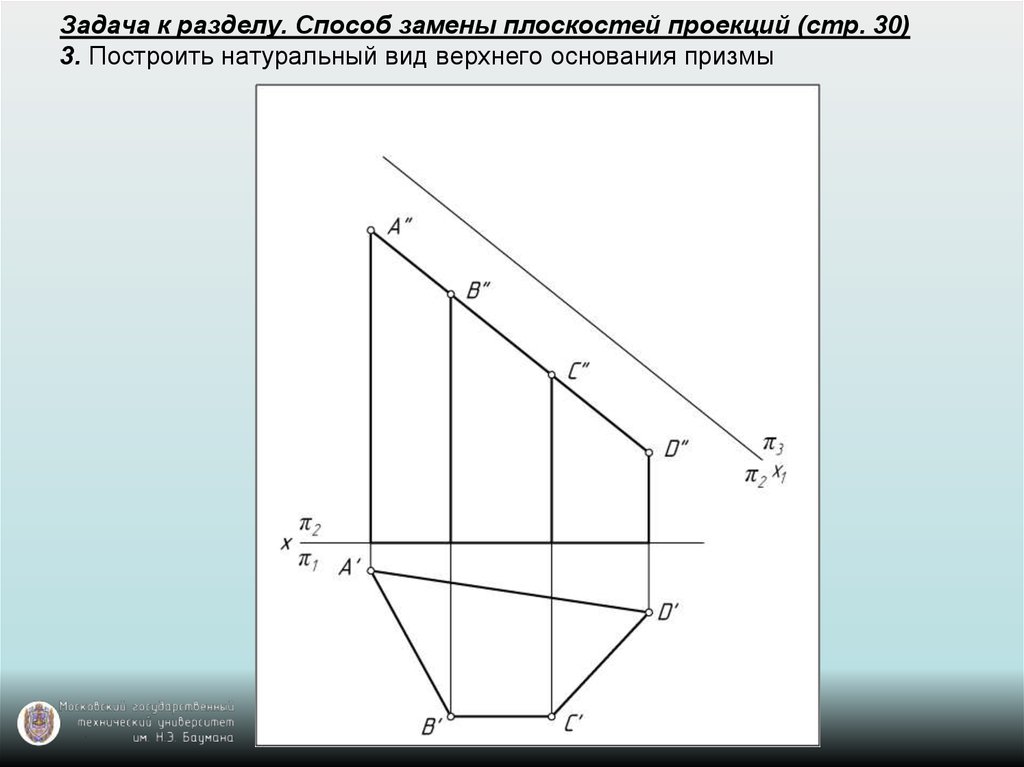

Наклонные чертежи

Наклонный вид похож на изометрический вид, за исключением одного существенного отличия. В наклонном чертеже две из трех осей чертежа всегда находятся под прямым углом друг к другу. [Рисунок 6C]

Чертежи в разобранном виде

Чертеж в разобранном виде — это наглядный чертеж двух или более деталей, которые соединяются вместе как сборка. . Вид показывает отдельные части и их положение относительно других частей до того, как они будут собраны. [Рисунок 7]

Рис. 7. Чертеж в разобранном виде

Чертежи в разобранном виде часто используются в IPC, которые используются для заказа деталей. Чертеж в разобранном виде имеет номера, и номера соответствуют списку номеров деталей. Покомпонентные изображения также используются в руководствах по техническому обслуживанию (MIM) для сборки и ремонта компонентов самолета. Эти чертежи часто сопровождаются примечаниями, поясняющими процесс сборки.

Диаграммы

Диаграмма может быть определена как графическое представление сборки или системы, показывающее различные части и выражающее методы или принципы работы. Есть много типов диаграмм; однако те, с которыми сталкивается авиамеханик во время выполнения своей работы, могут быть сгруппированы в четыре класса или типа: монтажные, принципиальные, блок-схемы и электрические схемы.

Схемы установки

На рис. 8 показан пример схемы установки. Это схема установки компонентов управления полетом самолета. Он идентифицирует каждый из компонентов в системах и показывает их расположение в самолете. Каждая цифра (1, 2, 3 и 4) на детали показывает расположение отдельных компонентов системы управления полетом в кабине экипажа самолета. Схемы установки широко используются в руководствах по техническому обслуживанию и ремонту самолетов и бесценны для идентификации и определения местоположения компонентов и понимания работы различных систем.

Рисунок 8. Пример схемы установки (компоненты системы управления полетом) фактического размера и формы компонентов, а скорее располагать компоненты относительно друг друга в системе. Схемы показывают принцип работы системы самолета и часто используются для устранения неполадок и в учебных целях. На рис. 9 схематично показана система кондиционирования воздуха самолета. Высокоскоростной воздух, отбираемый от двигателя, смешивается с холодным воздухом в смесительной камере и распределяется по коллектору в различные части самолета. Рис. 9. Принципиальная схема системы кондиционирования воздуха для B737 NG Обратите внимание, что каждая строка имеет код для удобства чтения и отслеживания потока. Каждый компонент идентифицируется по имени, и его положение в системе можно установить, отметив линии, которые ведут к устройству и выходят из него. Принципиальные схемы и схемы установки широко используются в руководствах по эксплуатации самолетов. Блок-схемы Блок-схемы используются для демонстрации упрощенной взаимосвязи более сложной системы компонентов. [Рисунок 10] Отдельные компоненты изображаются в виде прямоугольника (блока) с линиями, соединяющими его с другими компонентами (блоками), с которыми он взаимодействует во время работы. Рис. 10. Блок-схема [Рисунок 11] Эти диаграммы даже для относительно простых схем могут быть довольно сложными. Для техников, занимающихся ремонтом и установкой электрооборудования, необходимо доскональное знание электрических схем и электрических схем. Рисунок 11. Схема подключения Блок-схемы Блок-схемы используются для иллюстрации последовательности или потока событий. В авиационной отрасли наиболее часто используются два типа блок-схем: блок-схемы устранения неполадок и логические блок-схемы. Блок-схема поиска и устранения неисправностей Блок-схемы поиска и устранения неисправностей часто используются для обнаружения неисправных компонентов. Они часто состоят из серии вопросов «да» или «нет». Если ответ на вопрос положительный, следует один курс действий. Если ответ отрицательный, следует другой курс действий. Таким простым способом может быть достигнуто логическое решение проблемы. На рис. 12 показана блок-схема для определения вариантов ремонта композитной конструкции. 9Рисунок 12. Блок-схема поиска и устранения неисправностей [Рисунок 13] В логической блок-схеме используются стандартные символы для обозначения определенных типов логических вентилей и их отношения к другим цифровым устройствам в системе. Поскольку цифровые системы используют двоичную математику, состоящую из 1 и 0, напряжения или отсутствия напряжения, светового импульса или отсутствия светового импульса и т. д., логические блок-схемы состоят из отдельных компонентов, которые принимают вход и обеспечивают выход, который является тем же как ввод или наоборот. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт