Кривые и поверхности на экране компьютера
Кривые и поверхности на экране компьютера
ОглавлениеПредисловиеПочему сплайны? Часть I. Сплайн-функции Глава 1. Сплайн-функции одной переменной 1.1. Интерполяционные кубические сплайны 1.1.2. Определение интерполяционного кубического сплайна 1.1.3. Граничные (краевые) условия 1.1.4. Построение интерполяционного кубического сплайна 1.1.5. Советы пользователю 1.1.6. Выбор интерполяционной функции (плюсы и минусы) 1.1.7. Свойства интерполяционного кубического сплайна 1.1.8. Программная реализация 1.2. Сглаживающие кубические сплайны 1.2.2. Определение сглаживающего кубического сплайна 1.2.3. Граничные (краевые) условия 1.2.4. Построение сглаживающего кубического сплайна 1.2.5. Выбор весовых коэффициентов 1.2.6. Построение сглаживающих сплайновых кривых при помощи сплайн-функций 1.2.7. Программная реализация 1.3. Другие сплайны 1.3.1. Линейное пространство кубических сплайн-функций 1.  3.2. Кубические В-сплайныГлава 2. Сплайн-функции двух переменных 2.1. Интерполяционные бикубические сплайны 2.1.2. Определение интерполяционного бикубического сплайна 2.1.3. Граничные (краевые) условия 2.1.4. Построение интерполяционного бикубического сплайна 2.1.5. Свойства интерполяционного бикубического сплайна 2.1.6. Построение сплайновых поверхностей при помощи сплайн-функций 2.1.7. Программная реализация 2.2. Сглаживающие бикубические сплайны 2.2.2. Определение сглаживающего бикубического сплайна 2.2.3. Граничные (краевые) условия 2.2.4. Построение сглаживающего бикубического сплайна 2.2.5. Построение сплайновых поверхностей при помощи сплайн-функций 2.2.6. Программная реализация Часть II. Геометрические сплайны Глава 3. Сплайновые кривые 3.1. Элементарные сведения из дифференциальной геометрии кривых 3.1.5. Кривизна и кручение кривой 3.1.6. Плоские кривые 3.1.7. Составные кривые 3.  1.8. Геометрическая непрерывность3.2. Кривые Безье 3.2.2. Свойства кривых Безье 3.2.3. Составные кривые Безье 3.2.4. Рациональные кривые Безье 3.2.5. Программная реализация алгоритма 3.3. В-сплайновые кривые 3.3.2. Составные кубические B-сплайновые кривые 3.3.3. Кратные и воображаемые вершины 3.3.4. Рациональные кубические В-сплайновые кривые 3.3.5. Форма Безье составных кубических B-сплайновых кривых 3.3.6. Программная реализация алгоритма 3.4. Бета-сплайновые кривые 3.4.2. Составные Бета-сплайновые кривые 3.4.3. Кратные и воображаемые вершины 3.4.4. Программная реализация алгоритма 3.5. Другие сплайновые кривые 3.5.1. Интерполяционные кубические кривые Эрмита 3.5.2. Сплайновые кривые Catmull-Rom 3.5.3. Составные плоские кубические кривые, заданные в неявной форме Глава 4. Сплайновые поверхности 4.1. Элементарные сведения из геометрии поверхностей 4.1.2. Гладкие и регулярные поверхности 4.1.3. Первая квадратичная форма поверхности 4.  1.4. Кривая на поверхности4.1.5. Угол между кривыми на поверхности 4.1.6. Площадь поверхности 4.1.7. Вторая квадратичная форма поверхности 4.1.8. Линии кривизны 4.1.9. Гауссова и средняя кривизны 4.1.10. Геометрическая непрерывность 4.1.11. Вектор скручивания и билинейная поверхность 4.2. Поверхности Безье 4.2.1. Параметрические уравнения поверхности Безье 4.2.2. Свойства элементарных поверхностей Безье 4.2.3. Составные поверхности Безье 4.2.4. Рациональные поверхности Безье 4.2.5. Программная реализация 4.3. В-сплайновые поверхности 4.3.1. Параметрические уравнения элементарной бикубической В-сплайновой поверхности 4.3.3. Составные бикубические В-сплайновые поверхности 4.3.4. Кратные и воображаемые вершины 4.3.5. Рациональные бикубические B-сплайновые поверхности 4.3.6. Программная реализация 4.4. Бета-сплайновые поверхности 4.4.2.  Свойства элементарных Бета-сплайновых поверхностей4.4.3. Составные Бета-сплайновые поверхности 4.4.4. Кратные и воображаемые вершины 4.4.5. Программная реализация 4.5. Другие сплайновые поверхности 4.5.1. Интерполяционные бикубические поверхности Эрмита 4.5.2. Программная реализация 4.5.3. Составные неявно заданные кубические поверхности |
Кривые и поверхности на экране компьютера
Кривые и поверхности на экране компьютера
ОглавлениеПредисловиеПочему сплайны? Часть I. Сплайн-функции Глава 1. Сплайн-функции одной переменной 1.1. Интерполяционные кубические сплайны 1.1.2. Определение интерполяционного кубического сплайна 1.1.3. Граничные (краевые) условия 1.1.4. Построение интерполяционного кубического сплайна 1.1.5. Советы пользователю 1.1.6. Выбор интерполяционной функции (плюсы и минусы) 1.1.7. Свойства интерполяционного кубического сплайна 1.1.8. Программная реализация 1.  2. Сглаживающие кубические сплайны1.2.2. Определение сглаживающего кубического сплайна 1.2.3. Граничные (краевые) условия 1.2.4. Построение сглаживающего кубического сплайна 1.2.5. Выбор весовых коэффициентов 1.2.6. Построение сглаживающих сплайновых кривых при помощи сплайн-функций 1.2.7. Программная реализация 1.3. Другие сплайны 1.3.1. Линейное пространство кубических сплайн-функций 1.3.2. Кубические В-сплайны Глава 2. Сплайн-функции двух переменных 2.1. Интерполяционные бикубические сплайны 2.1.2. Определение интерполяционного бикубического сплайна 2.1.3. Граничные (краевые) условия 2.1.4. Построение интерполяционного бикубического сплайна 2.1.5. Свойства интерполяционного бикубического сплайна 2.1.6. Построение сплайновых поверхностей при помощи сплайн-функций 2.1.7. Программная реализация 2.2. Сглаживающие бикубические сплайны 2.2.2. Определение сглаживающего бикубического сплайна 2.2.3. Граничные (краевые) условия 2.  2.4. Построение сглаживающего бикубического сплайна2.2.5. Построение сплайновых поверхностей при помощи сплайн-функций 2.2.6. Программная реализация Часть II. Геометрические сплайны 3.1. Элементарные сведения из дифференциальной геометрии кривых 3.1.4. Трехгранник Френе 3.1.5. Кривизна и кручение кривой 3.1.6. Плоские кривые 3.1.7. Составные кривые 3.1.8. Геометрическая непрерывность 3.2. Кривые Безье 3.2.2. Свойства кривых Безье 3.2.3. Составные кривые Безье 3.2.4. Рациональные кривые Безье 3.2.5. Программная реализация алгоритма 3.3. В-сплайновые кривые 3.3.2. Составные кубические B-сплайновые кривые 3.3.3. Кратные и воображаемые вершины 3.3.4. Рациональные кубические В-сплайновые кривые 3.3.5. Форма Безье составных кубических B-сплайновых кривых 3.3.6. Программная реализация алгоритма 3.4. Бета-сплайновые кривые 3.4.2. Составные Бета-сплайновые кривые 3.4.3. Кратные и воображаемые вершины 3.  4.4. Программная реализация алгоритма3.5. Другие сплайновые кривые 3.5.1. Интерполяционные кубические кривые Эрмита 3.5.2. Сплайновые кривые Catmull-Rom 3.5.3. Составные плоские кубические кривые, заданные в неявной форме Глава 4. Сплайновые поверхности 4.1. Элементарные сведения из геометрии поверхностей 4.1.2. Гладкие и регулярные поверхности 4.1.3. Первая квадратичная форма поверхности 4.1.4. Кривая на поверхности 4.1.5. Угол между кривыми на поверхности 4.1.6. Площадь поверхности 4.1.7. Вторая квадратичная форма поверхности 4.1.8. Линии кривизны 4.1.9. Гауссова и средняя кривизны 4.1.10. Геометрическая непрерывность 4.1.11. Вектор скручивания и билинейная поверхность 4.2. Поверхности Безье 4.2.1. Параметрические уравнения поверхности Безье 4.2.2. Свойства элементарных поверхностей Безье 4.2.3. Составные поверхности Безье 4.2.4. Рациональные поверхности Безье 4.2.5. Программная реализация 4.3.  4.3.1. Параметрические уравнения элементарной бикубической В-сплайновой поверхности 4.3.2. Свойства элементарных бикубических B-сплайновых поверхностей 4.3.3. Составные бикубические В-сплайновые поверхности 4.3.4. Кратные и воображаемые вершины 4.3.5. Рациональные бикубические B-сплайновые поверхности 4.3.6. Программная реализация 4.4. Бета-сплайновые поверхности 4.4.2. Свойства элементарных Бета-сплайновых поверхностей 4.4.3. Составные Бета-сплайновые поверхности 4.4.4. Кратные и воображаемые вершины 4.4.5. Программная реализация 4.5. Другие сплайновые поверхности 4.5.1. Интерполяционные бикубические поверхности Эрмита 4.5.2. Программная реализация 4.5.3. Составные неявно заданные кубические поверхности |
Разница между сплайном, B-сплайном и кривыми Безье
Улучшить статью
Сохранить статью
- Последнее обновление: 16 июн, 2020
Улучшить статью
Сохранить статью
1.
Сплайн:
Кривая сплайна — это математическое представление, для которого легко построить интерфейс, который позволит пользователю проектировать и контролировать форму сложных кривых и поверхностей.
2. B-сплайн :
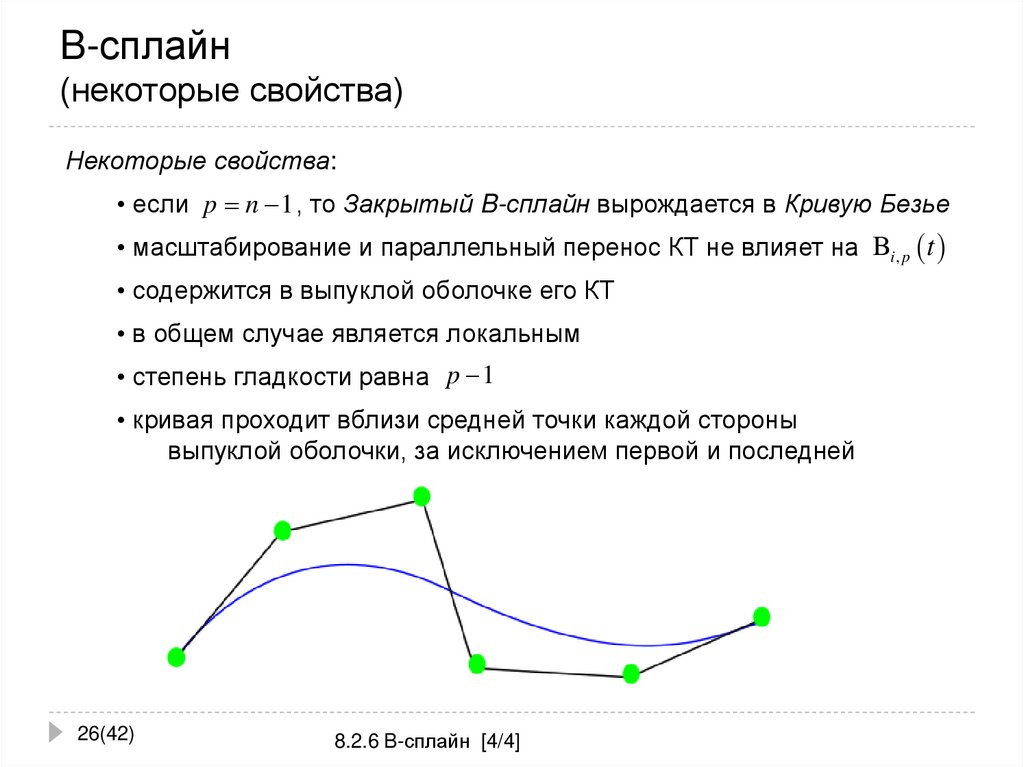
B-сплайн — это базовая функция, содержащая набор контрольных точек. Кривые B-сплайна задаются базисной функцией Бернштейна, которая имеет ограниченную гибкость.
3. Безье:
Эти кривые задаются граничными условиями, матрицей характеристик или функцией смешивания. Участок кривой Безье может быть заполнен любым количеством контрольных точек. Количество аппроксимируемых контрольных точек и их взаимное расположение определяют степень многочлена Безье.
Разница между спланией, B-спланией и бэзиером:
| Spline | B-Spline | Bezier |
|---|---|---|
| . называются контрольными точками, которые указывают общую форму кривой. | Кривые B-сплайна задаются базисной функцией Бернштейна, которая имеет ограниченную гибкость. | Кривые Безье могут быть заданы с граничными условиями, с матрицей характеристик или с функцией смешивания. |
| Он повторяет общую форму кривой. | Эти кривые являются результатом использования открытой универсальной базисной функции. | Кривая обычно повторяет форму определяющего многоугольника. |
| Типичное применение сплайна в САПР включает проектирование корпусов автомобилей, поверхностей самолетов и космических кораблей, а также корпусов кораблей. | Эти кривые можно использовать для построения кривых смешения. | Их можно найти в пакетах рисования и черчения, а также в приложениях САПР. |
| Обладает высокой степенью гладкости в местах соединения полиномиальных частей. | B-сплайн допускает порядок базисной функции и, следовательно, степень результирующей кривой не зависит от количества вершин. | Степень полинома, определяющего сегмент кривой, на единицу меньше, чем номер определяющей точки многоугольника. |
| Кривая сплайна представляет собой математическое представление, для которого легко построить интерфейс, который позволит пользователю проектировать и контролировать форму комплекса кривые и поверхности. | В B-Spline существует локальное управление поверхностью кривой, и каждая вершина влияет на форму кривой. | Параметрическая кривая, используемая в смежных областях. |
Статьи по теме
Что нового
Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта. Используя наш сайт, вы подтверждаете, что вы прочитали и поняли наши Политика использования файлов cookie & Политика конфиденциальности
Кривая Безье. Поймите математику Безье… | by Omar Aflak
Понимание математики кривых Безье
Кривые Безье часто используются в компьютерной графике, часто для создания плавных кривых, и тем не менее они являются очень простым инструментом.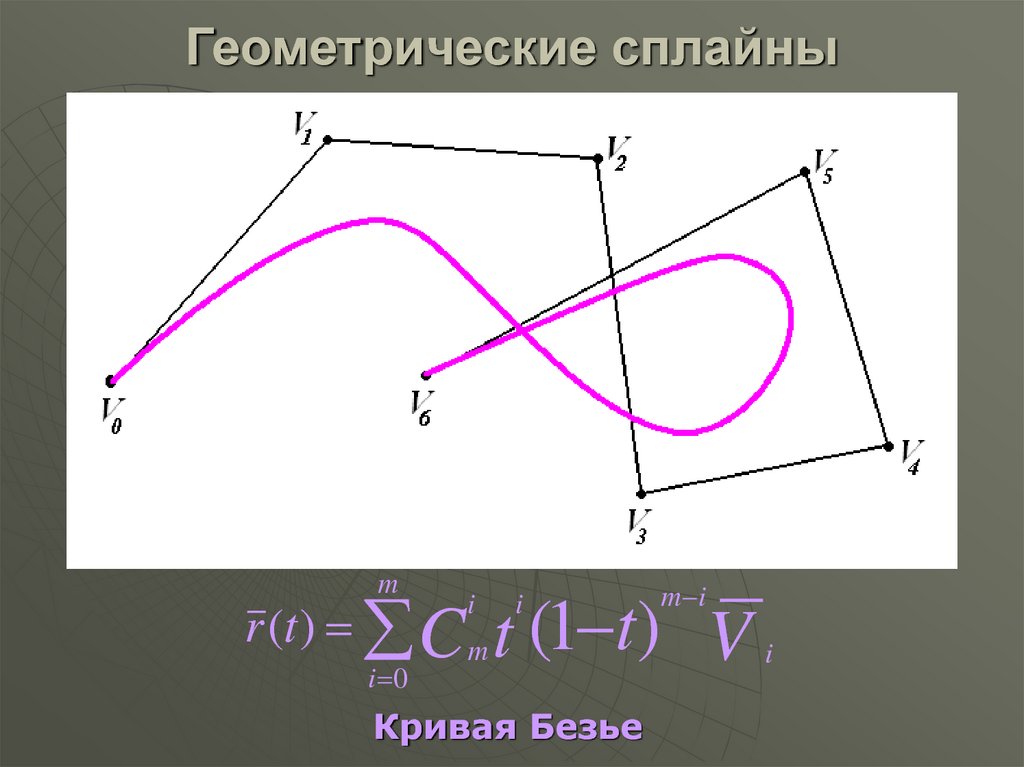
Если вы когда-либо использовали Photoshop, вы, возможно, наткнулись на этот инструмент под названием «Якорь», где вы можете ставить опорные точки и рисовать с их помощью некоторые кривые… Да, это кривые Безье. Или, если вы использовали векторную графику, SVG, они тоже используют кривые Безье. Посмотрим, как это работает.
Учитывается N+1 точки (P0,…, PN) называется Контрольные точки , . Бёзье DELID DEFINDE DEFINDINDINDE:
. 1Где B(t) — полином Бернштейна, а:
экв. 2Вы заметите, что этот многочлен Бернштейна очень похож на член k(th) в биномиальной формуле Ньютона, который равен:
экв. 3 На самом деле многочлен Бернштейна есть не что иное, как 9n = 1. Вот почему, если вы суммируете все Bi до n , вы получите 1 .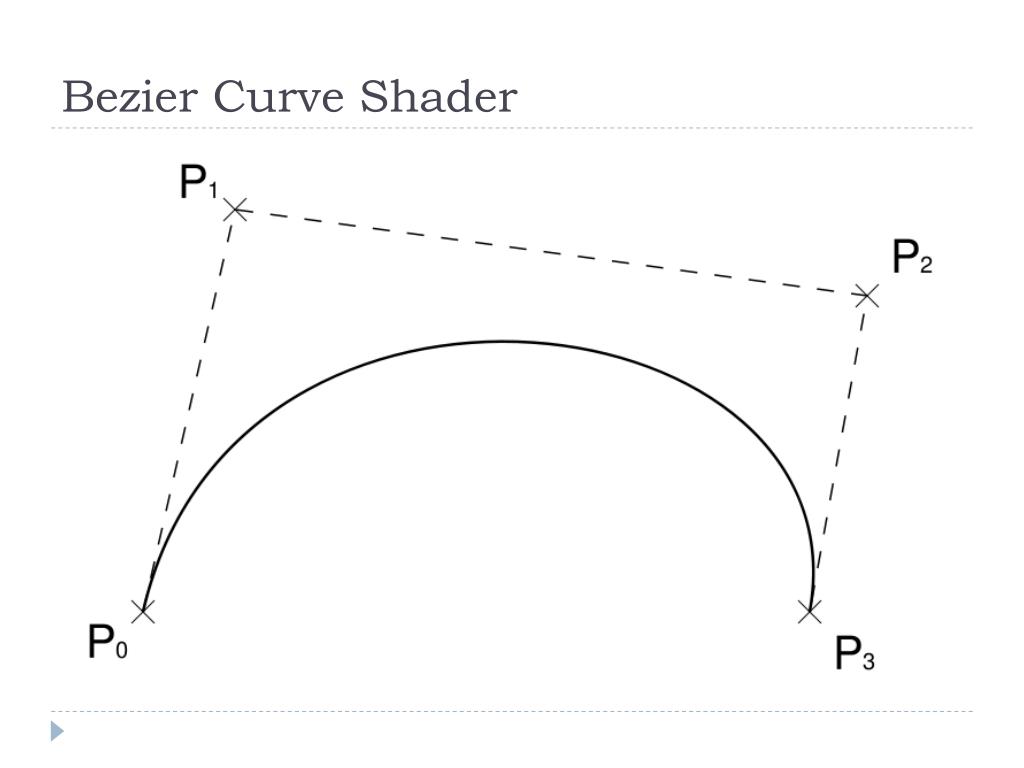
В любом случае.
Квадратичная кривая Безье — это то, как мы называем кривую Безье с 3 контрольными точками, поскольку степень P(t) будет равна 2. Давайте рассчитаем кривую Безье с учетом 3 контрольных точек и исследуем некоторые свойства, которые мы можем найти! Помните, экв. 1 соответствует n+1 точек, поэтому в нашем случае n=2.
Имейте в виду, что P(t) возвращает не число, а точку на кривой. Теперь нам осталось выбрать три контрольные точки и оценить кривую в диапазоне [0, 1] . Мы можем сделать это в Python довольно легко.
Вы можете заметить, что кривая начинается и заканчивается в первой и последней контрольных точках. Этот результат будет верным для любого количества точек. Поскольку t варьируется от 0 до 1 , мы можем доказать это, оценив P(t) при t=0 и t=1 .
Используя экв. 1 :
Поскольку кривая идет от P0 до P2 , в этом случае P1 полностью определяет форму кривой . Перемещаясь P1 вокруг вы можете заметить кое-что:
Кривая Безье всегда содержится в многоугольнике, образованном контрольными точками. Этот многоугольник поэтому называется контрольный многоугольник , или многоугольник Безье. Это свойство также сохраняется для любого количества контрольных точек, что делает управление ими интуитивно понятным при использовании программного обеспечения.
На самом деле мы можем представить формулу Безье, используя умножение матриц, что может быть полезно в других случаях, например, для разделения кривой Безье. Если мы вернемся к нашему примеру, мы можем переписать P(t) следующим образом:
экв. 6 Итак, вся информация о квадратичной кривой Безье сжата в одну матрицу, М .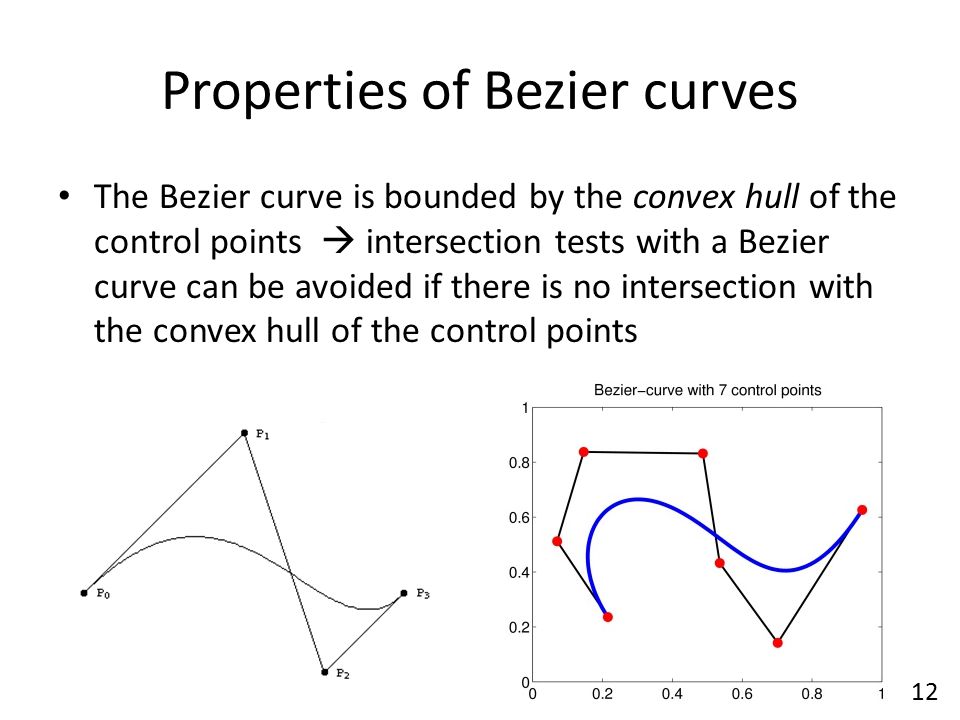
Теперь мы можем захотеть найти коэффициенты этой матрицы, не выполняя все эти шаги и легко программируемым способом. Поскольку коэффициенты матрицы — это просто коэффициенты полинома перед каждым Pi , то, что мы ищем, — это расширенная форма полинома Бернштейна ур. 2 .
Еще одно: если мы разложим Bi(t) на , мы получим многочлен перед Pi , что соответствует i(му) столбцу в матрице. Однако это не очень удобно, и было бы проще программировать, если бы вместо этого мы могли получать строки. Тем не менее, вы можете заметить, что i (я) строка матрицы точно такая же, как перевернутый (n-i) (th) столбец , и коэффициенты перевернутого (n-i) (th) столбца есть не что иное, как коэффициенты B(n-i)(t) , взятые в убывающей степени t .
экв. 7 Вы можете обратиться к экв.