Спираль нарисовать: Как нарисовать спираль (56 фото) » Рисунки для срисовки и не только

Спирали и паттерны | Школа-комьюнити «Юниверс»

Казалось бы — что может быть проще, чем простая спиралька? Но выясняется, что в Illustrator заложена возможность рисовать лишь расходящиеся, логарифмические спирали, а вот ту, что называется «Архимедова» — с равным шагом, нарисовать куда сложнее. Вообще-то, мы хотели сделать урок про паттерны, но на фоне сложностей со спиралью урок получился совсем про другое. Впрочем, паттерн у нас все равно получится!

Шаг 1.

Паттерн будет состоять из множества спиралей. Начнем с создания одной из них. Возьмите инструмент Line Segment Tool и нарисуйте несколько горизонтальных параллельных друг другу линий. Количество линий – это количество витков будущей спирали.

Обратите внимание на расстояние между ними – оно должно быть везде одинаковым. В примере мы задали шаг в 10 мм. Получить строго горизонтальную линию можно, если при перемещении курсора удерживать клавишу Shift. Включите направляющие, которые покажут, на какое расстояние вы сдвигаете каждую линию (меню View > Smart Guides). Чтобы ускорить процесс создания линий, просто нарисуйте первую, а затем, с зажатой клавишей Alt, потяните ее вниз, сделав таким образом ее копию. После этого несколько раз нажмите сочетание клавиш  Cmd + D. Программа автоматически скопирует линию с заданным шагом. 

 

Александр Сераков: Обратите внимание: количество этих линий — это количество витков спирали.

Шаг 2.

Выделите все линии с правой стороны инструментом Direct Selection Tool (белая стрелка)…

 

…и нажмите Enter – это откроет диалоговое окно Move, где вам нужно задать значение для Distance, равное расстоянию между линиями, то есть 10 мм.

Шаг 3. 

Откройте палитру Brushes через меню Window > Brushes. Выделите все линии инструментом Selection Tool и перетащите в палитру.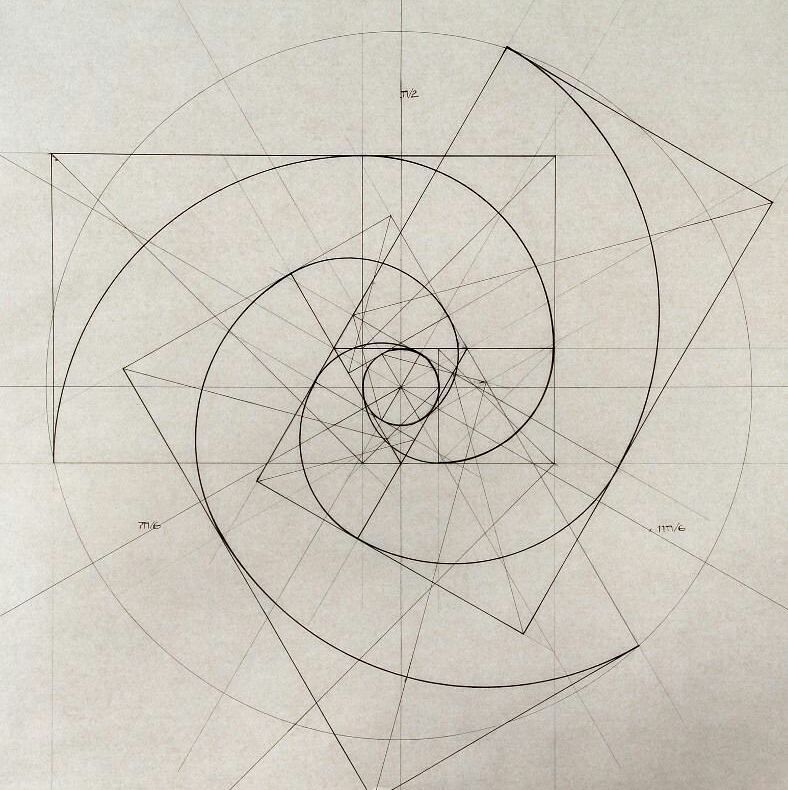   Сразу после этого откроется диалоговое окно New Brush, где вам нужно выбрать тип кисти Art Brush.

В настройках художественной кисти (Art Bush Options) в разделе Brush Scale Options выберите Stretch to Fit Stoke Lenght, чтобы растянуть линии по всей длине заданного контура, к которому она применена, а в разделе Direction можно указать, как будут располагаться линии вдоль этого же контура.

 

Шаг 4.

Линии, которые вы нарисовали в первом шаге, больше не понадобятся, поэтому удалите их. Перейдем к созданию спирали. Нарисуйте круг инструментом Ellipse Tool, а в палитре Brushes выберите только что созданную кисть.

Шаг 5.

Для дальнейшей работы со спиралью примените комнату Expand Appearance, чтобы превратить кисть в обычный контур.

Поскольку наша спираль состоит из отдельных пяти линий, если вы попробуете сделать спираль толще, то увидите разрывы в нескольких местах. 

Чтобы убрать их, вам нужно соединить линии. Выделите спираль > перейдите в меню Path > Join.

Шаг 6.

Продолжим редактировать спираль. В результате применения команды Expand Appearance на ней появились лишние точки. Контур с небольшим количеством точек удобнее редактировать, а также выводить на экран или печать.  Чтобы упростить его, перейдите в меню Object > Path > Simplify.

Для начала в появившемся окне установите ползунок Curve Precision на 100%, а Angle Threshold оставьте на 0%. После этого начните немного сдвигать ползунок Curve Precision до приемлемого результата, чтобы сделать упрощенный контур максимально похожим на оригинальный, но с уменьшенным количеством опорных точек. Постарайтесь не исказить форму спирали.

А.С.: Конечно, эту спираль можно применять теперь как угодно, но мы все же хотели рассказать про паттерн! И вторую часть урока вы можете рассматривать как отдельную тему «Как быстро и легко сделать паттерн».

Шаг 7.

Теперь вы можете изменить размер спирали, настроить  ее толщину, задав значение для Stroke, а также выбрать подходящий цвет в палитре Swatches.

При помощи круга другого цвета, сделайте фон под спиралью.

Шаг 8.

Приступим к созданию паттерна. Точно также как мы переносили линии в палитру Brushes, перенесите только что созданный элемент паттерна в палитру Swatches, предварительно выделив его черной стрелкой.

Оставшаяся на артборде спираль больше не нужна, удалите ее.

А.С.: При желании вы сможете получить ее обратно, вытащив на артборд из палитры Swatches.

Шаг 9.

Дважды щелкните по паттерну, который вы только что поместили в палитру Swatches. Все, что попадает в выделенный участок, становится частью повторяющейся области паттерна.

Далее действуйте по своему усмотрению. При создании паттерна я использовала следующие опции: подбирала гармоничные сочетания цветов через палитру Golor Guide; копировала спирали, перетаскивая их в пределах выделенной области с зажатой клавишей Alt; использовала сочетание клавиш Cmd + Shift + [ ] , чтобы разместить спирали друг под другом.

Шаг 10.

Подтвердите создание паттерна, нажав Done сверху на серой полосе окна. Этим действием вы одновременно  вышли из режима создания паттерна и сохранили новый паттерн в панели Swatches.

С этого момента вы можете применять паттерн объектам. Например, создайте прямоугольник инструментом Rectangle Tool, а в панели Swatches выберите для заливки новый паттерн. 

Кстати…

У вас всегда есть возможность изменить размер примененного к объекту паттерна. Перейдите в меню Window > Transform. Через меню палитры Transform выберите команду Transform Pattern Only. После этого измените значения для ширины, высоты или угла наклона, используя числовые значения в окне Transform.

А.С.: О, да! Как настроить примененный паттерн — этот вопрос регулярно мне задают на мастер-классах. Конечно, тут бы Illustrator имел бы все шансы выиграть в конкурсе «как запрятать поглубже нужную вещь»! Но теперь нас этим не напугать.

Рисование спирали Python turtle — Stack Overflow на русском

Вопрос задан 3 года 7 месяцев назад

Изменён 1 месяц назад

Просмотрен 14k раз

Задано: нарисовать Архимедову спираль в Python с помощью turtle. Нарисовал круг:

import turtle
turtle.shape('turtle')
i = 1
while i <= 360:
    turtle.left(1)
    turtle.forward(1)
    i += 1

Дальше приходит в голову только вручную менять значения угла поворота черепахи через определенные пройденные ей расстояния (четверти координат). А как можно написать правильный алгоритм для именно для спирали?

• python
• python-3.x
• алгоритм
• turtle

2

Найдено на просторах интернета

from turtle import Turtle, Screen
from math import pi, sin, cos
from random import randint, random
RADIUS = 180  # roughly the radius of a completed spiral
screen = Screen()
WIDTH, HEIGHT = screen. window_width(), screen.window_height()
turtle = Turtle(visible=False)
turtle.speed('fastest')  # because I have no patience
turtle.up()
for _ in range(3):
    x = randint(RADIUS - WIDTH//2, WIDTH//2 - RADIUS)
    y = randint(RADIUS - HEIGHT//2, HEIGHT//2 - RADIUS)
    turtle.goto(x, y)
    turtle.color(random(), random(), random())
    turtle.down()
    for i in range(200):
        t = i / 20 * pi
        dx = (1 + 5 * t) * cos(t)
        dy = (1 + 5 * t) * sin(t)
        turtle.goto(x + dx, y + dy)
    turtle.up()
screen.exitonclick()

Нужно было подключить модуль math, а дальше уже математика.

from math import pi, sin, cos
import turtle
turtle.shape('turtle')
for i in range(200):
    t = i / 10 * pi
    dx = t * cos(t)
    dy = t * sin(t)
    turtle.goto(dx, dy)

import turtle
for i in range(1000):
    turtle.forward(i * 0.001)
    turtle.left(1)

рисует спираль, не очень понимаю зачем усложнять.

2

import turtle as t
    
t. shape('turtle')  
circles = 10  
sectors = 20  
space_btw_cls = 10  
turn = 360 / sectors  
angle = 0  
    
for i in range(circles*sectors):  
    angle += turn  
    radius = space_btw_cls / 360 * angle  
    t.circle(radius, turn)

1

import turtle
turtle.shape('turtle')
x = 0.5
for i in range(20):
    for j in range(30):
        turtle.forward(x)
        turtle.left(6)
    x += 0.5

1

import turtle
turtle.title("rainbow!")
turtle.speed(0.5)
turtle.bgcolor("black")
r,g,b = 255,0,0
for i in range(255*2):
    turtle.colormode(255)
    if i < 255//3:
        g += 3
    elif i <255*2//3:
        r -= 3
    elif i < 255:
        b += 3
    elif i < 255*4//3:
        g -= 3
    elif i < 255*5//3:
        r += 3
    else:
        b -= 3
    turtle.fd(50+i)
    turtle.rt(91)
    turtle. pencolor(r,g,b)

1

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Что такое Золотая спираль? Чтобы узнать, давайте нарисуем один.

Пол Мироча

Это обсуждение представляет собой отрывок из семинара, организованного The Desert Lab 30 января 2021 года: «Фибоначчи и агавы», часть серии Seeing Math in Nature .

---

Как странная последовательность чисел, случайно открытая Фибоначчи около 1200 года, является ключом к золотой пропорции, золотому прямоугольнику, золотой спирали — и жизни, вселенной и всему остальному.

---

Эти геометрические спирали встречаются в природе. Как только вы нарисуете один, вы будете видеть их повсюду.

Что такое Фибоначчи на самом деле?

Леонардо Пизанский, которого звали Фибоначчи, был средневековым математиком  (1170 – ок.  1240). Он не проектировал падающую башню, но, скорее всего, вы слышали, как кто-то произносил имя Фибоначчи, возможно, в художественной галерее или на коктейльной вечеринке. Вы, наверное, слышали, что это часть сакральной геометрии, лежащей в основе Жизни, Вселенной и Всего Всего. Но произвело ли на вас впечатление само знание этого? И я нет.

Фраза, которую я люблю использовать в начале урока рисования или мастер-класса: «Вы не поймете что-то по-настоящему, пока не попытаетесь это нарисовать». Давайте сделаем это.

Эта числовая последовательность действительно образует закономерности и геометрию, встречающиеся повсюду в природе. Почему Вселенной так нравятся эти числа? Может быть, это потому, что природа всегда меняется и растет, и это геометрия роста и формы.

Но сначала займемся цифрами.

Числа Фибоначчи

Знаменитая числовая последовательность Фибоначчи была проста: чтобы получить следующее число в последовательности, нужно сложить два предыдущих числа. Это был его ответ на популярную загадку чисел: предположим, что пара кроликов, самец и самка, способны спариваться, и каждый месяц их потомство производит пару кроликов мужского и женского пола. Сколько кроликов будет через год?

Ответ: 144, число Фибоначчи. Как мы увидим, эту последовательность и геометрию, которую она образует, можно найти повсюду в мире природы.

Странный факт: Количество лепестков на цветке обычно равно числу Фибоначчи. Что с этим?
Об этом мы поговорим в другом посте.

Затем есть еще один номер

, называемый Phi

Вот где это становится странным. Что математики обнаружили в последовательности Фибоначчи, так это то, что отношения последовательных чисел в последовательности Фибоначчи, то есть деление одного числа в последовательности на предыдущее, становятся все ближе и ближе к особому числу, 1,618…

8\5= 1,6  

377/233= 1,61802575…

1,618… для краткости называется Фи. Я поставил многоточие после него, потому что десятичные дроби идут до бесконечности). Поскольку фи — иррациональное число, оно стремится к бесконечности, никогда не повторяясь, приближаясь к фи, но никогда не достигая точной, поддающейся определению величины. Для вашего взгляда на этот кусочек бесконечности я вычислил Фи до 100 000 разрядов.

1,618, одно из самых известных иррациональных чисел, также называемое золотым сечением, 1:1,618…. Эта пропорция на протяжении всей истории так восхищала архитекторов, художников и математиков, что ее называли «золотой» и даже «священной». Некоторые называют эти числа и их результирующую геометрию основой нашего восприятия красоты.

Чтобы доказать это, я представлю следующий 5-секундный видеоролик.

Одной из причин такого восхищения этим отношением является то, что оно находится в золотом прямоугольнике. Пропорции сторон этого прямоугольника равны 1 к 1,618 . И почему эта пропорция вызывает такое восхищение?

Открыв его в природе, художники, философы, математики и архитекторы использовали это соотношение в своей работе. Они передали эту секретную формулу через века, чтобы создать то, что считается наиболее гармоничным соотношением между визуальными элементами. Просто в этом что-то есть. Это динамическая форма — мозг пытается, но не может точно отобразить этот прямоугольник с помощью простых чисел. Это потому, что он основан на иррациональном числе.

Это золотой прямоугольник: отношение его длинной стороны к короткой равно 1,618…

До сих пор речь шла о прямых пропорциях. Но самое интересное заключается в том, как числа Фибоначчи, Золотая пропорция и Золотой прямоугольник содержатся в Золотой спирали.

Швейцарский математик Якоб Бернулли был настолько впечатлен этой спиралью, что придал ей мистический смысл. Когда он умер в 1705 году, Бернулли попросил вырезать эту спираль на его надгробии вместе с латинской фразой «9».0036 eadem mutata resurgo », («Хоть и изменился, но воскресну прежним»).

Рисование золотой спирали

Я собираюсь нарисовать это от руки карандашом по двум причинам:
1. рисование только рукой и мозг создает более глубокое обучение. Рука – это продолжение вашего мозга.
2. Это помогает нашим навыкам рисования практиковаться в оценке основных форм. Он не должен быть идеальным или прямым. Грубые формы будут работать так же хорошо или даже лучше, чем использование линейки и циркуля.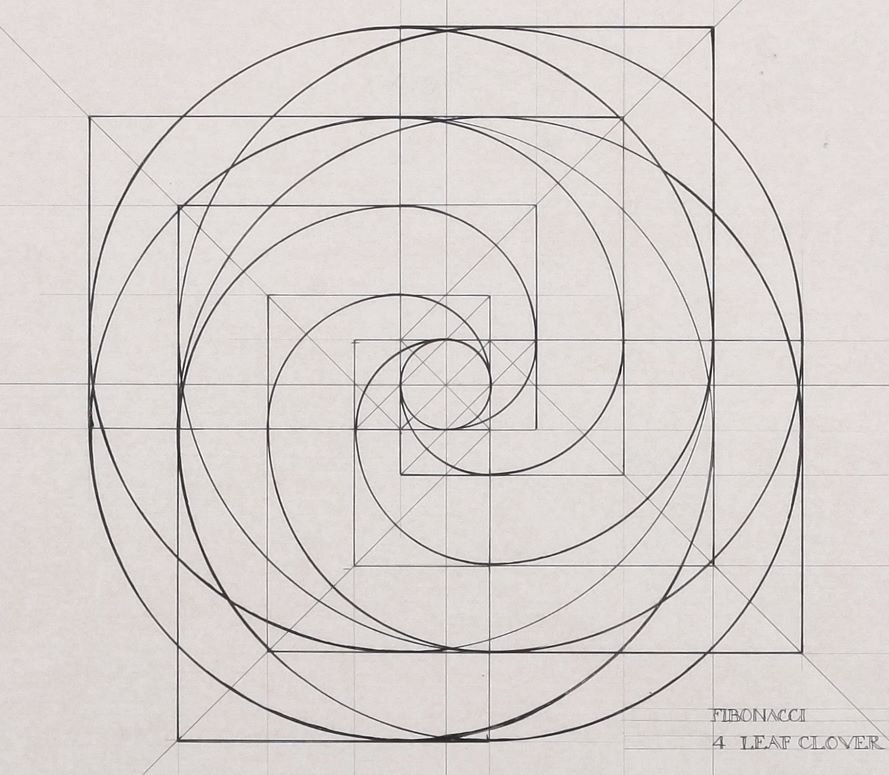

Вот быстрый 1,5-минутный предварительный просмотр того, как я рисую спираль. Тогда мы сделаем это вместе. Нарисовав это, некоторые люди сообщают о кратковременной искре просветления.

Ускоренное видео рисования спирали

1. Нарисуйте один крошечный квадрат в нижней правой четверти страницы. I лист бумаги для принтера подойдет. Это семя фрактальной модели.

2. Нарисуйте еще один квадрат того же размера от руки выше и разделите верхнюю сторону первого.

3. Нарисуйте еще один квадрат справа, той же высоты, что и два сложенных квадрата. (Подсказка: это неуловимый золотой прямоугольник)

4. Нарисуйте еще один квадрат поверх предыдущего прямоугольника. Это делает еще один золотой прямоугольник. Когда мы добавляем квадраты, результирующая общая форма всегда будет золотым прямоугольником. Это называется «самоподобием» и представляет собой простую фрактальную геометрию. Каждый прямоугольник, который мы создадим таким образом, будет точно таким же — изменится только размер.

5. Нарисуйте еще один квадрат той же высоты, что и предыдущая стопка, но ниже нее. (Да, еще один золотой прямоугольник) Получается однобоко, но это не имеет значения.

6. Нарисуйте еще один квадрат ниже предыдущей группы с одной стороной такой же ширины, как предыдущий золотой прямоугольник.

6. Нарисуйте еще один квадрат ниже предыдущей группы с одной стороной такой же ширины, как предыдущий золотой прямоугольник.

9. Теперь, если вы разметите квадраты по их размеру, исходя из того, что первый квадрат равен 1 единице, вы получите: ЧИСЛА ФИБОНАЧЧИ! По мере добавления квадратов длина каждой стороны будет основываться на том, что первый квадрат равен единице. Длина сторон каждого нового квадрата всегда будет соответствовать последовательности Фибоначчи.

10. Если начертить диагональ каждого квадрата, то можно начать видеть каркас спирали.

Обратите внимание, что мы рисуем диагонали квадратов, создавая еще одно значимое иррациональное число, встречающееся в природе: квадратный корень из двух, 1,414 … Это также гипотенуза прямоугольного треугольника, центральное понятие для пифагорейцев. Итак, оба этих загадочных числа присутствуют в Золотой Спирали.

Открытие того, что диагональ квадрата является иррациональным, не поддающимся определению числом, вызвало сдвиг парадигмы среди древнегреческих философов. Основной принцип их мировоззрения заключался в том, что Вселенная исчисляема, определяема целыми числами и дробями. Открытие иррационального свело их с ума.

Легенда гласит, что около 500 г. до н. э. пифагорейцы выбросили Гиппаса из Метапонта за борт за то, что он опубликовал свое доказательство того, что квадратный корень из двух — длина диагонали квадрата или гипотенузы прямоугольного треугольника — является бесконечным неисчисляемым десятичным числом. Может быть, с тех пор культура научных кругов изменилась — или у академиков теперь есть более изощренные, но не менее эффективные средства разрешения споров.

В конце концов, пифагорейцы приняли это доказательство, и иррациональная природа гипотенузы стала дверью в тайный мистицизм, основанный на Культе Чисел.

Чтобы закончить этот рисунок, я нарисовал спираль оранжевым маркером.

Чтобы увидеть одну из причин, по которым Золотая спираль произвела такое впечатление на Якоба Бернулли, обратите внимание ниже на то, что это фрактал, другими словами, «самоподобный». Когда он становится больше, он всегда одинаков. Это верно, будь то раковина улитки или спиральная галактика.

---

Двухчасовой семинар UA Tumamoc «Фибоначчи и агавы» прошел онлайн 30 января 2021 года. Вы все еще можете приобрести билет с доступом к записи на это и другие мероприятия из серии онлайн-семинаров Desert Lab.

Спиральный рисунок — Etsy.de

Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.

Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.