СОПРЯЖЕНИЕ ДВУХ ОКРУЖНОСТЕЙ
Возможны два варианта построений сопряжений двух окружностей:
· Задан радиус сопряжения.
· Задана точка сопряжения на одной из окружностей.
Сопряжение может быть внешним, внутренним и смешанным.
1. Сопряжение двух окружностей дугой заданного радиуса R (Рисунок16)
Рисунок 16
При внешнем сопряжении (рисунок 16) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R1 + R и R2 + R, проведенных соответственно из центров сопрягаемых дуг, то есть из точек О1 и О2. Точки сопряжения А и В определяются как точки пересечения заданных дуг с прямыми ОО1 и ОО2.
Рисунок 17
При внутреннем сопряжении (рисунок 17) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R – R1 и R – R2, проведенных соответственно из О1 и О2(рисунок 17).
Рисунок 18
При смешанном сопряжении (рисунок 18) центр сопряжения О определяется в пересечении вспомогательных окружностей радиусов R — R1 и R + R2, проведенных соответственно из О1и О2. Точки сопряжения А и В лежат на пересечении линий центров ОО1 и ОО2 с дугами заданных окружностей.
2. Сопряжение двух окружностей, если задано точка сопряжения А на одной из окружностей (рисунок 19).
Соединяют точку А с центром О1 и откладывают на этой прямой отрезок АС, равный R2. К середине отрезка СО2 восставляют перпендикуляр до пересечения с продолжением линии О1А. Точка О пересечения и является центром сопряжения. Вторая точка сопряжения В лежит на пересечении линии центров ОО2 с дугой второй окружности.
Рисунок 19
ПОСТРОЕНИЕ КАСАТЕЛЬНЫХ
Построение касательных к окружности основано на том, что касательная перпендикулярна к радиусу, проведенному в точку касания.
1. Касательная к окружности из точки А, лежащей вне окружности (рисунок 20).
Рисунок 20
Отрезок ОА, соединяющий данную точку с центром окружности, делят пополам и из полученной О1, как из центра описывают вспомогательную окружность радиусом R = О1А. Вспомогательная окружность пересекает заданную в точке С. Прямая АС является касательной к окружности, так как угол АСО прямой, как вписанный в окружность и опирающийся на ее диаметр.
2. Касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон от касательных.
2.1 Внешняя касательная к окружностям радиусов R1 и R2 (рисунок 21).
Рисунок 21
Из центра О1 большей окружности проводят вспомогательную окружность радиусом R1 – R2. Отрезок О1О2 делят пополам и проводят вспомогательную окружность радиусом R = О3О1. Точки пересечения этих окружностей соединяют с центром О1 и продолжают до пересечения с окружностью радиуса R1 в точках В и D. Эти точки являются точками касания окружности большего диаметра. Из центра О2 проводят прямые О2А и О2С, соответственно параллельные О1В и ОD, до пересечения с контуром окружности в точках А и С. Прямые АВ и СD – искомые внешние касательные к двум окружностям.
2.2 Внутренняя касательная к двум окружностям радиусов R1 и R2 (рисунок 22).
Рисунок 22
Из центра окружности О1 проводят вспомогательную окружность радиусом R1 + R2. Делят отрезок О1О2 пополам, и из полученной точки О3проводят вторую вспомогательную окружность радиусом R = О3О1. Точки пересечения этих окружностей соединяют с центром О1 и на пересечении с окружностью радиуса R1 получают точки касания А и С. Из точки О2 проводят прямую, параллельную прямой О1А, и получают точку касания В на малой окружности. Аналогично построена точка касания D. Прямые АВ и СD – искомые внутренние касательные к двум окружностям.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Конспект урока по теме «Сопряжения.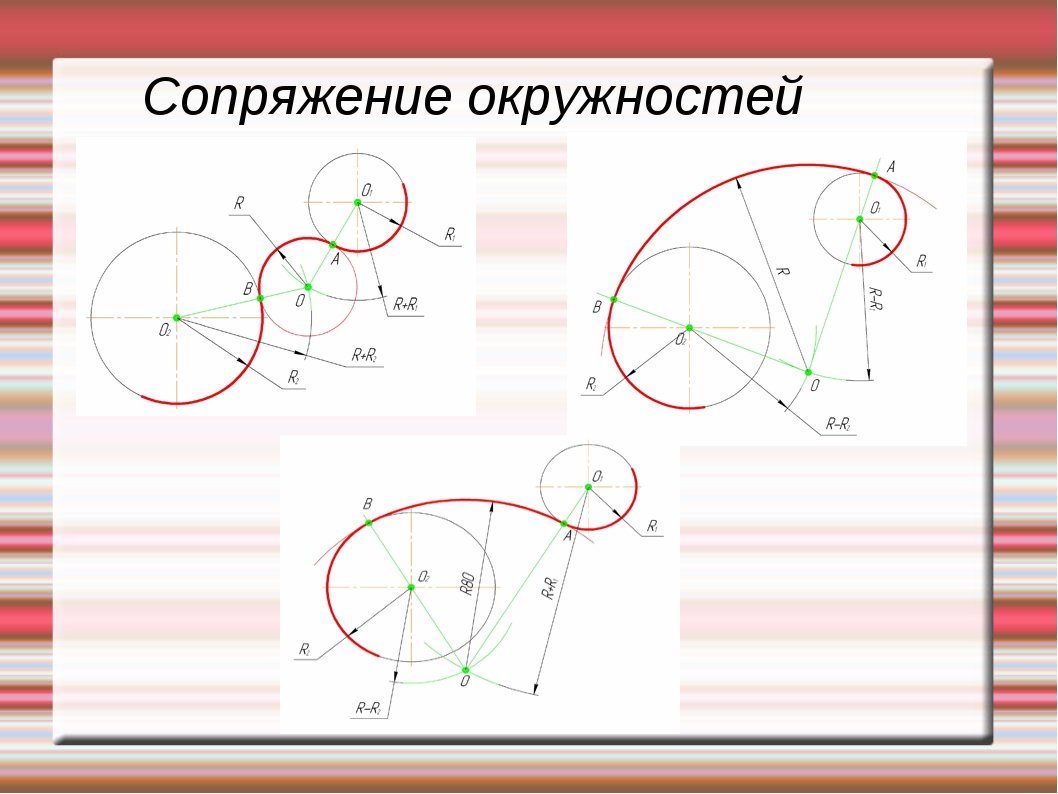 Виды сопряжений»
Виды сопряжений»
Урок черчения в 8 классе
Тема: Сопряжения. Виды сопряжений, их элементы, последовательность построений.Слайд 1.
Цели: привитие интереса к предмету «Черчение», развитие умений использовать полученные знания в практической деятельности.
Задачи урока:
познакомить обучающихся с применением сопряжений в технических формах;
научить выполнять основные виды сопряжений, понимать принцип построения сопряжений;
развивать логическое мышление, познавательный интерес, умение работать чертежными инструментами; воспитывать точность и аккуратность, внимательность и усидчивость.
Оборудование:
Визуальный ряд: мультимедийная презентация, технические детали, имеющие плавные переходы, классная доска.
Материалы и инструменты: рабочая тетрадь, чертежная бумага формата А4 и инструменты.
Ход урока
І. Организационный момент (2 мин.)
Учитель:
Добрый день, я приветствую Вас!
На хорошей волне начинаем урок!
Я уверен: все свершится у нас.
И знания пригодятся нам впрок!
Объявление темы и целей урока.
ІІ. Актуализация опорных знаний
(5 мин.)Учитель. В окружающей жизни мы часто встречаемся с предметами, форма которых имеет плавные переходы. Это: мобильные телефоны, автомобили, посуда и др. В предыдущих классах на уроках изобразительного искусства вы выполняли изображения различных животных, фигуры, которых также имели плавные переходы(см. рис. 1).Слайд 2.
Рис. 1
ІІІ. Изложение нового материала (10 мин.)
Изложение нового материала (10 мин.)
Сопряжением называется плавный переход от одной линии к другой.
Применение сопряжений очень разнообразно и многопланово в технической деятельности человека.
Сопряжения используют:
Слайд 3.
Рис.2Рис.3
(см. рис.5).Слайд 4.
Рис.4Рис.5
Сопряжения в технических деталях, предметах, изделиях применяют с целью: увеличения прочности, удобного и безопасного обращения, уменьшения коррозии деталей, учета эстетических требований.
При изучении сопряжений очень важно понять принцип их выполнения.
Для построения сопряжения надо найти центры, из которых проводят дуги, т.е.центры сопряжений.Необходимо найти также точки, в которых одна линия переходит в другую, т. е.точки сопряжений.Слайд 5.
е.точки сопряжений.Слайд 5.
Рассмотрим несколько видов сопряжения (обучающиеся делают записи в рабочих тетрадях, выполняют построения вслед за учителем). Слайды 6-9.
На внешнем сопряжениицентры сопрягаемых окружностей находятся за пределами радиуса сопряжения.
На внутреннем сопряжении центры сопрягаемых окружностей находятся внутри радиуса сопряжения.
ІV. Практическая работа(20 мин.)
Выполним заготовки трех изображений фигур, которые будем сопрягать.
Сопряжение двух прямых R15Внешнее сопряжение R10 Внутреннее сопряжение R80
Физкультминутка(2 мин.)(выполняется обучающимися вслед за демонстрацией на мультимедийном проекторе).
Продолжение практической работы.
Учащиеся получают карточки-задания (одну на парту – работа в парах) с алгоритмами различных видов сопряжений (Сопряжение двух прямых R15, Внешнее сопряжение R10, Внутреннее сопряжение R80). Слайд 11,12.
Слайд 11,12.
По истечении отведенного времени (10 мин.), учитель выявляет учащихся, справившихся с заданием. Затем демонстрирует выполнение данных видов сопряжений на доске.
Алгоритм выполнения сопряжений
Внешнее сопряжение R10
Из центра большей окружности проводим вспомогательные дуги радиусом, равным сумме радиуса сопряжения и радиуса окружности (30+10=40).
Из центра меньшей окружности проводим вспомогательные дуги радиусом, равным сумме радиуса сопряжения и радиуса окружности (20+10=30).
В пересечении этих дуг находим центры сопряжения О1 и О2, соединяем их с центрами сопрягаемых окружностей и находим на них точки сопряжения. Затем из этих центров проводим сопрягаемые дуги R10, ограничивая их точками сопряжения.
Контур сопряженной фигуры обводим сплошной толстой линией.

Внутреннее сопряжение R80
1. Из центра большей окружности проводим вспомогательные дуги радиусом, равным разнице радиуса сопряжения и радиуса окружности (80-30=50).
2. Из центра меньшей окружности проводим вспомогательные дуги радиусомравным разнице радиуса сопряжения и радиуса окружности (80-20=60).
3. В пересечении этих дуг находим центры сопряжения О1 и О2, соединяем его с центрами сопрягаемых окружностей и находим на них точки сопряжения. Затем из этих центров проводим сопрягаемые дуги R80, ограничивая их точками сопряжения.
4. Контур сопряженной фигуры обводим сплошной толстой линией.
Сопряжение двух прямых (углов) R15
Из вершин трапеции выполняем дугиR15. Проводим касательные линии к этим дугам и, на пересечении их, находим центры сопряжений О1, О2, О3, О4.
Из этих центров проводим перпендикуляры к сопрягаемым сторонам углов трапеции, находим точки сопряжения и выполняем сопряжение всех углов R15.

Контур сопряженной фигуры обводим сплошной толстой линией.
Сопряжение окружности и прямой,
двух параллельных прямых R10
Проводим вспомогательные линии, на удалении от прямых на расстоянии радиуса сопряжения R10.
Из центра окружности проводим вспомогательные дуги радиусом, равным сумме радиуса сопряжения и радиуса окружности (20+10=30) до пересечения с вспомогательными линиями.
Из полученных центров сопряжения проводим перпендикуляры к линиям и к окружности,находим точки сопряжения и выполняем сопряжение R10.
Контур сопряженной фигуры обводим сплошной толстой линией.
V. Итог урока (5 мин.)
Оценивание работ обучающихся. Рефлексия. Слайд 13.
— Что называется сопряжением?
— Какие виды сопряжений были изучены на уроке?
— Что необходимо построить для выполнения сопряжений?
— Чем отличается внешнее сопряжение от внутреннего?
VI.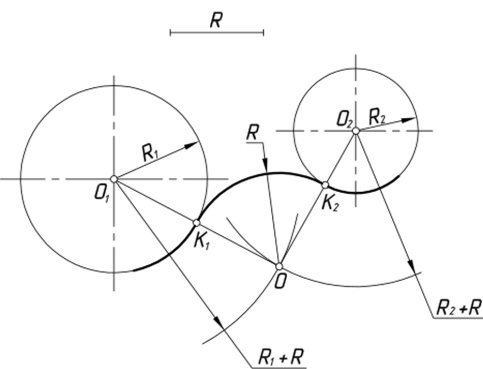 Домашнее задание (1 мин.)
Домашнее задание (1 мин.)
Изучить §15 пункт 3. Выполнить творческий эскиз « Сопряжение любимого предмета (мобильный телефон, игрушка и т. п.)». Слайд 14.
Заключение
На примере данного урокабыло показано, как можно объяснить детям назначение сопряжений, заинтересовать их примерами на практике через демонстрацию форм предметов с плавными переходами. Представлен алгоритм сопряжения углов, окружности и прямой и двух окружностей. Показан способ применения этих видов сопряжений при построении различных фигур.
Сопряжение окружностей (дуг) Внешнее сопряжение дуг окружностей
Внешним сопряжением
считается сопряжение, при котором центры
сопрягаемых окружностей (дуг) O1 ( радиус R1)
и O2 (радиус R2)
располагаются за сопрягающей дугой
радиуса R.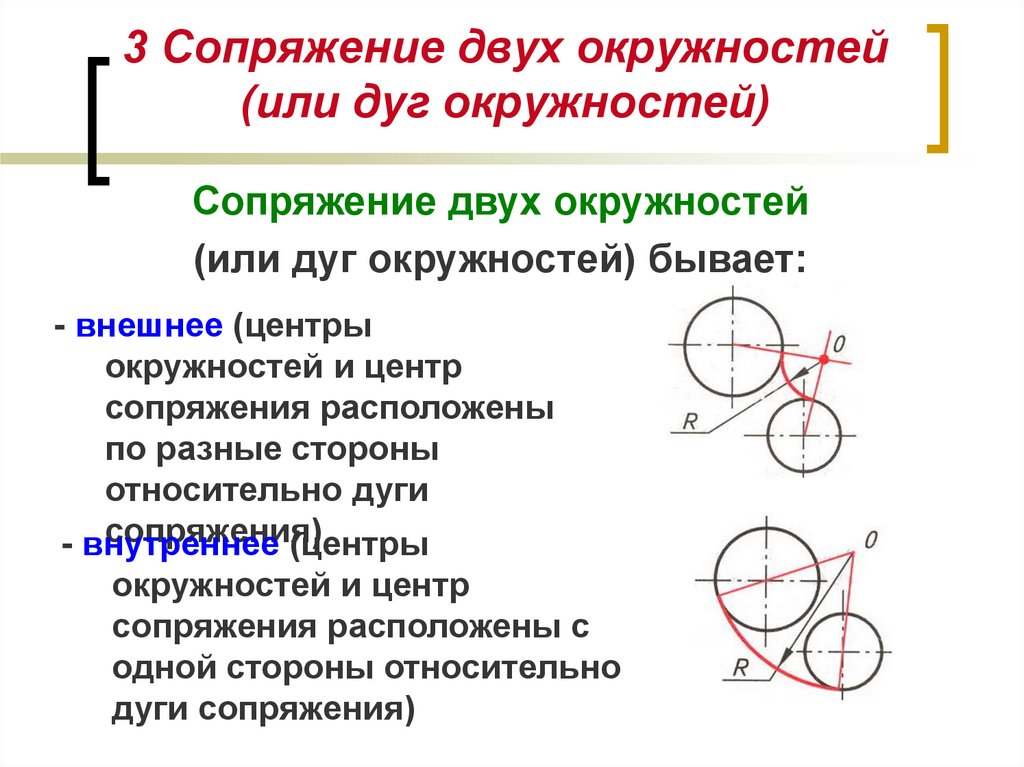 На примере рассмотрено внешнее
сопряжение дуг (рис.5). Сначала находим
центр сопряжения. Центром сопряжения
является точка пересечения дуг окружностей
с радиусами R+R1 и R+R2,
построенных из центров окружностей
O1(R1)
и O2(R2)
соответственно. Затем центры окружностей
O1 и O2 соединяем прямыми с центром сопряжения,
точкой O, и на пересечении линий с
окружностями O1 и O2 получаем точки сопряжения A и B. После
этого, из центра сопряжения строим дугу
заданного радиуса сопряжения R и соединяем
ей точки A и B.
На примере рассмотрено внешнее
сопряжение дуг (рис.5). Сначала находим
центр сопряжения. Центром сопряжения
является точка пересечения дуг окружностей
с радиусами R+R1 и R+R2,
построенных из центров окружностей
O1(R1)
и O2(R2)
соответственно. Затем центры окружностей
O1 и O2 соединяем прямыми с центром сопряжения,
точкой O, и на пересечении линий с
окружностями O1 и O2 получаем точки сопряжения A и B. После
этого, из центра сопряжения строим дугу
заданного радиуса сопряжения R и соединяем
ей точки A и B.
Рисунок 5. Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Внутренним
сопряжением называется сопряжение, при
котором центры сопрягаемых дуг O1,
радиуса R1,
и O2,
радиус R2,
располагаются внутри сопрягающей их
дуги заданного радиуса R. На рис.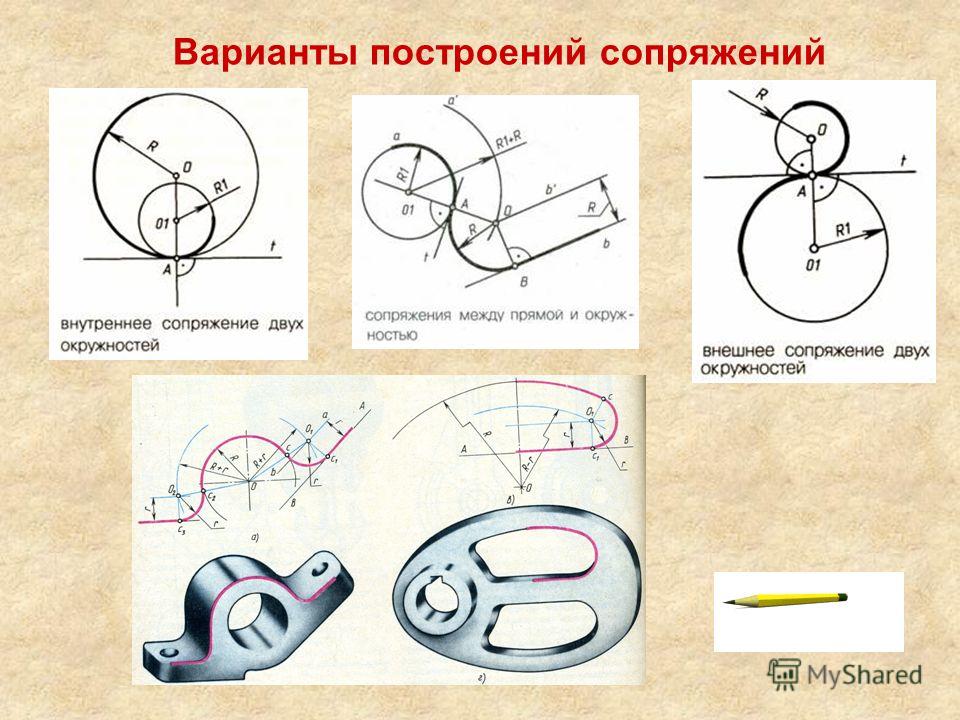 6 приведён
пример построения внутреннего сопряжения
окружностей (дуг). Вначале мы находим
центр сопряжения, которым является
точка O, точка пересечения дуг окружностей
с радиусами R-R1 и R-R2 проведённых из центров окружностей O1 и O2 соответственно. После чего соединяем
центры окружностей O1 и O2 прямыми линиями с центром сопряжения
и на пересечении линий с окружностями
O1 и O2 получаем точки сопряжения A и B. Затем
из центра сопряжения строим дугу
сопряжения радиуса R и строим сопряжение.
6 приведён
пример построения внутреннего сопряжения
окружностей (дуг). Вначале мы находим
центр сопряжения, которым является
точка O, точка пересечения дуг окружностей
с радиусами R-R1 и R-R2 проведённых из центров окружностей O1 и O2 соответственно. После чего соединяем
центры окружностей O1 и O2 прямыми линиями с центром сопряжения
и на пересечении линий с окружностями
O1 и O2 получаем точки сопряжения A и B. Затем
из центра сопряжения строим дугу
сопряжения радиуса R и строим сопряжение.
Рисунок 6. Внутреннее сопряжение дуг окружностей | Рисунок 7. Смешанное сопряжение дуг окружностей |
Смешанное сопряжение дуг окружностей
Смешанным сопряжением
дуг является сопряжение, при котором
центр одной из сопрягаемых дуг (O1)
лежит за пределами сопрягающей их дуги
радиуса R, а центр другой окружности(O2)
– внутри её.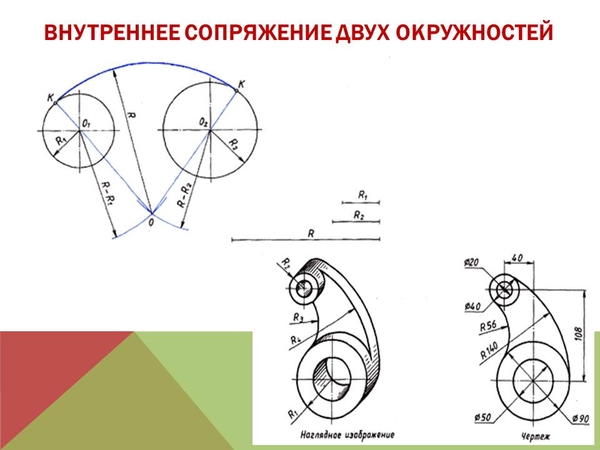 На рис.7 приведён пример
смешанного сопряжения окружностей.
Сначала находим центр сопряжения, точку
O. Для нахождения центра сопряжения
строим дуги окружностей с радиусами R+
R1,
из центра окружности радиуса R1 точки O1,
и R-R2,
из центра окружности радиуса R2 точки O2.
После чего соединяем центр сопряжения
точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями
соответствующих окружностей получаем
точки сопряжения A и B. Затем строим
сопряжение.
На рис.7 приведён пример
смешанного сопряжения окружностей.
Сначала находим центр сопряжения, точку
O. Для нахождения центра сопряжения
строим дуги окружностей с радиусами R+
R1,
из центра окружности радиуса R1 точки O1,
и R-R2,
из центра окружности радиуса R2 точки O2.
После чего соединяем центр сопряжения
точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями
соответствующих окружностей получаем
точки сопряжения A и B. Затем строим
сопряжение.
Построение кулачка
Построение очертания кулачка в каждом варианте следует начинать с нанесения осей координат Ох и Оу. Затем строят лекальные кривые по их заданным параметрам и выделяют участки, входящие в очертание кулачка. После этого можно вычертить плавные переходы между лекальными кривыми. При этом следует учесть, что во всех вариантах через точку D проходит касательная к эллипсу.
Обозначение Rx показывает, что величина радиуса
определяется построением. На чертеже
вместо Rx надо проставить соответствующее число
со знаком «*».
На чертеже
вместо Rx надо проставить соответствующее число
со знаком «*».
Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.
Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.
Эллипс — кривая второго порядка. Одним из способов построения эллипса является способ построения эллипса по двум осям рис.8. При построении проводим окружности радиусами r и R из одного центра О и произвольную секущую ОА. Из точек пересечения 1 и 2 проводим прямые, параллельные осям эллипса. На их пересечении отмечаем точку М эллипса. Остальные точки строим аналогично.
Рисунок 8. | Рисунок 9. Построение параболы |
Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки называемой фокусом параболы, расположенных в той же плоскости.
На рисунке 9 приведен один из способов построения параболы. Даны вершина параболы О, одна из точек параболы А и направление оси – ОС. На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника в задании – А1 и В1, делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4… 10. Вершину О соединяют с точками деления на А1, а из точек деления отрезка В1 проводят прямые параллельные оси ОС. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.
Синусоидой называют плоскую кривую, изображающую
изменение синуса в зависимости от
изменения его угла.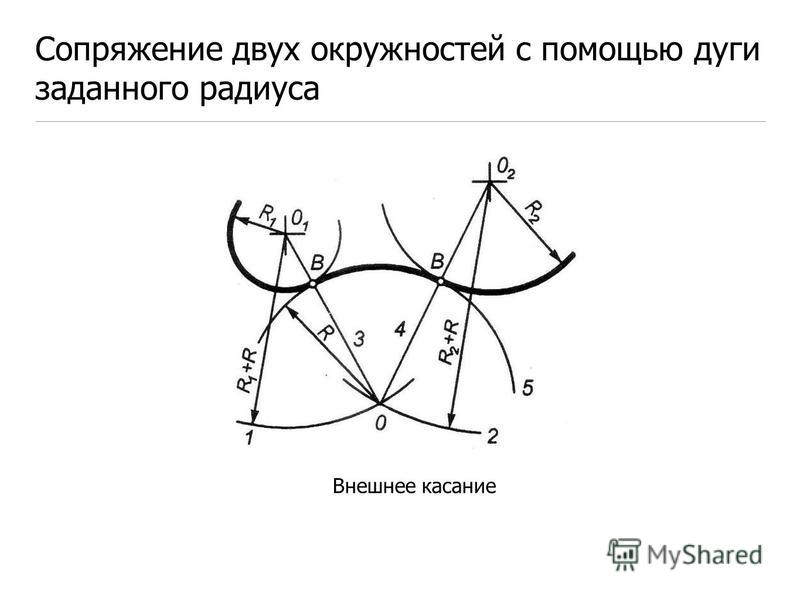 Для построения
синусоиды (рис. 10) нужно разделить
окружность на равные части и на такое
же количество равных частей разделить
отрезок прямой АВ
= 2лR. Из одноименных точек деления провести
взаимно перпендикулярные линии, в
пересечении которых получают точки,
принадлежащие синусоиде.
Для построения
синусоиды (рис. 10) нужно разделить
окружность на равные части и на такое
же количество равных частей разделить
отрезок прямой АВ
= 2лR. Из одноименных точек деления провести
взаимно перпендикулярные линии, в
пересечении которых получают точки,
принадлежащие синусоиде.
Рисунок 10. Построение синусоиды
Эвольвентой называют плоскую кривую, являющуюся
траекторией любой точки прямой линии,
перекатываемой по окружности без
скольжения. Построение эвольвенты
выполняют в следующем порядке (рис.11):
окружность делят на равные части;
проводят касательные к окружности,
направленные в одну сторону и проходящие
через каждую точку деления; на касательной,
проведенной через последнюю точку
деления окружности, откладывают отрезок,
равный длине окружности 2лR,
который делят на столько же равных
частей. На первой касательной откладывают
одно деление 2лR/n,
на второй – два и т. д.
д.
Рисунок 11. Построение эвольвенты | Рисунок 12. Спираль Архимеда |
Спираль Архимеда – плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра О по равномерно вращающемуся радиусу (рис.12).
Для построения спирали Архимеда задается шаг спирали – а, и центр О. Из центра О описывают окружность радиусом Р = а (0-8). Делят окружность на несколько равных частей, например, на восемь (точки 1, 2, …, 8). На столько же частей делят отрезок О8. Из центра О радиусами О1, О2, и т.д. проводят дуги окружностей, точки пересечения которых с соответствующими радиусами-векторами принадлежат спирали (I, II, …,YIII)
Таблица 2
1 Кулачок
| ||||||||||||||||||||||||||
2 Кулачок
|
3 Кулачок
| ||||||||||||||||||||||||||||
4 Кулачок
| ||||||||||||||||||||||||||||
5 Кулачок
| ||||||||||||||||||||||||||||||
6 Кулачок
|
Виды сопряжений
Лекция 9. СОПРЯЖЕНИЕ ОКРУЖНОСТЕЙ
СОПРЯЖЕНИЕ ОКРУЖНОСТЕЙ
Касание окружностей.
При касании двух окружностей между собой точка касания А является их
общей точкой. Она находится на пересечении окружностей с прямой, проходящей через центры касающихся ок-
ружностей.
Касание называется внешним, если расстояние между центрами касаю-
щихся окружностей равно сумме их ра-
диусов (R1+R2). Рис. 1.
Касание называется внутренним, если расстояние между центрами касающихся окружностей равно разности
их радиусов (R1-R2). Рис. 2.
Рис. 1 | Сопряжения окружностей дугами | ||
| окружностей. | ||
| Плавный переход от одной дуги к | ||
| другой достигается при том условии, | ||
| когда точка их касания расположена | ||
| на прямой, соединяющей центры этих | ||
| окружностей. | ||
| В этом случае мы также сталкиваемся | ||
| с различными вариантами. | ||
| Сопряжение двух дуг окружностей | ||
| третьей дугой окружности может быть | ||
| внешнее и внутреннее. | ||
| Внешним называется сопряжение, ко- | ||
| гда сопрягаемые окружности остаются | ||
| вне сопрягающей дуги. | ||
| Внешнее сопряжение. |
|
|
Рис. 2 | (Рис. 3). |
| |
| |||
|
|
|
|
Даны две дуги радиусов R1 и R2 соответственно с центрами О1 и О2, а также
радиус сопрягающей дуги R.
Центр сопрягающей дуги должен быть
равно удален от заданных дуг окружно-
стей на расстояние R. Поэтому проводим вспомогательные дуги из центра О1 ра-
диусом R1+R, а из центра О2 радиусом
R2+R до взаимного их пересечения в ис-
комом центре сопрягающей дуги. Для Рис. 3 определения точек касания (сопряжения)
1 и 2 проводим прямые, соединяющие центры окружностей О1 и О2 с найденным центром сопрягающей дуги. В за-
ключение радиусом R проводим сопрягающую дугу между точками 1 и 2.
Рис. 6
Внутреннее сопряжение. (Рис. 4).
Даны две дуги окружностей с радиусами R1 и R2 и центрами О1 и О2. За-
дан радиус R сопрягающей окружности. Сопрягаемые окружности находятся
внутри сопрягающей дуги. Расстояние между искомым центром
сопрягающей дуги и центрами задан-
ных окружностей равно разнице радиусов. Поэтому из центра О1 делаем за-
сечку R-R1, а из центра О2 засечку R-
R2 до их взаимного пересечения, яв-
ляющегося центром сопрягающей дуги.
Из полученного центра проводим пря- Рис. 4 мые через центры О1 и О2 для опре-
деления точек сопряжения 1 и 2, между
которыми очерчиваем сопрягающую дугу радиусом R.
Сложное сопряжение. (Рис. 5).
Даны две дуги окружностей с радиу-
сами R1 и R2 и центрами О1 и О2. За-
дан радиус R сопрягающей окружности.
С окружностью радиусом R1 и дугой
радиуса R мы имеем внутреннее со-
пряжение, а с окружностью радиуса R2
и дугой радиуса R – внешнее сопряжение.
Приводим построение к известному: Рис. 5 из центра О1 радиусом R-R1 делаем засечку, из центра О2 радиусом R+R2
до их взаимного пересечения, который является центром сопрягающей дуги. Из полученного центра проводим прямые через центры О1 и О2 для опре-
деления точек сопряжения 1 и 2, между которыми очерчиваем сопрягающую дугу радиусом R.
Сопряжение двух параллельных прямых двумя дугами окружностей.
(Рис. 6).
Дано: две параллельные прямые МН и PF с точками сопряжения на них А и В. На прямой АВ задается точка каса-
ния С сопрягающих дуг окружностей. Их центры и размеры радиусов опре-
деляем, строя перпендикуляры из точек касания А и В. Затем восставляем перпендикуляры в серединах отрезков
АС и СВ, на которых в точках пересе-
чения находим центры сопрягающих
дуг. Линия, соединяющая центры двух дуг, должна пройти через точку С (как контроль графического построения).
Если точка сопряжения С задается в середине АВ, то радиусом R1=R2 (на-
пример, гусек).
Сопряжение дуги окружности с прямой линией дугой заданного радиуса. (Рис. 7).
Дано: прямая АВ, дуга окружности радиуса R1 и радиус R. Проведем вспомо-
гательную линию, параллельную АВ, на
расстоянии R.
Зная, что центр сопрягающей дуги должен отстоять от заданной прямой и
дуги окружности радиуса R1 на равное
расстояние, проведем вспомогательную линию, параллельную АВ, на расстоянии
R, а из центра О1 вспомогательную дугу
Рис. 7 радиусом R1+R. В их пересечении нахо-
дится искомый центр О1.
Для нахождения точек сопряжения проведем прямую, соединяющую центры О1 и О2 (найдем точку 1), и опустим перпендикуляр из О2 на прямую АВ (най-
дем точку 2).
Из точки О2 опишем сопрягающую дугу радиусом R от точки 1 до точки 2.
Сопряжения двух параллельных прямых — Энциклопедия по машиностроению XXL
Построение сопряжения двух параллельных прямых I и 1 при условии, что расстояние между этими прямыми равно сумме сопрягаемых радиусов R 4- RА (Рис. 23). Дана точка сопряжения А. Линия центров в этом случае будет параллельна сопрягаемым прямым. Построение производят аналогично построениям, приведенным на рис. 22. [c.19]Построение сопряжения двух параллельных прямых I и li по данным точкам сопряжения А и В и произвольной точке 1 сопряжения двух дуг (рис. 24). Из середины отрезков 1—В и 1—А восставляют [c.19]
Для построения плавного сопряжения двух параллельных прямых АВ и СО с помощью дуги окружности (рис. 45) необходимо, чтобы точки касания прямых с дугой лежали на перпендикуляре, [c.50]
При сопряжении двух параллельных прямых дугами окружностей могут быть различные случаи. Рассмотрим некоторые из них на отдельных примерах. [c.42]
Выявление операций, необходимых для построения чертежа, облегчает выбор способа его выполнения. Если нужно вычертить, например, пластину, изображенную на рис. 39, то анализ контура ее изображения приводит нас к выводу, что мы должны применить следующие геометрические построения в пяти случаях провести взаимно перпендикулярные центровые линии (цифра 1 в кружке), в четырех случаях вычертить параллельные линии (цифра 2), вычертить две концентрические окружности (0 50 и 70 мм), в шести случаях построить сопряжения двух параллельных прямых дугами заданного радиуса (цифра 3), а в четырех — сопряжения дуги и прямой дугой радиуса 10 мм (цифра 4), в четырех случаях построить сопряжение двух дуг дугой радиуса 5 мм (цифра 5 в кружке). [c.28]
Сопряжение двух параллельных прямых. Заданы две параллельные прямые [c.36]
На рис. 20, б изображен аналогичный случай построения сопряжения двух параллельных прямых 1 п даны технические примеры с применением указанных сопряжений. [c.24]| Рис. 34. Сопряжение двух параллельных прямых |
На рис. 34 дано сопряжение двух параллельных прямых АВ и ОС дугами окружностей, проходящих через произвольную точку К. Точки А и О соединяют прямой и на ней задаются точкой К- Прямая АВ является касательной к сопрягающей дуге окружности, а точка А — точкой касания, следовательно, центр О1 сопрягающей дуги должен быть на перпендикуляре, восставленном в точке А к прямой АВ. Отрезок АК есть хорда сопрягающей дуги, а следовательно, центр этой дуги должен быть на перпендикуляре, проведенном через середину хорды АК. Пересечение этих двух перпендикуляров определит положение центра 0( сопрягающей дуги АК. Аналогично определяется центр О2 сопрягающей дуги ОК. Эта задача допускает несколько решений в зависимости от положения точки К на прямой АО. [c.21]
Сопряжение двух параллельных прямых дугами окружностей проводится в следующей последовательности. Соединяем точку А с точкой В и продолжаем прямую АВ до пересечения с прямой (точка Б). В точках Л и Б восставляем перпендикуляры к соответствующим прямым. Затем восставляем перпендикуляры к серединам отрезков прямых АВ и ВБ. Точки пересечения этих перпендикуляров и определят центры О1 и О2 сопрягающих окружностей. Из центра 0 радиусом, равным отрезку О1Л, а из центра О2 радиусом ОгБ проводим дуги окружности, которые проходят через точку В и сопрягают заданные прямые (рис. 17, в). [c.27]
Сопряжение двух параллельных прямых двумя дугами (рис. 21). Заданные на прямых точки А и В соединяются отрезком АВ, на котором отмечают произвольную точку М. В середине отрезков АМ и ВМ проводят к ним перпендикуляры в точках А н В также восставляют перпендикуляры к данным прямым. В пересечении соответствующих перпендикуляров находятся центры Ох и 0 . Радиусы закругления кх = = ОхА R2=0iB. Касание дуг происходит в точке М, находящейся на линии центров ОхО . Если точку М выбрать на середине АВ, то Rx=Ri [c.69]
Сопряжение двух параллельных прямых двумя дугами при заданных точках сопряжения (рис. 16.38). Для построения центров сопряжения [c.449]
Сопряжение двух параллельных прямых а и дугой радиуса (рис. 101). Проводят перпендикулярную к прямым с и Ь прямую с и получают точки А п В сопряжения. Делят отрезок АВ пополам и из точки О, как из центра, проводят дугу сопряжения радиусом = ОА. На чертеже (рис. 102) выполнены два сопряжения параллельных прямых (радиусами 8 и 28 мм). [c.94]
Сопряжение двух параллельных прямых а и 6 в пределах ограниченной длины этих прямых выполняют аналогично показанному на рис. 105, а, б. [c.95]
Сопряжение двух параллельных прямых а и Ь, если заданы точка А сопряжения и точка С касания дуг сопряжения (рис. 106, а, б). Соединив точки Л и С, находят точку В сопряжения. Из середины отрезка АС восставляют перпендикуляр до пересечения с перпендикуляром, восставленным к прямой а в точке Л. В пересечении перпендикуляров получают центр 0 первой дуги сопряжения. Аналогично находят центр О второй дуги сопряжения. Радиусами = ЛО и — ВО проводят дуги сопряжения. Конфигурация сопряжения и радиусы R и зависят, как это видно из рис. 106, а, б, от взаимного расположения точек Л и С. [c.95]
Сопряжение двух параллельных прямых а ш Ь, если задана точка А, через которую должна пройти дуга сопряжения (рис. 107). Для получения центра О дуги сопряжения проводят прямую, параллельную заданным прямым, посредине между этими прямыми. На пересечении полученной прямой с дугой проведенной из заданной точки Л, как из центра, радиусом, равным h 2, находится [c.95]
Сопряжения промежуточными дугами. 1. Сопряжение двух сторон прямого (рис. 68, а), острого (рис. 68,в) или тупого (рис. 68,й) углов дугой радиуса R выполняют следующим образом. Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии и находят точку О пересечения этих прямых. Точка [c.39]Построение сопряжения двух пересекающихся прямых I и h с дугами данных радиусов R и Ra (рис. 22). На перпендикуляре, восставленном к прямой I в точке А, откладывают от заданной точки А величину радиуса R и получают центр сопряжения О. Для нахождения второго центра Oi проводят на расстоянии от заданной прямой /i прямую /а, параллельную li- [c.19]
В черчении чаще приходится строить сопряжение двух пересекающихся прямых (фиг. 77, а) двух параллельных прямых (фиг. 77, б) сопряжение дуги окружности и прямой линии дугой окружности (фиг. 78, а, б) сопряжение двух окружностей прямой линией (фиг. 79, а, б я фиг. 80 — прямая МКУ, сопряжение двух окружностей дугами окружностей (фиг. 81, а, б, в, г и фиг. 82). [c.38]
Задача 18. Построить сопряжение двух параллельных отрезков прямых линий при помощи двух дуг одинакового радиуса. Точки сопряжений В п С должны совпадать с концевыми точками отрезков. [c.33]
Сопряжение двух пересекающихся прямых 1 и 1 дугами радиусов и (рис. 20, а) (точка сопряжения А задана). На перпендикуляре, восставленном к прямой 1 в точке А, откладывают отрезок АО , равный радиусу Ях, и получают центр сопряжения О1. Для получения второго центра сопряжения О2 строят два геометрических места точек прямую /2, параллельную и отстоящую от нее на расстоянии Я,,, и окружность из центра О1 радиусом концентричную окруж- [c.24]
На рис. 38, в показано сопряжение дугой радиуса Я двух окружностей разных диаметров. При этом одной окружности сопрягающая дуга касается внешней стороной, а другой — внутренней. Центр сопряжения О в этом случае будет в точке пересечения окружностей радиусов и / —/ 2-На рис. 39 показано построение сопряжения двух параллельных линий АЕ и ОВ двумя дугами. При этом точки сопряжений О, Е и М заданы. Такая задача может встретиться, например, при построении профиля карниза. Центры сопрягающих дуг Ох и О2 будут расположены в пересечении перпендикуляров к заданным прямым, проведенных из точек О и Е, и прямых, делящих отрезки ОМ и МЕ пополам и перпе
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости | Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 | |
| Каждая из окружностей лежит вне другой | Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 | |
| Внешнее касание двух окружностей | Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 | |
| Внутреннее касание двух окружностей | Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 | |
| Окружности пересекаются в двух точках | Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 | |
| Одна из окружностей лежит внутри другой | Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
| Две окружности на плоскости | |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 | |
| Каждая из окружностей лежит вне другой | |
Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 | |
| Внешнее касание двух окружностей | |
Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 | |
| Внутреннее касание двух окружностей | |
Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 | |
| Окружности пересекаются в двух точках | |
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 | |
| Одна из окружностей лежит внутри другой | |
Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 | |
| Две окружности на плоскости |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей d = O1O2 |
| Каждая из окружностей лежит вне другой |
Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 |
| Внешнее касание двух окружностей |
Расстояние между центрами окружностей равно сумме их радиусов d = r1 + r2 |
| Внутреннее касание двух окружностей |
Расстояние между центрами окружностей равно разности их радиусов d = r1 – r2 |
| Окружности пересекаются в двух точках |
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 < d < r1 + r2 |
| Одна из окружностей лежит внутри другой |
Расстояние между центрами окружностей меньше разности их радиусов d < r1 – r2 |
Общие касательные к двум окружностям
| Фигура | Рисунок | Свойства |
| Внешняя касательная к двум окружностям | Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. | |
| Внутренняя касательная к двум окружностям | Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой. | |
| Внутреннее касание двух окружностей | Существует единственная общая внешняя касательная. Других общих касательных нет. | |
| Окружности пересекаются в двух точках | Существуют две общих внешних касательных. Других общих касательных нет. | |
| Внешнее касание двух окружностей | Существует единственная общая внутренняя касательная, а также | |
Каждая из окружностей лежит вне другой | Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет | |
Формулы для длин общих касательных и общей хорды двух окружностей
Доказательства формул для длин общих касательных и общей хорды двух окружностей
Утверждение 1. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
Доказательство. Для того, чтобы найти длину отрезка K1K2, опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.1).
Рис.1
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K2 , K1K3 = r2 , O1K3 = r1 – r2 .
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:
Следовательно,
что и требовалось доказать.
Утверждение 2. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей внутренней касательной к этим окружностям вычисляется по формуле
Доказательство. Для того, чтобы найти длину отрезка K1K2 , опустим из точки O2 перпендикуляр O2K3 на прямую O1K1 (рис.2).
Рис.2
Поскольку четырёхугольник O2K2K1K3 – прямоугольник, то справедливы равенства
O2K3 = K1K3 , K1K3 = r2 , O1K3 = r1 + r2 .
Воспользовавшись этими равенствами, из прямоугольного треугольника O1O2K3 получаем:
Следовательно,
что и требовалось доказать.
Утверждение 3. Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d, то длина общей хорды AB этих окружностей вычисляется по формуле
где
Доказательство. Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,
Рис.3
следующие обозначения:
O2C = y, CB = x .
Тогда, воспользовавшись теоремой Пифагора для треугольников O1CB и O2CB, получим
Поэтому
Таким образом, справедлива формула:
где
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Сопряжение двух параллельных прямых, проводящих касательную к …
Сопряжение двух параллельных прямых
Даны две параллельные прямые и на одной из них точка сопряжения M (рис. 2.19, а ). Требуется построить сопряжение.
Строится следующим образом:
1) найти центр сопряжения и радиус дуги (рис. 2.19, б). Для этого из точки M перпендикуляр проводят до пересечения с линией в точке N. Отрезок MN разделен пополам (см. Рисунок 2.7)
2) от точки O — центр сопряжения с радиусом OM = ON описывают дугу из сопряженных точек M и N (рисунок 2.19, в ).
Рис. 2.19. Построение сопряжения двух параллельных прямых
Проведите касательную к окружности
Дана окружность с центром O и точкой A.Требуется провести касательную к окружности от точки A .
1. Точка A соединяет прямую с заданным центром O окружности.
Постройте вспомогательную окружность диаметром OA (рис. 2.20, a ). Чтобы найти центр 0 1, разделите сегмент OA пополам (см. Рисунок 2.7).
2. Точки M и N пересечения вспомогательной окружности с данной окружностью являются необходимыми точками касания.Точка A соединена прямыми линиями с точками M или N (рис. 2.20, b ). Прямая AM будет перпендикулярна линии OM, , поскольку угол AMO поддерживается диаметром.
Рис. 2.20. Проведите касательную к окружности
Проведение прямой касательной к двум окружностям
Даны две окружности радиусами R и R 1.Требуется построить касательную к ним прямую.
Возможны два случая контакта: внешний (рисунок 2.21, b ) и внутренний (рисунок 2.21, в ).С external touch построение выполняется следующим образом:
1) от центра O начертите вспомогательную окружность с радиусом, равным разности радиусов данных окружностей, т.е. R — R 1 (рис. 2.21, а ). К этой окружности из центра O1 проведем касательную Ο 1 Ν. Построение касательной показано на рис. 2.20;
2) радиус, проведенный из точки O в точку Ν, продолжается до пересечения в точке M с заданной окружностью радиуса R. Параллельно радиусу OM проведите радиус Ο 1 P малого круга. Прямая, соединяющая точки сопряжения M и P, является касательной к заданным окружностям (рисунок 2.21, б ).
Рис. 2.21. Проведите касательную к двум окружностям
Для внутреннего касания конструкция аналогична, но вспомогательная окружность нарисована с радиусом, равным сумме радиусов R + R 1 (рис. 2.21, в ). Затем из центра O 1 проведите касательную к вспомогательной окружности (см. Рис. 2.20). Точка N соединена радиусом с центром O. Параллельно радиусу ON проводится радиус O1 P меньшего круга. Искомая касательная проходит через точки сопряжения M и P.
Сопряжение дуги и прямой дуги заданного радиуса
Дана дуга окружности радиусом R и прямая линия. Их требуется соединить дугой радиуса R 1.
1. Найдите центральную пару (рис. 2.22, и ), которые должны находиться на расстоянии R 1 дуги и прямой. Поэтому проведена вспомогательная линия, параллельная данной линии, на расстоянии, равном радиусу R1 дуги муфты) (рис. 2.22, , ). Решение компаса, установленное равным сумме радиусов R + R 1, описывает дугу от центра O до пересечения с вспомогательной линией. Получившаяся точка O1 является центром сопряжения.
2. Как правило, находим точки сопряжения (рис. 2.22, b ) : соединяют центры прямых сопряженных дуг O1 и O и опускают из центра сопряжения Ο 1 перпендикуляр к заданной прямой.
3. Из центра сопряжения χ между сопряженными точками M и Ν проведите дугу с радиусом R 1 (рис. 2.22, b ).
Рис. 2.22. Построение сопряжения окружности и прямой
Сопряжение двух дуг дугой заданного радиуса
Даны две дуги с радиусами R 1 и R 2.Требуется построить сопряжение по дуге, радиус которой задан.
Возможны три случая контакта: внешний (рисунок 2.23, a, b ), внутренний (рисунок 2.23, в ) и смешанный (см. Рисунок 2.25). Во всех случаях центры сопряжения должны располагаться от заданных дуг на расстоянии радиуса дуги сопряжения.Рис. 2.23. Построение сопряжения двух дуг окружности
Строится следующим образом:
Для внешнего сенсорного ввода:
1) вспомогательные дуги от центров Ο 1 и O2 по решению циркуля, равному сумме радиусов заданной и сопряженной дуг (рис.2.23, а ) ; Радиус дуги, проведенной из центра Ο 1, равен R 1 + R 3; и радиус дуги
2D обнаружение столкновений — Разработка игры
Алгоритмы обнаружения столкновения в 2D-играх зависят от типа фигур, которые могут столкнуться (например, прямоугольник в прямоугольник, прямоугольник в круг, круг в круг). Как правило, у вас будет простая общая форма, которая покрывает объект, известный как «хитбокс», поэтому, даже если столкновение может не быть идеальным по пикселям, оно будет выглядеть достаточно хорошо и работать с несколькими объектами.В этой статье представлен обзор наиболее распространенных методов, используемых для обнаружения столкновений в 2D-играх.
Одна из более простых форм обнаружения столкновений — между двумя прямоугольниками, выровненными по оси, то есть без вращения. Алгоритм работает, гарантируя отсутствие зазора между любой из 4 сторон прямоугольника. Любой разрыв означает, что столкновения не существует.
var rect1 = {x: 5, y: 5, width: 50, height: 50}
var rect2 = {x: 20, y: 10, width: 10, height: 10}
если (rect1.x rect2.x &&
rect1.y rect2.y) {
}
если (5 <30 &&
55> 20 &&
5 <20 &&
55> 10) {
}
Рек. Код
Перемещайте прямоугольник с помощью клавиш со стрелками. Зеленый цвет означает столкновение, синий - отсутствие столкновения.
Crafty.init (200, 200);
var dim1 = {x: 5, y: 5, w: 50, h: 50}
var dim2 = {x: 20, y: 10, w: 60, h: 40}
var rect1 = Crafty.e ("2D, холст, цвет"). attr (dim1) .color ("красный");
var rect2 = Crafty.e ("2D, холст, цвет, клавиатура, четыре направления"). fourway (2) .attr (dim2) .color ("синий");
rect2.bind ("EnterFrame", function () {
если (rect1.x rect2.x &&
rect1.y rect2.y) {
this.color ("зеленый");
} else {
this.color ("синий");
}
});
Еще одна простая форма для обнаружения столкновений — между двумя кругами. Этот алгоритм работает, беря центральные точки двух окружностей и обеспечивая, чтобы расстояние между центральными точками было меньше двух сложенных радиусов.
Игровой код
Перемещайте круг с помощью клавиш со стрелками.Зеленый цвет означает столкновение, синий - отсутствие столкновения.
# cr-stage {
позиция: статично! важно;
высота: 200 пикселей! важно;
}
Crafty.init (200, 200);
var dim1 = {x: 5, y: 5}
var dim2 = {x: 20, y: 20}
Crafty.c ("Круг", {
круг: функция (радиус, цвет) {
this.radius = радиус;
this.w = это.h = радиус * 2;
this.color = color || «# 000000»;
this.bind ("Переместить", Crafty.DrawManager.drawAll)
вернуть это;
},
draw: function () {
var ctx = Crafty.canvas.context;
ctx.save ();
ctx.fillStyle = this.color;
ctx.beginPath ();
ctx.arc (
this.x + this.radius,
this.y + this.radius,
this.radius,
0,
Math.PI * 2
);
ctx.closePath ();
ctx.fill ();
ctx.restore ();
}
});
var circle1 = Лукавый.e («2D, холст, круг»). attr (dim1) .circle (15, «красный»);
var circle2 = Crafty.e ("2D, холст, круг, четыре пути"). fourway (2) .attr (dim2) .circle (20, "синий");
circle2.bind ("EnterFrame", function () {
var dx = (circle1.x + circle1.radius) - (circle2.x + circle2.radius);
var dy = (circle1.y + circle1.radius) - (circle2.y + circle2.radius);
var distance = Math.sqrt (dx * dx + dy * dy);
if (distance var circle1 = {радиус: 20, x: 5, y: 5};
var circle2 = {радиус: 12, x: 10, y: 5};
var dx = circle1.x - circle2.x;
var dy = circle1.y - circle2.y;
var distance = Math.sqrt (dx * dx + dy * dy);
if (distance Примечание : Вот еще один пример без Canvas или внешних библиотек.
Хотя некоторые из этих алгоритмов обнаружения столкновений достаточно просты для вычисления, тестирование * каждого * объекта с любым другим объектом может оказаться пустой тратой циклов.Обычно игры разделяют столкновение на две фазы: широкую и узкую.
Широкая фаза
Широкая фаза должна дать вам список объектов, которые * могут * конфликтовать. Это может быть реализовано с помощью пространственной структуры данных, которая даст вам приблизительное представление о том, где существует объект и что существует вокруг него. Некоторыми примерами пространственных структур данных являются Quad Trees, R-Trees или Spacial Hashmap.
Узкая фаза
Если у вас есть небольшой список объектов для проверки, вы захотите использовать алгоритм узкой фазы (например, перечисленные выше), чтобы дать определенный ответ относительно того, есть ли коллизия или нет.
Теорема Монжа о трех окружностях и общих касательных
Пусть есть три окружности разного радиуса, полностью лежащие вне друг друга. Чтобы исключить тривиальный случай, предположим также, что их центры не коллинеарны, то есть три центра не лежат на одной прямой. В этих условиях шесть внешних касательных к двум из трех окружностей, взятых попарно, пересекаются в трех точках. Тогда три точки лежат на одной прямой.
Это известно как теорема Монжа о круге .
Эта задача почти сравнима с задачами «4 путешественника» и «9 точек». Она имеет «трехмерное решение», но ее также можно решить, не покидая самолета. Д. Уэллс рассказывает о Джоне Эдсоне Свите, инженере, чьей реакцией на приведенную выше диаграмму было: «Да, это совершенно очевидно».
Решения| Контакты | | Первая страница | | Содержание | | Геометрия | | Вверх |
Copyright © 1996-2018 Александр Богомольный
Решение 1
Ниже приводится фрагмент, выдвинутый Джоном Эдсоном Суитом [Wells, p. 172-174, Gardner, p.119].
Представьте, что у вас есть три разных сферы, лежащих на одной плоскости, скажем, на плоскости №1. В одном частном случае, когда существует вторая плоскость, плоскость № 2, касательная к трем сферам, но покрывающая их сверху, доказательство особенно интуитивно понятно. Ведь тогда плоскости №1 и №2 обязательно должны иметь общую линию l, линию их пересечения. Биссектриса телесного угла, образованного плоскостями №1 и №2, проходит через центры всех трех сфер. Это будет самолет №3, изображенный вверху страницы.По определению, самолет №3 проходит через l.
С другой стороны, любые две сферы можно вписать в конус. Любая плоскость (внешняя), касающаяся двух сфер, также будет касательной к охватывающему конусу. Следовательно, плоскости №1 и №2 касаются каждого из трех конусов. Теперь касательная к конусу плоскость обязательно содержит его вершину. Наконец, вершины конусов принадлежат обеим плоскостям №1 и №2, следовательно, прямой l и, следовательно, плоскости №3.
Обратите внимание, что плоскость № 3 пересекает конусы по общим касательным линиям, как на диаграмме.
Хьюберт Шатрик упростил доказательство, сократив количество плоскостей до двух.
Решение 1 '
Рассмотрим три окружности как экваториальные большие окружности трех сфер. Существует общая касательная плоскость, касающаяся каждого в северных полушариях (плоскость №2 выше), и ее пересечение с данной плоскостью (плоскость №3 выше) является необходимой линией, потому что линии, соединяющие пары точек контакта, являются образующими тангенциальных конусов. (см. Решение 1), которые также включают исходные касательные в качестве образующих.
Еще одно трехмерное решение было предложено Натаном Боулером:
Решение 2
Постройте 3 прямых конуса на трех кругах в качестве оснований с равными углами при вершинах. Внешняя общая касательная два a пара окружностей принадлежит плоскости, определяемой образующими конуса в точках касания. Это потому, что образующие образуют один и тот же угол с плоскостью окружностей. Таких общих касательных плоскостей три пары. Они пересекаются по трем прямым A ', B' и C ', соответствующим трем точкам A, B и C в теореме.Теперь A 'и B' пересекаются на вершине одного из конусов. Точно так же пересекаются B 'и C', а также C 'и A'. Таким образом, A ', B' и C 'компланарны, а значит, A, B и C коллинеарны.
Решение 3
Это решение принадлежит Стюарту Андерсону.
Назовите три окружности a, b и c так, чтобы общие касательные точек a и b пересекались в точке C, касательные точек a и c в точке B, а касательные точек b и c в точке A. Присваиваем каждой окружности массу (ma , mb или mc) обратно пропорционально его радиусу. Если мы используем положительную массу для каждой окружности, тогда центр масс каждой пары окружностей будет находиться на пересечении их внутренних касательных, но если мы сделаем одну массу положительной, а другую отрицательной, центр масс будет находиться на пересечении их внешние касательные.Это легко доказать, используя аналогичные треугольники и определение центра масс. (Если вам не нравится идея отрицательной массы, подумайте о силах, приложенных либо направленными в экран, либо из него, и используйте вместо этого центр силы.)
Теперь это известный факт, что координаты центра масс комбинированной системы - это просто средневзвешенное значение координат центров каждой системы в отдельности и, следовательно, коллинеарны с ними. Если я выберу системы {ma, -mb}, {mb, -mc} и {ma, -mc}, то наложение первых двух систем даст третью, следовательно, ее центр масс будет коллинеарен их.QED
Между прочим, это также показывает, почему вы не можете доказать теорему для внутренних касательных пар: если все массы положительны, вы не можете объединить две пары окружностей, чтобы получить оставшуюся пару, потому что отмена невозможна. Теорема снова работает с одной внешней касательной парой и двумя внутренними касательными парами: {ma, mb} {mc, -mb} = {ma, mc}.
Решение 4
Это решение принадлежит Мартину Ребасу.
Рассматривайте три круга как три сферы равного размера, но проецируемые в трехмерном пространстве, поэтому самый большой круг представляет сферу, ближайшую к зрителю, и так далее.Затем три пары касательных определяют три бесконечно длинных цилиндра, которые, очевидно (находясь в одной плоскости), должны отступать к одной и той же линии горизонта.
Решение 5
Это векторное решение взято из книги М. Эриксона Beautiful Mathematics:
Предположим, что это три окружности: C 1 , C 2 , C 3 , с центрами c 1 , c 2 , c 3 и радиусами r 1 , r 2 , r 3 .(Обратите внимание, что символы, выделенные жирным шрифтом, обозначают векторы.) Пусть p ij , i ≠ j, 0
p ij = c i + [r i / (r i - r j )] ( c i - c j ) = (r i c j - r j c i ) / (r i - r j ).
Отсюда следует, что
r 1 (r 2 - r 3 ) p 23 + r 2 (r 3 - r 1 ) p 13 + r 3 (r 1 - r 2 ) p 12 = 0,
и, следовательно, p 13 , p 12 , p 23 коллинеарны, поскольку сумма скалярных коэффициентов равна 0.
Замечание
Другое доказательство (и обобщение) можно получить с помощью теоремы Менелая.Кроме того, любые две окружности подобны и могут быть получены друг из друга преобразованием подобия (гомотетии) с центром в точке пересечения их общих касательных. Известно, что, как правило, если одна фигура гомотетична другой, а вторая - третьей, и произведение коэффициентов гомотетии положительно, но отлично от 1, то произведение двух гомотетий является гомотетией, а три центры гомотетии коллинеарны, см. Яглом, с. 27. Дополнительные доказательства также легко следуют из теоремы Дезарга.
Применительно к окружностям две окружности могут иметь 0, 1 или 2 пары общих касательных. В последнем случае одна пара называется внутренняя , другая внешняя . (На схеме показаны три пары внешних касательных, но любые две окружности имеют также внутренние касательные, которые пересекаются между окружностями.) Если количество внешних касаний нечетное (1 или 3), то центры гомотетий коллинеарны. . Чтобы понять это правило, представьте, что окружности и прямые линии ориентированы - к любому из них прикреплена стрелка, указывающая в положительном направлении обхода.Противоположное направление считается отрицательным.
Ориентированный круг может касаться другого ориентированного круга или ориентированной линии одним из двух способов. Либо направления обхода двух фигур в точке касания совместимы, либо «против волокон» - в зависимости от того, имеют ли фигуры противоположную ориентацию или одинаковую.
Приведенное выше правило становится понятным, если применить его к ориентированным линиям. Из трех кругов либо все имеют одинаковую ориентацию, либо ориентация одного отличается от ориентации двух других.В обоих случаях теорема применима к ориентированным касательным линиям, ориентация которых совместима с ориентацией окружностей.
Линия, проходящая через центры гомотетии трех (ориентированных) окружностей, известна как их ось гомотетии или ось подобия .
Список литературы
- М. Эриксон, Beautiful Mathematics , MAA, 2011
- M. Gardner, Колоссальная книга коротких головоломок и задач , W.W. Norton & Co., 2006 г.
- Д. Уэллс, Вы математик , John Wiley & Sons, 1995
- И. М. Яглом, Геометрические преобразования II , МАА, 1968
Теорема Монжа
- Три окружности и общие касательные
- Monge из Desargue
- Monge via Desargue
2D-задачи, которые можно решить с помощью 3D-Outlook
- Четыре путешественника, Решение
- Теорема Дезарга
- Круги Содди и точки Эппштейна
- Симметрии в треугольнике
- Три круга и общие аккорды
- Три окружности и общие касательные
- Три равных круга
- Менелай из 3D
- Стереографическая проекция и инверсия
- Стереографическая проекция и радикальные оси
- Сумма квадратов равностороннего треугольника
| Контакты | | Первая страница | | Содержание | | Геометрия | | Вверх |
Copyright © 1996-2018 Александр Богомольный
Сопряженная система - Simple English Wikipedia, бесплатная энциклопедия
В химии сопряженная система - это система связанных p-орбиталей с делокализованными электронами.Сопряженные системы создаются несколькими множественными связями, каждая из которых разделена одинарной связью. В общем, сопряженные системы могут снизить общую энергию молекулы и повысить ее устойчивость. Они могут содержать неподеленные пары, радикалы или ионы карбения. Соединение может быть циклическим, ациклическим, линейным или смешанным. В большинстве случаев атомы в молекуле удерживаются вместе одинарными связями (где орбитали соседних атомов перекрываются). Молекулы, которые имеют сопряженную систему, обладают уникальными свойствами, отличными от обычных соединений, созданных разделением делокализованных электронов между многими атомами.
Конъюгация - это перекрытие одной р-орбитали с другой через сигма-связь (или одинарную связь), которая находится между ними. (D-орбитали более крупных атомов также могут вносить вклад в сопряженную систему). [1]
Сопряженная система имеет область перекрывающихся p-орбиталей, соединяющих одинарные связи между ними. Они позволяют делокализовать пи-электроны по всем соседним выровненным p-орбиталям. [2] Пи-электроны принадлежат не одинарной связи или атому, а скорее группе атомов.
крупнейших сопряженных систем (с наибольшим числом общих электронов) находятся в графите, проводящих полимерах и углеродных нанотрубках.
Конъюгация с разными видами р-орбитальных донорных группРазличные типы молекулярных структур могут приводить к конъюгации. Для сопряжения все соседние атомы в цепочке должны иметь доступную p-орбиталь. Во многих случаях сопряженные системы представляют собой серию одинарных связей, за каждой из которых следует двойная связь. Существуют и другие системы.Например, фуран (см. Рисунок) представляет собой пятичленное кольцо с двумя чередующимися двойными связями и кислородом в позиции 1. Кислород в фуране имеет две неподеленные пары, одна из которых заполняет p-орбиталь в этой позиции. Неподеленный электрон пары делает возможным сопряжение на пятичленном кольце. Присутствие азота в кольце может быть источником пи-орбиталей, необходимых для конъюгации. Кроме того, пи-орбитали, необходимые для конъюгации, могут поступать от замещающих групп α к кольцу, например: карбонильная группа (C = O), иминная группа (C = N), винильная группа (C = C) или анион.
Хромофоры [изменить | изменить источник]
Сопряженные системы - это основные составляющие хромофоров. Хромофоры - это светопоглощающие части молекулы, которые могут вызывать видимый цвет соединения. Хромофоры часто присутствуют в различных органических соединениях, а иногда и в полимерах, которые окрашены или светятся в темноте. Хромофоры часто состоят из серии сопряженных связей и / или кольцевых систем, которые могут включать связи C-C, C = C, C = O или N = N. Часто хромофоры имеют ароматические кольца.
Химическая структура бета-каротина. Одиннадцать сопряженных двойных связей, образующих хромофор молекулы, выделены красным.неправильных глаголов | АНГЛИЙСКИЙ СТРАНИЦА
Словарь неправильных глаголов для изучающих английский язык на сайтеEnglishpage.com содержит более 370 неправильных глаголов, используемых в современном английском языке, а также карточки и упражнения для отработки этих форм. Чтобы просмотреть наш расширенный словарь неправильных глаголов , который содержит более 470 глаголов, включая редкие и устаревшие формы, щелкните здесь.
Список неправильных глаголов
Карточки и упражнения на неправильные глаголы
Если вы хотите выучить неправильные глаголы, вам нужно практиковаться, практиковаться, практиковаться. Ниже мы создали пять наборов карточек, а также простые упражнения на неправильные глаголы, чтобы помочь изучающим английский язык выучить 100 самых распространенных неправильных глаголов в английском языке.
Общие вопросы об английских неправильных глаголах
Что такое неправильные глаголы?
Неправильные глаголы - это глаголы, которые не подчиняются обычным правилам спряжения.Например, неправильный глагол быть имеет несколько уникальных форм ( я , вы , он ), которые сильно отличаются от обычных глаголов, таких как готовить ( я готовлю , вы готовите , он готовит ).Сколько неправильных глаголов в английском языке?
Englishpage.com провел обширный анализ текста более 2000 романов и ресурсов, и на данный момент мы обнаружили 680 неправильных глаголов, включая префиксные глаголы ( неправильно понимают, , перечитывают, ), а также редкие и устаревшие формы ( цветов, , между прочим). ).Какие примеры неправильных глаголов?
Хорошие примеры неправильных глаголов: иметь , понимать и рисовать . Обратите внимание, что в их прошлых формах было , понималось, и нарисовали. сильно отличаются от обычных глаголов, которые заканчиваются на -d или -ed. Дополнительные примеры см. В списке неправильных глаголов Englishpage.com.Какие неправильные глаголы встречаются в английском языке чаще всего?
Согласно анализу текста более 2000 романов и ресурсов, проведенного Englishpage.com, наиболее распространенными неправильными глаголами в английском языке являются: быть , иметь , сказать , сделать , знать , получить , см. , думаю, , идут и принимают .Есть ли большие различия в неправильных формах глаголов в британском и американском английском?
В то время как многие ссылки показывают сильные различия между британским и американским английским в употреблении неправильных глаголов, исследование Englishpage.com показывает, что существует гораздо больше пересечений, чем можно предположить из многих из этих ссылок. (Там, где мы действительно обнаружили реальную статистическую разницу, мы перечислили британские формы курсивом.)Какие времена глаголов имеют неправильные формы в английском языке?
В английском языке неправильные формы глаголов встречаются в простом настоящем и простом прошедшем времени, а также в причастиях прошедшего времени.Помните, что причастия прошедшего времени используются во многих формах глаголов, включая: совершенное настоящее, совершенное прошедшее время, совершенное будущее, пассивные формы и условные формы прошедшего времени.Подробнее о словаре неправильных глаголов
Для получения дополнительной информации о нашем словаре неправильных глаголов и наших исследованиях щелкните здесь.Четыре спряжения | Комментарии колледжа Дикинсона
171. Глаголы классифицируются по четырем регулярным спряжениям, которые различаются по основному гласному, который появляется перед -re в действующем инфинитиве настоящего.
| СОЕДИНЕНИЕ | БЕСКОНЕЧНОЕ ОКОНЧАНИЕ | ШТОК |
| 1-й | - ( - ) | -ā- |
| 2-я | -ēre ( mon-ēre ) | -ē- |
| 3-й | -re ( reg-ĕre ) | -ĕ- |
| 4-я | -īre ( aud-īre ) | -ī- |
172. Основные части глагола, показывающие три основы, определяющие его спряжение повсюду, -
- Индикатив настоящего времени ( amō ), показывающий стержень настоящего времени.
- Инфинитив настоящего времени ( amā-re ), показывающий основу настоящего.
- Идеальный указатель ( amāv-ī ), показывающий идеальный стержень.
- Средний причастия Совершенного причастия ( amāt-um ) или, если эта форма не используется, Будущего активного причастия ( amāt-ūrus ), демонстрирующего лежачий ствол.
173. Правильные формы четырех конъюгаций показаны ниже.
1-е спряжение:
Активный - amāre , amāre , amāvī , amātum [любовь]
Пассивный - amātum , amārī , amātu
Present Stem amā-
Perfect Stem
Perfect Stem
Шток для лежа на спине amāt-
2-е спряжение:
Активный - dēleō , dēlēre , dēlēvī , dēlētum [сглаживание]
Пассивный - dēleor , dēlērī , dēlētus
Present Perfect Stem- 97 Present Perfect
Шток для лежа на спине dēlēt-
Однако во втором спряжении характеристика -ē- редко появляется в Совершенном и Совершенном причастии.Таким образом, общий тип:
Активный - монет , монет , монумент , Монитум [предупреждающий]
Пассивный - монет , монет , Монитус
Настоящий стержень монет-
Идеальный стержень монумент-
Супинатор monit-
3-е спряжение:
Активный - тегов , тегов , тегов , тегов [обложка]
Пассивный - тегов , тегов , тегов
Настоящий стержень тегов -
Perfect Stem 797 Perfect Stem 39
Шток для лежа на спине tēct-
4-е спряжение:
Активный - audiō , audīre , audīvī , audītum [слышать]
Пассивный - audītus , audīrī , audītus
Present Stem audī-
97 Perfect Stem 39
- Шток лежа на спине audīt-
а. Во многих глаголах главные части принимают формы, принадлежащие двум или более различным спряжениям (см. § 189 ).
1-й и 2-й - dom , domāre , domuī , domitum [subdue]
2-й и 3-й - maneō , manēre , mānsī , mānsum [остаток]
3-й и 4-й - petō , petre , petīvī , petītum [seek]
4-й и 3-й - vinciō , vincīre , vīnxī , vīnctum [привязать]
Такие глаголы классифицируются в соответствии с тем, к какому спряжению принадлежит основа Present.
. Способ
построения эллипса по двум осям
Способ
построения эллипса по двум осям