Сопряжение радиусов – Сопряжения - Сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг

Содержание

Сопряжения — Сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

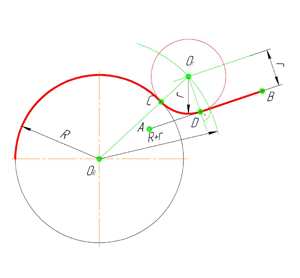
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.

Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

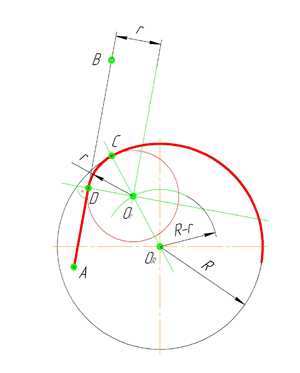
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

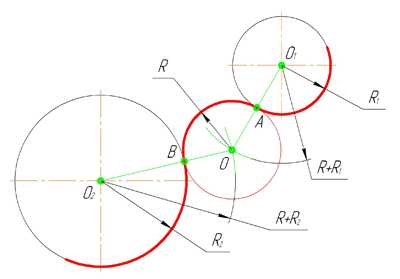
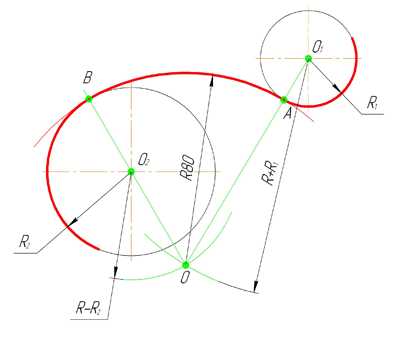
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

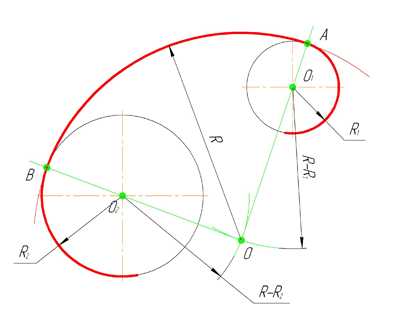
Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

chertimvam.ru

Учебно-методическое пособие «Техника выполнения сопряжений» — Информио

При изучении дисциплины «Начертательная геометрия и инженерная графика» студенты должны усвоить правила и последовательность выполнения геометрических построений и сопряжений. В этом отношении лучшим способом приобретения навыков построения являются задания по вычерчиванию контуров сложных деталей.

Прежде чем приступить к выполнению контрольного задания, нужно изучить технику выполнения геометрических построений и сопряжений по методическому пособию.

Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти:

Центр сопряжения – центр, из которого проводят дугу;
Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.

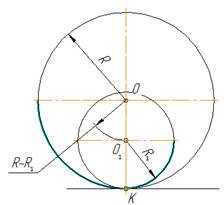
Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R. Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой (рис. 1)

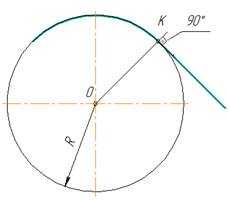
рис. 1

Переход от одной окружности к другой будет плавным, если окружности касаются.

Различают два случая касания дуг окружностей: внешнее (рис. 2) и внутреннее (рис.3).

При внешнем касании центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО₁ равно сумме радиусов окружностей R+R₁ и точка касания лежит на прямой ОО₁, соединяющей их центры.

При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО

1 равно разности их радиусов R-R₁ и точка касания К окружностей лежит на продолжении прямой ОО₁ (рис. 3).


рис. 2	рис. 3

Касание дуг окружностей:

рис. 2 – сопряжение двух окружностей (внешнее касание)

рис. 3 – сопряжение двух окружностей (внутреннее касание)

Сопряжение двух пересекающихся прямых

Даны пересекающиеся под прямым, острым и тупым углами прямые линии.

Требуется построить сопряжения этих прямых дугой заданного радиуса R.

рис. 4

Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и будет центом дуги сопряжения (рис. 4).
Перпендикуляры, опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки касания К и N.
Из точки О, как центра, описывают дугу заданного радиуса R.

рис. 5

Примечание.Для прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).

Сопряжение дуги окружности и прямой линии дугой заданного радиуса.

Внешнее касание

Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.

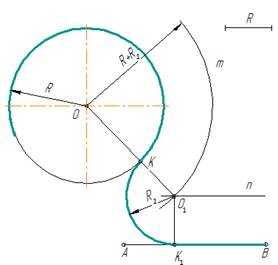
рис. 6

Для нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R₁и на расстоянии R₁– прямую n // AB. Точка О₁пересечения прямой n и дуги m будет центром сопряжения.
Для получения точек сопряжения: К и К₁ проводят линию центров ОО₁и восстанавливают к прямой АВ перпендикуляр ОК₁.
Из центра сопряжения О₁между точками К и К₁ проводят дугу сопряжения радиусом R₁

Внутреннее касание

В случае внутреннего касания выполняют те же построения, но дугу m вспомогательной окружности проводят радиусом R — R₁.

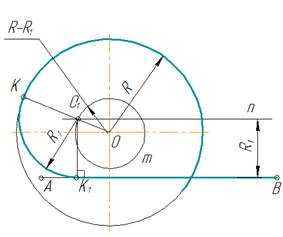
рис. 7

Сопряжение двух окружностей дугой заданного радиуса

Заданы две окружности радиусом R₁ и R₂. Требуется построить сопряжение дугой заданного радиуса R.

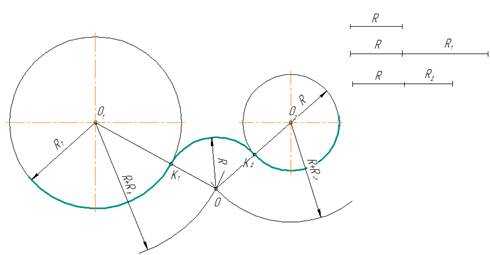
рис. 8

Внешнее касание

Для определения центра сопряжения О проводят вспомогательные дуги: из центра О₁окружности радиусом R + R₁ и из центра О₂ окружности радиуса R + R₂. Точка О пересечения этих дуг является центом сопряжения.
Соединяя центры О и О₁, а так же О и О₂ , определяют точки сопряжения (касания) К₁ и К₂.
Из центра О радиусом R проводят дугу сопряжения между точками К₁ и К₂

Внутреннее касание

При внутреннем касании выполняют те же построения, но дуги проводят радиусами

R -R₁ и R — R₂.

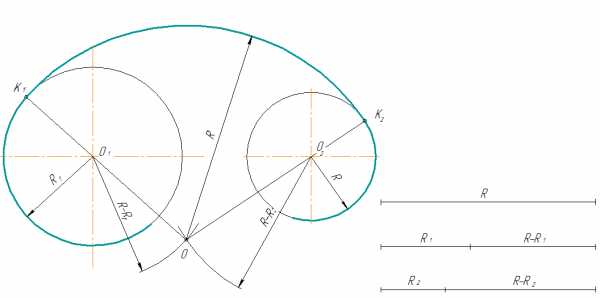
рис. 9

Смешанное касание

рис. 10

Центр сопряжения О находится в пересечении двух дуг, описанных из центра О₁радиусом R — R₁ и из центра О₂радиусом R + R₂

Примечание. При смешанном сопряжении центр О₁ одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R , а центр О₂ другой дуги – вне ее.

Частные случаи

Нахождение центра дуги заданного радиуса.

Задана дуга радиусом R, соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.

рис. 11

В основу построения положено нахождение точки О, равноудаленной от заданных прямых (рис. 11).

Из точки А ∈ m, как из центра, проводят дугу вспомогательной окружности с заданным радиусом R.
Проводят вспомогательную прямую l, параллельную прямой n, на расстоянии, равном заданному радиусу R.
Точка О – точка пересечения этих вспомогательных линий является центром заданной дуги. (рис. 12)

рис. 12

Боголюбов С.К. Инженерная графика: Учебник для средних специальных учебных заведений. – 3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392: ил.
Куприков М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил.
Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение. 1976. 336 с.

www.informio.ru

Сопряжение — Техническое черчение

Сопряжением называется плавный переход по кривой от одной линии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендикулярным к прямой в точке касания.

Сопряжение циркульных кривых возможно тогда, когда точка сопряжения будет являться одновременно и точкой касания сопрягаемых дуг. Следовательно, точка касания должна находиться на линии центров дуг окружностей.

Сопряжение пересекающихся прямых:

Пример 1. Даны пересекающиеся прямые AB и ВС и радиус сопряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в).

Сопряжение будет возможным, если прямые AB и ВС будут касательными к окружности радиуса R. Для нахождения центра этой окружности

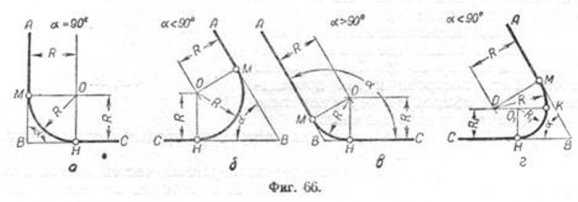
необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О.

Пример 2. Даны пересекающиеся прямые AB и ВС и радиусы сопряжения R и R1 Построение сопряжения возможно, если угол а<90.

Способ построения такого сопряжения приведён на фиг. 66,г.

Сопряжение параллельных прямых

Пример 1. Даны две параллельные прямые AB и СЕ и точки сопряжения В и С (фиг. 67).

Надо построить плавное сопряжение циркульными кривыми так, чтобы оно проходило через заданную точку K, посредине отрезка ВС.

Для определения радиусов и центров дуг сопряжения делим отрезки BK и КС прямыми так, чтобы они были перпендикулярны этим отрезкам и делили их пополам. Так как радиус сопряжения должен быть перпендикулярным к прямой в точке сопряжения, то для нахождения центров О дуг сопряжения восстанавливаем из точек В и С перпендикуляры до пересечения их с ранее проведёнными перпендикулярами к прямой ВС.

Точки пересечения этих перпендикуляров определят положение центров сопряжений О—О, а равные между собой отрезки 05 и ОС дадут величины радиусов сопряжений.

Пример 2 (фиг. 68), Этот пример отличается от предыдущего

тем, что точка К взята на прямой ВС произвольно, на некотором расстоянии e от прямой СЕ; следовательно, радиусы сопряжений R и R1— разные по величине. Ход построения сопряжений такой же, как и в предыдущем примере.

П p и м e p 3. Даны: расстояние между двумя параллельными прямыми AB и СЕ, равное сумме сопрягаемых радиусов R и R1, и точка сопряжения В (фиг. 69).

Для построения сопряжения проводим параллельно AB на расстоянии R вспомогательную прямую 0—01. Центр сопряжения 0 для радиуса R будет находиться на пересечении перпендикуляра, проведённого из точки В к вспомогательной прямой. Описывая из точки О дугу радиусом R, найдём точку К, из которой радиусом R1 делаем на вспомогательной прямой засечку, определяющую центр сопряжения O1. Из точки О1 опускаем перпендикуляр на прямую СЕ и, найдя точку сопряжения С, сопрягаем точки К и С дугой радиуса R1.

Сопряжение дуги окружности с прямой

Пример 1. Построим сопряжение дуги радиуса R с прямой AB радиусом R1 (фиг. 70). Для этого необходимо найти центр сопряжения 0 и точки сопряжения С и а. Точка С является одновременно точкой их касания и должна лежать на линии центров этих дуг. Радиус сопряжения должен быть перпендикулярен к прямой AB в точке касания а. Поэтому из центра О описываем радиусом, равным сумме R+R1, дугу.

На ней будет находиться центр сопряжения 0, для определения которого проводим параллельно AB на расстоянии R1 вспомогательную прямую ее до пересечения с проведённой дугой. Соединив точки O1и О, найдём точку сопряжения С. Для определения точки а опускаем из О1 перпендикуляр на AB. Далее, радиусом R1 из центра O1 сопрягаем точки а и С.

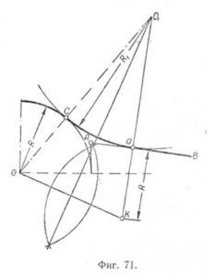
Пример 2. Даны: дуга радиуса R, прямая AB и точка сопряжения а. Требуется найти точку сопряжения С и радиус сопряжения R1 (фиг. 71). Проводим через точку а перпендикуляр к AB, на котором откладываем вниз отрезок aK, равный R. Соединяем центр О с точкой К. Для нахождения центра сопряжения O1 проводим через середину отрезка OK перпендикулярную прямую, которая пересечётся с прямой aK в точке O1Соединив О1 с О, найдём точку сопряжения С.

Сопряжение дуг окружностей дугой окружности

Сопряжение дуг окружностей может быть внешним (фиг. 72) или внутренним (фиг. 73). В обоих случаях сопряжения выполнимы: 1) если расстояние С между центрами О и 01сопрягаемых дуг больше суммы их радиусов R и R1 (фиг. 72, а и 73, а), т.е. C>R+R1 и 2) когда C<R+R1(фиг. 72, б и 73, б). Сопряжение выполнить невозможно, если один из радиусов сопрягаемых дуг окажется большим или равным сумме величины радиуса второй сопрягаемой дуги и расстояния между центрами сопрягаемых дуг, т. е. если получится соотношение R>=C+R1 или R1>=C+R. Для внешнего сопряжения дуг сопряжение окажется также невозможно, если радиус сопрягающей дуги R2 будет меньше полуразности С — (R+R1), т. е. R2 <

<(C-(R+R1))/2. Во всех случаях решение задачи сводится к нахождению центра 02сопрягающей дуги радиуса R2 и точек сопряжения A и В.

Внешнее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 72,a). Требуется построить сопряжение при условии, что C>R+R1.

Для построения сопряжения необходимо определить центр 02 и точки сопряжения Л и В. Для нахождения центра 02 проводим из центра О дугу радиуса R2+R, а из центра О1 дугу радиуса R2+R1 Пересечение этих дуг определит центр 02. Соединив прямыми центры О и 01 с центром 02, найдём на пересечении этих прямых с соответствующими дугами точки сопряжения A и В. Полученные точки сопрягаем радиусом R2.

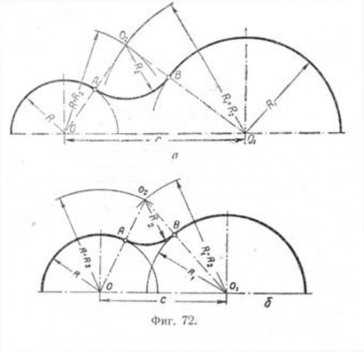
Построение сопряжения для случая, когда C<R+R1, дано на фиг. 72, б. Построение этого сопряжения ничем не отличается от предыдущего построения.

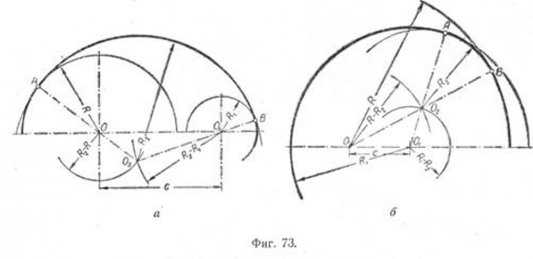
Внутреннее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 73, а). Требуется построить сопряжение, если C>R+R1 Решение этой задачи такое же, как и предыдущей, с той лишь разницей, что из центров О и О1 проводятся дуги радиусами R2 — R и R2 — R1.

На фиг. 73, б приведено построение сопряжения для случая, когда C<R+R1. Это построение ничем не отличается от построения, приведённого в предыдущем примере (фиг. 73,a).

www.nacherchy.ru

Урок по черчению «Сопряжение»

Сопряжения

(Показать несколько деталей, имеющих скругления).

Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе.

На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением.

При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т.е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно разделить на 3 группы.

Первая группа задач включает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построим окружность, касательную к прямой.

Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.

Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 1).

Рис. 1

Точка касания выбирается произвольно.

Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (О1 , О2 и т.д.) будут находиться на одинаковом расстоянии от заданной прямой, т.е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 1). Назовем эту линию линией центров.

Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например, точку О.

Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

Запишите в свои тетради в клетку следующие правила:

Если в сопряжении участвует прямая линия, то:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

2) точка касания лежит на перпендикуляре, проведенном из центра окружности к заданной прямой.

Сопряжение двух прямых.

На плоскости две прямые могут располагаться параллельно или под углом друг к другу.

Чтобы построить сопряжение двух прямых, необходимо провести окружность, касательную к этим двум прямым.

Откройте рабочие тетради на странице 31.

Рассмотрим сопряжение двух непараллельных прямых.

Две непараллельные прямые располагаются друг к другу под углом, который может быть прямым, тупым или острым. При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса (рис.1). Скругление углов на чертеже есть не что иное, как сопряжение двух непараллельных прямых дугой окружности заданного радиуса. Для выполнения сопряжения необходимо найти центр дуги сопряжения и точки сопряжения.

Известно, что если в сопряжении участвует прямая линия, то центр дуги сопряжения находится на линии центров, которая проводится параллельно заданной прямой на расстоянии, равном радиусу R дуги сопряжения.

Поскольку угол образован двумя прямыми, то проводят две линии центров параллельно каждой прямой на расстоянии, равном радиусу R дуги сопряжения. Точка их пересечения будет центром дуги сопряжения.

а)

б)

в)

Рис.2

Для нахождения точек сопряжения из точки О опускают перпендикуляры на заданные прямые и получают точки сопряжения К и К1. Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.

При построении сопряжения прямого угла упрощается проведение линии центров, так как стороны угла взаимно перпендикулярны. От вершины угла откладывают отрезки, равные радиусу R дуги сопряжения, и через полученные точки К и К1, которые будут точками касания, проводят две линии центров, параллельные сторонам угла. Они будут являться одновременно и линиями центров, и перпендикулярами, определяющими точки сопряжения К и К1 (стр. 31, рис.1).

Стр. 31, задание 4. Сопряжение двух параллельных прямых.

Чтобы построить сопряжение двух параллельных прямых, необходимо провести дугу окружности, касательной к этим прямым (рис.3).

а)

б)

в)

Рис.3

Радиус этой окружности будет равен половине расстояния между заданными прямыми. Так как точка касания не задана, подобных окружностей можно провести множество. Центры их будут находиться на прямой, проведенной параллельно заданным прямым на расстоянии, равном половине расстояния между ними. Эта прямая будет линией центров.

Точки касания (К1 и К2) лежат на перпендикуляре, опущенном из центра касательной окружности на заданные прямые (рис. 3а). Так как центр касательной окружности не задан, перпендикуляр проводится произвольно. Отрезок КК1 делят пополам (рис.3б), проводят через точки пересечения засечек прямую линию параллельно заданным прямым, на которой будут располагаться центры окружностей, касательных к заданным параллельным прямым, т.е. эта линия будет линией центров. Поставив ножку циркуля в точку О, проводят дугу сопряжения (рис. 3в) от точки К до точки К1.

Построение прямых, касательных к окружностям

(Р.Т. стр.33).

Задание 1. Проведите прямую, касательную к окружности через точку А, лежащую на окружности.

Из точки О проводим прямую OB через точку А. Из точки А любым радиусом проводим окружность. При пересечении с прямой получили точки 1 и 2. Из этих точек любым радиусом проводим дуги до пересечения между собой в точках Cи D. Из точки Cили Dпроводим прямую через точку А.

Она и будет касательной к окружности, так как касательная всегда перпендикулярна радиусу, проведенному в точку касания.

Задание 2.

Это построение аналогично построению перпендикуляра к прямой через заданную точку, которое можно выполнить с помощью двух угольников.

Сначала угольник 1 кладется так, чтобы его гипотенуза совпадала с точками O и A.Затем кугольнику 1 прикладывается угольник 2, который будет направляющим, т.е. по которому будет сдвигаться угольник 1. Потом угольник 1 приставляем другим катетом к угольнику 2. Затем катаем угольник 1 по угольнику 2 до тех пор, пока гипотенуза не совпадет с точкой A. И проводим прямую, касательную к окружности через точку A.

Задание 3. Проведите прямую, касательную к окружности через точку, не лежащую на этой окружности.

Даны окружность радиусом R и точка А, не лежащая на окружности, требуется провести из точки А прямую, касательную к данной окружности в верхней ее части. Для этого необходимо найти точку касания. Мы знаем, что точка касания лежит на перпендикуляре, проведенном из центра окружности к касательной прямой. Следовательно, касательная и перпендикуляр образуют прямой угол.

Зная, что всякий угол, вписанный в окружность и опирающийся на ее диаметр, является прямым, соединив точки А и О, принимают отрезок АО за диаметр описанной окружности. В пересечении описанной окружности и окружности радиуса R будет находиться вершина прямого угла (точка К). Отрезок АО делим пополам при помощи циркуля, получаем точку О1 (рис.4, б).

Из центра О1 радиусом, равным отрезку АО1, проводим окружность, получаем точки К и К1 в пересечении с окружностью радиуса R (рис.4 ,в).

Так как нужно провести только одну касательную к верхней части окружности, выбирают нужную точку касания. Этой точкой будет точка К. Точку К соединяем с точками А и О, получаем прямой угол, который опирается на диаметр АО описанной окружности радиусом R1. Точка К – вершина этого угла (рис.4, г), отрезки ОК и АК – стороны прямого угла, следовательно, точка К будет искомой точкой касания, а прямая АК – искомой касательной.

б)

а)

г)

в)

Рис.4

Проведение прямой, касательной к двум окружностям.

Даны две окружности радиусами R и R1 , требуется построить касательную к ним. Возможны два случая касания: внешнее и внутреннее.

При внешнем касании касательная прямая находится с одной стороны от окружностей и не пересекает отрезок, соединяющий центры данных окружностей.

При внутреннем касании касательная прямая находится с разных сторон от окружностей и пересекает отрезок, соединяющий центры окружностей.

Стр. 33. Задание 5. Проведите прямую, касательную к двум окружностям. Касание внешнее.

Прежде всего необходимо найти точки касания. Известно, что они должны лежать на перпендикулярах, проведенных из центров окружностей (О и О1) к касательной.

Из точки О проводим окружность радиусом R — R1 ,так как касание внешнее.

Разделим расстояние ОО1 пополам и проведем окружность радиусом R=ОО2=О1О2

Эта окружность пересекает окружность с радиусом R-R1 в точке К. Соединяем эту точку с О1.

Из точки О через точку К проводим прямую до пересечения с окружностью радиусом R. Получили точку К1 – первую точку касания.

Из точки О1 проводим прямую, параллельную КК1, до пересечения с окружностью радиусом R1. Получили вторую точку касания К2. Соединяем точки К1 и К2. Это и есть касательная к двум окружностям.

Задание 6. Проведите прямую, касательную к двум окружностям. Касание внутреннее.

Построение аналогичное, только при внутреннем касании радиус вспомогательной окружности, проводящейся из точки О равен сумме радиусов окружностей R+R1.

Вторая группа задач на сопряжения включает в себя задачи, в которых участвуют только окружности и дуги. Плавный переход одной окружности в другую может происходить или непосредственно касанием, или через третий элемент – дугу окружности.

Касание двух окружностей может быть внешним (РТ: стр.32, рис.3) или внутренним (РТ: стр.32, рис.4).

Задание 3 (стр. 32)

При внешнем касании двух окружностей расстояние между центрами этих окружностей будет равно сумме их радиусов.

Из точки О радиусом R+RC проведем дугу. Из точки О1 радиусом R1+RCпроведем дугу до пересечения с первой дугой. Получили точку ОС — центр сопряжения.

Соединяем точки О и О1 с центром сопряжения ОС. На окружностях получили точки касания (сопряжения).

Из точки ОС радиусом сопряжения RC30 соединяем точки касания.

Задание 4 (стр. 32)

При внутреннем касании двух окружностей одна из касательных окружностей находится внутри другой окружности, и расстояние между центрами этих окружностей будет равно разности их радиусов.

Из точки О радиусом (RC– R)проведем дугу. Из точки О1 радиусом (RC– R1)проведем дугу до пересечения с первой дугой. Получили точку ОС — центр сопряжения.

Центр сопряжения ОС соединяем с точками О и О1 с и продлеваем прямую дальше.

На окружностях получили точки касания (сопряжения).

Из точки ОС радиусом сопряжения RC60 соединяем точки касания.

Третья группа задач на сопряжения включает в себя задачи на сопряжения прямой и дуги окружности дугой заданного радиуса.

Выполняя такое задание, решают как бы две задачи: проведение касательной дуги к прямой и касательной дуги к окружности. Касание в этом случае может быть как внешним, так и внутренним.

РТ: стр. 32. Задание 1. Сопряжение окружности и прямой. Касание внешнее. RC 20.

Заданы прямая и окружность радиусом R, требуется построить сопряжение дугой радиуса RC 20.

Так как в сопряжении участвует прямая линия, то центр дуги сопряжения находится на прямой, проведенной параллельно заданной прямой на расстоянии, равном радиусу сопряжения RC 20. Поэтому параллельно заданной прямой на расстоянии 20 мм проводим еще одну прямую.

А центр дуги сопряжения при внешнем касании двух окружностей находится на окружности радиуса, равного сумме радиусов Rи RC. Поэтому из точки О радиусом (R+ RC) проводим дугу до пересечения с новой прямой (линией центров). Получим точку ОС, которая является центром сопряжения.

Затем находим точки касания. Первая точка касания — это перпендикуляр, опущенный из центра сопряжения на заданную прямую. Вторую точку сопряжения находим, соединив центр сопряжения ОС и центр окружности R. Точка касания будет лежат на первом пересечении с окружностью, так как касание внешнее.

Затем из точки ОС радиусом RC 20 соединяем точки сопряжения.

РТ: стр. 32. Задание 2. Сопряжение окружности и прямой. Касание внутреннее. RC60.

Параллельно заданной прямой проводим линию центров на расстоянии 60 мм. Из точки О радиусом (Rс- R) проводим дугу до пересечения с новой прямой (линией центров). Получим точку ОС, которая является центром сопряжения.

Из ОС проводим прямую через центр окружности точку О и перпендикуляр на заданную прямую. Получаем две точки касания. И затем из центра сопряжения радиусом 60 мм соединяем точки касания.

infourok.ru

Радиус сопряжения — Энциклопедия по машиностроению XXL

Для пояснения всех последующих построений на рис. 70, б отдельно вынесены элементы геометрических построений контура, распределенные по следующим группам скругление углов, касательные к дугам окружностей, сопряжение прямой и дуги окружности дугой заданного радиуса, сопряжение двух дуг окружностей дугой заданного радиуса, сопряжение двух дуг окружностей дугой, проходящей через заданную точку. [c.91]
В конструкциях деталей следует избегать выступов, пазов и отверстий, расположенных перпендикулярно к оси прессования (рнс. 8.11, а). Их следует заменять соответствующими элементами, расположенными в направлении прессования. Процесс формообразования деталей из композиционных материалов сопровождается значительной усадкой, поэтому в их конструкциях нельзя допускать значительной разностенности, которая вызывает коробление и образование трещин (рис. 8.11,6—г). Разностенность не должна превышать 1 3. В зависимости от габаритных размеров детали, используемого материала и других факторов оптимальной толщиной стенок считается 0,5—5 мм, а минимальными радиусами сопряжений — 0,5—2 мм. [c.439]

В первой части таблицы приводят обозначение сопрягаемой цепи. Во второй части таблицы указывают параметры звездочки число зубьев, профиль зуба со ссылкой на стандарт и указанием о смещении, класс точности, радиус впадины, радиус сопряжения, радиус головки зуба, половину угла впадины, угол сопряжения. [c.352]

При расчете геометрические параметры сварного соединения (см. рис. 1.14) и механические свойства стали ЮХСНД [262] были приняты следующие s = 20 мм /t/s = 0,6 b/s = 3 R/s = = 0,025 R — радиус сопряжения шва с основным металлом) I/s = 20 ат = 400 МПа Е = 2- 0 МПа = 2-10з МПа (От, Е и Ей — соответственно предел текучести, модули Юнга и упрочнения исследуемого материала). Принималось, что реология деформирования стали ЮХСНД описывается схемой транс- [c.46]

Радиус впадин зуба Диаметр окружности впадин Радиус сопряжения [c.293]

При определении минимальных радиусов сопряжения стенок различной толщины можно пользоваться приведенными выше соотношениями, заменив 5 средним арифметическим 5о = 0,5 (5 4- s) толщин сопрягаемых стенок (виды 3, и). При небольшой разнице толщин можно принимать 5о = 5. [c.80]

Следует избегать соединения стенок под острым углом (вид. /). Если это неизбежно, то радиус сопряжения принимают не менее (0,5 ч- 1)5о. [c.80]

Найденные из приведенных ориентировочных соотношений радиусы округляют до ближайших стандартных размеров Р = 1, 2, 3, 5, 8, 10, 15, 25, 30, 40 мм). Так как небольшое изменение радиусов сопряжений мало влияет на качество отливки, то рекомендуется унифицировать радиусы. [c.81]

Для испытанных труб магистральных трубопроводов радиус сопряжения основного металла с наплавленным равен 0,25—0,5 мм, средние значения высоты выступа сварного шва и его ширины составляли соответственно 3 и 20 мм. Значение коэффициента концен- [c.171]

При отливке образцов в металлические формы радиус сопряжения (галтель) принимается равным 50 мм. [c.456]

Радиус сопряжения рабочей части с головкой принимается равным 25—40 мм в зависимости от диаметра фрезы, применяемой при изготовлении образцов, при этом принимает значения 20 — 25 мм соответственно. [c.458]

Радиус сопряжения г поверхностей смежных участков профиля i [c.65]

Проточки за резьбой в том случае, когда диаметр тела болта равен диаметру резьбы, желательно делать длиной, равной (0,5 -т- 0,6)[c.187]

Допуск на толщину днищ у борта не более-1-10 /о—0. Допуск на размеры большой и малой осей лаза не более 1 мм. Допуск на радиус сопряжения выпуклой поверхности днища с бортом лаза не более + 5 мм. [c.536]

Предел прочности при растяжении в кг мм Задний угол Передний угол у Угол в > плане Радиус сопряжения задних граней г в мм Угол наклона главной режущей кромки [c.91]

Чтобы повысить прочность детали толщина стенок в углах должна быть не менее 0,8 мм и на 0,5—1,0 мм больше толщины сопрягаемых стенок. Плавность утолщения в углах будет обеспечена, если радиусы сопряжения внутренних и наружных поверхностей одинаковы. [c.54]

Минимальные радиусы сопряжений прямых или кривых частей контура при вырубке и пробивке обычными штампами [c.153]

У резцов с передней поверхностью по первой и второй формам величина радиуса сопряжения берется по формуле [c.304]

Геометрические сопряжения можно y jjOBHO разделить на непосредс венные сопряжения, когда одна линия (например, дуга окружносги) плавно переходит в другую (например, в прямую) без промежуточных линий и сопряжения промежуточными дугами окружностей радиуса R. Эти дуги называются дугами сопряжения, а радиусы — радиусами сопряжения. [c.39]

Таблица параметров еостоич из двух частей, разделенных сплошной основной линией. В первой части таблицы приводят обозначение сопрягаемой цепи. Во второй части указывают параметры звездочки число зубьев, профиль зуба со ссылкой иа стандарт и указанием о смещении, класс точности, радиус впадины, радиус сопряжения, радиус головки зуба, половину угла впадины, угол сопряжения. [c.322]

Другие параметры звездочки определяют радиус впадины г по формуле, приведенной на с. 273 радиус сопряжения (рис. 19.1, а), r = , 3025d + -(-0,05 мм радиус головки зуба Г2 = = п ,(1,24со5(р 4- 0,08соз р — 1,3025) -— 0,05 мм, где половина угла зуба Ф=17° — 64°/г угол сопряжения р= = 18°—60°/2 половина угла впадины и=55°—60°/г 1 — диаметр ролика [c.352]

Канавку для выхода шлифовального круга, которая существенно повышает концентрацию напряже1ий, следует заменить галтелью, по возможности увеличивая радиус сопряжения. Шлицевое соединение, особенно эвольвентное, меньше снижает выносливость вала, чем шпоночное. Упрочнение носа ,очной поверхности вала обкаткой роликами или шариками може повысить предел выносливости вала на 80… 100 %. Существует рзд других конструктивных и технологических приемов по повышенрю выносливости валов. Выходные концы валов редукторов выполняют цилиндрическими и коническими. Посадка на конус обеспечивает легкость сборки и разборки, точность базирования, надежность крепления. [c.62]

Влияние галтелей, скосов и конусов. Массу деталей можно заметно снизить увелпчение.м радиусов сопряжения стенок детали, т. е. приданне.м им более плавных очертаний. [c.118]

Диаметр отверстия диафрагмы и трубки подвода дополнительного потока = 0,7d . Длина трубы в зависимости от решаемых задач и технических условий выбирается L = 3d или L = 9d . Щелевой зазор диффузора 5 = 0,06rf , радиус сопряжения R = 0,3rf и длина ввода трубки подвода дополнительного потока = 0,33й1 . Наружный диаметр диффузора составляет (4—5)rf . Т. е. все размеры, необходимые для конструкторской прорисовки трубы, определены. [c.229]

Размеры детали или отверстия прямоугольной формы указывают на полке линии-выноски в виде произведения большей стороны на меиьн1ую (рис. 6.41, а). Размеры элементов, образованных сопрягающимися параллельными линиями, допускается проставлять, не указывая радиус сопряжения (рис. 6.41, б). [c.111]

Radius (раДиус) — позволяет задать радиус скругления, то есть радиус дуги, соединяющей сопрягаемые объекты. По умолчанию радиус сопряжения равен 0.5000 или последнему введенному значению. Изменение радиуса действует только на выполняемые после этого сопряжения, оставляя неизменными существующие. [c.281]

Радиусы сопряжения R Радиусы сопряжений необраба тываемых поверхностей лопатки [c.129]

В команде PILLET сначала нужно задать радиус сопряжения, а затем указать сопрягаемые линии. В команде HAMFER нужно задать размеры фаски а и Ь (рис. 141), а затем указать первую и вторую линии. [c.155]

В случае необходимости выбирают размеры ребер и расстояния между ними. К основным размерам поковок с ребрами (рис. 5.33) относятся радиусы сопряжений R, радиусы закруглений R[, высота ребра h, толщина ребра, равная 2R], углы наклона полотна -у-Максимальное расстояние а между ребрами для всех марок материалов зависит от высоты ребра при высоте ребра /г 1б мм а = = (30…35) s при /1 35,5 мм а=(25…30) s при /i125 мм —от О до Г 30. [c.126]

Рис. 4.27. Кривые распределения осевых термоупругих напряжений на внешней (сплоишые линии) и внутренней (штрих-1 ктирные) поверхностях ререходной зоны модельного цилиндрического корпуса в зависимости от радиуса сопряжения фланца с оболочкой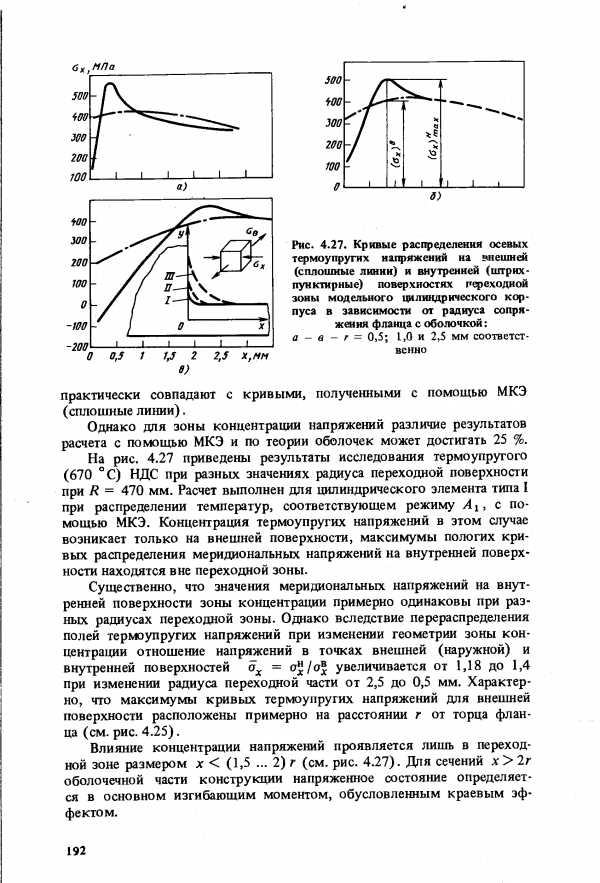

После определения усилий несложно произвести расчет методом конечных элементов иапря кенного и деформированного состояния фланцев и болтов ио заданным нагрузкам. Результаты расчета соединения (см. рис. 8.2), стянутого восемью болтами с резьбой М12, ирн Р=120 кН и Qo = 25 кН показаны на рис. 8.5. Несложно заметить, что в зоне сопряжения фланца с трубой имеется концентрация напряжений, которая может быть снижена увеличением радиуса сопряжения. [c.146]

Дополнительная режущая кромка должна быть прямолинейной и установлена строго параллельно подаче. При нежесткой системе станок—деталь—инструмент радиус сопряжения главной и дополнительной кромок г = 1,0-г-1,5 мм, при жесткой г —до 3 мм. [c.271]

На рис. 4.1 показана принятая расчетная схема патрубковой зоны ВВЭР, включающая в себя щшиндрическую оболочку переменной толщины (патрубок) и кольцевую пластину толщиной, равной толщине стенки корпуса реактора. Эта пластина заменяет собой часть оболочки корпуса, примыкающей к патрубку. При этом сохраняется реальная геометрия перехода патрубка в корпус — толщины, радиусы сопряжения, расположение и разделка сварного шва приварки патрубка к воротнику обечайки корпуса реактора. [c.121]

М1иш.мальный радиус (для мелких изделий) R = 0,5 мм для средних и крупных изделий следует применять радиусы R = 1 3 мм. Большие радиусы требуют применения пальцевых фрез с sanpaBKoii торца фрезы по сфере или тороиду с большим радиусом, что определяет диаметр фрезы, а следовательно, и радиус сопряжений вертикальных стенок друг с другом в илаие. [c.246]

Испытания производятся с оптимальными углами заточки—передним ч и задним а, которые устанавливаются экспериментально при постоянных значениях главного угла в плане главной режущей кромки Х=0 ,. радиуса сопряжения задних граней г — 1,5 мм, Оптимальные углы определяются при постоянной скорости резания 1г=сопб1, глубине резания / — 2 мм, подаче 5 = 0.5 мм об и стойкости резцов не менее 10 мин. Об- Г работка стали производится с охлаждением 54/о-ным раствором эмуль-сола в количестве 10 л/мин, обработка чугуна—всухую. [c.281]

mash-xxl.info

Использование сопряжения при построении чертежей. Черчение сопряжений

Форма многих деталей имеет плавный переход одной поверхности в другую (рис. 59). Для построения на чертежах контуров таких поверхностей используются сопряжения — плавный переход одной линии в другую.

Для построения линии сопряжений необходимо знать центр, точки и радиус сопряжения.

Центром сопряжения является точка, равноудаленная от сопрягаемых линий (прямых или кривых). В точках сопряжений происходит переход (касание) линий. Радиусом сопряжения называется радиус дуги сопряжения, с помощью которой происходит сопряжение.

Рис. 59. Примеры плавного соединения поверхностей хлебницы и линий на проекции ее боковой стенки

Рис. 60. Сопряжение углов на примере построения проекции боковой стенки хлебницы

Центр сопряжения должен находиться на пересечении дополнительно построенных линий (прямых или дуг), равноудаленных от заданных линий (прямых или дуг) либо на величину радиуса сопряжения, либо на специально рассчитываемое для данного типа сопряжения расстояние.

Точки сопряжения должны находиться на пересечении заданной прямой с перпендикуляром, опущенным из центра сопряжения на заданную прямую, либо на пересечении заданной окружности с прямой, соединяющей центр сопряжения с центром заданной окружности.

Сопряжение углов. Рассмотрим последовательность сопряжения углов (рис. 60) на примере построения проекции боковой стенки хлебницы:

1) построим трапецию, условно принимая ее за изображение формы заготовки для стенки хлебницы;

2) найдем центры сопряжения как точки пересечения вспомогательных линий, равноудаленных от сторон трапеции на расстояние, равное радиусу сопряжения, и параллельных им;

3) найдем точки сопряжения — точки пересечений перпендикуляров, опущенных на стороны трапеции из центров сопряжения;

4) из центров сопряжения проведем дуги радиусом сопряжения от одной точки сопряжения до другой; при обводке полученного изображения вначале обведем дуги сопряжений, а затем — сопрягаемые линии.

Сопряжение прямой и окружности дугой заданного радиуса. Рассмотрим это на примере построения фронтальной проекции детали «Опора» (рис. 61). Будем считать, что большая часть построения проекции уже сделана; необходимо отобразить плавный переход цилиндрической части поверхности к плоской. Для этого необходимо выполнить сопряжение окружности (дуги окружности) с прямой линией заданным радиусом:

1) найдем центры сопряжения как точки пересечения четырех вспомогательных линий: двух прямых, параллельных верхнему ребру основания «Опоры» и удаленных от нее на расстояние, равное радиусу сопряжения, и двух вспомогательных дуг, отстоящих от заданной дуги (цилиндрической поверхности) «Опоры» на расстояние, равное радиусу сопряжения;

2) найдем точки сопряжения как точки пересечения: а) заданных прямых (ребер «Опоры») с перпендикулярами, опущенными к ним из центров сопряжения; б) заданной дуги, изображающей на чертеже цилиндрическую поверхность опоры, с прямыми, соединяющими центры сопряжения с центром сопрягаемой дуги;

3) из центров сопряжения проводим дуги радиусом сопряжения от одной точки сопряжения до другой. Обводим изображение.

Сопряжение дуг окружностей дугами заданного радиуса. Рассмотрим это на примере построения фронтальной проекции формы для выпечки печенья (рис. 62), имеющей плавные переходы одной поверхности в другую:

1) проведем вертикальную и горизонтальные осевые линии. На них найдем центры и проведем три дуги радиусом R;

2) найдем центр сопряжения двух верхних окружностей как точку пересечения вспомогательных дуг радиусами, равными сумме радиусов заданной окружности (R) и сопряжения (R₁), т .e.R + R₁;

3) найдем точки сопряжения как точки пересечения заданных окружностей с прямыми, соединяющими центр сопряжения с центрами окружностей. Такое сопряжение называют внешним сопряжением;

Рис. 61. Сопряжение дуги и прямых линий на примере построения фронтальной проекции детали «Опора»

Рис. 62. Сопряжение трех дуг окружностей дугами заданных радиусов на примере
построения фронтальной проекции формы для выпечки печенья

4) построим сопряжения двух окружностей дугой заданного радиуса сопряжения R₂. Сначала найдем центр сопряжения перассечением дуг вспомогательных окружностей, радиусы которых равны разности радиуса сопряжения R₂ и радиуса окружности R, т. е. R₂ — R. Точки сопряжения получены на пересечении окружности с продолжением линии, соединяющей центр сопряжения с центром окружности. Из центра сопряжения проведем дугу радиусом R₂. Такое сопряжение называется внутренним сопряжением;

5) аналогичные построения выполним с другой стороны от оси симметрии.

cherch.ru

Как сделать сопряжение?

Здравствуйте! Рада видеть вас на втором уроке по 2D моделированию. Изучив его, вы с легкостью выполните чертежи деталей, содержащие сопряжения. Что такое сопряжение?

Сопряжение – это плавный переход одной линии в другую. Например, переход прямой линии в дугу, двух дуг.

Сопряжение окружностей:

При внутреннем сопряжении центры сопрягаемых окружностей находятся внутри радиуса сопрягающей их дуги.

При внешнем сопряжении центры сопрягаемых окружностей находятся вне радиуса сопрягающей дуги.

При смешанном сопряжении центр одной из окружностей находится внутри радиуса сопрягающей дуги, а центр другой вне его.

Учиться будем на примере детали «подвеска», задачник Р. С. Мироновой, 2001 год, стр. 18, вариант 6.

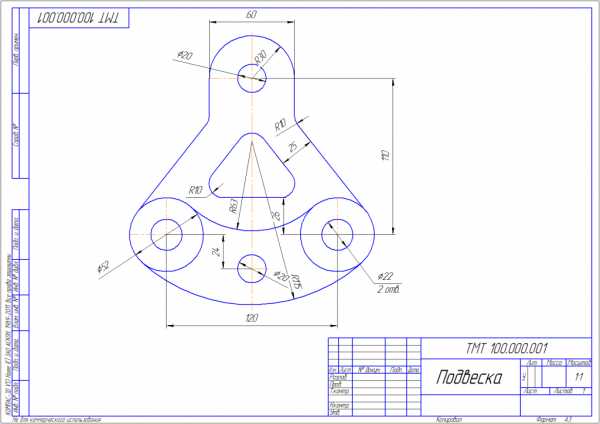
готовый чертеж детали с сопряжением

Анализ чертежа

1. Габаритные размеры 172*180 мм. Формат А4 не подойдет. Выбираем А3, ориентация горизонтальная.

2. Порядок вычерчивания пусть будет таким: сначала намечаем центры всех окружностей, вычерчиваем их, обводим контур, строим сопряжения, проставляем размеры, заполняем основную надпись.

3. Специальных требований к детали нет.

Приступаем. Смотрим видеоурок.

Скачать чертеж детали бесплатно здесь

veselowa.ru

Сопряжение радиусов – Сопряжения — Сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг