|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 2 Внешнее касание
Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.
рис. 6
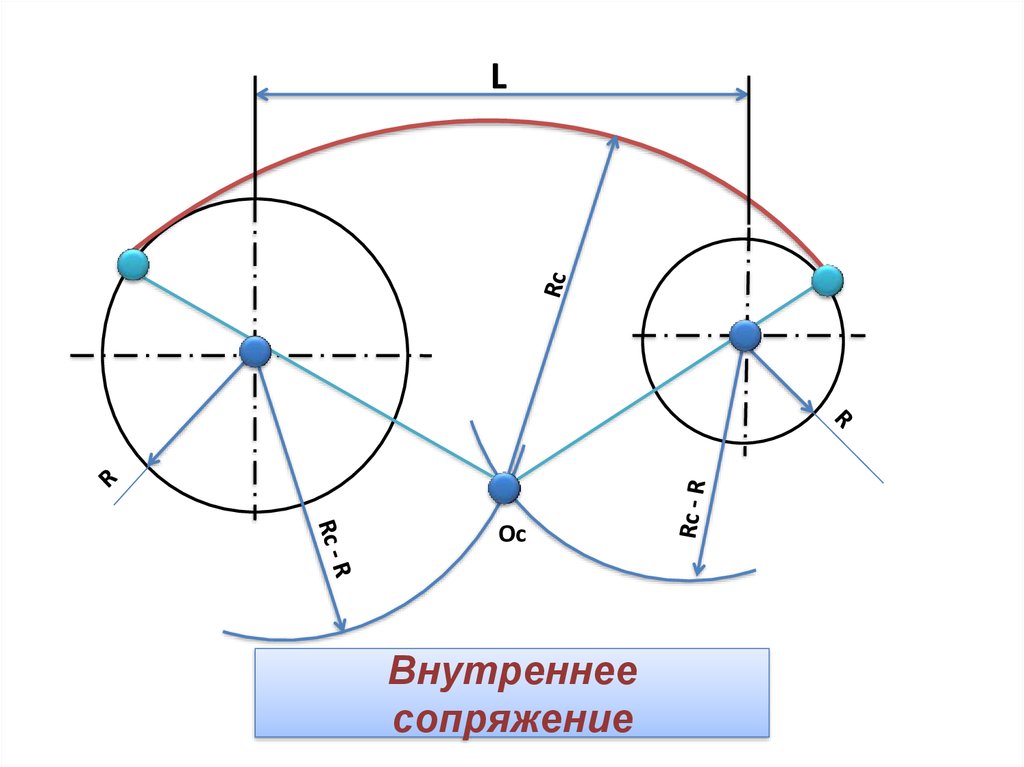
Внутреннее касание
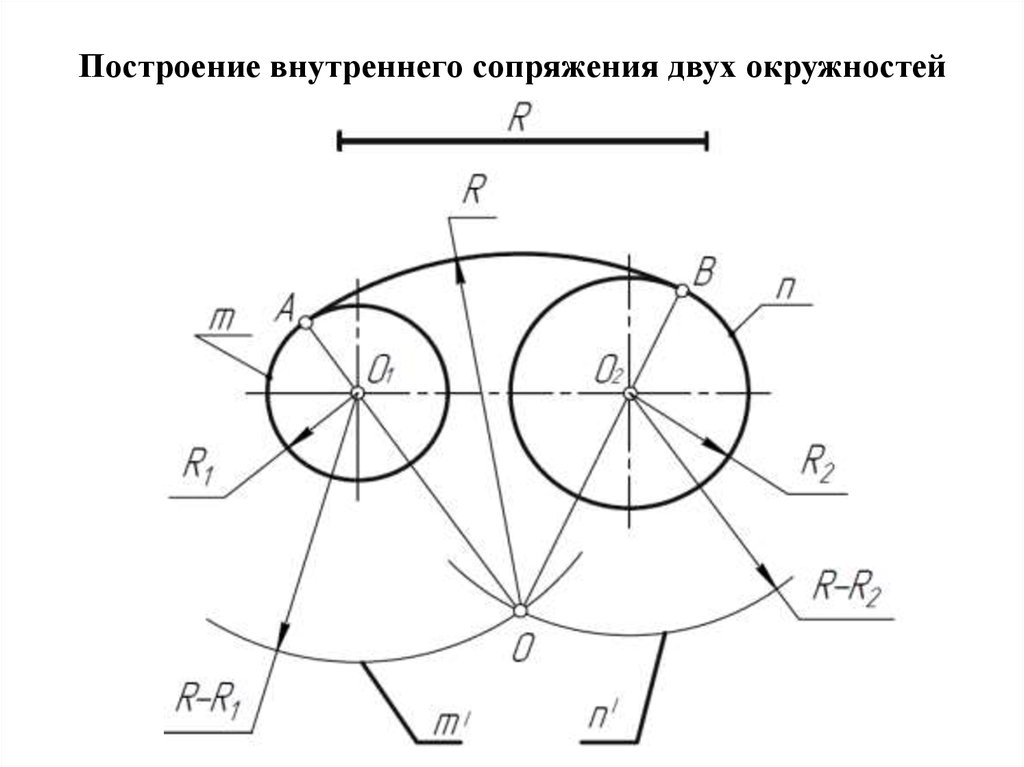
В случае внутреннего касания выполняют те же построения, но дугу m вспомогательной окружности проводят радиусом R — R
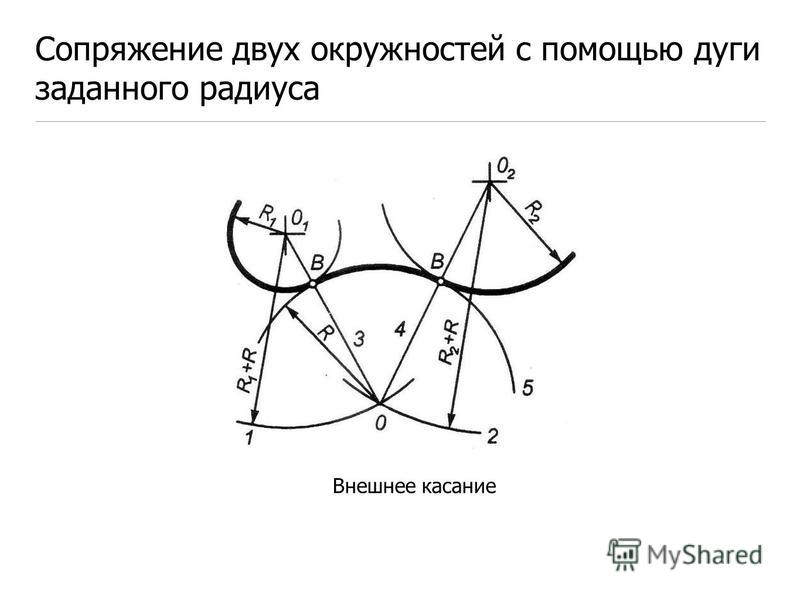
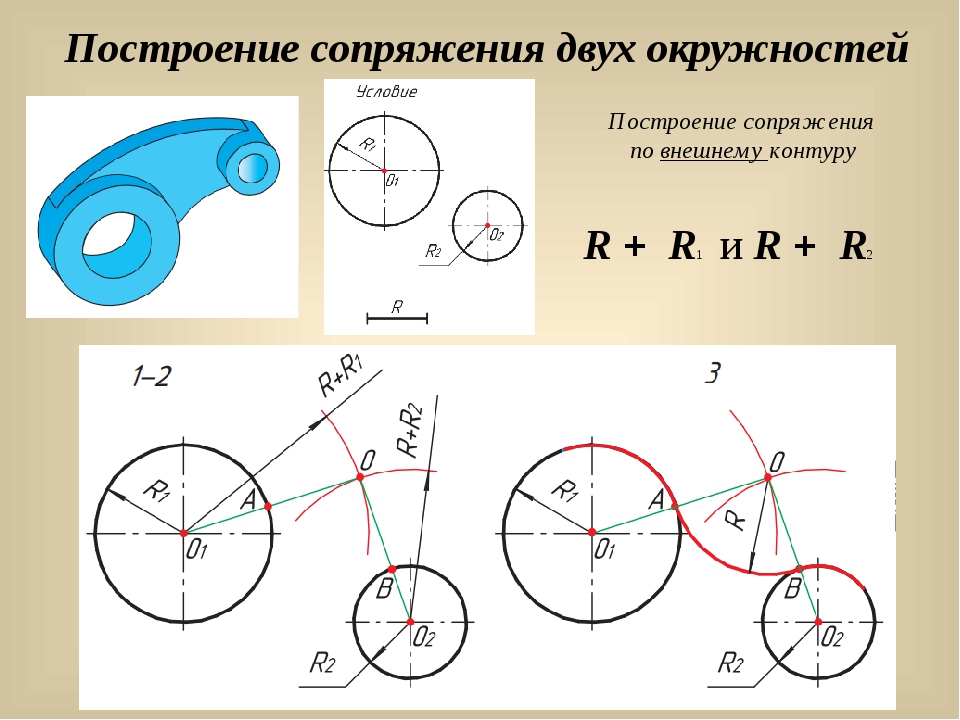
рис. 7 Сопряжение двух окружностей дугой заданного радиуса
Заданы две окружности радиусом R1 и R2. Требуется построить сопряжение дугой заданного радиуса R. рис. 8
Внешнее касание
Внутреннее касание
При внутреннем касании выполняют те же построения, но дуги проводят радиусами R -R1 и R — R2.
рис. 9
Смешанное касание рис. 10
Центр сопряжения О находится в пересечении двух дуг, описанных из центра О1 радиусом R — R1 и из центра О2 радиусом R + R2 Примечание. При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.
Частные случаи
Нахождение центра дуги заданного радиуса. Задана дуга радиусом R, соединяющая две параллельные прямые mи n и проходящая через точку А ∈
рис. 11
рис. 12
В основу построения положено нахождение точки О, равноудаленной от заданных прямых (рис. 11).
Построение и деление окружности Термины при построениях окружности Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром. Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R. Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D. Части окружностей называются дугами. Прямая СD, соединяющая две точки на окружности, называется хордой. Прямая МN,которая имеет только одну общую точку с окружностью называется касательной. Часть круга, ограниченная хордой СD и дугой, называется сигментом. Часть круга, ограниченная двумя радиусами и дугой, называется сектором. Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности Угол, образованный двумя радиусами КОА, называется центральным углом. Два взаимно перпендикулярных радиуса составляют угол в 900 и ограничивают 1/4 окружности. ⇐ Предыдущая12 Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Внутреннее сопряжение прямой линии с дугой — МегаЛекции
Контрольная работа не рецензируется и возвращается студенту обратно без проверки, если отсутствует хотя бы один из этапов данной работы.
Преподаватель вправе аннулировать представленное контрольное задание, если при собеседовании убедится, что студент выполнил их не самостоятельно.
Индивидуальные задания на контрольные работы берутся из таблиц в соответствии с вариантами. Номер варианта определяется по двум последним цифрам шифра студенческого билета (смотреть таблицу в конце методички).
Каждый чертеж выполняется на листах чертежной бумаги формата А3 (297×420 мм) с помощью чертежных инструментов карандашом. Надписи и буквенно-цифровые обозначения на листах выполняют шрифтом по ГОСТ 2.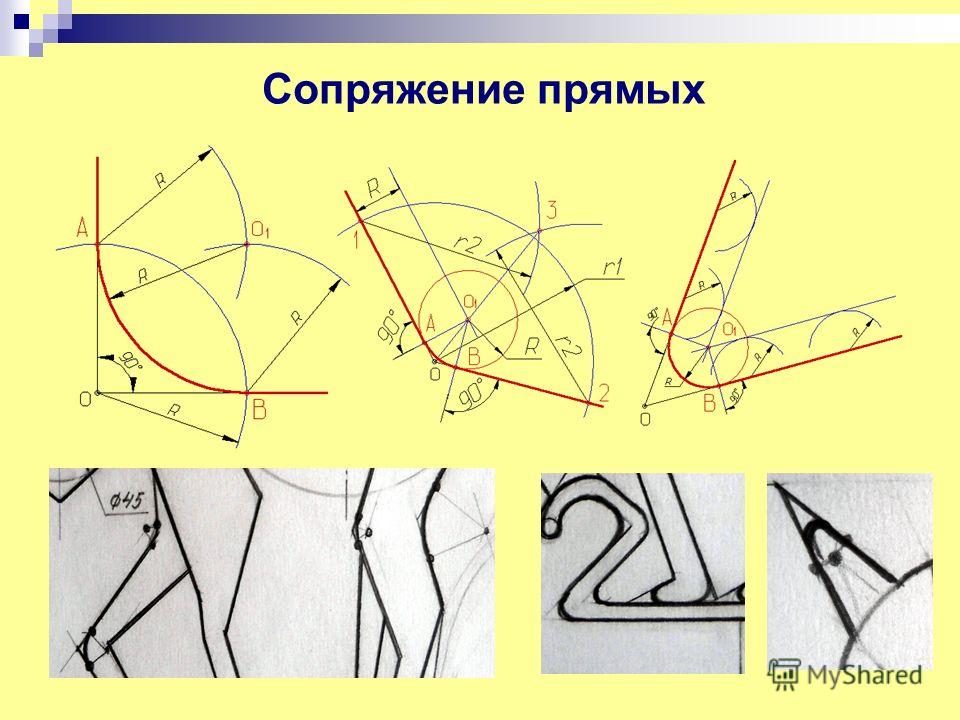
Рисунок 1. Пример заполнения основной надписи чертежа
ТЕМА 1. ВЫЧЕРЧИВАНИЕ КОНТУРОВ ТЕХНИЧЕСКИХ ДЕТАЛЕЙ.
Задание по теме 1. (Лист 1)
1. Вычертить контур детали, применяя правила построения сопряжений и деления окружностей на равные части. Данные для своего варианта взять из таблицы 1.
2. Построить очертание кулачка. Данные для своего варианта взять из таблицы 2.
Пример выполнения дан на рис. 2.
Графическую работу выполнять на листе бумаги формата А3 карандашом.
Рисунок 2. Образец выполнения листа 1
Порядок выполнения
. Изучить основные положения ГОСТ 2.301-68, 2.302-68, 2.303-68, 2.304-68, 2.306-68, 2.307-68, данные в сборнике стандартов «Единая система конструкторской документации», и рекомендуемую литературу.При вычерчивании контура детали, содержащего элементы сопряжения, нужно помнить, что без точного построения центра и точек сопряжения невозможно правильно выполнить и обвести чертеж.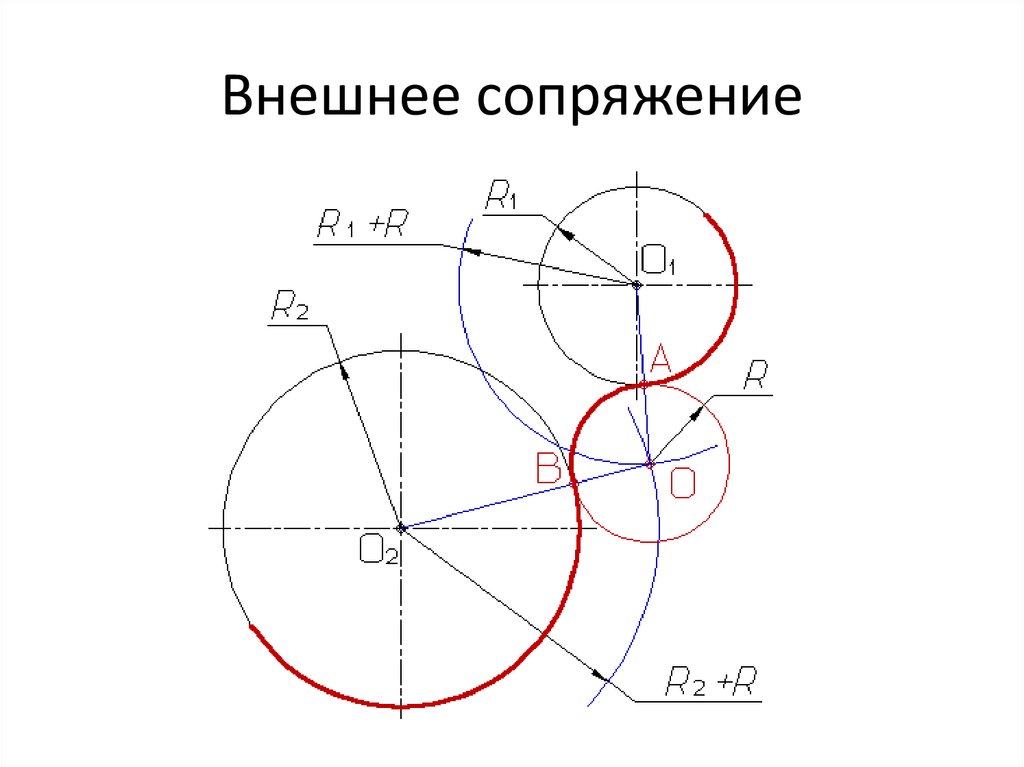 Выполняя задание, следует сохранять линии построения при определении центра и точек сопряжения.
Выполняя задание, следует сохранять линии построения при определении центра и точек сопряжения.
Таблица 1
| Корпус | Прокладка |
| Кронштейн | Корпус |
| Корпус |
|
| Крышка | Пластина |
| Стойка | Опора |
| Основание | Подвеска |
| Крышка | Корпус |
| Кронштейн | Опора |
| Кронштейн | Кронштейн |
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
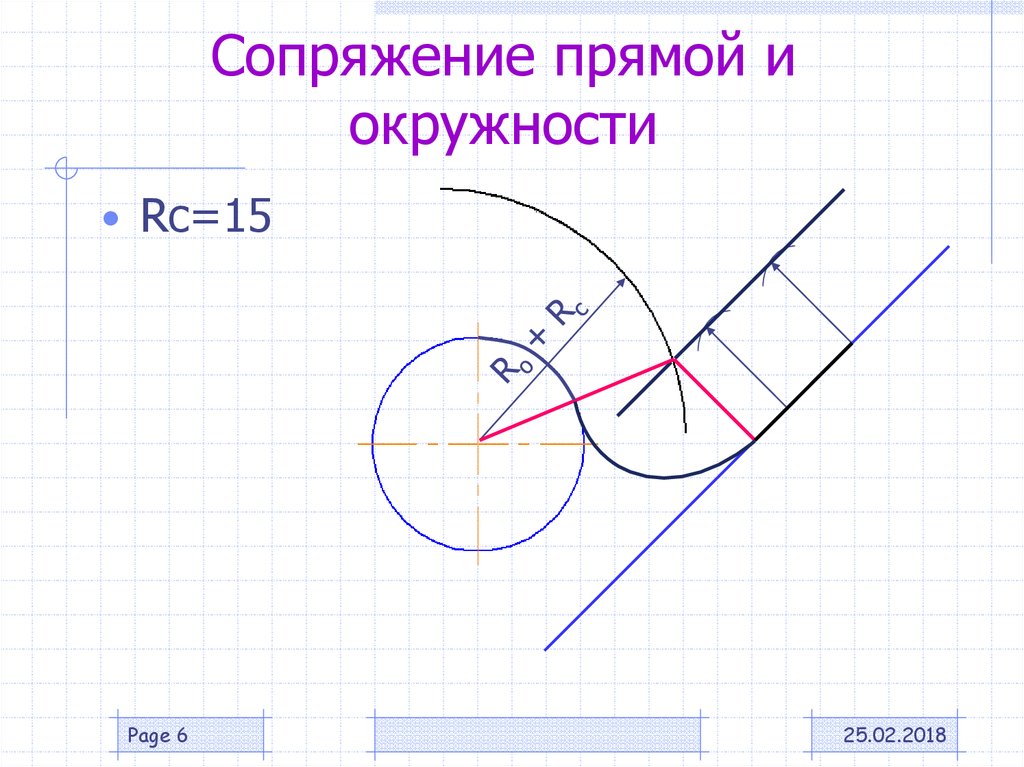
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R. (рис.3)
(рис.3)
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
| Рисунок 3. Внешнее сопряжение дуги и прямой линии | Рисунок 4. Внутреннее сопряжение дуги и прямой линии |
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой.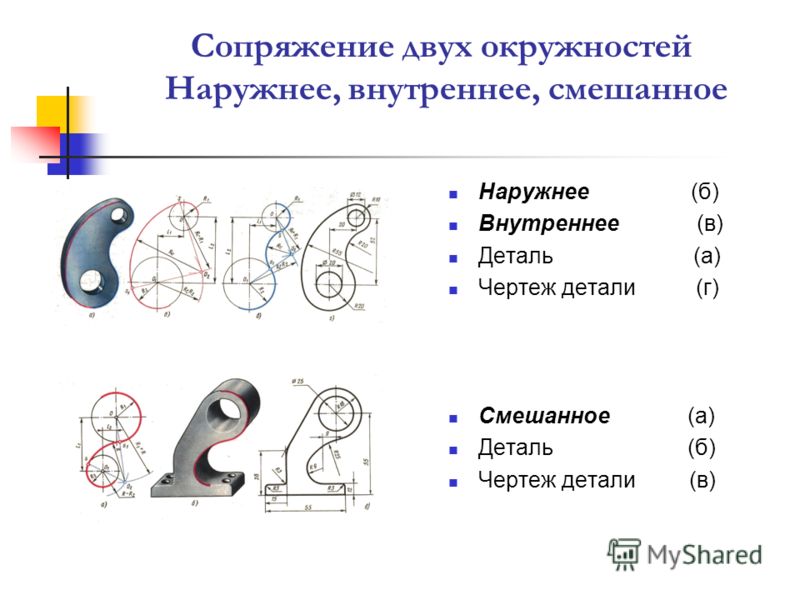 Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R (рис. 4) Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R (рис. 4) Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Воспользуйтесь поиском по сайту:
Сопряжение. Центр сопряжения. Точки сопряжения презентация, доклад
Урок – презентация
по черчению
СОПРЯЖЕНИЕ
Предисловие.
Основной целью школьного курса черчения является формирование у учащихся умений и навыков в чтении и выполнении чертежей. Использование на уроках черчения компьютерных разработок, доступных для понимания учащимися, будет способствовать повышению качества обучения черчению в целом, позволит разнообразить формы и методы ведения урока. Разработать урок может как учитель так и учащиеся. Это поможет значительно облегчить ведение урока и объяснения материала педагогу.
Данное пособие представляет собой учебный проект по теме «Сопряжение», который раскрывает цели материала по обучению построения сопряжения; дает алгоритм построения; расширяет ряд средств наглядности, используемых в процессе урока; предлагает методику, построенную с учетом вовлечения в активную работу мышления, памяти и органов чувств школьников.
Основное назначение проекта – наглядно, в доступной форме показать учащимся последовательность работы над построением сопряжения. Поэтому весь проект выполнен с использованием цветового оформления.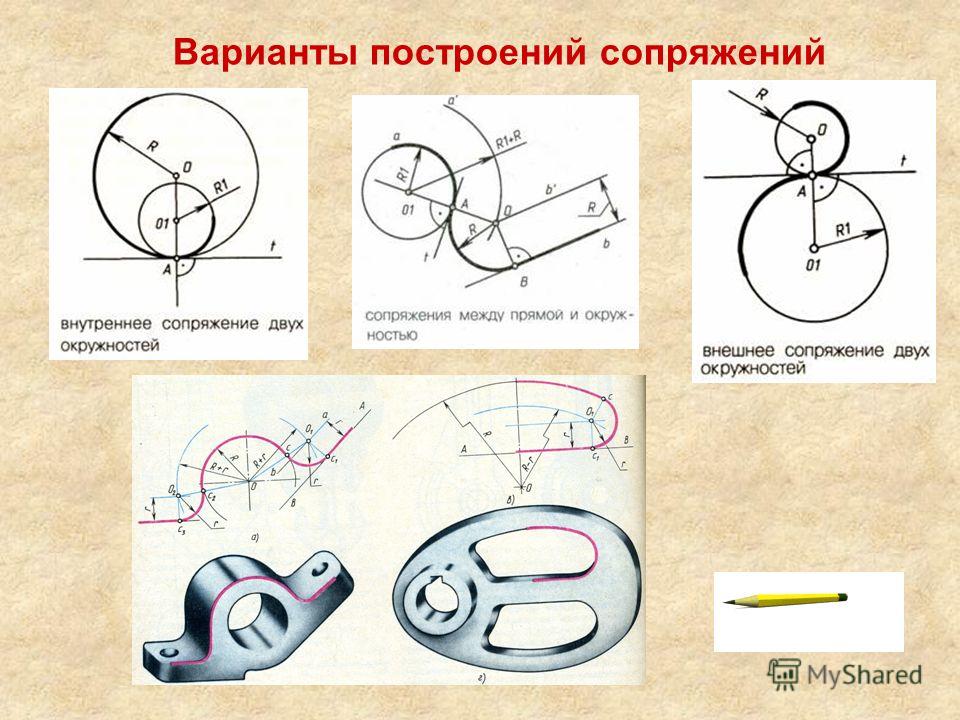
Продолжительность урока 2 академических часа. Урок разбит на три модуля с перерывами 5-10 минут.
1 модуль. Ставятся цели урока, дается определение сопряжения и объясняется общий способ построения сопряжений двух пересекающихся прямых. Учащиеся по ходу урока задают возникающие вопросы, записывают определение и делают соответствующие чертежи.
2 модуль. Применение геометрических построений на практике. Предлагается учащимся выполнить в тетради чертеж шаблона, предварительно разобрав этапы построения на компьютере. Один из учащихся выполняет задание на доске.
3 модуль. Дается еще три различных способа построения сопряжения, с наглядной демонстрацией и разбором последовательности. Учащиеся выполняют их в тетради.
При возникновении вопросов и непонятных моментов у учащихся, во время выполнения заданий, учитель с помощью компьютера легко может вернуться к моменту затруднения, что было бы сложнее сделать просто на доске.
В конце урока дается задание на дом. И демонстрируются варианты графических работ. Варианты работ приближены к знакомы предметам учащихся по урокам труда и рисования.
Тема: «Сопряжения»
Цели работы:
Знакомства с правилами сопряжения
Воспитание культуры труда, формирование навыков самостоятельной работы
Развитие пространственных представлений, пространственного мышления школьников.
Сопряжение – это плавный переход одной линии в другую.
Ребята, скажите на каких уроках вы уже встречали виды сопряжения? Назовите предметы или вещи содержащие сопряжения.
Для того чтобы линии плавно переходили одна в другую надо найти центр сопряжения и точки сопряжения. Все этапы построения выполняются сплошной тонкой основной линией.
1. Пусть R=20мм, тогда от основных линий надо провести дополнительные параллельные линии на расстоянии R20. Пересекаясь, они образуют центр сопряжения.
2. Для того чтобы найти точки сопряжения, из найденного центра сопряжения к основным линиям проводим перпендикуляры. Пересечение перпендикуляра и основной линии образуют точку сопряжения.
3. Из найденного центра сопряжения проводим дугу радиусом 20, соединяя точки сопряжения.
4. И последний этап, обвести получившееся сопряжение сплошной толстой основной линией. Вначале обводят дугу, затем вертикальную и горизонтальную линии.
Еще раз внимательно посмотрите на мониторе этапы построения сопряжения и вычертите их в тетради. Если что-то непонятно и возникают вопросы, спрашивайте.
1 модуль
R
R
R
Центр сопряжения
Точки сопряжения
R
R
Центр сопряжения
Точки сопряжения
R
Центр сопряжения
Точки сопряжения
R
R
R 25
R 25
R 15
R 15
80
50
60
А теперь для закрепления материала выполним практическое задание:
«Построить сопряжения в заданной фигуре».
Выполняется в тетради с предварительным разбором и демонстрацией.
2 модуль
Мы разобрали три разных вида сопряжения двух пересекающихся прямых с общим способом построения. Теперь рассмотрим переход от прямой к окружности. Посмотрите на монитор. Переход от прямой к окружности будет плавным, если прямая касается окружности. Точка сопряжения лежит на радиусе, перпендикулярном данной прямой.
3 модуль
0
Переход одной окружности к другой будет плавным, если окружности касаются. Точка сопряжения находится на прямой, соединяющей их центры.
R30
R20
R30+20
Сопряжение окружности и прямой дугой заданного радиуса. Даны окружности радиуса R130, радиус дуги сопряжения R220, отрезок.
Этапы построения:
Для нахождения центра сопряжения из центра окружности проводят дугу вспомогательной окружности радиуса R1+R2. От заданной прямой на расстоянии R2 проводят параллельную ей прямую до пересечения с дугой R1+R2. Точка пересечения будет центром сопряжения.
От заданной прямой на расстоянии R2 проводят параллельную ей прямую до пересечения с дугой R1+R2. Точка пересечения будет центром сопряжения.
Соединив прямой центр окружности и центр сопряжения получим точку сопряжения на дуге. Проведя из центра сопряжения перпендикуляр к заданной прямой определим вторую точку сопряжения.
Соединив дугой R2 точки сопряжения получим плавный переход от окружности к прямой.
Задание на дом:
Подготовиться к графической работе. Принести формат А4.
Задание выполняется на формате А4 (формат располагается вертикально).
Масштаб-1:1.
Цель работы: Изучение типов линий и приобретение навыков их выполнения (ГОСТ 2.303-68). Изучение построений сопряжений в очертаниях технических форм. Ознакомление с основными правилами нанесения размеров (ГОСТ 2.307-68). Изучение приемов написания букв и цифр чертежным шрифтом (ГОСТ 2.304-81).
Задание: Построить изображение плоского контура детали с выполнением сопряжений.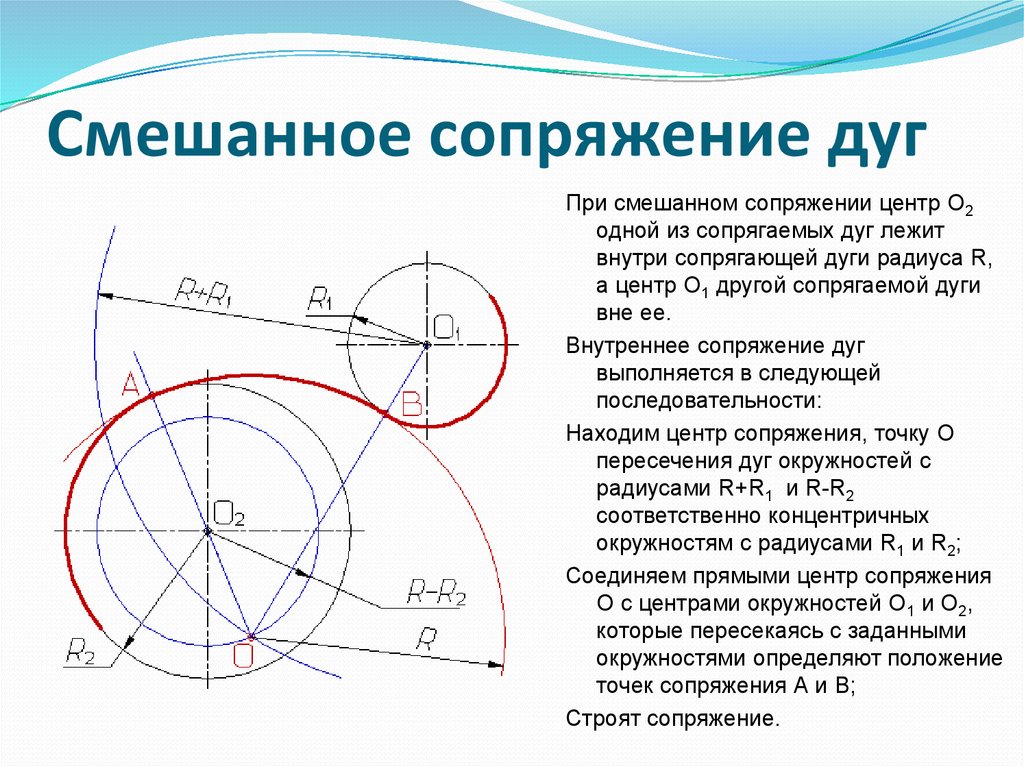 Исходные данные приведены ниже.
Исходные данные приведены ниже.
Методика оформления и последовательность выполнения задания «Очертания технических форм»:
Подготовить формат А4. Нанести внутреннюю рамку и прямоугольник основной надписи .
По размерам, нанесенным на исходные данные, установить габариты изображения и спланировать габаритный прямоугольник на чертеже так, чтобы очерк детали расположился примерно в середине поля формата.
Выбрать базовые линии очерка детали и нанести их на чертеже. Вычертить в тонких линиях контур детали, проведя все вспомогательные построения для центров и точек сопряжения линий.
Нанести выносные и размерные линии (ГОСТ 2.307-68. Разд.2). Особое внимание следует обратить на расположение размерных чисел над размерными линиями.
Сделать обводку чертежа.
Заполнить основную надпись, для чего сначала разобраться с конструкцией букв по рабочей тетради.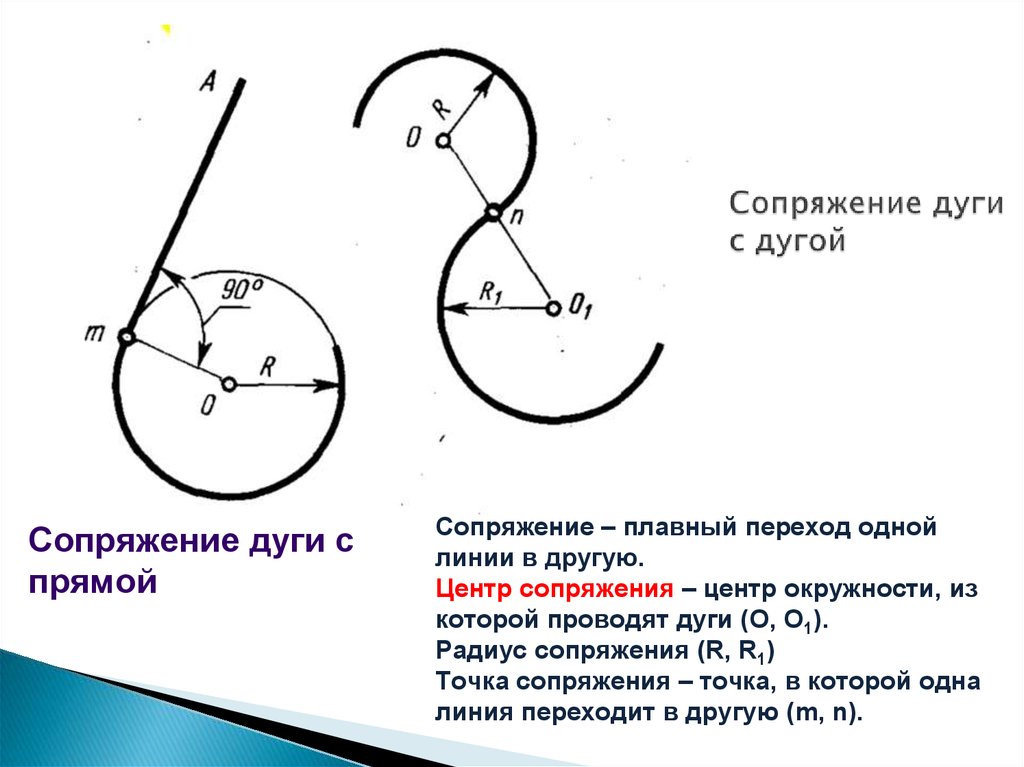
R20
R30
R20
R40
R5
R12
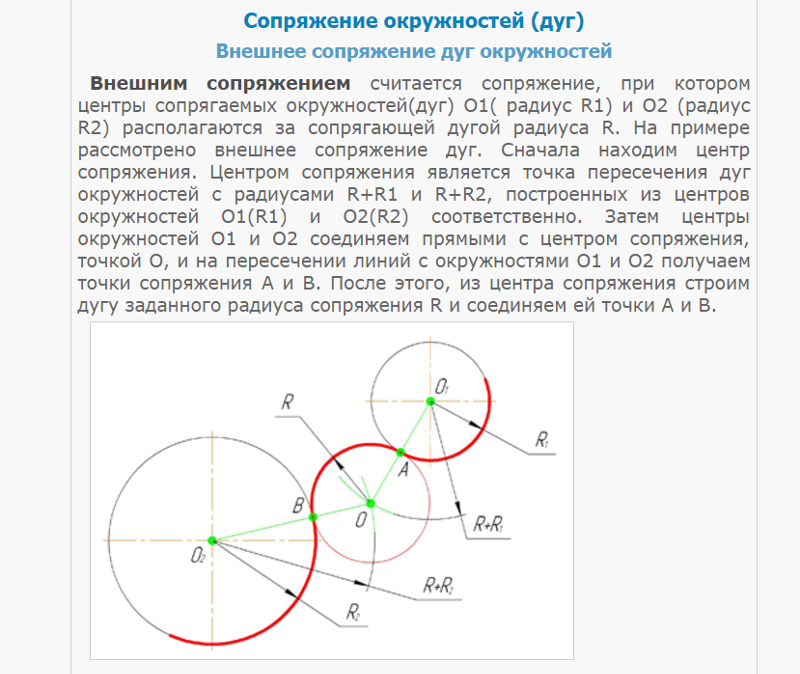
Внешнее сопряжение дуг
При внешнем сопряжении центры О1 и О2 сопрягаемых дуг радиусов R1 и R2 лежат вне сопрягающей дуги радиуса R.
Внешнее сопряжение дуг выполняется в следующей последовательности:
Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R1+R и R2+R соответственно концентричных окружностям с радиусами R1 и R2;
Соединяем прямыми центр сопряжения О с центрами окружностей О1 и О2, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;
Строят сопряжение.
Скачать презентацию
QL-Tf1: конъюгат Клоусона-Шмидта
QL-Tf1: конъюгат Клоусона-Шмидта
Сопряжение Клоусона-Шмидта точки P — это преобразование точки P таким образом, что каждая определяющая линия контрольного четырехугольника преобразуется в описанную окружность треугольника, образованного тремя другими линиями контрольного четырехугольника.
Это сопряжение, потому что двукратное применение этого преобразования приводит к исходной точке.
Преобразование часто обозначается аббревиатурой CSC .
Происхождение конъюгата
Джон Вентворт Клоусон предложил преобразование инверсии относительно некоторой окружности с точкой Микеля в центре (см. Ref-22 и Ref-40). Эккарт Шмидт придал очень полезную форму этой инверсии, изменив ее следующим образом:
В каждом четырехугольнике четырехугольника у нас есть 4 точки A, B, C, D в этом порядке. Пусть M — точка Микеля. Теперь биссектрисы угла Пусть окружность с центром окружности M и радиусом = √[MA.MC] = √[MB.MD] называется окружностью Шмидта. Сопряжение Клоусона-Шмидта точки P является инверсией относительно круга Шмидта отражения в 1-й линии Штейнера. Более того, отражение и инверсию можно выполнять в обратном порядке. Результатом является сопряжение, которое преобразует каждую определяющую линию исходного четырехугольника в описанную окружность треугольника, образованного тремя другими линиями исходного четырехугольника. 
Связь с правилами Штейнера
1-й и 2-й оси Штейнера описаны в правилах Штейнера (8) и (9). Вот почему они названы в честь Штайнера.
Правила 8, 9, 10 Штейнера о четырехугольниках говорят (см. Ref-4):
(8) Каждый из четырех возможных треугольников в четырехугольнике имеет вписанную и три вписанные окружности. Центры этих 16 окружностей лежат четыре на четыре на восьми новых окружностях.
(9) Эти восемь новых кругов образуют два набора из четырех, каждый круг одного набора равен
ортогонален каждой окружности другого набора. Центры окружностей каждого
Центры окружностей каждого
набор лежат на одной линии. Эти две линии перпендикулярны.
(10) Наконец, эти две последние прямые пересекаются в точке F (точка Микеля).
Оба набора из 4 окружностей, как описано в (9), соосны. Один набор имеет ось с реальными точками пересечения 4 окружностей, другой набор имеет ось с воображаемыми точками пересечения 4 окружностей. Эти оси называются 1 st Ось Штейнера (ось с 2 реальными общими точками пересечения 4 окружностей) и 2 nd Ось Штейнера (ось с 2 воображаемыми общими точками пересечения 4 окружностей). Общие точки пересечения на оси Штейнера 1 st являются единственными точками на реальной плоскости, которые инвариантны относительно сопряжения Клоусона-Шмидта. См. Ref-15d. Оси Штейнера также могут быть построены как биссектрисы угла QL-P1.QL-P4 и оси вписанной параболы QL-Co1. См. Ref-34, Эккарт Шмидт, QFG #9.Лж.
 Нарисуйте окружность Ci1 через P и 2 вершины на стороне L1 четырехугольника. Нарисуйте окружность Ci2 через P и 2 вершины на противоположной стороне L3 четырехугольника. Пусть X будет 2 и точками пересечения Ci1 и Ci2.
Нарисуйте окружность Ci1 через P и 2 вершины на стороне L1 четырехугольника. Нарисуйте окружность Ci2 через P и 2 вершины на противоположной стороне L3 четырехугольника. Пусть X будет 2 и точками пересечения Ci1 и Ci2.Координаты:
Пусть Q (u : v : w) — случайная точка, не принадлежащая одной из определяющих прямых четырехугольника отсчета.
Конъюгат Клоусона-Шмидта в координатах CT дает следующий результат:
(a 2 m n (a 2 (l-m) ( l — n) v w + b 2 (l — m) w ( l u +n v+n w) + c 2 (l — n) v (l u+m v+m w)) :
b 2 l n (b 2 (m-l) (m-n) u w + c 2 (m -n) u (l u+m v+ l w) + a 2 (m — l) w (n и+м v+n ш)) :
c 2 l m (c 2 (n — l) (n-m) u v + a 2 (n – l) v (m u+m v+n w)+ b 2 (n -m) u (l u+ l v + n w)))
Сопряжение Клоусона-Шмидта в DT-координатах дает следующий результат:
(б 4 Л Н у (и + в — ш) + в 4 L M u (u — v + w) — a 4 M N u (u + v + w) — 2 b 2 c 2 L u (N v + M w)
+ 2 а 2 б 2 Н ((у + в) (Н 2 и + М 2 в) — Н 2 ш 2 ) — 2 0 1 0 907 M (-M 2 v 2 + (u + w) (M 2 u + N 2 w)) :
а 4 M N v (u + v — w) + c 4 L M v (-u + v + w) — b 4 L N v (u + v + w) — 2 a 2 c 2 M v (N u + L w)
— 2 A 2 B 2 N ((U + V) (L 2 U + N 2 В) — N 2 W 2 ) + 2 B 2 C 2 L (-L 2 u 2 + (v + w) (L 2 v + N 2 w)) :
— 2 a 2 b 2 N (M u + L v) w + a 4 M N w (u — v + w) + b 4 L N w (-u + v + w) — с 4 L M w (u + v + w)
— 2 b 2 c 2 L (-L 2 u 2 + (v + w) (M 2 v + L 2 w )) + 70 2 0 9 0 2 M (-M 2 v 2 + (u + w) (L 2 u + M 2 w)))
где:
L = M 2 — N 2 M = N 2 — L 2 n = L 2 — м 2
Координаты с треугольником Микеля в качестве опорного треугольника
Если мы возьмем треугольник Микеля в качестве опорного треугольника ABC (C в точке Микеля),
, то сопряжение Клоусона-Шмидта QL-Tf1 принимает очень простую форму для квадригонов: +б 2 г х+с 9L1 = P1 = (T : b 2 w : c 2 v)
, где T = -(a 2 v w+b 2 w u+c 2 u v) / (u+v +ж).
См. Ref-34, QFG #338 Эккарта Шмидта.
Примеры конъюгатов Клоусона-Шмидта:
Точка/линия/кривая -1 | Точка/линия/кривая -2 |
|
|
Общие | |
Определение четырехугольных линий: L1, L2, L3, L4 | Окружность соответствующего треугольника QL-компонента |
Линия не через QL-P1 | Окружность через QL-P1 |
Линия A через QL-P1 | Линия A через QL-P1 |
Круг с центром QL-P1 | Другой круг с QL-P1 в центре |
Точки/линии/кривые | |
QL-P1: точка Микеля | Некоторые (неопределенные) точки в бесконечности |
QL-P4: Циркумцентр Микеля | Отражение QL-P1 в QL-L2 (линия Штейнера) |
QL-L2 Линия Штайнера | QL-Ci3 Круг Микеля |
QL-Co1: вписанная парабола | QL-Qu1: Моно QL-кардиоид Морли |
Круг через X(186) точек в QL-CT См. | Обведите через X(265) точек в QL-CT См. QL-P29, центр этого круга. |
QG-P1: диагональная точка пересечения | QA-P4: Изогональный центр |
QG-P17: Проекция QG-P1 на QG-L1 | QG-P18: Квазиизогональная точка пересечения |
QG-L1: 3 рд Диагональ | QG-Ci3: квазиизогональный круг |
QA-Ci1: QA-окружность Диагональный треугольник | Окружность через QG-2P2a, QG-2P2b, QA-P4, QG-P19 |
|
|
Инвариантность |
|
Биссектриса Штейнера-i (i=1-8) (кружки в правиле 9 Штейнера) | Та же биссектриса Штайнера-i (i=1-8) |
Круг Шмидта | Круг Шмидта |
Точка пересечения 9Круг Шмидта (переключающие пункты) | |
QL-Cu1: квазиизогональный кубический | QL-Cu1: квазиизогональный кубический |
Выступления в четырехугольниках:
Особые сюрпризы при применении Сопряжения Клоусона-Шмидта относительно четырехугольников:
- QL-Tf1 создает на уровне квадригона с использованием QG-P1 (точка пересечения диагонали) точку-четырехугольник: QA-P4 (изогональный центр), которая действительна для всех своих квадригонов QA.
 См. Ref-15d.
См. Ref-15d. QL-Tf1 создает на уровне квадригона с использованием QG-P16 (точка Шмидта) точку четырехугольника: QA-P3 (точка Гергонна-Штайнера), которая действительна для всех его квадригонов QA (Eckart Schmidt, 26 ноября 2012 г.) .
- Рассмотрим 4 точки QL-квадригона как QA-квадригона, также определяющего четырехугольник. Пусть M2 и M3 — точки Микеля двух других QA-квадригонов. Теперь M2 и M3 являются взаимными конъюгатами Клоусона-Шмидта относительно 1 st QA-Quadrigon. См. Ref-15b и Ref-15d.
- Для четырехугольника существуют три сопряжения Клоусона-Шмидта относительно четырехугольников
P1P2, P2P3, P3P4, P4P1 (CSCa),
P1P2, P2P4, P4P3, P3P1 (CSCb),
P1P4, P4P2, P2P3, P3P1 (CSCc).
Теперь произведение двух таких сопряженных дает третье.
Продукт всех трех достигает идентичности. См. Ref-15d. Кубика QA-DT-P4 (QA-Cu1) четырехугольника инвариантна относительно этих трех преобразований.
- Пусть P — некоторая точка на Кубике QA-DT-P4 (QA-Cu1) и пусть Pa = CSCa(P), Pb = CSCb(P), Pc = CSCc(P). Касательные в точках P, Pa, Pb, Pc к кубу QA-Cu1 совпадают в изогональном центре (QA-P4) четырехугольника P.Pa.Pb.Pc. См. Ref-15b.
Свойства:
- Пересечения прямых от L до P и касательных T в QL-Tf1-образной окружности L в QL-P1 дают ортогональную гиперболу с центром в средней точке P.QL-P1 с асимптотами, параллельными осям Штейнера . См. Ref-34, Eckart Schmidt, QFG-сообщение №1666.
- Пусть Q2 будет средней точкой QL-P1 и случайной точкой Q1. Теперь QL-Tf1[Q1) будет средней точкой QL-P1 и QL-Tf1(Q2). См. Re-34, QFG-сообщение №1689.
- Пусть Q2 — точка, коллинеарная QL-P1 и случайная точка Q1 (следовательно, QL-P1, QL-Tf1(Q1) и QL-Tf1(Q2) тоже будут коллинеарны). Теперь Q1.QL-Tf1(Q2) будет параллелен Q2.QL-Tf1(Q1). См. Ref-34, QFG-сообщение №1689.
- Обозначает QL-Tf1a=QL-Tf1, применяемый в 1-м QA-квадригоне, QL-Tf1b=QL-Tf1, применяемый во 2-м QA-квадригоне, QL-Tf1c=QL-Tf1, применяемый в 3-м QA-квадригоне.
 QL-Tf1a(QL-Tf1b(QL-Tf1c(P))) = P. 3 версии QL-Tf1 в четырехугольнике применяются в любом порядке.
QL-Tf1a(QL-Tf1b(QL-Tf1c(P))) = P. 3 версии QL-Tf1 в четырехугольнике применяются в любом порядке.
| Когда имеешь дело с практической реализацией радиочастотных приложений, всегда возникают какие-то кошмарные задачи. Одной из них является необходимость согласования различных импедансов взаимосвязанных блоков. Обычно они включают в себя подключение антенны к малошумящему усилителю (LNA), выход усилителя мощности (RFOUT) к антенне и выход LNA/VCO к входам микшера. Задача согласования требуется для правильной передачи сигнала и энергии от «источника» к «нагрузке». На высоких радиочастотах паразитные элементы (такие как индуктивность проводов, межслойные емкости и сопротивления проводников) оказывают значительное, но непредсказуемое влияние на согласующую цепь. Для частот выше нескольких десятков мегагерц теоретических расчетов и моделирования часто бывает недостаточно. Существует множество способов согласования импеданса, в том числе:
A Quick PrimerПрежде чем представить утилиты диаграммы Смита, было бы разумно кратко рассказать о явлении распространения волн для проводки ИС в условиях радиочастот (выше 100 МГц). Это может относиться к непредвиденным обстоятельствам, таким как линии RS-485, между усилителем мощности и антенной, между малошумящим усилителем и преобразователем/смесителем с понижением частоты и т. д. Это может относиться к непредвиденным обстоятельствам, таким как линии RS-485, между усилителем мощности и антенной, между малошумящим усилителем и преобразователем/смесителем с понижением частоты и т. д.Хорошо известно, что для обеспечения максимальной передачи мощности от источника к нагрузке импеданс источника должен быть равен комплексно-сопряженному импедансу нагрузки, или: R S + jX S = R L — jX L Рис. 2. Схема R S + jX S = R L — jX L . В этом случае энергия, передаваемая от источника к нагрузке, максимальна. Кроме того, для эффективной передачи мощности это условие необходимо, чтобы избежать отражения энергии от нагрузки обратно к источнику. Это особенно верно для высокочастотных сред, таких как видеолинии, радиочастотные и микроволновые сети. Что это такоеДиаграмма Смита представляет собой круговой график с множеством переплетенных кругов. При правильном использовании согласование импедансов с кажущейся сложной структурой может быть выполнено без каких-либо вычислений. Единственное усилие, которое требуется, это чтение и отслеживание значений по кругам. При правильном использовании согласование импедансов с кажущейся сложной структурой может быть выполнено без каких-либо вычислений. Единственное усилие, которое требуется, это чтение и отслеживание значений по кругам.Диаграмма Смита представляет собой полярный график комплексного коэффициента отражения (также называемого гаммой и обозначаемого буквой Γ). Или он определяется математически как параметр однопортового рассеяния s или s 11 . Диаграмма Смита составляется путем исследования нагрузки, полное сопротивление которой должно быть согласовано. Вместо того, чтобы рассматривать его импеданс напрямую, вы выражаете его коэффициент отражения Γ L , который используется для характеристики нагрузки (например, полной проводимости, усиления и крутизны). Γ L более полезен при работе с радиочастотами. Мы знаем, что коэффициент отражения определяется как отношение между отраженной волной напряжения и падающей волной напряжения: Количество отраженного сигнала от нагрузки зависит от степени несоответствия между импедансом источника и импедансом нагрузки. Его выражение было определено следующим образом: Поскольку импедансы являются комплексными числами, коэффициент отражения также будет комплексным числом. Чтобы уменьшить количество неизвестных параметров, полезно заморозить часто встречающиеся и распространенные в приложении параметры. Здесь Z 0 (характеристический импеданс) часто является постоянной величиной и представляет собой реальное промышленное нормализованное значение, например 50 Ом, 75 Ом, 100 Ом и 600 Ом. Затем мы можем определить нормализованный импеданс нагрузки как: С этим упрощением мы можем переписать формулу коэффициента отражения как: Здесь мы можем видеть прямую зависимость между импедансом нагрузки и ее коэффициентом отражения. К сожалению, сложный характер зависимости практически бесполезен, поэтому мы можем использовать диаграмму Смита как тип графического представления приведенного выше уравнения. Чтобы построить диаграмму, необходимо переписать уравнение, чтобы извлечь стандартные геометрические фигуры (такие как круги или случайные линии). Во-первых, уравнение 2.3 переворачивается, чтобы получить: и Уравнивая действительные и мнимые части уравнения 2.5, мы получаем два независимых новых соотношения: Уравнение манипулируют путем преобразования уравнений с 2.8 по 2.13 в окончательное уравнение 2.14. Это уравнение представляет собой соотношение в виде параметрического уравнения (x — a)² + (y — b)² = R² в комплексной плоскости (Γr, Γi) окружности с центром в координатах [r/(r + 1 ), 0] и радиусом 1/(1 + r). См. Рисунок 4a для получения дополнительной информации. При построении диаграммы Смита необходимо соблюдать определенные меры предосторожности. Это одни из самых важных:
Назад к чертежной доскеДвигаясь дальше, мы используем уравнения с 2.15 по 2.18 для дальнейшего преобразования уравнения 2.7 в другое параметрическое уравнение. Это приводит к уравнению 2.19.Опять же, 2.19 представляет собой параметрическое уравнение типа (x — a)² + (y — b)² = R² в комплексной плоскости (Γr, Γi) окружности с центром в координатах (1, 1/x ) и радиусом 1/x. См. Рисунок 4b для получения дополнительной информации. Получить представление?Чтобы завершить нашу диаграмму Смита, мы накладываем друг на друга два семейства кругов. Тогда можно увидеть, что все круги одного семейства пересекаются со всеми кругами другого семейства. Зная импеданс в виде r + jx, можно определить соответствующий коэффициент отражения. Нужно только найти точку пересечения двух окружностей, соответствующую значениям r и x.Он тоже совершает возвратно-поступательное движениеВозможна и обратная операция. Зная коэффициент отражения, найдите две окружности, пересекающиеся в этой точке, и прочтите соответствующие значения r и × на окружностях. Процедура для этого следующая:
ЭкстраполироватьПоскольку метод разрешения диаграммы Смита в основном является графическим методом, точность решений напрямую зависит от определений графика. Вот пример, который может быть представлен диаграммой Смита для ВЧ-приложений:Пример: Рассмотрим волновое сопротивление 50-омной нагрузки и следующие импедансы: | Z 2 = 75 — j100 Ом | Z 3 = j200 Ом | Z 4 = 150 Ом |
| Z 5 = ∞ (обрыв цепи) | Z 6 = 0 (короткое замыкание) | Z 7 = 50 Ом | Z 8 = 184 — j900 Ом |
Затем нормализуйте и постройте график (см. Рисунок 5 ). Точки нанесены следующим образом:
| z 1 = 2 + j | z 2 = 1,5 — j2 | z 3 = j4 | г 4 = 3 |
| г 5 = 8 | z 6 = 0 | z 7 = 1 | z 8 = 3,68 — j18 |
Для увеличенного изображения (PDF, 502K)
Рис.
 5. Точки, нанесенные на диаграмму Смита.
5. Точки, нанесенные на диаграмму Смита. Теперь можно напрямую извлечь коэффициент отражения Γ на диаграмме Смита на рис. 5. После нанесения точки импеданса (точка пересечения круга постоянного сопротивления и круга постоянного реактивного сопротивления) просто прочтите проекцию прямоугольных координат по горизонтальной и вертикальной оси. Это даст Γr, действительную часть коэффициента отражения, и Γi, мнимую часть коэффициента отражения (см. 9).0719 Рисунок 6 ).
Также можно взять восемь случаев, представленных в примере, и извлечь соответствующие им Γ непосредственно из диаграммы Смита на рис. 6. Числа:
| Γ 1 = 0,4 + 0,2j | Г 2 = 0,51 — 0,4j | Г 3 = 0,875 + 0,48j | Г 4 = 0,5 |
| Г 5 = 1 | Г 6 = -1 | Г 7 = 0 | Г 8 = 0,96 — 0,1j |
Рис.
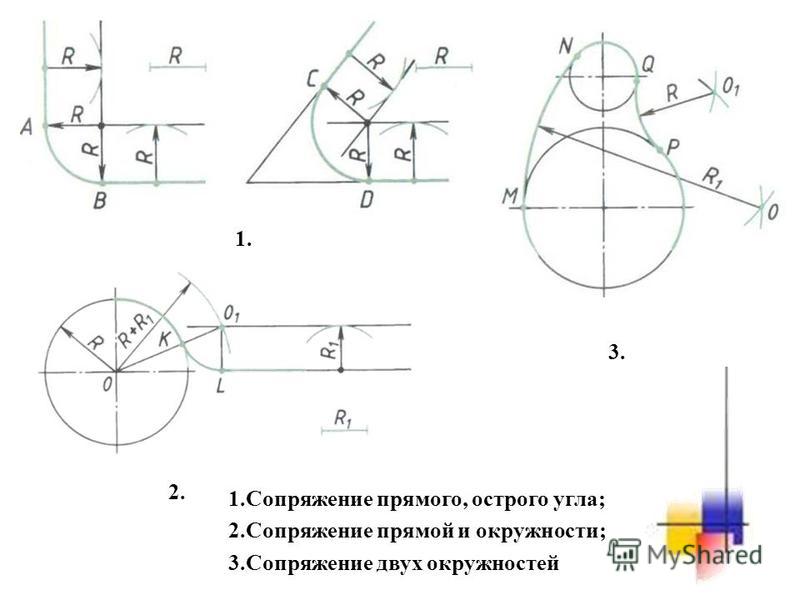 6. Прямое извлечение коэффициента отражения Γ, действительного и мнимого по оси X-Y.
6. Прямое извлечение коэффициента отражения Γ, действительного и мнимого по оси X-Y. Работа с допуском
Диаграмма Смита построена с учетом импеданса (резистора и реактивного сопротивления). После построения диаграммы Смита ее можно использовать для анализа этих параметров как в рядовом, так и в параллельном мирах. Добавление элементов в серию очень просто. Можно добавлять новые элементы и определять их эффекты, просто перемещаясь по кругу к соответствующим значениям. Однако суммирование элементов параллельно — это другое дело. Это требует учета дополнительных параметров. Часто проще работать с параллельными элементами в мире допуска.Мы знаем, что по определению Y = 1/Z и Z = 1/Y. Адмиттанс был выражен в mhos или Ω -1 , хотя теперь выражается в сименсах, или S. И, поскольку Z является комплексным, Y также должен быть комплексным.
Следовательно, Y = G + jB (2.20), где G называется «проводимостью», а B — «электрической проводимостью» элемента. Однако важно соблюдать осторожность.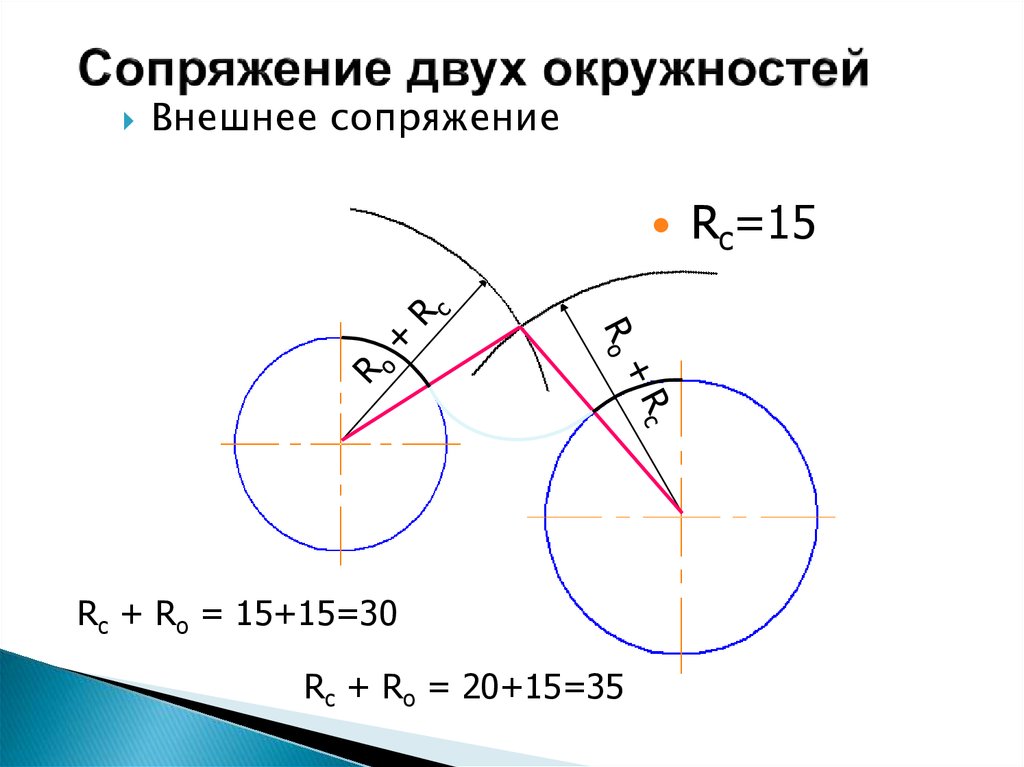 Следуя логическому предположению, мы можем заключить, что G = 1/R и B = 1/X. Однако это не так. При использовании этого предположения результаты будут неверными.
Следуя логическому предположению, мы можем заключить, что G = 1/R и B = 1/X. Однако это не так. При использовании этого предположения результаты будут неверными.
При работе с допусками первое, что мы должны сделать, это нормализовать y = Y/Y 0 . Это приводит к y = g + jb. Итак, что происходит с коэффициентом отражения? Проработав следующее:
Выясняется, что выражение для G противоположно по знаку z, и Γ(y) = -Γ(z).
Зная z, мы можем инвертировать знаки Γ и найти точку, расположенную на том же расстоянии от (0, 0), но в противоположном направлении. Тот же результат можно получить, повернув угол на 180° вокруг центральной точки (см. рис. 7).
Рис. 7. Результаты поворота на 180°.
Конечно, хотя Z и 1/Y представляют один и тот же компонент, новая точка отображается как другой импеданс (новое значение имеет другую точку на диаграмме Смита, другое значение отражения и т. д.). Это происходит потому, что график представляет собой график импеданса. Но новая точка — это, по сути, допуск. Следовательно, значение, указанное на графике, должно быть прочитано как Сименс.
Но новая точка — это, по сути, допуск. Следовательно, значение, указанное на графике, должно быть прочитано как Сименс.
Хотя этого метода достаточно для выполнения преобразований, он не работает для определения разрешения схемы при работе с параллельными элементами.
Диаграмма Адмиттанса Смита
В предыдущем обсуждении мы видели, что каждую точку на диаграмме Смита импеданса можно преобразовать в ее аналог полной проводимости, повернув ее на 180° вокруг начала координат комплексной плоскости Γ. Таким образом, диаграмму Смита полной проводимости можно получить, повернув всю диаграмму Смита полного сопротивления на 180°. Это очень удобно, так как избавляет от необходимости строить еще один график. Точка пересечения всех окружностей (постоянные проводимости и постоянные проводимости) автоматически находится в точке (-1, 0). С этим графиком добавление элементов параллельно также становится проще. Математически построение диаграммы Смита с проводимостью создается следующим образом:затем, обращая уравнение:
Далее, приравнивая действительную и мнимую части уравнения 3. 3, мы получаем два новых независимых соотношения:
3, мы получаем два новых независимых соотношения:
Составляя уравнение 3.4, мы получаем следующее:
, которое снова является параметрическим уравнением типа (x — a)² + (y — b)² = R² (уравнение 3.12) в комплексной плоскости (Γr, Γi) окружности с ее координатами в центре [ -g/(g + 1), 0] и радиусом 1/(1 + g).
Кроме того, разрабатывая уравнение 3.5, мы показываем, что:
, которое снова является параметрическим уравнением типа (x — a)² + (y — b)² = R² (уравнение 3.17).
Эквивалентное разрешение импеданса
При решении задач, в которых последовательно и параллельно смешиваются элементы, мы можем использовать одну и ту же диаграмму Смита и вращать ее вокруг любой точки, где существуют преобразования от z к y или от y к z. Рассмотрим сеть Рисунок 8 (элементы нормированы с Z 0 = 50 Ом). Последовательное реактивное сопротивление (x) положительно для индуктивности и отрицательно для емкости. Электрическая проводимость (b) положительна для емкости и отрицательна для индуктивности.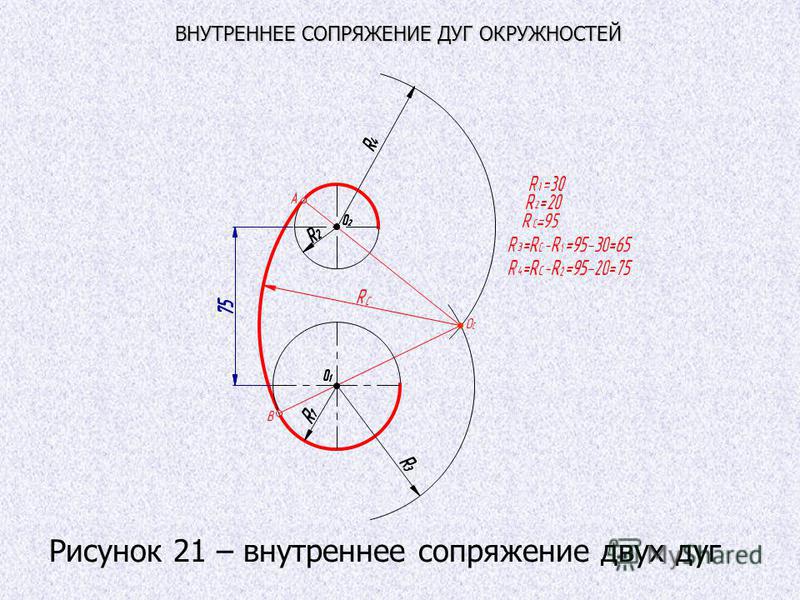
Рис. 8. Многоэлементная схема.
Схема должна быть упрощена (см. рис. 9 ). Начиная с правой стороны, где есть резистор и катушка индуктивности со значением 1, мы наносим точку ряда, где r окружность = 1 и l окружность = 1. Это становится точкой A. Поскольку следующим элементом является элемент в шунтирующем (параллельном) переходе на диаграмму Смита проводимости (поворотом всей плоскости на 180°). Однако для этого нам нужно преобразовать предыдущую точку в допуск. Это становится А’. Затем мы поворачиваем плоскость на 180°. Сейчас мы находимся в режиме приема. Шунтирующий элемент можно добавить, пройдя по окружности проводимости на расстояние, соответствующее 0,3. Это нужно сделать в направлении против часовой стрелки (отрицательное значение) и получить точку B. Затем у нас есть еще один элемент ряда. Мы снова возвращаемся к диаграмме импеданса Смита.
Рисунок 9. Сеть на рисунке 8 с ее элементами, разорванными для анализа.
Прежде чем это сделать, необходимо снова пересчитать предыдущую точку в импеданс (это был адмиттанс).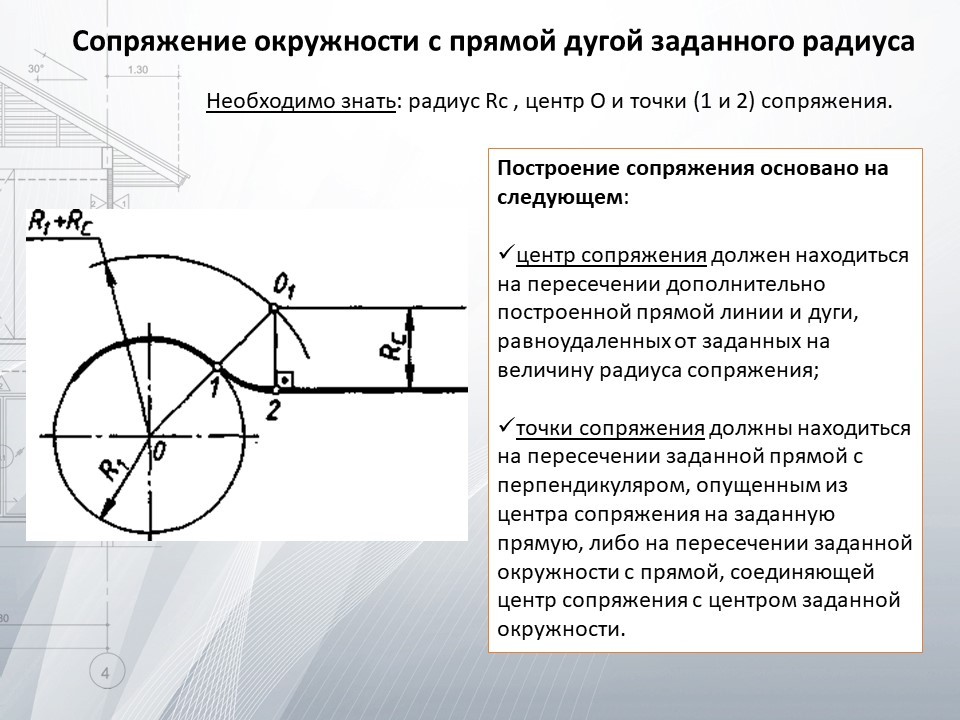 После преобразования мы можем определить B’. Используя ранее установленную процедуру, диаграмма снова поворачивается на 180°, чтобы вернуться в режим импеданса. Элемент ряда добавляется, следуя по кругу сопротивлений на расстояние, соответствующее 1,4 и отмечая точку С. Это нужно делать против часовой стрелки (отрицательное значение). Для следующего элемента выполняется та же операция (преобразование в адмиттанс и поворот плоскости). Затем переместите заданное расстояние (1.1) по часовой стрелке (поскольку значение положительное) вдоль круга постоянной проводимости. Мы помечаем это как D. Наконец, мы возвращаемся обратно в режим импеданса и добавляем последний элемент (последовательный индуктор). Затем мы определяем требуемое значение z, расположенное на пересечении круга сопротивления 0,2 и круга реактивного сопротивления 0,5. Таким образом, z определяется как 0,2 + j0,5. Если волновое сопротивление системы равно 50 Ом, то Z = 10 + j25 Ом (см. 9).0719 Рисунок 10 ).
После преобразования мы можем определить B’. Используя ранее установленную процедуру, диаграмма снова поворачивается на 180°, чтобы вернуться в режим импеданса. Элемент ряда добавляется, следуя по кругу сопротивлений на расстояние, соответствующее 1,4 и отмечая точку С. Это нужно делать против часовой стрелки (отрицательное значение). Для следующего элемента выполняется та же операция (преобразование в адмиттанс и поворот плоскости). Затем переместите заданное расстояние (1.1) по часовой стрелке (поскольку значение положительное) вдоль круга постоянной проводимости. Мы помечаем это как D. Наконец, мы возвращаемся обратно в режим импеданса и добавляем последний элемент (последовательный индуктор). Затем мы определяем требуемое значение z, расположенное на пересечении круга сопротивления 0,2 и круга реактивного сопротивления 0,5. Таким образом, z определяется как 0,2 + j0,5. Если волновое сопротивление системы равно 50 Ом, то Z = 10 + j25 Ом (см. 9).0719 Рисунок 10 ).
Для увеличенного изображения (PDF, 600K)
Рис.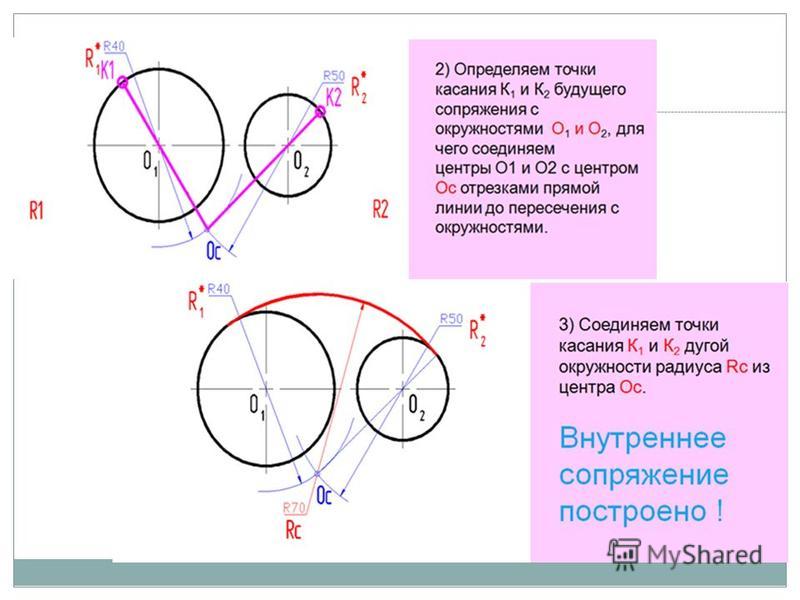 10. Элементы сети, нанесенные на диаграмму Смита.
10. Элементы сети, нанесенные на диаграмму Смита.
Согласование полных сопротивлений по шагам
Еще одной функцией диаграммы Смита является возможность определения соответствия импеданса. Это обратная операция нахождения эквивалентного импеданса данной сети. Здесь импедансы фиксированы на двух концах доступа (часто источник и нагрузка), как показано на Рисунок 11 . Цель состоит в том, чтобы спроектировать сеть для вставки между ними, чтобы обеспечить надлежащее согласование импедансов.
Рис. 11. Репрезентативная схема с известным импедансом и неизвестными компонентами.
На первый взгляд кажется, что это не сложнее, чем найти эквивалентное сопротивление. Но проблема в том, что может существовать бесконечное количество совпадающих комбинаций сетевых компонентов, дающих одинаковые результаты. Также может потребоваться учитывать другие входные данные (такие как структура типа фильтра, коэффициент качества и ограниченный выбор компонентов).
Подход, выбранный для достижения этой цели, требует добавления последовательностей и шунтирующих элементов на диаграмме Смита до тех пор, пока не будет достигнуто желаемое сопротивление. Графически это выглядит как поиск способа связать точки на диаграмме Смита. Опять же, лучший способ проиллюстрировать подход — обратиться к требованию в качестве примера.
Цель состоит в том, чтобы согласовать импеданс источника (Z S ) с нагрузкой (z L ) на рабочей частоте 60 МГц (см. рис. 11). Структура сети была зафиксирована как низкочастотная, L-типа (альтернативный подход состоит в том, чтобы рассматривать проблему как заставить нагрузку появиться как импеданс со значением = Z S , комплексно-сопряженным Z S ). Вот как находится решение.
Для увеличенного изображения (PDF, 537K)
Рис. 12. Сеть на Рис. 11 с точками, нанесенными на диаграмму Смита.
Первое, что нужно сделать, это нормализовать различные значения импеданса.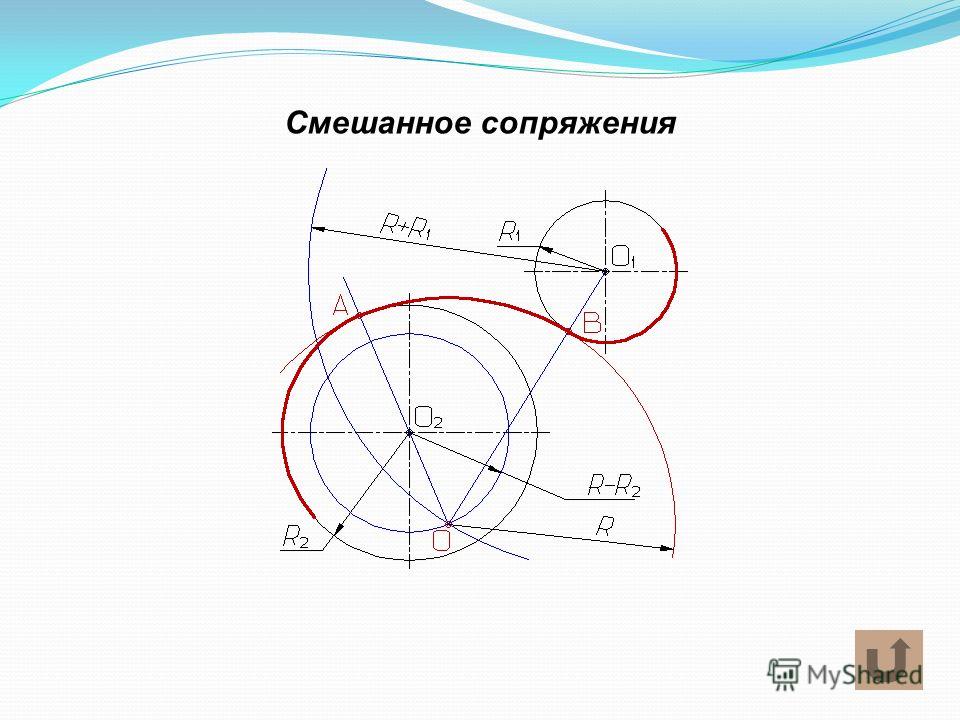 Если это не указано, выберите значение, которое находится в том же диапазоне, что и значения нагрузки/источника. Предположим, что Z 0 равно 50 Ом. Таким образом, z S = 0,5 — j0,3, z* S = 0,5 + j0,3 и z L = 2 — j0,5.
Если это не указано, выберите значение, которое находится в том же диапазоне, что и значения нагрузки/источника. Предположим, что Z 0 равно 50 Ом. Таким образом, z S = 0,5 — j0,3, z* S = 0,5 + j0,3 и z L = 2 — j0,5.
Затем расположите две точки на графике. Отметьте A для z L и D для z* S .
Затем определите первый элемент, подключенный к нагрузке (шунтирующий конденсатор), и преобразуйте его в проводимость. Это дает нам точку A’.
Определить участок дуги, где появится следующая точка после подключения конденсатора C. Поскольку мы не знаем значение C, мы не знаем, где остановиться. Однако мы знаем направление. C в шунте означает движение по часовой стрелке на диаграмме Смита полной проводимости до тех пор, пока не будет найдено значение. Это будет точка B (допуск). Поскольку следующий элемент является последовательным элементом, точка B должна быть преобразована в плоскость импеданса. Затем можно получить точку B’.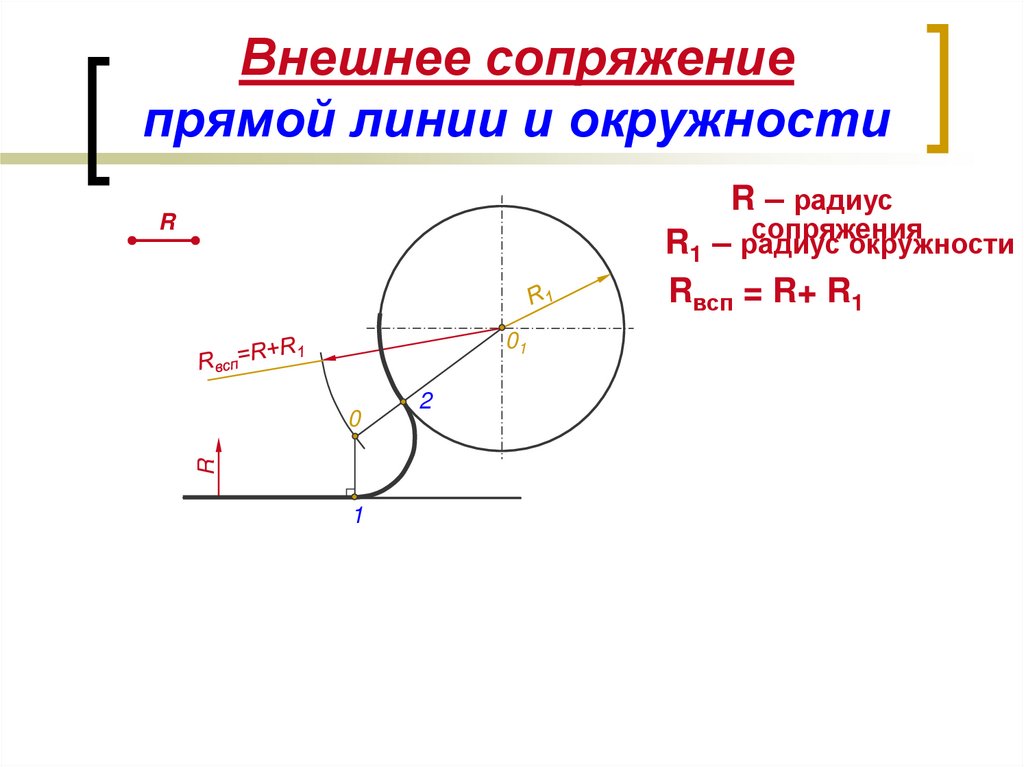 Точка B’ должна располагаться на той же окружности сопротивлений, что и D. Графически существует только одно решение от A’ до D, но промежуточная точка B (и, следовательно, B’) должна быть проверена с помощью «проверки и проверки». «попробовать» настройку. Найдя точки B и B’, мы можем измерить длину дуги A’ через B и дуги B’ через D. Первая дает нормированное значение активной проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Дуга A ‘ через B измеряет b = 0,78 и, таким образом, B = 0,78 × Y 0 = 0,0156 с. Поскольку ωC = B, то C = B/ω = B/(2πf) = 0,0156/[2π(60 × 10 6 )] = 41,4 пФ.
Точка B’ должна располагаться на той же окружности сопротивлений, что и D. Графически существует только одно решение от A’ до D, но промежуточная точка B (и, следовательно, B’) должна быть проверена с помощью «проверки и проверки». «попробовать» настройку. Найдя точки B и B’, мы можем измерить длину дуги A’ через B и дуги B’ через D. Первая дает нормированное значение активной проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Дуга A ‘ через B измеряет b = 0,78 и, таким образом, B = 0,78 × Y 0 = 0,0156 с. Поскольку ωC = B, то C = B/ω = B/(2πf) = 0,0156/[2π(60 × 10 6 )] = 41,4 пФ.
Длина дуги от B’ до D равна x = 1,2, поэтому X = 1,2 × Z 0 = 60 Ом. Поскольку ωL = X, то L = X/ω = X/(2πf) = 60/[2π(60 × 10 6 )] = 159 нГн.
Рис. 13. Типовая рабочая схема MAX2472.
Второй пример соответствует выходному сигналу MAX2472 с импедансом нагрузки 50 Ом (z L ) на рабочей частоте 900 МГц (см.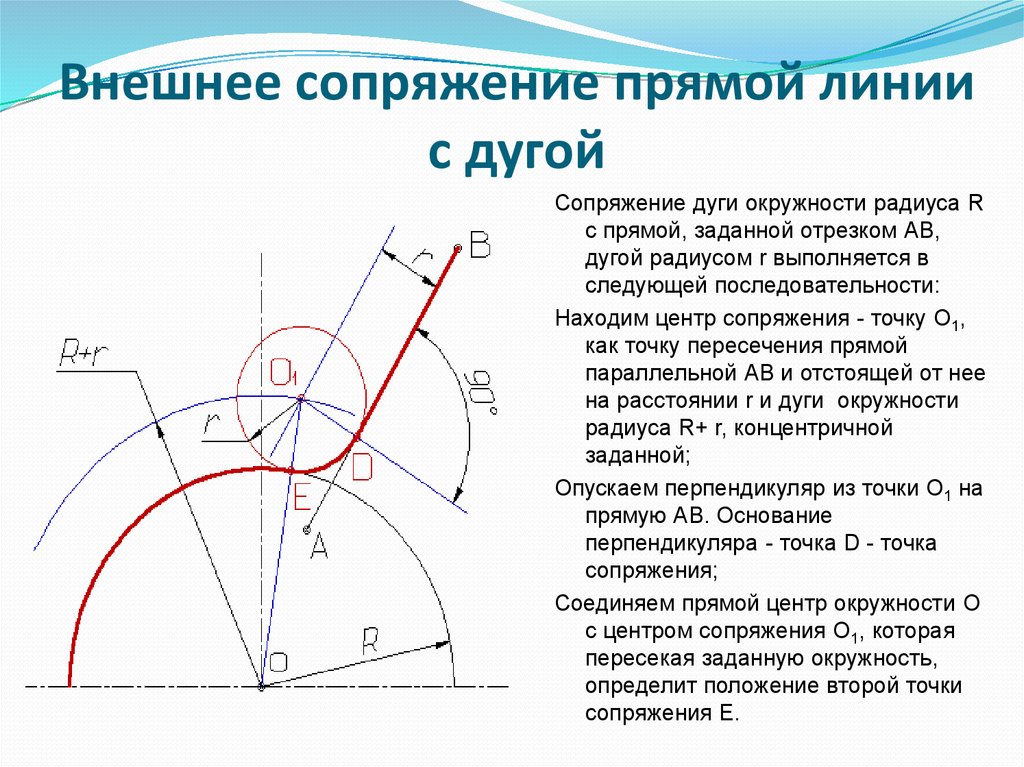 Рисунок 14 ). Эта сеть будет использовать ту же конфигурацию, что и в описании MAX2472. На приведенном выше рисунке показана согласующая сеть с шунтирующей катушкой индуктивности и последовательным конденсатором. Вот как находится решение.
Рисунок 14 ). Эта сеть будет использовать ту же конфигурацию, что и в описании MAX2472. На приведенном выше рисунке показана согласующая сеть с шунтирующей катушкой индуктивности и последовательным конденсатором. Вот как находится решение.
Рис. 14. Сеть на Рис. 13 с точками, нанесенными на диаграмму Смита.
Первое, что нужно сделать, это преобразовать параметр рассеяния S 22 в его эквивалентный нормализованный импеданс источника. MAX2472 использует Z 0 на 50 Ом. Таким образом, S 22 = 0,81/-29,4° становится z S = 1,4 — j3,2, z L = 1 и z L * = 1.
Затем расположите две точки на диаграмма. Метка A для z S и D для z L *. Поскольку первым элементом, подключенным к источнику, является шунтирующая катушка индуктивности, преобразуйте импеданс источника в адмиттанс. Это дает нам точку A’.
Определить участок дуги, где появится следующая точка после подключения индуктора L СПИЧКА . Поскольку мы не знаем значения L MATCH , мы не знаем, где остановиться. Однако мы знаем, что после добавления L MATCH (и преобразования обратно в импеданс) результирующий импеданс источника должен лежать на круге r = 1. Поэтому дополнительный последовательный конденсатор С МАТЧ может довести результирующий импеданс до z = 1 + j0. Поворачивая круг r = 1 на 180° вокруг начала координат, мы наносим все возможные значения полной проводимости, которые соответствуют кругу r = 1. Пересечение этого отраженного круга и круга постоянной проводимости, используемого с точкой A’, дает нам точку B (адмиттанс). Отражение точки B к импедансу становится точкой B’.
Поскольку мы не знаем значения L MATCH , мы не знаем, где остановиться. Однако мы знаем, что после добавления L MATCH (и преобразования обратно в импеданс) результирующий импеданс источника должен лежать на круге r = 1. Поэтому дополнительный последовательный конденсатор С МАТЧ может довести результирующий импеданс до z = 1 + j0. Поворачивая круг r = 1 на 180° вокруг начала координат, мы наносим все возможные значения полной проводимости, которые соответствуют кругу r = 1. Пересечение этого отраженного круга и круга постоянной проводимости, используемого с точкой A’, дает нам точку B (адмиттанс). Отражение точки B к импедансу становится точкой B’.
Найдя точки B и B’, мы можем измерить длину дуги A’ через B и дуги B’ через D. Первое измерение дает нормализованное значение проводимости L MATCH . Второй дает нормализованное значение реактивного сопротивления C MATCH . Дуга от A’ до B измеряет b = -0,575 и, таким образом, B = -0,575 × Y 0 = 0,0115S.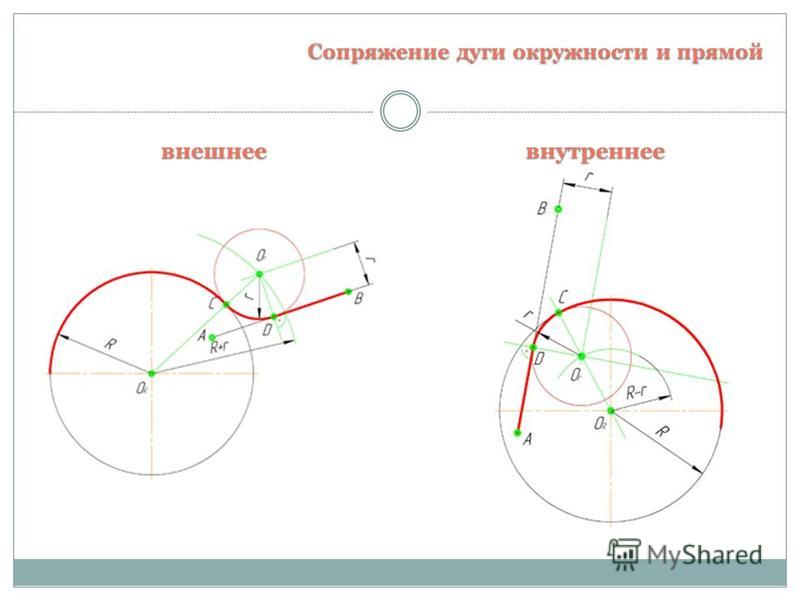 Поскольку 1/ωL = B, то L MATCH = 1/Bω = 1/(B2πf) = 1/(0,01156 × 2 × π × 900 × 10 6 ) = 15,38 нГн, что округляется до 15 нГн. Дуга B’ через D измеряет × = -2,81, таким образом, X = -2,81 × Z 0 = -140,5 Ом. Поскольку -1/ωC = X, то C MATCH = -1/Xω = -1/(X2πf) = -1/(-140,5 × 2 × π × 900 × 10 6 ) = 1,259 пФ, что округляет до 1пФ. Хотя эти расчетные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в технических характеристиках: L MATCH = 12 нГн и C MATCH = 1 пФ.
Поскольку 1/ωL = B, то L MATCH = 1/Bω = 1/(B2πf) = 1/(0,01156 × 2 × π × 900 × 10 6 ) = 15,38 нГн, что округляется до 15 нГн. Дуга B’ через D измеряет × = -2,81, таким образом, X = -2,81 × Z 0 = -140,5 Ом. Поскольку -1/ωC = X, то C MATCH = -1/Xω = -1/(X2πf) = -1/(-140,5 × 2 × π × 900 × 10 6 ) = 1,259 пФ, что округляет до 1пФ. Хотя эти расчетные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в технических характеристиках: L MATCH = 12 нГн и C MATCH = 1 пФ.
Заключение
Учитывая сегодняшнее изобилие программного обеспечения и доступность высокоскоростных мощных компьютеров, можно поставить под сомнение необходимость в таком базовом и фундаментальном методе определения основ схемы. На самом деле инженера настоящим инженером делает не только академическое знание, но и способность использовать ресурсы всех типов для решения проблемы.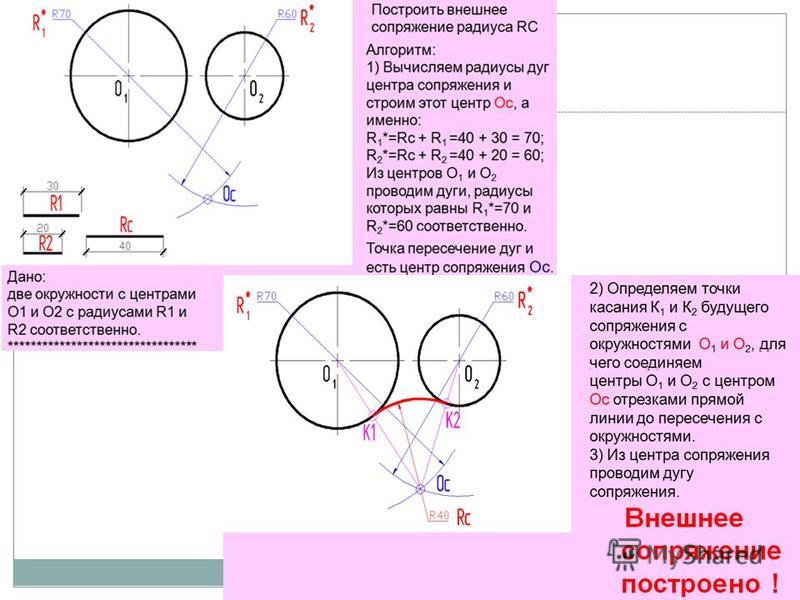 Легко ввести несколько чисел в программу, и она выдаст решение. Когда решения сложные и многогранные, наличие компьютера для выполнения черновой работы особенно удобно. Однако знание лежащей в основе теории и принципов, которые были перенесены на компьютерные платформы, и того, откуда они взялись, делает инженера или дизайнера более всесторонним и уверенным в себе профессионалом, а результаты — более надежными.
Легко ввести несколько чисел в программу, и она выдаст решение. Когда решения сложные и многогранные, наличие компьютера для выполнения черновой работы особенно удобно. Однако знание лежащей в основе теории и принципов, которые были перенесены на компьютерные платформы, и того, откуда они взялись, делает инженера или дизайнера более всесторонним и уверенным в себе профессионалом, а результаты — более надежными.
Аналогичная версия этой статьи появилась в выпуске RF Design за июль 2000 года.
| ||||||||||||||||
Спряжение глаголов в испанском языке511
Что такое глагол?
Вообще говоря, глагол — это слово в предложении, которое передает действие.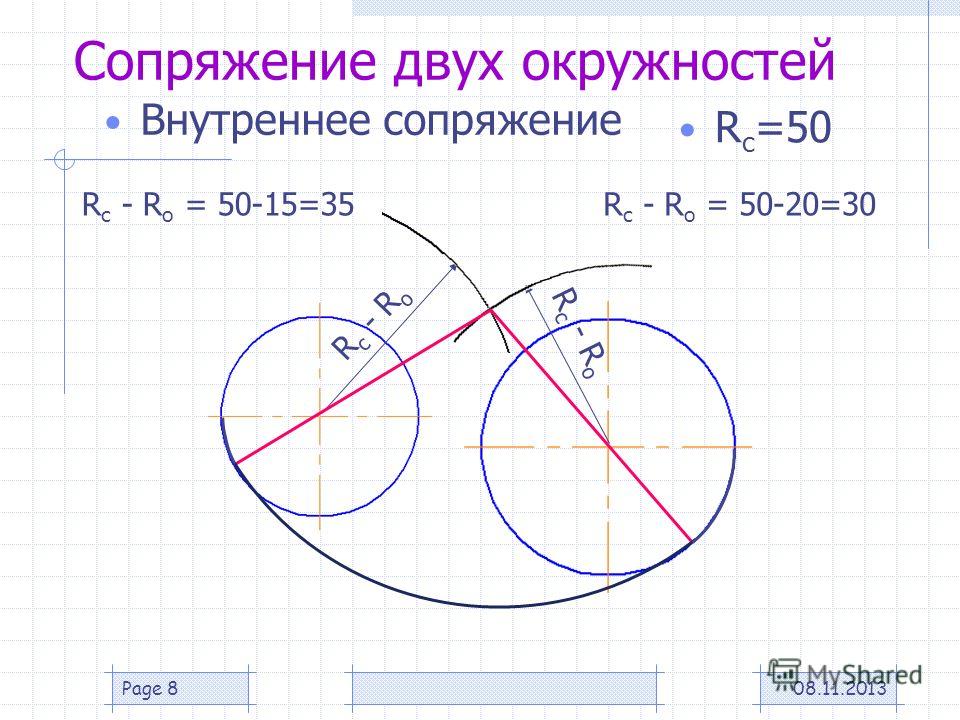 Глаголы в следующих предложениях подчеркнуты:
Глаголы в следующих предложениях подчеркнуты:
Лионель Месси играют в футбол.
Тейлор Свифт поет «Ты принадлежишь мне».
Марта, Иоланда и я вместе учимся на уроке химии .
Джордж Клуни
и Брэд Питт звезда в «11 друзей Оушена».
Глаголы также могут выражать состояние бытия:
Они очень счастливы.
Что такое сопряжение?
Спряжение — это действие, при котором глагол берется и изменяется таким образом, чтобы он «согласовывался» со своим подлежащим. Например, давайте изменим подлежащее в этом предложении «У нас есть лестница» с «мы» на «Мануэль»:
У нас есть лестница. → Мануэль имеет лестницу.
Для подлежащего и глагола чтобы согласиться, нам нужно было заменить глагол «иметь» на «имеет». Это сопряжение.
Звучит смешно, когда глагол неправильно спрягается:
I есть лестница.
Если вы выросли, говоря по-английски, вы можете спрягать глаголы, даже не задумываясь об этом; это просто естественно. Однако спрягать глаголы в испанском языке будет непросто. Вам нужно каждый раз останавливаться и думать, и практиковаться, практиковаться, практиковаться, пока это не станет вашей второй натурой.
Однако спрягать глаголы в испанском языке будет непросто. Вам нужно каждый раз останавливаться и думать, и практиковаться, практиковаться, практиковаться, пока это не станет вашей второй натурой.
Инфинитивы
Глагол без спряжения известен как «инфинитив». Поскольку не указывается подлежащее, инфинитив имеет «бесконечные» возможности спряжения. Английские инфинитивы включают слово to. Посмотрите на таблицу ниже и сравните инфинитивы с некоторыми сопряженными аналогами. Обратите внимание, что нет указания на предмет инфинитива:
инфинитив: | сопряжено: | |
|---|---|---|
играть | → | он играет |
петь | → | она поет |
иметь | → | у нас есть |
будет | → | они |
В отличие от английских инфинитивов, испанские инфинитивы состоят из одного слова, но их довольно легко распознать.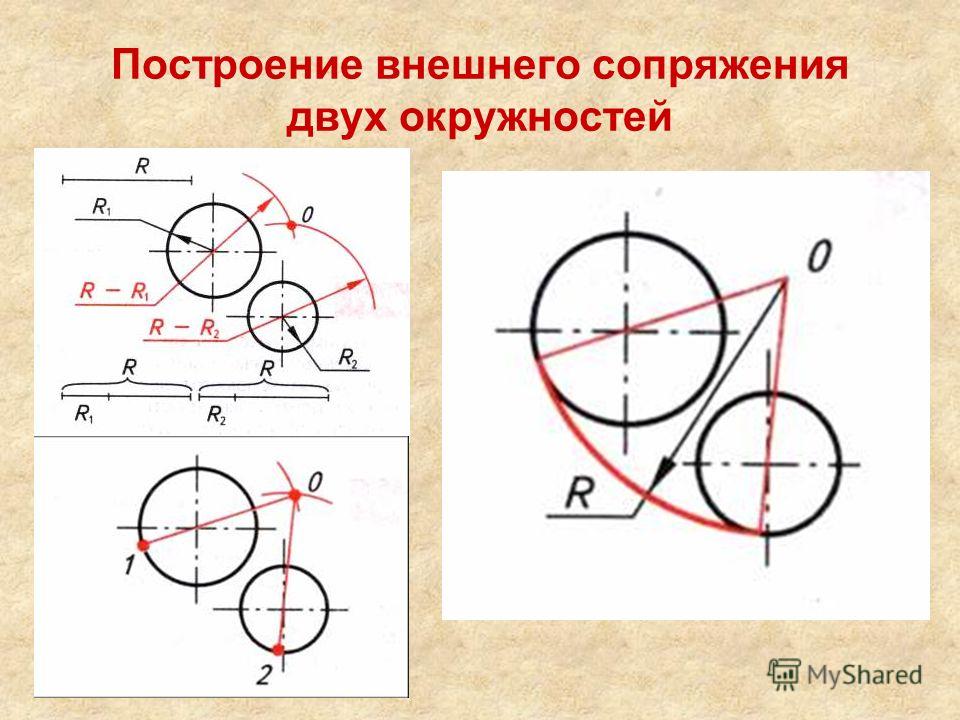
Три типа испанских инфинитивов
Примечание: Не все слова, оканчивающиеся на -ar, -er, или -ir, являются глаголами. Например. lugar — это существительное, означающее «место».
Все инфинитивы в испанском языке имеют одно из трех окончаний: -ar, -er, или -ir. Например:
хабл ар
говорить
ком э
есть
viv ir
жить
Испанские глаголы довольно уместно подразделяются на категории -ar, -er глаголы или -ir глаголы. Еще несколько примеров:
-AR глаголы: |
|---|
не могу ар estudi ar toc ar |
-ER глаголы: |
|---|
beb er корр. ле er |
-IR глаголы: |
|---|
abr ir записать ir recib ir |
Спряжение испанских глаголов
Времена глаголов
Прежде чем мы перейдем к спряжению глаголов, нам нужно кратко поговорить о «времях». Есть три основных времени: прошедшее, настоящее и будущее:
Я бежал.
Я бегу.
Я побегу.
Но есть и другие времена (как в английском, так и в испанском). Например:
Я побежал.
Я побежал.
Я побегу.
На этом сайте есть специальные уроки для каждого времени, но пока мы будем работать с настоящим временем.
См. также: Тематические местоимения на испанском языке
Представьте, что мы хотим сказать «я говорю» на испанском языке.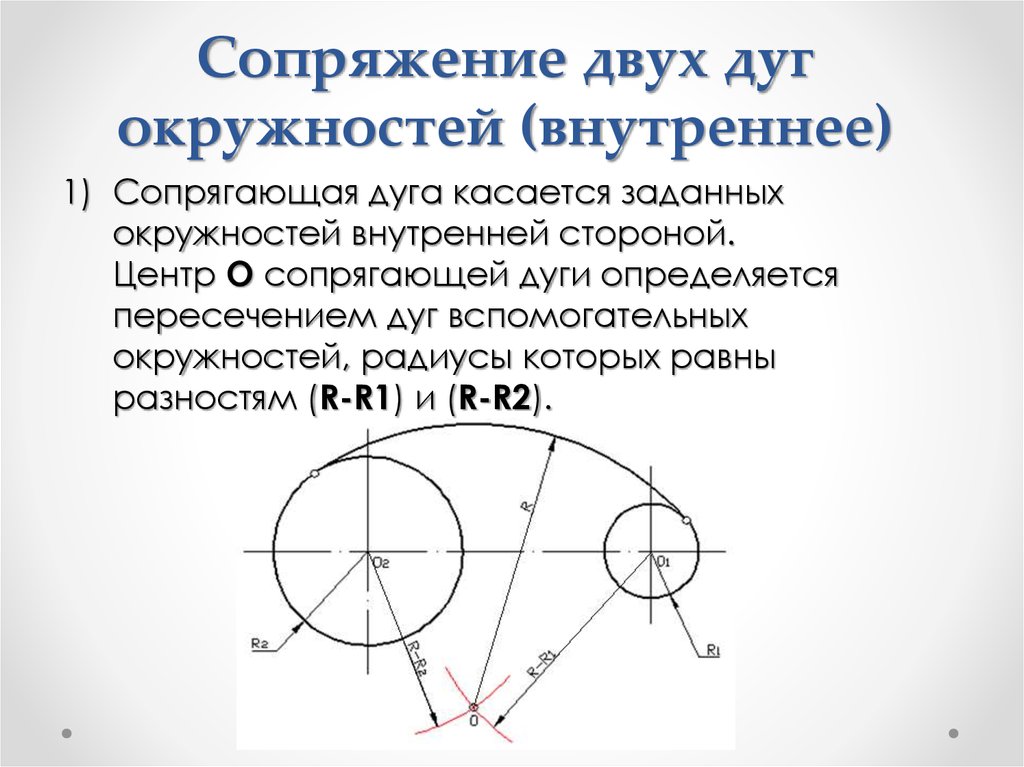 Первый шаг – определение предмета. Вот краткое напоминание о возможных подлежащих местоимениях из предыдущего урока:
Первый шаг – определение предмета. Вот краткое напоминание о возможных подлежащих местоимениях из предыдущего урока:
единственное число: | во множественном числе: | |
|---|---|---|
первое лицо: | лет | нозотрос, нозотрас |
второе лицо, неформальное: | вт | восотрос, восотрас |
второе лицо, формальное: | б/у | используется |
третье лицо: | эль, элла | Эллос, Эллас |
Итак, нам нужно использовать йо (I) в качестве темы.
Следующий шаг — найти нужный нам инфинитив и разбить его на две части: основу и окончание.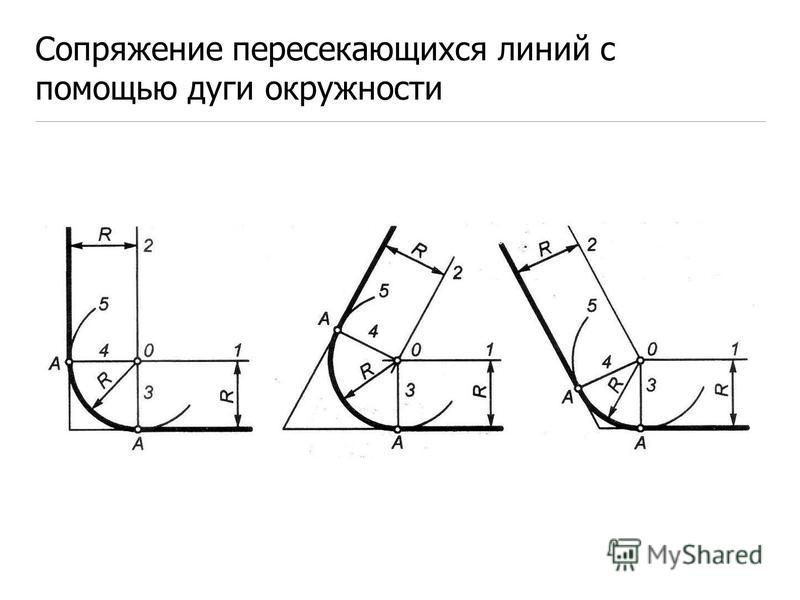 Хороший словарь скажет нам, что «говорить» — это 9.0737 хаблар на испанском языке. Основа hablar — «habl», а окончание — «-ar»:
Хороший словарь скажет нам, что «говорить» — это 9.0737 хаблар на испанском языке. Основа hablar — «habl», а окончание — «-ar»:
инфинитив: | стержень : | окончание: |
|---|---|---|
хаблар | хабл | -ар |
Таблицы окончаний глаголов
Теперь нам нужно найти (или еще лучше запомнить) соответствующую таблицу окончаний глаголов. Окончания глаголов «-ar» в настоящем времени перечислены в таблице ниже справа. (Помните, что мы используем таблицы глаголов с «-ar», потому что hablar — это глагол с «-ar».) Слева снова находятся подлежащие местоимения. Обратите внимание, что каждая ячейка в таблице подлежащих местоимений соответствует ячейке в таблице окончаний глаголов. Это не совпадение:
подлежащие местоимения:
| ↔ | Окончания «-ar»:
|
Нам нужно найти концовку, которая соответствует нашей теме.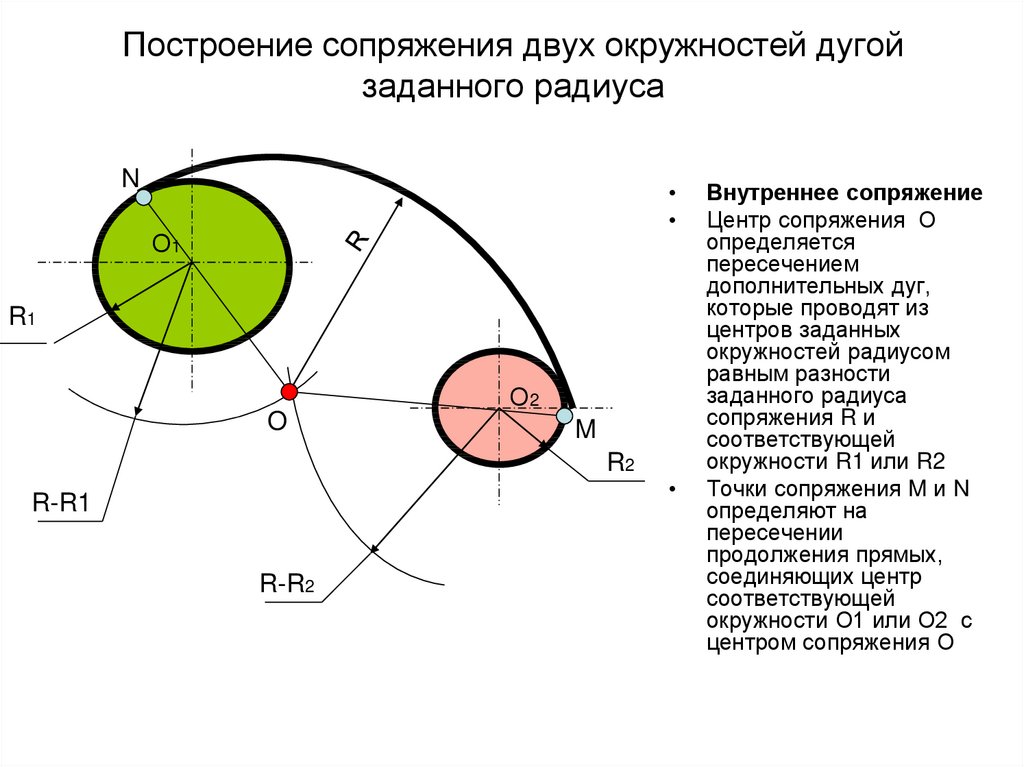 Так как наше подлежащее yo , мы добавим глагол с окончанием «-o» к нашей основе («habl»):
Так как наше подлежащее yo , мы добавим глагол с окончанием «-o» к нашей основе («habl»):
подлежащие местоимения:
| ↔ | Окончания «-ar»:
|
Складываем все вместе и получаем:
Йо хабло.
Я говорю.
Попробуем еще. Инфинитив dibujar означает «рисовать». Как его спрягать в значении «мы рисуем»? Удалите окончание, определите подлежащее местоимение ( nosostros ) и добавьте соответствующее окончание («-amos») к основе («dibuj»):
подлежащие местоимения:
| ↔ | Окончания «-ar»:
|
Добавьте местоимение подлежащего, и мы получим:
Nosotros dibujamos.
Рисуем.
Хорошо, а как насчет глаголов -er и -ir? Мы будем следовать той же процедуре, но нам нужно использовать разные графики. Вот все три (настоящего времени) графика вместе. Обратите внимание на сходства и различия:
Окончания «-ar»:
-o | -амос |
-как | — |
-а | -ан |
-а | -ан |
окончания «-er»:
-o | -эмо |
-эс | — |
-е | -en |
-е | -en |
Окончания «-ir»:
-o | -Имос |
-эс | -ис |
-е | -en |
-е | -en |
Инфинитив correr означает «бежать». Давайте использовать его, чтобы сказать «Вы бежите». корр. Окончание (из схемы -er) — -es. Добавляем подлежащее местоимение и получаем:
Давайте использовать его, чтобы сказать «Вы бежите». корр. Окончание (из схемы -er) — -es. Добавляем подлежащее местоимение и получаем:
Соответ.
Ты бежишь.
(Помните, что мы берем окончание из таблицы -er, потому что correr является глаголом -er.)
Как насчет глагола -ir? Vivir означает «жить». Давайте используем его, чтобы сказать «Мы живем».
Мы живем.
Неправильное спряжение глаголов в испанском звучит так же плохо, как и в английском. Если вы скажете «У меня есть лестница» на английском языке, люди посмотрят на вас смешно. То же самое, если вы скажете «Nosotros viven» по-испански.
Упрощенные таблицы окончаний глаголов
Вы не часто будете видеть таблицы глаголов, подобные показанным выше. Почему? Потому что они немного сложнее, чем должны быть. Обратите внимание, что окончания usted совпадают с окончаниями el / ella ? И почему окончания ustedes совпадают с окончаниями ellos / ellas ? Это верно не только для окончаний глаголов в настоящем времени; это верно и для всех других времен.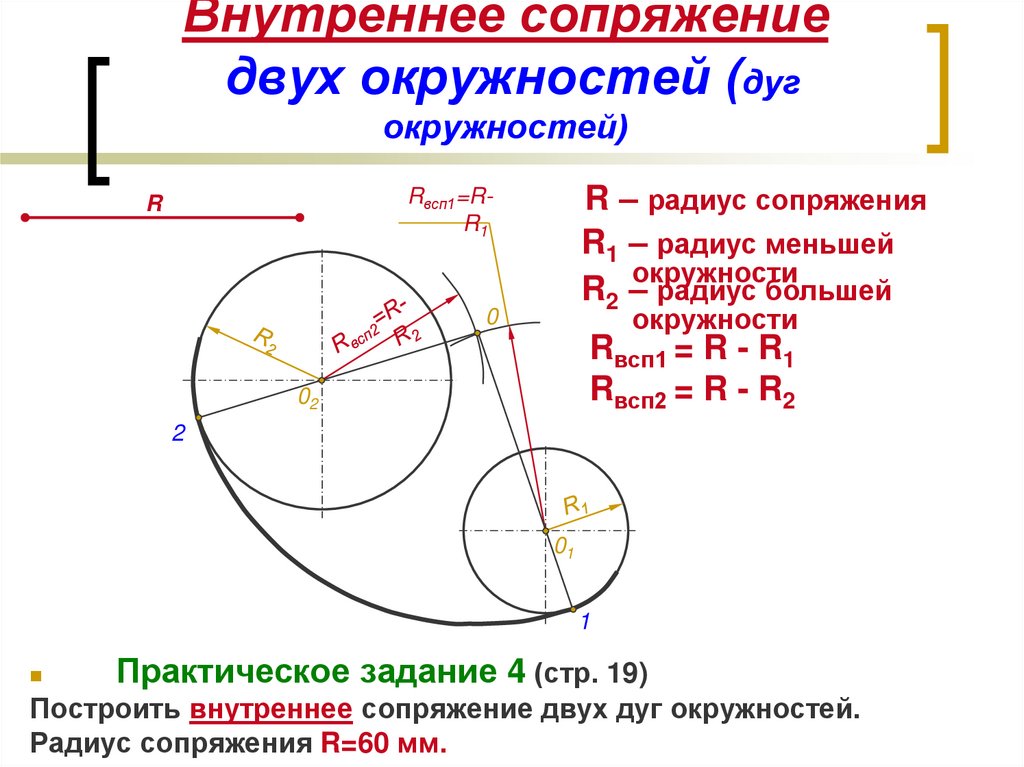 Поэтому гораздо проще сжать окончания в шесть сеток блоков, например:
Поэтому гораздо проще сжать окончания в шесть сеток блоков, например:
Окончания «-ar»:
-o | -амос |
-как | — |
-а | -ан |
окончания «-er»:
-o | -эмо |
-эс | — |
-e | -en |
Окончания «-ir»:
-o | -Имос |
-эс | — |
-е | -en |
Это означает, что ваша соответствующая таблица подлежащих местоимений должна выглядеть так:
подлежащих местоимений:
год | носотрос,-как |
вт | восотрос,-as |
эл, элла, уд. | Эллос, Эллас, Удс. |
Но помните, что мы ставим Ud. в поле él / ella просто для упрощения, а не потому, что это означает «он» или «она». Аналогично, помните, что Uds. не означает «они». Это просто в ellos / ellas коробка, потому что окончания глаголов одинаковы.
Убедитесь, что вы понимаете эта сетка. Это очень важно; вы будете видеть много из этого, когда будете изучать испанский язык.
Темы, которых нет в таблице?
Что делать, если вы хотите использовать тему, которой нет в таблице тем? Помните, что это местоимения или слова, которые заменяют другие существительные. Вам не нужно использовать местоимение, но вам все равно нужно вытащить окончание из соответствующего места на графике:
Барак Обама ≈ эль | → | Хабла Барака Обамы. |
Рамон и я ≈ носотрос | → | Рамон и йо корремос. |
Сусана и Рамон ≈ Эллос | → | Сусана и Рамон Живен. |
Неправильные глаголы
Вся эта чепуха со спряжениями уже может показаться ошеломляющей, но вы должны знать, что (почти) у каждого времени глагола есть определенные глаголы, которые не подчиняются обычным правилам спряжения. Эти глаголы известны как «неправильные» глаголы. Вам придется специально запоминать их спряжения, потому что обычные процедуры не работают. Вот пример печально известного неправильного глагола в настоящем времени: сер. (будет):
соевый | сом |
или | сой |
или | сын |
Ни одно из спряжений не следует ни одному из правил.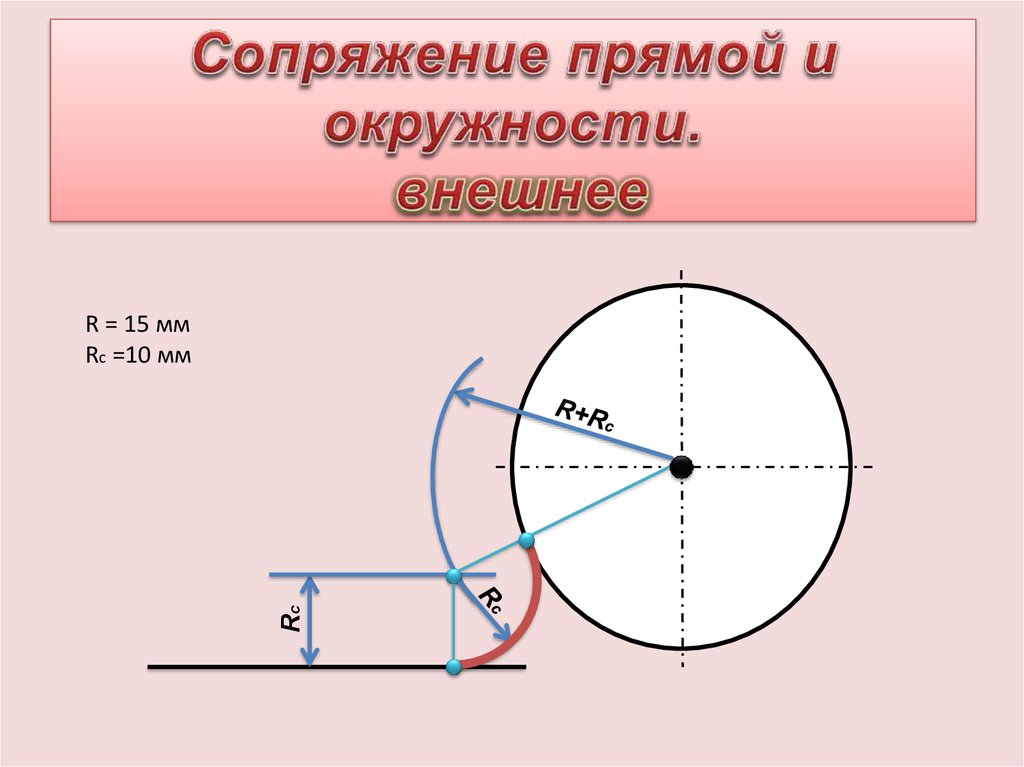 Мило, не так ли?
Мило, не так ли?
Но прежде чем вы начнете жаловаться на неправильные испанские глаголы, подумайте, каким неправильным может быть английский. Представьте, если бы вы, говорящий по-испански, должны были выучить это:
| . для игры (обычный): | будет (нерегулярно): |
|---|---|
я играю | Я |
Вы играете | Вы |
Он играет | Она |
Мы играем | Мы |
Они играют | Они |
Опускание подлежащих местоимений
Из-за того, что многие спряжения английских глаголов одинаковы, подлежащие местоимения очень важны. Посмотрите, что произойдет, если мы опустим одно:
Играет в футбол.
Какой предмет? Он она оно? Мы не можем сказать.
 Все правила по сольфеджио
Все правила по сольфеджио

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)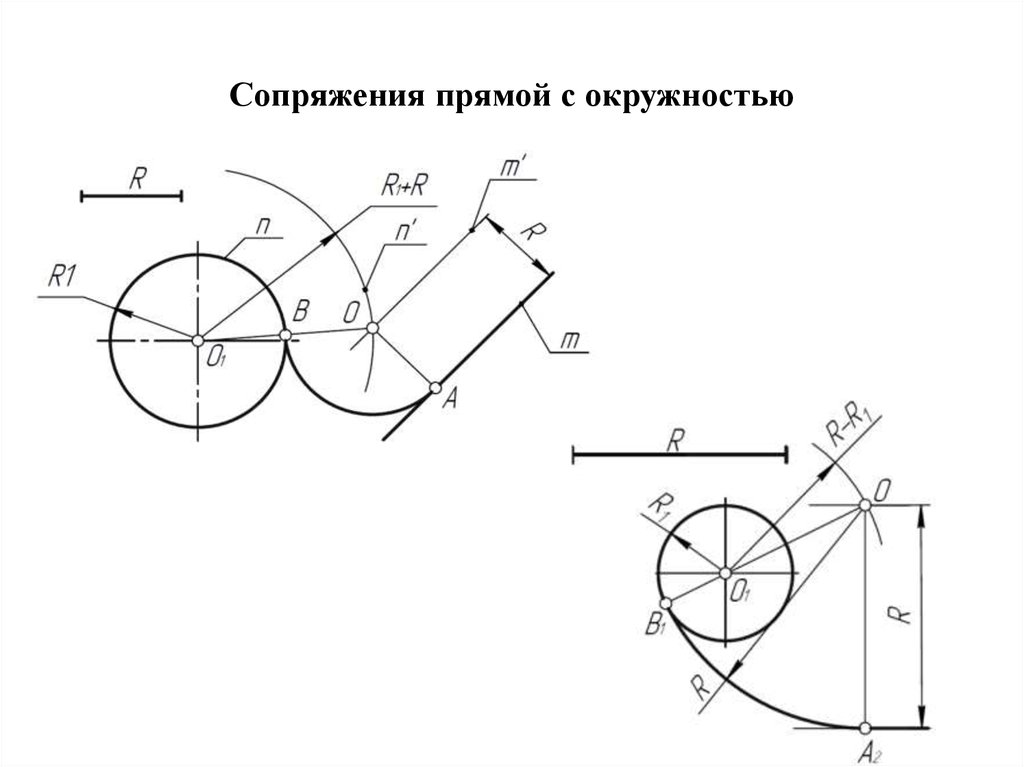 Лабораторные РЧ-измерения на месте, наряду с работой по настройке, необходимо учитывать для определения правильных окончательных значений. Расчетные значения необходимы для установки типа структуры и значений целевых компонентов.
Лабораторные РЧ-измерения на месте, наряду с работой по настройке, необходимо учитывать для определения правильных окончательных значений. Расчетные значения необходимы для установки типа структуры и значений целевых компонентов.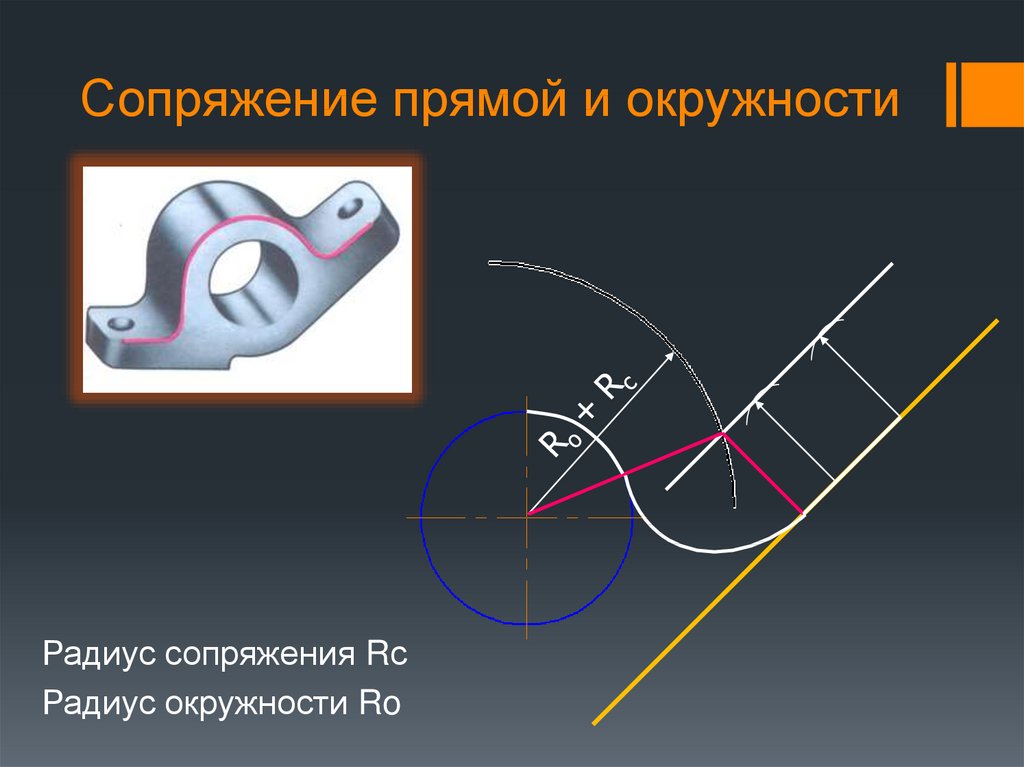
 3. Полное сопротивление на нагрузке.
3. Полное сопротивление на нагрузке. 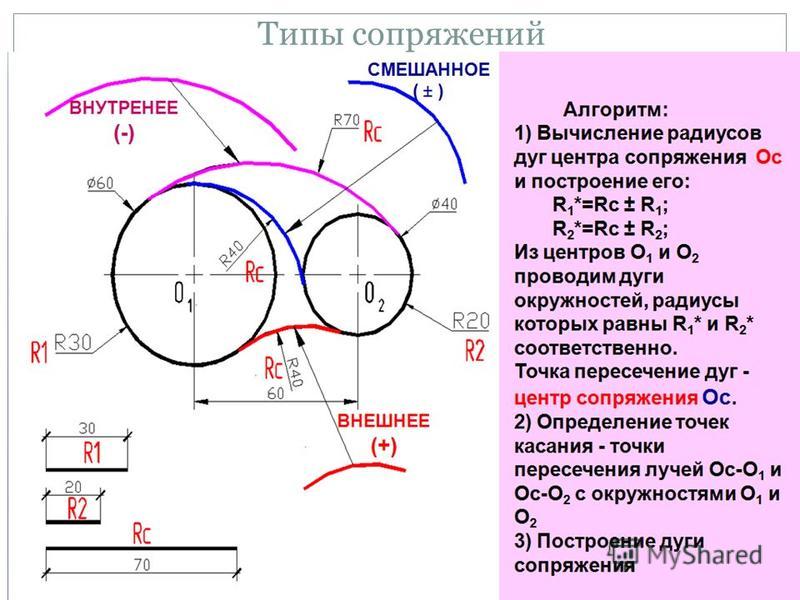
 В него входит точка (0, 0), являющаяся нулевой точкой отражения (нагрузка согласована с волновым сопротивлением). Короткое замыкание, как нагрузка, представляет собой окружность с центром в координате (0, 0) и имеет радиус 1. Для нагрузки холостого хода окружность вырождается в одну точку (с центром в 1, 0 и с радиус 0). Это соответствует максимальному коэффициенту отражения, равному 1, при котором вся падающая волна полностью отражается.
В него входит точка (0, 0), являющаяся нулевой точкой отражения (нагрузка согласована с волновым сопротивлением). Короткое замыкание, как нагрузка, представляет собой окружность с центром в координате (0, 0) и имеет радиус 1. Для нагрузки холостого хода окружность вырождается в одну точку (с центром в 1, 0 и с радиус 0). Это соответствует максимальному коэффициенту отражения, равному 1, при котором вся падающая волна полностью отражается. 
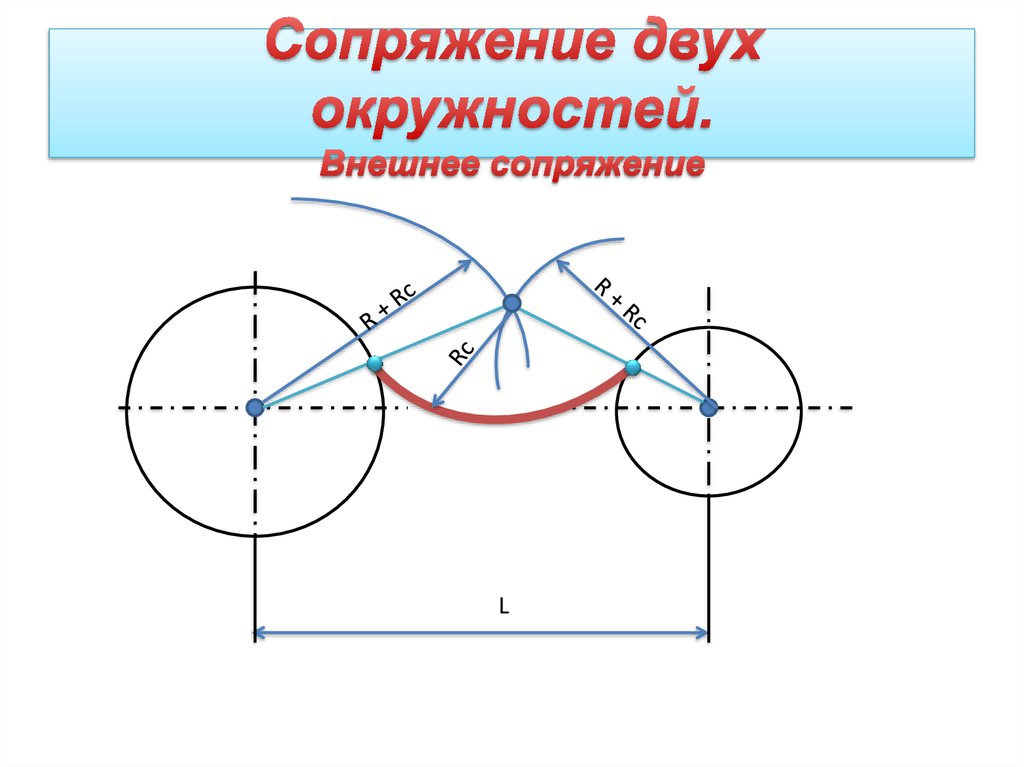
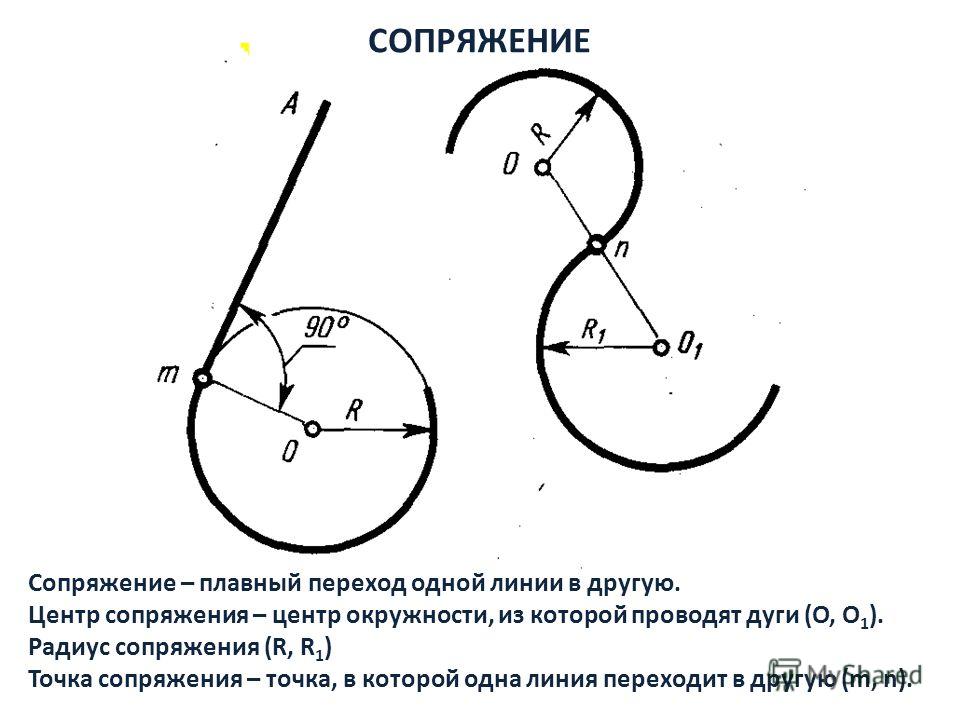 Рисунок 7 ).
Рисунок 7 ).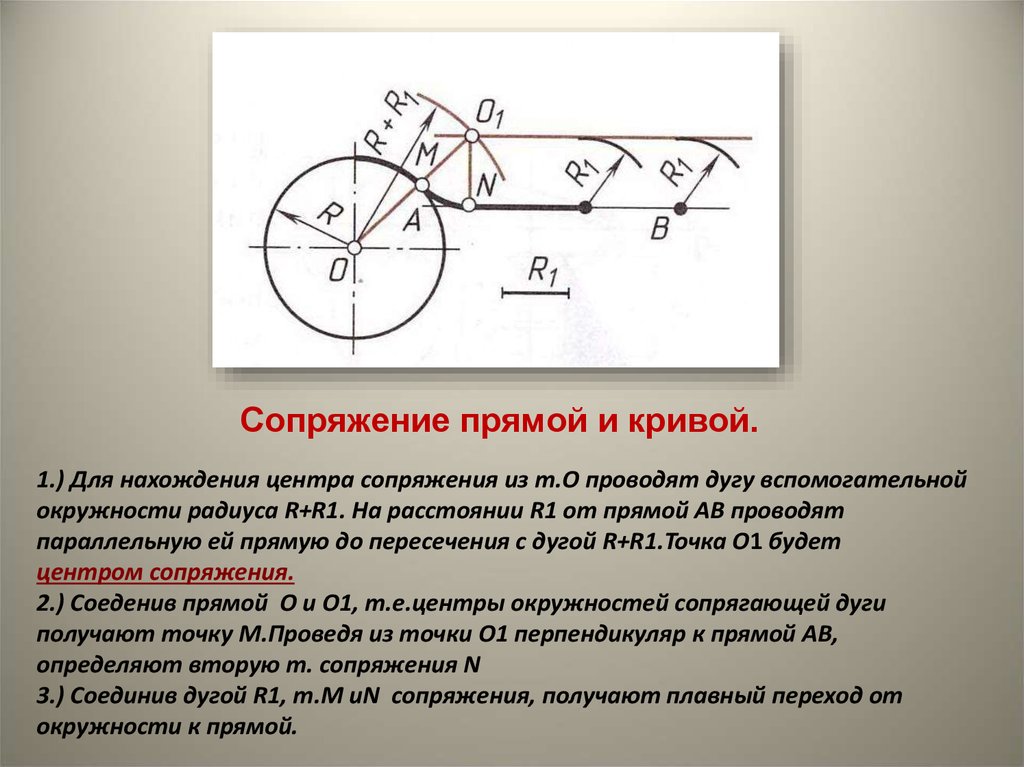 er
er 
