Сопряжение окружности и прямой как построить: Сопряжение прямой с окружностью

Методические рекомендации по теме «Сопряжения»

 

Министерство образования и молодежной политики Республики Коми

Государственное профессиональное образовательное учреждение

«Сыктывкарский политехнический техникум»

 

 

 

 

 

 

 

 

 

 

 

 

 

Л. В. Кочанова

 

Основы инженерной графики

 

Методические рекомендации

по выполнению самостоятельных работ

по теме «Сопряжение»

 

 

 

 

 

 

 

 

 

 

 

 

 

Сыктывкар 2020г.

 

        Министерство образования и молодежной политики Республики Коми

Государственное профессиональное образовательное учреждение

«Сыктывкарский политехнический техникум»

 

 

 

Л. В. Кочанова

 

Основы инженерной графики

 

 

 

Методические рекомендации по выполнению самостоятельных работ по теме «Сопряжение»

 

для профессии: 15.01.05 Сварщик (ручной и частично механизированной сварки (наплавки)

 

 

Составлено в соответствии с  Государственными требованиями к минимуму содержания и уровню подготовки выпускников по профессии: для профессии: 15.01.05 Сварщик (ручной и частично механизированной сварки (наплавки)

 

 

 

 

 

       Настоящие методические  указания содержат необходимые теоретические и практические сведения для самостоятельного освоения темы «Сопряжение». Пособие может быть использовано студентами техникума для самостоятельных работ.

 

 

 

 

 

 

 

 

 

 

 

Введение

       В этой методической работе будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

 

    Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

 

        Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

 

        Ниже будут рассмотрены основные типы сопряжений, упражнения по теме «Сопряжения».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла.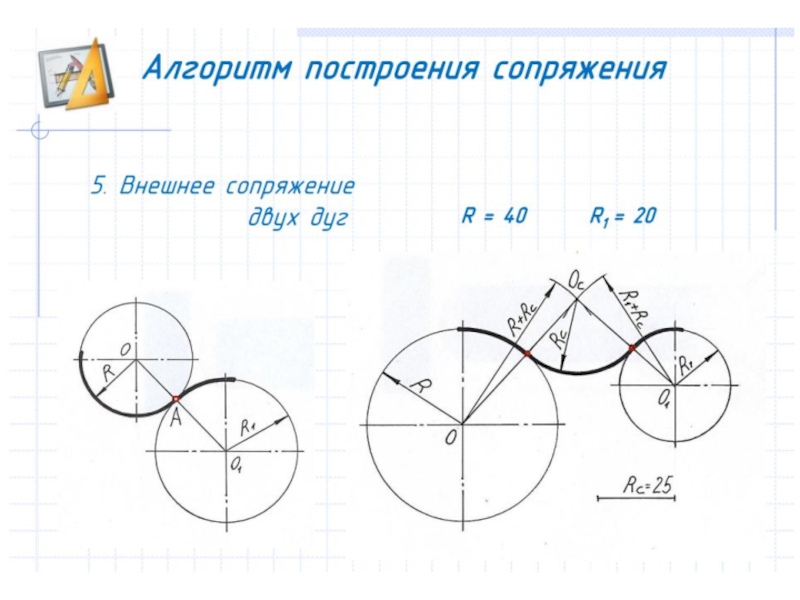

(Сопряжение пересекающихся прямых под прямым углом)

 

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

 

Сопряжение острого угла. (Сопряжение пересекающихся прямых под острым углом)

 

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение острого угла. Для построения сопряжения острого угла раствором циркуля, равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a и b. Сопряжение острого угла построено.

 

Сопряжение тупого угла. (Сопряжение пересекающихся прямых под тупым углом)

 

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

 

 

Сопряжение параллельных прямых линий

 

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

 

Сопряжение окружностей (дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.

      Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией.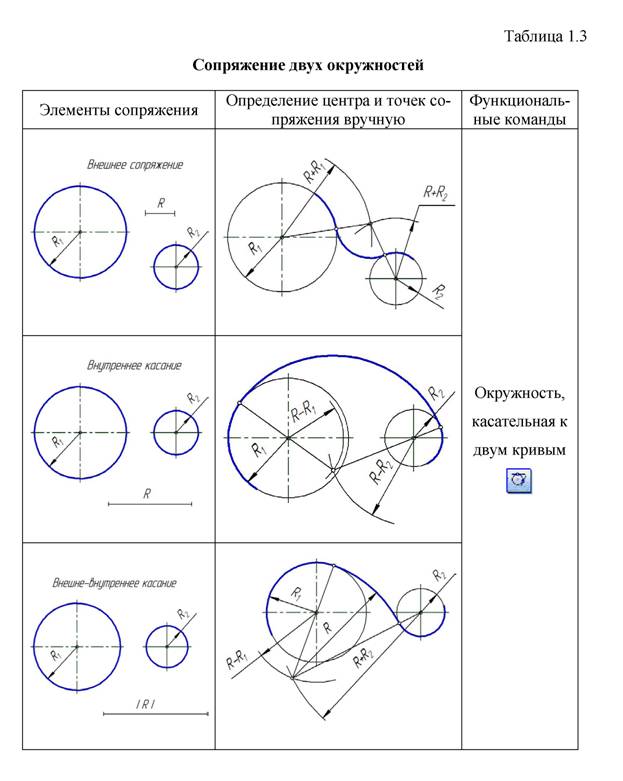 На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

                        

 

 

 

Сопряжение окружностей (дуг)

 

Внешнее сопряжение дуг окружностей

 

Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

 

 

 

 

 

 

 

Внутреннее сопряжение дуг окружностей

 

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

 

 

 

 

 

 

Смешанное сопряжение дуг окружностей

 

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её.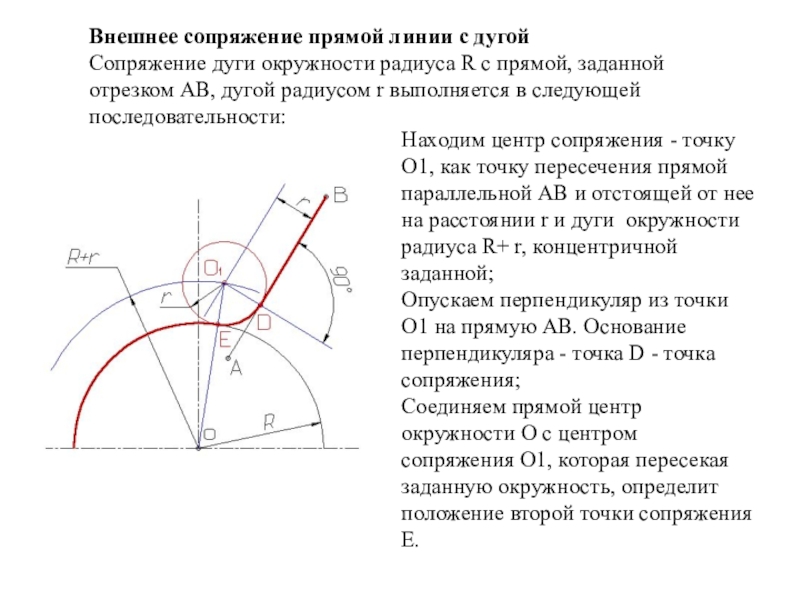

На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

 

 

 

 

 

 

 

Различные случаи сопряжений при черчении чертежей.

Анализ чертежа

       Пусть требуется построить чертеж прокладки (рис. 1, а). Как видно из чертежа, контур прокладки образуется в результате построения сопряжения окружностей, имеющих радиус 20 мм, дугой окружности R112. Изобразив в стороне этот случай сопряжения (рис. 1, б), замечают, что центр дуги сопряжения О должен находиться от центров малых окружностей на расстояниях, равных сумме радиусов окружностей: 20 + 112 = 132 мм. Для построения центра О из центров малых окружностей дугой радиуса 132 мм делают засечки. Соединив точку О с центрами малых дуг, получают точки сопряжения Л и В, между которыми и проводят дугу R 112. В рассматриваемом примере имеет место внешнее касание дуг, при котором центры находятся по разные стороны от точек сопряжения.

      Сопряжение прямых; линий с окружностями часто встречается в таких деталях, как гаечные ключи, шатуны, различные рычаги.

     Пусть требуется начертить контур головки шатуна (рис. 2, а). В чертеже имеет место сопряжение окружности R 20 с прямой, идущей параллельно оси шатуна на расстоянии 11 мм от нее, дугой радиуса R 15.

      Центре (рис. 2, б) должен находиться от окружности на расстоянии 15 мм, а от центра окружности на pacстоянии 20 + 15 = 35 мм; в то же самое время он должен находиться на расстоянии 11 + 15 = 26 мм от оси шатуна.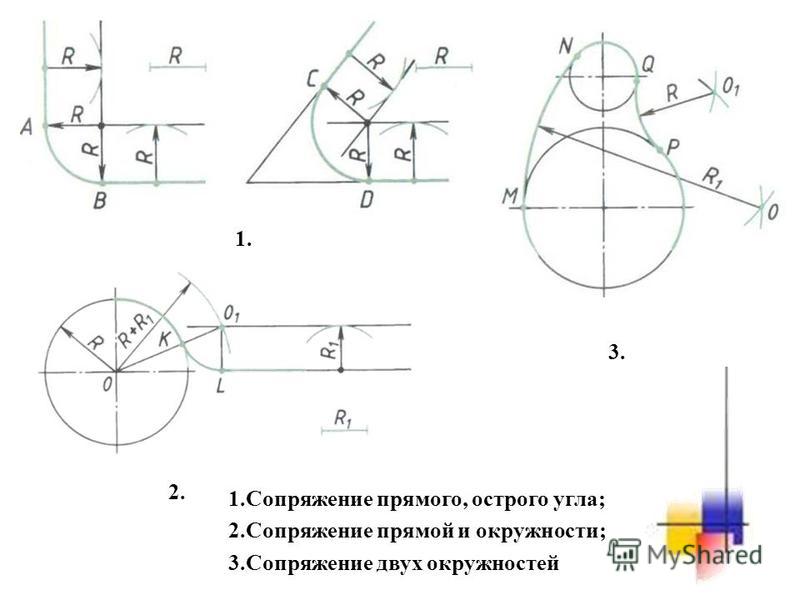

      Для нахождения центра О проводят дугу радиусом 35 мм и прямую, -параллельную оси шатуна на расстоянии 26 мм от этой оси. Точка пересечения дуги и прямой определит искомый центр.

Рис. 1. Сопряжение окружностей

Рис. 2. Сопряжение прямой с окружностью

Рис. 3. Практический пример сопряжения

    Соединяют центр дуги сопряжения О с центром окружности, находят первую точку сопряжения Л; опускают перпендикуляр из точки С на прямую, находят вторую точку сопряжения Б. Между точками сопряжения А и В проводят дугу сопряжения R 15.

      Пусть требуется начертить рычаг криволинейной формы (рис. 3, а). Предполагают, что задача решена: центр дуги R 105 найден (рис. 3, б). Определяют, чему будет равно расстояние от центра дуги сопряжения О до центра окружности 0 40. Очевидно, что оно будет равно разности радиусов 105—20 = 85 мм. Таким же путем находят расстояние от центра дуги сопряжения О до центра окружности 0 60 (105 — 30 = 75 мм). Пользуясь найденными величинами, из центров окружностей делают засечки, пересечение которых определит точку О. Соединяя найденный центр О с центрами окружностей 0 40 и 0 60, на продолжении линий находят точки сопряжения А и В. В примере имеет место внутреннее касание дуг, при котором центры находятся по одну сторону от точек касания.

        Центр Ох для проведения дуги R 58 предлагается найти самостоятельно. Подобный случай сопряжения уже рассматривался на рис. 1. Точки сопряжения находят по общему правилу, известному из геометрии: центры касающихся дуг и точки их касания (сопряжения) всегда лежат на одной прямой.

 

     Построение окружности, проходящей через заданную точку А и касающейся данной окружности в заданной точке В.

          Находим середину прямой линии АВ. Через середину линии АВ поводим перпендикуляр. Пересечение продолжения линии ОВ и перпендикуляра дает точку О1. О1 — центр искомой окружности с радиусом R = O1B = O1A.

Внутреннее касание окружности и дуги.

 

Построение сопряжения окружности с прямой линией в заданной на прямой точке А.

        Из заданной точки А линии LM восстанавливаем перпендикуляр к прямой линии LM. На продолжении перпендикуляра откладываем отрезок АВ. АВ = R. Соединяем точку В с центром окружности О1 прямой.

Из точки А проводим прямую линию параллельно ВО1 до пересечения с окружностью. Получим точку К – точку касания. Соединим точку К с центром окружности О1. Продлим линии О1К и АВ до пересечения. Получим точку О2, которая является центром дуги сопряжения с радиусом О2А = О2К.

                       

Сопряжение окружности с прямой в заданной точке.

Построение сопряжения окружности с прямой линией в заданной на окружности точке А.

                                             Внешнее касание.

Проводим касательную к окружности через точку А. Пересечение касательной с прямой линией LM даст точку В.

Делим угол, образованный касательной и прямой линией LM, пополам. Пересечение биссектрисы угла и продолжения радиуса ОА даст точку О1. О1 — центр дуги сопряжения с радиусом О1А = О1К.

                   

Сопряжение окружности с прямой в заданной точке на окружности.

 

   Внутреннее касание.

Проводим касательную к окружности через точку А. Пересечение касательной с прямой LM даст точку В. Делим угол, образованный касательной и прямой линией LM, пополам. Пересечение биссектрисы угла и продолжения радиуса ОА даст точку О1. О1 — центр дуги сопряжения с радиусом О1А = О1К.

                 

Сопряжение окружности  с прямой в заданной точке на окружности.

        Построение сопряжения двух неконцентрических дуг окружностей дугой заданного радиуса.

         Проводим из центра дуги О1 вспомогательную дугу радиусом R1-R3. Проводим из центра дуги О2 вспомогательную дугу радиусом R2+R3. Пересечение дуг даст точку О. О — центр дуги сопряжения с радиусом R3. Точки касания К1 и К2 лежат на линиях ОО1 и ОО2.

            

      Сопряжение 2-х неконцентрических дуг окружностей дугой.

 

Построение лекальной кривой подбором дуг.

  Подбирая  центры дуг, совпадающих с участками кривой, можно циркулем вычертить любую лекальную кривую.

 Для того чтобы дуги плавно переходили одна в другую, необходимо, чтобы точки их сопряжения (касания) находились на прямых линиях, соединяющих центры этих дуг.

 Последовательность построений.

 Подбираем центр 1 дуги произвольного участка ab.

На продолжении первого радиуса подбираем центр 2 радиуса  дуги участка bc.

На продолжении второго радиуса подбираем центр 3 радиуса  дуги участка cd и т. д.

Так строим всю кривую.

                  Подбор дуг.

Построение сопряжения двух параллельных прямых двумя дугами.

         Заданные на прямых параллельных линиях точки А и В соединяем линией АВ.

 Выбираем на прямой АВ произвольную точку М.

Делим отрезки АМ и ВМ пополам.

Восстанавливаем в серединах отрезков перпендикуляры.

В точках А и В, заданных прямых, восстанавливаем перпендикуляры к прямым.

Пересечение соответствующих перпендикуляров даст точки О1 и О2.

О1 центр дуги сопряжения с радиусом О1А = О1М.

О2 центр дуги сопряжения с радиусом О2В = О2М.

Если точку М выбрать на середине линии АВ, то радиусы дуг сопряжения будут равны.

Касание дуг в точке М, находящейся на линии О1О2.

                

Сопряжение параллельных прямых двумя дугами.

 

 

 

 

Выполнить упражнения.

 

 

 

Варианты для выполнения индивидуальных заданий.

 

1

2

 

3

4

 

5

6

 

7

8

 

9

10

 

11

12

 

13

14

 

 

15

16

 

17

18

 

19

20

 

21

22

 

23

24

 

25

27

 

28

29

 

30

 

 

Литература использованная для работы.

 

   Куликов В.П., Кузин А.В. Инженерная графика: учебник/ В.П. Куликов, А.В. Кузин. – 5-е изд. – М.: ФОРУМ, 2012. 368 с. – (Профессиональное образование).

 

     Боголюбов, С. К. Индивидуальные задания по курсу черчения [Текст]:Практическое пособие для учащихся техникумов/ С. К. Боголюбов. — М.: Высшая школа, 2000-368с.:ил.

       

     Короев  Ю.Н. Черчение для строителей. [Текст]:  учебник для СПТУ/ Ю.Н. Короев – 3е издание, переработанное и дополненное —  М.: Высшая школа, 1987-256с.

 

    Якубович, А.А. Задания по черчению для строителей. [Текст]:  практическое пособие/ А.А.  Якубович,  — 2-е издание, переработанное — М.: Высшая школа, 1989-232с.:ил.

 

    Чекмарев А.А., Верховский А.В., Пузиков А.А. Начертательная геометрия. Инженерная и машинная графика. Программа, контрольные задания и методические указания для студентов – заочников инженерно-технических специальностей вузов [Текст]/Под редакцией А.А. Чекмарева – 2-е издание, исправленное – М.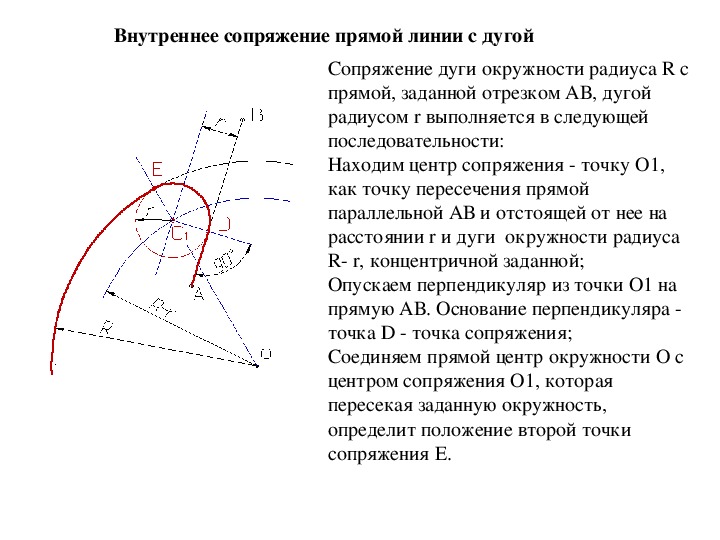 :Высшая школа, 2004-334с.:ил.

 

    Виноградов В.Н., Жукова Е.Т., Малышинков С.И., Орещенко А.Ф., Пилецкий И.В., Рыбакова Т.И., Коваленко Л.Н., Соловьев В.Е. «Словарь-справочник по черчению», Москва «Просвещение» 1993 г.

 

 

Касание к окружности — Умскул Учебник

На этой странице вы узнаете

• Сколько вариантов “окружность + прямая” можно начертить на листе бумаги?
• Что такое сопряжение и с чем его едят?
• Какие окружности изображены на олимпийском флаге? 

В жизни мы ежедневно сталкиваемся с касаниями. Касаемся предметов или друг друга. А может ли окружность, подобно человеку, чего-то касаться?  Давайте узнаем в этой статье.

Взаимное расположение прямой и окружности

Перед нами стоит задача начертить прямую и окружность на бумаге. Задумайтесь на секунду: как бы вы сейчас выполнили эту задачу? 

Поскольку их взаимное расположение не уточнено, то есть несколько вариантов, как их начертить.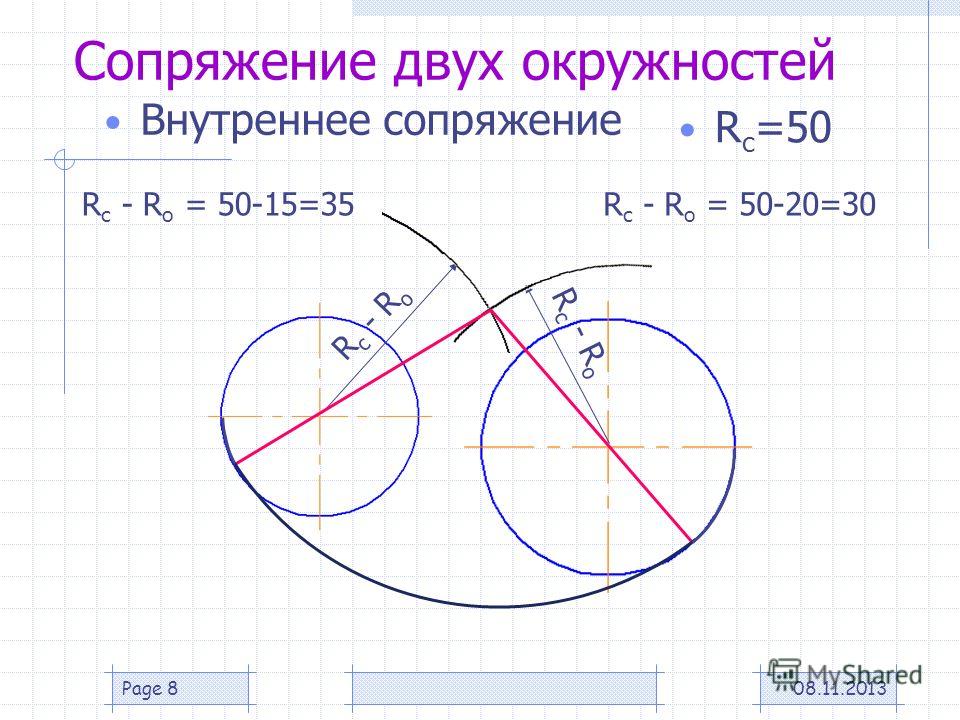  

1 случай. Прямая и окружность будут лежать в разных местах на листе и никак не пересекутся друг с другом. 

2 случай. Прямая будет только касаться окружности. 

3 случай. Прямая пересечет окружность. 

Сколько вариантов “окружность + прямая” можно начертить на листе бумаги? Каждый человек изобразит эти элементы в разных положениях относительно друг друга. Но так ли много разнообразия будет? На самом деле, существует всего три варианта расположения фигур:  — Они не касаются и не пересекаются; — Прямая касается окружности; — Прямая пересекает окружность.

Оказывается, в математике существуют термины для второго и третьего случая. Начнем их рассматривать с касательной к окружности. 

Касательная

Касательная – это прямая, которая имеет с окружностью только одну общую точку. 

На рисунке АВ – касательная, которая касается окружности в точке А.  

Что такое сопряжение и с чем его едят? Многие вещи, которые нас окружают, имеют плавные формы. Например, если мы посмотрим на цепь велосипеда, она имеет изогнутую форму.  Все такие детали можно вычертить, а называться эти чертежи будут сопряжениями. Сопряжение в черчении – это плавный переход линии в окружность или окружности до окружности. Чтобы построить сопряжения, есть целые законы, которые основаны на касании к окружности.

Свойства касательной

1 свойство. Касательная перпендикулярна радиусу, проведенному из центра окружности в точку касания. 

Проведем радиус ОА, тогда ОА ⟂ АВ. 

2 свойство. Если провести две касательных из одной точки, то их отрезки будут равны.

Проведем из точки В еще одну касательную ВС, тогда АВ = ВС. 

Если перевернуть рисунок, то можно заметить, что он отдаленно напоминает воздушный шар. А в воздушных шарах, также как и в свойстве касательных, используются равные по длине веревки. 

3 свойство. Угол между хордой и касательной равен половине дуги, которая заключена между этими касательной и хордой. 

Проведем хорду АС, тогда угол САВ равен \(\frac{1}{2}⋃АС\). 

Секущая

Теперь обратим внимание на третий случай, когда прямая пересекает окружность. Такая прямая называется секущей.

Секущая – это прямая, которая пересекает окружность в двух точках. 

Пусть на рисунке АВ – секущая, тогда точки А и В – точки пересечения окружности и секущей. 

Вспомни, как мы нарезаем пиццу или пирог. Каждый разрез будет секущей, то есть будет разделять круг на несколько частей. 

Свойства секущей 

1 свойство. Если из одной точки провести секущую и касательную к окружности, то квадрат касательной равен произведению секущей на ее внешнюю часть.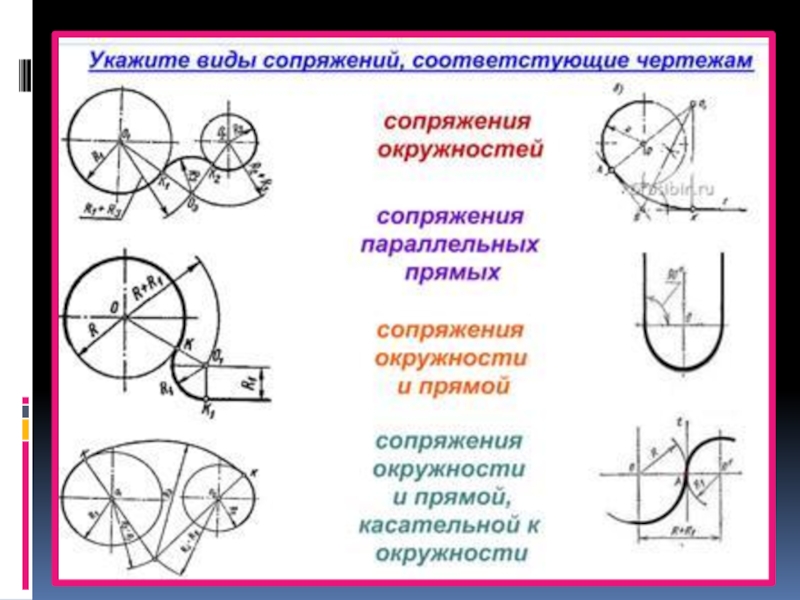  

Проведем из точки А касательную АВ и секущую АС. Пусть секущая будет пересекать окружность в точках С и Е. Тогда выполняется равенство АВ² = АС * АЕ. 

2 свойство. Если из одной точки провести две секущих к окружности, то произведение первой секущей на ее внешнюю часть равняется произведению второй секущей на ее внешнюю часть. 

Проведем секущие АВ (пересекает окружность в точках Е и В) и АС (пересекает окружность в точках С и D). Тогда выполняется равенство АС * AD = АВ * АЕ. 

3 свойство. Угол между двумя секущими равен половине разности градусных мер большей и меньшей дуг, которые заключены между секущими. 

Допустим, необходимо найти угол САВ. Тогда угол \(CAB = \frac{1}{2}(⋃CB-⋃DE)\). 

Не стоит пугаться знака “⋃” – в математике таким образом обозначают дугу окружности. 

Касание окружностей

Мы рассмотрели касание прямой и окружности, но могут ли две окружности касаться друг друга? Если у окружностей одна общая точка, то они являются касающимися друг к другу.  

И есть даже несколько вариантов такого касания: 

• Внешнее, когда окружности лежат по разные стороны от точки касания. 

В данном случае точка С – точка касания. 

• Внутреннее, когда одна окружность как бы “лежит” в другой. 

В данном случае точка С также является точкой касания. 

Касание окружностей нередко применяется при создании ювелирных украшений. Такое решение создает неповторимые и очень красивые образы. 

Какие окружности изображены на олимпийском флаге?  Как мы уже определили, окружности могут касаться друг друга. Но есть еще один вариант их взаимного расположения: окружности пересекаются друг с другом. В этом случае они будут иметь две общие точки.  Пересекающиеся окружности изображены на олимпийском флаге, их там целых 5. По одной из версий, они обозначают 5 частей света.

Рассмотрим свойство касающихся окружностей: 

•  Прямая, построенная через центры таких окружностей, включает точку касания.  

Если мы построим прямую через центры окружностей А и В, то на этой же прямой будет лежать точка касания С. 

Фактчек

• Прямая и окружность имеют три варианта взаимного расположения: не пересекаться, касаться или пересекать друг друга. 
• Касательная – это прямая, которая проведена к окружности и имеет с ней только одну общую точку. Касательная перпендикулярна радиусу, который проведен в точку касания. 
• Секущая – это прямая, которая проходит через окружность и имеет с ней две точки пересечения. 
• Если провести из одной точки касательную и секущую, то квадрат касательной будет равен произведению секущей на ее внешнюю часть. 
• Две окружности также могут касаться друг друга. Касание может быть как внешним, так и внутренним. При этом если соединить центры окружности прямой, то на этой же прямой будет лежать точка касания. 

Проверь себя

Задание 1.
Как называется прямая, которая проведена к окружности и имеет с ней одну общую точку?

1. Секущая;
2. Хорда;
3. Касательная;
4. Диаметр.

Задание 2. 
Дуга, заключенная между касательной и хордой, равняется 50^\(\circ\). Чему равен угол между касательной и хордой?

1. 25^\(\circ\);
2. 50^\(\circ\);
3. 100^\(\circ\);
4. 180\^(\circ\).

Задание 3. 
Длина секущей равна 9, а ее внешняя часть равняется 4. Чему равна касательная к окружности, проведенная из той же точки, что и секущая?

1. 36;
2. 6;
3. 9;
4. 5.

Задание 4. 
Между секущими заключены дуги окружности, которые равняются 70 и 30 градусам. Чему равен угол между секущими?

1. 40;
2. 10;
3. 80;
4. 20. 

Задание 5. 
Каким бывает касание двух окружностей?

1. Только внешним;
2. Только внутренним;
3. Внешним и внутренним;
4. Две окружности не могут касаться друг друга.  

Ответы: 1. – 3 2. – 1 3. – 2 4. – 4 5. – 3

Две прямые образуют круг

Думать трудно. Качество глубокого сна, который вы получаете каждый день, в равной степени пропорционально тому, сколько мозга вы используете. По словам моей жены (К.Д.), эта ее теория так же верна, как и гравитация. Это ее стандартный ответ на мою извечную жалобу на то, что она хорошо спит, а я нет.

 

Все теории верны, пока не доказано обратное. Итак, чтобы проверить эту теорию, я решил еще больше продвинуть свое мышление (а также проверить, есть ли еще что-то, что можно было бы продвинуть).

 

Первое, что пришло мне в голову, это проблема, с которой сталкивается моя нынешняя команда. Я сразу же записал это так. Вот так все выглядело с точки зрения нашей команды. Линейный. Причина и следствие.

 

Если вы работали в индустрии программного обеспечения, приведенный выше пример не должен показаться вам чем-то «новым».

 

Бизнес тоже так видит? Конечно нет. С точки зрения бизнеса все выглядит примерно так. Линейный. Причина и следствие.

 

Осмелюсь сказать, что многие из нас (все вы, читатели) видят вещи именно так — события разворачиваются по прямой линии. Однако реальность редко бывает линейной. Если вы внимательно посмотрите (изображение ниже), эти две линии образуют круг. А здесь это выглядит порочно.

Проблема есть проблема. Обозначение проблемы (проблема технической группы, проблема бизнеса и т. д.) — это всего лишь точка зрения человека, который смотрит на проблему. В приведенном выше примере, чтобы разорвать этот вечный цикл, обе стороны должны признать, что их «автономная» точка зрения на самом деле не является автономной и влияет на точку зрения других. Обе команды являются частью организации. Организация — это система, целью/функцией которой является решение проблем клиентов и создание благосостояния для себя. И технические, и бизнес-команды взаимодействуют друг с другом, и их взаимодействие влияет на общее функционирование системы (т.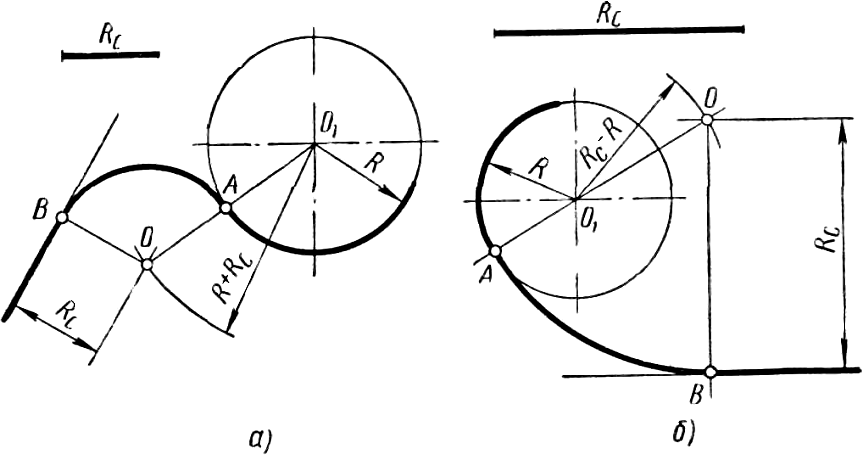 е. организации).

 

Пришло время представить, что такое система?

 

«Система — это целое, которое нельзя разделить на независимые части без потери своих основных свойств или функций». [1]

 

При попытке решить проблему размышления о взаимодействии между этими частями и о том, как они влияют друг на друга и на общие функции системы, называется «системным мышлением».

 

Невероятно. Согласен, но последствия есть.

 

Здесь важно отметить, что свойства системы являются результатом взаимодействия ее частей, а не их (частей) действий, взятых по отдельности. Таким образом, когда производительность отдельных частей системы улучшается, производительность в целом может не улучшаться (и обычно не улучшается).

 

Вспомните любую проблему, с которой вы недавно столкнулись. Что вы сделали, когда узнали об этой проблеме? Проанализировал его и поместил в определенное ведро (например, вопрос технической команды, вопрос бюджета, вопрос возможностей и т. д.). И почему бы нет? Нас так учили — изолировать проблемную зону, а потом исправлять. Это работает для определенных проблем, но, конечно, не для сложных. Такое мышление заставляет нас сосредоточиться на улучшении конкретной проблемной области (части системы) и игнорировать взаимодействие между этой областью и другими частями системы.

 

Представьте, что вы занимаетесь бизнесом и, как объяснено в приведенном выше примере, вас не устраивает скорость и качество работы, которую выполняет техническая команда. Вы проанализировали и выделили это как проблему возможностей и приверженности технической команды». Что бы вы сделали сейчас? Усилить давление на техническую команду, следить за каждым их шагом, пригрозить увольнением или вообще избавиться от него? И это решит ваши проблемы? Скорее всего нет.

 

Как упоминалось выше, проблема есть проблема, и нам не нужно присваивать ей метку. Вместо этого нам нужно изучить другую точку зрения и найти, какая из них или комбинация точек зрения даст нам лучшее решение.

 

При системном мышлении мы бы не просто смотрели на события (т. е. ошибки, возникшие в последней итерации), а углублялись и искали закономерности/тенденции. Попытка понять причину этих паттернов/тенденций → базовая структура и, в конечном счете, то, что позволяет этим структурам сохраняться → ментальные модели.

 

При таком понимании «целого» мы сможем найти решение, которое не только улучшит часть, но и улучшит общую производительность системы.

 

Конечно, в системном мышлении есть еще много чего, но основные принципы упомянуты выше. Позвольте мне также порекомендовать вам несколько книг[2], которые вы можете изучить, когда вам будет удобно, чтобы глубже вникнуть в концепцию.

 

Системное мышление — это целостный подход, который ведет к осознанному выбору, лучшим решениям и, конечно же, к лучшему сну (чтобы думать таким образом, требуется много умственных способностей).

 

К сожалению, теория моей жены не сработала для меня. Я все еще плохо сплю. Она настаивает на том, что моих усилий недостаточно, и просит меня еще подумать.

 

[1] Доклад Рассела Акоффа

[2] Введение в общее системное мышление Джеральда Винберга

[2] Цель Эллияху М. Голдратта и

[2] Пятая дисциплина Питера М. Сенге

 

Искусство решения задач

Изогональные сопряжения — это пары точек на плоскости относительно определенного треугольника.

Содержание

• 1 Изогональная теорема
• 2 параллельных сегмента
• 3 Перпендикулярность
• 4 Фиксированная точка
• 5 Биссектриса
• 6 Изогона диагонали четырехугольника
• 7 Изогоналей трапеции
• 8 Изогоналей полного четырехугольника
• 9 Изогона биссектрисы треугольника
• 10 точек на изогоналях
• 11 Трапеция
• 12 IMO 2007 Short list/G3
• 13 Определение изогонального сопряжения точки
• 14 Три точки
• 15 Второе определение
• 16 Расстояние до сторон треугольника
• 17 Знак изогонально сопряженных точек
• 18 Окружность треугольников педалей
• 19 Общая описанная окружность педальных треугольников как знак изогонально сопряженных точек
• 20 Две пары изогонально сопряженных точек
• 21 круг
• 22 1995 USAMO Проблемы/проблема 3
• 23 2011 USAMO Проблемы/проблема 5

Теорема об изогонах

Определение изогональных линий

Пусть даны прямая и точка, лежащие на ней. Пару прямых, симметричных относительно точки и содержащих ее, назовем изогоналами относительно пары

Иногда удобно взять за базовую одну пару изогоналей, например, и являются парой оснований. Тогда оставшиеся пары назовем изогоналами относительно угла

Проективное преобразование

Известно, что преобразование, переводящее точку с координатами в точку с координатами, является проективным.

Если ось абсцисс совпадает с прямой, а начало координат совпадает с точкой, то уравнения определяют изогонали, а их изображениями становятся линии, симметричные относительно прямой.

Ясно, что при обратном преобразовании (тоже проективном) такие пары прямых становятся изогоналями, а точки, равноудаленные от них, лежат на изогоналях.

Изогональная теорема

Пусть даны две пары изогоналей и относительно пары. Обозначим

Докажите, что и являются изогоналями относительно пары

Доказательство

Выполним проективное преобразование плоскости, переводящее точку в бесконечно удаленную точку, а прямую — в саму себя.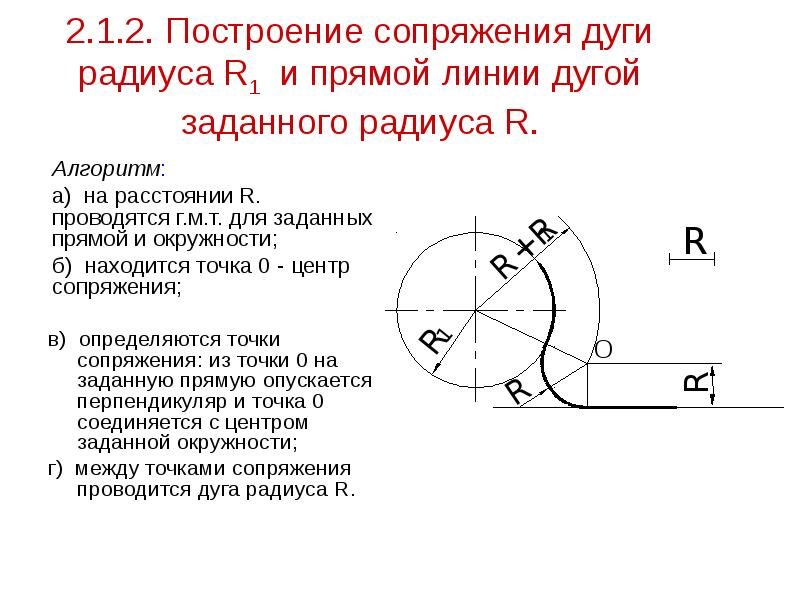 В этом случае изогонали превращаются в пару прямых, параллельных и равноотстоящих от

Обратное (тоже проективное) преобразование отображает точки, равноудаленные от на изогонали. Обозначим образ и прообраз одними и теми же символами.

Пусть изображения изогоналей — вертикальные линии. Пусть координаты образов точек Уравнение прямой

Уравнение прямой

Абсцисса точки

Уравнение прямой

Уравнение прямой

Абсцисса точки

Прообразы точек и лежат на изогонали.

Теорема изогоналей в случае параллельных прямых

Пусть и изогональны относительно

Пусть прямые и пересекаются в точке

Докажите, что прямые и параллельны изогонали относительно

Доказательство

Прообраз расположен в бесконечности на прямой

Из равенства следует равенство наклонов по модулю и к биссектрисе

Обратная теорема

Пусть прямые и пересекаются в точке

Пусть и изогоналы относительно

Докажите, что и изогоналы относительно

Доказательство

Прообраз расположен в бесконечности на прямой, поэтому наклон известен.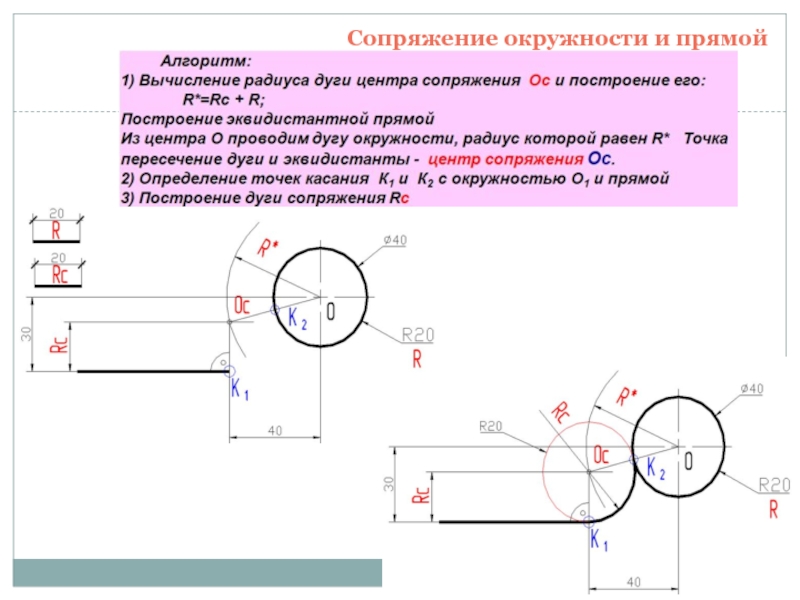

Предположим, что

Отрезок и прямые зафиксированы

пересекаются в

но есть единственная точка пересечения прямых Противоречие.

[email protected], vvsss

Параллельные отрезки

Пусть дан треугольник. Пусть и будут изогоналями относительно Пусть

Докажите, что лежит на биссектрисе и

Доказательство

Оба утверждения следуют из Изогональная теорема в случае параллельных прямых

[email protected], ввсс

Перпендикулярность

Пусть дан треугольник. Прямоугольные треугольники и с гипотенузами и построены по сторонам и к внешней (внутренней) стороне Пусть Докажите, что

Доказательство

Пусть — биссектриса

и изогональны по отношению к паре

и изогональны по отношению к паре

и изогональны по отношению к паре в соответствии с Изогональная теорема.

диаметр описанной окружности

Радиус окружности и высота изогональны относительно биссектрисы и вершины треугольника, поэтому

• Радиус окружности

[email protected], vvss с

Фиксированная точка

Пусть задан фиксированный треугольник. Пусть точки и на обочинах и соответственно будут произвольными точками.

Пусть это точка на боковой линии такая, что

Докажите, что линия проходит через фиксированную точку.

Доказательство

Докажем, что симметричная относительно точки лежит на .

и являются изогональными относительно

точек и лежат на изогональных относительно Теорема об изогонах.

Симметричная относительно точки лежит на изогональной относительно нее

[email protected], vvsss

Биссектриса

Пусть дан выпуклый четырехугольник. Позвольте и быть incenters треугольников и соответственно.

Позвольте и быть A-эксцентрами треугольников и соответственно.

Докажите, что это биссектриса числа

Доказательство

и являются изогональными относительно угла

и являются изогональными относительно угла в соответствии с Теорема об изогонах.

Обозначается

WLOG,

[email protected], vvsss

Изогона диагонали четырехугольника

Дан четырехугольник и точка на его диагонали такие, что

Пусть

Докажите, что

Доказательство

Выполним проективное преобразование плоскости, переводящее точку в бесконечно удаленную точку и прямую в себя.

В этом случае образы точек и равноудалены от изображения

точки (средняя точка лежит на

содержит середины и

есть линия Гаусса биссектрисы полного четырехугольника

прообразы точек и лежат на изогоналях и

vladimir.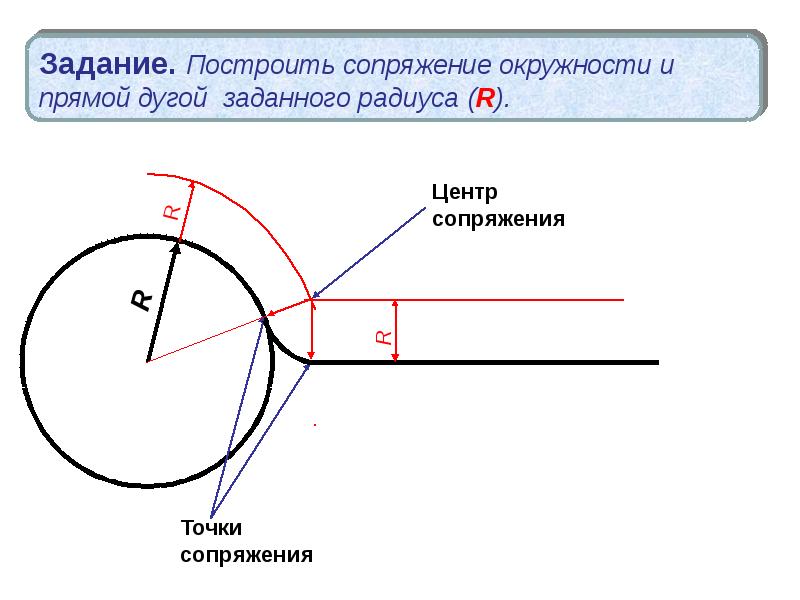 [email protected], vvsss

Изогонали трапеции

Пусть дана трапеция. Обозначим

Точка на меньшем основании такова, что

Докажите, что

Доказательство

Следовательно, и изогональны относительно

. Выполним проективное преобразование плоскости, переводящее точку в бесконечно удаленную точку и прямую в себя.

В этом случае образы точек и равноудалены от образа содержит середины и , то есть является линией Гаусса полного четырехугольника

биссектрисы

Прообразы точек и лежат на изогонали и

[email protected], ввсс

Изогонали полного четырехугольника

Пусть дан полный четырехугольник. Пусть точка Микеля

Докажите, что она изогональна и изогональна относительно

Доказательство

[email protected], ввсс

Изогональ биссектрисы треугольника

Дан треугольник. Точка, выбранная на биссектрисе

Обозначим Докажите, что

Доказательство

Выполним проективное преобразование плоскости, переводящее точку в бесконечно удаленную точку и прямую в себя.

В этом случае изображения отрезков и равноудалены от изображения

Изображение точки является средней точкой изображения и изображением средней точки

Изображение является параллелограммом

расстояния от и до равны

Прообразы и являются изогональными относительно

[email protected], vvsss 9 0094

Точки на изогоналях

Дан треугольник. Точка, выбранная на Точка выбрана так, что и являются изогональными относительно

Докажите, что

Доказательство

Обозначим

Используем закон синусов и получаем:

[email protected], ввсс

Трапеция

Боковая сторона трапеции перпендикулярна основаниям, точка — точка пересечения диагоналей.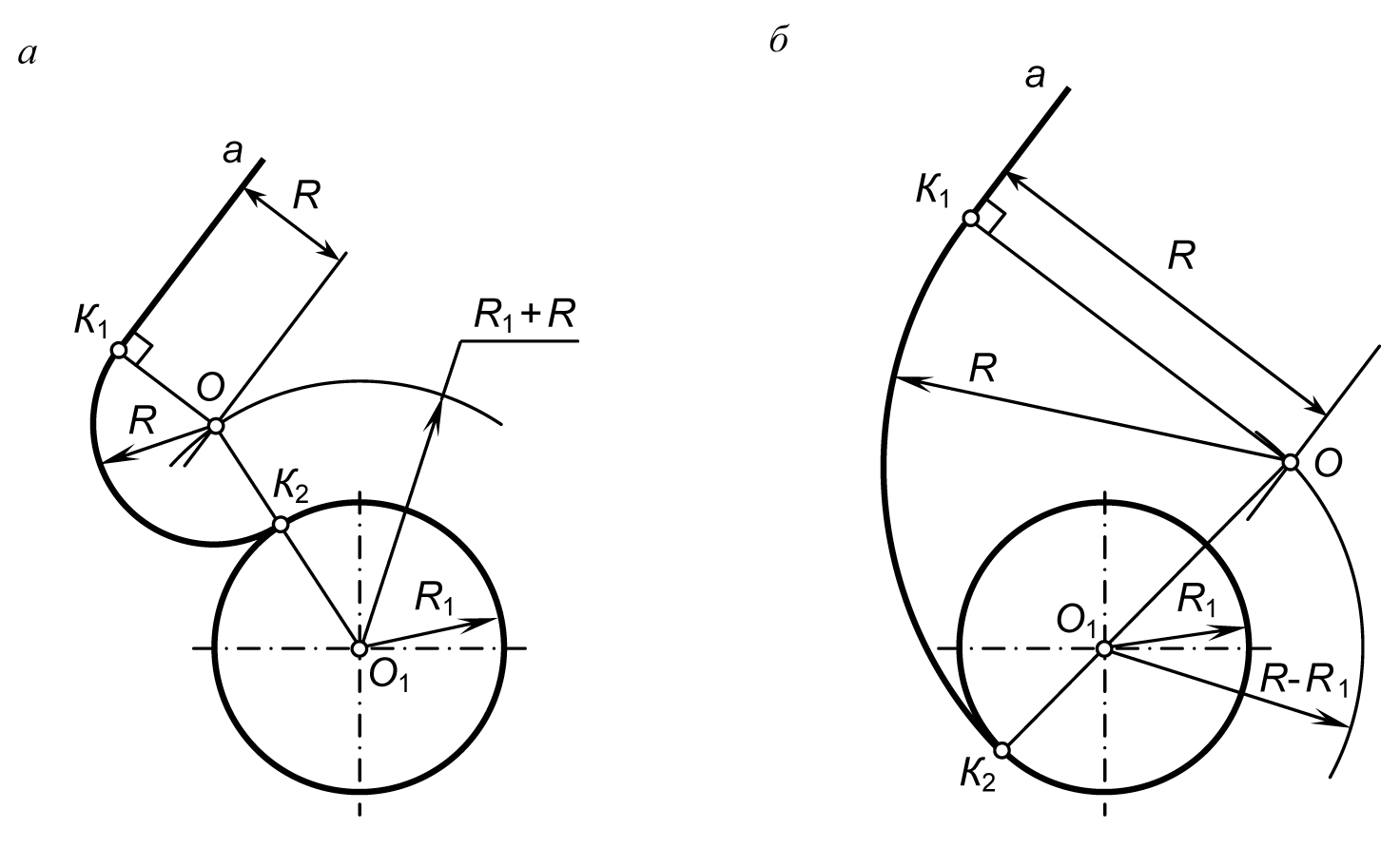

На описанной окружности треугольника взята точка, диаметрально противоположная точке

Докажите, что

Доказательство

WLOG, не диаметр Пусть боковые и пересекаются в точках и соответственно.

прямоугольник

изогональ относительно

изогональна относительно

В соответствии с Теорема об изогональности в случае параллельных прямых

в соответствии с Обратная теорема Теорема об изогонах в случае параллельных прямых.

[email protected], vvsss

IMO 2007 Short list/G3

Диагонали трапеции пересекаются в точке

Точка лежит между параллельными прямыми и такая, что и прямая разделяет точки и

Докажите, что

Доказательство

и изогональны относительно

изогональны относительно

[email protected], vvsss

Определение изогонального сопряжения точки

Пусть будет точка на плоскости, и пусть будет треугольник. Обозначим линиями . Обозначим линии , , , соответственно. Пусть , , будут отражениями , , над биссектрисами углов , , , соответственно. Тогда линии , , сходятся в точке , называемой изогональной сопряженной по отношению к треугольнику .

Доказательство

По нашим конструкциям линий , , и это утверждение остается верным после перестановки . Следовательно, по тригонометрической форме теоремы Чевы таким образом, опять же, согласно тригонометрической форме Чевы, линии совпадают, что и требовалось доказать.

Следствие

Пусть точки P и Q лежат на изогоналях относительно углов и треугольника

Тогда эти точки лежат на изогоналях относительно угла

[email protected], vvsss

Три точки

Пусть задан фиксированный треугольник. Пусть произвольная точка не лежит на обочине Пусть точка на изогонали относительно угла Позвольте быть точкой пересечения изогонали относительно угла и изогонали относительно угла

Докажите, что прямые и пересекаются.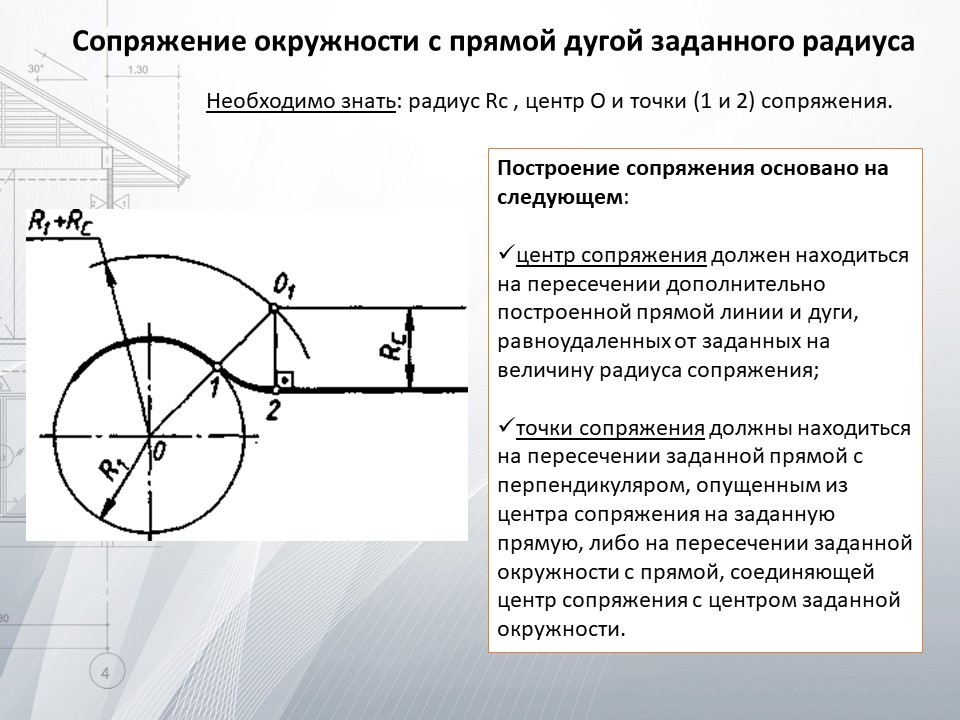

Доказательство

Обозначим

и являются изогоналями относительно

и S лежат на изогоналях

изогонально сопряжены относительно

и лежат на изогоналях

9000 2 Следовательно, точки и лежат на одной прямой, изогональной с с уважением

[email protected], vvsss

Второе определение

Пусть дан треугольник. Пусть точка лежит в плоскости Пусть отражения от боковых линий равны

Тогда центр описанной окружности является изогонально сопряженным

точек и не имеет изогонально сопряженных точек.

Другие точки боковых линий имеют соответственно изогонально-сопряженные точки.

Доказательство распространен поэтому Точно так же центр описанной окружности

Из определения 1 мы получаем, что это изогональное сопряжение

Ясно, что каждая точка имеет единственную изогональную сопряженную точку.

Пусть точка будет точкой с барицентрическими координатами Тогда имеет барицентрические координаты

vladimir. [email protected], vvsss

Расстояние до сторон треугольника

Пусть — изогональное сопряжение точки относительно треугольника

Пусть и — проекция на стороны и соответственно.

Пусть и — проекция на стороны и соответственно.

Затем

Доказательство

Лет [email protected], vvsss

Знак изогонально сопряженных точек

Пусть задан треугольник и точки и внутри него.

Пусть — проекции на стороны соответственно.

Пусть — проекции на стороны соответственно.

Пусть Докажите, что точка изогонально сопряжена с точкой относительно треугольника

Аналогичную теорему можно доказать и в случае вне

Доказательство

Обозначение Сходным образом Следовательно, точка является изогональным сопряжением точки относительно треугольника

[email protected], vvsss

Окружность педальных треугольников

Позвольте быть изогональным сопряжением точки относительно треугольника

Позвольте быть проекцией на стороны соответственно.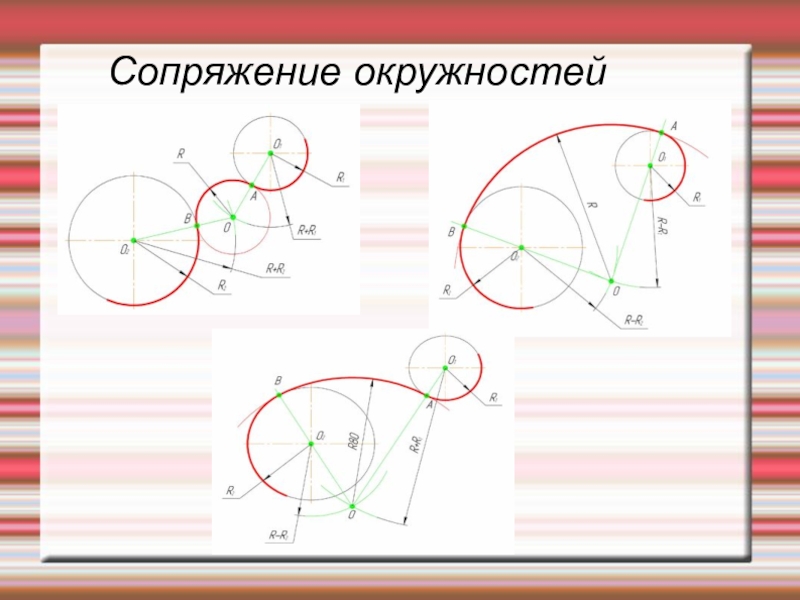

Пусть — соответственно проекция на стороны.

Докажите, что точки концикличны.

Середина окружности

Доказательство

Пусть

Следовательно, точки концикличны.

— трапеция,

середина — центр описанной окружности

Точно так же точки концикличны и концикличны.

Следовательно, точки концикличны, значит, их середина — центр описанной окружности

[email protected], vvsss

Общая описанная окружность педальных треугольников как знак изогонально сопряженных точек

Пусть дан треугольник и точки внутри него. Пусть — проекции на стороны соответственно. Пусть — проекции на стороны соответственно.

Пусть точки концикличны и ни одна из них не лежит на сторонах

Тогда точка является изогонально сопряженной точкой относительно треугольника

Это следует из единственности сопряженной точки и того факта, что прямая пересекает окружность не более чем в двух точках.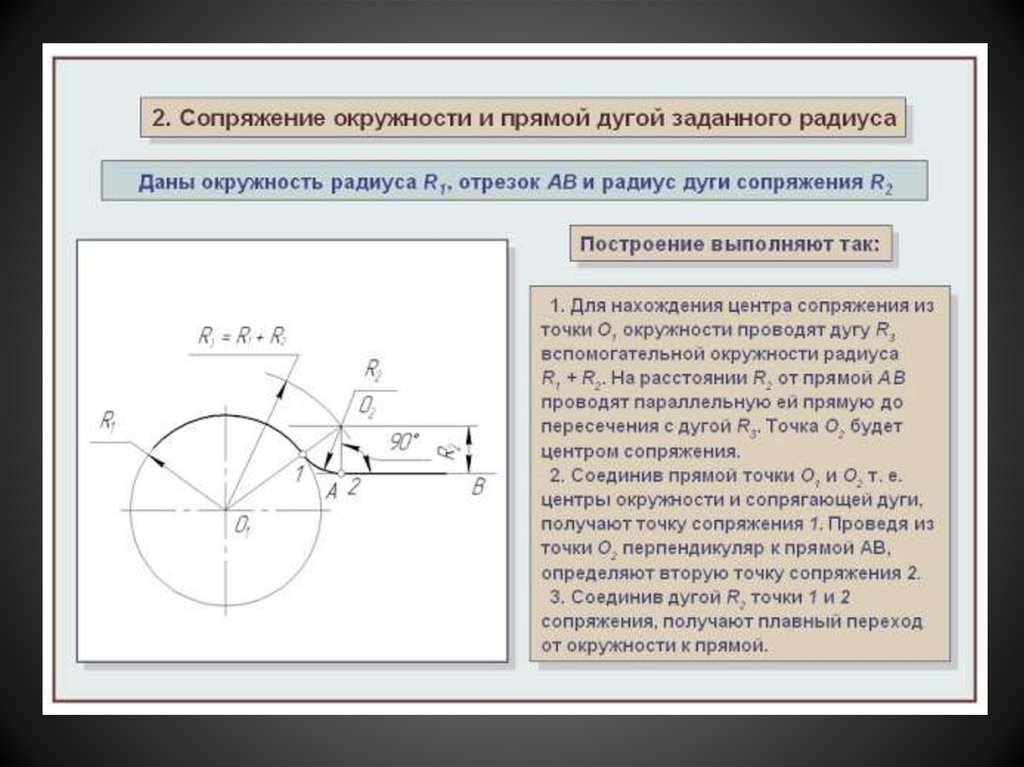

[email protected], ввсс

Две пары изогонально сопряженных точек

Пусть даны треугольник и точки и . Пусть точки и будут изогонально-сопряженными точек и относительно треугольника соответственно.

Пересечь и пересечь

Доказать, что точка изогонально сопряжена с точкой относительно

Доказательство

Имеются две пары изогоналей и по отношению к углу являются изогоналями по отношению к в соответствии с Изогональная теорема .

Аналогично изогонали относительно

Следовательно, точка является изогональной сопряженной точки относительно

[email protected], vvsss

Окружности

Пусть будет изогонально сопряженной точкой относительно треугольника

Пусть будет центром описанной окружности

Пусть будет центром описанной окружности

Докажите, что точки и обратны относительно описанной окружности

Доказательство

Центр описанной окружности точки и точек и лежит на серединном перпендикуляре к Аналогично

vladimir.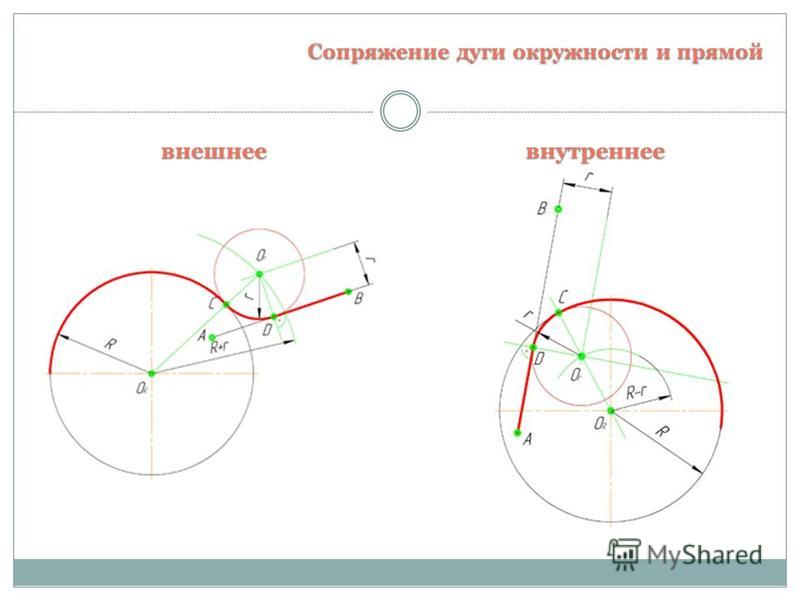 [email protected], vvsss

1995 USAMO Problems/Problem 3

Дан неравнобедренный непрямоугольный треугольник, через который обозначим центр описанной окружности, а через и — середины сторон и соответственно. Точка расположена на луче так, что подобна . Аналогично определяются точки и на лучах и соответственно. Докажите, что прямые и пересекаются.

Решение

Пусть будет высота Следовательно, и изогональны относительно угла и изогональны относительно угла

Аналогично и изогональны относительно

Аналогично и изогональны относительно

Пусть центр

изогонально сопряжен точка относительно треугольника

Следствие

Если медиана и симедиана начинаются из любой вершины треугольника, то угол, образованный симедианой и стороной угла, имеет ту же меру, что и угол между медианой и другой стороной угла.

являются медианами, следовательно, являются симедианами, поэтому три симедианы встречаются в точке, которая является центром треугольника, называемой точкой Лемуана.