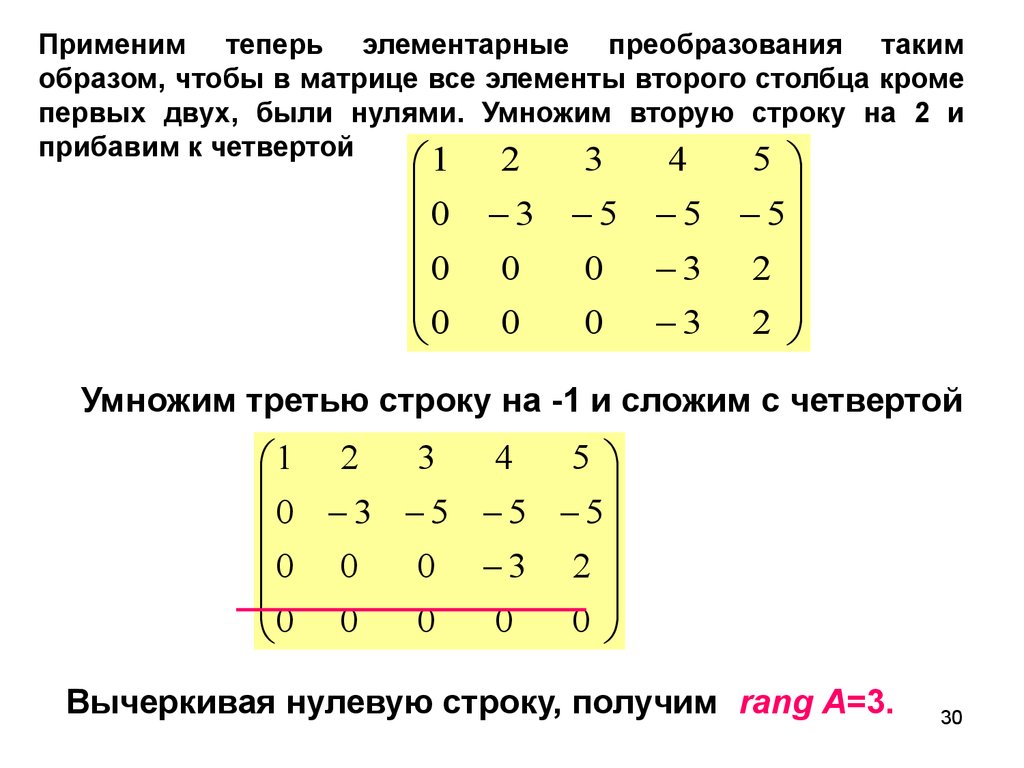
Сложение строк матрицы: Действия с матрицами

Содержание

Матрицы и действия над ними. Ступенчатая матрица. Элементарные преобразования.

Главная

» Общенаучные дисциплины

» Математика (1 семестр)

» Матрицы и действия над ними. Ступенчатая матрица. Элементарные преобразования.

Определения.

Матрицей называется прямоугольная таблица чисел или буквенных выражений, содержащая m строк и n столбцов: называют элементами матрицы.

Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы

Элементы образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной.

Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E .

Если все элементы матрицы равны 0, то матрица называется нулевой и ее обозначают буквой O.

Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны

Сложение матриц.

Суммой матриц одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Пример1.

Свойства сложения матриц.
1. Коммутативность.
A+B=B+A
2. Ассоциативность.
(A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α

Пример 2.

Произведением матрицы размерности на матрицу размерности называется матрица размерности.
Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 4.

Результатом транспонирования матрицы размерности является матрица размерности.

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц:
(A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице:
(A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^Tсовпадает с данной матрицей A, то матрица A называется симметрической.

Преобразования, не меняющие ранг матрицы, называются элементарными. К ним относятся:
1). Умножение строки или столбца на число, не равное нулю.
2). Перестановка строк или столбцов местами.
3). Прибавление к элементам одной строки или столбца элементов другой строки или столбца, умноженных на одно и то же число.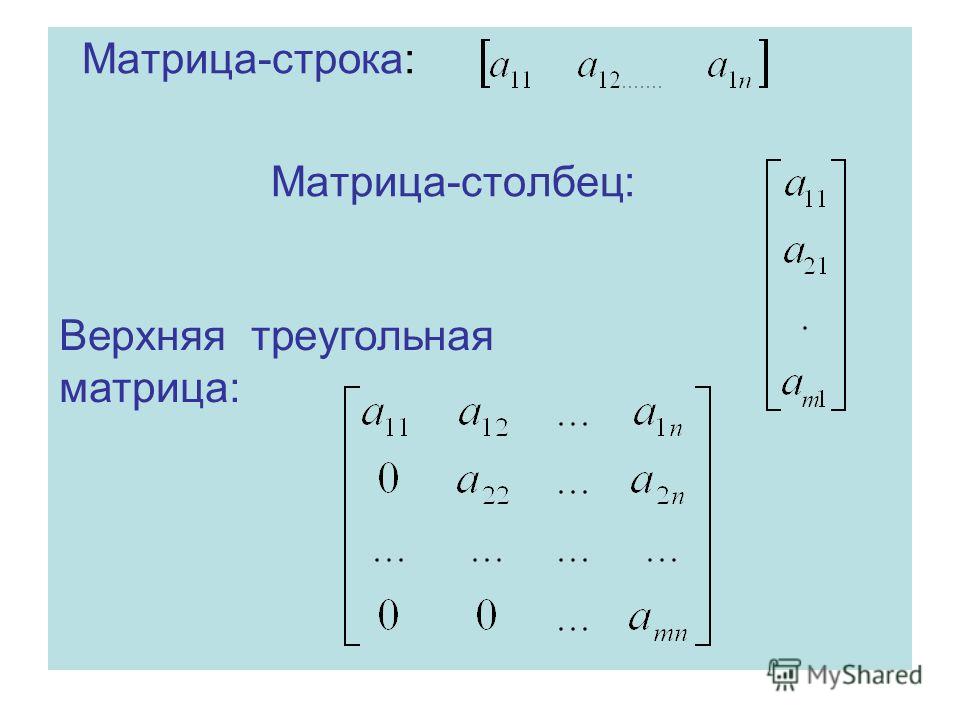
4). Вычеркивание строки или столбца, состоящего из нулей.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Почему умножение матриц такое / Хабр

Наверное, каждый задавался вопросом, почему умножение матриц такое. В этой статье мы разберём из каких соображений оно вводится именно так.

Маленькое предисловие

В дальнейшем нам понадобится такая структура, как векторное пространство, а точнее его частный случай — пространство столбцов высотынад Кратко напомню, что под этим понимается.

Во-первых, — это следующее множество

где таким образом обозначен вектор-столбец высотыто есть

Во-вторых, для любых векторовопределено сложение

и для любого вектораопределено умножение на скаляр

В-третьих, каждый векторединственным образом представим в следующем виде

где — скаляры, а — следующая система векторов

Такая система векторов называется базис, а скаляры, участвующие в разложение вектора, называются координатами этого вектора в данном базисе. Стоит отметить, что в это не единственный базис, но везде далее под «зафиксируем базис» можно понимать именно эту систему векторов.

Умножение матрицы на вектор

Прежде чем переходить к умножению матриц, посмотрим, из каких соображений вводится умножение матрицы на вектор. Для этого рассмотрим линейное отображение

То, что— линейное отображение, означает, что для любых векторови любого скаляравыполняются следующие два условия:

Или их можно объединить в одно

Нас интересует, как линейное отображениедействует на произвольный вектор Для этого зафиксируем в базис а в базис Теперь мы можем разложить векторпо базису

и представитьв следующем виде

Заметим, что а поскольку в зафиксирован базис, то эти векторы также можно разложить по базису

или тоже самое в векторной записи

Подставляем в равенство выше и получаем

Но правая часть равенства есть не что иное, как формула умножения матрицы на вектор-столбец

где столбцы матрицы есть векторы

Получается, можно ввести умножение матрицы на вектор по следующему правилу

И такое определение умножения будет согласовано с тем, как линейное отображениедействует на вектор

Если теперь обозначить то координаты вектора выражаются через координаты вектора следующим образом

Кроме того, мы получили и другой важный результат, вернёмся к выражению для

Из него следует, что линейное отображениеполностью определяется своими значениями на базисных векторах, то есть, если нужно найтито достаточно знать

Далее, мы поместили эти векторы в матрицу и определили умножение так, чтоесть произведение соответствующей матрицынаПолучается, что линейному отображению можно поставить в соответствие матрицу, которая полностью его определяет

Такая матрица называется матрицей линейного отображенияв выбранных базисах пространств и

Если говорить более строго, то существует взаимно однозначное соответствие между линейными отображениями из в и матрицами размера

Теперь мы можем перейти к умножению матрицы на матрицу.

Умножение матрицы на матрицу

Рассмотрим линейные отображенияи

и их композицию

Легко проверяется, что будет линейным отображением

Поэтому, если зафиксировать в и базисы, то каждому линейному отображению можно поставить в соответствие его матрицу

Нас теперь интересует, как между собой они связаны. Для этого рассмотрим следующее равенство

и найдём координаты вектора через координаты вектора

Так както

Но из равенстваследует, что

Подставляем в равенство выше и получаем

С другой стороны,то есть

Сравнивая первое и второе равенство для координатполучаем такое соотношение

которое является формулой умножения матрицы на матрицу.

Таким образом, умножение матрицы на матрицу вводится исходя из того, как действует композиция линейных отображений.

Другими словами, если линейным отображениямипоставить в соответствие их матрицыито композиции этих отображенийставится в соответствие матрица, которая является произведением матриц

Отсюда, кстати, следует, что матрицыиможно умножить только тогда, когда число столбцов матрицыравно числу строк матрицы

Пусть — матрица размера а — матрица размера Тогда, если в пространствах и зафиксировать базисы, то этим матрицам ставятся в соответствие линейные отображенияи

Но композиция определена только тогда, когда то есть число столбцов матрицыравно числу строк матрицы

Заключение

Таким образом, умножение матриц вводится исходя из того, как действуют линейные отображения. И это намекает на некую связь между ними.

Ниже оставлю различные учебники по алгебре, где можно про всё это прочитать более подробно, и другие различные источники.

Ссылки на литературу и различные источники

Основное:

[1] Введение в алгебру. В 3 частях. Часть 1. Основы алгебры. Кострикин А.И.

Дополнительное:

[1] Введение в алгебру. В 3 частях. Часть 2. Линейная алгебра. Кострикин А.И.

[2] Линейная алгебра и геометрия, Кострикин А.И., Манин Ю.И.

Прочее:

Для создания графики использовался manimCE: https://github.com/manimCommunity/manim

Кому интересно, то вот видео к статье:

Какие три операции над строками матрицы?

Рабочий пример

Purplemath

Что такое «операции» в математике?

«Операции» на математическом языке означает «процедуры», которые вы можете делать с вещами. Например, четыре основные операции над числами — это сложение, вычитание, умножение и деление.

Содержимое продолжается ниже

MathHelp.com

Каковы три операции над строками матрицы?

Для матриц существуют три основные операции над строками; то есть есть три процедуры, которые вы можете сделать со строками матрицы. Эти операции:

Перестановка строк: Вы выбираете две строки матрицы и меняете их местами. Например, вы можете взять третью строку и переместить ее в пятую строку, а пятую строку поставить на то место, где была третья.
Умножение строк: Вы можете умножать любую строку на любое ненулевое значение. Например, если все записи в одной строке четные, вы можете умножить строку на ½, сделав записи меньше и, следовательно, с ними будет легче работать.
Добавление строки: вы можете взять записи одной строки и добавить их к записям другой строки. Например, если в одной строке начальный элемент равен −3, а в другом ряду начальный элемент равен 4, вы можете добавить первую строку ко второй, получив ведущую 1 вместо 4.

Как выглядит замена строк?

Перестановка строк включает в себя не что иное, как взятие двух строк и перестановку их позиций. Например, учитывая следующую матрицу:

…вы можете поменять местами строки, чтобы расположить матрицу в более удобном порядке, например:

Чтобы получить приведенную выше матрицу, первая строка исходной матрицы была перемещена в третью строку новой матрицы, вторая строка была перемещена в первую строку, а третья — во вторую строку.

Переключение строк часто обозначается стрелками, например:

При переключении строк следите за правильным копированием записей.

Как выглядит умножение строк?

Умножение строк — это не что иное, как выбор строки матрицы и ее умножение на некоторое число. Например, имея следующую матрицу:

… вы можете умножить первую строку на -1, чтобы получить положительное ведущее значение в первой строке:

Это умножение строк часто обозначается стрелкой с умножением, указанным вверху. из него, например:

-1 R ₁ указывает фактическую операцию, которая была выполнена для перехода от исходной матрицы к новой. -1 говорит, что мы умножили на отрицательную 1; R ₁ говорит, что мы работали с первым рядом.

Обратите внимание, что вторая и третья строки были скопированы без изменений в новую матрицу. Умножение применялось только к первой строке, поэтому записи для двух других строк просто переносились без изменений.

Вы можете умножать на что угодно. Например, чтобы получить ведущую единицу в третьей строке предыдущей матрицы, вы можете умножить третью строку на отрицательную половину:

Поскольку вы ничего не делали с первой и второй строками, эти записи были просто копируется без изменений в новую матрицу.

Вы можете выполнить более одного умножения строк за один и тот же шаг, поэтому вы могли бы выполнить два вышеуказанных шага всего за один шаг, например: и нижние индексы выше), чтобы вы могли отслеживать свою работу. Матрицы очень грязные, особенно если вы делаете их вручную, а заметки могут облегчить проверку вашей работы позже. Это также произведет впечатление на вашего учителя.

Как выглядит добавление строк?

Добавление строки — это не что иное, как взятие записей одной строки и добавление их к записям другой строки. Сложение строк аналогично методу сложения для решения систем линейных уравнений. Например, предположим, что у вас есть следующая система уравнений:

х + 3 у = 1
− x + y = 3

Вы можете начать решение этой системы, сложив столбцы, чтобы получить 4 y = 4:

Тогда вы бы нашли значение y , и обратное решение для значения x .

Нечто подобное можно сделать и с матрицами. Например, имея следующую матрицу:

… вы можете уменьшить (то есть получить больше ведущих нулей) вторую строку, добавив к ней первую строку.

(Общая цель работы с матрицами на этом этапе состоит в том, чтобы получить ведущую 1 — или начальные 0, за которыми следует 1 — в начале каждой строки матрицы.)
Когда вы сокращали линейную систему из двух уравнений путем сложения, вы чертили черту «равно» внизу второго уравнения и складывали. Когда вы используете сложение на матрице, вам нужно взять немного бумаги для заметок, потому что вы не хотите пытаться выполнять работу внутри матрицы. Так что добавьте две строки на свой черновой лист:
Набросок —
не сдавайте это!
Результатом добавления является ваша новая вторая строка; вы напишете его вместо старого второго ряда. Результат будет выглядеть так:
В приведенном выше обозначении R ₁ + R ₂ «на стрелке означает «Я добавил строку один ко второй строке, и это результат, который я получил, будучи новой строкой два». Поскольку первая строка на самом деле не изменилась, и поскольку мы ничего не делали с третьей строкой, эти строки копируются в новую матрицу без изменений

Примечание: вы можете работать со строкой или над ней, но не с тем и другим вместе. нельзя, например, умножить вторую строку на 5, а затем добавить результат во вторую строку. Однако вы можете добавить умноженные записи второй строки в любую из других строк. Это означает, что вы работаете с второй ряд, но в том или ином из других рядов.С или на, но не на обоих!
URL: https://www.purplemath.com/modules/mtrxrows.htm
Страница 2
Операции со строками — MathBootCamps системы уравнений, а позже просто построчно уменьшить матрицу для других целей. Мы можем выполнить три операции со строками, каждая из которых даст матрицу из
строк, эквивалентную матрицам. Это означает, что если мы работаем с расширенной матрицей, набор решений базовой системы уравнений останется прежним.
[adsenseWide]
Операции со строками
В следующих примерах символ ~ означает «эквивалент строки».
Поменять местами две строки
При работе с системой уравнений порядок написания вопросов не влияет на решение. Поскольку расширенная матрица представляет собой систему уравнений, где каждая строка является уравнением, мы можем поменять местами две строки.
Обратите внимание на обозначение двойной стрелкой. Когда вы выполняете операции со строками, используйте подобную запись, чтобы отслеживать, что вы сделали. Очень легко допустить арифметическую ошибку, и если это произойдет, эта запись позволит вам вернуться и легко найти ее.
Формальное обозначение этой операции со строками (используемое в некоторых книгах): .
Умножение строки на ненулевую константу
Бывают случаи, когда будет полезно умножить строку на что-то вроде 2 или 1/3. Это не изменит решение основной системы уравнений, поскольку умножение любого уравнения на ненулевую константу приводит к эквивалентному уравнению (при условии, что вы умножаете ОБЕ стороны уравнения).
В этом примере каждая запись в строке 2 была умножена на константу. Справедливым вопросом здесь будет «Зачем вам выполнять эту операцию со строками?». Мы вернемся к этому, когда будем говорить об исключении Гаусса-Жордана и сокращении строк, но сейчас я выбрал умножение строки 2 на 3 только для того, чтобы показать вам, как это будет работать.
Формальное обозначение для этой конкретной операции со строками: . (подумайте: умножьте строку 2 на 3 и верните ее туда, где была исходная строка 2)
Умножьте строку на ненулевую константу и добавьте ее к другой строке
Вспомните, когда вы впервые научились решать системы уравнений. Вероятно, вы научились исключать переменную, умножая одно уравнение на число, а затем складывая два уравнения. Мы можем воплотить ту же идею в операции со строками.
Обратите внимание, что вся работа выполнялась в строке 2. Из-за этого в нашей сокращенной записи рядом со строкой 2 находится строка. Чтобы выполнить фактическую операцию со строкой, мы взяли каждое значение в строке 1, умножили его на -5, а затем добавили к строке 2. соответствующая запись в строке 2.
Формальное обозначение для этого будет: . (стрелка указывает, куда пойдет вся работа)
Общая картина
Последний пример показывает истинную мощь операций со строками. Выбирая, чтобы добавить к строке 2, мы исключили во 2-м уравнении.