Системы счисления разных народов: Системы счисления разных народов

Содержание

Системы счисления разных народов

В Древнем Вавилоне примерно за 40 веков до нашего времени создалась по-местная (позиционная) нумерация, т.е. такой способ изображения чисел, при котором одна и та же цифра может обозначать разные числа в зависимости от места, занимаемого этой цифрой. Наша современная нумерация тоже поместная: в числе 52 цифра 5 обозначает пятьдесят, т.е.5х10, а в числе 576 эта же цифра обозначаёт пятьсот, т.е. 5х10х10. В вавилонской поместной нумерации ту роль, которую играет у нас число 10, играло число 60, и потому эту нумерацию называют шестидеситеричной. Числа, меньшие 60, обозначались с помощью двух знаков. Они имели клинообразный вид, так как вавилоняне писали на глиняных дощечках палочками треугольной формы. Эти знаки повторялись нужное число раз.

Шестидесятеричная система возникла позднее десятичной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор неизвестно, когда и как возникла у вавилонян шестидесятеричная система.

На этот счет строилось много гипотез, но ни одна пока не доказана. Мнения историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы. Первая исходит из того, что произошло слияние двух племен, одно из которых пользовалось шестеричной, другое — десятичной. Шестидесятеричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса. Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60.

Шестидесятеричная запись целых чисел не получила распространения за пределами ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: в страны Ближнего Востока, Средней Азии, в Северную Африку и Западную Европу. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т.е. до начала XVII в.

3.2 Римская пятеричная

Это, наверное, самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме.

I	1
V	5
X	10
L	50
C	100
D	500
M	1 000

Предполагаемое происхождение римских цифр

Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать не удобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание.

Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.

О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы — до XVI века.

В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.

Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.

3.3 Древнегреческая аттическая пятеричная

В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции – Аттики со столицей Афины.

В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок: , , , . Число 5 записывалось знаком (древнее начертание буквы «Пи», с которой начиналось слово «пять» — «пенте»). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:

Число 10 обозначалось — заглавной «Дельта» от слова «дека» — «десять». Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:

3. 4 Древнегреческая ионийская десятеричная алфавитная

Примерно в третьем веке до нашей эры аттическая система счисления в Греции была вытеснена другой, так называемой «Ионийской» системой (она возникла в Милеете – греческая малоазиатская колония Ионии). В ней числа 1 — 9 обозначаются первыми буквами древнегреческого алфавита:

числа 10, 20, … 90 изображались следующими девятью буквами:

числа 100, 200, … 900 последними девятью буквами:

Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка ‘. Любая буква с этим значком сразу же становилась в тысячу раз больше.

Для отличия цифр и букв писали черточки над цифрами.

Древние евреи, арабы и многие другие народы Ближнего Востока имели такие же системы счисления.

При ее помощи можно было просто записать числа до ста миллионов (100 000 000). Эта система по быстроте счета мало отличается от «арабской». И хоть она не позиционная, но в ней есть мультипликативность.

3.5 Славянская глаголическая десятеричная

Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.

1	10	100	1 000
2	20	200
3	30	300
4	40	400
5	50	500
6	60	600
7	70	700
8	80	800
9	90	900

Числа записывали из цифр так же слева, направо, от больших к меньшим цифрам. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Такая запись числа аддитивная, то есть в ней используется только сложение:

= 800+60+3 = 863

Для того чтобы не перепутать буквы и цифры, использовались титла — горизонтальные черточки над числами, или точки.

3.6 Славянская кириллическая десятеричная алфавитная

Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:

Читаем дословно «четырнадцать» — «четыре и десять». Как слышим, так и пишем: не 10+4, а 4+10, — четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.

Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:

= 800+60+3

Для того чтобы не перепутать буквы и цифры, использовались титла — горизонтальные черточки над числами, что мы видим на рисунке.

Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:

	Тысяча	1000
	Тьма	10 000
	Легион	100 000
	Леодр	1 000 000
	Ворон	10 000 000
	Колода	100 000 000

Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.

3.7 Древнеиндийские системы счисления

Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.

Наряду с этой системой существовала в Индии еще одна система счисления брахми.

Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы.

В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.

Проектная работа «Обозначение цифр у разных народов»

Слайд 1

ОБОЗНАЧЕНИЕ ЦИФР У разных народов Выполнила: ученица 5 «а»класса Скурихина Милана Руководитель: Калачева С.Ю. 2019 год

Слайд 2

Введение. ГИПОТЕЗА: Знакомые нам цифры и числа не всегда существовали в том виде, в котором мы их знаем. ОБЪЕКТ ИССЛЕДОВАНИЯ: Цифры разных народов в разные времена.

Слайд 3

Актуальность работы: С самого раннего возраста человек сталкивается с необходимостью считать. Однако, научившись считать, люди мало знают о том, откуда появились цифры, кто придумал использовать ту или иную форму записи числа, поэтому я решила расширить свой кругозор по этой теме и рассказать об этом одноклассникам.

Слайд 4

Цель: Изучить причины возникновения и способы записи цифр в разные времена Задачи: Совершить небольшой экскурс в историю происхождения цифр разных народов; Научиться с помощью цифр и чисел народов обозначать количество; Познакомить одноклассников с цифрами и записью народов мира.

Слайд 5

Обозначение чисел в Южной Америке. Система Майя включала позиционность и нуль . Оба этих понятия были полностью неизвестны европейцам в это время. Первые девятнадцать чисел системы счисления были представлены точками и черточками, согласно следующей таблице: Нуль записывался как символ, похожий на раковину (домик улитки). Многозначные числа большие 19 , записывались вертикально, начиная с единиц высшего разряда сверху вниз.

Слайд 7

Обозначение чисел в Египте. Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находились очень далеко одна от другой, их числовые системы очень похожи: использование засечек на дереве или камне для записи прошедших дней. Египетские жрецы писали на папирусе, изготовленном из стеблей определенных сортов тростника, а в Месопотамии на мягкой глине. В египетской системе цифрами являлись иероглифические символы; они обозначали числа 1, 10, 100 и т. д. до миллиона.

Слайд 8

Египетская нумерация 1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем должно быть столько же палочек сколько и в верхнем, или на одну больше. 10. Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. 100. Это мерная веревка, которой измеряли земельные участки после разлива Нила. 1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка. 10 000. «В больших числах будь внимателен!» — говорит поднятый вверх указательный палец. 100 000. Это головастик. Обычный лягушачий головастик. 1 000 000. Увидев такое число обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф 10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца

Слайд 9

Обозначение чисел в Вавилоне В древнем Вавилоне примерно за 40 веков до нашего времени создалась позиционная нумерация , то есть такой способ записи чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой.

Слайд 10

Вавилонская нумерация В вавилонской поместной нумерации ту роль, которую у нас играет число 10, играет число 60, и потому эту нумерацию называют шестидесятиричной. Числа менее 60 обозначались с помощью двух знаков для единицы, и для десятка

Слайд 11

Вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60 . Тем не менее изобретение вавилонянами позиционной системы счисления с нулем представляло собой огромное достижение, по своему революционному значению для математики сопоставимое разве лишь с более поздней гипотезой Коперника в астрономии.

Слайд 12

Обозначение чисел у арабов. До хиджры арабы записывали числа словами, но затем, как это делали ранее греки, они стали обозначать числа буквами своего алфавита. В 772 индийский трактат «Сидданта» был привезен в Багдад и переведен на арабский, после чего стали использоваться две системы записи чисел: 1. В астрономии по-прежнему употребляли алфавитную систему, 2. В торговых расчетах купцы стали применять систему, заимствованную из Индии. Но даже среди тех, кто пользовался индийской системой, начертания цифр, как и в Индии, сильно варьировали

Слайд 13

Из арабского языка заимствовано и слово «цифра» (по-арабски «сыфр»), означающее буквально «пустое место» (перевод санскритского слова «сунья», имеющего тот же смысл). Это слово применялось для названия знака пустого разряда, и этот смысл сохраняло до XVIII века, хотя еще в XV веке появился латинский термин «нуль» (nullum — ничто).

Слайд 14

Обозначение чисел у римлян. Древние римляне изобрели систему исчисление, основанную на использовании букв для отображения цифр. Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы. Для того чтобы прочесть римскую цифру, следует следовать пяти основным правилам: Буквы пишутся слева направо, начиная с самого большого значения. Например: X V (15), CCXLIII (243), ZCXV (2115). Буквы I, X, C и M могут повторяться до трёх раз подряд, например: III (3), XX (20), ССC (300), MCCXXX (1320). Буквы V, L, D не могут повторяться. Цифры 6, 8, 40, 80, 800 следует писать, комбинируя буквы: VII (6), VIII (8), XL (40), LXXX (80), CD (400), DCCC (800). Например, 48 следует писать, комбинируя буквы XLVIII, 449 – CDXLIX _ Горизонтальная линия над буквой увеличивает её значение в 1000 раз.

Слайд 15

Латинская (Римская) нумерация I 1 V 5 X 10 L 50 C 100 D 500 M 1 000 Возникла эта нумерация в древнем Риме. Использовалась она для аддитивной алфавитной системы счисления

Слайд 16

Славянская кириллическая нумерация

Слайд 17

Читаем дословно «четырнадцать» — «четыре на десять». Как слышим, так и пишем: не 10+4, а 4+10, — четыре на десять. И так для всех чисел от 11 до 19. Таким образом у славян мы прослеживаем десятеричную систему счисления. Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение: 800+60+3

Слайд 18

Обозначение чисел у китайцев. Эта нумерация одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную арабскую, которой мы с Вами пользуемся. Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае.

Слайд 19

10 100 100 1 000; 548 Такая запись числа мультипликативна, то есть в ней используется умножение: 10+8  100+4  1 000 и 5  1

Слайд 20

Слайд 21

Число-это сложная, но очень интересная загадка.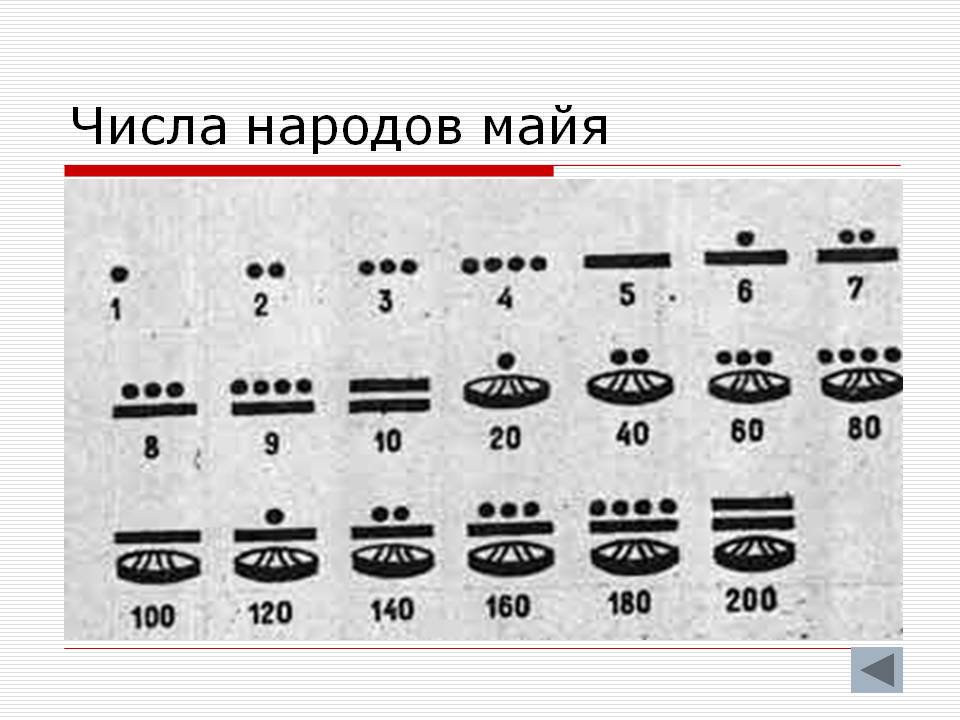 Итак, наиболее древними являются вавилонские и египетские цифры. Записи чисел были громоздкими, и лишь с изобретением позиционной системы счисления запись и вычисления упростились.

Слайд 22

Вывод: Проведенное мною исследование не исчерпывает всех аспектов истории возникновения цифр, но поиск и обобщение информации, позволяющее раскрыть данную тему, а также подбор интересных фактов расширили мой кругозор, усилили мотивацию изучения предмета.

Слайд 23

Числа Древней Руси Римские числа

Слайд 24

Древнеегипетские обозначения Вавилонская система счисления

Слайд 25

Обозначение чисел.

История возникновения цифр — древние числа и цифры Руси, Рима, Китая, Египта, Вавилона и Греции

Всматриваясь в причудливые знаки, не сразу поймешь, что символизируют древние числа и цифры. Мешки с крупами, орудия труда. В хвостатых, изогнутых знаках читается менталитет древнего народа, уровень его развития, навыки, экономическая обстановка. Обозначения цифр сотканы из глубоких абстракций и художественных представлений о мире. Рождение цифр неразрывно связано с возникновением письменности, но узелковое письмо шумерских народов появилось даже раньше. Оно было создано для счета. О чем это говорит? Уметь считать было важно во II в. до н.э., и в высокотехнологичном ХХI столетии.

Числа и бизнес пребывают в прочном тандеме. Числа нужны для основания и раскрутки бизнеса (для вычисления рентабельности, расчета конверсии, КПД), а бизнес нужен для хороших цифр на счету в банке. Счет стал неотъемлемой частью человеческого мышления и настолько влился в повседневную жизнь, что мы даже не замечаем его. Предприниматель должен числа не просто видеть, считать и предполагать, а читать. Созерцать не глазами, а разумом.

Вернуться к оглавлению

Как мир учился считать

Цифры и числа – это разные понятия. В обиходе мы их путаем, но существенная разница в сути слов от этого не исчезла. Цифра служит для условного обозначения числа. Число выражает количественную характеристику в цифрах, и представляет собой более обобщенное понятие.

Если проанализировать, какими были первые цифры, можно увидеть обширную историю культуры отдельного народа. Составление обозначений для чисел потребовало более высокого интеллектуального уровня. Поэтому наши предки оставляли тысячи зарубок на твердых материалах. Столько, сколько требовалось. Так, наивно, но достоверно, заполнялись древние отчетные документы, «чеки» и т.п. Первые цифры представляли собой примитивные засечки и значки.

Пример древних чисел и цифр

Генезис цифр останется для ученых неизведанной Марианской впадиной. Витиеватая история возникновения вызывает замешательство. Точно известно, что первые попытки письменной фиксации цифр были в Египте и Месопотамии: найденные древние математические записи тому свидетельство. Эти государства располагались далеко друг от друга, письменность и культура в каждом из них уникальна.

В Древнем Египте сформировалось скорописное иероглифическое письмо, месопотамские писцы использовали клинопись. Поэтому египетские первые цифры своей формой передавали природу всех окружающих предметов: животные, растения, предметы быта и т. д. Папирус Ринда (1650 г. до н.э.) и папирус Голенищева (1850 г. до н.э.) – числовые древнеегипетские документы — свидетельствуют о высоком культурном развитии народа. Месопотамская клинопись запечатлена на глиняных табличках, на которых цифры представлены небольшими клиньями, повернутыми в разные стороны соответственно своему значению.

И в египетских, и в месопотамских системах счисления есть цифры от 1 до 10, особые метки для обозначения десятков, сотен и тысяч, и ноль, который обозначали выделенным пустым местом.

Числа древнего Египта построены грамотно и логично. Рационализм и четкость отличают эти системы счисления от аналогичных попыток других народов. Цифры значением меньше десяти обозначались ׀. Например, цифра 6 выглядела как ׀׀׀׀׀׀. Число 10 обозначалось перевернутой подковой в иероглифической системе и особым символом – в иератической. Сколько десятков в числе, столько и «подков».

Иератическая система письменности предполагала для каждого числа, на десяток выше предыдущего, отдельный символ. Начиная от 100, это была стилизованная клюшка, над которой с каждой новой сотней ставили крохотную пометку.

В иероглифах все проще. Число 100 выглядело почти как арабская цифра 9, но египтяне назвали ее лотосом. Далее все аналогично — 200 – 2 «лотоса», 300 – 3 и т.д.

Египетские числа и цифры

Вы заметили, что в древнем Египте с самого начала сформировалась десятичная система? Однако Месопотамия все же превзошла Египет, когда на ее территории обрел независимость и возвысился Вавилон. Там вырастала отдельная культура, вскормленная достижениями соседних завоеванных государств.

Достижение Вавилона

Числа древнего Вавилона мало отличались от месопотамских: те же клиновидные знаки служили для обозначения единиц — ˅, и десятков — ˃. Комбинация этих знаков применялась для обозначения чисел 11-59. Число 60 в письме выглядело как зеркальное отражение буквы «Г». 70 – Г˃, 80 — Г˃˃ и так далее, принцип ясен, клинопись не отличается гениальностью.

Вавилонская система счисления

Основная ценность заключается в том, что один и тот же знак – обратите внимание – в зависимости от того, где он расположен в записи числа, имеет разное значение. Речь идет о поместном размещении знаков в системе счисления. Те же клиновидные знаки, указанные в разных разрядах, обладают разной значимостью. Поэтому Вавилонскую систему счисления с нулем принято называть позиционной. Математики могут с этим поспорить, потому что не найдено ни одного источника, в которой ноль располагался бы в конце числовой записи, что говорит об относительной позиционности.

Вавилонская система стала своеобразным трамплином, с которого человечество совершило прыжок на новый этап своего развития. Идея со временем попала в руки индусов. Они внесли свои коррективы, усовершенствовав систему счисления. Переняли идею итальянские торговцы, которые привезли ее в Европу вместе с товаром. Позиционная система счисления облетела весь мир, обогатив своим появлением не только математические науки, но и современный счет.

Знаете, откуда взялось деление часа на 60 минут, а минут – на 60 секунд? Из рассмотренной выше шестидесятеричной системы чисел. Взгляните, как обозначали числа древние вавилоняне, и в клиновидных значках увидите сакральный смысл современного, привычного для всех счисления.

Вернуться к оглавлению

История цифр разных народов

Цифры древней Греции

Под плеядой легендарных античных математиков и философов сформировалось две системы счисления. Каждая из них приносила свои преимущества, но они не были открыты или доработаны в связи с политико-культурными переменами.

Аттическую систему можно было бы назвать десятичной, если бы в ней не была выделена цифра 5. Аттическая запись чисел использовала повторы коллективных символов, что напоминало месопотамский метод. Единицу обозначала черта, написанная нужное количество раз. Таким образом записывались числа до 4. Цифра 5 была под первой буквой слова «пента», 10 – под первой буквой слова «дека» («десять») и т.д.

История чисел и цифр:

Алфавитная (или ионическая) система достигла своего расцвета в преддверии Александрийской эпохи. По сути, объединила десятеричную систему счисления и древневавилонский способ позиционности. Цифры записывались буквами и черточками. Система счисления довольно перспективна, но греки с их фанатичным стремлением к совершенству так и не довели ее до ума. Пытаясь достигнуть максимальной строгости и четкости в числовых записях, математики внесли существенные трудности в работу с ней.

Числа древнего Рима

Легкоузнаваемые, четкие, строгие и ясные обозначения стали весьма удачным изобретением римлян. Пройдя сквозь века, символы остались практически неизменными еще и потому, что Рим пользовался влиянием на древней государственной арене. А также перенимал некоторые культурные особенности у завоеванных народов. Бросается в глаза алфавитное обозначение цифр – главная «изюминка» аттической системы. Цифра V (5) – прототип ладони с раскрытыми пятью пальцами. Стало быть, Х (10) – две ладони. Палочками указывали единицы, а для сотен и тысяч предназначены прописные буквы алфавита.

Числа и цифры древнего Рима

Цифры древнего Китая

Система сложных, абстрактных иероглифов, в которую превратились невинные зарубки на гадальных костях, мало где применяется. Впрочем, иероглифы используются для формальных записей, а упрощенный набор символов применяется в повседневной жизни.

Числа в древней Руси

Как ни странно, Русь повторила алфавитную систему счисления. Каждая цифра была названа соответствующей ее рангу буквой алфавита. Цифра 1 выглядела как «А», 2 – «Б», 3 – «В» и т.д. Десятки и сотни также были подписаны соответствующими буквами славянского алфавита. Чтобы не путать в тексте слова с цифрами, над числовыми записями рисовали титло – горизонтальную волнистую линию.

числа и цифры Древней Руси

Древнеиндийские цифры

Сколько бы ни спорили ученые, сколько бы изменений ни претерпевала форма цифр, но возникновение арабских, «наших» цифр приписывают древней Индии. Возможно, арабы позаимствовали древнеиндийскую систему счисления или изобрели ее сами. Причиной научных мытарств стал фундаментальный математический труд Аль-Хорезми «Об индийском счете». Книга стала своеобразной «рекламой» десятичной позиционной системы. Иначе как объяснить внедрение индийской системы счисления на территории всего Халифата?

Эволюция индийских чисел и цифр

Полноценность позиционной системы укрепилась возникновением «нуля». В целом запись чисел не ушла далеко от аттической: для цифр 5, 10, 20… использовались коллективные символы, повторяющиеся нужное количество раз.

При таком подходе из древнеиндийских цифр не могли «вырасти» арабские. Это утверждение кажется логичным на первый взгляд, но история цифр загадочна, и демонстрирует непричастность древней Индии к возникновению знакомых нам символов.

Вернуться к оглавлению

Самые распространенные системы счисления

Арабские цифры значительно экономили время и материалы для письма. Один арабский ученый предложил обозначать цифру символом с определенным количеством углов. Количество углов должно равняться значению цифры. Например, «0» — «ничто», углов нет; 1 – 1 угол; 2 – 2 угла и т.д. Слово «цифра» также позаимствовано из арабских языков, где оно звучало как «сыфр», и обозначало «ничто», «пустота». У «сыфр» был синоним – «шунья». На протяжении веков «0» называли именно так. До тех пор, пока не появилось латинское «нуллум» («ничто»), как мы и называем «ноль».

Современный вариант символьного обозначения цифр выражен плавными, округлыми линиями. Это результат эволюции. В первозданном виде обозначения угловаты. Время действительно способно сглаживать углы – в прямом и переносном значениях. Неважно, откуда берет истоки история возникновения чисел, главное, они стали достоянием всего мира. Цифры легко пишутся и запоминаются, что облегчает и смысловое восприятие. Ведь перед вами не длинная вереница закорючек и букв.

Несмотря на то, что латынь называют «мертвым» языком, ее значимость в научной сфере подтверждена изучением в ВУЗах. Латинские цифры также нашли применение в документоведении, деловодстве, оформлении научных работ. Доступность, понятность и четкость сделали их завсегдатаями учебников и рефератов.

Как сделать латинскую запись числа? У вас есть 7 знаков, комбинируя которые вы составите необходимое обозначение. Эти знаки легко запомнить: I – 1, V – 5, Х – 10, L – 50, D – 500, M – 1000.

Если знак, обозначающий меньшее число, расположен за большим числом, меньшее прибавляется к большему. Например, ХI – 11.
Если символ меньшего числа стоит впереди, т.е. слева, нужно вычесть его от большего числа. Например, ХIХ – 19, а не 21.

Проанализировав указанные факты и взаимосвязь между ними, вы поймете, что история чисел и системы счисления не могут рассматриваться раздельно. Системы счисления формировались одновременно с числами. Культурная, экономическая, политическая ситуация каждого государства подготовила почву для их формирования, что объясняет различия между системами счисления.

Вернуться к оглавлению

«Биография» арабской цифры

История цифры 1.

Не только первая цифра в ряду, но и символ единства, совершенной целостности, как бог или космос. Смысл числительного «первый» семантически связано с именем Адама («первый человек»), а также с именами мифических персонажей Атум (созвучно со словом «атом», а мы знаем, что он неделимый), Один (от сканд. «первый», «верховный», «главенствующий»). Чувствуется фонетическое подобие слова «один» с «ЕДИНый», «жАДИНа». Улавливаете сходство?

История цифры 2

В названии цифры чувствуется парность, бинарное противопоставление, антонимичность, дуальность, четность. 2 – это защита от небытия и одиночества, противостояние единому. Вспомним, что Адам значит «первый», но после него не землю пришла Ева, она была «вторая». Ева значит «дева», а поскольку в древней Руси буквы «о» и «е» отсутствовали, то слово «дева» в письменном варианте выглядело как «дъва». Учитывая глубокую религиозную приверженность наших предков, имя «два» могло произойти из христианской мифологии.

История цифры 3

Недаром китайский цифровой ряд начинается с «тройки». Это совершенное число, за которым стоит ряд русских традиций – трижды постучать по дереву, трижды произнести «аминь» по окончанию молитвы, бог в православной вере существует в трех ипостасях. Цифра 3 обозначает крайнюю степень какой-либо характеристики. Например, «треклятый», «трисвятый». «Тройка» пишется практически одинаково с буквой «з», с которой начинается слово «земля». Как одна из стихий (1 – огонь, 2 – вода), земля вполне может оказаться третьей.

История цифры 4

Сравните русское слово «веер» с немецким словом «vier» («четыре»). Четвертая стихия – ветер — прячется под «четверкой». Кроме того, это четное число, «четыр». Оттуда и название.

История цифры 5

Одна из важнейших характеристик микро- и макрокосма. Ничего загадочного в этом нет. Вспомните, сколько у нас чувств, сколько классов животных, сколько элементов в буддийских упанишадах? Их пять. Цифра 5 находится у истоков навыков счета. В древней Руси считали «на пятках», то есть на пальцах руки. Выражение «знать, как пять своих пальцев», родом из той эпохи.

История цифры 6

На Руси цифру записывали под буквой «зело», пока не были введены арабские цифры. Сравните слова «зело» и «зло». Ведь 666 – три «зело» — обозначает абсолютное зло, треклятое (см. историю цифры 3).

История цифры 7

Цифра 7 начертанием и произношением сходна с латинской буквой Z («zet»). «Семь» созвучно с «земь», то есть «опора», «центр».

История цифры 8

Сразу слышится «осемь», т.е. «ось». Цифра 8 напоминает букву «В», с которой начинается ее буквенная запись.

История цифры 9

Мы слышим троекратное повторение триады. «Девятка» — это обобщение всего цифрового ряда и ее превосходство одновременно.

Зная историю возникновения чисел, вы будете смотреть на них через призму своих знаний, будучи осведомленным о том смысле, который они таят под своим начертанием. Может, вы интуитивно догадывались об этих смыслах?

Древние цифры.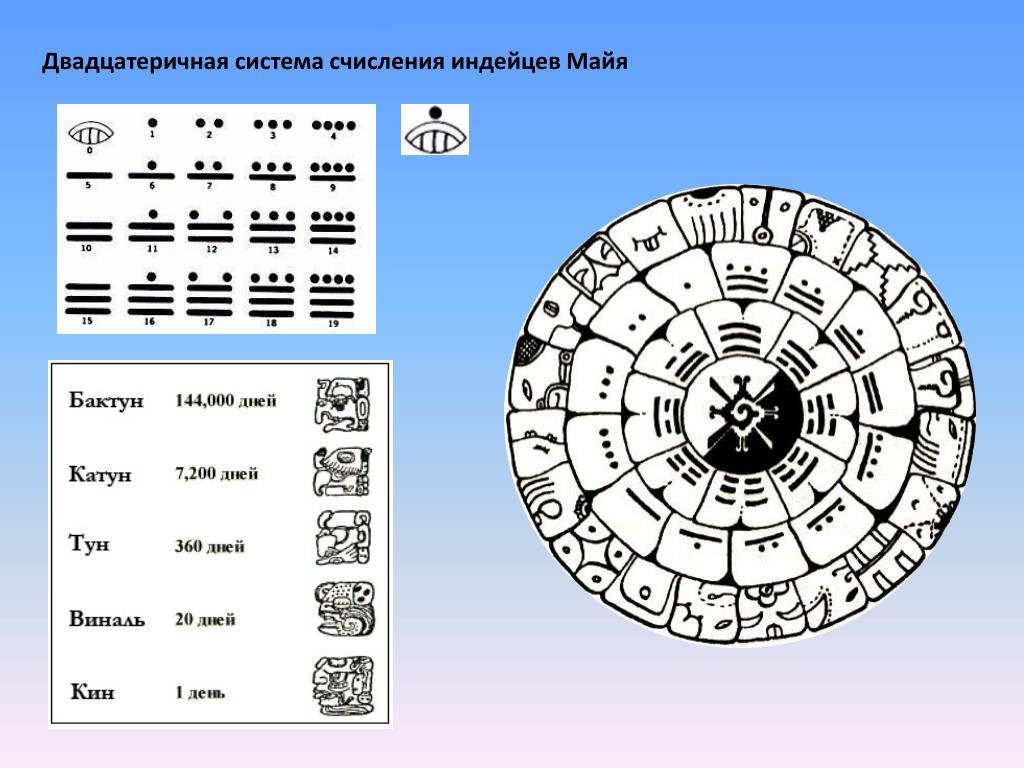 Самые старые системы счисления

Никто не знает как давно люди научились считать. Но, почти наверняка, нам известно как они это делали раньше. По крайней мере, с того момента, когда древние числа начали записывать. Система счисления, это просто метод, которым представляются числа, чаще всего для этого мы используем специальные знаки — цифры. Сейчас мы пользуемся (и то не всегда) десятичной системой, у нас 10 цифр, и основание тоже — десятка. Количество символов и основание не обязательно должны быть равны. В клинописи, например, только один символ — клин.

Древние цифры

Самой старой системой счисления была единичная или унарная. В ней была только одна цифра — единица. Так можно было сосчитать все, что угодно, интуитивно понятно и логично. Один это — I два, это — II три — III. Все просто, один палец, один предмет, если пальцы закончатся, можно взять палочки или камешки. Для удобства цифру (одну цифру) можно группировать по три или по четыре — IIII IIII IIII. Пока не нужно считать много, очень удобно. Но древним людям не приходилось много считать, они были заняты выживанием.

Единичную систему счисления применяют и сегодня… Попав на необитаемый остров, вы будете отмечать счастливые деньки именно в такой манере, зарубками на стволе дерева, например.

Двенадцатеричная система счисления

Она же Шумерская. Самая древняя система записи чисел из известных.

Шумерская цивилизация счистится древнейшей, и шумерская математика, скорее всего, тоже самая древняя. Итак почему 12, а не 5 или 10 (по числу пальцев).

На самом деле дело в пальцах, и у древних жителей Междуречья пальцев было тоже по 5 на каждой руке. Но считали они не пальцы, а фаланги. Посмотрите на картинку.

Прикасаясь большим пальцем к фалангам можно посчитать до 12. Эта система более удобна для счета, чем современна десятичная. Например, удобнее делить на 3.

Записывались все числа при помощи всего двух цифр: единицы (вертикальный клин) и десятки (горизонтальный клин). Цифра клин одна — а чисел записать можно много.

Запись чисел клинописью

В десятичной системе 1/3 = 0,33333333 (3). А в двенадцатеричной деление на 3 — это целое число. Ведь «дюжина» делится на 1,2,3,4,6 и само на себя. А десять, только на 1,2,5 и на 10. Нет ничего сложного в том, чтобы разделить одну пиццу на троих, но как это сделать в десятичной системе? Разрезать на 10 равных частей и взять по сколько….Целые куски не получатся. А вот если основа «дюжина», то деление на три даст 0,4. Двенадцать кусочков по 4 каждому.

Система настолько удобная, что мы пользуемся ею до сих пор…

Шестидесятеричная система счисления

От 12, сразу прыгаем к 60. Вавилонское царство возникло на месте шумерского. Поэтому, 12-ти и 60-ти, это фактически одна и та же система. Откуда взялось 60? Опять таки из пальцев. На одной руке 12 фаланг, а на другой — 5 пальцев. Досчитав до 12 на одно руке загибаем палец на другой и считаем снова до 12. Два загнутых пальца — две дюжины.

12х5=60.

И что же так считают? Время. На циферблате 12 часов по 60 минут в каждом.

Шумерские ученые первыми занялись астрономией, расчетом времени и календарем. Все остальные народы позаимствовали у них эти знания. И до сегодняшнего дня ничего не изменилось. Да и в окружности 360 градусов, а не 100, просто потому, что 360=12*30.

В Английской системе мер то же самое, в одном футе — 12 дюймов, в одном фунте — 12 унций. Во всем виноваты шумеры и удобство деления. Делить что-то на 2,3 и 4 приходится гораздо чаще, чем на 2 и на 5. Англичане точно знают, сколько это «треть фунта», а сколько будет «треть килограмма»?

Двадцатеричная система счисления

Ей пользовались индейцы майа. Но для записи использовались только три символа. Это «ноль», «единица» и «пять». Ноль изображался в виде ракушки, единица — точка, а пять — это линия. Чтобы записать число 18 делали так:

Выше написано буквально «три пятерки и три двойки», 5+5+5+3=18. В отличие от шумерской системы с двумя знаками для чисел, а индейцев Майа был самый настоящий ноль.

Десятичная система

Более молодая, чем вышеперечисленные. Использовалась в Египте, Древней Греции, Риме и, конечно, в Индии. Первыми, кто ее начал использовать были египтяне. Единица это — I двойка — II тройка — III…. Но для десятки был свой символ в виде дуги. Также и для сотни, тысячи, десяти тысяч.

Самым большой цифрой был миллион. Он изображался в виде человека с поднятыми вверх руками. Чтобы записать 12 делали так.

Впрочем, если написать «палочки» с другой стороны от дуги, число не изменится.

Древние греки тоже использовали десятичную систему, но вместо цифр — буквы. В самой древней, аттической системе египетский ряду цифр 1-10-100-1000 добавилась пятерка, которая записывалась буквой Π (пента, по-гречески «пять»). Интересно, что для денницы использовалась буква Ι.

Римская система счисления нам тоже хорошо известна. Она десятичная, так как пришла из Египта через Грецию. Единица римлян, такая же как и у египтян — I. Есть пятерка от греков — V. Многие историки считают, что такое изображение это упрощенный рисунок человеческой руки (пальцы не растопырены), а Х, это две скрещенные ладошки. У римлян, в отличие от египтян, позиция имеет значение. Так ХI — это одиннадцать, а IХ — девять.

После рассмотрения всех старых систем, становится понятно, как развивалась древняя арифметика. Когда в унитарной системе стало не хватать символов, вводились новые. Достаточно неудобно считать «палочки» IIII IIII IIII, когда их много, добавляли символы для 5 или 10. Индейцы Майа вместо палочек использовали камешки рисовали точки для единиц, а «черточка» это пять камешков. Все опять упирается в количество пальцев.

ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ | Энциклопедия Кругосвет

Содержание статьи

ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ. Интуитивное представление о числе, по-видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только «один», «два» и «много», подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово «три» использовалось только в сочетаниях «три дерева» или «три человека»; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова «один» и «первый», равно как «два» и «второй», во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета «один», «два», «много», слова «три» и «третий», «четыре» и «четвертый» ясно указывают на взаимосвязь между количественными и порядковыми числительными.

Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по-видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.

Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово «двадцать три» – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий «два раза по десять и три». Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерения или вычислений использовались основания 12 и 60.

Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.

ОБОЗНАЧЕНИЯ ЧИСЕЛ

Древний Египет.

Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. (См. сводную таблицу обозначений чисел.) Чтобы записанные таким образом числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона. Так, например, с помощью коллективных символов и повторений уже введенных символов число 6789 в иероглифических обозначениях можно было бы записать как

Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком, например, девять записывалось как вместо , а семьсот как вместо .

В этой записи число 6789 имело вид , причем знаки более высокого порядка располагались справа, а не слева. Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.

Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителям Месопотамии.

Вавилон.

Письменность шумеров является, по-видимому, столь же древней, как и письменность египтян. Развитие способов представления чисел в Месопотамской долине вначале шло так же, как и в долине Нила, но затем жители Междуречья ввели совершенно новый принцип. Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались на солнце или в печи. Эти записи оказались исключительно долговечными, а потому, в отличие от египетских папирусов, дошедших до нас в весьма малом числе экземпляров, в музеях мира хранятся десятки тысяч клинописных табличек. Однако жесткость материала, на котором жители Месопотамии делали записи, оказала глубокое влияние на развитие числовых обозначений. Через некоторое время после того, как Аккад завоевал шумеров, система счисления в Месопотамии стала шестидесятиричной, хотя сохранилось также и основание 10. Казавшееся правдоподобным предположение относительно того, почему выбор пал на число 60 как на основу вавилонской системы счисления, и утверждавшие, будто это связано с тем, что продолжительность земного года считалась равной 360 дням, не получило подтверждения. Ныне принято считать, что шестидесятиричная система была выбрана из метрологических соображений: число 60 имеет много делителей.

Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта (в раннешумерских табличках – небольшой полукруг) означала единицу; повторенный нужное число раз этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый коллективный символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку, (в раннешумерских текстах – небольшой кружок).

Повторенный соответствующее число раз, этот знак служил для обозначения чисел 20, 30, 40 и 50. Принцип повторного использования знаков позволял, например, записать число 59 в виде , т.е. 5·10 + 9.

Но для записи чисел больше 59 древние вавилоняне впервые использовали новый принцип – одно из самых выдающихся достижений в развитии систем обозначений чисел – принцип позиционности, т.е. зависимости значения символа от его местоположения в записи числа. Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять уже ранее использованные символы, если они будут занимать в записи числа новое положение левее предыдущих символов. Так, один клиновидный знак мог использоваться для обозначения и 1, и 60, и 60², и 60³, в зависимости от занимаемого им в записи числа положения, подобно тому, как единица в наших обозначениях используется в записях и 10, и 10², и 10³, и в числе 1111. При обозначении чисел больше 60 знаки, выступающие в новом качестве, отличались от старых тем, что символы разбивались на «места», или «позиции», и единицы более высокого порядка располагались слева. При таком способе записи для обозначения сколь угодно больших чисел уже не нужно было других символов, кроме уже известных. Например, число 6789 можно было записать так: , т.е. 1·(60)² + 53·(60) + 9. В Древнем Вавилоне, ок. 1650 до н.э., система счисления оставалась псевдопозиционной или лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной запятой, равно как и символа для обозначения отсутствующей позиции. Обозначал ли символ число 1·(60)² + 1 или 1·(60)² + 1·(60), приходилось догадываться из контекста. Однако в период правления селевкидов, ок. 300 до н.э., эта неоднозначность была устранена введением специального символа в виде двух небольших клиньев, помещаемого на пустующее место, т.е. обозначающего пустую позицию в записи числа. Таким образом, из системы счисления была устранена отмеченная выше неоднозначность. Например, символ означал число 3601, т.е. 1·(60)² + 0·(60) + 1. В то же время не было найдено ни одной таблички с записью, в которой символ нуля находился бы в конце числа. Именно поэтому вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60. Тем не менее изобретение вавилонянами позиционной системы счисления с нулем представляло собой огромное достижение, по своему революционному значению для математики сопоставимое разве лишь с более поздней гипотезой Коперника в астрономии.

Символы для обозначения чисел на вавилонских глиняных табличках не столь точны, как символы для обозначения чисел на древнеегипетских папирусах, несмотря на то, что вавилоняне использовали позиционный принцип. В исключительных случаях вавилоняне применяли сокращенные формы записи, иногда – с новыми символами для обозначения чисел 100 и 1000, или использовали принципы умножения или вычитания. Однако превосходство разработанной в Месопотамии системы счисления отчетливо видно в обозначении дробей. Здесь не требовалось вводить новые символы. Как и в нашей собственной десятичной позиционной системе, в древневавилонской системе подразумевалось, что на первом месте справа от единиц стоят величины, кратные 1/60, на втором месте – величины кратные 1/60² и т. д. Привычное нам деление часа и углового или дугового градуса на 60 минут, а одной минуты – на 60 секунд берет начало от вавилонской системы счисления.

Древняя Греция.

В Древней Греции имели хождение две основных системы счисления – аттическая (или геродианова) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова «пента» (пять) (буква Г употреблялась для обозначения звука «п», а не «г»). Дойдя до десяти, они ввели еще один новый символ Δ, первую букву слова «дека» (десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ H означал 100 (гекатон), X – 1000 (хилиои), символ M – 10000 (мириои или мириада). Используя число 5 как промежуточное подоснование системы счисления, греки на основе принципа умножения комбинировали пятерку с символами степеней числа 10. Так, число 50 они обозначали символом , 500 – символом , 5000 – символом , 50000 – символом . Еще бóльшие числа обычно описывались словами. Число 6789 в аттической системе записывалось в виде

Вторая принятая в Древней Греции ионическая система счисления – алфавитная – получила широкое распространение в начале Александрийской эпохи, хотя возникнуть она могла несколькими столетиями раньше, по всей видимости, уже у пифагорейцев. Эта более тонкая система счисления была чисто десятичной, и числа в ней обозначались примерно так же, как в древнеегипетской иератической системе. Используя двадцать четыре буквы греческого алфавита и, кроме того, еще три архаических знака, ионическая система сопоставила девять букв первым девяти числам; другие девять букв – первым девяти целым кратным числа десять; и последние девять символов – первым девяти целым кратным числа 100. Для обозначения первых девяти целых кратных числа 1000 греки частично воспользовались древневавилонским принципом позиционности, снова использовав первые девять букв греческого алфавита, снабдив их штрихами слева. Например, число 6789 в ионической системе записывалось как FΨΘП. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. Первоначально числа обозначались прописными буквами, но позднее сменились на строчные.

Ионическая система первоначально не сильно потеснила уже установившуюся аттическую или акрофоническую (по начальным буквам слов, означавших числительные) системы исчисления. По-видимому, официально она была принята в Александрии во времена правления Птолемея Филадельфийского и в последующие годы распространилась оттуда по всему греческому миру, включая Аттику. Переход к ионической системе счисления произошел в золотой век древнегреческой математики и, в частности, при жизни двух величайших математиков античности. Есть нечто большее, чем просто совпадение, в том, что именно тогда Архимед и Аполлоний работали над усовершенствованием системы обозначения больших чисел. Архимед, придумавший схему октад (эквивалентную современному использованию показателей степени числа 10) гордо заявлял в своем сочинении Псаммит (Исчисление песчинок), что может численно выразить количество песчинок, необходимых для того, чтобы заполнить всю известную тогда Вселенную. Изобретенная им система обозначения чисел включала число, которое ныне можно было бы записать в виде единицы, за которой следовало бы восемьдесят тысяч миллионов миллионов цифр.

С помощью простого введения диакритических знаков наподобие тех, которые греки применяли для обозначения тысяч, алфавитное обозначение целых чисел можно было бы легко приспособить для обозначения десятичных дробей, но этой возможностью они не воспользовались. Вместо этого для обозначения дробей греки использовали приемы древних египтян и вавилонян. Египетское влияние в Греции было достаточно сильным, чтобы навязать грекам употребление лишь аликвотных дробей, однако большие вычислительные удобства системы счисления вавилонян побудили живших позднее александрийских астрономов перейти к использованию шестидесятиричных дробей. Переняв систему счисления Древнего Вавилона, греки заменили месопотамскую клинопись своими буквенными обозначениями. Например, Птолемей записал длину хорды, стягивающей дугу в 120° окружности радиусом в 60 единиц, как PГNЕ‘КГ‘, т.е. 103 + 55/60 + 23/60² единиц. В более поздний период в вавилонской шестидесятиричной системе имелся специальный символ для обозначения «пустой» позиции, и греческие астрономы ввели для этой цели букву омикрон. Неясно, был ли такой выбор подсказан тем, что с этой буквы начиналось слово оуден (ничто). Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим, чем случайное совпадение, но у нас нет точных данных, позволяющих утверждать это со всей определенностью.

Поскольку греки работали с обыкновенными дробями лишь эпизодически, они использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятиричным дробям.

Недостатки греческих обозначений дробных чисел, включая использование шестидесятиричных дробей в десятичной системе счисления, объяснялись отнюдь не пороками основополагающих принципов. Недостатки греческой системы счисления можно отнести скорее за счет их упорного стремления к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали как набор единиц, поэтому то, что мы теперь рассматриваем как единое рациональное число – дробь, – греки понимали как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике. Кроме того, десятичные представления обыкновенных дробей в большинстве случаев бесконечны. А поскольку бесконечность была исключена из строгих рассуждений, теоретическая арифметика не нуждалась в такого рода представлениях. С другой стороны, областью, в которой практические вычисления испытывали величайшую потребность в точных дробях, была астрономия, а здесь вавилонская традиция была настолько сильна, что шестидесятиричная система обозначений угловых, дуговых и временных величин сохраняется и поныне.

Рим.

Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы.

Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Θ (или ⊕, или ⊗) и Φ (или , или ). Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Θ и φ. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX и XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.

В целом римляне не были склонны заниматься математикой, поэтому не испытывали особой потребности в больших числах. Тем не менее для обозначения 10000 они эпизодически использовали символ , а для числа 100000 – символ . Половинки этих символов иногда использовались для обозначения чисел 5000 () и 50000 (). Таким образом, в римских обозначениях число 6789 можно было бы записать как .

Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова uncia (унция), обозначавшего одну двенадцатую основной единицы длины.

Обозначения чисел у древних евреев.

Семитские народы могут претендовать на роль создателей алфавитного принципа обозначения чисел в том виде, как он использовался в ионической системе. Действительно, с небольшими модификациями этот принцип применялся евреями, сирийцами, арамейцами и арабами. И все же существует мало сомнений в том, что алфавитные обозначения чисел были заимствованы ими у древних греков, по-видимому из Милета, которые изобрели эти обозначения еще в 8 в. до н.э. У евреев использование алфавитных обозначений чисел окончательно вошло в обиход к 2 в. до н.э. Девять букв алфавита использовались для обозначения первых девяти целых чисел; еще девять букв означали первые девять кратных числа 10; остальные буквы использовались для обозначения сотен. Так как букв в алфавите для обозначения всех кратных числа 100 не хватало, в Талмуде числа, превосходящие 400, записывались путем комбинации: например, число 500 обозначалось символами, соответствующими числам 400 и 100, а 900 записывалось как 400 и 400 и 100. Позднее для обозначения чисел, кратных 100 и превосходящих 400, использовались окончательные варианты формы букв или других символов, в результате чего все девять кратных числа 100 получили свои индивидуальные обозначения в виде буквы или специального знака. (См. таблицу обозначений чисел.) Как и в ионической системе счисления, символы для обозначения первых девяти кратных числа 1000 были такими же, как символы, обозначающие первые девять чисел в разряде единиц. Число 6789 евреи записывали как. Так как запись числа 15 в обычном виде как 10 и 5 совпадает с первыми двумя буквами имени Бога Яхве, древние евреи записывали число 15 как 9 и 6. Высказывалось предположение, что по аналогичным причинам древние римляне избегали записывать число IV вместо IIII, т.к. символ IV совпадает с первыми двумя буквами старолатинского написания имени Юпитер.

Америка.

Исследователи, путешествовавшие в 16 в. по Центральной Америке, обнаружили цивилизации с высокоразвитыми системами счисления, отличными от тех, которые были известны в Европе. Самыми важными элементами в системе счисления майя были использование позиционного принципа и символа нуля. Если отвлечься от того, что принятая у индейцев майя система счисления была не шестидесятиричной, а двадцатиричной и вместо 10 использовала вспомогательное основание 5, то в остальном принципы были аналогичны тем, которые ранее были в ходу у жителей Древнего Вавилона. В схеме майя точка означала единицу, а повторяющиеся точки – числа до четырех; пятерку обозначала горизонтальная черта, а две и три горизонтальные черты обозначали, соответственно, числа десять и пятнадцать. Для обозначения числа двадцать майя воспользовались позиционным принципом, используя точку, помещенную над символом нуля. (Последний имел вид .)

Числа в системе счисления древних майя записывались в столбец, причем верхние символы были старшими. Самая нижняя позиция соответствовала разряду единиц; «этажом выше» располагалось число двадцаток. Еще выше единица соответствовала не кратным числа 400, как можно было бы ожидать, а кратным числа 360. За исключением этого разряда, связанного, насколько можно судить, с календарными соображениями и продолжительностью года, все остальные более высокие позиции соответствовали степеням числа 20. Число 6789 в системе счисления, принятой у майя, записывалось как

Система счисления у ацтеков в Мексике была более последовательно двадцатиричной, чем у майя, но в остальном менее тонкой, так как не использовала ни позиционный принцип, ни специальный символ для нуля. Точка означала у ацтеков единицу, а для обозначения степеней числа 20 были введены новые знаки: флаг для 20, дерево для 400 и кошелек для 8000. При необходимости другие числа представлялись с помощью повторения этих символов, а от их чрезмерного повторения они избавлялись, вводя специальные промежуточные коллективные знаки: ромбовидный знак для 10 и фрагменты дерева для 100, 200 или 300.

До появления в Северной Америке европейцев индейцы не имели письменности. Исследования древних систем счисления показывают, что используемые названия чисел были в основном прилагательными и лишь в отдельных случаях достигали уровня абстракции, когда они становились существительными. Тем не менее с помощью рисунков или устно индейцы могли выразить число вплоть до миллиона. Системы составления чисел были самыми различными, но примерно половина из них по существу была десятичной.

Китай.

Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять. (См. таблицу обозначений чисел.) Первые пять кратных числа 10 обозначались одной, двумя, ј, пятью горизонтальными палочками, а одна, две, три и четыре горизонтальные палочки, к которым сверху приставлялась вертикальная палочка, означали числа 60, 70, 80 и 90. Для обозначения чисел больше 99 использовался позиционный принцип. Число 6789 китайцы записали бы так: . Обозначения чисел с помощью палочек тесно связано со счетом на пальцах и счетной доске, но применялось оно также и в письменных вычислениях.

Во второй китайской системе счисления для обозначения первых девяти целых чисел или символов (см. таблицу обозначений чисел) используют девять различных знаков и одиннадцать дополнительных символов для обозначения первых одиннадцати степеней числа 10. В сочетании с умножением и вычитанием это позволяло записывать любое число меньше триллиона. Если один из символов, обозначающих первые девять целых чисел, стоит перед (при чтении слева направо) символом, означающим степень числа 10, то первое нужно умножить на второе, если же символ одного из девяти первых целых чисел стоит на последнем месте, то это число надлежит прибавить к обозначенному предыдущими символами. В такой системе счисления число 6789 выглядело бы так: , т.е. 6·1000 + 7·100 + 8·10 + 9.

Индия.

Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счисления вытеснила аттическую. Вполне возможно, что переход от кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно хоть как-то проследить или восстановить этот переход от древних индийских форм к системе, от которой произошли наши системы счисления. Надписи, найденные в Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками тех, которые получили теперь название индо-арабской системы. Первоначально в этой системе не было ни позиционного принципа, ни символа нуля. Оба эти элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари (см. таблицу обозначений чисел). В индийской системе число 6789 записывалось бы как . Здесь мы впервые встречаемся с элементами современной системы счисления: индийская система была десятичной, цифровой и позиционной. При желании можно даже усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.

Напомним, что позиционная система счисления с нулем возникла не в Индии, поскольку за много веков до этого она использовалась в Древнем Вавилоне в связи с шестидесятиричной системой. Поскольку индийские астрономы использовали шестидесятиричные дроби, вполне возможно, что это навело их на мысль перенести позиционный принцип с шестидесятиричных дробей на целые числа, записанные в десятичной системе. В итоге произошел сдвиг, приведший к современной системе счисления. Не исключена также возможность, что такой переход, по крайней мере отчасти, произошел в Греции, скорее всего в Александрии, и оттуда распространился в Индию. В пользу последнего предположения свидетельствует сходство кружка, обозначающего нуль, с начертанием греческой буквы омикрон. Однако происхождение индийского символа для нуля окутано тайной, так как первое достоверное свидетельство его появления в Индии датируется лишь концом 9 в. Как ни странно, ни греки, ни индийцы не включили в свои системы счисления десятичные дроби, но именно индийцам мы обязаны современной системой записи обыкновенных дробей с числителем, расположенным над знаменателем (но без горизонтальной черты, отделяющей числитель от знаменателя).

Аравия.

Современную систему обозначения чисел часто называют арабской, хотя ясно, что она берет начало не из Аравии. До хиджры арабы записывали числа словами, но затем, как это делали ранее греки, они стали обозначать числа буквами своего алфавита. В 772 индийский трактат «Сидданта» был привезен в Багдад и переведен на арабский, после чего стали использоваться две системы записи чисел: (1) в астрономии по-прежнему употребляли алфавитную систему, (2) в торговых расчетах купцы стали применять систему, заимствованную из Индии. Но даже среди тех, кто пользовался индийской системой, начертания цифр, как и в Индии, сильно варьировали. Эти две системы счисления были широко распространены и после распада арабского халифата. В его восточной части пользовались системой, аналогичной той, которая и сейчас встречается в арабском мире. Число 6789 в этой системе записывается как . Однако обозначения чисел в Испании 10 в. настолько сильно отличались по своим начертаниям от приведенных выше, что казались никак с ними не связанными. В испанских обозначениях, получивших название «гобар» или «песчаных», число 6789 выглядело бы так: . Свое название эти обозначения получили потому, что ими пользовались при вычислениях на «песчаном абаке». Как свидетельствует Бируни, индийцы часто производили вычисления на песке, что, возможно, и послужило поводом для такого названия. Тем не менее само происхождение этих цифр, от которых в свою очередь произошли наши современные цифры, остается неизвестным.

Западная Европа.

Первым европейским ученым, о котором достоверно известно, что он ввел в употребление в Европе арабские цифры, был Герберт, работавший в Испании и позднее (в 999-м) ставший папой Сильвестром II. В 12 в. Хуан из Севильи перевел на латынь трактат De numero indorum (Об индийских числах) арабского математика Аль-Хорезми. Когда в следующем веке индийские обозначения стали широко известными, новая система получила название алгоритм – от искаженного Аль-Хорезми. Через пару столетий европейские алгоритмики одержали верх и над абацистами, и над теми, кто пользовался римскими цифрами в вычислениях с целыми числами, но лишь с 1585 индо-арабская система обозначений, систематически расширяясь, стала использоваться и применительно к дробям. В том же году Симон Стевин опубликовал свой небольшой трактат De Thiende (Десятина), в котором он предложил записывать в виде или число, которое мы записали бы как 6789. В 17 в. вошла в употребление десятичная запятая (или точка), которой стали отделять целую часть числа от дробной, после чего европейцы отказались от предложенной Стевином индексации разрядов. После этих изменений развитие современной системы счисления завершилось. (Это отнюдь не означает, будто была достигнута полная стандартизация в названиях или обозначениях чисел. В Америке и Франции биллион означает тысячу миллионов, а в Англии и Германии – миллион миллионов; в континентальной Европе часто используется десятичная запятая, а в англосаксонских странах предпочитают ставить десятичную точку; англосаксы используют запятые, чтобы отделять степени тысячи, в некоторых странах для этой цели служит точка.)

ДВОИЧНАЯ СИСТЕМА

В последние годы в области прикладной математики, особенно в компьютерах, очень важное значение приобрела двоичная система счисления.

В то время как система счисления с основанием 10 требует десяти цифр (включая нуль), для двоичной арифметики необходимо всего два символа – 0 и 1.

Таблица: Десятичная система — Двоичная система
Десятичная система	Двоичная система	Десятичная система	Двоичная система
0	0	9	1001
1	1	10	1010
2	10	11	1011
3	11	12	1100
4	100	13	1101
5	101	14	1110
6	110	15	1111
7	111	16	10000
8	1000

В двоичной системе число 6789 записывается в виде 1101010000101, т. е. как

Переход от десятичной записи к двоичной осуществляется легко: десятичное число делится на два, затем на два делится частное, затем – новое частное и так до тех пор, пока не будет получено последнее частное (равное 1), причем каждый раз записывается остаток от деления. Выписав последнее частное (1) и вслед за ним в обратном порядке все остатки от деления исходного числа на два, мы получим двоичный эквивалент исходного числа. Чтобы записать двоичное число в десятичной системе, необходимо обратить процедуру: умножить первую цифру слева на 2, к полученному результату прибавить вторую цифру слева, полученную сумму прибавить к третьей цифре слева и т.д. до тех пор, пока мы не прибавим последнюю (самую правую) цифру двоичного числа.

Двоичной системой счисления пользовался в начале 17 в. Т.Харриот. Позднее Г.Лейбниц обратил на двоичную систему внимание миссионеров, отправлявшихся для проповеди христианства в Китай в надежде убедить китайского императора в том, что Бог (единица) сотворил все из ничего (нуля). Однако вплоть до 20 в. двоичную систему рассматривали как своего рода математический курьез, и время от времени раздавались предложения перейти от десятичной системы к восьмеричной или двенадцатиричной, но отнюдь не двоичной системе.

Однако именно в двоичной системе арифметические операции особенно просты. В двоичной системе не существует «таблицы сложения», которую нужно бы было запоминать, так как «перенос в старший разряд» начинается с 1 + 1 = 10. При сложении больших чисел необходимо лишь складывать по столбцам или разрядам, как в десятичной системе, памятуя лишь о том, что как только сумма в столбце достигает числа 2, двойка переносится в следующий столбец (влево) в виде единицы старшего разряда. Вычитание производится так же, как в десятичной системе, не задумываясь о том, что теперь в случае необходимости нужно «занимать» из столбца слева 2, а не 10.

В двоичной таблице умножения единственный результат, отличный от нуля, соответствует 1 x 1 = 1. Каких-нибудь других «табличных» произведений, требующих запоминания, не существует, так как любое целое число больше единицы в двоичной системе по крайней мере «двузначно». Умножение «столбиком» выполняется без труда, так как необходимость в «переносе в старший разряд» отпадает за исключением сложения частичных произведений при получении окончательного ответа. Однако за эту легкость приходится «платить» большим числом знаков при умножении даже небольших чисел.

Деление «углом» в двоичной системе выполняется быстро, при этом нет необходимости в пробных делителях. По существу, деление становится своего рода непрерывным вычитанием, которое отличается необычайной «прозрачностью».

В компьютерах двоичная система особенно удобна тем, что двоичные цифры соответствуют тому, что электронная система может находиться лишь в одном из двух состояний – либо «выключено» (цепь разомкнута, двоичная цифра 0), либо «включено» (цепь замкнута, двоичная цифра 1). Числа, записанные в двоичной системе, требуют большего числа знаков, чем их аналоги в десятичной системе, но при проектировании компьютеров, предназначенных для работы с числами, не превышающими 10 миллионов, оказалось, что легче оперировать с 24-разрядными двоичными числами (т. е. 24 реле или переключателя типа «вкл.» – «выкл.»), чем с семизначными десятичными числами (реле или переключателями, которые могут находиться в 10 состояниях). И в двоичной, и в десятичной системе суть состоит в позиционном принципе записи чисел, поэтому ясно, что современные суперкомпьютеры стали возможны благодаря тому, что четыре тысячи лет назад в Месопотамии было совершено важнейшее открытие в области обозначения чисел (см. также КОМПЬЮТЕР).

ДВЕНАДЦАТИРИЧНАЯ И ВОСЬМЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ

Хотя десятичная система счисления является наиболее широко применимой, это отнюдь не означает, что она самая лучшая. Широкое распространение во многом объясняется тем анатомическим обстоятельством, что у нас на руках и ногах по десять пальцев. Что же касается позиционного принципа и цифровых обозначений, то они с равным успехом могут быть приспособлены к системе счисления с любым основанием, независимо от того, равно ли оно 2, 10 или какому-нибудь другому целому положительному числу, кроме единицы. Например, подставив в полиномиальное представление 7x² + 6x¹ + 5x⁰ + 4x^–1 + 3^–2 вместо x значение 10, мы получим число 765,43 в нашей обычной десятичной системе. Но без малейшего ущерба для позиционного принципа обозначения целых чисел и дробей вместо x можно подставить и любое другое целое положительное число. Вместо числа 10 в качестве основания системы счисления чаще других предлагалось использовать числа 8 и 12. Системы, получающиеся при таких заменах, известны под названием восьмеричной и двенадцатиричной. В восьмеричной системе вместо переменной x в полиномиальном представлении следует подставить 8, и тогда число, равное в десятичной системе 765,43, в восьмеричной системе окажется равным (8²) + 6(8¹) + 5(8⁰) + 4(8^–1) + 3(8^–2), т.е. числу . В двенадцатиричной системе то же самое полиномиальное представление при x = 12 дает (12²) + 6(12¹) + 5(12⁰) + 4(12^–1) + 3(12^–2), или в наших обычных обозначениях . Что касается вычислений, то они во всех трех системах счисления, десятичной, восьмеричной и двенадцатиричной, производятся практически одинаково и с одной и той же легкостью. Различие в основном заключается в таблицах сложения и умножения, поскольку они изменяются от одной системы счисления к другой. Например, сумма семь плюс семь равна сумме восемь плюс шесть в восьмеричной системе, десять плюс четыре – в десятичной и двенадцать плюс два – в двенадцатиричной. Символически эти суммы и произведения можно записать следующим образом:

Мы видим, что переход от десятичной системы к восьмеричной или двенадцатиричной действительно требует полного пересмотра таблиц сложения и умножения; это объясняет, почему предложения о переходе к этим системам счисления не получили широкого признания. Преимущества, которые сулит этот переход, сводятся на нет сопряженными с ним трудностями. Главные преимущества восьмеричной и двенадцатиричной систем счисления связаны с делимостью их оснований. Рассматривая только целые числа, меньшие половины основания (поскольку ни одно число не может быть делителем основания, если это число больше половины основания, но меньше его), нетрудно понять, что число 10 имеет два неделителя – числа 3 и 4, тогда как в восьмеричной системе единственный неделитель, меньший половины основания, есть число 3, а в двенадцатиричной системе единственный неделитель основания равен числу 5. Иначе говоря, преимущество числа 12 как основания системы счисления заключается в том, что оно имеет делителями числа 2, 3, 4 и 6, тогда как число 10 имеет делителями числа 2 и 5. Число 8 имеет делителями только числа 2 и 4, однако его основное преимущество перед другими в том, что непрерывное деление пополам неизменно приводит к «одноместному» дробному представлению в полиномиальной форме. Например, если 8 разделить на 2¹⁰, то результат окажется в точности равным ^(0,004)₈, тогда как если 12 разделить на 2¹⁰, то получится (приближенно) (0,0183)₁₂, а при делении на 2¹⁰ числа 10 результат (также приближенный) будет равным (0,0097656)₁₀.

В метрологии большое значение имеет факторизуемость (разложимость на множители) числа, вот почему 8 и 12 играют столь заметную роль в неметрических системах весов и мер. На американских фондовых биржах дроби обычно выражают в восьмых долях, а время делится на 12 и существенно использует деление единиц на 60 частей. Особая роль числа 60 в наших измерениях времени и углов связана с тем, что около четырех тысяч лет назад древние вавилоняне осознали, что число 60 имеет много делителей, и выбрали его не только за основу своих весов и мер, но и своей системы счисления. Позиционный принцип вошел в обиход в связи с шестидесятиричной, а не десятичной системой. Но основание 60 обладает одним серьезным недостатком: оно слишком велико для того, чтобы его можно было использовать в современной цифровой полиномиальной форме, т.к. для этого потребовалось бы 60 различных символов, которые обозначали бы первые шестьдесят неотрицательных целых чисел. Кроме того, таблицы сложения и умножения включали бы числа от 1 до 59, что потребовало бы чрезмерно большой нагрузки на память. Этим же недостатком обладает и любое другое основание большее 12, поэтому двенадцатиричная система является наибольшим практически возможным основанием. Сама двенадцатиричная система требует введения двух новых цифр – для обозначения чисел 10 и 11. Для этой цели были предложены буквы t и e. Преимущество двоичной системы в том, что для нее необходимо всего лишь две цифры, но она располагается на другом конце шкалы относительно шестидесятиричной системы, для большинства практических целей основание ее слишком мало и поэтому число знаков при записи чисел в двоичной системе оказывается слишком большим. (См. предыдущий раздел.) Числа 8, 10 и 12 очень близки к оптимальной величине основания системы счисления, и вычисления в восьмеричной, десятичной и двенадцатиричной системах выполняются сравнительно легко.

Аргументы в пользу двенадцатиричной системы счисления не следует путать с аргументами в защиту двенадцатиричной монетарной и метрологической систем. Уже вавилоняне прекрасно понимали желательность согласованности системы счисления и метрологической системы. Однако продолжительное использование десятичной системы вместе с двенадцатиричными и шестидесятидесятиричными единицами измерения затушевало проблему их несогласованности. Более того, возникла тенденция преувеличивать те трудности, которые могла бы породить любая попытка их унифицировать. Внутренняя согласованность, по-видимому, играет более важную роль, чем любой выбор единого основания систем, будь то 8, 10 или 12. Во времена Великой французской революции, на заседаниях Революционной комиссии по весам и мерам, высказывались мнения о введения двенадцатиричных систем мер и весов, но окончательное решение склонилось в пользу унификации мер и весов на основе десятичной системы счисления. Результатом такого решения стала метрическая система, получившая ныне почти всеобщее признание.

В тех случаях, когда вместе с десятичной системой счисления параллельно используются двенадцатиричные и другие единицы измерения, неизбежно возникает непростая задача перевода из одной системы единиц в другую.

Следует иметь в виду, что трудности перехода от одной системы счисления к другой не имеют никакого отношения к преимуществам или недостаткам выполнения арифметических операций целиком в рамках одной системы, будь то восьмеричная, десятичная или двенадцатиричная система. Десятичная система не может не признать небольших преимуществ двух других систем: восьмеричная система имеет меньшие по объему таблицы сложения и умножения и особенно хорошо приспособлена к делению на 2, а двенадцатиричная удобнее для выполнения операции деления и представления простых дробей. Достаточны ли эти преимущества для того, чтобы настаивать на придании универсального характера той или иной системе счисления, – вопрос достаточно спорный, однако основанное в 1944 Двенадцатиричное общество Америки стало центром, объединяющим активную деятельность тех, кто хотел бы, чтобы число 12 играло столь же важную роль, какую во многих цивилизациях на протяжении прошлых полдюжины тысячелетий играло число 10.

Системы счисления: Какие бывают системы счисления

Какие бывают системы счисления

Позиционные системы счисления

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.

Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.

, где — это целые числа, называемые цифрами, удовлетворяющие неравенству .

Каждая степень в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя (номером разряда). Обычно, в ненулевых числах , левые нули опускаются. Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число записывают в виде последовательности его -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

Например, число сто три представляется в десятичной системе счисления в виде:

Наиболее употребляемыми в настоящее время позиционными системами являются:

В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.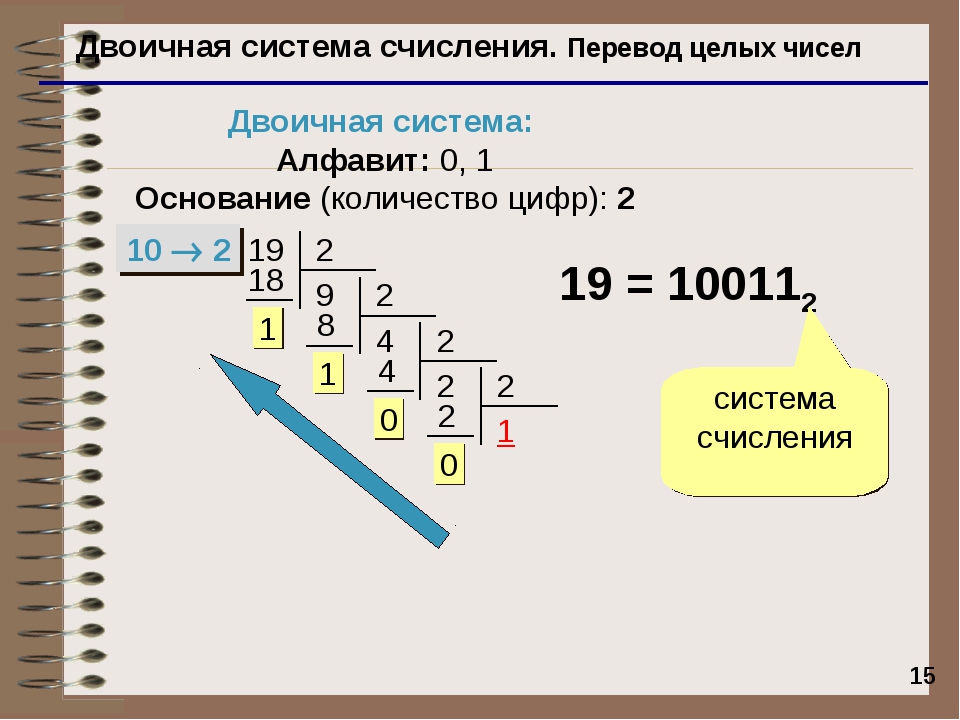

Смешанные системы счисления

Смешанная система счисления является обобщением -ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел , и каждое число в ней представляется как линейная комбинация:

, где на коэффициенты , называемые как и прежде цифрами, накладываются некоторые ограничения.

Записью числа в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса , начиная с первого ненулевого.

[править]Факториальная система счисления

В факториальной системе счисления основаниями являются последовательность факториалов , и каждое натуральное число представляется в виде:

, где .

Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: число, на единицу меньшее номера (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i! будет обозначать число инверсий для элемента i+1 в том множестве, в котором производятся перестановки (число элементов меньших i+1, но стоящих правее его в искомой перестановке)

[править]Фибоначчиева система счисления

Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число в ней представляется в виде:

, где — числа Фибоначчи, , при этом в коэффициентах есть конечное количество единиц и не встречаются две единицы подряд.

[править]Непозиционные системы счисления

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

[править]Биномиальная система счисления

, где .

[править]

[править]Система счисления Штерна–Броко

Система счисления Штерна–Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна–Броко.

[править]Системы счисления разных народов

[править]Единичная система счисления

По-видимому, хронологически первая система счисления каждого народа, овладевшего счётом. Натуральное число изображается путём повторения одного и того же знака (чёрточки или точки). Например, чтобы изобразить число 26, нужно провести 26 чёрточек (или сделать 26 засечек на кости, камне и т.д.). Впоследствии, ради удобства восприятия больших чисел, эти знаки группируются по три или по пять. Затем равнообъёмные группы знаков начинают заменяться каким-либо новым знаком — так возникают прообразы будущих цифр.

[править]Древнеегипетская система счисления

Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н. э. Для обозначения чисел 0, 1, 10, 10², 10³, 10⁴, 10⁵, 10⁶, 10⁷ использовались специальные цифры. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи.^[1]

[править]Вавилонская система счисления

[править]Алфавитные системы счисления

Алфавитными системами счисления пользовались древние армяне, грузины, греки (ионическая система счисления), арабы (абджадия), евреи (см. гематрия) и другие народы Ближнего Востока. В славянских богослужебных книгах греческая алфавитная система была переведена на буквы кириллицы.^[1]

[править]Еврейская система счисления

[править]

[править]Римская система счисления

Каноническим примером почти непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы:
I обозначает 1,
V — 5,
X — 10,
L — 50,
C — 100,
D — 500,
M — 1000

Например, II = 1 + 1 = 2
здесь символ I обозначает 1 независимо от места в числе.

На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:

IV = 4, в то время как:
VI = 6

[править]Система счисления майя

Майя использовали 20-ричную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году. Для записи основными знаками были точки (единицы) и отрезки (пятёрки).

[править]

Как разные страны мира ценят пунктуальность

Опоздать на полчаса в Греции, но вовремя в Японии: как разные страны по всему миру ценят пунктуальность

Сайт бесплатных онлайн-игр Г-н Гамез исследовал 15 разных стран не поощряется
Но Япония и Германия очень плохо реагируют на все, что не так пунктуально

Харриет Мэллинсон Для Mailonline

Опубликовано: 14:34 GMT, 26 июля 2016 г. | Обновлено: 18:40 GMT, 26 июля 2016 г.

Пунктуальность — это то, с чем многие люди борются, особенно в эпоху, когда благодаря технологиям стало проще, чем когда-либо, сообщить людям, что вы можете опоздать.

Как бы опоздавшие ни были рады узнать, что в Мексике опоздание на полчаса вполне приемлемо, а в Марокко вы можете опоздать на час или на день, не моргнув глазом.

Но тем, кто стремится придерживаться расписания, не стоит паниковать, поскольку Япония и Германия являются приверженцами пунктуальности, причем последняя даже требует, чтобы вы приходили на встречи раньше, как показывает новая инфографика.

Сайт бесплатных онлайн-игр Г-н Гамез провел исследование, чтобы выяснить, насколько и как мало разные страны мира придают значение пунктуальности, и результаты сильно разнятся.

В Южной Корее опоздание считается признаком неуважения.

Но в Малайзии опоздание на пять минут обычно означает час, а опоздание — это общепринятая норма, не требующая извинений.

В Китае не считается опозданием, если вы прибываете в течение 10 минут до согласованного времени, но в Японии, если поезд прибывает более чем на одну минуту позже запланированного, считается опозданием.

На другой стороне Тихого океана люди нередко опаздывают на запланированную встречу в Мексике на полчаса.

Благодаря промышленному прошлому в Германии ожидается, что вы приедете как минимум на 10 минут раньше. запланированная встреча.

Но в Нигерии, если встреча назначена на 13:00, это означает, что встреча начнется в любое время с 13:00 до 14:00.

Точно так же в Саудовской Аравии время не является таким важным товаром, поскольку люди часто опаздывают на встречи на полчаса. Глядя на часы во время мероприятия, также считается невежливым.

При назначении встречи в Бразилии от вас не требуется приходить вовремя, если только не используется фраза «английское время», что означает, что вы должны быть пунктуальными.

В Гане большинство графиков встреч считается гибким, даже если указано точное время. Очень часто это может означать любой момент в течение дня.

Точно так же пунктуальность не считается добродетелью в Индии. Люди ценят это, но не могут ответить взаимностью.

«Марокканское время» может означать опоздание на личную встречу от часа до дня.

В Греции пунктуальность не считается такой важной, но иностранцы по-прежнему должны приходить вовремя на встречи.В социальном плане вы должны опаздывать как минимум на 30 минут.

Про казахскую пунктуальность ходит много шуток, в Казахстане даже допустимо опаздывать на свадьбу.

В русской культуре терпение считается очень важным качеством, а пунктуальность — нет. Ожидается, что вы, как иностранец, придете вовремя, но не ждете того же или извинений от своего российского коллеги.

Поделитесь или прокомментируйте эту статью:

Русский народ и национальная идентичность — Россия в глобальной политике

Поиск Все Около вопросы Аналитика События ру | en РИНЦ Scopus О журнале Информация о журнале Инструкции для авторов Фонд исследований внешней политики Авторы Совет попечителей Редакционная коллегия Совет консультантов Редакция Реклама Архивы Предыдущие выпуски Текущий номер

Лекция 5.Системы баз данных.

Цель: предоставить обзор систем управления базами данных (СУБД) и представить одну из СУБД: SQL

План:

1. Основы систем баз данных: понятие, характеристика, архитектура. Модели данных. Нормализация. Ограничение целостности данных. Настройка запросов и их обработка.

2. Основы SQL. Параллельная обработка данных и их восстановление.

3. Проектирование и разработка баз данных.Технология программирования ORM. Распределенные, параллельные и гетерогенные базы данных.

Введение в базы данных. База данных — это структурированный набор записей или данных. Компьютерная база данных — это разновидность программного обеспечения для организации хранения данных. Базы данных помогают вам организовать эту связанную информацию логическим образом для облегчения доступа и поиска.Для разработки базы данных используется несколько моделей, таких как иерархическая модель, сетевая модель, реляционная модель, объектно-ориентированная модель и т. Д.

Иерархическая модель. В иерархической модели данные организованы в виде перевернутой древовидной структуры. Эта структура упорядочивает различные элементы данных в иерархии и помогает установить логические отношения между элементами данных нескольких файлов. Каждая единица в модели — это запись , которая также известна как узел .У каждой записи есть единственный родитель.

Рисунок 1- Иерархическая модель

Сетевая модель. Сетевая модель имеет тенденцию хранить записи со ссылками на другие записи. Каждая запись в базе данных может иметь несколько родителей, то есть отношения между элементами данных могут иметь отношения «много-много». Таким образом, эта модель является расширением иерархической структуры, допускающей отношения «многие ко многим» в древовидной структуре, допускающей наличие нескольких родителей.

Сетевая модель обеспечивает большее преимущество, чем иерархическая модель, в том, что она способствует большей гибкости и доступности данных.

Рисунок 2- Сетевая модель

Реляционная модель. Реляционная модель для управления базой данных — это модель базы данных, основанная на отношениях. Базовая структура данных реляционной модели — это таблица , в которой информация о конкретной сущности (скажем, студенте) представлена в столбцах и строках.В столбцах перечислены различные атрибутов (т.е. характеристики) объекта (например, имя студента, адрес, регистрационный _number). Строки (также называемые записями) представляют экземпляров объекта (например, конкретного студента).

Объектно-ориентированная модель. В этой модели мы должны обсудить функциональность объектно-ориентированного программирования. Это требует большего, чем просто хранение объектов языка программирования. Он обеспечивает полнофункциональные возможности программирования баз данных, в то же время обеспечивая совместимость с родным языком.Он добавляет функциональность базы данных в языки объектного программирования. Этот подход аналогичен разработке приложений и баз данных в постоянной модели данных и языковой среде. Приложениям требуется меньше кода, используется более естественное моделирование данных, а базы кода легче поддерживать. Разработчики объектов могут писать полные приложения для баз данных с приличным количеством дополнительных усилий. Но разработка объектно-ориентированных баз данных обходится дороже.

Система управления базами данных. Система управления базами данных (СУБД) — это компьютерное программное обеспечение, предназначенное для управления базами данных на основе различных моделей данных. СУБД — это сложный набор программ, которые контролируют организацию, хранение, управление и поиск данных в базе данных. СУБД классифицируются в соответствии с их структурами данных или типами, иногда СУБД также называют диспетчером баз данных. Задачи управления данными относятся к одной из четырех общих категорий, как указано ниже:

Внесение данных в базу данных.

Служебные задачи, такие как обновление данных, удаление устаревших записей и резервное копирование базы данных.

Сортировка данных: организация или перегруппировка записей базы данных.

Получение подмножеств данных.

СУБД имеет несколько преимуществ, таких как снижение избыточности и несогласованности данных, улучшенная целостность данных, улучшенная безопасность и т. Д.

Нормализация баз данных — это процесс преобразования базы данных в вид, отвечающий нормализованным формам.

Классификация ограничений целостности

В теории реляционных баз данных принято выделять четыре типа ограничений целостности:

Ограничение базы данных — это ограничение на значения, которые разрешено принимать в указанную базу данных.

Ограничение переменной отношения — это ограничение на значения, которые разрешено принимать указанной переменной отношения.

Ограничение атрибута — это ограничение на значения, которые разрешено принимать указанному атрибуту.

Ограничение типа — это не что иное, как определение большого числа значений этого типа.

Пример распространенного ограничения уровня переменной отношения — потенциальный ключ; Примером распространенного ограничения уровня базы данных является внешний ключ.

Целостность и достоверность данных в БД

Целостность БД не гарантирует достоверности (истинности) содержащейся в ней информации, но обеспечивает как минимум правдоподобие этой информации, отвергая заведомо невероятные, невозможные значения.Таким образом, не следует путать целостность (непротиворечивость) БД с истинностью БД. Истина и последовательность не одно и то же.

Достоверность (или истина) — это соответствие фактов, хранящихся в базе данных, реальному миру. Очевидно, что для определения надежности БД необходимо владение полными знаниями как о содержимом БД, так и о реальном мире. Для определения целостности БД требуется только знание содержимого БД и установленных для него правил.Поэтому СУБД не может гарантировать наличие в базе данных только истинных выражений; все, что она может сделать, — это гарантировать отсутствие каких-либо данных, вызывающих нарушение ограничений целостности (то есть гарантировать, что она не содержит данных, несовместимых с этими ограничениями).

Настройка запроса

Компонент SQL СУБД, который определяет, как реализовать навигацию по физическим структурам данных для доступа к требуемым данным, называется оптимизатором запросов (оптимизатором запросов).

Логика навигации (опция алгоритма) для доступа к требуемым данным называется способом или методом доступа (путем доступа).

Последовательность операций, выполняемых оптимизатором, которые обеспечивают выбранные пути доступа, называется планом выполнения (планом выполнения).

Процесс

, используемый оптимизатором запросов для определения пути доступа, называется настройка запроса (оптимизация запроса).

В процессе оптимизации запросов доступа для всех типов команд SQL DML определяются.Однако команда SQL SELECT представляет наибольшую сложность в решении задачи выбора способа доступа. Поэтому этот процесс обычно называют оптимизацией запроса, а не оптимизацией способов доступа к данным. Далее следует отметить, что термин «оптимизация запросов» не совсем точен в том смысле, что нет никакой гарантии, что в процессе оптимизации запроса действительно будет получен оптимальный способ доступа.

Таким образом, оптимизацию запросов можно определить как количество всех методик, которые применяются для повышения эффективности обработки запросов.

2. Основы SQL. Параллельная обработка данных и их восстановление.

Структурированный язык запросов (Structured Query Language) — стандарт взаимодействия с базой данных, поддерживаемый ANSI. Большинство твердотельных баз данных придерживаются стандарта ANSI-92. Почти каждая отдельная база данных использует некоторый уникальный набор синтаксиса, хотя очень похожий на стандарт ANSI. В большинстве случаев этот синтаксис является расширением базового стандарта, хотя бывают случаи, когда такой синтаксис приводит к разным результатам для разных баз данных.

В общих чертах «SQL база данных» — это общее название системы управления реляционными базами данных (RDMS) . Для некоторых систем, «база данных» также относится к группе таблиц, данных, конфигурационной информации, которые являются принципиально отдельной частью от других, подобных конструкций. В этом случае каждая установка SQL базы данных может состоять из нескольких баз данных. В других системах они упоминаются как таблицы.

Построение таблицы базы данных, которая состоит из столбцов , содержащих строк данных.Обычно таблицы создаются для хранения связанной информации. В одной базе данных можно создать несколько таблиц.

Каждый столбец представляет собой атрибут или набор атрибутов объектов, например идентификационные номера сотрудников, рост, цвет машин и т. Д. Часто в отношении столбца используется термин поле с указанием имени, например «в поле Имя» используемый. Поле строки — это минимальный элемент таблицы. Каждый столбец в таблице имеет определенное имя, тип данных и размер.Имена столбцов в таблице должны быть уникальными.

Каждая строка (или запись) представляет собой набор атрибутов конкретного объекта, например, строка может содержать идентификационный номер сотрудника, размер его зарплаты, год его рождения и т. Д. Строки таблиц не имеют имен. Для адресации конкретной строки пользователю необходимо указать какой-то атрибут (или набор атрибутов), уникальность которого он определяет.

Одной из основных операций, которые выполняет операция с данными, является выбор информации, хранящейся в базе данных.Для этого пользователь должен выполнить запрос (запрос).

Типы запросов данных

В SQL есть четыре основных типа запросов данных, которые относятся к так называемому языку манипуляции данными (DataManipulationLanguage или DML):

ВЫБРАТЬ для выбора строк из таблиц;

INSERT для добавления строки в таблицу;

ОБНОВЛЕНИЕ для изменения строк в таблице;

DELETE для удаления строк в таблице;

Каждый из этих запросов имеет разные операторы и функции, которые используются для выполнения некоторых действий с данными.SELECT QUERY имеет самое большое количество вариантов. Также существуют дополнительные типы запросов, используемые вместе с SELECT, типом JOIN и UNION. Но пока остановимся только на основных запросах.

Использование запроса Select для выбора необходимых данных

Для получения информации, хранящейся в базе данных, используется запрос Select. Основное действие этого запроса ограничено одной таблицей, хотя есть конструкции, обеспечивающие выбор из нескольких таблиц одновременно.Для получения всех строк данных по конкретным столбцам используется запрос такого вида:

ВЫБРАТЬ column1, column2 FROM table_name;
Также, можно получить все столбцы из таблицы, используя подстановочный знак «*»:
ВЫБРАТЬ * ИЗ имя_таблицы;
Это может быть полезно в том случае, когда вы собираетесь выбирать данные с определенным условием WHERE. Следующий запрос вернет все столбцы из всех строк, где «column1» содержит 3 значения:
ВЫБРАТЬ * ИЗ имя_таблицы ГДЕ column1 = 3;
3.Дизайн и разработка баз данных. Технология программирования ORM. Распределенные, параллельные и гетерогенные базы данных.
Проектирование баз данных Процесс создания схемы базы данных и определение необходимых ограничений целостности.
Основные задачи проектирования баз данных:
Поддержка хранения в БД всей необходимой информации.
Возможность сбора данных по всем необходимым запросам.
Сокращенное обозначение избыточности и дублирования данных.
Поддержка целостности базы данных.
Основные этапы проектирования баз данных
Эскизный проект
Концептуальный дизайн создание модели семантической области, то есть информационной модели самого высокого уровня абстракции. Такая модель создается без ориентации на какую-либо конкретную СУБД и модель данных. Термины «семантическая модель», «концептуальная модель» являются синонимами.
Конкретный тип и содержание концептуальной модели базы данных определяется формальным устройством, выбранным для этой цели.Обычно используются графические обозначения, похожие на диаграммы ER.
Чаще всего в концептуальную модель БД входят:
описание информационных объектов или концепций предметной области и связи между ними.
описание ограничений целостности, то есть требований к допустимым значениям данных и связям между ними.
Логическая схема
Логический дизайн создание схемы базы данных на основе конкретной модели данных, например, реляционной модели данных.Для реляционной модели данных логическая модель данных — это набор диаграмм отношений, обычно с указанием первичных ключей, а также «связей» между отношениями, представляющими внешние ключи.
Преобразование концептуальной модели в логическую, как правило, осуществляется по формальным правилам. Этот этап можно существенно автоматизировать.
На этапе логического проектирования рассматривается специфика конкретной модели данных, но не может быть учтена специфика конкретной СУБД.
Физическая конструкция
Физическая конструкция создание схемы базы данных для конкретной СУБД. Специфика конкретной СУБД может включать в себя ограничения на именование объектов базы данных, ограничения для поддерживаемых типов данных и т. Д. Кроме того, специфика конкретной СУБД в случае физической конструкции включает выбор решений, связанных с физическим носителем хранения данных (выбор методов управления дисковой памятью, разделения БД по файлам и устройствам, методов доступа к данным), создания индексов и т. д.
Что такое ORM?
ORM или Объектно-реляционное отображение — это технология программирования, которая позволяет преобразовывать несовместимые типы моделей в ООП, в частности, между хранилищем данных и предметами программирования. ORM используется для упрощения процесса сохранения объектов в реляционной базе данных и их извлечения, при этом ORM сам заботится о преобразовании данных между двумя несовместимыми состояниями. Большинство инструментов ORM в значительной степени полагаются на метаданные базы данных и объектов, поэтому объектам не нужно ничего знать о структуре базы данных, а базе данных ничего не знать о том, как данные организованы в приложении.ORM обеспечивает полное разделение задач на хорошо запрограммированные приложения, в случае которых и база данных, и приложение могут работать с данными каждая в корневой форме.
Fugure3- Работа ОРМ

:
Мировая статистика пользователей Интернета и статистика мирового населения за 2020 год
МИРОВОЕ ИСПОЛЬЗОВАНИЕ ИНТЕРНЕТА И СТАТИСТИКА НАСЕЛЕНИЯ
Оценка за третий квартал 2020 г.
Мир Регионы
Население
(Оценка 2020 г.)
Население
% Мира
Интернет-пользователи
30 сен 2020
Проникновение
Рейтинг (% населения)
Рост
2000-2020
Интернет
Весь мир%
Африка
1,340,598,447
17.2%
631 940 772
47,1%
13 898%
12,8%
Азия
4 294 516 659
55,1%
2,555,636,255
59.5%
2136%
51,8%
Европа
834,995,197
10,7%
727 848 547
87,2%
593%
14.8%
Латиница Америка / Карибский бассейн
654,287,232
8,4%
467,817,332
71,5%
2,489%
9,5%
Средний Восток
260,991,690
3.3%
184,856,813
70,8%
5 527%
3,7%
Север Америка
368 869 647
4,7%
332 908 868
90.3%
208%
6,8%
Океания / Австралия
42,690,838
0,5%
28 917 600
67,7%
279%
0.6%
МИР ИТОГО
7,796,949,710
100,0%
4,929,926,187
63,2%
1,266%
100,0%
ПРИМЕЧАНИЯ. (1) Оценки статистики использования Интернета и мирового населения приведены для 20 октября 2020 года.(2) НАЖМИТЕ на название каждого региона мира для получения подробной информации об использовании в регионе. (3) Демографические данные (численность населения) основаны на данных Отдела народонаселения ООН. (4) Информация об использовании Интернета взята из данных, опубликованных Nielsen. В Интернете Международный Союз Телекоммуникаций, по GfK, местными регуляторами ИКТ и другие надежные источники. (5) Определения, справка по навигации и заявления об отказе от ответственности: пожалуйста, обратитесь к Руководству по просмотру веб-сайтов.(6) Информация с этого сайта может быть цитирована, отдав должное и разместив обратную ссылку на www.internetworldstats.com. Авторские права © 2020, Маркетинговая группа Miniwatts. Все права защищены по всему миру.
ВТО | Понимание WTO
вверх
Торговля без дискриминации
1. Режим наибольшего благоприятствования (НБН): равное отношение к другим людям Согласно соглашениям ВТО, страны обычно не могут проводить различия между своими торговыми партнерами.Окажите кому-то особую услугу (например, более низкую ставку таможенной пошлины на один из его товаров), и вы должны сделать то же самое для всех остальных членов ВТО.
Этот принцип известен как принцип наибольшего благоприятствования. (MFN) ( см. Вставку ). Это настолько важен, что это первая статья Общего Соглашение о тарифах и торговле (ГАТТ), регулирующее торговлю товарами. НБН также является приоритетом в Генеральном соглашении по торговле услугами. (GATS) (статья 2) и Соглашение по торговым аспектам интеллектуальной Права собственности (TRIPS) (Статья 4), хотя в каждом соглашении принцип трактуется несколько иначе.Вместе эти три соглашения охватывают все три основные области торговли, которыми занимается ВТО.
Допускаются некоторые исключения. Например, страны могут заключить соглашение о свободной торговле, которое распространяется только на товары, которыми торгуют внутри группы. дискриминация товаров извне. Или они могут предоставить развивающимся странам особый доступ к своим рынкам. Или страна может установить барьеры против товаров, которые считаются несправедливыми по продаже из определенных стран.А в сфере услуг странам разрешено в определенных обстоятельствах проводить дискриминацию. Но соглашения допускают эти исключения только при строгих условиях. В целом, режим наибольшего благоприятствования означает, что каждый раз, когда страна снижает торговый барьер или открывает рынок, она должна делать это для одних и тех же товаров или услуг от всех своих торговых партнеров. будь то богатый или бедный, слабый или сильный.
2. Национальный режим: равное отношение к иностранцам и местным жителям Импортеры и товары местного производства должны рассматриваться одинаково, по крайней мере, после на рынок вышли иностранные товары.То же самое должно относиться к иностранные и внутренние услуги, а также иностранные и местные торговые марки, авторские права и патенты. Этот принцип национального режима (дающий с другими такое же обращение, что и со своими гражданами) также встречается во всех три основных соглашения ВТО (статья 3 ГАТТ, Статья 17 GATS и статья 3 TRIPS), хотя, опять же, в каждый из них.
Национальный режим применяется только после того, как продукт, услуга или объект интеллектуальной собственности вышли на рынок. Таким образом, взимание таможенной пошлины с импорта не является нарушением национального режима, даже если с продукции местного производства не взимается эквивалентный налог.
вернуться наверх
Свободная торговля: постепенно, договорная
Снижение торговых барьеров — одно из самых очевидных средств поощрения торговли.Соответствующие барьеры включают таможенные пошлины (или тарифы) и такие меры, как запреты на импорт или квоты, которые выборочно ограничивают количество. Время от времени обсуждаются и другие вопросы, такие как бюрократизм и политика обменного курса.
С момента создания ГАТТ в 1947-48 годах было проведено восемь раундов торговых переговоров. Сейчас идет девятый раунд в рамках Дохинской повестки дня в области развития. Сначала они были направлены на снижение тарифов (таможенных пошлин) на импортные товары. В результате переговоров индустриальный тарифные ставки стран на промышленные товары неуклонно снижались до менее 4%.
Но к 1980-м годам переговоры расширились, охватив нетарифные барьеры на товары и новые области, такие как услуги и интеллектуальная собственность.
Открытие рынков может быть полезным, но также требует корректировки. Соглашения ВТО позволяют странам вносить изменения постепенно, через прогрессивная либерализация. Развивающимся странам обычно дается больше времени на выполнение своих обязательств.
вернуться наверх
Предсказуемость: через переплет и прозрачность
Иногда обещание не повышать торговый барьер может быть так же важно, как его снижение, потому что обещание дает предприятиям более четкое представление об их будущих возможностях.Благодаря стабильности и предсказуемости поощряются инвестиции, создаются рабочие места, и потребители могут в полной мере пользоваться преимуществами конкуренции. выбор и более низкие цены. Многосторонняя торговая система — это попытка правительств сделать бизнес-среду стабильной и предсказуемой.
Уругвайский раунд, усиленные крепления
Процент тарифов, связанных до и после 1986-94 переговоры
Перед
После
Развитые страны
78
99
Развивающиеся страны
21
73
Страны с переходной экономикой
73
98
(Это тарифные позиции, поэтому процентные ставки не взвешиваются в соответствии с объемом торговли или стоимостью)
В ВТО, когда страны соглашаются открыть свои рынки для товаров или услуг, они связывать свои обязательства.Для товаров эти привязки представляют собой ограничения по ставкам таможенных тарифов. Иногда страны облагают импорт налогами по ставкам ниже связанных ставок. Часто это имеет место в развивающихся странах. В развитых странах фактически взимаемые и связанные ставки, как правило, совпадают.
Страна может изменить свои привязки, но только после переговоров со своими торговыми партнерами, что может означать компенсацию им потерь в торговле. Одним из достижений Уругвайского раунда многосторонних торговых переговоров было увеличение объема торговли в рамках связывающих обязательств. ( см. Таблицу ).В сельском хозяйстве 100% продуктов теперь имеют связанные тарифы. Результат всего этого: существенно более высокая степень безопасности рынка для трейдеров и инвесторов.
Система пытается улучшить предсказуемость и стабильность и другими способами. Один из способов — воспрепятствовать использованию квот и других мер, используемых для установления ограничений на количество импорта. введение квот может привести к еще большей бюрократии и обвинениям в нечестной игре. Другой — сделать правила торговли стран как можно более четкие и публичные (прозрачные).Многие соглашения ВТО требуют, чтобы правительства раскрывали свою политику и практику публично внутри страны или путем уведомления ВТО. Регулярный надзор за национальной торговой политикой через Механизм обзора торговой политики обеспечивает дополнительное средство поощрения прозрачности как на внутреннем, так и на многостороннем уровне.
вернуться наверх
Содействие честной конкуренции
ВТО иногда называют институт свободной торговли, но это не совсем так.Система допускает тарифы и, в некоторых случаях, другие формы защиты. Точнее, это система правил, посвященная открытой, честной и неискаженной конкуренции.
Правила о недискриминации НБН и национального режима предназначены для обеспечения справедливых условий торговли. То же самое и с теми, кто пользуется демпингом (экспорт по цене ниже себестоимости для увеличения доли рынка) и субсидиями. Вопросы сложны, и правила пытаются установить, что является справедливым, а что несправедливым, и как правительства могут реагировать, в частности, взимая дополнительные импортные пошлины, рассчитанные для компенсации ущерба, причиненного несправедливой торговлей.
Многие другие соглашения ВТО направлены на поддержку честной конкуренции: например, в сельском хозяйстве, интеллектуальной собственности, услугах. Соглашение о государственных закупках (a плюрилатеральное соглашение, поскольку оно подписано всего несколькими членами ВТО) распространяет правила конкуренции на закупки тысяч государственных организаций во многих странах. И так далее.
вернуться наверх
Поощрение развития и экономическая реформа
Система ВТО способствует развитию.С другой стороны, развивающимся странам необходима гибкость в отношении времени, необходимого для реализации системные соглашения. А сами соглашения наследуют более ранние положения ГАТТ, которые допускают особую помощь и торговые уступки для развивающихся стран.
Более трех четвертей членов ВТО — развивающиеся страны и страны с переходной экономикой. В течение семи с половиной лет Уругвайского раунда более 60 из этих стран самостоятельно реализовали программы либерализации торговли.В то же время развивающиеся страны и страны с переходной экономикой были гораздо более активными и влиятельными в переговорах Уругвайского раунда, чем в любом предыдущем раунде, и тем более в нынешней Дохинской повестке дня в области развития.
По окончании Уругвайского раунда развивающиеся страны были готовы взять на себя большую часть обязательств, которые требуются от развитых стран. Но соглашения давали им переходные периоды для адаптации к более незнакомым и, возможно, сложным положениям ВТО. особенно это касается беднейших, наименее развитых стран.В решении, принятом на уровне министров в конце раунда, говорится, что более благополучные страны должны ускорить выполнение обязательств по доступу на рынок для товаров, экспортируемых наименее развитыми странами, и требует увеличения технической помощи для них.

	Перед	После
Развитые страны	78	99
Развивающиеся страны	21	73
Страны с переходной экономикой	73	98

Системы счисления разных народов

3.2 Римская пятеричная

3.3 Древнегреческая аттическая пятеричная

3.<img src='/800/600/https/ds04.infourok.ru/uploads/ex/0784/0001056b-79750acc/3/img13.jpg' /> 4 Древнегреческая ионийская десятеричная алфавитная

3.5 Славянская глаголическая десятеричная

3.6 Славянская кириллическая десятеричная алфавитная

3.7 Древнеиндийские системы счисления

Проектная работа «Обозначение цифр у разных народов»

История возникновения цифр — древние числа и цифры Руси, Рима, Китая, Египта, Вавилона и Греции

Как мир учился считать

Достижение Вавилона

История цифр разных народов

Цифры древней Греции

Числа древнего Рима

Цифры древнего Китая

Числа в древней Руси

Древнеиндийские цифры

Самые распространенные системы счисления

«Биография» арабской цифры

История цифры 1.<img src='/800/600/https/ds04.infourok.ru/uploads/ex/0c83/000319c2-ddd9b48f/13/hello_html_m7c6eaea0.jpg' />

История цифры 2

История цифры 3

История цифры 4

История цифры 5

История цифры 6

История цифры 7

История цифры 8

История цифры 9

Древние цифры.<img src='/800/600/https/image1.slideserve.com/3442685/slide17-l.jpg' /> Самые старые системы счисления

Древние цифры

Двенадцатеричная система счисления

Шестидесятеричная система счисления

Двадцатеричная система счисления

Десятичная система

ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ | Энциклопедия Кругосвет

ОБОЗНАЧЕНИЯ ЧИСЕЛ

Древний Египет.

Вавилон.

Древняя Греция.

Рим.

Обозначения чисел у древних евреев.

Америка.

Китай.

Индия.

Аравия.

Западная Европа.

ДВОИЧНАЯ СИСТЕМА

ДВЕНАДЦАТИРИЧНАЯ И ВОСЬМЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ

Системы счисления: Какие бывают системы счисления

Какие бывают системы счисления

[править]Факториальная система счисления

[править]Фибоначчиева система счисления

[править]Непозиционные системы счисления

[править]Биномиальная система счисления

[править]

[править]Система счисления Штерна–Броко

[править]Системы счисления разных народов

[править]Единичная система счисления

[править]Древнеегипетская система счисления

[править]Вавилонская система счисления

[править]Алфавитные системы счисления

[править]Еврейская система счисления

[править]

[править]Римская система счисления

[править]Система счисления майя

[править]

Как разные страны мира ценят пунктуальность

Опоздать на полчаса в Греции, но вовремя в Японии: как разные страны по всему миру ценят пунктуальность

Поделитесь или прокомментируйте эту статью:

Русский народ и национальная идентичность — Россия в глобальной политике

Лекция 5.Системы баз данных.

:

Мировая статистика пользователей Интернета и статистика мирового населения за 2020 год

ВТО | Понимание WTO

Торговля без дискриминации

Свободная торговля: постепенно, договорная

Предсказуемость: через переплет и прозрачность

Содействие честной конкуренции

Поощрение развития и экономическая реформа

Добавить комментарий Отменить ответ

3. 4 Древнегреческая ионийская десятеричная алфавитная

История цифры 1.

Древние цифры. Самые старые системы счисления