Шестнадцатеричные числа | это… Что такое Шестнадцатеричные числа?
ТолкованиеПеревод
- Шестнадцатеричные числа
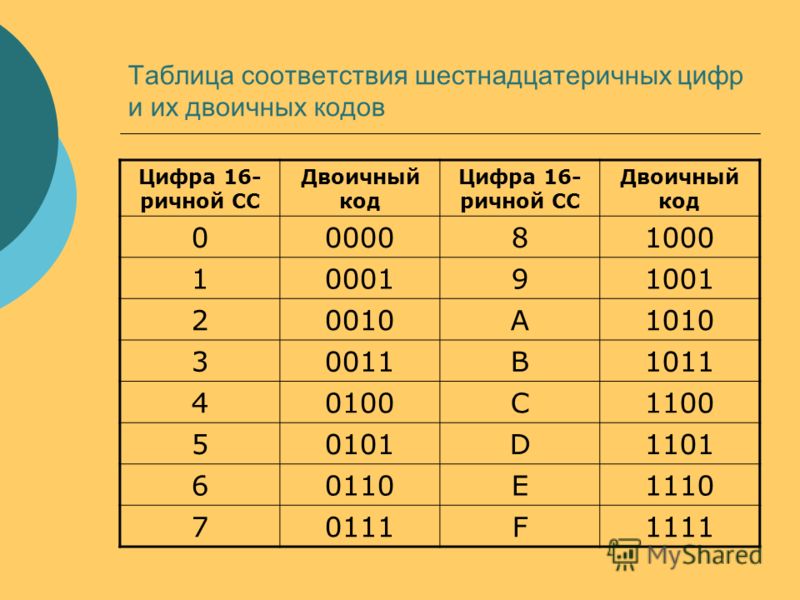
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См.
 также
также - 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа.
 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510) - Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Игры ⚽ Нужно сделать НИР?
- Шестнадцатиричная система счисления
- Шестнадцать
Полезное
Шестнадцатеричные числа | это… Что такое Шестнадцатеричные числа?
ТолкованиеПеревод
- Шестнадцатеричные числа
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.

Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 144310 или как 5A3 16.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.
 д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3. - Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Игры ⚽ Нужно сделать НИР?
- Шестнадцатиричная система счисления
- Шестнадцать
Полезное
Шестнадцатеричный — SparkFun Learn
- Главная
- Учебники
- Шестнадцатеричный
≡ Страниц
Авторы: Джимблом
Избранное Любимый 32
Вы когда-нибудь чувствовали себя скованно, составляя числа всего из 10 цифр? Или хотели представить большие числа с меньшим количеством цифр? Или легко идентифицировать значения байтов, не глядя на гипнотическую бинарную строку из 1 и 0? Для подобных приложений шестнадцатеричная система часто становится предпочитаемой инженером системой счисления.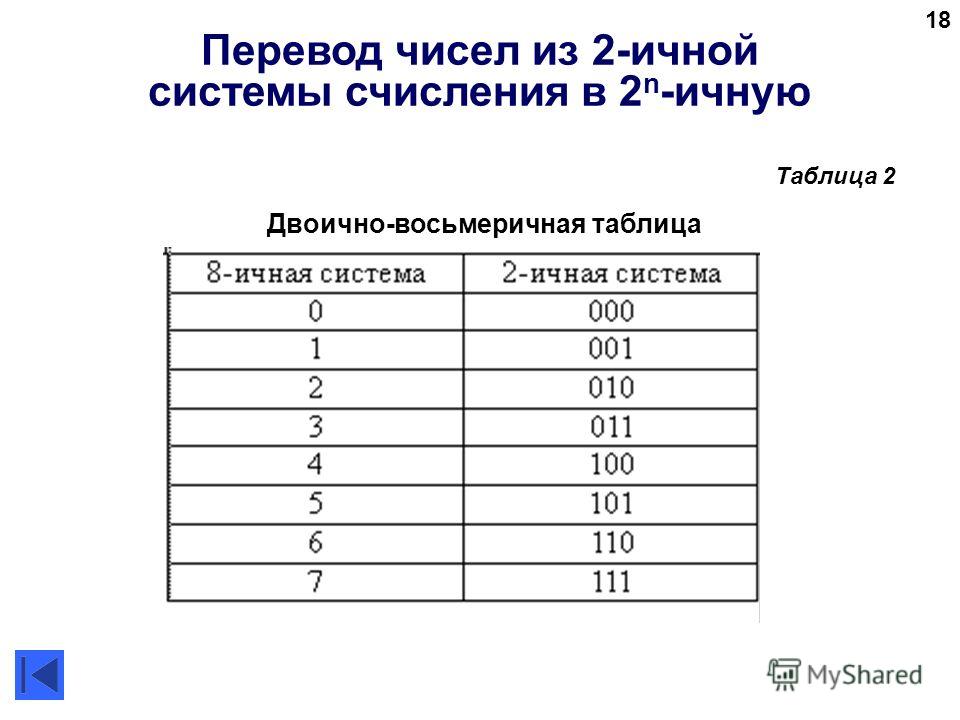
Как только вы разберетесь с шестнадцатеричным кодом, следующим шагом будет декодирование матрицы!
Шестнадцатеричное число — также известное как hex или base 16 — это система, которую мы можем использовать для записи и обмена числовыми значениями. В этом смысле она ничем не отличается от самой известной из систем счисления (той, которую мы используем каждый день): десятичной. Десятичная система счисления — это система счисления с основанием 10 (идеально подходит для существ с 10 пальцами), в ней используется набор из 10 уникальных цифр, которые можно комбинировать для позиционного представления чисел.
Шестнадцатеричный, как и десятичный, объединяет набор цифр для создания больших чисел. Так уж получилось, что hex использует набор из 16 уникальных цифр . Hex использует стандартные числа 0-9, но также включает шесть цифр, которые вы обычно не ожидаете увидеть при создании чисел: A, B, C, D, E и F.
Существует множество (бесконечное!) других систем счисления. там. Двоичный (с основанием 2) также популярен в инженерном мире, потому что это язык компьютеров. Двоичная система с основанием 2 использует только двухзначные значения (0 и 1) для представления чисел.
Hex, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как работает шестнадцатеричный формат, потому что во многих случаях имеет смысл представлять число в шестнадцатеричной системе счисления, а не в двоичной или десятичной.
Описано в этом руководстве
В этом руководстве рассматриваются все, что связано с шестнадцатеричными числами, с которыми вы можете столкнуться в электронике или программировании. Он разделен на следующие разделы:
- Hex Basics — Обзор шестнадцатеричного кода. На этой странице рассказывается о 16 шестнадцатеричных цифрах, о том, как мы представляем шестнадцатеричные числа и как считать в шестнадцатеричном формате.

- Преобразование в/из десятичного числа — На этой странице описаны наши предпочтительные методы преобразования между шестнадцатеричным и десятичным числом.
- Преобразование в/из двоичного файла — На этой странице показано, как можно преобразовать двоичный файл в шестнадцатеричный.
- Калькуляторы преобразования — Здесь вы найдете простой автоматический калькулятор для переключения между шестнадцатеричным, двоичным и десятичным форматами.
Рекомендуемая литература
Прежде чем углубляться в этот учебник, вы должны кое-что знать о десятичных числах. Помните длинное деление? Остатки? Коэффициенты? Продукты? Суммы? Экспоненты? Все это вернется, чтобы преследовать вас, когда вы узнаете о шестнадцатеричной системе счисления и ее связи с десятичной.
Помимо освежения арифметики, мы рекомендуем прочитать наш учебник по двоичным кодам перед этим (или параллельно с ним).
Посмотреть как одну страницу
Следующая страница →
Шестнадцатеричные основы
Компьютерные системы счисления 101: Двоичные и шестнадцатеричные преобразования
Главная/Блог/Компьютерные системы счисления 101: Двоичные и шестнадцатеричные преобразования
01 октября 2020 г. — 8 мин чтения
— 8 мин чтения
Аманда Фосетт
Когда мы печатаем слова на компьютере, он переведет их в числа. На самом деле для компьютера вся информация записывается в виде последовательности единиц и нулей. Компьютерные системы счисления — это то, как мы представляем числа в архитектуре компьютерной системы.
Системы счисления — одна из самых фундаментальных концепций, которую должны изучить компьютерщики. Это важный шаг для всех, кто хочет стать компьютерщиком или программистом.
Сегодня мы познакомим вас с системами счисления, которые необходимы для компьютерного ученого. Мы углубимся в двоичную и шестнадцатеричную системы счисления.
Сегодня мы узнаем:
- Что такое система счисления в информатике?
- Что такое двоичная система счисления?
- Что такое шестнадцатеричная система счисления?
- Как преобразовать между двоичным и шестнадцатеричным
- Что такое восьмеричная система счисления?
- Что узнать дальше
Что такое система счисления в информатике?
Люди давно умеют считать. Для этого мы используем системы, которые связывают уникальные символы с конкретными значениями. Это называется системой счисления , и это метод, который мы используем для представления чисел и манипулирования ими 9.0011
Для этого мы используем системы, которые связывают уникальные символы с конкретными значениями. Это называется системой счисления , и это метод, который мы используем для представления чисел и манипулирования ими 9.0011
Система счисления должна иметь уникальные символы для каждого значения, быть последовательной, предоставлять сопоставимые значения и быть легко воспроизводимой.
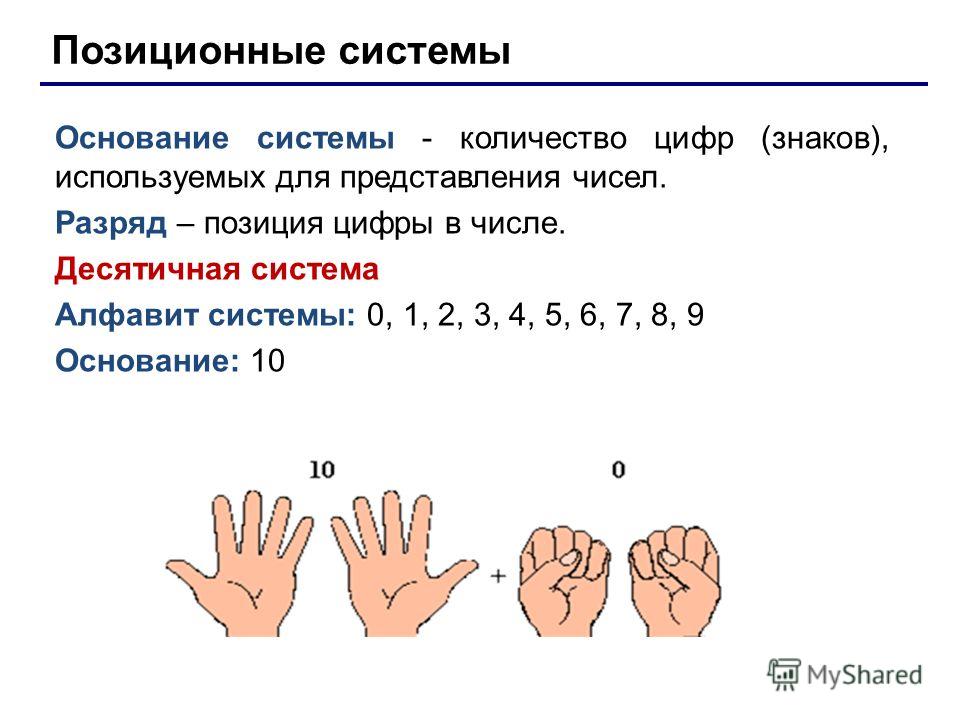
Вероятно, вы больше всего знакомы с десятичной системой , которая лежит в основе того, как люди считают. Десятичная система имеет основание 10 , потому что она предоставляет 10 символов для представления всех чисел:
Люди используют десятичную систему, потому что у нас есть 10 пальцев, чтобы считать, но машины не могут позволить себе такую роскошь. Итак, мы создали другие системы счисления, выполняющие те же функции. Компьютеры представляют информацию не так, как люди, поэтому нам нужны разные системы для представления чисел.
Компьютеры поддерживают следующие системы счисления:
- Двоичная
- Восьмеричный
- Десятичный
- Шестнадцатеричный
Знакомство с двоичной системой счисления
Компьютер использует бита для представления информации. Бит — это самая основная единица хранения данных в компьютере. Важный компонент компьютеров называется транзистор . Подобно выключателю света, транзистор либо позволяет, либо предотвращает протекание тока. Итак, у него всего два состояния: на и на .
Каждое число в компьютере представляет собой электрический сигнал. На заре компьютеров электрические сигналы представлялись в состоянии «включено» (отрицательный заряд) и в состоянии «выключено» (положительный заряд). Это формирует своего рода двоичный переключатель.
Эти два состояния могут быть представлены одним из двух символов: 1 и 0 . Это означает, что двоичная система счисления имеет основание 2. Для представления каждого числа нужны только символы.
Это означает, что двоичная система счисления имеет основание 2. Для представления каждого числа нужны только символы.
Базовые цифры для двоичной системы просты: 0 соответствует низкому уровню, а 1 соответствует высокому уровню.
Вместо того, чтобы представлять числа как отдельные единицы (например, число 10 или 400), мы используем группы единиц и нулей. Например, вот как это выглядит, когда компьютер считает от 0 до 10:
Это называется двоичной системой счисления. Каждая двоичная цифра обозначается как бит . Например, 011001100110 состоит из 4 битов: 000, 111, 111 и 000. Когда дело доходит до размещения значений битов (то есть цифр) в этой системе, мы размещаем значения, соответствующие возрастающим степеням числа 2, справа налево. левый.
Крайний правый бит называется младшим битом (LSB) , а крайний левый бит — старшим битом (MSB) .
Вы можете манипулировать битами слева и справа с помощью побитовых операторов для эффективного изменения значения числа на уровне машинного кода.
Преобразование между десятичной и двоичной
Теперь, когда мы знаем основы двоичной системы, давайте узнаем, как мы будем преобразовывать десятичную в двоичную. Начнем с преобразования двоичного кода в десятичный.
Мы знаем, что в двоичной системе есть разрядные значения степеней двойки. Эти значения являются весами цифр (0 или 1) в этих разрядах. Вот как это работает:
- Умножаем каждую цифру на ее вес (ее положение умножается на 2)
- Суммируем их все, чтобы получить десятичное число
Итак, возьмем двоичное число 11111010 и переведем его в десятичную систему счисления.
1 из 4
1 из 4
1 из 4
1 из 4
А теперь попробуем наоборот. Как преобразовать десятичное число в двоичное? Одним из способов сделать это является повторное деление, которое является удобным сокращением.
Итак, возьмем число 19. Начнем с деления его на два и записи остатка. Когда мы делим 19 на 2, мы получаем 9 с остатком 1.
Начнем с деления его на два и записи остатка. Когда мы делим 19 на 2, мы получаем 9 с остатком 1.
Затем мы берем 9 и делим его на 2, что дает нам результат 4 с остатком 1. Этот процесс продолжается до тех пор, пока мы не достигнем нуля. Остатки, которые мы собрали, образуют наше двоичное число!
Многократное деление на 2 и отслеживание остатков — это быстрый способ преобразования десятичной дроби в двоичную!
Попробуйте сами!
Каково двоичное представление числа 94?
A)
1001110
B)
0111101
C)
1011110
Вопрос
1
из
20
1
из
20
1
из
20
1
из
20
1
из
20
1
из
20
. 0099
0099
Теперь, когда мы немного узнали о двоичной системе, давайте узнаем о другой распространенной системе, используемой компьютерами: , шестнадцатеричной системе счисления .
Двоичные числа просты для компьютеров, но не так просты для понимания людьми. А когда вы работаете с большими числами, становится трудно писать без ошибок. Итак, чтобы решить эту проблему, мы можем организовать двоичные числа в группы по четыре бита, образуя шестнадцатеричную систему счисления.
Шестнадцатеричная система представляет собой более компактный способ представления чисел на компьютере, поскольку для представления значения цифры требуется всего 4 бита.
Шестнадцатеричная система (часто называемая «шестнадцатеричной») состоит из 16 символов , поэтому ее основание равно 16. Шестнадцатеричная система использует 10 чисел десятичной системы и шесть дополнительных символов, A, B, C, D , E и F.
Значения разрядов в шестнадцатеричном формате представляют собой степени 16. Давайте посмотрим, каким будет шестнадцатеричное число XYZ в десятичном виде. Как вы можете видеть ниже, шестнадцатеричным числам предшествует #, чтобы указать, что они имеют основание 16.
Давайте посмотрим, каким будет шестнадцатеричное число XYZ в десятичном виде. Как вы можете видеть ниже, шестнадцатеричным числам предшествует #, чтобы указать, что они имеют основание 16.
Как преобразовать двоичное число в шестнадцатеричное
Теперь, когда мы понимаем как двоичную, так и шестнадцатеричную системы счисления, давайте узнаем, как преобразовать двоичное число в шестнадцатеричное число. Начнем с двоичного в шестнадцатеричный.
Мы сгруппируем двоичные цифры в наборы по четыре (начиная справа). Затем мы заменяем каждый квартет соответствующим шестнадцатеричным представлением.
1 из 4
1 из 4
1 из 4
1 из 4
Теперь шестнадцатеричный код в двоичный! Давайте рассмотрим пример. Ниже мы расширяем каждую шестнадцатеричную цифру, заменяя ее эквивалентным двоичным квартетом.
1 из 3
1 из 3
1 из 3
Что такое восьмеричная система счисления?
Восьмеричная система счисления не так широко используется, как шестнадцатеричная или двоичная. Она была разработана с той же идеей, что и шестнадцатеричная система: сделать двоичную систему более компактной.
Она была разработана с той же идеей, что и шестнадцатеричная система: сделать двоичную систему более компактной.
Мы используем восемь основных символов для восьмеричной системы, которые заимствованы из десятичной системы. Двоичные триплеты могут иметь значения в диапазоне от 0–70 до 70–7.
Таким образом, разрядность будет возрастать в степени 888 справа налево.
Чтобы преобразовать из двоичного числа в восьмеричное , мы следуем этой базовой методике:
- Группируем двоичное число в наборы по три (аналогично тому, что мы делали с шестнадцатеричным)
- Довести каждую группу цифр до числа, кратного трем, путем добавления нулей
- Напишите соответствующий восьмеричный символ под каждой группой
- Теперь у вас будет восьмеричное число .
Преобразование восьмеричного числа в двоичное число аналогично, но немного проще:
- Запишите двоичное представление для каждой восьмеричной цифры
- Соедините эти числа вместе
- У вас не будет двоичного числа
НАПИСАЛ Аманда Фосетт
Присоединяйтесь к сообществу, насчитывающему более 1,4 миллиона читателей.
 также
также