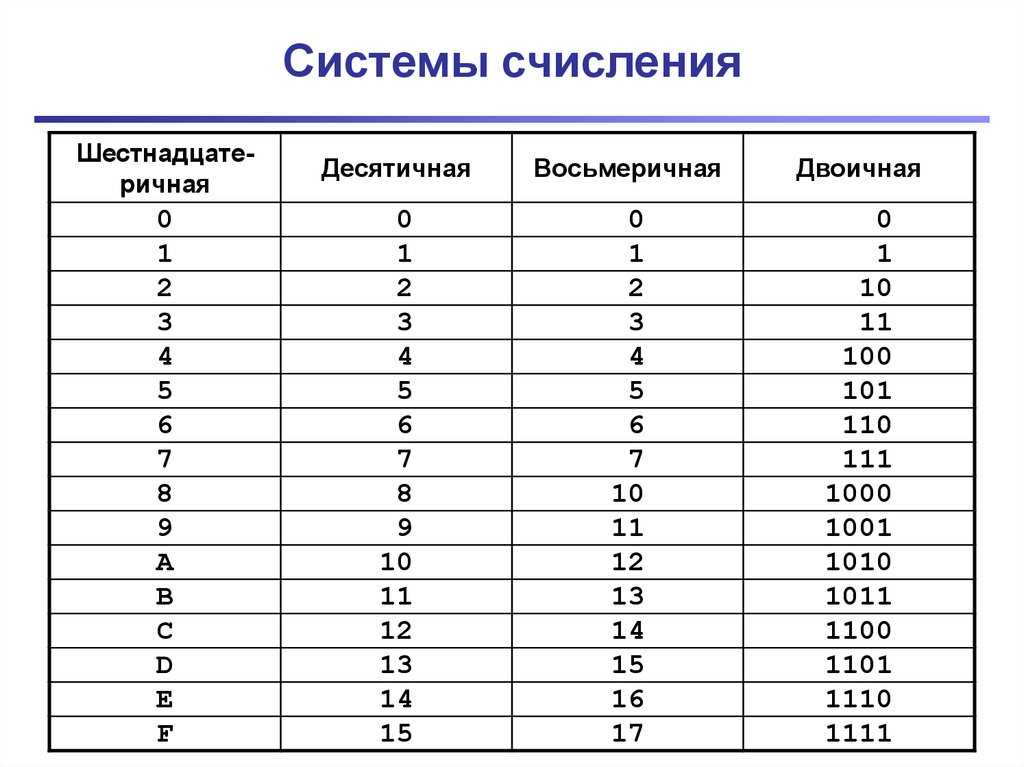
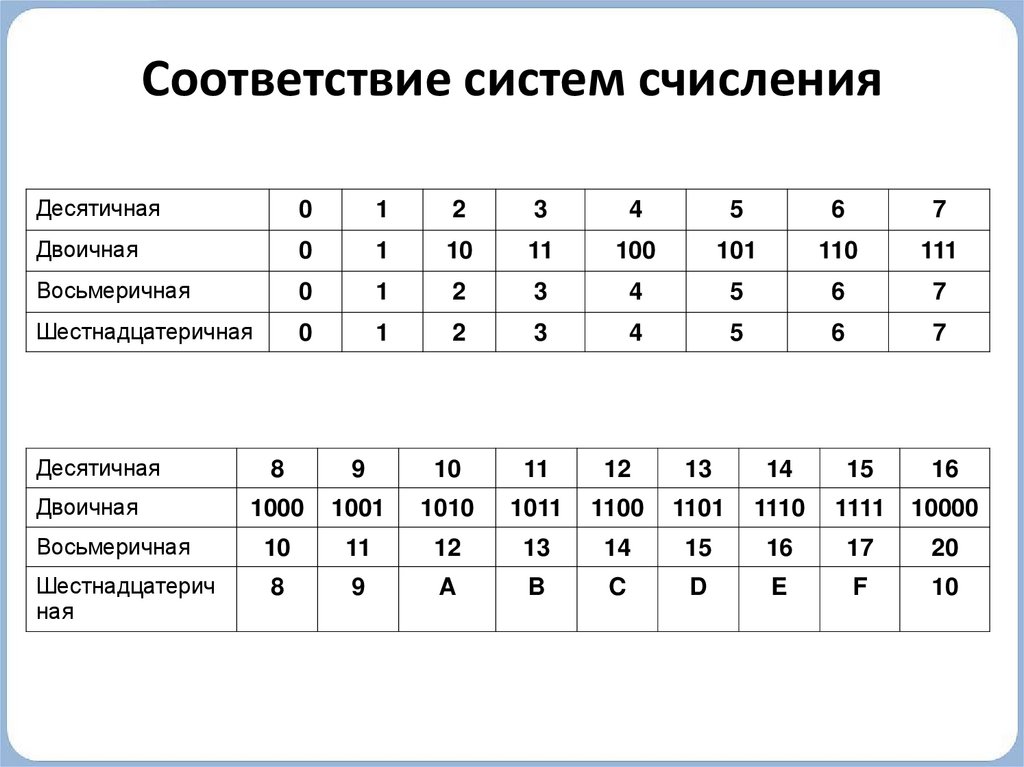
Шестнадцатиричная система счисления. Таблица для сложения и вычитания чисел в шестнадцатиричной системе счисления используется также, как и таблицы для двоичной и восьмиричной систем счисления.
Таблица 4
0 1 2 3 4 5 6 7 8 9 A B C D E F
00 1 2 3 4 5 6 7 8 9 A B C D E F
1 1 2 3 4 5 6 7 8 9 A B C D E F 10
2 2 3 4 5 6 7 8 9 A B C D E F 10 11
3 3 4 5 6 7 8 9 A B C D E F 10 11 12
4 4 5 6 7 8 9 A B C D E F 10 11 12 13
5 5 6 7 8 9 A B C D E F 10 11 12 13 14
6 6 7 8 9 A B C D E F 10 11 12 13 14 15
7 7 8 9 A B C D E F 10 11 12 13 14 15 16
8 8 9 A B C D E F 10 11 12 13 14 15 16 17
9 9 A B C D E F 10 11 12 13 14 15 16 17 18
A A B C D E F 10 11 12 13 14 15 16 17 18 19
B B C D E F 10 11 12 13 14 15 16 17 18 19 1A
C C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B
D D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C
E E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D
F F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E
Пример:
9 + В = 14 1A – F = B
Алгоритм
операции деление:
С=А:В.
Операция деления выполняется с использованием правил десятичного деления с помощью методов умножения и вычитания.
Сначала делаем сдвиг делителя к старшему разряду делимого на n разрядов. Потом от делимого отнимаем сдвигаемый делитель до тех пор, пока остаток будет меньше, чем сдвигаемый делитель. Цифра частного определяется количеством вычитаний сдвигаемого делителя.
Остаток сдвигается на один разряд влево и определяется следующая цифра частного. Количество разрядов целой части частного на 1 больше количества сдвигов разрядов делимого, то есть n+1.
Пример:
256 (10)| 2 Делитель = 002; n = 2;
— 200 1 2 8 Сдвигаемый делитель = 200;
56 Количество разрядов целой части частного = 3.
560
-400
160
1600
-1600
0000
2.
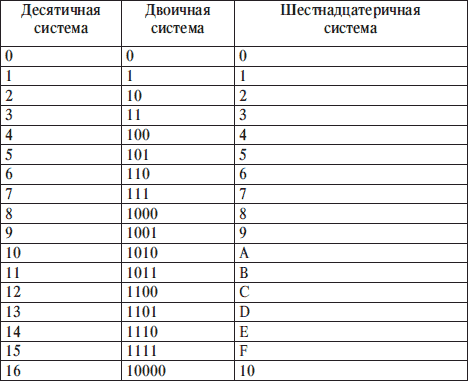 4. Представление чисел в эвм
4. Представление чисел в эвмВ зависимости от способа представления в них чисел машины делятся на машины с фиксированной запятой и машины с плавающей запятой.
В машинах с фиксированной запятой применяется естественная форма записи чисел: число представляется в виде последовательности цифр, разделенной на целую и дробную часть.
Ячейка памяти такой машины состоит из знакового разряда и цифровых разрядов. Постоянное количество числовых разрядов отведено для хранения целой части числа, остальные цифровые разряды предназначены для изображения ее целой части.
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
знак | Целая часть | Дробная часть | |||||||||||||
Название «машина
с плавающей запятой (точкой)» происходит
от того, что при записи чисел в ячейках
запятая помещается (с помощью записи в
указателе положения запятой) после
любого цифрового разряда ячейки.
При этом используются числа в так называемой нормализованной форме.Числа с плавающей запятой представляются в ЭВМ по формуле:
А = М*q p,
где М ‑ мантисса;
q ‑ основание системы счисление;
р ‑ порядок числа.
Мантисса числа ограничена диапазоном
q –1< |M| < 1.
Мантисса
нормализуется таким образом, чтобы
первой цифрой после запятой была
значащая цифра, а не нуль. Если
после вычисления мантисса имеет в
старших разрядах нули, то она при
нормализации сдвигается влево на
количество нулевых разрядов и при этом
порядок уменьшается на столько же
единиц, сколько сдвигов влево было
в мантиссе. Например, отобразим число
А =
-13,75
-13,75 (10) = -1101,11 (2) = -D,C (16) = -DC*16 1
При этом: М = -0,DC00 (16) = -0,1101 1100 0000 0000 (2)
В
современных ЭВМ используется не порядок,
а характеристика (Х),
которая более
порядка
на 64 единицы.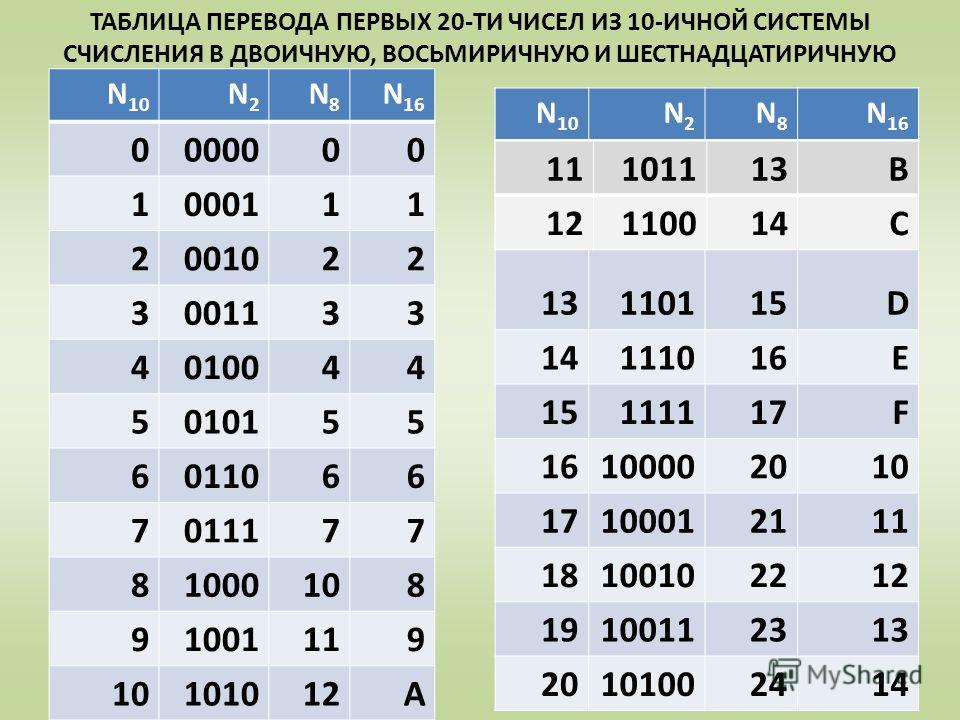 Таким образом, характеристика числа
будет:
Таким образом, характеристика числа
будет:
Х = р+64 (10) =р+40 (16) = р+01000001 (2)
[A]п.к. = 1.11011100*101000001
знак мантиссы
31 0
Х = р+40 (16) Мантисса от 3 до 7 байтХарактеристика
Рис.1. Формат чисел с плавающей запятой
Диапазон порядка находится от –64 к +63: -64 (10)< p < 63 (10), а диапазон характеристики — 0 < X < 127 (10)
Рассмотрим пример записи числа [A]п.к. = 1.11011100*101000001 в регистр ЭВМ с плавающей запятой (рис.2.).
1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | . | 0 | 0 | 0 | 0 |
Х М
Рис. 2. Пример записи числа с плавающей запятой
где 0,1 m <1,
m — мантисса,
p — показатель степени.
знак | Цифровые разряды мантиссы | Знак порядка | Порядок | |||||||||||
КОДИРОВАНИЕ ЧИСЕЛ. Для записи и хранения числовой информации
в памяти ЭВМ используются не сами числа,
а их коды.
Для записи и хранения числовой информации
в памяти ЭВМ используются не сами числа,
а их коды.
Кодом числа называется условное изображение числа в машине для выполнения арифметических операций. Двоичные числа могут быть представлены в прямом, обратном и дополнительных кодах.
Для кодирования знака числа используется один двоичный разряд, в котором знак «+» изображается цифрой 0; знак «-» изображается цифрой 1. Поскольку положительные числа в различных кодах одинаковы, то специальное кодирование относится только к отрицательным числам.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют различное изображение, но знак числа «-» кодируется как «1» для всех видов кодов.
Отрицательное число в прямом коде сохраняет свое изображение, в обратном коде разряды нулей заменяются единицами, а единицы — нулями. Дополнительный код отрицательного числа соответствует обратному коду числа с прибавлением единицы к младшему разряду.
Прямой
код используется при вводе
и выводе чисел, а также при сохранении
чисел в
памяти ЭВМ.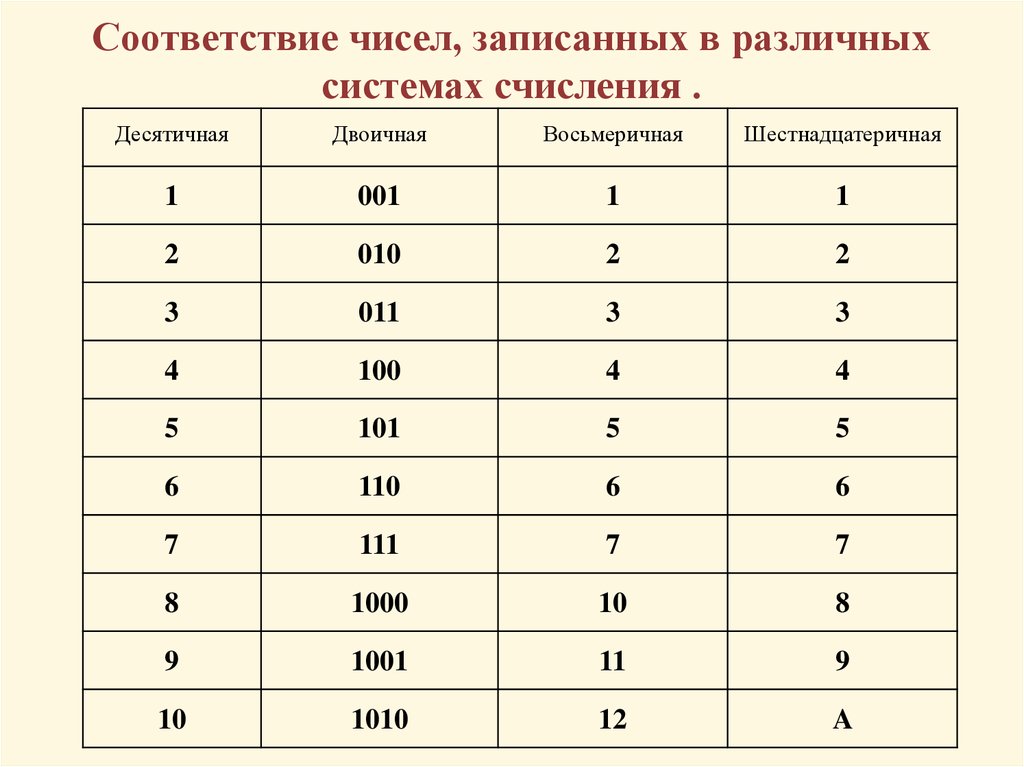
В прямом коде все разряды числа остаются неизменными. Например,
А (2) =1101 [A]п.к. = 0.1101; А (2) = — 0,1101 [A]п.к.= 1.1101
Прямой код используется при умножении чисел. Например,
С=А*В; А (2) =1011; B (2) = -1010;
Сначала вычисляем знаковые разряды путем сложения по модулю 2:
| 0 | 1 |
0 | 0 | |
1 | 1 | 0 |
‑ обозначение
операции «сложение по модулю 2».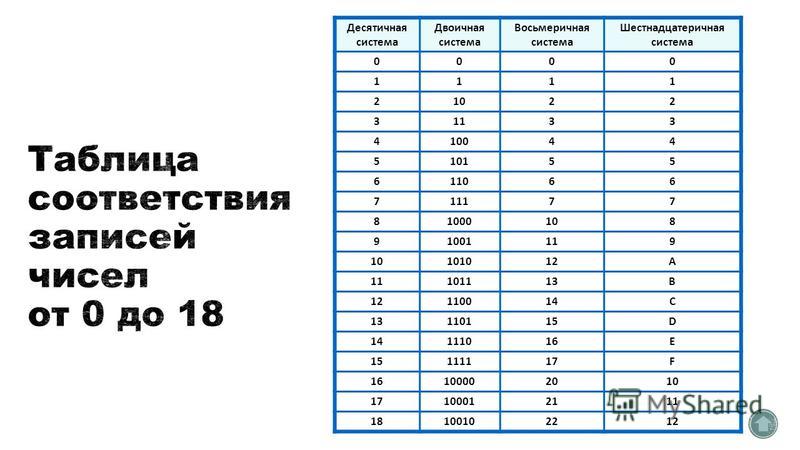
Получаем 0+1=1. Таким образом, результат будет иметь знак в прямом коде 1, что отображает знак минус.
1011
х1010
10110
+ 10110
1101110
Результат: [C]пк. = 1.1101110 (2).
С (2) = — 1101110 = — (1*26+1*25+1*23+1*22+0*20) = — (64+32+8+4+2) = — 110(10)..
Вычитание в ЭВМ выполняется как операция сложения в обратном или дополнительном коде.
Если число А>0, то обратный код пишется как прямой: [A] обр.к.= [A]пк.
Если число А<0, то все разряды числа, кроме знакового, инвертируются. Операция инверсии выполняется по формуле:
b и=
(q — 1) – b и.
Нуль в обратном коде в двоичной системе счисления имеет два изображения: “+0” = 0.00…0; “-0” = 1.11…1. В десятичной системе счисления нуль имеет такие изображения: “+0” = 0.00…0; “-0” = 9.99…9.
Переход от обратного кода к прямому осуществляется как и при переходе от прямого к обратному с помощью операции инверсии.
Рассмотрим пример сложения чисел с разными знаками в обратном коде в двоичной и десятичной системах счисления. С = А+(-В):
В двоичной системе счисления: В десятичной системе счисления:
А (2) = 1011; [A]обр.к.= 0.1011; 0.1011 А (10) = 11; [A]обр.к.= 0.11; 0.11
В (2)= —
101; [A]обр.к.=
1.1010; +1.1010 А (10) =
-5; [A]обр.к.= 9. 94; +9.94
94; +9.94
(1)0.0101 (1)0.05
+ 1 + 1
0.0110 0.06
При сложении в обратном коде перенос из старшего (знакового) разряда прибавляется к младшему разряду суммы для получения верного результата.
Если число А>0, то дополнительный код пишется как прямой:
[A]д.к.= =[A]п.к.
Если число А<0, то все разряды числа, кроме знакового, инвертируются и к младшему разряду прибавляется 1.
Пример:
А (2) = —
1010; [A]д.к.=
[A]обр.к. + 0.0001
= 1.0101+0.0001 = 1.0110.
+ 0.0001
= 1.0101+0.0001 = 1.0110.
Переход от дополнительного кода к прямому осуществляется как и при переходе от прямого к дополнительному (сначала преобразуется в обратный код, а потом к этому числу добавляется 1 младшего разряда).
Рассмотрим примеры сложения чисел с разными знаками в дополнительном коде:
В двоичной системе счисления: В десятичной системе счисления:
А (2) = 1011; [A]д.к.= 0.1011; 0.1011 А (10) = 11; [A]о.к.= 0.11; 0.11
В (2)= — 101; [A]д.к.= 1.1011; +1.1011 А (10) = -5; [A]о.к.= 9.95; +9.95
(1)0.0110 (1)0.06
Результаты:
А (2) =
110; А (10) =
6.
При сложении в дополнительном коде перенос из старшего (знакового) разряда отбрасывается для получения верного результата.
Переполнение разрядной сетки ведет к ошибке вычисления. Рассмотрим переполнения разрядной сетки на примерах:
1) А (2) = 1011,0111; [A]м.п.к. = 00.1011,0111
В (2) = 1101,1011; [B]м.п.к. = 00.1101,1011
01.1001,0010
2) А (2) = — 1011,0111; [A]м.д.к.= 11.0100,1001
В (2) = — 1101,1011 [B]м.д.к.= 11.0010,0101
10.0110,1110
При
сложении чисел с
одинаковыми знаками при переполнении
разрядной сетки знак результата
становится другим, что является признаком
переполнения.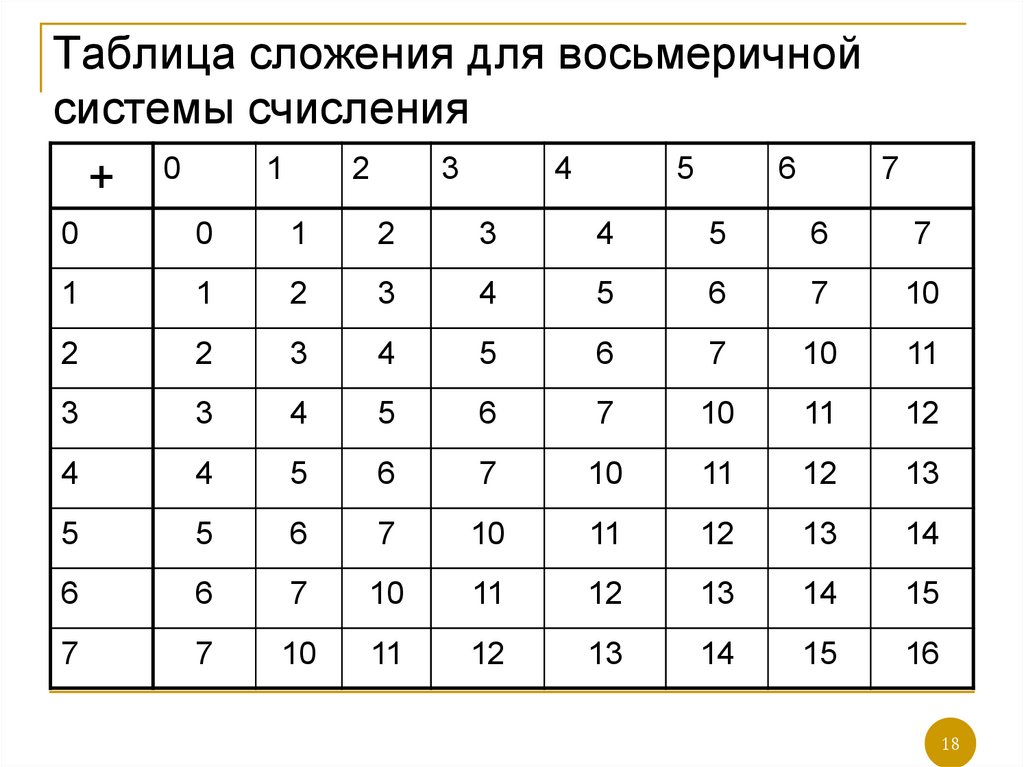 Для выявления в
ЭВМ признака
переполнения применяется модифицированный
дополнительный код, в котором под знак
числа отводятся два двоичных
разряда. При этом знак “+” отображается
как 00, а знак “-” ‑ 11. При переполнении
знаки результата
приобретают вид 01 (при сложении
положительных чисел ‑ А>0)
и 10 (при сложении отрицательных чисел
‑ А<0)
Для выявления в
ЭВМ признака
переполнения применяется модифицированный
дополнительный код, в котором под знак
числа отводятся два двоичных
разряда. При этом знак “+” отображается
как 00, а знак “-” ‑ 11. При переполнении
знаки результата
приобретают вид 01 (при сложении
положительных чисел ‑ А>0)
и 10 (при сложении отрицательных чисел
‑ А<0)
Интернет магазин китайских планшетных компьютеров |
|||||||||||||
Компьютеры — Троичная система счисления — Таблицы сложения в троичных системах счисления22 января 2011Оглавление: В троичной несимметричной системе счисленияС результатом в десятичной системе счисления:
С результатом в троичной несимметричной системе счисления:
В троичной симметричной системе счисленияС результатом в десятичной системе счисления:
С результатом в троичной симметричной системе счисления:
Симметричная троичная система счисленияПозиционная целочисленная симметричная троичная система счисления была предложена итальянским математиком Фибоначчи для решения «задачи о гирях». Симметричность при взвешивании на рычажных весах использовали с древнейших времён, добавляя гирю на чашу с товаром. Элементы троичной системы счисления были в системе счисления древних шумеров, в системах мер, весов и денег, в которых были единицы равные 3. Но только в симметричной троичной системе счисления Фибоначчи объединены оба этих свойства. Симметричная система позволяет изображать отрицательные числа, не используя отдельный знак минуса. Число 2 изображается цифрой 1 в разряде троек и цифрой в разряде единиц. Число −2 изображается цифрой в разряде троек и цифрой 1 в разряде единиц.
В соответствии 2. сохраняются числовые значения 0 и 1.
В троичной симметричной системе счисления знак 1 можно заменить знаком i или 2 и, во втором случае, использовать для троичной симметричной системы счисления {-1,0,+1} знаки троичной несимметричной системы {2,0,1}. СвойстваБлагодаря тому что основание 3 нечётно, в троичной системе возможно симметричное относительно нуля расположение цифр: −1, 0, 1, с которым связано пять ценных свойств:
Представление отрицательных чиселНаличие положительной и отрицательной цифр позволяет непосредственно представлять как положительные, так и отрицательные числа. ОкруглениеДругим полезным следствием симметричного расположения значений цифр является отсутствие проблемы округления чисел: абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа, соответствующей младшей значащей цифре младшего из сохраняемых разрядов. Следовательно, в результате отбрасывания младших цифр числа получается наилучшее при данном количестве оставшихся цифр приближение этого числа, и округление не требуется. Перевод чисел из десятичной системы в троичнуюПеревод чисел из десятичной системы в троичную и соответствующий ему вопрос о гирях подробно изложены в книгах . Там же рассказано о применении троичной системы гирь в русской практике. Перевод в другие системы счисленияВсякое число, записанное в троичной системе счисления с цифрами 0, 1, −1, можно представить в виде суммы целых степеней числа 3, причём если в данном разряде троичного изображения числа стоит цифра 1, то соответствующая этому разряду степень числа 3 входит в сумму со знаком «+», если же цифра −1, то со знаком «-», а если цифра 0, то вовсе не входит. Это можно представить формулой
причём коэффициенты K могут принимать значения { 1, 0, −1 }. Для того чтобы число, представленное в троичной системе, перевести в десятичную систему, надо цифру каждого разряда данного числа умножить на соответствующую этому разряду степень числа 3 и полученные произведения сложить. Практические применения
Просмотров: 23747 |
| DigiKey Electronics
Общие системы счисления для программирования включают двоичную (с основанием 2), десятичную (с основанием 10), восьмеричную (с основанием 8) и шестнадцатеричную
(база 16). Калькулятор преобразования системы счисления позволяет пользователю вводить число в любой системе и
преобразовать его в другие. Это также
работает как двоичный калькулятор сдвига битов, позволяя вам изменять значения, сдвигая биты вправо или влево
или путем изменения отдельных битов.
Сопутствующие инструменты
Манипуляции с двоичными битами
Объяснение преобразования чисел
Десятичная система счисления — это то, что мы используем ежедневно. В десятичной системе счисления положение цифр представляет степень числа 10 (основание 10). Это означает, что при движении влево от наименее значащий бит, вы будете увеличивать до следующая позиция после того, как вы достигнете 9. Значение 9представляет 9 «единиц», а 10 представляет 1 «десять».
Двоичная система с основанием 2, в которой используются только 1 и 0. Каждая позиция соответствует шагу 1. A
За двоичным числом 1 последовательно следует 10 (1 на месте «двойки» и «0» на месте единицы). Следующий
будет 11 (1 в двойках, +1 в единицах).
100 будет десятичным числом 4 (1 в четверках, 0 в 2, 0 в единицах).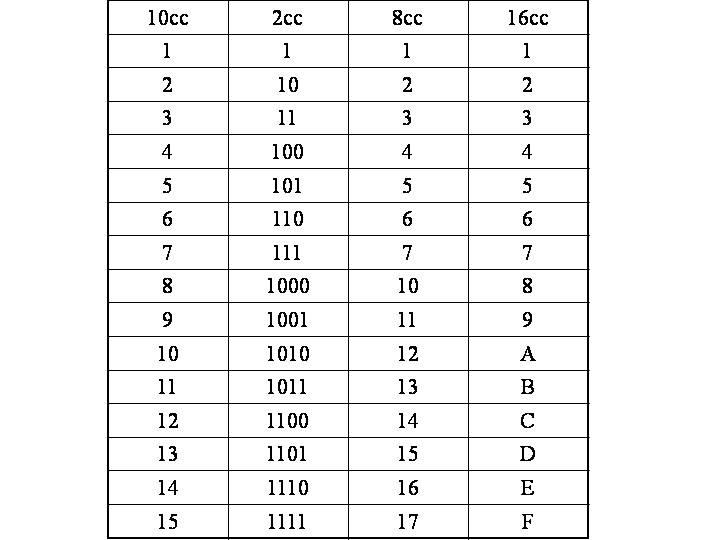 Самое большое преимущество а
двоичная система счисления, когда дело доходит до программирования, заключается в том, что схемы очень легко
представлять два государства. В электронике единицы и
0 можно использовать как выключенное или включенное состояние. Это делает Binary базой для всего программирования. Бинарный
падения происходят из-за того, что двоичные числа становятся очень длинными, если число большое.
Самое большое преимущество а
двоичная система счисления, когда дело доходит до программирования, заключается в том, что схемы очень легко
представлять два государства. В электронике единицы и
0 можно использовать как выключенное или включенное состояние. Это делает Binary базой для всего программирования. Бинарный
падения происходят из-за того, что двоичные числа становятся очень длинными, если число большое.
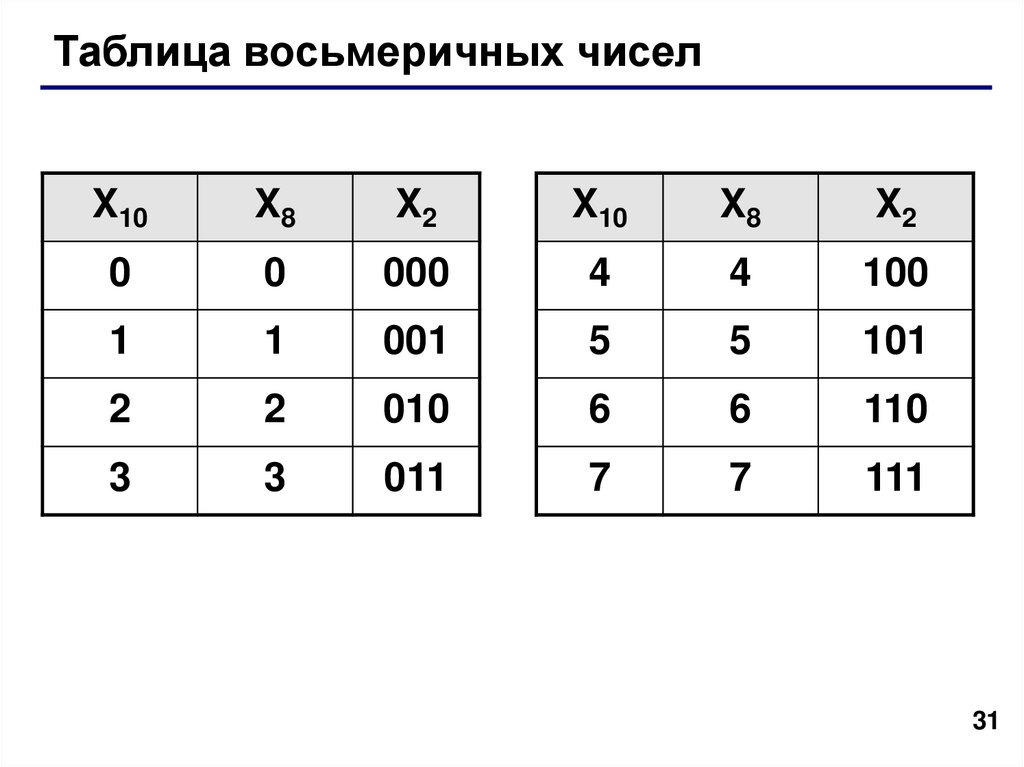
Восьмеричная система основана на 8, что означает позиционное указание чисел (от LSB) до единиц, 8, 64 и т. д. Например — в восьмеричной системе счисления 135 разбивается как 1×64 + 3×8 + 5×1 для всего 93. Восьмеричная система менее популярна сегодня и в значительной степени был заменен шестнадцатеричной системой с основанием 16.
Шестнадцатеричная система основана на базе 16 и использует числа 0-9 и буквы A~F. В этом
система позиция «единицы» увеличивается от 0 до 9но «10» обозначается буквой А, 11 — буквой В и т.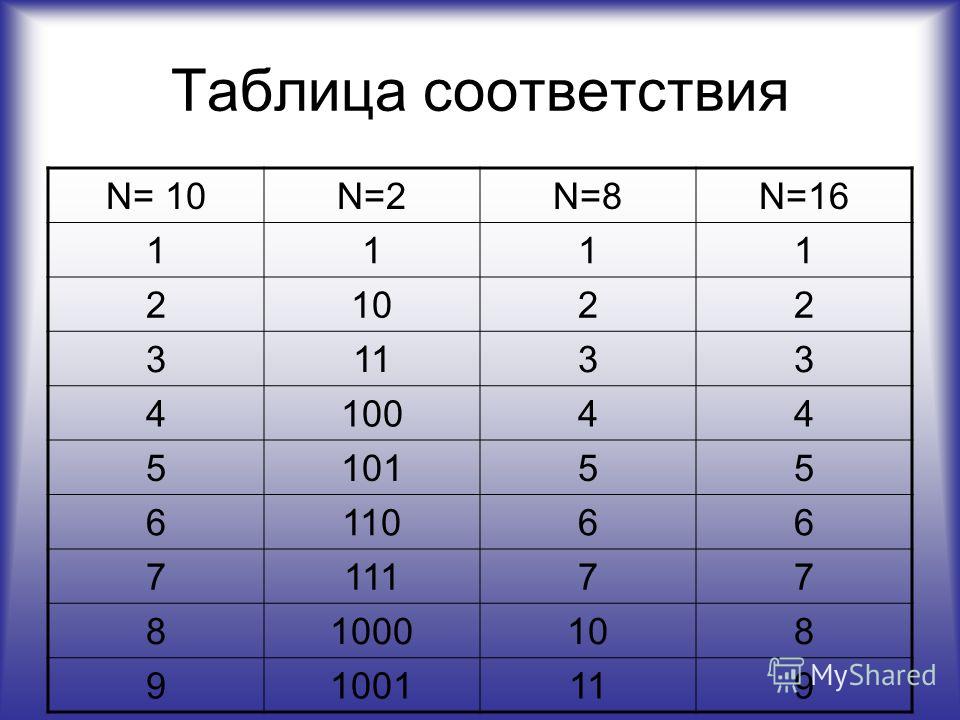 д.
Самым большим преимуществом шестигранной системы является то, что
это более простой способ представления очень больших чисел. Шестнадцатеричное значение 4B6 разбивается на 4 (двоичное
0100) B (двоичный 1011) 6 (двоичный 0110). Таким образом, это может занять очень длинную двоичную строку и
сжать его в более удобный для чтения формат.
д.
Самым большим преимуществом шестигранной системы является то, что
это более простой способ представления очень больших чисел. Шестнадцатеричное значение 4B6 разбивается на 4 (двоичное
0100) B (двоичный 1011) 6 (двоичный 0110). Таким образом, это может занять очень длинную двоичную строку и
сжать его в более удобный для чтения формат.
Сопутствующие инструменты
×
Системы счисления и преобразования – Блог Бекима Даути
[Далее выдержка из книги: CCENT/CCNA: ICND1 100-105 Certification Guide]
Нас научили пользоваться десятичной системой счисления, и мы можем сказать, что каждый раз чувствуем себя комфортно мы должны играть с числами в этой системе. Однако помимо десятичной системы счисления существуют и другие системы счисления, нашедшие применение в определенных технологических областях.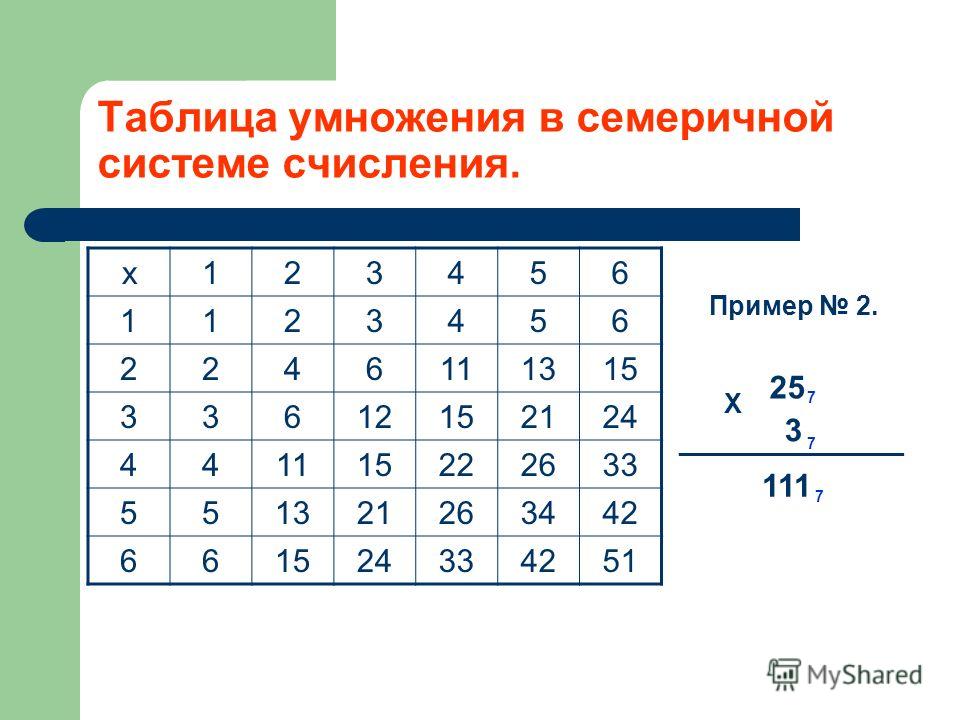 Некоторые из этих систем счисления: двоичная, восьмеричная и шестнадцатеричная.
Некоторые из этих систем счисления: двоичная, восьмеричная и шестнадцатеричная.
Двоичная система счисления
В отличие от десятичной системы счисления, которая имеет основание 10 и использует десять цифр, двоичная система счисления основана на 2 и использует две цифры, то есть 0 и 1. Таким образом, двоичная система счисления имеет ряд приложений в технике, особенно в области электроники.
Таблица 1. Представляет как десятичную, так и двоичную системы счисления
Преобразование десятичной системы в двоичную
Для меня самый простой метод преобразования десятичной системы в двоичную — использование следующей таблицы:
Таблица 2. Преобразование десятичного числа в двоичное
Пример: Преобразование десятичного числа 196 в двоичное число ???(2) справа начните размещать 0 и 1, пока не достигнете десятичного числа 196. Вы будете вводить 1 для чисел, которые являются частью вычисления, и 0 для чисел, которые не являются частью вычисления. Таким образом, вы получите числа 128 + 64 + 4 = 196. Наконец, строка, состоящая из 0 и 1, представляет собой результат преобразования десятичного числа в двоичное. При этом 196 в десятичном виде равно
Таким образом, вы получите числа 128 + 64 + 4 = 196. Наконец, строка, состоящая из 0 и 1, представляет собой результат преобразования десятичного числа в двоичное. При этом 196 в десятичном виде равно
11000100 в двоичном (см. Таблицу 3).
Таблица 3. Преобразование десятичного числа 196 в двоичное число 11000100
Преобразование двоичного числа в десятичное
Как и в случае с преобразованием десятичного числа в двоичное
Таблица C.2 преобразование десятичного числа в двоичное. будет использоваться для преобразования чисел из двоичных в десятичные. В этом случае 0 и 1 располагаются справа налево, как показано в таблице 4.
Пример: Преобразование двоичного числа 101011002 в десятичное число ???(10)
Таблица 4. Преобразование двоичного числа 11000100 в десятичное число 196
Таким образом, 11000100 Таким образом, 11000100 Восьмеричная система счисления — это старая система счисления, используемая в компьютерах. Таблица 5. Представляет как восьмеричную, так и двоичную системы счисления. Как объяснялось ранее, для преобразования десятичного числа в шестнадцатеричное удобно использовать двоичное число. Во-первых, десятичное число должно быть преобразовано в двоичное. Затем двоичное число разбивается на наборы по три бита в каждом, а затем из этого вычисляется восьмеричное число. Пример: Преобразование десятичного числа 196 в восьмеричное ???(8) Поскольку мы уже завершили преобразование десятичного числа 196 в двоичное число 11000100, давайте разделим двоичное число на наборы по три бита в каждом следующим образом: 011| 000| 100 – двоичное число 11000100, разделенное на три набора по три бита 3 | 0 | 4 – восьмеричный результат, относящийся к представлению нумерации в Обратите внимание, что мы добавили ноль в левую часть двоичного числа 11000100. Это делается для того, чтобы иметь возможность иметь три набора по три бита в каждом. Добавление нуля в правую часть числа не меняет его значения. Однако избегайте добавления нулей справа от числа в любой системе счисления. Таким образом, десятичное число 196 в восьмеричной системе равно 304. В отличие от восьмеричной системы счисления, шестнадцатеричная система счисления широко используется в математике и вычислениях. Это система счисления с основанием шестнадцать (16), состоящая из шестнадцати цифр, то есть от 0 до 9.и от A до F. Как и при преобразовании десятичного числа в восьмеричное, вам необходимо использовать двоичное число между ними всякий раз, когда вы конвертируете десятичное число в шестнадцатеричное. Таблица 6. Как объяснялось ранее, для преобразования десятичного числа в шестнадцатеричное число вступает в игру. Во-первых, десятичное число должно быть преобразовано в двоичное. Затем двоичное число разбивается на группы из четырех битов (полубайт), а затем преобразуется в шестнадцатеричное число. Пример: Преобразование десятичного числа 196 в шестнадцатеричное ???(16) Поскольку мы уже завершили преобразование десятичного числа 196 в двоичное число 11000100, давайте разделим двоичное число на два набора по четыре битов каждый следующим образом: 1100 | 0100 – двоичное число 11000100, разделенное на два набора по четыре бита C | 4 – результат в шестнадцатеричном формате, относящийся к представлению нумерации Таким образом, десятичное число 196 при преобразовании в шестнадцатеричное равно C4. Подписывайтесь на меня в Twitter или LinkedIn. Посмотрите мой блог или видеоблог здесь. Беким Даути [участник] Я являюсь автором руководства по сертификации CCENT/CCNA: ICND1 100-105 и основателем Dautti, виртуальной обучающей платформы под руководством инструктора, которая предоставляет компьютерные курсы в режиме реального времени. Я публиковал статьи о компьютерах на порталах PC World в Албании и CIO в Албании, а также книги о компьютерах, изданные Packt и Amazon. Мои книги продаются через различные онлайн-каналы продаж и в вашем распоряжении 24 часа в сутки, 7 дней в неделю. Я сертифицированный инструктор Cisco Academy (CCAI) и сертифицированный тренер Microsoft (MCT), регулярно веду компьютерные курсы. Примеры взаимодействия включают Dautti, InfoTech и QuickStart. У меня есть степень магистра. получил степень бакалавра информационных технологий в Университетском колледже Мэрилендского университета в Европе. Я получил степень бакалавра наук. в области информатики из Университета Тираны — Албания. Восьмеричная система счисления
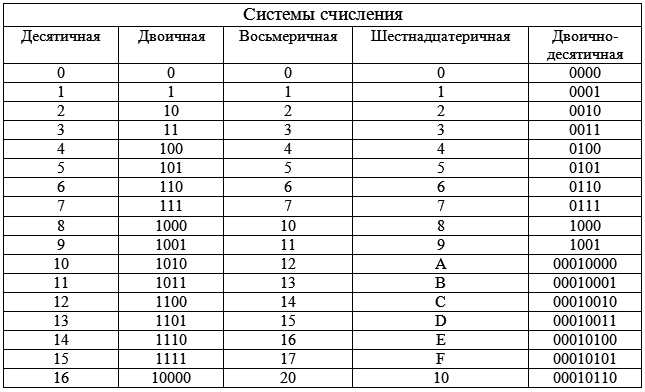 Это система счисления с основанием восемь, состоящая из восьми цифр: 0, 1, 2, 3, 4, 5, 6, 7. Чтобы преобразовать десятичную систему в восьмеричную, вам нужно использовать двоичную систему между ними. Двоичные числа служат мостом для облегчения преобразования между десятичными и восьмеричными числами.
Это система счисления с основанием восемь, состоящая из восьми цифр: 0, 1, 2, 3, 4, 5, 6, 7. Чтобы преобразовать десятичную систему в восьмеричную, вам нужно использовать двоичную систему между ними. Двоичные числа служат мостом для облегчения преобразования между десятичными и восьмеричными числами. Преобразование десятичного числа в восьмеричное
в каждом
. значение двоичного числа, в отличие от добавления нулей справа, которое изменяет значение двоичного числа.
значение двоичного числа, в отличие от добавления нулей справа, которое изменяет значение двоичного числа. Шестнадцатеричная система счисления
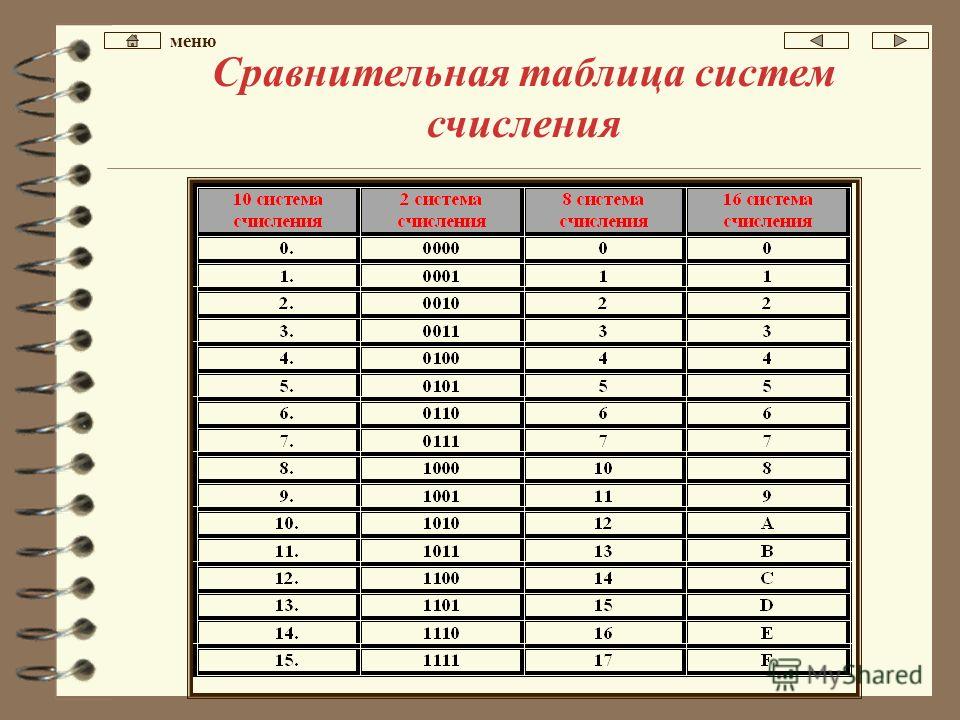 Представляет десятичную, двоичную и шестнадцатеричную системы счисления
Представляет десятичную, двоичную и шестнадцатеричную системы счисления Преобразование десятичного числа в шестнадцатеричное
в Таблице 6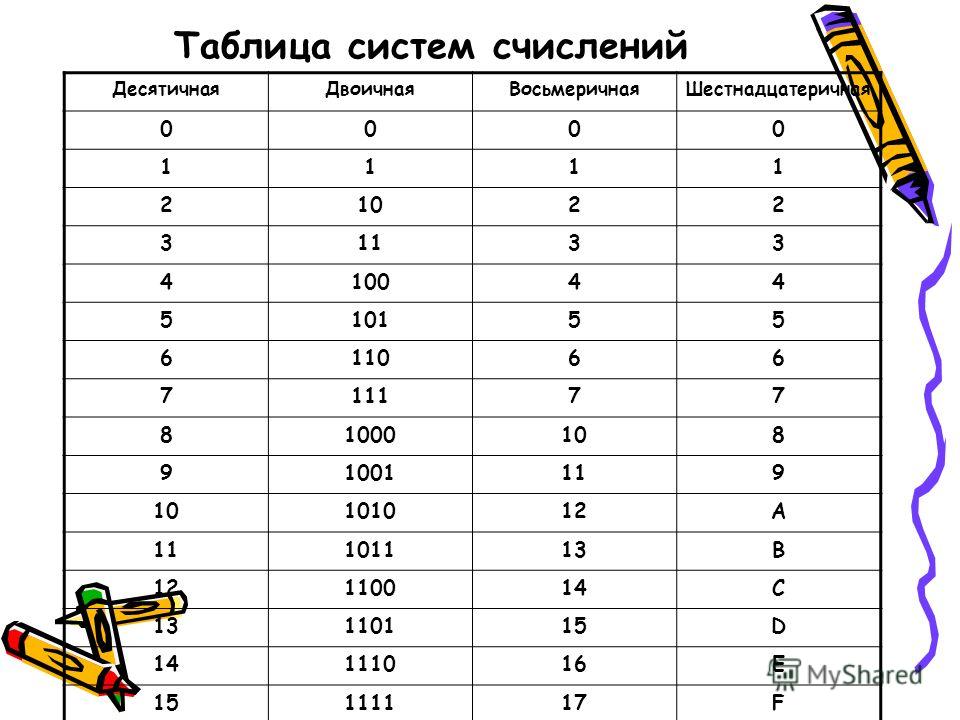
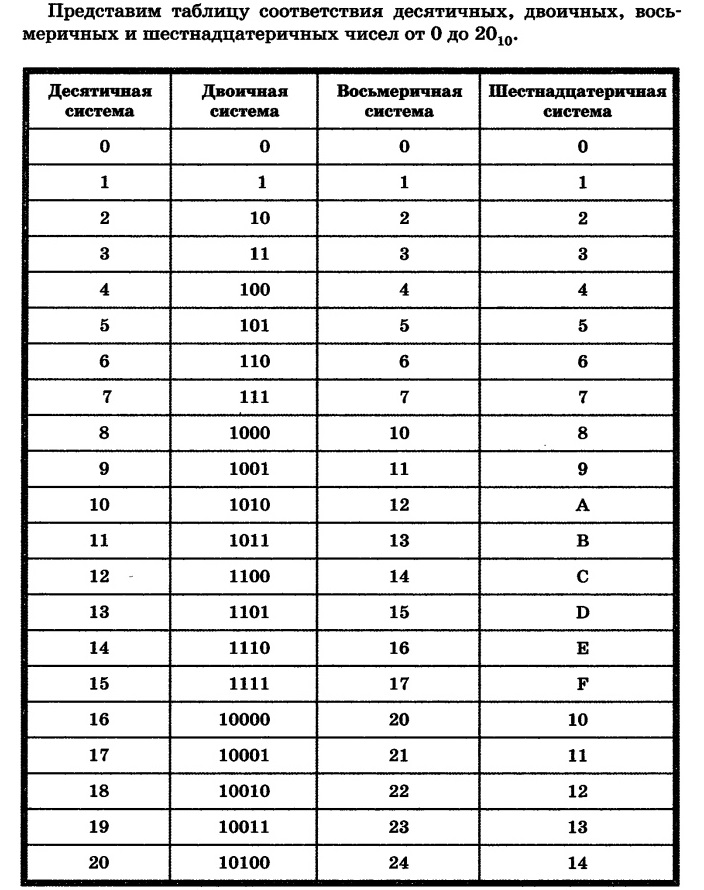
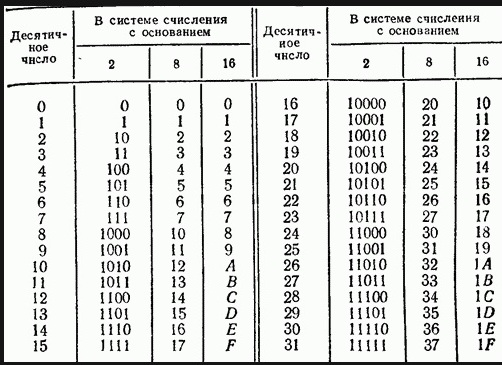 ..
..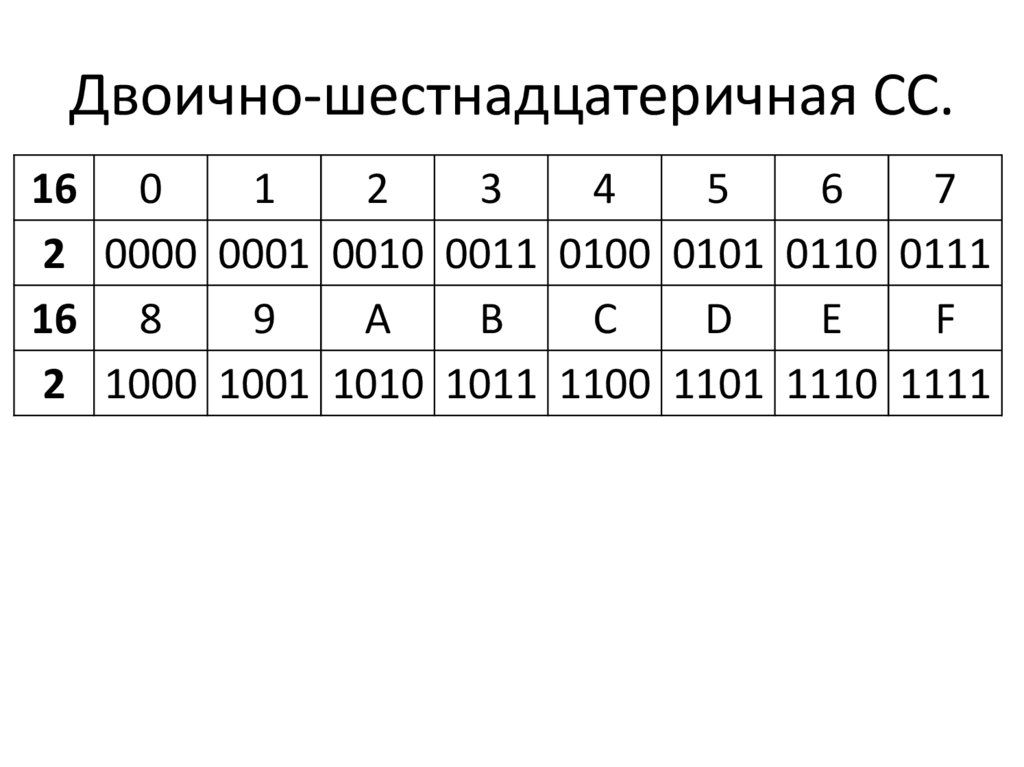 Задачу о наилучшей системе гирь рассматривал Лука Пачоли. Частный случай этой задачи был опубликован в книге французского математика Клода Баше де Мезириака «Сборник занимательных задач» в XVII веке в 1612 г. Русский перевод книги К. Г. Баше «Игры и задачи, основанные на математике» вышел в Петербурге в 1877 г. Позже этой задачей занимался петербургский академик Леонард Эйлер, интересовался Д. И. Менделеев.
Задачу о наилучшей системе гирь рассматривал Лука Пачоли. Частный случай этой задачи был опубликован в книге французского математика Клода Баше де Мезириака «Сборник занимательных задач» в XVII веке в 1612 г. Русский перевод книги К. Г. Баше «Игры и задачи, основанные на математике» вышел в Петербурге в 1877 г. Позже этой задачей занимался петербургский академик Леонард Эйлер, интересовался Д. И. Менделеев.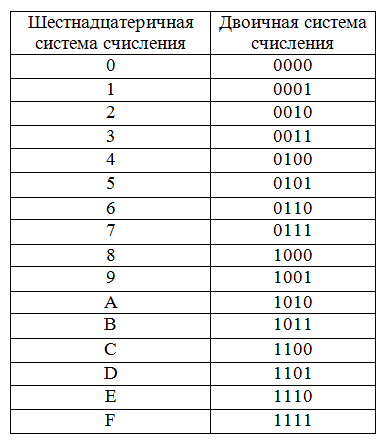
 При этом нет необходимости в специальном разряде знака и не надо вводить дополнительный код для выполнения арифметических операций с отрицательными числами. Все действия над числами, представленными в троичной системе счисления с цифрами 0, 1, −1, выполняются естественно с учётом знаков чисел. Знак числа определяется знаком старшей значащей цифры числа: если она положительна, то и число положительно, если отрицательна, то и число отрицательно. Для изменения знака числа надо изменить знаки всех его цифр. Например:
При этом нет необходимости в специальном разряде знака и не надо вводить дополнительный код для выполнения арифметических операций с отрицательными числами. Все действия над числами, представленными в троичной системе счисления с цифрами 0, 1, −1, выполняются естественно с учётом знаков чисел. Знак числа определяется знаком старшей значащей цифры числа: если она положительна, то и число положительно, если отрицательна, то и число отрицательно. Для изменения знака числа надо изменить знаки всех его цифр. Например: