Система координат у х z: Координаты точки и вектора

Содержание

Системы координат — UWP applications

Twitter LinkedIn Facebook Адрес электронной почты

Статья
09/24/2022
Чтение занимает 2 мин

Как правило, в приложениях с трехмерной графикой используется один или два типа Декартовой системы координат: левостороннюю и правостороннюю. В обеих системах координат положительная ось x указывает вправо, а положительная ось y — вверх.

Координаты слева и правой руки

Можно запомнить, в каком направлении указывает положительная ось z, указав пальцами левой или правой руки в направлении положительной оси x и скруглив их в направлении положительной оси y. Направление, в котором указывают ваши пальцы (к вам или от вас), — это направление, в котором указывает положительная ось z в этой системе координат. На следующем рисунке показаны эти две системы координат.

В Direct3D используется левосторонняя система координат. Несмотря на то что левосторонние и правосторонние системы координат относятся к наиболее распространенным, в программном обеспечении для работы с трехмерными объектами существует множество других систем координат. Например, приложения для трехмерного моделирования часто используют систему координат, в которой ось y указывает в направлении смотрящего или от него, а ось z — вверх.

Вершины и векторы

В системе координат координата x, y или z может определять точку в пространстве («вершину») или трехмерное направление («вектор»).

Коллекцию вершин можно использовать для определения строк и фигур. Простейшие объекты, определяемые вершинами, называются Примитивы, а более сложный объект, определяемый набором примитивов, — «сетка».

Ключевые операции, выполняемые с сетками, которые определены в трехмерной системе координат: преобразование, поворот и масштабирование. Можно комбинировать эти базовые трансформации и создавать матрицу трансформаций. Подробные сведения см. в разделе Преобразования.

При объединении этих операций результаты не будут коммутативными; важен порядок умножения матриц.

Перенос из правой системы координат

При переносе приложения, основанного на правосторонней системе координат, необходимо внести два изменения в данные, передаваемые Direct3D:

Измените порядок вершин треугольников так, чтобы система обходила их по часовой стрелке от передней. Другими словами, если имеются вершины v0, v1, v2, передайте их в Direct3D как v0, v2, v1.
Используйте матрицу представления для масштабирования пространства на -1 по оси z. Для этого переверните знак структуры матрицы _31, _32, _33 и _34, используемой для матрицы представления.

Системы координат и геометрия

Система координат станка с ЧПУ

Для определения координатного пространства внутри станка и пространства для перемещения инструмента (фрезы, резца, экструдера, лазерного луча и др.) во всех современных станках используются декартова система координат с осями X, Y и Z.

Декартова система координат — прямолинейная система координат с взаимно перпендикулярными осями. Это наиболее простая и поэтому часто используемая система координат:

Помимо линейных осей, станок может иметь несколько поворотных осей. Их обозначение зависит от того, вокруг какой линейной оси они вращаются. Ниже приведена схема системы координат с поворотными осями:

Для позиционирования инструмента в системе координат могут использоваться разные технические устройства и механизмы.

В этой статье рассматриваются системы координат, используемые в станках с ЧПУ, включая рабочую систему координат (WCS), машинную систему координат (MCS) и систему смещения.

Роль системы координат

Станок должен понимать положение заготовки в физическом пространстве — просто поместить кусок металла в ЧПУ станок и нажать кнопку «Пуск» недостаточно. Для решения этой задачи используется рабочая система координат станка.

Задача усложняется, когда в процессе обработки используется несколько инструментов. Каждый из них имеет различную длину, которая изменяет расстояние между базовой точкой шпинделя и заготовкой. Например, точка начала для 3-мм фрезы с небольшой длиной будет отличаться от точки начала для 6-мм сверла, предназначенного для сверления глубоких отверстий.

Система координат позволяет сообщить управляющей программе:

где в пространстве находится заготовка;

как далеко от неё находится инструмент;
как должен двигаться инструмент в процессе обработки детали.

Используя декартову систему координат, можно управлять движением инструмента вдоль каждой оси, что уже позволит сделать из заготовки деталь.

Система координат классического фрезерного станка с точки зрения оператора:

ось X задаёт перемещение «влево» и «вправо»;
ось Y — «вперед» и «назад»;
ось Z — «вверх» и «вниз».

Система координат классического токарного станка:

Многие современные токарные станки с ЧПУ оснащаются фрезерным инструментом. Но как быть, если токарный станок имеет всего две оси, а требуется обработать квадрат или шестигранник? Производители оборудования предлагают для таких случаев два решения.

1. Перейти от декартовой системы координат к полярной

Полярная система координат — это двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. В случае с токарным станком полярный угол это угол поворота шпинделя относительно инструмента, а полярный радиус это положение инструмента по оси Х.

Иными словами, чтобы определить точку в пространстве, необходимо указать радиус и угол отклонения от оси Х. На практике использовать такую систему координат, как правило, неудобно, поэтому ЧПУ преобразовывает угловое значение поворота шпинделя в более понятную линейную координату. При программировании в полярных координатах необязательно пересчитывать углы. Кроме того, обработка в полярных координатах не позволяет выполнять некоторые фрезерные операции.

2. Использовать дополнительную ось перемещения

Вторым способом является установка дополнительной оси перемещения (ось Y). Такая опция позволяет значительно расширить возможности станка, и, в отличие от полярных координат, пригодна для выполнения любых фрезерных операций. Недостаток такой опции — это её стоимость и сравнительно небольшой диапазон перемещений.

Движение вдоль системы координат всегда основано на том, как движется инструмент, а не стол с заготовкой. Например, увеличение значения координаты X приведёт к смещению стола влево, но если смотреть с точки зрения инструмента, он движется вправо вдоль заготовки.

Кроме трёх или двух осей, в любой системе координат задаётся исходная точка. Каждый станок с ЧПУ имеет свою собственную внутреннюю исходную точку, которая называется Machine Home или Референтная позиция.

Привязка системы координат

Чтобы упростить написание программ ЧПУ, используется система рабочих координат или WCS. WCS определяет конкретную исходную точку в блоке материала, обычно в программном обеспечении САМ.

Перед началом выполнения управляющей программы станку необходимо указать расположение заготовки относительно его системы координат (MCS).

Для этого оператор должен указать величину смещения по каждой оси станка. Это можно сделать несколькими способами, но на многих современных станках существует возможность оснащения его автоматической системой измерения заготовки.

Такая система представляет собой высокоточный датчик, который устанавливается в шпинделе станка (фрезерный станок) или в инструментальной револьверной головке (токарный станок). Датчик на медленной подаче производит касание заготовки и передает сигнал на ЧПУ, которая в свою очередь заносит в память величину смещения вдоль соответствующей оси. Такое устройство позволяет значительно ускорить наладку станка.

Выбор исходной точки для WCS требует тщательного планирования. Необходимо учитывать несколько условий:

исходная точка должен быть найдена механическими средствами с помощью искателя края или зонда;
одинаковые исходные точки помогают экономить время при замене деталей;
исходная точка должна учитывать требуемые допуски для всех последующих операций.

Если на станке обрабатывается несколько деталей в одном задании, для каждой детали может быть назначено собственное смещение. Это позволяет станку с ЧПУ точно связать свою систему координат с системами нескольких деталей в разных местах и выполнять несколько настроек одновременно.

Коррекция инструмента

Обычно для изготовления одной и той же детали используется несколько инструментов. Как отмечалось выше, разный инструмент имеет разные геометрические параметры, которые станок должен учитывать при перемещении. Для этого в станке существует таблица смещения инструмента, в которой указываются геометрические параметры инструмента (для токарных резцов: смещение от нулевой точки станка, для фрезерного инструмента длина и диаметр). Для записи коррекции используют несколько способов:

Измерения касанием. Этот способ не требует каких либо специальных технических средств или дополнительного оснащения, но вместе с этим является наименее точным.
Суть заключается в касании заготовки инструментом либо напрямую, либо через концевые меры.
Использование пресетера (необходимо наличие в цеху специального устройства — пресетора).

Пресетер позволяет точно измерить длину и диаметр инструмента. Это наиболее точный метод измерения, но вместе с тем наиболее затратный и наименее удобный, так как для проведения измерений инструмент необходимо извлекать из станка.

Измерение при помощи датчика измерения инструмента. В зависимости от типа датчика этот способ не уступает по точности предыдущему, но при этом менее затратный и наиболее эффективный, так как привязку инструмента можно осуществлять в автоматическом режиме. Суть данного способа заключается в установке в рабочую зону станка высокоточного датчика для измерения инструмента:

Инструмент касается контактной поверхности датчика, а датчик в свою очередь передает сигнал на ЧПУ, которая фиксирует данные в таблице инструментов. Измерение может проводиться как в ручном режиме, так и в автоматическом (в зависимости от типа датчика).

С помощью инструментов нашего портала Вы сможете легко сравнить между собой станки от разных производителей и принять верное решение о покупке оборудования!

Также вы можете обратиться за помощью к специалистам Центра технологической поддержки портала СТАНКОТЕКА — для этого оставьте заявку на сайте или позвоните по телефону, указанному на странице «Контакты».

1.2 Система координат XYZ – инженерная механика: статика

Глава 1: Основные понятия

Нам нужен стандарт, чтобы иметь возможность использовать общий язык. Декартова система координат позволяет нам выразить местоположение точки, чтобы другие могли понять, о чем мы говорим. В этом разделе мы рассмотрим системы координат 2d и 3d.

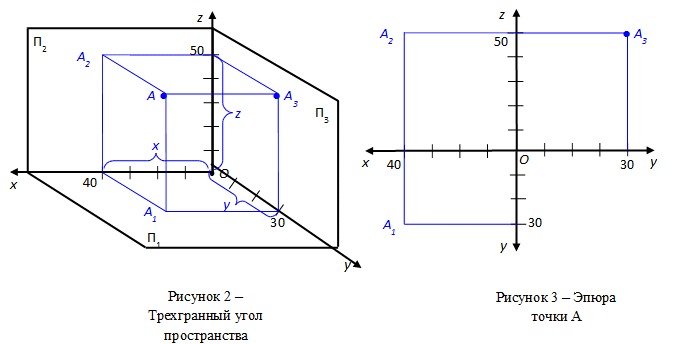
Векторы обычно описываются с точки зрения их компонентов в системе координат . Даже в повседневной жизни мы естественным образом пользуемся понятием ортогональных проекций в прямоугольной системе координат. Например, если вы спросите у кого-нибудь, как добраться до определенного места, вам, скорее всего, скажут пройти 40 км на восток и 30 км на север, чем 50 км в направлении 37° северо-востока.

В прямоугольной (декартовой) системе координат x-y на плоскости точка на плоскости описывается парой координат ( x , y ). Аналогичным образом вектор [latex]\vec A[/latex] на плоскости описывается парой своих вектор координаты. Координата x вектора A→» role=»presentation»>[latex]\vec A[/latex] называется его x-компонентой, а y-координата вектора A→» role=»presentation»>[ латекс]\vec A[/латекс] называется его y -компонентом. Компонента вектора x – это вектор, обозначаемый как [latex]\vec A_x[/latex]. Вектор y -component представляет собой вектор, обозначаемый как [latex]\vec A_y[/latex]. В декартовой системе x и y 9Компоненты вектора 0011 вектора являются ортогональными проекциями этого вектора на оси x и y соответственно. Таким образом, следуя правилу параллелограмма для сложения векторов, каждый вектор на декартовой плоскости может быть выражен как векторная сумма его векторных компонентов:

[латекс]\vec A =\vec A_x+\vec A_y[/latex]

Как показано на рисунке ниже, вектор [latex]\vec A[/latex] — это диагональ прямоугольника, где x -компонент [latex]\vec A_x[/latex] — это сторона, параллельная x -ось, а y -компонент [латекс]\vec A_y[/latex] является стороной, параллельной y -оси. Компонента вектора [latex]\vec A_x[/latex] ортогональна компоненте вектора [latex]\vec A_y[/latex].

Обычно принято обозначать положительное направление оси x единичным вектором i и положительное направление оси y единичным вектором j. Единичные векторы осей i и j определяют два ортогональных направления на плоскости. Как показано на рисунке выше, x — и y — компоненты вектора теперь можно записать в терминах ортов осей:

[латекс]\vec A_x = A_x\underline{\hat{i}}[/latex]

[латекс]\vec A_y = A_y\underline{\hat{j}}[/latex]

Векторы [latex]\vec A_x и \vec A_y[/latex], определенные на рисунке выше, являются вектором компоненты вектора [latex]\vec A[/latex] A→» role=»presentation»>. Числа A _x и A _y , определяющие компоненты вектора выше, являются скалярными компонентами вектора [latex] \vec A[/latex] A→» role=»presentation»>A→» role=»presentation»>. Комбинируя приведенную выше диаграмму с приведенными выше уравнениями, мы получаем компонентная форма вектора:

[латекс]\vec A=A_x\underline{\hat {i}} + A_y\underline{\hat {j}}[/latex]

Если мы знаем координаты b(x _b , y _b ) начальной точки вектора (где b означает «начало») и координат e(x _e , y _e ) конечной точки вектора вектора (где e обозначает «конец»), мы можем получить скалярные компоненты вектора, просто вычитая координаты исходной точки из координат конечной точки:

[латекс]A_x = x_e — x_b[/латекс]

[латекс]A_y = y_e — y_b[/латекс]

Чтобы задать положение точки в пространстве, нам нужны три координаты ( x , y , z ), где координаты x и y определяют местоположение на плоскости, а координата z задает положение по вертикали над или под плоскостью. Трехмерное пространство имеет три ортогональных направления, поэтому нам нужно не два, а , три единичных вектора, чтобы определить трехмерную систему координат. В декартовой системе координат первые два единичных вектора являются единичным вектором 9″ role=»presentation»>i-j-k, определяет стандартную правую систему координат (положительная ориентация).

В трехмерном пространстве вектор [латекс]\vec A[/латекс] A→» role=»presentation «> имеет три векторных компонента: x -компонент [латекс]\vec A_x = A_x\underline{\hat{i}}[/latex] , который является частью вектора[latex]\vec A[/latex ] A→» role=»presentation»> по оси x ; компонент y [latex]\vec A_y = A_y\underline{\hat{j}}[/latex] , который является частью [latex]\vec A[/latex] A→» role=»presentation»> по и -ось; и z -компонента [латекс]\vec A_z = A_z \underline{\hat{k}}[/latex], которая является частью вектора вдоль z -оси. Вектор в трехмерном пространстве представляет собой векторную сумму трех его векторных компонентов:

[латекс]\vec A= A_x\underline{\hat{i}}+A_y\underline{\hat{j}}+A_z\ underline{\hat{k}}[/latex]

Если мы знаем координаты его начала b(x _b , y _b , z _b ) и его конца e(x _e , у 9{2}}[/latex] и его квадрат добавляется к квадрату A _z ², чтобы получить A ² . Обратите внимание, что когда z -компонента равна нулю, вектор полностью лежит в плоскости x-y , и его описание сводится к двум измерениям.

Источник: University Physics Volume 1, OpenStax CNX, https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/2-2-coordinate-systems-and-components-of-a-vector/

Декартова система координат является право-ортогональной системой. Это будет иметь значение, когда мы начнем рассматривать правило правой руки в разделе 3.1. Это означает, что когда вы рисуете два направления (скажем, x и y), то z должен идти либо вверх, либо вниз. Мы вернемся к этому позже.

В основном : Декартова система координат дает нам способ сообщить местоположение точки в пространстве. В 2-d мы используем [x, y], а в 3-d мы также включаем z: [x, y, z].

Применение: Если я пытаюсь пройти через комнату, я могу пройти по прямой линии 5 шагов или могу сделать 3 шага вправо и 4 шага вперед. Если бы я хотел описать положение, куда я попал в декартовой системе координат, это было бы [3, 4], предполагая, что x находится справа, а y — прямо.

Заглядывая вперед : Это будет связано со всем, что мы делаем в этом классе, особенно с перекрестными произведениями (1.5), крутящим моментом (1.6) и уравнениями равновесия (везде).

Земные координаты

Декартова система координат

Обычная декартова система координат, связанная с Землей, определяется следующим образом:

Начало координат — центр Земли.
Ось Z является осью вращения. Он пронзает Землю на полюсах и его положительное направление к северному полюсу. Земля вращается в положительном направлении вокруг этой оси Z: когда вы кладете правую руку на земной шар так, чтобы большой палец показывает на северный полюс, то Земля вращается в направлении пальцев («правило правой руки»).
Большие круги, проходящие через полюса, называются меридианами. Начальный меридиан проезд через Гринвич (Лондон).
Плоскость, ортогональная оси Z, является экваториальной плоскостью. а большой круг, расположенный в этой плоскости, есть экватор.
Ось x указывает на пересечение нулевого меридиана с экватором.
Ось Y находится в плоскости экватора, она ортогональна оси X и ориентированы так, что координаты образуют правую систему. Когда пальцы правой руки перемещаются от оси x к оси y, то большой палец показывает в направлении оси Z.

Каждая точка на Земле определена однозначно по его декартовым координатам (x, y, z). На самом деле будет достаточно только 2 координат, потому что каждая точка находится на поверхности сферы:

x ² + y ² + z ² = R ²

(1)

, где R радиус Земли = 6371,010 км.

Поскольку эта декартова система координат привязана к Земле, это вызов Земля-центрированная Земля-фиксированная (ECEF).

Сферическая система координат

Точки на Земле обычно задаются в сферической системе координат.

Сферические координаты произвольной декартовой точки P(x, y, z) :

Широта φ , которая представляет собой угол между и экватора.
Долгота λ , которая является углом между нулевым меридианом и меридиан, проходящий через OP .
Радиус r , который является расстоянием P от начала координат.

Поскольку радиус постоянный, два угла ( φ, λ ) равны достаточно указать точку на Земле:

-90° ≤ φ ≤ 90° (широта по меридиану)

(2a)

-180° < λ ≤ 180° (долгота по экватору)

(2b)

Долгота на полюсах произвольная и обычно устанавливается равной 0° по соглашению.

Мы можем легко найти связь между декартовыми и сферическими координатами. Пусть P(x, y, z) — декартова точка, а P’ — ее проекция. на плоскости x/y. Длина OP’ равна

r’ = r cos φ

(3)

Теперь мы можем вычислить декартовы координаты из сферических координат:

x = r’ cos λ = r cos φ cos λ

(4a)

y = r’ sin λ = r cos φ sin λ

(4b)

z = r sin φ

(4c)

Решение этих уравнений для ( φ, λ, r ) дает противоположное соотношение:

r = √ x ² + y ² + z ²

(5a)

)

(5с)

Здесь простодушное λ = arctan( y/x ), что справедливо только для -90° < λ < 90°, был заменен правильным atan2( y, x ), что дает -180° < λ ≤ 180°.

Геодезическая система координат

Сферическая система координат тесно связана с геодезической системой . В геодезической системе точки обозначаются широтой, долготой и возвышение (высота х ). Высота измеряется ортогонально базовой поверхности. который обычно представляет собой земной эллипсоид. Когда мы аппроксимируем Землю сферой с радиус R , затем

h = r — R.

(6)

Система координат ENU

Система координат ENU является локальной системой, характерной для любой точки P на земле. Он образован плоскостью, касательной к поверхность Земли в точке P . В этой плоскости
единичный вектор E указывает на восток,
единичный вектор N указывает на север.
Единичный вектор U точек вверх,
, т. е. ортогонален касательная плоскость.

Практическая система координат ENU используется напр. от Google Планета Земля и другие приложения для таргетинга и отслеживания.

Вектор E = (E _x, E _y, E _z) касается окружности постоянной широты, проходящей через P . Этот круг также называют «параллельным кругом», потому что он параллелен экватору. Тангенс получается взятием частных производных выражений (4) относительно λ и нормирование полученного вектора на длину 1:

E _x = — sin λ.

(7а)

E _y = cos λ.

(7b)

E _z = 0.

(7c)

Вектор N = (N _x, N _y, N _z) касается окружности меридиана, проходящей через P . Итак, взяв частные производные от выражений (4) по φ и нормируя полученный вектор на длину 1, получаем:

N _x = — sin(φ) cos(λ).

(8а)

N _y = — sin(φ) sin(λ).

(8b)

N _z = cos(φ).

(8с)

Единичный вектор U = (U _x, U _y, U _z) указывает в направлении P . Итак, положив в выражениях (4) r = 1, получим:

U _x = cos(φ) cos(λ).

(9а)

U _y = cos(φ) sin(λ).

(9b)

U _z = sin(φ).

(9c)

Преобразование ENU в ECEF

Рассмотрим точку Q , имеющую координаты (x, y, z) в системе ECEF и координаты Q’ = (e, n, u) в системе ENU расположен по адресу P = (P _x, P _y, P _z) . Сферические координаты P равны (φ, λ, R) . Затем следующее уравнение преобразует (e, n, u) в (x, y, z) :

-sin (λ)

-sin (φ) cos (λ)

cos (φ) cos (λ)

P _x

cos (λ)

-sin (φ) sin (λ)

cos (φ) sin (λ)

P _y

(10)

cos (φ)

sin (φ)

P _z

Обратите внимание, что столбцы матрицы преобразования M ^{2 ^{2
равны векторам Е , Н , У соответственно. Следовательно,
матрица M ортонормирована. Это соответствует
вращение системы XYZ вокруг начала координат в системе ENU (с центром в начале координат).
Преобразование строится путем первого поворота векторов X , Y , Z вокруг начала координат в Э , Н , У ,
а затем переводим эту систему на вектор P в свое конечное положение.}}

Преобразование может быть записано в краткой форме с использованием векторной и матричной записи:

Q = M Q’ + P

(11)

Преобразование ECEF в ENU

Преобразование ECEF в ENU получается путем обращения преобразования (11):

Q’ = M ^-1 ( Q — 7771 M 90 193 772 7 772 7 772 7 90 7 7 7 7 9 9 0 9 7 7 T ( Q — P )

(12)

Здесь мы использовали тот факт, что обратная ортонормированная матрица равна преобразованной матрице. Это уравнение в явном виде выглядит следующим образом:

-sin (λ)

cos (λ)

x — P _x

-sin (φ) cos (λ)

-sin (φ) sin (λ)

cos (φ)

y — P _y

(13)

cos (φ) cos (λ)

cos (φ) sin (λ)

SIN (φ)

Z — P _Z

(e, n, u)

(P _x, P _y, P _z)

(φ, λ, R)

Вдумчивый читатель наверняка заметил асимметрию в соответствующих преобразованиях (11) и (12), даже если они оба выражают повороты и переносы. Это очевидное проблема решается следующим образом. Уравнение (12) можно записать в виде:

Q ‘ = M ^-1 Q — M ^-1 P

(14)

. Р обратным вращением так, что его оси параллельны системе XYZ. Затем он транслируется вектором M ^-1 P таким образом, что его происхождение перемещено в начало координат O системы XYZ. Действительно, выражение М ^-1 П обозначает начало координат O = (0, 0, 0) ^T системы XYZ, выраженной в системе ENU, как мы можем видеть применив уравнение (14) к точке P = — M ^-1 P

(15)

Итак, уравнения (12) или (14) соответственно можно записать так:

Q’ = M ^-1 Q + O’

(16)

5 что равно

полностью симметричны уравнению (11).

Система координат у х z: Координаты точки и вектора — урок. Геометрия, 11 класс.