Символьные вычисления в matlab: Символьные вычисления в Matlab — CodeTown.ru

Symbolic Math Toolbox — Выполнение символьных математических вычислений

Транскрипция содержимого страницы

Если ваш браузер не отображает страницу правильно, пожалуйста, читайте содержимое страницы ниже

Symbolic Math Toolbox
Выполнение символьных математических вычислений
                Symbolic Math Toolbox™ содержит функции для решения и обработки символьных математиче-
                ских выражений, а также выполнения арифметических операций с произвольной точностью.
                Продукт позволяет осуществлять аналитическое дифференцирование, интегрирование,
                упрощения, преобразования, а также решать уравнения. Также можно преобразовывать
                символьные математические выражения в код для MATLAB ®, Simulink ® и Simscape™.
                Symbolic Math Toolbox™ включает язык MuPAD®, оптимизированный для обработки символь-
                ных математических выражений. Он содержит библиотеки функций MuPAD® как в общих
                математических областях (математический анализ и линейная алгебра), так и в специализиро-
                ванных (комбинаторика и теория чисел).   Кроме того, предусмотрена возможность писать
                собственные функции и разрабатывать библиотеки на языке MuPAD®. Встроенный редактор
                MuPAD позволяет перемежать текст с математическими формулами, форматированным
                текстом и выводом решений MuPAD, включая двух- и трехмерную графику. Документы,
                составленные в редакторе MuPAD, легко преобразовать в HTML или PDF-формат для публика-
                ций, отчетов и передачи коллегам.
                Symbolic Math Toolbox включен в студенческие версии MATLAB и Simulink.
                Основные особенности
                • Функции для символьного решения уравнений, дифференцирования, интегрирования,
                  упрощения, а так же вычисления трансформант и специальные функции.
                • Арифметика с произвольной точностью.
                • Язык символьной математики MuPAD.
                • Редактор MuPAD с возможностью встраивать текст, графику и символьную математику для
                  документирования и управления вычислениями, выполненными на языке MuPAD.
  • Библиотека функций MuPAD для общих математических областей, таких как линейная
                  алгебра и математический анализ, а также специализированных, таких как теория чисел и
                  комбинаторика.
                • Функции для генерации кода из символьных выражений для MATLAB, Simulink, Simscape,
                  C, Fortran, MathML и TeX.
                Расчеты в Symbolic Math Toolbox
                Symbolic Math Toolbox включает полный набор инструментов для символьных вычислений, что
                увеличивает возможности MATLAB. Непосредственно из командной строки MATLAB или из
                редактора MuPAD предоставляется доступ к обширному набору символьных функций. Функ-
                циональные возможности инструмента можно расширить, написав на языке MuPAD собствен-
                ные символьные функции или библиотеки. Symbolic Math Toolbox также позволяет преобразо-
                вывать символьные результаты для использования в MATLAB, Simulink и Simscape.  
1

Поверхность, созданная по символьному выражению и построенная из командной строки MATLAB
Параметрическая поверхность зависимости скорости от массы и упругости для системы
масса-пружина-демпфер, построенная с помощью редактора MuPAD
                                                                                           2

Арифметика с произвольной точностью
    Symbolic Math Toolbox позволяет задавать произвольную точность переменным и арифметиче-
    ским операциям. Арифметика с произвольной точностью особенно полезна в ситуациях, когда
    необходима повышенная точность вычислений. Порог точности можно установить настолько
    высоко, насколько это необходимо для всех математических функций и операций.
    Программирование с использованием арифметики произвольной точности
    Символьные вычисления в MATLAB
    Symbolic Math Toolbox позволяет выполнить символьные вычисления из командной строки
    MATLAB с определением символьных математических выражений и их обработкой.
  Функции
    вызываются с помощью синтаксиса, аналогичного синтаксису MATLAB, и доступны для
    широкого круга задач в различных областях.
    Математический анализ
    Возможности Symbolic Math Toolbox обширны и включают дифференцирование, вычисление
    определенного и неопределенного интеграла, нахождение пределов функций, выполнение
    суммирования и произведения рядов, нахождение ряда Тейлора и Лорана, Z и Фурье, прямое и
    обратное преобразование. Также доступно проведение векторного анализа, включая расчет
    ротора, дивергенции, градиента, Якобиана, Лапласиана и потенциала.
    Линейная алгебра
    Матричный анализ с символьными матрицами включает вычисление нормы, числа обуслов-
    ленности, детерминанта и характеристического полинома. Symbolic Math Toolbox поддержива-
    ет выполнение матричных операций и преобразование функций для вычисления обратной
    матрицы, экспоненциала и работы с колонками и строками матрицы. Также возможно выпол-
    нение сингулярного разложения матрицы в символьном виде и получение символьных выра-
    жений для собственных векторов и значений.  
    Преобразование формул и упрощения
    Symbolic Math Toolbox позволяет упрощать длинные выражения, трансформировать выраже-
    ния в конкретные формы или переписывать их для заданных условий, заменять часть выраже-
    ний на конкретные символы или численные значения.
    Решение уравнений
    Symbolic Math Toolbox включает символьную версию многих математических функций. Среди
    них функции Дирака, Бесселя, Гамма, Эйри, логарифмы, функция ошибок и др.
3

Выполнение MuPAD выражений
Из среды MATLAB можно выполнять выражения, записанные на языке MuPAD, что позволяет
получить полный доступ к функционалу библиотеки MuPAD, включенной в инструмент.
Интерактивные вычисления в редакторе MuPAD
Редактор MuPAD обеспечивает интерактивную среду для выполнения символьных вычислений
на языке MuPAD. Он включает панель символов для доступа к общим функциям MuPAD. Все
результаты отображаются в математическом виде, который может быть преобразован в
MathML или TeX. Для управления и документирования работы в редакторе можно вставлять
графики, анимации, пояснения. 
Symbolic Math Toolbox содержит функции для совместного использования редактором MuPAD
и рабочей средой MATLAB символьных переменных и выражений, что позволяет объединить
работу, которая делается в этих средах.
Использование редактора MuPAD для анализа явления Гиббса для периодически-ступенчатой функции.
Редактор MuPAD позволяет выполнять и документировать символьные вычисления
Программирование в среде MuPAD
Для создания пользовательских символьных функций и библиотеки языка MuPAD в редакторе
MuPAD имеется отладчик и другие программные утилиты. Язык MuPAD поддерживает не-
сколько стилей программирования, включая процедурное, функциональное и объектно-
ориентированное. Он также оптимизирован для обработки символьных математических
выражений и по умолчанию рассматривает переменные как символьные.
                                                                                                 4

Процедура MuPAD для вращения вектора в трех измерениях. Язык MuPAD оптимизирован для обработки
    символьных математических выражений
    Генерация кода для MATLAB, Simulink и Simscape
    Symbolic Math Toolbox предоставляет возможности для генерации функций MATLAB, блоков
    Simulink и языка Simscape на основе уравнений, состоящих из символьных выражений.
  Преобразование результатов анализа для использования в MATLAB, Simulink и Simscape
5

Результат символьных вычислений можно конвертировать в численные вычисления на основе
                         функций, которые, в свою очередь, можно использовать в других частях программы. Также
                         возможна конвертация символьных выражений в Cи, Fortran, MathML, и TeX-код.
                         Автоматическое создание функции MATLAB из символьных выражений
Дополнительная информация и контакты
Информация о продуктах                                      Сообщество пользователей
sl-matlab.ru/products                                       matlab.exponenta.ru
Пробная версия                                              Тренинги
sl-matlab.ru/trial                                          sl-matlab.ru/training
Запрос цены                                                 Контакты
sl-matlab.ru/price                                          sl-matlab.ru
                                                            E-mail: matlab@sl-matlab.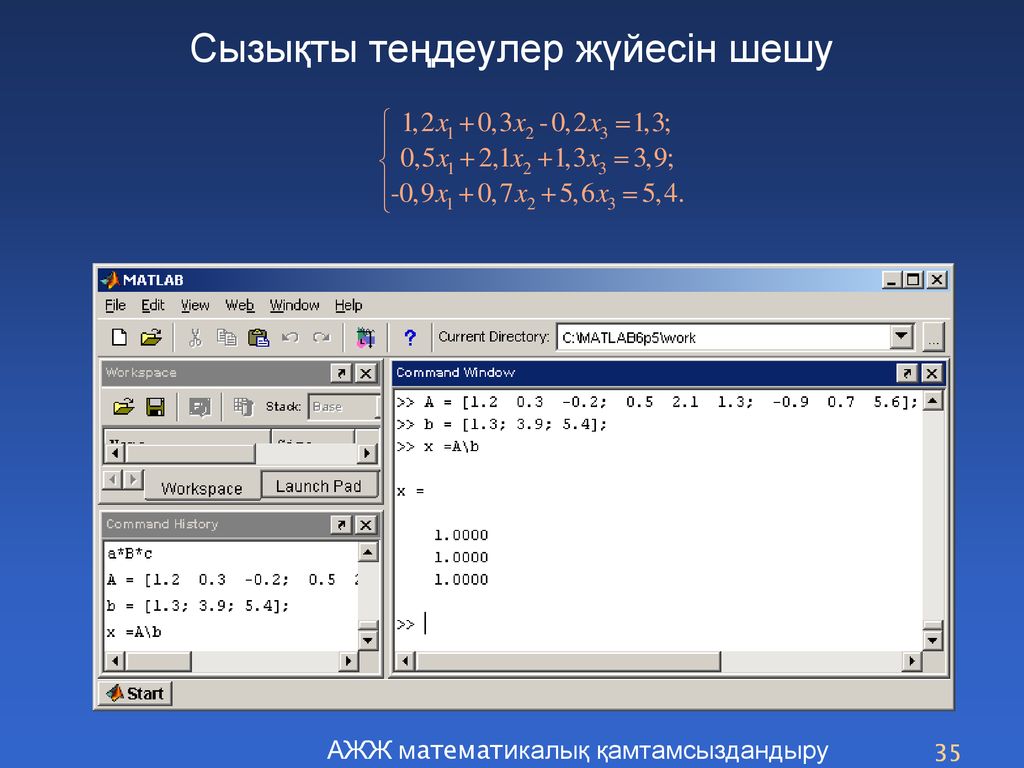  ru
Техническая поддержка
                                                            Тел.: +7 (495) 232-00-23, доб. 0609
sl-matlab.ru/support
                                                            Адрес: 115114 Москва, Дербеневская наб., д. 7, стр. 8
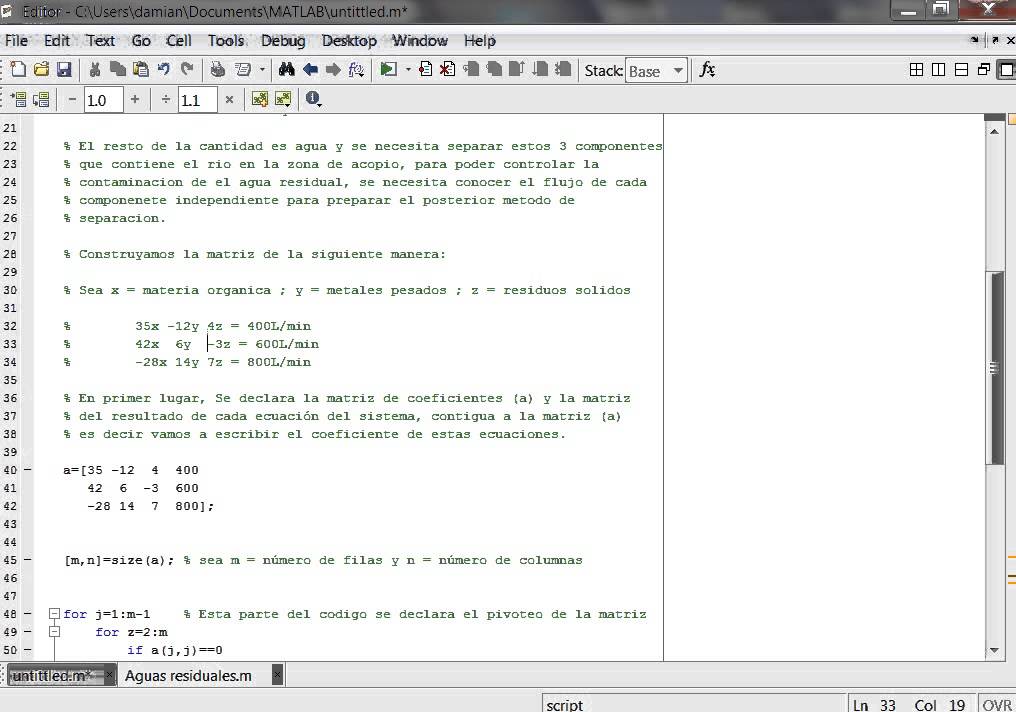
                                                                                                                    6

Символьные вычисления при помощи нейронных сетей

Нейронные сети хороши в решении статистических задач, в распознавании и генерации речи и изображений. В новой статье, опубликованной на arxiv.org, исследователи из Facebook AI Research показали, что нейросети позволяют получать отличные результаты также в символьном интегрировании и решении дифференциальных уравнений. Причём результаты нейросетей превосходят результаты в решении аналогичных задач коммерческих систем компьютерной алгебры, таких как Matlab или Mathematica.

Сама идея «механизировать» символьные вычисления появилась ещё на рубеже девятнадцатого и двадцатого веков.

В чём тут смысл?

Если у нас есть некоторое арифметическое выражение, например

2 + 10 × 6,

то для получения ответа нам не обязательно привлекать лучшего математика планеты. Вообще говоря, сойдёт и аккуратный исполнитель, который проводить математические исследования, быть может, и не умеет, но зато способен точно исполнять инструкции вида: «если встретились два числа, разделённые знаком +, то надо следовать алгоритму [описание алгоритма сложения в столбик]», или: «если встретились два числа, разделённые знаком ×, то надо следовать алгоритму [описание алгоритма умножения в столбик]».

Иными словами, арифметику и даже более сложную математику таким способом можно превратить в аналог «конвейера по сборке чего-то там»: вычисление разбивается на этапы, каждый из которых можно выполнить, следуя заранее описанной последовательности действий, почти без раздумий, и потому выполнять эти действия могут самую малость обученные «работники конвейера», а не только «топовые математические инженеры».

Однако «арифметикой чисел» дело не ограничивается. Превратить в конвейер можно и «арифметику символов». Это несколько сложнее, однако вполне достижимо.

Для этого выражение, содержащее не только числа и знаки операций с ними, но и буквы, следует трактовать, как «текст» на некотором языке, для которого определены правила допустимых «замен».

Например, правило может быть таким:

a_ × c_ + b_ × c_ → (a+b) × c

Это правило трактуется следующим образом: «если нам встретилось какое-то выражение, в дальнейшем называемое a, потом символ ×, потом ещё какое-то выражение, называемое c, потом символ +, потом какое-то выражение, называемое b, потом символ ×, потом точно то же, что и в прошлый раз, выражение c, то такую конструкцию можно заменить на (a + b) × c, где на место a, b и c подставлены соответствующие выражения».

Расшифровка может показаться громоздкой, однако, если понять смысл самого процесса, то его краткая символьная запись окажется довольно понятной. Мы, например, взглянем на выражение

2 × x + (3+y) × x

и поймём, что его можно преобразовать в

(2+3+y) × x,

поскольку 2 играет роль a в вышеописанном правиле, (3 + y) — роль b, а x — роль c.

Задав через такие правила все возможные алгебраические преобразования, мы можем поручить «работнику конвейера» перебрать все возможные трансформации интересующего нас выражения: пусть он возьмёт выражение, найдёт все места, соответствующие правилу 1, и применит к ним это правило, получив столько возможных «альтернатив» для исходного выражения, сколько было найдено таких мест. Потом он то же самое проделает с правилом 2. И так далее, пока не переберёт все правила. Потом пусть с каждым элементом получившегося списка «альтернатив» он проделает то же самое.

Если среди правил нет таких, которые делают выражение длиннее, то за — пусть довольно большое — но конечное количество шагов он переберёт все возможные трансформации исходного выражения.

Среди них мы можем найти, например, самую короткую форму — это будет «конвейерное» упрощение выражений. Или, если в выражении был знак «=», то мы можем найти такое преобразование, где слева от «=» стоит «x», и это будет решением уравнения относительно x.

Таков общий смысл «автоматизированных символьных вычислений», который раскрывается особенно эффектно, когда в качестве «работника конвейера» выступает компьютер — не устающий, быстро работающий и не ошибающийся. Ведь с его помощью от чисто механической деятельности в этой области можно освободить не только академиков, но и вообще всех людей в целом.

И такие системы на данный момент реализованы в относительном изобилии: Mathematica, Maple, Matlab и ряд других программ/библиотек содержат реализацию данного алгоритма вместе с довольно обширным набором правил преобразования, позволяющий им упрощать выражения, решать уравнения, брать производные и т. п.

Единственная проблема со всем этим в том, что полный перебор хоть и возможен, но для некоторых исходных выражений займёт очень много времени.

Подобная ситуация, кстати, аналогична тому, что имело место при реализации искусственного интеллекта для игры в шахматы: полный перебор позволяет найти наилучший ход, но займёт очень много времени. А потому и решение проблемы напрашивается аналогичное: некоторые «ветви» дерева перебора надо отсекать как бесперспективные, ещё на самых ранних этапах. Если это сделать, то смартфон будет в состоянии обыгрывать чемпионов мира — даже с ограничениями на время «обдумывания» каждого хода, а не за время жизни вселенной.

В шахматах, как мы знаем, это сработало. И вот недавно группа исследователей, состоящая из Гийома Лампла (Guillaume Lample) и Франсуа Шартона (François Charton), попробовала проделать аналогичное с символьным интегрированием и решением дифференциальных уравнений.

Существуют способы записи математических выражений в «линейной» форме.

Например, выражение

Может быть записано, как

(a+b)/c

Если пойти дальше и ввести понятие «бинарных» (с двумя аргументами) и «унарных» (с одним аргументом) операторов, то форма записи может стать ещё более регулярной.

Divide(Plus(a,b),c)

А отсюда уже один шаг до того, чтобы прийти к записи

Divide,Plus,a,b,c

Здесь уже нет понятия «приоритета операций» («сначала выполняется умножение, а потом сложение», и т. п.) и скобок, однако всё равно любая запись в такой форме имеет единственный смысл и, наоборот, любое математическое выражение можно преобразовать в такую форму.

Преимуществом же такой формы оказывается то, что записанное таким образом математическое выражение становится очень похожим на фразу на каком-то языке, а применение к нему некой операции (например, «интегрирования по переменной икс») — аналогичным переводу фразы с одного естественного языка на другой (роль «слов» здесь играют наборы символов, разделённые в вышеприведённом примере запятыми).

Мэйнстримом машинного перевода сейчас являются нейронные сети, преобразующие одну последовательность слов в другую.

Непричастным нейронные сети могут казаться какой-то очень сильной магией, но смысл их устройства довольно прост. У нас есть некоторая функция от набора входных параметров, возвращающая некоторое значение. Внутри этой функции есть коэффициенты, которые как раз и подбираются во время обучения. Обучение же состоит в том, что сначала мы выбираем совершенно случайные коэффициенты, а потом начинаем последовательно брать данные из обучающего набора, на каждом шаге слегка модифицируя коэффициенты так, чтобы то, что выдала функция для текущих входных параметров, стало поближе к известному нам значению, соответствующего этим входным параметрам.

На простом примере это можно представить так. Есть у нас набор точек на плоскости.

Мы, предположим, видим, что они расположены вроде бы почти на одной прямой. Мы можем взять уравнение прямой

y(x) = a × x + b

и попытаться подобрать a и b так, чтобы получившаяся прямая прошла как можно ближе ко всем этим точкам.

Сначала мы берём какие-то случайные числа в качестве a и b, потом берём первую известную нам точку и смотрим, как сильно игрек, вычисленный от её икса, отличается от того, который нам известен. После этого слегка подправляем a и b, чтобы отклонение стало поменьше. Потом берём вторую известную нам точку и повторяем для неё то же самое. И так далее, пока отклонения не станут достаточно для нас малыми.

В нейронных сетях функция сложнее, а коэффициентов существенно больше, но идея примерно та же самая.

Однако роль «иксов» и «игреков» могут играть не просто какие-то числа, а номера слов языка (предположим, что мы все возможные слова пронумеровали), роль же входных данных в этом случае будет играть набор предложений, переводы которых нам известны (например, их сделал человек-переводчик).

Правда, нейронная сеть в данном случае будет использоваться не для «угадывания» номера слова, а для оценки того, насколько хорошо слово с таким-то номером подходит к ситуации.

Тогда для перевода каждого слова в предложении мы можем пройти по всему списку слов второго языка и выбрать те, которым нейронная сеть проставила наилучшие оценки, в качестве гипотез. И повторять это, пока не получится предложение с наилучшей совокупной оценкой.

Несмотря на то, что это всё аналогично перебору вариантов, есть большой плюс: мы можем задать количество отбираемых на каждом шаге наилучших гипотез и таким образом радикально сократить количество перебираемых вариантов.

Аналогично действуют и современные системы ИИ для игры в шахматы — они тоже некоторым образом оценивают каждый из возможных на данном этапе ходов и выбирают некоторое количество тех, у которых оценка наилучшая, для анализа возможных последующих ходов. Из которых для анализа последующих тоже будут выбраны не все, а лишь некоторое количество с наилучшими оценками.

Ключевое же отличие шахматного интеллекта и машинного перевода в том, что последний даёт хорошие результаты, если в качестве входных данных брать не только несколько «текущих» слов, а ещё и что-то вроде «текущего состояния» нейронной сети, в которое она пришла после перевода предыдущих слов. Это оказывается аналогом «понимания контекста» — ведь слова естественных языков обретают смысл не только сами по себе, но ещё и в зависимости от того, какие слова стоят в относительной от них близости.

Нейронная сеть, которая «помнит контекст», как раз и была использована для символьных вычислений в данном исследовании.

Однако что взять в качестве данных для обучения такому «переводу»?

Тут, внезапно, ситуация даже проще, чем с естественными языками. Ведь для генерации набора примеров на последних нам нужен человек-переводчик, предоставивший нам правильные переводы фраз, которые будут использоваться для обучения нейронной сети делу оценки гипотез. В случае же с математическими выражениями мы можем просто генерировать их случайным образом, потом автоматически брать их производную (в отличие от интегрирования, взятие производной — гораздо более простая операция) и считать её входным «подынтегральным» выражением с известным ответом (этим самым случайным выражением).

Кроме того, мы можем сгенерировать случайные выражения и попытаться взять их интеграл при помощи систем компьютерной алгебры, отбирая в данные для обучения те, с которыми используемая нами система справилась.

Наконец, при помощи известной закономерности — правила «интегрирования по частям» — мы можем скомбинировать выражения из предыдущих пунктов, чтобы получить ещё одну порцию данных.

Именно таким образом в данном исследовании были получены данные для обучения интегрированию. И похожим по подходу способом — для решения дифференциальных уравнений.

В итоге алгоритм действительно заработал: нейронная сеть стала «предсказывать» ответ, собирая его по частям из наилучших гипотез, аналогично тому, как предложение на одном языке переводится на другой язык при помощи нейронных сетей.

Более того, согласно авторам исследования, этот метод справлялся с целым рядом тех выражений, с которыми не справлялись наиболее мощные из существующих системы компьютерной алгебры.

Правда, тут надо учесть, что у этих систем ограничивалось время поиска, а потому нельзя утверждать, что они бы вообще не нашли ответ — возможно, нашли бы, но не за тридцать секунд и не за три минуты, а, например, за пять часов.

Тем не менее, результаты всё равно впечатляют и вдохновляют: 99,6% успешных взятий интеграла у этой системы против 84% у Mathematica (с ограничением в 30 секунд) и 65,2% у Matlab.

97% успешных решений дифференциальных уравнений первого порядка против 77,2% у Mathematica.

81% успешных решений дифференциальных уравнений второго порядка против 61,6% у Mathematica.

Наконец, весьма интересна и ещё одна составляющая данного процесса.

Человек, конечно, тоже может решать задачу механическим перебором, однако ещё он на основе своего опыта может «видеть» перспективные направления этого перебора, чем радикально сокращать время поиска. Ранее, аналогичный процесс был сымитирован для игр в шахматы и го, но теперь есть пример его имитации для решения математических задач. Это — ключ как к лучшему пониманию работы человеческого интеллекта, так и к совершенствованию алгоритмов работы искусственного.

символьных вычислений в MATLAB — MATLAB и Simulink

Перейти к содержимому

Основное содержание

Символьные переменные, выражения, функции, преобразования между символьным и числовым

Symbolic Math Toolbox™ позволяет вам выполнять символьные вычисления из командной строки MATLAB ^® , задав специальный тип данных — символические объекты. Функции вызываются с использованием знакомого синтаксиса MATLAB. и доступны для интеграции, дифференциации, упрощения, решение уравнений и другие математические задачи. Символьные вычисления расширить числовые возможности MATLAB. Вы можете конвертировать символические результаты в числовые результаты и использовать их вне Symbolic Math Toolbox.

Категории

• Символьные переменные, выражения, функции и настройки
  Создание символьных переменных, выражений, функций, и установить настройки
  
• Операторы и элементарные операции
  Выполнение арифметических, реляционных и логических операций над символическими объекты
  
• Преобразование между символьными и числовыми
  Преобразование символьных данных в числовые, преобразование числовых значений в символьные объекты
  
• Единицы измерения
  Использовать физические единицы, конвертировать единицы, проверять согласованность единиц и совместимость
  

Избранные примеры

Физика затухающего гармонического осциллятора

Исследует физику затухающего гармонического осциллятора путем решения уравнений движения в случае отсутствия движущих сил. Этот пример исследует случаи недо-, сверх- и критического демпфирования.

Моделирование движения периодического качания маятника

Смоделируйте движение простого маятника с помощью Symbolic Math Toolbox™. Выведите уравнение движения маятника, затем решите уравнение аналитически для малых углов и численно для любого угла.

Оценка средней мощности, вырабатываемой ветровой турбиной

Использует Symbolic Math Toolbox™ и Statistics and Machine Learning Toolbox™, чтобы исследовать и получить параметрическое аналитическое выражение для средней мощности, вырабатываемой ветровой турбиной.

Разработка алгоритма для неискажения изображения

Разрабатывает математическую модель с использованием Symbolic Math Toolbox™, чтобы неискажать изображение и имеет локальную функцию в живом сценарии.

Электрический дипольный момент и мощность излучения

Находит среднюю мощность излучения двух притягивающих зарядов, движущихся по эллиптической орбите (электрический диполь).

Подтвердите модель Simulink с помощью Symbolic Math Toolbox

Смоделируйте прыгающий мяч, представляющий собой классическую гибридную динамическую систему. Эта модель включает в себя как непрерывную динамику, так и дискретные переходы. Он использует Symbolic Math Toolbox™, чтобы помочь объяснить некоторые теории, лежащие в основе решения ОДУ в моделировании прыгающего мяча.

Использование Symbolic Mathematics с решателями Optimization Toolbox

Используйте функции Symbolic Math Toolbox™ jacobian и matlabFunction для предоставления аналитических производных решателям оптимизации. Решатели Optimization Toolbox™ обычно более точны и эффективны, когда вы предоставляете градиенты и гессианы функций цели и ограничений.

Аналитическая модель консольной ферменной конструкции для Simscape

Найдите параметризованные аналитические выражения для смещения соединения тривиальной консольной ферменной конструкции как в статической, так и в частотной областях.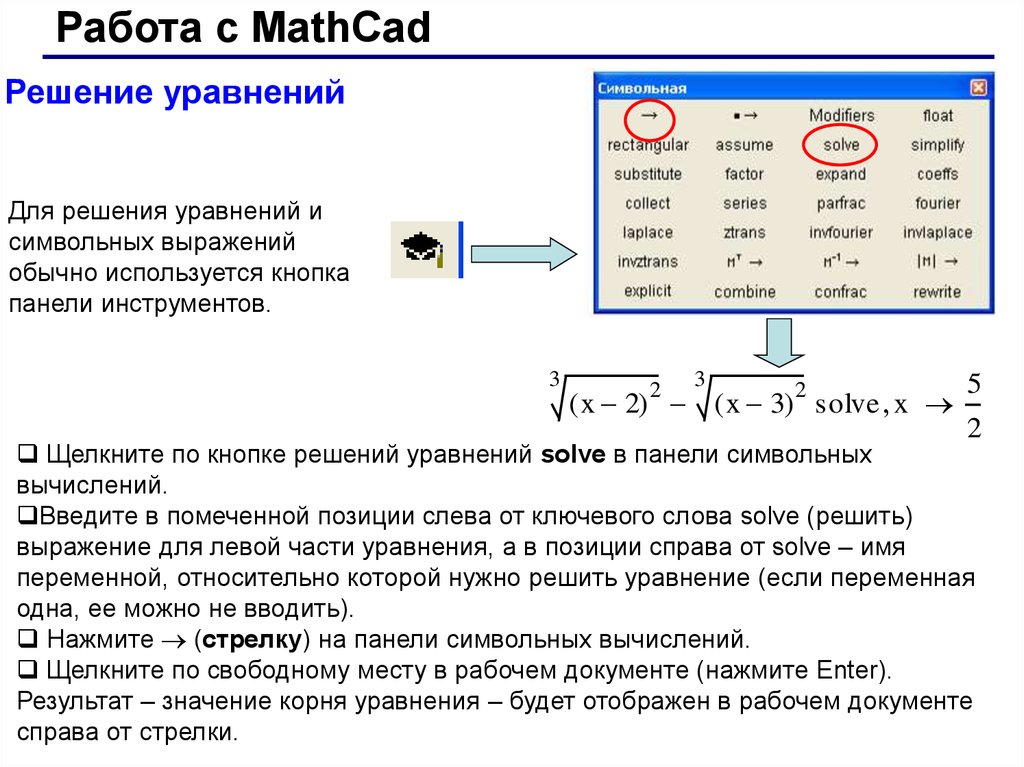 Аналитическое выражение для статического случая является точным. Выражение для функции частотной характеристики является приблизительной версией фактической частотной характеристики уменьшенного порядка.

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .

Вы также можете выбрать веб-сайт из следующего списка:

Европа

Свяжитесь с местным офисом

• Пробная версия ПО
• Пробная версия ПО
• Обновления продуктов
• Обновления продуктов

Начало работы с Symbolic Math Toolbox

Выполнение символьных математических вычислений

Symbolic Math Toolbox™ предоставляет функции для решения, построения графиков и управления символьными математическими операциями уравнения. Вы можете создавать, запускать и совместно использовать символьный математический код. В МАТЛАБ ^® Live Editor, вы можете получить предложения по следующим шагам для символических рабочих процессов. набор инструментов предоставляет функции в общих математических областях, таких как исчисление, линейная алгебра, алгебраические и дифференциальные уравнения, упрощение уравнений и уравнение манипуляция.

Symbolic Math Toolbox позволяет аналитически выполнять дифференцирование, интегрирование, упрощение, преобразований и решения уравнений. Вы можете выполнять размерные вычисления и конвертировать между единицами. Ваши расчеты могут быть выполнены либо аналитически, либо с использованием арифметика с переменной точностью, результаты отображаются в математическом наборе.

Вы можете поделиться своей символической работой с другими пользователями MATLAB в виде живых сценариев или преобразовать их в документы HTML, Word, LaTex или PDF.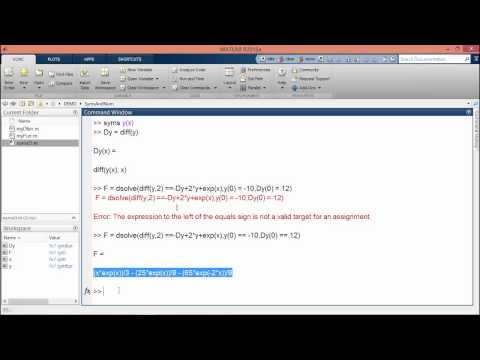 Вы можете генерировать функции MATLAB, функциональные блоки Simulink ^® и уравнения Simscape™ непосредственно из символьных выражений.

Учебные пособия

• Создание символьных чисел, переменных и выражений

  Использование символьных значений и переменных для выполнения аналитических вычислений.

• Создание символьных функций

  Использовать символьные функции, которые принимают символьные входные данные для аналитических целей. расчеты.

• Создание символьных матриц

  Использование матриц, содержащих символьные значения.

• Создание переменных символьной матрицы

  Использование переменных символьной матрицы.

• Использование символических объектов для представления математических объектов

  Использование символических объектов для представления математических объектов.

• Выполнение символьных вычислений

  Выполнение операций над символическими объектами.

• Использование предположений о символических переменных

  Смоделируйте проблему и получите более простые результаты с помощью предположения.

Дополнительная информация

Рекомендуемые примеры

Computational Mathematics in Symbolic Math Toolbox

Содержит обзор Symbolic Math Toolbox™, который предлагает полный набор инструментов для вычислительной и аналитической математики.

Изучайте исчисление в Live Editor

Изучайте исчисление и прикладную математику с помощью Symbolic Math Toolbox™. В примере показаны вводные функции fplot и diff.

Дифференциация

Аналитически найдите и оцените производные с помощью Symbolic Math Toolbox™. В примере вы найдете 1-ю и 2-ю производную f(x) и используете эти производные для нахождения локальных максимумов, минимумов и точек перегиба.