Шестнадцатиричная система счисления сообщение: Чему равно основание шестнадцатеричной системы счисления. Шестнадцатеричная нумерация и адресация

Шестнадцатеричная система счисления

Использует шестнадцать цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 в их обычном смысле, а затем A=10, B=11 , C=12 , D=13 , E=14 , F=15 . Также использует символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа. Внедрена американской корпорацией IBM. Широко используется в программировании для IBM-совместимых компьютеров. С другой стороны, в некоторых языках сохранились и следы использования этой системы счисления в прошлом.

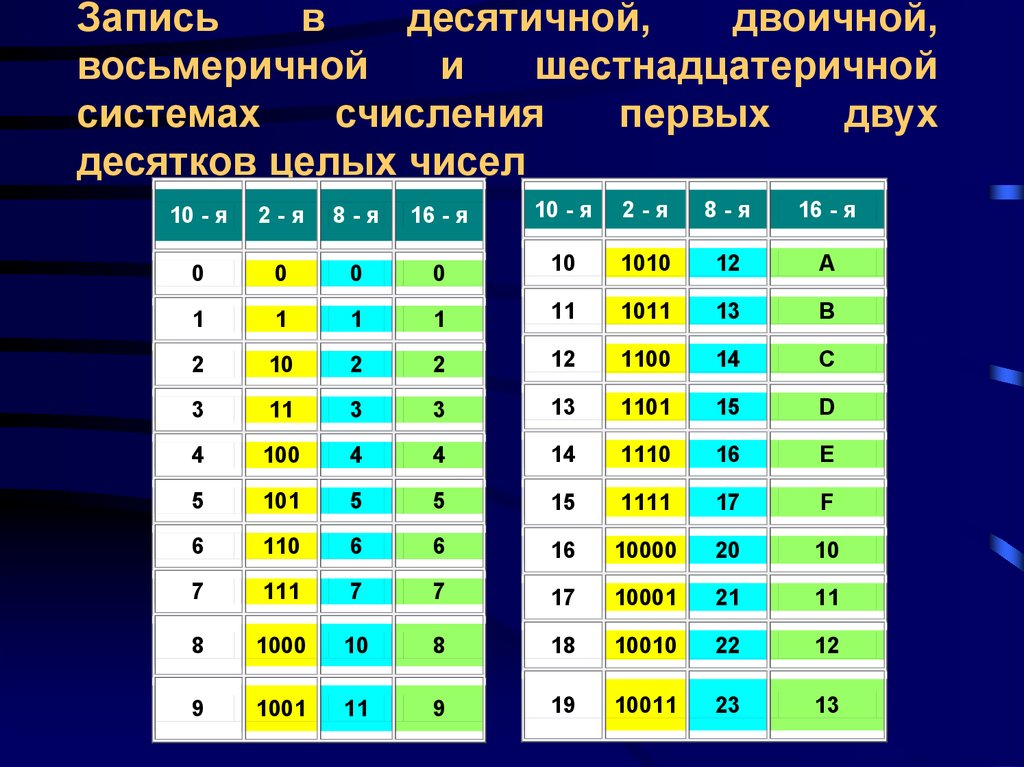
BIN	OCT	DEC	HEX
0	0	0	0
001	1	1	1
010	2	2	2
011	3	3	3
100	4	4	4
101	5	5	5
110	6	6	6
111	7	7	7
1 000	10	8	8
1 001	11	9	9
1 010	12	10	A
1 011	13	11	B
1 100	14	12	C
1 101	15	13	D
1 110	16	14	E
1 111	17	15	F
10 000	20	16	10

Для перевода чисел из восьмеричной и шестнадцатеричной систем в двоичную существует простой способ: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) — для восьмеричной системы или тетрадой (четверкой цифр) — для шестнадцатеричной системы.

Переведем число 6238 в двоичную систему. Для этого каждую цифру заменим на ее перевод в двоичную систему. Каждое полученное число при необходимости дополним слева нулями до трех цифр. Эти нули называются незначащими.

Полученное число равно 110 010 011₂.

Таким образом, 623₈ = 110 010 011₂.

Аналогично делаем для перевода из шестнадцатеричной системы в двоичную, но дополняя слева нулями до четырех цифр.

Переведем число A01F16 в двоичную систему:

Полученное число равно 1010 0000 0001 1111₂.

Значит, A01F₁₆ = 1010 0000 0001 1111₂.

Для перевода двоичного числа в восьмеричное, его надо раз_ бить на группы по три цифры справа налево и заменить каждую группу одной восьмеричной цифрой.

Примеры

Аналогично, для перевода двоичного числа в шестнадцатеричное, нужно разбить число на группы по четыре цифры справа налево и заменить каждую группу одной шестнадцатеричной цифрой.

Примеры

Заметьте, что максимальное двоичное число, которое можно записать тремя цифрами — 111, и оно равно десятичному (или восьмеричному) числу 7. А максимальное двоичное число, которое можно записать четырьмя цифрами, — 1111, и оно равно десятичному числу 15

или шестнадцатеричному F.

Шестнадцатеричная система счисления — презентация

1

Первый слайд презентации: Шестнадцатеричная система счисления

Работу выполнил: Кудряев Кирилл

Изображение слайда

2

Слайд 2: Понятие :

Шестнадцатеричная система счисления — это позиционная система счисления с основанием 16. Для записи чисел в шестнадцатеричной системе используется 10 цифр от нуля до девяти (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и латинские буквы A, B, C, D, E, F, обозначающие числа от 10 до 15. Таким образом, все символы шестнадцатеричной системы : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Изображение слайда

3

Слайд 3: История:

Шестнадцатеричная система счисления внедрена американской корпорацией IBM. Широко используется в программировании для IBM-совместимых компьютеров. Минимальной адресуемой (пересылаемой между компонентами компьютера) единицей информации является байт, состоящий, как правило, из 8 бит (англ. bit — binary digit — двоичная цифра, цифра двоичной системы), а два байта, то есть 16 бит, составляют машинное слово (команду). Таким образом, для записи команд удобно использовать систему с основанием 16.

Изображение слайда

4

Слайд 4: Применение:

Шестнадцатеричная система используется в цифровой электронике и компьютерной технике, в частности в низкоуровневом программировании на языке ассемблера для различных ЭВМ.

Изображение слайда

5

Слайд 5

Для шестнадцатеричной системы, как и для восьмеричной, характерен легкий перевод в двоичную систему счисления и обратно с помощью простой таблицы, в которой все цифры шестнадцатеричной системы от 0 до F(15) представлены в виде двоичных тетрод (четверок): 0 16 0000 2 1 16 0001 2 2 16 0010 2 3 16 0011 2 4 16 0100 2 5 16 0101 2 6 16 0110 2 7 16 0111 2 8 16 1000 2 9 16 1001 2 A 16 1010 2 B 16 1011 2 C 16 1100 2 D 16 1101 2 E 16 1110 2 F 16 1111 2. Виды переводов:

Изображение слайда

6

Слайд 6

Обратный перевод из шестнадцатеричной системы счисления в двоичную также прост. Для этого в двоичной записи числа нужно выделить тетроды (четверки) и заменить каждую тетроду соответствующей шестнадцатеричной цифрой. Отсчитывать тетроды нужно справа налево. В случае необходимости неполные тетроды дополняются нулями. Например: 1110111101 2 = 0011 1011 1101 2 = 3BD 16

Изображение слайда

7

Слайд 7: Использование 16-тиричной системы счисления:

Сейчас шестнадцатеричная система используется для обозначения цвета в языке гипертекстовой разметки HTML, графических программах. Чтобы задать определенный цвет применяются комбинации RGB-значения цвета (Red Green Blue — красный, зеленый, синий), записанные в шестнадцатеричном виде. Перед обозначением цвета ставят символ решетки (префикс). Например: # 7B917B — Первое число — 7B — отвечает за красную составляющую, второе — 91 — за зеленую и третье — 7B — за синюю.

Изображение слайда

8

Слайд 8: Синтаксис использования:

В различных системах и языках программирования используется разный синтаксис для обозначения шестнадцатеричных чисел.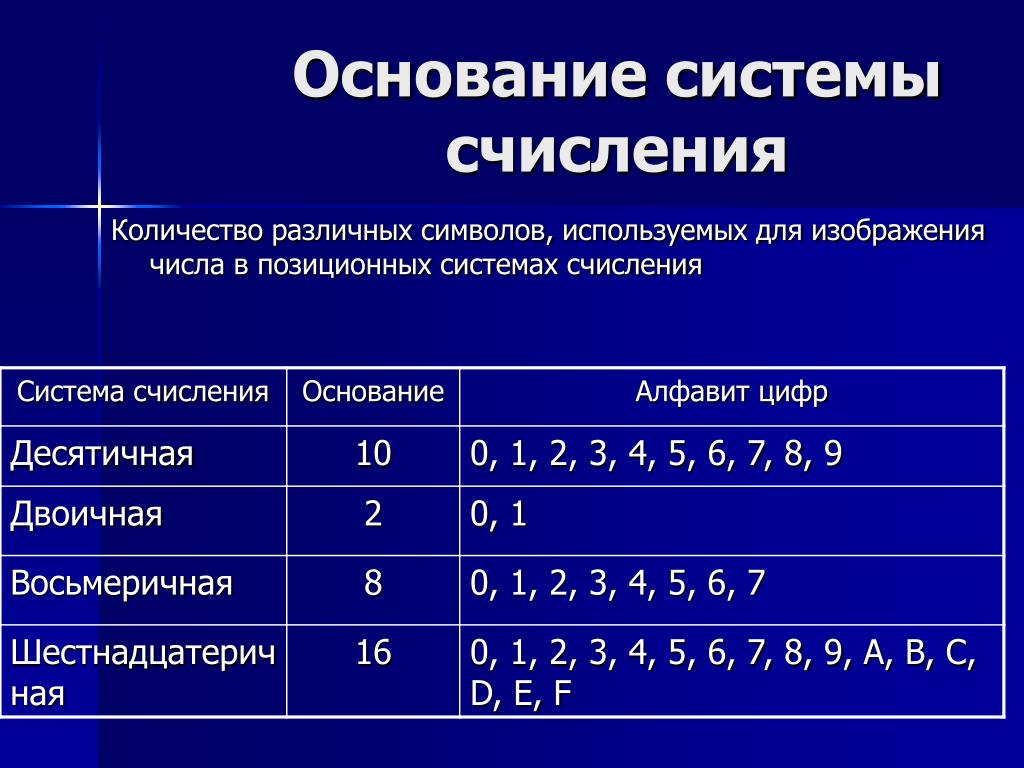 В ассемблерах используют букву h (от англ. hexadecimal ) в конце числа, например: 5A3h 16 = 1443 10, при этом, если число начинается не с цифры, а с буквы, впереди ставится 0, например: 0FFh 16 = 255 10, для того, чтобы отличать число от других идентификаторов. В Паскале (Pascal) и Бейсике (Basic) используют префикс $, например: «$5A3», в некоторых версиях Бейсика используется также сочетание «&h».

Изображение слайда

9

Слайд 9: Переводы:

В двоичную: В Десятеричную: В Восьмеричную:

Изображение слайда

10

Слайд 10: Правило перевода 10 – тичной :

Для перевода чисел из шестнадцатеричной системы счисления в десятичную сосчитаем количество разрядов шестнадцатеричного числа N и запишем степени шестнадцати от нулевой до N — 1 справа налево (помним, что каждая последующая степень получается умножением предыдущей на 16). Запишем под ними шестнадцатеричное число в прямом порядке. Умножим записанные числа на соответствующие им степени. Найдем сумму всех произведений. Результатом будет десятичное число, представленное в виде суммы различных степеней числа 16, умноженных на соответствующие коэффициенты.

Изображение слайда

11

Слайд 11: Пример:

Перевести число 21 16 в десятичную систему. Считаем число разрядов — 2, значит, нужно записать справа налево степени шестнадцати от нулевой до первой: 16 1 16 0 16 1 Запишем под степенями наше шестнадцатеричное число (слева направо, как есть): 16 1 2 1 Умножим числа на соответствующие степени шестнадцати и сложим их: 2 * 16 + 1 * 1 = 32 + 1 = 33, это и есть результат перевода: 21 16 = 33 10 Таким образом, шестнадцатеричное число 21 1 представлено в виде суммы ряда степеней числа 16 (основание шестнадцатеричной системы):

Изображение слайда

12

Слайд 12: И для общего кругозора:

С помощью специальной программы — шестнадцатеричного редактора чисел, можно просмотреть любой файл в виде набора байтов, представленных в шестнадцатеричном коде и внести определенные изменения. Это широко используется как для отладки, так и для взлома программ.

Изображение слайда

13

Последний слайд презентации: Шестнадцатеричная система счисления

Спасибо за внимание

Изображение слайда

Tech Stuff — Hexadecimal, Decimal and Binary

Основной единицей, используемой в компьютерном мире, является байт (также известный как октет), байт (или октет) состоит из 8 битов (также известных как двоичные цифры). Большинство современных систем используют кратные байты, таким образом, 16-битная система состоит из 2 байтов (2 x 8 = 16), 32-битная система состоит из 4 байтов (4 x 8 = 32), а 64-битная система состоит из 2 байтов (4 x 8 = 32). имеет 8 байт (8 x 8 = 64). Термин слово , как и в описании 32-битное слово, в значительной степени исчез из технического лексикона.

Содержимое любого байта, например, в ячейке памяти или в сети, может быть выражено во многих системах нумерации . Наиболее часто используемые системы нумерации: Десятичная , Шестнадцатеричная и Двоичная :

Система нумерации	База	Диапазон	Примечания
Десятичный	база 10	0 — 1,2,3…	Самая распространенная система счисления — долларовая, метрическая и т.д. Байт (8 бит) имеет 256 возможных значений в диапазоне 0 — 255
Двоичный	база 2	0 — 1	Базовый уровень, на котором работает электронная схема компьютера — один бит.
Шестнадцатеричный	база 16	0-9, А-Ф	Каждый шестнадцатеричный символ представляет 4 бита (0 — 15 десятичных), которые называются полубайтом (маленький байт — честно!). Байт (или октет) состоит из 8 бит, поэтому он всегда представлен двумя шестнадцатеричными символами в диапазоне от 00 до FF.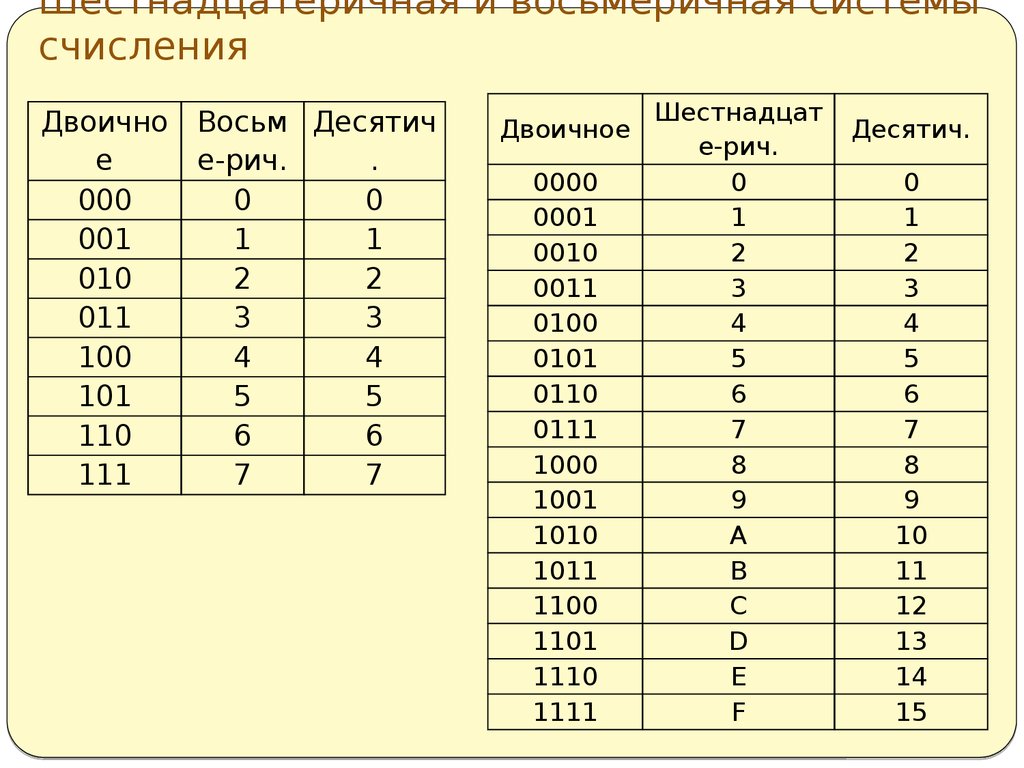

Историческая справка: Когда-то, когда мир и даже автор этой страницы были молоды, компьютеры были построены с 12-битными, 24-битными и даже 36-битными словами (в этом был какой-то смысл тогда просто выглядит странно сегодня). Каждый из этих размеров слова делится на 3 и использует восьмеричную систему счисления (с основанием 8). Каждый 3-битный элемент содержит 8 значений в диапазоне от 0 до 7. Таким образом, ячейка памяти с 12-битным двоичным значением 000.001.100.111 будет записана в восьмеричной форме как 0147.

Нумерация битов

При работе с двоичными данными каждый бит внутри байта (октета) может потребоваться идентифицировать с помощью метода, называемого нумерацией битов. Нумерация битов может быть очень запутанной, поскольку различные стандартные органы принимают разные соглашения. Ниже приведены все допустимые и используемые соглашения о нумерации битов для описания 8-битного байта (октета).

Содержимое памяти	0	0	0	0	0	0	0	0
Правила нумерации битов
Слева направо основание 0 (IETF)	0	1	2	3	4	5	6	7
Основание слева направо 1	1	2	3	4	5	6	7	8
Справа налево основание 1 (ITU)	8	7	6	5	4	3	2	1
Степень числа 2	7	6	5	4	3	2	1	0

Всегда проверяйте, какое соглашение используется в любой спецификации. Мы смирились с неизбежным и используем стандарт слева направо с основанием 0 (IETF) , поскольку благодаря Интернету он широко используется и, надеюсь, столь же широко понятен. Обоснование IETF для этого стандарта заключается в том, что он также однозначно представляет то, что называется сетевым порядком , то есть бит 0 идет в сеть первым, бит 1 вторым и так далее. Биты также имеют тенденцию выходить из сети в том же порядке, в котором они были отправлены. Использование сетевого порядка необходимо, поскольку внутреннее (машинное) представление данных может сильно различаться (вся эта ерунда с обратным порядком байтов и прямым порядком байтов), но когда данные загружаются в сеть, они должны быть в согласованном порядке, который может быть использован любая система, независимо от ее внутреннего представления, которая хочет использовать данные.

Наконец, при работе с двоичными файлами вы часто будете сталкиваться с терминами «старший значащий бит» (MSB) и «наименее значащий бит» (LSB). MSB всегда находится СЛЕВА, а LSB — СПРАВА. Таким образом, при использовании нумерации битов IETF старший бит — это бит 0, а младший бит — бит 7, тогда как при использовании нумерации битов ITU старший бит — это бит 8, а младший бит — бит 1. Совершенно ясно, верно?

8-битный байт (октет) Таблица преобразования:

Преобразование IPv4 из десятичного числа в шестнадцатеричное

Десятичное число	Шестнадцатеричный	Двоичный	Десятичный	Шестнадцатеричный	Двоичный
0	00	0000 0000	128	80	1000 0000
1	01	0000 0001	129	81	1000 0001
2	02	0000 0010	130	82	1000 0010
3	03	0000 0011	131	83	1000 0011
4	04	0000 0100	132	84	1000 0100
5	05	0000 0101	133	85	1000 0101
6	06	0000 0110	134	86	1000 0110
7	07	0000 0111	135	87	1000 0111
8	08	0000 1000	136	88	1000 1000
9	09	0000 1001	137	89	1000 1001
10	0А	0000 1010	138	8А	1000 1010
11	0Б	0000 1011	139	8Б	1000 1011
12	0С	0000 1100	140	8С	1000 1100
13	0Д	0000 1101	141	8Д	1000 1101
14	0Е	0000 1110	142	8Е	1000 1110
15	0Ф	0000 1111	143	8Ф	1000 1111
16	10	0001 0000	144	90	1001 0000
17	11	0001 0001	145	91	1001 0001
18	12	0001 0010	146	92	1001 0010
19	13	0001 0011	147	93	1001 0011
20	14	0001 0100	148	94	1001 0100
21	15	0001 0101	149	95	1001 0101
22	16	0001 0110	150	96	1001 0110
23	17	0001 0111	151	97	1001 0111
24	18	0001 1000	152	98	1001 1000
25	19	0001 1001	153	99	1001 1001
26	1А	0001 1010	154	9А	1001 1010
27	1Б	0001 1011	155	9Б	1001 1011
28	1С	0001 1100	156	9С	1001 1100
29	1Д	0001 1101	157	9Д	1001 1101
30	1Э	0001 1110	158	9Е	1001 1110
31	1F	0001 1111	159	9Ф	1001 1111
32	20	0010 0000	160	А0	1010 0000
33	21	0010 0001	161	А1	1010 0001
34	22	0010 0010	162	А2	1010 0010
35	23	0010 0011	163	А3	1010 0011
36	24	0010 0100	164	А4	1010 0100
37	25	0010 0101	165	А5	1010 0101
38	26	0010 0110	166	А6	1010 0110
39	27	0010 0111	167	А7	1010 0111
40	28	0010 1000	168	А8	1010 1000
41	29	0010 1001	169	А9	1010 1001
42	2А	0010 1010	170	АА	1010 1010
43	2Б	0010 1011	171	АБ	1010 1011
44	2С	0010 1100	172	АС	1010 1100
45	2D	0010 1101	173	н. э.	1010 1101
46	2Е	0010 1110	174	АЕ	1010 1110
47	2F	0010 1111	175	АФ	1010 1111
48	30	0011 0000	176	В0	1011 0000
49	31	0011 0001	177	В1	1011 0001
50	32	0011 0010	178	В2	1011 0010
51	33	0011 0011	179	В3	1011 0011
52	34	0011 0100	180	В4	1011 0100
53	35	0011 0101	181	В5	1011 0101
54	36	0011 0110	182	В6	1011 0110
55	37	0011 0111	183	В7	1011 0111
56	38	0011 1000	184	В8	1011 1000
57	39	0011 1001	185	В9	1011 1001
58	3А	0011 1010	186	БА	1011 1010
59	3Б	0011 1011	187	ББ	1011 1011
60	3С	0011 1100	188	до н. э.	1011 1100
61	3D	0011 1101	189	БД	1011 1101
62	3Е	0011 1110	190	БЭ	1011 1110
63	3F	0011 1111	191	БФ	1011 1111
64	40	0100 0000	192	С0	1100 0000
65	41	0100 0001	193	С1	1100 0001
66	42	0100 0010	194	С2	1100 0010
67	43	0100 0011	195	С3	1100 0011
68	44	0100 0100	196	С4	1100 0100
69	45	0100 0101	197	С5	1100 0101
70	46	0100 0110	198	С6	1100 0110
71	47	1100 0111	199	С7	1100 0111
72	48	0100 1000	200	С8	1100 1000
73	49	0100 1001	201	С9	1100 1001
74	4А	0100 1010	202	КА	1100 1010
75	4Б	0100 1011	203	КБ	1100 1011
76	4С	0100 1100	204	СС	1100 1100
77	4Д	0100 1101	205	CD	1100 1101
78	4Е	0100 1110	206	СЕ	1100 1110
79	4F	1100 1111	207	КФ	1100 1111
80	50	0101 0000	208	Д0	1101 0000
81	51	0101 0001	209	Д1	1101 0001
82	52	0101 0010	210	Д2	1101 0010
83	53	0101 0011	211	Д3	1101 0011
84	54	0101 0100	212	Д4	1101 0100
85	55	0101 0101	213	Д5	1101 0101
86	56	0101 0110	214	Д6	1101 0110
87	57	1101 0111	215	Д7	1101 0111
88	58	0101 1000	216	Д8	1101 1000
89	59	0101 1001	217	Д9	1101 1001
90	5А	0101 1010	218	ДА	1101 1010
91	5Б	0100 1011	219	ДБ	1101 1011
92	5С	0101 1100	220	DC	1101 1100
93	5Д	0101 1101	221	ДД	1101 1101
94	5Е	0101 1110	222	ДЭ	1101 1110
95	5F	1101 1111	223	ДФ	1101 1111
96	60	0110 0000	224	Э0	1110 0000
97	61	0110 0001	225	Е1	1110 0001
98	62	0110 0010	226	Е2	1110 0010
99	63	0110 0011	227	Е3	1110 0011
100	64	0110 0100	228	Е4	1110 0100
101	65	0110 0101	229	Е5	1110 0101
102	66	0110 0110	230	Е6	1110 0110
103	67	1110 0111	231	Е7	1110 0111
104	68	0110 1000	232	Е8	1110 1000
105	69	0110 1001	233	Е9	1110 1001
106	6А	0110 1010	234	ЕА	1110 1010
107	6Б	0110 1011	235	ЭБ	1110 1011
108	6С	0110 1100	236	ЕС	1110 1100
109	6D	0110 1101	237	ЭД	1110 1101
110	6Е	0110 1110	238	ЕЕ	1110 1110
111	6F	1110 1111	239	ЭФ	1110 1111
112	70	0111 0000	240	Ф0	1111 0000
113	71	0111 0001	241	Ф1	1111 0001
114	72	0111 0010	242	Ф2	1111 0010
115	73	0111 0011	243	Ф3	1111 0011
116	74	0111 0100	244	Ф4	1111 0100
117	75	0111 0101	245	Ф5	1111 0101
118	76	0111 0110	246	Ф6	1111 0110
119	77	1111 0111	247	Ф7	1111 0111
120	78	0111 1000	248	Ф8	1111 1000
121	79	0111 1001	249	Ф9	1111 1001
122	7А	0111 1010	250	ФА	1111 1010
123	7Б	0111 1011	251	ФБ	1111 1011
124	7С	0111 1100	252	ФК	1111 1100
125	7Д	0111 1101	253	ФД	1111 1101
126	7Э	0111 1110	254	ФЭ	1111 1110
127	7Ф	0111 1111	255	ФФ	1111 1111

Преобразование десятичного IPv4 в шестнадцатеричный

Чтобы преобразовать десятичный IPv4-адрес с точками в шестнадцатеричный, возьмите каждое десятичное значение с точками и преобразуйте его с помощью шестнадцатеричного калькулятора (подойдет стандартный калькулятор Windows в научном режиме или режиме программиста). Это даст:

IP-адрес в десятичном формате с точками = 192.168.0.5
Десятичный 192 = Шестнадцатеричный = C0
Десятичный 168 = Шестнадцатеричный = A8
Десятичный 0 = Шестнадцатеричный = 00
Десятичный 5 = Шестнадцатеричный = 05
IP-адрес в шестнадцатеричном формате с точками = C0.A8.00.05
 

---

Проблемы, замечания, предложения, исправления (включая битые ссылки) или что-то добавить? Пожалуйста, найдите время от занятой жизни, чтобы «написать нам» (вверху экрана), веб-мастеру (ниже) или в информационную поддержку на zytrax. У вас будет теплое внутреннее сияние до конца дня.

Шестнадцатеричное сложение/вычитание и дополнение до 2 | Penji

В этой статье рассматриваются сложение и вычитание без знака, а также сложение и вычитание в дополнении до 2 по основанию 16 (шестнадцатеричное). В этой статье также будет затронута тема переполнения в связи с этими операциями.

Что такое шестнадцатеричный формат?

Шестнадцатеричная система — это система счисления с основанием 16.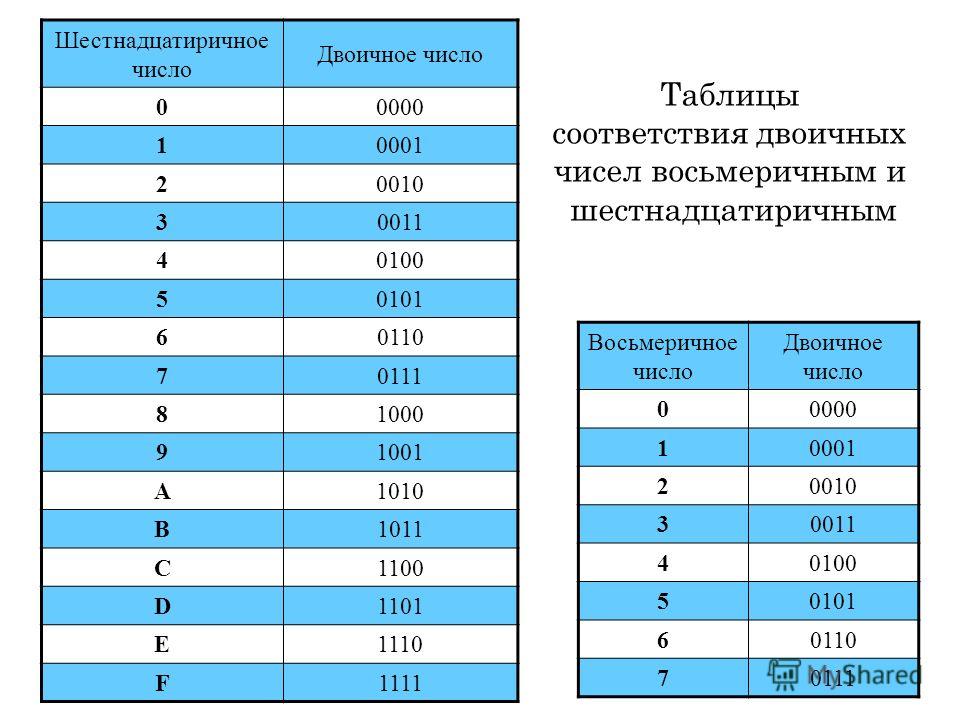 Она состоит из 16 различных символов, 0–9 для представления соответствующих двоичных значений и A, B, C, D, E и F для представления 10–15 соответственно. .

Для полноты картины давайте начнем с преобразования шестнадцатеричного числа в его десятичный эквивалент. Каждая позиция в шестнадцатеричном числе представляет степень 16, очень похожую на двоичную, за исключением того, что вместо этого мы используем основание 16. Возьмем, к примеру, 19FDE_16. Десятичный эквивалент рассчитывается так:

1) Запишите, на что будет умножаться каждый символ, чтобы основываясь на его позиции

2) Теперь преобразуйте буквы в их десятичные значения

3) Теперь умножьте и прибавьте, и вы получите ответ! Помните, что базы поднимаются справа налево, а не слева направо!

Сложение в шестнадцатеричном формате

Вы вводите шестнадцатеричное сложение только в том случае, если ваше число превышает 15. В остальном это почти то же самое, что и десятичное сложение. Начнем с небольшого примера.

Начните справа и добавьте.

1) 6 + 3 = 9 без переноса

2) A + B = 10 + 11 = 21 (> 15), значит перенос есть! Вычтите 16 из 21 и перенесите 1 (это похоже на обычное сложение, но вместо вычитания 10 просто вычтите 16, так как мы находимся в базе 16).

3) 4 + 1 + 1 (перенос) = 6

И вы получите ответ:

= 659_16 = 1190_10 + 435_10 = 1625_10

Взято из предыдущего курса ECS :

Теперь давайте сделаем часть а.

Переполнение — это когда у вас недостаточно места для хранения всего ответа, поэтому, если номер крайнего левого столбца больше 15, для этого вычисления возникает переполнение. Для этой конкретной части нет переполнения.

Вычитание в шестнадцатеричном формате

Это похоже на обычное десятичное вычитание, но заимствованное число отличается. В десятичной системе вы заимствуете группу 10_10, а в шестнадцатеричной системе вы заимствуете группу 16_10.

Вычтем наш предыдущий пример:

Теперь давайте сделаем часть b.

Опять же, здесь тоже нет переполнения!

Дополнение до 2

Чтобы получить отрицательное представление числа в дополнении до 2, запишите двоичную форму числа, инвертируйте биты и добавьте 1.

Предположим, мы хотим узнать, как выглядит -14, используя 7 биты для простоты.

1) Сначала запишем 14 в двоичном виде: 0 0 0 1 1 1 0

2) Затем мы инвертируем биты, 0 становится 1, а 1 становится 0: 1 1 1 0 0 0 1

3) Теперь мы добавляем 1:

Это -14 в дополнении до 2. ПРИМЕЧАНИЕ. Чтобы узнать, является ли число отрицательным в дополнении до 2, первый бит известен как «знак», но 0 означает, что число положительное, а 1 означает, что число отрицательное.

Теперь, чтобы преобразовать шестнадцатеричное число в дополнение до 2, вы хотите преобразовать шестнадцатеричное число в двоичное, а затем двоичное в дополнение до 2 (если вы хотите отрицание числа, которое вы конвертируете).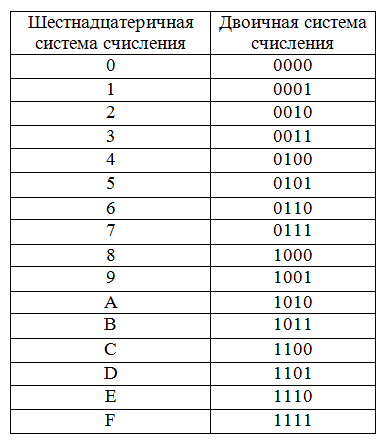

Чтобы преобразовать шестнадцатеричный код в двоичный, используйте следующую таблицу:

Каждая шестнадцатеричная цифра преобразуется в 4 двоичных: Возьмем, к примеру, (4E)_16

4_16 = 0100_2

E_16 = 1110_2

40001 Итак, 6E)_1 =(01001110)_2

Дополнение до 2 полезно для вычитания, но сложение с дополнением до 2 такое же, как обычное сложение, но переполнение отличается.

Давайте сделаем часть c .

Но для этого есть переполнение!

2 Complement Overflow

Переполнение происходит при добавлении двух подписанных 2 дополнительных чисел и 1) если оба операнда положительные, но результат отрицательный или 2) когда оба операнда отрицательные, но результат положительный. Итак, вернемся к части c.

Теперь часть d , вычитание дополнения до 2.

Сначала запишите двоичные формы обоих чисел.

Теперь получите дополнение до 2 для B8FDE3.