Шестнадцатеричное число 10 в десятичной системе счисления имеет вид: Перевод чисел из десятичной системы в шестнадцатиричную

Содержание

Шестнадцатеричная система счисления

Содержание:
Что такое шестнадцатеричная система счисления
Как перевести целое десятичное число в шестнадцатеричную систему счисления
Как перевести десятичную дробь в шестнадцатеричную систему счисления
Как перевести число из шестнадцатеричной системы счисления в десятичную
Как перевести дробное шестнадцатеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в шестнадцатеричной системе счисления

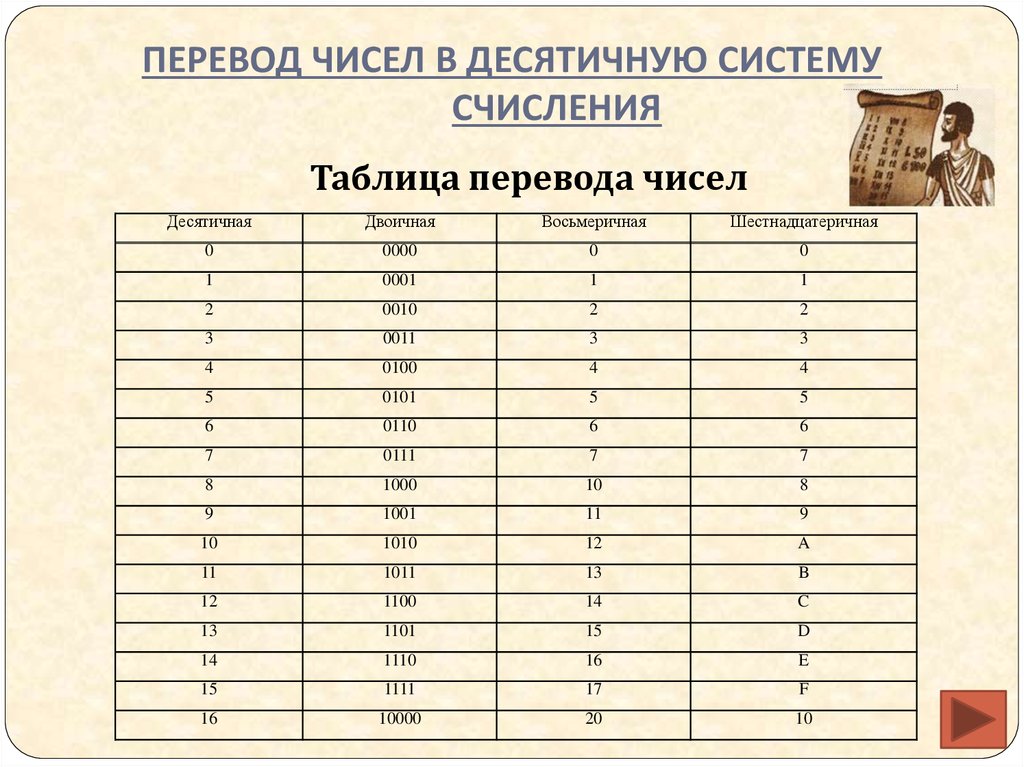
шестнадцатеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в шестнадцатеричной системе счисления используется десять цифр и шесть букв 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется

основанием системы счисления.

Например, F245₁₆ или 123A₁₆

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в шестнадцатеричную систему счисления

Для того, чтобы перевести целое десятичное число в шестнадцатеричную систему счисления нужно десятичное число делить на 16 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 323947₁₀ в шестнадцатеричную систему счисления:

323947 : 16 = 20246 остаток: 11, 11 = B
20246 : 16 = 1265 остаток: 6
1265 : 16 = 79 остаток: 1
79 : 16 = 4 остаток: 15, 15 = F
4 : 16 = 0 остаток: 4

323947₁₀ = 4F16B₁₆

Как перевести десятичную дробь в шестнадцатеричную систему счисления

Для того чтобы перевести десятичную дробь в шестнадцатеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в шестнадцатеричную систему счисления, а затем дробную часть, последовательно умножать на 16, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 842.990820885₁₀ в шестнадцатеричную систему счисления:

Переведем целую часть

842 : 16 = 52 остаток: 10, 10 = A
52 : 16 = 3 остаток: 4
3 : 16 = 0 остаток: 3

842₁₀ = 34A₁₆

Переведем дробную часть

0.990820885 · 16 = 15.85313416, 15 = F
0.85313416 · 16 = 13.65014656, 13 = D
0.65014656 · 16 = 10.40234496, 10 = A
0.40234496 · 16 = 6.43751936
0.43751936 · 16 = 7.00030976
0.00030976 · 16 = 0.00495616
0.00495616 · 16 = 0.07929856
0.07929856 · 16 = 1.26877696
0.26877696 · 16 = 4.30043136
0.30043136 · 16 = 4.80690176

0.990820885₁₀ = 0. FDA6700144₁₆

842.990820885₁₀ = 34A.FDA6700144₁₆

Шестнадцатеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной шестнадцатеричной. В данном примере получается бесконечная шестнадцатеричная дробь, поэтому умножение на 16 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 842.990820885

10 не может быть точно представлена в шестнадцатеричной системе счисления.

Как перевести число из шестнадцатеричной системы счисления в десятичную

Для того, чтобы перевести число из шестнадцатеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число на 16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем число AE19₁₆ в десятичную систему счисления:

Позиция в числе	4	3	2	1	0
Число	A	F	2	D	6

A₁₆ = 10₁₀
D₁₆ = 13₁₀
F₁₆ = 15₁₀

AF2D6₁₆ = 10 ⋅ 16⁴ + 15 ⋅ 16³ + 2 ⋅ 16² + 13 ⋅ 16¹ + 6 ⋅ 16⁰ = 717526₁₀

Как перевести дробное шестнадцатеричное число в десятичное

Для того, чтобы перевести дробное шестнадцатеричное число в десятичное, необходимо записать дробное шестнадцатеричное число, убрав точку и затем сверху расставить индексы.

Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число на 16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное шестнадцатеричное число 69.F3₁₆ в десятичное:

Позиция в числе	1	0	-1	-2
Число	6	9	F	3

F₁₆ = 15₁₀

69.F3₁₆ = 6 ⋅ 16¹ + 9 ⋅ 16⁰ + 15 ⋅ 16

-1 + 3 ⋅ 16^-2 = 105.94921875₁₀

Таблица значений десятичных чисел от 0 до 100 в шестнадцатеричной системе счисления

Значение числа в десятичной системе счисления	Значение числа в шестнадцатеричной системе счисления
0₁₀	0₁₆
1₁₀	1₁₆
2₁₀	2₁₆
3₁₀	3₁₆
4₁₀	4₁₆
5₁₀	5₁₆
6₁₀	6₁₆
7₁₀	7₁₆
8₁₀	8₁₆
9₁₀	9₁₆
10₁₀	A₁₆
11₁₀	B₁₆
12₁₀	C₁₆
13₁₀	D₁₆
14₁₀	E₁₆
15₁₀	F₁₆
16₁₀	10₁₆
17₁₀	11₁₆
18₁₀	12₁₆
19₁₀	13₁₆
20₁₀	14₁₆
21₁₀	15₁₆
22₁₀	16₁₆
23₁₀	17₁₆
24₁₀	18₁₆
25₁₀	19₁₆
26₁₀	1A₁₆
27₁₀	1B₁₆
28₁₀	1C₁₆
29₁₀	1D₁₆
30₁₀	1E₁₆
31₁₀	1F₁₆
32₁₀	20₁₆
33₁₀	21₁₆
34₁₀	22₁₆
35₁₀	23₁₆
36₁₀	24₁₆
37₁₀	25₁₆
38₁₀	26₁₆
39₁₀	27₁₆
40₁₀	28₁₆
41₁₀	29₁₆
42₁₀	2A₁₆
43₁₀	2B₁₆
44₁₀	2C₁₆
45₁₀	2D₁₆
46₁₀	2E₁₆
47₁₀	2F₁₆
48₁₀	30₁₆
49₁₀	31₁₆
50₁₀	32₁₆

Значение числа в десятичной системе счисления	Значение числа в шестнадцатеричной системе счисления
51₁₀	33₁₆
52₁₀	34₁₆
53₁₀	35₁₆
54₁₀	36₁₆
55₁₀	37₁₆
56₁₀	38₁₆
57₁₀	39₁₆
58₁₀	3A₁₆
59₁₀	3B₁₆
60₁₀	3C₁₆
61₁₀	3D₁₆
62₁₀	3E₁₆
63₁₀	3F₁₆
64₁₀	40₁₆
65₁₀	41₁₆
66₁₀	42₁₆
67₁₀	43₁₆
68₁₀	44₁₆
69₁₀	45₁₆
70₁₀	46₁₆
71₁₀	47₁₆
72₁₀	48₁₆
73₁₀	49₁₆
74₁₀	4A₁₆
75₁₀	4B₁₆
76₁₀	4C₁₆
77₁₀	4D₁₆
78₁₀	4E₁₆
79₁₀	4F₁₆
80₁₀	50₁₆
81₁₀	51₁₆
82₁₀	52₁₆
83₁₀	53₁₆
84₁₀	54₁₆
85₁₀	55₁₆
86₁₀	56₁₆
87₁₀	57₁₆
88₁₀	58₁₆
89₁₀	59₁₆
90₁₀	5A₁₆
91₁₀	5B₁₆
92₁₀	5C₁₆
93₁₀	5D₁₆
94₁₀	5E₁₆
95₁₀	5F₁₆
96₁₀	60₁₆
97₁₀	61₁₆
98₁₀	62₁₆
99₁₀	63₁₆
100₁₀	64₁₆

Перевод чисел из одной системы счисления в другую

Перевод чисел из десятичной системы счисления в другую позиционную

Как мы уже отмечали, человек привык работать в десятичной системе счисления, а ЭВМ ориентирована на двоичную систему. Поэтому общение человека с машиной невозможно без создания простых и надёжных алгоритмов перевода чисел из одной системы в другую и наоборот. Итак, как осуществить перевод чисел из десятичной системы в двоичную?
Допустим, надо перевести число 11 в двоичную систему счисления. Разделим 11 на 2. Получим частное 5 и остаток 1. Следовательно, в двоичной записи числа 11 последняя цифра равна 1. Для нахождения второй цифры разделим найденное нами частное 5 снова на 2. Получим частное 2 и остаток 1. Следовательно, вторая цифра с конца в двоичной записи числа 11 тоже равна 1. Частное 2 снова делим на 2. Получим 1 и 0 в остатке. Полученная 1 и есть первая цифра в двоичной записи числа 11. Остаток от последнего деления 0 — вторая цифра.

    Если необходимо преобразовать нецелое число — десятичную дробь, то производим следующие действия:
    1. Целую часть числа преобразовываем в двоичную систему способом, описанным выше.
    2. Дробную часть необходимо преобразовывать умножением на основание системы, в которую мы переводим число.

В результате умножения дробной части — числа 0,7 на основание системы — число 2 получим 1,4. Целую часть данного числа (цифру 1) выделяем, а дробную часть — число 0,4 снова умножаем на 2.
Очевидно, что процесс перевода числа 0,7 может продолжаться бесконечно. Действительно, за шесть шагов мы можем получить число 0,101100, а за семь шагов получили бы 0,1011001, которое является более точным представлением числа 0,7 в двоичной системе. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа. В результате перевода получим ответ:

Для перевода десятичных чисел в другие позиционные системы счисления пользуются теми же правилами, лишь меняется лишь основание системы, в которую надо перевести числа.

Перевод чисел из двоичной системы счисления в системы, родственные двоичной и обратно.

    Большие числа в двоичной системе счисления имеют очень громоздкие записи. Конечно, можно перевести число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоёмки. На помощь приходят системы, родственные двоичной — восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме.
    Системами счисления родственными двоичной считаются такие системы, основания которых являются значением степени числа 2.
    Например, четверичная, восьмеричная и шестнадцатеричная системы счисления являются системами, родственными двоичной.

    Для перевода чисел из двоичной системы счисления в системы, родственные двоичной, необходимо выполнить следующие действия:
    1. Разбить число на некоторое количество разрядов, равное степени числа 2 основания системы, в которую переводим.
    2.Если в старших и младших разрядах после разбиения не хватает знаков, то добавить их нулями.
    3.По таблице определить значение пары, триады, тетрады и т.п. разрядов, записанных в двоичной системе счисления, соответственно значению в той системе, в которую переводим.
    Например, дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в восьмеричную систему счисления разобьём число на триады (т.к. основание числа 2 равно 3), начиная от запятой, вправо и влево: 1.111.010.111.010,011.1 . Разбиение показано точками. В старшей и младшей триадах не хватает разрядов. Дополним их нулями: 001.111.010.111.010,011.100. По таблице определим восьмеричные цифры, соответствующие триадам. Получается восьмеричное число 17272,34.
    Рассмотрим ещё один пример: дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в шестнадцатеричную систему счисления разобьём число на тетрады (т.к. основание числа 2 равно 4): 1.1110.1011.1010,0111. В старшей тетраде не хватает разрядов. Дополним их нулями: 0001.1110.1011.1010,0111. По таблице определим шестнадцатеричные знаки, соответствующие тетрадам. Получается шестнадцатеричное число 1EBA,7.
     Пусть дано то же число. Для перевода его в четверичную систему счисления разобьём число на пары (т.к. основание числа 2 равно 2): 1.11.10.10.11.10.10,01.11. В старшей паре не хватает одного разряда. Дополним его нулём: 01.11.10.10.11.10.10,01.11. Определим четверичные цифры, соответствующие парам. Получается четверичное число 1322322,13.

Как осуществить обратный перевод:

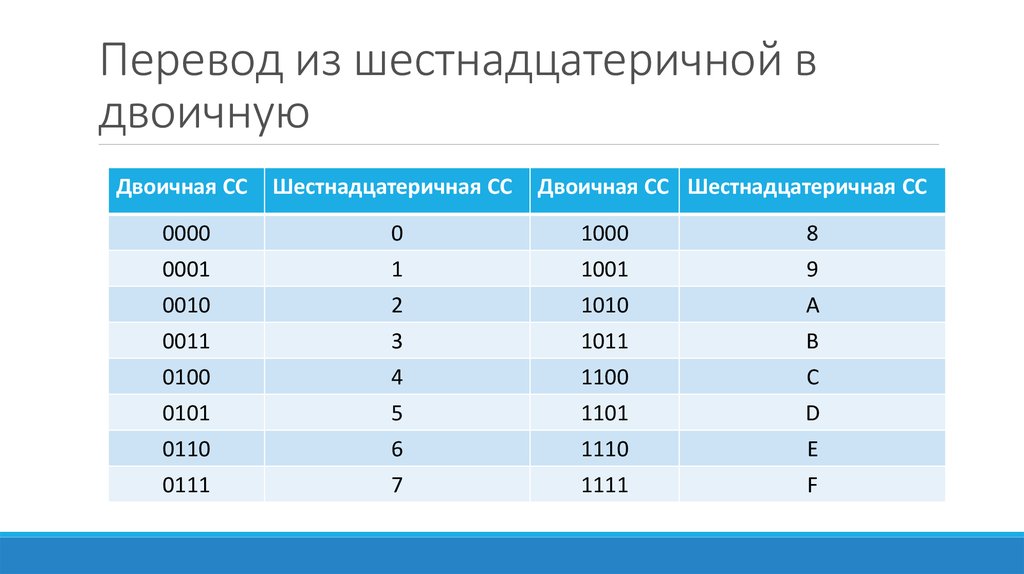
Пусть дано число 73,62 , записанное в восьмеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру числа запишем в виде триады из 0 и 1, соответствующей значению восьмеричной цифры в двоичной системе счисления: 111. 011,110.010.

Рассмотрим ещё один пример: дано число 7В3,Е6, записанное в шестнадцатеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру шестнадцатеричного числа запишем в виде тетрады из 0 и 1,соответствующей значению знака в двоичной системе счисления: 0111.1011.0011,1110.0110.

Перевод чисел из р-ичной позиционной системы счисления в десятичную.

Все позиционные системы счисления, о которых мы говорили выше, строятся по одному общему принципу. Выбирается некоторое число р — основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, т.е. произвольное число в системе счисления с основанием р имеет вид:

Если необходимо перевести двоичное число 1011011,11 в десятичную систему, воспользуемся этой формулой. Основание системы р=2, к — коэффициент, указывающий количество знаков в числе влево от запятой, к=7; а — знаки числа с соответствующими им коэффициентами.

Воспользуемся формулой для перевода шестнадцатеричного числа ВF,1D в десятичную систему. Основание системы р=16, к=2.

Пусть необходимо перевести восьмеричное число 254,262 в десятичную систему. Основание системы р=8, к=3

Шестнадцатеричное в десятичное — Преобразование, Формула, Метод, Примеры

Шестнадцатеричное в десятичное — это процесс преобразования одного числа в другое в системе счисления. Система счисления представляет собой представление чисел с помощью последовательного использования цифр или других символов. Существует четыре типа систем счисления, а именно: двоичная, восьмеричная, десятичная и шестнадцатеричная. Каждая из них имеет свой уникальный базовый номер, который различает системы.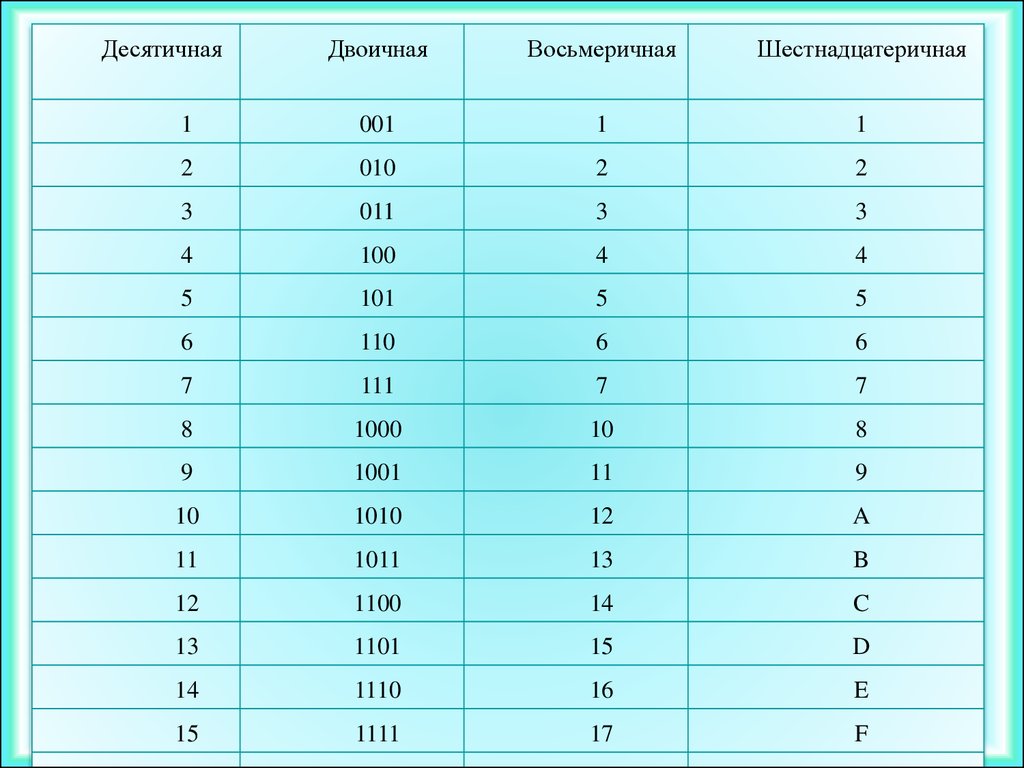 Шестнадцатеричная система счисления имеет базовое число 16, тогда как десятичная система счисления имеет базовое число 10. Давайте узнаем, как преобразовать шестнадцатеричное число в десятичное, таблицу преобразования и решим несколько примеров, чтобы лучше понять концепцию.

1.	Что такое преобразование шестнадцатеричных чисел в десятичные?
2.	Как преобразовать шестнадцатеричное число в десятичное?
3.	Преобразование шестнадцатеричной системы счисления в десятичную Формула
4.	Часто задаваемые вопросы о преобразовании шестнадцатеричной системы счисления в десятичную

Что такое преобразование шестнадцатеричных чисел в десятичные?

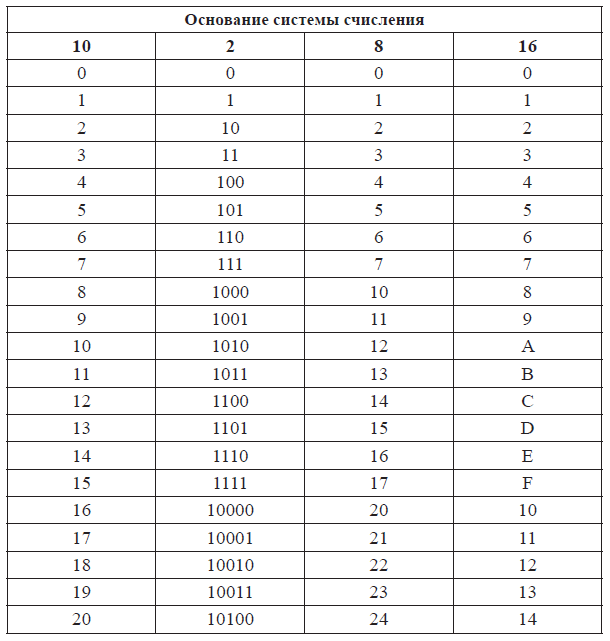
Преобразование шестнадцатеричных чисел в десятичные выполняется с учетом основных чисел каждой из систем счисления. Шестнадцатеричная система счисления работает как с цифрами, так и с символами, особенно для представления двузначных, используются символы. Всего существует 16 обозначений: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., 10, 11, 12, 13, 14, 15 и 10-15 представлены как A, B, C, D, E, F. Тогда как в десятичной системе счисления 10 обозначений представлены как 0, 1, 2, 3 , 4, 5, 6, 7, 8 и 9. Чтобы преобразовать шестнадцатеричное число в десятичное, мы сначала получаем десятичный эквивалент шестнадцатеричного числа из таблицы преобразования, умножаем как цифру на 16 в степени разрядности и складываем все вместе. Таблица преобразования приведена ниже:

Определение шестнадцатеричной системы счисления

Шестнадцатеричная система счисления также известна как позиционная система счисления, поскольку каждая цифра имеет вес в степени 16. Каждая цифра в 16 раз значительнее предыдущей. . Следовательно, когда мы преобразуем любое шестнадцатеричное число в любую другую систему счисления, мы умножаем цифры по отдельности, учитывая степень числа 16 в соответствии с их положением. Эта система счисления использует шестнадцать цифр/алфавитов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. и A, B, C, D, E, F с базовым числом 16. Например, 7DE ₁₆, E5F ₁₆, 9B4A ₁₆.

Определение десятичной системы счисления

Десятичная система счисления имеет основание 10 с цифрами от 0 до 9. Числа в повседневной жизни обычно представлены в этой форме. Например, 24 ₁₀, 654 ₁₀, 2012 ₁₀.

Как преобразовать шестнадцатеричное число в десятичное?

Преобразование шестнадцатеричного числа в десятичное выполняется с использованием основного числа 16. Шестнадцатеричная цифра расширяется, чтобы умножить каждую цифру на степень 16. Степень начинается с 0 справа и движется вперед вправо с увеличением мощности . Для завершения преобразования умноженные числа складываются.

Десятичный номер = d _n-1 × 16 ^r-1 +….+ d ₂ × 16 ² + d ₁ × 16 4 4 ¹ ⁰ .

Где,

n = количество цифр.
r = размещение цифры.

Шаги для преобразования шестнадцатеричного числа в десятичное:

Получите десятичный эквивалент шестнадцатеричного числа из таблицы преобразования. (таблица указана выше)
Умножьте каждую цифру в степени 16, начиная с 0 справа.
Сложите все числа вместе.

Давайте рассмотрим пример, чтобы лучше понять это.

Например: преобразовать шестнадцатеричное число \((25)_{16}\) в его десятичную форму.

\((25)_{16}\) = 2 × 16 ¹ + 5 × 16 ⁰

= 2 × 16 + 5 × 1

= 32 + 5

= 37 , \((25)_{16}\) = \((37)_{10}\).

Преобразование шестнадцатеричной системы счисления в десятичную Формула

Преобразование формулы из шестнадцатеричной в десятичную использует следующий метод:

Основание числа для преобразования здесь равно 16.
Умножьте каждую цифру данного числа, начиная с самой правой цифры, на показатели степени по основанию 16.
Показатель степени должен начинаться с 0 и увеличиваться на 1 каждый раз при движении справа налево.
Мы просто упрощаем каждый из продуктов и добавляем их. 90 \text{(decimal)}\)
☛Связанные темы
Ниже перечислены несколько интересных тем, связанных с преобразованием шестнадцатеричного в десятичное, взгляните.
- Шестнадцатеричный код в двоичный
- Десятичный в восьмеричный
- Восьмеричный в десятичный
- Десятичный в шестнадцатеричный
- Двоичный код в шестнадцатеричный
Часто задаваемые вопросы о шестнадцатеричной системе счисления
Что означает преобразование шестнадцатеричной системы счисления в десятичную?
Преобразование шестнадцатеричных чисел в десятичные выполняется с учетом основных чисел обеих систем счисления. При преобразовании шестнадцатеричного в десятичное используется основание числа 16. В шестнадцатеричной системе счисления используется 16 цифр/алфавитов: цифры 0,1, 2, 3, 4, 5, 6, 7, 8, 9 и символы A, B, C, D, E, F, таким образом, имеющие основание 16. , Десятичная система счисления использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, и поэтому имеет основание 10.
Как преобразовать шестнадцатеричное число в десятичное?
Преобразование шестнадцатеричного в десятичное выполняется с использованием основного числа 16. Шаги следующие:
- Получите десятичный эквивалент шестнадцатеричных символов, обратившись к таблице преобразования.
- Расширьте цифры, чтобы умножить каждую цифру на степень 16, которая начинается с 0 справа налево.
- После завершения процесса умножения найдите сумму.
- Окончательный ответ — десятичное число.
Что такое шестнадцатеричная формула для десятичной?
Формула преобразования шестнадцатеричной системы счисления в десятичную: 90 \текст{(десятичный)}\).
Как использовать формулу преобразования шестнадцатеричной системы счисления в десятичную?
Шестнадцатеричная формула в десятичную помогает преобразовать число, заданное в системе счисления с основанием 16, в системе счисления 10. В этом методе используется формула:
- При необходимости измените символы на цифры с помощью таблицы преобразования.
- Умножьте каждую цифру данного числа, начиная с самой правой цифры, на показатели степени по основанию 16.
- Показатель степени должен начинаться с 0 и увеличиваться на 1 каждый раз при движении справа налево.
- Мы просто упрощаем каждый из продуктов и добавляем их.
Какие существуют четыре типа системы счисления?
В математике существует четыре типа систем счисления, а именно:
- Двоичная система счисления — Основание числа 2
- Восьмеричная система счисления — Основание числа 8
- Десятичная система счисления — Базовое число 10
- Шестнадцатеричная система счисления — Базовое число 16
Двоичные и шестнадцатеричные целые форматы
Содержание
- 1 Целые числа
- 2 Десятичная запись
- 3 Шестнадцатеричная запись
- 4 Двоичная запись
- 5 См. также
Целые числа
Целые числа — это положительные или отрицательные целые числа или нуль. Целочисленные значения в диапазоне от -9 223 372 036 854 775 808 (-2 ⁶³ ) до 9 223 372 036 854 775 807 (2 ^{63 — 1} ) могут храниться в Analytica точно, без потери точности. Когда вводится целочисленный литерал в пределах этого диапазона, он сохраняется как целочисленное значение, а результаты целочисленных арифметических операций приводят к целочисленным результатам, если операнды не включают нецелочисленные значения или потенциально нецелочисленные значения. Как только встречается операция, которая включает число с плавающей запятой или ожидается, что она создаст число с плавающей запятой, результирующие значения сохраняются как 64-битные числа с плавающей запятой, известные как 9.0239 double s, с диапазоном целых чисел от -9 007 199 254 740 992 (-2 ⁵² ) до 9 007 199 254 740 992 (2 ⁵² ) — это означает, что каждое целое число в этом диапазоне может храниться точно без потери точности.
Каждое атомарное значение в Analytica имеет тип данных. Существует четыре типа данных для числовых значений: вещественное число с плавающей запятой (также известное как двойное), целое число, вещественное число с фиксированной точкой и комплексное число. Пока вы используете целочисленные операции над целочисленным типом данных, вы сохраняете 64-битное целочисленное значение (от -2 ⁶³ до 2 ^{63 — 1}). Вы можете использовать функцию TypeOf для проверки типа данных, который возвращает «Число» (для вещественных чисел с плавающей запятой), «Целое число», «FixedPointReal» или «ComplexNumber».
Десятичное представление
Обычно мы записываем целые числа в десятичной системе счисления, используя цифры от 0 до 9. При выборе целочисленного числового формата целые числа отображаются с полной точностью, не прибегая к экспоненциальному представлению, если базовое значение представляет собой целочисленный тип данных. Нецелые значения отображаются в экспоненциальном формате, если они имеют величину 10 ¹⁶ или больше.
При преобразовании числа в текст укажите «Integer» для параметра «format» при использовании функции NumberToText, чтобы получить ту же запись с основанием 10 с полной точностью для целых значений.
Шестнадцатеричная запись
Целые числа иногда записываются или вводятся в системе счисления с основанием 16, известной как шестнадцатеричная или просто «шестнадцатеричная». В шестнадцатеричном формате используются стандартные цифры от 0 до 9 плюс буквы от A до F . Когда шестнадцатеричная запись используется для ввода или отображения целочисленного значения в Analytica, ему всегда предшествует цифра 9.0263 0x , как в этих примерах:
0x25 = 37
0xa = 10
0x100 = 256
0xabcd9876 = _99254740992
Вы можете настроить отображение чисел в шестнадцатеричном виде, выбрав Шестнадцатеричное в диалоговом окне Формат чисел.
Вы также можете привести числа к шестнадцатеричному виду в тексте, таким образом:
NumberToText(34567, "Hex") → "0x8707"
При вводе шестнадцатеричных значений до 0x7ffffffffffffffff значение является целым числом с полной точностью. Более того, положительные значения превышают 2 ⁶³ и сохраняются как вещественные числа с плавающей запятой с возможной потерей точности. Чтобы ввести отрицательное значение, просто поставьте перед ним знак минус, например,
-0xabc → -2748
Однако, когда отрицательные числа отображаются в шестнадцатеричном представлении, они отображаются в шестнадцатеричном формате с использованием дополнения до двух, где установлен старший бит, и, следовательно, оно будет иметь 16 шестнадцатеричных цифр. 962, «Hex») → 0xc000000000000000
Двоичная запись
В двоичной записи по основанию 2 целые числа записываются с использованием только 0 и 1.