Системы счисления
Основные понятия систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
где S — основание системы счисления;
— цифры числа, записанного в данной системе счисления;
n — количество разрядов числа.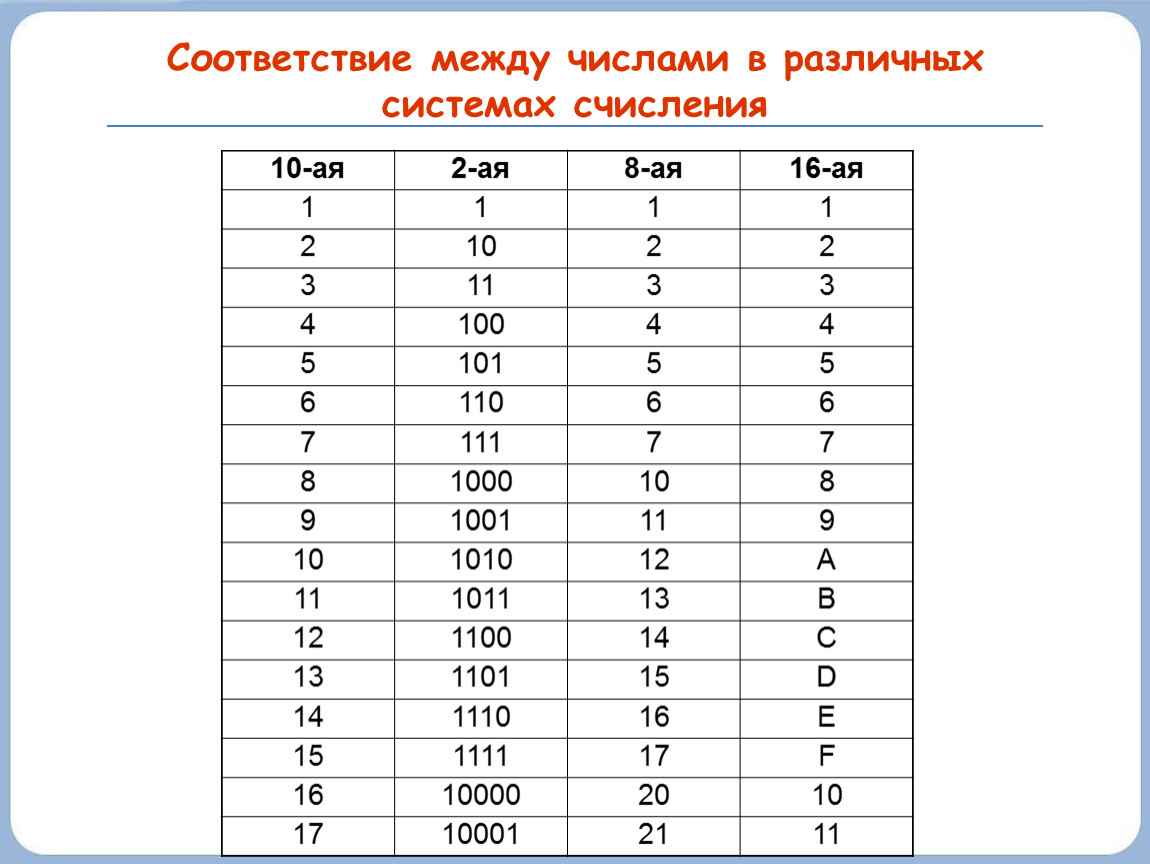
Пример. Число запишется в форме многочлена следующим образом:
Виды систем счисления
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква — V пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т.д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 2. Запись чисел в римской системе счисления
|
1 |
2 |
3 |
4 |
5 |
|
I |
II |
III |
IV |
V |
|
6 |
7 |
8 |
9 |
10 |
|
VI |
VII |
VIII |
IX |
X |
|
11 |
13 |
18 |
19 |
22 |
|
XI |
XIII |
XVIII |
XIX |
XXII |
|
34 |
39 |
40 |
60 |
99 |
|
XXXIV |
XXXIX |
XL |
LX |
XCIX |
|
200 |
438 |
649 |
999 |
1207 |
|
CC |
CDXXXVIII |
DCXLIX |
CMXCIX |
MCCVII |
|
2045 |
3555 |
3678 |
3900 |
3999 |
|
MMXLV |
MMMDLV |
MMMDCLXXVIII |
MMMCM |
MMMCMXCIX |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами.
По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичня система счисления – в настоящее время наиболее известная и используемая. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Люди привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев на руках.
Древнее изображение десятичных цифр (рис. 1) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.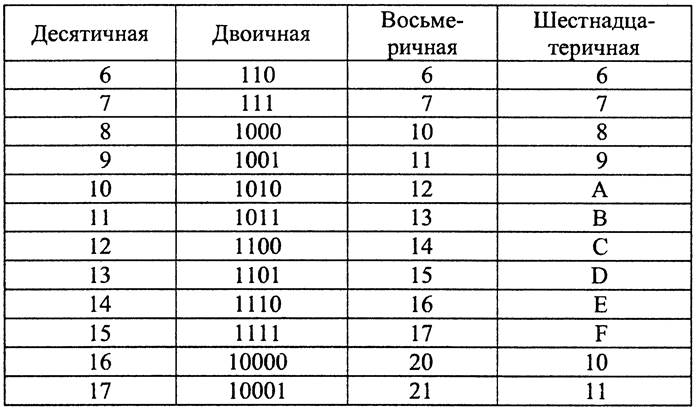
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке — наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы — триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост.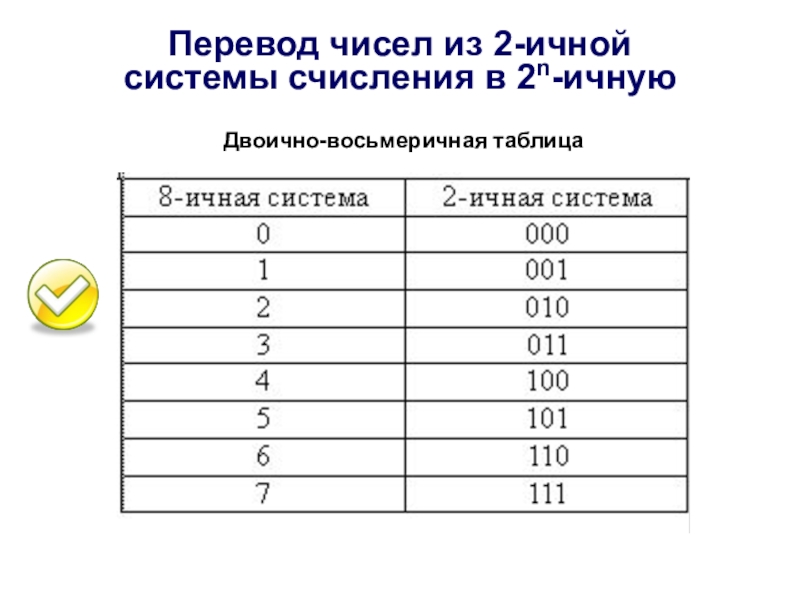
Таблица 3. Соответствие чисел, записанных в различных системах счисления
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
1 |
001 |
1 |
1 |
|
2 |
010 |
2 |
2 |
|
3 |
011 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики.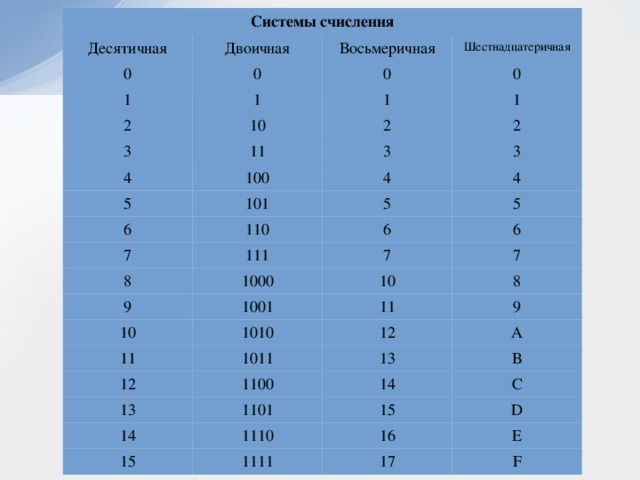
Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
Пример .
Число перевести в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
Пример .
Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
16 |
256 |
4096 |
65536 |
1048576 |
16777216 |
Пример .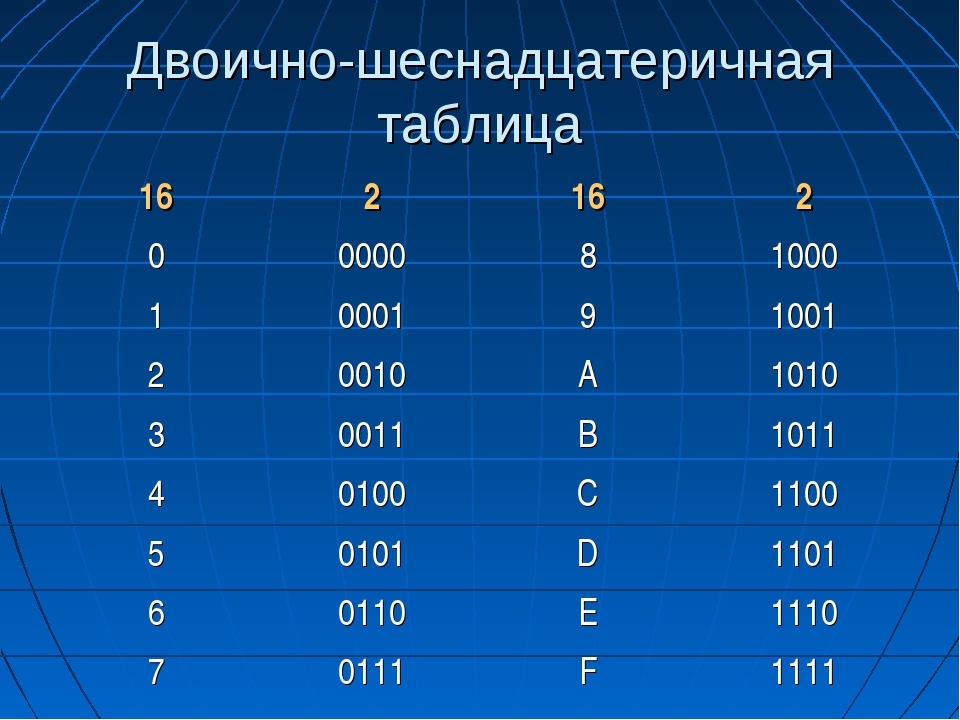
Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15.
Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в восьмеричную систему счисления.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в шестнадцатеричную систему счисления.
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.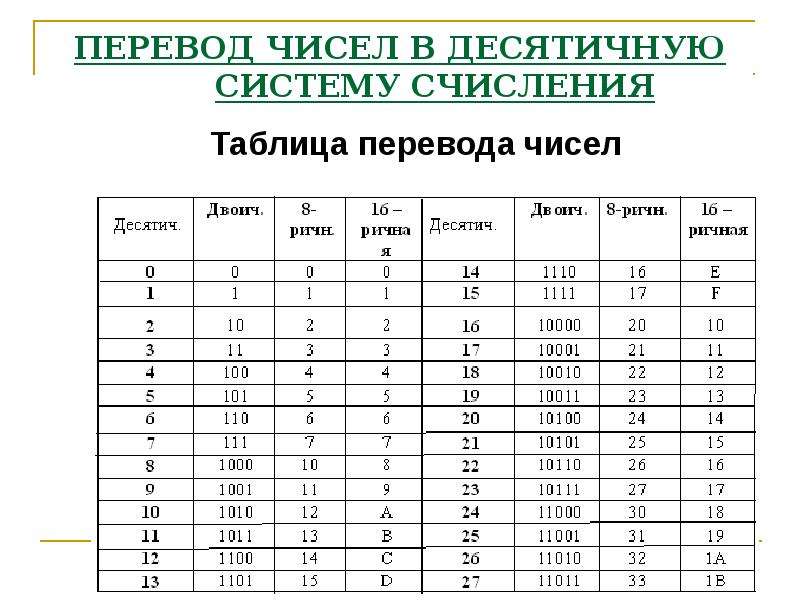
Пример. Число перевести в двоичную систему счисления.
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число перевести в двоичную систему счисления.
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число перевести в восьмеричную систему счисления.
Пример 2. Число перевести в шестнадцатеричную систему счисления.
Конвертер чисел в различных системах счисления. • Популярные конвертеры единиц • Определения единиц • Онлайн-конвертеры единиц измерения
Определения единиц конвертера «Конвертер чисел в различных системах счисления.»
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.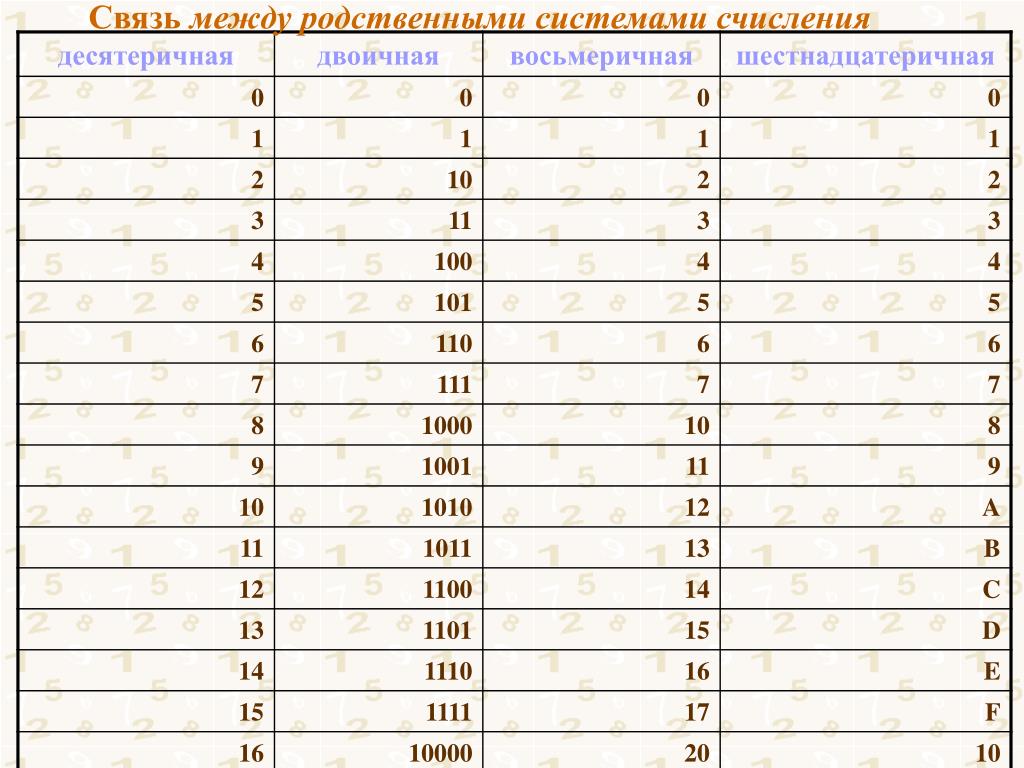
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
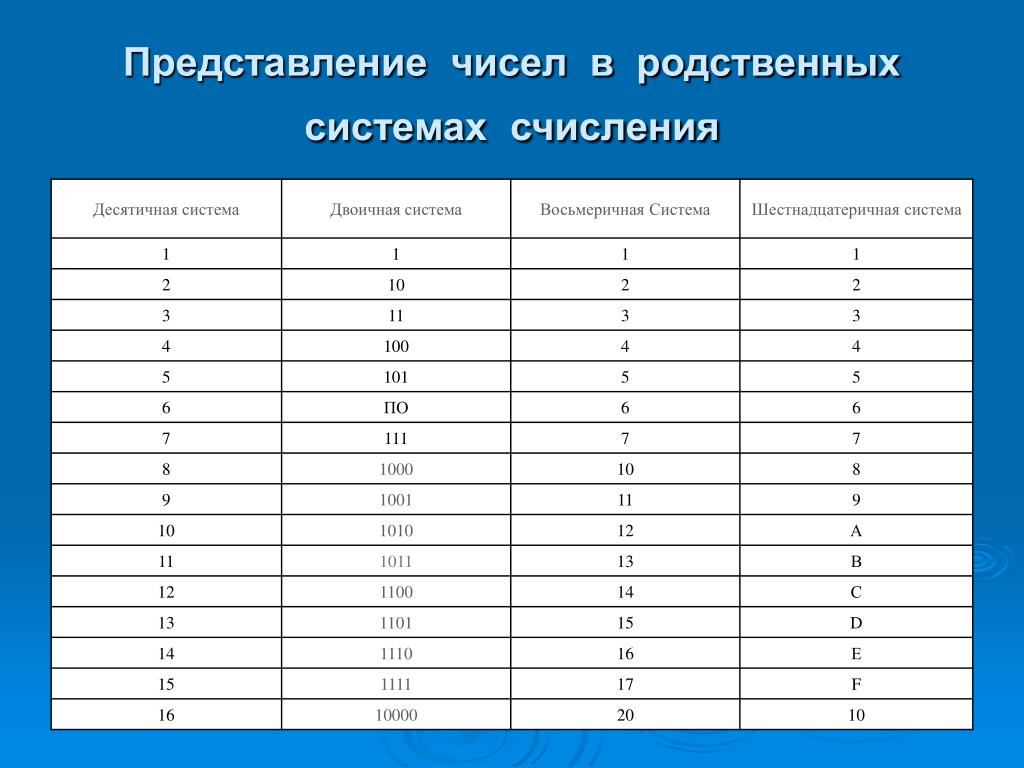единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Определения единиц конвертера «Конвертер чисел в различных системах счисления.» на русском и английском языках
двоичноеДвоичная система — позиционная система счисления с основанием 2. В этой системе числа записываются с помощью двух символов 0 и 1. Двоичная система используется во всех цифровых устройствах, таких как компьютеры и мобильные телефоны, так как ее проще всего реализовать в цифровой схемотехнике с помощью логических вентилей.
Пример: в двоичной системе двойка записывается как 10 и десять записывается как 1010.
Восьмеричная система — позиционная система счисления с основанием 8. В этой системе для записи любого числа используются символы 0–7.
Пример: в восьмеричной системе семерка записывается как 10 и шестьдесят шесть записывается как 100.
Десятичная система — позиционная система счисления с основанием 10. В этой системе для записи любого числа используются символы 0–9. Эта система наиболее широко использовалась во всех современных цивилизациях.
шестнадцатеричноеШестнадцатеричная система — позиционная система счисления с основанием 16. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–F.
Пример: в шестнадцатеричной системе пятнадцать записывается как F и двести пятьдесят шесть записывается как 100.
Эта система широко используется в низкоуровневом программировании современных компьютеров, начиная с IBM System/360, аналогом которых в СССР были машины серии ЕС ЭВМ.
Двоичная система — позиционная система счисления с основанием 2. В этой системе числа записываются с помощью двух символов 0 и 1. Двоичная система используется во всех цифровых устройствах, таких как компьютеры и мобильные телефоны, так как ее проще всего реализовать в цифровой схемотехнике с помощью логических вентилей.
Пример: в двоичной системе двойка записывается как 10 и десять записывается как 1010.
Троичная система — позиционная система счисления с основанием 3. В этой системе числа записываются с помощью символов 0–2. Эта система используется в логике и в вычислительной технике реализуется с помощью устройств, имеющих три устойчивых состояния, например, высокий уровень, низкий уровень, неизвестное состояние (открытый выход или открытый коллектор).
Пример: в троичной системе тройка записывается как 10 и десять записывается как 101.
Четвертичная система — позиционная система счисления с основанием 4.
В этой системе для записи любого числа используются символы 0–3.
Пример: в четвертичной системе четверка записывается как 10 и десять записывается как 22.
Пятеричная система — позиционная система счисления с основанием 5. В этой системе для записи любого числа используются символы 0–4.
Пример: в пятеричной системе пятерка записывается как 10 и двадцать пять записывается как 100.
Шестеричная система — позиционная система счисления с основанием 6. В этой системе для записи любого числа используются символы 0–5.
Пример: в шестеричной системе шестерка записывается как 10 и тридцать шесть записывается как 100.
Семеричная система — позиционная система счисления с основанием 7. В этой системе для записи любого числа используются символы 0–6.
Пример: в семеричной системе семерка записывается как 10 и сорок девять записывается как 100.
Восьмеричная система — позиционная система счисления с основанием 8.
В этой системе для записи любого числа используются символы 0–7.
Пример: в восьмеричной системе восьмерка записывается как 10 и шестьдесят четыре записывается как 100.
Девятеричная система — позиционная система счисления с основанием 9. В этой системе для записи любого числа используются символы 0–8.
Пример: в девятеричной системе девятка записывается как 10 и восемьдесят один записывается как 100.
Десятичная система — позиционная система счисления с основанием 10. В этой системе для записи любого числа используются символы 0–9. Эта система наиболее широко использовалась во всех современных цивилизациях.
основание 11Одиннадцатеричная система — позиционная система счисления с основанием 11. В этой системе для записи любого числа используются цифры 0–9 и буква латинского алфавита A.
Пример: в одиннадцатеричной системе десятка записывается как A и сто двадцать один записывается как 100.
Двенадцатеричная система — позиционная система счисления с основанием 12.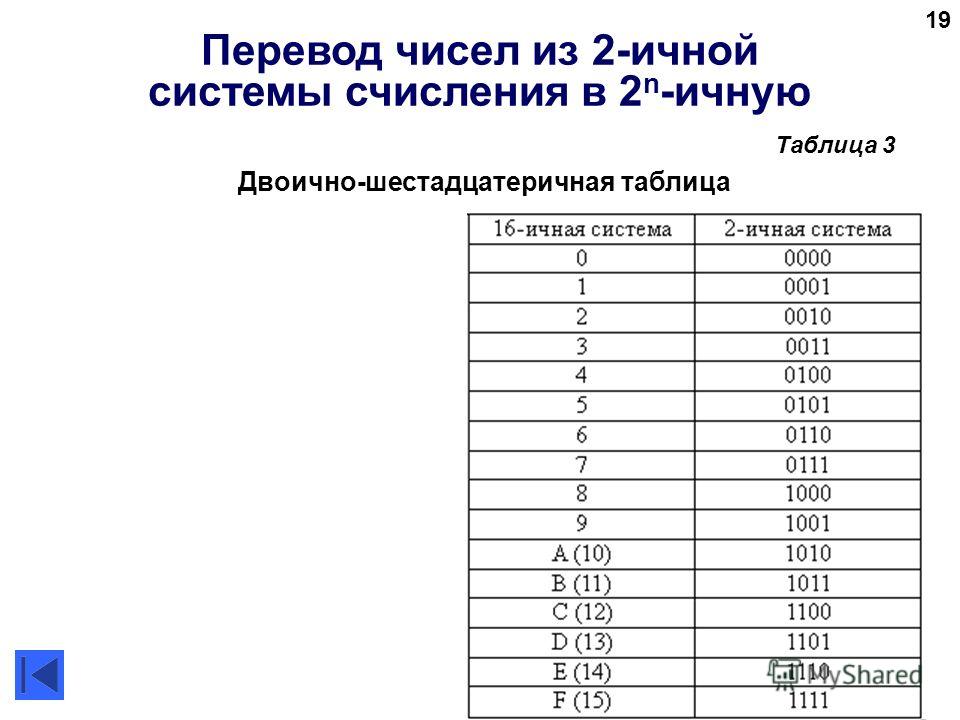
В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–B.
Пример: в двенадцатеричной системе одиннадцать записывается как B и сто сорок четыре записывается как 100.
Тринадцатеричная система — позиционная система счисления с основанием 13. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–С.
Пример: в тринадцатеричной системе двенадцать записывается как С и сто шестьдесят девять записывается как 100.
Четырнадцатеричная система — позиционная система счисления с основанием 14. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–D.
Пример: в четырнадцатеричной системе тринадцать записывается как D и сто девяносто шесть записывается как 100.
Пятнадцатеричная система — позиционная система счисления с основанием 15. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–E.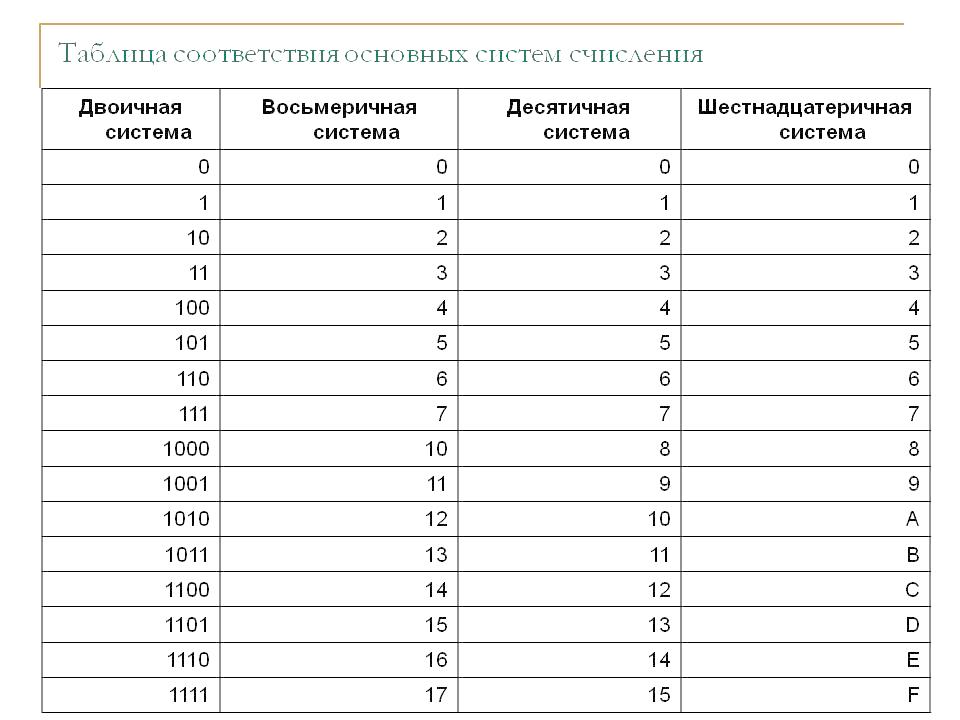
Пример: в пятнадцатеричной системе четырнадцать записывается как E и двести двадцать пять записывается как 100.
Шестнадцатеричная система — позиционная система счисления с основанием 16. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–F.
Пример: в шестнадцатеричной системе пятнадцать записывается как F и двести пятьдесят шесть записывается как 100.
Эта система широко используется в низкоуровневом программировании современных компьютеров, начиная с IBM System/360, аналогом которых в СССР были машины серии ЕС ЭВМ.
Семнадцатеричная система — позиционная система счисления с основанием 17. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–G.
Пример: в семнадцатеричной системе шестнадцать записывается как G и семнадцать записывается как 10.
Восемнадцатеричная система — позиционная система счисления с основанием 18.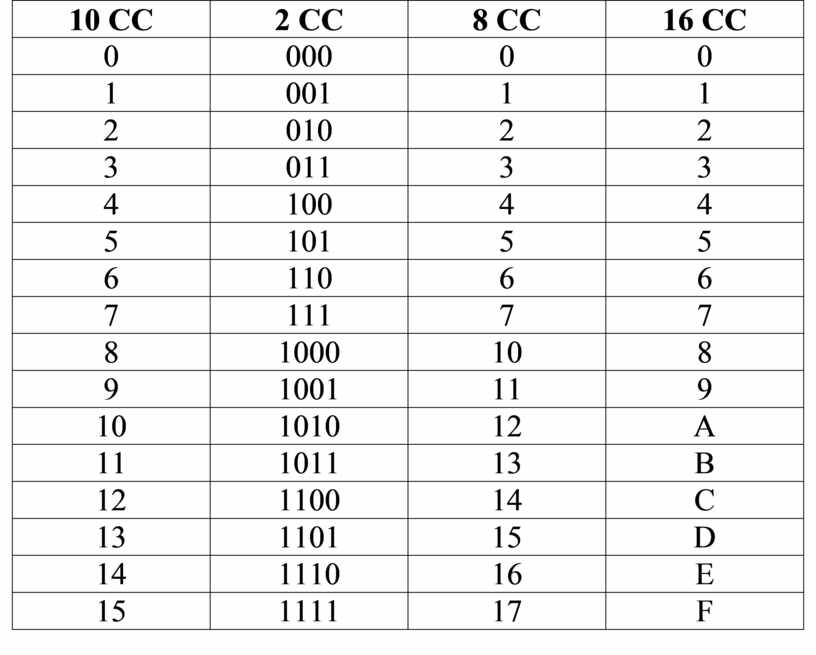
В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–H.
Пример: в восемнадцатеричной системе семнадцать записывается как H и восемнадцать записывается как 10.
Девятнадцатеричная система — позиционная система счисления с основанием 18. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–I.
Пример: в девятнадцатеричной системе восемнадцать записывается как I и девятнадцать записывается как 10.
Двадцатеричная система — позиционная система счисления с основанием 20. В этой системе для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–J.
Пример: в двадцатеричной системе девятнадцать записывается как J и четыреста записывается как 100.
В позиционной системе счисления с основанием 21 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–K.
Пример: в системе с основанием 21 десятичное число двадцать записывается как K и двадцать один записывается как 10.
В позиционной системе счисления с основанием 22 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–L.
Пример: в системе с основанием 22 десятичное число двадцать один записывается как L и двадцать два записывается как 10.
В позиционной системе счисления с основанием 23 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–M.
Пример: в системе с основанием 23 десятичное число двадцать два записывается как M и двадцать три записывается как 10.
В позиционной системе счисления с основанием 24 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–N.
Пример: в системе с основанием 24 десятичное число двадцать три записывается как N и двадцать четыре записывается как 10.
В позиционной системе счисления с основанием 25 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–O.
Пример: в системе с основанием 25 десятичное число двадцать четыре записывается как O и двадцать пять записывается как 10.
В позиционной системе счисления с основанием 26 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–P.
Пример: в системе с основанием 26 десятичное число двадцать пять записывается как P и двадцать шесть записывается как 10.
В позиционной системе счисления с основанием 27 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–Q.
Пример: в системе с основанием 27 десятичное число двадцать шесть записывается как Q и двадцать семь записывается как 10.
В позиционной системе счисления с основанием 28 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–R.
Пример: в системе с основанием 28 десятичное число двадцать семь записывается как R и двадцать восемь записывается как 10.
В позиционной системе счисления с основанием 29 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–S.
Пример: в системе с основанием 29 десятичное число двадцать восемь записывается как S и двадцать девять записывается как 10.
В позиционной системе счисления с основанием 30 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–T.
Пример: в системе с основанием 30 десятичное число двадцать девять записывается как T и тридцать записывается как 10.
В позиционной системе счисления с основанием 31 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–U.
Пример: в системе с основанием 31 десятичное число тридцать записывается как U и тридцать один записывается как 10.
В позиционной системе счисления с основанием 32 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–V.
Пример: в системе с основанием 32 десятичное число тридцать один записывается как V и тридцать два записывается как 10.
В позиционной системе счисления с основанием 33 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–W.
Пример: в системе с основанием 33 десятичное число тридцать два записывается как W и тридцать три записывается как 10.
В позиционной системе счисления с основанием 34 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–X.
Пример: в системе с основанием 34 десятичное число тридцать три записывается как X и тридцать четыре записывается как 10.
В позиционной системе счисления с основанием 35 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–Y.
Пример: в системе с основанием 35 десятичное число тридцать четыре записывается как Y и тридцать пять записывается как 10.
В позиционной системе счисления с основанием 36 для записи любого числа используются цифры 0–9 и буквы латинского алфавита A–Z.
Пример: в системе с основанием 36 десятичное число тридцать пять записывается как Z и тридцать шесть записывается как 10.
Преобразовать единицы с помощью конвертера «Конвертер чисел в различных системах счисления.
»
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Онлайн перевод чисел из одной системы счисления в любую другую
« — Что общего между женщиной и математикой?
— А то, что женщину, как и математику, не каждому идиоту дано понять.»
А я ведь помню те стародавние времена, когда без всяких онлайн приблуд, шестнадцатиразрядный счётчик лёгким движением
руки превращался в делитель частоты с изменяемым коэффициентом деления.
Хотя нет, вру — не лёгким. Беспрестанный перевод гигантских чисел в двоичную систему, перепроверка полученных итогов и
выуживание неизбежных ошибок вызывали скорбь и фатальное желание тихо, но выразительно материться.
Приведённая ниже таблица позволяет без излишнего напряга, калькулятора и деревянных счёт перевести число из десятичной системы в
двоичную, из двоичной в десятичную, да и что уж там скромничать — умеет переводить числа из произвольной системы счисления в любую другую.
К тому же, гулять, так гулять — она легко справится и с дробными числами, независимо от исходной системы счисления.
А для чего, собственно говоря, нам нужна эта таблица вместе со всем многообразием систем счисления?
Если с переводом чисел из двоичной системы в десятичную, или, наоборот, из десятичной в двоичную более-менее всё понятно,
то на кой ляд нам сдались эти: троичная, четверичная, пятеричная, шестеричная, семеричная, ну да и ладно, хватит уже роботов накручивать,
и прочие-ичные системы.
Ладно, ещё шестнадцатеричная позиционная система счисления — используется в низкоуровневом программировании,
компьютерной документации и записи кодов ошибок. А остальные?
Сами-то мы не местные, то бишь не математики, поэтому поковыряемся в интернете.
Поковырялись слегка в святых просторах и поняли, что нужны они в Париже — как в русской бане лыжи.
Хотя именно французы неоднократно и пытались перейти на двенадцатеричную систему счисления.
Однако у господ лягушатников ни шиша не сложилось, зато сложилось у некоторых народов Нигерии и Тибета, в связи с тем, что
считать до 12 они привыкли сидя, загибая не только 10 пальцев рук, но и 2 ноги.
Поэтому, по большому счёту, таблицу эту можно было бы изрядно подсократить, если бы не высокие традиции отечественного интернационализма, и не чувство глубокого уважения к биологической и культурной самобытности народов Нигерии, Мали и Папуа-Новой Гвинеи.
«Расскажите, пожалуйста, как называется знак, выражающий отсутствие значения данного разряда в позиционной системе счисления? А то я в математике полный ноль.»
«В мире есть 10 категории людей — те, которые понимают двоичную систему счисления, и те, которые ее не понимают. »
Это не вопрос-ответ, если кто не понял, а искромётный юмор из рублики «математики шутят», а для вопросов, критики и пожеланий милости просим на электронную почту [email protected]
Вычитание в столбик в любой системе
Вычитание в столбик в любой системе счисления
Система счисления – это форма записи чисел по определенным правилам.
Мы пользуемся в быту десятичной системой, но бывают и другие позиционные системы счисления (двоичная, пятеричная, восьмеричная, 16-ичная и т.д.).
Вы можете просмотреть цикл видеоуроков по системе счисления, чтобы понять, что к чему (автор видеоуроков – Максим Семенихин, он же автор данного сайта):
- Введение в системы счисления.
- Перевод чисел из десятичной системы в недесятичную.
- Быстрый переход из двоичной системы в восьмеричную.
- Шестнадцатеричная система счисления.
Вычитание в столбик в любой системе счисления производится по тому же принципу, что и в десятичной системе. Отличаются лишь сами по себе правила вычитания цифр.
Если уменьшаемая цифра больше вычитаемой, то разницы не наблюдается: 5 – 3 = 2, например, в любой системе счисления, в которой существуют цифры 5, 3 и 2.
Если же уменьшаемая цифра меньше вычитаемой, то нужно занять единицу из ближайшего следующего (старшего) разряда, цифра которого не равна нулю, и выполнить вычитание по правилам n-ичной системы.
При этом все следующие разряды-нули, начиная от того, из которого заняли, и заканчивая уменьшаемым разрядом, становятся вместо нулей равными основанию системы счисления, уменьшенному на единицу (как и в десятичной системе).
Онлайн калькулятор
для вычитания в столбик
в любой системе счисления
Для того, чтобы вычесть любые два числа в любой системе счисления, вы можете воспользоваться калькулятором, который находится на данной странице вверху. Введите любые два числа, а затем нажмите кнопку «Вычесть».
Замечание. Иногда калькулятор будет выдавать нули впереди числа в результате, например 00123. Это НЕ специфика записи числа в другой системе счисления (в любой системе число не может начинаться с нуля). Это лишь объяснение подробностей вычитания (на самом деле 00123 – это просто число 123).
A в системе счисления с основанием p вычисляется
Время выполнения заданий 180 минут
Время выполнения заданий 180 минут 1.
Алфавит племени Пиджен состоит из четырех букв. Аборигены закодировали слово BADC с использованием следующей кодовой таблицы: A B C D 10 0 1 01 и передали его, не
Тема: Системы счисления
Коротко о главном Тема: Системы счисления Системы счисления — это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, который существовали раньше
Подробнее16 (повышенный уровень, время 2 мин)
16 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем, 15, из системы
ПодробнееУкажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12,, 17 в системе счисления с основанием 5.
Уравнения и различные системы счисления 1. Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12,, 17 в системе счисления с основанием 5. 2. 121 x + 1 10 = 101 7 Ответ запишите в троичной
Подробнее6-1 (базовый уровень, время 4 мин)
6-1 (базовый уровень, время 4 мин) Тема: Выполнение и анализ простых алгоритмов. Что нужно знать: сумма двух цифр в десятичной системе счисления находится в диапазоне от 0 до 18 (9+9) в некоторых задачах
Подробнее18 (повышенный уровень, время 3 мин)
18 (повышенный уровень, время 3 мин) К. Поляков, 2009-2016 Тема: Основные понятия математической логики. Про обозначения К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной»
ПодробнееДелимость целых чисел в задачах
Югорский физико-математический лицей В.
П. Чуваков Делимость целых чисел в задачах Сборник задач Ханты-Мансийск 05 Делимость целых чисел в задачах: Сборник задач, — Ханты-Мансийск, Югорский физико-математический
16 (повышенный уровень, время 2 мин)
К. Поляков, 009-016 16 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
ПодробнееB4 (высокий уровень, время 10 мин)
B4 (высокий уровень, время 1 мин) Тема: Преобразование логических выражений. Про обозначения К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (,, ),
ПодробнееB7 (повышенный уровень, время 2 мин)
К Поляков, 009-01 B7 (повышенный уровень, время мин) Тема: Кодирование чисел Системы счисления Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
ПодробнееДелимость целых чисел
Делимость целых чисел Число а делится на число b (или b делит а) если существует такое число с, что а=bc При этом число c называется частным от деления а на b Обозначения: a — а делится на b или ba b делит
ПодробнееПЕРЕСТАНОВКИ.
Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
ПодробнееЛогические операции трехзначной логики
ВА Бубнов Московский городской педагогический университет Электронный научный журнал «Вестник Омского государственного педагогического университета» Выпуск 6 wwwomskedu Логические операции трехзначной
ПодробнееЕГЭ Н. В. Потехин
ЕГЭ 2017 Н. В. Потехин 1. Сколько существует натуральных чисел x, для которых выполнено неравенство 11011100 2 < x < DF 16? В ответе укажите только количество чисел, сами числа писать не нужно. 2. Логическая
B15 (высокий уровень, время 10 мин)
B5 высокий уровень, время 0 мин) Тема: Преобразование логических выражений. Про обозначения К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике,, ), неудобны,
ПодробнееСистемы счисления Пример 1.
Системы счисления В наше время человек всё время сталкивается с числами. Все мы с детства знакомы с общепринятой записью чисел при помощи арабских цифр. Однако этот способ записи использовался далеко не
Подробнееn q 1 a 1 a a q n A = n n q n m s 2
Лекция 5 Основы представления информации в цифровых автоматах Позиционные системы счисления Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками.
Любая предназначенная
B8 (повышенный уровень, время 2 мин)
К. Поляков, 009-011 B8 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем,
Подробнее23 Лабораторная работа 3
23 1. Общие сведения о комбинационных схемах Комбинационные схемы состоят из логических элементов. При использовании интегральных микросхем такими элементами обычно являются элементы типа И-НЕ, ИЛИ-НЕ,
ПодробнееКР ЕГЭ 20 Модуль 2. Вариант 3
КР ЕГЭ 20 Модуль 2 Вариант 3 Задание 1. Ниже записана программа. Получив на вход число x, эта программа печатает два числа, L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает
ПодробнееB10 (высокий уровень, время 10 мин)
B0 (высокий уровень, время 0 мин) Тема: Преобразование логических выражений.
Про обозначения К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (,, ),
А1 (базовый уровень, время 1 мин)
А1 (базовый уровень, время 1 мин) Тема: Системы счисления и двоичное представление информации в памяти компьютера. Что нужно знать: перевод чисел между десятичной, двоичной, восьмеричной и шестнадцатеричной
ПодробнееТождества Булевой алгебры
Тождества Булевой алгебры Основная задача математической логики на основании ложности или истинности простых высказываний определить значение сложного высказывания. Логические операции алгебре высказываний
ПодробнееСистемы счисления (СС)
Системы счисления (СС) I. Двоичная система счисления. Как устроено число в десятичной СС: 579 0 =5 0 7 0 9 0 0 ( a 0, a 0).
В любой другой позиционной системе счисления числа устроены точно таким же образом.
сайт Шпаргалка ЕГЭ Подготовка к ЕГЭ
B15 Укажите значения переменных K, L, M, N, при которых логическое выражение (K M) (L K) N ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке).
ПодробнееСимвол N O P Q R S T U V W X Y Z Код символа
Открытая олимпиада школьников «Информационные технологии» 2017-18 Решения заданий заключительного этапа для 7 и 8 класса 1. Системы счисления (1 балл) [Торрент] Петя решил скачать файл используя торрент-клиент.
ПодробнееТема 1. Элементы теории погрешностей
— 1 — Тема 1 Элементы теории погрешностей 11 Источники и классификация погрешностей Численное решение любой задачи, как правило, осуществляется приближенно, те с некоторой точностью Это может быть обусловлено
ПодробнееОсновные понятия формальной логики
Основные понятия формальной логики Элементы логики Умение правильно рассуждать необходимо в любой области человеческой деятельности.
Логика, как наука о том какие формы рассуждений правильны возникла немногим
B15 (высокий уровень, время 10 мин)
B высокий уровень, время 0 мин) К. Поляков, 009-0 Тема: Преобразование логических выражений. Про обозначения К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической
ПодробнееПример решения: данному уравнению. Здесь
Задание : Постройте таблицу истинности логической функции F A B C F Вычислите десятичный номер функции по формуле: Значения функции удовлетворяют системе линейных уравнений в поле, эквивалентной уравнению
ПодробнееОСНОВЫ АЛГОРИТМИЗАЦИИ И ПРОГРАММИРОВАНИЕ
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Владимирский государственный университет имени
ПодробнееБлок Системы счисления
Блок 2.
2.1. Системы счисления Знать основные понятия позиционных систем счисления: цифра, алфавит, размерность алфавита (основание системы), разряд числа, базис; развернутую формулу записи числа; числа
МОДУЛЬНАЯ АРИФМЕТИКА
МОДУЛЬНАЯ АРИФМЕТИКА В некоторых приложениях удобно выполнять арифметические операции над целыми числами, заданными в так называемом модульном представлении Это представление предполагает, что целое число
ПодробнееЗадания к 1.1 СИСТЕМЫ СЧИСЛЕНИЯ
Задания к 1.1 СИСТЕМЫ СЧИСЛЕНИЯ 15. В древнеегипетской нумерации для записи целых чисел использовались следующие иероглифы: Запишите числа, представленные древнеегипетскими иероглифами, в десятичной системе
ПодробнееЗадания А5 по информатике
Задания А5 по информатике 1.
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ Основная задача теории погрешностей состоит в оценке погрешности результата вычислений при известных погрешностях исходных данных. Источники и классификация погрешностей результата
ПодробнееA9 (базовый уровень, время 2 мин)
A9 (базовый уровень, время 2 мин) Тема: Построение таблиц истинности логических выражений. Про обозначения К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической
ПодробнееID_3519 1/7 neznaika.pro
Числа и их свойства Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел.
Запишите ответ без пробелов, запятых и других дополнительных символов. 1 Натуральные числа
«Олимпиада по информатике»
Министерство образования и науки Российской Федерации Российский совет олимпиад школьников Санкт-Петербургский государственный университет информационных технологий механики и оптики «Олимпиада по информатике»
ПодробнееЛекция 28 Глава 1. Векторная алгебра
Лекция 8 Глава Векторная алгебра Векторы Величины, которые определяются только своим числовым значением, называются скалярными Примерами скалярных величин: длина, площадь, объѐм, температура, работа, масса
ПодробнееЛабораторная работа по информатике для ТулГУ, пример оформления
Лабораторная работа по дисциплине «Информатика»
1. Цель работы
Познакомиться правилами перевода чисел из одной позиционной системы счисления в другую.
2. Задание на лабораторную работу
Перевести число из одной позиционной системы счисления в другую в соответствии с полученным вариантом (таблица 1).
Таблица 1 — Варианты заданий на работу
Вариант Число Исходная система
счисления Система
счисления Система
счисления Система
счисления
5 1212 7 3 5 6
3. Ход работы
1. Переведем число 1212 из семеричной системы счисления в троичную.
а) Для перевода числа из семеричной системы счисления в троичную сначала переведем исходное число в десятичную систему счисления.
12127 = 1∙73+2∙72+1∙71+2∙70 = 343+98+7+2 = 45010
Получили: 45010
б) Переведем 45010 в троичную систему.
Приведем целую часть числа 450 в систему счисления 3 последовательным делением на число 3 (таблица 2).
Таблица 2 — Перевод числа из одной позиционной системы счисления в другую
Делимое Делитель Частное Остаток
450 / 3 150 0
150 / 3 50 0
50 / 3 16 2
16 / 3 5 1
5 / 3 1 2
1 / 3 0 1
Ответ: 1212003
2.
Переведем число 1212 из семеричной системы счисления в пятеричную.
а) Для перевода числа из семеричной системы счисления в пятеричную сначала переведем исходное число в десятичную систему счисления.
12127 = 1∙73+2∙72+1∙71+2∙70 = 343+98+7+2 = 45010
Получили: 45010
б) Переведем 45010 в троичную систему.
Приведем целую часть числа 450 в систему счисления 5 последовательным делением на число 5 (таблица 3).
Таблица 3 — Перевод числа из одной позиционной системы счисления в другую
Делимое Делитель Частное Остаток
450 / 5 90 0
90 / 5 18 0
18 / 5 3 3
3 / 5 0 3
Ответ: 33005
3. Переведем число 1212 из семеричной системы счисления в шестеричную.
а) Для перевода числа из семеричной системы счисления в шестеричную сначала переведем исходное число в десятичную систему счисления.
12127 = 1∙73+2∙72+1∙71+2∙70 = 343+98+7+2 = 45010
Получили: 45010
б) Переведем 45010 в троичную систему.
Приведем целую часть числа 450 в систему счисления 6 последовательным делением на число 6 (таблица 4).
Таблица 4 — Перевод числа из одной позиционной системы счисления в другую
Делимое Делитель Частное Остаток
450 / 6 75 0
75 / 6 12 3
12 / 6 2 0
2 / 6 0 2
Ответ: 20306
4. Ответы на контрольные вопросы
1. Какая система называется позиционной? Приведите примеры таких систем.
Позиционные системы счисления — это системы счисления, в которых значение цифры напрямую зависит от её положения в числе.
Например, число 01 обозначает единицу, 10 — десять.
Позиционные системы счисления позволяют легко производить арифметические расчёты.
Представление чисел с помощью арабских цифр — самая распространённая позиционная система счисления, она называется «десятичной системой счисления». Десятичной системой она называется потому, что использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Заметьте: максимальная цифра (9) на единицу меньше количества цифр (10).
Для составления машинных кодов удобно использовать не десятичную, а двоичную систему счисления, содержащую только две цифры, 0 и 1.
Обратите внимание, что в двоичной системе максимальная цифра 1.
Программисты для вычислений также пользуются ещё восьмеричной и шестнадцатеричной системами счисления.
Количество цифр, используемых в системе счисления, называется её «основанием». В десятичной системе основание равно десяти, в двоичной системе — двум, ну а в восьмеричной и шестнадцатеричной — соответственно, восьми и шестнадцати. То есть в ручной системе счисления количество цифр равно р и используются цифры от 0 до р-1.
В общем случае в позиционной системе счисления числа представляются следующим образом: an-1 … a1a0f , где a0, a1, …, an-1 — цифры, а f — основание системы счисления. Если используется десятичная система, то — можно опустить.
Примеры чисел:
• 2510 — число в десятичной системе счисления, a0=5, a1=2;
• 318 — это же число в восьмеричной системе счисления, a0=1, a1=3;
• 2213 — это же число в несимметричной троичной системе счисления, a0=1, a1=2, a2=2;
• 110012 — это же число в двоичной системе счисления, a0=1, a1=0, a2=0, a3=1, a4=1;
2.
Какая система называется непозиционной? Приведите примеры таких систем.
Непозиционная система счисления — это такая система счисления, в которой положения цифры в записи числа не зависит величина, которую она обозначает. Система может накладывать определенные ограничения на порядок цифр (расположение по возрастанию или убыванию).
Существуют такие непозиционные системы счисления:
— Единичная система счисления,
— Пятеричная система счисления (Счёт на пятки́),
— Древнеегипетская система счисления,
— Вавилонская система счисления,
— Алфавитные системы счисления,
— Еврейская система счисления,
— Греческая система счисления,
— Римская система счисления,
— Система счисления майя,
— Кипу инков.
Отличие позиционной системы счисления от непозиционной.
В позиционных системах счисления значение цифры зависит от местонахождения в записи числа. Например, в числе 12 цифра 1 означает десять, а в числе 122 — сотню. В непозиционных системах счисления, где бы цифра не находилась, она имеет одно и то же значение.
Например, в римской системе счисления IV и XI цифра I означает единицу.
3. Правила какой арифметики используются при переводе числа из одной системы счисления в другую делением на основание новой системы?
Чтобы перевести целое число из одной десятичной системы счисления в другую позиционную систему, необходимо число одной системы счисления последовательно делить на основание той системы, в которую переводится данное число. При этом деление производится до тех пор, пока частное не окажется меньше основания получаемой системы счисления. Число в новой системе счисления формируется из остатков от деления, начиная с последнего. Иначе говоря, последнее частное становится высшим разрядом числа.
4. Какое максимально возможное число можно записать с помощью шестнадцатеричной системы счисления?
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF.
Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов.
Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние.
5. Перечислите цифры, используемые для записи числа в восьмеричной системе.
В восьмеричной системе счисления основание равно 8, для записи чисел используются цифры от 0 до 7. Для записи каждой цифры восьмеричной с.с. требуется максимум 3 разряда.
6. Возможен ли перевод дробных чисел из одной системы счисления в другую?
Да, можно.
Алгоритм перевода правильной дроби с основанием p в дробь с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления числа.
3. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
5. Выводы по проделанной работе
Изучил позиционные системы счисления, освоил алгоритмы перевода чисел из одной системы счисления в другую. Получил практические навыки по выполнению арифметических действий над двоичными числами, сложению и вычитанию двоичных и десятичных чисел в прямом, обратном и дополнительном кодах.
Набор задач по теме «Системы счисления»
Системы счисления:
Результат сложения чисел, записанных в восьмеричной системе счисления:
178+17008+1700008+170000008,
перевели в шестнадцатеричную систему счисления.
Напишите в ответе, в порядке возрастания, какие цифры встретились в получившейся записи. (Ответ: 3 C F)
Дети играли кубиками и решили сложить пирамиду. Для того, что бы пирамида была устойчивой, они решили всегда ставить кубик меньшего размера на кубик большего размера. Помогите ребятам правильно расположить кубики, если известна длина ребра каждого кубика:
Номер кубика | Длина ребра |
1 | 1019 |
2 | 1318 |
3 | 2027 |
4 | 2226 |
5 | 3035 |
6 | 3134 |
В ответе укажите без пробелов последовательность номеров кубиков в пирамиде сверху вниз.
Ответ: 651423
Петя загадал последовательность из 4 чисел, в которой каждое следующее число на единицу больше предыдущего. После этого он записал каждое число в системе счисления с определенным основанием, не меняя порядка чисел. Все числа записаны в системах счисления с разными основаниями. Получилась следующая запись:
37 35 33 31
Определите, в какой системе счисления записано последнее число, если известно, что одно из чисел записано в восьмеричной системе счисления. В ответе укажите натуральное число, равное основанию этой системы счисления.
Ответ: 11
Для написания сообщений используется алфавит, включающий в себя следующий набор пронумерованных символов:
Символ | пробел | а | б | в | г | д | е | ё | ж | з | и | й |
Номер символа | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Символ | к | л | м | н | о | п | р | с | т | у | ф | х |
Номер символа | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
Символ | ц | ч | ш | щ | ъ | ы | ь | э | ю | я | запятая | точка |
Номер символа | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
Для шифрования сообщений, написанных с использованием этого алфавита, принят следующий алгоритм:
1.
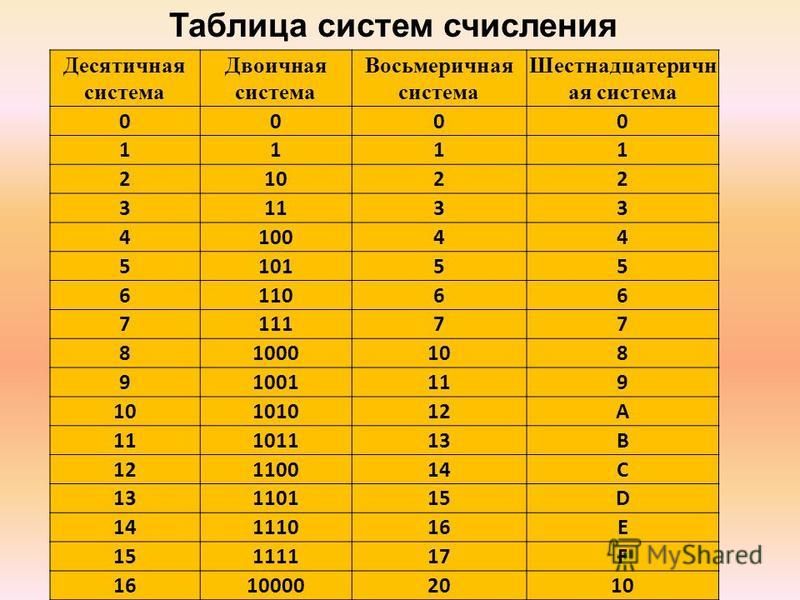По приведенной таблице определяется номер очередного символа исходного сообщения и переводится в шестеричную систему счисления. При записи результата всегда используется 2 разряда (при необходимости дописывается незначащий ноль).
2. Старший и младший разряд полученной записи меняются местами, и полученное число переводится обратно в десятичную систему счисления – получается номер символа по приведенной таблице, на который заменяется исходный символ.
В процессе шифрования, каждый символ исходного сообщения заменяется на другой символ по приведенному алгоритму (легко заметить, что будут существовать символы, которые в результате шифрования не изменят своего значения).
Расшифруйте сообщение, полученное в результате применения описанного алгоритма:
ршжб азн сеэгар.
В ответе запишите исходное сообщение.
Ответ: волк ест зайцев.
Вычислите значение выражения:
В ответе укажите целое число.
Ответ: 2
6. Вася не любил много писать и решил при записи больших чисел сокращать написание повторяющихся цифр. Он завел правило: если при записи числа слева направо встречаются две идущие подряд одинаковые цифры, то он пишет только одну такую цифру и ставит над ней точку. Вася записал пять примеров и точно помнит, что только в одном из них и только один раз встречались идущие подряд две одинаковых цифры, но при записи этого примера он поторопился и не поставил в примере точку. Помогите Васе определить нужный пример и расшифровать число, записанное в сокращенной форме. В ответе через запятую дайте, сначала номер примера, затем полную запись того числа, в котором Вася сократил запись без указания основания системы счисления.
1. 12031045 + 1012015 = 13043105
2. 12023 + 1013 = 20103
3. 4124536278 + 12315168 = 4247053458
4. 4724729 + 8752109 = 14576829
5. 12А2367911 + 9452А411 = 1386897211
7. Дано следующее равенство:
ABC + ABC = 13С(B+А)
A, B и C – натуральные числа, не превышающие 16, которые равны значениям отдельных цифр чисел или определяют значения оснований систем счисления, в которых эти числа записаны, если указаны в нижних индексах.
Найдите комбинацию значений A, B и C, при которой указанное равенство выполняется. В ответе приведите через пробел сначала десятичную запись числа, соответствующего значению А, затем десятичную запись числа, соответствующего значению В, и в конце десятичную запись числа, соответствующего значению С. Если существует несколько наборов A, B и C удовлетворяющих условию, приведите любой из них.
Ответ: 7 2 8 || 11 5 14
8. Найдите натуральное число такое, что его запись в шестеричной системе счисления имеет ровно четыре значащих разряда и при этом выполняются следующие условия:
1. Две первые цифры его записи являются одинаковыми между собой, и две последние цифры также одинаковы между собой.
2. Две первые цифры отличны от последних двух цифр.
3. Число является полным квадратом, то есть оно является квадратом некоторого целого числа.
В ответе укажите четырехзначное число в шестеричной системе счисления.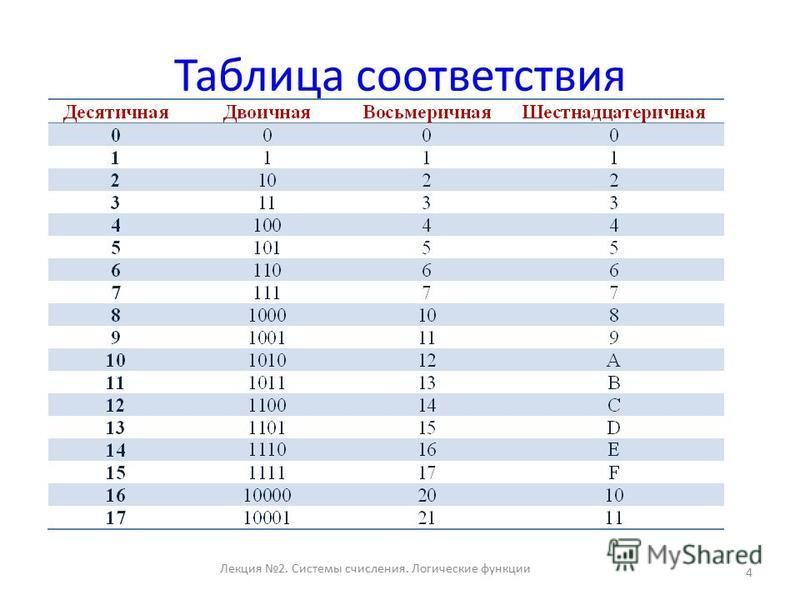
Ответ: 3344
Решение
Задачи, связанные с системами счисления целесообразно решать, используя полную степенную запись числа.
Перепишем условие:
А*63+А*62+В*6+В=Х2, где
А – первая и вторая цифра числа в шестеричной системе,
В – третья и четвертая цифра числа в шестеричной системе.
Упростим выражение
(36*А + В)*7= Х2
Проанализируем данное равенство.
Из условия задачи понятно, что А может принимать значения от 1 до 5, а В может принимать значения от 0 до 5.
Следовательно максимальное значение Х2 может быть равно 1295, а минимальное равно 252.
Таким образом можно утверждать что:
15,87
Поскольку по условию Х целое, то нас интересует ряд целых чисел от 16 до 35.
Кроме того, из равенства видно, что Х должно быть кратно 7. Что сокращает ряд чисел до трех: 21, 28, 35.
Далее нужно решить независимо три уравнения:
(36*А + В)*7= 212
(36*А + В)*7= 282
(36*А + В)*7= 352
Из полученных уравнений только второе имеет решение, при котором A и B будут целыми числами, попадающими в
диапазоны, определенные выше. Получаем А = 3 и В = 4.
9. Сколько существует натуральных чисел, для которых одновременно выполняются следующие условия:
1. Запись числа в семеричной системе счисления имеет ровно три значащих разряда.
2. Если перевести это число в шестеричную систему счисления, то запись числа останется трехразрядной, но значение каждого разряда увеличится на единицу по сравнению со значениями соответствующих разрядов в записи этого числа в семеричной системе счисления.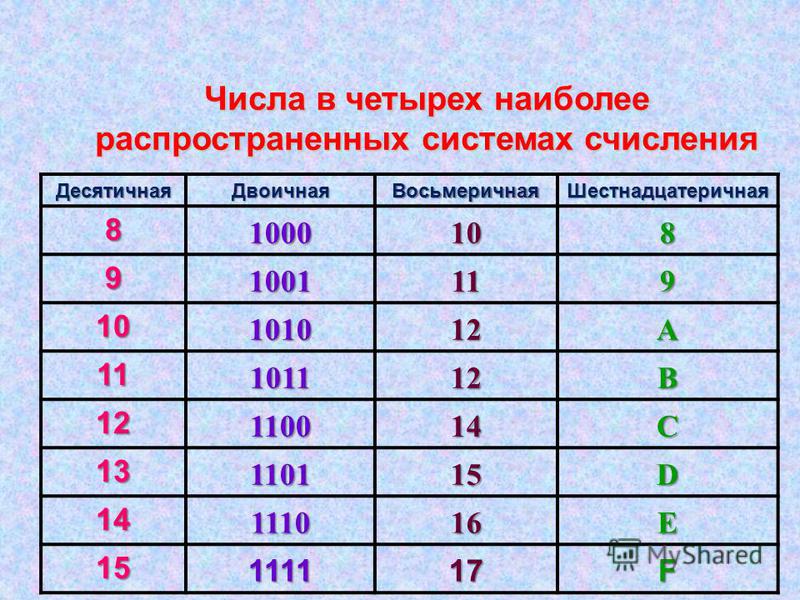
В ответе укажите целое число.
Ответ: 5
10. Дано арифметическое выражение, все числа которого записаны в шестнадцатеричной системе счисления:
Посчитайте сумму цифр числа, являющегося результатом вычисления этого выражения и записанного также в шестнадцатеричной системе счисления. Запишите полученную сумму в ответ в десятичной системе счисления.
Ответ: 61
11.Запись некоторого натурального числа X в шестнадцатеричной системе счисления имеет ровно три значащих разряда. Это число увеличили в два раза, и оказалось, что запись получившегося числа Y в шестнадцатеричной системе также имеет ровно три значащих разряда, причем сумма цифр шестнадцатеричной записи исходного числа X равна сумме цифр шестнадцатеричной записи полученного числа Y. Сколько существует таких чисел X, которые удовлетворяют указанным условиям и при этом содержат хотя бы одну цифру 2 в своей шестнадцатеричной записи? В ответе укажите целое число.
Ответ: 23
12. В троичной системе счисления три различные цифры зашифровали буквами А, В и С. Определите их значения, если известно: ВАС + СВА = САВС. В ответе последовательно без пробелов и запятых укажите сначала цифру, зашифрованную буквой А, затем цифру, зашифрованную буквой В и затем цифру, зашифрованную буквой С.
Ответ: 021
13. Даны четыре арифметических выражения. Выберите выражение с корректной записью чисел в указанных системах счисления и вычислите его результат. В ответе запишите одно десятичное число, получаемое в результате решения корректно записанного выражения.
178 – 324 + АВ11 – XCIV(римск.) = 10
467 – 12313 + CXI (римск.) – B12 = 10
2911 – 335 + XCIX (римск.) – 1F16 = 10
266 – 100102 +XCIX(римск.) – 1B13 = 10
Ответ: 81
14. В четверичной системе счисления каждую из цифр зашифровали буквами А, В, С и D.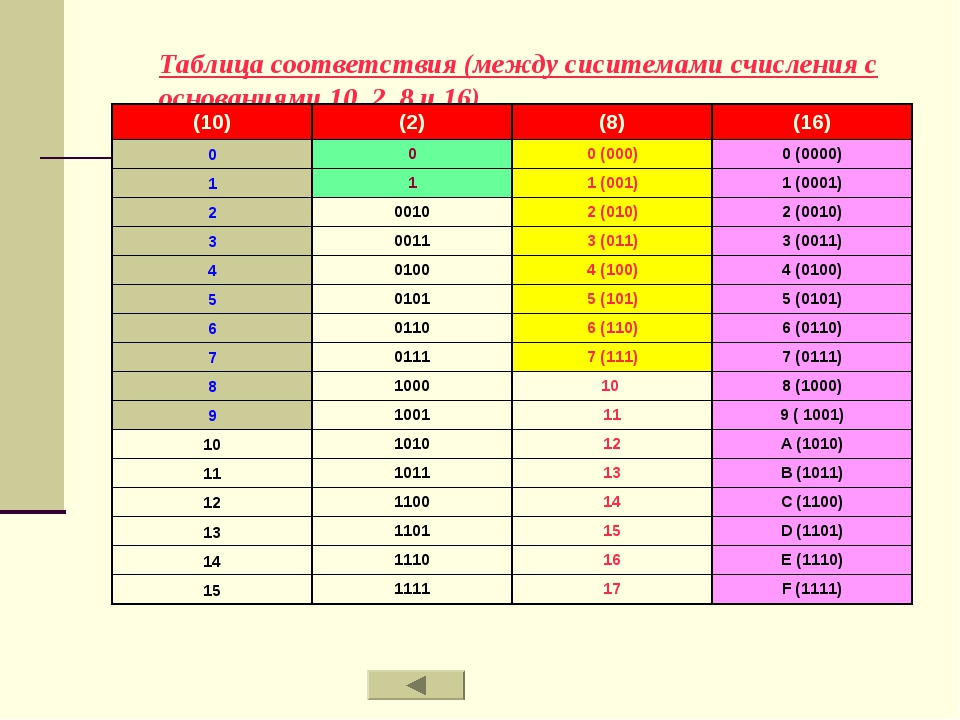
Определите их значения, если известно: ACAB + DBBD = ACCAA. В ответе последовательно без пробелов и запятых укажите сначала, букву, шифрующую цифру 0, затем букву, шифрующую цифру 1, затем букву, шифрующую цифру 2, и, наконец, букву, шифрующую цифру 3.
Ответ: CADB
. 15.Даны три произведения чисел, записанных в различных системах счисления. Символом N обозначена одна, допустимая в использующихся системах счисления, цифра. Найдите максимальное значение N, такое, что в результате вычисления все представленные произведения чисел будут четными числами. В ответе укажите целое число.
1. 40323N5 x B2750412
2. 23201N4 x 21AF5819
3. 1434N45 x 1B034A13
Ответ 2
16. Число X = (3232 + 44 -1) * 1616 + 88 -1 перевели из десятичной в двоичную систему счисления. Сколько единиц получилось в двоичной записи числа? В ответе укажите целое число.
17.
В числе, записанном в римской системе счисления, поменяли местами вторую и третью от начала цифры, а затем перевели результат в десятичную систему счисления. Получилось число 193. Определите исходное число, переведите его в десятичную систему счисления и запишите результат. Напомним, что для записи чисел в римской системе счисления используется набор из семи цифр (I, V, X, L, C, D, M).
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Шестнадцатеричная система счисления 1-100
Шестнадцатеричная система счисления — это система счисления с основанием 16.
Представляет числовые значения с использованием шестнадцати символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. В таблице ниже представлены шестнадцатеричные числа от 1 до 64, что эквивалентно десятичным числам от 1 до 100.
| Шестнадцатеричное | Десятичное | Шестнадцатеричное | Десятичное | |||
|---|---|---|---|---|---|---|
| 1 | 1 | 33 | 51 | |||
| 2 | 335 | 53 | ||||
| 4 | 4 | 36 | 54 | |||
| 5 | 5 | 37 | 55 | |||
| 6 | 0009 56000||||||
| 7 | 7 | 39 | 57 | |||
| 8 | 8 | 3A | 58 | |||
| 9 | 9 | 3B | 00000093C | 60 | ||
| B | 11 | 3D | 61 | |||
| C | 12 9000 9 | 3E | 62 | |||
| D | 13 | 3F | 63 | |||
| E | 14 | 40 | 64 | |||
| 65 | ||||||
| 10 | 16 | 42 | 66 | |||
| 11 | 17 | 43 | 67 | |||
| 12 | 18 | 44 | 1 | 45 | 69 | |
| 14 | 20 | 46 | 70 | |||
| 15 | 21 | 47 | 71 | |||
| 16 | 72 | 0009 1723 | 49 | 73 | ||
| 18 | 24 | 4A | 74 | |||
| 19 | 90 004 254B | 75 | ||||
| 1A | 26 | 4C | 76 | |||
| 1B | 27 | 4D | 77 | |||
| 1D | 29 | 4F | 79 | |||
| 1E | 30 | 50 | 80 | |||
| 1F | 31 | 900051 | 900 | 52 | 82 | |
| 21 | 33 | 53 | 83 | |||
| 22 | 34 | 54 | 84 | |||
| 23 | ||||||
| 24 | 36 | 56 | 86 | |||
| 25 | 37 | 57 | 87 | |||
| 38 | 58 | 88 | ||||
| 27 | 39 | 59 | 89 | |||
| 28 | 40 | 5A | 90 | 91 | ||
| 2A | 42 | 5C | 92 | |||
| 2B | 43 | 5D | 93 | |||
| 2C | 000945 | 5F | 95 | |||
| 2E | 46 | 60 | 96 | |||
| 2F | 47 | 61 | 97 | 0000009 98|||
| 31 | 49 | 63 | 99 | |||
| 32 | 50 | 64 | 100 | 900 19
Статьи по теме
Выбрать этикетку
Подробнее
Преобразование системы счисления — Schoolelectronic
В предыдущих постах мы обсуждали представление чисел в различных системах счисления.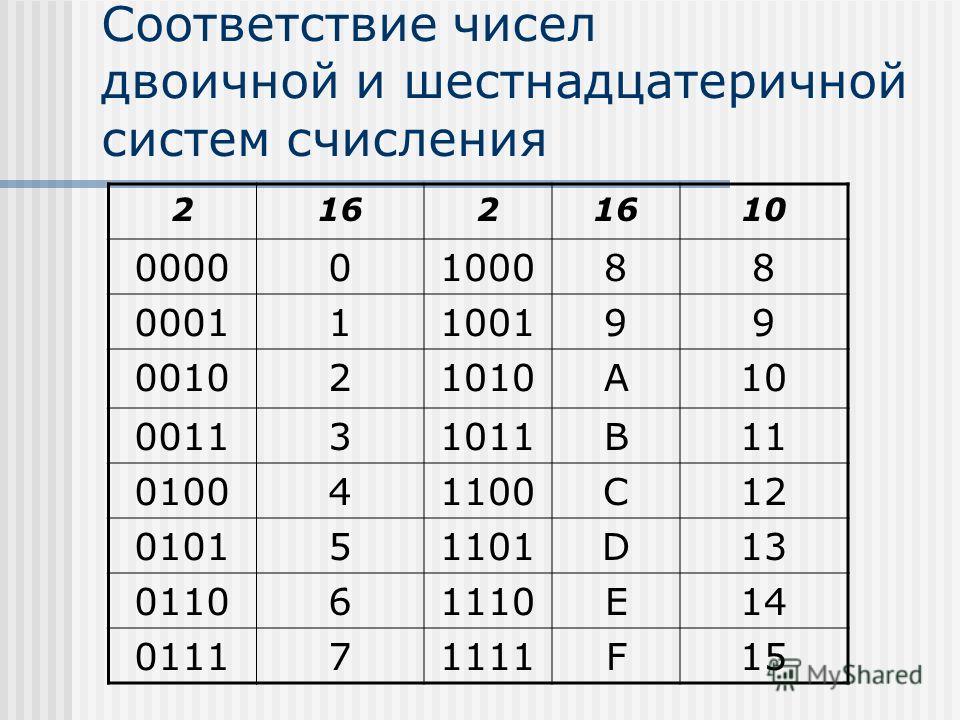
Мы также пошагово решили примерные задачи и попробовали несколько ярлыков. Здесь мы кратко обсудим преобразование системы счисления. Другими словами, мы бы увидели, как мы можем представить данное число в другой системе счисления без каких-либо изменений в значении.
В следующих постах мы обсудим основные методы преобразования любого заданного числа из одной системы счисления в другую.
В этот момент вы спросите меня: «Эй, а зачем нам делать это преобразование чисел? «.
Этот вопрос абсолютно верен, потому что в электронике правильное решение системы счисления в первую очередь зависит от типа приложения. Чтобы лучше выразиться, возьмем пример.
Вы предоставляете номер своего мобильного телефона одному из одноклассников. Например, это ваш номер мобильного телефона (123) -456-0123 в десятичной системе счисления, и вы решили указать его в двоичном формате как (1111011) -111001000-1111011 .
Однако, когда вы даете то же число в десятичном формате вашему компьютеру.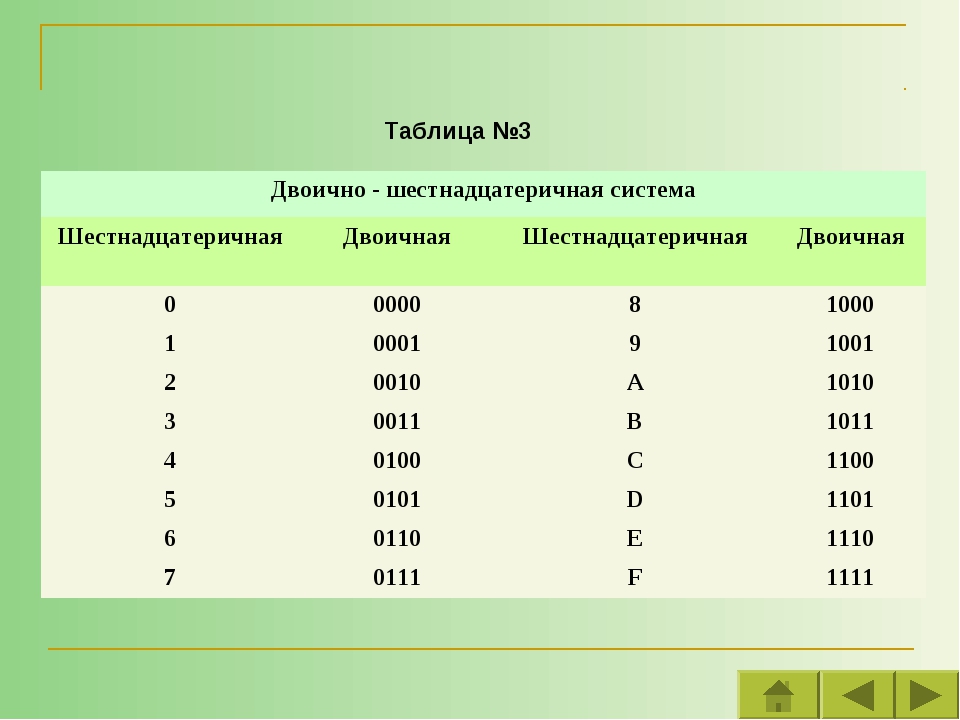
Число будет преобразовано в его двоичный эквивалент, как показано выше, и сохранено. (компьютер понимает только нули и единицы).
Из приведенного выше примера мы можем четко различить, когда нам нужна десятичная система счисления и двоичная система счисления.
Восьмеричная система счисления и шестнадцатеричная система счисления были введены в основном для того, чтобы машинные коды были более удобными для человека, вместо нулей и единиц.
Восьмеричная система счисления отступила назад и редко находит применение в современных приложениях.Шестнадцатеричная система счисления является сегодня наиболее широко используемой системой счисления. Современные компьютеры используют шестнадцатеричный формат для адресов памяти и значительно упрощают отладку, когда компьютер выдает ошибку с шестнадцатеричным адресом вместо длинной строки из нулей и единиц.
Мы начнем изучать методы преобразования с десятичной системы счисления, поскольку мы больше знакомы с десятичной системой счисления.
Под преобразованием десятичной системы счисления мы узнаем следующие преобразования
- Десятичная система счисления в двоичную систему счисления
- Десятичная система счисления в восьмеричную систему счисления
- Десятичная система счисления в шестнадцатеричную систему счисления
- Двоичная система счисления в десятичную систему счисления
- Восьмеричная система счисления в десятичную систему счисления
- Шестнадцатеричная система счисления в десятичную систему счисления
Таблица преобразования десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
В предыдущих постах подробно описывалась процедура, шаг за шагом, для преобразования заданного числа из одной системы счисления в другую с помощью экзаменов.
В таблице ниже приведены эквивалентные числа в четырех системах счисления, которые мы будем использовать в базовой электронике.
Эта таблица преобразования представляет собой не что иное, как простую шпаргалку для выполнения математических и логических операций с различными системами счисления, с которыми мы сталкивались ранее, подобно таблицам умножения (от 1 до 20), которые мы просили запомнить в классе математики младших классов. быстрее выполнять сложные операции умножения и деления.
Эта таблица будет действовать как простой бонус к ускорению, чтобы быстрее выполнять математические операции между системами счисления.Мы также можем использовать эту таблицу для быстрого преобразования системы счисления.
| Десятичный Базовый 10 | Двоичный Базовый 2 | Восьмеричный Базовый 8 | Шестнадцатеричный Базовый 16 | ||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 00091 | 1 | |
| 2 | 10 | 2 | 2 | ||
| 3 | 11 | 3 | 3 | ||
| 10019 4 | 0009|||||
| 5 | 101 | 5 | 5 | ||
| 6 | 110 | 6 | 6 | ||
| 7 | 111 | 7 | 10 | 8 | |
| 9 | 1001 | 11 | 9 | ||
| 10 | 1010 | 12 | 9000 4 A|||
| 11 | 1011 | 13 | B | ||
| 12 | 1100 | 14 | C | ||
| 13 | 1101 | 1110 | 16 | E | |
| 15 | 1111 | 17 | F | ||
| 16 | 10000 | 20 | 10 | 20 | 10 | Система десятичного преобразования
Таблица преобразования десятичных, двоичных, шестнадцатеричных и ASCII чисел
Это таблица преобразования с десятичными числами рядом с их двоичными и шестнадцатеричными эквивалентами .
Соответствующие символы ASCII также перечислены с более подробным описанием некоторых символов на этой странице. Если ни одно из этих слов для вас ничего не значит, перейдите в конец страницы, чтобы получить дополнительную информацию по адресу:
коды ASCII от 0 до 127
| № | двоичный | Шестигранник | ASCII | Описание |
| 0 | 00000000 | 0ч | null | |
| 1 | 00000001 | 1 ч. | начало товарной позиции | |
| 2 | 00000010 | 2 ч. | начало текста | |
| 3 | 00000011 | 3 ч. | конец текста | |
| 4 | 00000100 | 4ч | конец передачи | |
| 5 | 00000101 | 5ч | запрос | |
| 6 | 00000110 | 6ч | подтвердить | |
| 7 | 00000111 | 7ч | звонок | |
| 8 | 00001000 | 8ч | возврат | |
| 9 | 00001001 | 9ч | горизонтальный выступ | |
| 10 | 00001010 | Ач | перевод строки | |
| 11 | 00001011 | Bh | вертикальный язычок | |
| 12 | 00001100 | шасси | подача формы | |
| 13 | 00001101 | Dh | возврат каретки | |
| 14 | 00001110 | Eh | сдвиг | |
| 15 | 00001111 | Fh | смена | |
| 16 | 00010000 | 10ч | выход канала передачи данных | |
| 17 | 00010001 | 11ч | устройство управления 1 | |
| 18 | 00010010 | 12ч | устройство управления 2 | |
| 19 | 00010011 | 13ч | устройство управления 3 | |
| 20 | 00010100 | 14ч | устройство управления 4 | |
| 21 | 00010101 | 15ч | отрицательное подтверждение | |
| 22 | 00010110 | 16ч | синхронный холостой ход | |
| 23 | 00010111 | 17ч | конец блока | |
| 24 | 00011000 | 18ч | отменить | |
| 25 | 00011001 | 19ч | конец среднего | |
| 26 | 00011010 | 1 Ач | заменить | |
| 27 | 00011011 | 1Bh | побег | |
| 28 | 00011100 | 1Ч | разделитель файлов | |
| 29 | 00011101 | 1Dh | разделитель групп | |
| 30 | 00011110 | 1Eh | разделитель записей | |
| 31 | 00011111 | 1Fh | блок сепаратора | |
| 32 | 00100000 | 20ч | место | |
| 33 | 00100001 | 21ч | ! | восклицательный знак |
| 34 | 00100010 | 22ч | “ | двойные кавычки |
| 35 | 00100011 | 23ч | # | числовой знак или хэш-тег |
| 36 | 00100100 | круглосуточно | $ | знак доллара |
| 37 | 00100101 | 25ч | % | знак процента |
| 38 | 00100110 | 26ч | и | амперсанд |
| 39 | 00100111 | 27ч | ‘ | одинарная кавычка |
| 40 | 00101000 | 28ч | ( | левая скобка |
| 41 | 00101001 | 29ч | ) | правая скобка |
| 42 | 00101010 | 2Ач | * | звездочка |
| 43 | 00101011 | 2Bh | + | плюс |
| 44 | 00101100 | 2Ч | , | запятая |
| 45 | 00101101 | 2Dh | – | дефис или знак минус |
| 46 | 00101110 | 2Eh | . | период |
| 47 | 00101111 | 2Fh | / | слэш |
| 48 | 00110000 | 30ч | 0 | ноль |
| 49 | 00110001 | 31ч | 1 | один |
| 50 | 00110010 | 32ч | 2 | два |
| 51 | 00110011 | 33ч | 3 | три |
| 52 | 00110100 | 34ч | 4 | четыре |
| 53 | 00110101 | 35ч | 5 | пять |
| 54 | 00110110 | 36ч | 6 | шесть |
| 55 | 00110111 | 37ч | 7 | семь |
| 56 | 00111000 | 38ч | 8 | восемь |
| 57 | 00111001 | 39ч | 9 | девять |
| 58 | 00111010 | 3Ач | : | толстая кишка |
| 59 | 00111011 | 3Bh | ; | точка с запятой / td> |
| 60 | 00111100 | 3Ч | < | меньше знака |
| 61 | 00111101 | 3Дч | = | знак равенства |
| 62 | 00111110 | 3Eh | > | знак больше |
| 63 | 00111111 | 3Fh | ? | вопросительный знак |
| 64 | 01000000 | 40ч | @ | при символе |
| 65 | 01000001 | 41ч | A | заглавная |
| 66 | 01000010 | 42ч | Б | столица b |
| 67 | 01000011 | 43ч | С | капитал c |
| 68 | 01000100 | 44ч | D | заглавная d |
| 69 | 01000101 | 45ч | E | заглавная е |
| 70 | 01000110 | 46h | Ф | заглавная f |
| 71 | 01000111 | 47ч | G | заглавная г |
| 72 | 01001000 | 48ч | H | заглавная h |
| 73 | 01001001 | 49ч | I | капитал i |
| 74 | 01001010 | 4Ач | Дж | заглавная j |
| 75 | 01001011 | 4Bh | К | заглавная k |
| 76 | 01001100 | 4Ч | л | большой l |
| 77 | 01001101 | 4Dh | M | столица м |
| 78 | 01001110 | 4Eh | N | заглавная n |
| 79 | 01001111 | 4Fh | O | капитал o |
| 80 | 01010000 | 50ч | П | заглавная |
| 81 | 01010001 | 51ч | Q | капитал q |
| 82 | 01010010 | 52ч | R | заглавная |
| 83 | 01010011 | 53х | S | заглавная s |
| 84 | 01010100 | 54ч | т | капитал т |
| 85 | 01010101 | 55ч | U | столица у |
| 86 | 01010110 | 56ч | В | капитал v |
| 87 | 01010111 | 57ч | Вт | заглавная w |
| 88 | 01011000 | 58ч | Х | заглавная x |
| 89 | 01011001 | 59ч | Y | капитал у |
| 90 | 01011010 | 5Ah | Z | заглавная буква z |
| 91 | 01011011 | 5Bh | [ | левый кронштейн |
| 92 | 01011100 | 5Ч | \ | обратная косая черта |
| 93 | 01011101 | 5Dh | ] | кронштейн правый |
| 94 | 01011110 | 5Eh | ^ | каретка или циркумфлекс |
| 95 | 01011111 | 5Fh | _ | подчеркивание |
| 96 | 01100000 | 60ч | ` | могильный акцент |
| 97 | 01100001 | 61ч | а | строчная |
| 98 | 01100010 | 62ч | б | строчная b |
| 99 | 01100011 | 63ч | c | строчная c |
| 100 | 01100100 | 64ч | д | строчная d |
| 101 | 01100101 | 65h | e | строчная e |
| 102 | 01100110 | 66ч | f | строчная f |
| 103 | 01100111 | 67ч | г | строчная г |
| 104 | 01101000 | 68h | ч | строчная h |
| 105 | 01101001 | 69ч | я | строчная i |
| 106 | 01101010 | 6Ач | j | строчная j |
| 107 | 01101011 | 6Bh | к | строчная k |
| 108 | 01101100 | 6Ч | л | строчная l |
| 109 | 01101101 | 6Dh | кв. м | строчная m |
| 110 | 01101110 | 6Eh | п | строчная n |
| 111 | 01101111 | 6Fh | или | строчная o |
| 112 | 01110000 | 70ч | п. | строчная |
| 113 | 01110001 | 71h | кв. | строчная q |
| 114 | 01110010 | 72ч | r | строчная r |
| 115 | 01110011 | 73h | с | строчная s |
| 116 | 01110100 | 74h | т | строчная t |
| 117 | 01110101 | 75h | u | строчная u |
| 118 | 01110110 | 76h | v | строчная v |
| 119 | 01110111 | 77h | Вт | строчная w |
| 120 | 01111000 | 78h | x | строчная x |
| 121 | 01111001 | 79ч | л | строчная y |
| 122 | 01111010 | 7Ah | z | строчная z |
| 123 | 01111011 | 7Bh | { | распорка левая |
| 124 | 01111100 | 7Ч | | | бар |
| 125 | 01111101 | 7Dh | } | распорка правая |
| 126 | 01111110 | 7Eh | ~ | тильда или знак эквивалентности |
| 127 | 01111111 | 7Fh | DEL |
Расширенные коды ASCII
Ниже приведены расширенные коды ASCII для кодов символов от 128 до 255.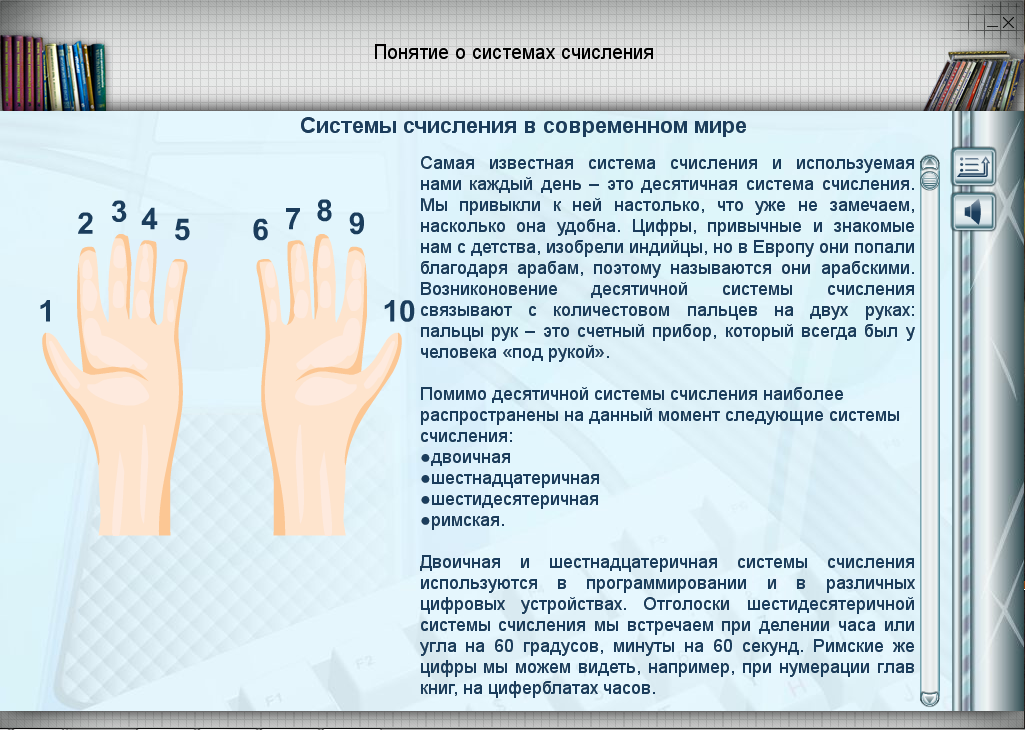
В этой таблице используется кодировка ISO 8859-1 или ISO Latin-1 . Коды 128-159 содержат расширенные символы Microsoft Windows Latin-1. Существуют и другие варианты, но это наиболее часто используемый набор кодов символов.
| № | двоичный | Шестигранник | ASCII | Описание |
| 128 | 10000000 | 80ч | € | знак евро |
| 129 | 10000001 | 81h | ||
| 130 | 10000010 | 82h | ‚ | одинарная кавычка low-9 |
| 131 | 10000011 | 83х | ƒ | строчная f с крючком |
| 132 | 10000100 | 84х | „ | двойные низкие кавычки |
| 133 | 10000101 | 85х | … | многоточие горизонтальное |
| 134 | 10000110 | 86ч | † | кинжал |
| 135 | 10000111 | 87ч | ‡ | двойной кинжал |
| 136 | 10001000 | 88х | ˆ | с акцентом с циркумфлексом |
| 137 | 10001001 | 89ч | ‰ | знак промилле |
| 138 | 10001010 | 8Ah | Š | заглавные буквы s с кароном |
| 139 | 10001011 | 8Bh | ‹ | котировка с одинарным левым углом |
| 140 | 10001100 | 8Ч | Œ | лигатура OE |
| 141 | 10001101 | 8Dh | ||
| 142 | 10001110 | 8Eh | Ž | заглавная буква z с кароном |
| 143 | 10001111 | 8Fh | ||
| 144 | 10010000 | 90ч | ||
| 145 | 10010001 | 91h | ‘ | левая одинарная кавычка |
| 146 | 10010010 | 92ч | ’ | правая одинарная кавычка |
| 147 | 10010011 | 93h | “ | левая двойная кавычка |
| 148 | 10010100 | 94ч | ” | правая двойная кавычка |
| 149 | 10010101 | 95h | • | пуля |
| 150 | 10010110 | 96ч | – | и тире |
| 151 | 10010111 | 97h | – | тире |
| 152 | 10011000 | 98h | ˜ | маленькая тильда |
| 153 | 10011001 | 99h | ™ | знак товарного знака |
| 154 | 10011010 | 9Ah | š | строчная буква s с кароном |
| 155 | 10011011 | 9Bh | › | Одинарная кавычка, указывающая вправо |
| 156 | 10011100 | 9Ч | – | строчная лигатура oe |
| 157 | 10011101 | 9Dh | ||
| 158 | 10011110 | 9Eh | ž | строчная буква z с кароном |
| 159 | 10011111 | 9Fh | Ÿ | заглавная буква y с тремой |
| 160 | 10100000 | A0h | неразрывный пробел | |
| 161 | 10100001 | A1h | ¡ | перевернутый восклицательный знак |
| 162 | 10100010 | A2h | ¢ | центов знак |
| 163 | 10100011 | A3h | £ | знак фунта |
| 164 | 10100100 | A4h | ¤ | знак валюты |
| 165 | 10100101 | A5h | ¥ | йен знак |
| 166 | 10100110 | A6h | ¦ | вертикальная ломаная |
| 167 | 10100111 | A7h | § | знак раздела |
| 168 | 10101000 | A8h | ¨ | умляут |
| 169 | 10101001 | A9h | © | знак авторского права |
| 170 | 10101010 | AAh | ª | женский порядковый указатель |
| 171 | 10101011 | ABh | « | кавычки с двойным левым углом |
| 172 | 10101100 | АЧ | ¬ | не подписывать |
| 173 | 10101101 | ADh | мягкий перенос | |
| 174 | 10101110 | AEh | ® | зарегистрированный товарный знак, знак |
| 175 | 10101111 | AFh | ¯ | над строкой |
| 176 | 10110000 | B0h | ° | знак градуса |
| 177 | 10110001 | B1h | ± | знак плюс-минус |
| 178 | 10110010 | B2h | ² | 2 куба |
| 179 | 10110011 | B3h | ³ | 3 куба |
| 180 | 10110100 | B4h | ´ | острый акцент |
| 181 | 10110101 | B5h | мк | микроподпись |
| 182 | 10110110 | B6h | ¶ | знак Pilcrow |
| 183 | 10110111 | B7h | · | средняя точка |
| 184 | 10111000 | B8h | ¸ | седилья |
| 185 | 10111001 | B9h | ¹ | надстрочный один |
| 186 | 10111010 | BAh | º | мужской порядковый показатель |
| 187 | 10111011 | BBh | » | прямые двойные угловые кавычки |
| 188 | 10111100 | БЧ | ¼ | дробь одна четверть |
| 189 | 10111101 | BDh | ½ | дробь половинная |
| 190 | 10111110 | БЭх | ¾ | дробь три четверти |
| 191 | 10111111 | BFh | ¿ | перевернутый вопросительный знак |
| 192 | 11000000 | C0h | À | капитель а с могилой |
| 193 | 11000001 | C1h | Á | заглавная а с острым |
| 194 | 11000010 | C2h | Â | заглавная А с циркумфлексом |
| 195 | 11000011 | C3h | Ã | заглавная буква А с тильдой |
| 196 | 11000100 | C4h | Ä | заглавная а с тремой |
| 197 | 11000101 | C5h | Å | заглавная а с кольцом сверху |
| 198 | 11000110 | C6h | Æ | заглавная AE |
| 199 | 11000111 | C7h | Ç | заглавная c с седилем |
| 200 | 11001000 | C8h | È | заглавная е с могилой |
| 201 | 11001001 | C9h | É | заглавная е с острым углом |
| 202 | 11001010 | CAh | Ê | заглавная e с циркумфлексом |
| 203 | 11001011 | CBh | Ë | заглавная е с тремой |
| 204 | 11001100 | ГЧ | Ì | заглавная я с могилой |
| 205 | 11001101 | CDh | Í | заглавная i с острым углом |
| 206 | 11001110 | CEh | Î | заглавная i с циркумфлексом |
| 207 | 11001111 | CFh | Ï | заглавная буква i с тремой |
| 208 | 11010000 | D0h | Ð | капитал eth |
| 209 | 11010001 | D1h | Ñ | заглавная буква n с циркумфлексом |
| 210 | 11010010 | D2h | Ò | заглавная o с циркумфлексом |
| 211 | 11010011 | D3h | Ó | заглавная о с острой / тд> |
| 212 | 11010100 | D4h | Ô | заглавная o с циркумфлексом |
| 213 | 11010101 | D5h | Õ | заглавная o с тильдой |
| 214 | 11010110 | D6h | Ö | заглавная o с тремой |
| 215 | 11010111 | D7h | × | знак умножения |
| 216 | 11011000 | D8h | Ø | заглавная o с косой чертой |
| 217 | 11011001 | D9h | Ù | заглавная u с могилой |
| 218 | 11011010 | DAh | Ú | заглавная u с острым углом |
| 219 | 11011011 | DBh | Û | заглавная буква U с циркумфлексом |
| 220 | 11011100 | ДЧ | Ü | заглавная буква U с тремой |
| 221 | 11011101 | ДДх | Ý | заглавная y с острым |
| 222 | 11011110 | DEh | Þ | главный шип |
| 223 | 11011111 | DFh | ß | строчная ess-zed |
| 224 | 11100000 | E0h | до | строчная а с могилой |
| 225 | 11100001 | E1h | á | строчная а с острым ударением |
| 226 | 11100010 | E2h | â | строчная a с циркумфлексом |
| 227 | 11100011 | E3h | ã | строчная a с тильдой |
| 228 | 11100100 | E4h | ä | строчная а с тремой |
| 229 | 11100101 | E5h | å | строчная буква a с кольцом сверху |
| 230 | 11100110 | E6h | æ | строчная ae |
| 231 | 11100111 | E7h | ç | строчная c с седилем |
| 232 | 11101000 | E8h | и | строчная е с могилой |
| 233 | 11101001 | E9h | é | строчная е с острым ударением |
| 234 | 11101010 | EAh | ê | строчная e с циркумфлексом |
| 235 | 11101011 | EBh | ë | строчная е с тремой |
| 236 | 11101100 | ЭЧ | м | строчная е с могилой |
| 237 | 11101101 | EDh | – | строчная i с острым ударением |
| 238 | 11101110 | EEh | до | строчная i с циркумфлексом |
| 239 | 11101111 | EFh | ï | строчная i с тремой |
| 240 | 11110000 | F0h | ð | строчная eth |
| 241 | 11110001 | F1h | – | строчная буква n с тильдой |
| 242 | 11110010 | F2h | шт | строчная o с могилой |
| 243 | 11110011 | F3h | — | строчная o с острым ударением |
| 244 | 11110100 | F4h | ô | строчная o с циркумфлексом |
| 245 | 11110101 | F5h | х | строчная o с тильдой |
| 246 | 11110110 | F6h | ö | строчная o с тремой |
| 247 | 11110111 | F7h | ÷ | разделительный знак |
| 248 | 11111000 | F8h | ø | строчная o с косой чертой |
| 249 | 11111001 | F9h | ù | строчная u с могилой |
| 250 | 11111010 | FAh | ú | строчная буква U с ударением |
| 251 | 11111011 | FBh | û | строчная буква U с циркумфлексом |
| 252 | 11111100 | FCh | ü | строчная u с тремой |
| 253 | 11111101 | FDh | ý | строчная y с острым ударением |
| 254 | 11111110 | FEh | þ | шип строчный |
| 255 | 11111111 | FFh | ÿ | строчная y с тремой |
Двоичные числа
Компьютерная система счисления, состоящая из 2 цифр: 0 и 1.
Иногда его называют базой-2.
Поскольку у компьютеров нет 10 пальцев, весь подсчет внутри самого компьютера выполняется с использованием только двух цифр: 0 и 1 (или «включено» и «выключено», или «ложь» и «истина»).
Шестнадцатеричные числа
В шестнадцатеричной системе (сокращенно hex) используются числа от 0 до 15. Она начинается как десятичная система: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, но затем идет A, которое равно 10, а затем B, C, D, E и F (что, конечно, равно 15). Следующее число — 10, что на самом деле 16 в десятичной системе счисления и так далее….
Поскольку может быть невозможно различить шестнадцатеричное и десятичное число (является ли это «25» десятичным 25 или 25 в шестнадцатеричном формате, что равно 37 десятичному числу?), После каждого шестнадцатеричного числа обычно ставят строчную букву «h». . Итак, 25 — десятичное число, а 25h — шестнадцатеричное.
ASCII
ASCII означает Американский стандартный код для обмена информацией .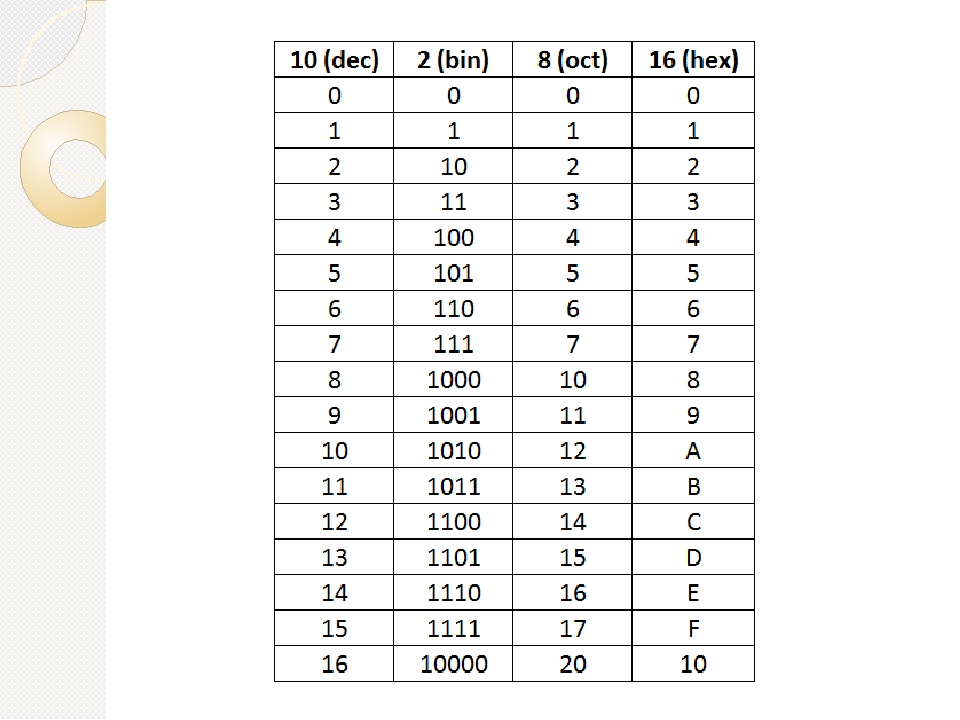
Это стандарт, который был определен в 1963 году, чтобы позволить компьютерам обмениваться информацией независимо от производителя.
- Поскольку компьютеры в основном работают с числами, набор символов ASCII состоит из 128 десятичных чисел в диапазоне от 0 до 127, присвоенных буквам, цифрам, знакам препинания и наиболее распространенным специальным символам. Поскольку компьютеру требуется 7 бит для представления чисел от 0 до 127, эти коды иногда называют 7-битным ASCII .
- Цифры от 0 до 31 используются для управляющих кодов — специальных инструкций, таких как указание на то, что компьютер должен издать звук (код ASCII 7) или принтер должен начать работу с нового листа бумаги (код ASCII 12).
- Коды ASCII с 32 по 47 используются для специальных символов, начиная с символа пробела.
- После чисел от 0 до 9 (коды ASCII от 48 до 57) вы снова получаете некоторые специальные символы, от двоеточия до символа @.
- Буквы начинаются с заглавной A, начиная с кода ASCII 65 и далее.
Строчные символы от a до z занимают коды ASCII от 97 до 122. Вы можете задаться вопросом, почему символы нижнего регистра просто не следуют за своими заглавными собратьями. Помните: это ASCII, это компьютерные вещи из темных веков.Если вы возьмете заглавную U (код ASCII 85) и прибавите 32 к этому коду, вы получите код символа 117, который является строчной буквой u. 32 — это магическое «расстояние» между заглавными и строчными буквами, а 32 — поистине волшебное и эффективное число, с которым может столкнуться любой компьютер или ботаник. Даже я люблю 32. - Коды с 123 по 127 снова являются специальными символами, включая тильду (~).
- Все компьютерные системы также используют числа от 128 до 255 для представления дополнительных символов, но этот список на самом деле не стандартизирован для всех.Вот почему приведенная выше таблица разделена на две части. Первая таблица с 7-битными кодами ASCII универсальна для всех компьютеров. Вторая расширенная таблица ASCII — нет — это то, что используют современные машины Windows.
- Поскольку 256 символов недостаточно для представления всех символов, используемых в азиатских языках, и для решения досадных проблем совместимости с различными кодами, используемыми для кодов от 128 до 255, появился новый стандарт. Набор символов Unicode содержит более 32000 символов.
Строчные символы от a до z занимают коды ASCII от 97 до 122. Вы можете задаться вопросом, почему символы нижнего регистра просто не следуют за своими заглавными собратьями. Помните: это ASCII, это компьютерные вещи из темных веков.Если вы возьмете заглавную U (код ASCII 85) и прибавите 32 к этому коду, вы получите код символа 117, который является строчной буквой u. 32 — это магическое «расстояние» между заглавными и строчными буквами, а 32 — поистине волшебное и эффективное число, с которым может столкнуться любой компьютер или ботаник. Даже я люблю 32.
Шестнадцатеричная система счисления. Факты для детей
Шестнадцатеричная система счисления , также известная как шестнадцатеричная система счисления , представляет собой систему счисления, состоящую из 16 символов (основание 16). Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. Шестнадцатеричный использует десятичные числа и включает шесть дополнительных символов. Здесь нет символов, означающих десять, одиннадцать и т. Д., Поэтому эти символы представляют собой буквы английского алфавита: A, B, C, D, E и F.Шестнадцатеричный A = десятичный 10 и шестнадцатеричный F = десятичный 15.
Люди в основном используют десятичную систему счисления. Вероятно, это потому, что у людей десять пальцев (десять пальцев). Однако у компьютеров есть только включение и выключение, называемое двоичной цифрой (или для краткости битом). Двоичное число — это просто строка из нулей и единиц: например, 11011011. Для удобства инженеры, работающие с компьютерами, склонны группировать биты вместе. Раньше, например, в 1960-х годах, они группировали по 3 бита за раз (подобно тому, как большие десятичные числа сгруппированы по тройкам, например, 123 456 789).Три бита, каждый из которых включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7. Это называется восьмеричным.
По мере того, как компьютеры становились больше, было удобнее группировать биты по четырем, а не по трем. Дополнительный бит может быть включен или выключен, 0 или 1. Таким образом, это удваивает числа, которые будет представлять символ.
Это 16 чисел. Hex = 6 и Decimal = 10, поэтому он называется шестнадцатеричным. Четыре бита называются полубайтом (иногда пишется полубайтом ).Полубайт — это одна шестнадцатеричная цифра, записываемая с использованием символа 0-9 или A-F. Два полубайта — это байт (8 бит). В большинстве компьютерных операций используется байт или кратное байту (16 бит, 24, 32, 64 и т. Д.). Шестнадцатеричный код упрощает запись этих больших двоичных чисел.
Чтобы избежать путаницы с десятичной, восьмеричной или другими системами счисления, шестнадцатеричные числа иногда пишутся с буквой «h» после числа. Например, 63h означает 63 в шестнадцатеричной системе счисления. Разработчики программного обеспечения нередко перед числом (0x63) используют 0x .
Шестнадцатеричные значения
Шестнадцатеричная система счисления похожа на восьмеричную систему счисления (основание 8), потому что каждую из них можно легко сравнить с двоичной системой счисления.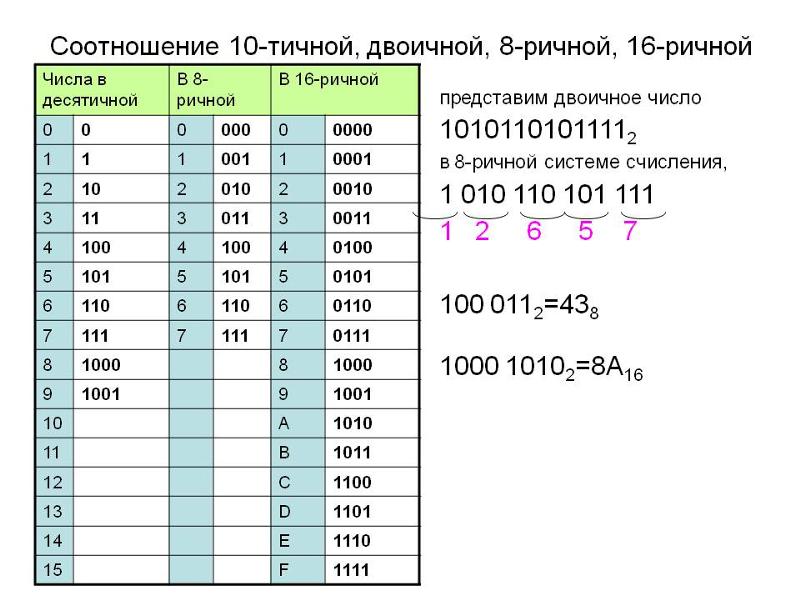
В шестнадцатеричном формате используется четырехбитное двоичное кодирование. Это означает, что каждая цифра в шестнадцатеричном формате совпадает с четырьмя цифрами в двоичном формате. Octal использует трехбитную двоичную систему.
В десятичной системе первая цифра — это , это разрядов, следующая цифра слева — это десятков, , следующая — сотен, , и т. Д.В шестнадцатеричном формате каждая цифра может иметь 16 значений, а не 10. Это означает, что у цифр — это место, — шестнадцать — , а следующая — , 256 — . Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 в десятичном.
Примеры значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
|
Преобразование
Двоичное в шестнадцатеричное
Для изменения числа с двоичного на шестнадцатеричный используется метод группировки.
Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные числа, как показано на приведенной выше диаграмме для шестнадцатеричных чисел от 0 до F. Для перехода с шестнадцатеричного числа выполняется обратное. Каждая шестнадцатеричная цифра заменяется двоичной, и группировка обычно удаляется.
| Двоичный | Группы | шестигранник | |||
|---|---|---|---|---|---|
| 01100101 | 0110 | 0101 | 65 | ||
| 010010110110 | 0100 | 1011 | 0110 | 4B6 | |
| 1101011101011010 | 1101 | 0111 | 0101 | 1010 | D75A |
Шестнадцатеричное и десятичное
Существует два распространенных способа преобразования числа из шестнадцатеричного в десятичное.
Первый метод чаще используется при преобразовании вручную:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0–9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму преобразованных чисел на каждом шаге ниже.
- Начать с младшей шестнадцатеричной цифры. Это цифра на правом конце. Это будет первый предмет в сумме.
- Возьмем вторую наименьшую значащую цифру. Это рядом с цифрой на правом конце.Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей младшей значащей цифры, но умножьте ее на 16 2 (то есть на 16 в квадрате или 256). Добавьте это к сумме.
- Продолжайте для каждой цифры, умножая каждое место на другую степень 16. (4096, 65536 и т. Д.)
| Расположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 1048576 (16 5 ) | 65536 (16 4 ) | 4096 (16 3 ) | 256 (16 2 ) | 16 (16 1 ) | 1 (16 0 ) |
Следующий метод чаще используется при программном преобразовании числа.
Ему не нужно знать, сколько цифр у числа до его начала, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0–9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму преобразованных чисел на каждом шаге ниже.
- Начните со старшей цифры (цифра в крайнем левом углу). Это первая позиция в сумме.
- Если существует другая цифра, умножьте сумму на 16 и добавьте десятичное значение следующей цифры.
- Повторяйте вышеуказанный шаг до тех пор, пока цифры не исчезнут.
Пример: 5Fh и 3425h в десятичном формате, метод 1
|
|
Пример: 5Fh и 3425h в десятичном формате, метод 2
|
|
Связанные страницы
Картинки для детей
Шестнадцатеричная схема подсчета пальцев.
Предложение Брюса Алана Мартина о шестнадцатеричной системе счисления
Преобразование двоичных, десятичных и шестнадцатеричных значений
Обновлено: 12.06.2020, Computer Hope
двоичный
Компьютеры работают по принципу манипулирования числами. Внутри компьютера числа представлены в битах и байтах. Например, число три представлено байтом с битами 0 и 1, установленными на «00000011», что является системой нумерации с основанием 2.Люди обычно используют десятичную систему счисления или десятичную систему счисления.
Это означает, что в Base 10 вы считаете от 0 до 9, прежде чем добавить еще одну цифру. Например, число 22 в базе 10 означает, что у нас есть два набора десятков и два набора единиц.
База 2 также известна как двоичный , так как может быть только два значения для определенной цифры; либо 0 = ВЫКЛ, либо 1 = ВКЛ. Вы не можете представить число 22 в двоичной системе счисления.
Десятичное число 22 представлено в двоичном виде как 00010110.Следуя приведенной ниже диаграмме, мы получаем:
| Положение бита | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Десятичное | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
22 или 00010110:
Все числа, представляющие 0, не учитываются, 128, 64, 32, 8, 1 , потому что 0 означает ВЫКЛ.
Однако подсчитываются числа, представляющие 1, 16 + 4 + 2 = 22, потому что 1 представляет ВКЛ.
Таблица десятичных значений и двоичных эквивалентов
| Десятичное | двоичный |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 16 | 10000 |
| 32 | 100000 |
| 64 | 1000000 |
| 100 | 1100100 |
| 256 | 100000000 |
| 512 | 1000000000 |
| 1000 | 1111101000 |
| 1024 | 10000000000 |
Шестнадцатеричный
Другая система нумерации, используемая компьютерами, — шестнадцатеричная, или Base 16.
В этой системе числа считаются от 0 до 9, затем буквы от A до F перед добавлением еще одной цифры. Буквы от A до F представляют десятичные числа от 10 до 15 соответственно. На приведенной ниже диаграмме показаны значения шестнадцатеричной позиции по сравнению с 16 в степени и десятичными значениями. С большими числами легче работать с шестнадцатеричными значениями, чем с десятичными.
Чтобы преобразовать значение из шестнадцатеричного в двоичное, вы просто переводите каждую шестнадцатеричную цифру в ее 4-битный двоичный эквивалент.Шестнадцатеричные числа имеют префикс 0x или суффикс h .
Например, рассмотрим шестнадцатеричное число:
0x3F7A
Используя двоичную диаграмму и шестнадцатеричную диаграмму ниже, это переводится в двоичное значение:
0011 1111 0111 1010
| Десятичное | Шестнадцатеричный | двоичный |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | А | 1010 |
| 11 | Б | 1011 |
| 12 | С | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | Ф | 1111 |
Двоичные десятичные и шестнадцатеричные числа и преобразования
Двоичная система счисления — это система счисления, основанная на 2.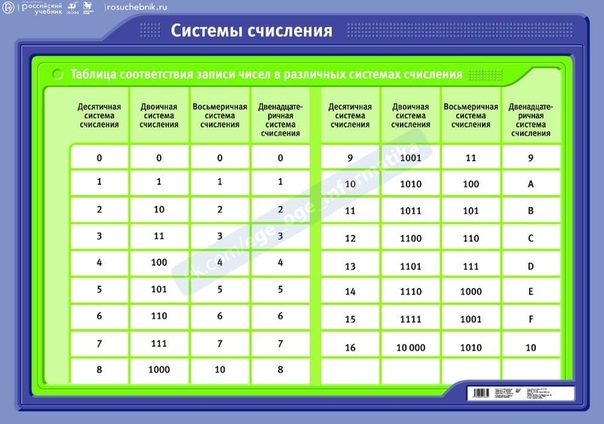
Что именно такое «основано на 2» ?? Итак, у вас есть только два символа («0» и «1») для определения и представления целых чисел в двоичной системе счисления.
Десятичная система счисления — это система счисления, основанная на 10. Что такое «основано на 10» ?? Итак, у вас есть 10 символов («0», «1», «2», «3», «4», «5», «6», «7», «8», «9») для определения и представляют целые числа в десятичной системе счисления.
Шестнадцатеричная система счисления — это система счисления, основанная на 16.Что именно такое «на основе 16» ?? Итак, у вас есть 16 символов («0», «1», «2», «3», «4», «5», «6», «7», «8», «9», «A» , «B», «C», «D», «E», «F») для определения и представления целых чисел в шестнадцатеричной системе счисления.
Как это возможно? Читай ниже.
Двоичная система счисления
Двоичные числа позволяют нам представить любое число, используя всего два символа «0» и «1». Двоичные числа представлены на основе степени двойки.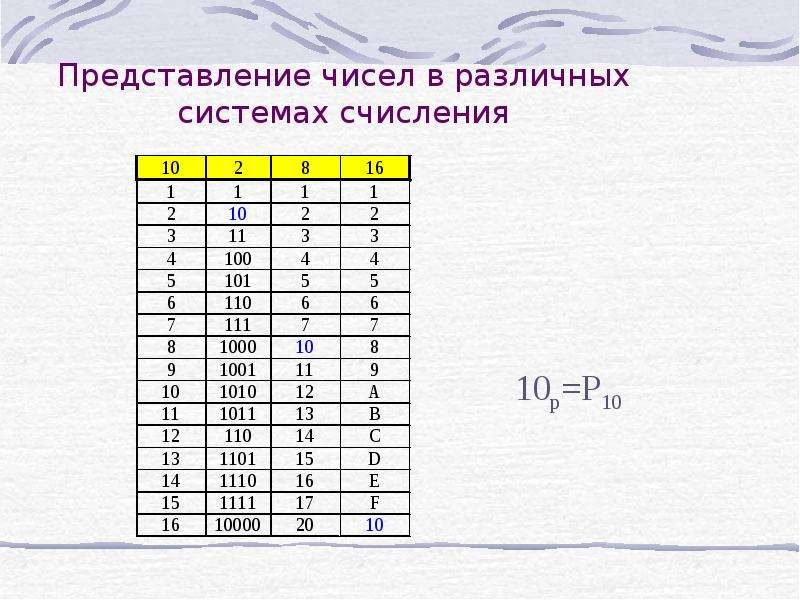
Чтобы понять эту концепцию более четко, прочтите приведенную ниже таблицу и запомните эти числа.Эта таблица ограничена 8-битными двоичными числами и их преобразованиями, потому что вы будете иметь дело с 8-битными двоичными числами больше в своем исследовании CCNA (когда вы изучаете IPv4-адреса, подсети, VLSM, суперсети (суммирование маршрутов) и т. Д.).
Если вы хотите научиться преобразовывать двоичные числа большего размера в битах, просто добавьте больше степеней двойки, например 512, 1024, 2048 и т. Д.
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Десятичные значения | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
В приведенной выше таблице самый правый бит (2 0 ) известен как младший бит, а самый левый бит (2 7 ) известен как самый старший бит.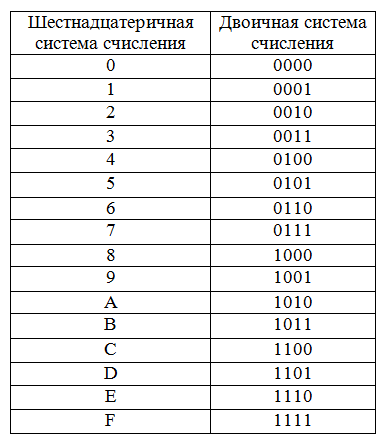
Всякий раз, когда вас просят преобразовать десятичное число в двоичное или двоичное в десятичное, помните приведенную выше таблицу. Как инженер сети и сетевой безопасности, вам нужно будет выполнять много преобразований из двоичных чисел в десятичные числа и обратно.
Пример 1 — Преобразование 172 (в десятичных дробях) в его двоичный эквивалент.
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| Десятичные значения | 128 | 0 | 32 | 0 | 8 | 4 | 0 | 0 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 5 (= 32), 2 3 (= 8) и 2 2 (= 4) бит » on «и остальные биты» off «, вы получите 172.
То есть 128 + 32 + 8 + 4 = 172
Следовательно, двоичный эквивалент 172 равен 10101100.
Пример 2 — Преобразование 192 (десятичных знаков) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Десятичные значения | 128 | 64 | 0 | 0 | 0 | 0 | 0 | 0 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 6 (= 64) бит «включенными», а оставшиеся биты «выключенными», вы получите 192.
То есть 128 + 64 = 192.
Следовательно, двоичный эквивалент 192 равен 11000000.
Пример 3 — Преобразование 168 (в десятичных дробях) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| Десятичные значения | 128 | 0 | 32 | 0 | 8 | 0 | 0 | 0 |
Из приведенной выше таблицы, если вы включите 2 7 (= 128), 2 5 (= 32) и 2 3 (= 8) бит, а остальные биты отключите, вы получится 168.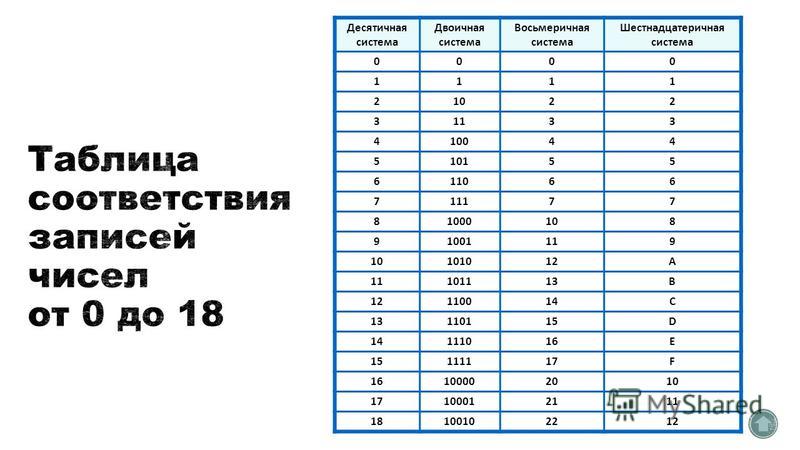
То есть 128 + 32 + 8 = 168
Следовательно, двоичный эквивалент 168 равен 10101000.
Пример 4 — Преобразование 224 (десятичных знаков) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Десятичные значения | 128 | 64 | 32 | 0 | 0 | 0 | 0 | 0 |
Из приведенной выше таблицы, если вы включите 2 7 (= 128), 2 6 (= 64) и 2 5 (= 32) бит, а остальные биты отключите, вы получится 224.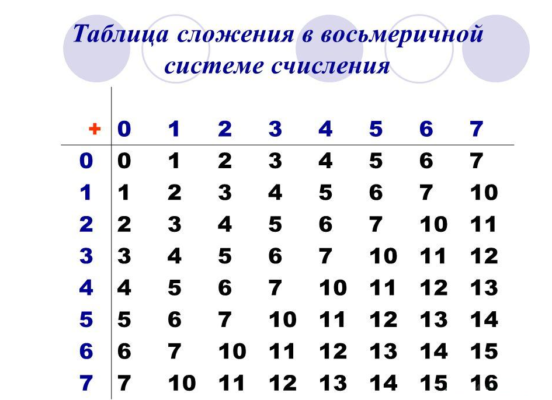
То есть 128 + 64 + 32 = 224
Следовательно, двоичный эквивалент 224 равен 11100000.
Пример 5 — Преобразование 240 (десятичных знаков) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Десятичные значения | 128 | 64 | 32 | 16 | 0 | 0 | 0 | 0 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 6 (= 64), 2 5 (= 32) и 2 4 (= 16) бит «на «и оставшиеся биты» выключены, вы получите 240.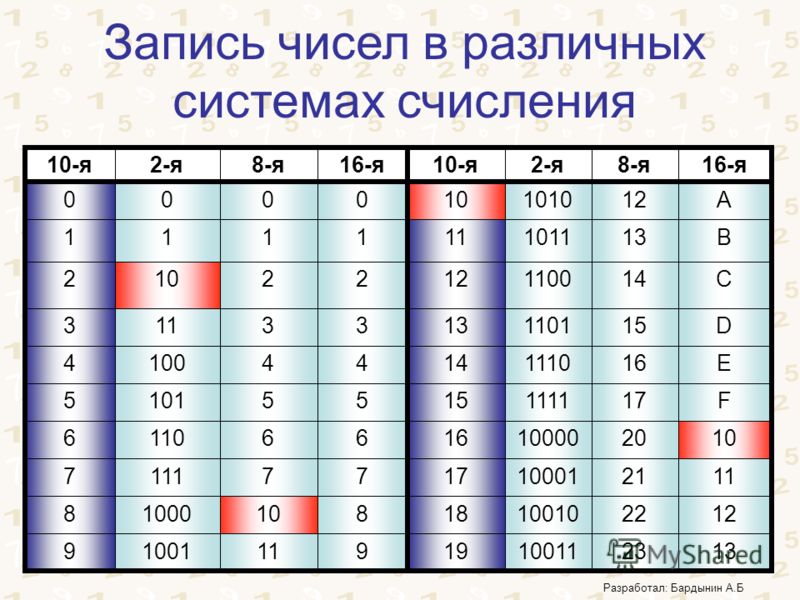
То есть 128 + 64 + 32 + 16 = 240
Следовательно, двоичный эквивалент 240 равен 11110000.
Пример 6 — Преобразование 248 (в десятичных дробях) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Десятичные значения | 128 | 64 | 32 | 16 | 8 | 0 | 0 | 0 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 6 (= 64), 2 5 (= 32), 2 4 (= 16) и 2 3 (= 8) битов «включено», а оставшиеся биты «выключены», вы получите 248.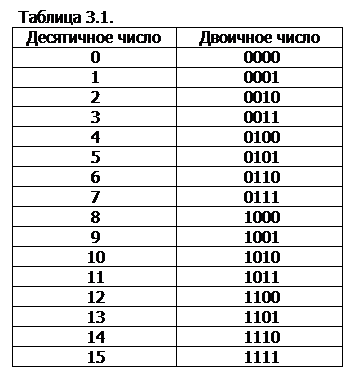
То есть 128 + 64 + 32 + 16 + 8 = 248
Следовательно, двоичный эквивалент 248 равен 11111000.
Пример 7 — Преобразование 252 (в десятичных дробях) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| Десятичные значения | 128 | 64 | 32 | 16 | 8 | 4 | 0 | 0 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 6 (= 64), 2 5 (= 32), 2 4 (= 16), 2 3 (= 8) и 2 2 (= 4) бит «включены», а оставшиеся биты «выключены», вы получите 252.
То есть 128 + 64 + 32 + 16 + 8 + 4 = 252
Следовательно, двоичный эквивалент 252 равен 11111100.
Пример 8 — Преобразование 254 (в десятичных дробях) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Десятичные значения | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 0 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 6 (= 64), 2 5 (= 32), 2 4 (= 16), 2 3 (= 8), 2 2 (= 4) и 2 1 (= 2) бит «включен», а оставшиеся биты «выключены», вы получите 254.
То есть 128 + 64 + 32 + 16 + 8 + 4 + 2 = 254
Следовательно, двоичный эквивалент 254 равен 11111110.
Пример 9 — Преобразование 255 (в десятичных дробях) в его двоичный эквивалент
Ответ:
| Степень двойки (для 8 бит) | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Двоичные биты («0» или «1») | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Десятичные значения | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Из приведенной выше таблицы, если вы сделаете 2 7 (= 128), 2 6 (= 64), 2 5 (= 32), 2 4 (= 16), 2 3 (= 8), 2 2 (= 4), 2 1 (= 2) и 2 0 (= 1) бит «включен» (все биты «включены») вы получите 255.
То есть 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
Следовательно, двоичный эквивалент 255 равен 11111111. Теперь все биты в восьмибитном двоичном числе включены. Если вы оставите все биты двоичного числа «включенными», вы получите максимально возможное десятичное значение для этого двоичного числа.
Максимально возможное десятичное значение для восьмибитового двоичного числа — 255.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — это система счисления, основанная на 16.У вас 16 символов («0», «1», «2», «3», «4», «5», «6», «7», «8», «9», «A», « B »,« C »,« D »,« E »,« F ») для определения и представления целых чисел в шестнадцатеричной системе счисления.
В шестнадцатеричной системе счисления, 10 (в десятичной системе счисления) представлено символом «A», 11 (в десятичной системе счисления) представлено символом «B», 12 (в десятичной системе счисления) представлено символом «C», 13 (в десятичной системе) обозначается символом «D», 14 (в десятичном формате) обозначается символом «E», а 15 (в десятичном формате) обозначается символом «F».
Примечание. Мы используем «0x» перед шестнадцатеричным числом, чтобы указать, что это шестнадцатеричное число, а не десятичное.
В десятичной системе счисления (которая основана на 10, которую мы используем в повседневной жизни) числа сгруппированы по 10. Мы считаем от 0 до 9, от 10 до 19, от 20 до 29 и так далее.
В шестнадцатеричной системе счисления мы считаем от 0x0 до 0xF (от 0 до 9 с использованием шестнадцатеричных чисел от 0x0 до 0x9 и от 10 до 15 с использованием шестнадцатеричных чисел от «0xA» до «0xF»), от 0x10 (16 в десятичной системе) до 0x1F (31 в десятичных разрядах), от 0x20 (32 в десятичных) до 0x2F (47 в десятичных) и так далее.
См. Следующую таблицу для более четкого представления.
| Десятичное число | двоичный | Шестнадцатеричный |
|---|---|---|
| 0 | 0 | 0x0 |
| 1 | 1 | 0x1 |
| 2 | 10 | 0x2 |
| 3 | 11 | 0x3 |
| 4 | 100 | 0x4 |
| 5 | 101 | 0x5 |
| 6 | 110 | 0x6 |
| 7 | 111 | 0x7 |
| 8 | 1000 | 0x8 |
| 9 | 1001 | 0x9 |
| 10 | 1010 | 0xA |
| 11 | 1011 | 0xB |
| 12 | 1100 | 0xC |
| 13 | 1101 | 0xD |
| 14 | 1110 | 0xE |
| 15 | 1111 | 0xF |
| 16 | 10000 | 0x10 |
| 17 | 10001 | 0x11 |
| 18 | 10010 | 0x12 |
| 19 | 10011 | 0x13 |
| 20 | 10100 | 0x14 |
| 21 | 10101 | 0x15 |
| 22 | 10110 | 0x16 |
| 23 | 10111 | 0x17 |
| 24 | 11000 | 0x18 |
| 25 | 11001 | 0x19 |
| 26 | 11010 | 0x1A |
| 27 | 11011 | 0x1B |
| 28 | 11100 | 0x1C |
| 29 | 11101 | 0x1D |
| 30 | 11110 | 0x1E |
| 31 | 11111 | 0x1F |
| 32 | 100000 | 0x20 |
| 33 | 100001 | 0x21 |
| 34 | 100010 | 0x22 |
| 35 | 100011 | 0x23 |
| 36 | 100100 | 0x24 |
| 37 | 100101 | 0x25 |
| 38 | 100110 | 0x26 |
| 39 | 100111 | 0x27 |
| 40 | 101000 | 0x28 |
| 41 | 101001 | 0x29 |
| 42 | 101010 | 0x2A |
| 43 | 101011 | 0x2B |
| 44 | 101100 | 0x2C |
| 45 | 101101 | 0x2D |
| 46 | 101110 | 0x2E |
| 47 | 101111 | 0x2F |
| 48 | 110000 | 0x30 |
| 49 | 110001 | 0x31 |
Как специалист по сетевой и сетевой безопасности, вам нужно больше сосредоточиться на преобразовании 16-разрядных двоичных чисел из двоичного в шестнадцатеричное, поскольку адреса IPv6 представлены в виде 16-разрядных блоков шестнадцатеричных чисел.
При преобразовании двоичного числа в шестнадцатеричное одна шестнадцатеричная цифра напоминает группу из четырех смежных двоичных битов, называемую полубайтом. Минимально возможное десятичное значение для 4-битного двоичного числа — 0, а максимальное — 15 (0xF).
Пример 1 — Преобразуйте следующее 16-битное двоичное число 0010001100000001 в шестнадцатеричное.
Ответ:
| Полубайты | 0010 | 0011 | 0000 | 0001 |
| Шестнадцатеричные числа | 2 | 3 | 0 | 1 |
Шестнадцатеричный эквивалент 16-битного двоичного числа 0010001100000001 — 0x2301
Пример 2 — Преобразуйте следующее 16-битное двоичное число 0010100101000101 в шестнадцатеричное.
Ответ:
| Полубайты | 0010 | 1001 | 0100 | 0101 |
| Шестнадцатеричные числа | 2 | 9 | 4 | 5 |
Шестнадцатеричный эквивалент 16-битного двоичного числа 0010100101000101 — 0x2945
Пример 3 — Преобразуйте следующее 16-битное двоичное число 0011111111100111 в шестнадцатеричное.
Ответ:
| Полубайты | 0011 | 1111 | 1110 | 0111 |
| Шестнадцатеричные числа | 3 | Ф | E | 7 |
Шестнадцатеричный эквивалент 16-битного двоичного числа 0011111111100111 — 0x3FE7
Пример 4 — Преобразуйте следующее 16-битное двоичное число 1111111010000000 в шестнадцатеричное.
Ответ:
| Полубайты | 1111 | 1110 | 1000 | 0000 |
| Шестнадцатеричные числа | Ф | E | 8 | 0 |
Шестнадцатеричный эквивалент 16-битного двоичного числа 1111111010000000 — 0xFE80
.