|
|
|
Презентация-проект на тему «Графики функций»
Скрыть
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Красота в математике.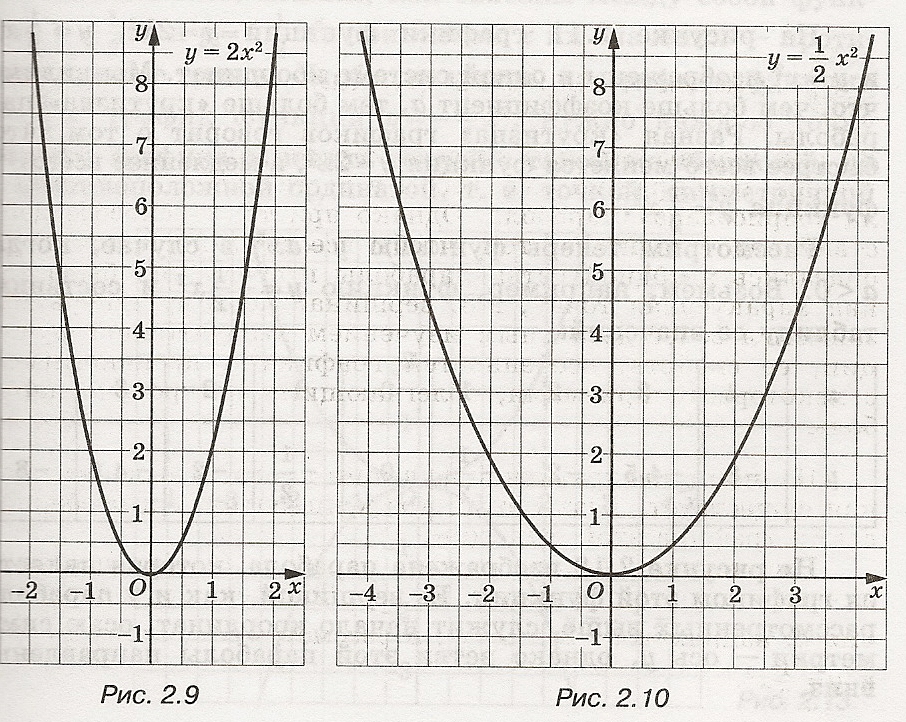
Графики функций Проектную работу выполнили ученицы 8 «А» класса МБОУ СОШ №141 Яброва Евгения и Люфт Марина
Актуальность проекта Преобразование графиков функции является одним из фундаментальных математических понятий Обучение учащихся построению и преобразованию графиков функции является одной из главных задач обучению математике в школе.
3 слайд Описание слайда:Цель проекта Рассмотреть графический метод решения уравнений, неравенств, систем уравнений. Научиться строить графики с помощью преобразований и графики функций с модулем. Задачи Рассмотреть графики различных функций и их свойства. Научиться применять графический способ решения: Уравнений; систем уравнений; неравенств.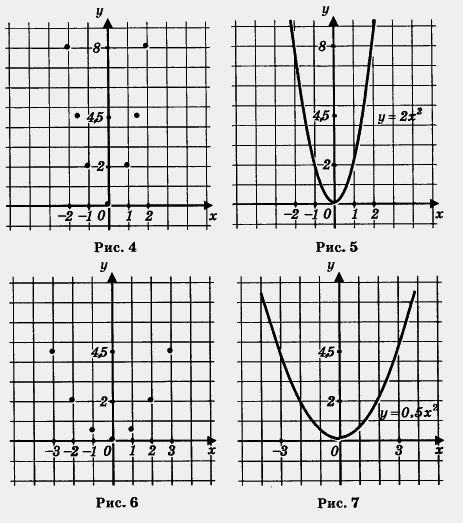
Определения Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной x соответствует единственное значение переменной y. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты – соответствующим значениям функции.
5 слайдИз истории… Понятие функции уходит своими корнями в ту далёкую эпоху, когда люди впервые поняли, что окружающие их предметы взаимосвязаны.
Они ещё не умели считать, но уже знали, что: чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела; чем дольше горит костёр, тем теплее в пещере.
Понятие переменной величины было введено в науку французским учёным и математиком Рене Декартом (1596-1650).
7 слайд Описание слайда:Линейная функция y=kx+b Свойства функции: D(f)=(- ∞;+∞) E(f)=(- ∞;+∞) Функция монотонна унаим. — не сущ., унаиб.- не сущ. Непрерывная Неограниченная
8 слайд Описание слайда:Квадратичная функция у = ax²+bx+c Свойства функции: D(f)=(- ∞;+∞) E(f)=[0;+∞) y=0, при x=0, у>0, при х (- ∞;+∞) Убывает на луче (-∞;0], возрастает на луче [0;+∞).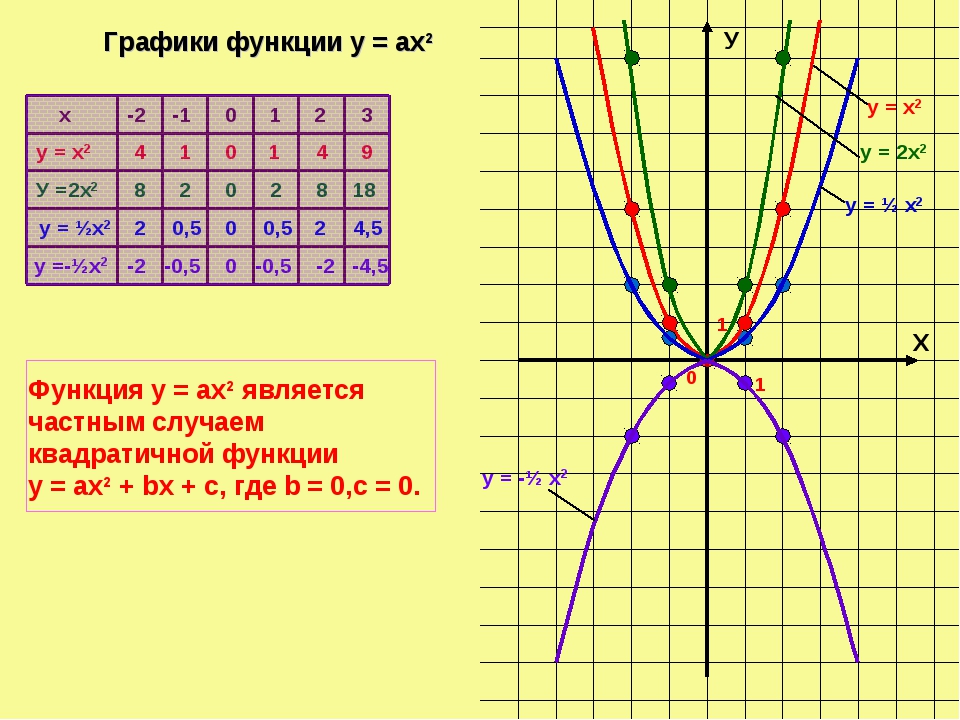
унаим.=0, унаиб.- не сущ. Непрерывная Выпукла вниз Ограничена снизу
Функция y= Свойства функции: D(f)=[0;+∞) E(f)=[0;+∞) y=0, при x=0, y>0, при x>0 Возрастает на луче [0;+∞) унаим.=0, унаиб.- не сущ. Непрерывная Выпукла вверх Ограничена снизу
Функция y=|x| Свойства функции: D(f)=(- ∞;+∞) E(f)= [ 0;+∞) у=0, при х=0, у>0, при х (- ∞;+∞) Убывает на луче (-∞;0], возрастает на луче [0;+∞). унаим.=0, унаиб.- не сущ. Непрерывная Ограничена снизу
11 слайд Описание слайда:Функция обратной пропорциональности у= Свойства функции: D(f)=(-∞;0) (0;+∞) E(f)= (-∞;0) (0;+∞) у>0 при х>0, y<0 при х<0 Убывает на промежутке (-∞;0) и (0;+∞) унаим.
— не сущ., унаиб.- не сущ. Неограниченная Выпукла и вверх, и вниз Прерывная
Алгоритм решения уравнений графическим способом. Рассмотреть две функции. В одной системе координат построить графики этих функций. Найти точки пересечения построенных графиков Абсциссы точек пересечения – это корни уравнения. Записать их в ответ.
13 слайд Описание слайда:Пример 1 Решим уравнение графическим способом: =2x y= — гипербола y=2x- прямая x 1 2 4 0,5 -1 -2 -4 -0,5 x 1 2 3 -1 -2 -3 y 2 1 0,5 4 -2 -1 -0,5 -4 y 2 4 6 -2-4 -6 Ответ: x=±1
14 слайд Описание слайда:Пример 2 Решим уравнение графическим способом: x²=x+2 y=x²-парабола y=x+2-прямая x 0 1 2 -1 -2 x 0 1 2 y 0 1 4 1 4 y 2 3 4 Ответ:x1=-1, x2=2.
Алгоритм применения графического метода при решении систем уравнений Выразить у через х в каждом уравнении. Построить в одной системе координат графики этих функций. Определить координаты всех точек пересечений графиков (если они есть). Координаты этих точек и будут решениями системы.
16 слайд Описание слайда:Пример 1 Решим систему уравнений графическим способом: y=-x² y=-x-6 y=-x²-парабола y=-x-6- прямая x 0 1 2 -1 -2 x 0 -1 -2 y 0 -1 -4 -1 -4 y -6 -5 -4 Ответ: (-2;-4) (3;-9).
17 слайд Описание слайда:Алгоритм решения неравенств графическим методом Рассмотреть две функции.
В одной системе координат построить графики этих функций. Определить абсциссы точек пересечения графиков (приближённо). Определить промежуток, на котором график 1-й функции лежит выше или ниже 2-й функции (в соответствии со знаком неравенства). Записать полученное множество в ответ.
Пример 1 Решим неравенство графическим способом: >2х-2 у= — гипербола у=2х-2-прямая х 1 2 4 0,5 -1 -2 -4 -0,5 х 0 1 2 у 4 2 1 8 -4 -2 -1 -8 y -2 0 2 Ответ: (- ∞;-1), (0;2).
19 слайдПреобразование графиков функций Различают три вида геометрических преобразований графика функции: Первый вид — масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
Второй вид — симметричное (зеркальное) отображение относительно координатных осей. Третий вид — параллельный перенос (сдвиг) вдоль осей Х и У.
Масштабирование Масштабирование — операция сжатия или растяжения графика функции вдоль осей абсцисс и ординат. у=х² — парабола х 0 1 2 -1 -2 у 0 3 12 3 12 у=0,5х² — парабола х 0 1 2 -1 -2 у 0 0,5 2 0,5 2 у=3х² — парабола х 0 1 2 -1 -2 у 0 1 4 1 4
21 слайд Описание слайда:Симметричное (зеркальное) отображение относительно координатных осей у= у=- х 0 1 4 9 х 0 1 4 9 у 0 1 2 3 у 0 -1 -2 -3
22 слайд Описание слайда:Параллельный перенос Параллельный перенос — сдвиг вдоль осей X и Y.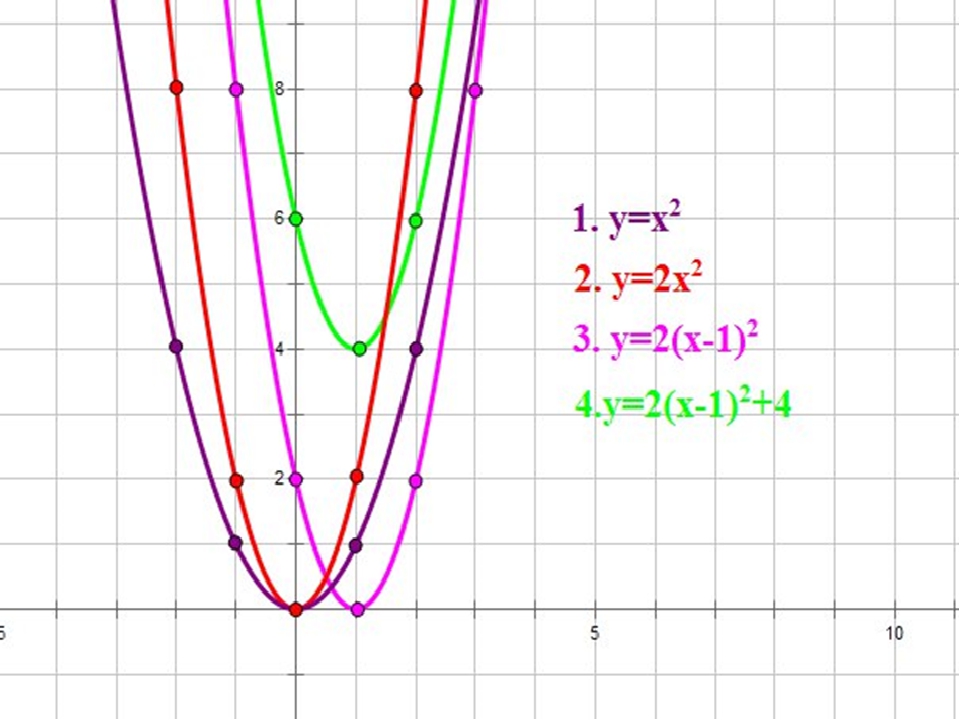
Алгоритм 1.Перейти к новой системе координат, проведя (пунктиром) вспомогательные прямые x=-l, y=m. 2. «Привязать» график функции y=f(x) к новой системе координат.
Дробно-линейная функция Дробно-линейной называют обычно функцию вида y= . Для построения графика дробно-линейной функции выделяют из неправильной дроби целую часть. y= = = = — =2- y=- +2 – гипербола получена пар-ным переносом графика функции y=- по оси х вправо на 2 ед., по оси у вверх на 2 ед. х 1 2 0,5 0,25 -1 -2 -0,5 -0,25 у -1 -0,5 -2 -4 1 0,5 2 4
24 слайд Описание слайда:Алгоритм построения графика функции y=|f(x)| Построить график функции y=|f(x)| . Оставить без изменений те части графика функции y=f(x), которые лежат не ниже оси x.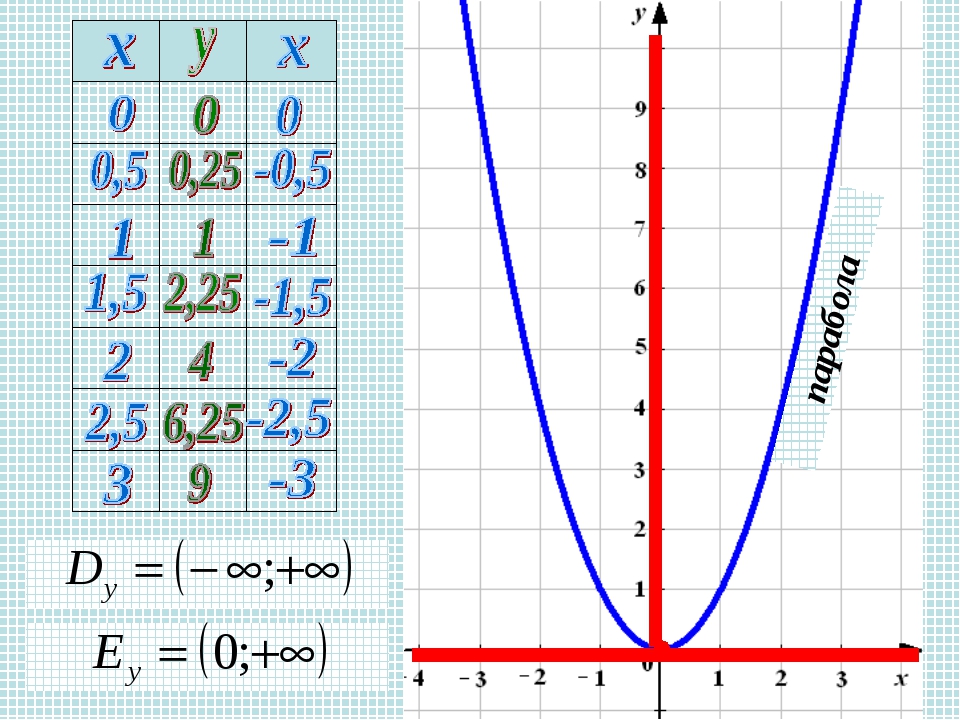
Части графика функции y=f(x), которые лежат ниже оси x, заменить на симметричные им относительно оси x. Алгоритм построения графика функции y=f(|x|) Построить график функции y=f(x) при x 0. Добавить ветви, симметричные построенным относительно оси y.
Пример 1 y=| | Построим график функции y= = = = + = 1+ y= +1 – гипербола получена пар-ным переносом графика функции y= по оси Х вправо на 2 ед. и по оси У вверх на 1 ед. х 1 2 0,5 5 -1 -2 -0,5 -5 у 5 2,5 10 1 -5 -2,5 -10 -1
26 слайд Описание слайда:Пример 2 Построить график функции: у= | | у= х 0 1 4 9 у 0 1 2 3
27 слайд Описание слайда:Алгоритм решения квадратного уравнения вида ax²+bx+c=0 графическим способом.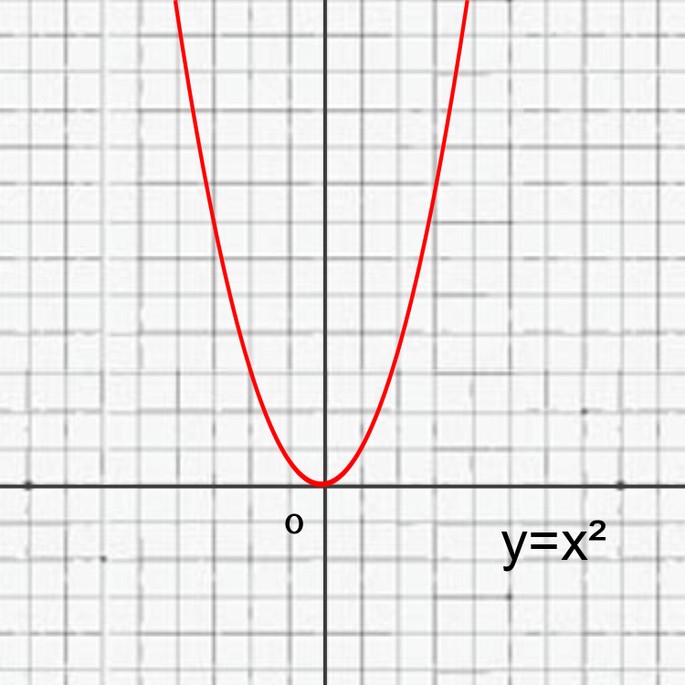
Рассмотреть квадратичную функцию у= ax²+bx+c. Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось параболы. Отметить на оси х 4 точки, симметричные относительно оси параболы. Через полученные точки провести параболу. Координаты точек пересечения параболы с осью Х и будут решением уравнения.
Пример 1 х²-4x+3=0 a=1 b=-4 c=3 X0= = =2 Y0=f(X0)=2²-4*2+3=4-8+3=-1 (2;-1)-вершина параболы, ветви . х 0 1 2 3 4 у 3 0 -1 0 3 Ответ: х1=1, х2=3.
29 слайд Описание слайда:Решим задание из тестов ОГЭ Построить график функции: у= = — =-х²+1 у=-х²+1-парабола График получен пар-ным переносом графика функции у=-х² на 1 ед.
вверх. у=-х² х 1 2 3 -1 -2 -3 у -1 -4 -9 -1 -4 -9
Заключение В ходе работы над проектом мы познакомились с различными видами функций, систематизировали всю информацию о них. Изучили применение графического способа при решении уравнений, неравенств, систем уравнений, квадратных уравнений, которое мы представили в своей работе. Практическая значимость нашей работы заключается в том, что мы создали диск учебных видеороликов, который может использоваться учащимися 8-х и 9-х классов.
31 слайд Описание слайда:Список литературы Учебник Алгебра 8 класс А.Г. Мордкович, Н.П. Николаев (2013 год) Часть 1 Задачник Алгебра 8 класс А.Г. Мордкович, Н.П. Николаев (2013 год) Часть 1 Контрольные работы по алгебре 7‐9 класс Мордкович А.
Г. ФГОС ОГЭ. Математика : типовые экзаменационные варианты: 36 вариантов / под ред. И.В. Ященко – М. :Издательство «Национальное образование», 2018 http://matematikam.ru/calculate-online/grafik.php https://ru.wikipedia.org/wiki
Курс повышения квалификации
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель математики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп.
образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Проверен экспертом
Общая информация
Номер материала: ДБ-269433
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Разработка урока по математике на тему ИСПОЛЬЗОВАНИЕ ШАБЛОНОВ ПАРАБОЛ ДЛЯ ПОСТРОЕНИЯ ГРАФИКА ФУНКЦИИ у = а (х – m)2 + n
У р о к 14.
Использование шаблонов парабол для построения графика функции у = а (х – т)2 + п
Цель: продолжить формирование умения строить график функции у = а (х – т)2 + п, используя при этом шаблоны парабол.
Ход урока
I. Организационный момент.
II. Устная работа.
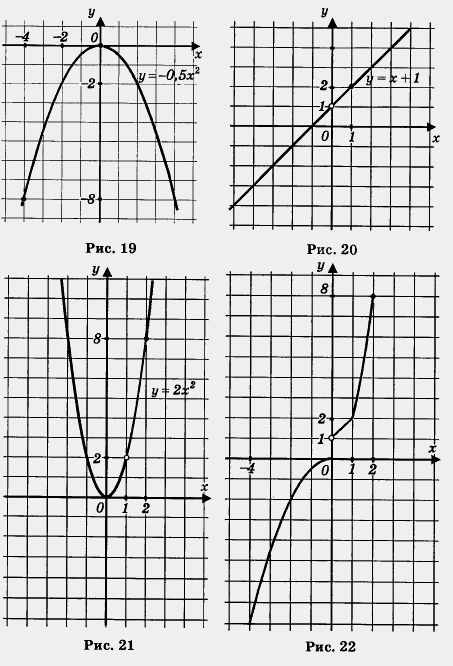
Для каждого из графиков, изображенных на рисунке, найдите соответствующую функцию:
а) у = ; б) у = –2х2 + 1; в) у = (х – 1)2 – 2; г) у = х2 + 1; д) у = ; е) у = (х + 1)2 – 2.
Формирование умений и навыков.
Учащиеся выполняют з а д а н и я двух групп:
– построение графика функции у = а (х – т)2 + п с использованием шаблонов;
– построение графика функции у = а (х – т)2 + п с помощью преобразований.
№ 107, № 112.
Используя шаблон параболы у = 2х2, постройте график функций:
а) у = 2 (х + 1)2 – 4; б) у = –2 (х – 3)2 + 2.
Используя шаблон параболы у = х2, постройте график функции:
а) у = ; б) у = .
Постройте графики функции:
а) у = ; б) у = –3(х – 1)2 + 4; в) у =
Проверочная работа.
В а р и а н т 1
1. Изобразите схематически графики функций:
а) у = –(х – 3)2; б) у = х2 + 1; в) у = 2 (х + 1)2 – 3.
2. Используя шаблон параболы у = х2, постройте график функций:
а) у = (х + 2)2 – 3; б) у = –(х – 1)2 + 4.
В а р и а н т 2
1. Изобразите схематически графики функций:
а) у = –2х2 + 3; б) у = (х + 2)2; в) у = –(х – 1)2 – 2.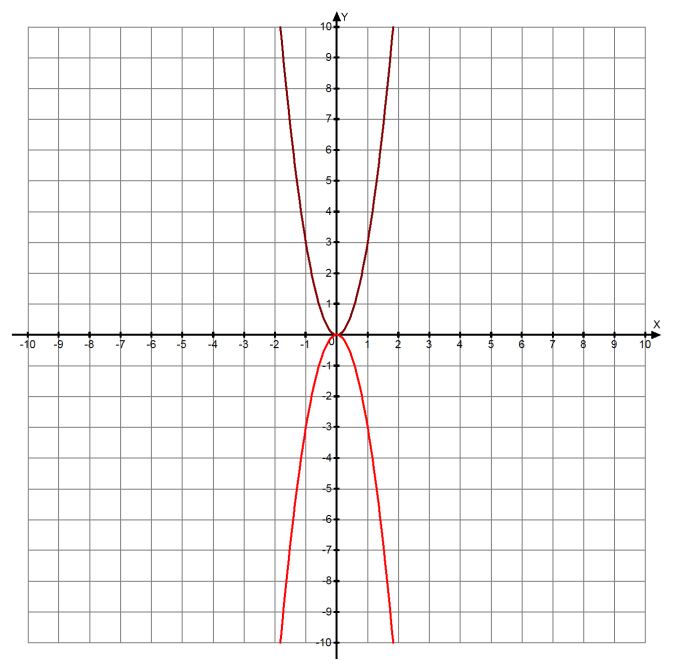
2. Используя шаблон параболы у = х2, постройте графики функций:
а) у = (х – 3)2 – 2; б) у = –(х + 1)2 + 5.
Итоги урока.
– Что является графиком функции у = а (х – т)2 + п?
– Как может быть получен график функции у = а (х – т)2 + п из графика функции у = ах2?
д/з № 108, № 113 Постройте графики функций у = –2 (х – 1)2 + 3
Элементы шаблона графика Окна графиков создаются из файлов шаблонов графиков. Файлы шаблонов исходных графов имеют расширение OTP . Origin поставляется с большим количеством встроенных шаблонов графиков (системных шаблонов). Эти шаблоны используются для создания всех более чем 100 типов графиков Origin, и их можно изменять и сохранять, чтобы сохранить ваши пользовательские настройки. Файл шаблона графика отличается от файла окна графика (.OGG) в этих шаблонах не хранят данные. Скорее, файлы шаблонов графиков хранят важные характеристики страниц и слоев (размер страницы, количество слоев, масштабирование текста и графических объектов и т. Д.), А также информацию о стиле печати данных (тип графика, цвета графика, метки данных и т. Д.) . Для получения дополнительной информации см. «Атрибуты, сохраненные с шаблоном графика» ниже. Сохранение настроек графика в файл шаблонаЧтобы сохранить активное окно графика как файл шаблона графика (.OTP):
или
Оба действия открывают диалоговое окно template_saveas . Для получения информации об элементах управления диалогового окна см. Атрибуты, сохраненные с шаблоном графикаСтраница графика, каждый слой графика на странице, оси, метки, метки осей, текст или аннотации объектов, а также графики данных имеют свойства, которые можно сохранить в шаблоне графика. Атрибуты, управляемые из диалогового окна Plot Details сохраняются с шаблоном графика:
Атрибуты, управляемые этими диалоговыми окнами, сохраняются с шаблоном графика:
Кроме того, в шаблоне сохраняются следующие свойства окна графика:
Примечание о держателях стилей графика данныхДетали (или стили графиков данных) каждого графика данных в окне графика сохраняются в держателях стилей графика данных. Держатели стилей графика данных содержат информацию о типе графика данных (например, разброс, линия или столбец) и настройках графика данных (например, параметры на вкладке «Символ сведений о графике»).Когда вы сохраняете окно графика в качестве шаблона, каждый график данных в каждом слое окна графика имеет связанный держатель стиля графика данных. Таким образом, когда вы создаете график на основе этого настраиваемого шаблона, для каждого слоя на вашем графике первый график данных в слое будет отображаться в соответствии с информацией, хранящейся в первом держателе стиля графика данных для этого слоя. Второй график данных в слое будет отображаться в соответствии с информацией, хранящейся во втором держателе стиля графика данных для этого слоя, и так далее. |
Сохранение настроенного окна как шаблона.
Вы можете предварительно установить длинное имя для графа, созданного из этого шаблона.
Этот предварительный просмотр используется для представления вашего шаблона в меню Plot и в библиотеке шаблонов .
Когда вы добавляете графики данных в слой, Origin выполняет поиск держателя стиля графика данных, который в настоящее время не используется (например, если вы удалили график данных из содержимого слоя), и отображает график данных с использованием первого стиля графика данных. найден держатель. Если вы добавите в слой больше графиков данных, чем имеется держателей стилей, Origin отобразит график данных, используя информацию из последнего держателя стиля графика данных.Линейные функции и их графики
Обзор линий графика
Напомним, что множество всех решений линейного уравнения может быть представлено на прямоугольной координатной плоскости с помощью прямой линии, проходящей по крайней мере через две точки; эта линия называется ее графиком.Например, чтобы построить график линейного уравнения 8x + 4y = 12, мы сначала решим относительно y .
8x + 4y = 12 Вычтем 8x с обеих сторон.
4y = −8x + 12 Разделим обе части на 4.y = −8x + 124 Упростим. Y = −8×4 + 124y = −2x + 3
В таком виде мы видим, что y зависит от x ; другими словами, x — это независимая переменная, которая определяет значения других переменных. Обычно мы думаем о x -значении упорядоченной пары ( x , y ) как о независимой переменной.и y — зависимая переменная — переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о y -значении упорядоченной пары ( x , y ) как о зависимой переменной. Выберите по крайней мере два x -значения и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.
x | y | y = −2x + 3 | Решения |
|---|---|---|---|
−2 | 7 | y = −2 (−2) + 3 = 4 + 3 = 7 | (-2, 7) |
-1 | 5 | y = −2 (−1) + 3 = 2 + 3 = 5 | (-1, 5) |
0 | 3 | y = −2 (0) + 3 = 0 + 3 = 3 | (0, 3) |
4 | −5 | y = −2 (4) + 3 = −8 + 3 = −5 | (4, −5) |
6 | −9 | y = −2 (6) + 3 = −12 + 3 = −9 | (6, −9) |
Постройте точки и проведите через них линию с помощью линейки.
Обязательно добавьте стрелки на обоих концах, чтобы указать, что график неограничен.
Результирующая линия представляет все решения 8x + 4y = 12, которых бесконечно много. Вышеупомянутый процесс описывает метод построения графиков, известный как построение точек A
Функции — Документация Grafana-Zabbix
Функции Переменные
Есть несколько встроенных переменных шаблона, доступных для использования в функциях:
-
$ __ range_ms— диапазон времени панели в мс -
$ __ range_s— диапазон времени панели в секундах -
$ __ range— временной диапазон панели, строковое представление (30s,1m,1h) -
$ __ range_series— вызвать функцию для всех значений серии
Примеры:
groupBy ($ __ диапазон, сред.)
процентиль ($ __ range_series, 95) - 95-й процентиль по всем значениям
Преобразовать
ГруппаПо
groupBy (интервал, функция)
Берет каждую временную серию и объединяет свои точки, попавшие в заданный интервал , в одну точку с помощью функции , которая может принимать одно из следующих значений: avg , min , max , median .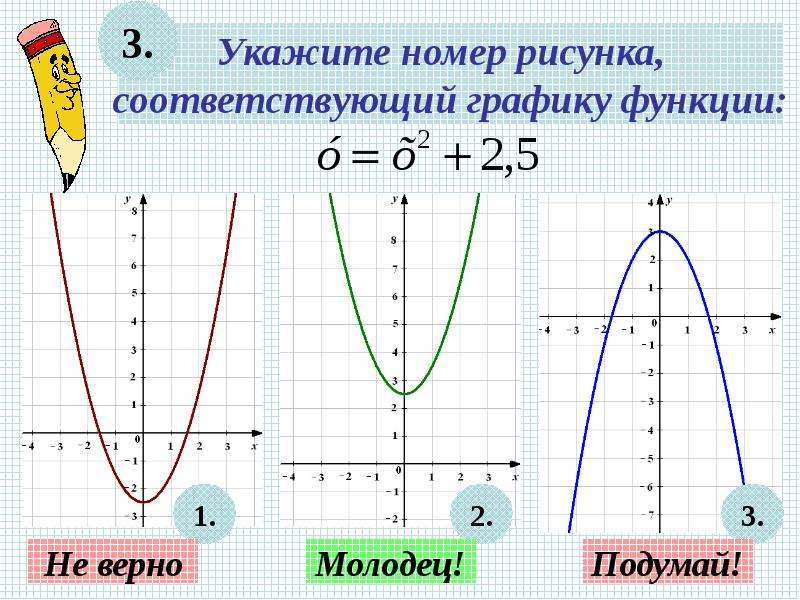
Примеры:
groupBy (10м, средн.)
groupBy (1 час, медиана)
масштаб
шкала (фактор)
Берет таймсерии и умножает каждую точку на заданный коэффициент .
Примеры:
шкала (100)
шкала (0,01)
дельта
дельта ()
Преобразует абсолютные значения в дельту. Эта функция просто вычисляет разницу между значениями.Посекундно
расчет использовать скорость () .
скорость
оценка ()
Вычисляет скорость увеличения временного ряда в секунду. Устойчив к сбросу счетчика. Подходит для преобразования увеличение счетчиков до скорости в секунду.
подвижное Среднее
movingAverage (размер окна)
Графики скользящего среднего показателя по фиксированному количеству прошлых точек, заданному параметром windowSize .
Примеры:
подвижное Среднее (60)
вычисляет скользящее среднее по 60 точкам (если метрика имеет разрешение в 1 секунду, она соответствует 1-минутному окну)
экспоненциальный средний
exponentialMovingAverage (windowSize)
Принимает ряд значений и размер окна и создает экспоненциальную скользящую среднюю по следующей формуле:
ema (current) = constant * (Current Value) + (1 - constant) * ema (previous)
Константа рассчитывается как:
constant = 2 / (windowSize + 1)
Если windowSize <1 (0.1, например), Константа не будет вычисляться и будет взята непосредственно из windowSize (Константа = размер окна).
Немного сложно построить график EMA от первой точки ряда (не от Nth = windowSize). Чтобы это сделать,
плагин должен сначала получить предыдущие N точек и рассчитать для них простую скользящую среднюю. Чтобы этого избежать, плагин использует это
Хак: предположим, что предыдущие N точек имеют те же средние значения, что и первые N (размер окна).